Identification and handling of artifactual gene expression profiles emerging in microarray hybridization experiments

Abstract

Mathematical methods of analysis of microarray hybridizations deal with gene expression profiles as elementary units. However, some of these profiles do not reflect a biologically relevant transcriptional response, but rather stem from technical artifacts. Here, we describe two technically independent but rationally interconnected methods for identification of such artifactual profiles. Our diagnostics are based on detection of deviations from uniformity, which is assumed as the main underlying principle of microarray design. Method 1 is based on detection of non-uniformity of microarray distribution of printed genes that are clustered based on the similarity of their expression profiles. Method 2 is based on evaluation of the presence of gene-specific microarray spots within the slides’ areas characterized by an abnormal concentration of low/high differential expression values, which we define as ‘patterns of differentials’. Applying two novel algorithms, for nested clustering (method 1) and for pattern detection (method 2), we can make a dual estimation of the profile’s quality for almost every printed gene. Genes with artifactual profiles detected by method 1 may then be removed from further analysis. Suspicious differential expression values detected by method 2 may be either removed or weighted according to the probabilities of patterns that cover them, thus diminishing their input in any further data analysis.

INTRODUCTION

High-density cDNA microarrays are currently widely used to assess differential expression of thousands of genes in various biological conditions (1). The resulting profiles of expression of differential genes obtained in a set of microarray hybridizations are regarded as the most valuable information in interpretation and evaluation of the results. Almost all the methods of advanced mathematical analysis of microarray hybridizations (clustering, extraction of genes essential for class separation, networking, etc.) deal with gene expression profiles (a profile is a series of differential expression values of a gene according to the series of microarray hybridizations) as elementary data units (2–4). However, generation of the large quantity of data is always associated with the generation of a significant amount of noise. Therefore, it is anticipated that a substantial proportion of the gene expression profiles will not actually reflect the influence of the applied biological conditions, but will rather result from various technical problems encountered in one or several microarray experiments within the hybridization set. Numerous undefined technical factors may influence the quality of microarray hybridization results on different slides, producing artifactual expression profiles of genes. Such factors may include local microscopic glass defects occurring during production of slides, defects of printing pins, problems with scanning of particular slide areas via one or both channels, fingerprints, scratches, excessive slide drying, defects of washing, etc. Indeed, it could easily happen that the main features of the expression profiles that underlie their clustering stem exclusively from the local technical artifacts of one or several microarray slides used for the analysis of hybridization set. Genes with completely or partially artifactual expression profiles are present practically in any hybridization set and, depending on the hybridization quality, may include up to 80% of the printed clones.

Unfortunately, the problem of distinguishing between biological and artifactual profiles cannot be easily solved by the application of the common quality control strategies for decreasing data noise since they mostly deal only with the quality of printed spots (5–7), leaving aside the biological relevance of data. For example, establishment of an arbitrary general threshold for fold change in gene expression may well mask biologically significant changes while preserving the artifacts if they produce significant differential ‘expression’ values (8–10).

A popular approach for pinpointing the biological relevance of the detected expression profiles consists of technical replication of hybridizations (11) or of microarray elements (printing of several spots containing one and the same cDNA on the same slide) (12,13), with an underlying assumption that erroneous data are non-stable and are poorly repeated in different experiments. However, such an assumption is true only when error-producing factors randomly fluctuate among repeated experiments (14). If a certain technical factor acts stably in numerous hybridizations (or in many spots), its constant influence will be superimposed with the influences of real biological factors and may even outweigh them. In this case, repeated hybridizations will produce fairy stable, but probably partly non-biological results. Unfortunately, experimental design employing randomization of the influence of error-producing factors is hardly possible because of the limited knowledge about their nature and mechanism of action. The only known example that can be considered as an attempt of randomization is a dye swap between Cy3 and Cy5 probe labels for two-color microarrays (15). However, this type of control has limited value and seems unnecessary for common reference design (16–18) when labeling bias does not affect class comparisons (19).

Another approach proposed for the estimation of the biological validity of microarray hybridization data is based on the analysis of the correspondence between the dendrogram presenting hierarchical clustering of hybridization expression vectors and the dendrogram of similarity of applied biological conditions (16). Needless to say, such an approach is poorly applicable to experiments where unexpected proximity of vectors is anticipated, e.g. for molecular classification of human tumor samples (20). Moreover, though the approach in general is able to reveal a hybridization experiment of a poor quality, it is not sensitive to individually erroneous gene expression values. The same is true for hierarchical clustering (correlation analysis) of common control probes for two-color hybridization sets (17).

Large groupings of gene behavior are usually intuitively regarded as biological, whereas singleton gene expression profiles are viewed as potential artifacts. Actually, such an intuition may also be misleading, since the existence of a large highly correlated cluster of genes with similar behavior does not necessarily imply that this behavior is biologically meaningful. Large clusters may consist of genes with purely artifactual expression profiles resulting from technical problems involving relatively extensive slide areas in one or several hybridizations.

Thus, it appears that clusters of genes displaying artifactual expression profiles may have all the typical characteristics usually attributed to a true biological behavior: they may be reproducible (stable) and include numerous genes displaying statistically significant levels of differential expression.

Here, we propose two novel approaches for distinguishing between biological and artifactual gene expression profiles. These approaches do not deal with the traditionally used criteria of technical quality or biological validity. Instead, our diagnostics are based on detection of deviations from uniformity (randomization), which is assumed as the main underlying principle in microarray design. Indeed, all microarrays of the same series keep the same geometrical position for every printed gene within the microarray geometrical template. Since there is no clustered printing of co-regulated genes or genes having interconnected functions, such genes should yield a uniform (random) distribution of spots. On the other hand, if data are processed via a clustering algorithm, then biologically interconnected and/or co-regulated genes are expected to react similarly to applied biological conditions, thus displaying correlated expression profiles, which will in turn lead to their gathering within a single cluster. Therefore, one anticipates a uniform distribution of spots corresponding to the genes within a cluster characterized by a biologically valid profile. On the contrary, if a non-uniform distribution of spot positions of co-clustered genes over the microarray is observed, it may indicate that some locally acting technical factors rather than genuine biological factors have contributed to the observed ‘expression’ pattern. Random printing of co-regulated genes over the microarray template should also lead to uniform distribution of various values of differential gene expression within the same template. Therefore, any analogous differential expression values of genes printed within the same concentrated microarray area may be suspected of having an artifactual nature due to some local technical problems.

Thus, our method of detection of erroneous data is based on the evaluation of two interconnected characteristics: (i) non-uniformity of the distribution over the microarray geometrical template of the printed genes that are clustered together based on the similarity of their expression profiles; and (ii) the presence of gene-specific microarray spots within the slides’ areas characterized by an abnormal concentration of low/high differential expression values, which we define as ‘patterns of differentials’. Though formally these two methods of quality control are completely independent, in fact they handle the same kind of noise. This becomes obvious in simple cases, when a small number of patterns appear in the series of hybridizations. In such instances, the microarray geometrical distribution of genes included in non-uniform clusters of profiles perfectly matches the geometrical distribution of patterns of differential expression values on individual slides. When the number of patterns increases, the correspondence becomes less obvious, and the first method appears to be more sensitive in detection of artifacts.

Applying two novel algorithms, one for nested clustering (the basis of the first method) and one for pattern detection (the basis of the second method), a dual estimation of the profile’s quality for almost every printed gene is possible. Genes with artifactual profiles detected by the first method may then be removed from further analysis. Alternatively, suspicious differential expression values detected by the second method could be weighted according to the probabilities of patterns that cover them, in order to diminish their input in any further analysis.

MATERIALS AND METHODS

Microarray hybridizations

The examples shown in this report are derived from the analysis of several microarray hybridization experiments performed in the course of various gene discovery projects conducted at Quark Biotech Inc. The utilized microarrays (several types) contained approximately 10 000 clones derived from custom disease-oriented non-redundant cDNA libraries and were hybridized to pairs of Cy3- and Cy5-labeled cDNA probes. Probe synthesis and labeling was performed using the GEMBright probe labeling kit (Incyte Genomics, Palo Alto, CA) according to the manufacturer’s instructions. Microarray printing, hybridization, washing and scanning of the slides were performed as previously described (21). The experimental design was always based on using common biologically relevant reference probes. Cy3 and Cy5 signals were balanced according to signal intensities of all printed genes, using a proprietary non-linear balancing algorithm.

Nested clustering

The procedure of nested clustering consists of sequential repetitions of three basic steps given below.

(i) Detection of the optimal neighborhood for a gene’s expression profile. The optimal neighborhood of a profile is defined according to a chosen measure of similarity (typically, Pearson’s correlation coefficient). The optimality implies that for a given neighborhood radius, the minimum probability for this neighborhood to collect a given number of gene expression profiles is attained. All probabilities are calculated under the hypothesis of the uniformity of distribution of vectors of all gene expression profiles in a much wider neighborhood. Let k be a dimension of the vector of a gene’s expression profile equal to the number of hybridizations under analysis. Let us take a deliberately wide neighborhood of profile x with radius R. Then, the volume of neighborhood with radius R will be defined as V_R. Let it contain n points (gene expression profiles). As is well known (22), if n points are uniformly distributed in a volume V_R, then the number of points in a neighborhood with radius r and with volume V_r will be a random variable having a Poisson distribution with the parameter λ · r^k that is proportional to V_r (λ = ). Thus, the probability (P) of finding more than m points in a neighborhood with radius r will be

For large enough m (m > λr^k), the sum is well approximated by its first member

Let us imagine that point (gene expression profile) x has an expanding sequence of neighborhoods with radii r₁, r₂, r₃…< R. The optimal neighborhood (with radius r_i) for a given gene (x) will be the one for which the probability P_{mi(ri) reaches a minimum, where m1, m2, m3… correspond to the actual number of points observed in the neighborhoods with radii r1, r2, r3, respectively, and where Pm1(r1), Pm2(r2), Pm3}(r₃),… are evaluated according to equation 1b.

(ii) Defining the initial set of non-intersecting clusters is formed by a greedy procedure. The most populated optimal neighborhood of a gene expression profile out of the whole set of detected neighborhoods is designated as cluster 1. The next most populated neighborhood out of the whole set of detected neighborhoods, which, however, does not intersect with cluster 1, is designated as cluster 2, and so on. Genes that are not included in any of the obtained clusters are distributed among the numbered clusters according to their proximity to the clusters’ centers.

(iii) Improvement of clustering. To make the clustering procedure more accurate, a popular k-means technique is applied to the initial set of defined clusters. Specifically, by iterations, all the genes are redistributed among the clusters in such a way that every gene is moved into the cluster whose center is closest to the genes profile. In the next step, the centers of all the clusters are recalculated, and the next iteration begins (23).

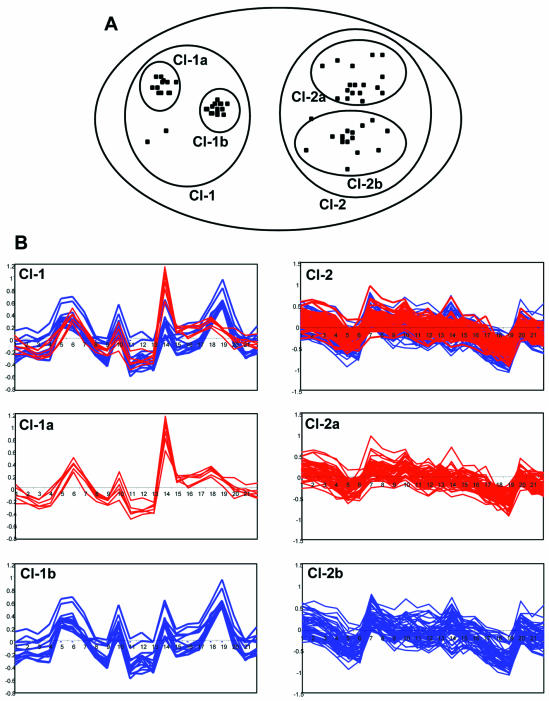
These three steps of the algorithm are initially applied to the expression profiles of all genes, thus producing first level clusters. Next, the same three steps are applied to the epicenters of the first level clusters (a cluster’s epicenter is closest to the cluster’s center real gene expression profile, whereas the center of the cluster is calculated as an average of all gene expression profiles included in a given cluster). This produces clusters of the next (e.g. the second) level (Fig. 1A and B). The procedure is repeated until either the necessary number of levels of nested clustering is reached, or all the genes are united within a single cluster. As a result, every gene is attributed to a series of nested (enclosed) clusters.

Figure 1.

Nested clustering of gene expression profiles. (A) Two-dimensional representation of the nested clustering procedure. The gene expression profiles are shown as separate points in a two-dimensional space. Higher level cluster 1 (Cl-1) contains two compact lower level clusters, Cl-1a and Cl-1b. Higher level cluster 2 (Cl-2) contains two poorly separated lower level clusters, Cl-2a and Cl-2b. (B) Actual expression profiles of genes included in Cl-1 and 2. The x-axis shows the hybridization experiments and the y-axis shows the ln of values of differential expression. See text for details.

The statistical validity of splitting higher level clusters into lower level clusters is verified by application of the Kolmogorov–Smirnov (KS) criterion (22) testing the maximal distance between two cumulative distributions: the distribution of real distances (correlations) between gene expression profiles within the higher level cluster and the cumulative distribution of correlations between uniformly distributed vectors (gene expression profiles) within the area of multidimensional space, which is covered by the same cluster. If all lower level clusters within a higher level cluster are poorly separated from each other, then the distribution of distances among all the gene expression profiles within a higher level cluster should be similar to that of a uniformly distributed set. An example of higher level cluster 2 (Cl-2) consisting of ‘friable’ lower level poorly separated (KS P-value = 0.23) clusters, Cl-2a and Cl-2b, is shown in Figure 1. Alternatively, if lower level clusters are compact and are clearly separated one from another, then the distribution of correlations among all the gene expression profiles within a higher level cluster will differ from the distribution expected for a uniformly distributed set. This type of higher level cluster is also shown in Figure 1 as cluster 1 (Cl-1), mainly consisting of compact clusters Cl-1a and Cl-1b (KS P-value = 0.002).

Defining the uniformity of the microarray distribution of spots corresponding to the genes included within one and the same cluster

Following the ideas appearing in Rassokhin and Agrafiotis (24), the same KS statistic was used as a criterion of uniformity of distribution of spots over the microarray. The distance between microarray spots was defined as a ‘city-block’ distance (|x₂ – x₁| + |y₂ – y₁|), where (x₁, y₁) and (x₂, y₂) are coordinates of two spots on the microarray. (We use a city-block distance because it adequately reflects non-uniformity of the distribution of spots over a microarray, whilst corresponding formulae are less complex in comparison with Euclidean distance.) The cumulative distribution of city-block distances between the spots corresponding to the genes of the same cluster is compared with the cumulative distribution of distances between spots randomly distributed over the microarray. The theoretical cumulative distribution of city-block distances between spots uniformly distributed over the microarray is calculated as described below.

The relevant random variable is the city-block distance ξ = ρ ((x₁, y₁), (x₂, y₂)) = |x₂ – x₁| + |y₂ – y₁| between two spots, randomly chosen from a uniform distribution of spots in the rectangle with sides L_x and L_y.

Let

f(u) = P{ξ = u} = P{ρ((x₁, y₁), (x₂, y₂)) = u} (1≤u≤L_x + L_y)    2

Then

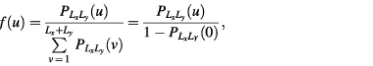
where

and

Calculations of all the theoretical cumulative distributions can be performed using equations 3a and 3b. The resultant maximal difference between the real and theoretical cumulative distributions is the KS statistic. The KS quality of a cluster is thus defined as the P-value of KS statistics for a given cluster.

Detection of patterns (over-populated areas)

Pattern is defined as a spatially concentrated (e.g. located in close proximity to one another on the microarray) set of spots with value characteristics belonging to the same predefined interval. These values can refer to the values of Cy3 or Cy5 hybridization signals, or to background signals, or (which is the most important for our purposes) to the calculated values of balanced differential expression. For automatic detection of patterns, the following algorithm is applied.

Let the distance between two spots on a microarray slide be the city-block distance: (|x₂ – x₁| + |y₂ – y₁|); k the city-block radius of the neighborhood; n(T) the total number of spots characterized by values belonging to a predefined class T; p = the probability of a random spot within the neighborhood of a chosen spot x of class T belonging to the same class, where N is a total number of spots on the microarray; a(k) the total number of spots in the neighborhood of radius k; and u_k(x) the number of spots of class T in the neighborhood of radius k of spot x.

On average, u_k(x) is equal to p·a(k). For the uniform distribution of all the spots of class T over the microarray, the probability of finding more than u_k(x) spots belonging to class T in the neighborhood of spot x belonging to class T is

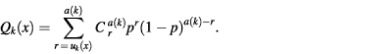
For large enough a(k), this distribution is close to a Poisson distribution (22):

Therefore, as in the case of equation 1, for large enough u_k(x) (u_k(x) > a(k)·p), we can use the first member of the sum as an approximation of Q_k(x):

For every spot x, there is a sequence of probabilities: Q₁, Q₂, Q₃… The minimal Q_i will define the optimal radius k(x) = i of the neighborhood of spot x, for which the appearance of the actual number of spots belonging to the same class as spot x is the least probable.

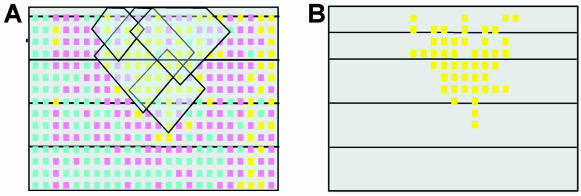
Let λ be the threshold of significance for probability Q_i (e.g. 0.001). Then, the interconnected union of all the neighborhoods x_i with Q_k(xi) < λ will represent a ‘zone of pattern’ of class T: the interconnected union of significantly over-populated optimal neighborhoods (shown as an area covered by semi-transparent rhombi in Fig. 2A). The pattern itself is then defined as a set of spots with differential expression values belonging to a certain interval (e.g. class T), which are covered by a ‘pattern zone’ generated by union of neighborhoods with class T spot centers. For example, in Figure 2A, though the ‘pattern zone’ generated as a union of neighborhoods of yellow spots covers both yellow (class T) and pink spots (another class), only the yellow spots are detected as a pattern (Fig. 2B).

Figure 2.

Automatic identification of patterns using a city-block distance. (A) An example of the distribution of differential expression values over a slide. Yellow, blue and pink spots have differential expression values belonging to high value (>2), low value (<0.5) or intermediate value intervals, respectively. Semi-transparent rhombi represent some of the optimal city-block neighborhoods of spots with high values of differentials. The interconnected union of these rhombi constitutes a ‘pattern zone’. (B) Detected pattern of high differentials; the spots with high differential expression values that were covered by a detected ‘pattern zone’.

The probability of the pattern occurrence, equal to the probability of occurrence of the ‘pattern zone’, similarly to equation 4, may be estimated as

where z is the area of a given ‘pattern zone’ (the total number of spots covered by the zone), and u is the number of spots of class T covered by the ‘pattern zone’.

RESULTS AND DISCUSSION

First method of quality control of gene expression profiles: evaluation of non-uniformity of distribution of cluster-related spots over the microarray geometrical template as a sign of an artifactual nature of cluster

This method employs a newly developed clustering procedure as a tool for quality control of gene expression profiles. It is assumed that due to a random printing of co-regulated genes over the microarray template, the genes having correlated expression profiles (and clustered together on this basis) should be uniformly distributed over the microarray. Thus, any deviation from such uniformity may indicate that an expression profile typical for a certain cluster has a non-biological origin and rather stems from some locally acting technical factors. Indeed, it could easily happen that the main features of the expression profiles that underlie their clustering stem exclusively from the local technical artifacts of one or several microarray slides used for the analysis of hybridization set.

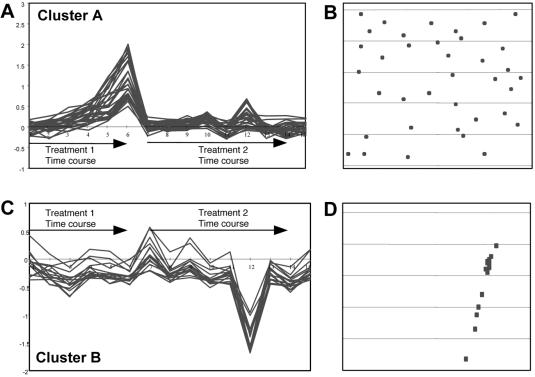
The above point is illustrated in Figure 3. The spots corresponding to genes within cluster A (Fig. 3A) are uniformly distributed over the microarray (Fig. 3B). At the same time, the expression profile of these genes truly reflects the applied biological conditions, because the genes are upregulated by a certain treatment in a time-dependent manner and are non-responsive to another treatment, exactly as expected. On the other hand, all the spots corresponding to the genes of cluster B (Fig. 3C) are concentrated within a certain microarray area (Fig. 3D). Note that the main feature of these genes’ behavior is their high downregulation only in hybridization 12, while in the rest of hybridizations the genes do not display any significant differential expression. Taken together, these features of cluster B point to its potential artifactual nature.

Figure 3.

Uniformity versus non-uniformity of cluster distribution over the microarray. (A and C) Examples of gene clusters (cluster A and cluster B) detected in the same microarray experiment consisting of 15 hybridizations. The probes for hybridizations 1–6 were derived from cells subjected to ‘treatment 1’ in a time-course manner. Hybridizations 7–14 relate to a time-course treatment of the same cells with another agent (‘treatment 2’). Hybridization 15 represents untreated control cells. The x-axis shows hybridization experiments and the y-axis shows the ln of values of differential expression. (B) Microarray distribution of spots corresponding to the genes included in cluster A. (D) Microarray distribution of spots corresponding to the genes included in cluster B.

Accordingly, we reasoned that the uniformity of distribution of cluster-related spots over the microarray template might be used as a quantitative measure of the biological relevance of a cluster. A specific procedure of nested clustering was worked out (for details, see Materials and Methods) as an essential part of our approach for detection of biologically valid and artifactual expression profiles. As a result of this procedure, the expression profile of almost every gene appears in a chain of enclosed clusters. The uniformity of the distribution of nested clusters of different levels over the microarray is calculated using the KS statistic (see Materials and Methods). The P-value corresponding to the median of the distribution of ln of KS qualities (ln of P-values) of the enclosed chain of clusters serves for the calculation of the KS quality of the included individual gene expression profiles. We considered gene expression profile as biological when the corresponding median KS P-value was ≥0.2, and as artifactual when the median KS P-value was ≤0.001. Gene expression profiles with intermediate KS P-values were considered as belonging to a ‘gray zone’ and probably have both biological and artifactual features.

As a next step, we experimentally tested our ability to distinguish between biological and artifactual gene expression profiles based on KS statistics of the uniformity of microarray distribution of the corresponding nested clusters. Hybridiz ation expression vectors originating from biologically related samples (e.g. from the same type of similarly treated cells) tend to be close to one another (highly correlated). Thus, the correspondence between correlation distances among the vectors of differential expression values of certain samples (probes) and their expected biological ‘proximity’ is a popular method for testing the hybridization quality. If a certain hybridization appears in a ‘wrong’ position of the hierarchical clustering dendrogram, it raises suspicion as to the quality of this hybridization or as to its biological attribution. Clearly, if for repeated hybridizations, the position of only one of the hybridizations of a pair is non-consistent, the primary doubt concerns its quality. (However, this is correct only in cases when there are no doubts regarding its anticipated position within the dendrogram.) Dendrograms of correlation proximity of hybridizations may be constructed either according to all the genes employed in the experiment or according to a gene’s subset. It is natural to suggest that dendrograms constructed only according to genes with biologically relevant expression profiles will better correspond to the assumed biological proximity among the probes than dendrograms constructed according to genes with artifactual expression profiles.

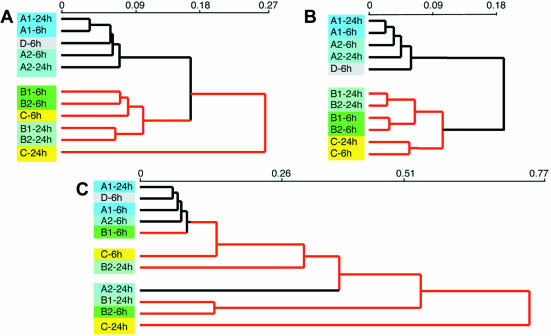
Therefore, in order to test whether our assumption regarding the non-biological nature of expression profiles of genes included in non-uniformly distributed clusters is correct, we performed a hierarchical clustering of several hybridization sets according to the following profiles: (i) all the genes printed on the microarray; (ii) genes that comply with the criterion of biological nature of profiles (median KS P-value ≥0.2); (iii) genes that do not comply with the criterion of biological nature of profiles (median KS P-value ≤0.001); and (iv) a similar number of randomly selected genes. An example of such an analysis is shown in Figure 4. The experiment consisted of microarray analysis of gene expression in the same type of cells plated at the same initial density while grown under different conditions. Specifically, the cells were treated with 1 ng/ml platelet-derived growth factor β (PDGFβ) (A1) for 6 or 24 h; 10 ng/ml PDGFβ (A2) for 6 or 24 h; 1 ng/ml transforming growth factor β (TGFβ) (B1) for 6 or 24 h; 10 ng/ml TGFβ (B2) for 6 or 24 h; or hypoxia (C) for 6 or 24 h. Control cells were grown under normoxic conditions in regular basal medium (D) for 6 h. The resulting hybridization data were not subjected to standard quality control evaluation and no data filtering according to the thresholds of signals or differential expression values was performed. Hierarchical Pearson correlation clustering of hybridizations according to expression profiles of all 10 000 printed genes is shown in Figure 4A. The major separation was obtained between three groups of treatments: (i) all PDGFβ treatments and control; (ii) all TGFβ treatments and 6 h hypoxia; and (iii) 24 h hypoxia. While the close proximity of TGFβ- and hypoxia-driven expression profiles could be explained by involvement of similar signal transduction pathways triggered by these treatments (25–29), a prominent separation of the 24 h hypoxia sample had no straightforward biological explanation. Similarly, there was no straightforward biological explanation for the presence of the control sample among the PDGF samples. However, when hierarchical clustering of probes was performed according to 6283 expression profiles corresponding only to the genes complying with the KS criterion of biological quality, the resulting tree became obviously more relevant to the underlying biology (Fig. 4B): (i) the major separation occurred between only two groups of hybridizations, one including all the PDGF treatments and control, and the other including all the TGFβ treatments and all the hypoxia treatments; (ii) within the latter group, TGFβ treatments became clearly separated from the hypoxia treatments; (iii) both hypoxia treatments appeared together; (iv) the control probe was now separated from all the PDGF probes; and (v) the proximity between the 6 or the 24 h profiles obtained with different concentrations of TGFβ also became more significant. In contrast, when hierarchical clustering was performed according to 1847 expression profiles corresponding only to the genes not complying with the KS criterion of biological quality, the resulting tree became almost completely biologically unordered (Fig. 4C), indicating the non-biological nature of the analyzed expression profiles. The distribution of Cy3 signals, Cy5 signals and balanced differential expression values in both analyzed gene subsets was similar, indicating that indeed artifactual gene expression profiles are not generally removed from the analysis by establishing arbitrary thresholds. Hierarchical clustering of 6000 or 2000 randomly selected expression profiles produced dendrograms identical to the one shown in Figure 4A.

Figure 4.

Influence of gene sorting according to the KS criterion of biological quality on hierarchical clustering of probes. (A) Hierarchical clustering of probes within the hybridization set according to gene expression profiles of all 10 000 genes printed on the microarray. (B) Hierarchical clustering of probes within the same hybridization set according to expression profiles of 6283 genes with a median KS P-value ≥0.2, predicted to have biological expression profiles. (C) Hierarchical clustering of probes within the same hybridization set according to expression profiles of 1847 genes with a median KS P-value ≤0.001 predicted to have artifactual expression profiles. Probes: A1, PDGFβ 1 ng/ml; A2, PDGFβ 10 ng/ml; B1, TGFβ 1 ng/ml; B2, TGFβ 10 ng/ml; C, hypoxia (0.5% O₂, 5% CO₂). For details, see text.

Thus, we conclude that our procedure is indeed able to usefully distinguish between biologically relevant and artifactual expression profiles of individual genes and their clusters.

Second method of quality control of gene expression profiles: evaluation of biological validity of individual differential gene expression values by calculation of probability of patterns of high/low differential expression values on the individual slide

Expression profiles of genes are formed by the values of their balanced differential expression in hybridizations included in the set. Accordingly, we wished to investigate the uniformity of distribution of these calculated differential expression values over the corresponding slides. Our assumption was that in certain hybridizations, prominently contributing to the generation of artifactual profiles, this distribution would not be uniform. Rather, many spots with similar calculated differential expression values would be concentrated within limited slide areas, indicating local technical problems. The whole range of detected differential expression values was divided into three intervals: (i) values higher than a selected threshold for meaningful high differentials (for the examples presented herein, the balanced Cy5/C3 ratio was selected to be higher than 2); (ii) values lower than the selected threshold for meaningful low differentials (for the examples presented herein, the balanced Cy5/C3 ratio was selected to be less than 0.5); and (iii) an interval of values lying between these two thresholds. Individual slide regions characterized by concentration of spots with value characteristics attributed to the same predefined interval were called ‘patterns of differentials’. At the heart of method 2, there is a special algorithm that was developed for automatic pattern detection (for details, see Materials and Methods). Thus, all the individual differential expression values obtained in every hybridization of the set get an additional characteristic that is the probability of the pattern that covers the corresponding spot (under conditions of uniform distribution of high/low values). Differential expression values corresponding to the spots (per hybridization) that are covered by patterns of small probability are considered as artifactual.

The next question to ask is how to handle the data that were found to be artifactual by application of method 2. The easiest solution will be filtering out of the suspicious gene profiles. Indeed, removal of genes having artifactual expression profiles detected by method 1 from the analysis has significantly improved the biological relevance of the thierarchical clustering dendrogram (Fig. 4B).

However, it is clear that along with the purely biological and purely artifactual profiles, there must also exist profiles (and probably, they are the most abundant ones) of a mixed nature, in which only part of the gene’s differential expression values is corrupted. Therefore, simple filtering out of all the genes whose profiles contain one or several suspicious differential expression values cannot be considered as the best solution because it will lead to a loss of potentially important biological information.

A more feasible way of handling the artifactual differential expression values is their correction. The correction (normalization) of individual differential expression values derived from the slides where the corresponding spot is covered by the pattern may be performed according to the average of expression values of the entire unpatterned area of the same slide. A more accurate correction may be achieved using the algorithm proposed by Yang et al. for within-print-tip-group normalization (30). The robust local regression across the range of gene expression intensity can be used here as is proposed in Colantuoni et al. (31).

We propose an alternative way to handle the artifactual data detected by method 2: diminishing the impact of a patterned expression value on results of further data analysis. This type of data processing can be easily applied to any kind of data analysis by decreasing the input of suspicious values in the corresponding function. Here it will be demonstrated on an example of clustering of gene profiles.

For a facilitated analysis of hybridization results, it is worth having a clustering procedure that collects all the genes with biologically similar behavior regardless of different artifactual features that influence their profiles. Unfortunately, the standard Pearson correlation measure equally weights both artifactual and biological details. Moreover, as was shown for the example in Figure 3, clustering may be mainly defined by erroneous profile features (that usually tend also to be the most prominent ones) while ignoring the biological behavior. All this leads to a biologically meaningless gene partition into clusters or, alternatively, to generation of a large number of small clusters differing in terms of certain profile characteristics, which may be biologically irrelevant.

To tackle this problem, we have developed a special procedure of weighted clustering aimed at collection of all the genes with similar/identical biological behavior regardless of the contamination of their expression profiles with artifactual features. The idea of this procedure is to perform the clustering of profiles not on the basis of the standard correlation coefficient but rather according to a weighted coefficient. The correlation coefficient between two gene profiles, x and y, is calculated based on the differential expression values (x_i and y_i) constituting these profiles. The weight attributed to the x_i differential is equal to the probability P_patt of the pattern, which includes a corresponding spot in the ith hybridization. Differential expression values obtained from the spots included in low probability patterns have smaller input in weighted correlation coefficient between the profiles.

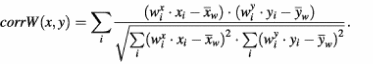
Here

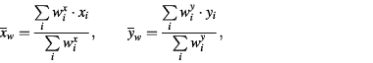
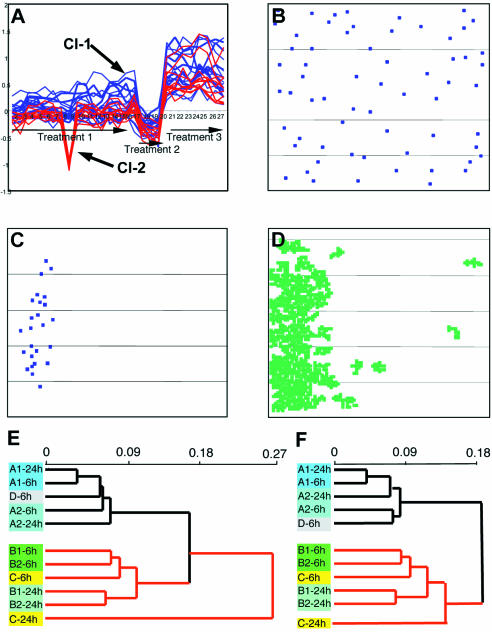
and where weight w_i^x is equal to the probability of a pattern that covers a given spot in a given hybridization. If there are no patterns covering the spot, w_i^x = 1. It is obvious that this weighted measure of distance is applicable not only for the clustering of gene expression profiles (Fig. 5A–D), but also for the hierarchical clustering of probes (Fig. 5E and F) and for any other type of statistical analysis of microarray results involving a measure of distance. Figure 5A illustrates an application of this procedure to clustering of gene expression profiles, that results in gathering within one cluster of two (‘red’ and ‘blue’) otherwise separately clustered groups of genes. The biological nature of the ‘blue’ profile is confirmed (i) by the profile characteristics corresponding to the treatments applied; and (ii) by a uniform microarray distribution of spots corresponding to the clustered genes (Fig. 5B). The artifactual origin of the ‘red’ cluster is confirmed (i) by a non-uniform microarray distribution of the corresponding genes (Fig. 5C); and (ii) by the coincidence of this distribution with the ‘zone of pattern’ of low differentials on the slide, corresponding to hybridization 8, which contributes the major negative peak of the ‘red’ cluster profile.

Figure 5.

Application of weighted measure of distance for clustering of gene expression profiles and hierarchical clustering of hybridizations. (A) A cluster obtained from the application of the weighted clustering procedure represents a combination of two otherwise separated clusters (shown in blue and red). The x-axis shows the hybridization probes and the y-axis shows the ln of values of differential expression. (B) Microarray distribution of spots corresponding to the genes within the ‘blue’ cluster. (C) Microarray distribution of spots corresponding to the genes within the ‘red’ cluster. (D) Pattern of low differentials on the slide corresponding to probe 8. (E) Hierarchical clustering of probes within the hybridization set according to gene expression profiles of all 10 000 genes printed on the microarray (same as shown in Fig. 4A). (F) Hierarchical clustering of the same hybridization set using a weighted measure of distance, based on the expression profiles of all 10 000 printed genes. Note the improvement of the probe clustering in accordance with the underlying biological conditions (for details, see the text and the legend to Fig. 4).

Thus, the biological quality of gene expression profiles may be determined not only by their inclusion in a chain of non-uniformly distributed clusters (method 1), but also by estimation of the presence of their corresponding individual slide spots within the patterns of differentials (method 2). On the other hand, calculation of the cumulative size of the ‘patterned’ areas may serve as a measure of quality control of the slide itself: the more patterns of differentials are detected in a certain hybridization, the poorer its technical quality (L. Brodsky, A. Leontovich, M. Shtutman and E. Feinstein, manuscript in preparation).

Comparison of the two methods of quality control of gene expression profiles

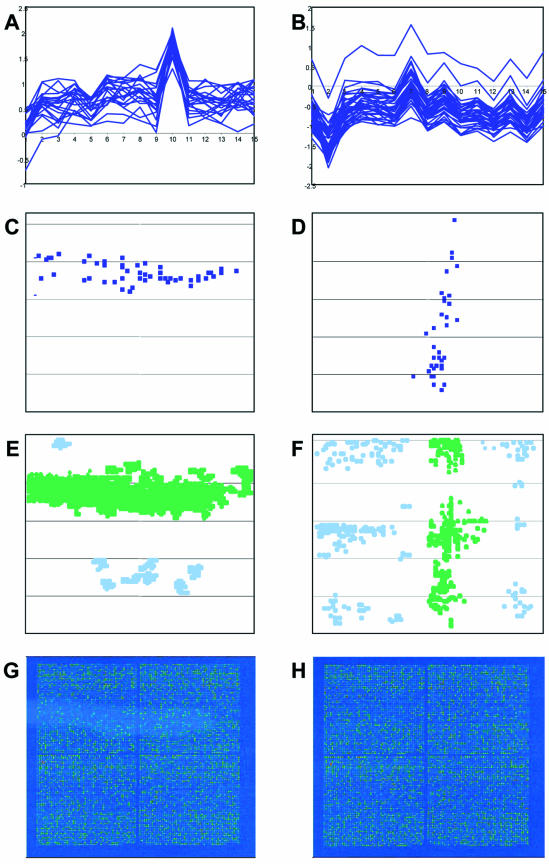
The interconnection of the two methods presented above is easily demonstrated in simple cases where there is high coincidence of areas of distribution of artifactual clusters over the microarray template with the zones of patterns of high/low differential expression values on the individual slides of a hybridization set. An example shown in Figure 6 clearly demonstrates that the microarray locations of genes included in artifactual clusters (Fig. 6C and D) indeed coincide with the positions of some of the patterns of high/low differentials (Fig. 6E and F; the relevant patterns are colored in green) detected on slides corresponding to the hybridizations (hybridization 10 for the left panel and hybridization 2 for the right panel), which predominantly contributed to the features of calculated gene expression profiles (Fig. 6A and B). Additional patterns detected on these or other slides contributed to formation of other artifactual clusters (not shown). Interestingly, while in some cases these patterns clearly overlapped with visually distinguishable slide defects (Fig. 6G), in other cases the existence of pattern of differentials could be detected only by the algorithm (Fig. 6F).

Figure 6.

Coincidence of microarray distribution of artifactual clusters with the zones of patterns of differential expression values. (A and B) Two gene clusters detected in the same microarray experiment, comprising 15 hybridizations. The x-axis shows the hybridization probes and the y-axis shows the ln of values of differential expression. (C and D) Microarray distribution of spots corresponding to the genes included in the clusters shown in (A) and (B), respectively. (E and F) Patterns of differentials appearing on the slides corresponding to hybridizations 10 and 2, respectively. The patterns whose position coincides with the microarray distribution of clusters shown in (A) and (B) are colored green. (G and H) Deduced Cy5 microarray images of slides corresponding to hybridizations 10 and 2, respectively.

When there are many patterns on different individual slides of a given series of hybridizations, the correspondence between areas of non-uniformly distributed clusters and slide patterns becomes less obvious. Indeed, for this case, the geometry of cluster distributions is defined by the interplay of patterns on different slides.

According to our observations, nested clustering-based detection of artificial profiles is more sensitive than pattern-based detection. Exclusion of artificial gene profiles detected by the first method renders the dendrogram of probe proximity closer to the biologically expected one (Fig. 4B, probes C-8h and C-24h are together) than the dendrogram obtained after correction of the patterned expression values (see Fig. 5B, where probes C-8h and C-24h are rather far from each other). We believe that the higher sensitivity of the first method stems from the fact that the results of pattern detection are strongly dependent on such parameters of the procedure as threshold for high/low values and threshold for probability of significant pattern.

Conclusions

We have developed a novel approach for quality control of microarray hybridizations. Unlike other quality control approaches, its main purpose is distinguishing between truly biological expression data and artifactual data. Moreover, the method not only helps in detecting erroneous data but also struggles with at least some of the artifacts hampering high throughput gene expression analysis. In contrast to other approaches, which are based on a spot-wise quality control, in our method detection of irrelevant data is a result of simultaneous processing of the entire set of hybridization values, thus providing more reliable statistics. As a consequence, the method is very sensitive for the detection of differential expression values that are under the influence of hidden technical factors.

The method is supported by a group of novel algorithms, enabling (i) nested clustering of gene expression profiles; (ii) analysis of the non-uniformity of microarray distribution of spots corresponding to the genes included in a cluster; and (iii) detection of patterns (non-uniform distribution of signals, differentials, etc.) on the hybridization slides.

The lack of biological relevance of a gene expression profile is determined according to its inclusion in a nested chain of non-uniformly distributed clusters, while the lack of biological relevance of each balanced differential expression value forming the gene’s expression profile may be estimated according to the probability of a ‘zone of pattern’ to cover the corresponding microarray spots on the corresponding slides. The ability to distinguish between biological and artifactual data may be further translated into decision making in three ways. (i) Exclusion of genes with artifactual expression profiles from further analysis. (ii) Weighting of patterned expression values (proposed in this manuscript). For example, weighted clustering of gene expression profiles gathers genes with common biological behavior into the same group regardless of the contamination of their profiles with technical artifacts. (iii) Normalization (correction) of patterned expression values as was proposed by other authors (30,31).

Standard quality control procedures tend to disregard low differential expression values or sufficiently high differential expression values obtained from microarray spots characterized by low hybridization signals because of doubts concerning their technical/biological quality. The developed ability to estimate the biological relevance of the gene’s behavior supports the possibility of a more comprehensive analysis of this potentially important though automatically disregarded information. Keep in mind that expression of many regulatory biological factors is normally very low. Finally, the latest attempts to create microarray data depositories (e.g. the Gene Expression Omnibus project at NCBI, http://www.ncbi.nlm.nih.gov/geo/) are expected to encounter problems that stem from data of variable quality originating from different sources utilizing different quality control procedures and different technological platforms for microarray printing and data acquisition. Our method is independent of spot-wise quality control parameters and mainly relies only on knowledge of acquired hybridization signals and distribution of the printed genes over the microarrays. As such, it may be helpful for handling the heterogeneous data supplied to the depositories by various groups. Though random printing of genes is currently assumed as a basis for the whole approach, this procedure of printing may be established as a necessary attribute of microarray design. At present, our algorithms support 10 000 spot microarrays printed in the former Incyte facility. However, the algorithms may be easily adjusted to any technological platform.