ANALYSIS ON CENSORED QUANTILE RESIDUAL LIFE MODEL VIA SPLINE SMOOTHING

Abstract

We propose a general class of quantile residual life models, where a specific quantile of the residual life time, conditional on an individual has survived up to time t, is a function of certain covariates with their coefficients varying over time. The varying coefficients are assumed to be smooth unspecified functions of t. We propose to estimate the coefficient functions using spline approximation. Incorporating the spline representation directly into a set of unbiased estimating equations, we obtain a one-step estimation procedure, and we show that this leads to a uniformly consistent estimator. To obtain further computational simplification, we propose a two-step estimation approach in which we estimate the coefficients on a series of time points first, and follow this with spline smoothing. We compare the two methods in terms of their asymptotic efficiency and computational complexity. We further develop inference tools to test the significance of the covariate effect on residual life. The finite sample performance of the estimation and testing procedures are further illustrated through numerical experiments. We also apply the methods to a data set from a neurological study.

1. Introduction

Residual life is defined as the remaining time to event given the fact that the survival time T of a patient is at least t, i.e., T − t|T ≥ t. In many clinical studies, especially when the associated diseases are chronic or/and incurable, knowing residual life is the major concern to patients. Modeling and estimating the mean of residual life has generated a large literature, for example, Oakes and Dasu (1990, 2003), Chen and Cheng (2005, 2006), Chen, Jewell and Cheng (2005), Müller and Zhang (2005), and Chen (2007). Compared with mean residual life models, quantile residual life models provide more complete and informative interpretation, especially when the distribution of the residual life is non-symmetric or skewed. Researches in this area are fairly recent, and include Jeong, Jung, and Costantino (2008), Jung, Jeong, and Bandos (2009), and Ma and Yin (2010). The quantile residual life models considered in the current literature focus on modeling and estimation at a single fixed t. Our interest here is in investigating the covariate effects along a range of times t. We take the covariate effects to be time variant, smooth functions of t in a varying coefficient quantile residual life model.

Our research is initially motivated by a clinical study on MELAS (mitochondrial myopathy, encephalopathy, lactic acidosis, and stroke-like episodes), which is a rare genetically-inherited neuroglial disease. Once the disease starts, MELAS patients suffer from progressive encephalopathy and stroke-like episodes that lead to disability and early death. There is as yet no effective treatment for this devastating condition, hence at each patient’s hospital visit, both the patient and the clinician are mainly interested in how much longer the patient can survive. When a patient is known to be a carrier of such genotype as yet without the disease, the time to disease onset becomes of central interest. Quantile analysis is more informative comparing to the classical mean approach. For example, the patients might be more interested in knowing how long their remaining time is with a 90% probability, rather than in knowing the average residual time. Our proposed method answers such questions, taking into consideration the patient’s characteristics.

We first represent the coefficient functions in the quantile residual life models by normalized B-splines, and estimate the spline coefficients using the residual life model jointly at different time points. This is what we refer to as one-step estimation. A second approach is a modification, in which we estimate the time varying coefficient function values at a set of different time points first, and then use a spline representation to approximate the coefficient functions based on estimated function values. This is what we refer to as two-step estimation. A similar two-step estimation is also used in a longitudinal data setting in Fan and Zhang (2000). We show a close link between the two estimation procedures, and point out computational advantage of the two-step procedure. We also study the large sample properties of the estimation procedures. To the best of our knowledge, this is the first time the residual life model has been considered simultaneously over a range of times.

The remainder of the paper is organized as follows. In Section 2, we present the quantile residual life model in its general form and show that the model is well-defined. We introduce two estimation procedures in Section 3. The one-step estimation procedure is discussed in Section 3.1, where we establish its root-n consistency and asymptotic normality. We further develop a simplified two-step estimation procedure in Section 3.2, and point out how the two estimation procedures are related in Section 3.3. Testing procedures are subsequently developed in Section 4, and we perform numerical analysis through simulation studies and a data analysis on the MELAS study in Section 5. We finish the paper with some discussion in Section 6, and collect the technical details and proofs in a web Appendix.

2. Censored Quantile Residual Life Model

Let (X_i, T_i, C_i), i = 1, …, n, be identical and independently distributed (i.i.d.), where X_i is a covariate vector, T_i is the event (death) time, and C_i is a competing censoring time. Assume the censoring time C_i to be independent of the event time T_i and the covariate X_i. Let Y_i = min(T_i, C_i) and D_i = I(T_i ≤ C_i), the binary index of censoring. As a typical situation in survival data analysis, we take the actual observations to be (X_i, Y_i, D_i) for i = 1, …, n. For notational convenience, we assume the observations are sorted in increasing order, 0 < Y₁ ⋯ ≤ Y_n. The quantile residual life model we consider has the general form

$$Q_{\tau }(T_i-t|X_i,T_i\ge t)=m\{X_i,\mathit{\beta }(t)\},t\ge 0,$$ (2.1)

where Q_τ (T|A) denotes the τth conditional quantile function of a random variable T conditional on an event A, τ is a quantile level ranging between 0 and 1, and t is the time at which the residual life is considered. Here, m(·) is a parametric function of covariate X, while the parameter β(t) = {β₁(t), β₂(t), …, β_p(t)}^T consists of p unknown smooth functions of t. Model (2.1) basically assumes that, given the covariate X_i, and the fact that T_i > t, the τth conditional quantile of the residual life T_i − t can be characterized by a parametric function m with its coefficient β(t) varying with time t. Our main interest is in estimating β(t), as well as testing the effect of certain components in the covariate vector X. A special case of the model is the familiar linear varying-coefficient model,

$$Q_{\tau }(T_i-t|X_i,T_i\ge t)=X_i^{\mathrm{T}}\mathit{\beta }(t),t\ge 0.$$

Here we let the first component of X_i be 1, hence the model includes a time-dependent intercept term. By taking into consideration that β(t) is a smooth function of t, we can obtain a unified presentation of the residual life over a period of time, which is of interest in many applications. Moreover, compared to estimating the residual life at given times separately, we can achieve a more efficient estimator by estimating β(t) globally.

Before proceeding to the estimation of β(t), we first establish that there indeed exists a survival model that satisfies the quantile restriction in (2.1), simultaneously for all t ≥ 0. Note that if the model is only required to hold at an arbitrary fixed t, identifiability is not an issue. If S(t|X) = Pr(T ≥ t|X) is the survival function of T given the covariate X, then (2.1) can be written as

$$S[t+m\{X,\mathit{\beta }(t)\}|X]=(1-\tau )S(t|X)$$

for any t ≥ 0. This functional equation can be recognized as a special case of a Schröder’s equation, and a solution for S exists as long as for all t ≥ 0, m{X, β(t)} is positive and continuous with respect to t, and t + m{X, β(t)} is strictly increasing as a function of t (Gupta and Langford (1984)). These are moderate conditions and are easily satisfied for a large class of m functions. Hence the model in (2.1) is well defined and self-coherent. In the next section, we proceed to describe the estimation algorithm for β(t).

Here and throughout the text, the o_p or O_p notation is component-wise in the case of vectors; ‖·‖ refers to the L₂ or l₂ norm according to the content.

3. Estimation

3.1. One-step estimation of β(t)

In this section, we propose one-step estimation equations for β(t) based on normalized B-spline approximation. Specifically, we take b(t) = [π₁(t), …, π_kn (t)]^T as k_n B-spline basis functions given a set of internal knots and the order of spline, and then approximate β(t) by β(t) ≈ αb(t), where α is a p × k_n matrix of unspecified parameters. Although many other nonparametric methods exist in the literature, we use B-spline approximation due to its convenience in implementation. In this notation, (2.1) can be approximated by

$$Q_{\tau }(T_i-t|X_i,T_i\ge t)=m\{X_i,\mathit{\alpha }\mathbf{b}(t)\},t\ge 0.$$

For a fixed basis b(t), this can be treated as a parametric model. At any fixed t = t₀ and for a general m function, a slight modification of the estimator in Jung, Jeong, and Bandos (2009) yields the estimating equation

$$\sum _{i=1}^n\frac{\partial m\{X_i,\mathit{\alpha }\mathbf{b}(t_0)\}}{\partial \alpha }(\frac{I[Y_i\ge t_0+m\{X_i,\mathit{\alpha }\mathbf{b}(t_0)\}]}{G[t_0+m\{X_i,\mathit{\alpha }\mathbf{b}(t_0)\}]}-(1-\tau )\frac{I(Y_i\ge t_0)}{G(t_0)})=0.$$ (3.1)

Here α is a length pk_n vector formed by concatenating all the rows of α, G is the censoring process survival function, G(t) = Pr(C ≥ t). In practice, G is typically estimated by a Kaplan-Meier estimator.

A careful inspection of ∂m{X_i, αb(t₀)}/∂α reveals that it equals ∂m{X_i, αb(t₀)}/∂{αb(t₀)} ⊗ b(t₀), where ⊗ denotes a Kronecker product. Hence (3.1) includes only p independent estimating equations, hence does not suffice to estimate all the pk_n elements in α. However, since (2.1) holds for all t > 0, one can estimate α by assembling a collection of equations of type (3.1) at (t_j : j = 1, …, J), a set of distinctive values of the observed Y_i’s. Specifically, we propose to obtain α through minimizing

$$s(\mathit{\alpha })=\sum _{j=1}^J{\left\{\sum _{i=1}^n\frac{\partial m\{X_i,\mathit{\alpha }\mathbf{b}(t_j)\}}{\partial \{\mathit{\alpha }\mathbf{b}(t_j)\}}\right(\frac{I[Y_i\ge t_j+m\{X_i,\mathit{\alpha }\mathbf{b}(t_j)\}]}{Ĝ[t_j+m\{X_i,\mathit{\alpha }\mathbf{b}(t_j)\}]}-(1-\tau )\frac{I(Y_i\ge t_j)}{Ĝ(t_j)}\left)\right\}}^{\otimes 2},$$ (3.2)

where υ^⊗2 denotes υ^Tυ for any vector υ. Using α̂ to denote the estimate obtained from minimizing (3.2), the estimator of β(t) is β̂(t) = α̂b(t). Obviously, several tuning parameters need to be decided in this procedure. First, to select the number of basis functions k_n, we could use some standard selection criterion such as BIC. Specifically, we estimate α̂(k_n) for a fixed candidate k_n, and form s{α(k_n)}. We then select the optimal k_n through minimizing s{α(k_n)} + log(n)k_n. In the following, we discuss the selection of the other tuning parameters J and the t_j’s that are more specific to the residual life model.

The choice of t_j’s. One can choose an arbitrary set of times t₁,…, t_J in (3.2) as long as at least k_n of the J corresponding equations of the form (3.1) are linearly independent, for then the estimator given in (3.2) is uniquely defined. Note that this requires that J ≥ k_n, so the number of distinctive event/censor times is larger than the number of B-spline basis functions. Our subsequent theoretical development further requires that there exist ε > 0 so that J = o(n^1/2−ε). A natural choice is to let t₁ = 0 and t_j+1 = Y_j, the jth event or censoring time, for j = 1, …, J − 1. Since the distribution of the Y_i is usually continuous over [0, T], this choice generally satisfies the requirement. Computationally, when t_j increases, fewer observations contribute to the corresponding estimating equation. In addition, the estimated Ĝ also becomes less reliable. Hence, we recommend in practice to stop the summation over j in (3.2) at a value between k_n and one third of the total number of distinct Y_i values. The same rule is also applied to the two-step estimation approach introduced later in Section 3.2.

Asymptotic properties

In this section, we give the convergence rate and asymptotic distribution of β̂(t) and α̂ obtained from minimizing (3.2). Let t = (t₁, …, t_J) and

$$s_i\{t,\mathit{\beta }(t),G\}=\frac{\partial m\{X_i,\mathit{\beta }(t)\}}{\partial \mathit{\beta }(t)}(\frac{I[Y_i\ge t+m\{X_i,\mathit{\beta }(t)\}]}{G[t+m\{X_i,\mathit{\beta }(t)\}]}-(1-\tau )\frac{I(Y_i\ge t)}{G(t)}),f_i\{\mathit{\alpha }\mathbf{b}(\mathbf{t}),G\}=(\frac{\partial E[s_i^{\mathrm{T}}\{t_1,\mathit{\alpha }\mathbf{b}(t_1),G\}]}{\partial \alpha },\dots ,\frac{\partial E[s_i^{\mathrm{T}}\{t_J,\mathit{\alpha }\mathbf{b}(t_J),G\}]}{\partial \alpha })\left[\begin{array}{c}\hfill s_i\{t_1,\mathit{\alpha }\mathbf{b}(t_1),G\}\hfill \\ \hfill ⋮\hfill \\ \hfill s_i\{t_J,\mathit{\alpha }\mathbf{b}(t_J),G\}\hfill \end{array}\right].$$

It is easy to see that the estimator in (3.2) satisfies an estimating equation of the form

$$n^{-1/2}\sum _{i=1}^n{f}_i\{\mathit{\alpha ̂}\mathbf{b}(\mathbf{t}),Ĝ\}=o_p(J{n}^{\epsilon }),$$

for any ε > 0. In what follows, we outline conditions under which we derive the asymptotic properties of α̂.

A1 : The true time-varying coefficient vector β₀(t) consists of p smooth functions defined on a closed interval [0, T], and each of them has a bounded rth derivative with r ≥ 2.

Under Condition A1, there exists a B-spline approximation α₀b(t) and a constant C₁ such that ${\text{sup}}_{t\in [0,T]}|{\mathit{\beta }}_0(t)-{\mathit{\alpha }}_0\mathbf{b}(t)|<C_1{k}_n^{-r}$ (Schumaker (1981)).

A2 : The quantile function m(x, β) has a bounded second derivative with respect to β.

Let

$$S_n\{\mathit{\beta }(t)\}=\sum _{i=1}^n{s}_i\{t,\mathit{\beta }(t),G\}=\sum _{i=1}^n\frac{\partial m\{X_i,\mathit{\beta }(t)\}}{\partial \mathit{\beta }(t)}(\frac{I[Y_i\ge t+m\{X_i,\mathit{\beta }(t)\}]}{G[t+m\{X_i,\mathit{\beta }(t)\}]}-(1-\tau )\frac{I(Y_i\ge t)}{G(t)}),$$

be the functional estimation equations for β(t) (without B-spline approximations).

A3 : The functional estimating equation ES_n{β(t)} = 0 has a unique solution β₀(t). In addition, there exist a compact set Ω ∈ R^p+1 such that the p curves contained in β₀(t) form an interior point of Ω. Note that this implies each curve in β₀(t) is uniformly bounded.

A4 : The censoring survival function G(t) and the event survival function S(t) are differentiable; g(t) = G′(t), and s(t) = S′(t) are bounded away from zero and infinity and are bounded for all t ∈ [0, T].

A5 : max_i sup_t E‖s_i{t, β(t), G}‖² = O(1).

A6 : The first derivative of each component of f_i{β(t), G} with respect to G is uniformly bounded. That is, there exists a constant C > 0 such that |∂ f_i{β(t), G}/∂G| < C for all β(t), G and i = 1, …, n.

With those conditions, we summarize the asymptotic properties of α̂ in two theorems. The proofs are deferred to a web Appendix.

Theorem 1. Under A1–A6, if the number of B-spline basis function, k_n, satisfies n^1/4r << k_n << n^1/4 for r ≥ 2, then

$${\Vert \mathit{\alpha ̂}-{\mathit{\alpha }}_0\Vert }^2=O_p\left(\frac{k_n}{n}\right).$$ (3.3)

It follows from the Theorem 1 that β̂(t) is uniformly consistent for t ∈ [0, T], i.e. sup_t∈[0,T] ‖β̂(t) − β(t)‖² = O_p(k_n/n). We now define the following notations relate to the asymptotic distribution of α̂. Let

$$M=(\frac{\partial E[s_i^{\mathrm{T}}\{t_1,{\mathit{\alpha }}_0\mathbf{b}(t_1),G\}]}{\partial \alpha },\dots ,\frac{\partial E[s_i^{\mathrm{T}}\{t_J,{\mathit{\alpha }}_0\mathbf{b}(t_J),G\}]}{\partial \alpha }),𝒟=\text{cov}\left[{\{{\nu }_i^{\mathrm{T}}(t_1,{\mathit{\beta }}_1,G),\dots ,{\nu }_i^{\mathrm{T}}(t_J,{\mathit{\beta }}_J,G)\}}^{\mathrm{T}}\right],$$

where

$${\nu }_i(t_j,{\mathit{\beta }}_j,G)=s_i(t_j,{\mathit{\beta }}_j,G)-{\mathbf{q}}_2({\mathit{\beta }}_j,t_j){\int }_{-\infty }^{t_j}{h}^{-1}(s)\{dI(Y_i\le s,D_i=0)-I(Y_i\ge s)d{\mathrm{\Lambda }}_G(s)\}+{\int }_{-\infty }^{\infty }{G}^{-1}(s){\int }_{-\infty }^s{h}^{-1}(\upsilon )\{dI(Y_i\le \upsilon ,D_i=0)-I(Y_i\ge \upsilon )d{\mathrm{\Lambda }}_G(\upsilon )\}d{\mathbf{q}}_1({\mathit{\beta }}_j,s).$$

Here h(s) = E(Y₁ ≥ s), Λ_G is the cumulative hazard function of the censoring process, and

$${\mathbf{q}}_1({\mathit{\beta }}_j,s)=E[\frac{\partial m(X_i,{\mathit{\beta }}_j)}{\partial {\mathit{\beta }}_j}I\{t_j+m(X_i,{\mathit{\beta }}_j)\le \text{min}(s,Y_i)\}],{\mathbf{q}}_2({\mathit{\beta }}_j,t_j)=(1-\tau )G{(t_j)}^{-1}E\{I(Y_i\ge t_j)\frac{\partial m(X_i,{\mathit{\beta }}_j)}{\partial {\mathit{\beta }}_j}\}.$$

The difference of s_i and ν_i is a consequence of the Kaplan-Meier estimation of G(t). With this notation, the following theorem summarizes the asymptotic distribution of α̂.

Theorem 2. Under A1–A6, for any η ∈ R^pk_n and ‖η‖ = 1, n^1/2η^T(α̂ − α₀)/σ → N (0, 1) in distribution when n → ∞, where σ² = η^T𝒱η, and 𝒱 = ℬ𝒟ℬ^T, ℬ = (MM^T)⁻¹M.

From Theorem 2, we can see that estimating the censoring process survival function G(t) does not bring additional bias while it has an impact on the estimation variance. With β̂(t) = α̂b(t) = α̂^T{I_p ⊗ b(t)}, it follows from Theorem 2 that, for any given time t, β̂(t) is asymptotically normal with mean β(t) and variance-covariance matrix {I_p ⊗ b(t)}^T𝒱{I_p ⊗ b(t)}/n.

The one-step estimation procedure introduced here requires intensive computation, since the dimension of the unknown parameter α in (3.2) is pk_n. In Section 3.2, we propose a two-step approach to reduce the computational burden. A discussion comparing the two approaches is provided in Section 3.3.

3.2. An alternative two-step estimation approach

It is worth noting that the nonparametric function estimation for β(t) differs from the conventional one in an important aspect. In a classical regression, β(t) contributes to a relation as a function of all t’s in a valid range; in the residual life model, β(t) contributes to a relation only as a function value at a fixed t. At different t_j, β(t_j) is subject to a different requirement. Other than β(t) being sufficiently smooth, β(t_j) at different t_j values are not inherently related via these requirements. Thus, intuitively, one can estimate β(t) at a large set of t values to obtain {t_j, β̌ (t_j)}, j = 1, …, J, and then use these as pseudo observations to perform a nonparametric fitting using, say, splines.

To be precise, select t_j, j = 1, …, J, as in Section 3.1. At each t_j, obtain β̌(t_j) from

$$\sum _{i=1}^n{s}_i\{t_j,\mathit{\beta }(t_j),Ĝ\}=\sum _{i=1}^n\frac{\partial m\{X_i,\mathit{\beta }(t_j)\}}{\partial \mathit{\beta }(t_j)}(\frac{I[Y_i\ge t_j+m\{X_i,\mathit{\beta }(t_j)\}]}{Ĝ[t_j+m\{X_i,\mathit{\beta }(t_j)\}]}-(1-\tau )\frac{I(Y_i\ge t_j)}{Ĝ(t_j)})=0,$$ (3.4)

then obtain an estimator of α from minimizing ${\sum }_{j=1}^J{\{\mathit{\alpha }\mathbf{b}(t_j)-\mathit{\beta ̌}(t_j)\}}^{\otimes 2}$. The minimizer α̃ has the explicit form

$$\mathit{\alpha ̃}=\{\sum _{j=1}^J\mathit{\beta ̌}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}{\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}}^{-1}.$$

As before, we construct the two-step estimator of β(t) using β̃(t) = α̃b(t).

Note that the estimator α̃ can be written as

$$\mathrm{\alpha ̃}=\sum _{j=1}^J{I}_p\otimes [{\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}}^{-1}\mathbf{b}(t_j)]\mathit{\beta ̌}(t_j)=𝒞{(\mathit{\beta ̌}{(t_1)}^{\mathrm{T}},\dots ,\mathit{\beta ̌}{(t_J)}^{\mathrm{T}})}^{\mathrm{T}},$$ (3.5)

where

$$𝒞\equiv (I_p\otimes [{\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathbf{T}}(t_j)\}}^{-1}\mathbf{b}(t_1)],\dots ,I_p\otimes [{\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}}^{-1}\mathbf{b}(t_J)\left]\right),$$

and I_p stands for p-dimensional identity matrix. Since β̌(t_j) → β(t_j) for any 1 ≤ j ≤ J, as long as the B-spline basis is adequate, α̃b(t) is a consistent estimate of the true coefficient function β(t). Let ℳ = diag(∂E [s_i{t₁, β(t₁), G}]/∂β(t₁)^T, …, ∂E [s_i{t_J, β(t_J), G}]/∂β(t_J)^T),,

Theorem 3. Under the regularity conditions of Theorem 1, for any η ∈ R^k_n and ‖η‖ = 1, we have n^1/2η^T(α̃ − α₀)/σ → N (0, 1) in distribution when n → ∞, where σ² = η^T𝒲η, where 𝒲 = 𝒞ℳ⁻¹𝒟(ℳ⁻¹)^T𝒞^T.

Theorem 3 can be proved similarly as Theorem 2 by grouping J estimating equations in (3.4) together and using the relation (3.5). We omit the proof.

As before, it follows from Theorem 3 that, for any given time t, β̃(t) is asymptotically normal with mean β(t) and variance-covariance matrix {I_p ⊗ b(t)}^T𝒲{I_p ⊗ b(t)}.

3.3. Relation between one-step and two-step approaches

The two estimation approaches are essentially two ways of linking point-wise curve estimation and the spline curve representation. Specifically, the one-step estimation imposes the spline representation before forming an estimate, with α̂ obtained through a one-step optimization. In contrast, the two-step approach forms an estimate at various time points first, then links the results to the spline representation. In terms of computational cost, the one-step estimation is more expensive, since it means solving a pk_n-dimensional estimation equation, while the two-step approach solves J separate p-dimensional estimating equations, followed by a simple matrix-vector multiplication. Both estimators are consistent and enjoy asymptotically normality. We now investigate in detail the estimation efficiency of the two approaches.

Recall that 𝒱 and 𝒲 are limiting variance-covariance matrices for the one-step estimator α̂ and two-step estimator α̃, respectively. The two matrices share the same pivotal component 𝒟. To understand the it differences, we first establish the association between M and ℳ.

Let (M^T)_jl be the (j, l)th size p × k_n block of M^T, ℳ_jj the (j, j)th size p × p block of ℳ, 𝒞_jl the (j, l)th size k_n × p block of 𝒞, e_l the length p vector with ith entry 1 and all others 0. Then

$${(M^{\mathrm{T}})}_{jl}=\frac{\partial E\{s_i(t_j,\mathit{\alpha }\mathbf{b}(t_j),G)\}}{\partial {\alpha }_l^{\mathrm{T}}}={ℳ}_{jj}{e}_l{\mathbf{b}}^{\mathrm{T}}(t_j),{𝒞}_{lj\prime }=e_l^{\mathrm{T}}\otimes [{\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}}^{-1}\mathbf{b}(t_{j\prime })],{(M^{\mathrm{T}}𝒞)}_{jj\prime }={ℳ}_{jj}\sum _{l=1}^p{e}_l{\mathbf{b}}^{\mathrm{T}}(t_j)(e_l^{\mathrm{T}}\otimes [{\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}}^{-1}\mathbf{b}(t_{j\prime })\left]\right)={\mathbf{b}}^{\mathrm{T}}(t_j){\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}}^{-1}\mathbf{b}(t_{j\prime }){ℳ}_{jj}.$$

Assembling the blocks of M^T𝒞, and defining a hat matrix

$$H={\{\mathbf{b}(t_1),\dots ,\mathbf{b}(t_J)\}}^{\mathrm{T}}{\{\sum _{j=1}^J\mathbf{b}(t_j){\mathbf{b}}^{\mathrm{T}}(t_j)\}}^{-1}\{\mathbf{b}(t_1),\dots ,\mathbf{b}(t_J)\},$$

we obtain the relationship between M and ℳ that M^T𝒞 = ℳ(H⊗I_p). Therefore,

$$𝒜(𝒲-𝒱){𝒜}^{\mathrm{T}}=M\{M^{\mathrm{T}}𝒞{ℳ}^{-1}𝒟{({ℳ}^{-1})}^{\mathrm{T}}{𝒞}^{\mathrm{T}}M-𝒟\}{M}^{\mathrm{T}}=M\{ℳ(H\otimes I_p){ℳ}^{-1}𝒟{({ℳ}^{-1})}^{\mathrm{T}}{(H\otimes I_p)}^{\mathrm{T}}{ℳ}^{\mathrm{T}}-𝒟\}{M}^{\mathrm{T}}=Mℳ\{(H\otimes I_p){ℳ}^{-1}𝒟{({ℳ}^{-1})}^{\mathrm{T}}(H\otimes I_p)-{ℳ}^{-1}𝒟{({ℳ}^{-1})}^{\mathrm{T}}\}{ℳ}^{\mathrm{T}}{M}^{\mathrm{T}}.$$

Consequently, 𝒲 can be written as

$$𝒲=\{{𝒜}^{-1}Mℳ(H\otimes I_p){ℳ}^{-1}\}D{\{{𝒜}^{-1}Mℳ(H\otimes I_p){ℳ}^{-1}\}}^{\mathrm{T}},$$

while the component H ⊗ I_p is simply replaced by the identity matrix in the expression for 𝒱. We conclude the following,

1. If J = k_n, then 𝒲 = 𝒱, and the two estimators are equivalent. For, in this case, H = I_kn.

2. If J > k_n, then 𝒲 − 𝒱 can have zero, positive, and negative eigenvalues, and hence there is no definitive winner between the two estimators in terms of efficiency.

In practice, a relative small k_n is often sufficient to approximate the smooth components in β(t). However, to fully utilize the model structure in (2.1), as long as computational stability is retained, one would choose a large J. Thus, J = k_n almost never happens in reality. The two-step estimator has appealing computational advantages over the one-step estimator and, at the same time, is not inferior in terms of estimation efficiency. We hence recommend using the two-step procedure in practice. In fact, both the one-step and the two-step procedures can be improved through better weighting, as we now discuss.

Equivalence between optimized α̂ and α̃

We could view the one-step estimator α̂ and the two-step estimator α̃ as special cases of two families of estimations. First, instead of forming the sum of squares of the estimating equation terms, we could form the sum of weighted squares using the Generalized Method of Moments (GMM). We define a family of GMM estimator by

$$\mathit{\alpha ̂}{\mathbf{w}}_1=\text{arg}\underset{\mathit{\alpha }}{\text{min}}{\left(\sum _{i=1}^n\right[\begin{array}{c}\hfill s_i\{t_1,\mathit{\alpha }\mathbf{b}(t_1),Ĝ\}\hfill \\ \hfill \dots \hfill \\ \hfill s_i\{t_J,\mathit{\alpha }\mathbf{b}(t_J),Ĝ\}\hfill \end{array}\left]\right)}^{\mathrm{T}}{\mathbf{W}}_1\left(\sum _{i=1}^n\right[\begin{array}{c}\hfill s_i\{t_1,\mathit{\alpha }\mathbf{b}(t_1),Ĝ\}\hfill \\ \hfill \dots \hfill \\ \hfill s_i\{t_J,\mathit{\alpha }\mathbf{b}(t_J),Ĝ\}\hfill \end{array}\left]\right),$$ (3.6)

where W₁ is a pJ × pJ-dimensional weight matrix. It is easy to see that, when W₁ = I_pJ is the identity matrix, the GMM estimating equations at (3.6) reduce those at (3.2), and consequently α̂ is a special case of a GMM estimator. Second, we define a family of Weighted Least Squares (WLS) estimators by

$$\mathit{\alpha ̃}{\mathbf{w}}_2=\text{arg}\underset{\mathit{\alpha }}{\text{min}}{\left\{\begin{array}{c}\hfill \mathit{\alpha }\mathbf{b}(t_1)-\mathit{\beta ̌}(t_1)\hfill \\ \hfill \dots \hfill \\ \hfill \mathit{\alpha }\mathbf{b}(t_J)-\mathit{\beta ̌}(t_J)\hfill \end{array}\right\}}^{\mathrm{T}}{\mathbf{W}}_2\left\{\begin{array}{c}\hfill \mathit{\alpha }\mathbf{b}(t_1)-\mathit{\beta ̌}(t_1)\hfill \\ \hfill \dots \hfill \\ \hfill \mathit{\alpha }\mathbf{b}(t_J)-\mathit{\beta ̌}(t_J)\hfill \end{array}\right\},$$

where W₂ is a pJ × pJ-dimensional weight matrix. Similarly, the two-step estimator α̃ is a special case of an WLS estimator when W₂ = I_pJ is the identity matrix.

It is well-known that the most efficient WLS estimator is reached when the weight matrix W₂ is the inverse of the variance-covariance matrix of β̌. i.e. W₂ = {ℳ⁻¹𝒟(ℳ⁻¹)^T}⁻¹. The same results in Theorem 3 holds for the optimal WLS estimator with limiting matrix 𝒲 replaced by 𝒲̃ = (Fℳ^T𝒟⁻¹ℳF^T)⁻¹, where F = {I_p ⊗ b(t₁), …, I_p ⊗ b(t_J)}. On the other hand, the most efficient GMM estimator is the one with W₁ = 𝒟⁻¹, the inverse of the variance-covariance matrix of the estimating equations that invokes (3.1) at t₁, …, t_J. The resulting optimal GMM estimator has a limiting variance-covariance matrix 𝒱̃ = ((M𝒟⁻¹M^T)⁻¹ to the first order. It is not difficult to verify that M = Fℳ^T to the first order, hence the estimation variance of the optimal one-step GMM estimator is the same to the first order as the optimal two-step WLS estimator, that is, they are effectively equivalent.

Although ideally a weighted approach should be used, it is not recommended in practice, because the optimal weights involve density estimation in the quantile regression framework. This is known to be unreliable. One could use the bootstrap to generate the variance estimation, but it is computationally undesirable. For these reasons we focus our discussion on the unweighed estimations β̂(t) and β̃(t).

We summarize the differences between the two estimations as follows. First, their constructions are different. The one-step estimation incorporates the spline representations first to reduce the problem into a parameter estimation problem, it then constructs different estimating equations at various times. Because the number of parameters is likely smaller than the number of the resulting estimating equations, it falls in the category of GMM estimation. The two-step approach estimates the function values at various individual time points, then links the results to the spline representation. Because the number of spline coefficients is likely smaller than the function values obtained, this falls to the linear regression category and calls for a LS criterion. Computational complexities are also different. The two-step approach reduces a pk_n-dimensional estimation equation to J p-dimensional estimations. Hence it is computationally less challenging and more efficient. Finally, in terms of estimation variance, the two approaches are equally efficient when the respective optimal weights are used. The proposed α̂ and α̃ use equal weights, which leads to different efficiency losses. The efficiency loss of α̂ is the type of loss seen in the regression context with heteroscedastic error when the error variance is treated as a constant. Hence the amount of loss in practice depends on the error variance structure. The efficiency loss of α̃ is the type of loss seen under the GMM framework when the performance difference of available estimation equations and their correlations are ignored. Hence the amount of loss in practice depends on how different and how correlated these estimating equations are. Neither of α̂ and α̃ is uniformly better than the other. When we reduce the dimension of the estimation equations to the parsimonious case of J = k_n, the two estimators are again equivalent. Accordingly, we recommend the two-step approach in practice.

4. Inference Tools

Once we obtain the estimate of β(t), the next step is to test the covariate effect on the τth quantile of residual life. To this end, we write $\mathit{\beta }(t)={\{{\mathit{\beta }}_1^{\mathrm{T}}(t),{\mathit{\beta }}_2^{\mathrm{T}}(t)\}}^{\mathrm{T}}$, where β₁ (t) and β₂(t) are p₁- and p₂-dimensional sub-vectors of β(t), (p₁ ≤ p, p₂ ≤ p). We assume that, through proper parameterization, interest is in testing whether β₂(t) is a zero function. Thus, the null and alternative hypotheses are respectively

$$H_0:{\mathit{\beta }}_2(t)=0{\forall }_t\text{and}{H}_1:{\mathit{\beta }}_2(t)\ne 0\text{for at least one}t\in [0,T].$$ (4.1)

Under the same spline representation for β(t), testing (4.1) is equivalent to testing

$$H_0:{\mathit{\alpha }}_2=0,\mathrm{v}\mathrm{s}{H}_1:{\mathit{\alpha }}_2\ne 0.$$

Here, $\mathit{\alpha }={({\mathit{\alpha }}_1^{\mathrm{T}},{\mathit{\alpha }}_2^{\mathrm{T}})}^{\mathrm{T}}$, where α₁ and α₂ are sub-matrixes of α with dimensions p₁ × k_n and p₂ × k_n, respectively, the spline coefficients associated with β₁(t) and β₂(t). Under Theorems 2 and 3, we could construct Wald-type statistics

$$T_{n,1}=n{\mathit{\alpha ̂}}_2^{\mathrm{T}}{𝒱}_{22}^{-1}{\mathrm{\alpha ̂}}_2\text{and}{T}_n{,}_2=n{\mathit{\alpha ̃}}_2^{\mathrm{T}}{𝒲}_{22}^{-1}{\mathrm{\alpha ̃}}_2,$$

where 𝒱₂₂ and 𝒲₂₂ are, respectively, p₂k_n × p₂k_n lower-right sub-matrixes of 𝒱 and 𝒲 associated with α₂. Under the null hypothesis, T_n,1 and T_n,2 are asymptotically chi-square distributed with degrees of freedom p₂k_n.

Both 𝒱₂₂ and 𝒲₂₂ involve unknown components that need to be estimated empirically. Two estimation approaches exist. In large sample situations, we can use asymptotic results. To estimate M in 𝒱. we use the sample average to replace the expectation, i.e., $E[s_i^{\mathrm{T}}\{t,{\mathit{\alpha }}_0\mathbf{b}(t),G\}]\approx n^{-1}{\sum }_{i=1}^n{s}_i^{\mathrm{T}}\{t,\mathit{\alpha ̂}\mathbf{b}(t),Ĝ\}$, and use a numerical difference for the derivative. Following the same line, we can estimate ℳ in 𝒲. In the web Appendix we show that 𝒟 can be approximated by

$$\mathrm{𝒟̂}=n^{-1}\sum _{i=1}^n{\{{\mathrm{\nu ̂}}_i{(t_1,\mathit{\beta ̂}(t_1),Ĝ)}^{\mathrm{T}},\dots ,{\mathrm{\nu ̂}}_i{(t_J,\mathit{\beta ̂}(t_J),Ĝ)}^{\mathrm{T}}\}}^{\mathrm{T}}\{{\mathrm{\nu ̂}}_i{(t_1,\mathit{\beta ̂}(t_1),Ĝ)}^{\mathrm{T}},\dots ,{\mathrm{\nu ̂}}_i{(t_J,\mathit{\beta ̂}(t_J),Ĝ)}^{\mathrm{T}}\},$$

where

$${\mathrm{\nu ̂}}_i^{\mathrm{T}}(t_j,\mathit{\beta ̂}(t_j),Ĝ)=s_i\{t_j,\mathit{\beta ̂}(t_j),Ĝ\}+n^{-1}\sum _{l=1}^n\frac{\partial m\{X_l,\mathit{\beta ̂}(t_j)\}}{\partial \mathit{\beta ̂}(t_j)}{Ĝ}^{-1}[t_j+m\{X_l,\mathit{\beta ̂}(t_j)\left\}\right]I[t_j+m\{X_l,\mathit{\beta ̂}(t_j)\}\le Y_l]\times \{{ĥ}^{-1}(Y_i)(1-D_i)I[Y_i\le t_j+m\{X_l,\mathit{\beta ̂}(t_j)\}]-n^{-1}\sum _{k=1}^n{ĥ}^{-2}(Y_k)(1-D_k)I(Y_k\le \text{min}[Y_i,t_j+m\{X_l,\mathit{\beta ̂}(t_j)\left\}\right]\left)\right\}-{\mathbf{q̂}}_2(\mathit{\beta ̂}(t_j),t_j)[{ĥ}^{-1}(Y_i)(1-D_i)I(Y_i\le t_j)-n^{-1}\sum _{k=1}^n{ĥ}^{-2}(Y_k)(1-D_k)I\{Y_k\le \text{min}(Y_i,t_j)\}],$$ (4.2)

$ĥ(s)=n^{-1}{\sum }_{i=1}^{n}I(Y_i\ge s)$, and

$${\mathbf{q̂}}_2\{\mathbf{b̂}(t_j),t_j\}=(1-\tau )Ĝ{(t_j)}^{-1}{n}^{-1}\sum _{i=1}^n[I(Y_i\ge t_j)\frac{\partial m\{X_i,\mathit{\beta ̂}(t_j)\}}{\partial \mathit{\beta ̂}(t_j)}].$$

We then assemble empirical estimates of 𝒱₂₂ and 𝒲₂₂, and substitute for the true ones in T_n,1 and T_n,2.

A more precise and stable approach is to use the bootstrap method to estimate 𝒱₂₂ and 𝒲₂₂, especially when sample size is not large. The cost of bootstrap is in computation intensity. This is the standard bootstrap used in quantile regression, so we omit implementation details. We also do not propose the score test for the quantile residual life model because, in the model we consider, the score test loses its typical advantage over Wald test. Since the residual life model holds for all t, we also need $E\{f_{T|X}(t|X)X_2{X}_1^{\mathrm{T}}\}=0$ for all t to enjoy the advantage of the score test. Such condition cannot be satisfied without violating the original model assumptions. For this reason, the score test is not recommended in our context.

5. Numerical Results

5.1. Simulation

We conducted simulation studies to investigate the finite sample performance of the proposed method. The first quantile residual life we study has the form Q_τ (T_i − t|X_i, T_i ≥ t) = β₁(t) + β₂(t)X_i, where X_i is the ith subject’s covariate, τ = 0.5, and β₁(t) and β₂(t) are time varying intercept and slope coefficients that are linear functions of t: β₁(t) = β_1c + β_1lt and β₂(t) = β_2c + β_2lt. We write β_c = β_1c + β_2c and β_l = β_1l + β_2l. To generate data sets, we adopt the model with survival function

$$S(t|X_i)={\{1+\frac{t(X_i^{\mathrm{T}}{\beta }_l)}{X_i^{\mathrm{T}}{\beta }_c)}\}}^{\text{log}(1-\tau )/\text{log}(1+X_i^{\mathrm{T}}{\mathrm{\beta }}_l)}={(1-\tau )}^{\text{log}\{1+t{X}_i^{\mathrm{T}}{\beta }_l/(X_i^{\mathrm{T}}{\beta }_c)\}/\text{log}(1+X_i^{\mathrm{T}}{\beta }_l)}.$$

Data generated here satisfy the quantile residual life model as long as β₁(t) and β₂(t) do not simultaneously degenerate to a constant function. In fact, when the slopes in both β₁(t) and β₂(t) are zero, the above survival function does not exist, and we need to generate data from

$$S(t|X_i)=e^{t\text{log}(1-\tau )/X_i^{\top }{\beta }_c}={(1-\tau )}^{t/X_i^{\top }{\beta }_c}$$

in order to satisfy the corresponding quantile residual life model. We study all four situations, in which β₁(t), β₂(t) can be either a linear function or a constant function.

We generated the covariates X_i’s from a uniform distribution in [0, 2], and we generated the censoring distribution from a mixture of infinity and an exponential distribution, so that the censoring rate was approximate 15%–20%. The sample sizes were n = 100, 200, 300, and 1,000, and we chose the first one-third of the y_i values to form the t_j values in calculating the β̂_j’s. One could of course put more values into the collection of t_j’s, but, as pointed in Section 3.1, the effective samples participating in the estimation of β̂_j are the ones with Y_i ≥ t_j. Thus, a larger value of t_j yields less efficient estimation of β̂_j. When the effective sample size is too small, the asymptotic results may not be relevant, and various numerical issues also occur. For computational stability, we chose the t_j values to ensure that there were at least one third of the observations contributing to the estimation of β̂_j. The quadratic spline basis functions were selected, we put four knots at the boundary and equally spaced positions between the boundaries. A total of 1,000 simulations was conducted in each model.

To illustrate the performance of the method on a non-polynomial functional form of β(t), we conducted a second simulation study with the quantile residual function m{X, β(t)} = e^−2Xβ₁(t) + e^−Xβ₂(t). Here β₁(t) = {log(1 − τ)}² and ${\beta }_2(t)=-2\sqrt{a+t}\text{log}(1-\tau )$ at a = 0.01. It can be verified that the random process with survival function

$$S(t|X_i)=\text{exp}\{-e^{X_i}(\sqrt{t+a}-\sqrt{a})\}$$

yields a τth quantile residual of the desired form. We generated the covariate X_i’s from a uniform distribution in [−1.5, 0.5] and a censoring time from a mixture of infinity and exponential distribution as before to retain a similar censoring rate.

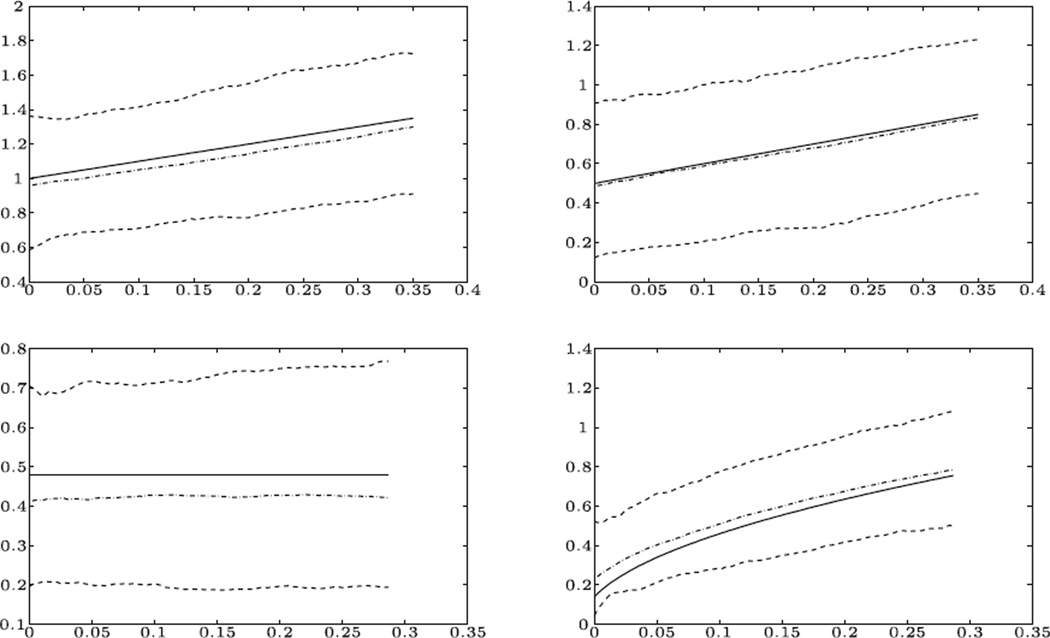
We present the mean squared error (MSE) of the estimation for different models and sample sizes in Table 1. Here for each function β_j(t), the MSE was calculated using ∑_i(β̂_j(t_i) − β_j(t_i))², where t_i’s are equally spaced on the range of t considered. For comparison, we also present the MSE of the estimation with smoothing the pointwise estimates of β(t). Clearly, for all the models and the sample sizes, our method yields an estimate with smaller MSE than the pointwise procedure. The improvement is especially dramatic when sample size is small or moderate. When sample sizes are 1,000, presented for comparison purposes, the improvement becomes less impressive, although still quite important. To provide a visual inspection of the estimation for both the linear and nonlinear model, we also plotted the mean estimated curves together with the true curves and 90% pointwise confidence bands in Figure 1. As can be seen, the estimated average curves are rather close to the truth, indicating the validity of our proposal. We point out here that the confidence bands in Figure 1 contain a constant curve, hence at the 10% level, one may not conclude that the varying coefficient model is really necessary. This is caused by the small sample size. With n =1,000, the 90% confidence bands corresponding to the nonlinear true function no longer contain any constant curve.

Table 1.

MSE of un-smoothed and smoothed curve fitting.

	True functions		MSE un-smoothed		MSE smoothed
n	β1(t)	β2(t)	β1(t)	β2(t)	β1(t)	β2(t)
	1	0.5	0.0693	0.0553	0.0381	0.0302
	1	0.5 + t	0.1211	0.1154	0.0634	0.0498
100	1 + t	0.5	0.1341	0.1014	0.0612	0.0448
	1 + t	0.5 + t	0.1700	0.1483	0.0769	0.0600
	(log2)2	$2\text{log}2\sqrt{0.01+t}$	0.0561	0.1288	0.0347	0.0605
	1	0.5	0.0456	0.0432	0.0296	0.0310
	1	0.5 + t	0.0800	0.0924	0.0425	0.0535
200	1 + t	0.5	0.0903	0.0688	0.0447	0.0374
	1 + t	0.5 + t	0.1350	0.1029	0.0623	0.0453
	(log2)2	$2\text{log}2\sqrt{0.01+t}$	0.0433	0.0946	0.0307	0.0410
	1	0.5	0.0340	0.0352	0.0254	0.0290
	1	0.5 + t	0.0581	0.0828	0.0354	0.0574
300	1 + t	0.5	0.0778	0.0633	0.0453	0.0423
	1 + t	0.5 + t	0.1078	0.0968	0.0526	0.0547
	(log2)2	$2\text{log}2\sqrt{0.01+t}$	0.0376	0.0676	0.0287	0.0276
	1	0.5	0.0150	0.0152	0.0118	0.0130
	1	0.5 + t	0.0238	0.0407	0.0185	0.0345
1,000	1 + t	0.5	0.0287	0.0287	0.0200	0.0229
	1 + t	0.5 + t	0.0419	0.0561	0.0295	0.0440
	(log2)2	$2\text{log}2\sqrt{0.01+t}$	0.0167	0.0226	0.0152	0.0139

Figure 1.

Curve fitting for β₁(t) and β₂(t) in different models. Top row: m(x, β) = β₁(t) + β₂(t)X, β₁(t) = 1 + t, β₂(t) = 0.5 + t. Bottom row: m(x, β) = e^−2X β₁(t) + e^−X β₂(t), β₁(t) = (log(2))², ${\beta }_2(t)=2\text{log}2\sqrt{0.01+t}$. True curve (’−’), median estimated curve (’−.’), and 90% pointwise confidence band (’−’). Sample size n = 300.

We also implemented the Wald test procedure, where the interest is in testing whether the slope function in the linear models or the coefficient function of e^−X in the nonlinear model β₂(t) is the zero function. To test the level precision, we let β₁(t) = 1 and 1 + t for the linear models, and generated the data from S(t|X_i) = exp {te^2X_i/log(1 − τ)} for the nonlinear model. We considered the levels 0.01, 0.05 and 0.1. The results for various sample sizes are given in Table 2. They indicate that the test levels are close to the nominal values when the sample size is n = 300 for the linear models, while they generally perform well even for smaller sample sizes for the nonlinear model. We point out that, because of the nature of the model, the residual life at t practically relies only on the observations that are both uncensored and still surviving at t; the sample size n = 200, for instance, only yields an effective sample size of about 100 in our simulation set up. Thus it is not a surprise to see this kind of level performance. To demonstrate the local power of the test, in the linear models we kept the same β₁(t) with ${\beta }_2(t)=c/\sqrt{n}$ and $c(1+t)/\sqrt{n}$ for c = 5, 10. For the nonlinear model, we set β₁(t) = {clog(1 − τ)}²/n, ${\beta }_2(t)=-2c\text{log}(1-\tau )\sqrt{(t+a)/n}$ for c = 40 and a = 0.01. and generated data from $S(t|X_i)=\text{exp}\{-e^{X_i}\sqrt{n}/c(\sqrt{t+a}-\sqrt{a})\}$. The local power results for various sample sizes are given in Table 3. One notices that the power does not necessarily increase as the sample size increases. This is because we are performing a local test where the local alternative is at a root n distance from the null, while the typical convergence rate of β(t) is slower than root n. We view the results in Table 3 as a worst case scenario of the power result.

Table 2.

Level precision of the Wald tests for H₀ : β₂(t) = 0, H₁ : β₂(t) ≠ 0.

	n	0.01	0.05	0.1
		linear model
	100	0.1170	0.2350	0.3050
β1(t) = 1	200	0.0650	0.1610	0.2270
	300	0.0090	0.0500	0.1050
	100	0.0590	0.1230	0.1790
β1(t) = 1 + t	200	0.0460	0.1120	0.1580
	300	0.0150	0.0550	0.0940
		nonlinear model
	100	0.0240	0.0490	0.0800
β1(t) = {log(1 − τ)}2	200	0.0260	0.0590	0.0960
	300	0.0160	0.0520	0.0900

Table 3.

Power of the Wald tests for H₀ : β₂(t) = 0, H₁ : β₂(t) ≠ 0.

	n	0.01	0.05	0.1
			${\beta }_2(t)=5/\sqrt{n}$
	100	0.8640	0.9390	0.9650
β1(t) = 1	200	0.5470	0.7240	0.7980
	300	0.2840	0.5110	0.6270
			${\beta }_2(t)=5(1+t)/\sqrt{n}$
	100	0.9660	0.9920	0.9970
β1(t) = 1	200	0.7470	0.8480	0.8920
	300	0.4900	0.7050	0.7850
			${\beta }_2(t)=5/\sqrt{n}$
	100	0.3510	0.5680	0.6760
β1(t) = 1 + t	200	0.2530	0.4450	0.5750
	300	0.1140	0.2610	0.3830
			${\beta }_2(t)=5(1+t)/\sqrt{n}$
	100	0.4000	0.6160	0.7170
β1(t) = 1 + t	200	0.2970	0.4850	0.6010
	300	0.1290	0.2790	0.3820
			${\beta }_2(t)=10/\sqrt{n}$
	100	0.7700	0.8590	0.8940
β1(t) = 1 + t	200	0.7240	0.8530	0.8850
	300	0.5900	0.7410	0.8090
			${\beta }_2(t)=10(1+t)/\sqrt{n}$
	100	0.8330	0.9070	0.9340
β1(t) = 1 + t	200	0.7520	0.8560	0.9050
	300	0.6000	0.7480	0.8100
			${\beta }_2(t)=-80\text{log}(1-\tau )\sqrt{(t+0.01)/n}$
	100	0.7470	0.8140	0.8340
β1(t) = {40log(1 − τ)}2/n	200	0.6600	0.8230	0.8820
	300	0.4080	0.5830	0.6930

5.2. Application: MELAS study

For illustrative purpose, we applied Model (2.1) to part of the data from the aforementioned MELAS study, consisting of 135 MELAS mutation carriers followed up over the past 10 years (Kaufmann et al. (2009)). We chose the disease onset as the time when the patient fails to perform the daily activities of healthy people. The Karnofsky score is common measurement for functional impairment, ranging from 0 to 100. A healthy subject should be scored at 100. We take T_i to be first year that the ith patient’s Karnofsky score is at 90 or lower. About 30% patients are censored since they are still neurologically fully functional at the end of the study. The researchers found that male patients tend to have earlier disease onset. It is of clinical interest to confirm whether MELAS affects male and female patients differently in terms of residual life time. Using gender of a patient as a predictor, we applied a varying coefficient linear median residual life model.

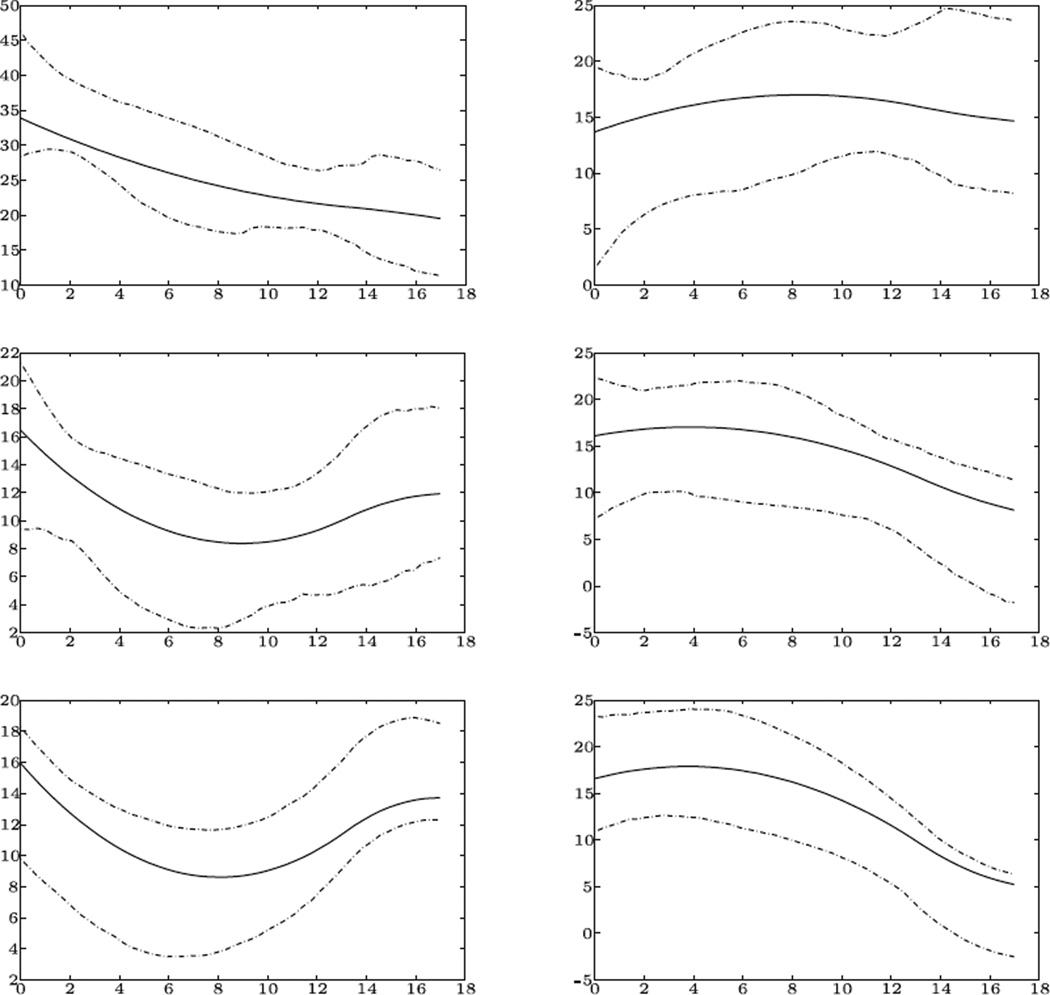
The estimation of the constant coefficient function β₁(t) and the time varying gender effect β₂(t), along with their upper and lower 5% quantile bootstrap confidence bands are given in Figure 2. Specifically, β₁(t) depicts the median residual life time to disease onset of male MELAS patients at various ages. For example, at birth, the median time to disease onset of a male MELAS patient is about 34 years, while at year 16, the median residual time is about 20 years. Here β₂(t) describes the difference in median residual time between male and female patients, with confidence bands largely situated above the zero level. Indeed, a formal testing procedure using the method developed in Section 4, yields a p-value 2.35e⁻⁷ that strongly suggests a gender difference. In Particular, the female residual survival is superior to that of the male, with the median residual time of female patients about 15 years longer than that of male patients. Such a difference slightly increases after birth, and decreases again after age 8.

Figure 2.

Estimated time varying intercept function (left) and slope function (right), and their confidence bands (upper and lower 10% quantile) in MELAS study for median (upper), lower quartile (middle) and 10% quantile (lower) residual life time.

We also estimated the male and female residual life time at the 0.25 and 0.1 quantile levels. As with the median, the female has later disease onset time at each age. For example, given that a patient survived to age 4, a female’s residual life is 17 years longer than that of a male, with probability 0.9. This is the age at which the female 10% residual life advantage is the largest. This advantage slowly declines when the patient continues to survive. At age 16, 90% of the surviving females have at least 6 years advantage over males, and 75% of them have at least 11 years advantage. The plots of the 25% and 10% residual life and their corresponding confidence intervals are also in Figure 2. Similar to the median, a test on no gender differences at these two quantile levels yield p-values of 3.94e⁻⁴ and 0.0255 respectively, hence it is quite clear that a female has superior residual survival time at these two quantile levels as well.

One may notice from Figure 2 that, at the 80% confidence level, some confidence bands contain a constant curve. In other words, one might adopt a constant coefficient assumption to model the residual life in those cases. This is a rather typical trade-off between the model complexity and flexibility – whether or not to use a constant coefficient model here depending on how comfortable one feels to make this simplification at a 80% confidence level. One also needs to note that a constant coefficient model may be sufficient at one τ, but may not be so for other τ values. Our methods can help in the decision of whether or not to adopt a constant coefficient assumption.

6. Discussion

We have proposed a time-varying coefficient residual life quantile model. This model allows one to simultaneously model the residual life at different times, yet still ensure the self coherence of the model. Compared to modeling the survival time directly, it allows more flexibility and enables one to describe the residual life directly. We proposed a practically feasible estimation procedure using the spline representation to approximate the time-varying coefficient function, and demonstrated its validity through asymptotic properties. We emphasize here that slightly more complex, yet still feasible, estimation procedures based on quadratic inference functions (Qu, Lindsay, and Li (2000)) can be used to improve the efficiency of the unweighted estimation procedure. We further proposed inference procedures to test the covariate effect. We applied both the estimation and testing procedures in simulations studies as well as to MELAS data.

We have not included the special case where some coefficient might be fixed instead of varying with time. It is easy to see that this can be handled by restricting the spline approximation to the time varying coefficient functions that include the fixed unknown parameter in the set of α’s. The developed inference tools can be used to determine whether a certain coefficient indeed varies with time. Specifically, we can reparameterize to a coefficient function ${\beta }_j(t)=c_0+{\beta }_j^{*}(t)$, where ${\beta }_j^{*}(0)=0$, and proceed to test ${\beta }_j^{*}(t)=0$. As in Jung, Jeong, and Bandos (2009) we have assumed the censoring process to be independent of the covariates X, a reasonable assumption for MELAS data. If, however, this assumption is violated, we only need replace the Kaplan-Meier estimator of the censoring survival function with a suitable local Keplan-Meier estimator for G(t|x). For example, we can use

$$Ĝ(t|x)=\prod _{i=1}^n{[1-\frac{K\{(x_i-x)/h\}}{{\sum }_{j=1}^{n}I(Y_j\ge Y_i)K\{(x_j-x)/h\}}]}^{I(Y_i\le t,{\delta }_i=0)}$$

to replace Ĝ(t), where K is a kernel function and h is a bandwidth, and keep all the remaining procedures unchanged. In the simulation, we used quadratic spline basis functions with a fixed number of knots. If this is not sufficient and more sophisticated spline smoothing techniques, for example the P-spline or the regression spline, are needed, one can use smoothing parameter selection techniques on the pseudo observations (t_j, β̂_j), j = 1, …, J. Because the β̂_j’s are estimated at a root-n rate, while the spline smoothing rate is slower than that, the consistency of the estimated coefficient functions is preserved without any special treatment of the β̂_j’s. Finally, instead of splines, other basis functions, such as wavelets or a Fourier basis, can be implemented. A kernel based approach can also be explored, but research in these areas is clearly beyond the scope of this paper.