CA3 Retrieves Coherent Representations from Degraded Input: Direct Evidence for CA3 Pattern Completion and Dentate Gyrus Pattern Separation

Summary

Theories of associative memory suggest that successful memory storage and recall depends on a balance between two complementary processes: pattern separation (to minimize interference) and pattern completion (to retrieve a memory when presented with partial or degraded input cues). Putative attractor circuitry in the hippocampal CA3 region is thought to be the final arbiter between these two processes. Here we present the first direct, quantitative evidence that CA3 produces an output pattern closer to the originally stored representation than its degraded input patterns from the dentate gyrus (DG). We simultaneously recorded activity from CA3 and DG of behaving rats when local and global reference frames were placed in conflict. CA3 showed a coherent population response to the conflict (pattern completion), even though its DG inputs were severely disrupted (pattern separation). The results thus confirm the hallmark predictions of a longstanding computational model of hippocampal memory processing.

Introduction

The hippocampus is crucial for spatial, contextual, and episodic memory (Eichenbaum, 2004; O'Keefe and Nadel, 1978; Squire et al., 2004), but the precise computations performed by the hippocampus in support of these functions are unknown. It is thought that the hippocampus integrates external sensory information from the lateral entorhinal cortex (LEC) with self-motion-based spatial information from the medial entorhinal cortex (MEC) to create context-specific representations necessary for the recall of individual events (Knierim et al., 2006; Manns and Eichenbaum, 2006; Suzuki et al., 1997). A longstanding computational theory suggests that, to maximize the storage of information with minimal interference, associative networks such as the hippocampus perform two competing, yet complementary, processes (Guzowski et al., 2004; Hasselmo and Wyble, 1997; McClelland and Goddard, 1996; McNaughton and Morris, 1987; McNaughton and Nadel, 1990; O'Reilly and McClelland, 1994; Rolls and Treves, 1998). Pattern separation refers to the ability of the network to reduce the overlap between similar input patterns before they are stored, in order to reduce the probability of interference in memory recall. Pattern completion refers to the ability of the network to retrieve stored output patterns when presented with partial or degraded input patterns. In many models of the hippocampus, the dentate gyrus (DG) region is regarded as a preprocessing stage that performs pattern separation on entorhinal cortex inputs. In contrast, the extensive network of recurrent collaterals in CA3 may produce attractor dynamics that result in pattern completion (or generalization) when input representations are similar to stored memories (attractor basins), or pattern separation when input representations are more distinct (Guzowski et al., 2004; Rolls and Treves, 1998).

Previous studies have provided evidence consistent with the hypothesized roles of the DG and CA3 in pattern separation and pattern completion (for reviews, see Santoro, 2013; Yassa and Stark, 2011). However, a rigorous test of these functions requires measuring both the input and output representations of the brain structures, to test explicitly whether the outputs are more similar (pattern completion) or less similar (pattern separation) than the inputs. Previous investigations of CA3 and DG lacked critical information about the inputs, making it uncertain whether the putative pattern separation/completion was inherent to the region under investigation or merely a reflection of processing that already occurred upstream (e.g., Gilbert et al., 2001; Rolls and Kesner, 2006; Kesner et al., 2000; McHugh et al., 2007; Nakazawa et al., 2002; Lee et al., 2004). This uncertainty is magnified by the paucity of published studies on the nature of DG neural representations in freely moving animals. Other studies that investigated both input and output patterns worked under experimental conditions in which CA3 reflected pattern separation, precluding a test of its hypothesized pattern completion functions (Bakker et al., 2008; Leutgeb et al., 2007).

An experimental protocol utilizing local-global reference frame conflicts has been shown to result in CA3 neural responses that resemble pattern completion. Lee et al. (2004) showed that the population of CA3 cells responded to the local-global conflict more coherently than did the population of CA1 cells. In the present study, we recorded single-unit activity simultaneously from CA3 and DG in the same protocol to directly test whether the DG input patterns to CA3 were degraded in the cue-conflict environment (as predicted from pattern separation hypotheses) and whether the CA3 representation of the altered environment was more similar to the familiar environment, compared to its DG inputs. The results show that CA3 produced an output pattern closer to the originally stored representation than the degraded input patterns from the DG, providing the first direct, quantitative, neurophysiological evidence for pattern completion of severely degraded inputs in the DG-CA3 circuit.

Results

Single unit activity was recorded from the DG and CA3 of freely moving rats using multi-tetrode arrays (Fig. 1A, B). The CA3 tetrodes were localized to the pyramidal cell layer, primarily in the CA3a and CA3b regions. The DG tetrodes were localized in (or just external to) the granule cell layer (n = 33) or in the hilus (n = 23); none of the tetrode tips encroached upon the CA3c layer. As discussed at length in a paper that presented data from the same animals as those reported here (Neunuebel and Knierim, 2012), it is impossible to distinguish from histology alone whether any individual, extracellularly recorded unit is a mature granule cell; an adult-born, immature granule cell; or a cell in the hilus. The cells recorded here had properties that are consistent with previous publications of DG neural activity (Gothard et al., 2001; Jung and McNaughton, 1993; Leutgeb et al., 2007; Neunuebel and Knierim, 2012). Approximately half of the cells in our sample fired in multiple, irregularly spaced subfields as rats ran in a large, open field after the main experiment each day (Figure S1 & S2). This pattern of activity was ascribed to granule cells by Leutgeb and colleagues (2007) (subsequent work has suggested that such patterns may be preferentially associated with newborn granule cells or hilar cells; Alme et al., 2010; Neunuebel and Knierim, 2012). Other cells that were included in the analysis either fired at a low rate (< 1 Hz) with little spatial specificity or had a single place field in the open field. These cells were considered by Neunuebel and Knierim (2012) as likely candidates for mature granule cells. Because it is unknown whether the different firing profiles corresponded to different morphological cell types, we did not segregate different subtypes of DG cells in the primary analyses (but we confirmed the main results by analyzing different subclasses in the supplementary material).

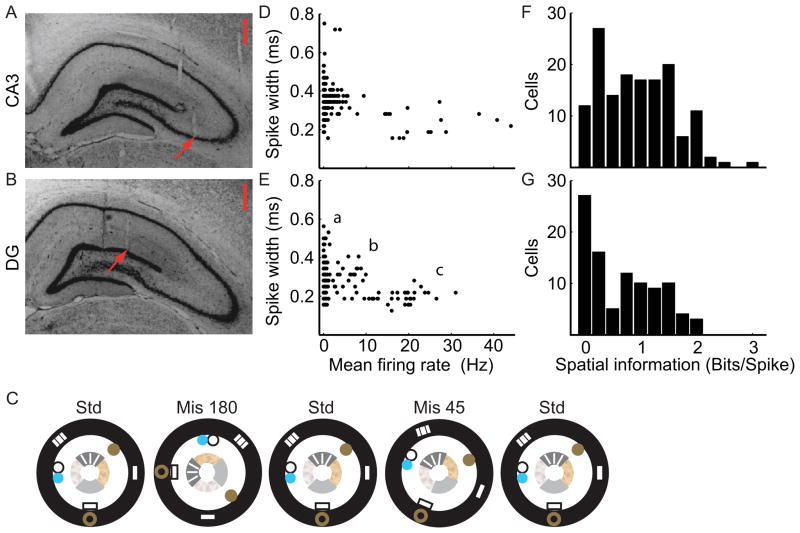
Figure 1.

Basic properties of CA3 and DG neural firing and experimental procedure. (A–B) Recording location examples show tetrodes targeting CA3 (A) and DG (B). Because the transverse axis of the hippocampus is angled relative to the midline, the DG tetrodes targeted sites medial and posterior to the regions sampled by CA3 tetrodes. Scale bar equals 500 μm and arrows indicate the end of the tetrode tracks. Other tracks are visible that ended in adjacent sections. (C) One day of the experimental protocol consisted of three standard sessions interleaved with two cue-mismatch sessions. The mismatch angles depicted are 180° and 45°. (D–E) Putative cell types from CA3 (D) and DG (E) were differentiated by the mean firing rates (Hz; abscissa) and spike widths (ms; ordinate) of all well-isolated cells recorded in the first standard session of the day. For CA3 cells, two distinct groups were observed (putative principal cells with a mean firing rate < 10 Hz and putative interneurons with a mean firing rate ≥10 Hz). Three groups of cells were apparent in DG: (a) < 2 Hz, (b) 2–10 Hz, and (c) > 10 Hz. (F–G) The distribution of spatial information scores (Skaggs et al., 1996) from CA3 (F) was significantly higher than for DG (G) (Mann-Whitney U-test, Z = 3.1, p < 0.03). See Figure S6 for the information score distribution of the DG neurons that fired < 2 Hz.

Rats ran clockwise (CW) around a track centered in a black-curtained, circular environment (Figure 1C). Four local cues tiled the surface of the track and six global cues were placed on or near the curtains (Knierim, 2002). The rats experienced a standard configuration of these cue sets for an average of 16 days before the experiments started. Recording sessions consisted of three standard sessions (Std) separated by two mismatch sessions (Mis), in which graded changes in sensory input were produced by rotating the global cues CW and the local cues counterclockwise (CCW) by the same amount, for net cue mismatches of 45°, 90°, 135°, and 180°. Over the course of 4 days, the rats experienced each mismatch amount twice. During the experiment, 399 CA3 units and 341 DG units were recorded during baseline sessions in which the rat sat quietly or slept in a towel-lined dish. These baseline sessions were used to judge stability of the recordings within a day. Subsets of these cells were active during any given behavioral session and were analyzed quantitatively.

During behavior on the track, the CA3 cells could be classified into putative principal cells and putative interneurons on the basis of firing rates and spike widths (Figure 1D), with putative principal cells having lower firing rates and wider spikes and putative interneurons having higher firing rates and narrower spikes. The DG units, on the other hand, segregated into three clusters of points (Figure 1E). Preliminary analysis of the data showed that some DG units fired at very low rates on the track, but the locations of these spikes were consistent across individual laps. The DG mossy fiber synapse onto CA3 is very large and it is conceivable that even these low-rate cells might exert a significant influence on the CA3 network response. Therefore, to include these very low-rate cells and to exclude the high-firing-rate putative interneurons, we restricted our analyses to cells with ≥20 spikes in a given session and a mean firing rate <10 Hz, respectively. We applied these criteria to both CA3 and DG to remain consistent between regions and to remain consistent with the criteria of our previous report on the entorhinal inputs to the DG and CA3 (Neunuebel et al., 2013), thus allowing direct comparison to those results. Approximately 37% of CA3 (146) and 28% of DG (96) units met these inclusion criteria during the first standard session of the day (although many additional cells met the inclusion criteria in later sessions of the day; Figure S1, S2, & S3). Figure 1F & 1G show that both CA3 and DG had a similar range of spatial information scores, although the median score of the CA3 neurons was greater than the DG neurons (CA3: median 0.9, IQR 0.4–1.4; DG: median 0.6, IQR 0.1–1.2; Mann–Whitney U test, z =3.1, p < 0.03).

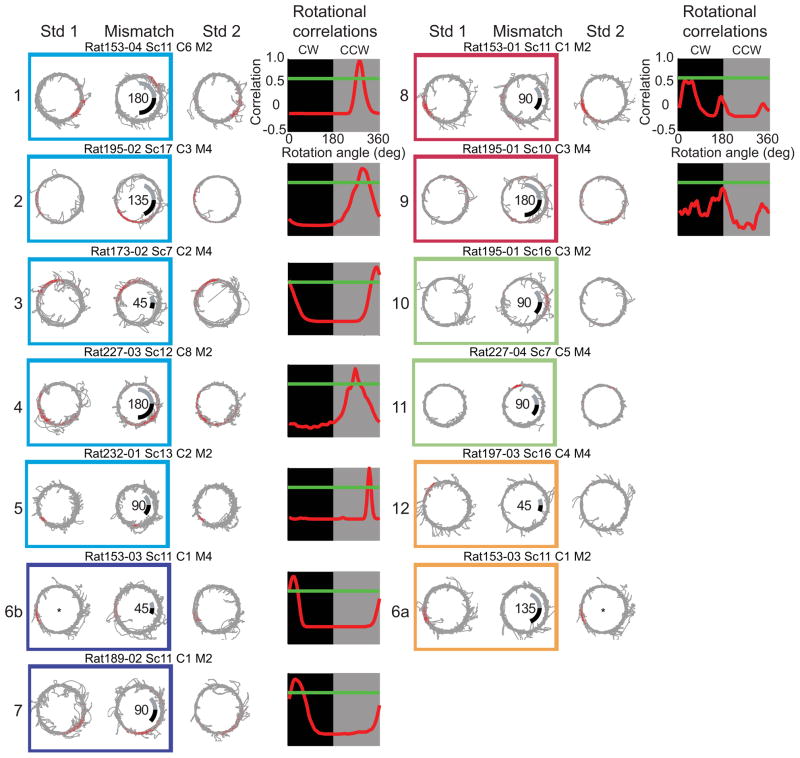
Similar to previously published reports of hippocampal subregions CA3 and CA1 (Lee et al., 2004) and their entorhinal inputs (Neunuebel et al., 2013), individual cells responded differently to the double rotation manipulation. Classification of cells into different response types leads to arbitrary distinctions in many cases, and therefore we did not perform statistical or quantitative analyses on these categories. We present them here to provide a useful description of the types of single-unit responses that underlie the quantitative, population analyses presented below. The firing fields of some cells rotated CCW with the local cues or CW with the global cues. This rotation was determined by correlating the Mis rate map with the Std 1 rate map at each of 72 rotational increments (each increment was 5°) and using the location of the peak correlation as an indicator of cue control. The peak correlation was required to exceed a threshold set at 0.6, which was a level that most reliably captured experienced observers’ evaluations of the similarity between two rate maps. Figure 2 shows examples of CA3 cells that were classified as CCW (cells 1–5) and CW (cells 6b & 7). Cell 1 had a firing field near the 4 o’clock position on the track in both standard sessions (Std 1 and Std 2). In the 180° cue-mismatch session, the firing field rotated CCW, which indicated local cue control. The maximum correlation occurred when the rate map was rotated 275° degrees CW (i.e., 85° CCW) and surpassed the 0.6 threshold (green line). Cells 2–5 are other examples of local-cue controlled cells. A smaller number of CA3 place fields were controlled by the global cues, rotating their firing fields CW (cells 6b and 7). In agreement with Lee et al. (2004), the local-cue-dominated firing fields (n = 101) far outnumbered the global-cue-dominated fields (n = 40).

Figure 2.

CA3 cellular responses. Example spike (red points) and trajectory (grey line) plots of CA3 cells. Values in the center of mismatch sessions indicate the total mismatch angle. The grey and black lines show the amount of the local and global cue rotations, respectively. Boxes enclosing rate maps from Std1 and Mis sessions indicate cells categorized as clockwise (navy blue), counterclockwise (cyan), appear (green), disappear (orange), or ambiguous (maroon). A plot of the rotation correlation analysis between the Std1 and Mis sessions (red line) is shown to the right of each set of rate maps. Peak correlations above 0.6 (green line) located in the black or grey box indicated that the fields rotated CW or CCW, respectively. Asterisks indicate that the standard sessions for cell were the same sessions.

A number of cells (n = 60) had place fields that met inclusion criteria in both the standard and mismatch sessions, but their responses were considered ambiguous (i.e., the peak rotational correlation was < 0.6). Many of these cells had fields that became more diffuse during the mismatch session (cells 8 & 9). For other cells, the activity criteria were reached in only one of the two sessions. Cells 10 and 11 are examples of strong fields (n = 64) that developed during the mismatch session despite firing only a few spikes in the standard session. Cells 6a and 12 are examples of fields (n = 64) that were present in the standard session but were silent in the mismatch session. Cell 6 is classified as disappear during the first mismatch session (labeled as 6a) and as CW for the second mismatch session (labeled 6b), showing that, as in prior reports (Knierim, 2002; Lee et al., 2004), the same cell could respond differently to the manipulation in different sessions. The appearance or disappearance of the fields was not an artifact of recording instability, since the tetrode cluster patterns were similar during baseline sessions recorded before and after the behavioral sessions, indicating that the same cells were present throughout the experiment.

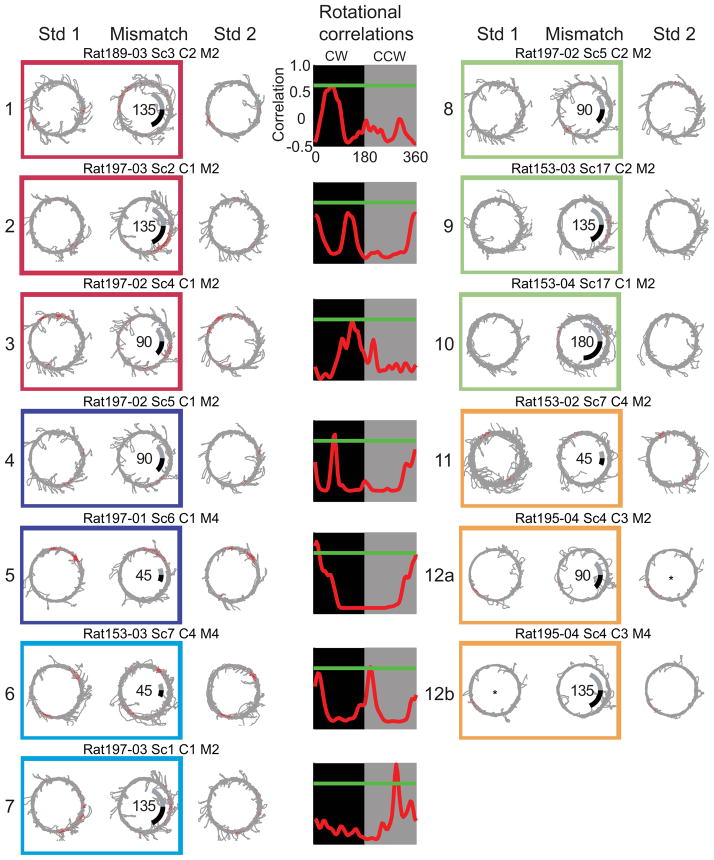
Examples of DG responses to the double rotation are shown in Figure 3. Similar to CA3, DG cells could also be classified as CCW, CW, ambiguous, appear, or disappear. Many of the DG cells fired in single or multiple locations on the track (Jung and McNaughton, 1993; Leutgeb et al., 2007; Neunuebel and Knierim, 2012) and fired consistently across the standard sessions. For example, cell 1 had two small fields (at 3 and 8 o’clock) in both standard sessions. During the 135° mismatch session, one field apparently rotated to the 10 o’clock position and stretched in length while the other field rotated to 6 o’clock while the size remained similar. Because the peak correlation was just below the threshold, the cell’s response was considered ambiguous, a classification consistent with the changes in field size that indicated that the response was not simply a rotation of the firing fields. Cells 2 and 3 are other examples of cells that met activity criteria in both sessions and could not be described as simple rotations (n = 49). Other cells had place fields that rotated either CW or CCW (cells 4–7), according to the > 0.6 rotational correlation threshold. Unlike CA3, there was not a large difference between the number of rate maps that rotated CCW (n = 36) or CW (n = 23). Similar to CA3, some of the cells were classified as appear (n = 49; e.g., cells 8–10) or disappear (n = 29; e.g., cells 11–12b).

Figure 3.

DG cellular responses. The figure format is identical to the CA3 cellular responses seen in figure 2. See also Figures S1 and S2.

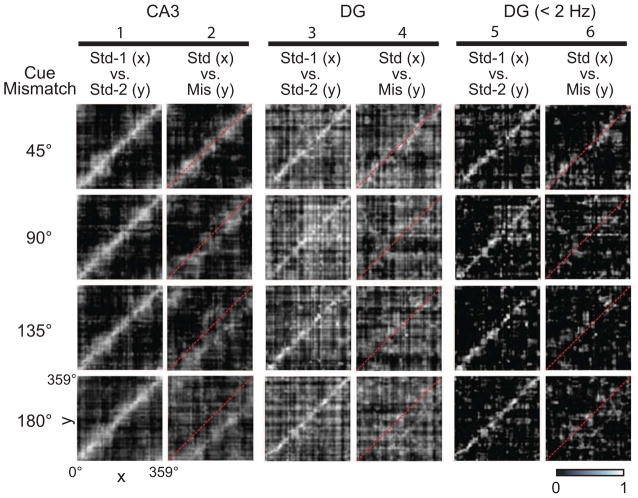
To analyze at the neural population level the differences between CA3 and DG in response to the double rotation manipulation, we created spatial correlation matrices from the population firing rate vectors at each location on the track (Figure S4) (Gothard et al., 2001; Lee et al., 2004; Neunuebel et al., 2013; Yoganarasimha et al., 2006). The mean firing rate of every cell in the sample (normalized to its peak rate) was calculated for each 1° bin of the circular track to create 360 firing rate vectors. The firing rate vectors of a standard session (Std 1) were correlated with the firing rate vectors from either the next mismatch session (Mis) or the next standard session (Std 2). The Std 1 vs. Std 2 correlation matrices for CA3 produced a band of high correlation on the main diagonal, showing that most CA3 cells fired at a similar location in both standard sessions (Fig. 4, column 1). In every mismatch session, CA3 maintained a band of highly correlated activity (Std 1 vs. Mis; Figure 4, column 2). This band shifted downward from the main diagonal (red line), indicating that the CA3 representation was controlled coherently by the local cues (see below for analyses demonstrating that the high correlation bands match precisely the angles of rotations of the local cues). However, the correlation structure degraded with increasing mismatch amounts, indicating that increasing cue-mismatches caused increasing changes to the CA3 representation (Lee et al., 2004).

Figure 4.

Population responses to cue-mismatch manipulations. Spatial correlation matrices were produced by correlating the normalized firing rate vectors for a standard session with those of the following mismatch or standard session (Figure S4). CA3 representations maintained coherence in all mismatch sessions (column 2), indicated by the bands of high correlation (white) shifting below the identity line (red dash), despite the decorrelated DG representations found in the input (columns 4 and 6). See also Figures S4, S5, and S6.

The critical question for the present study is (a) whether the coherence in the CA3 response was a reflection of an active pattern completion (or pattern generalization / error correction) computation performed by CA3 circuitry on degraded or corrupted input patterns, or (b) whether the coherence was merely a passive reflection of input patterns that were already coherent prior to CA3. To answer this question, we analyzed the input representations from the cells recorded from the DG in the same animals. In the Std 1 vs. Std 2 correlation matrix (Fig. 4, column 3), the DG showed a band of high correlation at the main diagonal, consistent with a reproducible pattern between standard cue configuration sessions (although the correlation matrices showed a noisier overall distribution compared to CA3; see below). In the critical Std 1 vs. Mis matrices, the DG showed only weak evidence of a high-correlation band (Fig. 4, column 4), consistent with the computational models that propose a pattern separation function for the DG. These results demonstrate that the CA3 representation remains stable in the presence of a severely degraded input from DG, implying that CA3 can retrieve a previously stored pattern based on that degraded input.

The Std 1 vs. Std 2 matrices for the DG (Fig. 4, column 3) showed less coherence than their CA3 counterparts (Fig. 4, column 1) (i.e., in addition to the high correlations along the main diagonal of the DG Std 1 vs. Std 2 matrices, there were additional pixels with high correlations away from the main diagonal). This finding raises the question of whether the DG supported coherent spatial representations even in the standard sessions. The matrices used all of the putative principal cells with mean firing rates < 10 Hz. As shown in Figure 1D, the DG population shows three clusters of cells in the spike width vs. firing rate scatter plot: (a) a group of cells with very low rates (< 2 Hz) and a wide distribution of spike widths; (b) a group of cells with moderate firing rates (2–10 Hz) and medium spike widths; and (c) a group of cells with high firing rates (> 10 Hz) and narrow spike widths. The last group consisted of presumed interneurons that were dropped from the analysis. It is possible that the middle class of cells was not as spatially modulated as the low-rate cells, and inspection of the rate maps confirmed this suspicion for most (but not all) of these cells (Figures S1 and S2). We thus generated the correlation matrices based only on the low-rate cluster of cells (group a). These matrices showed a cleaner coherence band in the Std 1 vs. Std 2 matrices compared to the larger data set (Fig. 4, column 5), demonstrating that the low-rate cells had highly reproducible firing patterns in the standard sessions. Moreover, the Std 1 vs. Mis matrices still showed a strong lack of spatial coherence, especially in the mismatch sessions > 45° (Fig. 4, column 6). When we restricted analysis further to include only the cells that meet minimum spatial information criteria, the correlation matrix patterns were preserved (Figure S5). Because it is not known which of these cell classes are the principal neurons that project to CA3 (and therefore constitute the input pattern to that region), to be conservative, we continued to analyze the combined data from all cells with firing rates < 10 Hz (i.e., groups a and b in Fig. 1E; columns 3–4 of Fig. 4).

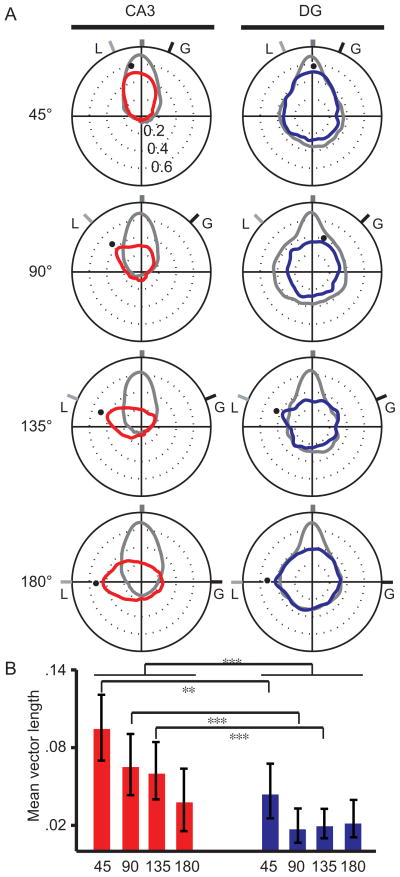
To statistically analyze the population responses, the mean correlations of pixels in each of the 360 diagonals of the correlation matrix were calculated and plotted in polar coordinates (Fig. 5). The stability of the CA3 representations was evidenced by the peak correlation that occurred near 0° for all Std 1 vs. Std 2 correlation matrices (gray polar plots). For all mismatch sessions (red plots), the peak correlations shifted CCW by approximately the same amount that the local cues were rotated. For DG, the peak correlations for the Std 1 vs. Std 2 comparison occurred near 0° (gray plots), indicating that the DG spatial representations were stable (see Figure S6 for the very low-rate [< 2 Hz] DG cells included in Fig. 4, columns 5–6, and Figure S5 for the polar plots of the cells that met the minimum spatial information criteria). The correlations between the standard and 45° mismatch sessions maintained a peak centered near 0° (blue plots), but the distributions became much more circular with the larger mismatch angles, indicating a lack of coherence. The maximum correlations for DG corresponded to either CW (45° and 90° mismatch) or CCW (135° and 180° mismatch) rotations, although a small peak was also evident at the local-cue predicted angle for the 90° mismatch.

Figure 5.

Quantifying input and output representations. (A) Polar plots were created from the spatial correlation matrices to represent the population activity between standard-1 vs. standard-2 (grey) and standard vs. mismatch (color) sessions. Each polar plot was created by calculating the average correlation along each diagonal of the corresponding correlation matrix to convert the 2D matrix into a 1D polar plot. The grey and black tick marks labeled “L” and “G” indicate the rotation angles of the local and global cue sets, respectively. The black dots indicate the angle at which the population correlations for the Std-Mis comparisons were maximum. For CA3, the maximum correlations closely followed the rotation of the local cues. (B) Mean vectors were calculated to quantify the coherence of the representations between sessions. Error bars represent the 95% confidence interval calculated with a bootstrap analysis. Collapsed across mismatch angles, CA3 had significantly larger mean vectors than its DG input. With respect to individual mismatch angles, the CA3 mean vectors were significantly larger than the DG mean vectors for the 45°. 90°, and 135° angles. ***, p < .001; **, p < .002.

The degree of coherence between the representations of the standard session and the mismatch session is reflected in the sharpness and unimodality of the polar plots. To compare the different brain regions, we calculated the mean vector for each Std-Mis polar plot (i.e., the mean of all vectors originating at the origin of the plot and ending at each data point on the plot) and used bootstrapping statistical methods (Efron and Tibshirani, 1991) to compare the length of the mean vector between the hippocampal subregions (see Experimental Procedures). Collapsed across the four mismatch angles, CA3 mean vectors were significantly greater than DG mean vectors (p < 0.001) (Fig. 5B). When comparing individual mismatch angles, the CA3 mean vectors were significantly greater than DG for the 45° (p < 0.002), 90° (p < 0.001), and 135° (p < 0.001) mismatch angles. The mean vectors were not significantly different for the 180° mismatch (p = 0.166), although inspection of the polar plots shows a much narrower tuning curve for CA3 than DG (see also Figures S5 and S6).

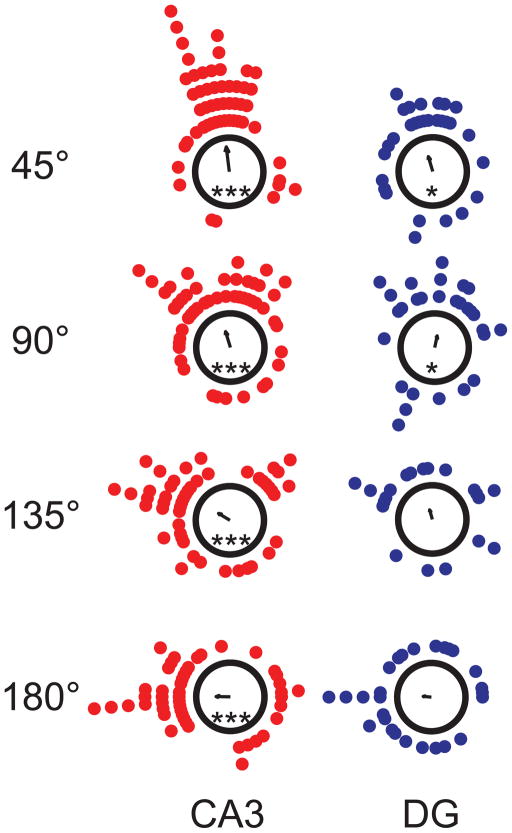
To determine if the patterns observed in the population were mirrored in the firing properties of single cells, we examined the coherence of control that the local and global cues had on individual units (Fig. 6). Cue control was determined by conducting a rotational analysis (see Experimental Procedures) on the subset of cells that met activity criteria in consecutive standard and mismatch sessions. The mean vector length for CA3 cells was significant for all mismatch angles (Rayleigh test, p < 0.001), indicating significant clustering of the cell responses. Furthermore, the direction of the mean vector in all mismatch sessions corresponded to a local cue rotation. DG responses were more variable and only the mean vectors of the smallest two mismatch angles were significant (Rayleigh test; 45° and 90°; p < 0.04). The angle of the mean vector corresponded to the direction of a local cue rotation for 3 of the 4 mismatch angles (45°, 135°, & 180°).

Figure 6.

Analysis of Individual Cell Rotation Amounts. Each dot indicates the amount that the cell’s spatial firing rotated between the standard and mismatch sessions (CA3, red; DG, blue). The arrows at the centers of the polar plots denote the mean vector. The mean vector length for CA3 cells was significant for all mismatch angles, whereas the mean vector length for the DG was variable (Rayleigh test; CA3, all angles, p < 0.001; DG, 45° and 90°, p < 0.04). CA3 followed the local cues for all mismatch angles and DG followed the local cues for 3 out of the 4 mismatch angles (45°, 135°, and 180°). ***, p < 0.001; *, p < 0.04.

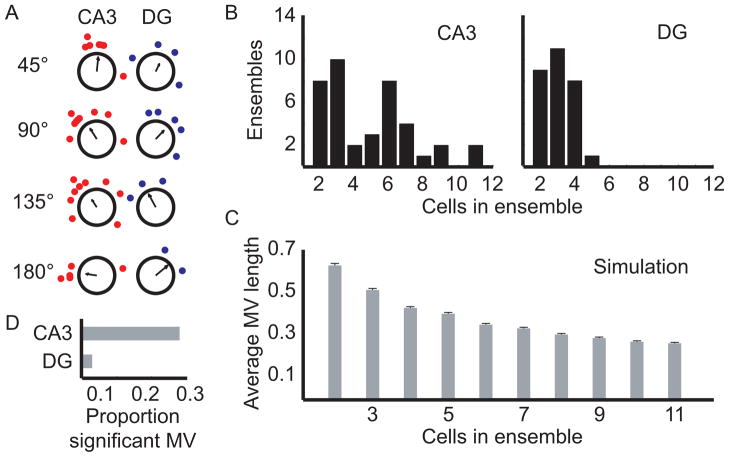
The preceding analyses pooled data that were recorded across many sessions and rats. Because this pooling may have combined heterogeneous patterns of responses across data sets, it is important to know whether these results hold up at the level of individual data sets with simultaneously recorded neurons (Lee et al., 2004). Due to the sparse firing in DG, there were limited data sets with large ensembles of active cells in both CA3 and DG. Thus, we examined data sets with ≥2 simultaneously recorded cells from CA3 or ≥2 simultaneously recorded cells from DG, in which all cells met activity criteria in both the standard and the mismatch sessions (examples of simultaneous recordings for each area and mismatch angle are shown in Fig. 7A). On average, there were more cells recorded simultaneously in CA3 than in DG (Figure 7B). Because the size of the mean vector is dependent on the number of cells in the ensemble, we were unable to perform a simple comparison of the average lengths of the mean vectors between the regions. To illustrate the problem, Figure 7C shows the results of a simulation in which the mean vectors of ensembles of increasing size were calculated for angles randomly distributed around a circle. As the ensemble size increased, the magnitude of the mean vector decreased, even though the data were randomly distributed in all cases. Thus, a positive result may occur by chance due to unequal average ensemble sizes. To circumvent this problem, rather than comparing the magnitude of the mean vector itself, we compared the proportion of data sets in each region that were significantly clustered (Fig. 7D). Significant clustering of a data set was determined by comparing the mean vector length of a sample with the randomized data produced for a sample of identical size. If the vector length from the data was greater than 95% of the vectors from the randomized data (Fig. 7C), the vector length was considered significant. CA3 had a larger proportion of significantly clustered data sets than its DG input (CA3 [11/40], DG [1/29]; χ²(1) = 6.77, p < 0.01). When we restricted the analysis to the subset of data in which 2 or more cells were recorded simultaneously from CA3 together with 2 or more cells recorded simultaneously from DG, the proportions were almost identical, although the smaller number of data sets reduced the statistical significance to a trend (CA3[5/19], DG[1/23]; χ²(1) = 3.05, p = 0.08). These results provide strong evidence that simultaneously recorded CA3 cells respond more cohesively than the input from DG.

Figure 7.

Ensemble coherence. (A) Examples of simultaneous recordings from each region. Data within a circular plot were recorded simultaneously, but different plots come from different data sets. (B) Histograms show the number of cells in each simultaneously recorded data set for the four regions. On average, CA3 had more cells per data set than DG. (C) Simulations showed that small sample sizes could artificially increase the size of the mean vector. Data points (i.e., rotation angles) were randomly selected with replacement from a uniform distribution of orientations (1–360°) to calculate the expected value of the mean vector based on the samples coming from a random distribution. Simulations were run 1000 times for each of 10 sample sizes (n = 2–11 samples) and the average length of all 1000 mean vectors (average MV length) was plotted as a function of sample size. The mean vector length was largest for ensembles with two cells and decreased nonlinearly as the sample size increased. To account for the effect of sample size on the real data, the mean vector length of an ensemble was considered significant at α = 0.05 when it was greater than 950 of the 1000 mean vector lengths from the simulated data run with an equal number of cells in the sample. Error bars show SEM. (D) The proportion of significant mean vector lengths for each region. CA3 showed more significant clustering than its DG input (CA3 [11/40], DG [1/29]; χ² (1) = 6.77, p < 0.01).

Discussion

One of the key goals of systems and cognitive neuroscience is to understand the transformations of neural representations, and the rules governing these transformations, as information is processed from one stage of a circuit to another stage. This goal is aided by theoretical and computational studies that make explicit predictions about the different processing stages. One of the best known and oldest computational theories of neural information processing postulates that the DG region of the hippocampus performs a pattern separation process on its input from the EC, whereas attractor circuitry in the downstream CA3 region can perform pattern separation or pattern completion based on the relative strengths of the embedded attractors and the exact nature of the external inputs from the EC and DG regions (Marr, 1971; McNaughton and Morris, 1987; McNaughton and Nadel, 1990; Rolls and Treves, 1998). Numerous studies have shown evidence consistent with a pattern separation function in both DG and CA3 and a pattern completion function in CA3 (e.g., Gilbert et al., 2001; Rolls and Kesner, 2006; Kesner et al., 2000; McHugh et al., 2007; Nakazawa et al., 2002; Lee et al., 2004; for review see Yassa and Stark, 2011). However, most of the evidence in these studies was indirect, as the studies typically measured the output of the region without measuring the input representations, or they used behavioral tasks to try to assess the underlying neural representations. Because pattern separation and pattern completion, by definition, require knowledge of the transformation of an input representation to an output representation (Guzowski et al., 2004; McClelland and Goddard, 1996; O'Reilly and McClelland, 1994; Santoro, 2013), it is impossible to know whether the output reflects an operation intrinsic to a particular brain region without knowledge of the properties of the inputs to that region. In conjunction with previously published data (Neunuebel et al., 2013) on the EC representations under the same manipulation, the present study provides direct evidence that the DG performs a pattern separation operation on its EC inputs and that CA3 performs a pattern completion operation on its DG and EC inputs.

Neunuebel et al. (2013) demonstrated that cells from the superficial layers of MEC (the layers that project to the hippocampus) were predominantly controlled by the global cues. Cells from the superficial layers of LEC, in contrast, showed a weak spatial representation, as expected, but there was a detectable signal at the population level that was controlled by the local cues. The LEC and the MEC are the primary inputs to the DG; therefore, the strong loss of coherence of the DG cells in the current experiment, given the coherent response of the MEC input, is a strong indication of a pattern separation function of the DG. In contrast, the data from CA3 provide the strongest neurophysiological evidence to date of a pattern completion (error correction) function in this region. The CA3 response was controlled more strongly by the local cues on the track, in agreement with a prior study using the same protocol (Lee et al., 2004). Because the MEC cells were controlled predominately by the global cues, consistent with their relationship to the global-cue dominated head direction cell system (Hargreaves et al., 2007; Sargolini et al., 2006; Yoganarasimha et al., 2006; Zugaro et al., 2001), the MEC input could not have simply driven the local-cue-dominated CA3 response (although a weak subset of MEC cells that were local-cue driven might have contributed). The LEC response, although controlled by local cues, was spatially very weak, and thus seemingly incapable of solely driving the strong spatial response patterns of CA3. The DG response was inconsistent and clearly less correlated than the CA3 response. Thus, these data provide conclusive evidence that the CA3 representations of the standard and altered environments were more correlated with each other than any of the input representations were correlated with each other, fulfilling the classic, computational definition of pattern completion.

This work bears some resemblance to the study of Gothard and colleagues (Gothard et al., 2001), who recorded DG and CA1 on a track that was parametrically changed in length by sliding a start box along the track on each trial. As the rat ran on the track, both the DG and CA1 representations switched abruptly from a reference frame defined by the start box to a global reference frame defined by the room. There was no evidence, however, of pattern separation occurring in that experiment. The experiment that most closely resembles the current work is a study by Leutgeb and colleagues (Leutgeb et al., 2007), who recorded from the DG and CA3 regions during manipulations in which they gradually morphed the geometry of a recording enclosure from a square to a circle. Both the Leutgeb study and the present study investigated how DG and CA3 representations recorded from the same animals changed as the result of parametric changes to the environment. Leutgeb et al. (2007) showed that DG neurons gradually changed their firing fields in response to the increasing changes in the geometry. Importantly, the authors also recorded from 3 units in the molecular layer of the DG that were grid cells; because the molecular layer is the site of synaptic connect between MEC and DG, the authors inferred that these units were probably axons of MEC grid cells. The firing fields of these grid cells did not change appreciably in response to the morphing manipulation. Thus, these data showed clear evidence that the DG representation changed more than its putative MEC input. It is not known how this manipulation affected the LEC inputs. Nonetheless, as it is unlikely that the LEC provides a strong spatial signal to the DG, these data show pattern separation in DG (although not of the classic “expansion recoding” type; Marr, 1969; McNaughton and Nadel, 1990).

Interestingly, the pattern separation in the Leutgeb et al. (2007) study appeared fairly linear, as the population vector changed gradually with increasing amounts of change to the environment. This result is in sharp contrast to the nonlinear effects in the present data, in which the DG population remained coherent in the 45° mismatch session and then abruptly became highly noncoherent in the larger mismatch sessions (especially evident in Figures S5 and S6). In the Leutgeb study, the CA3 population responses also changed gradually with the increasing morphing of the geometry, suggesting that this apparent pattern separation in CA3 was primarily driven by the upstream pattern separation performed by the DG, and not a reflection of any active computational processing of CA3 itself. Although Leutgeb et al. ( 2007) suggested tentatively that the slightly greater correlation between CA3 representations of small changes to the environment geometry, compared to DG representations, may reflect a pattern completion process, it is just as likely that these greater correlations were the result of CA3 receiving highly correlated patterns of activity directly from the MEC, rather than pattern-completing the slightly altered DG representations. The present study, on the other hand, in conjunction with the EC data from Neunuebel et al. (2013), provides clear and convincing evidence that CA3 does indeed perform a pattern completion function (as defined computationally) on degraded input from DG and EC. Thus, the present study is a critical complement to the Leutgeb study, as well as other studies from those investigators (Leutgeb et al., 2004; Leutgeb et al., 2005). Under certain conditions, CA3 representations are completely orthogonal in different environments, which may reflect a pattern separation function imposed by the DG as well as attractor dynamics in CA3. However, under other conditions, CA3 performs the long-hypothesized pattern completion/error correction functions long attributed to its recurrent collateral circuitry, conclusively demonstrated in the present study.

An important question arising from these results is why the pattern-completed CA3 representation follows the weak local cue signal provided by the LEC input, rather than the strong global cue signal provided by the MEC input. When grid cells were discovered in MEC (Hafting et al., 2005) and poor spatial selectivity was shown in LEC (Hargreaves et al., 2005), it was assumed by many investigators that grid cells were the primary spatial drive onto place cells (e.g., Hafting et al., 2005; McNaughton et al., 2006; Monaco and Abbott, 2011; Savelli and Knierim, 2010; Solstad et al., 2006; but see Burgess et al., 2007; Kropff and Treves, 2008; O'Keefe and Burgess, 2005). More recent data have shown that this simple model is at best incomplete, as (a) major disruption of grid cells can leave a significant amount of spatial tuning intact in place cells (Brandon et al., 2011); (b) during development, adult-like place field firing patterns appear before well-formed grid-cell firing patterns (Langston et al., 2010; Wills et al., 2010); (c) cue-card manipulations in a cylindrical environment can cause discordant responses of grid cells and place cells (Song et al., 2012); and (d) inactivation of hippocampal place cells can cause the loss of gridness in MEC cells (Bonnevie et al., 2013). Neunuebel et al. (2013) proposed one model of how the LEC inputs may cause the CA3 attractor to form at the local-cue predicted location based on a speculation that the rats pay attention first to the local cues when they are placed on the track. Another possible explanation is related to the different subtypes of cells in the DG. Immature, adult-born granule cells are hyperexcitable and hyperplastic (Ge et al., 2007), and these cells may dominate the responses of the DG (Alme et al., 2010; Neunuebel and Knierim, 2012). A recent study has shown that immature granule cells receive input preferentially from the LEC than from the MEC (Vivar et al., 2012). If these cells are the dominant drive onto the CA3 population, at least when the rat initially enters an environment, then they may override the input from the MEC cells. Simulations show that only a small bias input is required to cause an attractor bump to form at a particular location (Zhang, 1996), and it is possible that the bias caused by LEC-driven, highly active immature neurons may drive the CA3 response by seeding the recurrent collateral circuitry of CA3 to form the CA3 activity bump at locations corresponding to the local cues. Different physiologically defined DG cell types have different spatial firing profiles (Neunuebel and Knierim, 2012), but it is not known how these profiles map onto specific, morphologically defined cell types (e.g., developmentally born granule cells, adult-born mature granule cells, adult-born immature granule cells, hilar cells, interneurons, etc.). Understanding this mapping will be necessary to further understand the computations of the DG and how they influence the downstream, putative attractor circuitry in CA3.

Experimental Procedures

Subjects and Surgery

Seven male, Long-Evans rats (Charles River Laboratories) were individually housed with ad libitum access to food and water during a 12-hour light/dark circadian cycle (lights off at noon). When rats were ~5–6 months old and had been habituated for ~14 days, a custom-built recording drive that contained 18 independently moveable tetrodes and 2 references was surgically implanted in the right hemisphere. The drives were positioned such that the most anterior-lateral tetrodes (n = 5) targeted CA3a and the most posterior-medial tetrodes (n = 13) targeted the DG. To optimize drive placement, recordings were performed during surgery to find the lateral edge of CA3, which served as a landmark for the medial/lateral placement the drives; the most lateral tetrode ranged from 3.2–4.9 mm lateral to bregma and 3.2–4.4 mm posterior to bregma. The Institutional Animal Care and Use Committees at John Hopkins University and the University of Texas Health Science Center at Houston approved surgical protocols, which were performed under aseptic conditions and complied with standards from the National Institutes of Health.

Training and Recording

Prior to surgery, rats were familiarized daily to human contact and sleeping in a small dish (~ 25.4 cm) located on a pedestal (each lasting 30 minutes/day over a two week period). Rats recovered from the surgical procedure for 5–7 days and then their body weight was reduced to 80–90% of the free-feeding weight. After a daily session of advancing tetrodes, rats were trained in a cue-controlled environment to run laps around a circular track (outside and inside diameters of the track were 76 cm and 56 cm, respectively) for an average of 16 days. The track, which was centered in a black-curtained enclosure with six salient cues located at the periphery, was divided into four 90° segments that were textured with different materials (Knierim, 2002). During the initial training sessions, chocolate sprinkles were dispersed around the track and rats gradually learned to continuously navigate CW for the reward. A cardboard panel was placed in front of any rats attempting to move CCW. As behavior progressively improved, the reward was eventually reduced to one to two random locations per lap.

The double rotation experiments were conducted for 4 days. Two baseline sessions (BL1 lasting 1 hour and BL2 lasting 30 minutes), which were separated by two hours as the rat was returned to its home cage, were recorded prior to the start of the experiment. The baseline sessions consisted of periods when the rat slept or was resting quietly in its holding dish. During behavior, rats ran five track sessions. Track sessions consisted of three standard sessions (Std: local and global cue relationship remained constant) interleaved with two mismatch sessions (Mis: local and global cues were rotated by equal increments, but in opposite directions, producing mismatch angles of 45°, 90°, 135°, or 180°). For example, a 180° mismatch represents a 90° CCW local cue rotation plus a 90° CW global cue rotation. Mismatch angles were chosen in pseudorandom order such that each angle was chosen once during the first 2 days of recording and once again during the second two days. After the fifth session of the day, the cells were recorded as the rats foraged in an open field (135 x 135 cm) surrounded by white wooden walls (30 cm high) in the room that housed the recording equipment and where the baseline sessions were recorded. All experiments concluded with a 30-minute baseline session.

Electrophysiological Recordings

A Cheetah Data Acquisition System (Neuralynx, Bozeman, MT) concurrently obtained up to 72 channels (18 tetrodes) of single-unit data and 21 channels of local field potential (LFP) activity. Neural signals were detected simultaneously on four fine microwire electrodes (gold-plated nichrome [12 μm] or unplated platinum-iridium [17 μm]) that were wound together to form a tetrode. The signals were amplified 1,000 – 5,000 times and filtered between 0.6 and 6 KHz (for units) or 1 Hz and 300 Hz (for LFP). The spike waveforms above a threshold of 30–70 μV were sampled for 1 ms at 32 kHz, whereas LFPs were continuously sampled at 1 kHz. The rat’s position was tracked with an overhead camera recording a circular array of light emitting diodes (red and blue) positioned over the head of the rat and a 13 cm extension behind the head with additional diodes (green) at 30 Hz.

Tetrodes were independently advanced by small increments every day for approximately three weeks. After entering the CA1 layer, tetrodes were advanced at ~40–148 μm (the larger movements occurred after leaving CA1) each day for an additional 300 μm. For tetrodes targeting DG, advancement was significantly reduced to 10–20 μm per day once gamma activity and dentate spikes in the LFP were detected (Bragin et al., 1995a,b). A tetrode was no longer advanced after it detected well-isolated units that fired during behavior. Tetrodes that did not show active cells during behavior (even though they may have had active cells during the quiet baseline sessions) were advanced by 10 μm. This procedure continued until at least five putative DG cells that fired during behavior were present on any combination of tetrodes. For tetrodes targeting CA3, tetrodes were advanced daily by ~50 μm in an attempt to enter the CA3 layer at the same time that DG units were detecting cells. No attempt was made to track cells through the experiment; therefore, some of the same units may have been recorded over multiple days. However, our primary analyses of individual ensembles do not depend on the number of cells; moreover, because the data are analyzed separately for different mismatch amounts, any unit is counted at most twice.

Unit Isolation

Multiple waveform characteristics (i.e., spike amplitude peak, area under the waveform, and valley depth) recorded simultaneously on the four wires of a tetrode were used to isolate single-units offline with a custom, interactive software program. A cell’s isolation quality was rated on a subjective scale from 1 (very good) to 5 (poor) depending on the distance each cluster was separated from other clusters and from background noise. Cluster isolation was judged prior to examining any of the behavioral firing correlates of the cells. All cells rated as fair or better (categories 1, 2, and 3) were potentially included in all analyses.

Data Analysis

Analysis was performed on data restricted to times when the animal’s head was within the boundaries of the track and traveling with a velocity greater than 1 cm/s. The circular, two-dimensional data for each cell was transformed into a 1-D linear representation by converting the rat’s Cartesian position into units of degrees on the track and the mean firing rate for every degree of the track was calculated. A gaussian smoothing algorithm (σ = 5.34°) was applied to the linearized firing rate maps.

Population correlation matrices were created by forming normalized firing rate vectors for the sample of cells at each 1° bin of the track and correlating these vectors with the vectors for every location in a comparison (Figure S4). A band of high correlation along one of the diagonals of this matrix indicates a high degree of coherence of the representation between the two sessions. The correlation matrix was reduced to 1-D polar plots by averaging the correlation values along each of the 360 diagonals of the matrix. Bootstrap procedures were used to estimate the 95% confidence intervals of the mean vectors of the polar correlation plots (Efron and Tibshirani, 1991). For each region and mismatch angle, the sample of cells was randomly resampled with replacement to generate a new sample of the same number of data points as the original. These data points were used to calculate 2D correlation matrices and polar plots, and the mean vector was calculated. The procedure was repeated 1000 times, and the 2.5^th and 97.5^th percentile values were taken as the limits of the 95% confidence interval. To test for statistical differences between CA3 and DG, we first looked at overall differences collapsed across mismatch angles based on the mean vectors from the bootstrapped samples as follows:

$${\text{MV}}_{\text{CA}3-\text{DG}}={\sum }_{\mathrm{i}}(\text{MV}{(\mathrm{i})}_{\text{CA}3}-\text{MV}{(\mathrm{i})}_{\text{DG}})$$

where MV is the mean vector, and i is a member of the set [45°,90°, 135°, and 180°]. The MV_CA3-DG was calculated each time for 1000 random resamplings with replacement of the original sample, and a p value was assigned as the number of times that the ΔMV_CA3-DG was < 0. For example, if MV_CA3-DG > 0 in all 1000 bootstraps, the p value associated with this was p≤0.001. To look at differences between brain regions for individual mismatch angles, we created bootstrapped distributions based on the difference in the MV for each particular mismatch angle and pair of brain regions.

The rotation angle and direction that each cell’s rate map rotated between consecutive standard and mismatch sessions was determined for every cell that met the inclusion criteria in both sessions. The linearized rate map in the standard session was correlated with the linearized rate map for the mismatch session. The mismatch session rate map was then shifted in increments of 5° and correlated with the standard session rate map at each increment. A cell’s rotation angle was assigned to the shift producing the maximum correlation.

Statistical test were calculated in Excel (Microsoft Corp.), Matlab (MathWorks), or Statistica (StatSoft, Inc.). Functions from the Matlab circular statistics toolbox were used to determine circular statistics. Every statistical analysis was two-tailed and considered significant at p < 0.05, unless a different significance level was indicated.

Histological Procedures

For a subset of tetrodes, 10 μA of positive current was passed for 10 seconds to generate lesions used to aid in identifying the location of the tetrodes during histological reconstruction. Lesions were made 0–10 days after finishing the double rotation experiments. The day after lesioning, rats were euthanized with formalin perfused through the heart. Two rats (227 and 232) were euthanized immediately after making the lesions. Brains were sliced (40 μm) in the coronal plane with a freezing microtome, mounted on microscope slides, and stained with Cresyl Violet. A Moticam 2000 camera (Motic Instruments Inc., Richmond, BC, Canada) or IC Capture DFK 41BU02 camera (The Imaging Source, Charlotte, NC, USA) attached to a Motic SMZ-168 stereoscope was used to image the brain slices. All tetrode tracks were identified and the lowest point of the track was used to determine the recording location. Recording tips that were located in or near the CA3a and CA3b pyramidal layers were assigned to CA3. Consistent with published examples from other groups (Jung and McNaughton, 1993; Leutgeb et al., 2007), tetrode tracks that terminated in the granule cells layer or at the interface between the granule cell layer and the polymorphic layer were considered (for descriptive purposes) to be located in the granule cell layer. Tetrode tracks that terminated below the granule layer but above the CA3 pyramidal layer were considered to be located in the hilus. As described in the results, the final histological location of the recording tips is not necessarily a valid indication of the identity of the recorded cells. However, all recordings assigned to the DG came from tetrodes that showed no indication of having encroached upon the CA3 pyramidal layer.