Summary
Protein molecules often undergo conformational changes. In order to get insights about the forces that drive such changes, it would be useful to have a method that computes the per-residue contributions to the conversion free energy. Here, we describe the “Confine-Convert-Release” (CCR) method, which is applicable to large conformational changes. We show that CCR correctly predicts the stable states of several “chameleon” sequences that have previously been challenging for molecular simulations. CCR can often discriminate better from worse predictions of native protein models in CASP. We show how the total conversion free energies can be parsed into per-residue free-energy components. Such parsing gives insights into which amino acids are most responsible for given transformations. For example, here we are able to “reverse-engineer” the known design principles of the chameleon proteins. This opens up the possibility for systematic improvements in structure-prediction scoring functions, in the design of protein conformational switches, and in interpreting protein mechanisms at the amino-acid level.
Introduction
It is often useful to know the relative stabilities of two different conformations A vs. B of a protein molecule. We call this the conversion free energy, ΔG = GB − GA. Also useful is to know the contributions to those stability differences that are made by the individual amino acids. Such a method could help address questions such as: (1) Which amino acids are most responsible for allosteric or conformational change from A to B? (2) Which amino acids most strongly determine the transition state in an enzyme mechanism? (3) If you have a computational model that mispredicts a target structure, which amino-acid sites are the biggest sources of prediction error? Knowledge of this type could be useful for refining protein-structure-prediction algorithms. (4) If you want to design a protein conformational switch, which amino acids are most controlling of the switching behavior? These applications could be advanced considerably by a computer method that begins with knowledge of the structures A and B, computes the conversion free energy, and then parses that free energy into approximate component free energies from individual amino acids or secondary structures.
To date, such a tool has not been available because: (a) such computations are quite expensive, (b) it is not clear that molecular simulation forcefields would be sufficiently accurate, and (c) because ‘per-residue’ free energy quantities are fraught with non-additivities (Dill, 1997; Mark and van Gunsteren, 1994). One widely explored strategy is to use molecular dynamics simulations along some putative reaction coordinate pathway from conformation A to B (Cheng et al., 2006; Chipot et al., 2007; Dellago et al., 2002; E and Vanden-Eijnden, 2007; Elber, 2005; Haas and Chu, 2009; Hamelberg et al., 2004; J´onsson et al., 1998; E and Vanden-Eijnden, 2007; West et al., 2007). The free energy along this reaction coordinate can then be determined using methods such as umbrella sampling (Mascarenhas and Kastner, 2013; Torrie and Valleau, 1977) and the weighted histogram analysis method (WHAM) (Kumar et al., 1992). However, such approaches have limitations. First, it is necessary to know an efficient reaction pathway from A to B. If conformations A and B are quite different, then it can be challenging to find such paths. Second, these methods are computationally slow. To get an accurate estimate of the total free energy difference ΔG = GB − GA requires accurate determinations of many small free energy differences A → 1 → 2. . . → B, and each step requires substantial amounts of sampling. Third, large errors can accumulate along the pathway as a sum of errors along the steps. Even so, some groups have successfully calculated protein conformational free energies (Cecchini et al., 2009; Christ and van Gunsteren, 2007; Ovchinnikov et al., 2013; Park et al., 2008; Shell, 2010; Spichty et al., 2010; Strajbl et al., 2000; Tyka et al., 2006; Ytreberg et al., 2006; Ytreberg and Zuckerman, 2006; Zheng et al., 2008).
Some strategies for computing a conversion free energy do not require knowing a pathway from A to B. Examples include the reference system method (Ytreberg and Zuckerman, 2006), deactivated morphing (Park et al., 2008), Enveloping distribution sampling (Christ and van Gunsteren, 2007) and the confinement method (Cecchini et al., 2009; Ovchinnikov et al., 2013; Tyka et al., 2006).
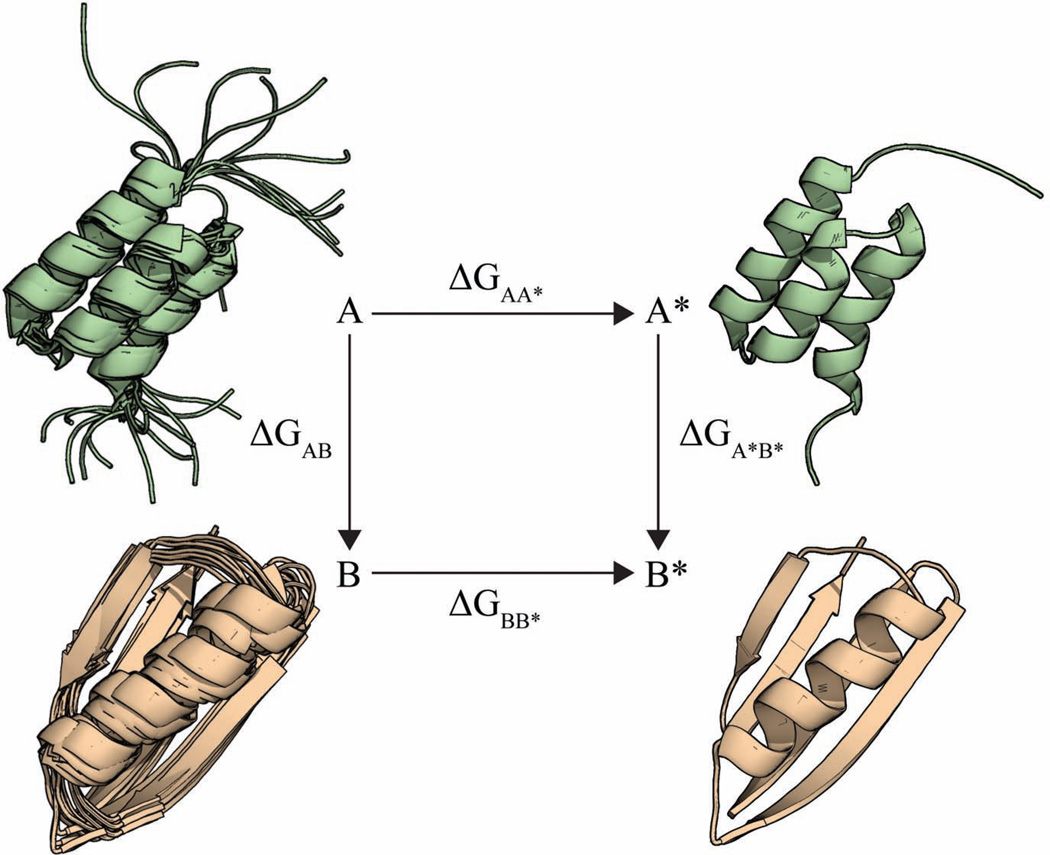
Our approach follows from the confinement method of Tyka et al. (Tyka et al., 2006) and Cecchini et al. (Cecchini et al., 2009), from the ‘confine-and-release’ method for computing binding affinities (Mobley et al., 2006, 2007), and from related methods (Lybrand et al., 1986; Strajbl et al., 2000; Woo and Roux, 2005). To distinguish between the different confinement methods used recently, we call the present method Confine-Convert-Release (CCR), named after the three steps of its thermodynamic cycle shown in Figure 1, described briefly below and in more detail in Supporting Information.
Figure 1.
Graphical representation of the thermodynamic cycle employed in the Confine-Convert-Release method.
CONFINE
Conformational state A of the protein is an ensemble that describes the thermal motions of the molecule in macrostate A. Our first computational step is to impose restraints that restrict the ensemble of A to a reference state, A*, which is much ``tighter'', nearly a single microstate. We do this by applying positional harmonic restraints in a series of MD simulations.
CONVERT
We then convert conformation A* to conformation B*, a highly restricted version of the ensemble of the B macrostate. We compute the free energy of the conversion step between A* and B* using either normal-mode analysis (Brooks and Karplus, 1983; Case, 1994) or the quasi-harmonic method (Karplus and Kushick, 1981; Levy et al., 1984). Because both A* and B* are highly restrained in this transformation, the normal-mode method gives an accurate measure of the free energy difference between them. And, because there is little remaining conformational entropy in the ensembles A* and B*, this conversion free energy is mostly an enthalpy.
RELEASE
Then, we release the restraints on the restricted state B*, allowing it to become the broader ensemble, macrostate B. We do this by gradually decreasing the positional harmonic restraints in a series of MD simulations.
This approach has been previously validated on small model peptides (Cecchini et al., 2009; Tyka et al., 2006). Here, we do two things. First, we validate the CCR method on substantially larger proteins and larger conformational changes. We show that it gives correct conversion free energies across a spectrum of challenging problems. Second, we introduce modification in the CONVERT step that allows us to parse the full conversion free energies, ΔG, into per-residue conversion free-energy components using the same thermodynamic cycle.
Results: (A) Validating the CCR method on various conformational changes
Consistency checks using a prior test on a 16-mer β-hairpin from protein G
We verified that our implementation of the CCR method produces results similar to those previously reported in the literature. The method has been applied to a 16-amino-acid β-hairpin from protein G, known as BHP (Cecchini et al., 2009). We calculated the free energy difference between the native conformation (called bhp1, which has a two-stranded β-sheet) and a non-native conformation (called bhp3, which has a three-stranded β-sheet). Our calculation shows that bhp1 is more stable by 1.7 kcal/mol, which is consistent with 200 εs equilibrium molecular dynamics simulations showing that bhp1 is favored by 1.8 kcal/mol, also in agreement with previous calculations (Cecchini et al., 2009).
CCR can often distinguish CASP-model predictions from true native structures
Next, we looked at 6 target proteins from the CASP9 experiment (Moult et al., 2011). For each target, we examined up to 5 submitted models. We computed the conversion free energy between the experimental native structure and the best model. As is common in the CASP experiment, we assess our results in terms of Global Distance Test Total Score (GDT-TS) (Zemla, 2003), which is a Cα based measure of structural accuracy. It can be understood roughly as the percentage of residues that are correctly positioned in the model (range 0 to 100, higher is better). In 5 out of 6 cases, the CCR method assigns a lower free energy to the experimentally determined structure than to any of the model submissions (see Supplementary Figure S1 and Table S1 for details). This is simply a basic consistency check; other discriminators can also successfully tell native structures from computer generated models (Sheffler, 2009; Zhou and Zhou, 2002).
CCR can correctly rank-order the CASP models submitted from a given prediction team
We tested whether the CCR method can correctly rank-order different putative native structures predicted using a single CASP team’s prediction algorithm. We examined three targets: T0559, T0560 and T0540 (see SI Table S2 for details regarding CASP targets, corresponding PDB Identifier and description of proteins used in this study).
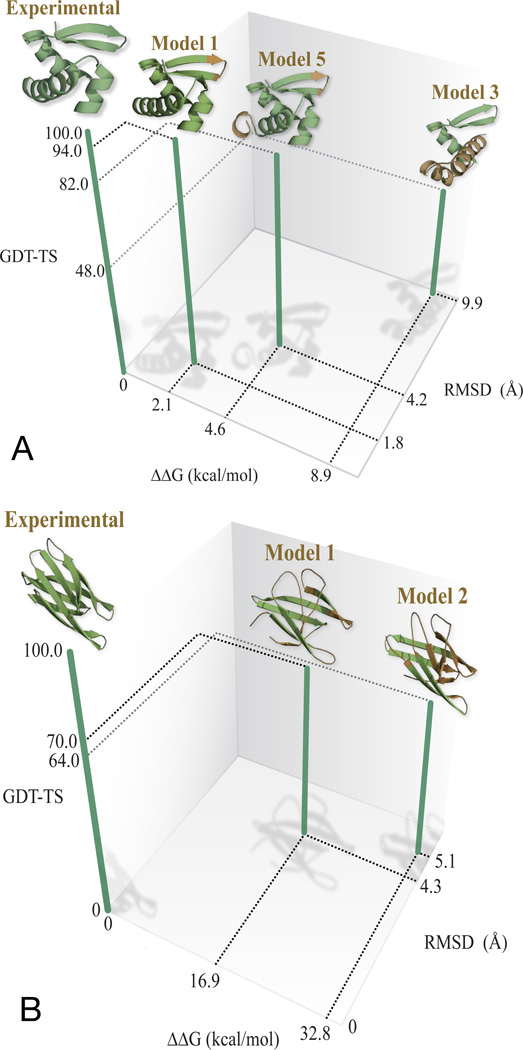
In CASP 9, the best predictor group for the 69-amino-acid target protein T0559 was “BAKER-ROSETTASERVER”. We excluded two models that were very similar to other models that we did include. We find that our CCR method correctly rank-orders the remaining three models submitted for this target (Figure 2(A)). In comparison, the order of submitted model 3 and 5 were incorrectly predicted during CASP experiments (Figure 2(A)).
Figure 2.
(A) The confine-convert-release method ranks correctly the native structure and the three predicted models from BAKER-ROSETTASERVER for CASP target T0559. The backbone regions of the predicted structures that differ substantially from the experimental structures upon superposition are colored brown. The corresponding GDT-TS scores and RMSD values are also plotted along with free energy values. (B) The CCR method correctly rank- orders the native structure and two models submitted by different prediction groups for CASP target T0540.
We performed a similar calculation for target T0560 comparing two models from the group called “Splicer”. The remaining three models were discarded, as they were too similar to the rest of the models. Again, the CCR free-energy calculation correctly identifies the native state and gives rankings that agrees well with CASP’s GDT-TS scores (Supplementary Figure S2 in the supporting information).
Finally, we used the free energies calculated using CCR method to compare models for target T0540 that were produced by different prediction groups. We compared the best models from groups “LTB” (Model 1) and “Mufold” (Model 2). Again, we find that the CCR-based free energies rank order the models in good correlation with the GDT-TS based score (Figure 2(B)).
CCR can be useful for quality assessment in CASP
A part of the CASP experiment entails the quality assessment (QA) of predictors’ models (Kryshtafovych and Fidelis, 2011). Predictors are asked to pro- duce an overall score (called QMODE1) for each model on a scale from 0 to 1, with higher values corresponding to better models (Kryshtafovych and Fidelis, 2011). Many of the groups use consensus strategies in such experiments. Here, we chose two computer-generated models from CASP target T0538, where the top performing group “MUFOLD-WQA” (Wang et al., 2011) failed to identify the best model. We examined two models, one from “PconsR” (GDT-TS= 96), which MUFOLD-WQA gave a QMODE1 = 0.54. The second model was from “MULTICOM-NOVEL” (GDT-TS=83); it is a poorer model, but MUFOLD-WQA assigned it a higher QMODE1 = 0.59. The CCR method gave a conversion free energy that favored the PconsR model by 3.9 kcal/mol, which correctly identified the more accurate model. Although consensus methods are often very effective, they can miss good predictions that are non-consensus, i.e. that are found by only a few methods. At least in this case, the confinement method captures a structure that was otherwise missed.
CCR can predict the conformational preferences of ‘chameleon’ sequences
We tested the ability of the CCR method to calculate the conversion free energies of a series of chameleon sequences from Alexander et al. (Alexander et al., 2007, 2009; Bryan and Orban, 2010; He et al., 2008, 2012). These are pairs of highly similar sequences that fold into remarkably different structures. They have designed a protein-G-like sequence of 56-residues that is marginally stable in one of two possible folds. By mutating key residues in this sequence, they are able to stabilize one fold or the other (see Supplementary Figure S3). We refer to the 4β + α structure as the β conformation, and the 3α structure as the α conformation. We denote sequences that prefer the α fold as GA and sequences that prefer β as GB. One pair of sequences (GA88/GB88) is 88 percent identical in sequence, differing at seven positions. Another pair (GA95/GB95) is 95 percent identical, differing at three positions. Accurately predicting the structural preferences of such similar sequences has posed a challenge for computational methods (Allison et al., 2011).
CCR method identifies the correct structure, α vs. β, for all four sequences (See supporting information Figure S3 for conversion free energy values. For that purpose we compared two different computer-generated models for each sequence, not simulation to experiment. One model is based on the α structure and the other on the β. See Supporting Information for details on the modeling procedure). And, there is indirect evidence that the magnitudes are reasonable. From experiments, it is expected that the free-energy differences between α and β must be small, otherwise they would not be chameleons. Consistent with this, our calculated free energy differences range from around 3.5 to 5.0 kcal/mol. In a more recent study (He et al., 2012), the amino acid residue at position 45 (Tyr for β and Leu for α) was found to be important for switching between α and β conformations. This inspired us to introduce another mutation at this position, Y45A, which we refer to as GA98. Our calculations predicted that this mutation shifts the equilibrium to the α conformation, which is now more stable than the β by 3.8 kcal/mol. Although this result has not yet been confirmed experimentally, it is consistent with the previously observed effect of Y45L (He et al., 2012).
Results: (B) CCR can parse A → B conversion free energies into its per-residue components
So far, we have described how the CCR method computes the total conversion free energy ΔG between two conformations A and B. Now we describe how we parse ΔG into component amino-acid-level per-residue free energies (PRFEs). In general, total protein free energies can rarely be parsed into additive component free energies (Dill, 1997; Mark and van Gunsteren, 1994). Non-additivities can typically be large. However, the CCR framework enables an approach to minimizing non-additivities, allowing us to parse the total free energy into components. Here’s a brief summary; more detail is given in SI. First, the steps for confinement (AA*) and release (BB*) are small conformational changes; they are just restrictions of the ensembles A and B to their mean values, so they are dominated by local interactions. Second, the corresponding free energy changes, ΔGAA* and ΔGBB* are obtained by thermodynamic integration of small steps along the corresponding pathways, A → A* and B → B* . Each such pathway step is sufficiently small that it is given exactly in Taylor expansion as a sum of per-residue terms (Tyka et al., 2006). And third, even though the conformational transition A* → B* can be arbitrarily large, it is essentially between two microstates (highly constrained), so there is nearly zero conformational entropy change, ΔSA*B* · 0. Hence ΔGA*B* · ΔHA*B*. Such enthalpies are component wise decomposable (This is only approximate, and not exact, for two reasons. First, we do not include the residual conformational entropy from the normal mode or quasi-harmonic steps. However, we show in the SI that these entropies are small. Second, we do not include solvent entropies. For implicit-solvent modeling, such as we use here, solvation free energies are predominantly contact enthalpies because they are potentials of mean force that are averaged over solvent freedom). Below, we show that such per-residue conversion free energies give useful insights for identifying the driving forces in chameleon proteins and for finding errors in CASP models.
CCR PRFEs give insights into what drives the conformational switching in chameleon proteins
Here, we use the computed per-residue conversion free energies to shed light on the chameleon sequences of Alexander et al and He et al. (Alexander et al., 2007, 2009; Bryan and Orban, 2010; He et al., 2008, 2012). The PRFE’s, ΔΔG(β − α), are shown in Figure 3 and Figure 4.
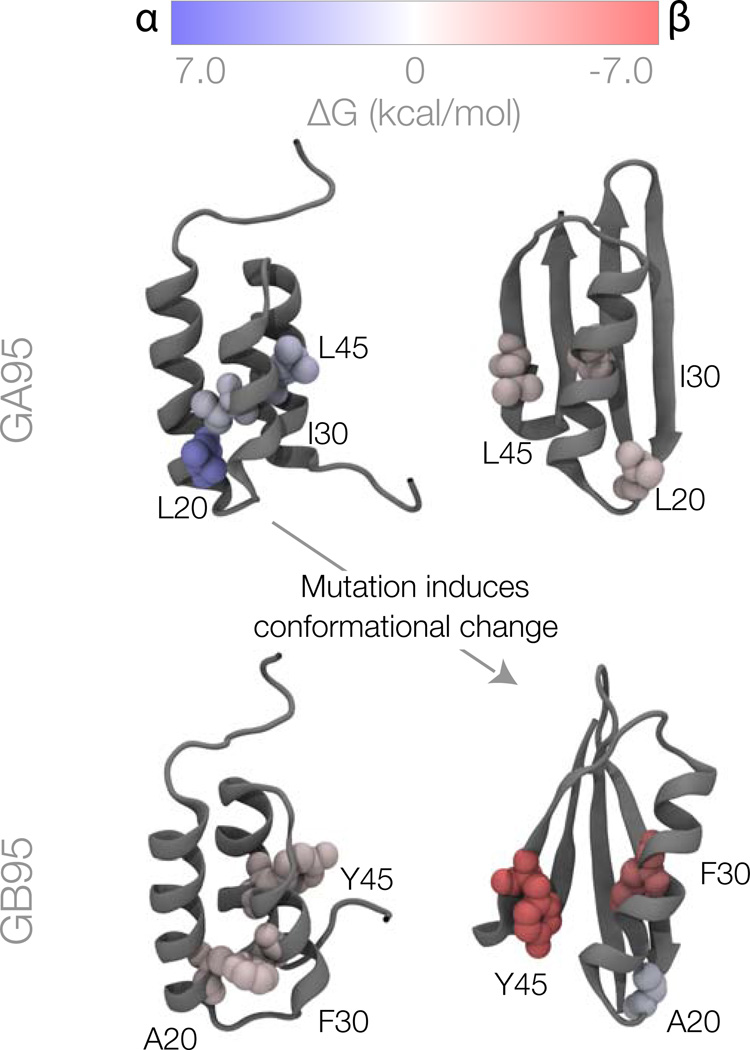
Figure 3.
Per-residue conversion free energies for the α and β conformations of the GA95 and GB95 sequences. Residues colored in blue favor the α structure; residues in red favor the β structure; and white residues have no preference. The residues mutated between GA95 and GB95 are shown as space filling.
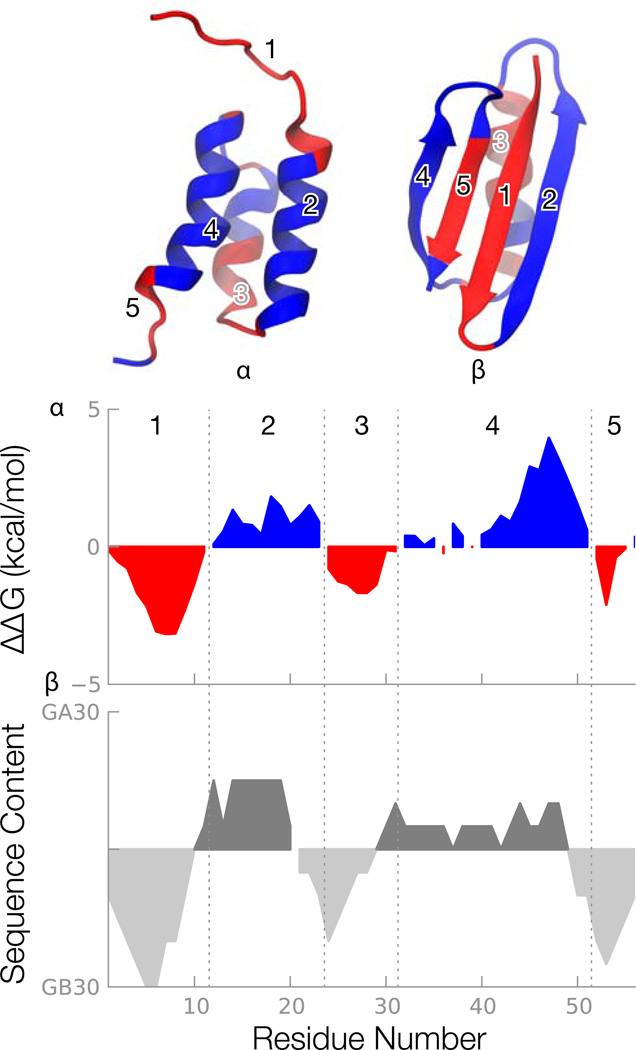
Figure 4.
Per-residue free energy calculations reveal alternating preferences of the individual secondary structures. Upper: residues favoring the either the α or β structure form a stable core in the corresponding structure. Each residue is colored identically in the two structures according to the per-residue free energies shown in the middle panel. Middle: per-residue free energies reveal regions of the sequence that favor the α or β structure. Lower: the per-residue free energies can largely be traced back to the source (either GA30 or GB30) of the amino acid at each position. All plots are smoothed with a 6-residue running average.
Why does GA95 (which contains L20, I30 and L45) favor the α structure, while GB95 (which contains A20, F30 and Y45) favor the β structure? The top left of Figure 3 shows the GA sequence put into the α structure. The top right shows the GA sequence put into the β structure. And the bottom two figures show the GB sequence put into each of the two possible structures. First, look at the top row: Why does the L20-I30-L45 sequence prefer the top left structure over the top right structure? In short, L20, which is hydrophobic, is buried in a hydrophobic core in the GA structure, but it is exposed to solvent when the chain is configured in the GB structure. Why does the A20-F30-Y45 sequence prefer the bottom right structure over the bottom left structure? In short, F30, which is hydrophobic, is buried in a hydrophobic core in the GB structure, but it is exposed to solvent when the chain is configured in the GA structure. Also, Y45 forms a hydrogen bond with D47 in the β structure. (Interestingly, residue A20 favors the α structure, but only weakly, so it is not sufficient to drive GB to GA.) In addition to the direct effects of mutations, there are also indirect effects due to small perturbations in the environment around the mutations. For example, the L20A mutation causes a slight repacking around residue 20. This causes large changes in the per-residue free energies of nearby residue A26.
Our PRFEs give insights about how other residues in protein G – besides those at the three mutation sites – support either the structure GA or GB. First, we find that most of the residues in the region 1– 8 stabilize the β structure. This is because they are hydrophobic and the GB structure provides them with a locally well-packed hydrophobic environment. In contrast, residues 1–8 would be in a random coil in the GA structure. This effect is most prominent in case of L7 (see SI figure S4 for per residue free energy preferences). In addition, residue A26 is a big driver towards the GB fold. A26 is part of well-packed hydrophobic core in the β fold but is solvent exposed in the α fold. Other residues support the GA fold. For example, Q11 stabilizes the α fold by forming a hydrogen bond with E15. The residue that most strongly drives toward the GA fold is I49, because it is part of the hydrophobic core in the α fold but is solvent exposed in the β fold. These points are illustrated in more detail in Supplementary Figures S5.
Figure 4 makes two interesting points; namely that these chameleon sequences have alternating runs of preferences for α, then β, etc. and that our CCR calculations are able to “reverse-engineer” the information that was used to design the original sequences in the first place. Alexander et al (Alexander et al., 2007) used an iterative approach and relied on previous experiments that used random mutagenesis to design these two heteromorphic pairs. On the other hand our calculations can rationalize such approach. The middle panel of Figure 4 shows a smooth version of the computed per-residue conversion free energy, ΔΔG(β − α) relative to the GA95 sequence (see SI figure S4 for raw peaks). The red regions are parts of the sequence that favor β and the blue regions favor α. In these chameleon molecules, each of the 5 secondary structure sequences mostly favors either α or β structure monolithically, without ambiguity. The bottom panel shows the patterns that Alexander et al used to develop the chameleon sequences. They took stretches of chain as binary mixtures from GA30 and GB30 (Alexander et al., 2007). That is, at each position, there are at most two possible amino acids, rather than twenty, coming from either GA30 or GB30. Our bottom panel of Figure 4 shows a running average of the origin of the amino acid at each position. Comparison of the middle and bottom panels of Figure 4 show that our CCR free energies reflect the design origins of the chameleon sequences. Hence we believe that the CCR free-energy method may also be useful for reflecting the energetic tendencies and origins of amino acids in proteins.
Our results show, at least for these chameleon proteins, that the overall net stability of a structure is very small, but it results from quite strong preferences of a few individual amino acids to be in one conformation or the other. Hence, for these and possibly other switch-like proteins, only a handful of amino acids can control a protein’s conformation.
The per-residue free energy reports conformational driving forces
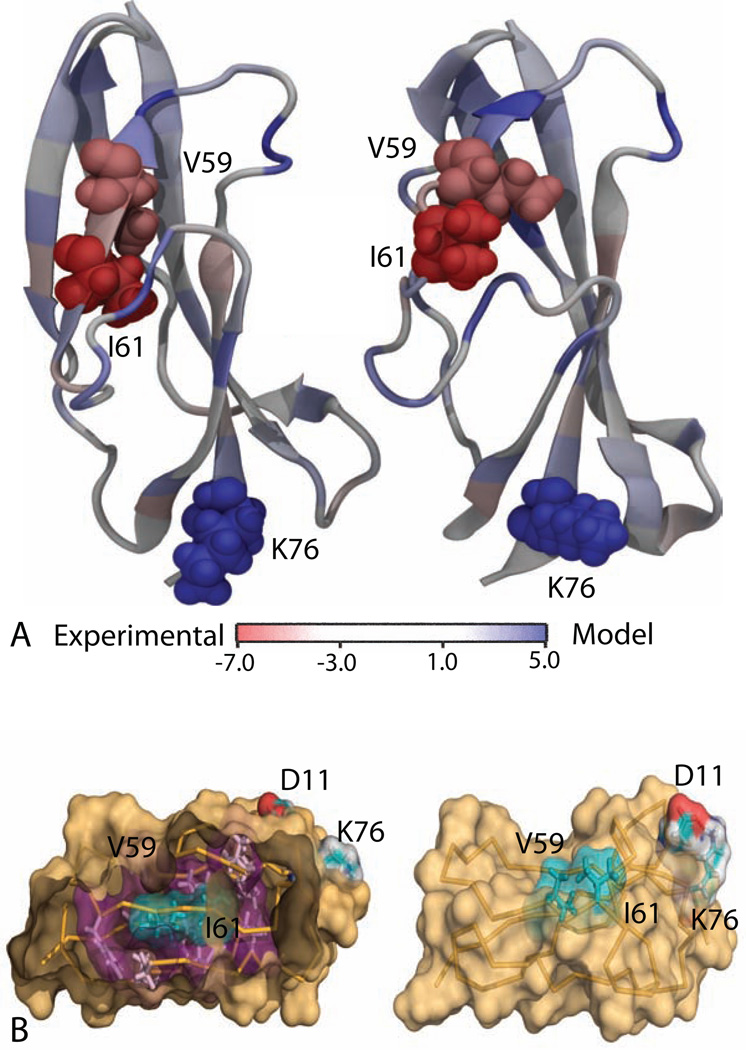
Our per-residue conversion free energies are also useful for diagnosing which residues are most responsible for conformational differences. Here, we compare the best computer model prediction for the native structure of CASP target T0569 (from the “Mufold” group, having GDT-TS=78) vs. the experimental NMR structure. Our result using CCR method predicts that the experimental structure is more stable by 20 kcal/mol. It predicts that the two hydrophobic residues V59 and I61 are destabilizing in the CASP model relative to the experimental structure (Figure 5). Figure 5(B) shows that the side chains of these hydrophobic residues are oriented towards the protein hydrophobic core in the native NMR structure but are oriented towards the exterior of the protein, exposing them to solvent, in the model. These residues are part of a beta-sheet in the experimental structure, but because of their sidechain orientation, the corresponding beta-sheet becomes disordered in the predicted model (Figure 5 and Figure S6). There is also a large difference around K76, which forms a salt-bridge with D11 in the predicted model, but not in the experimental structure. This suggests that salt-bridge interactions are too favorable for the combination of forcefield and implicit solvent model we use, which has been a problem noted in the past (Roe et al., 2007).
Figure 5.
(A) Per-residue free energy between the experimental NMR structure and the best prediction for CASP target T0569. The amino acid residues that are colored in deep red and deep blue stabilizes the NMR structure and the prediction, respectively; the residues with light blue color do not have a strong preference. (B) Key differences between the two structures as predicted by PRFE. The side chains of hydrophobic residues V59 and I61 are well packed and oriented towards the hydrophobic core in in the experimental structure (left) but they are exposed to the solvent in computer-generated model (right). A salt bridge between K76 and D11 stabilizes the computer-generated structure.
Not all CCR predictions are correct
Despite the successes we observe in most cases we have studied, there are also some failures, especially for pairs of structures A and B having very similar GDT-TS scores. One example is Target T0538, where we compared the experimental structure with three models (Model 1: “PconsR”—GDT-TS=96; Model 2: “Shell”—GDTTS= 90; Model 3: “FOLDIT”—GDT-TS=86). In this case, the CCR method incorrectly predicts that computer model 1 is more stable than the crystal structure (see Supplementary Figure S7(A)). Per-residue free energy calculations (not shown) show that despite only small variations at the backbone level, the side chains are oriented in very different ways (see Supplementary Figure S7(B)), giving rise to large differences in the stabilization of certain residues. In particular, some of the differences arise from different salt bridge patterns and certain flexible polar residues exposed to the surface. This unexpected result shows that the CCR method is very sensitive to local interactions (including side chain reorientation) and may indicate issues with the forcefield and implicit-solvent models used in our calculations.
Discussion
We have described a computational method called Confine-Convert- Release for computing the difference free energy between two conformational ensembles. We showed: that the conversion free energy can be calculated on proteins of up to around 100 residues, even for large conformational changes; that it can discriminate the folding preferences of a series of chameleon proteins; that it can discriminate between the native structure and structure predictions, and that it can often identify the best prediction. We have also shown that it can be used to give residue-level insights into the dominant structural factors that are responsible for the conversion free energies in conformations of a protein. The CCR method should be useful for protein design, structure prediction, and understanding the mechanism of conformational change.
Experimental Procedures
In this section we briefly describe the confine-convert-release (CCR) method. This method was previously known as confinement method and originally developed by Tyka et al. (Tyka et al., 2006) and Cecchini et al. (Cecchini et al., 2009). We follow their treatments, but with some small technical differences. Below, we summarize our approach.
From the given ensembles A and B, we first establish much more tightly defined reference ensembles A* and B*. The reference ensembles are simply taken to be the ensemble average structures of A and B.
We now compute the free energy for confinement by imposing positional restraints (springs) of gradually increasing strengths, to force A into state A*. This is done by running 20 molecular dynamics simulations(each 20 ns long) along the confinement reaction coordinate. The harmonic restraint force constant is scaled up, starting from 0.00005 kcal/mol (mostly free) to 81.92 kcal/mol (tightly restrained).
The tightly restrained reference state, (A*) is then converted to (B*). The free energy of this conversion is computed using normal mode analysis (Brooks and Karplus, 1983; Case, 1994). We also found similar results using quasi-harmonic analysis (Karplus and Kushick, 1981; Levy et al., 1984). The free energy calculated in this way is shown as ΔGA*B* in Figure 1.
In the release step, the highly restrained reference state, (B*) is released to a free ensemble (B) by using a series of progressively looser position restraints. This is done through a procedure that is simply the revers of the confinement process.
The free energy of confinement, ΔGAA* and release, ΔGBB* are estimated by numerically integrating over the atomic fluctuations taken at different force constants (Tyka et al., 2006) (see SI).
The full confinement free energy, ΔGA,B between the two states A and B is calculated as ΔGAB = ΔGAA* − ΔGBB* + ΔGA*B*
One advantage of the CCR method is that none of the simulations during the restraining step depends on any other. Therefore, it can be fast to compute with available computer resources. We ran each confinement calculation on a single graphics-processing unit (GPU). For a 56-residue protein, this leads to a calculation time of only 4 hours on 40 GPUs (1 GPU per confinement calculation × 20 calculations per structure × 2 structures). All calculations were performed with the Amber 11 suite of programs (Case et al., 2005, 2012; Goetz et al., 2012) in combination with the ff99SB forcefield (Hornak et al., 2006) and the GBneck generalized born implicit solvent model (Mongan et al., 2006; Roe et al., 2007).
We calculated the approximate per-residue free energy as follows. The free energy, ΔGAA* and ΔGBB* of each residue was calculated numerically as described by Tyka et al. (Tyka et al., 2006). We call this method approximate as we ignore the entropic contribution from the normal mode or quasi-harmonic analysis at the highly restrained state. Thus, ΔGA*B* · ΔHA*B*. The internal energy of each residue was calculated with Amber’s “decomp” module using the final two restrained trajectories.
Supplementary Material
Computation of free energy due to large conformational changes in protein
Total conversion free energies parsed into per-residue free-energy components
Interpreting protein mechanisms at the amino-acid level
Design of protein conformational switches, structure prediction
Acknowledgements
We thank Sarina Bromberg for help with the figures. KD appreciates the support of the Laufer Center and NIH grant GM34993.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Supplemental Information
Supplemental Information is available in the online version of the paper.
References
- Allison JR, Bergeler M, van Gunsteren WF. Can computer modeling explain why two highly similar sequences fold into different structures? Biochemistry. 2011;50:10965–10973. doi: 10.1021/bi2015663. [DOI] [PubMed] [Google Scholar]
- Alexander PA, He Y, Chen Y, Orban J, Bryan P. The design and characterization of two proteins with 88% sequence identity but different structure and function. Proc. Natl. Acad. Sci. 2007;104:11963–11968. doi: 10.1073/pnas.0700922104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander PA, He Y, Chen Y, Orban J, Bryan P. A minimal sequence code for switching protein structure and function. Proc. Natl. Acad. Sci. 2009;106:21149–21154. doi: 10.1073/pnas.0906408106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks BR, Karplus M. Harmonic dynamics of proteins: Normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. 1983;80:6571–6575. doi: 10.1073/pnas.80.21.6571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryan PN, Orban J. Proteins that switch folds. Curr. Opin. Struct Biol. 2010;20:482–488. doi: 10.1016/j.sbi.2010.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case D. Normal-mode analysis of protein dynamics. Curr. Opin. Struct. Biol. 1994;4:285–290. [Google Scholar]
- Case DA, Cheatham TE, III, Darden T, Gohlke, Luo HR, Merz KM, Jr, Onufriev A, Simmerling C, Wang BR, Woods R. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case DA, Darden TA, Cheatham TE, III, Simmerling CL, Wang J, Duke RE, Luo R, Walker RC, Zhang W, Merz KM, Roberts B, Hayik S, Roitberg A, Seabra J, Swails AW, Goetz AW, KolossvAry I, Wong KF, Paesani F, Vanicek J, Wolf RM, Liu J, Wu X, Brozell SR, Steinbrecher T, Gohlke H, Cai Q, Ye X, Wang J, Hsieh M-J, Cui G, Roe DH, Mathews DH, Seetin MG, Salomon-Ferrer R, Sagui C, Babin V, Luchko T, Gusarov S, Kovalenko A, Kollman PA. Amber12. San Francisco: University of California; 2012. [Google Scholar]
- Cecchini M, Krivov SV, Spichty M, Karplus M. Calculation of free-energy differences by confinement simulations. Application to peptide conformers. J.Phys.Chem. B. 2009;113:9728–9740. doi: 10.1021/jp9020646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng X, Wang H, Grant B, Sine SM, McCammon JA. Targeted Molecular Dynamics Study of C-Loop Closure and Channel Gating in Nicotinic Receptors. Plos Comp. Biol. 2006;2:1173–118. doi: 10.1371/journal.pcbi.0020134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chipot C, Shell MS, Pohorille A. Introduction, Free Energy Calculations: Theory and Applications in Chemistry and Biology. In: Chipot C, Pohorille A, editors. Springer Series in Chemical Physics. vol. 86. Berlin and Heidelberg: Springer; 2007. pp. 1–32. [Google Scholar]
- Christ CD, van Gunsteren WF. Enveloping distribution sampling: A method to calculate free energy differences from a single simulation. J. Chem. Phys. 2007;126:184110, 1–10. doi: 10.1063/1.2730508. [DOI] [PubMed] [Google Scholar]
- Dellago C, Bolhuis PG, Geissler PL. Transition Path Sampling. Adv. Chem. Phys. 2002;123:1–84. doi: 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
- Dill KA. Additivity Principles in Biochemistry. Biochemistry. J. Biol. Chem. 1997;272:701–704. doi: 10.1074/jbc.272.2.701. [DOI] [PubMed] [Google Scholar]
- E W, Ren W, Vanden-Eijnden E. Simplified and improved string method for computing the minimum energy paths in barrier-crossing events. J Chem Phys. 2007;126:164103–164108. doi: 10.1063/1.2720838. [DOI] [PubMed] [Google Scholar]
- Elber R. Long-timescale simulation methods. Cur. Opin. in Str. Biol. 2005;15:151–156. doi: 10.1016/j.sbi.2005.02.004. [DOI] [PubMed] [Google Scholar]
- Goetz AW, Williamson MJ, Xu D, Poole D, Le Grand S, Walker RC. Routine microsecond molecular dynamics simulations with AMBER - Part I: Generalized Born. J. Chem. Theory Comput. 2012;8:1542–1555. doi: 10.1021/ct200909j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas K, Chu JW. Decomposition of energy and free energy changes by following the flow of work along reaction path. J Chem Phys. 2009;131:144105–144111. doi: 10.1063/1.3243080. [DOI] [PubMed] [Google Scholar]
- Hamelberg D, Mongan J, McCammon JA. Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules. J Chem. Phys. 2004;120:11919–11929. doi: 10.1063/1.1755656. [DOI] [PubMed] [Google Scholar]
- He Y, Chen Y, Alexander PA, Orban J. NMR structures of two designed proteins with high sequence identity but different fold and function. Proc. Natl. Acad. Sci. 2008;105:14412–14417. doi: 10.1073/pnas.0805857105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Chen Y, Alexander PA, Bryan PN, Orban J. Mutational tipping points for switching protein folds and functions. Structure. 2012;20:83–91. doi: 10.1016/j.str.2011.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- J´onsson H, Mills G, Jacobsen KW. In: Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions in Classical and Quantum Dynamics in Condensed Phase Simulations. Berne BJ, Ciccotti G, Coker DF, editors. World Scientific; 1998. 385 pp. [Google Scholar]
- Karplus M, Kushick J. Method for estimating the configurational entropy of macromolecules. Macromolecules. 1981;14:325–332. [Google Scholar]
- Kryshtafovych A, Fidelis K, Tramontano A. Evaluation of model quality predictions in CASP9. Proteins. 2011;79:91–106. doi: 10.1002/prot.23180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. The weighted histogram analysis method for free-energy calculations on biomolecules. I. J. Comp. Chem. 1992;13:1011–1021. [Google Scholar]
- Levy R, Karplus M, Kushick J, Perahia D. Evaluation of the configurational entropy for proteins: application to molecular dynamics simulations of an α-helix. Macromolecules. 1984;17:1370–1374. [Google Scholar]
- Lybrand TP, McCammon JA, Wipff G. Theoretical Calculation of Relative Binding Affinity i n Host-Guest Systems. Proc. Nat. Aca. Sci. 1986;83:833–835. doi: 10.1073/pnas.83.4.833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mark AE, van Gunsteren WF. Decomposition of the Free Energy of a System in Terms of Specific Interactions: Implications for Theoretical and Experimental Studies. J. Mol. Biol. 1994;240:167–176. doi: 10.1006/jmbi.1994.1430. [DOI] [PubMed] [Google Scholar]
- Mascarenhas NM, Kastner J. How maltose influences structural changes to bind to maltose-binding protein: Results from umbrella sampling simulation. Proteins. 2013;81:185–198. doi: 10.1002/prot.24174. [DOI] [PubMed] [Google Scholar]
- Mobley DL, Chodera JD, Dill KA. On the use of orientation restraints and symmetry corrections i n alchemical free energy calculations. J. Chem. Phys. 2006;125:084902, 1–16. doi: 10.1063/1.2221683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley DL, Chodera JD, Dill KA. The combining and release method: obtaining correct binding free energies in the presence of protein conformational change. Journal of Chemical Theory and Computation. 2007;3:1231–1235. doi: 10.1021/ct700032n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moult J, Fidelis K, Kryshtafovych A, Tramontano A. Critical assessment of methods of protein structure prediction (CASP)-round IX. Proteins. 2011;79:1–5. doi: 10.1002/prot.23200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mongan J, Simmerling C, McCammon JA, Case D, Onufriev A. J. Chem. Theory Comput. 2006;3:156–169. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ovchinnikov V, Cecchini M, Karplus M. A Simplified Confinement Method for Calculating Absolute Free Energies and Free Energy and Entropy Differences. J. Phys. Chem. B. 2013;117:750–762. doi: 10.1021/jp3080578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S, Lau A, Roux B. Computing conformational free energy by deactivated morphing. J. Chem. Phys. 2008;129:134102, 1–5. doi: 10.1063/1.2982170. [DOI] [PubMed] [Google Scholar]
- Roe DR, Okur A, Wickstrom L, Hornak V, Simmerling C. Secondary structure bias in generalized Born solvent models: comparison of conformational ensembles and free energy of solvent polarization from explicit and implicit solvation. J Phys Chem B. 2007;111:1846–1857. doi: 10.1021/jp066831u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strajbl M, Sham YY, Vill J, Chu Z-T, Warshel A. Calculations of Activation Entropies of Chemical Reactions in Solution. J.Phys.Chem. B. 2000;104:4578–4584. [Google Scholar]
- Sheffler W, Baker D. RosettaHoles: Rapid assessment of protein core packing for structure prediction, refinement, design, and validation. Protein Science. 2009;18:229–239. doi: 10.1002/pro.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shell SM. A replica-exchange approach to computing peptide conformational free energies. Mol. Sim. 2010;7:505–515. [Google Scholar]
- Spichty M, Cecchini M, Karplus M. Conformational Free-Energy Difference of a Miniprotein from Non equilibrium Simulations. J. Phys. Chem. Lett. 2010;1:1922–1926. [Google Scholar]
- Torrie GM, Valleau JP. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977;23:187–199. [Google Scholar]
- Tyka M, Clarke A, Sessions R. An Efficient, Path-Independent Method for Free-Energy Calculations. J.Phys.Chem. B. 2006;110:17212–17220. doi: 10.1021/jp060734j. [DOI] [PubMed] [Google Scholar]
- Wang Q, Vantasin K, Xu D, Shang Y. MUFOLDWQA: A new selective consensus method for quality assessment in protein structure prediction. Proteins. 2011;79:185–195. doi: 10.1002/prot.23185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West AM, Elber R, Shalloway D. Extending molecular dynamics time scales with milestoning: example of complex kinetics in a solvated peptide. J Chem Phys. 2007;126:145104–1451014. doi: 10.1063/1.2716389. [DOI] [PubMed] [Google Scholar]
- Woo H-J, Roux B. Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. 2005;102:6825–6830. doi: 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ytreberg FM, Swendsen RH, Zuckerman DM. Comparison of free energy methods for molecular systems. J Chem Phys. 2006;125:184114, 1–11. doi: 10.1063/1.2378907. [DOI] [PubMed] [Google Scholar]
- Ytreberg F, Zuckerman D. Simple estimation of absolute free energies for biomolecules. J. Chem. Phys. 2006;124:104105, 1–6. doi: 10.1063/1.2174008. [DOI] [PubMed] [Google Scholar]
- Zemla A. LGA: a method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng L, Chen M, Yang W. Random walk in orthogonal space to achieve efficient free-energy simulation of complex systems. Proc. Natl. Acad. Sci. 2008;105:20227–20232. doi: 10.1073/pnas.0810631106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Zhou Y. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 2002;11:2714–2726. doi: 10.1110/ps.0217002. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.