Computational Approaches for Understanding Energy Metabolism

Abstract

There has been a surge of interest in understanding the regulation of metabolic networks involved in disease in recent years. Quantitative models are increasingly being used to i nterrogate the metabolic pathways that are contained within this complex disease biology. At the core of this effort is the mathematical modeling of central carbon metabolism involving glycolysis and the citric acid cycle (referred to as energy metabolism). Here we discuss several approaches used to quantitatively model metabolic pathways relating to energy metabolism and discuss their formalisms, successes, and limitations.

Introduction

The accumulated amount of biochemical work carried out over the years has elaborated complex metabolic systems and networks. This information includes the network architecture encoded in chemical reactions that are carried out by metabolic enzymes and the kinetic parameters that determine reaction mechanisms involved in each of these chemical reactions. Application of this knowledge has led to tremendous predictive capability in characterizing metabolic regulation in normal physiology including the growth of unicellular organisms and the successful simulation of energy metabolism in healthy red blood cells. However, there are far fewer instances in which these models have been applied to the characterization of pathophysiology. Applying our knowledge of metabolic regulation to the investigation of disease states such as cancer or neurodegeneration is currently a scientific frontier. In this review, we will revisit several classic techniques for the mathematical modeling of metabolic pathways and discuss instances where their application to biomedical science is beginning to yield fruitful dividends.

1. Linear Systems, Flux Balance Analysis

Linear models are mathematical models that containt a set of algebraic equations based on the stoichiometric relationships that define conservation relationships within a metabolic network. Linear models, to our knowledge, were first applied to biochemical systems in 1961 by Howard Shapiro¹. Shapiro discussed the possibility of using optimization in biochemical linear models in a 1969 publication². In 1984, a model incorporating glycolysis and the TCA cycle was employed running a variant of Dantzig’s algorithm with the assumed biological objective of minimized free energy dissipation^3,4. An enduring research program was initiated by Bernhard Palsson half a decade later^5,6.

An early work of Palsson showed that growth maximization in an E. coli model could correctly match 86% of 79 gene essentialities examined⁷. Subsequent modeling in S. cerevisiae was able to closely predict growth rates and exometabolic fluxes in various media, and nearly capture the in vivo phosphate/oxygen (P/O) ratio of 0.94 with a simulated P/O value of 1.04, showing that models of eukaryotes were also feasible⁸. If one chooses the biological objective function to reflect the appropriate physiological demands then it is possible to predict features of adaptation; this was shown to be the case for growth optimization in several E. coli mutants⁹. By this time it had become apparent that linear models held much promise, particularly when coupled with optimization.

1.1 Genome Scale Modeling

Today, when we refer to linear models, we most often mean Constraint Based Models (CBMs). We refer to a CBM as any model making use of the stoichiometric matrix, S, as a linear matrix constraint, e.g. S * F = 0, where F is a flux vector. In fact, this is a nearly universal constraint, as it guarantees conservation of mass during steady state processes such as exponential growth or tissue maintenance¹⁰. Other constraints commonly used include reversibility constraints when the direction of a reaction is known for physiological conditions of interest, bounds on the uptake of nutrients or efflux rates due to regulation or physiology, or bounds on enzyme reactions when the maximum enzyme velocity Vmax is known.

Because these constraints give rise to an underdetermined system, it will not be possible to identify a unique solution for the flux vector. A unique solution is often desirable as it allows investigators to analyze a putative metabolic phenotype. Indeed, this is one of the more convenient features of linear optimization: the ability to get meaningful solutions without explicitly taking into account any, or at least very few, free parameters. Flux Balance Analysis, or FBA, assumes a linear combination of fluxes to be maximized or minimized (Fig. 1). In microbes, perhaps the most popular FBA objective has been growth maximization, which consists of the biomass precursors and products formulated as a single pseudo-reaction. Additionally, an ATP maintenance constraint should be formulated as a sink reaction with the molar ATP required to keep one gram of dry weight biomass living for one hour¹¹. This empirically determined constraint, although assumed, is less discussed, perhaps due to its dependence on individual strains and environments. We note that for many expression-based methods in the CBM framework, the ATP maintenance constraint is not required (see Table and Fig. 2 for examples). Fixed biomass objectives by themselves also have some undesirable qualities; biomass composition likely has some measure of variability based on genetic background and environment. Robust FBA attempts to address this problem by allowing some variation in the biomass composition, as determined by variation of empirical assays of biomass ¹². Despite these caveats, FBA has recently been found to not only predict growth in microbes, but also has good agreement with gold standard ¹³C flux assays in vivo when the growth objective is used along with ATP synthesis maximization and minimization of absolute fluxes¹³.

Figure 1. (A) A simple geometric illustration of an FBA problem.

Constant constraints on the Vi limit the feasible solution to an n-dimensional cube (shown in gray). Further linear constraints from the S matrix create a cone of feasible solutions (blue). Linear programming algorithms find an optimal solution on a vertex (illustrated with orange circle). (B and C) Depiction of a simple metabolic network with compartmentalization and its associated stoichiometric matrix. The three compartments, denoted with subscripts b, e, and c represent the boundary, extracellular environment, and cytosol. The boundary is what separates the model from its environment, and mass balance is not assumed at the boundary; this allows for the implementation of source and sink reactions.

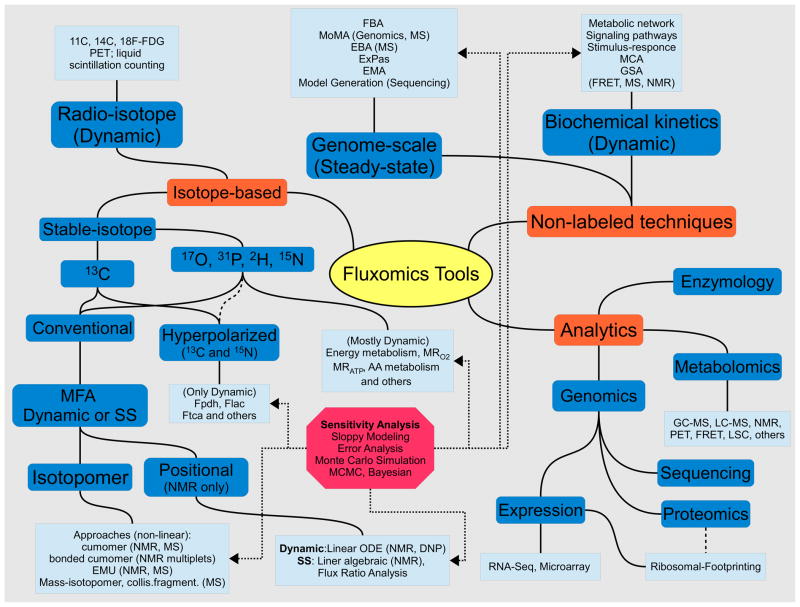
Figure 2. Schematic representation of Fluxomics tools.

Important to fluxomics are both the mathematical and computational tools for non-labeled and labeled techniques, as well as the analytical methods used to obtain data and parameters. Metabolite concentrations and kinetic parameters are obtained primarily from both Gas Chromatography and Liquid Chromatography Mass-Spectrometry (GC-MS and LC-MS), Nuclear Magnetic Resonance (NMR), UV-V is spectroscopy, electrochemistry, Förster (Fluorescence) resonance energy transfer (FRET), Positron Emission Tomography (PET), Liquid Scintillation Counting (LSC), and classical enzymology. Sequence data is employed in the construction of organism models, whereas proteomics and expression data find use in the creation of tissue or cell-type specific models. High-quality expression data such as RNA-Seq and Ribosomal Footprinting are beginning to find uses in flux prediction. Several prominent genome-scale techniques include Flux Balance Analysis (FBA), Minimization of Metabolic Adjustment (MoMA), Energy Balance Analysis (EBA), ExPas (Extreme Pathways), and Elementary Mode Analysis (EMA). Isotope-based approaches include stable isotope techniques (mostly convenient 13C MFA and other nuclei, namely 17O, 31P, 2H and 15N used to study central metabolism), hyperpolarized 13C (Dynamic Nuclear Polarization (DNP)) and radio-isotopes which are studied with PET and LSC. Well-established MFA tools include isotopomer and positional modeling which could be studied dynamically or at steady-state (SS). With hyperpolarized technique it is possible to extract energy-related fluxes like Pyruvate dehydrogenase flux Fpdh, Lactate production rate Flac and Tricarboxylic Acid Flux Ftca (e.g. with [1- or 2-13C]Pyr as tracers). With other nuclei, the metabolic rate of Oxygen consumption MRO2 and ATP production MRATP and Amino Acids fluxes (AA) could be accessed directly. Advanced isotopomer techniques include cumomer approach with Elementary Metabolite Units (EMU) and Bonded Cumomers frameworks designed to reduce the number of independent variables while retaining all measurable isotopomer information. Non-labeled techniques along with genome-scale analysis include biochemical kinetics modeling tools to study metabolic and signaling networks and their regulation architecture with established tools like Metabolic Control Analysis (MCA) and Global Sensitivity Analysis (GSA). Additional sensitivity analysis should be conducted e.g. with Monte-Carlo techniques like Markov Chain Monte-Carlo (MCMC, Bayesian) analysis to check the reliability of extracted metabolic parameters, including fluxes.

Minimization of absolute flux is a commonly used objective employed alongside other objectives, forming a minimax problem (i.e. finding the minimum absolute flux profile among all flux profiles that maximize biomass). This approximates the biological goal of being efficient with enzyme production costs and enzyme crowding constraints while also guaranteeing that no thermodynamically impossible loops are present, that is, ruling out some fluxes that might otherwise violate Kirchoff’s loop rule^14,15. This constraint will work whenever a sink reaction, such as growth, is being optimized. However, maximizing an internal flux, as in Flux Variability Analysis¹⁶, could still result in internal cycles¹⁵. Initial thermodynamic approaches involved nonlinear optimization^17–20. Constraints satisfying Kirchoff’s loop rule were later developed that were faster and more generally applicable than prior methods^15,21. Still, these involve integer constraints that put this problem in a slower class of algorithms than the convex minimized absolute flux problem. When available, thermodynamic data is valuable; it can not only be used to guarantee there are no internal cycles, but can also aid in determining reaction direction and potential regulatory targets^15,18,22,23. Application of this framework to concentration data allows unmeasured metabolite concentrations to be inferred and global concentrations to be resolved at the organelle level²⁰. CBMs have also found use in tracing individual atoms through pathways, which provides a more appealing framework for performing Metabolic Flux Analysis (MFA; discussed below) on stable isotope data due to the lack of bias compared to typical MFA models, which are often an order of magnitude smaller than genome-scale reconstructions²⁴. Recent insightful work has made it possible to simplify the computational complexity of loopless FBA to be nearly the same as conventional FBA, but some mathematical difficulties must still be overcome before bounds on exchange fluxes can be suitably incorporated for genome-scale modeling^10,25.

The metabolism of different tissues within the same organism is diverse; whereas the metabolism in liver is anabolic, neurons or red blood cells have a much more limited catabolic regime^26–28. The creation of tissue specific models for multicellular organism has become an important problem, and several automated algorithms taking as inputs tissue expression data and a generic model for the organism have been developed^28–30. Coupling multiple cellular models together will enable multi-scale modeling of tissues in multicellular models or entire ecosystems for microbes^26,31–33.

Automated generation of metabolic networks from genome sequence and pathway databases, especially in prokaryotes, has been developed^34–37. This will offer many advantages to modelers: a starting point for curated models (a draft reconstruction is estimated to often take several months even in prokaryotes), a means for doing population or ecological simulation³³, and personalized genomic modeling for patients with metabolic syndromes such as cancer where both the patient and possibly the disease have diverse genotypes^38,39. Eukaryotic models are somewhat more difficult to generate due to the necessity of protein localization and metabolite transporter information³⁴. Automatic reconstruction going beyond enzymatic gene information, such as rFBA models, should also be possible^40,41; the automated generation of boolean and higher-order discrete regulatory models using time-series expression data has been explored as well, though to date these regulatory models have not been coupled to metabolic reconstructions^42–45. These approaches and other families of genome-scale methods are discussed in Table 1.

Table 1.

Families of methods for constraint-based models. Broad classes of methods are described, along with references to some individual implementations or studies.

Method Family	Description	Benefits	Caveats	Solver Type	Notes	Refs
FBA	Flux Balance Analysis: Linear programming applied to the model.	Usually very fast and simple to use, especially when a biomass pseudo-objective is available.	Arguably has more limited use in non-microbial models. Only simple objectives or sequential (e.g. bi-level) optimization is practical.	Linear	Often constraint-based modeling (CBM) in general may be referred to as FBA, though this is not technically correct.	16
MOMA	Minimization of Metabolic Adjustment	Usually very fast and simple to use, especially when a reference or wild-type flux is available; useful for simulating mutations.	It has been argued that the closest distance to a flux doesn’t represent mutation as well as simulating the least number of flux changes (ROOM).	Linear, Quadratic Convex	Related, but slightly more sophisticated methods are being used to estimate flux profiles from expression data.	123,124
DFBA	Dynamic FBA: incorporates a step-wise simulation of FBA, along with update rules that relate biomass to uptake rate, solving for extracellular concentrations.	Allows for some non-steady state observations	Small timescale dynamics and intracellular dynamics may be difficult to model.	Linear (Iterative)	Other, but infrequently used (due to difficulty) methods involving regulation (rFBA) or multi-scale models of tissues build on this approach.	11
EBA	Energy Balance Analysis: FBA, but also incorporates thermodynamic constraints	Incorporates thermodynamic information, prevents futile cycles.	Usually much slower than LP methods like FBA.	nonlinear, MILP, or Monotropic	A highly active research area.	10,15,17,19
Tissue-specific Model Creation	Requires expression data for tissue of interest.	Tissues have vastly different regulatory schemes; these methods take this into account by finding which metabolic genes are likely to be expressed in a given tissue.	Still requires some other method and objective to estimate flux or do pathway analysis.	MILP	A highly active research area.	28–30
Expression-Flux mapping	Takes ideas from MOMA and tissue-specific model creation to estimate fluxes.	Unlike tissue-specific models, will actually estimate the flux since a MOMA-like objective is employed.	Requires high-quality (e.g. RNA-Seq) expression data, or for PROM, abundant microarray data from different conditions.	Linear optimization, but moderate number of simulations or preprocessing required.	Highly accurate predictions can be obtained.	125,126
Interaction Search	Epistasis, or genetic interactions, come up in many contexts, but are also important in energy metabolism, since energy is often related to very important phenotypes including growth, proliferation, and survival.	For such analyses, convex optimization may offer the only tractable method.	Simulating pairwise epistasis in the general case requires pairwise simulation of all double mutants of interest, which can be very time-consuming at the genome scale when different mutations in each gene, or different environments, are considered	Linear optimization, but often many simulations required. Min Cuts (exponential).	The sign of weak epistasis is difficult to predict, due to error propogation in growth rates	127–130

Several approaches have been used in applying CBMs to cancer and the Warburg effect, the preference for glycolytic ATP production over glucose-derived mitochondrial ATP production in cancer cells^46–48. An important study working with a simplified, small model of central-carbon metabolism showed that, while the TCA cycle predicts better ATP yield than glycolysis when only available glucose is considered as a constraint, the addition of enzyme solvent-capacity constraints creates a preference for ATP synthesis through glycolysis⁴⁸. More recently, the work of Vazquez et al. was extended to include a genome-scale model along with enzyme solvent-capacity constraints, which was able to show significant correlations between fluxes and expression in the NCI-60 cell line panel, as well as predicting an intermediate state in cancer metabolism transition exhibiting a temporary increase in OxPhos that was supported by two prior experimental observations⁴⁷. All of these approaches correctly predicted lactate production. Concurrent research on predicting cancer targets by screening for simulated negative epistasis in cancer tissue-specific models that have at least one known-drug target and no known effect on normal tissue revealed many epistatic interactions³⁹. A related study confirmed one of these synthetic lethalities between hemeoxygenase and fumarate hydratase, a mutation found in certain kidney cancers⁴⁹. The recent publication of Human Recon 2 promises to aid in the understanding of many human diseases; already 65 cell-type specific models based on it are available, and the model reports 77% accuracy in identifying metabolic markers across 49 inborn errors of metabolism⁵⁰. Although this model is a great step forward in consolidating much of the knowledge about human metabolism, it is only one of many steps to come. For instance, this model is still primarily only amenable to steady-state approaches, lacks corresponding enzyme-regulatory and signaling architecture, and has introduced more dead-end metabolites than it removed (1,176 versus 339).

1.2 Conclusions

Kinetic models for smaller pathways are possible when the data are present, but many energetic questions concern the entire cell, leaving only incorporation of CBMs as a viable option. The original efficiency and ease of use of FBA have helped propagate a field of more diverse algorithms that are often tractable on today’s computers using the same modeling and software frameworks^51,52. Numerous methods and successful applications in energy metabolism exist, including prevalent diseases such as heart disease, cancer, and Alzheimer’s⁵³.

Multiscale models, as were used in the Alzheimer’s models, will undoubtedly become more common. At the intracellular scale, CBMs are also beginning to incorporate information other than metabolic stoichiometry^54–56. A whole cell model for Mycoplasma genitalium incorporating information about all classes of macromolecular synthesis and degradation, in addition to stoichiometric and regulatory information, found a non-stochastic coupling between metabolism and the cell-cycle where DNA replication rates depended on the concentration of dNTP⁵⁵. Models like these are not easy to build, but substantial endeavors are underway to assist in their draft construction and refinement, and together with an increase in use of jamboree meetings of organism and model experts and online collaborative tools, will likely aid in creating public models of higher quality and the understanding of many biological processes outside the traditional scope of metabolism ^{35,50,57–61}.

2. Biochemical Kinetic Modeling

Biochemical kinetic models describe dynamic properties of metabolic and signaling networks, predicting a variety of different properties e.g. fluxes, metabolite concentrations or complex dynamic behavior with multiple steady states, oscillations and bifurcations over time⁶² (Fig. 2). These kinetic models form mechanistic descriptions of metabolic networks and are able not only to predict effects of environmental stresses or genomic changes but also allow for the investigation of network robustness and design principles. To generate such a model, kinetic parameters must be included in the model explicitly. In practice this requirement makes such models substantially underdetermined. As a result, extensive parameter sensitivity evaluations are required for all model calculations. In this section we discuss the basic formalism of kinetic models. Due to space limitations we do not consider here some important strategies like parameter estimation, model validation and other types of analysis of network models and instead we refer to others kinetic modeling pathway approaches reviewed recently^63,64.

2.1 Kinetic models of metabolic networks

To construct kinetic models, several types of data required. A component of all metabolic networks is stoichiometry and this was discussed above (stoichiometric matrix S: see also FBA part, eq.1).

$$\frac{dM}{dt}=S\ast F(M,p),$$ (1)

Where S is the stoichiometry matrix, M and F are the concentration and flux vectors, and p is the parameter vector.

Presently metabolic pathway charts are known for many organisms and tissues and there are several databases containing this information, e.g. KEGG metabolic pathways database (see Box 1). Construction of models requires the use of mechanistic enzyme flux equations and their reaction laws are included explicitly. The reaction rate (F, eq.1) depends on the concentration of metabolites and kinetic/thermodynamic parameters: Vmax – the maximum activity of the enzyme, turnover rates, Michaelis-Menten constants, effector constants and others. There is a lot of literature available for enzyme kinetics^65,66. A limiting factor in construction of complex dynamic models is the lack of knowledge of kinetic mechanisms and the difficulty in experimental identification of parameters. So the common strategy in computational biology is to reduce the number of unknown parameters and consequently to use simplified or generic rate equations^67,68. Another alternative modeling approach, hybrid dynamic modeling, combines detailed mechanistic kinetics for regulatory enzymes with simplified rate equations with a small number of parameters for the remaining reactions^69,70. To check the reliability of this approach, Bulik et al ⁷⁰ have applied it to two independent metabolic networks including one involving energy and redox metabolism of red blood cells. Calculations of stationary and temporary states under various physiological challenges demonstrate the good performance of the hybrid models.

Box 1. ONLINE RESOURCES FOR KINETIC MODELING.

Enzymes, Pathways and Metabolites

KEGG: (Kyoto Encyclopedia of Genes and Genomes). Comprehensive metabolic pathways database dealing with genes, protein, metabolites and pathways (http://www.genome.jp/kegg/)

BRENDA: (BRaunschweigENzymeDAtabase). Extensive enzyme database. Schomburg I et. al. Nucleic Acids Res. 2013; (http://www.brenda-enzymes.org/)

SABIO-RK (System for the Analysis of BIOchemicalpathways- Reaction Kinetics) Extension of SABIO biopathway database developed for biochemical reaction kinetics: http://sabio.h-its.org/ Wittig U, Kania R et. al. Nucleic Acids Res. 2012

STRENDA: Standards for Reporting Enzymology Data; (http://www.beilstein-institut.de/en/projects/strenda/

GTD: the Thermodynamics of Enzyme-Catalysed Reactions database, the National Institute of Standards and Technology (NIST, USA); Goldberg RN et. al. “Thermodynamics of Enzyme-Catalyzed Reactions -a Database for Quantitative Biochemistry”, Bioinformatics 2004; 20(16):2874–2877; http://xpdb.nist.gov/enzyme_thermodynamics/

ExplorEnz: a database of the IUBMB enzyme list; A.G. McDonald, S. Boyce and K.F. Tipton. Nucleic Acids Res. 37, D593–D597 2009; http://www.enzyme-database.org/index.php

ExPASy: Enzyme nomenclature database; http://enzyme.expasy.org/

MetaCyc: a database of experimentally elucidated metabolic pathways; Caspi et a, ”The MetaCyc Database of metabolic pathways and enzymes and the BioCyc collection of pathway/genome databases”, Nucleic Acids Research., 2012; http://metacyc.org/

HMDB: the Human Metabolome DataBase- contains detailed information about small molecule metabolites found in the human body; Wishart DS, Knox C, Guo AC, et al., HMDB: a knowledgebase for the human metabolome. Nucleic Acids Res. 2009 37(Database issue):D603–610.; http://www.hmdb.ca/

Metabolic Modeling

SBML: (Systems Biology Markup Language). A biomodels database for storing computational models of bioprocesses. (http://sbml.org/Main_Page)

GEPASI: Popular software package for kinetic metabolic analysis; Mendes, P. (1997) Biochemistry by numbers: simulation of biochemical pathways with Gepasi 3. Trends Biochem. Sci. 22, 361–363. http://www.gepasi.org/gepasi.html

Cellware: Modeling tool for cellular transactions; http://www.bii.a-star.edu.sg/achievements/applications/cellware/index.php

BISEN: Biochemical Simulation Environment- set of tools for generating equations for simulating biochemical systems in the Matlab (bbc.mcw.edu/BISEN); Vanlier, J. et al. BISEN: Biochemical Simulation Environment. Bioinformatics (Oxford, England)25, 836–7 (2009)

COPASY: a software for simulation and analysis of biochemical networks. http://www.copasi.org/tiki-view_articles.php

DIZZY: Chemical kinetics stochastic simulation software. http://systems-biology.org/software/simulation/dizzy.html

Constructions of dynamic models with multilevel hierarchical networks which include the integration of multiple biological processes including metabolism, signal transduction, genetic regulation⁷¹ and even living whole-cell⁵⁵ have also been carried out.

All enzyme-catalyzed reactions are reversible in principle and thermodynamic constraints have to be captured in kinetic modeling. There are several thermodynamic enzyme reactions databases available (see Box 1). Several databases have been developed for enzyme kinetic data such as BRENDA and SABIO-RK (see Box 1). In 2004 the STRENDA (STandards for Reporting Enzymology DAta)– a Commision of Beilstein-Institut in Germany were set-up to develop standardization of enzyme data. The STRENDA commission is accompanied by ESCEC (Experimental Standard Conditions of Enzyme Characterizations) conferences where the latest in enzymology and systems biology is presented. Other databases are also described in the Box 1.

Modeling of metabolic dynamics from the cellular to organ level is a powerful tool to interpret experimental data. Recently several kinetic models at the organ level were developed to study energy metabolism in brain^72–74, muscle^67,68 and heart^75,76. These modeling approaches allow for the evaluation of the relative significance of metabolic pathways and regulatory mechanisms, the prediction of responses to environmental stimuli which cannot be directly measured such as the introduction of a drug. These models are also being applied to bioenergetics of diseases such as Parkinson desease.⁷⁷

2.2 Sensitivity Analysis and Metabolic Control

Mechanism based models predict dynamics in a specified system for each set of determined system parameters. It is important however to further investigate the effect of parameter perturbations on the overall system. Identification of network control points, robustness and parameters sensitivities are most crucial to the prediction of the system output behavior. Local parameter sensitivity analysis has been used to identify critical parameters in dynamic models of e.g. muscle energetics⁶⁸ and excitable cell ATP dynamics⁷⁸. The local sensitivity coefficient is defined as:

$$S_p^R={\left(\frac{\partial R/R}{\partial p/p}\right)}_{ss},$$

Where p represents the parameter that is varied and R is a response of the system output such as a concentration or flux, subscript ss means differentiation at steady-state. Local sensitivity analysis allows only one parameter to vary for each calculation, deals with small perturbations and is most widely used in metabolic systems⁶². However, parameters can vary extensively, and for this reason it is more appropriate to explore the possibility of nonlinear effects from simultaneous variations of arbitrary magnitude by means of global parameter sensitivity analysis (GSA)^63,79. GSA has the advantage that it allows for a more comprehensive analysis by applying a Monte Carlo strategy to sample distributions of random parameters ⁷⁹. For each parameter set the sensitivity indices are calculated by minimization of an objective function, defined as a sum of squared errors between perturbed and reference or experimental output.⁷⁹ Metabolic Control Analysis (MCA) is a form of sensitivity analysis which is used in metabolic engineering. MCA computes the extent to which an enzyme controls a flux or concentration in the network. Control coefficients describe the relative sensitivities of dependent variables to independent systems parameters. Metabolic control analysis helps to elucidate the distribution of concentration and flux control coefficients. This approach was developed independently by two groups in the seventies^80,81. In particular, control coefficients describe the change in system variables as a result of perturbation of particular enzyme concentrations (independent parameter). The magnitude of change in pathway flux as response to enzyme concentration change is expressed as the Flux Control Coefficient (FCC)⁸¹

$$C_{E_i}^F={\left(\frac{\partial F/F}{\partial E_i/E_i}\right)}_{ss}={\left(\frac{\partial \mathit{lnF}}{\partial ln{E}_i}\right)}_{ss},$$ (2)

where $C_{E_i}^F$ is the FCC of the ith enzyme, F is the steady-state flux, Ei is the activity of ith enzyme, and the subscript ss means differentiation at new steady-state condition. One feature of MCA is that control properties result from log-log derivatives. As a result, summation theorems which state that e.g. for FCC the sum of all FCCs in metabolic network is equal to one⁸¹

Although sensitivity analysis widely used in kinetic modeling, it is rarely used in genome-scale modeling techniques such as FBA. This is despite the fact that early publications discuss the notion of shadow prices, which describe the rate of change in the objective function with respect to a particular flux, as well as prominent toolboxes featuring implementations of MCMC sampling strategies^5,82.

2.3 Conclusions

In summary, mechanism-based kinetic models, though applied to limited bionetworks, provide a thorough understanding of biological systems. To understand dynamic features of metabolic networks, parameter fits are not necessary, especially when experimental data is limited or not available. In these regards sensitivity analysis becomes a significant tool to study dynamic flux control and has the potential to develop models which possess prognostic power⁶³.

3. Stable Isotope Tracing and Metabolic Flux Analysis

Metabolic Flux Analysis (MFA) employs stable isotope tracing and aims to characterize fluxes based on the distribution of labeling patterns of heavy isotopes (most commonly ¹³C) that are introduced into cells. MFA can yield novel insight into the operation of biological systems, e.g. discovering features such as network mechanisms, novel pathways, futile cycles substrate cycling or alternative reactions. A large set of fluxes in a flux map is described as a fluxome and was defined by Sauer et al⁸³ as the array of fluxes for all of the reactions in a living system. The field of fluxomics aims to analyze this set of fluxes⁸³ (see Fig. 2). In metabolome-wide MFA the number of measurements from labeling experiments is usually much larger than the number of fluxes to be determined. This makes flux estimation an overdetermined problem in mathematical terms. The challenges of modern MFA have provided the motivation to develop additional theoretical frameworks to study the fluxome. For example, the details of flux analysis based on cumomers (see Box 2) are explained in series of papers ^84–86. Alternative methods such as Elementary Metabolite Units⁸⁷ and Bonded Cumomers⁸⁸ aim to minimize the number of necessary state variables and to reduce computational cost^89,90.

Box 2. GLOSSARY for MFA.

Isotopomer (or sometimes refer as isotopologue)-“isotopic” molecule which represents one possible labeled state of a given substrate and so differing in position of isotopes. For metabolite M with n different carbon atoms there are 2ⁿ possible isotopomers (if labeled with two isotopes –e.g. ¹²C or ¹³C isotopes). Particular isotopomer M(i1, i2…in) is the isotopomer with labeled atoms in i1, i2.positions. For example, the Glu(1,2)- isotopomer of glutamate is labeled with its first and second carbon atoms and all others atoms are unlabeled.

Mass-Isotopomer: A set of isotopomers with the same mass. For instance, the mass-isotopomer alanine M+2 (AlaM2) contains all isotopomers with two labeled atoms. A molecule with n carbon atoms has n+1 mass-isotopomers.

Cumomer: the set of isotopomers of metabolite M which contain a particular labeled fragment,⁸⁴ thus representing a “virtual” isotopic molecule. Cumomer M[i1, i2…ik] is the set of isotopomers with labeled i1, i2…ik atoms. For example Lac[1,2]- cumomer of lactate with labeled first and second atoms and the third atom is either labeled or unlabeled. Total number of cumomers for molecule with n different carbon atoms equal to total number of isotopomers, 2ⁿ.

Bonded cumomer: cumomer whose indices refer to adjacent carbons⁸⁸. Lac[1,2]- bonded cumomer and Lac[1,3]- nonbonded.

Flux(F): rate of reaction, expressed e.g. in mkmol/g/min. Reflect in vivo enzymes activity and pathways rate. Flux information is important for mechanistic metabolic and disease pathophysiology studies.

Net flux: difference between reaction forward and backward fluxes F_f-F_b.

Exchange flux (F_e): Often referred as a minimal flux between forward or backward fluxes, usually when F_f>=F_b, F_e=F_b(see above)

Fluxome: set of fluxes for the reactions in organism network. The term was introduced by Sauer et al in 1999⁸³.

Fluxomics: The discipline that applies different computational methods to analyze fluxome

FBA family: steady-state analysis of fluxes, based e.g. on measured input and output (transport) fluxes or whole gene, protein expression and linear programming.

MFA: steady state or dynamic analysis of fluxes based on the network stoichiometry and on the redistribution of labeled patterns of metabolites.

These fluxomics methods are classified as dynamic or static (steady state) depending on the manner of measurement of labeled metabolite patterns. Isotope-based MFA has been applied successfully to complex bionetworks with metabolic cycles, subcellular compartmentalization, reaction reversibility, and futile substrate cycling. Recently, MFA has become a widely used tool. The general methodology for both isotopically steady state and dynamic approaches for ¹³C MFA and ¹³C metabolic modeling has been reviewed recently, with applications to mammalian physiological systems-(e.g. brain),^91–95 microbial fluxome^96,97 and plants⁹⁸. Some important problems in MFA including its methodology, flux error analysis and model validation are discussed elsewere^91,99.

3.1 Metabolic Flux Analysis

MFA currently represents one of the most powerful fluxomics techniques to estimate network fluxes, allowing estimation of both net and exchange fluxes within multi- and sub-cellular compartments (Fig. 2). MFA differs from FBA by incorporating the data from experiments using isotope labeled nutrients (i.e. a tracer) into a metabolic model, and in general is a nonlinear problem. Tracers are supplied continuously to a biological system at metabolic steady state and labeling patterns of downstream metabolites are analyzed. However, it is possible to feed tissue or cells with a limited quantity of label, e.g. with a bolus or pulse, and this infusion technique is relatively common in physiological in vivo temporal studies⁹⁵. The propagation of labels through a network depends on the network’s structure, activity of network enzymes (fluxes), and pool sizes; larger pools slow down propagation and higher fluxes accelerate it⁹¹.

Isotopic enrichments or patterns in metabolites are usually measured by MS coupled with LC or GC and NMR. The isotopes most often used to study bioenergetics are ³¹P (e.g. brain ATP rate analyzed by NMR)^{100,101, 17}O (e.g. cerebral oxygen metabolism by NMR)^{101,102, 18}O (whole body energy balance by MS)^{103, 2}H (e.g. lactate recycling by NMR)¹⁰⁴ and most commonly ¹³C (see above, NMR and MS). The ability to use NMR spectroscopy to study energy metabolism was demonstrated for ³¹P¹⁰⁵ and for ¹³C^106,107 using suspension of microorganisms. Thereafter, seminal in vivo kinetics studies of energy metabolism have been made with ¹³C in perfused heart^108,109 and liver^110–112, and non-invasively in brain^113,114 and skeletal muscle^115,116 using different models.

Technological advances in NMR and MS have led to advances in metabolomics¹¹⁷. In parallel, analytical techniques for ¹³C MFA have been developed - from relatively simple to complex multi-compartmental models with extended bionetworks represented by large numbers of equations. These models were able to demonstrate that human brain energy metabolism has not only a neuronal but also glial component, and have further shown that in glia, TCA cycle and anaplerotic pyruvate carboxylase activity are significant¹¹⁸, and that neuronal TCA cycle activity increases during visual stimulation¹¹⁹, and decreases during normal aging, leading to a neuronal loss of oxidative capacity¹²⁰.

NMR and MS are both capable of measuring label distribution in glycolysis and TCA cycle associated intermediates. High resolution LC-MS methods allow the assessment of all mass-isotopomers (n+1 in total for a metabolite with n carbon atoms, Box 2) of glycolytic and TCA cycle intermediates, many of which are not detectable by NMR due to low sensitivity. NMR however gives more specific information about metabolites’ positional enrichments, via its analysis of ¹³C multiplet spectra (e.g. Glu4- glutamate labeled at C4 position and other amino acids associated with TCA cycle glutamine and aspartate). Still, even this technique is not able to quantify all possible molecules that differ only in their isotope distribution (i.e. isotopomers, see Box 2) (=2ⁿ for a molecule with n different carbon atoms) with one exception¹²¹. Therefore the combination of both methods could potentially give more valuable metabolic information about bionetworks and better precision for calculated fluxes.

High sensitivity could favor the use of radioisotopes (analyzed by liquid scintillation counting and/or PET) and ¹³C hyperpolarized compounds for flux studies. They are particularly convenient if there is no need for positional labeling information. An interesting use of ¹¹C isotope with PET and a mathematical model to study neuroenergetics was recently published¹²².

Detailed mathematical models are required for the correct interpretation of experimental data and to analyze isotopic patterns to calculate in vivo fluxes. Metabolic models differ depending on isotopic specificity of the input data, but three families can be distinguished: positional models, mass-isotopomer models and isotopomer models (see Fig. 2). Most metabolic labeled experiments are limited to measurement of positional fractional enrichments of metabolites (in the case of ¹³C NMR, the yield is at most n independent variables for a metabolite with n asymmetrical carbon atoms) and to only one or few mass-isotopomers from all MS data (n+1 mass-isotopomers). As a consequence there has been no complete description of isotopomer distribution dynamics, resulting in the loss of a lot of mechanistic biochemical information and the reliable determination of metabolic parameters. The main targets of modern isotopomer modeling approaches relate to the accurate determination of metabolic fluxes, improving their reliability, and providing maximal metabolic information which can be derived from the fine structure of ¹³C MR spectroscopy of metabolites and/or metabolome-scale ¹³C mass-isotopomers distributions

3.2 Conclusions

Various approaches for metabolic flux analysis have been employed recently, with the most advanced being cumomer modeling. Despite these advances in the theoretical basis for MFA, it is still an expanding and very active research field. Further progress will combine different analytical and experimental techniques, e.g. MS and NMR data with advanced dynamic and steady-state MFA techniques capable of handling heterogeneous data.

There is a significant value for metabolic flux analysis in many biomedical fields. High performance ‘omics’ tools expand the application of flux analysis further to understand in vivo metabolism and its mechanisms and regulation under different conditions, elucidating the pathological mechanism of diseases, providing information on bottle-neck reactions, and identifying specific steps for drug targets. Moreover, by providing information on flux in individual cells and tissues, MFA can significantly expand the potential of ‘omics’ techniques.

Summary

Fluxes through metabolism directly report in vivo enzyme reaction rates. To comprehensively understand metabolism and elucidate its regulation all three flux modeling approaches should be applied. Each of these modeling approaches (linear modeling, kinetic modeling, and metabolic flux analysis) has successes and limitations. There have been a variety of successes in modeling energy metabolism with steady-state techniques, from the better understanding of diseases as diverse as Alzheimer’s disease and host-pathogen diseases to predicting treatments for cancer. Despite such amazing successes, it must be cautioned that these models are far from perfect; 77% of metabolic biomarkers for inborn errors in metabolism can be predicted with correct directionality with the recently published Human Recon 2, and while a great achievement, still leaves much room for improvement. The yeast models, which have also shown much promise in predicting many phenotypes, have difficulty when predicting effects requiring greater precision, such as epistasis. Undoubtedly, this is largely due to the incompleteness of the reconstructions themselves. For several of the more popular model organisms, iterative improvements of reconstruction releases remain an active area of research. Other model organisms, such as drosophila melanogaster, a model organism often used for studying mitochondrial defects, do not yet possess even a draft reconstruction. The parallel advances in modeling techniques enable the reconstructions to serve a dually important role as mathematically and experimentally verified databases; errors can easily be found by computational procedures, showing us where more experiments are needed to fill the gaps.

A limitation of linear models themselves is their inability to simulate dynamics. But, this is a somewhat artificial constraint, as integrated techniques utilizing the same reconstructions have proven to be successful. Increasingly, integrated techniques and diverse types of data underlying organism or cellular modeling will also play a vital role in improving predictive capability and a systematic knowledge base for biology. When trying to study individual or small sets of pathways, kinetic models may be relatively easy to implement if data is available, and data is rapidly becoming easier to generate with advances in mass spectrometry. However, for many investigators, these methods may be neither easy to implement nor affordable to generate. Genome-scale models can cover more genes, with typically faster simulation times, making them particularly attractive to course-drained drug prediction or genetic interaction studies. In both cases, accuracy largely depends on the assumptions made by the user. Just because genome-scale methods such as FBA can be accurate and easy to run, does not mean a naive attempt will provide valuable predictions.

Box 3. ONLINE RESOURCES for 13C MFA and FBA.

OpenFLUX: software for 13C-based metabolic flux analysis; Quek LE, et. al. Microb Cell Fact. 2009, 8:25. doi: 10.1186/1475-2859-8-25

13CFLUX: software package for analyzing steady-state 13C labeling experiments; runs under Linux; Wiechert W et. al. Metabolic engineering 2001, 3(3):265–283; https://www.13cflux.net/13cflux/

iMS2Flux: MS data processing tool for isotope labeling experiments focusing on increasing throughput at multiple stages of the data analysis; Poskar CH et. al. BMC Bioinformatics. 2012;13(1):295. http://sourceforge.net/projects/ims2flux/

13CFLUX2: the new high-performance software suite for 13C-metabolic flux analysis; runs under Linux; Weitzel M. et. al. Bioinformatics. 2013 Jan 1;29(1):143–5; http://www.13cflux.net/13cflux2/

FiatFlux: a software for metabolic flux analysis from 13C-glucose experiments.

Zamboni N. et. al. BMC Bioinformatics, 2005, 6, 209

ETA: Extracellular Time-Course Analysis, MATLAB-based software for determination of cell specific rates from extracellular time courses. Murphy TA, Young JD. Biotechnol Bioeng. 2013 Jan 7.doi: 10.1002/bit.24836

NMR2Flux: software tool developed for plant metabolism based on two-dimensional NMR spectra; Sriram et. al. Plant Physiology, 2004, 136, 3043

CWave: software package designed for dynamic 13C MFA with positional enrichments based on in vivo NMR data. Mason G.F. et. al. Brain Res. Brain Res. Protoc. 2003, 10, 181

COBRA Toolbox: Open-source MATLAB and Python packages for use with genome-scale models, which includes implementations of many of the linear and constraint based algorithms discussed in this review; Hyduke et. al. Nature Prot. 2011; http://opencobra.sourceforge.net/openCOBRA/Welcome.html

BioMet: Web-based toolbox for stoichiometric analysis, provide the capabilities of genome-wide analysis of metabolism; Svijovic M. et. al. Nucleic Acids Research, 2010, 38, W149; www.sysbio.se/BioMet/

In Silico Organisms: A well-maintained list of curated genome-scale reconstructions and models; http://gcrg.ucsd.edu/InSilicoOrganisms/OtherOrganisms

COBRA Methods: A fairly comprehensive list of genome-scale methods http://cobramethods.wikidot.com/methods