Reconstruction and Identification of DNA Sequence Landscapes from Unzipping Experiments at Equilibrium

Abstract

Two methods for reconstructing the free-energy landscape of a DNA molecule from the knowledge of the equilibrium unzipping force versus extension signal are introduced: a simple and fast procedure, based on a parametric representation of the experimental force signal, and a maximum-likelihood inference of coarse-grained free-energy parameters. In addition, we propose a force alignment procedure to correct for the drift in the experimental measure of the opening position, a major source of error. For unzipping data obtained by Huguet et al., the reconstructed basepair (bp) free energies agree with the running average of the true free energies on a 20–50 bp scale, depending on the region in the sequence. Features of the landscape at a smaller scale (5–10 bp) could be recovered in favorable regions at the beginning of the molecule. Based on the analysis of synthetic data corresponding to the 16S rDNA gene of bacteria, we show that our approach could be used to identify specific DNA sequences among thousands of homologous sequences in a database.

Introduction

Single-molecule techniques make possible the unzipping of a single DNA or RNA molecule, that is, the separation of the two nucleotidic strands under a mechanical action, e.g., at fixed force (1–3), or at constant pulling rate (4–6). The output signal, e.g., the distance between the two ends of the open strands in a constant force experiment (1–3), or the force versus trap displacement in a constant pulling rate experiment (4–6), is known to reflect the basepairing free energies, which depend on the sequence of the biomolecule. A natural question is whether this signal can, in practice, be used to reconstruct the DNA or RNA sequence.

The development of second-generation, high-throughput DNA sequencing methods (7–11) has revolutionized molecular biology and medicine over the past decades. These methods, e.g., sequencing by synthesis, commercialized by Illumina (8,9) (San Diego, CA), sequencing by ligation, called SOLID, commercialized by Life Technologies (12) (Carlsbad, CA), or sequencing by hybridization of complementary DNA probes (13), achieve parallel sequencing of many short DNA fragments, which are then reassembled to obtain the whole genome. There is, however, still a need for improvement to achieve massive, cheap, accurate, fast and individual sequencing. In the third generation of sequencing techniques single-molecule experiments, which in principle avoid the amplification stage and the segmentation of the sequence in shorter subsequences (reads), hold promise for limiting sequencing errors. Two promising methods are sequencing in zero-mode waveguide developed by Pacific Bioscience (Menlo Park, CA), in which the incorporation of nucleotides during the synthesis of a new DNA is observed continuously in real time (14) and nanopore sequencing, based on the readout of the sequence-dependent electrical signal resulting from the passage of a DNA molecule through a nanopore (15). A recently developed method based on a combination of constant-force unzipping and hybridization of complementary probes allows for the accurate readout of the positions of the probe sequences on a single DNA molecule (16). Finally mechanical unzipping of a single-molecule has been shown to be effective to reconstruct small DNA sequences in constant-force experiments (3). Even if unzipping experiments will not be, in the immediate future, competitive with commercial sequencing technologies they can provide complementary techniques, which can be advantageous, as well as simpler and cheaper, for particular applications. Among these applications are the rapid classification of an individual sequence, e.g., to characterize which bacterium has infected a patient, and the detection of genetic variations responsible for diseases, such as variations in the copy number of repeated sequences, which are particularly difficult to quantify with current sequencing methods.

Apart from direct application to the development of sequencing technologies, unzipping experiments have become a good experimental system to test equilibrium and out-of-equilibrium theories in statistical mechanics. This is due both to the very high control of the experimental system and to the fact that unzipping is very well modeled by a one-dimensional random walk of the opening fork (the boundary between the open and closed portion of the DNA double helix) in a disordered potential caused by the DNA sequence (5,6,17–19). Theoretical works have, in particular, focused on the possibilities of reconstructing the features of the sequence-specific free-energy landscape through equilibrium (2,3,20) and out-of-equilibrium measurements (21–26).

An important issue in extracting information on the sequence from unzipping experiments is the limitations due to the experimental setup (6,20,27). Thompson and Siggia have stressed the difficulty of inferring the sequence because the position of the opening fork cannot be read out directly from the displacement of the optical trap (see Fig. 1), as the thermal fluctuations in the single-stranded (ss) DNA may exceed the average gain of ∼1 nm consecutive to the opening of one basepair (27). Other limitations of the experimental system are the thermal drift of the optical trap, the precision over the measured force, and the limited spatial resolution. Subnanometric spatial resolution, and a precision of measured forces on the order of a fraction of a piconewton, can nowadays be routinely achieved. However, the thermal drift of the optical trap remains a major problem in unzipping data, limiting the ability to associate local features of the force signal with an absolute position in the sequence.

Figure 1.

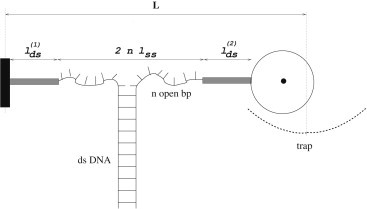
Sketch of the setup for the single DNA molecule unzipping experiment. The DNA molecule is attached to the surface (left) and a bead (right) held in an optical trap at distance L from the surface through rigid linkers of total length ${\ell }_{\text{ds}}$. When the unzipping force is equal to its average value $f_{\text{av}}$, the single strands corresponding to the n unzipped basepairs of the molecule have extension $2n{\ell }_{\text{ss}}$, and the bead is displaced by ${\ell }_{\text{av}}$ from the center of the trap. When the force deviates from $f_{\text{av}}$ the extension of the ssDNA strands and the displacement vary according to their stiffnesses, $K_{\text{ss}}\left(n\right)$ and $K_{\text{trap}}$.

In this work, we explicitly take into account in the inference model thermal fluctuations coming from the single strands of DNA, the linkers, and the bead in the optical trap. We express the average force at a given position as a convolution of the force signal over the possible positions of the opening fork with these distance fluctuations (4,6). Two techniques for inferring the sequence-specific free-energy landscape from the force signal at equilibrium are introduced. The first method, called saddle-point (SP) approximation, is fast and simple, and requires very little computational effort. The second method, called Box approximation, relies on the maximum likelihood inference of the free-energy parameters, coarse-grained over an appropriate number of basepairs, and is more demanding from a computational point of view. In addition, we show how multiple force signals corresponding to the same molecule can be aligned using an extension of alignment algorithms developed in bioinformatics. This alignment procedure can be used to reduce the drift effect in the data.

First, we use our alignment and inference methods to reanalyze experimental data from a study of unzipping at constant and low velocity by Huguet et al. (4). We show how the sequence free-energy landscape can be reconstructed on the scale of several basepairs, and we discuss how this characteristic scale depends on the setup features. Based on those findings, we then show that our approach can be used to identify specific DNA sequences among a large database of homologous sequences. A proof of principle is given from synthetic force data corresponding to the 16S rDNA genes of 2076 bacteria. We show that our procedure is capable of matching a 16S gene with the same gene in the database, and to distinguish it from homologous genes with a few mismatches.

The article is organized as follows. In the Materials and Methods section, the model for DNA unzipping (6) is exposed and a local harmonic approximation of ssDNA elastic properties around the unzipping force is introduced. We then describe the two inference methods, called SP approximation and Box approximation, which allow us to reconstruct the free-energy landscape from the measured forces. We also explain how force data obtained from the same DNA molecule can be aligned to remove the drift. In the Results and Discussion section, we investigate the inference performances of the SP and Box approximations along the sequence for two repetitions of the unzipping experiment on the same sequence (4). The inference procedures are applied to synthetic force data generated from the 16S rDNA genes of a bacterial database, and we discuss their ability to identify one gene across a family of thousands of homologous sequences. Perspectives and open problems are discussed in the Conclusion.

Material and Methods

Model for DNA unzipping

Let $s_i=A,C,G,T$ be the bases in the DNA sequence along the 5′-to-3′ strand, with $i=1,\dots ,N$ being the base index (Fig. 1). The free-energy cost for unzipping the first n basepairs of the double-stranded (ds) DNA molecule is given by

$$G_{\text{ds}}\left(n\right)=\sum _{i<n}{g}_0\left(s_i,s_{i+1}\right),$$ (1)

where $g_0\left(s_i,s_{i+1}\right)$ takes into account both pairing and stacking contributions between neighbor bases on the strand. The 10 independent values of $g_0\left(s_i,s_{i+1}\right)$ are given as functions of the temperature and ionic condition (28,4), and are reported for the data we have analyzed in the Section I in the Supporting Material.

Each one of the two unzipped strands of the molecule are modeled as harmonic springs, with stiffness constant $K_{\text{ss}}\left(n\right)$, rest length $n{\ell }_{\text{ss}}$ and rest free energy $n{g}_{\text{ss}}$; $K_{\text{ss}}\left(n\right)$, ${\ell }_{\text{ss}}$ and $g_{\text{ss}}$ are effective parameters obtained from a local harmonic approximation of the freely-jointed chain model, known to be accurate for ssDNA elastic properties (29,30), around the average unzipping force, $f_{\text{av}}$. In addition, the setup includes two very short dsDNA linkers with total length ${\ell }_{\text{ds}}$, which we consider to be rigid, and the optical trap, with stiffness constant $K_{\text{trap}}$. We denote by L the position of the trap (see Fig. 1).

After integrating out the degrees of freedom related to the unzipped strand extensions and the displacement of the bead in the trap, we obtained an effective free energy for the number of unzipped basepairs, n, as a function of the trap position, L, given by

$$G\left(n|L\right)=G_{\text{ds}}\left(n\right)-2n{g}_{\text{ss}}+\frac{1}{2}K\left(n\right){\left(L-{\ell }_{\text{av}}-{\ell }_{\text{ds}}-2n{\ell }_{\text{ss}}\right)}^2,$$ (2)

where the effective spring constant is given by $1/K\left(n\right)=\left(2/K_{\text{ss}}\left(n\right)\right)+\left(1/K_{\text{trap}}\right)$ and ${\ell }_{\text{av}}=f_{\text{av}}/K_{\text{trap}}$ is the displacement of the bead in the trap at the average unzipping force. It is important to stress that the effective stiffness, $K\left(n\right)$, is dominated at the beginning of the opening by the trap stiffness. When the number, n, of open bases is such that $K_{\text{ss}}\left(n\right)$ becomes small with respect to $K_{\text{trap}}$, the stiffness is, conversely, dominated by the single-strand thermal fluctuations, and decreases with n. For the experimental setup in Huguet et al. (4), the crossover takes place for a few hundreds of open basepairs (see Fig. S1 in the Supporting Material). The effective stiffness does not vary significantly when, for fixed L, the number of unzipped basepairs changes around its average number. Hereafter we will therefore consider that it is a function of L only, denoted by $K\left(L\right)$. Details about the harmonic approximation, the value of $K\left(L\right)$, and the derivation of Eq. 2 can be found in Section II of the Supporting Material.

The free energy of the system is a function of the trap position, L, given by (in units of $k_{\text{B}}T$)

$$G\left(L\right)=-\log Z\left(L\right),\text{with}Z\left(L\right)=\sum _{n=0}^N{e}^{-G\left(n|L\right)}.$$ (3)

Knowing the free energy, we can easily compute the value of the force at equilibrium for fixed L:

$$\langle f\rangle \left(L\right)=f_{\text{av}}-\frac{dG}{dL}\left(L\right).$$ (4)

Hereafter, we refer to $G_{\text{ds}}\left(n\right)$ (1) as the cumulative basepair free energy, and to the set of basepair free energies, $g_0\left(s_i,s_{i+1}\right)$, versus basepair index, i, as basepair free energies. We now present two procedures to infer the basepair free energies from the knowledge of the experimental unzipped force, $f_{\text{exp}}\left(L\right)$.

Inference of the basepair free-energy landscape: SP approximation

Given the position, L, of the trap, the most likely value of the number of unzipped basepairs is $n^{\text{SP}}\left(L\right)$, minimizing $G\left(n|L\right)$. The SP approximation consists of approximating the sum over the values of n in Eq. 3 for $Z\left(L\right)$ by its dominant contribution, coming from $n=n^{\text{SP}}\left(L\right)$. Within the SP approximation, the free energy simply corresponds to $G\left(L\right)=G\left(n^{\text{SP}}\left(L\right)|L\right)$, and the equilibrium force is given by

$$\langle f\rangle \left(L\right)-f_{\text{av}}\simeq -\frac{\partial G}{\partial L}\left(n^{\text{SP}}\left(L\right),L\right)\simeq K\left(L\right)\left(L-{\ell }_{\text{av}}-{\ell }_{\text{ds}}-2n^{\text{SP}}\left(L\right){\ell }_{\text{ss}}\right).$$ (5)

As the unzipping proceeds, dsDNA pairing and stacking free energy is converted into ssDNA elastic free energy, equal to

$$g\left(L\right)\equiv 2g_{\text{ss}}+2\left(\langle f\rangle \left(L\right)-f_{\text{av}}\right){\ell }_{\text{ss}}$$ (6)

per unzipped basepair within the harmonic model of ssDNA outlined above. $g\left(L\right)$ is, at equilibrium, equal to the mean value of the basepair free energy, $g_0\left(s_n,s_{n+1}\right)$, averaged over the distribution of the number, n, of unzipped basepairs at fixed L.

Upon replacement of the equilibrium force, $\langle f\rangle \left(L\right)$, with the experimental measure, $f_{\text{exp}}\left(L\right)$, in Eqs. 5 and 6, we obtain the number of unzipped basepairs,

$$n^{\text{SP}}\left(L\right)=\frac{1}{2{\ell }_{\text{ss}}}\left(L-{\ell }_{\text{av}}-{\ell }_{\text{ds}}-\frac{f_{\text{exp}}\left(L\right)-f_{\text{av}}}{K\left(L\right)}\right),$$ (7)

and the corresponding equilibrium basepair free energy,

$$g^{\text{SP}}\left(L\right)=2g_{\text{ss}}+2\left(f_{\text{exp}}\left(L\right)-f_{\text{av}}\right){\ell }_{\text{ss}},$$ (8)

respectively, at trap position L. The basepair free-energy landscape of the DNA molecule can then be parametrically plotted by representing $\left(n^{\text{SP}}\left(L\right),g^{\text{SP}}\left(L\right)\right)$ for various values of L (see Results).

Inference of the basepair free-energy landscape: Box approximation

The SP approximation is fast and easy to implement, but neglects all the fluctuations of the number of unzipped basepairs around its most likely value, $n^{\text{SP}}$. To take into account those fluctuations, we resort to another approximation scheme, where the average value of the force is computed exactly through the sum over all possible values of n as in Eq. 4, but where the cumulative basepair free energy, $G_{\text{ds}}$ in Eq. 1, depends on a limited number of parameters, which can be optimized to reproduce the experimental force signal. To do so, we write the cumulative free energy as a sum of box functions of width b,

$$G_{\text{ds}}^{\text{Box}}\left(n\right)=b\sum _{k=0}^{\text{integer}\text{part}\text{of}n/b}{g}_k.$$ (9)

Parameter $g_k$ represents the box average of the free energies over the basepairs in the interval $i=kb+1,\dots ,\left(k+1\right)b$. The value of b can be chosen at convenience; the order of magnitude coincides with the typical fluctuations over the position of the bead in the optical trap at fixed position L (in units of ${\ell }_{ss}$),

$$b_{\text{B}}\left(L\right)=\sqrt{\frac{k_{\text{B}}T}{4K\left(L\right){\ell }_{\text{ss}}^2}}.$$ (10)

We have chosen $b=b_B\left(L\right)/2$. In Section IVB of the Supporting Material, we indeed show that it is optimal to adapt b to the characteristic fluctuations of the apparatus or, equivalently, to choose the precision of the inference in accordance with the stiffness of the setup. Note that b varies with L due to the dependence of the effective stiffness, K, on the trap position (see Fig. S1).

The aim of the inverse problem is to infer the parameters $g_0,g_1,\dots ,g_{N/b-1}$ from the experimental unzipping curve, $f_{\text{exp}}\left(L\right)$. As a result of thermal fluctuations of the number of unzipped basepairs at fixed L, we expect the force measures, $f_{\text{exp}}\left(L\right)$ and $f_{\text{exp}}\left(L^{\prime }\right)$, to be correlated (influenced by the same part of the sequence) as long as $\left|L^{\prime }-L\right|<\sqrt{k_{\text{B}}T/K}\sim b{\ell }_{\text{ss}}$. To reduce redundancy in the data, we consider the set of measured forces, $f_{\text{exp}}\left(L_k\right)$, at discrete positions $L_k=L_0+k\times 2b{\ell }_{\text{ss}}$, with integer-valued k; the offset position $L_0$ encompasses the linker length, ${\ell }_{\text{ds}}$, and the average bead displacement, ${\ell }_{\text{av}}$. We further assume that the experimental error in measuring the force is a normal variable with zero mean and variance ${ϵ}^2$, with $ϵ=0.1$ pN. The logarithm of the probability of the set of measured forces at positions $L_k$ is

$$\log P\left(\left\{f_{\text{exp}}\left(L\right)\right\}|\left\{g_k\right\}\right)=-\frac{1}{2{ϵ}^2}\sum _{k=0}^{N/b-1}{\left(f_{\text{exp}}\left(L_k\right)-{\langle f\rangle }^{\text{Box}}\left(L_k\right)\right)}^2-\frac{1}{2{\Delta }^2}\sum _{k=0}^{N/b-1}{\left(g_k-\overline{g}\right)}^2$$ (11)

up to an additive constant independent of the $g_k$ parameters. ${\langle f\rangle }^{\text{Box}}\left(L_k\right)$ is the equilibrium force at trap position $L_k$, given by Eq. 4, with the true cumulative basepair free energy, $G_{\text{ds}}$, replaced with $G_{\text{ds}}^{\text{Box}}$. The second term in Eq. 11 represents the a priori contribution to the log probability; it regularizes the inference problem by imposing that the inferred free-energy parameters, $g_k$, should be around the typical value, $\overline{g}=2.5$. The penalty parameter, $\Delta \simeq 1$ (in units of $k_{\text{B}}T$), corresponds to the expected deviation of $g_k$ around $\overline{g}$.

In the spirit of maximum-likelihood inference, we maximize $\text{log}P$ over the $g_k$ coefficients using a gradient ascent procedure. The maximum does not seem to depend on the initial values of $g_k$. In addition we find that the optimum over $g_k$ depends weakly on the parameter $\gamma ={\left(ϵ/\Delta \right)}^2$ in the expected range ${10}^{-4}-{10}^{-2}$ (see Section IVA in the Supporting Material).

Alignment of experimental unzipping forces

We have reanalyzed the data of Huguet and collaborators (4), in which a part of a λ-DNA molecule of 6800 base pairs, of known sequence, is unzipped at low velocity (10 nm/s), at 1 M monovalent salt concentration. The two complementary strands of the DNA molecule are attached, through two 29-nucleotide-long dsDNA handles, to a bead and to a micropipette. The force on the bead is measured through the displacement in the optical trap (see Fig. 1) and acquired at 1 kHz frequency. We have filtered this signal at a frequency of 1 Hz to obtain the average force at each position. We have analyzed two unzipping curves (see Fig. 4) corresponding to two molecules with the same sequence, hereafter called Molecules 1 and 2. Notice that the unzipping curves do not start at the beginning of the sequence, as the first recorded forces correspond to ∼700 open basepairs for Molecule 1 and 950 open basepairs for Molecule 2.

Figure 4.

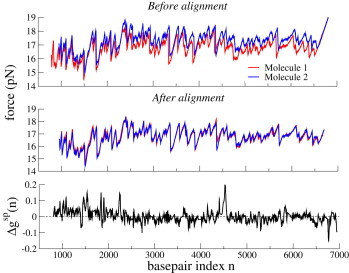
Force-curve alignment for Molecules 1 and 2. (Upper) Experimental force versus trap displacement for two unzipping experiments (Molecules 1 and 2) in Huguet et al. (4). (Middle) Coincidence between the force curves is strongly improved by our alignment procedure. We first globally shift the curve of Molecule 2 by $\simeq 0.5$ pN, then apply the Matlab routine for aligning the force curves along the basepair index axis, described in the main text. (Lower) Difference, $\Delta g^{SP}\left(n\right)$, between the SP free energies inferred from Molecules 1 and 2 after alignment. To see this figure in color, go online.

An important source of experimental error is a low-frequency drift of the instrument, resulting from dilatations or contractions after local changes in temperature. The drift adds extra noise in the measurement of position L of the optical trap. Experimental data were preprocessed by Huguet et al. to reduce experimental drift (see Huguet et al. (4) and their Supplementary Information). Even after this preprocessing, however, the two experimental force curves for Molecules 1 and 2 were not perfectly superimposed (see Fig. 4, upper), and the two corresponding sets of 10 free-energy parameters, $g_0$, calculated in Huguet et al. (4), referred to as best sets, differed by $10\text{\%}$ (see Fig. S19).

To align two force curves, we propose the following procedure, based on the celebrated Needleman-Wunsch alignment algorithm of bioinformatics (31). First, we compute the average unzipping forces, $f_1\text{and}{f}_2$, for the two molecules, and apply a global shift, $f_2-f_1=0.5$ pN, on the force curve of Molecule 2. This correction compensates a global error (offset) on the absolute force measure (typically of the order of some fractions of a piconewton). Second, we align the two force curves using the Matlab routine nwalign, which implements the Needleman-Wunsch algorithm. This routine aligns sequences of symbols (generally, bases or amino acids) according to a matrix of scores, expressing the similarities between pairs of symbols. Here, symbols are force values, and the score is a measure of how close two values are. In practice, we discretize trap positions L with a step of $\Delta L=1$ nm and the force values, $f\left(L\right)$, in $N_f=22$ increments, $\Delta f\sim 0.2$ pN. This choice allows us to cover the 4–5 pN total range of variations of the unzipping force along the molecules. Each force curve is therefore turned into a discretized sequence, $i\left(L\right)$, with $i=1$ for the minimal value of the force and $i=N_f$ for the maximal value. The score for aligning two force increments i and j at the same position is given by

$$S_{ij}\equiv S\left(i-j\right)=-\frac{{\left(i-j\right)}^2}{2{\sigma }^2}.$$ (12)

Parameter σ is related to the experimental resolution of the force (of the order of 0.1–0.5 pN) divided by the discretization interval, $\Delta f$; hereafter, we choose ${\sigma }^2=5$. The minimal score, $S\left(N_f\right)$, corresponding to the $\sim 4$ pN maximal difference between two unzipping forces, is $S\left(N_f\right)\simeq -35$. In addition, gaps can be inserted in the alignment, with a fixed score of $S_{\text{gap}}=-20$, about halfway between the scores $S\left(0\right)=0$ and $S\left(N_f\right)$. Gaps are necessary to compensate for the drift of the trap position in one force signal relative to the other one. We have verified that the force signal alignments are weakly affected by the choice of another set of parameters or of another number of discretization intervals, $N_f$ (Fig. S24).

In the Results section, we will compare the basepair free energies inferred using the data of Molecule 1 to the values computed from its best set and the λ-DNA sequence; results for Molecule 2 are reported in the Section V in the Supporting Material. Moreover, we will realign the force curves with the procedure described above and compare the two inferred basepair free-energy landscapes with the one obtained from the free energies given by the Mfold server (see Section VI in the Supporting Material). Finally, we will also generate synthetic force data by computing the equilibrium unzipping force as a function of the displacement, given the sequence and the Mfold free energies. These synthetic data allow us to infer the beginning of the sequence, which was lost in the experimental data. In addition, and of more importance, synthetic data are useful to estimate the performance of the inference method in ideal conditions (no drift, strict equilibrium).

Synthetic data on 16S bacterial genomes

A potential application of unzipping experiments is to identify an unknown DNA sequence from a database of reference sequences. To illustrate how DNA screening can be implemented, we focus on the 16S ribosomal RNA gene, of about $N=1540$ bp. The 16S rDNA gene is widely used for phylogenetic classification of bacteria, and is relatively long to have a good statistics in sequence comparison (32). To better understand the resolution that could be achieved with unzipping analysis, we have downloaded from the NCBI RefSeq database (33) ∼2500 well cured 16S bacterial sequences. The 16S rDNA sequence of one bacterium, hereafter called the test sequence, is chosen in the database. We then compute the theoretical unzipping force curves for all 16S bacterial sequences, infer the corresponding basepair free-energy landscapes, and compare them with the test landscape. We estimate their discrepancies, and whether they are large enough compared to the experimental uncertainty computed from the detailed analysis of the experimental data above.

Results and Discussion

SP inference: reconstructed basepair free-energy landscape

The inference of the basepair free energy is easily done using the SP approximation, as Eqs. 7 and 8 provide a parametric representation of g versus the number of unzipped basepairs, n, as a function of the trap position, L. The outcome for the data of Molecule 1 is shown in Fig. 2 and compared with its counterpart obtained from the sequence and the best free-energy parameters (Table S1), and averaged on a sliding window of 30 bp. The results of the SP inference for synthetic data generated from the model (4) are also plotted in Fig. 2. The difference between the basepair free energy inferred from the experimental data and that inferred from the synthetic data is small with respect to their common discrepancy with the true basepair free energies. This good agreement entails that our unzipping model based on the local harmonic approximation is accurate, and that out-of-equilibrium effects are weak: the unzipping velocity is low enough for the system to be effectively at equilibrium for each trap position L.

Figure 2.

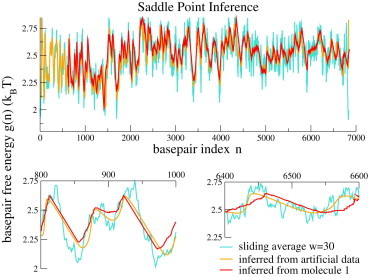
SP inference. The basepair free energies, $g\left(n\right)$, inferred from Molecule 1 force data (red curve) are compared to the true free energies (computed from Mfold, sliding average over $w=30$ bp; turquoise curve) and to the free energies inferred from synthetic data generated from the model (orange curve). (Upper) Complete sequence. (Lower) Magnifications of two regions, one at the beginning of the molecule (left) and one at the end (right). To see this figure in color, go online.

The performance of the SP procedure strongly depends on the local features of the free-energy landscape. The unzipping force signal is characterized by the so-called stick-slip phenomenon (34). When strong basepairs are followed by weaker base pairs the cumulative free energy, $G\left(n|L\right)$, Eq. 2, may have two local minima in $n_1$ and $n_2$, with $n_1<n_2$. The stick phase corresponds to the first minimum $\left(n=n_1\right)$: the single strands and the bead in the trap are pulled and stretched without breaking strong bases. In the slip phase (the second minimum, in $n=n_2$), not only the strong basepairs but also the contiguous weak basepairs have opened. The stick-slip phenomenon gives rise to the characteristic sawtooth behavior of the unzipping force. Conversely, in regions where weak basepairs are followed by strong basepairs, the cumulative free energy, $G\left(n|L\right)$, has generally a unique minimum.

Fig. 2 shows that the SP approximation, which replaces the sum of the contributions associated with different n in Eq. 3 with a unique contribution from $n^{\text{SP}}$ is accurate in the non-stick-slip regions (e.g., region $800<n<820$ in Fig. 2, lower), and less accurate in the stick-slip regions (e.g., region $820<n<860$ in Fig. 2, lower), where it cuts the true free-energy landscape. Detailed calculations presented in the Section III of the Supporting Material show how the error in reconstructing the landscape of stick-slip regions done by the SP approximation depends on the total stiffness of the apparatus, $K\left(L\right)$.

Box inference: reconstructed basepair free-energy landscape

In Fig. 3, the basepair free energies, $g\left(n\right)$, inferred with the Box approximation from the unzipping data of Molecule 1 and from the synthetic data are compared to their true counterparts, computed from the best free-energy parameters found in Huguet et al. (4), and averaged on a sliding window of 30 bp. Fig. 3 (middle row) shows how the Box inference allows us to better follow the variation of the basepair free-energy landscape along the sequence, whereas the SP inference tends to cut the free-energy barriers. The results for Molecule 2 are very similar (see Fig. S14). The strong similarity between the free-energy landscapes corresponding to experimental and synthetic data inferred with the Box approximation in the two regions magnified in the middle row of Fig. 3 (at the beginning and end of the data sets) provides further support for the validity of the model and the equilibrium assumption. In Fig. 3, lower, we show the basepair free-energy landscape inferred with the Box approximation and the true basepair free-energy landscape with a box average with the same window size, b. The value of b (see Eq. 10) ranges from 5 bp at the beginning of the unzipping curve to 10 bp at the end of the sequence.

Figure 3.

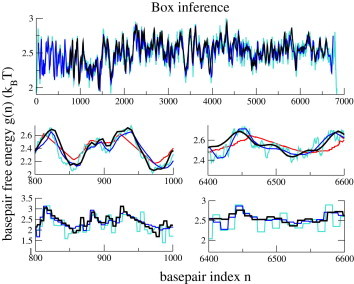
Box inference. Comparison of the basepair free energies, $g\left(n\right)$, inferred with the Box procedure from the force data of Molecule 1 ($b=5$; black curve) and from the synthetic data ($b=5$; blue curve) with the true free energies ($w=30$; turquoise curve). (Upper and middle) Sliding averages with width $w=30$ bp. Red curve (middle) shows the SP inference for Molecule 1, as in Fig. 2. (Lower) Box averages of widths 5 (left) and 10 bp (right). To see this figure in color, go online.

A detailed description of the reconstruction error along the sequence, i.e., of the difference between the true and the inferred basepair free-energy landscapes within the SP and Box approximations can be found in Section V of the Supporting Material. The reconstruction error does not show any systematic (monotonic) behavior with the number, n, of unzipped basepairs along the sequence. However, the error is larger in stick-slip regions (Fig. S10) and in regions for which the thermal drift of the optical trap has not been appropriately corrected, and the inferred basepair free-energy landscape is shifted with respect to the true landscape. This statement is corroborated by the fact that the inference error in the synthetic data set has much smaller peaks. The inference error in the real data are dominated by this drift problem, with the consequence that, apart from the very beginning of the sequence (700–1500 bp), it is not much lower with the Box approximation than with the SP approximation.

Alignment of unzipping force signals and experimental uncertainty in the inferred free-energy landscapes

To compare the inferred basepair free-energy landscapes of Molecules 1 and 2 with those obtained from the Mfold pairing parameters (Table S3 and Section VI in the Supporting Material), we aligned the two experimental force signals using the procedure described in Methods (see Fig. 4, middle). The agreement between the two force signals is much better than in the absence of alignment (Fig. 4, upper), though some differences are still visible, e.g., around $n=4400$ bp. These differences allow us to quantify the experimental resolution of the force signal for two unzipping experiments with the same sequence in the setup used by Huguet and collaborators. We estimate the resolution of the SP landscape through the discrepancy between the free energies inferred for the two molecules after alignment by

$$\Delta g_{av}^{SP}=\frac{1}{N}\sum _n\left|\Delta g^{SP}\left(n\right)\right|,\text{with}\Delta g^{SP}\left(n\right)=g_1^{SP}\left(n\right)-g_2^{SP}\left(n\right),$$ (13)

where subscripts 1 and 2 refer to Molecules 1 and 2, respectively. We find $\Delta g_{\text{av}}^{\text{SP}}\simeq 0.025$ (in units of $k_{\text{B}}T$). Hence, the resolution per basepair is very small compared to the differences in free energy between different basepair types, which proves the efficiency of the alignment procedure.

Fig. 4 (lower) shows that the discrepancy $\Delta g^{\text{SP}}\left(n\right)$ is not uniform along the sequence and can reach values about 10 times higher than $\Delta g_{\text{av}}^{\text{SP}}$ values in some regions.

Sequence identification of the bacterial gene from synthetic force signal

We now compare the inferred free-energy landscapes between one 16S rDNA gene (the test sequence) and three other reference sequences based on the synthetic data. The test sequence, which we have chosen at random from the NCBI database (33), is a Brevibacterium of the frigoritolerans species (B-F); it is responsible for foot odor and is used for cheese fabrication. The reference sequences are a cyanobacterium, Nostoc azollae (N-A), another Brevibacterium, B. halotolerans (B-H), and the bacterium Bacillus simplex of the DSM 1321 strain (B-S). N-A and B-F have quite different 16S genes (329 mismatches), whereas B-H and B-F are more similar (102 mismatches); B-S, though not classified in the same family, is very similar to B-F (18 mismatches).

The first plot of Fig. 5 shows the theoretical unzipping force curves corresponding to the B-F and N-A genes and computed according to Eq. 4. As the two sequences differ widely in composition and length ($N=1478$ and 1540 bp for N-A and B-F, respectively), the force curves are not well aligned, even if drift is not present in the synthetic data. We therefore align the two force curves using the force alignment procedure described in Methods (see Fig. 5, second plot). The SP free-energy landscapes of the two sequences are then inferred (Fig. 5, third plot). Remarkably, the SP inferred free-energy landscapes are well aligned, as are the true free-energy landscapes obtained from the directly aligned sequences (Fig. 5, bottom). Moreover, the locations (basepair indices) of the discrepancies between the two inferred landscapes coincide with those between the true landscapes.

Figure 5.

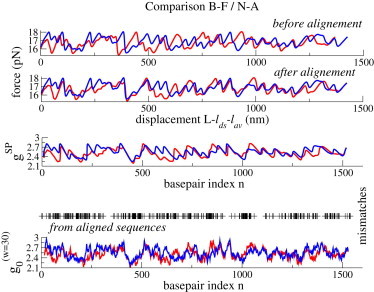
Comparison of the 16S gene of B-F and N-A bacteria from synthetic unzipping force signals. (Upper two plots) Equilibrium forces calculated from the 16S gene of the B-F (blue) and N-A (red) bacteria before (upper) and after (lower) alignment of the force signals. (Middle) Basepair free energies inferred from the aligned force signals with the SP procedure. (Lower) Basepair free energies computed from the aligned sequences and Mfold at 150 mM NaCl, averaged on a 30 bp sliding window; mismatch positions are shown with black crosses. To see this figure in color, go online.

For the comparison of the test sequence (B-F) with the more similar reference sequences (B-H and B-S), we show in Fig. 6 the basepair free-energy differences, $\Delta g\left(n\right)$, between the landscapes inferred from the equilibrium force curves of the test and reference sequences using the SP (Fig. 6, upper) and Box (Fig. 6, lower) approximations; the corresponding free-energy landscapes can be found in Figs. S29–S34. Fig. 6 (upper) shows in addition the differences between the true landscapes, averaged over 30 bp. B-F and B-H can clearly be distinguished on this scale based on their SP free-energy landscapes. The difference between the inferred SP landscapes is $\Delta g^{\text{SP}}=59$ k_BT in total or, equivalently, $\Delta g_{\text{av}}^{\text{SP}}\simeq 0.04$ k_BT/bp (see Eq. 13), which is larger than the resolution of $\simeq 0.02$ k_BT estimated from the experiments on the λ-phage Molecules 1 and 2. We therefore conjecture that B-F and B-H could be distinguished using the SP procedure on unzipping data obtained with the setup of Huguet et al. (4).

Figure 6.

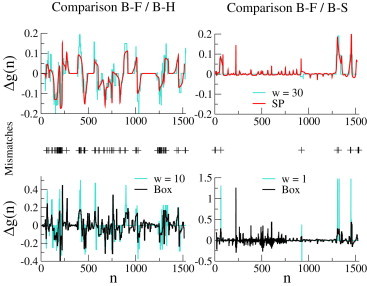
Comparison of the 16S gene of B-F bacterium with those of B-H (left) and B-S (right) bacteria from synthetic unzipping force signals. Differences, $\Delta g\left(n\right)$, between basepair free energies of the two bacteria after inferences with the SP (upper) and Box (lower) approximations. Sliding averages over $w=30$ (upper), 10 (lower left), and 1 (lower right) of the differences between the Mfold free energies at 150 mM NaCl are shown for comparison (turquoise line). (Middle) Mismatches between B-F and B-H (left) and between B-F and B-S (right) sequences, obtained from direct alignment of the sequences; there are 102 mismatches between B-F and B-H, and 18 between B-F and B-S. To see this figure in color, go online.

The 16S genes of B-F and B-S differ by 18 mismatches only, 12 of which are located at the extremities of the molecules. Mutations can nevertheless be detected from the SP landscapes (Fig. 6, upper right) inferred from the synthetic data. Small peaks in the SP free-energy difference in mutation-free regions come from local errors in the force alignment, presumably due to the finite increment ($\approx 0.2$ pN) in the discretization of the force signal. The total difference between the inferred SP landscapes is $\Delta g^{\text{SP}}=12$ k_BT, that is, $\Delta g_{\text{av}}^{\text{SP}}\simeq 0.008$ k_BT/bp. This small value suggests that B-F and B-S probably could not be distinguished with unzipping data obtained with the setup of Huguet et al. (4)

With the Box procedure (Fig. 6, lower) the differences, $\Delta g\left(n\right)$, between the inferred landscapes agree with the differences between the true landscapes, averaged over $w=10$ bp for B-F and B-H (Fig. 6, lower left) and over $w=1$ bp for B-F and B-S (Fig. 6, lower right). In the latter case, all six internal mismatches coincide with peaks in the difference between the inferred basepair free energies, and can be detected; an additional peak, around basepair 250, is due to a local error in the force alignment. However, the Box approximation method is slower than the SP method (it takes several hours to fit the parameters for the $\simeq 1500$ bp sequence on a commercial Desktop computer with Mathematica). In addition, the Box procedure is more sensitive than SP to small errors in the force alignment procedure, e.g., errors around $n=500$ in Fig. 6, lower right. The Box method should therefore be used as a refinement procedure to better quantify the differences in free-energy landscapes detected by the SP method.

Large-scale screening of bacterial database

We now carry out a large-scale screening of the bacterial database, keeping the test sequence (B-F) unchanged; the results of a similar large-scale screening where the test sequence is N-A are presented in Fig. S35. For each of the 2076 sequences in the database (see Section VIIF in the Supporting Material), we compute the synthetic equilibrium force curve, align it with the test force signal, and infer the SP free-energy landscape. The total free-energy difference with the test SP landscape is shown in Fig. 7 as a function of the number of mismatches in the pairwise sequence alignments (Fig. 7, left) and of the total difference between the true free-energy landscapes computed with Mfold (Fig. 7, right). The whole calculation for the 2076 sequences in the database, including the computation of the unzipping force curves, the alignments of the force signals, the SP inference, and the computation of free-energy differences is done with a Matlab code in ∼15 min on a Macbook Pro computer.

Figure 7.

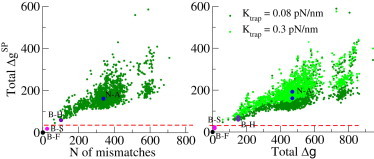
Large-scale comparison of the 16S gene in B-F with those in the other sequences of the database. (Left) SP free-energy differences versus the number of mismatches between B-F and the other sequences. (Right) SP versus Mfold (150 mM NaCl) free-energy differences between B-F and the other sequences. The straight line at $\Delta g=35$ represents the experimental resolution estimated from Fig. 4. To see this figure in color, go online.

Fig. 7 shows that there is a good correlation between the total SP free-energy difference and the number of mismatches. No simple linear relationship can be expected, as the difference in basepair free energy depends on the type of mismatch. In a similar way, the total differences between the inferred landscaped are strongly correlated to the total differences between the true landscapes (Fig. 7, right). As barriers are generally underestimated by the SP approximation, the former are generally smaller than the latter. We show in addition that the total SP free-energy differences increase when the synthetic data are generated with a fourfold-stiffer optical trap (Fig. 7, light green dots; see also Figs. S31 and S32).

The whole-database analysis with synthetic data and SP inference shows, as expected, that the only sequence with zero SP free-energy difference is the test sequence itself (B-F). The next most similar sequence is B-S. However, as discussed in the previous paragraph, the total difference in free energy is smaller than the experimental resolution between two identical molecules estimated from the data of Huguet and collaborators (4) and indicated in Fig. 7 by the red dashed line. It seems, however, that B-F can be distinguished from any other sequence in the database, including B-H, when experimental errors are taken into account. In Section VII of the Supporting Material, the 16S rDNA gene of N-A is compared to the other 2076 sequences in the database. The results are similar to what is shown in Fig. 7 for the B-F test sequence, with the difference that N-A could also be distinguished from its closest sequence with the estimated experimental resolution.

Conclusion

In this article, we have shown how the basepair free-energy landscape of a single DNA molecule with 6800 bases could be inferred from the unzipping data published in Huguet et al. (4) with a resolution of 30–40 basepairs. Sequencing techniques with low resolution but used on very long sequences could be interesting in practical applications, and could complement current techniques, which are limited to short reads.

The inference of the whole free-energy landscape is a difficult problem, as it requires determination of a large number of parameters, increasing in a linear fashion with the length of the molecule. We have proposed and compared two approximation approaches to solve this problem. The first approach, the SP method, is in practice a reparameterization of the force-extension curve and requires very little computational effort. The second procedure, called Box approximation, consists of approximating the free-energy landscape with a piecewise constant function on the scale of b bases and fitting the corresponding coarse-grained energetic parameters to match the equilibrium force computed from an unzipping model to the experimental signal. We find that the best value for b is about half the ratio of the length of thermal fluctuations of the bead in the optical trap over the typical length of two open basepairs. This choice allows us to adjust the procedure automatically to the precision of the experimental setup, and to avoid overfitting the data. As the size of ssDNA fluctuations increases with the number, n, of unzipped basepairs, so does the natural resolution, b, ranging from ∼5 bases at the beginning of the molecule to 20 bases at the end of the molecule (see Fig. S1) in the setup of Huguet et al. (4). It is important to stress that the value of b at the beginning of the opening depends on the stiffness of the optical trap and of the dsDNA linkers (assumed to be rigid here, since they are very short) and could easily be made smaller in other experimental setups. Indeed, the optical trap stiffness in the setup of Huguet and co-workers (4), $K_{\text{trap}}=0.08$ pN/nm, is relatively small. As a matter of comparison, consider the unzipping experiments of Woodside et al. (3), for which $K_{\text{trap}}=0.3-0.4$ pN/nm. With the Box inference method, we expect to be able to resolve the free-energy landscape over the first 200 bp of the sequence with a resolution of the order of $b\simeq 0.5\sqrt{k_{\text{B}}T/K4{\ell }_{\text{ss}}^2}\approx 2$ bp (Fig. S26). As a consequence, it seems possible to drastically improve the reconstruction scale of the inference by changing the setup for small n, until $K_{\text{ss}}$ becomes the smallest stiffness of the setup and ssDNA fluctuations are the dominant contribution to the bead fluctuations. Unfortunately, in the data sets analyzed, the unzipping signal starts at $n=700-900$ open basepairs (for Molecules 1 and 2, respectively), and the part of the unzipping dominated by the trap stiffness is missing. In this range, as shown with the synthetic data, the resolution on the inferred free-energy landscape is expected to be of the order of 5–10 bases.

Comparison with the synthetic unzipping data obtained from the known sequence show that the major source of error is the drift of the apparatus. The presence of drift, the intensity of which could be reduced by the use of specific setups, e.g., double optical traps, considerably affects the accuracy of inferred free-energy landscapes. We have proposed an alignment procedure of force curves, which makes use of the celebrated Needleman-Wunsch algorithm for aligning nucleotidic or protein sequences. We have shown that the procedure is efficient for aligning two experimental force signals (Molecules 1 and 2) affected by drift and corresponding to the same DNA sequence. We expect that drift could be practically eliminated and that the inferred free energy could be assigned to unambiguous basepair indices, even in the absence of any a priori information on the sequence, by aligning a large number of unzipping curves corresponding to the same sequence. A systematic check of the efficiency of our alignment procedure on other experimental data, with several unzipping signals, would therefore be very useful.

In the second part of the article, we have given a proof of principle, with synthetic force data, that unzipping experiments combined with our inference approach could be used as a method of identifying one among thousands of 16S rRNA bacterial sequences. The standard method for detecting homologous sequences is DNA-DNA hybridization. DNA-DNA association kinetics is informative about the similarity between test and reference DNA sequences. However, this hybridization method is quite involved, as it is time-consuming, labor-intensive, and expensive to perform (32). Moreover, it gives only a global measure of the difference between the test and reference sequences. Unzipping-based methods could, in principle, also give local information on similarities or dissimilarities between the sequences.

The gene screening procedure proposed here allows us to find, within experimental limitations, the sequence corresponding to the test gene in the database. If this sequence is not present, the SP inference procedure identifies the sequence most similar to that of the test gene, partially reconstructs the sequence of the test gene in the matching zones, and gives the coarse-grained differences between the two free-energy landscapes in the nonmatching regions on a 10–50 bp scale, which depends on the experimental resolution and on the inference method. In particular, the SP method is robust and fast, and can be carried out with no extra computation cost with respect to the comparison of unzipping forces. Once the most similar sequence has been found, a more precise resolution over the differences of the free-energy landscapes can be obtained by the Box approximation. Note that we used our force alignment procedure to compare theoretical free-energy landscapes of homologous (but distinct) sequences, which are free of drift. When comparing an experimental force curve to one or more theoretical force curves computed from a sequence database, the force alignment procedure will, in addition, be helpful in removing the drift from the data.

We stress that differences between the inferred free-energy landscapes are more meaningful than differences between the true and inferred landscapes. Although there may be important differences between the SP free-energy landscape and the true one, e.g., due to the stick-slip characteristics of the unzipping signal, we have shown that homologous sequences, even a few mutations away from one another, could be distinguished by comparing their SP landscapes. SP comparison provides information not at the basepair level, but on larger scales. To achieve basepair accuracy, one could combine unzipping experiments with the hybridization of oligonucleotide probes (16), which could be engineered to bind to the part of the sequence where a different landscape has been detected. It would be interesting to test the hybridization of different probes with nucleotide contents compatible with the average free-energy difference inferred from the unzipping signal and the SP or Box approximations.

The study described in this article could be extended in several ways. We based our inference on the equilibrium force signal by filtering the force data at a resolution of 1 Hz. However, the temporal resolution of the data acquisition is much higher (here, 1 kHz). The data therefore contain in principle more information than the average force at each position. Thus, one way to expand on this study would be to exploit for the inference not only the average force but the distribution of forces at each position. A second, and very interesting way would be to incorporate in the model elements of the unzipping dynamics by taking into account the bead, single strand, and linker relaxation dynamics (35). In addition, although we focused here on the basepair free-energy landscape associated with the sequence, we did not attempt to infer the sequence itself. Thus, a third way to extend this study would be to look for the most likely sequence capable of generating the inferred Box-averaged free energy, $g_k$. It would be useful to introduce more complicated priors over the energetic parameters used in this work, in particular to constrain the basepair free energies to take values from a set of only 10 possible known values.