Abstract
The microaerophilic magnetotactic bacterium Magnetospirillum gryphiswaldense swims along magnetic field lines using a single flagellum at each cell pole. It is believed that this magnetotactic behavior enables cells to seek optimal oxygen concentration with maximal efficiency. We analyze the trajectories of swimming M. gryphiswaldense cells in external magnetic fields larger than the earth’s field, and show that each cell can switch very rapidly (in <0.2 s) between a fast and a slow swimming mode. Close to a glass surface, a variety of trajectories were observed, from straight swimming that systematically deviates from field lines to various helices. A model in which fast (slow) swimming is solely due to the rotation of the trailing (leading) flagellum can account for these observations. We determined the magnetic moment of this bacterium using a to our knowledge new method, and obtained a value of A · m2. This value is found to be consistent with parameters emerging from quantitative fitting of trajectories to our model.
Introduction
Cells of magnetotactic bacteria (1) possess iron-bearing magnetosomes with permanent magnetic moments, so that they passively align parallel to and swim along magnetic field lines: they are flagella-propelled compass needles. The adaptive value of magnetotaxis is not fully understood. Since all known species live in stratified water columns or sediments, and many are obligate microaerophiles, it is likely that magnetotaxis works in tandem with oxygen-seeking behavior—magnetoaerotaxis—to guide organisms to preferred redox environments. Aligning to geomagnetic field lines provides an inexpensive (because passive) way of sensing up and down, which is the predominant direction of redox gradients.
Two types of magnetoaerotaxis have been identified (2), but they are not yet fully understood. In polar magnetoaerotaxis, cells swim toward geomagnetic north (south) in the northern (southern) hemisphere in oxidizing conditions, usually propelled by single polar flagella. In reducing conditions, organisms reverse their flagellar motors, and hence their velocity. Many live at oxic-anoxic interfaces, where oxidizing/reducing conditions prevail above/below, respectively. By contrast, Magnetospirilla are axial magnetoaerotactic. In a uniform environment, they swim toward both geomagnetic poles. Each cell senses the oxygen concentration along its trajectory as a function of time. If a cell detects an unfavorable gradient (that is, motion away from preferred conditions), the probability of reversing its flagellar motor, and therefore velocity, is increased. The opposite happens along a favorable gradient.
Such temporal gradient sensing is reminiscent of chemotaxis in Escherichia coli (3), where a rod-shaped cell body is propelled by a rotating bundle of rigid helical flagella (3). Propulsion in Magnetospirilla is quite different. Magnetospirilla are bipolarly flagellated, bearing one flagellum that is not helical in its quiescent state at each pole of a mature cell, which is helical (4). Propulsion is likely similar to that in the nonmagnetic species Spirillum voluntas, where each polar flagellum is actually a bundle of ∼75 thinner flagella (5). Dark-field observations (6,7) show that both flagella bundles in a mature cell rotate in the same direction during swimming. The simplest propulsion model (8) treats the cell body as a rigid helix, and the polar flagella as rigid rods. The rotating flagella cause the cell body to rotate in the opposite direction to render the whole organism torque free. The rotational-translational coupling of the body spiral then propels it forward. More sophisticated models take account of the chiral shapes adopted by the rotating flagella (9–11).
Understanding magnetotactic bacteria motility is interesting and important from many perspectives. The ecological niches they inhabit, which are intimately linked to their magnetoaerotaxis, give them a potentially important but as yet little understood role in global iron cycling (12). In the biophysics of micropropulsion (13), these organisms provide novel paradigms beyond the well-studied E. coli. Since motile bacteria increasingly function as models for the physics of active colloids (14), magnetotactic organisms open up the possibility of studying such systems in an easily tunable external field. For applications, magnetotactic bacteria guided by external fields have been used to manipulate mesoscopic cargoes (15), and have been proposed as drug delivery vehicles (16).
We study the swimming of M. gryphiswaldense, one of the better-characterized magnetotactic bacteria. Sampling of ≲ 300 organisms returned a broad speed distribution between 5 and 50 μm s−1 (15). Comparative genomics has pinned down core genes for magnetotaxis (17). The kinetics of its magnetosome formation has been followed using x-ray scattering (18). It is not yet possible to visualize the individual flagella of M. gryphiswaldense—significantly thinner than the bundles in S. voluntas—during swimming.
In a rotating magnetic field, M. gryphiswaldense shows a variety of complex trajectories (19); the same study also found incidentally that the organism could reverse its velocity during motion, though the mechanism by which it does so is unknown. Perhaps surprisingly, there has been no quantitative study in the simpler environment of constant external magnetic field to date. In this article, we report such a study, which yields an unexpected result: the speed distribution is strongly bimodal. Cells swimming in either direction at ≈15 μm s−1 or ≈45 μm s−1 can switch rapidly (in s) between the fast and slow modes. To elucidate the biomechanical origins of this behavior, we track cells next to a glass slide in an external magnetic field. Wall-cell hydrodynamic interaction competes with magnetic effects to generate a variety of trajectories, all of which can be accounted for by the hypothesis that the fast and slow swimming modes are associated with deploying the trailing and leading flagella, respectively. It is possible that such switching may be part of the organism’s strategy for exploring its environment perpendicular to magnetic field lines.
Materials and Methods
Bacteria strain and sample environment
Liquid cultures of M. gryphiswaldense, strain MSR-1, were grown undisturbed at room temperature (∼22°C) in closed 25 mL vials with 10 mm air above the surface over 3–5 days. The medium used was prepared according to the established protocol (20): it contained, per liter, deionized water, 2.38 g HEPES, 3.0 g sodium pyruvate, 0.1 g yeast extract, 3.0 g soybean peptone, 0.34 g NaNO3, 0.1 g KH2PO4, 0.15 g MgSO4 · 7H2O, and 3.0 g granular activated charcoal. The pH was adjusted to 7.0 with NaOH. Ferric citrate (0.5 mM) and 1.4-dithiothreitol (DTT; 1.0 mM) were added aseptically after autoclaving. The cultures had an average optical density of ∼0.3 (at 600 nm) and a few millimeters below the surface an accumulation of cells was observed. We selected motile cells with magnetosomes by loading a sterile 5 mL syringe with a fitted plastic tip with the culture. The tip was closed with a sterile cover and the syringe was placed for ∼4 h next to a permanent magnet (with S-pole toward the tip) so that motile cells would swim along field lines in a field of mT and accumulate close to the tip.
Magnetic field
The z-field was applied using a 20 mm diameter electromagnet mounted just below the sample. The y-field was due to two disc-shaped permanent magnets mounted at 20 mm to give mT in a central region of mm2 where the sample was placed.
Microscopy and image analysis
Movies containing ∼3000 images were collected at 100 frames/s using a Nikon Eclipse Ti inverted microscope equipped with a CMOS-camera (MC 1362, Mikrotron, Unterschleissheim, Germany) and frame grabber card (Inspecta 5, Mikrotron). A custom-made observation chamber—consisting of a coverglass with spacer (160-μm-thick coverglass) glued with ultraviolet curing glue (Loctite 358) on a microscopy slide—was filled with the bacterial suspension, taken from the syringe (used for the selection of the motile cells as described above), and sealed with Vaseline. We used a phase contrast objective (Nikon 10× Ph1) with ≈30–40 μm depth of field, which enabled us to view selectively bacteria swimming along either the bottom or the top of the observation chamber. We used a 100× objective to estimate the swimming distance of cells from the bottom surface.
Each collected movie contains ∼500 swimming cells in the field of view (see also Fig. S1 in the Supporting Material). Trajectories were extracted using standard tracking methods (21). We discarded trajectories that showed diffusive rather than ballistic (swimming) behavior using the method of Miño et al. (22). To achieve better statistics we used up to 15 movies for constructing swimming-speed distributions.
Magnetic moment determination
We used differential dynamic microscopy (DDM), recently applied to studying swimming of microorganisms (23,24) and generalized to anisotropic particles (25), to determine the effective translational diffusion coefficients of nonmotile M. gryphiswaldense parallel and perpendicular to an applied horizontal magnetic field. Nonmotile cells were obtained by heating wild-type organisms at 60°C for 1 h. In DDM, we analyze the intensity fluctuations from the spatial Fourier transform of a sequence of images to obtain the intermediate scattering function (ISF), , where q is the wave vector of the fluctuations being probed and t is time. The ISF measures dynamics on the spatial scale, . By analyzing in two sectors with q approximately perpendicular and parallel to the applied field, B, we can determine the effective translational diffusion coefficients of the particles in a dilute suspension as a function of B. Fitting the observed field dependence of these diffusivities gives a value for the magnetic moment m.
In a mean-field kinetic theory, the effective translational diffusivities of noninteracting ellipsoidal particles (each with fixed magnetic moment m) perpendicular, , and parallel, , to an applied magnetic field, B, are given by (26)
| (1) |
| (2) |
where is the reduced magnetic field, is Boltzmann’s constant, T the temperature, is the isotropic translational diffusion coefficient, and and are the translational diffusivities of a prolate spheroid along the major axis and minor axis, respectively, at B = 0. In the case of particles with m along the major axis, the second-order orientational order parameter is given by
| (3) |
This quantifies the mean alignment of the particles with increasing B and therefore the transition from isotropic to anisotropic dynamics. In the zero and infinity field limits, reduced to 0 and 1, respectively, giving
| (4) |
| (5) |
| (6) |
and were measured as functions of B using DDM over a range of spatial frequency of m−1 (Fig. 1). Fitting to the mean-field kinetic theory expressions given above gives estimates of , , and m (see Fig. 1 caption).
Figure 1.
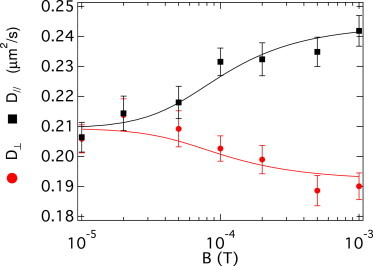
Effective translational diffusion coefficients versus the amplitude of the magnetic field in the direction perpendicular, , and parallel, , to the applied magnetic field. Error bars are standard deviations, obtained from averaging the measured diffusion coefficients over the range of spatial frequency, m−1, and representative of a slight q-dependency—a measure of systematic error. Lines are simultaneous fits (global fitting) to the experimental data using Eqs. 1 and 2 with m, , and linked for both fits. We obtained , /s, and /s. To see this figure in color, go online.
The diffusivities and are related to the corresponding drag coefficients of a prolate spheroid:
| (7) |
where (27)
| (8) |
and
| (9) |
Here η is the viscosity of the surrounding fluid and , with a and b the major and minor semiaxes, respectively. By solving numerically Eqs. 8 and 9, we found μm and μm, using the viscosity of water, Pa · s, and the measured diffusion coefficients μm2/s and μm2/s.
Results
The cultured cells were race-tracked and loaded into sealed sample chambers and observed at 10× magnification with a phase-contrast microscope. Movies were taken using a CMOS-camera, typically at 100 frames/s (see Materials and Methods for details).
Bimodal speed distribution
We first investigated swimming in the bulk, i.e., in the middle of the 160-μm-thick sealed sample chamber, under a homogeneous horizontal applied magnetic field, mT ( earth’s field in magnitude), . Here and throughout this work, the applied field is antiparallel to the y axis, which, together with an orthogonal x axis, defines the plane that is being imaged. The optical axis of our microscope defines the z axis in a right-handed system (Fig. 2). Approximately equal numbers of the cells swim toward the magnetic north pole (parallel to y) and toward the magnetic south pole (antiparallel to y).
Figure 2.
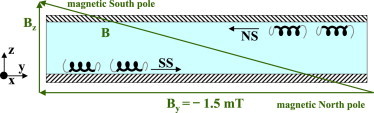
A schematic of our observation chamber, defining axes and showing how a magnetic field with finite y and z components separates NS and SS cells. To see this figure in color, go online.
These are south-seeking (SS) and north-seeking (NS), respectively, since the earth’s magnetic south pole is situated near the earth’s geographic North Pole. Note that SS and NS cells are not distinct populations, since axial magnetotactic cells switch ocasionally between SS and NS even in homogenous oxygen conditions. Fig. 3 a shows the distribution of swimming velocities in the xy plane, , calculated over 0.4 s sections of trajectories. For both SS and NS organisms, the distribution is clearly bimodal, with peaks corresponding to speeds of 15 μm s−1 and 45 μm s−1. We will refer to these peaks as SSslow, SSfast, NSslow, and NSfast.
Figure 3.
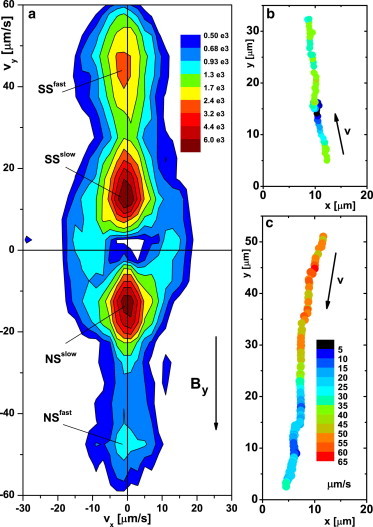
(a) Swimming velocity distribution (see color code) obtained by tracking M. gryphiswaldense in the bulk at a horizontal applied field of mT. (b and c) Trajectories of SS and NS cells, respectively, with color-coded swimming speed, illustrating mode switching of fast-stop-fast (b) and fast-slow (c). To see this figure in color, go online.
Examination of individual trajectories shows that this distribution results not from two distinct populations, but from cells varying their swimming speeds. Fig. 3 b shows the trajectory of an SSfast cell that stopped for 0.7 s before continuing SSfast; Fig. 3 c shows the trajectory of an NS organism that switched from fast to slow swimming. We found trajectories with all possible speed and velocity changes, although speed switching with no reversal is the most common.
Near-wall swimmers deviate from magnetic field lines
We next added a vertical component, , to the applied field so that NS (SS) cells are guided by the now slant field lines to, and accumulate at, the top (bottom) for ; for , the accumulation is on the opposite side (Fig. 2). Observations at a higher numerical aperture revealed that cells swam at μm from the wall at mT, increasing to μm at mT. Fig. 4 shows the of these near-wall swimmers at mT. Since the separation of NS and SS organisms was total, only the relevant half of is shown. In contrast to Fig. 3, where on average v is parallel to B, there is now a clear deviation of v, the projected xy velocity, from the direction of the field lines in the xy plane, which are along y. The angular deviation, β, has opposite signs for fast and slow swimmers (Fig. 4). Its mean magnitude, , increases with the vertical field (Fig. 5, a–d), so that approximately (Fig. 5 e). It is important to note that the bulk result ( (Fig. 3)) is recovered at a wall at .
Figure 4.
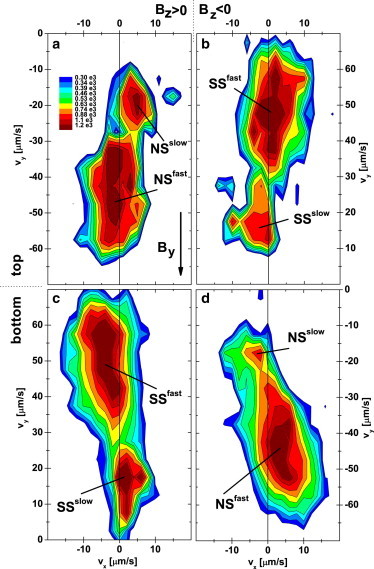
Swimming velocity distribution of cells swimming close to the top (a and b) and bottom walls (c and d) with horizontal field mT. The vertical fields were mT (a and c) and mT (b and d). To see this figure in color, go online.
Figure 5.
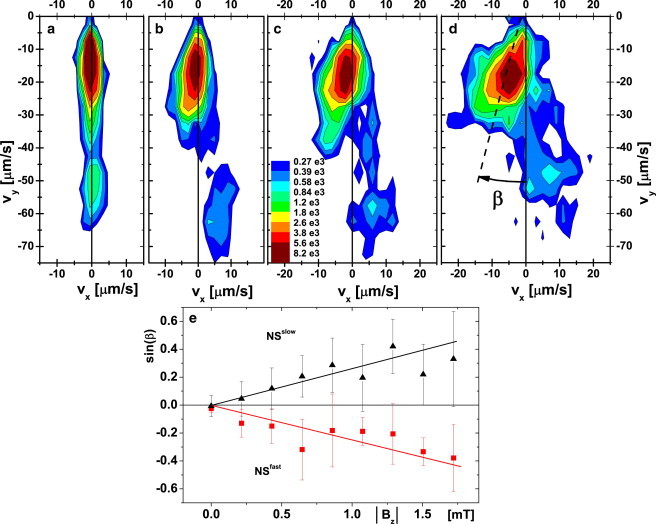
Swimming velocity distribution measured close to the bottom wall for vertical field strengths of : 0.0, , , and mT (a–d, respectively) and constant horizontal field, mT. (e) Swimming angle β (plotted as ) close to the bottom wall for slow (black triangles) and fast (red squares) north seekers. The points and error bars correspond to the mean values and full width at half-maxima of the peaks, respectively. The lines are guides to the eye. To see this figure in color, go online.
We discuss the origins of these deviations later. Here, we simply point out that they do not arise from a misalignment of or such that , because the observed sense of deviation is opposite for cells swimming along the top and the bottom of the sample chamber under the same conditions (i.e., comparing Fig. 4, a and c or Fig. 4, b and d).
Interestingly, there is no detectable change in the absolute swimming speeds near a wall from their values in the bulk: in both cases, the majority of cells swim at ≈45 μm s−1 and ≈15 μms−1 (Figs. 3 and 4). This means that although the field lines guiding cells to the wall are at an angle to horizontal of (Fig. 2), cells swim essentially parallel to the top and bottom surfaces. The origins of the torque (in the direction) giving rise to this state of affairs is unclear, but a similar torque has been observed for Caulobacter crescents cells swimming next to a surface (28).
Observing surface mode switching and loops
Fig. 6 a shows the trajectory of a cell switching from NSfast (red) to NSslow (blue) and back to NSfast (red), with deviations consistent with Fig. 4 a; Fig. 6 b shows an NSfast cell reversing to SSslow and then reverting to NSfast. Interestingly, β changes abruptly at the first reversal from to . The change from NS to SS means that the cell leaves the top surface (Fig. 2) and starts swimming into the bulk, where no deviation occurs (Fig. 3). After reversing to NS, the cell returns to the wall and shows again. Of 370 such trajectories, each of duration s, % contained swimming-mode changes. All possible combinations of mode switching between SSslow, SSfast, NSslow, and NSfast were observed. Each putative switching event was checked to ensure that it was not an artifact due to intersecting trajectories.
Figure 6.
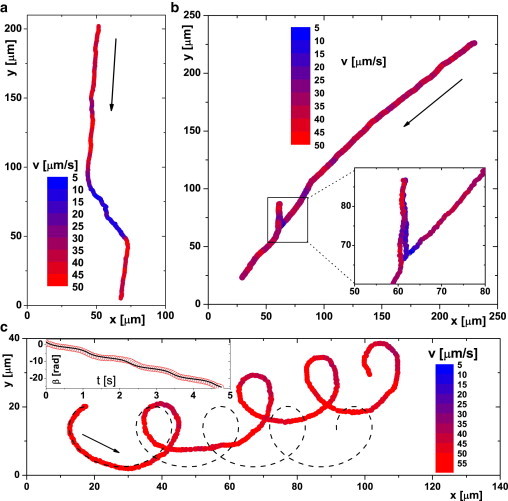
Trajectories of individual cells swimming in the indicated directions in a horizontal field of mT. The color code corresponds to the absolute swimming speed. Trajectories were recorded close to the top (Bz = +0.86 mT) (a and b) and close to the bottom (Bz = −1.0 mT) (c) of the observation chamber. The line in c shows a calculated trajectory with the best-fit parameters , rad s−1, and m s−1. (Inset) Calculated (line) and measured (points). To see this figure in color, go online.
A very small proportion (, found by automated scanning through 104 trajectories) of the trajectories at 1 mT contained loops (Fig. 6 c and Fig. S2). Loops were not observed at lower vertical fields. The sense of these loops depends on the swimming speed. At , we find clockwise (CW) loops on the bottom and counterclockwise (CCW) loops on the top of the sample cell (viewed from the top), whereas for , the sense of the loops is reversed. A mixture of these kinds of behavior was obtained at .
Modeling two-speed swimming
Our observations show that M. gryphiswaldense in an external magnetic field switches between four swimming modes: NSslow, NSfast, SSslow, and SSfast. Two velocity modes have been observed in S. voluntas. In a young cell, which possesses only a single flagella bundle immediately after cell division, propulsion by the trailing bundle is twice as fast as propulsion by the leading bundle (5). In a previous study of M. gryphiswaldense (19), an asymmetry of the swimming speed between NS and SS was reported. It was suggested that this asymmetry was due to a change of the flagella pitch upon reversal. In this work, we find that reversal and the switch between fast and slow swimming modes are independent phenomena, e.g., changing from NSfast to NSslow and back to NSfast without reversal is possible (Fig. 6 a). We therefore seek another explanation for two-speed swimming.
Wall hydrodynamic interactions
An important clue comes from the observation that cells next to a wall swim at a finite deviation to the direction of the horizontal magnetic field. Thus, each cell experiences a finite magnetic torque, which must be balanced by another torque; the latter is due to hydrodynamic interactions between cells and the wall.
In a rotating body close to a solid wall (29), the drag coefficient of any element of the body increases with decreasing distance from the wall, resulting in a net force perpendicular to the angular velocity and the wall normal. The direction of this force reverses if the sense of rotation reverses. Thus, E. coli swim in circles next to solid surfaces (30): the body and the flagella bundle rotate in opposite directions, giving rise to equal and opposite hydrodynamic forces that act on the body and the flagella bundle, respectively, so that the whole cell experiences a net hydrodynamic torque, which is balanced by the viscous torque due to the cell’s rotation in a viscous fluid.
Quantitative model
M. gryphiswaldense possesses a helical body with two polar flagella. We assume that each rotating flagellum adopts a spiral form, as is observed in S. voluntas. Our proposed physical picture is as follows. Suppose a cell swims by rotating both flagella. Then, borrowing directly from the analysis of E. coli next to surfaces (30), the system of hydrodynamic forces acting on a cell swimming next to a bottom wall is as shown in Fig. 7 a, with the (force-free) requirement that . If, to a first approximation, we take the front and back flagella to be equivalent, then , and the net hydrodynamic torque is zero, . With no need for any balancing magnetic torque, , or , i.e., cells should swim along field lines. This is not what is observed.
Figure 7.
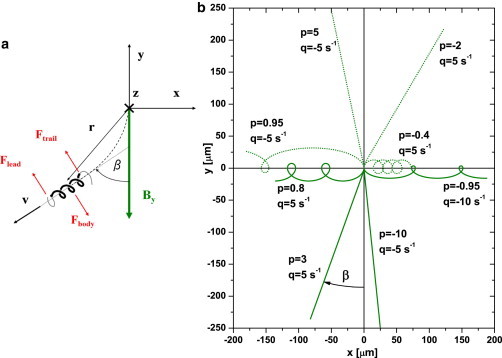
(a) Schematic of an NS cell swimming along the bottom of the observation chamber. Seen from behind, the right-handed helical body rotates CW and the flagella CCW. Red arrows show the directions of the surface-mediated hydrodynamic forces on the body and flagella when they are rotating in these respective senses. (b) Calculated trajectories for different parameters p and ω in a magnetic field, mT. Solid lines represent NS () and dotted lines SS () cells. All trajectories are calculated over 5 s for μm/s and with initial conditions . To see this figure in color, go online.
We therefore hypothesize that cells swim with either the leading or trailing flagella, which does give rise to net hydrodynamic torques along the z axis with opposite signs (Fig. 7 a). If the magnetic field is large enough, viz., , a solution can be found for . Cells will swim at a fixed to the field lines, with the sign of β dependent on the sign of , which in turn is a function of whether the leading or trailing flagellum is in use. Rotation of the leading flagella alone results in a deviation of swimming direction in CW sense with respect to the bulk swimming direction, whereas rotation of the trailing flagella alone leads to a deviation in CCW sense; this holds for SS and NS cells. Deviations of opposite senses are predicted for the upper surface. Fig. 4 shows that these predictions are correct. If the magnetic field is too small, viz., , so that the hydrodynamic torque always overcompensates the magnetic torque, more complex trajectories result.
In general, assuming that the speed in the xy plane, v, , m, and are constants, the position of a cell and the angle between its velocity and the horizontal magnetic field, β (Fig. 7), satisfy the equations
| (10a) |
| (10b) |
| (10c) |
where , , with ξ being the friction coefficient of a cell for rotation around the z axis (Fig. 7 a). With initial conditions and , we obtain
| (11a) |
| (11b) |
| (11c) |
where
| (12) |
| (13) |
For (i.e., ), straight trajectories result, as expected, with fixed deviation . For , these equations predict loops whose shape, size, pitch, and sense of rotation depend on ω and p. These loop swimmers should migrate along x, i.e., perpendicular to the horizontal field, at a rate that is essentially determined by . Predicted trajectories for different values of are shown in Fig. 7 b.
Trajectories and parameters
We now analyze observed looped trajectories to obtain the parameters of our model. From an observed trajectory, we measure the time-dependent angular deviation, . This function is first fitted to Eq. 11a to give , p, and ω. These values are then used in Eqs. 11b and 11c to calculate the expected trajectory, using the average speed over the measured trajectory for v in these expressions.
A sample prediction is shown in Fig. 6 c, where the inset shows the measured (points) of the trajectory observed in the main figure and the fitted function (solid line). The fit parameters obtained, , yield the predicted trajectory in the main figure (dashed curve), which shows all the important features (shape, size of loops, periodicity, migration predominantly along x) of the observed trajectory (red curve), and a reasonable quantitative fit up to and slightly beyond the first loop.
In our model, loops occur when , i.e., when the torque due to hydrodynamic interactions with the surface is larger than the magnetic torque due to the horizontal magnetic field. Two pieces of evidence suggest that this is indeed the case. First, we only observed loops when mT. We have already reported the observation from direct imaging that cells appear to swim closer to the surface at higher vertical fields. Although the origin of this effect is unclear, it is reasonable to assume that cells swimming closer to the surface will experience a higher , consistent with the observation of loops only when is high enough.
Second, in a population of cells experiencing the same , those cells with a lower , i.e., a smaller magnetic moment (because is constant for all cells), should be the ones that swim in loops. From fitting the 20 or so loop trajectories, we obtain an average value for the ratio of magnetic to hydrodynamic torque of . Under the same field conditions, straight-swimming cells yield an average of (obtained in this case from ). Since is in the same range for both cases, we take to be approximately constant. The observed values of then suggest that the magnitude of the magnetic moment, , of the loop swimmers is of that of the straight swimmers. Since the magnetic moment of each cell depends not only on the number of magnetosomes but also their intracellular arrangement (31), it is easy to envisage a distribution of . Presumably, the loop swimmers come from the low-end tail of such a distribution.
To proceed further, we need a value for the average magnetic moment of M. gryphiswaldense cells. We know of two estimates of this quantity in the literature. Analysis of trajectories in rotating magnetic fields gives an upper bound of A · m2 based on an estimated rotational friction coefficient, ξ (19). A measurement using static light scattering (32) returned a fitted moment of A · m2. However, this work used a homogeneous cylinder to model the scattering of the cells, and returned a fitted cell length of m, which is unrealistically short. In the closely related species M. magnetotacticum, values found were in the range 3.0– A · m2 (33,34). Our measurements of the magnetic moment of nonmotile M. gryphiswaldense cells using the DDM method (25) described in Methods and Materials yields a value of A · m2, comparable to previous values for M. magnetotacticum.
Assuming that at high enough vertical field, mT, ξ and are approximately constant for all trajectories, we average over all trajectories to obtain rad/s. At mT, straight trajectories gave us a fitted value of . These estimated values of together with the above measured value of m then allow us to estimate pN·nm·s. We compare this value to that of a prolate spheroid rotating around its minor axis (35). From fitting the diffusivity of nonmotile cells in a magnetic field using a prolate ellipsoid model (see Materials and Methods), we found μm and μm. Using Pa · s for water, we obtain pN · nm · s. The order-of-magnitude agreement with our estimate of pN · nm · s from parameters fitted to observed trajectories is reassuring, especially since modeling the drag of a helix with a prolate ellipsoid in which the radius of the former and semiminor axis of the latter are approximately equal will likely lead to a significant overestimation of the helix’s rotational drag coefficient.
Discussion and Conclusions
Our findings raise a number of intriguing questions for the biology of M. gryphiswaldense. In particular, since our results have unequivocally established the existence of fast and slow swimming modes for each cell, we may inquire into the molecular mechanism for such mode switching, and into its function in the cells’ natural environment. Turning first to the functional question, we suggest that this phenotype controls the ability of a swimming cell to explore its environment in directions perpendicular to the magnetic field, B. A self-propelled particle with finite magnetic moment in an external magnetic field will travel on average parallel to B; but its rotational Brownian motion will cause directional fluctuations, so that the particle will explore dimensions orthogonal to the field lines. The larger the particle’s propulsion velocity, the further the particle will move away from the original field line before the magnetic field restores its orientation along B. It is therefore possible that a cell uses these two swimming modes to tune how much it wanders away from swimming along B, e.g., as a function of how close it is to its preferred microaerophilic environment. A second suggestion is that M. gryphiswaldense somehow uses its two speeds directly in magnetoaerotaxis, analogous to how E. coli use speed modulation to navigate temperature gradients (thermotaxis) (36).
A final possibility is based on the result that the optimal sensing time required for detecting a (logarithmic) concentration gradient is proportional to (Eq. 58 in (37)). Thus, switching from a fast to a slow swimming mode such that allows a cell to sample a that is three times smaller, so that M. gryphiswaldense perhaps utilizes this mechanism to optimize oxygen sensing.
We observed that cells switched between fast and slow swimming modes rapidly. Indeed, the switching time is below our current experimental resolution. Since we constructed trajectories using running averages of 20 frames at 100 frames/s, we can give an upper bound: switching between swimming modes in M. gryphiswaldense occurs in s. Our theoretical model supports the suggestion that the switching is between using leading and trailing flagella. We may therefore, second, inquire into the molecular mechanism used by a cell to achieve such fast and coordinated changes in the motors situated at its two opposite poles.
Although only the most preliminary mechanistic suggestions could be offered at this stage, e.g., the use of a molecular clutch (as used in Bacillus subtilis to switch motility on and off rapidly and reversibly (38)), we can certainly set our upper bound for the switching time in the context of intracellular diffusion. Flagellar motion in E. coli is controlled by the diffusion of proteins such as CheY and CheZ, whose diffusion coefficients in the cytoplasm are in the range 5–10 μm2 s−1 (39). To diffuse from one pole to another, a distance of m, takes s, which is consistent with our upper bound, and with recent work concluding that diffusion of CheY suffices to explain subsecond coordinated switching between CCW and CW flagellar rotation in this organism (40). Presumably, intracellular diffusion of relevant analogous proteins also lies behind the coordinated switching between leading and trailing flagella in our organism. Interestingly, various ionic salts are known to disrupt the coordinated switching of polar bundles between CCW and CW rotation in S. voluntas (7). It would be interesting to perform similar experiments in M. gryphiswaldense.
Switching between swimming modes, and indeed between NS and SS behavior, requires the coordination of flagellar motors. Again, only the most preliminary suggestion could be made based on analogy with other organisms. Very recent work shows that the intracellular diffusion of phosphorylated CheY, long known to be a key molecule in chemotaxis in E. coli, is sufficient to explain the coordinated switching between CCW and CW rotation of flagellar motors in this species on a subsecond timescale. The similarity in cell size and switching timescales between E. coli and M. gryphiswaldense suggests that once the relevant protein(s) have been identified in the latter, their intracellular diffusion should again suffice to explain flagellar coordination.
Acknowledgments
Funding was from the Swiss National Science Foundation (PBFRP2-127867), FP7-PEOPLE (PIIF-GA-2010-276190), and the United Kingdom’s Engineering and Physical Sciences Research Council (EP/D071070/1, EP/E030173, and EP/I004262/1).
Supporting Material
References
- 1.Blakemore R.P. Magnetotactic bacteria. Annu. Rev. Microbiol. 1982;36:217–238. doi: 10.1146/annurev.mi.36.100182.001245. [DOI] [PubMed] [Google Scholar]
- 2.Frankel R.B., Williams T.J., Bazylinski D.A. Magneto-aerotaxis. In: Schüler D., editor. Magnetoreception and Magnetosomes in Bacteria. Springer; Berlin: 2006. pp. 1–24. [Google Scholar]
- 3.Berg H.C. Springer-Verlag; New York: 2004. E. coli in Motion. [Google Scholar]
- 4.Schüler D., Köhler M. The isolation of a new magnetic spirillum. Zentralbl. Mikrobiol. 1992;147:150–151. [Google Scholar]
- 5.Swan M.A. Trailing flagella rotate faster than leading flagella in unipolar cells of Spirillum volutans. J. Bacteriol. 1982;150:377–380. doi: 10.1128/jb.150.1.377-380.1982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Metzner P. Studien über die Bewegungsphysiologie niederer Organismen I. Naturwissenschaften. 1923;11:395–399. [Google Scholar]
- 7.Krieg N.R., Tomelty J.P., Wells J.S., Jr. Inhibition of flagellar coordination in Spirillum volutans. J. Bacteriol. 1967;94:1431–1436. doi: 10.1128/jb.94.5.1431-1436.1967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chwang A.T., Wu T.Y., Winet H. Locomotion of Spirilla. Biophys. J. 1972;12:1549–1561. doi: 10.1016/S0006-3495(72)86181-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Winet H., Keller S.R. Spirillum swimming: theory and observations of propulsion by the flagellar bundle. J. Exp. Biol. 1976;65:577–602. doi: 10.1242/jeb.65.3.577. [DOI] [PubMed] [Google Scholar]
- 10.Ramia M. Numerical model for the locomotion of spirilla. Biophys. J. 1991;60:1057–1078. doi: 10.1016/S0006-3495(91)82143-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ramia M., Swan M.A. The swimming of unipolar cells of spirillum volutans: theory and observations. J. Exp. Biol. 1994;187:75–100. doi: 10.1242/jeb.187.1.75. [DOI] [PubMed] [Google Scholar]
- 12.Simmons S.L., Edwards K.J. Geobiology of magnetotactic bacteria. In: Schüler D., editor. Magnetoreception and Magnetosomes in Bacteria. Springer; Berlin: 2006. pp. 77–102. [Google Scholar]
- 13.Lauga E., Powers T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009;72:096601. [Google Scholar]
- 14.Schwarz-Linek J., Valeriani C., Poon W.C.K. Phase separation and rotor self-assembly in active particle suspensions. Proc. Natl. Acad. Sci. USA. 2012;109:4052–4057. doi: 10.1073/pnas.1116334109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Martel S., Tremblay C.C., Langlois G. Controlled manipulation and actuation of micro-objects with magnetotactic bacteria. Appl. Phys. Lett. 2006;89:233904. [Google Scholar]
- 16.Felfoul O., Mohammadi M., Martel S. Magnetic resonance imaging of Fe3O4 nanoparticles embedded in living magnetotactic bacteria for potential use as carriers for in vivo applications. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2007;2007:1463–1466. doi: 10.1109/IEMBS.2007.4352576. [DOI] [PubMed] [Google Scholar]
- 17.Richter M., Kube M., Schüler D. Comparative genome analysis of four magnetotactic bacteria reveals a complex set of group-specific genes implicated in magnetosome biomineralization and function. J. Bacteriol. 2007;189:4899–4910. doi: 10.1128/JB.00119-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Staniland S., Ward B., Telling N. Rapid magnetosome formation shown by real-time x-ray magnetic circular dichroism. Proc. Natl. Acad. Sci. USA. 2007;104:19524–19528. doi: 10.1073/pnas.0704879104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ērglis K., Wen Q., Cēbers A. Dynamics of magnetotactic bacteria in a rotating magnetic field. Biophys. J. 2007;93:1402–1412. doi: 10.1529/biophysj.107.107474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Schultheiss D., Schüler D. Development of a genetic system for Magnetospirillum gryphiswaldense. Arch. Microbiol. 2003;179:89–94. doi: 10.1007/s00203-002-0498-z. [DOI] [PubMed] [Google Scholar]
- 21.Crocker J.C., Grier D.G. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 1996;179:298–310. [Google Scholar]
- 22.Miño G., Mallouk T.E., Clement E. Enhanced diffusion due to active swimmers at a solid surface. Phys. Rev. Lett. 2011;106:048102. doi: 10.1103/PhysRevLett.106.048102. [DOI] [PubMed] [Google Scholar]
- 23.Wilson L.G., Martinez V.A., Poon W.C.K. Differential dynamic microscopy of bacterial motility. Phys. Rev. Lett. 2011;106:018101. doi: 10.1103/PhysRevLett.106.018101. [DOI] [PubMed] [Google Scholar]
- 24.Martinez V.A., Besseling R., Poon W.C.K. Differential dynamic microscopy: a high-throughput method for characterizing the motility of microorganisms. Biophys. J. 2012;103:1637–1647. doi: 10.1016/j.bpj.2012.08.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Reufer M., Martinez V.A., Poon W.C.K. Differential dynamic microscopy for anisotropic colloidal dynamics. Langmuir. 2012;28:4618–4624. doi: 10.1021/la204904a. [DOI] [PubMed] [Google Scholar]
- 26.Ilg P. Anisotropic diffusion in nematic liquid crystals and in ferrofluids. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;71:051407. doi: 10.1103/PhysRevE.71.051407. [DOI] [PubMed] [Google Scholar]
- 27.Chwang A.T., Yao-Tsu Wu T. Hydromechanics of low-Reynolds-number flow. Part 2. J. Fluid Mech. 1975;67:787–815. [Google Scholar]
- 28.Li G., Tang J.X. Accumulation of microswimmers near a surface mediated by collision and rotational Brownian motion. Phys. Rev. Lett. 2009;103:078101. doi: 10.1103/PhysRevLett.103.078101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Happel J., Brenner H. Prentice Hall; Englewood Cliffs, NJ: 1965. Low Reynolds Number Hydrodynamics. [Google Scholar]
- 30.Lauga E., DiLuzio W.R., Stone H.A. Swimming in circles: motion of bacteria near solid boundaries. Biophys. J. 2006;90:400–412. doi: 10.1529/biophysj.105.069401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Faivre D., Fischer A., Gehring A.U. Development of cellular magnetic dipoles in magnetotactic bacteria. Biophys. J. 2010;99:1268–1273. doi: 10.1016/j.bpj.2010.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cătăln Logofău P., Ardelean I., Ioniţă B. Determination of the magnetic moment and geometrical dimensions of the magnetotactic bacteria using an optical scattering method. J. Appl. Phys. 2008;103:094911. [Google Scholar]
- 33.Chemla Y.R., Grossman H.L., Buchanan B.B. A new study of bacterial motion: superconducting quantum interference device microscopy of magnetotactic bacteria. Biophys. J. 1999;76:3323–3330. doi: 10.1016/S0006-3495(99)77485-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bahaj A.S., James P.A.B., Moeschler F.D. An alternative methode for the estimation of the magnetic moment of non-spherical magnetotactic bacteria. IEEE Trans. Magn. 1996;32:5133–5155. [Google Scholar]
- 35.Chwang A.T., Yao-Tsu Wu T. Hydromechanics of low-Reynolds-number flow. Part 1. J. Fluid Mech. 1974;63:607–622. [Google Scholar]
- 36.Demir M., Salman H. Bacterial thermotaxis by speed modulation. Biophys. J. 2012;103:1683–1690. doi: 10.1016/j.bpj.2012.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Berg H.C., Purcell E.M. Physics of chemoreception. Biophys. J. 1977;20:193–219. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Blair K.M., Turner L., Kearns D.B. A molecular clutch disables flagella in the Bacillus subtilis biofilm. Science. 2008;320:1636–1638. doi: 10.1126/science.1157877. [DOI] [PubMed] [Google Scholar]
- 39.Lipkow K., Andrews S.S., Bray D. Simulated diffusion of phosphorylated CheY through the cytoplasm of Escherichia coli. J. Bacteriol. 2005;187:45–53. doi: 10.1128/JB.187.1.45-53.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Terasawa S., Fukuoka H., Ishijima A. Coordinated reversal of flagellar motors on a single Escherichia coli cell. Biophys. J. 2011;100:2193–2200. doi: 10.1016/j.bpj.2011.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


