Reconciling disparate views of template-directed nucleation through measurement of calcite nucleation kinetics and binding energies

Significance

Organisms use specialized macromolecules to direct the timing and placement of crystals during biomineral formation. This phenomenon has inspired synthetic approaches to templating but remains poorly understood. One view holds that the organic matrix promotes nucleation through stereochemical matching to guide the organization of solute ions, while another equates binding strength to promotion of nucleation. Our study reconciles these views with a mechanistic explanation for template-directed nucleation. Through measurements of calcite nucleation kinetics and substrate–crystal binding we show that nucleation barriers and binding free energies are linearly related for all functional group chemistries and conformations as predicted from classical nucleation theory. This model reconciles long-standing concepts of stereochemical matching with the conventional wisdom that good binders are good nucleators.

Abstract

The physical basis for how macromolecules regulate the onset of mineral formation in calcifying tissues is not well established. A popular conceptual model assumes the organic matrix provides a stereochemical match during cooperative organization of solute ions. In contrast, another uses simple binding assays to identify good promoters of nucleation. Here, we reconcile these two views and provide a mechanistic explanation for template-directed nucleation by correlating heterogeneous nucleation barriers with crystal–substrate-binding free energies. We first measure the kinetics of calcite nucleation onto model substrates that present different functional group chemistries (carboxyl, thiol, phosphate, and hydroxyl) and conformations (C11 and C16 chain lengths). We find rates are substrate-specific and obey predictions of classical nucleation theory at supersaturations that extend above the solubility of amorphous calcium carbonate. Analysis of the kinetic data shows the thermodynamic barrier to nucleation is reduced by minimizing the interfacial free energy of the system, γ. We then use dynamic force spectroscopy to independently measure calcite–substrate-binding free energies, ΔG_b. Moreover, we show that within the classical theory of nucleation, γ and ΔG_b should be linearly related. The results bear out this prediction and demonstrate that low-energy barriers to nucleation correlate with strong crystal–substrate binding. This relationship is general to all functional group chemistries and conformations. These findings provide a physical model that reconciles the long-standing concept of templated nucleation through stereochemical matching with the conventional wisdom that good binders are good nucleators. The alternative perspectives become internally consistent when viewed through the lens of crystal–substrate binding.

Biological systems are unique in their ability to organize minerals into functional materials with complex patterns and architectures. A substantial body of evidence suggests specialized macromolecules, particularly proteins (1, 2) and carbohydrates (3, 4), provide preferential sites for nucleation to direct the placement, timing, and orientation of crystals (5), both intra- and extracellular. Within the biomineralization community, the conventional view of biologically directed nucleation is that macromolecular matrices present an interfacial match to the crystal lattice that assists in forming the crystal nucleus. This cooperative view of directed nucleation is rooted in the collective action of multiple residues that guide the organization of ions into a configuration defining the energetic minimum for the system. A series of in vitro observations have reinforced this picture by showing that highly ordered organic monolayers can control the location and orientation of calcite crystals precipitated from solution (6). In this approach, good templates are revealed through a direct functional assay, i.e., nucleation. Over the years, this view of mineralization, both in the context of natural structures such as bone (7) and in biomimetic systems such as Langmuir or self-assembled monolayers (SAMs), has come to define the conventional wisdom.

In contrast, the bioinspired materials community has approached the question of nucleation control from what would appear to be an alternative perspective. Efforts within that community to discover and use biomolecules that induce the formation of diverse inorganic materials have been guided by the assumption that good binders are good nucleators (8–12). For example, in the widely used method of phage display, libraries of M13 bacterial phage are screened for their ability to bind to the surface of an inorganic material. Once strong binders are identified, the sequences of the peptides expressed by those phage are determined, and synthetic versions of the peptides—absent the phage—are then used as template molecules to promote nucleation of the inorganic. This approach ignores the collective action of the ions inherent in template-directed nucleation and uses an indirect assay—binding strength—to identify good template sequences. However, the approach has been successfully applied to the synthesis of diverse materials that include metals, semiconductors, and insulators.

A closer look at the underlying factors controlling both the dynamics of nucleation and the strength of surface binding reveals a common source for these two perspectives. Classical nucleation theory predicts that the rate of nucleation J₀ on a surface is described by the relations (13, 14).

where A = a kinetic prefactor that includes rates of diffusion and desolvation, k_B = Boltzmann’s constant, T = temperature, Δg* is the thermodynamic barrier to forming a critically sized nucleus, γ = interfacial energy, ω = molecular volume [6.13 × 10⁻²³ cm³ per molecule for calcite (15)], F = a constant that depends on nucleus shape, and σ = the supersaturation as defined by

where a_i is the activity of species i and K_sp is the solubility product of calcite or amorphous calcium carbonate (ACC) (K_sp = 10^−8.48 or 10^−6.39, respectively, at 25 °C).

The interfacial energy γ is a composite term comprised of contributions from three interactions—the crystal–liquid (γ_CL), crystal–substrate (γ_CS), and substrate–liquid (γ_SL). These are related by the expression

where h is a constant that depends upon the relative surface areas of the crystal–substrate and crystal–liquid interfaces. Recent studies of calcite nucleation on self-assembled monolayers (16) or polysaccharide films (17) and calcium phosphate nucleation on collagen (18) show that Eqs. 1 and 3 give a reasonable description of template-directed nucleation and that the interfacial energy is indeed the governing parameter.

Now consider how Eqs. 1 and 3 are related to the strength of crystal–template binding. The free energy of binding ∆G_b for any given element of area a within the crystal–substrate contact area is given by the difference between the free energy of the crystal–substrate–liquid system when the crystal is bound to the substrate and the free energy in the unbound state such that

(Note that when a is the total contact area between the crystal and the substrate, then ∆G_b gives the total binding free energy of the crystal–substrate interface.) Combining Eqs. 3 and 4 reveals that

Because γ_CL depends only on the contact between the crystal and the liquid, it is independent of the template chemistry. Consequently, γ and ∆G_b should be linearly related and, from Eq. 1b, an explicit relationship between the barrier to nucleation and the strength of the crystal–substrate-binding energy should exist.

To test whether these two views of template-directed nucleation are indeed interchangeable, we first conducted a series of experiments to quantify the free energy barriers to calcite nucleation onto a suite of substrates. Self-assembled monolayers were prepared by established methods (19, 20) to obtain five types of substrates with different head group chemistries (COOH, PO₄, SH or OH) and chain lengths (C11 or C16). These choices were based on the macromolecules known to be associated with the formation of skeletal biominerals. Although a variety of functional group chemistries have been documented, nearly all are abundant in residues of the carboxylated amino acids, aspartic and glutamic. Although lower in abundance, thiols (SH) of cysteine residues and a number of phosphorylated (PO₄) amino acids are also widespread in calcification environments (Table 1) (21–31).

Table 1.

Summary of proteins associated with biogenic calcite

Organism	Protein description	Protein name	Solubility	Ref.
	poly(glycine) and Asp/Glu rich regions, Cys	MSI31	insoluble	21
Pinctada fucata (pearl oyster)	Gly rich	MSI7	insoluble	22
	Pro/Ile/Tyr/Arg regions, Gly/Trp rich region, Asp rich region	Prismalin-14	insoluble	23
Crassostrea nippona (Iwagaki oyster)	acidic, highly phosphorylated, Asp/Glu/Cys rich	MPP1	soluble	24
Crassostrea virginica (American oyster)	highly phosphorylated, Asp/Ser/Gly rich	None	soluble	25
Adamussium colbecki (American scallop)	highly phosphorylated, Asp/Ser/Gly rich	None	soluble	26
Patinopecten yessoensis (Yesso scallop)	Ser/Gly/Asp rich, basic terminal sequence	MSP1	insoluble	27
Pinna nobilis (Mediterranean fan mussel)	Ala/Asp/Thr/Pro rich, Cys rich terminal sequence	Calprismin	soluble	28
	Asp rich	Caspartin	soluble	28
Procambarus clarkia (crayfish)	Glu/Ala rich	GAMP	insoluble	29
Gallus gallus (chicken)	cysteic acid rich	Ovotransferrin	soluble	30
Anser anser (goose)	Ala/Glu/Ser/Gly/Trp rich	Ansocalcin	soluble	31

Most calcite-extracted proteins are rich in carboxylate groups due to aspartic acid (Asp) and glutamic acid (Glu). Many are also phosphorylated or contain thiol groups in cysteine (Cys) residues. GAMP, gastrolith matrix protein.

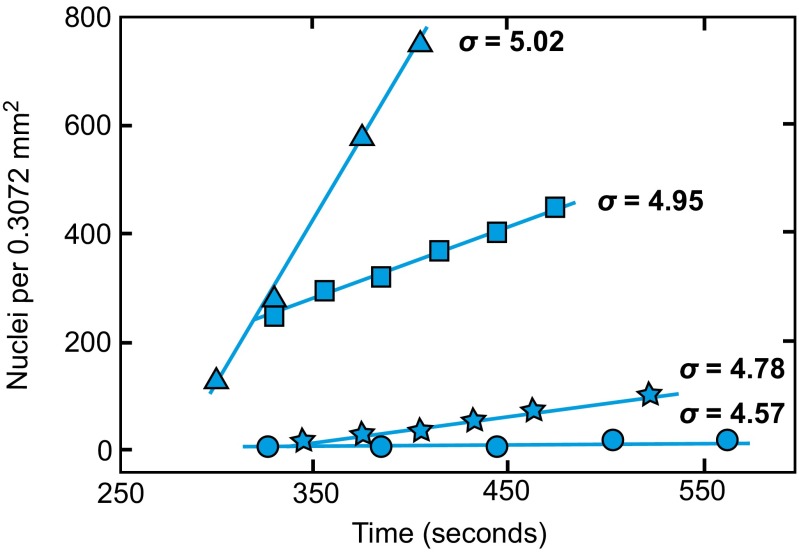
The nucleation experiments determined the rates of heterogeneous calcite nucleation onto these substrates over a series of supersaturations, σ. Using established methods (16, 17), the crystallite number density was measured over time. The data show a linear relationship with slopes that increase with σ. Fig. 1 illustrates typical rate data for calcite precipitation onto C16–COOH substrates. Rates increase in solutions with progressively higher supersaturations, and the rates are specific to each type of substrate. Data for all surfaces are provided elsewhere (Fig. S1). By determining the slope of number density vs. time, the steady-state rate of nucleation, J₀, was estimated from each experiment. Substituting Eq. 1b into 1a and transforming to a linear expression gives

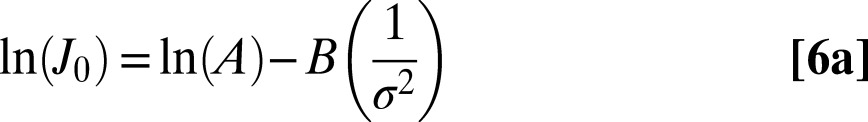where

Fig. 1.

The number of calcite nuclei on the surface of C16–COOH scales linearly with time during the early stages of each experiment. The slopes of the plotted lines for each supersaturation, σ, quantify steady-state nucleation rates, J₀. Rates of nucleation increase with the supersaturation of the mineralizing solution.

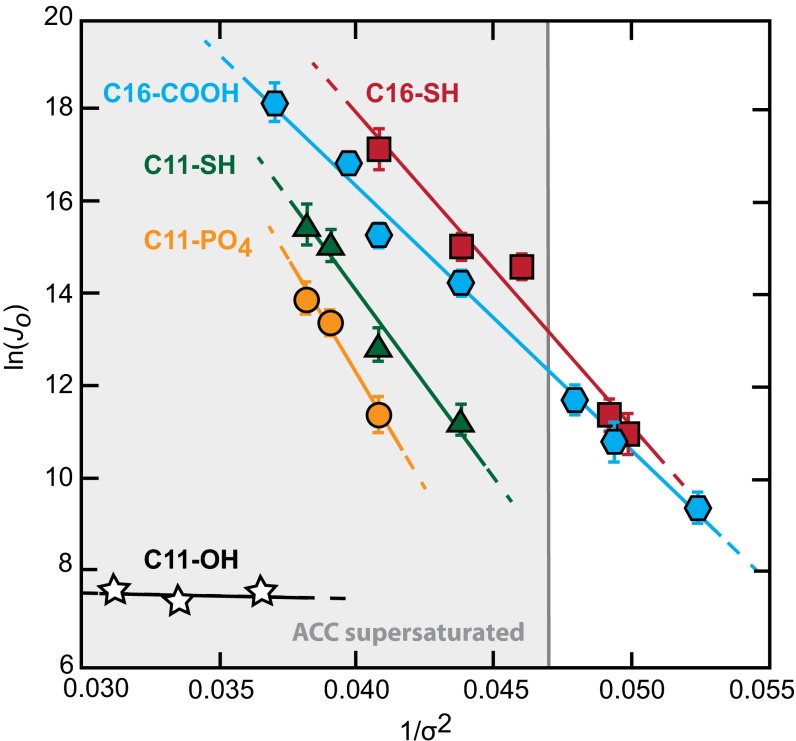
The good fit of Eq. 6a to the rate data (Fig. 2) suggests the simple classical model accurately describes the nucleation behavior for all of these surfaces. Using a shape factor of 19.1, which describes a calcite rhomb nucleating on the (012) face (16), from the slope B we find that γ ranges from 81 to 95 mJ/m² for nucleation onto the different substrates (Table 2). [Because γ is proportional to F^1/3, even if nucleation occurs on a completely different plane, the derived values of γ are nearly unchanged. For example, for nucleation on the (104) face, F decreases to 16, and the values of γ increase by only 6%.] As expected, these values for heterogeneous nucleation are smaller than the average value of 109 mJ m⁻² that is estimated for the crystal–liquid interface, which controls homogenous nucleation from solution (16, 32). Fig. S2 shows the effect of these differences on the magnitude of the barrier as a function of supersaturation.

Fig. 2.

Nucleation rate measurements obey the linear relationship predicted by Eq. 6a for all substrates. The slopes of the dependence, B, are proportional to the substrate-specific thermodynamic barriers to nucleation and are used to estimate calcite–substrate interfacial free energies, γ_cs. The shaded region indicates saturation with respect to ACC. Error bars denote two SEs of the measurements collected at each supersaturation.

Table 2.

Values of B, ln(A), and γ estimated from rates of heterogeneous calcite nucleation from solutions of varying Mg²⁺/Ca²⁺ and ΔG_ba estimated from force microscopy measurements in Mg-free solutions

Substrate	Mg2+/Ca2+	B	ln(A)	γ (mJ m−2)	ΔGba (kcal mol−1)
C16–COOH	0	−572	39	81	−7.4
C16–COOH	0.5	−582	39	81	—
C16–COOH	1.0	−511	35	79	—
C16–COOH	1.5	−485	33	77	—
C16–COOH	2.0	−539	35	80	—
C16–SH	0	−680	45	86	−4.4
C11–SH	0	−806	46	91	−2.9
C11–PO4	0	−983	52	95	−1.6

Calculations of γ assume rhombohedral nuclei. The interfacial tension²³ of calcite in solution is ∼110 mJ m⁻².

The results shown in Table 2 exhibit a substrate-specific dependence upon functional group chemistry and length of the alkanethiol chain. Monolayers with a constant chain length show chemistry-specific effects with lower values of γ for surfaces of (i) C16–COOH compared with C16–SH and (ii) C11–SH compared with C11–PO₄. Differences in chain length, likely through a combination of head group spacing and conformation (16, 20, 33–35), also affect γ as evidenced by the significantly lower value for C16–SH compared with C11–SH. The very low number of crystallites that formed on C11–OH surfaces prevented reliable estimation of nucleation rates, and these data were not further analyzed.

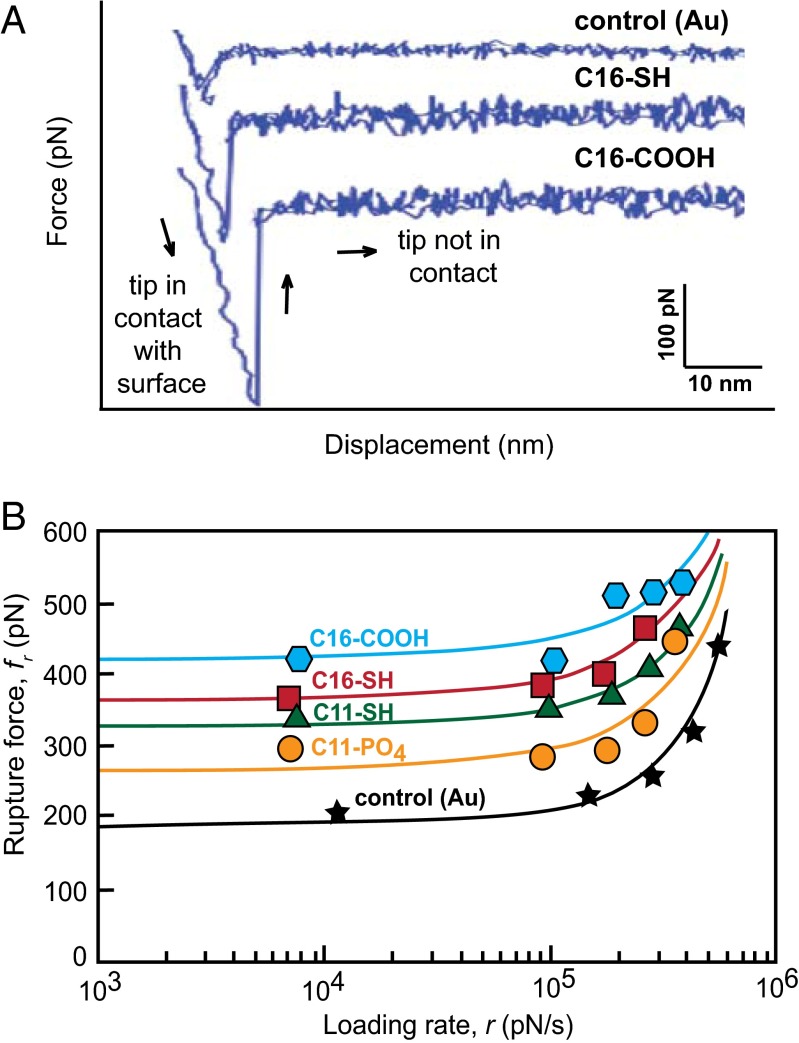
After obtaining the values of γ for the different SAM chemistries, we then conducted independent measurements to determine the magnitude of the binding free energy ∆G_b between the nucleating phase and the SAMs. We used dynamic force spectroscopy (DFS) (36, 37) to quantify ∆G_b for SAM-functionalized atomic force microscopy (AFM) tips binding to the {104} face of calcite (Materials and Methods). DFS measures the force required to rupture the bond between an AFM tip and a substrate (Fig. 3A). When the rupture force f_r is measured as a function of the rate r at which the tip is retracted from the substrate, a characteristic dependence of f_r on r is obtained (Fig. 3B). Extrapolating that dependence to zero pulling rate gives the equilibrium work required to rupture the tip–substrate bond. This is the binding free energy.

Fig. 3.

(A) Representative force curves for the control (Au-coated AFM tip) and two substrates (C16–COOH and C16–SH) show the differences in interaction strength with the calcite surface at the same tip retraction velocity (1 × 10⁻⁵ m/s). (B) Mean force of calcite–SAM rupture calculated from repeated force curve measurements decreases with the experimental loading rate, which is the product of cantilever spring constant and tip retraction velocity. All experimental substrates interact with the calcite (104) surface more strongly than the bare (gold-coated) tip. Solid lines denote exponential fits to the data.

By evaluating thousands of experiments for a series of retraction velocities we find that the alkanethiol functionalized tips are associated with significantly higher values of tip–calcite rupture force than the control (bare gold tip) and that the rupture force is indeed substrate-specific (Fig. 3B). The largest forces are associated with tips functionalized with C16–COOH, whereas the smallest forces correspond to C11–PO₄.

Due to the small size of the alkanethiol molecules (of order 10^–1 nm) compared with the curvature of the AFM tip (of order 10 nm), we expect that the measured forces correspond to the rupture of multiple (N) bonds between the tip and the surface (Fig. S3). The dependence of rupture force on loading rate (Fig. 3B) shows two distinct regimes, as expected from the theory of bond breaking (37). These include a region at small loading rate where adsorption and desorption rates are similar and fluctuations in N occur relatively rapidly and a region at large loading rate that is dominated by the kinetics of forced desorption so that fluctuations in N are less important. The multiple bond model (37) incorporates both regimes in its interpretation of force spectra and allows estimates of single-molecule–binding free energies (ΔG_b) independent of N. By fitting the rupture force data (Fig. 3B and Fig. S4) to this model, ΔG_b per molecule was estimated for each SAM alkanethiol (Table 2).

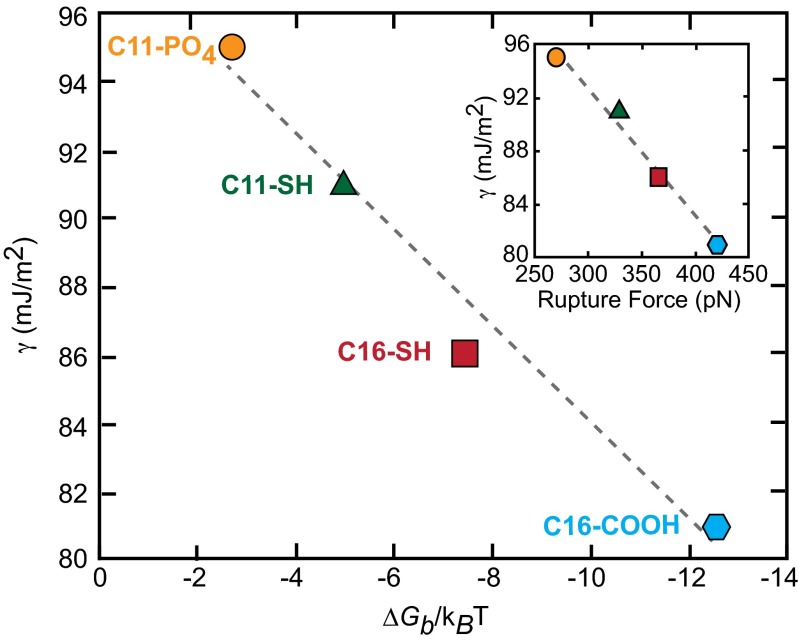
The binding energy measurements confirm the prediction that γ should scale linearly with ∆G_b (Fig. 4). Moreover, the slope of the line is close to what is expected from Eq. 5. For nucleation on the (104) face, h = 0.525 (16) whereas, for the (104) face, one can easily show it is 0.333. The value of a is at least as large as the area per SAM molecule for a perfectly ordered SAM, which is about (0.5 nm)² (38), but is certainly less than 1 nm² for a single molecule. Thus, h/a is in the range of ∼0.25–1 nm⁻². For comparison, the slope in Fig. 4 is 0.33 nm⁻². Considering the likely differences in binding to the (104) and (01 ) faces, which are likely to define the nucleation planes, and the slight uncertainties in F and a, the agreement is remarkably good.

Fig. 4.

Experimentally derived interfacial energies (γ) correlate with the free energy of binding (ΔG_b) for an alkanethiol SAM molecule with the calcite (104) surface as predicted by Eq. 4. Rupture forces which extrapolated a zero loading rate are also linearly related to γ (Inset). Lower γ correlates with strong calcite–SAM interactions (large ΔG_b or force).

The results in Fig. 4 demonstrate that lower barriers to nucleation and hence lower interfacial energies are associated with greater calcite–substrate-binding free energies. For the substrates used in this study, the trend is general across the different functional group chemistries as well as the odd/even chain lengths. Several insights arise from this analysis into how functional group chemistry can regulate the nucleation rate of calcite.

First, the findings challenge long-standing assumptions regarding the predominant role of carboxyl groups as dominant players in mineralization. Other chemical groups, albeit with lower abundance in calcifying environments, can reduce the energy barrier to nucleation and may also play significant roles in regulating patterns of mineralization. For example, Fig. 2 shows that some conformations of thiol and phosphate moieties can also significantly promote the onset of calcite formation. These results are supported by molecular modeling studies that find highly ionized substrates both exhibit strong adhesion to the calcite surfaces and promote calcite nucleation (34). The measurements also reiterate the importance of secondary structure in macromolecular activity. SAM structure and packing, which are strongly influenced by chain length (39, 40), have a strong control on calcite nucleation. A recent molecular dynamics analysis suggests these effects may be related to the degree of symmetry in interactions between SAM monomers and its impact on SAM order, highlighting once again the importance of cooperativity in both SAM–crystal-binding and template-directed nucleation (35).

Second, in agreement with previous findings for odd and even COOH SAMs (16) and polysaccharide films (17), the kinetics of crystal nucleation can be understood for all of these surfaces through a classical approach. As seen in Fig. 2, the dependence of J₀ upon supersaturation follows the predictions of classical nucleation theory and is unchanged as the driving force crosses into the regime that is supersaturated with respect to ACC. Under the conditions of this study, because the supersaturation with respect to calcite is so much larger than that with respect to ACC (16), the reduction in interfacial energy provided by the SAMs reduces the barrier to heterogeneous nucleation enough to favor precipitation of the crystalline polymorph without evidence of ACC formation in either the optical or SEM observations. The accuracy of the classical description is further demonstrated by the observed linear relationship between the interfacial and binding free energies (Fig. 4). Consequently, despite the recent reports of prenucleation clusters (41–43), liquid–liquid separation (44–46), and multiphase aggregation-based pathways of calcite formation (41, 42, 47) in bulk solutions, the results presented here provide strong evidence that the classical theory of nucleation provides a good description of calcite formation on ionized surfaces and that interfacial energy is a useful concept even when critical nuclei are in the nanometer range.

Finally, these findings unlock the secret to the success of methods that identify template molecules through binding assays. They provide a physical basis for the conventional wisdom that good binders are good nucleators: Because strong binders inherently possess a large value of ∆G_b, they lower the net interfacial energy γ, thereby reducing the barrier to nucleation.

Materials and Methods

Preparation of Functionalized Substrates.

Substrates for CaCO₃ nucleation were prepared from evaporated gold on mica (Agilent Technologies) using the template-stripped gold method (48). Self-assembled monolayers were deposited on the gold by submerging the substrates in ethanol-based (200 proof anhydrous, Sigma-Aldrich), 1.5-mM solutions of the following five alkanethiols (Sigma-Aldrich): 16-Mercaptohexadecanoic acid (C16–COOH), 1,16-Hexadecanedithiol (C16–SH), 1,11-Undecanedithiol (C11–SH), 11-Mercaptoundecylphosphoric acid (C11–PO₄), or 11-Mercapto-1-undecanol (C11–OH), for 12–15 h.

Nucleation Rate Measurements.

Solutions were prepared using calcium chloride dihydrate [99+%, (Alfa Aesar)], magnesium chloride hexahydrate [99%, (Sigma-Aldrich)], and sodium carbonate [99.997%, (Alfa Aesar)] and transferred to two polypropylene 140-cc syringes for the CaCl2/MgCl2 and Na2CO3 solutions. After rinsing with ethanol and water, the substrates were placed in a sealed flow chamber (volume = 0.5 mL) and connected to the syringes with Tygon tubing (1/16″ inner diameter, Cole Parmer). A high-precision syringe pump continuously flowed the solutions into the substrate chamber at 30 mL/h per syringe (total flow rate = 60 mL/h) to maintain steady-state conditions. This flow rate was selected after nucleation rate measurements made over a range of flow rates demonstrated this was the optimal value to prevent diffusion-limited conditions while also maintaining the reactant solutions in the chamber for sufficiently long residence time to observe nucleation for a wide variety of supersaturations. Solutions were mixed in the tubing 10 cm upstream of the substrate chamber to ensure that nucleation did not occur before the solution came into contact with the substrate (Figs. S5 and S6). The experiments were conducted at 25 °C and supersaturations of 4.66–5.12 (species activities calculated with Geochemist’s Workbench) at pH values of 10.55 ± 0.10.

CaCO₃ nucleation was monitored by optical microscopy (Olympus BX51, 10x or 20x objective). Because the resolution of the optical microscope was insufficient to directly observe the formation of critical nuclei, we estimated nucleation rates by making two assumptions.

• i)Each optically observed crystal developed from a single nucleus. That is, we assumed each nucleus that successfully crossed the energy barrier to achieve critical size grew into an optically observable crystallite. This assumption is reasonable because the data were collected only within the time interval where crystallite spacing was very large [separation between observed crystals was much greater than the size at which they became optically visible (Fig. S6)] and, during the period of constant nucleation, each crystal consisted of a single, well-faceted rhombohedrum. Moreover, the data show their appearance was linearly dependent on time (Fig. 1 and Fig. S1), which would not be true if nucleation events were not independent of one another.
• ii)All crystallites nucleated heterogeneously on the surface. Parallel experiments that used inverted substrates and an Olympus IX2 inverted microscope validated this assumption with measurements showing similar nucleation rates and through SEM observations showing that the crystals exhibited substrate-specific orientations with nucleation occurring on the (012) plane as reported previously by others (6, 16, 33, 38).

The steady-state nucleation rates were calculated directly as the slopes of crystallites versus time plots (in units of nuclei per m² per s) within the time interval where the number of nuclei increased linearly with time, typically within the first few hours of each experiment. Up to three replicate experiments were performed for each substrate/supersaturation condition, and the average J₀ from the replicates was used to calculate B and γ for each substrate.

Dynamic Force Spectroscopy.

Force measurements were made with the model MFP-3D AFM (Asylum Research) using Si3N4 cantilevers with triangular tips (Veeco). Cantilevers were cleaned under UV/ozone for 10 min, coated by thermal evaporation with 4 nm Cr followed by 40 nm Au, and recleaned under UV/ozone before placement in alkanethiol solutions for SAM deposition. Force measurements between the modified tips and a freshly cleaved calcite {104} surface (Iceland Spar, Wards) were conducted in a saturated (σ = 0) CaCO₃ solution at pH 10.55. The spring constants of individual cantilevers were calculated using the thermal calibration method (49) before beginning force measurements. Five tip retraction velocities (2 × 10⁻⁷ − 1 × 10⁻⁵ m/s) were sampled while using a constant approach velocity of 200 nm/s and a 1-s dwell time at the surface. Heterogeneity in the calcite surface was factored into the measurements by using a routine to randomly move the tip to different positions on the surface using 20-nm steps. For each surface, force curves were measured for each of the five velocities at 100 locations on the surface, resulting in 500 data points per sample.

To analyze the data and extract binding free energies, we used the theoretical treatment developed by Friddle et al. (37) for the case in which multiple bonds are broken upon retraction of the tip. This theory posits that force spectroscopy carried out over a sufficiently wide range of pulling rates naturally explores both the far-from-equilibrium regime, where bond rupture is always permanent, as well as a near-equilibrium regime where the pulling rate is sufficiently slow that both individual binding and unbinding events occur reversibly near the point of bond rupture. The rupture force exhibits a characteristic nonlinear dependence on log-pulling rate across the two regimes, with a plateau region at low pulling rates and linear rise at high pulling rates. When extrapolated to a pulling rate of zero, the force curve then gives the quasi-static work, i.e., the work required to break the bond at zero rate, which is equal to the free energy of binding ∆G_b.

Fitting this data with the dependence expected from this theory provides the value of the rupture force at zero pulling rate f_eq, as well as the parameter xt/N, which is the physical distance from the minimum of the bound state to the transition state normalized by the number of bonds. This estimate reflects both the slope of the curve in the regime of high pulling rate, as well as the force at which the transition from plateau to linear dependence is obtained. ∆G_b can then be determined by solving the transcendental equation

where W is the Lambert function.

Scanning Electron Microscopy.

SEM images were collected on a model FEI Quanta 600 FEG Environmental SEM operated at high vacuum and 10–20 kV accelerating voltage (Fig. S7). All samples were coated with ∼10 nm of Au/Pd before imaging.

Raman Spectroscopy.

The CaCO₃ polymorph of the crystallites that formed was determined by Raman spectroscopy. Spectra were recorded with a Jobin Yvon Horiba LabRam high resolution spectrometer using a 632.81-nm He–Ne laser focused through a 100x objective (Fig. S8).