Ranking and combining multiple predictors without labeled data

Significance

A key challenge in a broad range of decision-making and classification problems is how to rank and combine the possibly conflicting suggestions of several advisers of unknown reliability. We provide mathematical insights of striking conceptual simplicity that explain mutual relationships between independent advisers. These insights enable the design of efficient, robust, and reliable methods to rank the advisers’ performances and construct improved predictions in the absence of ground truth. Furthermore, these methods are robust to the presence of small subgroups of malicious advisers (cartels) attempting to veer the combined decisions to their interest.

Abstract

In a broad range of classification and decision-making problems, one is given the advice or predictions of several classifiers, of unknown reliability, over multiple questions or queries. This scenario is different from the standard supervised setting, where each classifier’s accuracy can be assessed using available labeled data, and raises two questions: Given only the predictions of several classifiers over a large set of unlabeled test data, is it possible to (i) reliably rank them and (ii) construct a metaclassifier more accurate than most classifiers in the ensemble? Here we present a spectral approach to address these questions. First, assuming conditional independence between classifiers, we show that the off-diagonal entries of their covariance matrix correspond to a rank-one matrix. Moreover, the classifiers can be ranked using the leading eigenvector of this covariance matrix, because its entries are proportional to their balanced accuracies. Second, via a linear approximation to the maximum likelihood estimator, we derive the Spectral Meta-Learner (SML), an unsupervised ensemble classifier whose weights are equal to these eigenvector entries. On both simulated and real data, SML typically achieves a higher accuracy than most classifiers in the ensemble and can provide a better starting point than majority voting for estimating the maximum likelihood solution. Furthermore, SML is robust to the presence of small malicious groups of classifiers designed to veer the ensemble prediction away from the (unknown) ground truth.

Every day, multiple decisions are made based on input and suggestions from several sources, either algorithms or advisers, of unknown reliability. Investment companies handle their portfolios by combining reports from several analysts, each providing recommendations on buying, selling, or holding multiple stocks (1, 2). Central banks combine surveys of several professional forecasters to monitor rates of inflation, real gross domestic product growth, and unemployment (3–6). Biologists study the genomic binding locations of proteins by combining or ranking the predictions of several peak detection algorithms applied to large-scale genomics data (7). Physician tumor boards convene a number of experts from different disciplines to discuss patients whose diseases pose diagnostic and therapeutic challenges (8). Peer-review panels discuss multiple grant applications and make recommendations to fund or reject them (9). The examples above describe scenarios in which several human advisers or algorithms provide their predictions or answers to a list of queries or questions. A key challenge is to improve decision making by combining these multiple predictions of unknown reliability. Automating this process of combining multiple predictors is an active field of research in decision science (cci.mit.edu/research), medicine (10), business (refs. 11 and 12 and www.kaggle.com/competitions), and government (www.iarpa.gov/Programs/ia/ACE/ace.html and www.goodjudgmentproject.com), as well as in statistics and machine learning.

Such scenarios, whereby advisers of unknown reliability provide potentially conflicting opinions, or propose to take opposite actions, raise several interesting questions. How should the decision maker proceed to identify who, among the advisers, is the most reliable? Moreover, is it possible for the decision maker to cleverly combine the collection of answers from all of the advisers and provide even more accurate answers?

In statistical terms, the first question corresponds to the problem of estimating prediction performances of preconstructed classifiers (e.g., the advisers) in the absence of class labels. Namely, each classifier was constructed independently on a potentially different training dataset (e.g., each adviser trained on his/her own using possibly different sources of information), yet they are all being applied to the same new test data (e.g., list of queries) for which labels are not available, either because they are expensive to obtain or because they will only be available in the future, after the decision has been made. In addition, the accuracy of each classifier on its own training data is unknown. This scenario is markedly different from the standard supervised setting in machine learning and statistics. There, classifiers are typically trained on the same labeled data and can be ranked, for example, by comparing their empirical accuracy on a common labeled validation set. In this paper we show that under standard assumptions of independence between classifier errors their unknown performances can still be ranked even in the absence of labeled data.

The second question raised above corresponds to the problem of combining predictions of preconstructed classifiers to form a metaclassifier with improved prediction performance. This problem arises in many fields, including combination of forecasts in decision science and crowdsourcing in machine learning, which have each derived different approaches to address it. If we had external knowledge or historical data to assess the reliability of the available classifiers we could use well-established solutions relying on panels of experts or forecast combinations (11–14). In our problem such knowledge is not always available and thus these solutions are in general not applicable. The oldest solution that does not require additional information is majority voting, whereby the predicted class label is determined by a rule of majority, with all advisers assigned the same weight. More recently, iterative likelihood maximization procedures, pioneered by Dawid and Skene (15), have been proposed, in particular in crowdsourcing applications (16–23). Owing to the nonconvexity of the likelihood function, these techniques often converge only to a local, rather than global, maximum and require careful initialization. Furthermore, there are typically no guarantees on the quality of the resulting solution.

In this paper we address these questions via a spectral analysis that yields four major insights:

1. Under standard assumptions of independence between classifier errors, in the limit of an infinite test set, the off-diagonal entries of the population covariance matrix of the classifiers correspond to a rank-one matrix.

2. The entries of the leading eigenvector of this rank-one matrix are proportional to the balanced accuracies of the classifiers. Thus, a spectral decomposition of this rank-one matrix provides a computationally efficient approach to rank the performances of an ensemble of classifiers.

3. A linear approximation of the maximum likelihood estimator yields an ensemble learner whose weights are proportional to the entries of this eigenvector. This represents an efficient, easily constructed, unsupervised ensemble learner, which we term Spectral Meta-Learner (SML).

4. An interest group of conspiring classifiers (a cartel) that maliciously attempts to veer the overall ensemble solution away from the (unknown) ground truth leads to a rank-two covariance matrix. Furthermore, in contrast to majority voting, SML is robust to the presence of a small-enough cartel whose members are unknown.

In addition, we demonstrate the advantages of spectral approaches based on these insights, using both simulated and real-world datasets. When the independence assumptions hold approximately, SML is typically better than most classifiers in the ensemble and their majority vote, achieving results comparable to the maximum likelihood estimator (MLE). Empirically, we find SML to be a better starting point for computing the MLE that consistently leads to improved performance. Finally, spectral approaches are also robust to cartels and therefore helpful in analyzing surveys where a biased subgroup of advisers (a cartel) may have corrupted the data.

Problem Setup

For simplicity, we consider the case of questions with yes/no answers. Hence, the advisers, or algorithms, provide to each query only one of two possible answers, either +1 (positive) or −1 (negative). Following standard statistical terminology, the advisers or algorithms are called “binary classifiers,” and their answers are termed “predicted class labels.” Each question is represented by a feature vector x contained in a feature space .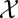

In detail, let 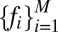be M binary classifiers of unknown reliability, each providing predicted class labels 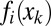to a set of S instances 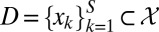, whose vector of true (unknown) class labels is denoted by 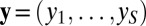.We assume that each classifier 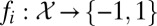was trained in a manner undisclosed to us using its own labeled training set, which is also unavailable to us. Thus, we view each classifier as a black-box function of unknown classification accuracy.

Using only the predictions of the M binary classifiers on the unlabeled set D and without access to any labeled data, we consider the two problems stated in the introduction: (i) Rank the performances of the M classifiers and (ii) combine their predictions to provide an improved estimate 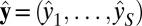of the true class label vector y.

We represent an instance and class label pair 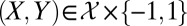as a random vector with probability density function 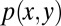, and with marginals 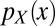and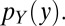

In the present study, we measure the performance of a binary classifier f by its balanced accuracy π, defined as

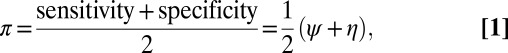where ψ and η are its sensitivity (fraction of correctly predicted positives) and specificity (fraction of correctly predicted negatives). Formally, these quantities are defined as

Assumptions.

In our analysis we make the following two assumptions: (i) The S unlabeled instances 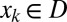are independent and identically distributed realizations from the marginal distribution 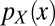and (ii) the M classifiers are conditionally independent, in the sense that prediction errors made by one classifier are independent of those made by any other classifier. Namely, for all 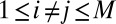, and for each of the two class labels, with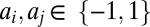

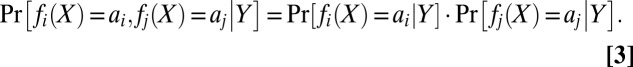Classifiers that are nearly conditionally independent may arise, for example, from advisers who did not communicate with each other, or from algorithms that are based on different design principles or independent sources of information. Note that these assumptions appear also in other works considering a setting similar to ours (15, 23), as well as in supervised learning, the development of classifiers (e.g., Naïve Bayes), and ensemble methods (24).

Ranking of Classifiers

To rank the M classifiers without any labeled data, in this paper we present a spectral approach based on the covariance matrix of the M classifiers. To motivate our approach it is instructive to first study its asymptotic structure as the number of unlabeled test data tends to infinity, 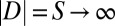. Let Q be the 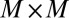population covariance matrix of the M classifiers, whose entries are defined as

where 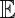denotes expectation with respect to the density 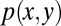and .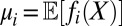

The following lemma, proven in SI Appendix, characterizes the relation between the matrix Q and the balanced accuracies of the M classifiers:

Lemma 1.

The entries q_ij of Q are equal to

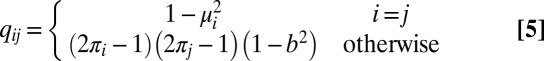where 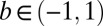is the class imbalance,

The key insight from this lemma is that the off-diagonal entries of Q are identical to those of a rank-one matrix 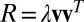with unit-norm eigenvector v and eigenvalue

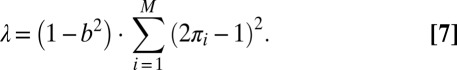Importantly, up to a sign ambiguity, the entries of v are proportional to the balanced accuracies of the M classifiers,

Hence, the M classifiers can be ranked according to their balanced accuracies by sorting the entries of the eigenvector v.

Although typically neither Q nor v is known, both can be estimated from the finite unlabeled dataset D. We denote the corresponding sample covariance matrix by . Its entries are

where Under our assumptions, is an unbiased estimate of Q, e.g., 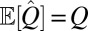. Moreover, the variances of its off-diagonal entries are given by

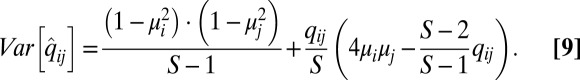In particular, 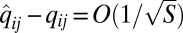and asymptotically 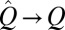as 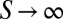. Hence, for a sufficiently large unlabeled set D, it should be possible to accurately estimate from 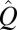the eigenvector v and consequently the ranking of the M classifiers.

One possible approach is to construct an estimate 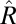of the rank-one matrix R and then compute its leading eigenvector. Given that 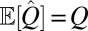, for all 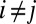we may estimate 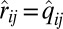, and we only need to estimate the diagonal entries of R. A computationally efficient way to do this, by solving a set of linear equations, is based on the following observation: Upon the change of variables 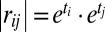, we have for all ,

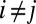Hence, if we knew q_ij we could find the vector t by solving the above system of equations. In practice, because we only have access to 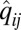we thus look for a vector 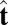with small residual error in the above 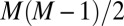equations. We then estimate the diagonal entries by 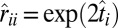and proceed with eigendecomposition of 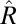. Further details on this and other approaches to estimate v appear in SI Appendix.

Next, let us briefly discuss the error in this approach. First, because 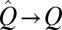as 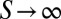, it follows that 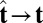and consequently 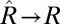. Hence, asymptotically we perfectly recover the correct ranking of the M classifiers. Because R is rank-one, 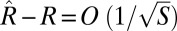and both R and 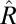are symmetric, as shown in SI Appendix, the leading eigenvector is stable to small perturbations. In particular, 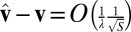. Finally, note that if all classifiers are better than random and the class imbalance is bounded away from ±1, then we have a large spectral gap with .

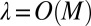SML

Next, we turn to the problem of constructing a metalearner expected to be more accurate than most (if not all) of the M classifiers in the ensemble. In our setting, this is equivalent to estimating the S unknown labels by combining the labels predicted by the M classifiers.

The standard approach to this task is to determine the MLE 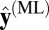of the true class labels y for all of the unlabeled instances (15). Under the assumption of independence between classifier errors and between instances, the overall likelihood is the product of the likelihoods of the S individual instances, where the likelihood of a label y for an instance x is

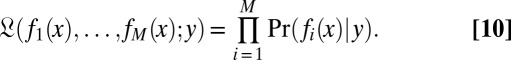As shown in SI Appendix, the MLE can be written as a weighted sum of the binary labels 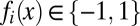, with weights that depend on the sensitivities ψ_i and specificities η_i of the classifiers. For an instance x,

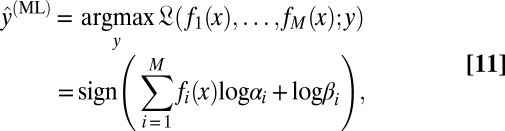where

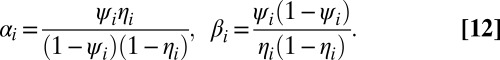Eq. 11 shows that the MLE is a linear ensemble classifier, whose weights depend, unfortunately, on the unknown specificities and sensitivities of the M classifiers.

The common approach, pioneered by Dawid and Skene (15), is to look for all S labels and M classifier specificities and sensitivities that jointly maximize the likelihood. Given an estimate of the true class labels, it is straightforward to estimate each classifier sensitivity and specificity. Similarly, given estimates of ψ_i and η_i, the corresponding estimates of y are easily found via Eq. 11. Hence, the MLE is typically approximated by expectation maximization (EM) (18–21, 23).

As is well known, the EM procedure is guaranteed to increase the likelihood at each iteration till convergence. However, its key limitation is that owing to the nonconvexity of the likelihood function the EM iterations often converge to a local (rather than global) maximum.

Importantly, the EM procedure requires an initial guess of the true labels y. A common choice is the simple majority rule of all classifiers. As noted in previous studies, majority voting may be suboptimal, and starting from it, the EM procedure may converge to suboptimal local maxima (23). Thus, it is desirable, and sometimes crucial, to initialize the EM algorithm with an estimate 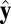that is close to the true label y.

Using the eigenvector described in the previous section, we now construct an initial guess that is typically more accurate than majority voting. To this end, note that a Taylor expansion of the unknown coefficients α_i and β_i in Eq. 12 around 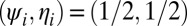gives, up to second-order terms, ,

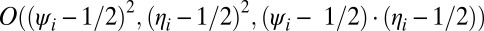Hence, combining Eq. 13 with a first-order Taylor expansion of the argument inside the sign function in Eq. 11, around 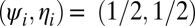yields

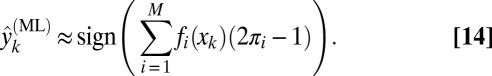Recall that by Lemma 1 up to a sign ambiguity the entries of the leading eigenvector of R are proportional to the balanced accuracies of the classifiers, 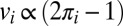. This sign ambiguity can be easily resolved if we assume, for example, that most classifiers are better than random. Replacing 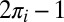in Eq. 14 by the eigenvector entries 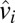of an estimate of R yields a novel spectral-based ensemble classifier, which we term the SML,

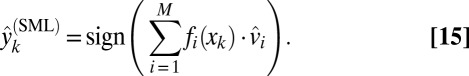Intuitively, we expect SML to be more accurate than majority voting as it attempts to give more weight to more accurate classifiers. Lemma S2 in SI Appendix provides insights on the improved performance achieved by SML in the special case when all algorithms but one have the same sensitivity and specificity. Numerical results for more general cases are described in Simulations, where we also show that empirically, on several real data problems, SML provides a better initial guess than majority voting for EM procedures that iteratively estimate the MLE.

Learning in the Presence of a Malicious Cartel

Consider a scenario whereby a small fraction r of the M classifiers belong to a conspiring cartel (e.g., representing a junta or an interest group), maliciously designed to veer the ensemble solution toward the cartel’s target and away from the truth. The possibility of such a scenario raises the following question: How sensitive are SML and majority voting to the presence of a cartel? In other words, to what extent can these methods ignore, or at least substantially reduce, the effect of the cartel classifiers without knowing their identity?

To this end, let us first introduce some notation. Let the M classifiers be composed of a subset P of 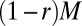“honest” classifiers and a subset C of rM malicious cartel classifiers. The honest classifiers satisfy the assumptions of the previous section: Each classifier attempts to correctly predict the truth with a balanced accuracy π_i, and different classifiers make independent errors. The cartel classifiers, in contrast, attempt to predict a different target labeling, T. We assume that conditional on both the cartel’s target and the true label, the classifiers in the cartel make independent errors. Namely, for all 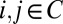, and for any labels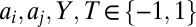

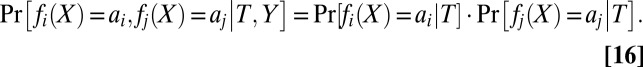Similarly to the previous sections, we assume that the prediction errors of cartel and honest classifiers are also (conditionally) independent.

The following lemma, proven in SI Appendix, expresses the entries of the population covariance matrix Q in terms of the following quantities: the balanced accuracies of the M classifiers, the balanced accuracy π_c of the cartel’s target with respect to the truth, and the balanced accuracies ξ_j of the rM cartel members relative to their target.

Lemma 2.

Given 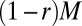honest classifiers and rM classifiers of a cartel C, the entries 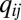of Q satisfy

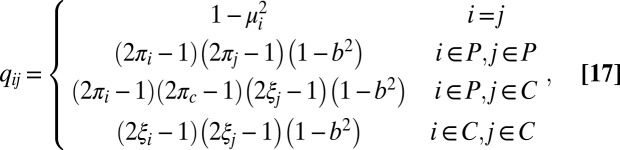where 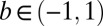is the class imbalance, as in Eq. 6.

Next, the following theorem shows that in the presence of a single cartel the off-diagonal entries of Q correspond to a rank-two matrix. We conjecture that in the presence of k independent cartels, the respective rank is .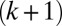

Theorem 1.

Given 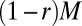honest classifiers and rM classifiers belonging to a cartel, 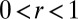, the off-diagonal entries of Q correspond to a rank-two matrix with eigenvalues

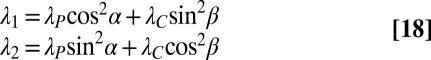and eigenvectors

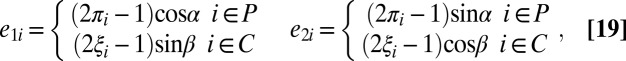where

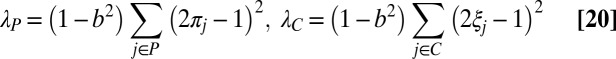and, with , ,

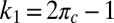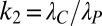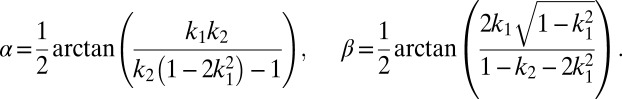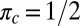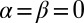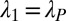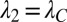As an illustrative example of Theorem 1, consider the case where the cartel’s target is unrelated to the truth, i.e., . In this case , so , and

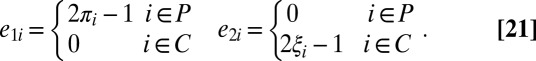Next, according to Eq. 15 SML weighs each classifier by the corresponding entry in the leading eigenvector. Hence, if the cartel’s target is orthogonal to the truth (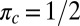) and 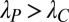, SML asymptotically ignores the cartel (SI Appendix, Fig. S3). In contrast, regardless of π_c, majority voting is affected by the cartel, proportionally to its fraction size r. Hence, SML is more robust than majority voting to the presence of such a cartel.

Application to Simulated and Real-World Datasets

The examples provided in this section showcase strengths and limitations of spectral approaches to the problem of ranking and combining multiple predictors without access to labeled data. First, using simulated data of an ensemble of independent classifiers and an ensemble of independent classifiers containing one cartel, we confirm the expected high performance of our ranking and SML algorithms. In the second part we consider the predictions of 33 machine learning algorithms as our ensemble of binary classifiers and test our spectral approaches on 17 real-world datasets collected from a broad range of application domains.

Simulations.

We simulated an ensemble of M = 100 independent classifiers providing predictions for S = 600 instances, whose ground truth had class imbalance b = 0. To imitate a difficult setting, where some classifiers are worse than random, each generated classifier had different sensitivity and specificity chosen at random such that its balanced accuracy was uniformly distributed in the interval 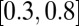. We note that classifiers that are worse than random may occur in real studies, when the training data are too small in size or not sufficiently representative of the test data. Finally, we considered the effect of a malicious cartel consisting of 33% of the classifiers, having their own target labeling. More details about the simulations are provided in SI Appendix.

Ranking of classifiers.

We constructed the sample covariance matrix, corrected its diagonal as described in SI Appendix, and computed its leading eigenvector 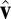. In both cases (independent classifiers and cartel), with probability of at least 80%, the classifier with highest accuracy was also the one with the largest entry (in absolute value) in the eigenvector 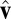, and with probability >99% its inferred rank was among the top five classifiers (SI Appendix, Fig. S4). Note that even if the test data of size S = 600 were fully labeled, identifying the best-performing classifier would still be prone to errors, because the estimated balanced accuracy has itself an error of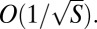

Unsupervised ensemble learning.

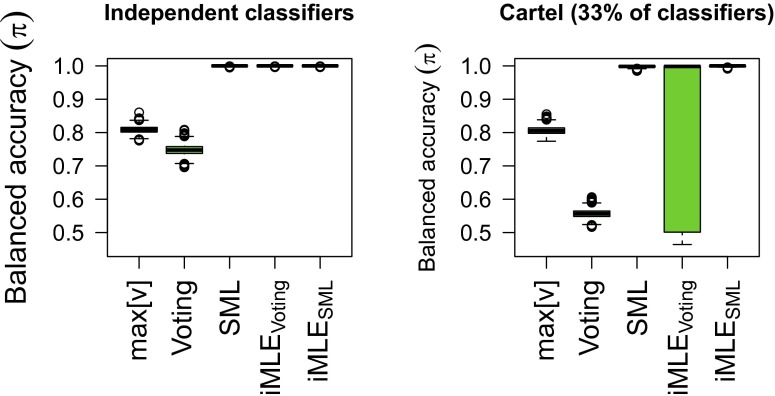
Next, for the same set of simulations we compared the balanced accuracy of majority voting and of SML. We also considered the predictions of these two metalearners as starting points for iterative EM calculation of the MLE (iMLE). As shown in Fig. 1, SML was significantly more accurate than majority voting. Furthermore, applying an EM procedure with SML as an initial guess provided relatively small improvements in the balanced accuracy. Majority voting, in contrast, was less robust. Moreover, in the presence of a cartel, computing the MLE with majority voting as its starting point exhibited a multimodal behavior, sometimes converging to a local maxima with a relatively low balanced accuracy.

Fig. 1.

Balanced accuracy of several classifiers: the classifier f_i with largest eigenvector entry, 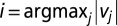; majority voting; SML; and iMLE starting from SML or from majority voting. (Left) One hundred independent classifiers; (Right) 67 honest classifiers and 33 belonging to a cartel with target balanced accuracy of 0.5. The boxplots represent the distribution of balanced accuracies of 3,000 independent runs.

A more detailed study of the sensitivity of SML and majority voting and their respective iMLE solutions versus the size of a malicious cartel with 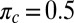is shown in SI Appendix, Fig. S5. As expected, the average balanced accuracy of all methods decreases as a function of the cartel’s fraction r, and once the cartel’s fraction is too large all approaches fail. In our simulations, both SML and iMLE initialized with SML were far more robust to the size of the cartel than either majority voting or iMLE initialized with majority voting. With a cartel size of 20%, SML was still able to construct a nearly perfect predictor, whereas the balanced accuracy of majority voting and iMLE initialized with majority voting were both far from 1. Interestingly, in our simulations, iMLE using SML as starting condition showed no significant improvement relative to the average balanced accuracy of SML itself.

Real Datasets.

We applied our spectral approaches to 17 different datasets of moderate and large sizes from medical, biological, engineering, financial, and sociological applications. Our ensemble of predictions was composed of 33 machine-learning methods available in the software package Weka (25) (Materials and Methods). We split each dataset into a labeled part and an unlabeled part, the latter serving as the test data D used to evaluate our methods. To mirror our problem setting, each algorithm had access and was trained on different subsets of the labeled data (SI Appendix).

Fig. 2 and SI Appendix, Figs. S6–S8 show the results of different metaclassifiers on these datasets. Let us now interpret these results and explain the apparent differences in balanced accuracy between different approaches, in light of our theoretical analysis in the previous section.

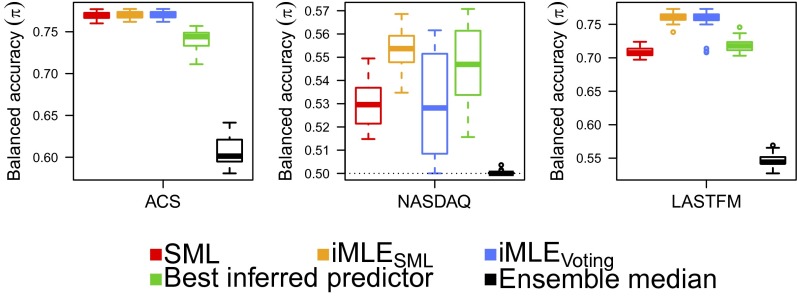
Fig. 2.

Comparison between SML, iMLE from SML or from majority voting, the best inferred predictor, and the median balanced accuracy of all ensemble predictors on real-world datasets. The ACS dataset (Left) approximately satisfied our assumptions. In the NASDAQ dataset (Center) many predictors had poor performances. For the LASTFM data (Right), the predictors did not satisfy the conditional independence assumption. In all cases iMLE starting from SML had equal or higher balanced accuracy than iMLE starting from majority voting. The boxplots represent the distribution of balanced accuracies over 30 independent runs.

In datasets where our assumptions are approximately satisfied, we expect SML, iMLE initialized with SML, and iMLE initialized with majority voting to exhibit similar performances. This is the case in the ACS data (Fig. 2, Left), and in all datasets in SI Appendix, Fig. S6. We verified that in these datasets Eq. 3 indeed holds approximately (SI Appendix, Table S3). In addition, in all these datasets, the corresponding sample covariance matrix of the 33 classifiers was almost rank-one with .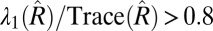

SI Appendix, Fig. S7 and Fig. 2, Center correspond to datasets where the median performance of the classifiers was only slightly above 0.5, with some classifiers having poor, even worse than random balanced accuracy. Interestingly, in these datasets, the covariance matrix between classifiers was far from being rank-one (similar to the case when cartels were present). The relative amount of variance captured by the first two leading eigenvalues 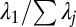and 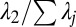was, on average, 51.4% and 15.0%, respectively. In these datasets, SML seems to offer a clear advantage: Initializing iMLE with SML rather than with majority voting avoids the poor outcomes observed in the NYSE, AMEX, and PNS datasets.

Finally, the datasets in SI Appendix, Fig. S8 and in Fig. 2, Right are characterized by very sparse (ENRON) or high-dimensional (LASTFM) feature spaces 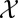. In these datasets, some instances were highly clustered in feature space, whereas others were isolated. Thus, in these datasets many classifiers made identical errors.

Remarkably, even in these cases, iMLE initialized with SML had an equal or higher median balanced accuracy than iMLE initialized with majority voting. This was consistent across all datasets, indicating that the SML prediction provided a better starting point for iMLE than majority voting.

Summary and Discussion

In this paper we presented a spectral-based statistical analysis for the problems of unsupervised ranking and combining of multiple predictors. Our analysis revealed that under standard independence assumptions the off-diagonal of the classifiers covariance matrix corresponds to a rank-one matrix, whose eigenvector entries are proportional to the classifiers balanced accuracies. Our work gives a computationally efficient and asymptotically consistent solution to the classical problem posed by Dawid and Skene (15) in 1979, for which to the best of our knowledge only nonconvex iterative likelihood maximization solutions have been proposed (18, 26–29).

Our work not only provides a principled spectral approach for unsupervised ensemble learning (such as our SML), but also raises several interesting questions for future research. First, our proposed spectral-based SML has inherent limitations: It may be suboptimal for finite samples, in particular when one classifier is significantly better than all others. Furthermore, most of our analysis was asymptotic in the limit of an infinitely large unlabeled test set, and assuming perfect conditional independence between classifier errors. A theoretical study of the effects of a finite test set and of approximate independence between classifiers on the accuracy of the leading eigenvector is of interest. This is particularly relevant in the crowdsourcing setting, where only few entries in the prediction matrix 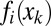are observed. Although an estimated covariance matrix can be computed using the joint observations for each pair of classifiers, other approaches that directly fit a low-rank matrix may be more suitable.

Second, a natural extension of the present work is to multiclass or regression problems where the response is categorical or continuous, instead of binary. We expect that in these settings the covariance matrix of independent classifiers or regressors is still approximately low-rank. Methods similar to ours may improve the quality of existing algorithms.

Third, the quality of predictions may also be improved by taking into consideration instance difficulty, discussed, for example, in refs. 18 and 23. These studies assume that some instances are harder to classify correctly, independent of the classifier used, and propose different models for this instance difficulty. In our context, both very easy examples (on which all classifiers agree) and very difficult ones (on which classifier predictions are as a good as random) are not useful for ranking the different classifiers. Hence, modifying our approach to incorporate instance difficulty is a topic for future research.

Finally, our work also provides insights on the effects of a malicious cartel. The study of spectral approaches to identify cartels and their target, as well as to ignore their contributions, is of interest owing to its many potential applications, such as electoral committees and decision making in trading.

Materials and Methods

Datasets and Classifiers.

We used 17 datasets for binary classification problems from science, engineering, data mining, and finance (SI Appendix, Table S1). The classifiers used are described in ref. 30 or are implemented in the Weka suite (25) (SI Appendix, Table S2).

Statistical Analysis and Visualization.

Statistical analysis and visualization were performed using MATLAB (2012a; The MathWorks) and R (www.R-project.org). Additional information is provided in SI Appendix.