Abstract
Adhesion of bacteria occurs on virtually all natural and synthetic surfaces and is crucial for their survival. Once they are adhering, bacteria start growing and form a biofilm, in which they are protected against environmental attacks. Bacterial adhesion to surfaces is mediated by a combination of different short- and long-range forces. Here we present a new atomic force microscopy (AFM)-based method to derive long-range bacterial adhesion forces from the dependence of bacterial adhesion forces on the loading force, as applied during the use of AFM. The long-range adhesion forces of wild-type Staphylococcus aureus parent strains (0.5 and 0.8 nN) amounted to only one-third of these forces measured for their more deformable isogenic Δpbp4 mutants that were deficient in peptidoglycan cross-linking. The measured long-range Lifshitz-Van der Waals adhesion forces matched those calculated from published Hamaker constants, provided that a 40% ellipsoidal deformation of the bacterial cell wall was assumed for the Δpbp4 mutants. Direct imaging of adhering staphylococci using the AFM peak force-quantitative nanomechanical property mapping imaging mode confirmed a height reduction due to deformation in the Δpbp4 mutants of 100 to 200 nm. Across naturally occurring bacterial strains, long-range forces do not vary to the extent observed here for the Δpbp4 mutants. Importantly, however, extrapolating from the results of this study, it can be concluded that long-range bacterial adhesion forces are determined not only by the composition and structure of the bacterial cell surface but also by a hitherto neglected, small deformation of the bacterial cell wall, facilitating an increase in contact area and, therewith, in adhesion force.
INTRODUCTION
Bacteria adhere to virtually all natural and synthetic surfaces (1, 2), as adhesion is crucial for their survival. Bacterial adhesion to surfaces is followed by their growth and constitutes the first step in the formation of a biofilm, in which organisms are protected against antimicrobial treatment and environmental attacks. Accordingly, the biofilm mode of growth is highly persistent and biofilms are notoriously hard to remove, causing major problems in many industrial and biomedical applications, with high associated costs. On the other hand, biofilms can be beneficial, too, as in the bioremediation of soil, for instance. Surface thermodynamics and (extended) DLVO (Derjaguin and Landau, Verwey, and Overbeek) approaches have been amply applied in current microbiology to outline that bacterial adhesion to surfaces is mediated by an interplay of different fundamental physicochemical interactions, including Lifshitz-Van der Waals, electric double-layer, and acid-base forces (3–5). Assorted according to their different effective ranges, these different fundamental interactions can be alternatively categorized into two groups, short-range and long-range forces (6), that act over distances of a few nm up to 10s of nm, respectively.
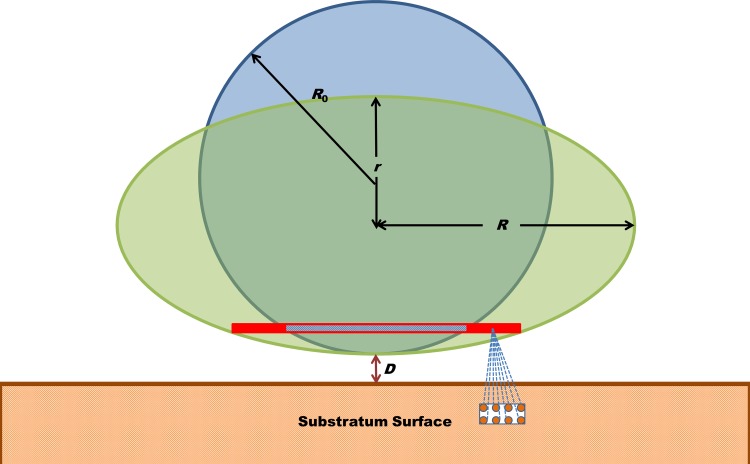
Long-range adhesion forces are generally associated with Lifshitz-Van der Waals forces (F) and can be theoretically calculated (7) for the configuration of a sphere with radius R0 versus a flat surface (Fig. 1) using the equation
| (1) |
in which A is the Hamaker constant (8), z is distance, and D indicates the separation distance between the sphere and the substratum surface. The Hamaker constant in equation 1 accounts for the materials properties of the interacting surfaces and the medium across which the force is operative. Since long-range adhesion forces result from the summation of all pairwise molecular interaction forces in the interacting volumes, any deformation that brings a bacterial cell surface closer to a substratum surface and allows it to extend over a larger contact area will increase the long-range adhesion force (Fig. 1). So far, this aspect of long-range adhesion forces between bacteria and substratum surfaces has been largely neglected, because deformation due to adhesion forces is small for naturally occurring bacteria, which possess a rigid, well-structured peptidoglycan layer. Nevertheless, it has recently been pointed out that even small deformations can have a considerable impact on the metabolic activity of adhering bacteria, a phenomenon for which the term “stress deactivation” has been coined (9). Thus, despite their small numerical values, minor variations in long-range adhesion forces may still strongly affect the behavior of bacterial cells at substratum surfaces.
FIG 1.
Pairwise summation of long-range Lifshitz-Van der Waals molecular interaction forces in the bacterial cell and substratum yields the long-range adhesion force between the interacting surfaces. Deformation of the bacterial cell wall brings more molecules in the bacterium into the close vicinity of the substratum, which increases the adhesion force. In this schematic, the undeformed bacterial cell is taken as a sphere with radius R0 deforming under the influence of the adhesion forces into an oblate spheroid with polar radius r and equatorial radius R. D indicates the separation distance.
In this paper, we propose a method to derive long-range adhesion forces between bacteria and substratum surfaces, based on a previously published elastic deformation model (10). Through the use of two isogenic Δpbp4 mutants and their wild-type parent strains (Staphylococcus aureus NCTC 8325-4 and ATCC 12600), long-range adhesion forces could be related with the nanoscale deformability of the cell wall. Note that the so-called Δpbp4 mutants are deficient in penicillin-binding proteins, which play an important role in cross-linking peptidoglycan strands, and are therefore more susceptible to deformation than their parent strains (11), for which reason they are ideal to demonstrate the role of deformation in long-range adhesion forces between bacteria and substratum surfaces.
MATERIALS AND METHODS
Bacterial strains and culture conditions.
Two pairs of staphylococcal strains were included in this study. Each pair comprised a wild-type parent strain and a so-called Δpbp4 mutant deficient in penicillin-binding proteins, which play an important role in cross-linking peptidoglycan strands in the cell wall. The Δpbp4 mutant of S. aureus NCTC 8325-4 was kindly provided by Mariana G. Pinho (Universidade Nova de Lisboa), while the Δpbp4 mutant of S. aureus ATCC 12600 was our own construct, prepared as described by Atilano et al. (12). Briefly, the strain was inoculated with the pMAD-pbp4 plasmid by electroporation and grown on tryptone soy agar (TSA; Oxoid, Basingstoke, England) plates containing erythromycin (Sigma-Aldrich, St. Louis, MO) and X-Gal (5-bromo-4-chloro-3-indolyl-β-D-galactopyranoside; Sigma-Aldrich) for 48 h at 30°C. To obtain bacteria with a chromosomally integrated copy of pMAD-pbp4, blue colonies were used to inoculate overnight cultures in tryptone soy broth (TSB; Oxoid) medium. Next, 10 ml TSB was inoculated with 100 μl of an overnight culture, and the bacteria were grown for 1 h at 30°C and then transferred to 42°C for 6 h. To select bacteria with a chromosomally integrated copy of pMAD-pbp4, dilutions (1,000×) of the culture were plated on TSA plates with erythromycin and X-Gal and incubated for 48 h at 42°C. To subsequently obtain bacteria that had excised pMAD-pbp4 from the chromosome, blue colonies with integrated pMAD-pbp4 were used to inoculate overnight cultures in TSB medium at 42°C. Next, 10 ml TSB was inoculated with 10 μl of the overnight culture, and growth was continued for 6 h at 30°C. Dilutions (1,000×) of the cultures were plated on TSA plates with X-Gal and incubated at 42°C for 48 h. White colonies were tested for erythromycin sensitivity and checked for the presence or absence of pbp4 by colony PCR.
Staphylococci were precultured from blood agar plates in 10 ml TSB. Precultures were grown for 24 h at 37°C. After 24 h, 0.5 ml of a preculture was transferred into 10 ml fresh medium and a main culture was grown for 16 h at 37°C. Bacteria were harvested by centrifugation at 5,000 × g for 5 min, washed twice with 10 mM potassium phosphate buffer, pH 7.0, and finally, suspended in the same buffer. When bacterial aggregates were observed microscopically, a 10-s sonication at 30 W (Vibra Cell model 375; Sonics and Materials Inc., Danbury, CT) was carried out intermittently three times, while cooling the suspension in a water-ice bath. Note that staphylococci are coccal organisms, possessing a nearly perfect spherical shape (13–15).
DLS.
In order to account for possible differences in the size of the Δpbp4 mutants with respect to that of their wild-type parent strains, the hydrodynamic radii (R0) of the staphylococci were determined using dynamic light scattering (DLS; Zetasizer Nano ZS; Malvern Instruments Ltd., United Kingdom) in 10 mM potassium phosphate buffer. For each strain, three separate cultures were included, and the measurements were repeated on three different aliquots from one culture.
AFM force spectroscopy.
Glass slides (Gerhard Menzel GmbH, Braunschweig, Germany) were sonicated for 3 min in 2% RBS35 (Omnilabo International BV, The Netherlands) and sequentially rinsed with tap water, demineralized water, methanol, tap water, and demineralized water.
Bacterial probes were prepared by immobilizing a bacterium onto a NP-O10 tipless cantilever (Bruker, Camarillo, CA). Cantilevers were first calibrated by the thermal tuning method, and spring constants were always within the range given by the manufacturer (0.03 to 0.12 N/m). Next, a cantilever was mounted to the end of a micromanipulator, and under microscopic observation, the tip of the cantilever was dipped into a droplet of 0.01% α-poly-l-lysine with a molecular weight of 70,000 to 150,000 (Sigma-Aldrich) for 1 min to create a positively charged layer. After 2 min of air drying, the tip of the cantilever was carefully dipped into a staphylococcal suspension droplet for 1 min to allow bacterial attachment through electrostatic attraction and dried in air for 2 min. Successful attachment of a staphylococcus on the cantilever follows directly from a comparison of the force-distance curves of a staphylococcal probe and the curve for a poly-l-lysine-coated cantilever (see Fig. S1 in the supplemental material). Although this attachment protocol is standard in the measurement of adhesion forces using atomic force microscopy (AFM) (16), it is possible that the attachment procedure disturbed the structure of the weakened mutant strains and therewith affected the results. However, bacterial probes produced similar force-distance curves, regardless of the different drying times for the wild-type parent strains and the Δpbp4 mutants (see Fig. S2 in the supplemental material). Thus, it can be ruled out that the attachment protocol disturbed the structure of the Δpbp4 mutants with their weakened cell walls. Bacterial probes were always used immediately after preparation.
All force measurements were performed in 10 mM potassium phosphate buffer (pH 7.0) at room temperature on a BioScope Catalyst atomic force microscope (Bruker). In order to verify that a bacterial probe had a single contact with the substratum surface, a scanned image in the AFM contact mode with a loading force of 1 to 2 nN was made at the onset of each experiment and examined for double contour lines. Double contour lines indicate that the AFM image was not prepared from the contact of a single bacterium with the surface but that multiple bacteria on the probe were in simultaneous contact with the substratum. Any probe exhibiting double contour lines was discarded. At this point, however, it must be noted that images containing double contour lines seldom or never occurred, since they represent the unlikely situation that the bacteria on the cantilever are equidistant to the substratum surface within the small range of the interaction forces. This is unlikely, because the cantilever was in contact with the substratum under an angle of 15 degrees.
Adhesion forces between the bacterial cell and glass surface were measured at multiple, randomly chosen spots. Before the actual measurements were taken, five force-distance curves of a bacterial probe toward a clean glass surface were measured at a loading force of 3 nN, and the maximal adhesion force upon retraction was recorded. Next, the maximal adhesion forces were separately measured at loading forces of 1, 3, 5, 7, and 9 nN. For each loading force, at least 20 force-distance curves were recorded (see Fig. S3 in the supplemental material for replicate measurements obtained with one probe), and after this series, the maximal adhesion force under the loading force of 3 nN was always measured again. Whenever this force differed from the initially measured value by more than 1 nN, the bacterial probe was considered damaged and replaced by a new one. Measurements for each strain at a single loading force typically included six bacteria and two probes, with the bacteria being taken out of three separate cultures.
Derivation of the long-range contribution to the total adhesion force.
The long-range force (FLR) between a bacterium and the substratum arises from pairwise attractive Lifshitz-Van der Waals forces between all molecules in the interacting bodies (Fig. 1) and decays slowly with increasing distance between a bacterium and the substratum surface. Therefore, as long as the bacterial cell surface is in contact with the substratum surface, FLR can be approximated as a constant, while the short-range force (FSR) can be assumed to be proportional to the contact area (S). Hence,
| (2) |
where Fadh is the total adhesion force and fSR is the short-range force per unit contact area. On the basis of a previously proposed elastic deformation model (10), Fadh can be expressed as
| (3) |
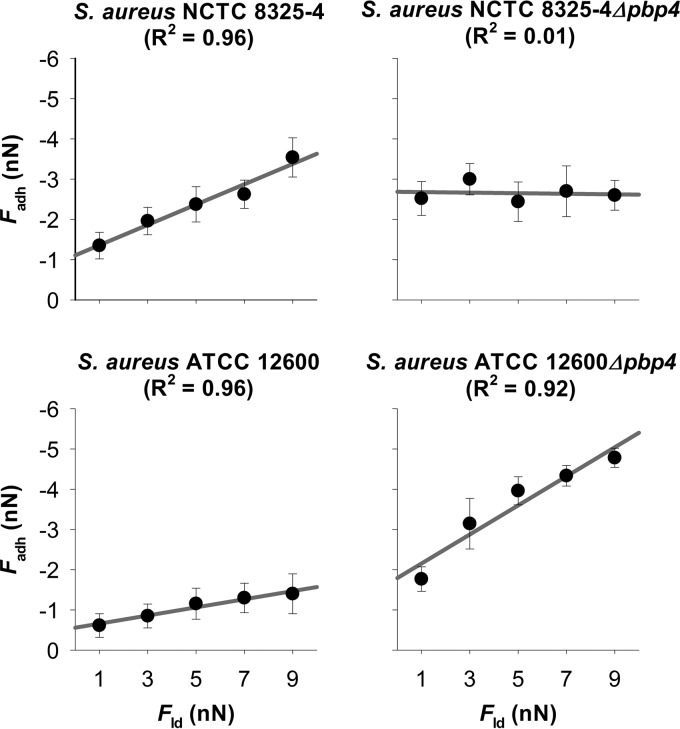
Equation 3 indicates a linear relationship between Fadh and the loading force (Fld) (see Fig. 2), while fSR, the reduced Young's modulus (E*), and the initial contact area (S0) are readily determined from our elastic deformation model (10). By fitting Fadh versus Fld according to equation 3, the value of FLR can be resolved immediately from the intercept (F0) by
| (4) |
FIG 2.
Adhesion force (Fadh) as a function of the loading force (Fld) applied during AFM measurements for two wild-type S. aureus strains (NCTC 8325-4 and ATCC 12600) and their isogenic Δpbp4 mutants. Error bars denote the standard deviations over at least 100 force curves (six bacteria divided over two different probes and taken from three separate cultures).
Theoretical evaluation of the cell wall deformation from a comparison of Lifshitz-Van der Waals forces between a sphere and an ellipsoid.
The Lifshitz-Van der Waals force between a sphere and a substratum surface () can be expressed as
| (5) |
where R0 is the radius of the undeformed sphere and D is the separation distance between the sphere and the substratum surface (Fig. 1) (7, 17). Assuming that adhering coccal bacteria deform to an ellipsoid with a shorter polar axis and a circular equatorial plane, the Lifshitz-Van der Waals force (()) can be calculated from
| (6) |
where R and r represent the lengths of the equatorial and polar radii, respectively. When the bacterial cell volume remains constant during the deformation,
| (7) |
Insertion of equation 7 into equation 6 leads to
| (8) |
The Hamaker constant of isogenic mutants can be considered similar to the one of their parental strains and, possibly, invariant with the bacterial strains involved (18, 19). Hence, dividing equation 8, as applied to the Δpbp4 mutant, by equation 5, as applied to the parent strain, yields the ratio k of the Lifshitz-Van der Waals forces between an ellipsoidally deformed Δpbp4 bacterium and an undeformed, spherical bacterium of the parent strain:
| (9) |
where and represent the hydrodynamic radii of the undeformed bacteria for the parent strain and its isogenic Δpbp4 mutant strain, respectively. Equation 9, at close approach (20) (D ≪ , r), simplifies into
| (10) |
The ratio k can be readily determined from the Lifshitz-Van der Waals adhesion forces of the parent strains and their isogenic Δpbp4 mutants, as summarized in Table 1. Subsequently, r can be calculated by
| (11) |
and substitution into equation 7 yields
| (12) |
TABLE 1.
Pairwise comparison of R0 of planktonic staphylococci, FLR, and the dimensions of ellipsoidally deformed bacterial cells from matching experimental and theoretically calculated Lifshitz-Van der Waals forces for wild-type S. aureus NCTC 8325-4 and ATCC 12600 and their isogenic Δpbp4 mutantse
| S. aureus strain | R0 (nm)a | FLR (nN)b | kb | rLW (nm)b | RLW (nm)b | R0 − rLW (nm)b | rheight image (nm)c | R0 − rheight image (nm)b |
|---|---|---|---|---|---|---|---|---|
| NCTC 8325-4 | ||||||||
| Parent strain | 618 ± 35 | −0.8 ± 0.2 | 3 ± 1 | 638 ± 44 | ||||
| Δpbp4 mutant | 570 ± 38 | −2.7 ± 0.3 | 304 ± 97 | 780 ± 202 | 266 ± 135 | 508 ± 40d | 82 ± 78 | |
| ATCC 12600 | ||||||||
| Parent strain | 678 ± 38 | −0.5 ± 0.1 | 3 ± 1 | 690 ± 31 | ||||
| Δpbp4 mutant | 620 ± 33 | −1.6 ± 0.4 | 327 ± 99 | 854 ± 197 | 293 ± 132 | 583 ± 27d | 49 ± 60 |
Data after the plus-or-minus signs indicate standard deviations in hydrodynamic radii over nine aliquots taken from three separate bacterial cultures of each strain.
Data after the plus-or-minus signs indicate standard deviations calculated by error propagation.
Data after the plus-or-minus signs indicate standard deviations in the height of bacterial cells over at least 60 staphylococci taken from three different cultures of each strain.
The polar radius (rheight image) determined in the AFM peak force-QNM mode is significantly smaller than the hydrodynamic radius (R0) measured by DLS, according to a one-sided Student's t test (P < 0.05).
For an explanation of the dimensional parameters, see Fig. 1. The deformation of the bacterial cell is expressed in terms of the difference between the hydrodynamic radius and the polar radius, i.e., (R0 − rLW) and (R0 − rheight image), in which rheight image is obtained from AFM imaging. For the shaded cells, results could not be calculated due to the assumption of undeformable wild-type strains.
Imaging of bacterial cell deformation using AFM in the peak force-QNM mode.
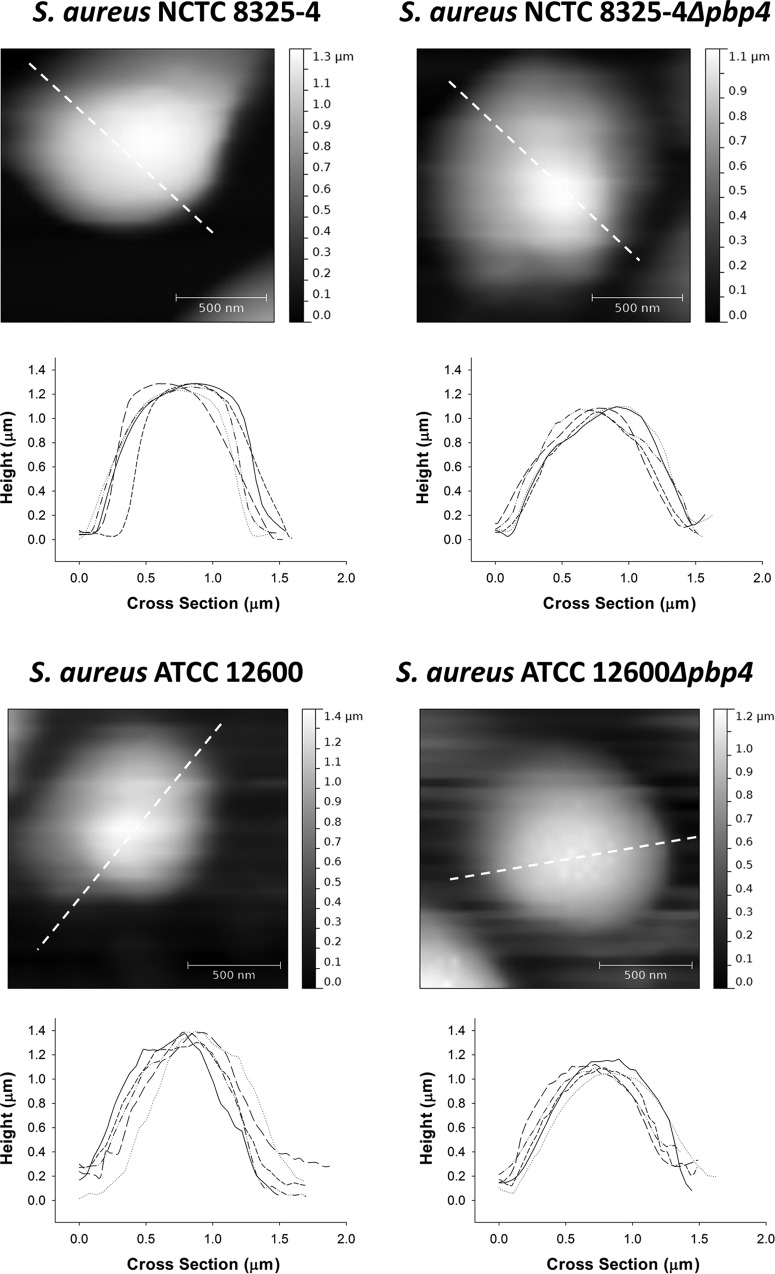
In order to directly image the possible deformation of staphylococci adhering to a surface, AFM was applied in the so-called peak force-quantitative nanomechanical property mapping (QNM) imaging mode, providing the possibility to obtain images while applying a minimal imaging force through the precise control of the force response. SCNASYST-FLUID tips (Bruker) for use in the peak force-QNM mode were calibrated as described above for NP-O10 tipless cantilevers. The tip radius was estimated by scanning the calibration surface provided by the manufacturer and image analysis with NanoScope analysis software (Bruker). First, a droplet of 0.01% α-poly-l-lysine was spread on a clean glass slide and air dried to create a positively charged surface (21). Next, a 200-μl droplet of a staphylococcal suspension was put on the slide. After 30 min, the suspension was washed off and immobilized bacteria within an area of 25 μm2 were scanned in 10 mM potassium phosphate buffer (pH 7.0) using a previously calibrated tip in the peak force-QNM mode on the BioScope Catalyst AFM at a scan rate of 0.5 Hz and peak force set point of 1 nN. The images were analyzed using Gwyddion (v2.30) software (22). The height of each individual bacterial cell was determined from the extracted height profile (see Fig. 3). For each strain, images of at least 60 different staphylococci, representing three separate cultures, were taken.
FIG 3.
Height images and profiles of individual staphylococci immobilized on a glass surface in the AFM peak force-QNM mode for two wild-type S. aureus strains (NCTC 8325-4 and ATCC 12600) and their isogenic Δpbp4 mutants. Five examples of height profiles are presented for each strain. The profiles plotted as solid lines are derived along the directions indicated by the dashed lines in the height images presented.
RESULTS
Hydrodynamic radii of planktonic staphylococci.
The hydrodynamic radii (R0) of planktonic staphylococci are presented in Table 1. According to a one-sided Student's t test performed at a significance level with a P value of <0.05, Δpbp4 mutants were slightly but significantly smaller than their wild-type parent strains. Importantly, the hydrodynamic radii of the strains were not affected by harvesting procedures, as demonstrated in Fig. S5a in the supplemental material.
Long-range contributions to bacterial adhesion forces and bacterial cell deformation.
In Fig. 2, the adhesion force (Fadh) is plotted versus the loading force (Fld) applied during AFM measurements, as derived from force-distance curves under different applied loading forces (see Fig. S4 in the supplemental material). Three out of four strains showed good linear relationships (R2 > 0.9), despite variations in the slope and intercept. However, for S. aureus NCTC 8325-4 Δpbp4, the adhesion force appeared to be independent of the loading force. Table 1 also summarizes the contribution of the long-range force (FLR) to the adhesion force for the two parent strains and their isogenic Δpbp4 mutants. All strains showed attractive long-range forces. Interestingly, the ratios k of these two forces for the parent strains and their respective isogenic mutant were very similar at about 3 for both S. aureus NCTC 8325-4 and ATCC 12600. Since the space separating the bacterial cell from the glass substratum is filled with potassium phosphate buffer of relatively high ionic strength (10 mM), electric double-layer interactions may be considered negligible (23, 24), and the ratio k between the long-range forces for the parent and mutant strains can be considered the ratio between their Lifshitz-Van der Waals forces. This consideration allows calculation of the change in the dimensions of the Δpbp4 staphylococcal mutants under the influence of attractive Lifshitz-Van der Waals forces. The long-range Lifshitz-Van der Waals adhesion forces measured matched those calculated from published Hamaker constants (18, 19), provided that an ellipsoidal deformation of the bacterial wall from its original undeformed, spherical shape with radius R0 was assumed for the Δpbp4 mutants (for details, see equations 11 and 12). Accordingly, it can be calculated that the deformation of the Δpbp4 mutants (R0 − rLW, where rLW is the polar radius of the ellipsoidally deformed bacterial cells from matching experimental and theoretically calculated Lifshitz-Van der Waals forces) amounts to 266 nm and 293 nm for S. aureus NCTC 8325-4 and ATCC 12600, respectively (Table 1), due to the built-in deficiency in their cell wall rigidity.
Direct measurement of staphylococcal cell deformation.
Comparative, quantitative data do not exist for the deformation of Δpbp4 mutants compared to that of their parent strains. Although the results from our elastic deformation model presented above are intuitively reasonable, we also measured the deformation directly using the AFM in the peak force-QNM mode (Fig. 3). Importantly, the polar radii of the strains were not affected by harvesting procedures, as demonstrated in Fig. S5b in the supplemental material. The height images and profiles of the respective wild-type parent and mutant strains were expressed in terms of the polar radii (rheight image) and are also presented in Table 1. According to a two-sided Student's t test performed at a significance level with a P value of <0.05, the rheight image values of the wild-type parent strains were not significantly different from their hydrodynamic radius (R0) values. However, according to a one-sided Student's t test performed at a significant level with a P value of <0.05, the rheight image values of both Δpbp4 mutants were significantly smaller than their hydrodynamic radius (R0) values determined using DLS. These direct measurements confirm the strong deformation of Δpbp4 mutants during adhesion to glass, although not to the same extent derived from our elastic deformation model.
DISCUSSION
Long-range, Lifshitz-Van der Waals adhesion forces between bacteria and substratum surfaces are of ubiquitous importance in facilitating adhesion of bacteria, since they cause attraction of bacteria from a long distance to a substratum surface, while they operate regardless of the details of the bacterial cell surface structure and composition. Moreover, in a long-range approach, surface appendages may be less important, as the concept of distance between bacteria and substratum surfaces is lost upon close approach. Long-range Lifshitz-Van der Waals adhesion forces can be derived from contact angles with liquids on the interacting surfaces and surface thermodynamic modeling (25, 26) or decoupling of AFM adhesion force measurements using Poisson analysis (27–30). However, among different strains, long-range adhesion forces vary considerably less than short-range forces (27–30). Similarity in long-range adhesion forces is to be expected, because these forces arise from the entire bacterial cell, i.e., its DNA content, cytoplasm, cell membrane, peptidoglycan layer, and outermost cell wall structures (Fig. 1). Whereas the outermost cell wall structures may vary the most across different strains, the overall composition of different bacterial strains is rather similar, which suggests that the variations in long-range adhesion forces observed hitherto may have sources other than differences in chemical composition. This is the first study to derive quantitative data on the nanoscale deformation of deformable Δpbp4 mutants and its relation with long-range adhesion forces between these staphylococci and substratum surfaces. The long-range adhesion forces of the deformable mutants were 3-fold stronger than those of their rigid parent strains, which suggests that long-range Lifshitz-Van der Waals forces between bacteria and substratum surfaces are strongly affected by the deformability of the bacterial cell wall. In this study, Staphylococcus aureus was used, since the undeformed bacterium is spherical and can be attached to the AFM cantilever without an orientational preference. Evaluation of cell wall deformation on the basis of the comparison of the Lifshitz-Van der Waals forces for other cell types, like rod-shaped organisms, is possible, but this requires different equations to derive the theoretical values of the Lifshitz-Van der Waals force and, moreover, precise control of the orientation of the organisms on the AFM cantilever.
An impact of bacterial cell wall deformation on long-range adhesion forces is new, as it is extremely difficult to reveal by other methods. Contact angle measurements with liquids on bacterial lawns, for instance, most likely yield information on the undeformed cell wall of the bacteria with the outer surface structures collapsed in a partly dehydrated state. Force values derived from combining contact angles on solid substrata and bacterial lawns using thermodynamic modeling therefore do not include an influence of deformation as a result of adhesion to a substratum surface. This implies that studies that aim to reveal an impact of deformation on long-range adhesion forces should, in one way or another, include cell wall deformation combined with an appropriate method. At this point, it should be admitted that even in the current study using our previously published elastic deformation model (10), we conclude that bacteria slightly deform under the influence of adhesion forces from an extrapolation of results obtained for highly deformable Δpbp4 staphylococcal mutants to the situation valid for rigid organisms.
Deformation of Δpbp4 staphylococcal mutants has never been quantified before, and hence, we have no independent comparative data. On the basis of the ellipsoidal deformation (Fig. 1), over 40% deformation along the polar axis occurred for the Δpbp4 mutants under a loading as high as 9 nN, using the assumption that the wild-type parent strains remained spherical under the same load. When directly imaging bacteria immobilized at the poly-l-lysine-coated glass slide, as mediated by attractive electrostatic interactions (16), the polar radii (rheight image) of the Δpbp4 mutants were smaller than their hydrodynamic radii (R0), but the differences appeared to be much smaller than the deformation obtained from our elastic deformation model (compare R0 − rheight image with R0 − rLW in Table 1). However, in AFM force spectroscopy, the loading force also contributes to the deformation of the bacterial cell wall. In the AFM peak force-QNM mode, the loading force hardly deforms immobilized bacteria and the cell wall deforms only under the influence of the adhesion force between the bacterium and the substratum surface. This difference in the origin of external loads likely explains why the deformation calculated from matching measured and theoretically calculated Lifshitz-Van der Waals forces is larger than that directly measured using the AFM in the peak force-QNM mode. Although they deviate quantitatively, results from our elastic deformation model and AFM support the suggestion that Δpbp4 mutants are mechanically softer than their parent strains and deform significantly under loading, which is consistent with the lack of cross-linked peptidoglycan strands in their cell wall (11, 12). At first glance, from the independence of the adhesion force (Fadh) from the applied loading (Fld), this may not seem true for S. aureus NCTC 8325-4 Δpbp4 (Fig. 2). However, this particular mutant readily reaches a strong adhesion force at low loading forces, which may be indicative of deformation over the entire range of loading forces applied; i.e., it may possess an extremely soft peptidoglycan layer.
Due to the lack of sufficiently sensitive techniques, like AFM peak force-QNM, it has hitherto been assumed that naturally occurring bacterial strains, including the parent strains of our isogenic mutants, do not deform during adhesion. Recent observations emphasize that deactivation of bacterial metabolism differs when bacteria adhere to different substrata (9, 31). Assuming that stress deactivation is related to cell deformation, it is inferred that naturally occurring bacteria suffer small, nanoscale deformation upon adhesion, causing stress deactivation (9, 32) and cell death as a fatal result when adhesion forces and accompanying deformation become too large (33–35). Yet, these studies do not provide direct evidence of bacterial cell wall deformation upon adhesion. On the basis of the results of this study, it can be concluded that minor differences in long-range Lifshitz-Van der Waals forces may be considered indicative of potential bacterial cell wall deformation.
In summary, differences in long-range Lifshitz-Van der Waals forces between adhering bacteria and substratum surfaces not only can be due to variation in the composition and structure of the bacterial cell surface but also can be caused by nanoscale deformation of the bacterial cell wall, facilitating an increase in contact area and, therewith, in adhesion force. Bacterial cell wall deformation has never been accounted for in bacterial adhesion studies, and therewith, the findings presented in the current paper pave the way for a better understanding of poorly understood phenomena like bacterial stress deactivation upon strong adhesion of micron-sized bacteria to a substratum surface.
Supplementary Material
ACKNOWLEDGMENTS
We are grateful to Mariana G. Pinho, Laboratory of Bacterial Cell Biology, and Sergio R. Filipe, Laboratory of Bacterial Cell Surfaces and Pathogenesis, Instituto de Tecnologia Quimica e Biológica, Universidade Nova de Lisboa, for providing S. aureus NCTC 8325-4 Δpbp4 and the pMAD-pbp4 plasmid.
Footnotes
Published ahead of print 8 November 2013
Supplemental material for this article may be found at http://dx.doi.org/10.1128/AEM.02745-13.
REFERENCES
- 1.Fletcher M. 1994. Bacterial biofilms and biofouling. Curr. Opin. Biotechnol. 5:302–306. 10.1016/0958-1669(94)90033-7 [DOI] [PubMed] [Google Scholar]
- 2.Hall-Stoodley L, Costerton JW, Stoodley P. 2004. Bacterial biofilms: from the natural environment to infectious diseases. Nat. Rev. Microbiol. 2:95–108. 10.1038/nrmicro821 [DOI] [PubMed] [Google Scholar]
- 3.Bos R, Van der Mei HC, Busscher HJ. 1999. Physico-chemistry of initial microbial adhesive interactions—its mechanisms and methods for study. FEMS Microbiol. Rev. 23:179–230. 10.1111/j.1574-6976.1999.tb00396.x [DOI] [PubMed] [Google Scholar]
- 4.Hermansson M. 1999. The DLVO theory in microbial adhesion. Colloids Surf. B Biointerfaces 14:105–119. 10.1016/S0927-7765(99)00029-6 [DOI] [Google Scholar]
- 5.Van Oss CJ. 1994. Interfacial forces in aqueous media. Marcel Dekker, New York, NY [Google Scholar]
- 6.Van Oss CJ. 2003. Long-range and short-range mechanisms of hydrophobic attraction and hydrophilic repulsion in specific and aspecific interactions. J. Mol. Recognit. 16:177–190. 10.1002/jmr.618 [DOI] [PubMed] [Google Scholar]
- 7.Israelachvili JN. 1992. Intermolecular and surface forces, 2nd ed. Academic Press, San Diego, CA [Google Scholar]
- 8.Hamaker HC. 1937. The London-van der Waals attraction between spherical particles. Physica 4:1058–1072. 10.1016/S0031-8914(37)80203-7 [DOI] [Google Scholar]
- 9.Liu Y, Strauss J, Camesano TA. 2008. Adhesion forces between Staphylococcus epidermidis and surfaces bearing self-assembled monolayers in the presence of model proteins. Biomaterials 29:4374–4382. 10.1016/j.biomaterials.2008.07.044 [DOI] [PubMed] [Google Scholar]
- 10.Chen Y, Norde W, Van der Mei HC, van der Busscher HJ. 2012. Bacterial cell surface deformation under external loading. mBio. 3(6):e00378–12. 10.1128/mBio.00378-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wyke AW, Ward JB, Hayes MV, Curtis NA. 1981. A role in vivo for penicillin-binding protein-4 of Staphylococcus aureus. Eur. J. Biochem. 119:389–393. 10.1111/j.1432-1033.1981.tb05620.x [DOI] [PubMed] [Google Scholar]
- 12.Atilano ML, Pereira PM, Yates J, Reed P, Veiga H, Pinho MG, Filipe SR. 2010. Teichoic acids are temporal and spatial regulators of peptidoglycan cross-linking in Staphylococcus aureus. Proc. Natl. Acad. Sci. U. S. A. 107:18991–18996. 10.1073/pnas.1004304107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lee JC, Betley MJ, Hopkins CA, Perez NE, Pier GB. 1987. Virulence studies, in mice, of transposon-induced mutants of Staphylococcus aureus differing in capsule size. J. Infect. Dis. 156:741–750. 10.1093/infdis/156.5.741 [DOI] [PubMed] [Google Scholar]
- 14.Touhami A, Jericho MH, Beveridge TJ. 2004. Atomic force microscopy of cell growth and division in Staphylococcus aureus. J. Bacteriol. 186:3286–3295. 10.1128/JB.186.11.3286-3295.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Madigan MT, Martinko JM, Stahl DA, Clark DP. 2011. Brock biology of microorganisms. Pearson Education, Limited, London, United Kingdom [Google Scholar]
- 16.Vadillo-Rodríguez V, Busscher HJ, Norde W, De Vries J, Dijkstra RJB, Stokroos I, Van der Mei HC. 2004. Comparison of atomic force microscopy interaction forces between bacteria and silicon nitride substrata for three commonly used immobilization methods. Appl. Environ. Microbiol. 70:5441–5446. 10.1128/AEM.70.9.5441-5446.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Parsegian VA. 2006. Van der Waals forces. Cambridge University Press, Cambridge, United Kingdom [Google Scholar]
- 18.Rijnaarts HHM, Norde W, Bouwer EJ, Lyklema J, Zehnder AJB. 1993. Bacterial adhesion under static and dynamic conditions. Appl. Environ. Microbiol. 59:3255–3265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rijnaarts HHM, Norde W, Lyklema J, Zehnder AJB. 1999. DLVO and steric contributions to bacterial deposition in media of different ionic strengths. Colloids Surf. B Biointerfaces 14:179–195. 10.1016/S0927-7765(99)00035-1 [DOI] [Google Scholar]
- 20.Van Kampen NG, Nijboer BRA, Schram K. 1968. On the macroscopic theory of Van der Waals forces. Phys. Lett. 26:307–308. 10.1016/0375-9601(68)90665-8 [DOI] [Google Scholar]
- 21.Camesano TA, Natan MJ, Logan BE. 2000. Observation of changes in bacterial cell morphology using tapping mode atomic force microscopy. Langmuir 16:4563–4572. 10.1021/la990805o [DOI] [Google Scholar]
- 22.Nečas D, Klapetek P. 2012. Gwyddion: an open-source software for SPM data analysis. Cent. Eur. J. Phys. 10:181–188. 10.2478/s11534-011-0096-2 [DOI] [Google Scholar]
- 23.Verwey EJW. 1947. Theory of the stability of lyophobic colloids. J. Phys. Colloid Chem. 51:631–636. 10.1021/j150453a001 [DOI] [PubMed] [Google Scholar]
- 24.Butt H-J, Graf K, Kappl M. 2006. Physics and chemistry of interfaces. John Wiley & Sons, Inc, Darmstadt, Germany [Google Scholar]
- 25.Absolom DR, Lamberti FV, Policova Z, Zingg W, Van Oss CJ, Neumann AW. 1983. Surface thermodynamics of bacterial adhesion. Appl. Environ. Microbiol. 46:90–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Van Oss CJ. 1989. Energetics of cell-cell and cell-biopolymer interactions. Cell Biophys. 14:1–16 [DOI] [PubMed] [Google Scholar]
- 27.Han T, Williams J, Beebe T. 1995. Chemical-bonds studied with functionalized atomic-force microscopy tips. Anal. Chim. Acta 307:365–376. 10.1016/0003-2670(94)00671-8 [DOI] [Google Scholar]
- 28.Williams J, Han T, Beebe T. 1996. Determination of single-bond forces from contact force variances in atomic force microscopy. Langmuir 12:1291–1295. 10.1021/la950500j [DOI] [Google Scholar]
- 29.Stevens F, Lo Y, Harris JM, Beebe TP. 1999. Computer modeling of atomic force microscopy force measurements: comparisons of Poisson, histogram, and continuum methods. Langmuir 15:207–213. 10.1021/la980683k [DOI] [Google Scholar]
- 30.Chen Y, Busscher HJ, Van der Mei HC, Norde W. 2011. Statistical analysis of long- and short-range forces involved in bacterial adhesion to substratum surfaces as measured using atomic force microscopy. Appl. Environ. Microbiol. 77:5065–5070. 10.1128/AEM.00502-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Busscher HJ, Van der Mei HC. 2012. How do bacteria know they are on a surface and regulate their response to an adhering state? PLoS Pathog. 8:e1002440. 10.1371/journal.ppat.1002440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rizzello L, Galeone A, Vecchio G, Brunetti V, Sabella S, Pompa PP. 2012. Molecular response of Escherichia coli adhering onto nanoscale topography. Nanoscale Res. Lett. 7:575. 10.1186/1556-276X-7-575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lewis K, Klibanov AM. 2005. Surpassing nature: rational design of sterile-surface materials. Trends Biotechnol. 23:343–348. 10.1016/j.tibtech.2005.05.004 [DOI] [PubMed] [Google Scholar]
- 34.Tiller JC. 2011. Antimicrobial surfaces, p 193–217 In Börner HG, Lutz J-F. (ed), Bioactive surfaces, vol 240 Springer, New York, NY [Google Scholar]
- 35.Schaer TP, Stewart S, Hsu BB, Klibanov AM. 2012. Hydrophobic polycationic coatings that inhibit biofilms and support bone healing during infection. Biomaterials 33:1245–1254. 10.1016/j.biomaterials.2011.10.038 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.