Classification of small lesions on dynamic breast MRI: Integrating dimension reduction and out-of-sample extension into CADx methodology

Abstract

Objective

While dimension reduction has been previously explored in computer aided diagnosis (CADx) as an alternative to feature selection, previous implementations of its integration into CADx do not ensure strict separation between training and test data required for the machine learning task. This compromises the integrity of the independent test set, which serves as the basis for evaluating classifier performance.

Methods and Materials

We propose, implement and evaluate an improved CADx methodology where strict separation is maintained. This is achieved by subjecting the training data alone to dimension reduction; the test data is subsequently processed with out-of-sample extension methods. Our approach is demonstrated in the research context of classifying small diagnostically challenging lesions annotated on dynamic breast magnetic resonance imaging (MRI) studies. The lesions were dynamically characterized through topological feature vectors derived from Minkowski functionals. These feature vectors were then subject to dimension reduction with different linear and non-linear algorithms applied in conjunction with out-of-sample extension techniques. This was followed by classification through supervised learning with support vector regression. Area under the receiver-operating characteristic curve (AUC) was evaluated as the metric of classifier performance.

Results

Of the feature vectors investigated, the best performance was observed with Minkowski functional ’perimeter’ while comparable performance was observed with ’area’. Of the dimension reduction algorithms tested with ’perimeter’, the best performance was observed with Sammon’s mapping (0.84 ± 0.10) while comparable performance was achieved with exploratory observation machine (0.82 ± 0.09) and principal component analysis (0.80 ± 0.10).

Conclusions

The results reported in this study with the proposed CADx methodology present a significant improvement over previous results reported with such small lesions on dynamic breast MRI. In particular, non-linear algorithms for dimension reduction exhibited better classification performance than linear approaches, when integrated into our CADx methodology. We also note that while dimension reduction techniques may not necessarily provide an improvement in classification performance over feature selection, they do allow for a higher degree of feature compaction.

1. Introduction

Computer Aided Diagnosis (CADx) aims to assist in the characterization of a previously annotated pattern in terms of its morphological or functional attributes, and in the estimation of its probability of pathological (or healthy) state [1]. Approaches to CADx typically involve three steps - (1) an extraction step where features characterizing the healthy or pathological patterns are computed, (2) a feature reduction step where the initial set of computed features are reduced to a smaller subset of features most relevant to the classification task and (3) a supervised learning step where the classification performance of the pattern characterizing features is evaluated. This has been widely demonstrated in the current literature in several contexts such as chest CT [2, 3], dynamic breast MRI [4–6], digital mammography [7, 8] etc.

Of particular interest in this study is feature reduction, which aims to efficiently represent the originally extracted high-dimension pattern characterizing feature vectors in a low-dimension space; this has been previously accomplished through feature selection in CADx [5, 6, 9]. Feature selection involves reducing the size of the originally extracted feature set through exclusion of features that are either irrelevant to the feature task, or are redundant in information content. Recently, dimension reduction was proposed as an alternative to feature selection in breast CADx [7, 10]. Rather than explicit inclusion or exclusion of specific features, such techniques allowed for algorithmic-dependent weighting of all features while computing a new feature set in the low-dimension space. While integration of dimension reduction into CADx presents an interesting innovation, the implementation is not without complications.

The supervised learning step, where features are evaluated in their ability to distinguish between healthy and pathological classes of patterns, is an important step in currently established CADx methodology. Here, a strict separation of training and test data is mandatory for proper execution of this step, especially since the performance of the features are evaluated on the test data. Feature selection can be easily integrated into CADx while maintaining this strict separation because it yields explicit selection of features that are best suited for the task. This allows simple selection of the best features from the training set alone for subsequent application to the test set. However, dimension reduction yields a new set of features in a different feature space; the mapping between the high-dimension feature set and the corresponding low-dimension representation is not as easy to interpret and subsequently replicate in the test set. Thus, the ideal approach to integrating dimension reduction in CADx while also maintaining strict training-test separation is not immediately clear. Previous approaches to integrating dimension reduction in CADx have taken to applying such algorithms to the entire dataset [7, 10] which unfortunately violates the requirement of strict seperation between training and test sets. This is attributed to the fact that dimension reduction imposes no such restriction regarding training-test data separation; data points from both sets are free to interact and influence the computation of their low-dimension representations. A direct consequence of such interaction between the training and test data, prior to the supervised learning step, is the contamination of the independent test set. Evaluating the performance of the classifier on such a test set is not representative of the real world application of CADx where all information about the test set would be completely hidden from the classifier until its training is complete.

To address this shortcoming, we propose an improved CADx methodology where the required strict separation between training and test data is maintained while concurrently integrating dimension reduction. This involves restricting the application of dimension reduction techniques to the training data alone. The low-dimension representation of data points in the test set are computed through out-of-sample extensions. A comparison of the CADx methodology proposed in this study and the one previously used is shown in Figure 1. As shown here, the use of such out-of-sample extension techniques allows for integration of dimension reduction in CADx while maintaining the integrity of the independent test set.

Figure 1.

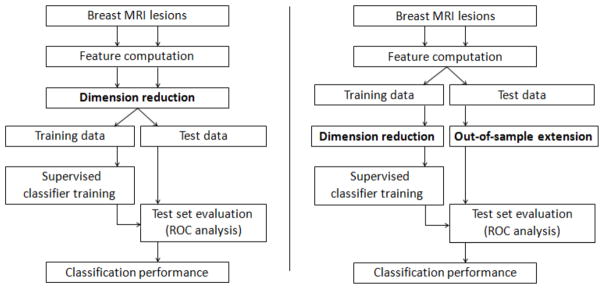
A comparison of the CADx approach previously used in the literature (A) and our CADx methodology proposed in this study (B). Note the splitting of the data into training and test sets at different stages in each approach. Our proposed methodology limits the application of dimension reduction to the training data alone, thus preserving the integrity (independence) of the test set.

We demonstrate our CADx methodology in the research context of classifying small diagnostically challenging lesions on dynamic breast magnetic resonance imaging (MRI). Breast cancer is among the leading causes of mortality for women in North America [11]. In this regard, dynamic contrast-enhanced MRI (DCE-MRI) has emerged as a promising diagnostic modality for detection and evaluation of suspicious mammographic lesions. However, while breast cancer diagnosis on DCE-MRI has been the subject of research in the area of CADx [4, 5, 12–21], not many studies have focused on evaluating the value of DCE-MRI in small lesions. Accurate diagnosis of such small lesions is clinically important for improving disease management in patients, where evaluating the dignity of breast lesions is specifically challenging as typical benign and malignant characteristics are harder to discern. In this regard, Leinsinger et al. reported a diagnostic accuracy of 75% in detecting breast cancer through cluster analysis of signal intensity time curves [22]. More recently, Schlossbauer et al., attempting to classify a dataset of small lesions (mean size 1.1 cm), reported an AUC value of 0.76 when using dynamic criteria [23].

Our work falls in the general research context of improving the classification performance of such small lesions on breast DCE-MRI. Here, we specifically focus on the evaluation of different feature reduction approaches through dimension reduction and feature selection using previously proposed topological feature sets derived from Minkowski Functionals [24]. Our goals in this work are to evaluate the ability of such feature reduction algorithms in terms of the classification performance of the reduced feature sets as well as the degree of feature compaction achieved by both approaches, as discussed in the following sections.

2. CADx methodology

2.1. Overview

Figure 1(B) shows the CADx methodology proposed and evaluated in this study; various components of this system are described in this section.

Feature computation is achieved through the use of novel topological texture features derived from Minkowski functionals [25] to dynamically capture properties of the lesion enhancement pattern. Previous studies have investigated a variety of textural approaches such as using gray-level co-occurence matrices [4, 18, 5, 26, 27], gabor texture and moment invariants [6, 26], shape descriptors [19] etc in characterizing the character of lesions on dynamic breast MRI. Such approaches usually require a pre-processing step involving precise lesion segmentation which is a challenging task for the radiologist given the small size of the lesions used in this study. Borders of such lesions can be ill-defined and harder to visualize leading to imperfect manual segmentation and significant inter-reader variability. However, the process involved in extracting Minkowski Functionals creates binary images of the lesion at several thresholds which performs an implicit segmentation without any external user input. Previous work has also shown that such texture features are also able to characterize the lesion margin at different gray-level thresholds which contributes to improved classifier performance [24]. In this work, texture analysis using Minkowski functionals is performed on all five post-contrast images of a dynamic breast MRI exam and then combined to form lesion characterizing high-dimension feature vectors; this follows a dynamic characterization approach previously explored in other studies [27, 26].

The extracted feature vectors are then split into a training and test set. The high-dimension feature vectors in the training set alone are subject to dimension reduction. While the literature boasts of a wide spectrum of dimension reduction algorithms, it is impossible to systematically evaluate our approach with all such documented algorithms. To showcase our CADx methodology with a balanced yet representative selection of algorithms, we focus on two classical and two recent dimension reduction techniques that can be considered as a balanced selection with respect to algorithmic properties, namely principal component analysis or PCA (non-parametric, linear) [28], Sammon’s mapping (classical gradient descent, non-linear) [29], t-distributed stochastic neighbor embedding or t-SNE (global optimization, non-linear) [30] and exploratory observation machine or XOM (local optimization, non-linear) [31–33].

After the training data is processed with such dimension reduction techniques, the corresponding low-dimension representations for the test set are obtained using out-of-sample extension techniques. In particular, we investigate the use of Shepard’s interpolation and radial basis function neural network function approximation (RBFN-FA).

For comparison with dimension reduction, feature selection through evaluation of mutual information criteria [9] is also used. Feature reduction is followed by supervised learning and classification, which is achieved through support vector regression (SVR) [34]. These processing steps were used to evaluate the classification performance achieved with proposed CADx methodology of maintaining training-test data separation while applying dimension reduction, as discussed in the following sections.

2.2. Texture analysis

Minkowski functionals were computed by first binarizing each specified region of interest (ROI) through the application of several thresholds. While different strategies may be pursued for choosing thresholds, we specified thresholds at equal intervals between its minimum and maximum intensity limits to cover the entire gray-level range. For each binary image obtained, three Minkowski functionals, i.e. area, perimeter and Euler characteristic, were computed as follows -

$$M{F}_{\mathit{area}}=n_s,$$ (1)

$$M{F}_{\mathit{perimeter}}=-4n_s+2n_e,$$ (2)

$$M{F}_{\mathit{Euler}}=n_s-n_e+n_v,$$ (3)

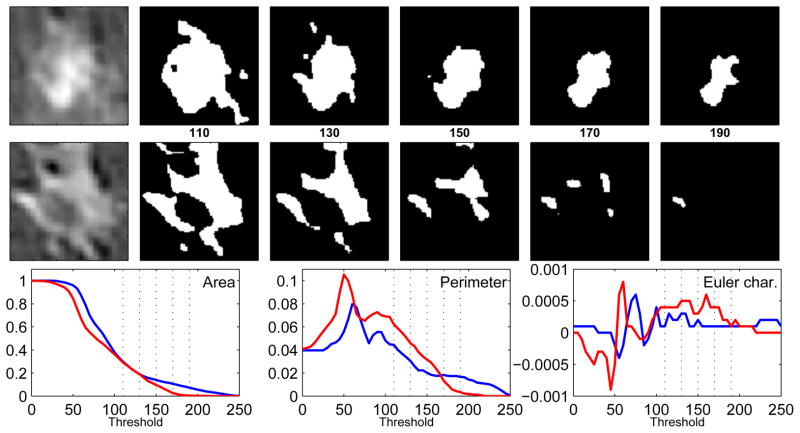
where n_s was the total number of white pixels, n_e was the total number of edges and n_v was the number of vertices [25]. The area feature recorded the area of the white pixel regions in the binary image, the perimeter feature calculated the length of the boundary of white pixel areas and the Euler characteristic was a measure of connectivity between the white pixel regions. This is further illustrated in Figure 2. The number of thresholds applied was a free parameter; different choices for this parameter are investigated here.

Figure 2.

Illustration of Minkowski functionals. The upper and middle rows correspond to benign and malignant lesion examples. Lesions on the far left are binarized for five thresholds in the interval [110, 190], where the values indicate a brightness level on a gray-level scale of [0 255]. In the bottom row, the three features - area, perimeter, and Euler characteristic, are plotted as a function of the threshold for the benign (blue) and malignant (red) lesions; the subset of the five thresholds used to create the binary images are marked as vertical dotted lines. These curves depict the morphological properties of the binary images and distinguish between the benign and malignant patterns.

Once computed for every binary image derived from a specific ROI, these values were stored in a high-dimension vector corresponding to each Minkowski functional, similar to an approach described in [3]. Such computations were performed for the same ROI on all five post-contrast images of the lesion and then combined. The dimension of such texture feature vectors was given by N×D, where N was the number of thresholds used to binarize each ROI and D was the number of post-contrast images acquired for each lesion (5 for all dynamic breast MRI exams used in this study). Thus, the overall dimension of the texture feature vectors was 100.

2.3. Feature reduction - dimension reduction

The goal of dimension reduction in this study was to transform high-dimension feature vectors into a set of low-dimension vectors for subsequent classification. Specifically, we investigated the classification performance achieved with such representations of dimensions 2, 3, 5, 10 and 20, as computed using the following methods.

PCA is an orthogonal linear transform that maps the original feature space to a new set of orthogonal coordinates or principal components [28]. This transformation is defined so that the first principal component accounts for highest global variance, and subsequent principal components account for decreasing amounts of variance. The corresponding low-dimension projections of the texture feature vectors can be determined by including the appropriate number of principal components. As mentioned above, we investigated using the first 2, 3, 5, 10 and 20 principal components to represent the high-dimension feature vectors.

Sammon’s mapping is based on a point mapping of high-dimension feature vectors to a low-dimension space such that inter-point distances in the high-dimension space approximate the corresponding inter-point distances in the low-dimension space [29].

Let X_i, i = 1, 2, ..N, represent a set of high-dimension feature vectors and Y_i, i = 1, 2, ..N, their corresponding low-dimension representations where N is the number of data points in the training set of this study. The distance between any two points X_i and X_j is represented by D_ij, and the distance between any two points Y_i and Y_j, by d_ij. Starting with a randomly chosen initial configuration for Y_i, the cost function E which represents how well the low-dimension representations Y_i represent the feature vectors X_i is given by

$$E=\frac{1}{{\sum }_{i<j}{D}_{ij}}\sum _{i<j}^N\frac{{(D_{ij}-d_{ij})}^2}{D_{ij}}.$$ (4)

A steepest descent procedure is used for minimizing E. The implementation of this algorithm was taken from a widely used dimension reduction toolbox for MATLAB [35].

Stochastic neighbor embedding (SNE) follows a non-linear approach where Euclidean distances between high-dimension texture feature vectors are converted into conditional probabilities representing similarities. The similarity of two feature vectors is defined as the conditional probability that one selects the other as a neighbor; the closer the feature vectors, the higher the similarity [30]. Once such conditional probability distributions are established for both the high-dimension feature vectors and their corresponding low-dimension representations, the goal is to minimize the mismatch between the two distributions.

Let X_i, i = 1, 2, ..N, represent a set of high-dimension feature vectors and Y_i, i = 1, 2, ..N, their corresponding low-dimension representations. Let p_j|i be the condition probability that X_i selects X_j as a neighbor, assuming that neighbors were picked in proportion to their probability density under a Gaussian centered at X_i. Similarly, q_j|i is the conditional probability in the low-dimension space. The goal of SNE is to reduce the mismatch between p_j|i and q_j|i, which is achieved through minimization of the sum of Kullback-Leibler (KL) divergences over all feature vectors using a gradient descent method. The cost function is given by

$$E=\sum _{i}KL(P_i||Q_i)=\sum _i\sum _j{p}_{j\mid i}log\frac{p_{j\mid i}}{q_{j\mid i}},$$ (5)

where P_i represents the conditional probability distribution over all other feature vectors given X_i, and Q_i represents the conditional probability distribution over all other low-dimension representations given Y_i.

t-SNE was developed as an improvement over SNE in two respects - (1) simplification of the cost function optimization and (2) addressing the so-called crowding problem inherent to SNE [30]. Details pertaining to this algorithm and its cost function minimization can be found in [30], and a review of the algorithm can be found in [7, 36]. The t-SNE implementation was taken from the dimension reduction toolbox for MATLAB [35]. This implementation had one free parameter perplexity, which can be defined as a smooth measure of the effective number of neighbors. The value of this free parameter was specified to provide the best separation between the two classes of lesions. Other internal parameters of t-SNE such as the degrees of freedom of the t-function and the number of iterations for which the cost function optimization is processed were defined through default settings provided by the toolbox.

Finally, we note that the t-SNE implementation provided in the MATLAB toolbox was specifically tuned for visualizing high-dimensional data in 2-D and 3-D; its behavior in general dimension reduction tasks (such as 5-D, 10-D, 20-D etc) is not fully understood [30]. Our inclusions of results that reduce the data to 5, 10 and 20 dimensions were simply for completeness, and to observe their corresponding effects on classification performance.

XOM maps a finite number of data points X_i in a high-dimension space to target points Y_i in the low-dimension embedding space [31–33]. The embedding space is equipped with a structure hypothesis which corresponds to the final target structure for embedding the high-dimension data. However, a key difference that separates XOM from other topology-preserving mappings, such as Kohonen’s Self-Organizing Map (SOM) [37], is that it projects the high-dimension data to the low-dimension embedding space (rather than projecting the sampling vectors of the structure hypothesis onto the high-dimension data space).

The initial setup of XOM involves - (1) defining the topology of the high-dimension data in the feature space through computation of distances d(X_i, X_j) between feature vectors X_i, (2) defining a structure hypothesis represented by sampling vectors S_k in the low-dimension space, and (3) initializing output vectors Y_i, one for each input feature vector X_i. While different choices may be considered for S_k, such as lattice structures, Gaussian distributions etc. [33], we use random samples from a uniform distribution in this application in order to enable occupation of the entire projection space. The output vectors Y_i are adapted iteratively during the training process; upon completion of the dimension reduction procedure, their final position represents the low-dimension projections of the high-dimension feature vectors.

Once the initial setup was complete, the goal of the algorithm is to reconstruct the topology induced by the high-dimension feature vectors X_i through displacements of Y_i in the low-dimension space. This is accomplished by incrementally updating the image vectors Y_i using a sequential learning procedure. For this purpose, neighborhood couplings between feature vectors in the high-dimension space are represented by a cooperativity function h, which was modeled in this study as a Gaussian

$$h(X_i,X^{\prime }(S(t)),\sigma (t))=e^{-\frac{{(X_i-X^{\prime }(S(t)))}^2}{2{\sigma }^2(t)}}.$$ (6)

Here, X′(S(t)) represents the best-match for a input feature vector X_i. For a randomly selected sampling vector S, the best-match feature vector X′ is identified by the criterion: ||S − Y′|| = min_i|| S − Yi||. Once the best-match feature vector is identified, the output vectors Y_i are incrementally updated by a sequential adaptation step according to the learning rule

$$Y_i(t+1)=Y_i(t)+\epsilon (t)h(X_i,X^{\prime }(S(t)),\sigma (t))(S(t)-Y_i(t)).$$ (7)

where t represents the iteration step, ε(t) is the learning rate and σ(t) is a measure of neighborhood width taken into account by the cooperativity function h. In this study, both ε(t) and σ(t) are changed in a systematic manner depending on the number of iterations by an exponential decay annealing scheme [33]. The algorithm is terminated when either the cost criterion is satisfied, or when the maximum number of iterations is completed. The above sequential learning rule can be interpreted as a gradient descent step on a cost function for XOM, whose formal derivation can be found in [36]. By systematically exchanging functional and structural components of topology preserving mappings such as SOM [37], XOM can be seen as a computational framework for structure-preserving dimensionality reduction [32, 33]. Further details of this algorithm can be found in [32, 36].

We note three parameters in this algorithm - (1) the learning parameter ε(2) the neighborhood parameter σ, and (3) the total number of iterations. Default settings were specified for internal parameters ε and number of iterations. Under these conditions, the value of free parameter σ that enabled the best separation between the two classes of lesions was identified.

2.4. Out-of-sample extension

Since feature reduction through dimension reduction was restricted in its application to the training data alone, the test data were out-of-sample points that had to be mapped to a low-dimension representation. For this purpose, the training set of high-dimension points X_i and their corresponding known low-dimension representations Y_i were used to define a mapping F such that Y_i = F (X_i). Once established, such a mapping could be used to determine the low-dimension representations of the test set.

The goal of out-of-sample extension algorithms in this context was to create or approximate the mapping F. For a high-dimension feature vector X whose low-dimension representation is unknown, F can be treated as an interpolating function of the form

$$F(X)=\sum _{i=1}^M{a}_i(X)Y_i,$$ (8)

where a_i are the weights that define the interpolating function and M is the number of data points in the test set. We investigated two approaches to defining these weights.

Shepard’s interpolation

This technique implements an inverse distance weighting approach in defining a_i described previously [38], i.e.,

$$a_i(X)=\frac{1/d{(X,X_i)}^p}{{\sum }_{j=0}^{M}1/d{(X,X_j)}^p}.$$ (9)

The power parameter p controlled how points at different distances from X contributed to the computation of F(X), i.e. large values of p ensured that only those points close to X made contributions to the weighting function.

Radial basis neural network function approximation (RBFN-FA)

As an alternative to Shepard’s interpolation, the mapping F was approximated using a radial basis function neural network. The weights a_i were defined as,

$$a_i(X)=\frac{e^{-\frac{{(X-X_i)}^2}{2{\rho }^2}}}{{\sum }_{j=0}^M{e}^{-\frac{{(X-X_j)}^2}{2{\rho }^2}}},$$ (10)

which represented the activity of the hidden layer of the radial basis function network. The ρ parameter controlled the shape of the radial basis function kernel, and defined the neighborhood of feature vectors that contributed to the computation of F(X).

Of the dimension reduction techniques investigated in this study, PCA was a special case that allowed for direct mapping of out-of-sample points into the lower-dimension space and did not require any special out-of-sample extension.

2.5. Treatment of free parameters for dimension reduction and out-of-sample extension

Most advanced non-linear dimension reduction and out-of-sample extension techniques have free parameters which must be specified. Typically, such free parameters were optimized using a variety of quality measures related to visualization, as described in the literature [29, 39–41]. We refrained from using such measures in this study for two reasons - (1) the best way to evaluate the quality of a lower-dimension projection is still unclear and under debate [40] and (2) the end goal for dimension reduction in this study is classification and not visualization. For these reasons, we instead specified values for such free parameters that provided the best separation between the benign and malignant classes of lesion patterns, as identified in cross-validation analysis performed independently with randomly chosen subsets of data.

2.6. Feature reduction - feature selection

Feature selection involves identifying a subset of features from the input feature space that makes the most relevant contribution to separating the two different classes of data points in the machine learning step. This study used mutual information analysis to identify a subset of features from the high-dimensional feature vectors that best contributed to the lesion character classification.

Mutual information (MI) is a measure of general independence between random variables [42]. For two random variables X and Y, the MI is defined as -

$$I(X,Y)=H(X)+H(Y)-H(X,Y),$$ (11)

where entropy H(·) measures the uncertainty associated with a random variable. The MI I(X, Y ) estimates how the uncertainty of X is reduced when Y has been observed. If X and Y are independent, their MI is zero.

For ROI data set in this study, the MI between each feature f_s, which is the feature stored in the s^th dimension of feature vector f, and the corresponding class labels y was calculated as

$$I(f_s,y)=\sum _{}^{n_c}\sum _{}^{n_f}P(f_s,y){log}_2\frac{P(f_s,y)}{P(f_s)P(y)},$$ (12)

where n_c was the number of classes and n_f was the number of histogram bins used for f_s. In this approach, the probability density function of each variable is approximated using histograms P(·) [43]. The number of classes n_c = 2 and the number of histogram bins for the texture features n_f was determined adaptively according to

$$n_f={log}_{2}N+1+{log}_2(1+\kappa \sqrt{N/6}),$$ (13)

where κ is the estimated kurtosis and N the number of ROIs in the training set [9].

2.7. Classification

The extraction of texture features and subsequent feature reduction was followed by a supervised learning step where the lesion patterns were classified as benign or malignant. In this work, support vector regression with a radial basis function kernel was used for the machine learning task [34]. Here, SVR treated the features as independent variables and their labels as the dependent variable and acted as a function approximator; this function was then used in conjunction with the texture features of the test data to predict their labels. The SVR implementation was taken from the libSVM library [44].

In this study, 70% of the data was used for the training phase while the remaining 30% served as an independent test set. The percentages for division into training and test set (and subsequent division of the training set into a training and validation set for cross-validation) were determined empirically; 50-50, 60-40, 70-30, 80-20 and 90-10 splits have all been used in the literature. The training data was sub-sampled from the complete dataset in such a manner that atleast 40% of each class (benign and malignant) were represented to ensure that class representation in the training set was not skewed toward one particular class. Special care was taken to ensure that lesion ROIs extracted from the same patient were used either as training or test data to prevent any potential for biased training. As mentioned earlier, the use of out-of-sample extension techniques ensured that training and test feature vectors did not interact during the feature reduction step. When evaluating feature selection, the best features of the texture feature vectors were selected by evaluating the mutual information criteria of the training data alone.

In the training phase, models were created from labeled data by employing a random sub-sampling cross-validation strategy where the training set was further split into 70% training samples and 30% validations samples. Such cross-validation was performed over 40 iterations where the training and validation samples were picked randomly from the original training set. The purpose of the training was to determine the optimal classifier parameters, i.e. those that best capture the boundaries between the two classes of lesion patterns. The free parameters for the classifiers used in this study were the cost parameter for SVR and the shape parameter of its radial basis function kernel. Then, during the testing phase, the optimized classifier predicted the label (benign or malignant) of lesion ROIs in the independent test dataset; a receiver-operating characteristic (ROC) curve was generated and used to compute the area under the ROC curve (AUC) which served as a measure of classifier performance. This process was repeated 50 times resulting in an AUC distribution for each feature set.

We use AUC as the metric of classifier performance in this study over simpler metrics such as accuracy in this study for the following reasons - (1) AUC, unlike accuracy, is not influenced by the prevalence of disease in the sample, and it is not calculated on the basis of only one cut-off point, which treats false-positive and false-negative results as if they were equally undesirable, but allows for a detailed evaluation of diagnostic accuracy at varying levels of sensitivity and specificity [45], (2) AUC is well established as a metric of classifier performance in various studies involving lesion classification on breast MRI [5–7, 10, 23, 26, 21, 20, 27, 24], (3) ) it serves as metric for quantitative comparison of classifier performance between different algorithmic approaches in our CADx methodology, and (4) it allows us to compare our approach to previous studies that have also reported AUC values while investigating lesion classification on a similar dataset of small lesions [23].

2.8. Statistical analysis

A Wilcoxon signed-rank test was used to compare two AUC distributions corresponding to different texture features. Significance thresholds were adjusted for multiple comparisons using the Holm-Bonferroni correction to achieve an overall type I error rate (significance level) less than α (where α = 0.05) [46, 47].

Texture, feature reduction, classifier and statistical analysis were implemented using Matlab 2008b (The MathWorks, Natick, MA).

3. Data

3.1. Patient data

Sixty diagnostically challenging breast tissue lesions were identified from DCE-MRI datasets of 54 female patients by two experienced radiologists who came to a consensus on evaluation of clinical findings. The mean patient age was 52 (standard deviation: 12 years, range: 27 to 78 years). In all cases, histopathologically confirmed diagnosis from needle aspiration/excision biopsy was available prior to this study; 32 of the lesions were diagnosed as benign and the remaining 28 as malignant. Mean lesion diameter was 1.1 cm (standard deviation of 0.73 cm). The histological distribution of the 32 benign lesions is as follows - 3 fibroadenoma, 10 fibrocystic changes, 5 fibrolipomatous change, 7 adenosis, 1 papilloma and 6 non-typical benign disease. The histological distribution of the 28 malignant lesions is as follows - 18 invasive ductal carcinoma, 5 invasive lobular carcinoma, 3 ductal carcinoma in-situ and 2 non-typical malignant disease.

3.2. Acquisition protocols

Patients were scanned in the prone position using a 1.5T MR system (Magnetom VisionTM, Siemens, Erlangen, Germany) with a dedicated surface coil to enable simultaneous imaging of both breasts. Images were acquired in the transversal slice orientation using a T1-weighted 3D spoiled gradient echo sequence with the following imaging parameters; echo repetition time (TR) = 9.1 ms, echo time (TE) = 4.76 ms and flip angle (FA) = 25°. Acquisition of the pre-contrast series was followed by the administration of 0.1 mmol/kg body weight of paramagnetic contrast agent (gadopentate dimeglumine, MagnevistTM, Schering, Berlin, Germany). Five post-contrast series were then acquired, each with a measurement time of 83 seconds, and at intervals of 110 seconds. All DCE-MRI datasets were acquired, based on routine clinical indication only, with informed consent from the patients. Purely retrospective use of strictly anonymized data was performed according to the institutional review board (IRB) guidelines of Ludwig Maximilians University, Munich, Germany.

In the collection of patient data used in this study, images in the dynamic series were acquired with two different settings of spatial parameters; for 19 patients, the images were acquired as 32 slices per series with a 512×512 matrix, 0.684×0.684 mm² in-plane resolution and 4 mm slice thickness, while in other cases, the same images were acquired as 64 slices per series with a 256×256 matrix, 1.37×1.37 mm² and 2 mm slice thickness. To maintain uniform image data for texture analysis, the images acquired with a 512×512 matrix were reduced to a 256×256 matrix through bilinear interpolation.

3.3. Lesion annotation

With the exception of two patients, for whom two separate lesions were chosen for analysis, one primary lesion was selected from each patient for analysis. Each identified lesion was annotated with a two-dimensional (2D) square ROI with dimensions of 11×11 pixels on the central slice of the lesion by two experienced radiologists in a consensus approach. The ROI annotations were made on difference images created by subtracting the fourth post-contrast image from the pre-contrast image; these difference images were acquired as part of the clinical imaging protocol and allowed for better localization of the small lesions through enhancement of lesion tissue. This ROI was subsequently translated to the pre-contrast and all five post-contrast images of the T1 dynamic series. The ROI size was chosen to minimize the included amount of surrounding healthy tissue. A single encapsulating ROI was used to capture the lesion in most cases. Four lesions (3 malignant and 1 benign), whose margins exceeded the ROI boundary, were captured with two non-overlapping ROIs to preserve lesion margin information. Three examples of the small lesions used in this study are shown in Figure 3.

Figure 3.

Examples of benign and malignant lesion ROIs at five different images of contrast uptake.

3.4. Pre-processing steps

Lesions were enhanced on each post-contrast ROI (S_i) by subtracting and dividing the i^th post-contrast ROI S_i, i = {1, 2, 3, 4, 5}, with the corresponding ROI annotated on the pre-contrast lesion (S₀), S_i = (S_i − S₀)/S₀. This step effectively suppresses the healthy tissue that surrounded the lesion in the ROI but can be problematic if patient motion during the acquisition results in improper registration between the various post-contrast and pre-contrast images. Datasets used in this study had only negligible motion artifacts over time and thus, compensatory image registration steps were not required.

4. Results

4.1. Extracting Minkowski functionals with different number of thresholds

Table 4.1 shows the classification performance in AUC achieved with the three Minkowski functionals when extracted with different number of binarizing thresholds. The extracted feature vectors were not subject to subsequent dimension reduction and out-of-sample extension and thus the size of these vectors was determined by the number of binarizing thresholds used. A significant improvement in performance was noted with perimeter when 20 such thresholds were used to binarize the ROI of the lesion (on each post-contrast image)(p < 0.05). The classification performance did not significantly improve when more thresholds were used (p < 0.05). All other results reported in this study used 20 thresholds when computing topological texture features from each post-contrast image. The resulting overall dimension of each Minkowski functional feature vector was 100. We also observed that while the performance of the feature vectors derived from area and perimeter were comparable to each other, both significantly outperformed Euler characteristic (p < 0.01).

Table 1.

Comparison of the best classification performance (mean AUC ± std) achieved achieved with Minkowski functionals when different thresholds are used for computation of features. A significant improvement is noted with perimeter when 20 thresholds are used. No further significant improvement in performance is noted when the thresholds are increased.

No. of thresholds	Area	Perimeter	Euler Char.
5	0.79 ± 0.11	0.77 ± 0.11	0.66 ± 0.09
10	0.81 ± 0.10	0.80 ± 0.10	0.68 ± 0.09
15	0.81 ± 0.09	0.78 ± 0.10	0.68 ± 0.10
20	0.83 ± 0.09	0.82 ± 0.10	0.68 ± 0.10
25	0.80 ± 0.10	0.84 ± 0.09	0.67 ± 0.10

4.2. Evaluating the best results obtained with dimension reduction

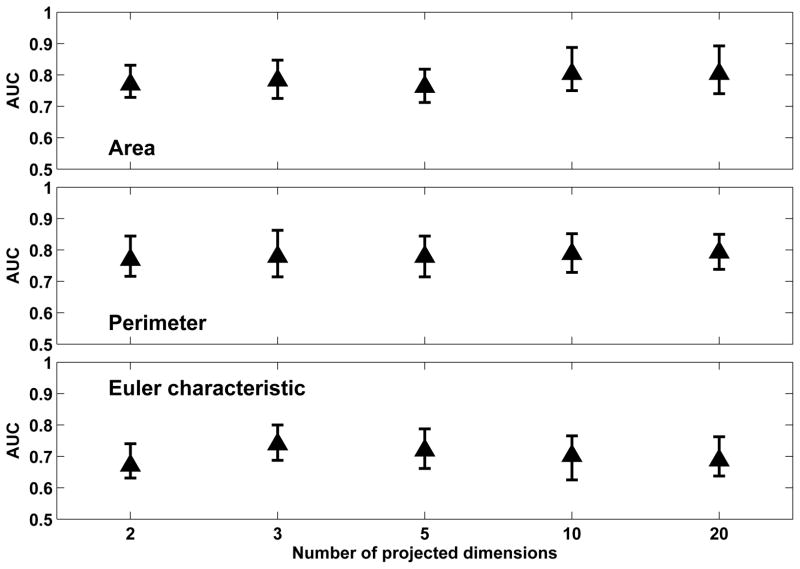
Figure 4 shows the classification performance achieved with the three Minkowski functionals when PCA was used to project the feature vectors to a low-dimension space defined by different numbers of principal components. The best classification performance was observed with ’Area’ (0.81 ± 0.09) and ’Perimeter’ (0.80 ± 0.10) which was obtained with 20-D projections from PCA. However, we note that this performance was not significantly better than that achieved with 2-D (0.78 ± 0.10 for area and perimeter) or 3-D projections (0.79 ± 0.10 for area and perimeter). Thus, a high degree of feature compaction was achieved from the original 100-D vectors. We also evaluated the percentage of variance accounted for when including different number of principal components of the original feature vectors. Inclusion of 20 principal components accounted for 99% of overall variance in both area and perimeter, while inclusion of 2 and 3 principal components accounted for approximately 65% and 75% of variance respectively, as seen in Table 4.2.

Figure 4.

Comparison of classification performance achieved with Minkowski functionals when PCA is used in conjunction with out-of-sample extension (through direct mapping) for different numbers of projected dimensions in the low-dimension space. For each distribution, the central mark corresponds to the median and the edges are the 25th and 75th percentile. The best results are obtained with ’area’ and ’perimeter’ for a 20-D low-dimension representation; however, comparable performance is also achieved with 2-D and 3-D representations.

Table 2.

Percentage of overall variance accounted for by different number of principal components.

No. of Principal Components	% of Overall Variance
	Area	Perimeter	Euler Char.
2	65.99	63.52	54.60
3	76.53	73.47	63.04
5	87.40	84.01	74.43
10	95.68	93.40	85.65
20	99.29	98.76	95.14

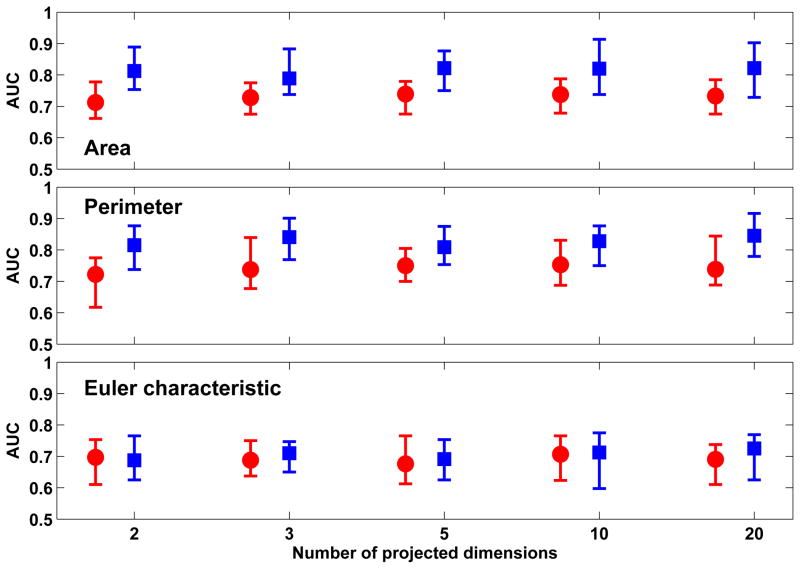
Figure 5 shows the classification performance achieved with the three Minkowski functionals when Sammon’s mapping is used to project the feature vectors to a low-dimension space. The best classification performance was observed with ’Area’ (0.83 ± 0.08) and ’Perimeter’ (0.84 ± 0.10) when 20-D projections were obtained using Sammon’s mapping in conjunction with out-of-sample extension through RBFN-FA. We note that the performance achieved with 20-D projections for ’Area’ were not significantly better than those achieved with 2-D (0.81± 0.10) or 3-D projections (0.80± 0.10). Similarly, the performance achieved with 20-D projections for ’Perimeter’ were not significantly better than those achieved with 3-D projections (0.83 ± 0.09). Thus, a high degree of feature compaction was achieved from the original 100-D vectors. When comparing out-of-sample extension techniques used in conjunction with Sammon’s mapping, we note that the performance achieved with RBFN-FA was significantly better than that achieved with Shepard’s interpolation (p < 0.01).

Figure 5.

Comparison of classification performance achieved with Minkowski functionals when Sammon’s mapping is used in conjunction with out-of-sample extension through Shepard’s interpolation (red) and RBFN-FA (blue) for different numbers of projected dimensions in the low-dimension space. For each distribution, the central mark corresponds to the median and the edges are the 25th and 75th percentile. The best results are obtained with ’area’ and ’perimeter’ with RBFN-FA for a 20-D low-dimension representation; however, comparable performance is also achieved with 2-D and 3-D representations.

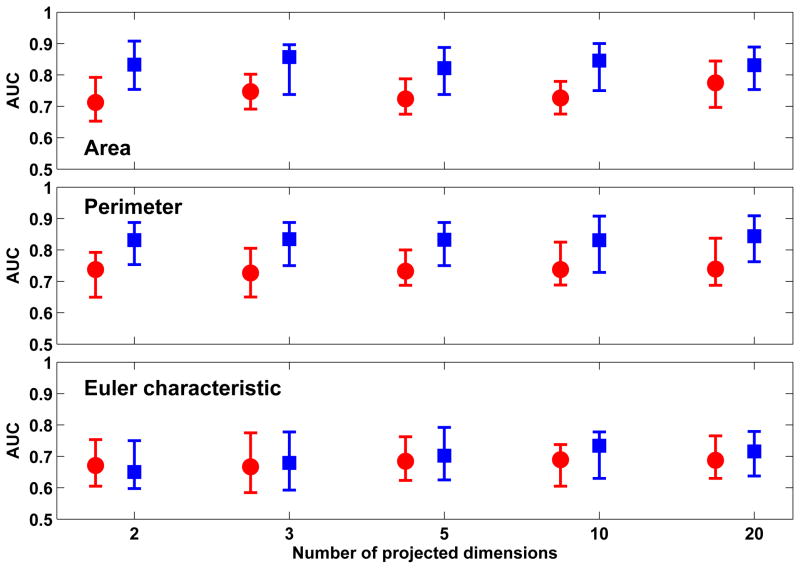
Figure 6 shows the classification performance achieved with the three Minkowski functionals when XOM was used to project the feature vectors to a low-dimension space of different dimensions. The best classification performance was observed with ’Area’ (0.83 ± 0.10) which was obtained with 2-D projections from XOM. Comparable performance was observed with ’Perimeter’ (0.82 ± 0.09), also with 2-D projections. The classification performance for both did not significantly improve or decline when dimensions of the XOM projections was increased. Of the two out-of-sample extension techniques used, the best classification performance was achieved with RBFN-FA which significantly outperformed Shepard’s interpolation (p < 0.01).

Figure 6.

Comparison of classification performance achieved with Minkowski functionals when XOM is used in conjunction with out-of-sample extension through Shepard’s interpolation (red) and RBFN-FA (blue) for different number of projected dimensions in the low-dimension space. For each distribution, the central mark corresponds to the median and the edges are the 25th and 75th percentile. The best results are obtained with ’area’ and ’perimeter’ with RBFN-FA for a 2-D low-dimension representation; no significant improvement in performance is observed when the number of projected dimensions is increased further.

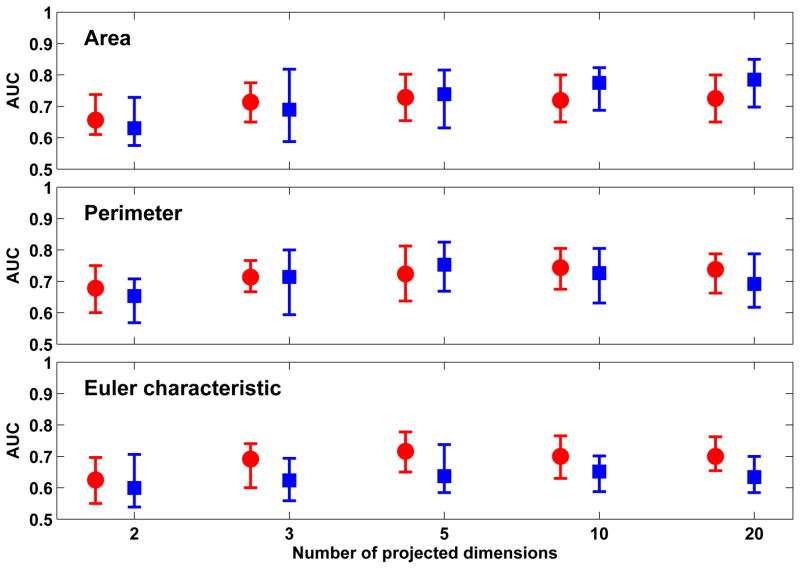
Figure 7 shows the classification performance achieved with the three Minkowski functionals when t-SNE was used to project the feature vectors to a low-dimension space of different dimensions. The best classification performance was observed with ’Area’ (0.76 ± 0.11) for 20-D projections and ’Perimeter’ (0.74 ± 0.12) for 5-D projections. In both cases, the performance was not significantly different than that achieved with 3-D projections. No significant differences were observed between using RBFN-FA and Shepard’s interpolation (p < 0.05).

Figure 7.

Comparison of classification performance achieved with Minkowski functionals when t-SNE is used in conjunction with out-of-sample extension through Shepard’s interpolation (red) and RBFN-FA (blue); and for different number of projected dimensions in the low-dimension space. For each distribution, the central mark corresponds to the median and the edges are the 25th and 75th percentile. The best results are obtained with ’area’ and RBFN-FA for a 20-D low-dimension representation.

4.3. Dimensionality reduction vs feature selection vs no feature reduction

Table 4.4 shows a comparison of the best classification performance obtained with the three Minkowski functionals when using PCA, Sammon’s mapping, XOM and t-SNE in conjunction with RBFN-FA to create low-dimension representations of the feature vectors. For comparison, the classification performance obtained with feature selection through evaluation of mutual information criteria, and with no feature reduction was also included. The number of projective dimensions required to achieve the reported classification performance is also shown.

Table 4.

Comparison of the best classification performance (mean ± std) achieved with Minkowski functionals for 2-D and 3-D projections (Proj.) using PCA, Sammon’s mapping, XOM and t-SNE. The third column (Sep.) indicates the state of training-test seperation in CADx methodology used, the one proposed in this study (Y) or the current approach specified in the literature where dimension reduction is applied to the entire dataset (N).

Proj.	Feature	Sep.	PCA	Sammon	XOM	t-SNE
2D	Area	Y	0.78 ± 0.10	0.81 ± 0.10	0.83 ± 0.10	0.67 ± 0.09
		N	0.79 ± 0.09	0.79 ± 0.11	0.77 ± 0.10	0.72 ± 0.11
	Perimeter	Y	0.78 ± 0.10	0.80 ± 0.11	0.82 ± 0.10	0.68 ± 0.10
		N	0.79 ± 0.11	0.79 ± 0.09	0.77 ± 0.11	0.70 ± 0.11
	Euler char.	Y	0.68 ± 0.09	0.69 ± 0.09	0.67 ± 0.11	0.63 ± 0.10
		N	0.71 ± 0.11	0.67 ± 0.09	0.69 ± 0.10	0.69 ± 0.09
3D	Area	Y	0.79 ± 0.10	0.80 ± 0.10	0.82 ± 0.10	0.71 ± 0.08
		N	0.79 ± 0.09	0.79 ± 0.09	0.77 ± 0.09	0.78 ± 0.11
	Perimeter	Y	0.79 ± 0.10	0.83 ± 0.09	0.82 ± 0.10	0.73 ± 0.09
		N	0.79 ± 0.11	0.79 ± 0.09	0.79 ± 0.10	0.76 ± 0.08
	Euler char.	Y	0.72 ± 0.09	0.70 ± 0.08	0.69 ± 0.11	0.68 ± 0.09
		N	0.75 ± 0.08	0.67 ± 0.08	0.70 ± 0.10	0.72 ± 0.09

The best classification performance with ’Area’ was observed when using Sammon’s mapping (0.83 ± 0.08) and XOM (0.83 ± 0.10). This was no significantly better than the performance achieved when no feature reduction was employed (p < 0.05). The best classification performance with ’Perimeter’ was observed with Sammon’s mapping (0.84 ± 0.10). This was not significantly better than either XOM (0.82± 0.09) or not using any feature reduction (0.82± 0.09) (p < 0.05). However, for both Minkowski Functionals, the worst classification performance was observed with t-SNE which was significantly outperformed by other algorithms (p < 0.05). For both features, the dimension reduction techniques were used in conjunction with RBFN-FA.

As seen Table 4.4, XOM achieved the reported results while using the least number of dimensions for its projections (2-D). While Sammon’s mapping required 20-D projections for its reported performance, this was not significantly better than the performance achieved with 2-D projections for ’Area’ or 3-D projections for ’Perimeter’, as seen in Figure 5. Thus, Sammon’s mapping and XOM were able to achieve high classification performance while simultaneously providing a high degree of compaction of the original feature set, especially when compared to feature selection through mutual information.

4.4. Comparing the CADx work flow proposed in this study with the previous approach

Table 5 shows the comparison in classification performance achieved with the two CADx methodologies (outlined in Figure 1) when using PCA, Sammon’s mapping, XOM and t-SNE for both 2-D and 3-D projections. As seen here, the classification performance achieved with all techniques did not significantly change when either CADx approach was used. The only exception to this trend was classification performance of Minkowski functional ’Area’ when processed with XOM, which showed a small but significant improvement in performance (p < 0.05) when the CADx methodology proposed in this study was used. In contrast, classification performance for t-SNE improved when the CADx approach did not properly maintain an independent test set, although this improvement was not statistically significant (p < 0.05) and its performance was still worse than other techniques.

5. Discussion

Dimension reduction has been previously proposed as an alternative for feature selection in CADx while evaluating the character of suspicious lesions on breast exams [7, 10]. However, such studies did not maintain a strict separation between training and test data while integrating dimension reduction into CADx, which is requirement for the supervised learning step. To address this shortcoming, we developed, tested and quantitatively evaluated an improved CADx methodology that integrates dimension reduction while concurrently maintaining strict separation between training and test sets. This was achieved by applying dimension reduction to the training data alone, while using out-of-sample extension techniques to compute low-dimension representations of the test set. Our methodology explored the integration of dimension reduction algorithms such as PCA, Sammon’s mapping, XOM and t-SNE in conjunction with out-of-sample extension techniques such as Shepard’s interpolation and RBFN-FA, as alternatives for explicit feature selection for the purpose of reducing the size of the originally extracted feature set. In this study, the original feature set included three 100-D vectors extracted for each of the Minkowski functionals, i.e., area, perimeter and Euler characteristic.

We demonstrated the applicability of our CADx methodology to a clinical problem, namely improving the classification performance achieved with small diagnostically challenging lesions (mean size 1.1 cm) on breast DCE-MRI. Accurate diagnosis of such small lesions is clinically important for improving disease management in patients, where evaluating the dignity of breast lesions is specifically challenging as typical benign and malignant characteristics are harder to discern. The best AUC value achieved by previous studies with such lesions was 0.76 when using dynamic criteria to characterize the lesions [23]. In this study, we were able to improve upon such results through the use of topological texture features derived from Minkowski functionals which were subsequently processed using non-linear dimension reduction techniques such as Sammon’s mapping (0.84 ± 0.10 for perimeter) and XOM (0.83 ± 0.10 for area) in conjunction with RBFN-FA when using our proposed CADx methodology. Improved classification performance can contribute to reducing (1) the likelihood of performing false positive biopsies of benign lesions, thereby eliminating risks associated with the biopsy and (2) missed breast cancers developing from misdiagnosed malignant lesions, while also enabling earlier diagnosis of suspicious lesions.

As seen in Table 4.1, the best classification performance among the feature vectors extracted from Minkowski Functionals was achieved with area and perimeter. These features characterize the size and boundary of the lesion pixel regions as a function of the gray-level threshold, thereby capturing aspects of lesion heterogeneity (or lack thereof), which is an important criterion for determining malignancy of lesions on breast DCE-MRI. This is also observed in Figure 2 where the benign and malignant lesion exhibit very different topological changes when binarized with different gray-level thresholds. We also note in Table 4.1 that Euler Characteristic performs significantly worse when compared to the other two Minkowski Functionals (p < 0.01). This suggests that connectivity does not make a significant contribution toward distinguishing between benign and malignant enhancement patterns when such small lesions are analyzed. Table 4.1 also shows a significant improvement in performance when using 20 binarizing thresholds, rather than 15 or lower, to extract the Minkowski Functionals. This suggests that using too few thresholds does not provide such features enough resolution to disccriminate between the two classes of lesions. Using more than 20 thresholds did not significantly improve classification performance which indicates that too many thresholds do not provide additional information at distinguishing between benign and malignant classes of lesions in our dataset.

As seen in Figures 4–7, the best classification performance was observed when non-linear dimension reduction methods such as Sammon’s mapping and XOM are used in conjunction with RBFN-FA, rather than with linear methods such as PCA. However, while such non-linear algorithms offer more sophistication in terms of their algorithmic properties, they also include more free parameters whose specification is not trivial. When one considers both the classification performance and the degree of feature compaction achieved, both XOM and Sammon’s mapping were able to achieve high classification performance using 2-D and 3-D projections. This clearly demonstrates that such methods can be successfully utilized in CADx methodology to maintain classification performance while simultaneously enabling a high degree of feature compaction. Such compaction allowed for an efficient representation of information that achieved the best separation between the two classes of patterns.

Table 4.4 compares the classification performance achieved with Sammon’s mapping and XOM, to that achieved with feature selection using mutual information. As seen here, both Sammon’s mapping and XOM were able to achieve comparable classification performance to mutual information. More importantly, Sammon’s mapping and XOM were able to achieve this classification performance while reducing the original 100-D feature set to a smaller feature set (2-D or 3-D) while mutual information required a significantly larger feature set to represent the reduced feature set. This can be related to the fact that feature selection calls for explicit inclusion or exclusion of features which does constitute some loss of information. Dimension reduction, on the other hand, allows all features to influence the final low-dimension representations in some weighted manner as determined by the algorithm used. This could potentially streamline the collection of information pertaining to the classification task while also making the representation of this information more compact, i.e., through a low-dimension output feature space.

Table 5 compares the performance achieved with 2-D and 3-D projections of all Minkowski functionals, obtained with different dimension reduction techniques, using both CADx methodologies outlined in Figure 1. The results observed here suggest that our proposed CADx methodology, while maintaining strict separation of training and test data, does not cause any deterioration in classification performance, when compared to the current approach used in the literature. However, we anticipate that the performance observed with our approach will deteriorate as the size of the data (and in turn the training set) becomes smaller, which could affect the performance of the non-linear dimension reduction algorithms. Given that small datasets are not uncommon in studies focused on CADx research, specifically in dynamic breast MRI [6, 26], this effect could be significant interest and will be studied in more detail in future studies.

One limitation of this study regards the treatment of t-SNE. As seen in Figure 7 and Table 4.4, the worst performance with this dataset of small lesions was noted with t-SNE regardless of which CADx methodology was used. The poor performance could be tied to the default settings used for the internal parameters of t-SNE. As acknowledged by the authors in [30], these default settings were best suited for tasks involving visualization of high-dimension data in 2-D or 3-D, and thus, perhaps not for processing the feature vectors of our dataset or for the classification task investigated in this study. Another limitation concerns the handling of datasets with different spatial resolution in this study. Since the feature extraction approach pursued in this study was not resolution-invariant, we processed all ROIs with higher spatial resolution with bilinear interpolation to match the lower spatial resolution of the remaining ROIs. While this ensured that such differences in spatial resolution did not contribute any bias to the feature extraction and subsequent classification, future studies should also investigate the development and use of resolution-invariant features for this task.

While integrating dimension reduction into CADx presents an interesting innovation and is accompanied by promising results such as those reported in this study, it is important to be aware of certain inherent drawbacks with this approach. The goal in CADx is to identify the separation between different classes of feature vectors in a collection of high-dimension data. Dimension reduction, on the other hand, aims to best represent high-dimension data in a low-dimension space through some optimization paradigm (preservation of distances, similarities, topologies etc). Thus, the goals of both may not always converge and as a result, integrating dimension reduction into CADx may not always yield desirable results. As future outlook, we propose to explore dimension reduction techniques that incorporate some form of class discrimination while computing the low-dimension representations of the high-dimension feature vectors. Supervised dimension reduction variants of learning vector quantization approaches such as generalized matrix learning vector quantization (GMLVQ) [48], limited rank matrix learning vector quantization (LiRAM LVQ) [49], or of the neighbor retrieval visualize (NeRV) algorithm [40], would be better suited to integration with our CADx methodology proposed in this study.

6. Conclusion

This study describes a new approach to integrating dimension reduction into the CADx methodology while concurrently maintaining a strict separation between training and test sets required for supervised learning components. Such a strict separation, achieved by restricting the application of dimension reduction to the training data alone while processing the test data with out-of-sample extension techniques, ensured that the integrity of the test set was not compromised prior to the classification task.

Our proposed CADx methodology was demonstrated in the research context of classifying small diagnostically challenging breast tissue lesions (mean lesion diameter of 1.1 cm) on DCE-MRI. The results observed suggest that incorporating such a methodology can facilitate improvements in the classification performance achieved with such lesions when compared to previous work in this area. Non-linear algorithms for dimension reduction exhibited better classification performance than linear approaches, when integrated into our CADx methodology. Finally, we note that while such dimension reduction techniques may not necessarily provide an improvement in achievable classification performance over feature selection, they do allow for a high degree of compaction in the feature reduction step.

We hypothesize that such an approach would have clinical significance given the inherent difficulty in evaluating the dignity of small breast lesions where typical benign and malignant characteristics are harder to identify. However, larger controlled trials need to be conducted in order to further validate the clinical applicability of our method.

Table 3.

Comparison of the best classification performance (mean ± std) achieved with feature reduction techniques - PCA, XOM, t-SNE and MI, as well as the corresponding dimensions of the output feature vectors. The classification performance achieved without feature reduction (none) is also included. As seen here, the best results are obtained for area and perimeter when used with Sammon’s mapping or XOM (in conjunction with RBFN-FA); XOM achieves this with the smallest lower-dimensional representation. All results for PCA, XOM and t-SNE were obtained with the CADx methodology proposed in this study.

Feature	Technique	AUC	Dimension
Area	PCA	0.81 ± 0.09	20
	Sammon	0.82 ± 0.08	20
	XOM	0.83 ± 0.10	2
	t-SNE	0.76 ± 0.11	20
	MI	0.81 ± 0.10	50
	none	0.83 ± 0.09	100
Perimeter	PCA	0.80 ± 0.10	20
	Sammon	0.84 ± 0.10	20
	XOM	0.82 ± 0.09	2
	t-SNE	0.74 ± 0.12	5
	MI	0.80 ± 0.09	30
	none	0.82 ± 0.09	100
Euler char.	PCA	0.72 ± 0.09	3
	Sammon	0.70 ± 0.08	3
	XOM	0.71 ± 0.11	5
	t-SNE	0.71 ± 0.09	5
	MI	0.69 ± 0.09	20
	none	0.68 ± 0.09	100