Modeling Seroadaptation and Sexual Behavior among HIV⁺ Study Participants with a Simultaneously Multilevel and Multivariate Longitudinal Count Model

Summary

Longitudinal behavioral intervention trials to reduce HIV transmission risk collect complex multilevel and multivariate data longitudinally for each subject with important correlation structures across time, level, and variables. Accurately assessing the effects of these trials are critical for determining which interventions are effective. Both numbers of partners and numbers of sex acts with each partner are reported at each time point. Sex acts with each partner are further differentiated into protected and unprotected acts with correspondingly differing risks of HIV/STD transmission. These trials generally also have eligibility criteria limiting enrollment to participants with some minimal level of risky sexual behavior tied directly to the outcome of interest. The combination of these factors makes it difficult to quantify sexual behaviors and the effects of intervention. We propose a multivariate multilevel count model that simultaneously models the number of partners, acts within partners, and accounts for recruitment eligibility. Our methods are useful in the evaluation of intervention trials and provide a more accurate and complete model for sexual behavior. We illustrate the contributions of our model by examining seroadaptive behavior defined as risk reducing behavior that depends on the serostatus of the partner. Several forms of seroadaptive risk reducing behavior are quantified and distinguished from non-seroadaptive risk reducing behavior.

1. Introduction

Behavioral interventions designed for people living with HIV represent a targeted method of reducing the sexual transmission of HIV and can potentially play a critical role in controlling the human immunodeficiency virus (HIV) epidemic (Aral and Eterman, 2002). The Health Living Project (HLP) (The Healthy Living Project Team, 2007) is one behavioral intervention program in recent years that targets this population.

A successful intervention works to reduce risky behaviors that can lead to future transmission. This can come from reducing the number of partners who are HIV negative and/or reducing the number of unprotected sex acts with each partner who is HIV negative. In HLP and similar studies, measures of risky behavior are traditionally summarized into a single outcome. These outcomes typically involve summing behaviors across partners, for example the total number of unprotected sex acts with all partners who are either HIV negative or of whom the HIV status is uncertain. These measures are aggregated outcomes. While an aggregated outcome can be conveniently modeled using a univariate longitudinal model, it fails to accurately describe the complexity of risky sexual behavior. We show that reduction in risk can come from several different behavioral changes and argue that these changes require different interventions. Seroadaptation is one specific strategy where the subject uses knowledge or perceived knowledge of their potential partner’s HIV serostatus to alter their behavior and limit their risk of transmission. The term HIV serostatus describes an individual’s status of being positive or negative for the HIV antibody. We use the terms HIV⁺ serostatus to describe an individual that is positive for the HIV antibody and HIV⁻ serostatus for an individual who is negative for the HIV antibody. The behaviors associated with enacting strategies for risk reduction based on HIV serostatus of potential partners are called seroadaptive behaviors.

Our model has the ability to quantify seroadaptive behavior and therefore provides a critical contribution towards understanding risky sexual behavior. When measuring the effects of behavioral interventions, changes may occur through seroadaptive behaviors and/or as a change in frequency. An HIV⁺ participant who changes from (5 HIV⁺, 5 HIV⁻) partners in a given unit of time to (8 HIV⁺, 2 HIV⁻) partners changes their behavior through seroadaptation. If that same participant instead changes from (5 HIV⁺, 5 HIV⁻) partners to (2 HIV⁺, 2 HIV⁻) partners, then the reduction in frequency is the source of risk reduction. Seroadaptation and changes in frequency are not mutually exclusive. The participant that changes from (5 HIV⁺, 5 HIV⁻) partners to (3 HIV⁺, 1 HIV⁻) partners decreases their risk from both seroadaptation and reduction in frequency. It is important that these two forms of risk reductions are distinguished from one another because seroadaptive behavior is contingent on accurate knowledge of partner serostatus but frequency changes are not. Seroadaptive behavior is not a guaranteed preventative strategy (Pinkerton, 2008; Wilson et al., 2010; Butler and Smith, 2007) and risks of infection with multiple strains of the virus exist (Poudel et al., 2007). However, seroadaptive behavior has been shown to be an effective form of risk reduction (Cassels et al., 2009; Jin et al., 2009; Golden et al., 2008). The study of seroadaptive behavior has been isolated almost exclusively in men who have sex with men (Parsons et al., 2005; Cox et al., 2004; Snowden et al., 2009, 2011). The HLP data presents an opportunity to examine seroadaptive behavior in a variety of other risk groups. Understanding the role of seroadaptive behavior is important in other prevention studies as well. Reniers and Helleringer (2011) argue that the importance of HIV testing and counseling can not be accurately measured without accounting for seroadaptive behavior. A similar observation has been made for condom effectiveness studies (Warner et al., 2004).

In this article, we propose to jointly analyze the number of HIV⁺ partners, the number of HIV⁻/unknown serostatus partners, and the numbers of protected and unprotected acts with each partner. The number of partners of each serostatus are observed once at each time point and the number of protected and unprotected acts with each partner form a bivariate outcome that is nested within both subject and time. We refer to treating the number of partners and behavior with each partner as a separate observation as disaggregation on a per partner basis and propose a Bayesian model for multivariate multilevel longitudinal count data for analysis of this type of outcome. While our methods are motivated by the HLP data, many other similar sexual behavior intervention studies involving people living with HIV have comparable data structures suitable for future analysis including Living in the Face of Trauma (LIFT) (Sikkema et al., 2007), Positive Choice: Interactive Video Doctor (Gilbert et al., 2008), and Healthy Relationships (Kalichman et al., 2001). In comparison with univariate models of longitudinal aggregated outcomes, our model offers the following advantages:

• Disaggregation of sex acts on a per partner basis allows us to model the full multivariate hierarchical nested structure of the data. This allows us to identify differences in behavior that previous analyses could not.

• Using a multivariate multilevel longitudinal model correctly models distinct levels of heterogeneity that were previously lumped into a single source of variation. Behavior variability exists both across different subjects as well as across partners within subjects. Previous analyses failed to account for variation across partners.

• Identification of seroadaptation in our population is critical to estimating the effects of behavioral interventions and can be determined directly from our model.

• Baseline eligibility criterions are correctly incorporated into the model.

We expand on each of these in turn.

Disaggregation on a per partner basis results in a separate bivariate outcome of the number of protected and unprotected sex acts for each partner. Modeling these outcomes separately differentiates a scenario of many partners with a few unprotected sex acts each from a scenario with a single partner and many unprotected acts. These different scenarios provide information for a more targeted counseling intervention focusing on reducing the number of casual relationships with HIV⁻ partners, increasing the use of protection, or both. In addition, these scenarios provide important information in deciding appropriate policy for prevention. The effectiveness of programs like PreExposure Prophylaxis (PrEP) where HIV⁻ people take antiretroviral medication daily to lower their chances of becoming infected may be viable and reasonable for the partners of our study population if only a few HIV⁻ partners that engage in many unprotected acts with the subject were involved.

The multilevel multivariate outcome separately models subject level and partner level variation. Typical analysis in the field that analyze total protected acts in an aggregated fashion ignores this differentiation. Using multilevel outcomes facilitates proper modeling of the longitudinal process. Modeling separate sources of variation correctly also provides some estimation benefits since all observed information is used. Subjects in the HLP study are followed over time but unfortunately partners are not identified and are not be traceable. This is reflected in our model through a time dependent process on subject specific latent effects leaving partner level variation independent of time. A simulation illustrating the benefits of modeling different sources of variation is given in Web Appendix A.

Our model enables us to quantify seroadaptive behavior. For the HLP data, we draw inference on 3 specific seroadaptive behaviors. Subjects can selectively choose (i) their partners, preferring HIV⁺ partners over HIV⁻/unknown serostatus partners, (ii) to have fewer sex acts with their HIV⁻/unknown serostatus partners compared to their HIV⁺ partners, and (iii) to use condoms a larger percentage of the time with partners who are HIV⁻/unknown. Case (i) is behavior associated with partner selection while cases (ii) and (iii) describe sexual behavior during a relationship once it is formed. When seroadaptation is examined with an HIV⁻ population, these seroadaptive behaviors still exist but in reverse form. The level of seroadaptation can change over time, differ between treatment and control groups, and differ across risk group, race, or by location.

Many studies, including HIV prevention studies, use eligibility criteria to initially screen for a high risk population. This recruitment method implies that some combination of observations that can occur at followup visits can not occur at baseline. For example, if only participants who reported unprotected sex with an HIV⁻ partner were recruited into the trial, we could have no zeros at baseline for this measure and a simple Poisson model would be inappropriate. If unaccounted for, the entire study population will appear more risky at baseline due to regression to the mean when no changes have actually occurred. The multivariate disaggregated data structure is necessary to model the complex eligibility criteria used in these trials. In our proposed model, we build this recruitment eligibility criterion directly into our conditional baseline distributions to remove bias due to the recruitment of a high risk population and to more accurately reflect the range of possible observations at baseline.

Previous multivariate count models (Chib and Winkelmann, 2001) and (Tunaru, 2002) model data without the multilevel structure using a single set of latent effects to model correlation between observations. A number of approaches extend modeling to multivariate multilevel data including Dunson (2000), Goldstein (2010), Rabe-Hesketh et al. (2005), and Browne and Draper (2006). Goldstein et al. (2009) specifically addresses multilevel models where data is observed on more than 1 level. This was later extended to model count data in Goldstein and Kounali (2009) by formulating a latent normal model where an extra step is inserted to sample an underlying latent normal variable from the count data. However, this method makes the fixed effect coefficients harder to interpret. None of these models examine the longitudinal component simultaneously with multilevel multivariate data. A common way to incorporate longitudinal dependence is through the inclusion of additive random effects that are correlated over time in the predictor. Alternatively, multivariate smoothing techniques such as Gaussian Markov random fields (Rue and Held, 2005; Fahrmeir and Lang, 2001) or dynamic Bayesian linear models (West et al., 1985; West and Harrison, 1997) can be used.

The model we propose is for multilevel multivariate count data with observations on multiple levels and is followed through time. The introduction of a second level of latent effects properly accounts for heterogeneity across partners. Correlation across time is modeled through a generalized autoregressive process which can be applied to each level of latent effects as needed. In our model, subjects are followed through time while partners are not so the process is applied only to the subject specific latent effects.

The remainder of the article is organized as follows. Section 2 provides a detailed description of the HLP data and outlines the multilevel structure. Terminology specific to HIV and sexual behavior is defined. Section 3 describes our model, specifies the prior structure, and outlines the algorithm for posterior computation. In Section 4, we outline how to draw inference on seroadaptive behavior with our model and define some specific terminology for the task. Section 5 presents the results of applying the presented model to the HLP dataset. Findings on seroadaptive behavior are explored in detail. Finally, we conclude with a discussion in Section 6.

2. Data Description

The Healthy Living Project is a multisite 2-group randomized controlled comprehensive behavioral intervention trial aimed at reducing risky sexual behavior among people living with HIV. After randomization, 469 eligible individuals were assigned to the control group and 467 were assigned to the behavioral intervention treatment group. HLP participants were surveyed longitudinally every 5 months in six equally spaced interviews over 25 months. Participant demographic information was collected at baseline and a summary can be found in Web Appendix B. Subjects were categorized into 4 risk groups by transmission risk as intravenous drug users (IDU) and, provided they were not IDU, then by sexual orientation as men who have sex with men (MSM), heterosexual males (HTM), or females (FEM). The study was conducted in Los Angeles, Milwaukee, New York, and San Francisco. Other demographic information that was stored include education status, race, gender, and age.

At each interview including the baseline interview, outcomes pertaining to risky sexual behavior in the previous 3 months were recorded. This included the total number of partners, the serostatus of each partner, and the total number of protected and unprotected sex acts across all partners. Specific partner information on the number of protected and unprotected sex acts with up to the 5 most recent partners is also recorded. In the HLP study, a partner was defined as someone with whom the participant had oral, vaginal, or anal sex. Sex acts in our analysis exclude oral sex and are defined as vaginal or anal intercourse only, due to the negligible transmission risk of HIV associated with oral sex leaving observations of 0 sex acts with a partner possible. The serostatus of each partner is categorized as HIV⁺, HIV⁻, or unknown. As usual in this field, we treat unknown serostatus partners as HIV⁻ and for the remainder of the article, use of the description HIV⁻ refers jointly to the HIV⁻ and unknown serostatus population.

Recruitment was designed to screen for a high risk population. Study participants were only enrolled if they reported at least one unprotected sex act with an HIV⁻ partner or with at least 1 HIV⁺ partner who was not categorized as their primary partner at the baseline interview. Zero truncated joint distributions are used for the appropriate outcomes at baseline to reflect this enrollment criterion.

The number of HIV⁺ partners, HIV⁻ partners, and total protected and unprotected acts across all partners are subject level observations recorded longitudinally over time. Disaggregating the number of total protected and unprotected sex acts by partner gives the number of protected and unprotected sex acts with each specific partner which are bivariate partner level observations nested within subject and time. In the cases when a subject reported more than 5 partners at an interview, the number of protected and unprotected sex acts with each of these additional partners are treated as random variables with a constrained sum to reflect the uncertainty in the data. After imputation of these outcomes, there was a total of 22,269 partner level bivariate observations spread over 4,695 separate interviews. Subject and partner level observations are jointly modeled as Poisson counts with mean parameters driven by participant and partner level covariates and random effects.

3. Model

3.1 Likelihood Specification

Let observations for subject i = 1, …, n occur at measurement times t_ij where j = 1, …, J_i and J_i varies by subject. At time t_ij, let V_ij denote the total number of partners associated with subject i in the previous 3 months, and let W_ijk=(P_ijk, U_ijk)^T denote the bivariate outcome composed of the number of protected sex acts P_ijk and unprotected sex acts U_ijk nested in subject i and time t_ij with partner k = 1, …, V_ij.

To model separate behavioral changes among HIV⁺ and HIV⁻ partners, we introduce an HIV serostatus indicator Z_ijk denoting the serostatus of partner k at time t_ij where Z_ijk = 1 indicates HIV⁺ and Z_ijk = 0 indicates HIV⁻/unknown status. Letting $V_{ij}^{+}$ be the number of HIV⁺ partners and $V_{ij}^{-}$ be the number of HIV⁻ partners at time t_ij, then

$$\begin{array}{l}{V}_{ij}=V_{ij}^{+}+V_{ij}^{-}\\ V_{ij}^{+}=\sum _{k=1}^{V_{ij}}{Z}_{\mathit{ijk}}.\end{array}$$

The complete outcome vector, Y_ij, for subject i at time t_ij is then modeled with a multivariate nested count model where

$${\mathbf{Y}}_{ij}={(V_{ij}^{+},V_{ij}^{-},{\mathbf{W}}_{ij1}^T,{\mathbf{W}}_{ij2}^T,\dots ,{\mathbf{W}}_{{\mathit{ijV}}_{ij}}^T)}^T$$

has length 2V_ij + 2 that will vary across subjects and times. Outcomes are correlated both between different outcomes and across time. We first present the cross sectional model and correlations between outcomes in Y_ij. Correlations across time are then introduced through a multivariate stationary process.

We model each component of Y_ij as Poisson distributed $V_{ij}^{+}~\text{Po}({\lambda }_{v,ij}^{+}),V_{ij}^{-}~\text{Po}({\lambda }_{v,ij}^{-})$, P_ijk ~Po(λ_p,ijk), and U_ijk ~Po(λ_u,ijk) conditional on corresponding mean parameters ${\lambda }_{v,ij}^{+},{\lambda }_{v,ij}^{-}$, λ_p,ijk, and λ_u,ijk for 1 ≤ i ≤ n, 1 ≤ j ≤ J_i, and 1 ≤ k ≤ V_ij. A log-linear random effects regression model characterizes these mean parameters

$$\left(\begin{array}{c}{\lambda }_{v,ij}^{+}\\ {\lambda }_{v,ij}^{-}\end{array}\right)=exp\left(\begin{array}{c}{\mathbf{x}}_{ij}^{\prime }{\mathit{\alpha }}_v^{+}+{\beta }_{v,ij}^{+}\\ {\mathbf{x}}_{ij}^{\prime }{\mathit{\alpha }}_v^{-}+{\beta }_{v,ij}^{-}\end{array}\right)$$ (1)

and

$$\left(\begin{array}{c}{\lambda }_{p,\mathit{ijk}}\\ {\lambda }_{u,\mathit{ijk}}\end{array}\right)=\{\begin{array}{c}exp\left(\begin{array}{c}{\mathbf{x}}_{\mathit{ijk}}^{\prime }{\mathit{\alpha }}_p^{+}+{\beta }_{p,ij}^{+}+{\delta }_{p,\mathit{ijk}}\\ {\mathbf{x}}_{\mathit{ijk}}^{\prime }{\mathit{\alpha }}_u^{+}+{\beta }_{u,ij}^{+}+{\delta }_{u,\mathit{ijk}}\end{array}\right),\text{if}{Z}_{\mathit{ijk}}=1,\\ exp\left(\begin{array}{c}{\mathbf{x}}_{\mathit{ijk}}^{\prime }{\mathit{\alpha }}_p^{-}+{\beta }_{p,ij}^{-}+{\delta }_{p,\mathit{ijk}}\\ {\mathbf{x}}_{\mathit{ijk}}^{\prime }{\mathit{\alpha }}_u^{-}+{\beta }_{u,ij}^{-}+{\delta }_{u,\mathit{ijk}}\end{array}\right),\text{if}{Z}_{\mathit{ijk}}=0\end{array}$$ (2)

where average number of protected and unprotected acts with partner k, λ_p,ijk and λ_u,ijk, are parameterized differently depending on partner serostatus. Here, x_ij is the vector of subject level covariates and x_ijk appends partner level covariates to x_ij. The set of fixed effects $\mathit{\alpha }=({\mathit{\alpha }}_v^{+},{\mathit{\alpha }}_v^{-},{\mathit{\alpha }}_p^{+},{\mathit{\alpha }}_u^{+},{\mathit{\alpha }}_p^{-},{\mathit{\alpha }}_u^{-})$ and subject specific latent effects ${\mathit{\beta }}_{ij}={({\beta }_{v,ij}^{+},{\beta }_{v,ij}^{-},{\beta }_{p,ij}^{+},{\beta }_{u,ij}^{+},{\beta }_{p,ij}^{-},{\beta }_{u,ij}^{-})}^T$ correspond to the number of HIV⁺ partners, HIV⁻ partners, protected acts with an HIV⁺ partner, unprotected acts with an HIV⁺ partner, protected acts with an HIV⁻ partner, and unprotected acts with an HIV⁻ partner respectively. Partner specific latent effects corresponding to partner k are denoted as δ_ijk = (δ_p,ijk, δ_u,ijk).

To complete specification of the hierarchical structure, random effects are modeled as Gaussian. Subject specific random effects β_ij evolve through time using a stationary multivariate autoregressive(1) process leading to correlation between observations within the same subject across time. At baseline j = 1, subject specific random effects β_i1 are normal with 6 ×6 covariance matrix L

$${\mathit{\beta }}_{i1}\mid \mathbf{L}~{\mathrm{N}}_6(\mathbf{0},\mathbf{L}).$$ (3)

Future time points j = 2, …, J_i model subject specific random effects as conditional normal

$${\mathit{\beta }}_{ij}\mid {\mathit{\beta }}_{ij-1},\mathbf{\sum }~{\mathrm{N}}_6(\mathbf{A}{\mathit{\beta }}_{ij-1},\mathbf{\sum })$$ (4)

where A is a diagonal matrix with each diagonal element taking values between −1 and 1, and Σ is a positive definite covariance matrix. We assume the process is stationary which implies

$$\mathbf{L}={\mathbf{ALA}}^T+\mathbf{\sum },$$

or equivalently elementwise

$$L_{st}=\frac{{\mathrm{\sum }}_{st}}{1-A_{ss}{A}_{tt}},$$

where L_st, Σ_st, and A_st denote the s^th row t^th column element of matrix L, Σ, and A respectively. Partner specific bivariate random effects δ_ijk are normal with covariance D

$${\mathit{\delta }}_{\mathit{ijk}}\mid \mathbf{D}~{\mathrm{N}}_2(\mathbf{0},\mathbf{D}).$$ (5)

Since partners are not followed over time and we can not determine if any of the same partners are kept between interviews, we assume no correlation between partner specific random effects.

Conditionally, observed outcomes for subject i, ${\mathbf{Y}}_i={({\mathbf{Y}}_{i1}^T,\dots ,{\mathbf{Y}}_{{iJ}_i}^T)}^T$ are multivariate Poisson-log normal as defined in Aitchison and Ho (1989). The expected value and correlation between outcomes after marginalizing over subject and partner specific random effects can be calculated using equations (1) and (2). Define conditional mean parameters $\mathrm{E}({\mathbf{Y}}_i\mid {\mathit{\lambda }}_i)\equiv {\mathit{\lambda }}_i={({\mathit{\lambda }}_{i1}^T,\dots ,{\mathit{\lambda }}_{{iJ}_i}^T)}^T$ where ${\mathit{\lambda }}_{ij}={({\lambda }_{v,ij}^{+},{\lambda }_{v,ij}^{-},{\lambda }_{p,ij1},{\lambda }_{u,ij1},\dots ,{\lambda }_{p,{\mathit{ijV}}_{ij}},{\lambda }_{u,{\mathit{ijV}}_{ij}})}^T$. From our hierarchical model specification in equations (3), (4), and (5), it follows naturally

$$log{\mathit{\lambda }}_i~\mathrm{N}({\mathit{\mu }}_i,\mathbf{\Omega })$$

where μ_i with r^th element μ_ir is a function of fixed effects α while covariance matrix Ω = (Ω_rq) is a function of A, L, and D. The mean and variance of the r^th component of Y_i are

$$\begin{array}{l}\mathrm{E}(Y_{ir})=exp({\mu }_{ir}+\frac{1}{2}{\mathrm{\Omega }}_{rr})\equiv {\phi }_{ir},\\ var(Y_{ir})={\phi }_{ir}+{\phi }_{ir}^2\{exp({\mathrm{\Omega }}_{rr})-1\}\end{array}$$ (6)

and the covariance between the q^th and r^th observations of Y_i is

$$cov(Y_{iq},Y_{ir})={\phi }_{iq}{\phi }_{ir}\{exp({\mathrm{\Omega }}_{qr})-1\}$$ (7)

where q ≠ r. Equation (7) shows that the sign and statistical significance of the covariance between observations can be determined directly from the Ω matrix since cov(Y_iq, Y_ir) is only positive when Ω_qr is positive and only negative when Ω_qr is negative. We define a parameter as statistically significant if the 95% posterior equal-tail credible interval of the parameter does not contain 0. The credible interval for Ω_qr is sufficient to determine if the credible interval for cov(Y_iq, Y_ir) contains 0.

The eligibility criterion for the study can not be correctly modeled in a univariate framework but is readily incorporated into the joint baseline distributions of our model. The eligibility criterion excludes two distinct events at baseline j = 1. The first excluded event is the number of HIV⁺ and HIV⁻ partners both reported as 0. The second excluded event is the number of unprotected sex acts with all HIV⁻/unknown serostatus partners and HIV⁺ casual partners all reported as 0. To incorporate this information into the model, two joint zero- truncated Poisson distributions replace the conditionally independent Poisson assumption for partners and separately for acts. We define (X₁, …, X_G) to be distributed joint zero-truncated Poisson if the joint density of (X₁, …, X_G) is

$${\left\{1-exp(-\sum _{g=1}^G{\lambda }_g)\right\}}^{-1}\frac{exp(-{\sum }_{g=1}^G{\lambda }_g){\prod }_{g=1}^G{\lambda }_g^{X_g}}{{\prod }_{g=1}^G{X}_g!}$$

for X_g = {0, 1, 2, … } where (X₁, …, X_G) are not all equal to 0.

3.2 Prior Specification

Proper prior distributions are chosen for model parameters (α, Σ, A, D) to ensure the posterior is well defined. In selecting values for parameterizing our prior distributions, we chose values that are neutral favoring no positive or negative effect and non-influential thus letting the data drive our posterior inference. We consider priors to be non-influential if a twofold increase in the variance of our priors changes our posterior mean estimates by less than 1%. Normal priors are assumed α_l ~ N(μ_α = 0, ${\sigma }_{\alpha }^2=10$) for each fixed effect covariate. Inference on the posterior mean number of partners and sex acts per partner involves exponentiating the diagonal terms of the covariance matrix as shown in equation (6). This results in a complication when the standard conjugate Inverse-Wishart density priors alone are used for covariance parameters Σ and D since the exponentiated diagonal terms have undefined posterior means due to long right tails. Details for the univariate case are shown in the Appendix. To correct this problem, priors for Σ and D are chosen to be proportional to the product of an Inverse-Wishart density distribution on the entire covariance matrix times independent left truncated normal density distributions on each of the diagonal elements truncated at 0. Letting Σ_s,s and D_t,t be the diagonal elements of Σ and D, for s = 1, … 6 and t = 1, 2, priors for Σ and D are

$$\begin{array}{l}\pi (\mathbf{\sum })\propto {\mid \mathbf{\sum }\mid }^{\frac{m_{\mathbf{\sum }}}{2}}exp\left[-\frac{1}{2}\left\{\text{tr}({\mathbf{\Psi }}_{\mathrm{\sum }}{\mathbf{\sum }}^{-1})+\sum _{s=1}^6{\left(\frac{{\mathrm{\sum }}_{s,s}-{\mu }_{\mathrm{\sum }}}{c_{\mathrm{\sum }}}\right)}^2\right\}\right]\mathrm{I}({\mathrm{\sum }}_{s,s}>0)\\ \pi (\mathbf{D})\propto {\mid \mathbf{D}\mid }^{\frac{m_D}{2}}exp\left[-\frac{1}{2}\left\{\text{tr}({\mathbf{\Psi }}_D{\mathbf{D}}^{-1})+\sum _{t=1}^2{\left(\frac{D_{t,t}-{\mu }_D}{c_D}\right)}^2\right\}\right]\mathrm{I}(D_{t,t}>0).\end{array}$$

This shortens the right tails resulting in less dispersion in the prior. Values for the parameters were chosen as m_Σ = 10, Ψ_Σ = I₆, m_D = 10, Ψ_D = I₂, μ_Σ = 2, μ_D = 2, c_Σ = 100, c_D = 100. Autoregressive factors A_l,l, the l^th diagonal element of A are given uniform priors A_l,l ~Unif(a_A = −1, b_A = 1).

3.3 Posterior Computation

Our posterior computations are sampled with Markov Chain Monte Carlo (MCMC) methods using the Metropolis algorithm (Metropolis et al., 1953; Hastings, 1970; Gelfand and Smith, 1990; Casella and George, 1992). We provide a brief summary here with a more detailed step by step algorithm in Web Appendix C. For sampling α, a second-order Taylor expansion around the current state of the Markov chain (Rue and Held, 2005) was used as the proposal function and this proposal substantially speeds convergence when compared to a random walk Gaussian proposal function. Sampling of subject specific random effects β_ij, partner specific random effects δ_ijk, and autoregressive matrix A use random walk Gaussian proposal functions with the proposal function for the diagonal elements of A truncated at −1 and 1. Covariance parameters Σ and D are sampled using the Metropolis algorithm with Inverse-Wishart proposal functions that approximate the posterior density. Specifically, we use the proposal functions q(Σ|β_ij) and q(D|δ_ijk) that are densities of Inverse-Wishart distributions IW(m_q1, Ψ_q1) and IW(m_q2, Ψ_q2) respectively where $m_{q1}=m_{\mathrm{\sum }}+{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}1,{\mathbf{\Psi }}_{q1}={\sum }_{i=1}^n{\sum }_{j=2}^6({\mathit{\beta }}_{ij}-\mathbf{A}{\mathit{\beta }}_{ij-1}){({\mathit{\beta }}_{ij}-\mathbf{A}{\mathit{\beta }}_{ij-1})}^T+{\mathbf{\Psi }}_{\mathrm{\sum }},m_{q2}=m_D+{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{V}_{ij},$ and ${\mathbf{\Psi }}_{q2}={\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{\sum }_{k=1}^{V_{ij}}{\mathit{\delta }}_{\mathit{ijk}}{\mathit{\delta }}_{\mathit{ijk}}^T+{\mathbf{\Psi }}_D$.

Let S_ij be the set of partners k for which P_ijk and U_ijk are not observed in the data. Then conditional on total protected acts, total unprotected acts, and mean parameters λ_ij, P_ijk and U_ijk are Multinomial distributed random variables and can be directly sampled.

The estimation procedure was implemented in R. A total of 100,000 iterations were collected after an initial 30,000 iterations were discarded as burn-in.

4. Seroadaptive behavior

Using our model, we make inference on 3 different forms of seroadaptive behavior to describe how the choice of (i) partner, (ii) level of sexual activity, and (iii) condom use differs depending on the serostatus of the partner. We define terms to help quantify these seroadaptive behaviors respectively as the (i) serodiscordant partner multiple (SPARM), (ii) serodiscordant activity multiple (SAM), and (iii) serodiscordant protection multiple (SPROM) and discuss them below.

The serodiscordant partner multiple measures whether partners of a specific serostatus are preferentially selected. To determine SPARM, we first calculate the expected probability that subjects with characteristics defined by x_ij would choose an HIV⁻ partner as

$${\pi }_{\mathit{SPARM},ij}={\mathrm{E}}_{{\mathit{\beta }}_{ij}}\left(\frac{{\lambda }_{v,ij}^{-}}{{\lambda }_{v,ij}^{+}+{\lambda }_{v,ij}^{-}}\right)$$

where E_θ(g(θ)) refers to the expectation of the function g(θ) with respect to the random variable θ. The corresponding serodiscordant partner multiple, SPARM_ij is then defined as the odds of picking an HIV⁻ partner

$${\text{SPARM}}_{ij}=\frac{{\pi }_{\mathit{SPARM},ij}}{1-{\pi }_{\mathit{SPARM},ij}}$$

and is interpreted to mean HIV⁻ partners are picked SPARM_ij times as often as HIV⁺ partners. The SPARM is a relative measure that depends on the prevalence and availability of HIV⁺ partners in the area and should not be used by itself to assess the presence of seroadaptive behavior. It is however possible to compare SPARM between different groups or time periods to determine differences or changes in seroadaptive behavior. A ratio of SPARMs less than 1 implies a difference in seroadaptive partner selection with individuals characterized by the numerator showing greater preference towards selecting partners who are also HIV⁺.

The serodiscordant activity multiple (SAM) measures differences in the level of sexual activity in relationships with partners of differing serostatus. Sexual activity level is measured by the total number of reported sex acts in the relationship regardless of protection status. The expected probability that subjects with characteristics defined by x_ij choose to engage in sex with an HIV⁻ over an HIV⁺ partner adjusting for differences in the number of partners of each serostatus is

$${\pi }_{\mathit{SAM},ij}={\mathrm{E}}_{{\mathit{\beta }}_{ij},{\mathit{\delta }}_{\mathit{ijk}}}\left(\frac{{\lambda }_{u,\mathit{ijk}}+{\lambda }_{p,\mathit{ijk}}}{{\lambda }_{u,\mathit{ijk}}+{\lambda }_{p,\mathit{ijk}}+{\lambda }_{u,{\mathit{ijk}}^{\prime }}+{\lambda }_{p,{\mathit{ijk}}^{\prime }}}\right)$$

where partner k is HIV⁻ and partner k′ is HIV⁺. Correspondingly, SAM_ij is defined as the odds of engaging in sex with an HIV⁻ partner,

$${\text{SAM}}_{ij}=\frac{{\pi }_{\mathit{SAM},ij}}{1-{\pi }_{\mathit{SAM},ij}}.$$

A SAM value of 1 implies no difference in sexual activity level between partners of different serostatus while values less than 1 imply seroadaptation towards lower levels of sexual activity with HIV⁻ partners.

The serodiscordant protection multiple (SPROM) measures selective use of protection based on partner serostatus. The SPROM measure describes differences in the tendency to use protection per sex act. The expected probability that a protected sex act is with an HIV⁻ partner instead of an HIV⁺ partner adjusting for differences in sexual activity level and the number of partners is

$${\pi }_{\mathit{SPROM},ij}={\mathrm{E}}_{{\mathit{\beta }}_{ij},{\mathit{\delta }}_{\mathit{ijk}}}\left(\frac{w_{\mathit{ijk}}{\lambda }_{p,\mathit{ijk}}}{w_{\mathit{ijk}}{\lambda }_{p,\mathit{ijk}}+w_{{\mathit{ijk}}^{\prime }}{\lambda }_{p,{\mathit{ijk}}^{\prime }}}\right)$$

where partner k is HIV⁻, partner k′ is HIV⁺, and w_ijk = (λ_p,ijk + λ_u,ijk)⁻¹ are weights to adjust for the sexual activity level of partner k. The corresponding SPROM_ij is defined as

$${\text{SPROM}}_{ij}=\frac{{\pi }_{\mathit{SPROM},ij}}{1-{\pi }_{\mathit{SPROM},ij}},$$

the odds a protected sex act is with an HIV⁻ partner assuming equal numbers of HIV⁺ and HIV⁻ partners and equal levels of sexual activity. A SPROM value of 1 implies no seroadaptive use of protection while values greater than 1 imply a greater tendency to use protection with HIV⁻ partners.

5. Results

5.1 Model Validation

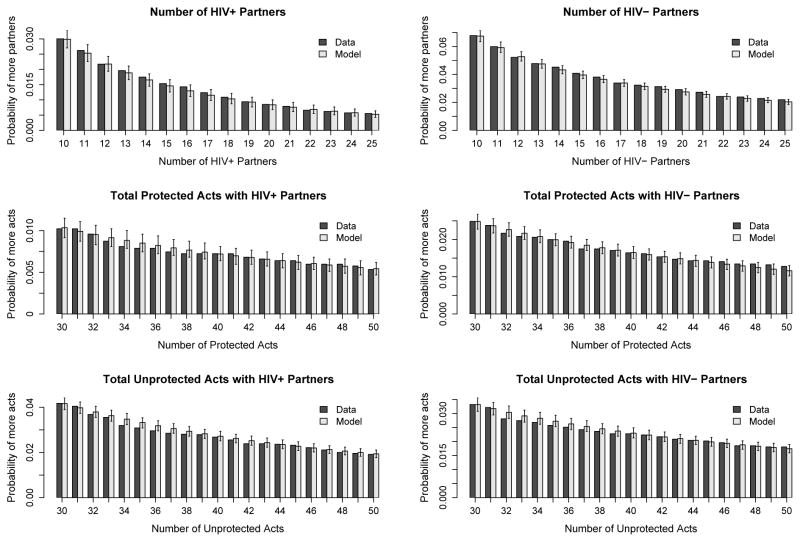
Accurate modeling of the high activity portions of the population is particularly important. These cases represent the greatest transmission risk and also test to see if our model adequately accounts for the high levels of variation in sexual behavior. To examine the accuracy of our model in this area, we compare the tail end of our posterior predictive distributions to the data for the number of HIV⁺ partners, number of HIV⁻ partners, total number of protected acts with all HIV⁺ partners, total number of protected acts with all HIV⁻ partners, total number of unprotected acts with all HIV⁺ partners, and total number of unprotected acts with all HIV⁻ partners at each time point. A total of 1000 datasets of new values for Y_ij are simulated using the sampled posteriors of parameters λ_ij for 1 ≤ i ≤ n and 1 ≤ j ≤ J_i.

Figure 1 shows a summary of the tail portions of our posterior predictive distribution. For comparison, we also plot the percentage of observations in the HLP data that fit into each bin. In all these outcomes, our model reasonably predicts the percentage of high activity in the study population.

Figure 1.

Comparison of tail probabilities between model posterior predictive distributions and the percentage of HLP data fitting the bin criterion. Each bin reflects the probability of observing values greater than or equal to the outcome value. Outcomes include the number of HIV⁺ partners, number of HIV⁻ partners, total number of protected acts with all HIV⁺ partners, total number of protected acts with all HIV⁻ partners, total number of unprotected acts with all HIV⁺ partners, and total number of unprotected acts with all HIV⁻ partners for all subjects over all time points.

5.2 HLP Covariate Effects

Analysis of the HLP data does not find the counseling intervention to be efficacious. Subjects in the treatment group did not show evidence for (a) fewer HIV⁻/unknown partners, (b) greater numbers of protected acts per HIV⁻/unknown partner, or (c) fewer unprotected sex acts per HIV⁻/unknown partner than their control group counterparts at any time point. The number of HIV⁺ and HIV⁻ partners does decrease over the course of the study across all study participants indicating a reduction in risky behavior as a result of being enrolled in the study regardless of treatment group assignment. Average number of unprotected acts per partner also decreases across both treatment and control groups while protected acts per partner stays fairly consistent throughout the duration of the study.

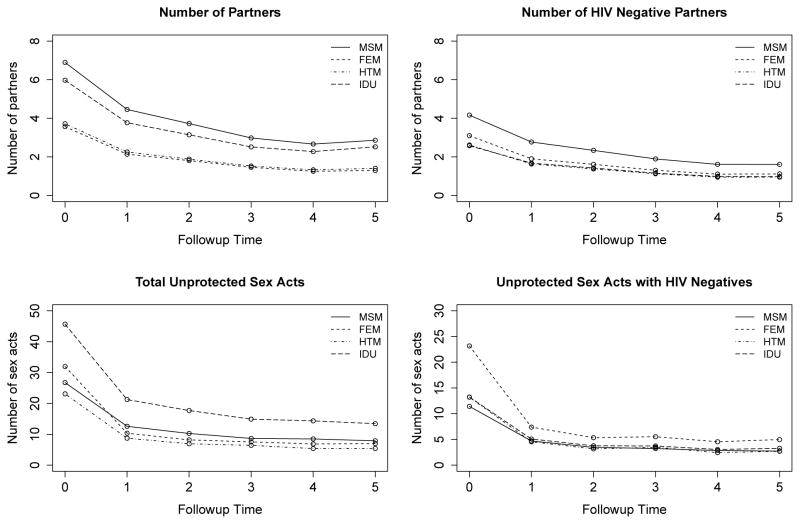
We find key differences in behavior across the different risk groups and summarize our findings in Figure 2. Females exhibited the riskiest sexual behavior, reporting the greatest numbers of unprotected sex acts with HIV⁻ partners. Even though the MSM group reported the largest numbers of HIV⁻ partners and the IDU group reported the largest numbers of total unprotected sex acts, both groups appear to mitigate their risk when their partner was HIV⁻ and reported fewer unprotected sex acts with those partners than the FEM group.

Figure 2.

Summary of sexual behavior across the 4 risk groups. All plots are average predicted outcomes with our model for participants who were white, assigned to the control group, less than 40 years old, from Los Angeles, did not graduate high school, were out of work, had no history of hard drug use, and reported only 1 main partner if any partners were reported.

A detailed analysis of covariates can be found in Web Appendix D. Estimates of the covariance parameters in the model can be found in Web Appendix E. We spend the remainder of this section on presenting the new findings specific to seroadaptive behavior in this study population.

5.3 HLP Seroadaption

We first examine seroadaptive behavior in white men who have sex with men (MSM) that are less than 40 years old from Los Angeles who did not graduate high school and were out of work with no history of hard drug use. Our model estimates these participants to have a SPARM of 1.50 (1.09, 1.99) entering relationships with HIV⁻ partners roughly 50% more often than with HIV⁺ partners. We denote inference estimates as a_M (a_L, a_U) where a_M is the posterior mean, a_L and a_U are respectively the 2.5% quantile and 97.5% quantile estimates of the posterior distribution. Over the course of the study, the SPARM stays around this level with a slight dip to 1.32 (0.93, 1.78) by the end of the study. Lower levels of sexual activity were reported when the relationship was with an HIV⁻ partner resulting in a SAM of 0.78 (0.56, 1.07) though the value is not significant. The SAM stays fairly consistent throughout the study staying below 1 at each followup with values reported at followup 2 and followup 4 being marginally significant. The SPROM of 1.48 (1.22, 1.77) provides significant evidence that participants were almost 50% more likely to use protection during sex if their partner was HIV⁻. This value increases somewhat during the course of the study to as much as 1.87 (1.44, 2.39) by followup 5 indicating participants may have further increased seroadaptive use of condoms while in the study although the difference in SPROMs at the two time points is not significant. Comparison with the treatment group shows that the treatment and control groups exhibit very similar behavior throughout the study. This shows that the counseling intervention did not significantly alter subjects’ seroadaptive strategies. Overall, clear evidence exists for seroadaptive use of protection in our study group.

Seroadaptive behavior varies also across the 4 risk groups of the study population. Since most studies of seroadaptive behavior study MSM, we examine seroadaptive behavior across the risk groups using MSM as the comparison group. Our findings show the 4 risk groups do not significantly differ in SAM or SPROM values indicating similar seroadaptive behavior once relationships are formed. However, females reported a significantly higher SPARM value of 4.26 (2.89, 5.93) compared to the SPARM value of 1.50 (1.09, 1.99) reported by the MSM population indicating that females chose HIV⁻ partners far more frequently over HIV⁺ partners compared to MSM. The HTM population also report a relatively high SPARM value of 2.05 (1.37, 2.93) choosing HIV⁻ partners about twice as often as HIV⁺ partners. Part of the observed difference in SPARM values between the heterosexual and MSM populations is likely a result of the higher percentage of HIV⁺ individuals in the MSM population though this does not account for differences between the heterosexual males and females. Our findings suggest interventions targeting females and heterosexual males may benefit from encouraging seroadaptive selection of partners to reduce the SPARM value.

Our analysis also examined seroadaptive behavior differences across race and location. Among the race categories of white, black, Hispanic, and other, seroadaptive behavior strategies were fairly similar with Hispanics choosing the largest percentage of HIV⁻ partners though differences were not significant. HLP was a multisite study across Los Angeles, Milwaukee, New York, and San Francisco. Our findings indicate participants in Milwaukee reported a significantly higher SPARM value of 3.16 choosing HIV⁻ partners far more often than participants in the other locations. This could be a result of differences in HIV⁺ partner availability in these respective areas. Nonetheless, it is important to recognize the increased percentage of HIV susceptible partners of people living with HIV in a location like Milwaukee and respond accordingly with the appropriate intervention.

A full summary of seroadaptive results is shown in Table 1.

Table 1.

Seroadaptive behavior comparison. Comparison group is white men who have sex with men (MSM) at baseline that are less than 40 years old from Los Angeles who did not graduate high school and were out of work with no history of hard drug use. For each group, we evaluated the serodiscordant partner selection (SPARM), serodiscordant activity multiple (SAM), and the serodiscordant protection multiple (SPROM).

Seroadaptive measures	SPARM	SAM	SPROM
Comparison group	1.50 (1.09, 1.99)	0.78 (0.56, 1.07)	1.48 (1.22, 1.77)*
Time
Followup 1	1.55 (1.10, 2.09)	0.74 (0.52, 1.03)	1.71 (1.36, 2.14)*
Followup 2	1.56 (1.10, 2.12)	0.67 (0.46, 0.93)*	1.80 (1.41, 2.28)*
Followup 3	1.58 (1.11, 2.16)	0.73 (0.51, 1.02)	1.69 (1.30, 2.15)*
Followup 4	1.47 (1.05, 2.00)	0.72 (0.50, 1.00)*	1.82 (1.39, 2.32)*
Followup 5	1.32 (0.93, 1.78)	0.88 (0.60, 1.23)	1.87 (1.44, 2.39)*
Treatment (Trt)
Trt Baseline	1.55 (1.10, 2.10)	0.82 (0.59, 1.13)	1.42 (1.16, 1.73)*
Trt Followup 1	1.48 (1.05, 2.03)	0.80 (0.56, 1.12)	1.62 (1.28, 2.03)*
Trt Followup 2	1.39 (0.98, 1.91)	0.82 (0.57, 1.15)	1.82 (1.42, 2.32)*
Trt Followup 3	1.41 (1.00, 1.94)	0.82 (0.56, 1.15)	1.91 (1.47, 2.49)*
Trt Followup 4	1.23 (0.87, 1.69)	0.90 (0.61, 1.27)	1.83 (1.33, 2.44)*
Trt Followup 5	1.35 (0.95, 1.87)	0.88 (0.58, 1.24)	1.75 (1.31, 2.30)*
Risk Group
FEM	4.26 (2.89, 5.93)	0.72 (0.49, 1.02)	1.44 (1.14, 1.73)*
HTM	2.05 (1.37, 2.93)	0.86 (0.56, 1.28)	1.48 (1.08, 1.95)*
IDU	0.96 (0.65, 1.34)	0.69 (0.45, 1.00)*	1.31 (1.10, 1.54)*
Race
Black	1.35 (0.99, 1.79)	0.79 (0.58, 1.05)	1.27 (1.01, 1.57)*
Hispanic	2.02 (1.47, 2.72)	0.75 (0.55, 1.01)	1.52 (1.18, 1.92)*
Other	1.59 (1.07, 2.28)	0.75 (0.51, 1.06)	1.53 (1.18, 1.93)*
Location
Milwaukee	3.16 (2.09, 4.65)	0.76 (0.49, 1.11)	1.58 (1.26, 1.93)*
New York	1.36 (0.95, 1.87)	0.89 (0.63, 1.25)	1.64 (1.27, 2.02)*
San Francisco	1.77 (1.26, 2.37)	0.82 (0.58, 1.13)	1.51 (1.25, 1.81)*

Values of SAM and SPROM with * indicate statistically significant evidence for seroadaptation.

Values in bold are significantly different from the value in the comparison group.

6. Discussion

Our Bayesian model for multilevel multivariate longitudinal count data has distinct advantages in the modeling of sexual behavior data and allows a more comprehensive evaluation of covariate effects such as the effects of counseling intervention. Our proposed model differentiates between different forms of risk reduction in sexual behavior. HIV transmission risk can be lowered through decreasing the number of partners, decreasing the number of sex acts per partner, or increasing the proportion of sex acts where condoms are used. Each of these risk reduction scenarios may also be selectively modified based on partner serostatus illustrating seroadaptation. The counseling to achieve and to respond to each of these scenarios can be very different. Identifying the specific areas of behavior that present the highest risk for transmission can highlight key points of interest for future intervention studies. For example, future intervention studies targeting females may prefer to focus on partner selection since that risk group chose a significantly larger proportion of HIV⁻ partners than any other risk group.

Our model is the first model to mathematically quantify different types of seroadaptive behavior providing a quantitative basis for future seroadaptation studies. In the HLP study, we find that subjects living with HIV already make some seroadaptive behavioral decisions that reduce the risk of transmission and that the current intervention under evaluation did not appear to alter these seroadaptive behaviors significantly. In addition, there is evidence that seroadaptive partner selection specifically varies based on the risk group and location. Individually tailored interventions focusing on enhancing these already existing seroadaptive behaviors may be another route of transmission risk reduction.

We also highlighted the importance of disaggregation on a per partner basis when analyzing sexual behavior data. Disaggregation of the number of protected and unprotected acts per partner treats behavior with each partner as separate events permitting partner level analysis and allowing the modeling of partner contributed variation, explicitly differentiating it from subject contributed variation. The situation of multiple unprotected sex acts with a single partner where only 1 possible HIV transmission could occur is now weighed differently than the situation of 1 unprotected sex act with multiple partners where multiple transmission acts could occur. The resulting multilevel model is ideal for sexual behavior data since we can separately model the effects of following subjects longitudinally through time even when their partners may be different at each followup. We make use of a generalized autoregressive stationary process on the subject specific latent effects accounting for heterogeneity of time trajectories across all outcomes.

Other intervention studies of sexual behavior may not record total number of acts across all partners. Instead, only partner specific information for the first few partners and the total number of partners are recorded. In this scenario, imputation of the acts data for the remaining partners without the constraint on total number of acts is theoretically still possible with our model.

Although our paper focuses on modeling longitudinal sexual behavior profiles, our model can readily be applied to any application with nested longitudinal count data.

Appendix Prior choice on variance hyperparameters

We consider the hierarchical Poisson model with random effects

$$\begin{array}{l}{Y}_i~\text{Po}({\lambda }_i)\\ {\lambda }_i=exp(\mu +{\beta }_i)\\ {\beta }_i~\mathrm{N}(0,{\sigma }^2)\end{array}$$

for i = 1, …, n. When prior independence is assumed between μ and σ², the sampling mean, E(Y_i), can be found using iterated conditional expections

$$\begin{array}{l}\mathrm{E}(Y_i)=\mathrm{E}(\mathrm{E}(Y_i\mid {\lambda }_i))=\mathrm{E}({\lambda }_i)=\mathrm{E}(\mathrm{E}({\lambda }_i\mid \mu ,{\sigma }^2))=\mathrm{E}(exp(\mu +\frac{1}{2}{\sigma }^2))\\ =\mathrm{E}(exp(\mu ))\mathrm{E}(exp(\frac{1}{2}{\sigma }^2)).\end{array}$$

Use of the conjugate inverse gamma prior for σ² ~ IG(a, b) results in a posterior density

$$f({\sigma }^2\mid {\beta }_i,Y_i)\propto exp\left(-\frac{b^{\ast }}{{\sigma }^2}\right){({\sigma }^2)}^{-{\alpha }^{\ast }-1}$$

where a^* = a + n/2 and $b^{\ast }=b+{\sum }_{i=1}^n{\beta }_i^2/2$ for σ² ∈ (0, ∞). Letting v = exp (σ²/2), the corresponding posterior density

$$f(v\mid {\beta }_i,Y_i)\propto \frac{1}{v}exp\left(-\frac{b^{\ast }}{2log(v)}\right){(logv)}^{-a^{\ast }-1}$$

has undefined mean E(v). As a direct result, E(Y_i) is also undefined. The use of a zero left truncated normal prior for σ² ~ truncN(c, d²) where c and d² are respectively the mean and variance of the untruncated normal density results in posterior densities

$$\begin{array}{l}f({\sigma }^2\mid {\beta }_i,Y_i)\propto {({\sigma }^2)}^{-n/2}exp\left(-\frac{1}{2}\left(\frac{{({\sigma }^2-c)}^2}{d^2}+\frac{{\sum }_{i=1}^n{\beta }_i}{{\sigma }^2}\right)\right)\\ f(v\mid {\beta }_i,Y_i)\propto \frac{1}{v}{(logv)}^{-n/2}exp\left(-\frac{1}{2}\left(\frac{{(2logv-c)}^2}{d^2}+\frac{{\sum }_{i=1}^n{\beta }_i}{2logv}\right)\right)\\ \propto \frac{1}{v}{(logv)}^{-n/2}{v}^{(2c-2logv)/d^2}exp\left(-\frac{{\sum }_{i=1}^n{\beta }_i}{4logv}\right)\end{array}$$

that avoids this complication and has a finite E(Y_i). In the multivariate case, use of zero left truncated normal priors on each diagonal element of the covariance matrix has the same effect.