Groupwise Segmentation with Multi-Atlas Joint Label Fusion

Abstract

Groupwise segmentation that simultaneously segments a set of images and ensures that the segmentations for the same structure of interest from different images are consistent usually can achieve better performance than segmenting each image independently. Our main contribution is that we adopt the groupwise segmentation framework to improve the performance of multi-atlas label fusion. We develop a novel statistical model to allow this extension. Comparing to previous atlas propagation and groupwise segmentation work, one key novelty of our method is that the error produced during label propagation is explicitly addressed in the joint label fusion framework. Experiments on hippocampus segmentation in magnetic resonance images show the effectiveness of the new groupwise segmentation technique.

1 Introduction

As a primary mechanism for quantifying the properties of anatomical structures and pathological formations from imaging data, image segmentation is an important task in medical image analysis. Typically, a segmentation algorithm is applied to segment one image at a time, i.e. segmenting one image is independent from segmenting other images. However, different segmentation tasks may not be independent, especially when images share common structures and similar appearances. When some images share similarities, one may expect that their segmentations should be related as well. By enforcing consistency in the segmentations produced for them, one may improve the robustness of automatic segmentation against random effects.

The idea of incorporating region coherence of same or similar objects across different images to reduce segmentation errors was initially addressed in the joint registration and segmentation framework, e.g. [2, 7, 10], motivated by the observation that image registration and image segmentation are highly correlated tasks. Improving one can help improve the other. By registering multiple images into a common space, appearance models of the same structure of interest from all images can be collected and re-enforced to ensure similar appearances for the segmented structures from different images. The estimated segmentations can then be used to improve registration such that segmentation alignments after registration are improved. With registrations between testing images, both appearance and shape consistencies can be enforced in groupwise segmentation.

Since the groupwise segmentation idea can be implemented with any non-groupwise segmentation algorithms, to directly improve upon the state of the art medical image segmentation techniques, we adopt the groupwise segmentation framework to improve the performance of multi-atlas label fusion (MALF). Through establishing one-to-one correspondence between a target image and a pre-labeled image, i.e. atlas, by image-based deformable registration, MALF transfers segmentation labels from the atlas to the target image and uses label fusion to combine solutions produced by different atlases. The highly competitive performance over many challenging applications, e.g. [5, 13, 15], show that the example-based knowledge representation and registration-based knowledge transfer model employed by MALF can produce highly accurate segmentation for medical applications.

Since pairwise or groupwise registration among testing images are often required in groupwise segmentation, it is a natural extension to apply techniques developed in MALF for groupwise segmentation. Our first contribution is to realize this extension through a novel statistical model for groupwise segmentation. Similar to the atlas propagation work [15] and the recent groupwise segmentation work [6], in our approach, each testing image and its estimated segmentation is applied as an additional atlas to help improve the segmentation accuracy for other testing images. However, when a testing image is applied as an atlas, due to the errors in producing its automatic segmentation, it is expected to be less reliable than the original atlases. Our second contribution is to extend the joint label fusion technique [14] to address this limitation. For validation, we apply our approach to segment the hippocampus from MRI and show significant performance improvements over MALF and other label propagation work.

2 Methods

Image segmentation can be addressed via estimating the conditional probability p(T_S|T_F, 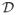), where T_F is the image to be segmented, T_S is a segmentation for T_F and 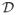is the training data, which, for example, may include some images and their gold standard segmentations. The conditional probability can be estimated through various methods, e.g. discriminative learning or MALF.

In the MALF framework, 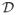contains all atlases. The conditional probability is estimated in the form p(l|x, T_F, 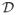) through warping each atlas to the target image, followed by label fusion, where l indexes through all labels and x indexes through all voxels in T_F. This technique is described in detail below. With accurate conditional probabilities, the true segmentation can be estimated by T_S(x) = argmax_lp(l|x, T_F, ).

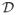2.1 Multi-Atlas Label Fusion

Since our work is based on MALF, we briefly describe the technique. Let $\mathcal{D}=\{A^1=(A_F^1,A_S^1),\dots ,A^n=(A_F^n,A_S^n)\}$ be n atlases, warped to the space of a target image by deformable registration. $A_F^i$ and $A_S^i$ denote the i_th warped atlas image and manual segmentation.

One simple and powerful label fusion technique is weighted voting, where each atlas contributes to the final solution according to a weight. Among the weighted voting approaches, similarity-weighted voting strategies with spatially varying weight distributions have been particularly successful [1, 13, 14]. The consensus votes received by label l are:

$$\widehat{p}(l\mid x,T_F,\mathcal{D})=\sum _{i=1}^n{w}_x^{i}p(l\mid x,A^i)$$ (1)

where p̂(l|x, T_F, 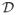) is the estimated probability of label l for the target image. p(l|x, Aⁱ) is the probability that Aⁱ votes for label l at x, with Σ_l∈{1,…L} p(l|x, Aⁱ) = 1. Typically, for deterministic atlases that have one unique label for every location, p(l|x, Aⁱ) is 1 if $l=A_S^i(x)$ and 0 otherwise. $w_x^i$ is the voting weight for the i_th atlas, with ${\sum }_{i=1}^n{w}_x^i=1$.

To estimate voting weights, similarity metrics employed by image-based registration such as sum of squared distance and normalized cross correlation can be applied such that atlases with more similar appearance to the target image at location x receives higher votes. One limitation of this approach is that the voting weights for each atlas is estimated independently from other atlases, ignoring potential correlations among the atlases. To address this problem, the joint label fusion algorithm estimates voting weights by simultaneously considering pairwise atlas correlations. As shown in [14], joint label fusion performed better than label fusion with independent weight estimation.

In the joint label fusion approach, segmentation errors produced by one atlas are modeled as $T_{S,l}(x)=A_{S,l}^i(x)+{\delta }^i(x)$. T_S,l(x), $A_{S,l}^i(x)\in \{0,1\}$ are the observed votes for label l produced by the target image and the i_th warped atlas, respectively. Hence, δⁱ(x) ∈ {−1, 0, 1} is the observed label error. Note that both T_S,l and δⁱ(x) are unknown. The probability that different atlases produce the same label error at location x are captured by a dependency matrix M_x, with $M_x(i,j)=p({\delta }^i(x){\delta }^j(x)=1\mid T_F,A_F^i,A_F^j)$ measuring the correlation between i_th and j_th atlases. In [14], the pairwise atlas correlation is estimated by appearance correlation as $M_x(i,j)~{\left[{\sum }_{y\in \mathcal{N}(x)}\mid A_F^i(y)-T_F(y)\mid \mid A_F^j(y)-T_F(y)\mid \right]}^{\beta }$, where 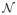(x) defines a neighborhood around x and β is a model parameter. The expected label difference between the combined solution and the target segmentation is:

$$E\left[{(T_{S,l}(x)-\sum _{i=1}^n{\mathbf{w}}_x^i{A}_{S,l}^i(x))}^2\mid F_T,F_1,\dots ,F_n\right]={\mathbf{w}}_x^t{M}_x{\mathbf{w}}_x$$ (2)

where t stands for transpose. To minimize the expected label difference, the voting weights are solved by ${\mathbf{w}}_x=\frac{M_x^{-1}{1}_n}{1_n^t{M}_x^{-1}{1}_n}$, where 1_n = [1; 1; …; 1] is a vector of size n.

2.2 Formulation for groupwise segmentation

Let ${\mathcal{T}}_F=\{T_F^1,\dots ,T_F^m\}$ be m testing images to be segmented. Groupwise segmentation can be formulated as jointly segmenting all testing images using the training set 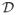and can be solved via estimating the joint conditional probability $p({\mathcal{T}}_S=\{T_S^1,\dots ,T_S^m\}\mid {\mathcal{T}}_F,\mathcal{D})$, where $T_S^1,\dots ,T_S^m$ are the estimated segmentations for $T_F^1,\dots ,T_F^m$, respectively. Since it is difficult to directly estimate the joint probability, we apply the pseudolikelihood approximation technique [3] and estimate the joint probability by:

$$\prod _{k=1}^{m}p(T_S^k\mid \mathcal{D},{\mathcal{T}}_F,{\mathcal{T}}_S\backslash \{T_S^k\})\prod _{k=1}^m\prod _{x}p(l^k(x)\mid x,\mathcal{D},{\mathcal{T}}_F,{\mathcal{T}}_S\backslash \{T_S^k\})$$ (3)

where $l^k(x)={\text{argmax}}_{l}p(l\mid x,\mathcal{D},{\mathcal{T}}_F,{\mathcal{T}}_S\backslash \{T_S^k\})$ is the estimated label for the k_th testing image. In this model, we assume that the label probability for each voxel is conditionally independent given the images and segmentations in (3). Note that the segmentation of each testing image is estimated by both the original atlases and the remaining testing images. Hence, the correlations between testing images are explicitly considered to make their solutions compatible.

Like the pseudolikelihood approach, the segmentations for all testing images are computed through iterative estimation. First, the segmentation of each testing image is independently estimated with MALF only using the atlases. In each of the following iterations, the estimated segmentation for each testing image is updated one at a time to maximize the joint probability (3). Using weighted voting based label fusion, we estimate the label probability for one testing image $T_F^k$ by:

$$p(l\mid x,\mathcal{D},{\mathcal{T}}_F,{\mathcal{T}}_S\backslash \{T_S^k\})=\sum _{i=1}^n{\mathbf{w}}^i{A}_{S,l}^i+\sum _{j=1,j\ne k}^m{\mathbf{w}}^{a^j}{a}_{S,l}^j$$ (4)

where a^j is the candidate segmentation produced by warping the segmentation produced for the j_th testing image to $T_F^k$. w^ajis the voting weight assigned to it, with ${\sum }_{i=1}^n{\mathbf{w}}^i+{\sum }_{j=1,j\ne k}^m{\mathbf{w}}^{a^j}=1$. Note that, for a simpler notation, the parametrization by x is implicit.

Potential risk in using testing images as atlases Due to registration and label fusion errors, it is reasonable to expect that the segmentation produced for each testing image is less accurate than those of the original atlases. Hence, when applying a testing image as an atlas to segment other testing images, in addition to the errors produced by image-based deformable registration, segmentation errors produced for the testing image are also propagated to other testing images. This potential risk may result in overall less accurate candidate segmentations produced by warping a testing image than by directly warping an original atlas.

Image similarity based label fusion is effective for detecting and reducing segmentation errors caused by registration errors. However, it can not detect whether the atlas contains errors in its segmentation. To address the unreliability of using testing images as additional atlases, we propose a solution based on the following observation. If an atlas produces more segmentation errors than other atlases, it is expected that its voting weight should be smaller than other atlases in the optimal solution. We propose to incorporate such prior knowledge in similarity-based weighted voting for more robust label fusion. To this end, we explicitly control the contribution from testing images in (4). Following the joint label fusion technique, we estimate the label probability for each testing image by solving the following optimization problem:

$$E\left[{(T_{S,l}^k-\sum _{i=1}^n{\mathbf{w}}^i{A}_{S,l}^i-\sum _{j=1,j\ne k}^m{\mathbf{w}}^{a^j}{a}_{S,l}^j)}^2\mid \mathcal{D},{\mathcal{T}}_F\right]={[\mathbf{w};{\mathbf{w}}^a]}^{t}M[\mathbf{w};{\mathbf{w}}^a]\text{subject}\text{to}\sum _{i=1}^n{\mathbf{w}}^i=1-\lambda ,\sum _{j=1,j\ne k}^m{\mathbf{w}}^{a^j}=\lambda$$ (5)

For segmenting one testing image, the contribution from the remaining testing images is controlled by the total weight assigned to them, 0 ≤ λ < 1. Typically, when the atlases cannot produce reliable segmentation, one may expect more contribution from testing images to regularize the results and vice versa.

Applying Lagrange multipliers, we can solve (5) in closed form by:

$${[\mathbf{w};{\mathbf{w}}^a]}^t=M^{-1}({\mu }_{c}c+{\mu }_{d}d)$$ (6)

where c = [1; …; 1; 0; …; 0], d = [0; …; 0; 1; …; 1]. Only the first n entries in c and the last m−1 entries in d are non-zero. $\left[\begin{array}{c}{\mu }_c\\ {\mu }_d\end{array}\right]={\left[\begin{array}{c}{c}^t{M}^{-1}c,c^t{M}^{-1}d\\ d^t{M}^{-1}c,d^t{M}^{-1}d\end{array}\right]}^{-1}[1-\lambda ;\lambda ]$.

3 Experiments

Imaging data and Experiment setup

Our study is conducted using 1.5 T baseline MR images from the Alzheimer’s Disease Neuroimaging Initiative (ADNI). Among these images, 57 are normal controls, 84 are patients with mild cognitive impairment (MCI) and 41 are patients with AD. Manual segmentations of the hippocampus are provided by ADNI as well. For cross-validation evaluation, we randomly selected 10 images to be the training images, i.e. the atlases, and another 50 images for testing. The cross-validation experiment was repeated for five times. In each experiment, a different set of atlases and testing images were randomly selected. The results reported below are averaged over the five experiments. To examine the performance with respect to the number of atlases used for producing the initial segmentation, in each cross-validation experiment, we also tested with different numbers of atlases, varying from 1 to 10.

For label fusion, we applied a 5 × 5 × 5 neighborhood for 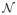. In our experiments, we fixed β = 2 for computing the atlas correlation matrix, which is shown to be optimal in [14] for hippocampus segmentation. For groupwise segmentation, we fixed λ = 0.5. Hence, the expected contribution from each testing image is significantly smaller than the contribution from each atlas.

Results

As shown in Fig. 1, our iterative optimization usually converges within a few iterations, with the first iteration producing the maximal performance improvement and dramatic diminishing performance gains in later iterations. In our experiment, we set the maximal iteration number to be 3. Fig. 1 also shows the performance produced by applying MALF alone and our groupwise segmentation method (MALF+groupwise). The results are shown in terms of average number of mislabeled voxels produced for each hippocampus. Fig. 2 shows some results produced by the two methods. As expected, the performance of MALF increases as the number of atlases increases. Our groupwise method produced consistently better results than applying MALF alone. The error reduction rates caused by groupwise segmentation vary from ~10% to ~30%.

Fig. 1.

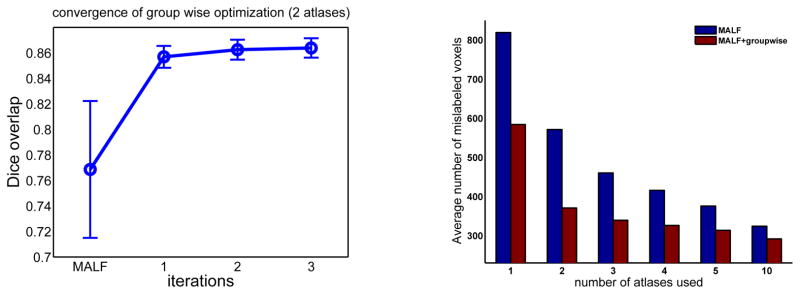
Left: Segmentation accuracy (in terms of Dice similarity coefficient $\frac{2\mid A\cap B\mid }{\mid A\mid +\mid B\mid }$) of our groupwise segmentation algorithm at each iteration. The results are averaged over 5 cross-validation experiments. Error bar is at 0.25 standard deviation. The segmentation produced by MALF used two atlases; Right: Segmentation performance in terms of average number of mislabeled voxels per hippocampus.

Fig. 2.

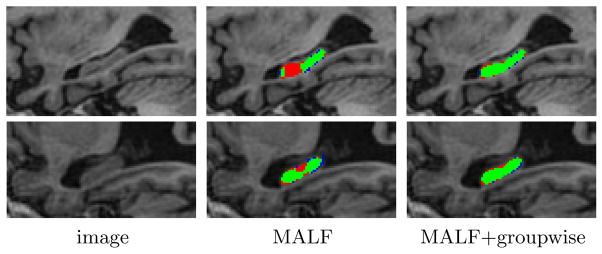
Sagittal views of hippocampus segmentation. Red: manual segmentation; Blue: automatic segmentation; Green: overlap between manual and automatic segmentation.

Fig. 3 (left) shows the Dice similarity coefficient (DSC)( $\frac{2\mid A\cap B\mid }{\mid A\mid +\mid B\mid }$) for controls, patients with MCI and AD, respectively. When only one or two atlases were used by MALF to produce initial segmentations, the improvement by our groupwise method is about 10 % DSC. Our results using one atlas are better than the hippocampus segmentation results, ~0.76, reported in [12], which also performed groupwise segmentation using one training image. When 5 and 10 atlases were used, the improvements caused by our groupwise approach are >2% and >1% DSC, respectively. To further test the generalization performance, we also repeated 5 cross-validation experiments, each with randomly selected 10 normal controls as atlases and 50 randomly selected subjects as testing images. As shown in Fig. 3 (right), our groupwise segmentation method produced an average DSC of 0.892, 1 % improvement over applying MALF alone. All improvements are statistically significant, with p<0.01 on the paired Students t-test for each cross-validation experiment. Our results also compare well to the state-of-the-art hippocampus segmentation performance, as summarized in Table 1¹. Overall, our results compare favorably over the state-of-the-art but we used many fewer atlases than the competing works.

Fig. 3.

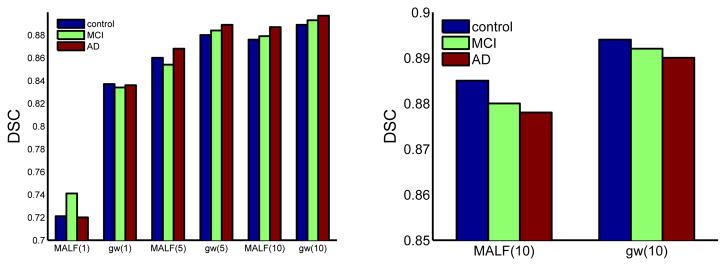
Segmentation accuracy produced by using randomly selected atlases (left) and normal control atlases (right). The number of atlases used by MALF and our groupwise method (gw) is given in parentheses. Results are averaged over 5 cross validations.

Table 1.

Hippocampus segmentation performance in the recent literature.

method : number of atlases used	Dice	JI	Tested Cohort
[13] : 38 atlases	0.87	-	normal control, AD
[4] : 79 atlases	0.887	-	normal control
[11]: 30 atlases	0.880	-	normal control
[8] : 55 atlases		0.80/0.81	normal control/MCI
[15] : 30 atlases	<0.85	-	normal control/MCI/AD
[14] : 20 atlases	0.892	-	normal control/MCI
[9] : 17 atlases	0.870	0.771	-
Our method : 10 atlases	0.893	0.805	normal control/MCI/AD

4 Conclusions and Discussion

We extended the powerful MALF technique to perform groupwise segmentation and validated our method in a hippocampus segmentation task. One drawback of groupwise segmentation is the additional computational cost for registrations among the testing images. However, this added cost is justified by the performance gain. For applications, where manually labeled atlases are limited and testing images are abundant, this technique will be more suitable to be applied.