Conformal piezoelectric energy harvesting and storage from motions of the heart, lung, and diaphragm

Significance

Heart rate monitors, pacemakers, cardioverter-defibrillators, and neural stimulators constitute broad classes of electronic implants that rely on battery power for operation. Means for harvesting power directly from natural processes of the body represent attractive alternatives for these and future types of biomedical devices. Here we demonstrate a complete, flexible, and integrated system that is capable of harvesting and storing energy from the natural contractile and relaxation motions of the heart, lung, and diaphragm at levels that meet requirements for practical applications. Systematic experimental evaluations in large animal models and quantitatively accurate computational models reveal the fundamental modes of operation and establish routes for further improvements.

Abstract

Here, we report advanced materials and devices that enable high-efficiency mechanical-to-electrical energy conversion from the natural contractile and relaxation motions of the heart, lung, and diaphragm, demonstrated in several different animal models, each of which has organs with sizes that approach human scales. A cointegrated collection of such energy-harvesting elements with rectifiers and microbatteries provides an entire flexible system, capable of viable integration with the beating heart via medical sutures and operation with efficiencies of ∼2%. Additional experiments, computational models, and results in multilayer configurations capture the key behaviors, illuminate essential design aspects, and offer sufficient power outputs for operation of pacemakers, with or without battery assist.

Nearly all classes of active wearable and implantable biomedical devices rely on some form of battery power for operation. Heart rate monitors, pacemakers, implantable cardioverter-defibrillators, and neural stimulators together represent a broad subset of bioelectronic devices that provide continuous diagnostics and therapy in this mode. Although advances in battery technology have led to substantial reductions in overall sizes and increases in storage capacities, operational lifetimes remain limited, rarely exceeding a few days for wearable devices and a few years for implants. Surgical procedures to replace the depleted batteries of implantable devices are thus essential, exposing patients to health risks, heightened morbidity, and even potential mortality. The health burden and costs are substantial, and thus motivate efforts to eliminate batteries altogether, or to extend their lifetimes in a significant way.

Investigations into energy-harvesting strategies to replace batteries demonstrate several unusual ways to extract power from chemical, mechanical, electrical, and thermal processes in the human body (1, 2). Examples include use of glucose oxidation (3), electric potentials of the inner ear (4), mechanical movements of limbs, and natural vibrations of internal organs (5–7). Such phenomena provide promising opportunities for power supply to wearable and implantable devices (6–8). A recent example involves a hybrid kinetic device integrated with the heart for applications with pacemakers (7). More speculative approaches, based on analytical models of harvesting from pressure-driven deformations of an artery by magneto-hydrodynamics, also exist (9).

Cardiac and lung motions, in particular, serve as inexhaustible sources of energy during the lifespan of a patient. Mechanical-to-electrical transduction mechanisms in piezoelectric materials offer viable routes to energy harvesting in such cases, as demonstrated and analyzed by several groups recently (10–17). For example, proposals exist for devices that convert heartbeat vibrations into electrical energy using resonantly coupled motions of thick (1–2 mm) piezoelectric ceramic beams on brass substrates (1). Although such models highlight the potential for self-powering devices, there are important practical challenges in the coupling of rigid mechanical systems with the soft, dynamic surfaces of the body in a manner that does not induce adverse side effects. An ideal device construct would enable power harvesting throughout the macroscale displacement cycles associated with natural motions of an organ, but in a manner that does not induce any significant constraints on those motions. Development of flexible devices based on arrays of piezoelectric ZnO nanowires (14, 15) represents an important step in this direction. Experiments performed with a linear motor to periodically deform the device indicate electrical outputs as large as 1–2 V (open-circuit voltage) and ∼100 nA (short-circuit current) (13). Initial in vivo tests on rabbit hearts yielded voltages and currents of ∼1 mV and ∼1 pA, respectively. The associated electrical power is substantially less than that required for operation of existing classes of implants, such as pacemakers. Some improvement in performance is possible with thin-film geometries, as demonstrated in bending experiments on devices based on barium titanate (16) and lead zirconate titanate (PZT) (11, 12, 17). In vivo evaluations are needed, however, to assess the suitability for realistic use and potential for producing practical levels of power.

The present work reports several advances in the materials science and engineering of biocompatible, flexible, energy harvesters. The key findings include in vivo demonstrations of PZT-based devices (i) with output open-circuit voltages and short-circuit currents that are greater by three and five orders of magnitude, respectively, than previous in vivo results; (ii) monolithically integrated with rectifiers and millimeter-scale batteries for simultaneous power generation and storage, including high-power, multilayer designs; (iii) in biocompatible forms, evaluated through cell cultures and large-scale, live animal models, on various locations/orientations on different internal organs, each approaching human scales; and (iv) for harvesting inside the body, via open and closed left thoracotomy experiments with a bovine model. Additional results demonstrate (i) power generation at a level necessary for continuous operation of a cardiac pacemaker; (ii) mechanically and electrically stable device behavior over 20 million cycles of bending/unbending in a moist, hydrogel environment; and (iii) quantitatively accurate analytical models that couple mechanical deformations and piezoelectric effects to predict electrical output as a function of key design parameters and materials properties, including multilayer configurations.

Results and Discussion

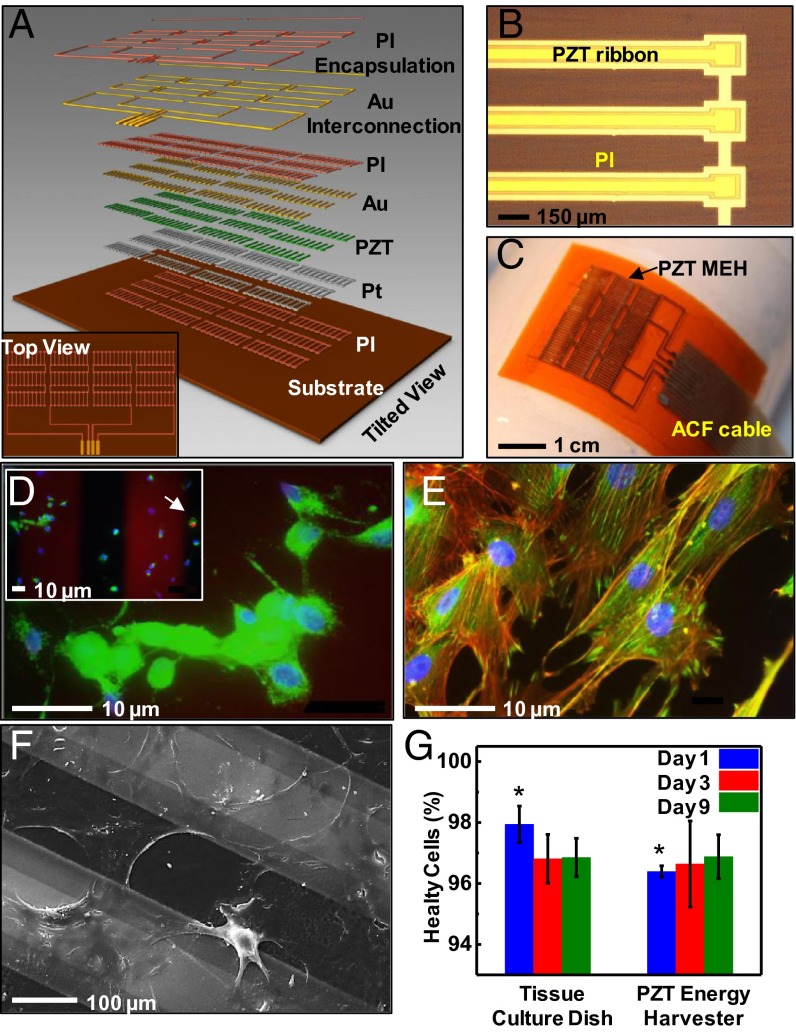
Fig. 1A and SI Appendix, Figs. S1 and S2 provide schematic diagrams of a flexible PZT mechanical energy harvester (MEH). An optical microscope image and a photograph appear in Fig. 1 B and C, respectively. The key functional element is a capacitor-type structure that consists of a layer of PZT (500 nm) between bottom (Ti/Pt, 20 nm/300 nm) and top (Cr/Au, 10 nm/200 nm) electrodes. See SI Appendix for details. An MEH module consists of 12 groups of 10 such structures that are electrically connected in parallel. Each of the 12 groups is connected in series to its neighboring group to increase the output voltage (SI Appendix, Fig. S2). Encapsulation of these devices with biocompatible materials isolates them from bodily fluids and tissue, thereby minimizing the risks of failure or immune response. A thin spin-cast layer of polyimide (PI) (SI Appendix) serves effectively in this role, as demonstrated in leakage tests performed in PBS (P-5368, pH 7.4; SIGMA) in a way that maintains excellent mechanical flexibility. The computed bending stiffness (per unit width) is 0.22 N⋅mm and 0.10 N⋅mm for regions coincident with and away from the PZT structures, respectively. For a bending radius of 2.5 cm, the maximum strain in the PZT is only 0.1%.

Fig. 1.

Flexible MEH based on thin ribbons of PZT, and tests of biocompatibility using rat smooth muscle cells. (A) Exploded-view schematic illustration with a top view (Inset). (B) Optical microscope image of PZT ribbons printed onto a thin film of PI. (C) Photograph of a flexible PZT MEH with cable for external connection. ACF, anisotropic conductive film. (D) Live/dead viability assay showing live cells (green) with intact nucleus (blue) and one dead cell (red) as indicated by the arrow (Inset). This image corresponds to day 9 of the experiment. (E) Fluorescent image showing Vinculin focal contact points (green), actin filaments (red), and nuclei (blue). (F) SEM image of cells on PZT ribbons encapsulated by a layer of PI. (G) Lactate dehydrogenase assay shows no indications of toxicity for cells on a membrane of PZT at day 9. (*P value ≤0.05 between the two groups.) Error bar is calculated standard error.

As a screen of the biocompatibility and absence of cytotoxicity of the constituent materials, we examined the adherence, growth, and viability of rat smooth muscle cells (SMCs), as a representative tissue cell, on the encapsulated PZT capacitor structures described above. SMCs readily adhere to fibronectin-coated structures, with evident spreading (Fig. 1D), and intact detectable cytoskeletal structures, i.e., Vinculin focal contacts via fluorescence (green in Fig. 1D) and cytoskeletal actin microfilaments (red in Fig. 1E). The scanning electron microscope (SEM) image shows spreading cells in Fig. 1F. No detectable cytotoxicity was observed in a live/dead assay that identifies calcein acetomethoxy derivative (green) for viable cells and ethidium homodimer (red) for damaged cells, suggesting that the majority of SMCs are healthy (green in Fig. 1D). In fact, more than 96% of cells were viable after 9 d of culture. Cells grown on device structures showed no differences from those grown on standard tissue culture plates at days 3 and 9 (Fig. 1G).

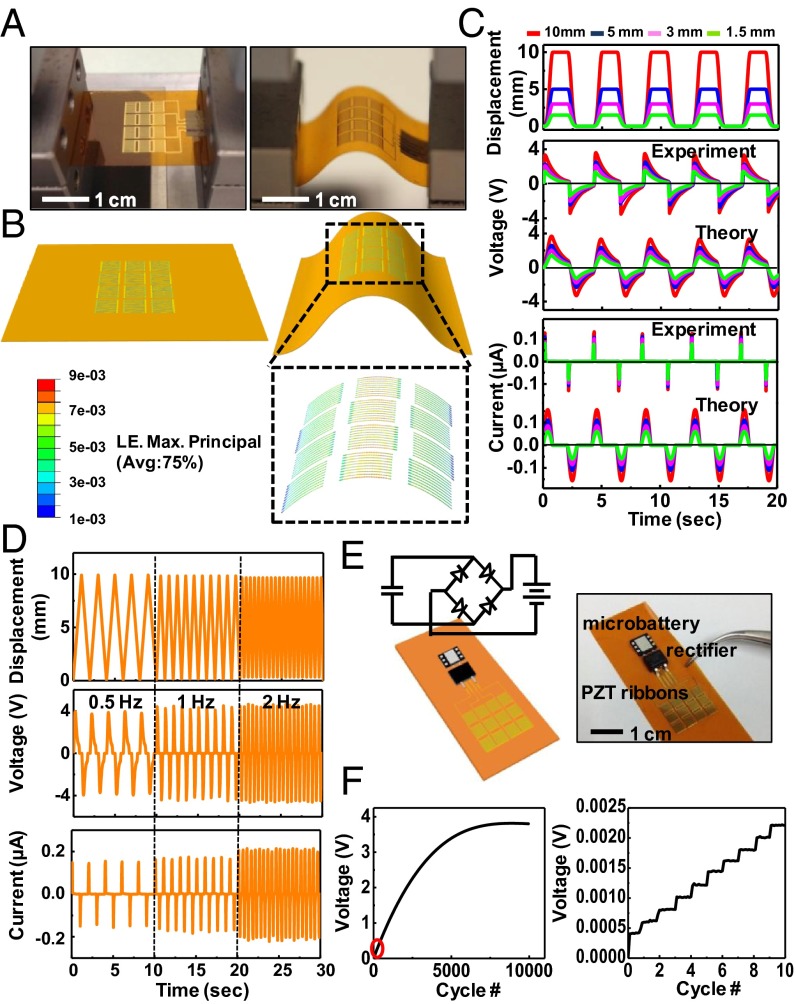
Measurements with a bending stage reveal dynamic mechanical properties, as shown in Fig. 2A. Fig. 2B illustrates 3D deformations of the PZT ribbons, with distributions of strain obtained by finite element analysis (FEA). The overall shapes match those observed in Fig. 2A. The strain distributions in SI Appendix, Figs. S3 and S4 quantitatively capture the nature of deformations in the various device layers. The results determine the electrical field and electrical displacement in the PZT through constitutive models of piezoelectric behavior. The voltage and current outputs of a representative device before (Fig. 2C) and after (SI Appendix, Fig. S5) rectification illustrate the nature of operation. See SI Appendix for details.

Fig. 2.

Experimental and theoretical studies of the electrical behavior of PZT MEHs under various mechanical loads. (A) Photographs of a PZT MEH clamped on a bending stage in flat (Left) and bent (Right) configurations. (B) Three-dimensional finite element method modeling for the device in A. The results highlighted by the black dashed box give the computed distributions of strain in the PZT ribbons for a displacement load of 5 mm along the horizontal direction. LE, logarithmic strain. (C) Experimental and theoretical results for displacement, voltage, and current as a function of time for PZT MEHs under bending loads similar to those shown in A and B. (D) Displacement, voltage, and current as a function of time curves, for bending loads with frequencies of 0.5, 1, and 2 Hz. (E) Schematic illustration (Left) and photograph (Right) of a PZT MEH connected to and cointegrated with a rectifier and rechargeable microbattery. A circuit schematic appears in Left. (F) Voltage across such a battery as a function of time during charging by a PZT MEH under cyclic bending load (Left). The peak voltage output of the PZT MEH is 4.5 V. The red oval (Left) highlights, approximately, the region plotted (Right). The results highlight the expected stepwise behavior in charging.

Experimental behaviors can be captured with an analytical model. Compression of a device with length L leads to buckling with an out-of-plane displacement 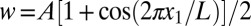as shown in SI Appendix, Fig. S6A, where the origin of coordinate x₁ is at the center of the device, and the amplitude A is related to the compression ΔL between the two ends by 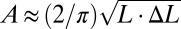. The PZT layers, together with the top and bottom electrodes, bend with the buckled substrate. The membrane strain in the PZT ribbons is given analytically by

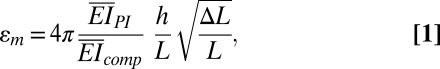(see SI Appendix for details), where 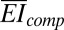and 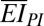are the bending stiffness (per unit width) of the PI with and without the PZT and electrodes, respectively; and h is the distance from the center of the PZT layers to the neutral mechanical plane of the cross-section as shown in SI Appendix, Fig. S6B. The bending strain in the PZT ribbons has opposite signs above and below the midpoint through the thickness of the PZT, and therefore does not contribute to the voltage or current output. For thin PZT layers, the bending strain is much smaller than the membrane strain; the total strain is therefore dominated by the membrane strain. See SI Appendix for details.

PZT is transversely isotropic with the polarization direction x₃ normal to the surface. The elastic, piezoelectric, and dielectric constants are denoted by c_ij, e_ij, and k_ij, respectively. For plane-strain deformation (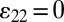) the strain 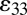and the electrical field E₃ along the polarization direction x₃ satisfy the constitutive relations 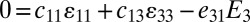and 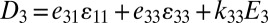, where the electrical displacement D₃ along the polarization direction is a constant to be determined. For measurements of current, the top and bottom electrodes connect to an ammeter, which has negligible electrical resistance. As a result, voltage between the top and bottom electrodes is zero, and 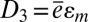, where the effective piezoelectric constant is 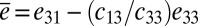and the membrane strain 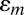is given in Eq. 1. For each group of devices in series, the charge induced by 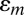gives the current 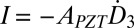(SI Appendix, Fig. S6C), i.e.,

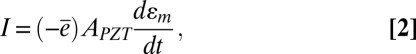where 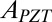is total area of the PZT ribbons in each group. In experiments, the compression ΔL between the two ends of the device is a periodic function of time t, given by

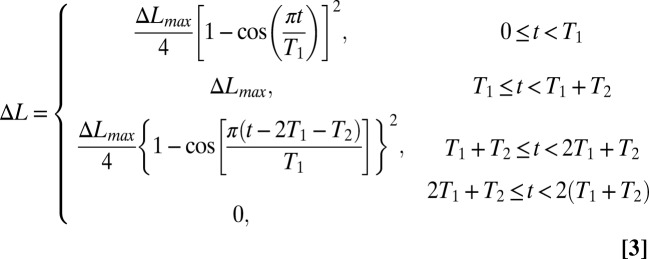in the first period, where ΔL_max is the maximum compression, and T = 2(T₁+T₂) is the period. Fig. 2C shows ΔL vs. t for T₁ = 0.8 s, T₂ = 1.3 s, and ΔL_max = 1.5, 3, 5, and 10 mm as in the experiments. Fig. 2C shows that the current obtained from Eq. 2 for these four values of ΔL_max agree reasonably well with the experiments, where L = 2.5 cm, , h = 24.7 µm, and = 2.24 mm² as in the experiments (see SI Appendix for details), and 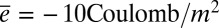, which is on the same order of magnitude as the literature values (18). The peak current ranges from 0.06 to 0.15 µA for ΔL_max from 1.5 to 10 mm, respectively.

In measurements of voltage, the potential drop across each group is V/N, where V is the total voltage for N groups of devices in series (SI Appendix, Fig. S6C). The electrical displacement is 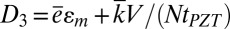, where 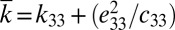is the effective dielectric constant and t_PZT is the thickness of PZT ribbons. The current 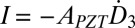is related to the voltage V and resistance R of the voltmeter by I = V/R, which gives 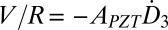, i.e.,

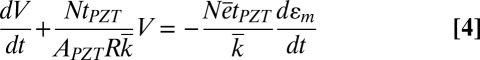For the initial condition V(t = 0) = 0, the voltage is given by

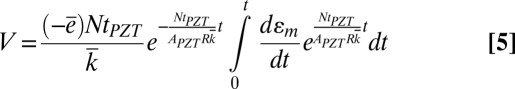For 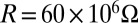in the experiment and 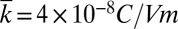(18), Fig. 2C shows the voltage V vs. time t obtained from Eq. 5, which agrees well with the experiments, including both the shape and peak value. The peak voltage can reach values as large as 3.7 V for the maximum compression ΔL_max = 10 mm. (The differences between the measured and predicted behavior of the output current in Fig. 2C arise because, according to Eqs. 1 and 2, the current is directly proportional to the rate of compression d∆L/dt, and is therefore sensitive to d∆L/dt when the compression reverses direction. The assumed displacement profile does not follow precisely the one in the experiment. By contrast, the voltage is relatively insensitive to d∆L/dt because Eqs. 1 and 5 involve the integration of d∆L/dt.)

Fig. 2D shows that the currents and voltages increase with frequency, even with the same load amplitudes, consistent with predicted dependence (Eqs. 2, 4 and 5) on the strain rate 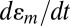. This behavior can be understood by recognizing that increasing the frequency with the same load amplitude increases the amount of work performed by the external force; as a result, the harvester produces enhanced output energy through increases in current and voltage.

This energy can be captured directly by use of a chip-scale rechargeable battery (EnerChip CBC012; Cymbet Corporation) and a Schottky bridge rectifier (MB12S; Micro Commercial Components) cointegrated on the same flexible substrate with the MEHs. Characterization can be performed using the setups shown in Fig. 2A. Fig. 2 E and F show the device and the output voltage of the battery measured in such a case; the results reveal stepwise increases in the stored energy with each cycle of bending and unbending (Fig. 2A). As the process continues, the voltage of the battery saturates at a value (∼3.8 V) characteristic of the battery specification.

The analytical framework can be modified to account for the rectifier via its resistance R_rectifier, as illustrated in SI Appendix, Fig. S6D. Here, the resistance in the current measurement is R_rectifier instead of 0, whereas the resistance R in the voltage measurement is replaced by R + R_rectifier. The voltage in Eq. 5 is replaced by its absolute value. See SI Appendix for details. The results (SI Appendix, Fig. S5) agree well with experiments. The amplitudes of the current and voltage are only slightly smaller than those without the rectifier.

An effective efficiency for conversion of mechanical energy to electrical energy can be defined as the ratio of energy stored in the battery W_stored to the total mechanical work W_total, i.e., 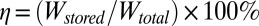. Here W_stored is estimated from the saturated voltage 3.8 V and capacity of the battery as 0.164 J. The total mechanical work is the product of the number of cycles for the battery voltage to saturate (e.g., 7,500 from Fig. 2F for ΔL_max = 10 mm) and work done (19) in each cycle 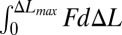, where 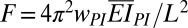is the bucking force (SI Appendix, Fig. S6A), and w_PI = 2 cm is the width. These calculations indicate an efficiency, at the system level, of η = 1.7%. This value can be improved by decreasing the thicknesses and Young’s moduli of the electrodes and PI encapsulation layer and/or by increasing the area coverage of the PZT. Reductions in viscoelastic dissipation of the substrate can also be helpful (19). [We note that alternative metrics for efficiency (13) lead to much higher values than those reported above.]

Additional in vitro characterization illustrates that these MEH devices can be wrapped onto various curved objects such as balloons, fingers, and wrists, as seen in SI Appendix, Fig. S7. Control experiments (SI Appendix, Fig. S8) reveal that reversing the electrical connections to measurement equipment reverses the signal polarity, as expected. The devices exhibit excellent fatigue properties. Bending and releasing more than 20 million times while in direct contact with a transparent layer of gelatin (Knox), to mimic a moist environment (SI Appendix, Fig. S9 A and B), induce no noticeable degradation in the properties, as in SI Appendix, Fig. S9 C and D.

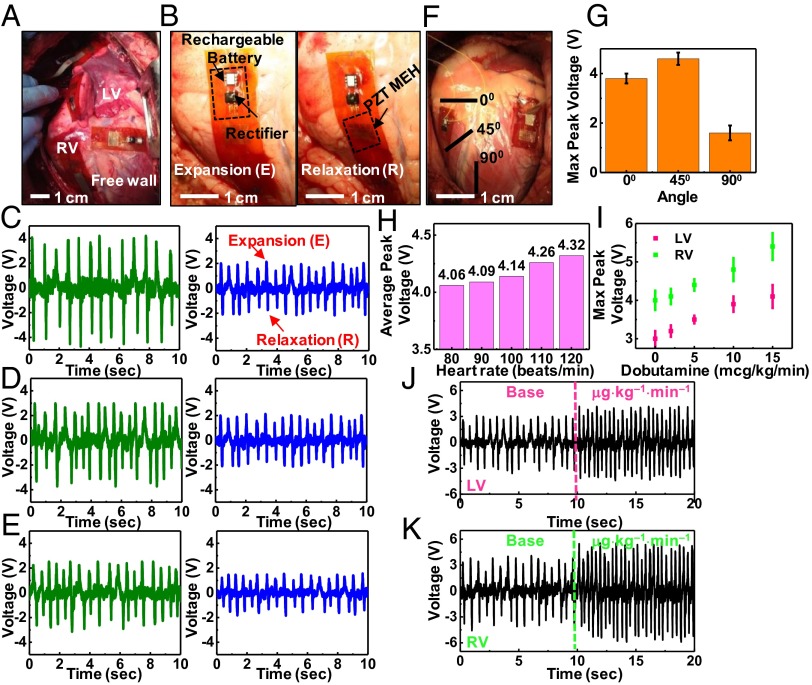
In vivo testing involved affixing the devices to epicardial sites on the right ventricle (RV), left ventricle (LV) base, and free wall of bovine and ovine hearts as shown in Fig. 3A and Movies S1 and S2. The anchoring scheme used sutures at three points, to maintain focal contact, although without rigid attachment so as to minimize any alteration or constraint on cardiac motion. Similar suturing techniques have been previously used to suture 3D patches onto the LV in a rat model (20). Furthermore, alternative suturing techniques, including running locked stitch and five-point lacerations can further reinforce the attachments. No detectable change in cardiac conduction or epicardial motion occurs following this simple procedure for fixing the device onto the epicardium. The PZT MEH maintains conformal contact, without delamination from the heart during the entire cycle of cardiac motion from contraction to relaxation. Evaluation of various mounting sites can identify locations for optimal power extraction (Fig. 3 A and B). Analysis of voltage outputs from devices placed on the RV, LV base, and free wall appear in Fig. 3 C, D, and E, respectively. The RV yields the best results, even though the LV has more muscular fibers (9–11 mm thick) than the RV (3–5 mm thick) (21). The differences in shape and other functional characteristics are, however, most important. The RV chamber is box- or wedge-shaped in form, with a concave free wall, which is thinner than the LV and is attached to the convex interventricular septum (22). The LV is roughly cylindrical in shape and has a thick wall structure with three spiraling layers of muscle to enable contractions with a twisting or torsional motion (23, 24). The RV ejects blood primarily by shortening its free wall, whereas ejection from the LV primarily involves a reduction in its diameter or circumference, associated with wall thickening (25). The contraction of the RV by shortening the free wall likely results in enhanced overall wall motion and hence increased bending of the MEH than the twisting contraction of the LV.

Fig. 3.

In vivo evaluation of the optimal placement and orientation of PZT MEHs on the heart, and assessment of voltage output by varying the heart rate via dobutamine infusion and use of a temporary pacemaker. (A) Photograph of PZT MEHs on the RV, LV, and free wall of a bovine heart. (B) PZT MEH cointegrated with a rectifier and rechargable battery, mounted on the RV of a bovine heart, shown during expansion (Left) and relaxation (Right). Open circuit voltage as a function of time for PZT MEHs on bovine (green) and ovine (blue) hearts, mounted on (C) RV, (D) LV, and (E) free wall at an orientation of 0° relative to the apex of the heart. Here, the heart rate is 80 beats per min. (F) Photograph of PZT MEHs oriented at different angles. (G) Measurements of maximum values of the peak open circuit voltages produced by these devices indicate peak output at 45°. Error bar is calculated standard error. (H) Average peak voltages of a PZT MEH on the RV of a bovine heart at 0° for various heart rates (80–120 beats per min) controlled by a temporary pacemaker. (I) Maximum peak voltage for various dosages of dobutamine infusion, for the case of a device on the RV (green points) and LV (pink points) of a bovine heart at 0°. Error bar is calculated standard error. Voltage as a function of time for PZT MEHs on the LV (J) and RV (K) of a bovine heart, with a base and maximum dose of dobutamine.

Orientation of the device is also important, as illustrated by the data in Fig. 3 F and G. Bending in the longitudinal direction (x₁ direction in SI Appendix, Fig. S3) relative to the orientation of the PZT ribbons provides the highest efficiency (see SI Appendix for details). To examine the dependence on orientation on the heart, measurements involve the longitudinal direction of PZT ribbons along the 0°, 45°, and 90° directions with respect to the apex of the heart. The 0° and 45° directions produce greater voltages than those at 90° (Fig. 3G). This behavior, for 0° and 45°, is expected because the myocardial tissue of the heart is anisotropic and contracts in a generally circumferential direction (26) with cardiac fibers aligned in a continuous manner from +60° on the endocardium to −60° on the epicardium (27); 90° is clearly out of this range. Theoretically, as shown in Eq. 5, the voltage is proportional to the strain rate, or equivalently, the strain amplitude for a given period. FEA confirms that the strain by bending along the x₁ direction is larger than that along x₂, as shown in SI Appendix, Figs. S3 and S4. Aligning the x₁ direction with the strongest bending direction optimizes the harvested energy.

The size of the heart, beat rate, and force of contraction are additional factors that affect voltage output. In the studies reported here (Figs. 3–5), the bovine heart is nearly twice the mass of the the ovine model. All devices deployed on the former yield significantly higher voltage outputs than those in the ovine model, for any site of implantation on the heart (SI Appendix, Figs. S10 and S11). Modulating the heart rate through electrical and chemical stimulation reveals the dependence on frequency. Fig. 3H demonstrates that increasing the bovine heart rate with a temporary pacemaker (Medtronic 5388) increases the voltage in direct proportion to heart rate (see SI Appendix, Figs. S10 and S11 and Movie S3), consistent with modeling results, assuming that the amplitude does not vary significantly with frequency. Similarly, increasing the force and degree of contractility of the myocardium via dobutamine infusion, i.e., the inotropic state (15 μg⋅kg⁻¹⋅min⁻¹), increases both the voltage and the frequency of the output (SI Appendix, Fig. S12). Such a response occurs for both the LV and RV, as shown in Fig. 3 I–K.

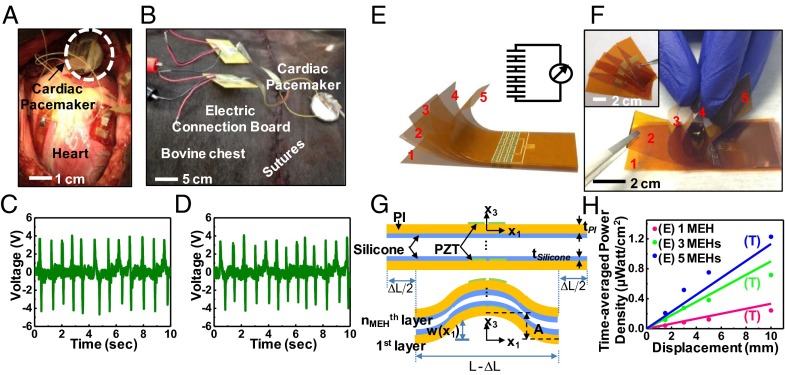
Fig. 5.

Performance of a PZT MEH evaluated with the chest open and closed and scaling of power output in multilayer stacked designs. Photograph of a PZT MEH without and with battery, rectifier, and pacemaker connection on a bovine heart when the chest is (A) open and (B) closed. Voltage as a function of time for a PZT MEH on the bovine RV with the chest open (C) and closed (D). (E) Schematic illustration of a multilayer stack of five independent PZT MEHs connected in series. A circuit schematic appears in the upper right-hand corner. (F) Photograph of such a stacked configuration, peeled apart at the left edge to show the separate layers. Each device appears just before stacking (Inset). (G) Schematic illustration of the theoretical shape for buckling of a stack of PZT MEHs with spin-cast layers of silicone elastomer (thickness = 10 μm) in-between and under compression. (H) Time-averaged power density as a function of the bending load displacement for stacks consisting of one (pink curve), three (green curve) and five (blue curve) PZT MEHs, connected in series. E, experimental data; T, theory.

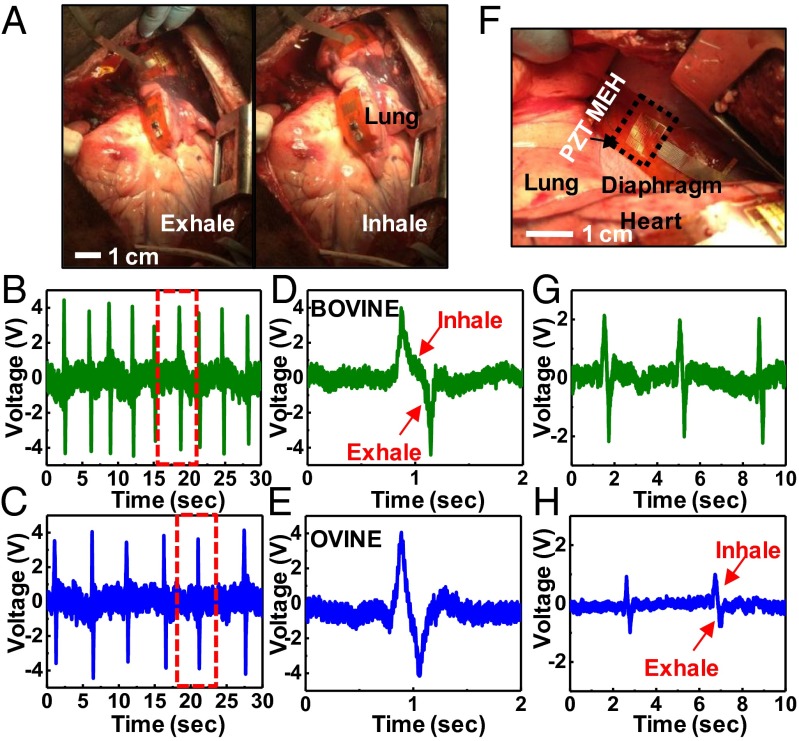
The lung represents another internal organ of interest for mechanical energy harvesting. Results for mounting on the bovine (Fig. 4A and Movie S4) and ovine lung of the bovine are consistent with expectation. In particular, in both models respiratory movement can be converted to voltage (Fig. 4 B and D). Unlike observations with the heart, data collected from the lung show no strong interspecies differences (Fig. 4 C and E). The diaphragm offers an additional option. Data indicate larger voltage response for the bovine (Fig. 4F) than the ovine, as shown in Fig. 4 G and H, respectively. Collectively, these results indicate that flexible PZT MEH systems are readily capable of harnessing energy from different locations across the body, with operational details that depend on the species and the organ.

Fig. 4.

In vivo evaluation of PZT MEHs on the lung and diaphragm. (A) Photograph of a PZT MEH cointegrated with a microbattery and rectifier, mounted on the bovine lung. Voltage as a function of time for such devices on the bovine (B) and ovine (C) lung. D and E show plots corresponding to the regions indicated by the red dashed boxes in B and C, respectively. (F) Photograph of a PZT MEH on the bovine diaphragm. Voltage as a function of time for such a device on the bovine (G) and ovine (H) diaphragm.

Any long-term practical use would, of course, require efficient operation upon closure of the chest postthoracotomy. Data collected with the chest open (Fig. 5A) and closed (Fig. 5B) show the same capabilities in power generation, as in Fig. 5 C and D. Similar in vivo tests on a pig model appear in SI Appendix, Fig. S13. Such results clearly suggest an ability to power implanted devices. The magnitude of power generation in this context is important. Operation of a cardiac pacemaker system provides a specific example of interest. State-of-the-art devices offer cardiac activity sensing, adaptive pacing, and programability, with average power consumption values as low as 0.3 μW (28, 29). The power output of a PZT MEH depends on its design. With layouts described previously, the time-averaged power density (electrical power output per unit area of PZT) corresponds to 0.12 and 0.18 µW/cm² for mounting on the RV at 0° and 45° as seen in SI Appendix, Fig. S14 A and B, respectively. Stacking multiple PZT MEH sheets (Fig. 5 E and F and SI Appendix, Fig. S15) increases the power output. Fig. 5G shows a stack of n_MEH PZT MEHs thin, spin casted of silicone layer in between as adhesives and strain isolating layers. The silicone, which is much more compliant (Young’s modulus 60 KPa) than the PI (Young’s modulus 2.5 GPa), does not significantly alter the modes of deformation of the PZT MEHs (SI Appendix, Table 1). As a result, for a stack of n_MEH PZT MEHs, Eq. 5 can be applied simply by replacing N with N⋅n_MEH. For ΔL_max = 10 mm, in multilayer stacks with n_MEH = 3 and 5, in vitro experiments show peak voltages of 5.8 and 8.1 V (SI Appendix, Fig. S16), respectively, consistent with Eq. 5. Both values are higher than that (3.7 V) for a single-layer device. In vivo demonstrations on the bovine heart are consistent with these results (SI Appendix, Fig. S17). The time-averaged power density increases with n_MEH, and can reach as large as 1.2 μW/cm² (Fig. 5H) for n_MEH = 5, which is sufficient to operate a cardiac pacemaker (1) (see SI Appendix for details).

Conclusions

The reported results provide evidence that piezoelectric MEHs can yield significant electrical power from motions of internal organs, up to and exceeding levels relevant for practical use in implants. Theoretical models establish design rules and provide predictive capabilities for efficiencies associated with various single and multilayer layouts. Practical applications demand long-term reliable operation in the closed body cavity. The extensive cycling tests and initial measurements of biocompatibility summarized here represent starting points for the sort of qualifications that are required. In addition to uses on internal organs, the same types of systems can be implemented in skin-mounted configurations for health/wellness monitors or nonbiomedical devices. The potential to eliminate batteries or, at least, the need to replace them frequently represents a source of motivation for continued work in these and related directions.

Materials and Methods

Detailed fabrication steps for the devices, designs for the data acquisition systems, and related hardware all appear in SI Appendix. In vitro biocompatibility study and in vivo implantation of the device on animal models are also described in the SI Appendix. All animal procedures and experiments were approved by the Institutional Animal Care and Use Committee at the University of Arizona.