Indistinguishability and correlations of photons generated by quantum emitters undergoing spectral diffusion

Abstract

Photon-based quantum information processing is based on manipulating multi photon interference. We focus on the Hong-Ou-Mandel (HOM) dip in the photon coincidence rate which provides a direct measure of interference of indistinguishable photons linked to their Bose statistics. The effect has been first observed with entangled photons generated by parametric down conversion and then extended to independent emitters. Fluctuations caused by coupling between emitters and a bath can erode the interference which causes the dip. Here we show how the magnitude and shape of the HOM dip is affected by spectral diffusion induced by coupling to a brownian oscillator bath. Conditions for maintaining and controlling the interference are specified.

The ultrafast optical control of quantum interference of single photons is of fundamental interest with broad applications to entanglement generation¹, quantum computing²,³,⁴, communication⁵, and information processing⁶,⁷,⁸. The HOM dip in the photon coincidence counting (PCC) rate¹ is an ultimate measure of photon indistinguishability⁹,¹⁰. It has been observed in a broad variety of systems including remote frequency-detuned organic molecules¹¹,¹², quantum wells¹³, quantum dots¹⁴,¹⁵,¹⁶, nano crystals¹⁷, nitrogen vacancies in diamond¹⁸,¹⁹,²⁰ and carbon nanotubes²¹. We examine photon interference in the setup shown in Fig. 1a. A pair of photons is generated by two remote two-level molecules a and b with ground g_α and excited state e_α, α = a, b. These photons then enter a beam splitter and are subsequently registered by time-and-frequency gated detectors s and r. There are two types of possible outcomes: two photons registered in one detector (s or r) or coincidence where one photon is detected in each. The ratio between these outcomes reflects the Bose statistics and degree of distinguishability of photons. If the two photons incident on the beam splitter are indistinguishable the PCC vanishes. This is known as the HOM dip. The dip is displayed by varying the position of the beam splitter which causes delay T between the two photons. The normalized PCC rate varies between 1 for completely distinguishable photons and 0 when they are totally indistinguishable. For classical fields and 50:50 beam splitter the PCC rate may not be less than 1/2. We denote the photons to be indistinguishable (distinguishable) if the PCC rate is smaller (larger) than 1/2.

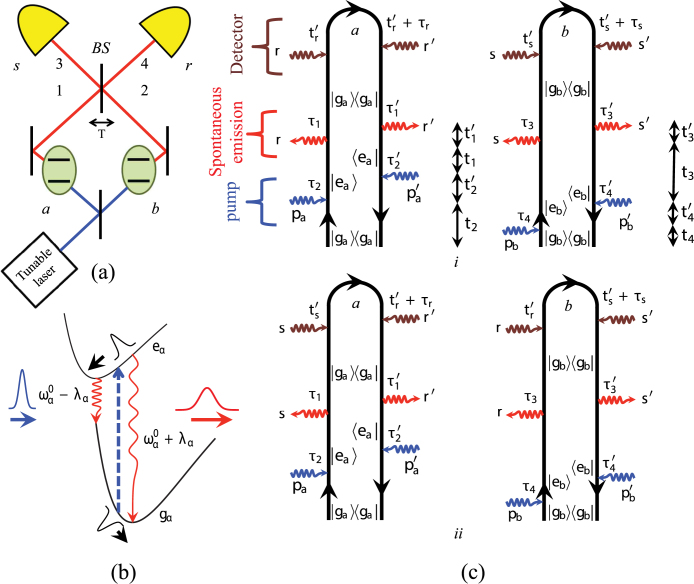
Figure 1. Time-and-frequency resolved measurement of PCC with spectral diffusion.

Schematic of the PCC experiment with two source molecules - (a), the two-level model of the molecule with SD used in our simulations - (b). (c) - Loop diagrams for the PCC rate of emitted photons from two molecules (for diagram rules see26). The left and right branches of each diagram represent interactions with ket- and bra- of the density matrix, respectively. Field-matter interactions with the pump pulses p_a and p_b (blue), spontaneously emitted s, s′, r, r′ photons (red) and detectors (brown).

PCC is typically measured using pure time-domain detection²²,²³. Originally performed with entangled photons generated by parametric down conversion (PDC)¹ the shape of the dip vs delay is usually related to the two-photon state envelope which is governed by an effective PDC Hamiltonian²⁴. Bath induced fluctuations can become important for remote emitters and have been introduced phenomenologically¹². Here we present a microscopic theory for PCC with bath fluctuations by formulating the signal in the joint field-matter space.

Results

Generation and detection of PCC by two remote emitters

The time-and-frequency gated PCC signal is described by the two pairs of loop diagrams shown in Fig. 1c. Each loop represents molecule (a or b) which undergoes four field-matter interactions and each detector interacts twice with the field. Fig. 1c shows that after interacting with pump (with its ket) at time t₂ molecule a evolves in the coherence 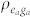during time interval 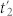. The second interaction of the pump with the bra then brings the molecule into a population state 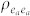which evolves during interval t₁ until the first interaction with spontaneous emission mode occurs with ket. The molecule then evolves into the coherence 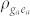during 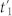until the second bra- interaction of spontaneous mode. During population and coherence periods, the characteristic timescale of the dynamics is governed by population relaxation and dephasing, respectively.

All relevant single-molecule information is given by the four point dipole correlation function 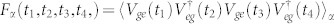, where V and V^† are the lowering and raising dipole transition operators, respectively. Diagrams i in Fig. 1c represent non-interfering term given by a product of two independent fluorescence contributions of the individual molecules. Diagrams ii represent interference described in the joint space of the two molecules and involve the interference of eight quantum pathways (four with the bra and four with the ket) with different time orderings. Each molecule creates a coherence in the field between states with zero and one photon |0〉〈1| and |1〉〈0|. By combining the contributions from a pair of molecules we obtain a photon population |1〉〈1| that can be detected²⁴,²⁵. For a pair of identical molecules, the beam splitter destroys the pathway information making the molecules indistinguishable and giving rise to quantum interference.

Bath induced fluctuations via e.g. spectral diffusion (SD) can destroy the quantum interference. Generally SD can manifest itself as either discrete random jumps of the emission frequency²¹,³¹,³² or as a broadening of a hole burnt in the spectrum by a narrowband pulse³³,³⁴. We focus on the SD in the “hole burning” limit (HBL) (see Methods for the precise conditions and Section S3 of SI). This is relevant to the crystals which store information in the form of reversible notches that are created in their optical absorption spectra at specific frequencies. Long storage times³⁵, high efficiencies³⁶, and many photon qubits in each crystal³⁷ can be achieved in this limit.

We have calculated the PCC signal (see Methods) for the output fields E₃ and E₄ of the beam splitter (see Fig. 1a) that contains all relevant field matter interactions (see Section S3 of SI) using the SD in HBL. It first assumes that the dephasing is much faster than the fluctuation timescale, i.e. 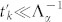, k = 1, 2, 3, 4. Second, if excitation pulse duration 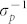and the inverse spectral 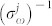, and temporal 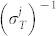, j = r, s gate bandwidths of the detectors and much shorter than the fluctuation time scales, one may neglect the dynamics during the delay between population evolution and its detection. Under these conditions the PCC signal is given by

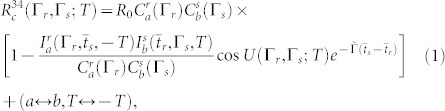where expressions in the last line represent permutation of the molecules a and b, 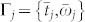represents a set of gating parameters for the detector j = r, s. C_α(Γ = {t, ω}) is the time-and-frequency resolved fluorescence of molecule α = a, b corresponding to diagram i in Fig. 1c:

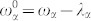is the mean absorption and fluorescence frequency. 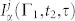and 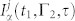with t₁ < t₂ are the interference contribution α = a, b, j = r, s corresponding to diagram ii in Fig. 1c

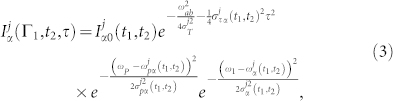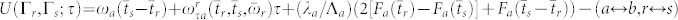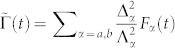, with 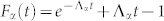, α = a, b and all the remaining parameters are listed in Eqs. (S24)–(S31) of the SI. The contribution of Eq. (2) enters signal in Eq. (1) as the amplitude square coming from each molecule in the presence of fluctuations. The interference term (3) generally cannot be recast as a product of two amplitudes²⁶. In the following we simulate the results of Eqs. (1)–(3) using the typical parameters of the TPI experiments⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰.

Variation of the HOM dip with gating

We first examine the effect of time and frequency gating on photon indistinguishability and PCC. In the absence of the SD and using identical detectors 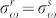, 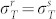the signal (1) for 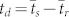is reduced to

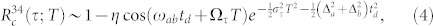where the parameters η, Ω_τ and σ_τ are given in Eqs. (S32)–(S35) of the SI. Eq. (4) is commonly derived in the field space alone by adding a phenomenological Gaussian function of the time delay¹. In the present analysis the Gaussian shape is characteristic to the harmonic bath.

Fig. 2a depicts Eq. (4) vs the delay between detectors 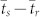for different values of the time gate bandwidth σ_T and fixed spectral gate bandwidth σ_ω. If the time gate bandwidth is smaller than the splitting 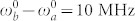the HOM dip is shallow and does not go below 1/2 which implies that photons generated by the two molecules are distinguishable. If the time gate bandwidth is larger than the splitting, the HOM dip drops below 1/2 indicating that the photons are indistinguishable. Similarly in Fig. 2b we fix the time gate bandwidth σ_T and vary the frequency gate σ_ω. As σ_ω is increased the photons gradually become more indistinguishable and the dip becomes larger. In the original HOM experiment¹ the PCC was plotted vs the delay T. Here we fix T and vary the delay between the detectors 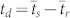. In the absence of fluctuations both T and t_d enter the signal (4) in a similar way. However once fluctuations are included Eq. (1), t_d is directly connected to fluctuations whereas the delay T is not. Below we study the PCC variation with t_d holding T fixed.

Figure 2. Effect of gating spectrograms on photon indistinguishability in the absence of spectral diffusion.

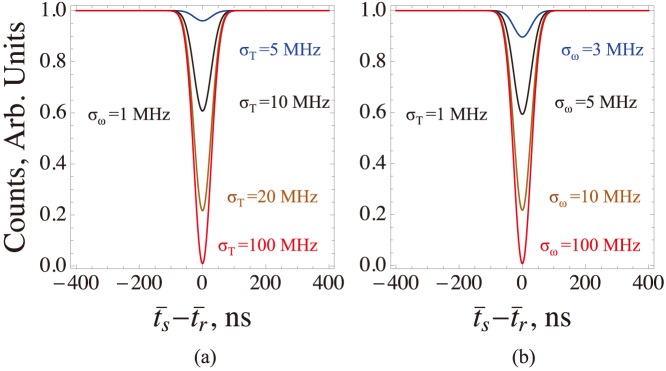
PCC signal for Λ_a = Λ_b = 0 given by Eq. (4) vs the delay between the detection for different values of the time - (a) and frequency - (b) gating bandwidths for the fixed frequency - (a) and time - (b) bandwidths, j = r, s. The parameters are chosen as 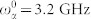, , 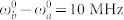T = 10 ns, σ_p = 3 MHz, Δ_a = Δ_b = 25 MHz, .

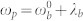Narrowband spectral filters are typically used in the experiments with broadband laser pulses. The broadband excitations degrade the quantum interference²⁷,²⁸,²⁹. This can be easily explained since the in addition to selecting a well defined frequency, the narrow frequency gate makes the ultrashort pulse longer and therefore two such photons are more likely to overlap in time and harder to distinguish, enhancing the HOM dip. In the present application we use narrowband excitation pulse and the degree of distinguishability is controlled by the interplay of spectral and temporal gating widths through the Wigner function. Therefore if the time gate is narrow, the broad frequency gate makes photons less distinguishable increasing the visibility of HOM dip.

Time-and-frequency resolved fluorescence with spectral diffusion

The simplest way to observe SD is by time-and-frequency resolved fluorescence. The molecular transition frequency is coupled linearly to an overdamped Brownian oscillator that represents the bath (see Fig. 1b). The absorption and emission lineshape functions for a pair of molecules are given by³⁰

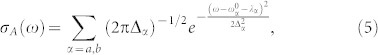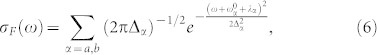where 2λ_α is the Stokes shift and 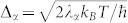is a linewidth parameter. Together with the relaxation rate Λ_α (see Eq. (11)) these parameters completely describe the SD model and govern the evolution of the emission linewidth between the initial time given by Eq. (5) (see Fig. 3a) and long time given by Eq. (6) (see Fig. 3b). Eqs. (5)–(6) are obtained in the slow nuclear dynamics limit: .

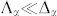Figure 3. Effect of SD on individual molecule emission lineshapes.

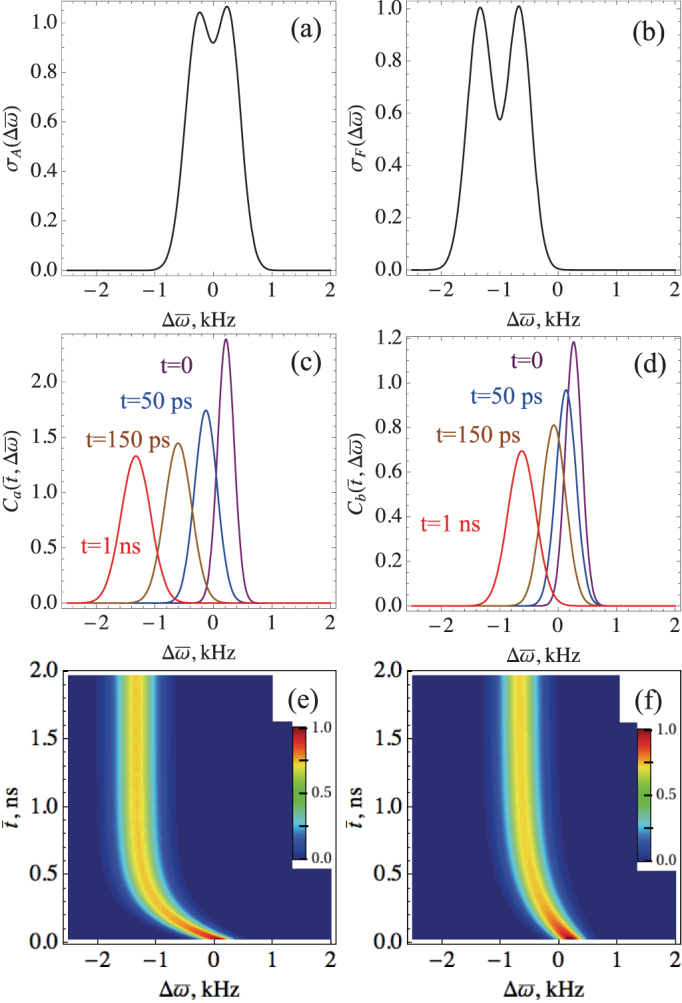
Absorption (5) - (a) and fluorescence (6) - (b) line shapes vs displaced frequency 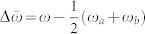. Time-and-frequency resolved fluorescence (2) displayed as a snapshot spectra for molecule a - (c) and b - (d) and depicted as a two-dimensional contour plot - (e) and (f), respectively. Parameters of the system are: 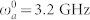, , 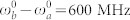Δ_a = 220 MHz, Δ_b = 205 MHz, Λ_a = 5 MHz, Λ_b = 3 MHz, 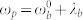, σ_p = 102 MHz, 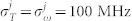, j = r, s, and the temperature is set to 10 K.

The time-and-frequency resolved fluorescence (Eq. (2)) is depicted as a series of the snapshot spectra at different times for molecule a in Fig. 3c. It shows a time dependent frequency redshift 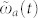and time dependent spectral broadening given by 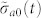(see Section S4 of SI). Initially 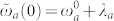whereas at long times 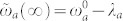, where 2λ_α is the Stokes shift. 2D representation of Eq. (2) is given in Fig. 3e. Fig. 3d and 3f show the same signals for molecule b. Because of the different reorganization energies λ_a, λ_b and relaxation rates Λ_a, Λ_b the Stokes shift dynamics and dispersion are different. Even when the absorption frequencies are the same ω_a = ω_b, the fluorescence can show a different profile due to SD. This affects the distinguishability of the emitted photons as will be demonstrated below.

Combined effect of gating and SD on the HOM dip

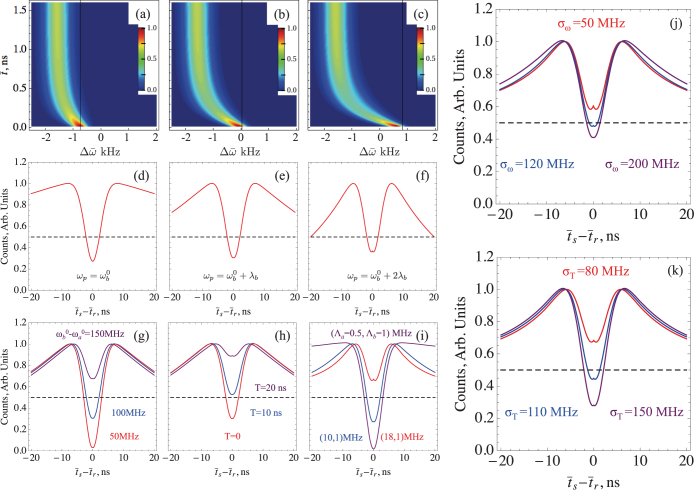
We depict the 2D fluorescence (2) in Fig. 4a. The vertical line marks the pump frequency 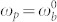- tuned midway between absorption and fluorescence at long time (see Eqs. (5-6)), the Stokes shift is ~1 kHz. Fig. 4b shows the same for 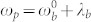where we have a larger Stokes shift ~2 kHz. At 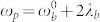the Stokes shift ~3 kHz as shown in Fig. 4c. Fig. 4d–f show the PCC signal (1) for the parameters corresponding to Fig. 4a–c, respectively. The HOM dip is less pronounced as the degree of indistinguishability drops from 0.275 - Fig. 4d, to 0.3 - Fig. 4e further to 0.375 in Fig. 4f.

Figure 4. The combined effect of SD and gating on photon indistinguishability.

Time-and-frequency resolved fluorescence from two molecules (vertical black line represents excitation frequency) - top row for different excitation frequencies: 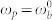- (a), 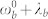- (b), 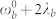- (c). The corresponding PCC signal vs delay between detector clicks: - (d) - (f) (middle row) for the values of the excitation frequencies in (a) - (c), respectively. Here 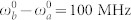, T = 1 ns, Λ_a = 5 MHz, Λ_b = 3 MHz. PCC for different transition energies of molecules excited at 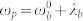- (g); PCC for different values of the delay T with 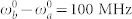- (h); PCC for different values of the SD time scale Λ_a and Λ_b and fixed linewidth Γ_a, Γ_b according to Eq. (12) - (i). Excitation pulse bandwidth σ_p = 102 MHz, gating bandwidths 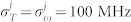, j = r, s, transition energies 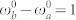. PCC for different frequency gate bandwidths - (j) at fixed time gate bandwidth σ_T = 100 MHz and for different time gate bandwidths - (k) at fixed frequency gate bandwidth σ_ω = 100 MHz. Molecules have distinct SD timescales Λ_a = 15 MHz, Λ_b = 1 MHz and .

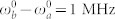The distinguishability is also affected by the molecular transition frequencies. Fig. 4g shows that for fixed time and frequency gate bandwidths 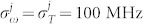, j = r, s the photons are distinguishabe as long as 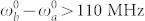and are indistinguishable otherwise. The effect of the time delay T caused by the position of the beam splitter is depicted in Fig. 4h. For T < 10 ns (>100 MHz bandwidth) the photons are indistinguishable, after that they become distinguishable. The SD timescale is one the key parameters affecting the degree of indistinguishability. Using Eq. (12) we fixed the absorption linewidth Γ_α and varied Λ_α and Δ_α. The PCC signal (1) depicted in Fig. 4i shows that if the molecules have nearly degenerate transition frequencies 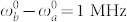for slower fluctuations Λ_a = 0.5 MHz, Λ_b = 1 MHz the photons are indistinguishable. Increasing the SD rate of one of the molecules increases the degree of distinguishability, e.g. for Λ_a = 10 MHz the HOM dip becomes 0.225, which is still less than classical 1/2 limit. However for fast SD Λ_a = 18 MHz, the HOM dip becomes 0.625 and photons are clearly distinguishable even though both time and frequency gates are broader than the difference in transition frequencies.

We further illustrate the effect of frequency and time gating in the presence of spectral diffusion. Fig. 4j shows that if two molecules have different SD timescales (Λ_a = 15 MHz and Λ_b = 1 MHz) and the frequency gate bandwidth is narrow (σ_ω = 50 MHz) the photons are rendered distinguishable and HOM dip is 0.6. By increasing the σ_ω the photons become indistinguishable and HOM dip is 0.48 for σ_ω = 120 MHz and 0.35 for σ_ω = 200 MHz. In all three cases we kept the time gate fixed at σ_T = 100 MHz. Alternatively we change the time gate bandwidth while keeping the frequency gate fixed at σ_ω = 100 MHz. Fig. 4k shows that initially indistinguishable photons at σ_T = 80 MHz with HOM dip 0.675 become indistinguishable at σ_T = 110 MHz with HOM dip 0.45 and at σ_T = 150 MHz with HOM dip 0.275. Thus, if the presence of the bath erodes the HOM dip the manipulation of the detection gating allows to preserve the quantum interference.

Discussion

To put our ideas into more practical perspective and connect with quantum processing technologies, we note that recent progress in long-term quantum memories using HBL where entanglement is achieved with telecom photons, proved the possibility of quantum internet³⁸,³⁹. Simultaneous time and frequency detection can be achieved using high-speed photodiode which converts fast optical signal into a fast electrical signal, fast oscilloscopes to observe the waveform, wide bandwidth spectrum analyzers and other elements. Short pulse characterization using time-frequency map such as frequency-resolved optical gating (FROG)⁴⁰, spectral phase interferometry for direct-field reconstruction (SPIDER)⁴¹ are well established tools for ultrafast metrology⁴²,⁴³. Extending these techniques to a single photon time and frequency resolved detection is challenging and can be achieved if combined with on-chip tunable detectors⁴⁴ or upconversion processes⁴⁵,⁴⁶.

In summary we have employed a time-ordered superoperator Green's function formalism to calculate the PCC from two remote emitters coupled to a bath. In the absence of a bath, time gating is sufficient to reveal quantum interference. Even if the emitters have well resolved transition frequencies with splitting Δω quantum interference manifests if the temporal resolution Δt is higher than 2π/Δω. Once the bath is included, time-and-frequency gating is necessary to resolve the dip. We showed how various model parameters affect the indistinguishability.

Methods

Coincidence measurements

The PCC signal is defined via the four point correlation function of the time-and-frequency gated electromagnetic fields E₃ and E₄ incident on the detector²²

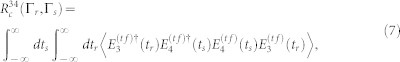where 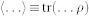is tracing with respect to ρ - the total field plus matter density operator. The fields in the output 3, 4 and input 1, 2 ports of the 50:50 beamsplitter are related by

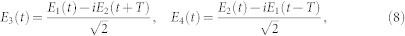where ±cT is small difference of path length in the two arms. In Section S1 and S3 of the SI we show that Eq. (7) may be recast as

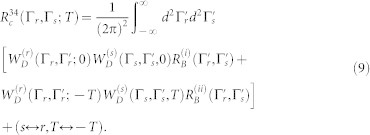Here 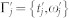represents the set of parameters of the matter plus field incident on the detector j = r, s. Eq. (9) is given by the spectral and temporal overlap of the Wigner spectrograms of detectors 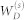, 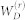Eqs. (S3) (Section S1) and bare signal pathways 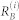and 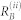(S12)–(S13) (Section S3) of SI. The detector provides a window of observation centered at time 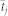and frequency 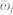, j = s, r. 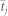and 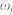can be varied independently. However the temporal 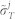and spectral 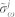resolutions are not independent and must satisfy 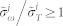²². We assume a point-size detector and omit all effects of spatial resolution only retaining temporal and spectral gating²⁵,⁴⁷.

Spectral diffusion

For an electronic system coupled to a harmonic bath the matter correlation function obtained by the second order cumulant expansion³⁰ (see Section S2 of SI)

where 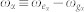is the absorption frequency, Φ_α(t₁, t₂, t₃, t₄) is the four-point lineshape function Φ_α(t₁, t₂, t₃, t₄) = −g_α(t₁ − t₂) − g_α(t₃ − t₄) + g_α(t₁ − t₃) − g_α(t₂ − t₃) + g_α(t₂ − t₄) − g_α(t₁ − t₄). We shall use the overdamped Brownian oscillator model for the spectral density. The lineshape function then depends on two parameters: the reorganization energy λ_α and the fluctuation relaxation rate Λ_α (see Section S2 of the SI) in the high temperature limit 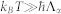we have

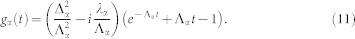For a given magnitude of fluctuations Δ_α, α = a, b the FWHM of the absorption linewidth³⁰

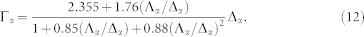Author Contributions

K.E.D. and S.M. designed the research and wrote the paper, K.E.D. performed the research.

Supplementary Material

Supplementary Information

Supplementary Information