Impact of Bulge Loop Size on DNA Triplet Repeat Domains: Implications for DNA Repair and Expansion

Abstract

Repetitive DNA sequences exhibit complex structural and energy landscapes, populated by metastable, non-canonical states, that favor expansion and deletion events correlated with disease phenotypes. To probe the origins of such genotype-phenotype linkages, we report the impact of sequence and repeat number on properties of (CNG) repeat bulge loops. We find the stability of duplexes with a repeat bulge loop is controlled by two opposing effects; a loop junction-dependent destabilization of the underlying double helix, and a self-structure dependent stabilization of the repeat bulge loop. For small bulge loops, destabilization of the underlying double helix overwhelms any favorable contribution from loop self-structure. As bulge loop size increases, the stabilizing loop structure contribution dominates. The role of sequence on repeat loop stability can be understood in terms of its impact on the opposing influences of junction formation and loop structure. The nature of the bulge loop affects the thermodynamics of these two contributions differently, resulting in unique differences in repeat size dependent minima in the overall enthalpy, entropy, and free energy changes. Our results define factors that control repeat bulge loop formation; knowledge required to understand how this helix imperfection is linked to DNA expansion, deletion, and disease phenotypes.

Introduction

Repetitive DNA sequences can adopt a variety of canonical and non-canonical DNA structures resulting in complex structural and energy landscapes with potentially profound biological consequences. In particular, the propensity of repeat sequences to adopt slipped-out bulge loop secondary structures has been implicated in DNA triplet repeat expansion and the associated DNA expansion diseases.^1–10 More than 30 known human diseases are attributed to the uncontrolled expansion of repeat DNA sequences.^11–14 It has been proposed that DNA repeat bulge loop structures are incorrectly recognized and processed by the DNA replication,^15–17 recombination^18–22 and repair machinery^{8, 23, 24} thereby causing DNA expansion to occur. In support of this view, a number of studies have shown incorrect processing of CAG/CTG-repeat secondary structures by reconstituted cell-free mismatch repair^25–28, double strand break repair,^{22, 29, 30} or base excision repair^{24, 31, 32} machineries leading to DNA expansion and deletion events in vitro. Recently, McMurray and coworkers also have shown in more detail that the conformational ensemble adopted by CAG repeat bulge loops traps a critical component of the mismatch repair system, the MSH2-MSH3 complex, in nonfunctional states.³³.

Using oligonucleotide based models, we³⁴ and others^35–38 have shown that repeat sequences can form bulge loop ensembles of closely related structures stabilized by intramolecular interactions between the loop bases. Reversion of these structures to the more stable duplex state is inhibited at ambient temperature but occurs at elevated temperature.^39–42 In other words, these bulge loops form metastable complexes that require input of external energy in order to revert to the more thermodynamically stable Watson-Crick duplex state. Moreover, these repeat loops are able to accommodate base lesions and repair intermediates disruptive to duplex DNA within the repeat domain without significant loss of stability, probably through readjustment of the ensemble of structures.^{43, 44} Recent reports have suggested that readjustment of repeat ensembles to reduce the energetic impact of lesions and repair intermediates favors DNA states that are less successfully processed by the DNA repair machinery than the same defects in conventional duplex DNA.^{38, 43, 45} These observations highlight the role of DNA damage and repair within or near slipped out DNA structures in favoring processes that may result in expansion events. More recently, the Pearson group has also drawn attention to the important role that repeat loop/duplex junctions may play in modulating repair processes and inducing expansion or deletion events.⁴⁶ Evidence is also accumulating on the importance of neighboring duplex domains on repeat loop stability.^{8, 47–49} When the slipped-out repeat loop is located within larger repeat sequence domains, the same bulge loop can be in multiple positions with relatively facile loop migration between these positions, thereby providing an additional entropic driving force stabilizing the bulge loop structures.⁴⁵ The presence of base lesions or repair intermediates influences the distribution and migration of slipped out repeat loops within larger repeat domains. Such Boltzman conformational entropy contributions due to multiple loop arrangements may contribute to the repeat size dependence of expansion events,⁵⁰ where DNA expansion becomes inevitable for repeat numbers ≥ 35 for most triplet repeat sequences.^{1, 3, 4}

The role of triplet repeat bulge loop structures in expansion processes is now well recognized. However, insights into the forces that stabilize repeat loop structures, and what causes such structures to facilitate DNA expansions or deletions, remain sparse. Experimental results for single strand (CNG)_n repeat oligonucleotides show a length dependence behavior for the thermal and thermodynamic properties of the CNG repeat self structure, consistent with longer repeat structures facilitating expansion events.^51–55 An intriguing pattern of even versus odd repeat number dependence in the thermodynamic properties of isolated repeats has been observed which may play a role in the formation and processing of repeat structures.^56–58 It has been suggested that the nature of the repeat loop changes with size. In this view, smaller repeat bulge loops (fewer than ~8 repeats/24 nucleotides) are more open and solvent accessible than larger repeat loops that are supposed to more closely resemble hairpin like structures.^{35, 36} Single base bulges and small non-repeat loops comprising a few bases are very disruptive to DNA stability and are generally repaired efficiently.⁵⁹ Smaller triplet repeat loops also appear to be more readily repaired than larger repeat bulge loops,^{25, 60, 61} possibly due to differences in the repair pathways involved.

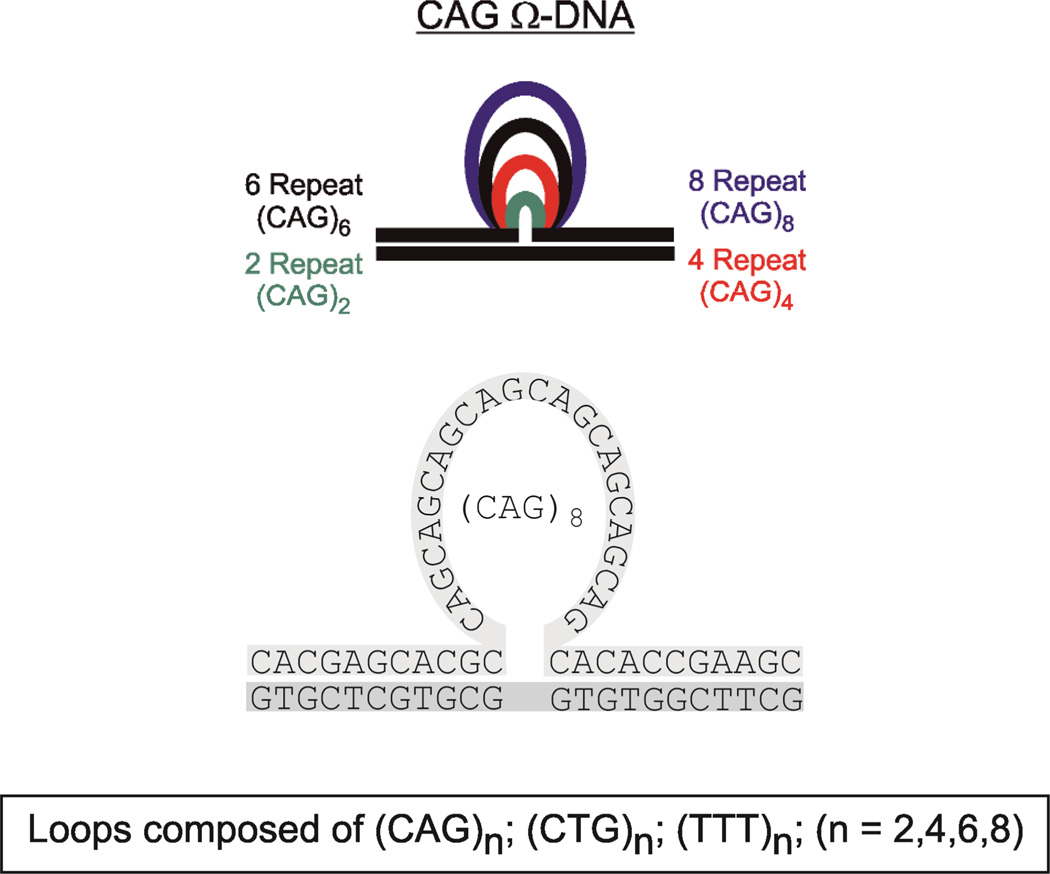
To better understand how repeat loop size, sequence, and number of repeats affect repeat bulge loop properties, we report here a systematic calorimetric and circular dichroism (CD) investigation of the thermodynamic impact of CAG and CTG Ω-DNA repeat bulge loops of variable size, as outlined in scheme 1. We find that the thermodynamic impact of repeat bulge loop size can be understood in terms of two opposing contributions; namely, a destabilizing contribution due to disruption of, or strain on, the underlying double helix associated with duplex-loop junction formation; and a counteracting stabilization due to loop self-structure. It is the relative impact of these opposing influences that determines the properties of a given repeat bulge loop.

Scheme 1.

Schematic representation of the constructs and sequences studied. The example shown is for the CAG repeat bulge loop. The CTG repeat bulge loop is located in the opposing strand.

Materials and Methods

Materials

Oligonucleotides were synthesized on a 10µmole scale by standard phosphoramidite chemistry using an Äkta DNA synthesizer, and were purified by DMT on and subsequent repeated DMT off reverse phase HPLC, as previously described.^{62, 63} The purities of the oligonucleotides were assessed by analytical HPLC and ion spray mass spectroscopy, and were found to be pure by analytical HPLC and better than 98% pure by mass spectroscopy. Purified oligonucleotides where dialyzed using dispo-dialyzers with MWCO 500 Da (Spectrum, CA) against at least two changes of pH 6.8 buffer containing 10 mM Cacodylic acid/Na-Cacodylate, and 0.1 mM Na₂ EDTA and sufficient NaCl to yield a final concentration of 100 mM in Na⁺ ions. Molar extinction coefficients of the parent DNA oligomers lacking repeats ((CAG)₀, (CTG)₀) were determined by phosphate assay under denaturing conditions (90°C)^{64, 65} and were found to be:; ε_{(CAG)0 (260nm, 90°C)}= 190400 M⁻¹ cm⁻¹; ε_{(CTG)0 (260nm, 90°C)}= 186200 M⁻¹ cm⁻¹. For all other oligonucleotides, extinction coefficients were determined from continuous variation titrations (Job plots)⁶⁶ with the complementary parent oligonucleotide, and were found to be: ε _{(CAG)2 (260nm, 90°C)}= 251400 M⁻¹ cm⁻¹; ε_{(CAG)4 (260nm, 90°C)}= 315500 M⁻¹ cm⁻¹; ε_{(CAG)6 (260nm, 90°C)}= 368400 M⁻¹ cm⁻¹; ε_{(CAG)8 (260nm, 90°C)}= 424900 M⁻¹ cm⁻¹; ε_{(CTG)2 (260nm, 90°C)}= 221700 M⁻¹ cm⁻¹; ε_{(CTG)4 (260nm, 90°C)}= 271100 M⁻¹ cm⁻¹; ε_{(CTG)6 (260nm, 90°C)}= 342900 M⁻¹ cm⁻¹; ε_{(CTG)8 (260nm, 90°C)}= 380500 M⁻¹ cm⁻¹.

DSC studies

DSC studies were conducted as previously described using a NanoDSCII differential scanning calorimeter (Calorimetry Science Corporation, Utah) with a nominal cell volume of 0.3 ml.^{34, 67, 68} Oligonucleotides, at a concentration of 50 µM in strand, were repeatedly scanned between 0°C and 90 or 95 °C with a constant heating rate of 1°C /min, while continuously recording the excess power required to maintain sample and reference cells at the same temperature. After conversion of the measured excess power values to heat capacity units (cal/K) and subtractions of buffer vs. buffer scans, the raw DSC traces were normalized for DNA concentration and analyzed using Origin software. The calorimetric enthalpy (ΔH_cal) was derived by integration of the excess heat capacity curve, and ΔC_p was derived from the difference in the linearly extrapolated pre- and post-transition baselines at T_m. ΔS was derived by ΔH/T_m, assuming “pseudomonomolecular” dissociation behavior in which propagation dominates initiation.^{69, 70} The T_m is defined as the temperature at the midpoint of the integrated excess heat capacity curve for a given conformational transition, which corresponds to half the sample being denatured for a process that exhibits pseudomonomolecularity. We fit the experimental excess heat capacity curves of our Ω-DNA’s to a model for 2 independent, two-state transitions as previously described.^{43, 47, 48, 48, 71, 72} We find that we can obtain good agreement between the experimental curves and the fitted curves for all Ω-DNA constructs with the repeat loops.

Circular Dichroism studies

CD spectra were recorded as a function of temperature using an AVIV model 400 spectropolarimeter (Aviv Biomedical, Lakewood, NJ). Spectra were recorded with an averaging time of 10 sec using a 1mm path length cell from 340 nm to 205 nm in steps of 1 nm between 0°C and 95°C in 5°C intervals. After subtraction of buffer scans recorded at corresponding temperatures, spectra were normalized for DNA concentration as previously described^{34, 63} and analyzed further. Oligonucleotide concentrations were 10µM in strand.

UV absorption studies

UV spectra and temperature dependent changes in UV absorbance were measured using an AVIV model 400 UV/VIS spectrophotometer (Aviv Biomedical, Lakewood, NJ). Temperature dependent changes in absorbance at 260 nm with a 1 nm bandwidth were recorded with an averaging time of 5 sec while the temperature was raised in steps of 0.5°C with 1 minute equilibration time. Oligonucleotide concentrations were 1.5 or 2 µM in strand.

Results and Discussion

The Impact of Loop Size and Sequence on CNG Repeat Bulge Loop Optical Properties

The CD spectroscopic signature for repeat bulge loops is nearly independent of loop size

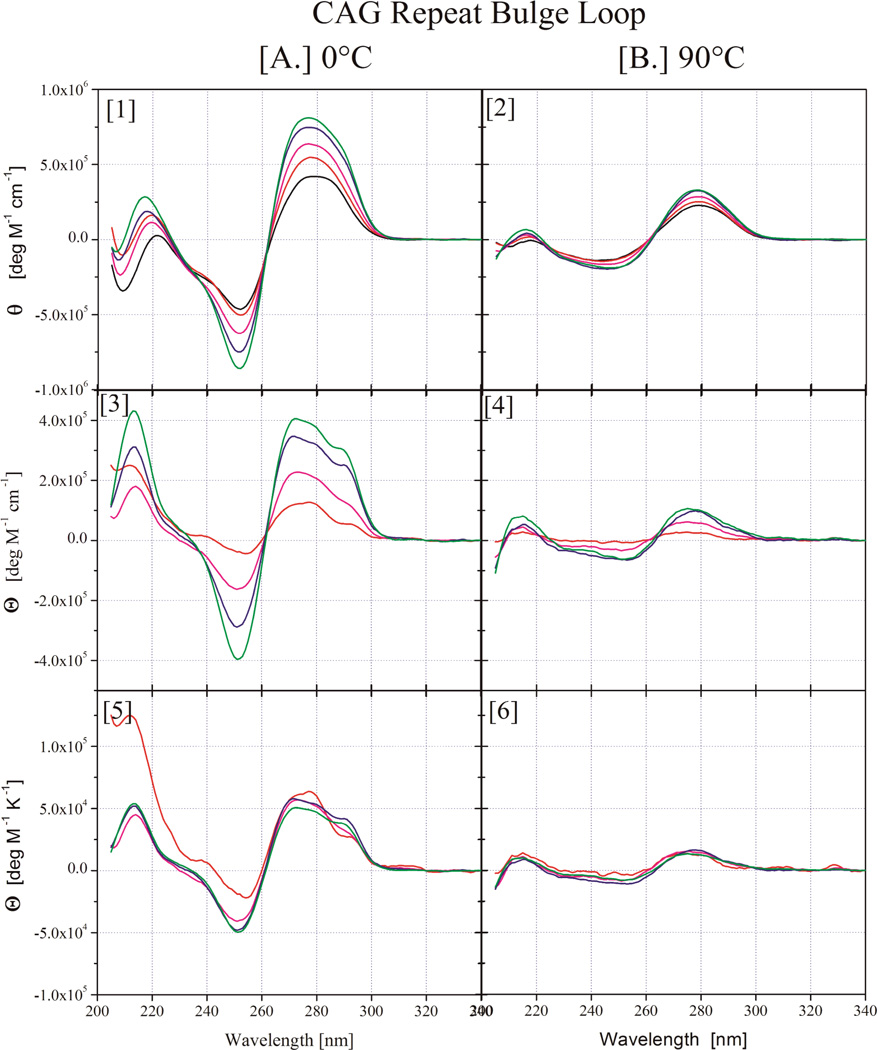
To understand how loop size affects repeat loop properties, we investigated the spectroscopic and thermodynamic properties of bulge loops with increasing numbers of (CNG)_n repeats (n=2,4,6,8). This range of repeat bulge loop sizes includes those for which an altered, more open state relative to larger loops has been postulated.³⁵ To avoid potential complications due to differential even versus odd repeat number behavior,^{56, 57} we focus only on loops with an even number of repeats. We used CD spectroscopy under native and denaturing conditions to assess how an increase in the number of repeats within the bulge loop domain impacts the overall DNA structure. The resulting data for the (CAG)_n (n=0,2,4,6,8) family of bulge loop Ω-DNA constructs in their native conditions (at 0°C, panel A (1)) and denaturing conditions (90°C, panel B(2)) are shown in Figure 1. Corresponding CD spectra for the (CTG)_n and (TTT)_n families of bulge loop Ω-DNA constructs are found in the Supplementary Information section.

Figure 1.

CD spectra for Ω-DNA bulge loop structures with increasing number of CAG repeats. ((CAG)₂ - red,(CAG)₄ - purple, (CAG)₆ - blue, (CAG)₈ - green, the parent 22mer duplex lacking a bulge loop is shown in black). In panels 1 & 2 the measured experimental data are shown, whereas panels 3 & 4 show the residual spectra after subtraction of the parent duplex contribution and panels 5 & 6 show the normalized residual spectra after normalization by the number of repeats in the loop domain. The native state spectra at 0°C are grouped together in Column A, whereas the denatured state spectra at 90°C are displayed in Column B.

The family of (TTT)_n bulge loops acts as model for bulge loops with an unstructured loop domain of equivalent size to that of the (CNG)_n repeat bulge loops in our CD^{73, 74} and DSC studies.⁷⁵

The overall spectral features of a given repeat sequence remain essentially the same for all loop sizes, consistent with no major impact of loop size on global conformation

The detailed spectral properties for a given repeat loop size differ subtly for different repeat sequences, likely reflecting the different optical properties of the bases and possibly subtle differences in loop or junction structure. The primary repeat size induced difference is a change in the intensities of the maxima and minima with increasing repeat number, reflective of the CD absorption of the additional bases in the construct. To compare results for constructs with different loop sizes, we subtracted from each CD spectrum the CD spectrum of the 22mer parent lacking a bulge loop ((CAG)₀) (Panel A(3) and Panel B(4)) and dividing by the number of repeats in the loop, thereby generating a set of ‘normalized residual spectra’ shown in Panel A (5) and Panel B (6). In so doing, we assume that the double helical domain and junction structure remain unchanged as a function of loop size and assign all bulge loop induced alterations in duplex CD spectra (e.g. possible DNA bending, altered base pairing at the duplex loop junctions) to the spectral contributions of the repeat bulge loop. Using this approach diminishes the impact of the junction and helix-turn on the CD spectra as the number of repeats increases. This approach is justified by the observation that normalized residual CD spectra under denaturing conditions at 90°C for all repeats are indistinguishable within experimental noise. The 90°C spectra solely reflect the contributions from the additional bases in the constructs with larger number of repeats absent any contribution from DNA structure. This approach is further justified by the observation that the native normalized residual CD spectra for the all-T bulge loop containing construct becomes increasingly similar to that of poly T with increasing loop size, as the relative contribution of the junction to the spectrum diminishes. Large T-loops are considered to approximate random coil like behavior.^76–79 Hence the CD spectrum should become increasingly similar to that of the random coil like poly T polymer as the loop size increases, as is indeed observed. We also note that the resultant normalized residual CD spectra for the (CNG)_n repeat loops show close similarities to the CD spectra recorded for isolated single stranded (CNG)_n repeats reported by Sheardy and coworkers.^{52, 53}

Significantly, the normalized residual native CD spectra (Figure 1, Panel A (5)) are essentially identical in shape and intensity for a given repeat for all repeat numbers larger then n=2. By contrast, for each 2 repeat loop construct (CAG)₂ (Figure 1, Panel A (5)), (CTG)₂, and (TTT)₂, (supplementary materials) we observe small differences in the normalized residual CD spectra, manifest predominantly in the low wavelength range of the spectra. The observed deviations from a uniform spectral contribution from insertion of 2 repeat units for the smallest repeat bulge loops (n=2/6 nucleotides) likely reflects structural adjustments to accommodate the small repeat loop size. These will be discussed in more detail below. For repeats larger than n=2/6 nucleotides, the CD data strongly suggest that the repeat loops adopt the same overall structure, insofar as this global feature can be assessed by CD spectroscopy.

The Impact of Loop Size and Sequence on CNG Repeat Bulge Loop Thermodynamic Properties

Calorimetrically Determined Melting Transitions

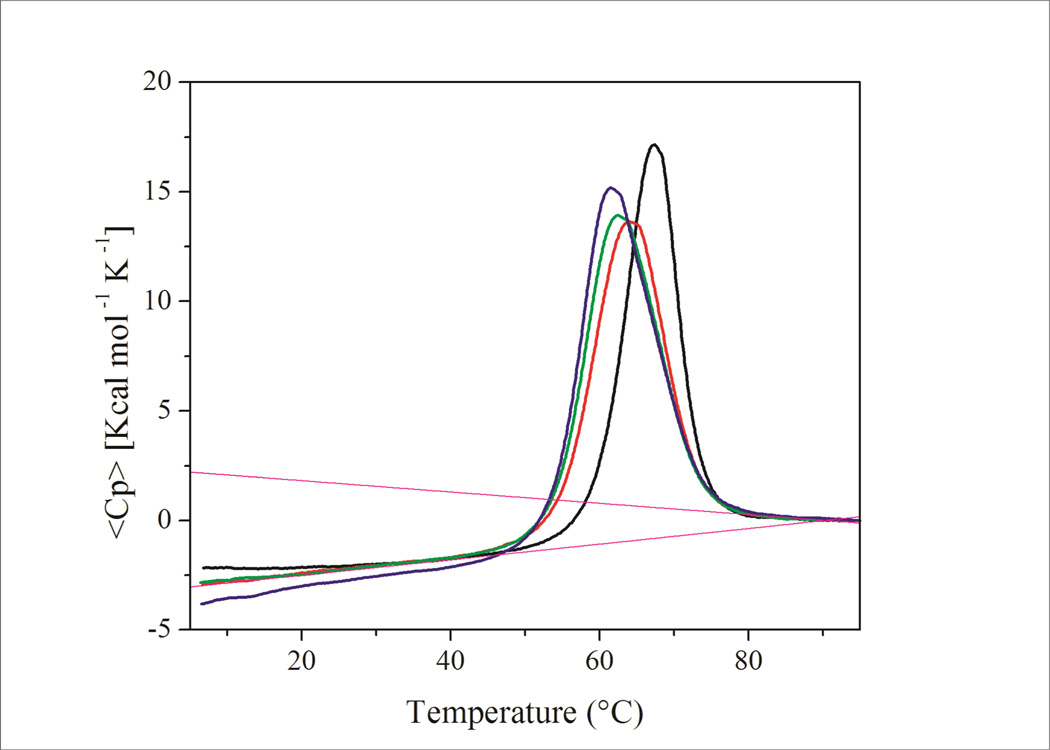
Excess heat capacity data for (CAG)_n repeats (n=2,4,6,8) are shown in Figure 2. Corresponding results for the (CTG)_n and (TTT)_n families of repeat bulge loop constructs are shown in the Supplementary Information section. The corresponding thermodynamic data derived from these excess heat capacity curves are listed in Table 1.

FIGURE 2.

Excess heat capacity curves for Ω-DNA constructs with increasing number of CAG repeats in the loop domain. (CAG)₂ – black, (CAG)₄ – red, (CAG)₆ – green, (CAG)₈ – blue. Average pre and post transition baselines are indicated by stippled lines in magenta. Note the clear indication of a heat capacity change at T_m for all constructs.

Table 1.

Thermodynamic data for different repeat bulge loop sizes:

Oligomer* Complex	Tm [°C]	ΔHcal [kcal mol−1]	ΔScal** [cal mol−1 K−1]	ΔCp [cal mol−1 K−1]	ΔGcal25°C [kcal mol−1]
CAG0·CTG0 duplex	79.1	173.4	492.3 ± 24	1100	21.8
CAG- loops
CAG2·CTG0	67.0	160.1	470.5	1260	16.4
CAG4·CTG0	63.7	164.3	487.7	1390	15.6
CAG6·CTG0	62.3	171.6	511.6	1540	15.7
CAG8·CTG0	61.3	192.2	574.6	1750	17.3
CTG-loops
CTG2·CAG0	67.1	157.4	462.7	380	18.5
CTG4·CAG0	63.1	162.3	482.7	890	16.4
CTG6·CAG0	61.9	185.5	553.6	1170	17.9
CTG8·CAG0	62.2	208.0	620.1	1570	19.7
T-loops***
T2·CTG0	65.2	155.2	458.2	1060	15.8
T4·CTG0	60.5	148.8	446.1	1330	13.2
T6·CTG0 ***	58.6	139.1	419.3	730	12.8
T8·CTG0	56.2	137.1	416.3	1230	11.1
				Ave 1090 ± 260

^*We estimate experimental errors to be T_m≈0.3°C, ΔH ≈ 2.5%, ΔS≈5% and ΔC_p ≈20%

^**Entropy values determined for pseudo-monomolecular process for Ct =50 µM, as bulge loops of different loop size show variable concentration dependence of Tm. To correct for bimolecular process a mixing term of 21.5 cal mol⁻¹ K⁻¹ needs to be added to the reported value.

^***These all T-bulge loops also form the basis of the DNA meter concept.^{97, 97}

^****Larger error for T6·CTG0 due to older commercially synthesized sample that was less well purified.

Inspection of Figure 2 reveals an intriguing trend in melting behavior of the (CAG)_n constructs. With increasing loop size, the melting curves for (CAG)₄, (CAG)₆ and (CAG)₈ reveal a trend of decreasing melting temperatures, but increasing peak area. The excess heat capacity curve for the construct with the (CAG)₂ repeat loop is visually distinct, showing a sharper melting transition at higher temperature. These observations correlate with the CD spectral changes discussed above. We detect very similar pre- and post-transition baselines and a distinct heat capacity change, ΔC_p at T_m, for all (CAG)_n constructs.^{34, 80–83} The same general trend is also observed for the (CTG)_n repeat loops. In the following sections, we dissect these excess heat capacity curves and the associated thermodynamic data.

Deconvolution of the Excess Heat Capacity Curves

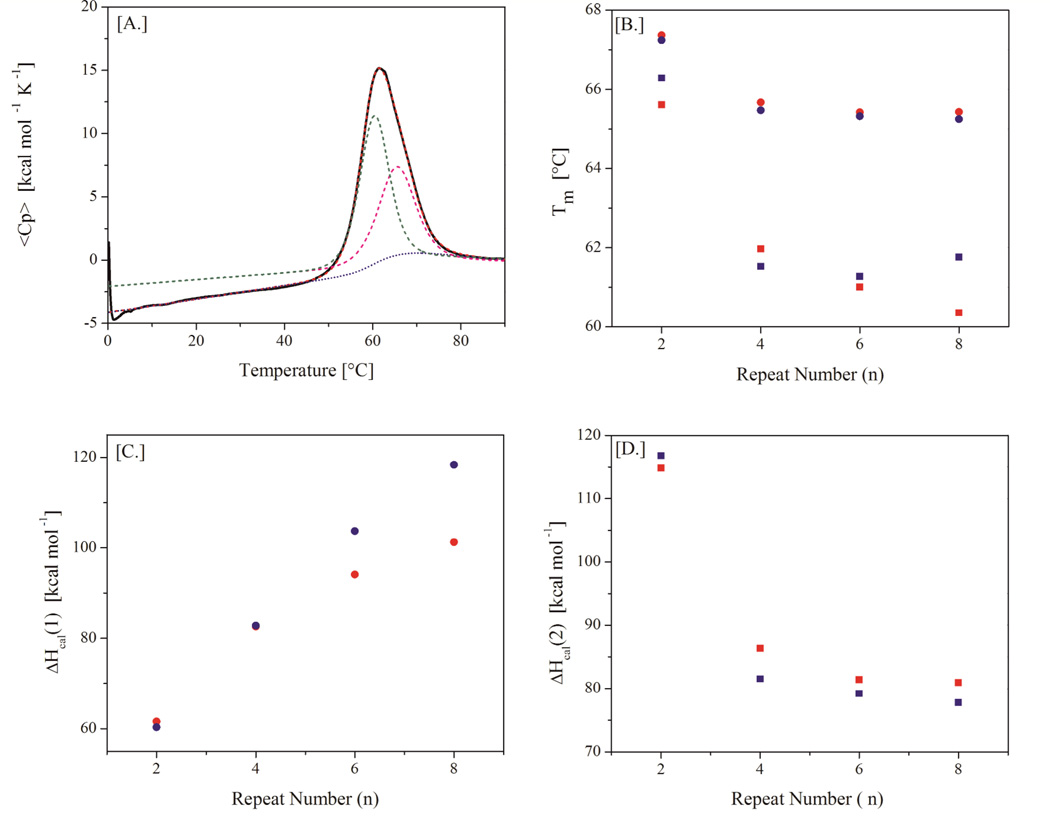
To extract the information embedded in these excess heat capacity curves, we apply the general allosteric state model of Wyman and Gill to deconvolute individual melting curves into their component two-state subtransitions.^{71, 72} While visual inspection suggests a single melting transition, we previously have shown that the calorimetric melting curve of the (CAG)₆ Ω-DNA bulge loop construct, with or without base lesions, cannot adequately be described in terms of a simple two-state transition.^{43, 47, 48} Instead, a model with at least two independent two-state transitions with significant ΔCp changes is needed to describe the DSC thermogram for that construct. Here we find that this two independent two-state transition model describes satisfactorily the melting curves of all the bulge loop constructs. A model dependent analysis of excess heat capacity curves of 3-way DNA junctions yields a similar deconvolution into two component transitions as we observe here for our bulge loop constructs.⁸⁴ Inspection of Figure 3 shows that the melting temperatures and enthalpies assigned to the two transitions exhibit intriguing dependencies on loop size.

FIGURE 3.

A–D: Deconvolution of the Ω-DNA excess heat capacity curves shown by the example of (CAG)₈ (panel A).The T_m’s (panel B) and enthalpy changes (panels C & D) of the two deconvoluted subtransitions are plotted against repeat loop size for CAG (red) and CTG (blue). While the T_m of the 1^st deconvoluted subtransition (circle) monotonically decrease with loop size, the enthalpy change for this transition monotonically increases over the range of loop sizes investigated. By contrast, the T_m and enthalpy change of the 2^nd subtransition (square) approach limiting values with increasing loop size for both CAG and CTG repeats.

Specifically, we find that only the low temperature fitted transition reflects contributions from an increase in the repeat loop size. We observe a decrease in the melting temperature coupled with an increase in the enthalpy change for this transition as a function of increasing loop size. Differences between CTG and CAG repeat loops are reflected predominantly in the enthalpy change for the low temperature fitted transition. Loop size dependent entropy change must be responsible for the observed decrease in T_m despite increasing enthalpy change. By contrast, with increasing loop size the melting temperature and enthalpy change for the second fitted transition (high temperature transition) asymptotically approach limiting values (T*= 65°C; ΔH*=78–80kcal/mol), independent of repeat loop composition. Intriguingly, this limiting enthalpy change is close to that measured for the isolated upstream 11mer duplex arm of our Ω-DNA construct (unpublished data), which is the more stable of the two duplex arms. It appears that the final melting step is increasingly dominated by dissociation of the upstream duplex arm as the loop size increases. Thus, while the Wyman and Gill model postulates discrete energy states and does not invoke specific structural transitions, taken together our data suggest a structural model; namely, the first (low temperature) part of the melting transition being dominated by the coupled melting of the less stable arm and the repeat loop, followed by the upper, high temperature part of the transition being dominated by subsequent melting of the more stable upstream duplex arm. For small loop sizes, the two two-state transitions overlap substantially and are un-resolvable in the deconvolution. With increasing loop size, the two component transitions are increasingly resolved. The overlap of the two transitions for small loop sizes explains the altered appearance of the (CNG)₂ DSC curves and the CD spectral differences relative to those of larger bulge loops. This sequential denaturation model also successfully describes the differential effects of upstream and downstream lesions on the melting of the repeat bulge loops^{43, 47} and for the melting behavior of (CNG)_n repeat loop rollamers⁴⁵ within larger repeat sequence domains, providing yet another demonstration of the importance of neighboring duplex domains on repeat loop stability.^{8, 47–49}

Analysis of the thermodynamic data

T_m measurements alone mask fundamental distinctions: Calorimetric measurements reveal repeat bulge loops to exhibit size and sequence dependent differential enthalpy, entropy, and free energy changes that pass through minima, even while the T_m decreases monotonically over the entire range of repeat loop sizes studied

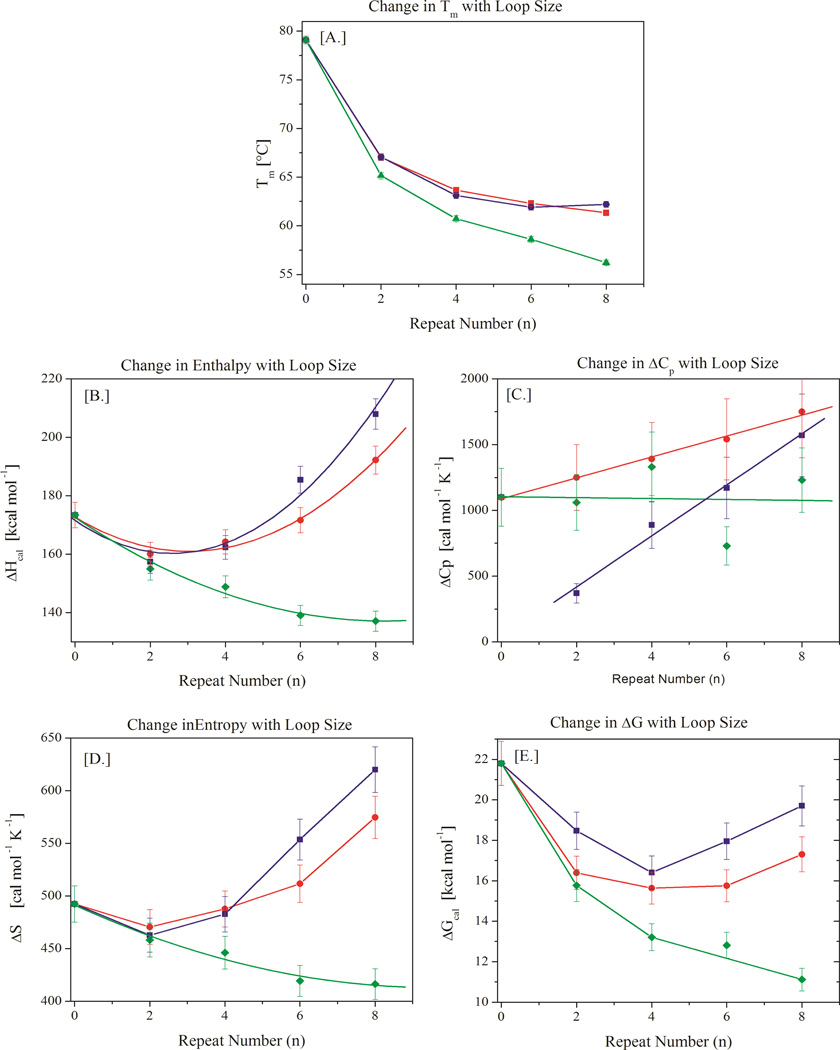
The experimentally determined, model-independent thermodynamic data listed in Table 1 are summarized graphically in Figure 4. We find that with increasing loop size the apparent melting temperature for the (CNG)_n constructs decreases monotonically (Fig 4A). The decrease in T_m is less pronounced for (CAG)_n and (CTG)_n than for unstructured bulge loops comprising only thymidines, (TTT)_n. There is also some indication that the T_m for (CNG)_n loops may increase for loop sizes larger than n=8/24 nucleotides; however, this cannot be confirmed with the current data set. Interestingly, there is very little difference in T_m between CAG repeats and CTG repeats. We have previously made a similar observation for hairpins with repeat loops,⁴¹ which contrasts with the reported behavior of single-stranded (CNG)_n repeats in isolation.^51–55

FIGURE 4.

A–E: Variation in thermal (T_m - panel A) and thermodynamic parameters (ΔH – panel B, ΔC_p – panel C, ΔS - panel D, and ΔG – panel E) with increasing loop size for CAG repeat bulge loops (blue), CTG repeat bulge loops (red), and TTT repeat bulge loops (green). Note the monotonic decrease in T_m in panel A despite the presence of distinct minima in the thermodynamic state functions displayed in panels B, D, and E.

In contrast to the monotonic decrease in T_m with loop size, the enthalpy change (Fig 4B) and entropy change (Fig 4D) values for the (CNG)_n repeats exhibit minima at n=2 repeats/6 nucleotides. The observed heat capacity changes for (CTG)_n and (CAG)_n increase linearly with loop size (Fig 4B), albeit with different slopes for CTG and CAG repeats. For small repeat loop sizes, the CTG repeat is marginally less enthalpic and entropic than the CAG repeat, while for larger repeat loop sizes the trend reverses. The changeover occurs near 4 repeats/12 nucleotides. This observation is unexpected as heretofore it has generally been assumed that CTG repeat structures are much more enthalpic than CAG repeat structures of corresponding size.^{42, 51, 53–55, 85} For comparison the enthalpy and entropy changes observed for the all-T bulge loop constructs decrease monotonically and there is no discernible change in heat capacity with increasing loop size, as expected for unstructured loops.^86–90 Similarly, the free energy change also passes through a minimum at n=4 repeats for both (CAG)_n and (CTG)_n constructs (Fig 4E). However, unlike the enthalpy and entropy changes, the free energy change for the (CTG)_n constructs is always larger than that of the (CAG)_n constructs, reflecting the impact of the difference in heat capacity change. As expected, the free energy change for the (TTT)_n constructs decreases monotonically with increasing loop size. Whereas for the all-T bulge loops T_m, enthalpy, entropy and free energy changes all vary in the same direction with increasing loop size, the repeat bulge loops reveal the unexpected feature of the enthalpy, entropy, and free energy changes passing through minima, while the T_m decreases monotonously over the entire range of repeat loop sizes studied. Moreover, the minima in the thermodynamic state functions occur at different loop sizes, depending on the state function. We note in passing that simple T_m measurements, which are often reported as proxies for DNA stability, would not have revealed these intriguing complexities. It is only when one analyzes the complete thermodynamic profile derived by means of directly measured calorimetric data that these unanticipated patterns become evident.

Small repeat bulge loops (≤ 2 repeats/6 nucleotides) are largely unstructured and show similarities to small T bulge loops (≤ 6 nucleotides) in their thermodynamic properties

To understand the complex dependences of thermal properties and thermodynamic state functions on bulge loop size, we note that the dependences of T_m, enthalpy, and entropy changes for small CAG and CTG repeat bulge loops mimic similar dependences for the all T-bulge loop controls. Previous work on all-T hairpin loops suggested that for T loops with fewer than 4 or 5 thymidines the stability of the complex is dominated by the enthalpic cost of disrupting the underlying duplex to accommodate the loop.^{86, 91–93} For T hairpin loops larger than 4 or 5 thymidines, changes in loop stability become primarily entropic in origin, reflecting the greater number of degrees of freedom for these unstructured loops and the absence of significant steric constraints.^{78, 79, 90, 94, 95} Bulge loops are not the same as hairpin loops, and we do detect a small loop size dependence of the enthalpy change up to a loop size of 24 thymidines ((TTT)₈). However, to a first approximation, we can assume that the same loop size dependence described for all-T hairpin loops also applies to our all-T bulge loops with loop size 6 nucleotides and larger. Indeed we find the loop size dependence on stability for bulge loop sizes larger than 6 thymidines to be predominantly entropic, with a roughly constant enthalpic contribution due to disruption of the duplex hosting the bulge loop. The similarity in the thermal and thermodynamic behavior of small repeat bulge loops and similar sized all-T bulge loops suggests that these same forces also dominate the thermodynamic properties of the repeat loops, although here the reasoning is different. The assumption of a largely unstructured small repeat bulge loop can be understood when one considers the results of foot printing studies^{38, 44, 56} that indicate a preference for NGCN turns comprising two of the three bases (NG and CN) from two adjacent repeat units in (CNG)_n repeats. If such a turn were to form for (CNG)₂, only one C and one G would be available to form additional interactions at the junction between the duplex and the turn - too little to be stable. The opposing tendency to optimize the turn and to form base pairing interactions likely result in the ensembles of small (CNG) loop structures to be predominantly unpaired. As a consequence, the thermodynamic properties of the small (CNG) bulge loops are likely dominated by the disruption of the duplex structure with little repeat loop self structure, similar to what we observe for the all-T bulge loop. In support of this view, we note that the observed changes in the CD spectra for (CNG)₂ discussed above are consistent with a disrupted or strained bulge loop state.

In contrast to large all-T bulge loops (>6 nucleotides), large repeat bulge loops (> 2 repeats/6 nucleotides) are stabilized by enthalpically favorable intra-loop interactions

By contrast to the small repeat bulge loops discussed above, as the number of repeats increases, it becomes progressively easier to form more and more of the intra-loop interactions that make up the repeat self-structure without disrupting the preferred turn and/or base pairing at the junction. Formation of an increasing amount of these repeat intra-loop interactions is stabilizing, so that the thermodynamics becomes increasingly dominated by the stabilizing contributions from repeat loop self-structure formation as the loop size increases. This assertion is supported by the CD data for larger bulge loop sizes discussed above. It is the interplay of these two opposing thermodynamic driving forces that cause the thermodynamic state functions for repeat bulge loops to go through minima as the number of repeats increases.

Forming a duplex/bulge loop junction is energetically costly while adding additional repeat units is energetically favorable

One of the consequences of the interplay between opposing forces is that one can estimate the incremental thermodynamic contributions of individual repeat units and the thermodynamic impacts of forming a bulge loop junction in the underlying duplex. The expectation for such an analysis is that, as the number of repeats increases, the thermodynamic data are increasingly dominated by contributions from the repeat self structure, with contributions from the junction and the turn becoming less significant. The incremental contribution of the repeat unit is estimated from the slope of the tangent of the thermodynamic parameter plotted as a function of loop size. The contributions of a “virtual’ bulge loop junction (e.g. a loop of 0 repeats) are estimated by extrapolation to 0 loop size and subtracting the measured values for the 22mer duplex. While the limited number of data points here restricts the precision of these estimates, we find that for larger bulge loop sizes the change in enthalpy becomes linear with increasing repeat number. From the tangent to the data we derive enthalpy change values of repeat self structure formation of approximately ΔH ≈ −11.4 kcal mol⁻¹ per CTG repeat and ΔH ≈ −7.0 kcal mol⁻¹ per CAG repeat. We also derive the corresponding entropy change values of approximately ΔS ≈ −34.5 cal mol⁻¹ K⁻¹ per CTG repeat and ΔS ≈ −21.7 cal mol⁻¹ K⁻¹ per CAG repeats. These values are somewhat larger than those we previously estimated from studies on triplet repeat hairpin data⁴¹, quite likely reflecting different underlying assumptions and methods of analysis. As expected, the enthalpy and entropy change values for CTG self structure are larger than those for CAG self structure. We also derive relatively unfavorable “virtual” junction formation enthalpies and entropies of ΔH≈ 40 kcal mol⁻¹, ΔS≈ 98 cal mol⁻¹ K⁻¹ for CAG, and ΔH≈ 56 kcal mol⁻¹, ΔS≈146 cal mol⁻¹ K⁻¹ for CTG from the difference in the intercept at 0 repeat number and the 22mer duplex enthalpy and entropy changes. The differences in these extrapolated junction enthalpy and entropy changes reflect differences in junction type for CAG and CTG repeat loops, as well as uncertainty in the extrapolation. We note that the repeat bulge loops in our constructs are located in complementary strands, such that the C·G base pairs are adjacent to the CAG bulge loop, whereas those adjacent to the GTC bulge loop are G·C base pairs. This observation reinforces recent views about the importance of the junction for repeat loop stability.⁴⁶ It is the larger cost of forming the CTG junction that is primarily responsible for the observed unexpected lower enthalpy change for small CTG bulge loops compared to CAG repeat bulge loops discussed above.

Repeat bulge loops, on either or both strands, are less stable than canonical repeat duplex DNA

We find that the experimentally determined enthalpy, entropy, and free energy changes for the corresponding family of duplexes with increasing number of (CAG)_n·(CTG)_n base pairs increase in close accordance with predictions from nearest neighbor models (Supplementary Information).

These values of thermodynamic functions for the duplexes are significantly larger than the sum of the corresponding repeat bulge loop values (ΔX_(CAG)n + ΔX_(CTG)n) by a component that can be attributed predominantly to the thermodynamic cost of forming the bulge loop junction. Additional small differences in enthalpy change between the duplex and the sum ((ΔH_(CAG)n + ΔH_(CTG)n) of the repeat bulge loops stabilizing the duplex may reflect heat capacity effects due to the differences in melting temperatures. The important observation here is that the energetic cost of bi-strand bulge loop formation (slipped homoduplex S DNA in the nomenclature of Pearson and coworkers^{60, 61}) is dominated by an initial cost of junction formation that is independent of repeat bulge loop size for loop sizes n≥ 4 repeats/12 nucleotides. As a consequence, repeat bulge loops are always thermodynamically less stable than the duplex state and can exist only as kinetically trapped states. As a further consequence of this observation it appears that once a certain loop size has been exceeded (>4 repeats/12 nucleotides) the energetic cost of loop formation relative to duplex formation remains relatively independent of loop size (assuming that that slipped out bulge loops form in both strands^{60, 61}). There is no significant gain in the thermodynamic driving forces for larger repeat bulge loops relative to the duplex state compared to smaller bulge loops. There may, however, be a more pronounced activation energy barrier/kinetic trap that makes larger repeat bulge loops persist more easily than smaller repeat bulge loops.^{39, 41, 42, 56, 96} There may also be potential higher order interactions within larger bulge loops; such as, branching or loops folded back on themselves. Such interactions may contribute additional stabilizing effects for large bulge loops that are not accounted for in our model system. Finally, we note that single slip outs (SI heteroduplex slip outs in the nomenclature of Person et al.^{60, 61}) are strongly disfavored thermodynamically compared to the fully base paired duplex state. Moreover, the cost of forming an SI slip-out in one strand only becomes ever more unfavorable compared to the duplex state as loop size increases.

Concluding remarks

We have shown that repeat bulge loop structure formation is driven by competing thermodynamic driving forces. The loop junction formation induced thermodynamic destablization of the underlying duplex dominates in small repeat bulge loops, while the repeat self structure induced stabilization dominates in larger repeat bulge loops. The thermodynamic properties of the repeat bulge loop can be understood in terms of the balance between these competing driving forces. Our results indicate that, while very small (n≤2) repeat (CNG) loops of 6 nucleotides may be more similar to unstructured bulge loops, the properties of repeat bulge loops of more than 4 repeats/12 nucleotides are dominated by the nature of the repeat self structure. Our analysis of the calorimetrically determined thermograms provides insights into the pathways by which repeat bulge loops melt, an observation that may be of relevance to processing of such structures by the DNA replication, recombination, and/or repair machineries. The observations reported here may explain in part the reported differences in repair efficiencies and repair outcomes of small versus large repeat slip-outs in plasmids.^{25, 60, 61} Our results add to the growing understanding of the energy landscapes of non-B DNA states adopted by repeat DNA sequences implicated in DNA expansion and deletion events. Such insights are a needed to better understand the processes that lead to DNA expansion events, and ultimately the development of disease phenotypes.

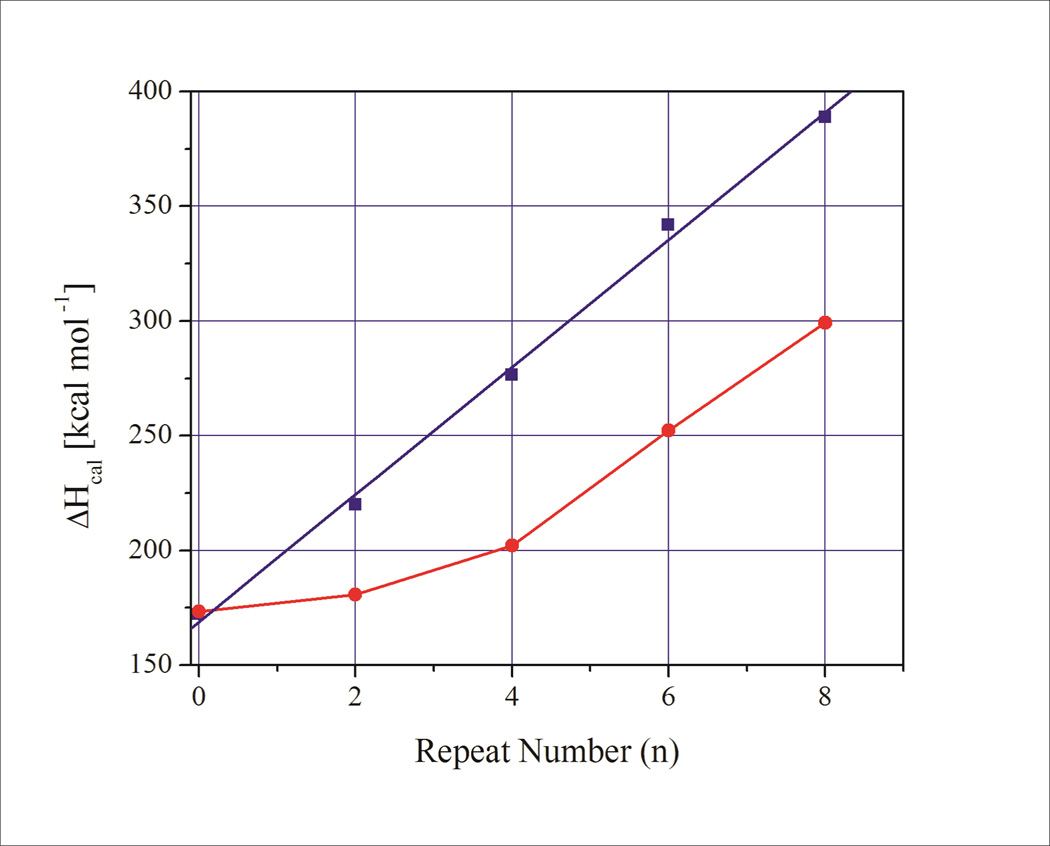
Figure 5.

Comparison of the calorimetrically measured enthalpy change for duplexes with increasing number of CAG·CTG base pairs (blue squares) with the enthalpy change calculated for bi-strand CAG and CTG bulge loops/slipped homoduplex S DNA⁶¹ (red circles) derived from the data described above. Note the enthalpy gap between the base paired repeats and those partitioned into bulge loop structures reflecting the cost of forming bulge loops from duplex DNA.