SUMMARY
Glioblastomas (GBMs) are the most common and malignant primary brain tumors and are aggressively treated with surgery, chemotherapy, and radiotherapy. Despite this treatment, recurrence is inevitable and survival has improved minimally over the last 50 years. Recent studies have suggested that GBMs exhibit both heterogeneity and instability of differentiation states and varying sensitivities of these states to radiation. Here, we employed an iterative combined theoretical and experimental strategy that takes into account tumor cellular heterogeneity and dynamically acquired radioresistance to predict the effectiveness of different radiation schedules. Using this model, we identified two delivery schedules predicted to significantly improve efficacy by taking advantage of the dynamic instability of radioresistance. These schedules led to superior survival in mice. Our interdisciplinary approach may also be applicable to other human cancer types treated with radiotherapy and, hence, may lay the foundation for significantly increasing the effectiveness of a mainstay of oncologic therapy.
INTRODUCTION
Patients suffering from glioblastoma (GBM), the most common and malignant primary brain tumor, have very poor survival. The standard of care is surgery when possible followed by radiation (Figure 1A) and chemotherapy (Stupp et al., 2005). This regime has seen little change over the past 50 years, as has the overall survival for this disease. Radiation is used in adjuvant therapy globally and provides a significant increase in the survival of GBM patients (Walker et al., 1980). Dose escalation studies demonstrated that survival improvements are observed up to an overall dose of 60 Gy (Walker et al., 1979). Beyond this point, there are little, if any, improvements in survival at the cost of increased toxicity (Bleehen and Stenning, 1991; Chan et al., 2002; Morris and Kimple, 2009). Typically, the dosing schedule is 2 Gy per day, 5 days per week, for 6 weeks. Several alternative schedules have been attempted, such as hypofractionated dosing of 3–6 Gy per session, hyperfractionated dosing of 1 Gy fractions two to three times per day, and accelerated dosing using multiple 2 Gy fractions a day to shorten the overall treatment time (Laperriere et al., 2002). None of these strategies, however, have resulted in consistent improvements in tumor control or survival and are thus not routinely used in the clinic.
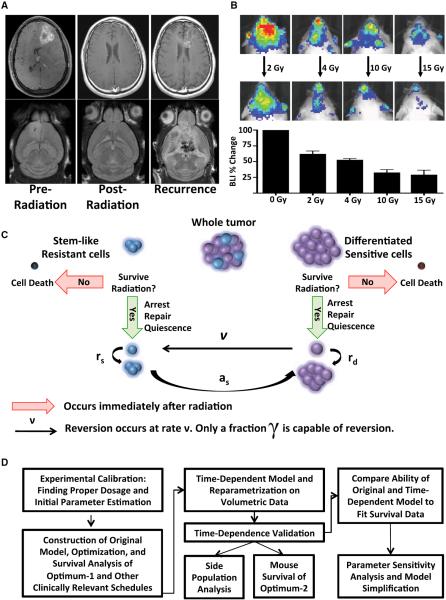
Figure 1. Human and Murine Gliomas Display Similar Recurrence Patterns in Response to Radiation.
(A) Representative MRIs showing human and mouse gliomas that are resolved by radiation treatment but then recur.
(B) Representative images and quantification of a radiation dose response assayed in E2f1-Luc glioma-bearing 24 hr after a given radiation dose. Error bars are SD.
(C) Schematic of the mathematical model used to describe the radiation response. The tumor is modeled as two separate cellular components: the stem-like resistant cells (SLRCs) and the differentiated sensitive cells (DSCs). SLRCs can repopulate the tumor, and some DSCs cells, represented by γ, are able to revert to SLRCs in response to radiation.
(D) Flow-chart summarizing the workflow described in the paper.
See also Figure S1.
Three recent advances provide insights into GBM biology that may impact therapy. First is the realization that GBM falls into several molecular subgroups that appear to be dominated by specific signaling pathways (Brennan et al., 2009; Phillips et al., 2006; Verhaak et al., 2010). These subgroups include proneural GBM that is related to abnormal platelet-derived growth factor (PDGF) signaling, classical GBM with canonical epidermal growth factor receptor (EGFR) amplification, and mesenchymal GBM with common loss of NF1 function. The second advance is the development and use of genetically engineered mouse models of GBM that provide genetically and histologically accurate models of these molecular subtypes of GBM (Hambardzumyan et al., 2011; Huse and Holland, 2009; Sharpless and Depinho, 2006). The third development is a series of work describing a subset of glioma cells that share many characteristics with stem cells (Galli et al., 2004; Ignatova et al., 2002; Singh et al., 2004). These cells are preferentially resistant to radiation and temozolomide and are considered an underlying cause of disease recurrence (Bao et al., 2006; Chen et al., 2012; Liu et al., 2006).
The PDGF-induced mouse model of GBM accurately mimics the 25%–30% of human GBMs in which aberrant PDGF signaling is present (Brennan et al., 2009; Shih et al., 2004; Verhaak et al., 2010). This model also contains a subpopulation of tumor cells that have similarities to stem cells (Barrett et al., 2012; Bleau et al., 2009; Charles et al., 2010). Stem-like cells are thought to reside in the perivascular niche and are maintained in that state at least partly by nitric oxide (NO) that signals through cyclic guanosine monophosphate, PKG, and NOTCH (Calabrese et al., 2007; Charles et al., 2010; Eyler et al., 2011). Within as little as 2 hr, NO can induce tumor cells to acquire a stem-like phenotype resulting in enhanced neurosphere and tumor formation upon transplantation (Charles et al., 2010). Other niche factors, such as hypoxic conditions, have also been shown to induce stemness (Heddleston et al., 2009; Li et al., 2009). Additionally, recent work has demonstrated that there are multiple tumorigenic cell types within a given tumor and that terminally differentiated astrocytes and neurons can dedifferentiate under oncogenic stress (Chen et al., 2010; Friedmann-Morvinski et al., 2012). These observations suggest that GBMs possess a dynamic heterogeneity of differentiation states that may allow them to rapidly and dynamically acquire a more resistant phenotype.
We hypothesized that mathematical modeling of this dynamic plasticity could be used to enhance radiation therapy. In the past few decades, the vast majority of mathematical modeling of the effects of radiation on cells has been based on the linear quadratic model. This model is widely accepted in the radiation literature due to its close agreement with experimental results for almost all radiation values of clinical interest (Hall and Giaccia, 2012). Several previous studies have specifically investigated the impact of radiotherapy on glioblastoma (Dionysiou et al., 2004; Harpold et al., 2007; Rockne et al., 2009; Stamatakos et al., 2006). These studies range from purely computational experiments to models fitting clinical data and have been utilized in predicting the outcomes of accelerated hyperfractionated schedules. Other recent work has successfully utilized mathematical modeling of cellular in vitro or rat-based in vivo systems to describe glioma behavior (Gao et al., 2013; Massey et al., 2012). Despite the multitude of work that has been done on optimal fractionation schedules, there has been very little success against aggressive gliomas in the clinic (Gupta and Dinshaw, 2005).
Here, we aimed to model a dynamic radiation response with the goal of identifying optimal schedules capable of improving radiation efficacy in a mouse model of PDGF-driven glioma. Our model considers two separate populations of cells: the largely radioresistant stem-like glioma cells and the radiosensitive differentiated glioma cells. We hypothesized that, after exposure to radiation, a fraction of the radiosensitive cells could rapidly revert to the radioresistant state. The inclusion of this dynamic hierarchical population structure and its plasticity induced by exposure to ionizing radiation is a feature of our framework. Based on this model, we described an optimized schedule that was predicted to prolong survival. Crucially, when tested in a clinically relevant glioma mouse model, this schedule markedly improved survival compared to a standard schedule. The fidelity of the model was improved by adding nonlinear temporal constraints to the acquisition of radioresistant properties based on the time since the previous radiation treatment. This second iteration of the model was able to generate a second optimized schedule that also improved survival in glioma-bearing mice. The mathematical model identifies the fraction of cells capable of acquiring radioresistance and the temporal constraints under which this process occurs as sensitive parameters for predicting radiation response. Specifically, our model predicts that if tumors were unable to rapidly acquire radioresistance, there would be no benefit to any of the optimum schedules. Our data support the functional importance of dynamic radioresistance to therapy and suggests that, at least in PDGF-driven glioma, the standard radiation schedule used may not be optimal. These findings may have broad implications for improving radiation therapy and provide a framework for future optimization of cytotoxic treatment delivery.
RESULTS
Initial Characterization of Radiation Dosing Using an Animal Model for PDGF-Driven GBM
We first performed a dose-response study to determine the effectiveness of various single-fraction doses of radiation (Figure 1B). We generated PDGF-B-induced tumors in Nestin-tv-a;E2f1-Luc mice using the replication-competent ASLV long-terminal repeat (LTR) with a splice acceptor (RCAS)/t-va mouse-model system (Uhrbom et al., 2004). These mice express firefly luciferase driven by the E2f1 promoter (E2f1-Luc), allowing for a noninvasive readout of cellular proliferation. This model is similar to human gliomas, in that glioma-bearing mice transiently respond to radiation treatment but ultimately succumb to disease recurrence (Figure 1A). We irradiated glioma-bearing mice with a variety of single doses: 2 Gy (approximately the daily dose used in humans), 4 Gy, 10 Gy, and 15 Gy. Twenty-four hours after irradiation, we found a progressive decrease in E2F1-drive bioluminescence activity with increasing radiation dose that appeared to plateau around 10 Gy (Figure 1B). For this reason, we chose a 10 Gy dose for further investigations.
Mathematical Modeling of GBM Cell Dynamics Predicts Treatment Response
We designed a mathematical model of GBM cell dynamics in response to radiation therapy. The model considers two distinct subpopulations of cells: stem-like/resistant cells (SLRCs) and differentiated/sensitive cells (DSCs) (Figure 1C). SLRCs reproduce symmetrically at rate rs to give rise to two SLRCs and asymmetrically at rate as to produce a SLRC and a DSC. Initially, the ratio of DSCs to SLRCs is given by R. Our model incorporates a bidirectional flow of cells between the SLRC and DSC states. In addition to SLRCs converting to a differentiated sensitive state, our model assumes that a fraction of DSCs may be capable of reverting to become SLRCs after exposure to ionizing radiation (Bleau et al., 2009; Charles et al., 2010; Chen et al., 2012; Li et al., 2009; Pistollato et al., 2010). The rate at which DSCs revert to a stem-like state is given by ν, and the fraction of DSCs that can revert is given by γ.
SLRCs are relatively radioresistant, whereas DSCs respond to radiation therapy via cell-cycle arrest, mitotic cell death, and apoptosis (Bao et al., 2006; Chen et al., 2012; Hambardzumyan et al., 2008). We modeled the cell-population response to radiotherapy using the linear quadratic model, which is widely accepted in the radiation literature due to its close agreement with experimental results (Dale, 1985; Fowler, 2010). The basic linear quadratic model states that the fraction of cells that survives a radiation dose of d Gy is given by exp[−αd −βd2]. The parameters α and β are specific to the type of tissue that is being irradiated; the parameter α represents cell killing resulting from a single radiation track causing damage to a specific chromosomal locus, whereas β represents cell killing via two tracks of radiation causing damage at the same locus. Within our mathematical framework, the parameters αs and βs characterize the response of SLRCs to radiation, whereas the parameters αd and βd denote the response of DSCs. In order to simplify the model, we considered the increased radiosensitivity of DSCs to be expressed in relation to the SLRC radioresistance, represented by the parameter ρ. In particular, we assumed that 0 ≤ ρ ≤ 1, αs = ρ αd, and βs = ρ βd. Therefore, the sensitivity of SLRCs to radiation can be characterized by a single parameter, ρ.
Our model also included radiation-induced cell-cycle arrest and attempted DNA-damage repair (Bao et al., 2006). In the context of our model, this arrest lasts for a minimum of Ls and Ld time units after radiation exposure in SLRCs and DSCs, respectively, and the rates at which these cells exit cell-cycle arrest are given by λs and λd. Further, newly converted DSCs take a minimum of Md units of time to begin reproducing again, and this event occurs at rate ηd.
Using this notation, we then formulated a mathematical model to describe the numbers of SLRCs and DSCs in response to radiation. At the time of diagnosis of the disease, there are SLRCs and DSCs. When these cells are exposed to the first dose of d Gy of radiation, there occurs a change in their numbers according to the linear quadratic model, producing SLRCs and DSCs. Additionally, there are γ DSCs that are capable reverting to the SLRC state. Using this description, we can then calculate the number of cells present at time t after exposure of the population to a dose of radiation. The number of DSCs is given by the number of DSCs that survived radiation and do not have the potential to revert to SLRCs plus any new growth and conversion from SLRCs since treatment; in addition, there are DSCs in the process of reversion. Similarly, the number of SLRCs is given by the population of cells that survived the dose of radiation plus any growth and reversion that has occurred since then:
where we use the notation x+ = x, x ≤ 0, and x+ = 0, x < 0. Further, note that, for the sake of readability, we have assumed that the rates λs, λd, and ηd are sufficiently large so they can be ignored; for the optimization described below, however, these terms were included (values listed in Table 1). For the full model without this assumption, see Equations 7 and 8 in the Supplemental Information available online.
Table 1.
Description and Values of the Mathematical Model Parameters
| Biological Process | Symbol | Original Parameter | Second Iteration | Final Iteration |
|---|---|---|---|---|
| Per Gy production of lethal DNA lesions from single-radiation track in DSC and SLRC | αd/αs | 0.0987/0.0395 | 0.0987/0.0429 | 0.0987/0.00987 |
| Per Gy2 production of lethal DNA lesions from two radiation tracks in DSC and SLRC | βd/βs | 1.14 × 10−7/4.58 × 10−8 | 1.14 × 10−7/4.96 × 10−8 | 1.14 × 10−7/1.14 × 10−8 |
| Rate at which newly converted DSC lead to clonal expansion (hr) | η d | 0.5 | 0.092 | 0.054 |
| Minimum time for newly converted DSC to being clonal expansion (hr) | Md | 24 | 313.256 | 366.3 |
| Minimum time DSC and SLRC are in quiescence (hr) | Ld/Ls | 24/36 | 461.46/464.99 | 193.32/477.02 |
| Rate at which DSC and SLRC exit quiescence | λd/λs | 0.5/0.35 | .011/.0001 | .1/.0328 |
| Proliferation rate of DSC and SLRC after exiting quiescence | rd/rs | .0088/.0001 | .0057/.0001 | .0038/.0008 |
| Initial ratio of DSC to SLRC | R | 20 | 20 | 20 |
| Rate at which SLRC convert to DSC | as | 0.0001 | 0.0001 | 0.0019 |
| Rate of reversion of DSC to SLRC | ν | 1.15 | 3.64 | 0.45 |
| Fraction of DSC capable of reverting to SLRC | γ | 0.15 | 0.353 | 0.4 |
| Time to peak reversion after irradiation | μ | - | 3.5 | 3.25 |
| Width of window of reversion | σ 2 | - | 2.5548 | 1.46 |
We can use the analytic description above to predict the response of the tumor to any course of radiation therapy.
Determination of an Optimal Radiation Schedule
To evaluate the response to a given radiation schedule in the context of our mathematical model, we considered the number of tumor cells present 2 weeks after treatment conclusion as an endpoint. To implement the optimization algorithm, an initial set of parameter values was derived from preliminary data (Figure 1B), previous studies (Galbán et al., 2012; Hambardzumyan et al., 2009; Pitter et al., 2011), or estimates (Table 1; Supplemental Information). We then predicted the survival outcomes for 10 Gy either administered as a single dose or in a clinically standard treatment (5 days of 2 Gy), finding that a standard fractionation schedule would perform significantly better than a single dose (Figures 2A and 2D).
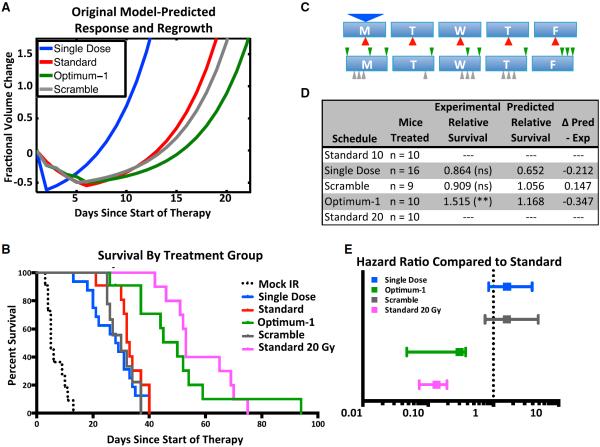
Figure 2. Mathematical Modeling of the Radiation Response Improves Survival in a Mouse Model of Proneural Glioma.
(A) Original model-predicted tumor response and growth following standard, single-dose, optimum-1, and scramble control radiation treatment schedules. Model parameters are listed under “Original Parameters” in Table 1.
(B) Kaplan-Meier survival plot of various radiation schedules. IR, ionizing radiation.
(C) Schematic depicting the various schedules tested. The arrow position represents the time of dose during the 8am–5pm treatment window. The size of the arrow correlates with the size of the dose.
(D) Table summarizing number of mice treated, the performance relative to standard therapy, and the original model-predicted performance of each group. ns, not significant.
(E) Hazard ratios of the various radiation schedules, compared to the standard radiation schedule. Error bars represent the 95% confidence interval (CI) of the hazard ratio (HR).
See also Figure S2.
We then aimed to identify an optimal fractionation schedule, with the goal of finding those schedules that minimized the number of tumor cells 2 weeks after the treatment conclusion. Mathematically identifying the global optimal schedule was not computationally feasible due to the complexity of our model, as well as the uncertainty of some of the parameters. Because of this, we utilized simulated annealing, a Monte-Carlo-based method (Kirkpatrick et al., 1983; Van Laarhoven and Aarts, 1987), to identify the best treatment strategies (see Supplemental Information; Table 2).
Table 2.
Description of the Tested Radiation Schedules
| Schedule | Day 1 | Day 2 | Day 3 | Day 4 | Day 5 |
|---|---|---|---|---|---|
| Standard | 2 Gy | 2 Gy | 2 Gy | 2 Gy | 2 Gy |
| Single dose | 10 Gy | – | – | – | – |
| Optimum-1 | 1 Gy | 1 Gy | 1 Gy | 1 Gy | 1 Gy- |
| 8am | 5pm | 3pm | 5pm | 3pm | |
| 2pm | 5pm | 4pm | |||
| 5pm | 5pm | ||||
| Scramble control | 1 Gy | 1 Gy | 1 Gy | 1 Gy | – |
| 10am | 4pm | 2pm | 1pm | ||
| 11am | 3pm | 2pm | |||
| 12pm | 4pm | 3pm | |||
| Hypofractionated | 5 Gy | – | – | – | 5 Gy |
| Hyperfractionated | 1 Gy | 1 Gy | 1 Gy | 1 Gy | 1 Gy |
| 9am | 9am | 9am | 9am | 9am | |
| 3pm | 3pm | 3pm | 3pm | 3pm | |
| Optimum-2 | 3Gy | 1 Gy | – | 1 Gy | 1 Gy |
| 8am | 4pm | 9am | 9am | ||
| 1pm | 1pm | ||||
| 5pm | 5pm |
A clinically motivated constraint set for our schedules is presented in the Supplemental Information. With this constraint set and using our initial set of parameters (Table 1), we identified an optimal schedule, “optimum-1,” that was predicted to do significantly better than standard treatment. We also created a control schedule by generating a scrambled sequence with a similarly clustered dosing scheme that was predicted to not perform significantly better than standard treatment (Figures 2A and 2D; Table 2).
Optimized Radiation Schedules Significantly Improve Survival in a Mouse Model of PDGF-Driven Glioma
We then returned to the RCAS/t-va mouse system to test the model's predictions in a survival assay. We performed survival experiments using PDGF-B-driven gliomas in Nestin-tv-a; Ink4a/Arf−/− mice. The genetic background of these mice is similar to human PDGF-driven tumors (Verhaak et al., 2010). As mice developed symptoms of glioma, such as lethargy, weight loss, seizures, etc., they were randomized into either the mock-treated group or one of the various 10 Gy radiation treatment groups, which consisted of a single dose, standard fractionation, optimum fractionation, and a scramble control (Table 2). The endpoint of survival was defined as the time point at which the animal had to be sacrificed because of excessive tumor burden: greater than 10% weight loss, lethargy, or seizure. Mock-treated mice quickly succumbed to their disease, with a median overall survival of 5 days after the onset of symptoms (Figure 2B). Animals in the single-dose and the clinical-standard groups had respective median survivals of 28.5 and 33 days after the onset of symptoms, which was significantly longer than the mock-treated group (p < 0.0001; Figure 2B). Although the median survival of the single-dose-treated animals was shorter than the standard treatment group, there was no significant difference between treatments (hazard ratio [HR] [95% confidence interval (CI)] = 1.619 [0.8450–3.932]; p value = 0.1742; Figures 2D and 2E).
We also analyzed two different mathematically predicted schedules: optimum-1 and the scrambled control sequence (Figures 2A and 2D; Table 2). The median survival of mice treated with the scrambled control schedule was 30 days (Figure 2B), which was not significantly different from the standard schedule (HR [95% CI] = 1.613 [0.7453–4.863]; p value = 0.2346; Figures 2D and 2E). Mice treated with optimum-1 had a median survival of 50 days (Figure 2B), which was significantly longer than the clinical standard schedule (Figures 2D and 2E; HR [95% CI] = 0.3015 [0.04708–0.3760]; p value = 0.001). Due to the increase in median survival observed with the optimized schedule, we next compared the optimized schedule to 2 weeks of clinical standard therapy; in the latter, mice were treated with 20 Gy, delivered in ten fractions given over 12 days, with a 2-day weekend break. The 20 Gy treatment group had a median survival of 53 days (Figure 2B), which was significantly greater than the 10 Gy clinical standard (Figures 2D and 2E; HR [95% CI] = 0.2084 [0.01295–0.1319]; p < 0.0001), but not significantly different from optimum-1 (Figure 2E, HR [95% CI] = 1.429 [0.6230–3.698]; p value = 0.3907).
Mathematical Modeling of Other Clinically Relevant Fractionation Schedules Leads to Iterative Updating of the Model
We then set out to investigate other fractionation schedules that have been clinically tested in GBM. Hyperfractionation schedules consist of a large number of smaller-dose treatments in an attempt to minimize damage to surrounding normal tissue, but according to clinical trials, this approach has not improved overall survival (Coughlin et al., 2000; Laperriere et al., 2002). Hypofractionation schedules involve a larger fraction size with fewer treatments, resulting in a shorter overall treatment time that again yields similar survival to conventional therapy (Laperriere et al., 2002). Surprisingly, our initial model predicted that both hypo- and hyperfractionated schedules would perform significantly differently than standard therapy: the hypofractionated schedule was predicted to be similar to a single dose of 10 Gy, whereas a standard hyperfractionated schedule was predicted to perform as well or slightly better than optimum-1 (Figures 3A and 3G).
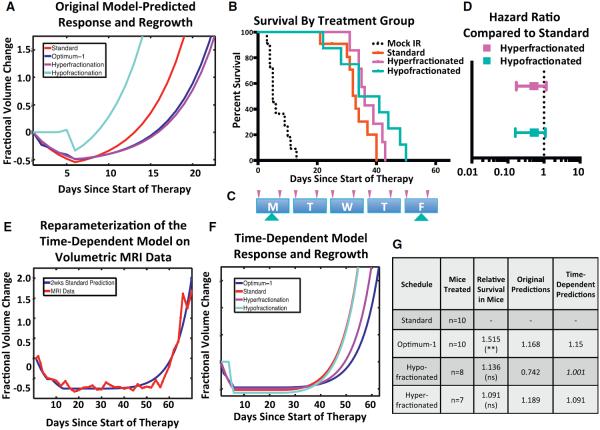
Figure 3. Comparison of Two Models: Incorporating Dedifferentiation Time Dependence Improves Fidelity.
(A) Predicted tumor growth in response to standard, hypofractionated, hyperfractionated, and optimum-1 radiation treatment schedules. These curves are based on the original model; parameters are listed under Original Parameters in Table 1.
(B) Kaplan-Meier survival plot of hypo- and hyperfractionated radiation schedules. Standard and optimum-1 survival are the same curves as Figure 2 and are shown for comparison.
(C) Schematic depicting the hyper- and hypofractionated schedules tested. The arrow position represents the time of dose during the 8am–5pm treatment window. The size of the arrow correlates with the size of the dose.
(D) Hazard ratios of the hypo- and hyperfractionated radiation schedules, compared to the standard radiation schedule. Error bars represent the 95% CI of the HR.
(E) Reparameterization of the time-dependent model based on volumetric MRI studies of mouse gliomas treated with 2 weeks of the standard schedule.
(F) Time-dependent model-predicted tumor growth in response to the various treatment schedules. Model parameters are listed under “Second Iteration” in Table 1.
(G) Table summarizing number of mice treated, the performance relative to standard therapy, and the predicted performance of the original and time-dependent model for each treatment group.
See also Figure S3.
We tested this prediction for both schedules by overall survival in mice. Mice were randomized as described above into either a hyperfractionated group or hypofractionated group and compared to standard therapy (Table 2). Mice treated with these schedules had a median survival of 37.5 days and 36 days, respectively (Figure 3B). Similar to results observed in human clinical trials, neither of these schedules was significantly different from the clinical standard schedule (Figure 3D; HRhyper [95% CI] = 0.5237 [0.1708–1.167]; p value = 0.1383; HRhypo [95% CI] = 0.3427 [0.1123–1.046]; p value = 0.0599). These results, and the hyperfractionated schedule in particular, highlighted a weakness in our model that we addressed with a second iteration of the model.
Time-Dependent Acquisition of Radioresistance Improves the Mathematical Model
To address the inaccurate predictions of the original model, we iteratively updated our model such that the fraction of cells rapidly acquiring resistance, γ, now depends on the time elapsed since the previous dose of radiation. Whereas the initial model treated γ as a time-independent constant following radiation, the updated model stipulates that γ varies over time and that there is a time where a maximum number of cells are prone to reversion in response to subsequent exposure to ionizing radiation. The updated model thus describes the acquisition of resistance with two additional time-dependent parameters: the time of maximal reversion after radiation, μ, and the width of the window during which reversion can occur after radiation, σ2. The model stipulates that, after the first dose of radiation, γ0 cells are capable of reversion; for a later dose given t hr after the previous dose of radiation, the fraction of cells capable of reversion is given by γ(t) = γoe−(t−μ)2/σ2. Other than these additional parameters added to further describe γ, the updated model is the same as the original model.
To investigate this time-dependent model, we first tested its predictions against volumetric time series data of mice after treatment with 2 weeks of standard therapy (Figure 3E). This comparison allowed us to identify parameter values capable of recapitulating the time-series data. Based on these model parameters, we found a closer concordance between predicted mouse survival times and observed experimental survival times of the optimum-1, hyperfractionated, hypofractionated, and standard schedules (Figures 3F and 3G). In addition to more accurately predicting the survival response, the model also makes significantly different predictions with regard to the enrichment of the SLRC population after radiation. Both models similarly predict that 1 day after the last dose, optimum-1 will lead to a larger number of SLRCs relative to standard therapy. However, the models offer differing predictions for the hyperfractionated schedule. The original model predicts that the hyperfractionated schedule maximally enriches the SLRC population among all schedules tested (Figure 4A), whereas the time-dependent model predicts that optimum-1 enriches the SLRC population to a greater extent than the hyperfractionated schedule (Figure 4B).
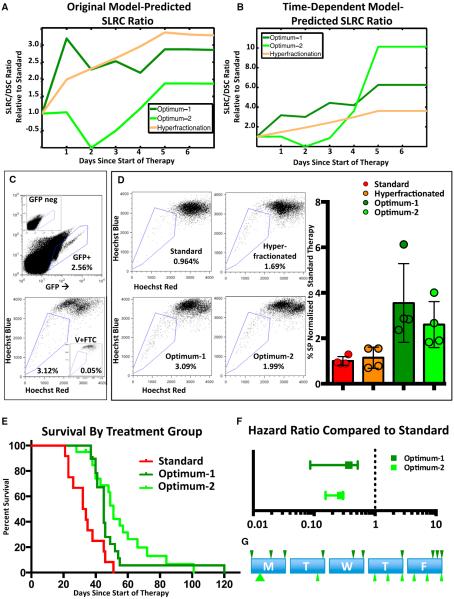
Figure 4. Optimized Radiation Schedules Enrich the Glioma Stem Cell Population.
(A and B) Graph showing predicted size of the stem-like resistant cell population for hyperfractionated, optimimum-1, and optimum-2 schedules, using the original model (A) or the time-dependent model (B). All values are normalized to predictions for standard therapy. Parameters in (A) and (B) are, respectively, from the Original Parameters and Second Iteration in Table 1.
(C) Representative gating strategy for eGFP+ tumor cell side-population (SP) analysis. The upper panel depicts the gate used to identify GFP-positive cells, based on a GFP-negative sample shown in the insert. The lower panel depicts the gate used to identify the SP, based on a Fumitremorgin C-verapamil-treated control shown in the insert.
(D) Representative images and quantification of SP analysis 24 hr after the conclusion of the standard, hyperfractionated, optimum-1, and optimum-2 schedules. For quantification, all values are normalized to the average SP of the standard schedule. Error bars represent the SD.
(E) Kaplan-Meier analysis comparing standard, optimum-1, and optimum-2 schedules. These mice represent an entirely independent cohort from mice in Figures 2 and 3.
(F) Hazard ratios of the optimum-1 and optimum-2, compared to standard radiation.
(G) Schematic briefly describing the optimum-1 and optimum-2 schedules. The arrow position represents the time of dose during the 8am–5pm treatment window. The size of the arrow correlates with the size of the dose. Error bars represent the 95% CI of the HR.
To test the effects of various schedules on the enrichment of SLRCs, we then treated mice with the standard, hyperfractionated, and optimum-1 schedules. Glioma tissue was harvested for side-population (SP) analysis on the sixth day, i.e., 1 day after the last dose of radiation. Stem-like cells are frequently identified from a variety of normal and malignant tissues by flow cytometry as the SP based their ability to efflux Hoechst dye via the ABC transporter, ABCG2 (Greve et al., 2012). Previous work has demonstrated that, in PDGF-driven murine gliomas, SP cells are enriched for canonical cancer stem cell properties, such as stem-marker expression, enhanced tumor-sphere formation, and enhanced tumorigenicity (Bleau et al., 2009). We generated tumors using a previously described RCAS vector that expresses both PDGF-B and enhanced GFP, which results in gliomas with GFP-positive tumor cells (Fomchenko et al., 2011). This system allowed us to limit the SP analysis to bona fide tumor cells (Figure 4C). We observed that tumors treated with the optimized schedule have a 3.55-fold enrichment when compared to standard therapy (p value = 0.0265; Figure 4D). However, as predicted by the time-dependent mathematical model, the hyperfractionated therapy was able to statistically significantly enrich the SP when compared to standard treatment (1.145-fold enrichment; p value = 0.5944; Figure 4D).
To further validate the time-dependent model, we used this model to derive an optimized schedule, “optimum-2” (Table 2). As with optimum-1, optimum-2 was predicted to lead to an enriched number of SLRCs 1 day after the last dose of radiation compared to standard treatment (Figure 4B). Tumors treated with the optimum-2 schedule had a 2.6-fold enrichment when compared to standard therapy (p value = 0.0210; Figure 4D). Although optimum-2 was predicted to enrich the SLRCs further than optimum-1, we saw no significant difference in the SP between the two groups (p value = 0.3805). We also tested the optimum-2 schedule using overall survival in mice and observed a significant improvement in survival compared to standard treatment (hazard HR [95% CI] 0.2720 [0.04074–0.2967] ratio; p value < 0.0001; Figure 4E). Optimum-2 was also predicted to have significantly longer survival than optimum-1 (Figure S3). The median survival of the optimum-2 group was longer than that of the optimum-1 group; this difference, however, did not reach statistical significance (Figure 4F; HR [95% CI] = 0.8788 [0.4572–1.689], p value = 0.1768).
To further improve the predictive accuracy of the model, we performed a final iteration by reparameterizing the model using the experimental survival data (Figures 5A and 5B). Performing this calculation led to a further confirmation that the time dependence of γ was essential to the model: fitting the time-dependent model to the survival data led to a smaller minimal mean square error as compared to the original model. The time-dependent model was able to fit the observed data to within an error of 5.2 days, in contrast to the original model, which could only fit the data to an error of 16.32 days. Thus, including time-dependent dedifferentiation increases the model's ability to match the survival data. We therefore concluded that the time-dependent form of γ is necessary to accurately explain the observed survival data and it is likely that any cell reversion due to ionizing radiation occurs in a time-dependent fashion.
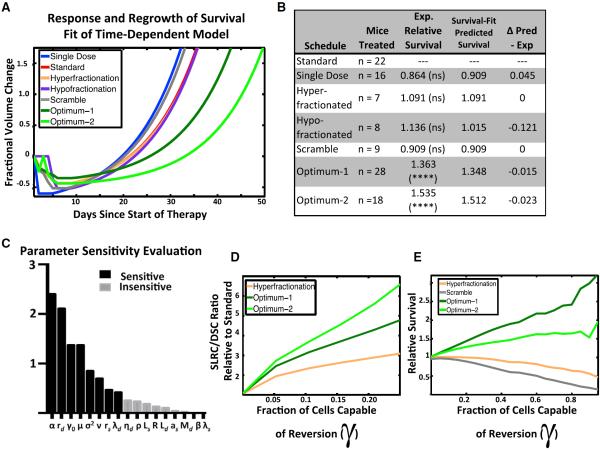
Figure 5. Growth Rate and Dynamic Dedifferentiation Are the Most Influential Parameters in Modeling Radiation Response.
(A) Survival-fit, model-predicted tumor growth in response to various radiation treatment schedules. These predictions are from the time-dependent model reparameterized to fit the mouse survival data with the parameters under “Final Iteration” in Table 1.
(B) Table summarizing the number of mice treated, the performance relative to standard therapy, and the predicted performance survival data reparameterized time-dependent model for each treatment group.
(C) Sensitivity analysis of the model's parameters, ranked from most to least sensitive, as determined by the sensitivity analysis (Supplemental Information).
(D) Predictions of the SLRC/DSC ratio while varying the fraction of cells capable of reversion (γo).
(E) Sensitivity plot showing the relative efficacy of several schedules while varying the fraction of cells capable of reversion (γo). An explanation of how we found the parameters for (E) can be found in Section 5 of the Supplemental Information.
See also Figure S4.
Lastly, we created a simplified version of the model that was more suitable for analysis and interpretation. The simplified model predictions for the tumor cell populations prior to dose i+1 (assuming t hours between doses i and i+1, and t0 hours between doses i−1 and i) are given by
According to this simplified form of the model, the optimized therapies optimum-1 and optimum-2 increase survival by converting cells from the fast-growing radiosensitive population to the slow-growing radioresistant population. Notably, sensitivity analysis of the simplified model identifies the parameters that describe reversion as novel sensitivity parameters (Figure 5C; Supplemental Information).
Finally, as a thought experiment, we considered this model in a setting where there is no reversion (γ0 = 0) and therefore no ability to rapidly acquire radioresistance. Under these conditions, the model reduces to the standard linear quadratic model, which highlights two important observations. First, in this scenario, all fractionation schedules would result in the same ratio of stem-like to differentiated cells (Figure 5D). This finding is in clear contradiction to the observations of our SP analysis (Figure 4D). Second, if there was no reversion, the model predicts all fractionation schedules would result in the same survival (Figure 5E), which is also contradicted by the observations from mouse survival experiments (Figures 2B and 4E). Taken together, these observations provide significant evidence for the fact that ionizing radiation encourages rapid reversion of a subset of glioma cells to a radioresistant stem-like state.
In sum, our iterative mathematical modeling approach, informed and validated by mouse modeling, allowed us to determine not only a radiation delivery schedule that prolonged survival in mice, but also to identify parameters of the biological processes guiding cellular behavior in gliomas that are responsible for radioresistance. This validated mathematical model can be used, in future work, to investigate the effectiveness of alternative schedules and test their effects on GBM cell populations.
DISCUSSION
Standard radiation delivery schemes are based on decades-old data that mostly predate recent findings on cancer stem cells. In GBM patients, many different radiation schedules have been tried in clinic based on classic radiobiological data, but thus far all have had roughly the same effectiveness. Here, we adopted a combined experimental and theoretical approach with the goal of identifying treatment schedules that would lead to better survival in animal models of the disease by accounting for dynamic transitions of cells between relatively radiosensitive and radioresistant pools. Our approach was based on the assumption that the tumor has a kinetic response to radiation causing some of the surviving cells to acquire resistance by adopting a more stem-like quiescent state over a matter of hours. Based on this approach, we successfully identified two treatment schedules that significantly extended survival in glioma-bearing mice, whereas a control schedule failed to do so, as predicted. The fact that optimized schedules clearly outperformed other schedules suggests that the response to radiation is dynamic and that the schedule of a given total dose of radiation can affect its ultimate efficacy.
Although the mathematical model presented here offers complexity, it does not include several potentially important biological factors, such as the immune system, stromal-tumor interactions, nutrient gradients, and others. For example, the work by Stamatakos et al. (2006) developed a sophisticated four-dimensional model for the response of high-grade gliomas to ionizing radiation. Based on their computational model, the authors are able to discuss the effects of cell-cycle time, reoxygenation times, and cell density on tumor response to therapy. Whereas these factors are important, using a simplified model focusing on a single factor, such as dynamic radioresistance, is a powerful way to isolate and better study that phenomenon. Additionally, it has previously been shown that working with a simplified model allows for a more thorough exploration of the mathematics behind the specific parameter, which often uncovers nonobvious predictions (Michor et al., 2005; Norton, 1988). Lastly, simplified models are amenable to more complex mathematical analysis, such as optimization of treatment schedules.
Glioma stem cells are functionally defined by their capacity to self-renew and to generate heterogeneous tumors upon transplantation (Vescovi et al., 2006). As stem-like cells are more therapeutically resistant and ultimately give rise to recurrent disease, it is commonly believed that decreasing the stem-like population will increase overall survival (Cheng et al., 2010; Scopelliti et al., 2009). However, our model predicts an improved overall survival for fractionation schedules that enrich the SLRC population. The side population, which is enriched for quiescent stem cells (Bleau et al., 2009; Deleyrolle et al., 2011; Harris et al., 2008), was elevated in the two optimized schedules that increased overall survival. However, the success of our model is driven by these cells acquiring a quiescent state and slower proliferation rate and therefore is not dependent on a complete dedifferentiation. Further characterization of the ability of radiation to induce other stem-like properties remains an exciting area for future studies.
Whereas eradicating all glioma cells, including the stem-like population, is essential for ultimately curing the disease, our model describes a phenomenon whereby utilizing alternatively fractionated schedules can increase the SLRC population and still result in a slower-growing residual tumor and prolonged time to recurrence. In this regard, our model joins a growing body of evidence suggesting that the relationship between cells with stem-like character and clinical outcomes might not be as straightforward as previously thought. A recent theoretical paper modeling tumor growth kinetics argues that, whereas cancer stem cells are necessary for tumor growth, the kinetics of growth are best described by the nonstem compartment (Morton et al., 2011). Additionally, a recent human GBM study compared the percentage of CD133+ glioma stem cells in patient-matched primary and recurrent samples (Pallini et al., 2011). Patients whose gliomas contained an increased percentage of CD133+ at recurrence demonstrated a significantly longer survival than those with decreased CD133+ cells at recurrence. These studies support our finding that a relative enrichment in the resistant stem-like population might prolong survival by increasing the time to recurrence.
Translating Optimized Schedules to Human Patients
There are some clear hurdles and open questions in regards to translating our findings from the mouse to the clinic. One measure of predicted toxicity and lethality of different fractionation schedules is given by the biologically effective dose (BED) (Fowler, 2010; Hall and Giaccia, 2012). This measure is frequently used to compare the effectiveness and toxicity of different schedules. It is difficult to use BED to compare the optimized schedules tested here, as the spacing of our doses is inconsistent. However, if we use the common assumption that doses separated by more than 6 hr are independent, then the optimum-1 schedule had one of the lowest BED values of all schedules tested. Because of this, it might even be possible to increase the dosage levels while keeping the toxicity of the schedule at or below the level of the standard therapy. An important avenue for extending these results to the clinical setting will be to consider optimizing fractionation schedules while stipulating that the schedule has an equal or lower BED than that of standard therapy.
Note also that this treatment approach enriches a slow-growing GSC population and therefore would not be curative. However, previous studies have shown that cancer stem cells are dependent on the NOTCH signaling pathway (Androutsellis-Theotokis et al., 2006; Charles et al., 2010; Eyler et al., 2011), and further studies have shown depletion and therapeutic sensitization of GSCs when treated with gamma-secretase inhibitors (Gilbert et al., 2010; Hovinga et al., 2010; Wang et al., 2010). Future studies that combine optimized radiation with therapeutics that specifically target GSCs, via NOTCH or other pathways, might further improve outcomes.
GBM is by definition a heterogeneous disease, and it is unclear how robust an optimized schedule developed for proneural glioma would perform across the various other GBM subtypes. The mouse model used in these studies is driven by PDGF signaling, which is characteristic of approximately 25%–30% of human GBMs. Of note, this mouse model might not reflect the biology of other commonly altered signaling pathways, such as EGFR amplification or NF1 loss, and further studies are needed to determine if the optimization will extend to those tumors. Additionally, even tumors with similar molecular underpinnings are likely to exhibit variability in the parameters used to optimize radiation delivery, such as proliferation rate and the fraction of cells capable of rapidly acquiring resistance. This observation brings up the possibility there may be no universal optimum schedule but rather multiple schedules where optimization for a given patient is dependent on detailed pathologic analysis of each resected tumor.
Additionally, the parameter values we used were determined iteratively based on the mouse model, and it is probable that the schedules presented here will not translate precisely to human tumors. Our investigation was performed for 1 week of therapy delivering a total of 10 Gy of radiation. Human patients receive 60 Gy of radiation over 6 weeks, and optimizing that schedule might not simply be six cycles of the 1 week optimized schedules. Nevertheless, our findings suggest that the gliomas respond dynamically and that the response follows kinetics with a timescale of hours, not weeks. It is therefore imperative to include such considerations into a theoretical framework in order to determine optimum radiation administration schedules for human patients.
Finally, our work studied radiation in isolation, whereas in man, radiation is usually administered after neurosurgical resection and with temozolomide. These treatment modalities need to be incorporated into models aimed at identifying dosing strategies for human patients. Nonetheless, our studies suggest that modeling glioma response to radiation as a dynamic heterogeneous process can predict a treatment schedule that improves overall survival. It also suggests that the schedule that patients are currently receiving may not be optimal.
EXPERIMENTAL PROCEDURES
Generation of Tumors Using RCAS/TVA
All of the animal experiments were conducted using protocols approved by the Institutional Animal Care and Use Committees of Memorial Sloan-Kettering Cancer Center, protocol 00-11-189. Tumors were generated as previously described by injecting RCAS-transfected DF1 cells into n-tva mice (Hambardzumyan et al., 2009). Mice were monitored carefully, and treatment began when they displayed neurological symptoms, such as lethargy or head tilt due to tumor burden, at which point they were irradiated for either bioluminescence (BLI) or survival assays. For BLI, mice were analyzed 24 hr after irradiation. For survival, mice were monitored until recurrence of symptoms. The various radiation schedules are described in Table 2; further details on mouse work can be found in the Supplemental Information online.
MRI Reconstruction and Analysis
Please see the Supplemental Information online.
SP Analysis
Hoechst 33342 staining was performed as previously reported (Bleau et al., 2009). Briefly, glioma-bearing mice were treated with standard, hyperfractionated, optimum-1, or optimum-2 schedules. Twenty-four hours after the last treatment, mice were euthanized and tissue was harvested for SP analysis. Bona fide tumor cells were identified based on eGFP+ expression, SP was based on Hoescht dye exclusion, and the data were analyzed by FlowJo. Further details on the SP analysis can be found in the Supplemental Information online.
Statistics
Please see the Supplemental Information online.
Mathematical Modeling
Please see the Supplemental Information online.
Supplementary Material
ACKNOWLEDGMENTS
The authors would like to thank the Holland and Michor labs and Jasmine Foo for discussions and comments and National Institutes of Health grants RO1 CA100688, U54 CA163167, U54 CA143798, U01 CA141502-01 (to E.C.H.), U54 CA143798 (to F.M.), NSF DMS-1224362, U54 CA143798 (to K.L.), MSTP GM07739, F31 NS076028 (to K.P.), and P01 CA085878 (to B.D.R.).
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information includes Extended Experimental Procedures, four figures, and three tables and can be found with this article online at http://dx.doi.org/10.1016/j.cell.2013.12.029.
REFERENCES
- Androutsellis-Theotokis A, Leker RR, Soldner F, Hoeppner DJ, Ravin R, Poser SW, Rueger MA, Bae SK, Kittappa R, McKay RD. Notch signalling regulates stem cell numbers in vitro and in vivo. Nature. 2006;442:823–826. doi: 10.1038/nature04940. [DOI] [PubMed] [Google Scholar]
- Bao S, Wu Q, McLendon RE, Hao Y, Shi Q, Hjelmeland AB, Dewhirst MW, Bigner DD, Rich JN. Glioma stem cells promote radioresistance by preferential activation of the DNA damage response. Nature. 2006;444:756–760. doi: 10.1038/nature05236. [DOI] [PubMed] [Google Scholar]
- Barrett LE, Granot Z, Coker C, Iavarone A, Hambardzumyan D, Holland EC, Nam HS, Benezra R. Self-renewal does not predict tumor growth potential in mouse models of high-grade glioma. Cancer Cell. 2012;21:11–24. doi: 10.1016/j.ccr.2011.11.025. [DOI] [PubMed] [Google Scholar]
- Bleau AM, Hambardzumyan D, Ozawa T, Fomchenko EI, Huse JT, Brennan CW, Holland EC. PTEN/PI3K/Akt pathway regulates the side population phenotype and ABCG2 activity in glioma tumor stem-like cells. Cell Stem Cell. 2009;4:226–235. doi: 10.1016/j.stem.2009.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bleehen NM, Stenning SP, The Medical Research Council Brain Tumour Working Party A Medical Research Council trial of two radiotherapy doses in the treatment of grades 3 and 4 astrocytoma. Br. J. Cancer. 1991;64:769–774. doi: 10.1038/bjc.1991.396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brennan C, Momota H, Hambardzumyan D, Ozawa T, Tandon A, Pedraza A, Holland E. Glioblastoma subclasses can be defined by activity among signal transduction pathways and associated genomic alterations. PLoS ONE. 2009;4:e7752. doi: 10.1371/journal.pone.0007752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabrese C, Poppleton H, Kocak M, Hogg TL, Fuller C, Hamner B, Oh EY, Gaber MW, Finklestein D, Allen M, et al. A perivascular niche for brain tumor stem cells. Cancer Cell. 2007;11:69–82. doi: 10.1016/j.ccr.2006.11.020. [DOI] [PubMed] [Google Scholar]
- Chan JL, Lee SW, Fraass BA, Normolle DP, Greenberg HS, Junck LR, Gebarski SS, Sandler HM. Survival and failure patterns of high-grade gliomas after three-dimensional conformal radiotherapy. J. Clin. Oncol. 2002;20:1635–1642. doi: 10.1200/JCO.2002.20.6.1635. [DOI] [PubMed] [Google Scholar]
- Charles N, Ozawa T, Squatrito M, Bleau AM, Brennan CW, Hambardzumyan D, Holland EC. Perivascular nitric oxide activates notch signaling and promotes stem-like character in PDGF-induced glioma cells. Cell Stem Cell. 2010;6:141–152. doi: 10.1016/j.stem.2010.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R, Nishimura MC, Bumbaca SM, Kharbanda S, Forrest WF, Kasman IM, Greve JM, Soriano RH, Gilmour LL, Rivers CS, et al. A hierarchy of self-renewing tumor-initiating cell types in glioblastoma. Cancer Cell. 2010;17:362–375. doi: 10.1016/j.ccr.2009.12.049. [DOI] [PubMed] [Google Scholar]
- Chen J, Li Y, Yu TS, McKay RM, Burns DK, Kernie SG, Parada LF. A restricted cell population propagates glioblastoma growth after chemotherapy. Nature. 2012;488:522–526. doi: 10.1038/nature11287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng L, Bao S, Rich JN. Potential therapeutic implications of cancer stem cells in glioblastoma. Biochem. Pharmacol. 2010;80:654–665. doi: 10.1016/j.bcp.2010.04.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coughlin C, Scott C, Langer C, Coia L, Curran W, Rubin P. Phase II, two-arm RTOG trial (94–11) of bischloroethyl-nitrosourea plus accelerated hyperfractionated radiotherapy (64.0 or 70.4 Gy) based on tumor volume (> 20 or < or = 20 cm(2), respectively) in the treatment of newly-diagnosed radiosurgery-ineligible glioblastoma multiforme patients. Int. J. Radiat. Oncol. Biol. Phys. 2000;48:1351–1358. doi: 10.1016/s0360-3016(00)01412-7. [DOI] [PubMed] [Google Scholar]
- Dale RG. The application of the linear-quadratic dose-effect equation to fractionated and protracted radiotherapy. Br. J. Radiol. 1985;58:515–528. doi: 10.1259/0007-1285-58-690-515. [DOI] [PubMed] [Google Scholar]
- Deleyrolle LP, Harding A, Cato K, Siebzehnrubl FA, Rahman M, Azari H, Olson S, Gabrielli B, Osborne G, Vescovi A, et al. Evidence for label-retaining tumour-initiating cells in human glioblastoma. Brain: a journal of neurology. 2011;134:1331–1343. doi: 10.1093/brain/awr081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dionysiou DD, Stamatakos GS, Uzunoglu NK, Nikita KS, Marioli A. A four-dimensional simulation model of tumour response to radiotherapy in vivo: parametric validation considering radiosensitivity, genetic profile and fractionation. J. Theor. Biol. 2004;230:1–20. doi: 10.1016/j.jtbi.2004.03.024. [DOI] [PubMed] [Google Scholar]
- Eyler CE, Wu Q, Yan K, MacSwords JM, Chandler-Militello D, Misuraca KL, Lathia JD, Forrester MT, Lee J, Stamler JS, et al. Glioma stem cell proliferation and tumor growth are promoted by nitric oxide synthase-2. Cell. 2011;146:53–66. doi: 10.1016/j.cell.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fomchenko EI, Dougherty JD, Helmy KY, Katz AM, Pietras A, Brennan C, Huse JT, Milosevic A, Holland EC. Recruited cells can become transformed and overtake PDGF-induced murine gliomas in vivo during tumor progression. PLoS ONE. 2011;6:e20605. doi: 10.1371/journal.pone.0020605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fowler JF. 21 years of biologically effective dose. Br. J. Radiol. 2010;83:554–568. doi: 10.1259/bjr/31372149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedmann-Morvinski D, Bushong EA, Ke E, Soda Y, Marumoto T, Singer O, Ellisman MH, Verma IM. Dedifferentiation of neurons and astrocytes by oncogenes can induce gliomas in mice. Science. 2012;338:1080–1084. doi: 10.1126/science.1226929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galbán S, Lemasson B, Williams TM, Li F, Heist KA, Johnson TD, Leopold JS, Chenevert TL, Lawrence TS, Rehemtulla A, et al. DW-MRI as a biomarker to compare therapeutic outcomes in radiotherapy regimens incorporating temozolomide or gemcitabine in glioblastoma. PLoS ONE. 2012;7:e35857. doi: 10.1371/journal.pone.0035857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galli R, Binda E, Orfanelli U, Cipelletti B, Gritti A, De Vitis S, Fiocco R, Foroni C, Dimeco F, Vescovi A. Isolation and characterization of tumorigenic, stem-like neural precursors from human glioblastoma. Cancer Res. 2004;64:7011–7021. doi: 10.1158/0008-5472.CAN-04-1364. [DOI] [PubMed] [Google Scholar]
- Gao X, McDonald JT, Hlatky L, Enderling H. Acute and fractionated irradiation differentially modulate glioma stem cell division kinetics. Cancer Res. 2013;73:1481–1490. doi: 10.1158/0008-5472.CAN-12-3429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert CA, Daou MC, Moser RP, Ross AH. Gamma-secretase inhibitors enhance temozolomide treatment of human gliomas by inhibiting neurosphere repopulation and xenograft recurrence. Cancer Res. 2010;70:6870–6879. doi: 10.1158/0008-5472.CAN-10-1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greve B, Kelsch R, Spaniol K, Eich HT, Gotte M. Flow cytometry in cancer stem cell analysis and separation. Cytometry Part A: the journal of the International Society for Analytical Cytology. 2012;81:284–293. doi: 10.1002/cyto.a.22022. [DOI] [PubMed] [Google Scholar]
- Gupta T, Dinshaw K. Modified optimal fractionation for poor prognosis malignant gliomas: an elusive search. Acta Oncol. 2005;44:105–113. doi: 10.1080/02841860510007611. [DOI] [PubMed] [Google Scholar]
- Hall EJ, Giaccia AJ. Radiobiology for the Radiologist. Lippincott Williams & Wilkins; Philadelphia: 2012. [Google Scholar]
- Hambardzumyan D, Becher OJ, Rosenblum MK, Pandolfi PP, Manova-Todorova K, Holland EC. PI3K pathway regulates survival of cancer stem cells residing in the perivascular niche following radiation in medulloblastoma in vivo. Genes Dev. 2008;22:436–448. doi: 10.1101/gad.1627008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hambardzumyan D, Amankulor NM, Helmy KY, Becher OJ, Holland EC. Modeling adult gliomas using RCAS/t-va technology. Transl. Oncol. 2009;2:89–95. doi: 10.1593/tlo.09100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hambardzumyan D, Parada LF, Holland EC, Charest A. Genetic modeling of gliomas in mice: new tools to tackle old problems. Glia. 2011;59:1155–1168. doi: 10.1002/glia.21142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harpold HL, Alvord EC, Jr., Swanson KR. The evolution of mathematical modeling of glioma proliferation and invasion. J. Neuropathol. Exp. Neurol. 2007;66:1–9. doi: 10.1097/nen.0b013e31802d9000. [DOI] [PubMed] [Google Scholar]
- Harris MA, Yang H, Low BE, Mukherjee J, Guha A, Bronson RT, Shultz LD, Israel MA, Yun K. Cancer stem cells are enriched in the side population cells in a mouse model of glioma. Cancer Res. 2008;68:10051–10059. doi: 10.1158/0008-5472.CAN-08-0786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heddleston JM, Li Z, McLendon RE, Hjelmeland AB, Rich JN. The hypoxic microenvironment maintains glioblastoma stem cells and promotes reprogramming towards a cancer stem cell phenotype. Cell Cycle. 2009;8:3274–3284. doi: 10.4161/cc.8.20.9701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hovinga KE, Shimizu F, Wang R, Panagiotakos G, Van Der Heijden M, Moayedpardazi H, Correia AS, Soulet D, Major T, Menon J, Tabar V. Inhibition of notch signaling in glioblastoma targets cancer stem cells via an endothelial cell intermediate. Stem Cells. 2010;28:1019–1029. doi: 10.1002/stem.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huse JT, Holland EC. Genetically engineered mouse models of brain cancer and the promise of preclinical testing. Brain Pathol. 2009;19:132–143. doi: 10.1111/j.1750-3639.2008.00234.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ignatova TN, Kukekov VG, Laywell ED, Suslov ON, Vrionis FD, Steindler DA. Human cortical glial tumors contain neural stem-like cells expressing astroglial and neuronal markers in vitro. Glia. 2002;39:193–206. doi: 10.1002/glia.10094. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick S, Gelatt CD, Jr., Vecchi MP. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Laperriere N, Zuraw L, Cairncross G, Cancer Care Ontario Practice Guidelines Initiative Neuro-Oncology Disease Site Group Radiotherapy for newly diagnosed malignant glioma in adults: a systematic review. Radiother. Oncol. 2002;64:259–273. doi: 10.1016/s0167-8140(02)00078-6. [DOI] [PubMed] [Google Scholar]
- Li Z, Bao S, Wu Q, Wang H, Eyler C, Sathornsumetee S, Shi Q, Cao Y, Lathia J, McLendon RE, et al. Hypoxia-inducible factors regulate tumorigenic capacity of glioma stem cells. Cancer Cell. 2009;15:501–513. doi: 10.1016/j.ccr.2009.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu G, Yuan X, Zeng Z, Tunici P, Ng H, Abdulkadir IR, Lu L, Irvin D, Black KL, Yu JS. Analysis of gene expression and chemoresistance of CD133+ cancer stem cells in glioblastoma. Mol. Cancer. 2006;5:67. doi: 10.1186/1476-4598-5-67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massey SC, Assanah MC, Lopez KA, Canoll P, Swanson KR. Glial progenitor cell recruitment drives aggressive glioma growth: mathematical and experimental modelling. J. R. Soc. Interface. 2012;9:1757–1766. doi: 10.1098/rsif.2012.0030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michor F, Hughes TP, Iwasa Y, Branford S, Shah NP, Sawyers CL, Nowak MA. Dynamics of chronic myeloid leukaemia. Nature. 2005;435:1267–1270. doi: 10.1038/nature03669. [DOI] [PubMed] [Google Scholar]
- Morris DE, Kimple RJ. Normal tissue tolerance for high-grade gliomas: is it an issue? Semin. Radiat. Oncol. 2009;19:187–192. doi: 10.1016/j.semradonc.2009.02.007. [DOI] [PubMed] [Google Scholar]
- Morton CI, Hlatky L, Hahnfeldt P, Enderling H. Non-stem cancer cell kinetics modulate solid tumor progression. Theor. Biol. Med. Model. 2011;8:48. doi: 10.1186/1742-4682-8-48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norton L. A Gompertzian model of human breast cancer growth. Cancer Res. 1988;48:7067–7071. [PubMed] [Google Scholar]
- Pallini R, Ricci-Vitiani L, Montano N, Mollinari C, Biffoni M, Cenci T, Pierconti F, Martini M, De Maria R, Larocca LM. Expression of the stem cell marker CD133 in recurrent glioblastoma and its value for prognosis. Cancer. 2011;117:162–174. doi: 10.1002/cncr.25581. [DOI] [PubMed] [Google Scholar]
- Phillips HS, Kharbanda S, Chen R, Forrest WF, Soriano RH, Wu TD, Misra A, Nigro JM, Colman H, Soroceanu L, et al. Molecular subclasses of high-grade glioma predict prognosis, delineate a pattern of disease progression, and resemble stages in neurogenesis. Cancer Cell. 2006;9:157–173. doi: 10.1016/j.ccr.2006.02.019. [DOI] [PubMed] [Google Scholar]
- Pistollato F, Abbadi S, Rampazzo E, Persano L, Della Puppa A, Frasson C, Sarto E, Scienza R, D'avella D, Basso G. Intratumoral hypoxic gradient drives stem cells distribution and MGMT expression in glioblastoma. Stem Cells. 2010;28:851–862. doi: 10.1002/stem.415. [DOI] [PubMed] [Google Scholar]
- Pitter KL, Galbán CJ, Galbán S, Tehrani OS, Li F, Charles N, Bradbury MS, Becher OJ, Chenevert TL, Rehemtulla A, et al. Perifosine and CCI 779 co-operate to induce cell death and decrease proliferation in PTEN-intact and PTEN-deficient PDGF-driven murine glioblastoma. PLoS ONE. 2011;6:e14545. doi: 10.1371/journal.pone.0014545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rockne R, Alvord EC, Jr., Rockhill JK, Swanson KR. A mathematical model for brain tumor response to radiation therapy. J. Math. Biol. 2009;58:561–578. doi: 10.1007/s00285-008-0219-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scopelliti A, Cammareri P, Catalano V, Saladino V, Todaro M, Stassi G. Therapeutic implications of Cancer Initiating Cells. Expert Opin. Biol. Ther. 2009;9:1005–1016. doi: 10.1517/14712590903066687. [DOI] [PubMed] [Google Scholar]
- Sharpless NE, Depinho RA. The mighty mouse: genetically engineered mouse models in cancer drug development. Nat. Rev. Drug Discov. 2006;5:741–754. doi: 10.1038/nrd2110. [DOI] [PubMed] [Google Scholar]
- Shih AH, Dai C, Hu X, Rosenblum MK, Koutcher JA, Holland EC. Dose-dependent effects of platelet-derived growth factor-B on glial tumorigenesis. Cancer Res. 2004;64:4783–4789. doi: 10.1158/0008-5472.CAN-03-3831. [DOI] [PubMed] [Google Scholar]
- Singh SK, Hawkins C, Clarke ID, Squire JA, Bayani J, Hide T, Henkelman RM, Cusimano MD, Dirks PB. Identification of human brain tumour initiating cells. Nature. 2004;432:396–401. doi: 10.1038/nature03128. [DOI] [PubMed] [Google Scholar]
- Stamatakos GS, Antipas VP, Uzunoglu NK, Dale RG. A four-dimensional computer simulation model of the in vivo response to radiotherapy of glioblastoma multiforme: studies on the effect of clonogenic cell density. Br. J. Radiol. 2006;79:389–400. doi: 10.1259/bjr/30604050. [DOI] [PubMed] [Google Scholar]
- Stupp R, Mason WP, van den Bent MJ, Weller M, Fisher B, Taphoorn MJ, Belanger K, Brandes AA, Marosi C, Bogdahn U, et al. European Organisation for Research and Treatment of Cancer Brain Tumor and Radiotherapy Groups; National Cancer Institute of Canada Clinical Trials Group Radiotherapy plus concomitant and adjuvant temozolomide for glioblastoma. N. Engl. J. Med. 2005;352:987–996. doi: 10.1056/NEJMoa043330. [DOI] [PubMed] [Google Scholar]
- Uhrbom L, Nerio E, Holland EC. Dissecting tumor maintenance requirements using bioluminescence imaging of cell proliferation in a mouse glioma model. Nat. Med. 2004;10:1257–1260. doi: 10.1038/nm1120. [DOI] [PubMed] [Google Scholar]
- Van Laarhoven PJ, Aarts EH. Simulated Annealing. Kluwer Academic; Dordrecht: 1987. [Google Scholar]
- Verhaak RG, Hoadley KA, Purdom E, Wang V, Qi Y, Wilkerson MD, Miller CR, Ding L, Golub T, Mesirov JP, et al. Cancer Genome Atlas Research Network Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell. 2010;17:98–110. doi: 10.1016/j.ccr.2009.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vescovi AL, Galli R, Reynolds BA. Brain tumour stem cells. Nat. Rev. Cancer. 2006;6:425–436. doi: 10.1038/nrc1889. [DOI] [PubMed] [Google Scholar]
- Walker MD, Strike TA, Sheline GE. An analysis of dose-effect relationship in the radiotherapy of malignant gliomas. Int. J. Radiat. Oncol. Biol. Phys. 1979;5:1725–1731. doi: 10.1016/0360-3016(79)90553-4. [DOI] [PubMed] [Google Scholar]
- Walker MD, Green SB, Byar DP, Alexander E, Jr., Batzdorf U, Brooks WH, Hunt WE, MacCarty CS, Mahaley MS, Jr., Mealey J, Jr., et al. Randomized comparisons of radiotherapy and nitrosoureas for the treatment of malignant glioma after surgery. N. Engl. J. Med. 1980;303:1323–1329. doi: 10.1056/NEJM198012043032303. [DOI] [PubMed] [Google Scholar]
- Wang J, Wakeman TP, Lathia JD, Hjelmeland AB, Wang XF, White RR, Rich JN, Sullenger BA. Notch promotes radioresistance of glioma stem cells. Stem Cells. 2010;28:17–28. doi: 10.1002/stem.261. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.