Coarse-grained simulations of the gating current in the voltage-activated Kv1.2 channel

Significance

Structure-based modeling of gating currents in voltage activation of ion channels presents a major challenge. A part of the challenge involves the difficulties of modeling explicitly the charge motion in the electrolytes between the membrane and the electrodes. The present work overcomes some of the above challenge by using a coarse-grained model in simulating the activation of the Kv1.2 channel. The model yields realistic gating charges and free energy landscapes and allows us to simulate the time dependence of the fast gating current and to elucidate its relationship to the landscape involved in the activation process.

Abstract

Quantitative structure-based modeling of voltage activation of ion channels is very challenging. For example, it is very hard to reach converging results, by microscopic simulations while macroscopic treatments involve major uncertainties regarding key features. The current work overcomes some of the above challenges by using our recently developed coarse-grained (CG) model in simulating the activation of the Kv1.2 channel. The CG model has allowed us to explore problems that cannot be fully addressed at present by microscopic simulations, while providing insights on some features that are not usually considered in continuum models, including the distribution of the electrolytes between the membrane and the electrodes during the activation process and thus the physical nature of the gating current. Here, we demonstrate that the CG model yields realistic gating charges and free energy landscapes that allow us to simulate the fluctuating gating current in the activation processes. Our ability to simulate the time dependence of the fast gating current allows us to reproduce the observed trend and provides a clear description of its relationship to the landscape involved in the activation process.

Advances in the elucidation of the action of voltage-activated ion channels (e.g., refs. 1–6) have provided key information about the relationship between the membrane voltage and the gating process. However, we still do not have a clear picture of the corresponding structure–function correlation. Furthermore, although there has been a significant progress in computational modeling of the energetics of ion channels (e.g., refs. 7–13), the understanding of the voltage activation process is rather limited. The problems include the fact that the exact structural changes have not been fully determined and the energetics of the conformational transition and the coupling to the external voltage are far from being understood.

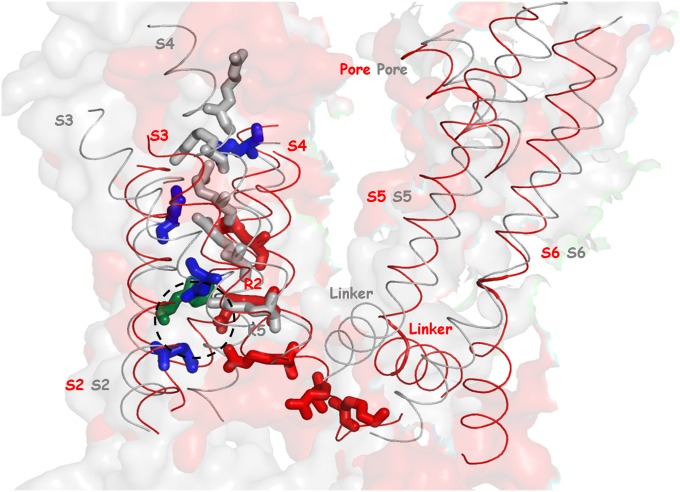
Voltage-activated ion channels regulate electrical activities in cells (e.g., see ref. 14). The voltage-sensing domains (VSDs) of such cannels are composed of four membrane spanning helices (S1–S4), with positively charged arginine and lysine residues in S4. The changes in membrane potential drive the conformational transitions of the VSD (15), which subsequently leads to the opening and closing of the pore domains formed by S5 and S6 helices (16) (Fig. 1).

Fig. 1.

The conformational transition of the full structural models of Kv1.2 between the open (gray ribbon) to the closed state (red ribbon): The gray and red sticks represent positively charged residues (R1, R2, R3, R4, and K5 from Top to Bottom) in the open and closed state, respectively. The blue sticks represent highly conserved negatively charged residues (E¹⁸³, E²²⁶, E²³⁶, and D²⁵⁹ from the closed state). Note that K³⁷⁴ (K5 from the open state) and R²⁹⁷ (R2 from the closed state) are located in the gating charge transfer center (a dashed circle), formed by D²⁵⁹, E²³⁶, and F²³³ (colored green from the closed state).

The gating transitions of the VSD are accompanied by the movements of the charged arginine and lysine residues of S4, generating a voltage-dependent nonlinear capacitance current [called gating current (17)] that precedes the ionic current upon channel opening. The gating charge, which corresponds to the gating current, was hypothesized by Hodgkin and Huxley (18) and was experimentally measured several decades later. This charge has been found to be around 13e in the Shaker K⁺ ion channels (19–21).

Reliable computer simulations of the gating current pose a great challenge. The difficulties start with the absence of an X-ray structure of the closed state. Nevertheless, intensive efforts have been made in building models of the closed state that is consistent with a vast amount of biochemical and biophysical data (9, 10, 12). These studies led to a reasonable model for the closed form of the K⁺ voltage-activated ion channel (see ref. 22 for review) where the S4 helix undergoes a predominant movement relative to the fixed S3 helix, sliding 10∼14 Å normal to the membrane axis and rotating counterclockwise (as viewed from the extracellular regions). However, this model is still tentative. Another problem is associated with the fact that the available calculations of the gating charge (except those reported in ref. 8) are based on the assumption that the normalized membrane potential is linear (11, 13) or is obtained by solving the linearized Poisson–Boltzmann equation with an unjustified dielectric constant (12, 23). Even a more microscopic approach (11) is based on the linearization assumption (see discussion in ref. 8). Furthermore, even a recent advance (13) that simulated a voltage activation event had to use a nonphysiological high external field (up to ±750 mV) to drive conformational transitions and has not determined the actual free energy barriers. Thus, it is still extremely challenging to extract reliable kinetic information (e.g., gating current) and the underlying free energy barriers by microscopic simulations.

To overcome the above difficulties, we extended our coarse-grained (CG) model (24) to include the effects of electrolyte and external potential on the energetics of the membrane system, with emphasis on reliable description of electrostatic effects (25). This model has been successfully applied to the voltage activation of the Kv1.2 channel (8), reproducing the energetics for the open and closed channel and providing a unique direct way of evaluating the gating charge, i.e., by simulating the actual electrolyte distribution that arises in response to the movements of charged residues in response to the changes in membrane potential.

Here, we moved in a more quantitative direction, focusing on simulating the gating current at different external membrane potentials by constructing the full structural models of intermediate Kv1.2 states and evaluating their energetics using our CG model. The simulations reproduced realistic free energy landscapes that allow us to simulate the fluctuating gating current in the activation processes. Our ability to simulate the time dependence of the fast gating provides a detailed picture of the molecular origin of the gating current, thereby relating it to detailed information about the activation process.

Key Elements of the Modeling Approach

Our CG treatment (which is outlined in Methods and SI Text) is aimed at modeling the protein/membrane system and its interaction with the external potential. The modeling of the protein/membrane system has been described in detail elsewhere (8), and we only want to emphasize that our simulation system (Fig. S1) includes explicitly all of the key elements of the system.

Overall, the explicit grid model reflects a compromise between the fully microscopic models of the electrolyte (in an implicit solvent) and a macroscopic model.

Results and Discussion

The Structural Model.

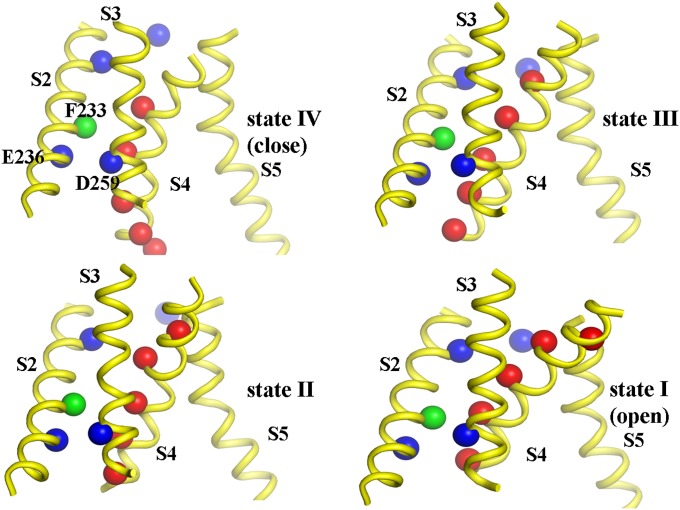
The structural models of Kv1.2 were constructed in accordance with the gating model of voltage sensing of Mackinnon and coworkers (5), whose study identifies the gating charge transfer center (formed by D²⁵⁹, E²³⁶, and F²³³) that is thought to facilitate the movements of the VSD by solvating a positively charged Arg or Lys residue (R1, R2, R3, R4, or K5, which corresponds to R²⁹⁴, R²⁹⁷, R³⁰⁰, R³⁰³, or K³⁰⁶) “inside” the membrane.

The present model extends directly the previous structural models of the VSD of the Shaker channel (10), by modeling the full intermediate structures of Kv1.2 that include pore domains (SI Text). Depending on a specific positively charged residue occupying the gating charge transfer center, the intermediate structures of Kv1.2 were classified as the O, C1, C2, C3, or C4 state (10); for example, K5, R4, R3, R2, and R1 interact with the gating charge transfer center in the O, C1, C2, C3, and C4 state, respectively, and was named as the first, second, third, fourth, and fifth states (Fig. 2). The fifth state was rejected due to the reason explained below and the four-states model is used in all simulations reported in the present study. Overall, the present model is similar to that of Henrion et al. (10), which supports the sliding-helix or helical screw model (26). More details about the structural modeling are given in SI Text.

Fig. 2.

The sequential movements of positively charged residues (red spheres) upon depolarization. The highly conserved hydrophobic residue (F²³³) in the gating charge transfer center (formed by F²³³, E²³⁶, and D²⁵⁹) is shown as a green sphere. The other key negatively charged residues (E¹⁸³, E²²⁶, E²³⁶, and D²⁵⁹) are shown as blue spheres. The gating transitions are associated with the predominant translational/rotational movements of the S4 helix along the relatively fixed S3 helix, sliding around 13 Å normal to membrane.

The Energetics of the Activation Process.

Obtaining the free energy landscape of conformational transitions of channel gating by explicit all-atom molecular dynamics (MD) simulations is still extremely challenging, although recent all-atom MD simulations of voltage sensing in the Kv1.2–2.1 channel appeared to provide a possible mechanism of conformational transitions and identified several intermediate states. However, the timescales of hopping between intermediate states are obscure due to high voltage applied (13), precluding one from obtaining quantitative free energy profiles at a given voltage.

Fortunately, our CG model, which emphasizes reliable electrostatic effects of proteins, overcomes some of the above problems by capturing a semiquantitative free energy landscape of the gating transitions between the closed and open states (8). Of course, this requires more systematic mapping than that used in our previous work that focused only on the initial and final states. Thus, we extended our previous study by the modeling intermediate states of the full Kv1.2 channel and evaluating their energetics, in order to obtain the complete free energy landscape at different voltages. In the current study, we used recent modifications of the CG energetics that included, in addition to the electrostatics effect of the protein, the electrolyte and the external voltage, also the hydrophobic contributions to the overall free energy using residue- and environment-specific hydrophobic scale with an implicit membrane model (27). The free energies were evaluated at two different voltages, −50 and 0 mV, taken as representative voltages for the low depolarization (less than −40 mV and greater than −90 mV) and the high depolarization regime (greater than −20 mV), respectively (28) (Table S1).

The calculated CG barriers for transitions between different states appeared to be much more reasonable than the barrier obtained in our previous work (that simply involved a very qualitative steered molecular dynamics simulation based only on the initial and final states). The improved results reflects the fact that the present work modeled all of the intermediate states of Kv1.2 and interpolated the transition structures (Methods and SI Text) along well-defined gating transition pathways that is consistent with the relevant experiments (5, 10). However, our error range for running with slightly different structures was found to be about 5 kcal/mol. Thus, in determining the free energy landscape, we sorted pairs of states (e.g., II and III) with energy differences that are closest to the corresponding observed energetics. We then evaluated the barrier for the transition between the two states of each sorted pair. This procedure reduced significantly the error limit in determining the barriers. After determining the optimal CG landscape, we moved to a related “consensus” landscape that has been based on the available experimental information. Both the raw CG landscape and the consensus landscape for 0 mV are given in Fig. S2.

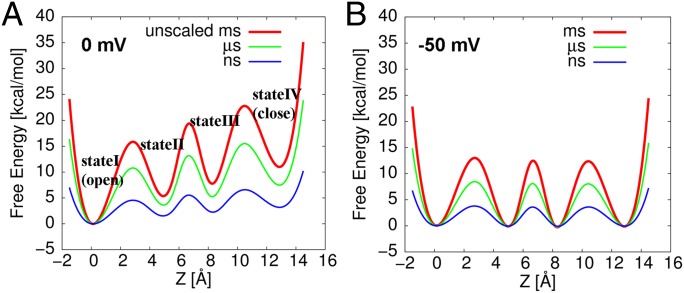
As seen from Fig. S2, the overall shape of the consensus free energy profile at 0 mV is characterized by unidirectional conformational transitions (29, 30). The overall free energy difference between the fourth (close) to first (open) state is approximately −12 kcal/mol, in agreement with the fact that the conformational equilibrium in this high depolarization regime is shifted toward to the first state (open state) (Table S1). That is, considering the observation that the experimental gating charge is close to its maximum value at this voltage (i.e., the channel is fully activated at this voltage), this overall free energy difference is qualitatively reasonable. In fact, the CG result is in good agreement with an experimental free energy difference of −14.6 kcal/mol at 0 mV, which is estimated from the observed Q–V (gating charge versus voltage) data for the Shaker channel (31). The free energy barrier for the initial transition (from the fourth to third state) is about ∼11 kcal/mol, which yields the dwell time of ∼1 ms with the effective frictional constant, determined below by our renormalization approach (Results and Discussion). It should be also noted that the energetics for transition between the first state and the second state coincidently matches well the barrier between the O and C1 states obtained (32) from all atom umbrella sampling free energy calculations. Notice that this slow component of gating transitions should be distinguished from the fast component of gating transitions that occurs at the timescale of ∼10 µs (33) and reflects the initial response of channel to the change in membrane potential from holding potential.

The consensus profiles for 0 and −50 mV are displayed in Fig. 3 A and B. Fig. 3A shows the (consensus) free energy profile (red curve) at 0 mV, and two other profiles (green and blue curve) obtained by scaling down the original profile for the renormalization treatment described below. In contrast to the trend for V = 0 mV, the overall shape of the free energy profile at −50 mV is characterized by bidirectional conformational transitions (Fig. 3B). The free energy differences between equilibrium states are close to 0 kcal/mol (Table S1), showing all states are almost equally populated at this voltage. Furthermore, the free energy barrier for the transition that opens the channel (the transition from the second to first state) is the highest (∼13 kcal). This is consistent with the qualitative experimental picture of a delayed channel opening in the low depolarization regime (28, 29, 34).

Fig. 3.

The free energy profiles along the gating transition pathway, estimated from our CG energetics, at (A) 0 mV and (B) −50 mV. The green and blue curves are obtained by scaling down the original free energy profile (red curve) by 0.29 and 0.68, respectively. The color code for the timescale of the gating transitions from each profile is included at the top right corner.

The contributions to the CG energies for all quasiequilibrium and transition states at 0 and −50 mV are summarized in Table S1. As seen from the table, the total free energy for both the high (0 mV) and low (−50 mV) depolarization is correlated with the calculated electrostatic free energy, indicating that the electrostatic effect is the main factor that determines the shape of the landscape. However, it is important to note that hydrophobic residues might play a larger role than that found here. For example, it has been suggested that hydrophobic residues in the VSD have a critical role on the formation of paddle motif in the open state (15, 35), stabilizing preferentially the open state. Obviously, this issue requires detailed analysis of the corresponding mutational effects. However, it seems to us that the observed effect of hydrophobic residues in the S4 helix may reflect the role of the hydrophobic region in controlling the gate for ion penetration (see figure 6 in ref. 8). In this case, the increased conductance observed upon mutations of the end of S3 and the beginning of S4 to more hydrophobic segment (15, 35) might not reflect a simple stabilization of the open form. It is possible that this mutational effect reflects hydrophobic destabilization of the penetrating ion in the gate region of the closed channel. In such a case, the destabilization can lead to a stronger force toward the open state. Of course, this hypothesis cannot be examined without simulating the ion conductance and this coupling with the gate opening, a task that can clearly be performed with our model.

A Renormalization Treatment of the Conformational Transitions.

The estimation of the timescales of gating transitions between equilibrium states of voltage-gated ion channels poses a great challenge for molecular simulations due in part to the incomplete description of the coupling between the molecular mechanics description of the proteins and the external voltage. To overcome this challenge, we used our consensus 1D surface and the renormalization approach (36). In this approach, the effective frictional constant in a 1D Langevin dynamics (LD) simulation is estimated for the reduced model (the 1D free energy surface) by applying a relatively strong harmonic potential to both the CG structure model and the reduced model, while adjusting free energy surface and frictional constant of the reduced model until the time-dependent response of both models is similar. The renormalization process is described in Figs. S3 and S4, where the resulting optimal friction is 50 ps⁻¹. Now, once we determine the friction, we can remove the extra harmonic potential and run LD on the potential of the reduced model. However, we can obtain the relevant results by using a scaled potential without the need of extremely long simulation time. That is, as was found in our early studies (e.g., ref. 37), it is useful to scale down the effective potential and run LD simulations in a shorter time, calculate the dwell time (or the first passage time), and then convert the results of the scaled potential to that of the real potential by multiplying the dwell time by the Boltzmann factor for moving from the real potential to the scaled potential. In the present case, we scale the potential by 0.29 and obtained for the initial transition (from the fourth to third state) an average dwell time of 0.68 ns, which is then extrapolated to 1.17 ms (Figs. S4A and S5) by using the correction associated with the change in the Boltzmann factor due to the difference between the scaled and unscaled potentials. It is also encouraging to note that the estimated time constant is ∼1 ms with our optimal friction of 50 ps⁻¹ and Kramer theory is consistent with the average observed dwell time of 1.17 ms (30).

Exploring the Nature of the Gating Current.

A major part of the present study focuses on the gating current. Thus, we would like to clarify some points, which are not widely recognized, about this quantity. That is, the gating charge is a parameter that represents the shift of the relative free energy difference between the closed and open configurations, due to the change in an external potential. This parameter, which was initially postulated by Hodgkin and Huxley (18), provides a qualitative explanation of the coupling of the external potential to the channel activation. The evaluation of the gating charge is usually done in an indirect way, using reasonable but not necessarily microscopic assumptions. This crucial problem is discussed in SI Text, section S2.

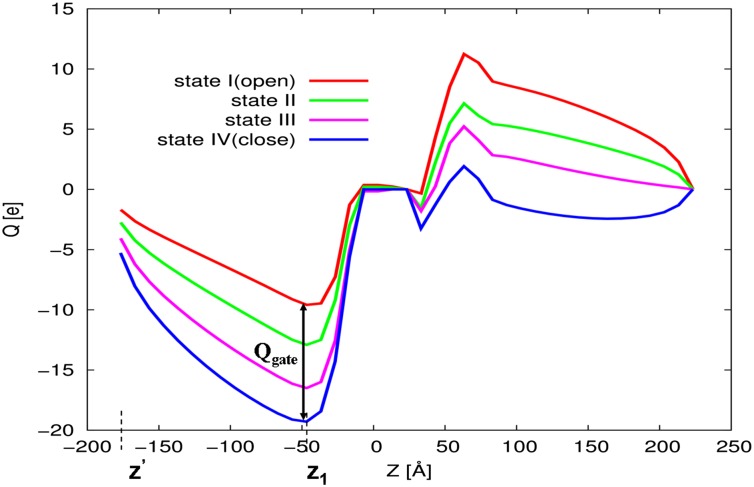
In view of the consideration of the SI Text, section S2, we focused here on obtaining the gating current, which is a real observable. This was done by starting from the fact that our CG model evaluates the charge distribution in the electrolytes rather that just the motion of the charges of the protein (as done by other approaches). This allowed us to determine the gating charges using the procedure described in Fig. 4, where we obtained the gating charge (for each protein configuration) by the following:

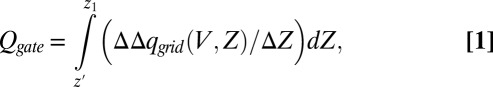where 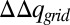is the difference between the accumulative sum of 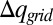of the open and closed channels, and z₁ is the point to the left of the membrane where the electrolyte charge distribution near the membrane changes sign. At this point, the integrated charge reaches a plateau and then starts to decrease. Note that integral evaluates the charges generated by the current after it equilibrates on the left side of the membrane, but before it actually penetrates the membrane.

Fig. 4.

The gating charges (calculated by Eq. 1 from the electrolyte charge distribution) for conformational transitions between the intermediate Kv1.2 states. The gating charge transferred for the last two transitions (from III to IV and II to III) are slightly larger than the gating charge for the initial transition (from IV to III).

Now the unique twist in the present work is the move from the gating charge to the gating current. That is, assuming an instant equilibration of the electrolyte charges with the protein charge, we obtain a parametric dependence of the electrolyte charges on the protein structure. Thus, we have the following:

Now, because we can evaluate 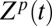(i.e., the z component of the center of mass of arginine residues R1, R2, R3, and R4 in the S4 helix of the VSD) by our renormalization approach, we can also evaluate I_gate. That is, the gating current can be simulated by using the results of the LD simulations with the scaled free energy surfaces (green and blue curves in Fig. 3) with effective frictional constant, determined from our renormalization approach (Results and Discussion). The free energy surface divides to four regions, each of which represents a quasiequilibrium state (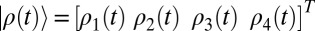), obtained from the normalized histogram of the population of the gating transitions. Then the slow component of the gating current is calculated by writing 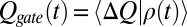and then differentiating 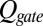and obtaining the following:

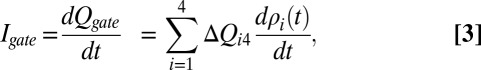where 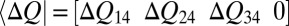is a gating charge vector and each element corresponds to the charge transferred from the fourth (close) to the other state (Eq. 1 and Fig. 4).

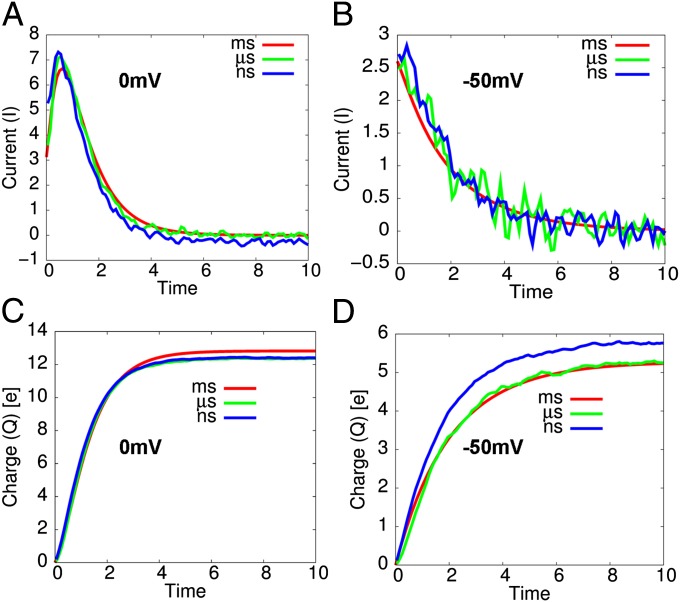
The above approach has been used to evaluate the gating current and charge profiles, where we applied the renormalization approach (while running LD with the renormalized friction) on the scaled free energy surfaces (green and blue curves in Fig. 3). The calculated results are summarized in Fig. 5, where as shown in Fig. 5A, the gating current in a high depolarization (0 mV) is characterized by a rising phase preceding a decay phase (see Fig. S6A for the convergence profiles of gating current). The rising phase has been observed in several experimental studies (34, 38) and its origin has been predicted by a kinetic modeling of the gating current with multiple states (29, 34), where the rate of initial transition is slower than the rates of the following transitions. The simulated dwell time distributions for transitions between states (i.e., from the fourth to third, the third to second, and the second to first) shows the same order of time constants as those from the kinetic study of gating current with experimental data (Fig. S5). In addition, the shape of the calculated gating current profile for the timescale of nanosecond (green curve in Fig. 5A) or the microsecond range (blue curve in Fig. 5A) is in excellent agreement with the gating current, occurring in the millisecond range (red curve in Fig. 5A), that is obtained using experimental rate constants [by solving kinetic master equation with the four equilibrium states assumed via spectral decomposition—often called the Q-matrix approach (39)]. Note that, in the millisecond range, the barriers are sufficiently high that the kinetics follows the Boltzmann probability and kinetic treatments are expected to be reliable. At any rate, as shown in Fig. 5C, the equilibrium gating charge is ∼13e, as expected from the unidirectional characteristic of gating transitions in the high depolarization regime (29, 30).

Fig. 5.

The gating current profiles at (A) 0 mV and (B) −50 mV with their corresponding gating charge profiles in C and D, respectively. (A) The rising phase of the gating current followed by a decay phase is observed at 0 mV. (B) The corresponding gating current profiles at −50 mV shows large fluctuations due to a bidirectional characteristic of gating transitions at this voltage.

In contrast to the trend for V = 0 mV, the gating current in a low depolarization (−50 mV) shows a single exponential-like decay (Fig. 5B), indicating that the timescale of transitions in the low depolarization regime is dominated by a single slower final transition that opens the channel (28, 29, 34). A single exponential-like gating current profile in this low depolarization regime is broadly consistent with the gating current profile observed experimentally (34, 38). In addition, we considered the gating current obtained from a voltage-dependent (phenomenological) rate constant expression (red curve in Fig. 5B). It was found that this gating current, which occurs in the timescale of milliseconds, is in excellent agreement with the gating current, occurring in the timescale of nanoseconds or microseconds (green curve or blue curve in Fig. 5B). In addition, the gating currents also show noisy profiles, fluctuating rapidly in a small timescale (Fig. S6B), which originates from the bidirectional characteristic of the gating transitions in this voltage range. As shown in Fig. 5D, the equilibrium gating charge is ∼5e, in a good agreement with the corresponding experimental result (34, 38).

At this stage, it is important to examine the initial response of the gating current to the change in the applied voltage, because this has been considered as a key probe for the property of the system (33). To accomplish this task, we run LD trajectories on g₁ (the surface with the initial potential) and then switched the potential to g₂ (the surface with the new potential) at different times and evaluated Z(t) (where Z is the average z component of the center of mass of four arginine residues). This procedure gave <Z(t)>₁, where the corresponding current is the desired short time behavior after turning on the new potential. The results of our simulations are summarized in Fig. S7, which shows the fast gating current (and charge), for an initial response of the channel to the change in the membrane potential [(A) from −50 to 0 mV and (B) the opposite change]. When the potential is switched from the lower (−50 mV) to the higher depolarization (0 mV) values, the fast gating current shows the same characteristic profile as the millisecond gating current (red curve in Fig. S7A), but with the faster timescale of approximately picoseconds (extrapolated to approximately microseconds). The fast gating current is also associated with barrier crossings from the state IV (closed) to state III (see green curve in Fig. S7A) and the corresponding contribution is larger than that for the relaxation within state IV. This contribution is given by blue curve in Fig. S7A. However, the fast gating current, responding to a drop in the membrane potential (from 0 to −50 mV), shows an inverted profile (red curve in Fig. S7B) with a predominant relaxation within the fourth state (blue curve in Fig. S7B).

The above fast gating current profiles appear to be consistent with the subtle difference of the free energy profiles in a low and high depolarization (Fig. 6). That is, since the barrier between state III and state IV is shifted toward state IV in the high depolarization case (when the membrane potential increases), the barrier crossing events and the corresponding positive peak are favored (although they are less probable than the relaxation events). Conversely, the relaxation events (that lead to a negative peak) are the predominant contributions, when the membrane potential drops. Finally, the purple curve in Fig. S7 A and B corresponds to the contribution of response from the right hand side of state IV. Note that we did not consider the transition of state V that might be important in deep hyperpolarization.

Fig. 6.

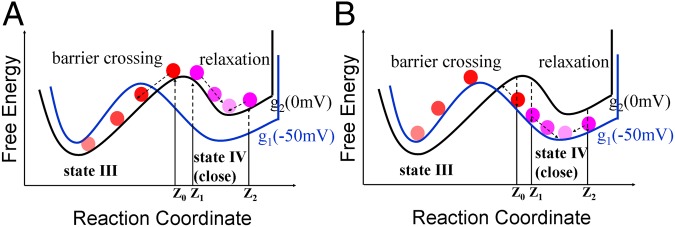
A schematic description of the origin of the fast current for the transition from −50 to 0 mV. (A) The gating transition due to the change of the membrane potential from −50 mV (blue curve) to 0 mV (black curve) at Z₀ results in the (forward) barrier crossing events (red spheres). However, the transitions at Z₁ and Z₂ result in the backward and forward relaxation events, respectively (purple spheres). In this case, the barrier crossing events contribute predominantly to the total fast gating current (Fig. S7 A and B). (B) The reverse gating transition due to the change of the membrane potential from 0 mV (black curve) to −50 mV (blue curve) at Z₀ results in the (forward) barrier crossing events (red spheres). However, the transitions at Z₁ and Z₂ result in the backward and forward relaxation events, respectively (purple spheres). In this case, the backward relaxation events contribute predominantly to the total fast gating current (Fig. S7 C and D). Also notice that the shift of transition state at 0 mV is caused by a combination of the destabilization of the fourth state (blue curve) and the stabilization of the third state (green curve).

To provide a qualitative rational for the above results, we consider the following probability:

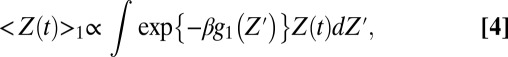where Z′ is the point where the potential is switched. Here, we take trajectories that start at different Z′ and follow their time dependency, Z(t), over g₂, while averaging the chance of having such trajectories over the Boltzmann distribution of g₁. The qualitative idea behind Eq. 4 is illustrated in Fig. 6. That is, a trajectories from Z₀ near to maximum of g₁ will move downhill to the left on g₂ and contribute dominantly to the short time gating current, although the chance for being at this point is small because of the factor 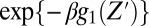. However, the trajectories from Z₁, which is further to the right, will not continue to the left on g₂ and these trajectories that contribute negatively to the short time gating current will be smaller. The other interesting trend is the response of the system to change from positive to negative potential (0 to −50 mV) or jumping from g₂ to g₁. In this case, we have two types of dominant trajectories, those that start from the right of the minimum of g₂ and those that start from Z₁. The most consistent picture emerges when we have small contribution from the Z₂ trajectories. This is consistent with the situation where the motion to the right is limited due to a large barrier for the state IV to state V transition. However, the slope on the right side should be smaller than that on the left, since fast moving trajectories would lead to a highly-peaked gating current. This type of landscape (see Fig. 6) has been incorporate in our model, by a reflective barrier in the far right side, and produced the observed behavior. Although this is not a fully first principal model, it reflects an plausible situation from calculation features. This will result in a negative current, which is consistent with the experimental observation.

Altogether, the fast gating current is thought to arise from an initial response of a channel to the change in membrane potential, which is in line with the origin of the fast gating current discussed by Bezanilla and coworkers (33). However, their 1D phenomenological free energy surface (with a shift of the minimum of the closed state at different membrane potentials) does not seem to provide a chance for barrier crossing events as a response to an increase in the membrane potential. On the other hand, our simulations indicate that the barrier crossing events are likely to predominantly contribute to the fast gating current in response to an increase in the membrane potential as the relaxation events are likely to prevail in response to a membrane potential drop.

Concluding Remarks

This work explored our ability to use our recently developed CG model to simulate reliably the effect of external electrode potentials on the gating current in ion channels as well as the molecular origin of the early gating current. The model involves our early CG model of the protein membrane system and a unique model of the electrolyte solution and the external electrodes. The electrolyte model allows us to navigate between the more microscopic Monte Carlo modeling to faster mean field models and helps in providing insight on the effect of external potentials.

Applying the CG model to the study, the energetics of the voltage-activated Kv1.2 channel captures the balance between the protein conformational energy and the applied potential, without the need of any specially adjusted parameter. The CG simulations also provided a clearer nonstandard description of the gating current and gating charge, allowing one to look directly at the change in the electrolyte charges rather than the interaction between the linearized external potential and the protein charges. Finally, our study has introduced a landscape-based simulation of the gating current fluctuations and converts it to the actual gating current.

The CG model may appear to some as an oversimplification that overlooks substates of the real surface and thus the origin of the fluctuating current. However, our renormalization approach generates an effective friction that should represent reliably the fluctuations between the different intermediate states. The model allows us to explore the fluctuating fast gating current and its time and voltage dependence.

It should be noted that we explore here a similar question to that examined by the studies of Bezanilla and coworkers (33). The difference is that we insist on obtaining the current from structure-based simulations, whereas the alternative approaches try to construct phenomenological effective potential based on “inverting” the observed trend. The difference reflects our long-standing philosophy that, in complex biological systems, it is practically impossible to construct a correct experimentally based effective potential. However, one can use experiment information to refine the shape of simulation-based effective landscapes. A relevant example is the issue of the temperature dependence of the fast gating current (33). Although reproducing this effect should be very instructive, it seems to us that it reflects the barrier crossing effect (Results and Discussion, Exploring the Nature of the Gating Current), which would require further studies. In fact, in view of our current successes with the CG potentials that have similar shapes in the different states, we find it unlikely that the observed effect reflects the phenomenologically deduced shape of the potential. However, the challenge of quantifying the observed effect is clearly a major benchmark for our approach.

The present work focused on our unique ability to model the short time gating current and explore its origin. The same approach can be applied to studies of the long time ion penetration current and its relationship to the applied voltage. Exploring the fundamental questions of the coupling between the channel conformational transitions and the energy of ion penetration should help to shed light on the effect of mutations that change the effect of the applied potential and provide improved molecular picture of the action of voltage-activated ion channels.

Methods

Our general strategy involves a refinement of our recent CG model and the extension of this model to the incorporation of an external potential in the simulation of protein/membrane system. The protein system is treated by a CG model that describes the main chains by an explicit model that represents the side chains as a simplified united atom model, whereas the membrane is described by a grid of nonpolar groups. This CG model provides a more advanced treatment of electrostatic effects than most current CG models (for more details, see ref. 25). Some details are provided in SI Text.