Strike a Balance: Optimization of Backbone Torsion Parameters of AMBER Polarizable Force Field for Simulations of Proteins and Peptides

Abstract

Based on the AMBER polarizable model (ff02), we have reoptimized the parameters related to the main-chain (Φ, Ψ) torsion angles by fitting to the Boltzmann-weighted average quantum mechanical (QM) energies of the important regions (i.e., β, P_II, α_R, and α_L regions). Following the naming convention of the AMBER force field series, this release will be called ff02pol.rl The force field has been assessed both by energetic comparison against the QM data and by the replica exchange molecular dynamics simulations of short alanine peptides in water. For Ace-Ala-Nme, the simulated populations in the β, P_II and α_R regions were approximately 30, 43, and 26%, respectively. For Ace-(Ala)₇-Nme, the populations in these three regions were approximately 24, 49, and 26%. Both were in qualitative agreement with the NMR and CD experimental conclusions. In comparison with the previous force field, ff02pol.rl demonstrated good balance among these three important regions. The optimized torsion parameters, together with those in ff02, allow us to carry out simulations on proteins and peptides with the consideration of polarization.

Introduction

In the last 2 decades, various molecular mechanics force fields have been developed based on ab initio quantum mechanical (QM) calculations and empirical experimental data. They successfully extended the ability of ab initio QM study and allowed studies of systems that are far beyond the capability of QM calculations. There are presently several types of molecular mechanics force fields. Among them, some have targeted the large audience of organic chemistry. Examples of these force fields include the work of Allinger’s group^1–4 and others who have been making efforts to achieve increasingly elaborate and accurate force fields for studying organic-related compounds. These force fields have found their ways in such applications as ligand binding. Another class of force fields is designed to study biological macromolecules such as proteins and DNAs. Some of the renowned physics-based force fields in this category include AMBER,^5–9 CHARMM,^10–12 OPLS,^13–16 and GROMOS.^17–19 Detailed accounts of the evolution and advances of these force fields have been reviewed recently.^20,21 With the growing computer power, simulations beyond nanoseconds have become increasingly routine. The constant updates in the force fields have also made them increasingly sophisticated. Together, physics-based molecular mechanics modeling has become an indispensable component of the theoretical tools to explore biomolecular structure and dynamics and biological processes.^22–26

Despite many successful examples,^22–26 molecular modeling is still far from reaching the accuracy and reliability demanded by the increasingly sophisticated applications. Among many contributing factors, the additive (fixed) partial charge model imposes serious limitations to the ability of molecular mechanics. One of the limitations is its inability to model varying solvation environment. However, the dynamic nature of biological molecules and the inherent heterogeneous environment in biological systems dictate the constantly changing solvation environment. For example, in the process of protein folding, a hydrophobic side chain may have strong preference to be buried inside the protein core in the native state. Yet, the same side chain may be partially exposed to water at the nonnative states. The substantial dielectric difference between the two states needs to be accounted for in the simulation. Therefore, development of the polarizable protein force field has also been the pursuit of many groups, including work of Berne–Friesner groups^27–29 and their attempt to implement their fluctuating charge model in the OPLS-AA force field,^30,31 work of Brooks–Mackerell–Roux groups^32–34 on the CHARMM force field, and work of the Ponder group^20,35,36 on their AMOEBA force field.

In the conventional models, the electrostatic interactions are modeled by fixed atomic charges. The average polarization effect due to the presence of surrounding can be modeled by increasing the atomic charges. Thus, the typical partial charges in the molecular mechanics force fields are about 10% larger than the gas-phase charges (e.g., the Cornell et al.⁹ charge set). Recently, in the development of the AMBER ff03 force field, Duan et al.³⁷ applied a continuum solvent model to calculate the electrostatic potentials in organic solvent for the derivation of partial charges. Despite these improvements in the fixed point charge models, in comparison, polarizable models have the advantage to be able to model the varying solvation environment with a unified treatment of the electrostatic interaction because the polarizable model can mimick the spontaneous polarization.

Studies on small systems with polarizable models appeared very early. Some of the pioneering studies^38,39 that have helped to lay the ground work for the development of polarizable model included those of Kollman and his coworkers.⁴⁰ It was found that the polarizable force field can provide good representation in both the gas phase and the condensed phase.

In AMBER family force fields, development of the nonadditive polarizable force field was the late Peter Kollman’s long-standing interest.^{41– 44} The first comprehensive implementation of a full-fledged polarizable force field for proteins (AMBER ff02) was released by late Kollman and Cieplak⁴⁰ in 2002, as part of the AMBER 7.0 simulation package.⁴⁵ Unfortunately, Kollman did not see a practical application before his untimely death. Because of the interruption, the ability of ff02 to model proteins and peptides has never been carefully examined, and its behavior remains largely unknown. Nevertheless, it has been shown that the inclusion of polarization improves the agreement of hydrogen bonding free energy of NMA–water with the ab initio value.⁴⁰ Therefore, it is clear that inclusion of polarization improves the accuracy of electrostatic representation. What remains untested and unoptimized is its accuracy to represent the important peptide conformations.

In this work, we first examined the AMBER ff02 polarizable force field using alanine dipeptide in water as the model system. A 30.0-ns MD simulation was performed at 300 K on an alanine dipeptide in a truncated octahedral box filled of 450 polarizable POL3⁴³ water molecules. Figure 1 shows the conformational distribution. In comparison to the Ramachandran plot derived from high-resolution known proteins structures there were obvious discrepancies.⁴⁶ Notably, the dominant area from the ff02 simulation was around (Φ = −150°, Ψ = 0°), which is not a highly populated area on the experimental Ramachandran plot. Instead, experiments have concluded that polyproline-like (P_II) is the dominant conformation of short peptides in aqueous solution. Obviously, the force field needs to be optimized before it can be applied.

Figure 1.

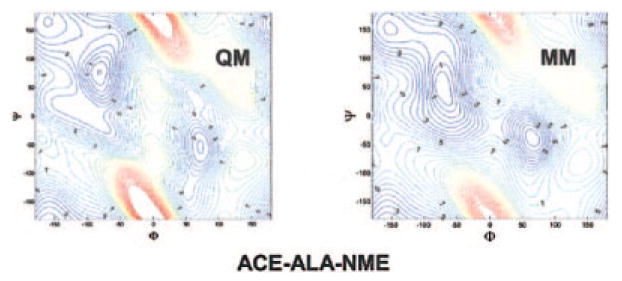
(Φ, Ψ) conformation distribution of Ace-Ala-Nme in POL3 water, simulated by ff02 for 30 ns. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The disagreement, however, is not surprising. Ideally, one may expect that the inclusion of the polarization effect in the conventional force fields would improve the accuracy, including the balance between the important conformations. However, the approximations in the model building and parameterization make some of the empirical parameters nontransferable. In particular, the torsion parameters account for both the backbone rotation energy and errors due to other factors (e.g., truncation of higher order terms). Therefore, backbone torsion parameters have been developed typically at the final step based on the QM energies. In the ff02 implementation, although the partial charges were refitted under the new polarizable model and a new energy term (polarization energy) was added, other parameters, including van der Waals, bond, bond angle, and torsions, were taken from the parm99 parameter set that was optimized for the Cornell et al charges.⁹ Strictly, it would be better to reoptimerize all parameters in the new model. However, the bond stretching, angle bending, and torsion rotation (except for the backbone torsion) only play minor roles in determining protein structures. At this stage, we elect to focus on the most crucial backbone torsion parameters as the first step of optimization. In this work (referred as ff02pol.rl hereafter), we adopt all parameters in ff02 except for the backbone torsion parameters.

Gnanakaran and Garcia^47,48 have recently showed how the AMBER94⁹ can be improved by just disabling the backbone torsion energy. They⁴⁷ found that the MD simulations of alanine-rich peptides with the modified AMBER94 can reproduce experimental results better.

The AMBER Polarizable Model

There are currently three major approaches to account for the polarization effect in protein force fields. The first is the induced dipole model, which is based on the conventional model with polarization energy terms. In this approach,^38,39 each atom is modeled as a monopole and an inducible dipole. The polarization effect is mimicked by the dipole–monopole interactions between permanent charges and inducible dipoles and the dipole–dipole interactions between the induced dipoles. In the fluctuating charge model, polarization is modeled by the variable charges. In this approach,^27–29 each atom is assigned a chemical potential that determines the charge flow. Results^30–33 of this approach in CHARMM and OPLS-AA force fields have been reported. The third approach³⁴ is based on the Drude oscillator,⁴⁹ in which each real atom is attached to a fictitious particle whose position is determined by its electrostatic environment.

The AMBER polarizable force field ff02 utilizes the first approach, which considers the induced dipoles. The total energy in ff02 is the minimalist (eq. 1) augmented by the polarization energy (eq. 2).

$$E_{\text{point}}=\sum _{\text{bonds}}{K}_r{(r-r_{\text{eq}})}^2+\sum _{\text{angles}}{K}_{\theta }{(\theta -{\theta }_{\text{eq}})}^2+\sum _{\text{dihedrals}}\frac{V_n}{2}[1+cos(n\phi -\gamma )]+\sum _{i<j}\left\{\left[\frac{A_{ij}}{R_{ij}^{12}}-\frac{B_{ij}}{R_{ij}^6}\right]+\frac{q_i{q}_j}{R_{ij}}\right\}$$ (1)

$$E_{\text{pol}}=-\frac{1}{2}\sum _i{\alpha }_i{\mathbf{E}}_i^{(0)}·{\mathbf{E}}_i.$$ (2)

In eq. (1), the four terms represent the bond stretching, angle bending, torsion rotating, van der Waals, and electrostatic energies, respectively. In eq. (2), α_i is the isotropic polarizabilities of the ith atom, E_i⁰ is the electrostatic field due to the permanent charges. E_i is the electrostatic field on atom i due to all other charges and induced dipoles

$${\mathbf{E}}_i^0=\sum _{j\ne i}{q}_j\frac{{\mathbf{r}}_{ij}}{r_{ij}^3}$$ (3)

$${\mathbf{E}}_i={\mathbf{E}}_i^0+\sum _{j\ne i}{\mathbf{T}}_{ij}·{\mu }_j{T}_{ij}=\frac{1}{r_{ij}^3}\left(3{\mathbf{r}}_{ij}\frac{{\mathbf{r}}_{ij}}{r_{ij}^2}-1\right).$$ (4)

Like the permanent charges, the induced dipoles also generate electrostatic field. The charges fitted by conventional RESP are thus no longer applicable. Cieplak and Kollman⁴⁰ have developed an iterative procedure to fit the charges. In this procedure, the point charges are first fitted to the difference between the QM electrostatic potential field and that generated by the induced dipoles [i.e.. ESP(QM)-ESP(induced)]. The fitted charges were then used to calculate the electrostatic fields due to the permanent charges, which also induces the dipoles is and due to the induced dipole. Such procedure was iterated until the convergence of total dipole moment reach 0.001 Deybe. The induced dipole of an atom due to other point charges was computed within the framework of AMBER used to calculate the electrostatic interactions. The 1–2 and 1–3 interactions were excluded, and the 1–4 interaction was included. In the polarizable force field (e.g., ff02), the charges were fitted against gas phase electrostatic potentials for its ability to take into account the polarizable effect averagely. In ff02, the charges were fitted at B3LYP/cc-pVTZ//HF/6-31G*. This is contrast to the condensed phase charges obtained in either Cornell et al.⁹ or Duan et al.³⁷ force fields.

Parameter Optimization Procedure

As a convention, alanine dipeptide (Ace-Ala-Nme) (Fig. 2) was chosen to model the backbone torsions (〈C–N–Cα–C, Φ, and 〈N–Cα–C–N, Ψ) of proteins. It merits mentioning that Sakae and Okamoto^50–52 have optimized AMBER, CHARMM, and OPLS force fields based on the known protein structures. Because the partial charges of Ace and Nme groups given in ff02 were fitted by a combined procedure over all dipeptides, Ace-X-Nme (X = 20 amino acids), the charges given in ff02 are different from the values fitted over the single model compound (Ace-Ala-Nme). The charge difference can contaminate the torsion parameters. Therefore, using the same approach as described in ref. 40, the atomic charges of alanine dipeptide were refitted. In the charge fitting, four important conformations with fixed standard (Φ, Ψ) angles, that is, β (−119°,113°), β_anti(−139°, 135°), α(−57°,−47°), and P_II(−79°,150°), were used. On the other hand, to keep consistency with ff02 charges to some extent, the atomic charges of alanine moiety (—NH—CHCH₃—CO—) in the model were restrained to the values in ff02. The resulting atomic charges are compared with the original ff02 values in Figure 2, which shows the appreciable difference in the atomic charges of Ace and Nme groups.

Figure 2.

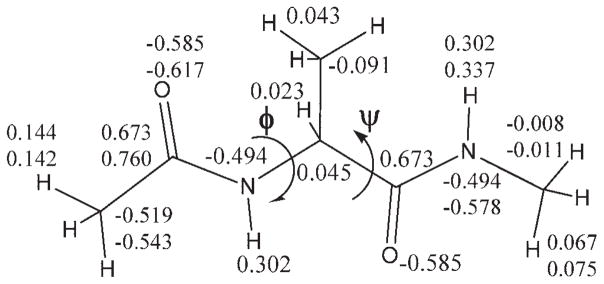
Alanine dipeptide model; the values are atomic charges (top) given by ff02 and refitted (bottom) as described in the text.

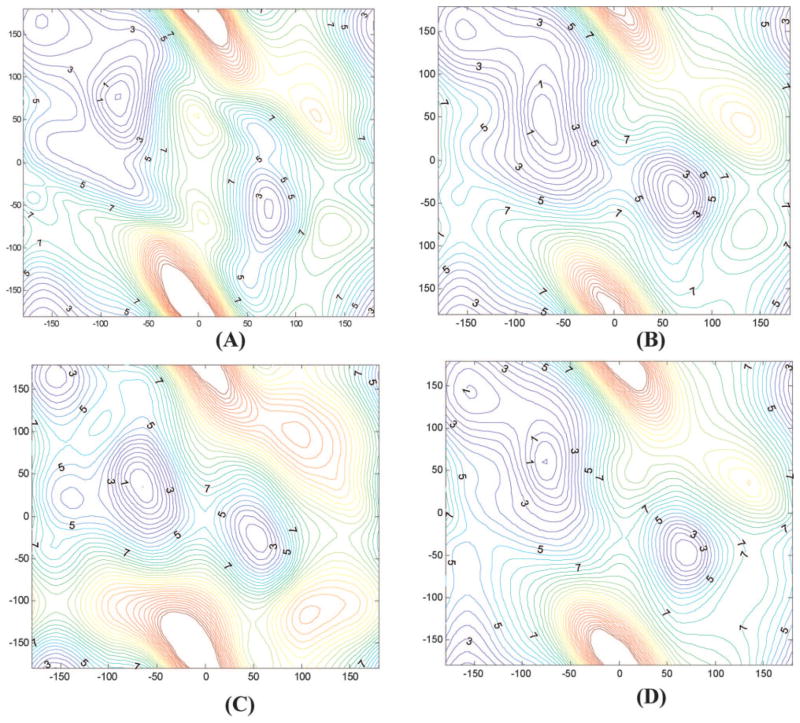
The gas phase (Φ, Ψ) energy map⁵³ of alanine dipeptide was used for torsion parameter fitting. The map, shown in Figure 3A, was computed at the MP2/cc-pVTZ//MP2/6-31G** level with a 20° increment in Φ and Ψ directions from −180–180°, respectively (324 grid points in total) and then interpolated by cubic spline to a finer map with 10° × 10° grid (1296 grid points in total). The interpolated map was used for the torsion parameter fitting.

Figure 3.

Comparison of (Φ, Ψ) energy maps of alanine dipeptide computed at various levels. (A) MP2/cc-pVTZ/MP2/6-31G**; (B) ff02pol.rl; (C) ff02; (D) parameters fitted without energy adjustment.

The fitting was to minimize the weighted error function defined in eq. (5).

$$\mathrm{\Delta }{\epsilon }^2=\sum _i{\omega }_i{(E_i^{\mathit{amb}}-E_i^{ab})}^2$$ (5)

where i is the index of grid points, ω_i = exp(−E_i^ab/k_BT) is the Boltzmann weighting factor, E_i^amb and E_i^ab are the AMBER and the ab initio torsion energies, respectively, excluding other terms. The temperature was set empirically to 450 K. The relatively high temperature was necessary because it gave a balanced coverage to the high- and low-energy areas. For example, the helix region of dipeptide is energetically high but important in determining protein structures. Attention should be paid to this region in fitting.

Force field development relies on quantitative comparisons with high-quality experimental and theoretical data. In the torsion parameter refinement, however, the typical practice is to refine against high level QM data. In the case of peptide main chain torsion parameters, the adjustment has been guided usually by comparing the relative energies of stable conformations of alanine dipeptide (Ace-Ala-Nme) with the corresponding QM values. A recent study by Mackerell et al.⁵⁴ indicated that such approach might be inadequate. By implementing the CMAP (grid-based energy correction map) approach in CHARMM, Mackerell et al.⁵⁴ were able to recover the QM map almost exactly. Yet, further adjustment was still necessary to obtain a reasonable conformational distribution in alanine dipeptide simulation. The main cause of the problem is the difference in the environment; the ab initio QM data was computed in the gas phase and the force field was developed to simulate systems in condensed phases. The energetic landscape can be significantly altered due to the change in solvent environment. For example, the lowest conformers (C7_eq) in the gas phase is not crucial in aqueous solution, and some of the crucial conformers (e.g., α-helix) in aqueous solution are unstable in the gas phase.⁵³ Therefore, empirical adjustments on target energy map are needed.

Moreover, the dynamic behavior of a flexible molecule is poorly represented by the individual stable conformers of fixed geometry. Yet, a conformational ensemble, which is determined by the overall terrain of the energy landscape, can provide better information because it includes the important regions (rather than points). Because it is rather difficult to mimic the entire energy map in the fitting, we chose to focus our attention on the important regions that correspond to the heavily populated areas on the experimental Ramachandran map. The focused regions included the β-sheet region (β, −140° ≤; Φ ≤ −100° and 120° ≤ Ψ ≤ 150°), poly proline region (P_II, −80° ≤Φ ≤ −50° and 130° ≤ Ψ ≤ 160°), right-handed α-helix region (α_R, −80° ≤ Φ ≤ −40° and −60° ≤ Ψ ≤ −30°), and left-handed α-helix region (α_L, 40° ≤ Φ ≤ 80° and 30° ≤ Ψ ≤ 60°). The Boltzmann-weighted average energies (simply called the average energy hereafter) at 300 K over the grid points in the four selected regions are 2.36, 2.53, 3.94, and 5.05 kcal/mol, respectively, and the relative average energies were, respectively, 0.0, 0.17, 1.58, and 2.69 kcal/mol.

In this work, the parameters of four torsion angles (〈C–N–C_α–C(Φ), 〈N–C_α–C–N(Ψ), 〈C–N–C_α–C_β, and 〈C_β–C_α–N–C) related to backbone N–C_α and C_α–C bonds were optimized. The energy of each torsion angle is mimicked by up to the thrid Fourier term. The fitting took two stages. At the first stage, all parameters of the four angles were optimized simultaneously. At the second stage, the parameters for 〈C–N–C_α–C_β and 〈C_β–C_α–N–C were fixed and the parameters for 〈C–N–C_α–C(Φ), 〈N–C_α–C–N(Ψ) were tuned, in comparison to the ab initio energies of the aforementioned four important regions.

Simulation Protocol

The optimized force field was tested by performing simulations on alanine peptides (Ace-Ala-Nme, Ace-(Ala)₇-Nme) in water. The replica exchange method⁵⁵ was applied to enhance the sampling to obtain reliable information about the force field. Using our AM-BER7-based⁴⁵ version implemented recently,⁵⁶ the replica exchange simulations were carried out.

For alanine dipeptide, a set of 28 replica molecular dynamics simulations was performed at the temperatures ranging from 295 to 470 K. Alanine dipeptide was placed in a truncated octahedral water box containing 381 POL3⁴³ water molecules. After relaxation by energy minimization, the system was initially equilibrated under NPT (constant particle, pressure, and temperature) condition at 300 K for 100.0 ps, during which the system density reached 1.0 g/cm³. The prepared system was then equilibrated under NVT (constant particle, volume, and temperature) at the respective replica temperatures for 100.0 ps. Each replica was run for 8.0 ns.

The same procedure was followed to prepare Ace-(Ala)₇-Nme for the replica simulations except that the truncated octahedron box for Ace-(Ala)₇-Nme contains 827 POL3⁴³ water molecules. A set of 32 replica exchange molecular dynamics simulations was performed at the temperatures ranging from 295 to 495K. Each replica was run for 8.0 ns. The replica exchange was attempted and the data was collected every 1.0 ps. It was observed that every replica traversed through all temperatures by many times during the MD simulations. In the following discussion the last 6.0 ns data were considered as production and the first 2.0 ns was ignored. The errors were estimated based on calculations of 1.0-ns windows.

Results and Discussion

Optimized Torsion Parameters

The optimized parameters for the four torsion angles are listed in Table 1. The average energies of P_II and α_R regions relative to the β-region were 0.17 and 1.57 kcal/mol (Table 2), respectively, which are close to the ab initio target values (0.17 and 1.58 kcal/mol). However, the relative energy of α_L region is 5.36 kcal/mol, which is notably higher than the target value (2.69 kcal/mol). Given that the α_L region is located on the right-hand side of the Ramachandran map, which is rarely present in protein structures, we feel the discrepancy is acceptable, certainly not as potentially deleterious as differences in the other three regions. Nevertheless, attempts were made to adjust the energy map to achieve agreement with the target values for all areas, but it was found that the relative average energy of the α_L region was not sensitive to the adjustment after the optimal parameters were obtained to achieve the target values for P_II, α_R, and β-regions. This was probably an indication of the difficulty to use Fourier terms to mimic the whole energy map. In comparison, the ff02 average energies of P_II, α_R, and α_L regions relative to β-region, are 1.54, 0.17, and 0.86 kcal/mol, respectively, which are notably different from the ab initio values, 0.17, 1.58, and 2.69 kcal/mol, respectively. As we will show later, this amount of energy difference causes significantly different conformation distribution of alanine dipeptide in aqueous solution.

Table 1.

Optimized Torsion Parameters for ∠C–N–C_α–C, ∠N–C_α–C–N, ∠C–N–C_α–C_β, and ∠C–_βC_α–N–C.

	Periodicity	A	Phase		Periodicity	A	Phase
C–N–Cα–C(φ)	1	0.692	0.0	C–N–Cα–Cβ	1	0.403	0.0
	2	0.498	180.0		2	0.692	180.0
	3	0.702	180.0		3	0.385	0.0
N–Cα–C–N(ψ)	1	0.898	180.0	Cβ–Cα–N–C	1	1.241	180.0
	2	0.965	180.0		2	0.195	0.0
	3	0.048	180.0		3	0.681	180.0

Table 2.

Boltzmann-Weighted Average Energies (in kcal/mol) of P_II, α_R, and α_L regions relative to the β region.

	β region	PII region	αR region	αL region
aAb initio	0.0	0.17	1.58	2.69
Ff02	0.0	1.54	0.17	0.86
ff02pol.rl	0.0	0.17	1.57	5.36
ff02pol-try	0.0	1.13	2.83	6.81

^aAt MP2/cc-pVTZ//MP2/6-31G**

Table 2 also includes the relative average energies computed by a set of torsion parameters (not shown in Table 1 and labeled as ff02-try in Table 2), which were fitted to the energy map without any adjustment. With respect to the ab initio values, the average energies of P_II, α_R, and α_L regions relative to the β- region produced by this set of parameters are 1.13, 2.83, and 6.81 kcal/mol, respectively. Because of their structural relevance, these are regions where our effort of fitting was focused upon. To obtain accurate fitting in these areas, because of inclusion of other regions in the fitting, adjustment was needed. The parameters in Table 1 were fitted to an adjusted energy map in which the ab initio energies of β, P_II, α_R, and α_L regions were scaled by factors of 1.2, 0.54, 0.51, and 0.7, respectively. It should be emphasized that, although the ab initio energies in these regions were scaled significantly during the fitting, the final relative average energies were close to the ab initio values. Therefore, the energy adjustment improves the agreement with the ab initio map in these important conformational regions. The approach of Boltzmann-weighted average ab initio energies of the focused regions is similar to the one used in the development of CHARMM param19 force field.⁵⁷

The energy maps computed by ff02pol.rl (B) and ff02 (C) are compared with the ab initio map in Figure 3A. Overall, the main features of ab initio map were well preserved on the refined map. There are also notable differences. For example, both ab initio (A) and ff02pol.rl (B) maps have C7_eq and C5 minima in the lower energy region (the third quadrant), but the flat area on (A) disappeared on (B). In contrast, the ff02 energy map (C) was notably different from (A). The differences are also reflected by the relative average energies in Table 2, which explains the conformational distribution of alanine dipeptide in water (Fig. 1). Figure 3D was computed by ff02pol-try. Although there was no major difference between (B) and (D), quantitative comparison (Table 2) and careful inspection indicate that the average energies in P_II and α_R regions are overestimated with respect to the β-region.

In our fitting process, the parameters were optimized based on the average energies of β, P_II, α_R, and α_L without paying attention to the relative energies of the individual conformers of the model compound. Thus, it would be interesting to assess the difference between the ff02pol.rl and ab initio relative energies of the individual conformers. Table 3 compares the relative energies of important conformers of alanine dipeptide at various levels. In ff02pol.rl, C5 is 1.39 kcal/mol higher in energy than C7eq, which is quite close to the ab initio energies of 1.47 kcal/mol at MP2/cc-pVTZ//MP2/6-31G** and 1.01 kcal/mol at LMP2/cc-pVTZ//MP2/6-31G*. The α-helix conformer with fixed standard (Φ, Ψ) angles⁵⁸ is 4.63 kcal/mol higher than C7eq in ff02pol.rl, in good agreement with 4.50 and 4.82 kcal/mol at the two ab initio levels, respectively. Note that the standard (Φ, Ψ) angles in ref. 58 is slightly different from the values we used (see Table 3). The energies of other three conformers (β, β_anti, and P_II) relative to C7_eq, 2.65, 1.74, and 2.27 kcal/mol, are also in agreement with the MP2/cc-pVTZ//MP2/6-31G** values, 2.72, 2.12, and 2.91 kcal/mol, respectively. As expected, the relative energies of C7_ax and left-handed helix are not reproduced by the current ff02pol.rl well. The ff02pol.rl values are also in reasonable agreement with the ab initio values. Because of the reasons stated above, the ff02 values, 0.0(C7eq), 2.15(C5), 6.42(α_R), 5.84(β), 3.77(β_anti), 5.40(P_II), 2.02(C7_ax), and 7.43 kcal/mol (α_L) are significantly different from the corresponding MP2/cc-pVTZ//MP2/6-31G* values, 0.0, 1.47, 4.82, 2.72, 2.12, 2.91, 2.50, and 5.03 kcal/mol, respectively.

Table 3.

Relative Energies (in kcal/mol) of Important Conformers Computed by Empirical Force Fields, Together with the Values Predicted at Various Ab Initio Levels.

	C7eq	C5	aαR-helix	aβ-sheet	aβanti-sheet	a PII	C7ax	αL-helix
ff02pol.rl	0.0	1.39	4.63	2.65	1.74	2.27	1.08	8.32
ff02	0.0	2.15	6.42	5.84	3.77	5.40	2.02	7.43
ff02pol-try	0.0	1.00	5.23	1.88	1.21	3.15	1.49	8.93
bAb initio	0.0	1.47	4.82	2.72	2.12	2.91	2.50	5.03
cAb initio	0.0	1.01	e4.50				2.20	5.19
dAb initio	0.0	0.91	e4.27				2.06	4.96

^aThe four conformers are not minima, their (φ ψ) are fixed at (−57°, −47°), (−119°, 113°), (−139°, 135°), and (−79°, 150°), respectively.

^bMP2/cc-pVTZ//MP2/6-31G**.

^cLMP2/cc-pVQZ(−g)//MP2/6-31G*.

^dLMP2/cc-pVQZ(−g)//MP2/6-311++G**.

^eFrom ref. ⁵⁸, the φ and ψ torsion angels were fixed at (−60°, −45°).

The Behavior of ff02pol.rl in Simulations of Short Peptides

In the past, QM energetic data has been almost the exclusive source for force field parameterization and calibration. An example was the work of Beachy et al⁵⁹ who assessed various force fields by comparing to the ab initio relative energies of tetrapeptide (Ace-(Ala)₃-Nme) conformers. In comparison to the energies of alanne dipeptides, tetrapeptide can help to assess the strength of peptide hydrogen bond, which is crucial to model proteins and peptides. However, the ultimate goal of a force field is to simulate proteins or peptides in physiological environments. Although the energetic comparisons do give valuable insight about a force field, their role for testing force fields is diminishing because of the exquisite accuracy required in force field parameters that is beyond the capability of any existing ab initio methods. Furthermore, studies⁵³ have revealed significant difference between the energy maps of alanine dipeptide in the gas phase and that in water. Even for the polarizable model, because of the approximations, the good agreement with the ab initio gas phase data does not guarantee a satisfactory force field for protein simulations. Instead, force fields should be judged based on realistic simulations.

Alternatively, similarity between experimental Ramachandran plot obtained from high-resolution protein structures and the conformational distribution of alanine dipeptide sampled in MD simulations has also been used to assess force fields.^37,60,61 Hu et al.⁶⁰ assessed earlier versions of AMBER, CHARMM, GROMOS, and OPLS force fields by comparing the conformational distribution maps sampled by these force fields with their QM/MM simulation results and experimental Ramachandran plot.⁶¹ They found that all of the early version force fields bias to some conformers and disfavor others. Indeed, such comparisons are valuable for the assessment of force fields. However, a major problem concerning this type of comparison is the absence of some key interactions (e.g., backbone hydrogen bonding) in the model compounds (ala-nine dipeptide). Because of their vital roles in secondary structures such as α-helix and β-sheet, the lack of main-chain backbone hydrogen bonds in alanine dipeptide model makes it rather difficult to assess the reliability of such comparisons. Thus, simple extrapolation of the results as treating the data as some sort of gold standard can be potentially misleading.

Protein simulations have also been applied to assess force fields. Although they have the advantage of being close to the environment to which the force fields are applied to, the limitation of sampling is a serious concern,⁶² which may prevent a full exposure of the problem in the examined force field. For example, most old force fields were able to maintain experimental protein structures within limited short simulations, ranging from 100 ps in early days to a few ns recently. Yet, problems were soon found when testing on other better designed systems. Several nanoseconds of simulation for a system with ten thousand atoms are far from convergent sampling. It is rather difficult to obtain reliable information about the behavior of a force field from such short simulations.

With the advancement of experimental methods such as NMR and CD,^63,64 two-dimensional infrared spectroscopy (2D-IR)^65,66 and polarized-Raman (PR)/FTIR,⁶⁷ increasing number of short peptides^{63– 67} in aqueous has been characterized (see below for more details), which offers us another way to examine force fields. Guanakaran and Garica⁴⁸ have recently examined their modified AMBER force field (AMBER94/MOD, in which the energy contribution from backbone torsions is set to zero). Mu et al.⁶⁸ assessed AMBER, CHARM, GROMOS, and OPLS force fields by comparing the simulation results of alanine tripeptide with the experimental measurements.⁶⁹ Recently, Pande and coworkers⁷⁰ also examined a series of variants of Cornell et al force field.

In the development of the AMBER ff03 force field, Duan et al.³⁷ proposed a method to use short peptide (Ace-(Ala)₄-Nme) simulation data for force field calibration. One important advantage of short peptides is their ability to model important intramolecular interactions including main-chain backbone hydrogen bonds. Also advantageous is their marginal stability. In fact, short peptides are typically disordered in solution and they have the ability to sample all relevant conformations within a relatively short time. The small peptides allow reliable sampling, which can unveil the dynamics completely, and allow quantitative assessment of the force field. In this study, we will extend the method and apply replica exchange MD simulations on alanine peptides (Ace-Ala-Nme and Ace-(Ala)₇-Nme) in water to examine the ff02pol.rl force field.

Figure 4A shows the conformational distribution of Ace-Ala-Nme in water at 300 K obtained from the replica exchange simulations using ff02pol.rl. The significant difference between Figure 4A and Figure 1 is quite evident, which is not surprising, given the significantly different energy maps (Fig. 3C and D) and the relative energies (Table 3) between ff02pol.rl and the original ff02. The population percentages in the β, P_II, and α_R regions are 30 ± 3%, 43 ± 5%, and 26 ± 4%, respectively. Note that the regions defined here (shown in Fig. 4A) for counting conformations are slightly different from those for calculating average energy (see above). There have been no reliable experimental data about the populations of various conformers in aqueous solution. However, based on NMR and CD measurement,⁴⁶ it was concluded that the P_II-like conformers dominate for alanine dipeptide in aqueous solution and helix conformers are secondarily important. The population percentages simulated by ff02pol.rl are in agreement with this qualitative experimental observation assessment. The quantitative data of alanine tripeptide -(Ala)₃- have been reported but are inconclusive. Based on the 2D-IR measurement and theoretical simulation, Woutersen et al.⁶⁹ deduced that the tripeptide in aqueous has approximately 80% P_II-like and 20% helix conformers. However, Schweiter–Stenner⁶⁷ found that their PR/FTIR measurement can be explained by a single extended β-like structure located at (−123°, 173°) or by simultaneous coexistence of both P_II and β, which implies the existence of additional β conformers. The most recent CD experiment carried out by Gokce et al.⁷¹ further confirmed the P_II dominance, which is attributed to the coupling of a peptide bond N-terminal to the chiral α-carbon. Considering the uncertainty in the experiments, we conclude that the ff02pol.rl gives reasonable description to the dynamic behavior of the short peptide. Figure 4B shows the changes of distribution fractions of the three important conformations at different temperatures. Overall, as the temperature increases, the most populated conformation at the low temperature, P_II, decreases, α and β conformations tend to increase. The net effect is leading a leveled distribution at high temperature, as dictated by favorable entropy toward disorder.

Figure 4.

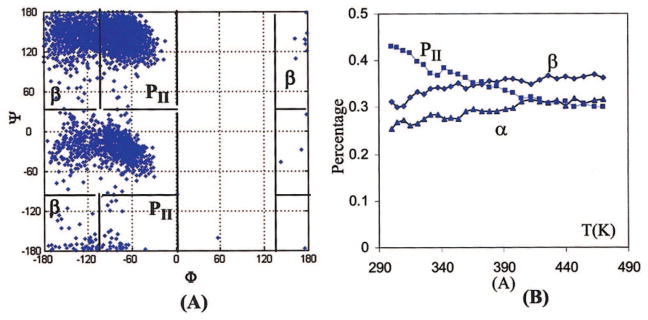
Conformation distribution maps (A) and the distribution changes with temperatures (B) of Ace-Ala-Nme, simulated by ff02pol.rl. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Conformational distributions of alanine dipeptide, sampled by AMBER94, CHARM27, and OPLS-AA force fields, have been reported elsewhere.⁶⁰ Table 4 lists the populations in the regions as given in ref. 60. These results²⁰ for AMBER 94, CHARM27, and OPLS-AA were obtained by 288 separate umbrella MD simulations, which were then stitched together with a 2D weighted histogram procedure. Although this method is different from our replica exchange simulation, it is reasonable to assume both methods sample the system extensively and the results in Table 4 are comparable. In ff02pol.rl, the α conformer was 26%, which was less than 57 and 46% of AMBER94 and CHARMM27, respectively, more than 14% of OPLS-AA, and close to the QM/MM value⁶⁰ of 27%. Like CHARMM27, the ff02pol.rl underrepresents the bridging area; the 1% population is compared with 3% by CHARMM27, 6% by AMBER94, 10% by OPLS-AA, and 16% by QM/MM. The population in the β-region is 71%, which is close to the OPLS-AA value (70%), and compared with the values (48, 29, and 49%, respectively) predicted by QM/MM, AMBER 94, and CHARMM27, respectively.

Table 4.

Population of Alanine Dipeptide Sampled by QM/MM and the Empirical Force Field.

	aα	a Bridge	aβ
DFT QM/MM	27	16	48
AMBER94	57	6	29
CHARMM27	46	3	49
OPLS-AA	14	10	70
ff02pol.rl	26	1	71

^aRegions are defined in ref. ⁶⁰, Alpha: −180° < φ < 0° and −120° < ψ < 30°; Bridge: −180° < φ < 0° and 30° < ψ < 90°, and Beta: −180° < φ < 0° and 90° < ψ < 180°//−180° < φ < 0° and −180° < φ < 0° and −120° < ψ < −180°.

The (Ala)₇ peptide, which is too short to form an α-helix, has served as an experimental model for testing the common features of denatured proteins as structureless random coils. The NMR and CD experiments^63,64 have concluded that, at 2°C, P_II-like conformations are the dominant species. In addition to the availability of the experimental data, we chose it as the model to examine the force field because it has several important advantages. First, unlike dipeptide, it is possible for the (Ala)₇ peptide to form intramolecular hydrogen bonds. This makes it possible to assess the competition between the intramolecular and intermolecular hydrogen bonds and to let us discern whether a force field biases to a helix or a β-sheet more clearly. For example, the simulation by the “helix-friendly” AMBER94 shows that the full helix is the major conformer for the peptide. Second, it allows us to minimize the terminal effects from blocking groups by excluding the first and last φ and Ψ angles in conformational statistics. This is a potentially important technical issue in force field refinement because in alanine dipeptide the Ace- and Nme- groups are together counted heavily, and their significance is artificially elevated to the level comparable to the -Ala- residue. In most studies of proteins and peptides, however, they are rarely present. Therefore, caution must be taken when assessing force fields based on dipeptide results. Extrapolation of the results can be potentially misleading and should be avoided. Finally, the peptide is small and structureless, as we stated earlier. Therefore, there are few energy traps and reliable sampling is much easier. Evidently, extensive conformational sampling of all relevant areas is the basis for quantitative comparison.

The conformational distribution of the (Ala)₇ peptide, sampled by ff02pol.rl, is shown in Figure 5A. After removing the first and last Φ and Ψ angles, the conformational populations in the β, P_II, and α-helix regions as defined in Figure 4A are 24 ± 3%, 49 ± 3%, and 26 ± 4%, respectively, which is in agreement with the experimental conclusion that P_II-like is the dominant conformers.^63,64 In comparison with alanine dipeptide, the distribution of the β conformer decreases, that of the P_II conformers increases, and that of the helix conformer remains nearly unchanged. Figure 5B shows changes of the distributions of three important conformations with temperature. In comparison with alanine dipeptide, as the temperature increases, the P_II conformations drop more rapidly and the α-helix form increases more obviously at low temperature (T < 337 K) and then remains unchanged at medium temperatures. Similar to the trends observed in the dipeptide, here the overall trend is toward a leveled distribution at high temperature, driven by conformational entropy. Regardless of which one is the most populated conformation at low temperature, high temperature always tends to reduce the most populated conformations to maximize the entropy of a system.

Figure 5.

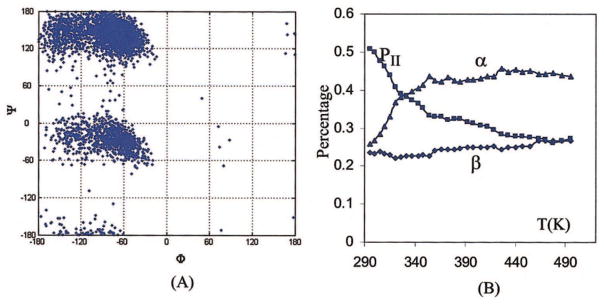
Conformation distribution maps (A) and the distribution changes with temperatures (B) of Ace-(Ala)7-Nme, simulated by ff92pol.rl. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Reaching a balance between helix and extended conformations has been a great challenge in the force filed parameterization. Recent experiments⁶³ and analyses⁷² on known protein structures show that the P_II conformations also play role in protein folding, which further complicates the issue and requires a balance among three important conformations, namely β-sheet, P_II, and α-helix regions. Obviously, the balance is crucial for studying protein folding. For instances, a bias of 0.5 kcal/mol/residue can be accumulated to 5.0 kcal/mol for a peptide with 10 resides. This amount of energetic bias is large enough to turn a β-sheet peptide to an α-helix in simulation or vice versa. However, experience and simulation study⁶⁸ on dipeptides and tripeptides showed that the available force fields always prefer some conformers while disfavor others. The AMBER 94 favors helices, whereas AMBER 96 prefers extended structures. The CHARMM 22 force field has a strong preference for helix conformations. OPLS-AA does not separate P_II and β-structures. GROMOS96 favors β conformers. The comparisons with the previous force fields (see Table 4) and the simulation results on Ace-(Ala)₇-Nme clearly indicate that the ff02pol.rl has a better balance among the three important conformational regions. However, as we gained the knowledge from previous force fields, a better understanding can be obtained only when it is applied to the various systems. Therefore, more tests on its ability to represent helix peptides (e.g., AK16) and β-sheets (e.g., the β-hairpin of G protein) are in progress.

The reasonable conformational distributions of the tested peptides, sampled by ff02pol.rl, do not necessarily implicate that we can improve a force field by fitting to increasingly accurate ab initio potential energy. We also compared the energies with the LMP2/cc-pVTZ(-Q)//MP2/6-31G* energy map (courtesy of A. MacKerell). In comparison to MP2, the LMP2 method has less BSSE (basis set superposition error) effect, and the LMP2 energy map should be more accurate than the currently used MP2 map. At LMP2 level, the relative average energies of P_II, α_R, and α_L to β regions are 0.49, 1.85, and 3.80kcal/mol, compared with 0.17, 1.58, and 2.69 kcal/mol at the MP2/cc-pVTZ//MP2/6-31G* level, respectively. If the LMP2 average energies were used for torsion parameterization, the resulting force field, with respect to the ff02pol.rl, will lead a population decrease in the P_II region and an increase in the β region. The helical population will also decrease relative to β-sheet conformations. However, the simulation on alanine dipeptide indicates that ff02pol.rl underrepresents P_II and overrepresents β regions slightly. Therefore, we did not change the target map to LMP2 map.

In summary, based on the AMBER polarizable model ff02, we have reoptimized the backbone parameters. We used the Boltzmann-weighted average energies of the important regions of ala-nine dipeptide as a criterion to adjust the energy map. The resulting force field (ff02pol.rl) was further assessed by simulations of alanine peptides (Ace-Ala-Nme and Ace-(Ala)₇-Nme). The conformation distributions for both peptides are in agreement with the experimental observation. In comparison to previous force fields, ff02pol.rl has good conformational balance among three important population regions (β, P_II, and α). Although polarizable protein force fields are still under development, the clear advantages in their ability to model spontaneous polarization in varying environments have them potentially attractive platforms for modeling protein dynamics, particularly when large-scale conformational change takes place. With the optimized torsion parameters, together with those in ff02, AMBER ff05pol is ready for realistic MD simulations on proteins and peptides.