Bayesian Inference for the Causal Effect of Mediation

Summary

We propose a nonparametric Bayesian approach to estimate the natural direct and indirect effects through a mediator in the setting of a continuous mediator and a binary response. Several conditional independence assumptions are introduced (with corresponding sensitivity parameters) to make these effects identifiable from the observed data. We suggest strategies for eliciting sensitivity parameters and conduct simulations to assess violations to the assumptions. This approach is used to assess mediation in a recent weight management clinical trial.

1. Introduction

Behavioral scientists and other applied researchers are often interested in both the causal effect of an intervention directly, and on the causal effect of the intervention on the outcome through its effect on other processes, called mediators (Kraemer et al. 2002). For example, interventions such as cognitive behavioral therapy (CBT) typically influence one or more processes, such as self efficacy or motivation, which in turn leads to a change in behavior, such as reduced consumption of alcohol or loss of weight. The graph below illustrates the basic idea in the setting of a single mediator, M:

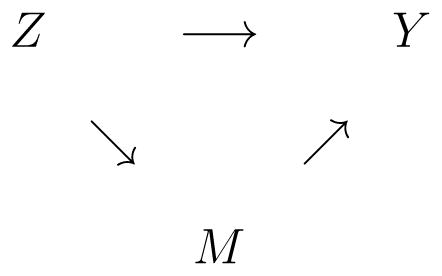
In this graph, the direct effect of exposure Z on outcome Y is the horizontal arrow at the top. The indirect effect of Z on Y passing through mediator M is captured by the arrows that flow from Z to M to Y. The statistical challenge is quantifying the direct and indirect effects. This is similar in structure to the surrogate endpoints problem (Joffe and Greene, 2009; Wolfson and Gilbert, 2010; Li et al., 2011).

We formalize the above as follows. First, let Z ∈ {0, 1} denote randomized intervention. Define the pair (M₀, M₁) as the potential values of a mediator variable under intervention z = 0, 1, with M_obs = ZM₁ + (1 − Z)M₀ observed. Each subject could be thought of as having a potential outcome Y_z,Mz for every combination of z and m. Two ways to characterize the effect of Z that passes around M (direct effect) have been proposed (Robins and Greenland, 1992; Pearl, 2001). In each case, comparisons are made between potential outcomes with a constant mediator but different treatments. The natural direct effect is defined by NDE = E(Y_1,M0 − Y_0,M0). This quantifies the effect of the intervention Z obtained by setting M to its ‘natural’ value M₀; i.e., its realization in the absence of the intervention. Note that here the value of the mediator will not be constant across subjects, but rather set to each subject’s value of M in the absence of treatment. Alternatively, one can define the controlled direct effect of treatment by E(Y_1m − Y_0m), for all m. Here, the direct effect of treatment involves setting M to a particular value for the whole population and varying the treatment.

In many trials of a behavioral intervention, the potential mediator is a behavior, symptom, or perception of an individual. For example, in a trial designed to examine the effect of therapy for depression on smoking cessation might trials, depressive symptoms could be viewed as a mediator. Many behavioral trials also examine measures of motivation or expectation of successful behavior change as potential mediators. Because these variables cannot be directly manipulated by the experimenter, the use of controlled effects can be difficult to justify.

The use of natural direct and indirect effects in behavioral intervention trials is conceptually easier to justify, particularly when the intervention being administered has multiple components designed to influence specific mediators (or paths toward change in the targeted behavior behavior). The natural indirect effect is defined as NIE = E(Y_1,M1 − Y_1,M0), or the effect of changing from M₀ to M₁, had everyone received the intervention. We can then define the total causal effect of Z on Y as TE = NDE + NIE = E(Y_1,M1) − E(Y_0,M0). Referring to the figure above, this captures the aggregate effect of Z that passes through and around M.

To interpret the meaning of natural direct and indirect effects, and particularly to interpret the meaning of Y_1,M0, we use the weight management trial (described at the end of this section) as an example. Suppose the intervention has a component that is targeted to help people track food intake. Then the direct effect is the effect of the intervention if the component of treatment that is affecting food intake monitoring were somehow to be removed. This implies that the path from the intervention to food intake monitoring will be blocked, but all other components of the treatment will be implemented and can potentially affect weight loss through paths that do not involve food intake monitoring.

In practice, mediation analysis is often based on solving linear systems of equations (MacKinnon 2008). For example, Baron and Kenny (1986) used the following three regression models:

$$\begin{array}{l}Y={\alpha }_1+{\beta }_{1}Z+{\epsilon }_1\\ M={\alpha }_2+{\beta }_{2}Z+{\epsilon }_2\\ Y={\alpha }_3+{\beta }_{3}Z+\gamma M+{\epsilon }_3,\end{array}$$

although, given the second two regressions, the first is redundant (Imai et al. 2010). Here, the proposed TE is β₃ + β₂γ, the NDE effect is β₃ and the NIE is β₂γ. The controlled direct effect of treatment is also β₃. However, causal interpretations of these parameters depend on sequential ignorability and no interaction assumptions (Imai et al. 2010); more detail on the former can be found in Section 2.3. The no interaction assumption is particularly strong for controlled effects, as it requires that, for example, E(Y_1m − Y_0m) does not depend on m. In addition to the randomization and no interaction assumptions, the model also requires correct specification of the linear system. A Bayesian version of the regression approach can be found in Yuan and MacKinnon (2009).

New semiparametric methods have recently been proposed for estimating mediation effects. Ten Have et al. (2007) proposed estimating mediation effects using models that make assumptions about structural interactions, rather than sequential ignorability. VanderWeele (2009) proposed using two marginal structural models (Robins 1999) to estimate natural direct and indirect effects. However, these methods can be problematic for continuous mediators due to unstable weights (Vansteelandt, 2009).

Parametric likelihood-based or Bayesian methods for mediation have primarily been proposed in a principal stratification (PS) framework (Frangakis and Rubin 2002), in which causal effects are defined within strata determined by post-randomization outcomes. See Gallop et al. (2009) and Elliott, Raghunathan, and Li (2010) for examples. In the mediation context, the PS approach has been used to define treatment effects conditional on M₀ and M₁, and hence focuses on latent subpopulations defined by pairs {M₀, M₁}. For a binary mediator, the direct effect of Z is defined as E(Y₁ − Y₀|M₁ = M₀), or the causal effect of Z among people whose value of M would not be affected by Z. When M is continuous rather than binary, the PS approach will generally require additional, untestable modeling assumptions because strata defined by M₀ = M₁ will be sparse or even empty in finite samples.

Because PS-based inferences apply to latent subpopulations, direct comparisons between PS and other methods is not straightforward; however, VanderWeele (2008) and Joffe and Greene (2009) provide detailed discussion and describe linkages between PS-based inferences and both controlled and natural direct and indirect effects.

Our approach is distinct from other mediation approaches in the literature in several ways. We take a fully Bayesian approach to inferring natural direct and indirect effects. Because we will focus on natural effects, we can focus on a subset of the potential outcomes Y_z,Mz: {Y_1,M1, Y_1,M0, Y_0,M0}, with Y_obs = ZY_1,M1+ (1 − Z )Y_0,M0 observed. For example, Y_1,M1 is the outcome that would be observed if we set Z = 1 and M = M₁. In this framework, we do not require that Y_zm be defined for all values of m; it is only necessary to define Y_zm for the realizations of M₀ and M₁. We model the marginal distributions of M₀ and M₁ non-parametrically, and then specify a copula model to obtain their joint distribution. We avoid making some of the strong assumptions that are required for some of the alternative methods described above. Instead, our model is identified if three sensitivity parameters are specified. Although our application has a binary outcome and continuous mediator, our general approach could be used for other types of outcomes and mediators.

We illustrate the methodology using data from a weight management trial, TOURS (Perri et al, 2008). Subjects were randomized to either extended care or to an education control group. Adherence to behavioral weight-management strategies, as measured by the number of days with self-monitoring records for food intake, is the proposed mediator of weight change. The outcome was a (binary) measure of weight change (described in Section 6). We estimate both the direct effect of the weight management programs on the weight change outcome, as well as the indirect effect of the programs on the outcome through the effect on adherence to food intake self-monitoring.

In Section 2, we discuss inference on the causal effect of mediation by first introducing some notation, then stating our assumptions, and finally showing that our assumptions are sufficient to identify the natural direct and indirect effects. We provide details on posterior computations in Section 3. Section 4 outlines our approach to elicitation for the sensitivity parameters and subsequent sensitivity analysis. Simulations to assess sensitivity to violations of assumptions can be found in Section 5. Section 6 contains our analysis of the TOURS trial. Finally, we wrap up and discuss extensions in Section 7.

2. Inference on causal effects

2.1 Notation

Let f_z,Mz′ (y) denote the distribution of Y_z,Mz′, for (z, z′) ∈ {0, 1}^⊗2. Similarly, we denote the conditional distribution [Y_z,Mz′|M_z′= m_z′] by f_z,Mz′(y|m_z′). Let D = (M₁ − M₀). The conditional distribution [Y_z,Mz′|M_z = m_z, $M_z^{\prime }=m_{z^{\prime }}$, D = d] is denoted by f_z,Mz′(y|m_z, m_z′, d). Multivariate distributions are defined using similar notation below.

2.2 Assumptions

Recall the observed data is M_obs = ZM₁ + (1 − Z)M₀ and Y_obs = ZY_1,M1 + (1 − Z )Y_0,M0. The observed data are not sufficient to identify the conditional distribution

$$f_{(1,M_1),(1,M_0),(0,M_0)}(y_{11},y_{10},y_{00}\mid m_1,m_0)$$

and the joint distribution, f_M0,M1(m₀, m₁) which are necessary to identify the joint posterior distribution of NIE and NDE without assumptions. Thus, we make the following assumptions.

Assumption 1. (Randomization assumption)

$$f_{(z^{\prime },M),M_z}(y_{z^{\prime },m},m_z\mid z)=f_{(z^{\prime },M),M_z}(y_{z^{\prime },m},m_z).$$ (1)

This assumption will hold in our application since the treatment was randomized.

Assumption 2 stratifies the population into those for whom the treatment has a large and small effect on the mediator.

Assumption 2a

For a fixed z and for some ε,

$$P(Y_{z,M_{z^{\prime }}}=1\mid M_{z^{\prime }}=m,\mid d\mid <\epsilon )=P(Y_{z,M_z}=1\mid M_z=m,\mid d\mid <\epsilon )$$

Note for binary responses, the above conditional probability uniquely determines the corresponding conditional distribution. The random variable D quantifies the treatment effect on the mediator. A consequence of the assumption is that, for example,

$$P(Y_{1,M_1}=1\mid M_0=m_0,M_1=m_1,\mid d\mid <\epsilon )=P(Y_{1,M_0}=1\mid M_0=m_1,M_1=m_0,\mid d\mid <\epsilon ).$$

It means that, among people for whom the treatment effect on the mediator is small (as quantified by ε), the distribution of the outcome is same whether that mediator value was induced by Z = 1 or Z = 0. It does not imply an exclusion restriction. That is, we are not assuming [Y_1,M0|M₀ = m] = [Y_0,M0|M₀ = m].

Assumption 2b

The next assumption is for the subgroup of subjects for whom Z has a greater than ε effect on M. For this group, for a fixed z, ε, and χ, we assume

$$P(Y_{z,M_{z^{\prime }}}=1\mid M_{z^{\prime }}=m,\mid d\mid \ge \epsilon )={\chi }^{sgn(d)}P(Y_{z,M_z}=1\mid M_z=m,\mid d\mid \ge \epsilon ).$$

where the sensitivity parameter χ is a relative risk with the following restriction:

$$\chi \in (0,1/P(Y_{z,M_z}=1\mid M_z=m,\mid d\mid \ge \epsilon ))\text{for}sgn(d)\equiv +$$

or

$$\chi \in (P(Y_{z,M_z}=1\mid M_z=m,\mid d\mid \ge \epsilon ),\infty )\text{for}sgn(d)\equiv -.$$

Note we differentiate m₁ > m_o + ε from m_o > m₁ + ε through the sgn(d) in the above expression. We discuss elicitation of χ and ε in Section 4.

Note that with Assumption 2, we implicitly assume a discontinous relationship (a step function at ε) between the conditional probabilities and the treatment effect on the mediator, D. There are not good alternatives to this, e.g., a smooth function of D, since this is not identifiable from the data (and would involve additional sensitivity parameters). We view the step function assumption as a reasonable alternative. By considering a several combinations of χ and ε, we should be able to capture many plausible scenarios. The key is differentiating the population into those where the intervention has a large versus small effect on the mediator.

Assumption 3

$$f_{M_{z^{\prime }}}(m_{z^{\prime }}\mid m_z,Y_{z,M_z})=f_{M_{z^{\prime }}}(m_{z^{\prime }}\mid m_z)$$

This assumptions says that the potential value of the mediator under treatment z′ is independent of the potential outcome under treatment z conditional on the potential value of the mediator under treatment z; for example, M₁ ⊥ Y_0,M0|M₀. This assumption also implies

$$f_{z,M_z}(y\mid m_z,m_{z^{\prime }})=f_{z,M_z}(y\mid m_z).$$

That is, the potential outcomes Y_z,Mz are independent of the mediator under the other treatment, m_z′ conditional on the mediator associated with the potential outcome, m_z; for example, Y_1,M1⊥ M₀|M₁. Thus this assumption says that no additional information is provided about the potential outcomes, Y_z,Mz from the mediator under the other treatment, M_z′ after we condition on the mediator under treatment z. Note it clearly does not imply Y_1,M1⊥ M₁|M₀.

This assumption is not required, but considerably simplifies computations. We examine sensitivity to this assumption via simulations in Section 5.

Assumption 4

We assume the joint distribution of the mediator follows a Gaussian copula model (Nelsen, 1999),

$$F_{M_0,M_1}(m_0,m_1)={\mathrm{\Phi }}_2\left[{\mathrm{\Phi }}_1^{-1}\{F_{M_0}(m_0)\},{\mathrm{\Phi }}_1^{-1}\{F_{M_1}(m_1)\}\right]$$

where Φ₁ is the univariate standard normal CDF and Φ₂ is the bivariate normal CDF with mean (0, 0)^T, variance (1, 1)^T and correlation ρ ∈ (−1, 1).

The joint distribution of the continuous mediators can be identified up to a sensitivity parameter ρ by first specifying the two marginal distributions. There is no information in the data about ρ because it represents the association between two variables that are never observed simultaneously. We will therefore treat ρ as known and vary it as part of a sensitivity analysis. The special case ρ = 1 implies equipercentile equating of the mediators (i.e., the ranks of M₀ and M₁ are the same). In Section 3, we discuss Bayesian nonparametric estimation of the marginal distributions which are identified from M_obs as outlined in Section 2.4.

The choice of the Gaussian copula here is for several reasons: 1) it allows complete flexibility in the marginals (which we model in Section 2.4.1 using a nonparametric Bayesian approach) and 2) it is parsimonious in terms of sensitivity parameters (here only one sensitivity parameter, ρ).

Assumption 5. (Conditional independence between potential outcomes)

$$\begin{gathered} f_{(1,M_1),(1,M_0),(0,M_0)}(y_{11},y_{10},y_{00}\mid m_0,m_1) \\ =f_{1,M_1}(y_{11}\mid m_0,m_1)f_{1,M_0}(y_{10}\mid m_0,m_1)f_{0,M_0}(y_{00}\mid m_0,m_1). \end{gathered}$$

Note that Assumption 5 is not necessary to estimate E[NIE|data] and E[NDE|data]; for these, we just need the marginal posterior distributions for the potential outcomes. However, it is necessary to estimate other features of the posterior distribution of NIE and NDE. In particular, the posterior mean of the NIE and NDE is not effected by this assumption; however the posterior variance is. In fact, this assumption provides an upper bound on the variance of the NIE assuming deviations only involving positive dependence between the potential outcomes. In particular, the difference (which we denote as A) between the variance of the NIE under Assumption 5 and under the case that Assumption 5 does not hold (with the strongest possible conditional dependence between the outcomes) is

$$A\le 2\int \theta \times s.d.(Y_{10})s.d.(Y_{11})f(m_0,m_1){dm}_0{dm}_1,$$

where

$$\theta =\frac{\sqrt{exp\{\mathit{sgn}(d)log\chi I(\mid d\mid \ge \epsilon )\}}p(Y_{11}=1\mid m_0,m_1)}{s.d.(Y_{10})s.d.(Y_{11})}-\frac{exp\{\mathit{sgn}(d)log\chi I(\mid d\mid \ge \epsilon )\}p{(Y_{11}=1\mid m_0,m_1)}^2}{s.d.(Y_{10})s.d.(Y_{11})}.$$

For further details on this and the entire derivation, see the Web appendix.

This assumption states that the correlation between the potential outcomes is completely explained by the two values for the potential mediator; implicitly, it is assuming there are no other mediators. We can weaken this assumption, but not without adding additional sensitivity parameters. In the data example, we provide information on the changes to the posterior variance under violations of Assumption 5. Another option to weaken this assumption would be to have it hold only conditional on baseline covariates; we discuss this extension in Section 7.

We emphasize that none of these assumptions are ‘checkable’ from the observed data.

2.3 Alternative assumptions required for non-parametric identification

The average NIE and NDE can be identified non-parametrically with an alternative set of assumptions (Imai et al. 2010; Robins 1999). In particular, Imai et al. (2010) showed that non-parametric identification required the treatment assignment ignorability (1) and ignorability of the mediator (i.e., sequential ingnorability),

$$f_{z^{\prime },M}(y_{z^{\prime },m}\mid m,z)=f_{z^{\prime },M}(y_{z^{\prime },m}\mid z)$$

for z, z′ = 0, 1. In addition, a positivity assumption is required for treatment and the mediator: P(Z = z) > 0 and P(M = m|Z = z) > 0 for all m, z. The above assumptions are typically made conditional on pre-treatment covariates. A sensitivity analysis can be used to quantify effects of unmeasured confounding (Imai et al., 2010a; Imai et al., 2010b; VanderWeele, 2010).

We do not make the sequential ignorability assumption. As stated earlier, this is typically not a reasonable assumption for mediators in behavioral trials. For example, our Assumption 2b allows for a dependence between M₀, M₁ and the potential outcomes that is not assumed to vanish after conditioning on Z (unlike with sequential ignorability). However, we require additional assumptions about the joint distribution of (M₀, M₁) because we need to identify the posterior distributions of NDE and NIE, not just the means.

2.4 Identification of joint distributions for computation of direct and indirect effects

In the following, we will demonstrate that Assumptions 1–4 are sufficient to identify the joint distribution of NIE and NDE. We state this formally in the following theorem. We also note that by randomization of the treatment, (1), the distributions f_Mz(M_z), f_MzYz(M_z|Y_z,Mz) and f_z,Mz(Y_z,Mz) are estimable from (Y_obs, M_obs).

Theorem

The joint posterior distribution of NIE and NDE is identified under Assumptions 1–5.

Proof

Consider the following factorization of the joint distribution of the two potential outcomes (one of which is observed), which we will denote as B,

$$\begin{gathered} f_{(0,M_0),(1,M_1),M_0,M_1}(y_{00},y_{11},m_0,m_1) \\ =f_{(M_0,Y_0),(M_1,Y_1)}(m_0,m_1\mid y_{00},y_{11})f_{(0,M_0),(1,M_1)}(y_{00},y_{11}). \end{gathered}$$ (2)

We can further factor B as

$$\begin{gathered} B=f_{(0,M_0),(1,M_1)}(y_{00},y_{11}\mid m_0,m_1)f_{M_0,M_1}(m_0,m_1) \\ =f_{0,M_0}(y_{00}\mid m_0,m_1)f_{1,M_1}(y_{11}\mid m_0,m_1)f_{M_0,M_1}(m_0,m_1)(\text{A}5) \\ =\frac{f_{M_0,M_1}(m_0,m_1\mid y_{00})f_{0,M_0}(y_{00})}{f_{M_0,M_1}(m_0,m_1)}\frac{f_{M_0,M_1}(m_0,m_1\mid y_{11})f_{1,M_1}(y_{11})}{f_{M_0,M_1}(m_0,m_1)} \\ \times f_{M_0,M_1}(m_0,m_1) \\ =\frac{f_{M_1}(m_1\mid m_0)f_{M_0,Y_0}(m_0\mid y_{00})f_{0,M_0}(y_{00})}{f_{M_0,M_1}(m_0,m_1)}{f}_{M_0}(m_0\mid m_1) \\ \times f_{M_1,Y_1}(m_1\mid y_{11})f_{1,M}(y_{11})(\text{A}2) \end{gathered}$$

where ‘A’ corresponds to ‘Assumption’ in the above. Each component in (2) is identified by randomization (Assumption 1) and/or Assumption 4. To obtain the posterior distribution of indirect effects, we need

$$f_{(1,M_1),(1,M_0)}(y_{11},y_{10})=\int f_{(1,M_1),(1,M_0)}(y_{11},y_{10}\mid m_0,m_1)f_{M_0,M_1}(m_1,m_0){dm}_0{dm}_1.$$

The second term in the integrand is a function of the estimable quantities in (2). Using Assumption 5, the first term in the integrand can be factored as

$$f_{(1,M_1),(1,M_0)}(y_{11},y_{10}\mid m_0,m_1)=f_{1,M_1}(y_{11}\mid m_0,m_1)f_{1,M_0}(y_{10}\mid m_0,m_1).$$

By Assumption 3, the first term is equal to f_1,M1 (y₁₁|m₀, m₁) = f_1,M1 (y₁₁|m₁) which can be estimated using the observed data via randomization (and a function of components in (2)). Also, we observe the pairs (Y_1,M1, M₁). The second term, f_1,M0(y₁₀|m₀, m₁) is identified by Assumptions 2 and 4. From Assumption 2, we identify f_1,M0(y₁₀|m₀, m₁)using f_1,M1(y₁₁|m₀, m₁) and the sensitivity parameters, (χ, ε). Using Assumption 4, we identify the distribution of M₀ given M₁ and estimate f_1,M1(y₁₁|m₀, m₁).

Similarly, to obtain the posterior distribution of direct effects, we need

$$f_{(1,M_0),(0,M_0)}(y_{10},y_{00})=\int f_{(1,M_0),(0,M_0)}(y_{10},y_{00}\mid m_0,m_1)f_{M_0,M_1}(m_0,m_1){dm}_0{dm}_1.$$

The first term, f_{(1,M0),(0,M0)}(y₁₀, y₀₀|m₀, m₁) can be factored via Assumption 5

$$f_{(1,M_0),(0,M_0)}(y_{10},y_{00}\mid m_0,m_1)=f_{1,M_0}(y_{10}\mid m_0,m_1)f_{0,M_0}(y_{00}\mid m_0,m_1).$$

The identification of the first term was outlined in the identification of the NIE. For the second term, f_0,M0(y₀₀|m₀, m₁) = f_0,M0(y₀₀|m₀) by Assumption 3, which is estimable from the observed data and randomization (since function of quantities in (2)).

2.4.1 Models and Estimation

The models required for inference in the previous section can be specified nonparametrically and estimated using the observed data. In particular, we need the following component nonparametric models:

$$Y_{z,M_z}~\mathit{Ber}({\pi }_{z,M_z}):z=0,1.$$

We specify Dirichlet process priors for the distributions F_Mz,y(m_z|Y_z,Mz= y): y = 0, 1; z = 0, 1. We also place independent Unif(0, 1) priors on π_z,Mz. The relevant posterior can be sampled in WinBUGS (see the supplementary materials).

Note that the identified quantities in the previous subsection, f_z,Mz(y|m) can be estimated quite easily using the models; this is clear if we rewrite f_z,Mz(y|m) as f_Mz,y(m|y)f_Yz,Mz (y)/f_Mz(m).

3. Posterior computations

We construct an algorithm to sample from the posterior distribution of the direct and indirect effects. We proceed using the following steps.

1. Fix the sensitivity parameters, (ρ, χ, ε).

2. Sample [F_M1,1, F_M1,0, F_M0,1, F_M0,0, π_1,M1, π_0,M0] ~ p(F_M1,1, F_M1,0, F_M0;,1, F_M0,0, π_1,M1, π_0,M0|m_obs, y_obs) where m_obs = {M_zi, i = 1, …, n} and y_obs = {Y_zi,Mzi, i = 1, …, n} using WinBUGS.

3. For each sample (F_M1,1, F_M1,0, F_M0,1, F_M0,0, π_1,M1, π_0,M0), compute NDE and NIE.

4. Repeat Steps 2–3 Q times.

If we place a prior on the sensitivity parameters, Step 1 is replaced by sampling the prior and Step 4 becomes repeat Steps 1–3 Q times. Details on WinBUGS in Step 2 and all of Step 3 can be found in the supplementary materials.

4. Sensitivity Analysis and Elicitation

Assumptions 2 and 4 contain three sensitivity parameters, (χ, ε, ψ). We discuss a general strategy to elicit a range for each sensitivity parameter.

Assumption 2

To help understand the first two sensitivity parameters, we assume, wlog, that the treatment has a non-negative (non-decreasing) effect on the mediator and using Assumption 2, we have the following expression

$$\frac{P(Y_{z,M_{z^{\prime }}}=1\mid m_z,m_{z^{\prime }},d\ge \epsilon )}{P(Y_{z,M_z}=1\mid m_z,m_{z^{\prime }},d\ge \epsilon )}=exp(log\chi )=\chi .$$ (3)

In the following, we choose Z = 1 (wlog) and assume (m₁ − m₀) > ε. In addition, we can simplify the expression in (3), which will facilitate elicitation, as follows,

$$\begin{array}{l}P(Y_{1,M_1}=1\mid M_1=m_1,M_0=m_0,d\ge \epsilon )=P(Y_{1,M_1}=1\mid M_1=m_1,M_0=m_0,d<\epsilon )\\ =P(Y_{1,M_0}=1\mid M_1=m_0,M_0=m_1,d<\epsilon ).\end{array}$$

The first equality comes from Assumption 3; the second from Assumption 2a. So we can rewrite (3) as

$$\frac{P(Y_{1,M_0}=1\mid m,d\ge \epsilon )}{P(Y_{1,M_0}=1\mid m,d<\epsilon )}=\chi .$$ (4)

where m is the value of the mediator under the control arm. The numerator corresponds to m₁ > (m₀+ε) (assuming a larger value for the mediator is better). If we assume the treatment has a larger effect on other mediators (not measured) or other relevant mechanisms, then we might expect the probability in the numerator to be larger than the denominator corresponding to a larger direct effect. We use expression (4) for eliciting.

To elicit likely values for ε, we consider how big d should be for the following ratio to be not equal to one,

$$\frac{P(Y_{1,M_0}=1\mid m_0,d=0[m_1=m_0])}{P(Y_{1,M_0}=1\mid m_0,d=\epsilon [m_1=m_0+\epsilon ])}.$$

Assumption 4

The parameter ρ in Assumption 4 corresponds to the rank correlation between the mediator values under the treatment and control arms, with ρ = 1 corresponds to a perfect correlation and ρ = 0 corresponding to independence. We use these two benchmarks to elicit a value. A conservative approach would be just to consider any value in [0, 1) (assuming the relationship was positive).

We elicit a range of values for each sensitivity parameter.

5. Simulation study to assess sensitivity to violations of Assumption 3

We explicitly suggest approaches for sensitivity analysis with sensitivity parameters for Assumptions 2 and 4. For Assumption 5, we derived analytic results that demonstrate its impact (only on the posterior variance). In the below, we assess, via simulations, sensitivity to violations of Assumption 3.

For the simulation, similar to the data example, we assume Y_1,M1 ~ Ber(0.71). We consider the following (simple) violations of assumption 3. We assume logit(M₀)|logit(M₁), Y_1,M1 ~ N (μ, σ²) μ = β₀ + β₁logit(M₁) + β₂Y_1,M1 and the logit transformation is on the interval [0, 350]. Based on the data (and setting ρ = .3 in Assumption 4), we obtain β₀ = −1.5241 and β₁ = 0.1842. We consider deviations from Assumption 3 (β₂ = 0) in terms of the following values for β₂, {1.07, 2.14, 4.28} which are half, full and twice of s.d. of m₀ after the logit transformation. For the simulation, we also consider varying the sensitivity parameters from Assumption 2 as follows: χ ∈ {1, 1.15, 1.3, 2} and ε ∈ {50, 75, 100}.

For each scenario, we compute the NIE assuming Assumption 3 holds and compare it to the true NIE when Assumption 3 does not hold. The results are in Table 1 (and Table S.1 in the supplementary materials).

Table 1.

Simulations to assess sensitivity of estimate of NIE to violations in Assumption 3: n=60

		χ = 1
		ε = 50		ε = 75		ε = 100
		NIE	s.d.	NIE	s.d.	NIE	s.d.
β2 = 0	Our Approach	0.024	(0.058)	0.030	(0.054)	0.029	(0.058)
	Truth	0.024	(0.058)	0.030	(0.054)	0.029	(0.058)
β2 = 1.28	Our Approach	0.0051	(0.058)	0.0065	(0.055)	0.0079	(0.060)
	Truth	0.0021	(0.058)	0.0036	(0.055)	0.0040	(0.058)
β2 = 2.56	Our Approach	−0.025	(0.051)	−0.017	(0.055)	−0.016	(0.047)
	Truth	−0.0034	(0.048)	0.0073	(0.051)	0.0067	(0.045)
β2 = 5.12	Our Approach	−0.058	(0.044)	−0.072	(0.048)	−0.062	(0.049)
	Truth	0.0045	(0.037)	0.0012	(0.038)	0.00075	(0.038)
		χ = 1.15
		ε = 50		ε = 75		ε = 100
		NIE	s.d.	NIE	s.d.	NIE	s.d.
β2 = 0	Our Approach	0.021	(0.053)	0.029	(0.052)	0.028	(0.061)
	Truth	0.021	(0.053)	0.029	(0.052)	0.028	(0.061)
β2 = 1.28	Our Approach	−0.0046	(0.056)	0.0026	(0.058)	0.0057	(0.049)
	Truth	−0.0075	(0.056)	0.00001	(0.056)	0.0032	(0.047)
β2 = 2.56	Our Approach	−0.015	(0.062)	−0.015	(0.055)	−0.016	(0.053)
	Truth	0.0042	(0.057)	0.0038	(0.055)	0.0033	(0.050)
β2 = 5.12	Our Approach	−0.060	(0.047)	−0.048	(0.051)	−0.075	(0.060)
	Truth	−0.0007	(0.031)	0.0072	(0.039)	−0.010	(0.044)
		χ = 1.3
		ε = 50		ε = 75		ε = 100
		NIE	s.d.	NIE	s.d.	NIE	s.d.
β2 = 0	Our Approach	0.020	(0.055)	0.030	(0.060)	0.017	(0.054)
	Truth	0.020	(0.055)	0.030	(0.060)	0.017	(0.054)
β2 = 1.28	Our Approach	0.00052	(0.055)	−0.0015	(0.053)	−0.0055	(0.058)
	Truth	−0.0014	(0.056)	−0.0049	(0.053)	−0.0076	(0.058)
β2 = 2.56	Our Approach	−0.012	(0.053)	−0.011	(0.054)	−0.015	(0.062)
	Truth	0.0044	(0.052)	0.0056	(0.051)	0.0022	(0.058)
β2 = 5.12	Our Approach	−0.040	(0.052)	−0.054	(0.051)	−0.051	(0.052)
	Truth	0.014	(0.037)	0.0021	(0.040)	0.0066	(0.042)
		χ = 2
		ε = 50		ε = 75		ε = 100
		NIE	s.d.	NIE	s.d.	NIE	s.d.
β2 = 0	Our Approach	0.015	(0.052)	0.010	(0.062)	0.021	(0.055)
	Truth	0.015	(0.052)	0.010	(0.062)	0.021	(0.055)
β2 = 1.28	Our Approach	−0.0053	(0.052)	0.010	(0.054)	0.012	(0.059)
	Truth	−0.0068	(0.053)	0.010	(0.052)	0.010	(0.057)
β2 = 2.56	Our Approach	0.016	(0.057)	0.00037	(0.058)	0.00064	(0.061)
	Truth	0.023	(0.052)	0.0098	(0.053)	0.012	(0.057)
β2 = 5.12	Our Approach	−0.0049	(0.064)	−0.018	(0.055)	−0.020	(0.055)
	Truth	0.030	(0.048)	0.022	(0.040)	0.020	(0.043)

The posterior mean and standard deviation of the NIE are not very sensitive to small to medium size violations of Assumption 3 with the estimates not differing by much more than .02. However, for the large violation (2 standard deviation change), the estimates can differ by as much as .05 to .08. There are no consistent patterns of bias, including bias toward the null.

6. TOURS: weight management trial

6.1 Description of Data

This was a randomized trial to compare the effectiveness of extended care programs designed to promote successful long term weight management. Participants completed a standard six month lifestyle modification program and then were randomly assigned to telephone counseling, face-to-face counseling or an education control group (Perri et al., 2008). This completed trial is referred to as TOURS. A very important question in this trial, and obesity research in general are identifying mediators of weight change. In this trial, different measures of adherence to behavioral weight-management strategies were recorded. Here, we focus on the (continuous) mediator, the number of days with self-monitoring records for food intake (which takes values 0 to 350) during the weight management phase of the trial, 6 to 18 months. Among those that lost at least 5% of their weight by 6 months, we define the (binary) outcome of interest to be whether or not they maintained the loss of at least 5% from 6 to 18 months.

In the analysis of the original trial, the telephone and face-to-face treatment arms resulted in similar weight maintenance that was considerably larger than the education control arm. Here, we assess the NIE and NDE of the mediator for the face-to-face (FTF) vs. education control (EC) arms. The sample sizes for the two treatment arms were 63 and 62, respectively.

6.2 Models

We assume the following prior for the conditional distribution of the mediators given the binary response (y ∈ {0, 1}), F_Mz,y(m_z|Y_z,Mz = y) ~ DP(K_z, W_z × Beta_[0,350](α_1z, β_1z) + (1 − W_z) × Beta_[0,350](α_2z, β_2z)), where the base measure is a mixture of Beta distributions on the interval [0, 350] and K_Z is the precision parameter. We place the following priors on the hyperparameters, K_z ~ DiscUnif [1, 20] and α_iz ~ Unif (0, 70) and β_iz ~ Unif (0, 70) for i = 1, 2 and W_z ~ Unif(0, 1): z = 1, 2.

6.3 Elicitation of sensitivity parameters

The combined expertise of the authors in weight management trials and causal inference were utilized the determine reasonable values for the sensitivity parameters.

Assumption 2

Regarding the sensitivity parameter ε, it was thought that a difference of at least one day per week in filling out the food intake records could be interpreted as clinically important and significant; we discuss this issue further in the discussion section. As a result, we consider values of ε ∈ (50, 100); roughly corresponding to a difference of 1 to 2 days per week. In addition, in terms of the ratio in (4), the impact of the treatment on the mediator being more than 50 days could reflect a positive impact on other factors innate to the individual up to a relative risk of about 1.3. Thus, we considered values χ ∈ (1.0, 1.3).

Assumption 4

For assumption 4, the correlation between m₀ and m₁ was thought to be positive. So, we followed the conservative approach from Section 4 and consider ρ ∈ [0, 1).

For the analysis, we also consider independent uniform priors over these ranges.

6.4 Results

For sampling from the posterior distribution of the models for the observed data in section 6.2, we ran 10000 iterations and discarded the first 5000 as burn-in. We ran multiple chains and trace plots indicated convergence.

The total effect of face-to-face (FTF) versus mail (EC) corresponded to a marginally significant risk difference of .081(−.073, .25) suggesting the efficacy of the FTF treatment (Tables 2–4). For all combinations of the sensitivity parameters considered, the conclusions were quite robust corresponding to a large NDE ranging from about .077 to .089, with credible intervals that covered zero (see Tables 2–4). The NIE was always much smaller in magnitude, less than .01 in absolute value with credible intervals centered close to zero.

Table 2.

Posterior means and credible intervals for NDE, NIE, and TE for ε ∈ {50, 75, 100}, χ ∈ {1.0, 1.15, 1.3} and ρ=0.

ε	χ	NDE	NIE	TE
50	1	0.077 (−0.078,0.25)	0.007 (−0.088,0.12)	0.085 (−0.070,0.25)
50	1.15	0.083 (−0.073,0.26)	0.001 (−0.10,0.11)	0.085 (−0.070,0.25)
50	1.3	0.089 (−0.085,0.26)	−0.003 (−0.10,0.10)	0.085 (−0.070,0.25)
75	1	0.078 (−0.070,0.25)	0.006 (−0.086,0.11)	0.085 (−0.070,0.25)
75	1.15	0.082 (−0.083,0.25)	0.002 (−0.095,0.11)	0.085 (−0.070,0.25)
75	1.3	0.086 (−0.073,0.26)	−0.001 (−0.10,0.099)	0.085 (−0.070,0.25)
100	1	0.078 (−0.075,0.25)	0.007 (−0.090,0.11)	0.085 (−0.070,0.25)
100	1.15	0.081 (−0.077,0.25)	0.004 (−0.091,0.11)	0.085 (−0.070,0.25)
100	1.3	0.086 (−0.072,0.26)	−0.0007 (−0.10,0.10)	0.085 (−0.070,0.25)

Table 4.

Posterior means and credible intervals for NDE, NIE, and TE for ε ∈ {50, 75, 100}, χ ∈ {1.0, 1.15, 1.3} and ρ=0.7.

ε	χ	NDE	NIE	TE
50	1	0.077 (−0.073,0.25)	0.007 (−0.092,0.13)	0.085 (−0.070,0.25)
50	1.15	0.082 (−0.079,0.25)	0.002 (−0.10,0.11)	0.085 (−0.070,0.25)
50	1.3	0.088 (−0.085,0.26)	−0.003 (−0.10,0.099)	0.085 (−0.070,0.25)
75	1	0.077 (−0.066,0.25)	0.007 (−0.088,0.12)	0.085 (−0.070,0.25)
75	1.15	0.082 (−0.075,0.25)	0.003 (−0.096,0.11)	0.085 (−0.070,0.25)
75	1.3	0.086 (−0.087,0.26)	−0.001 (−0.097,0.10)	0.085 (−0.070,0.25)
100	1	0.078 (−0.069,0.25)	0.007 (−0.091,0.12)	0.085 (−0.070,0.25)
100	1.15	0.080 (−0.076,0.25)	0.004 (−0.088,0.11)	0.085 (−0.070,0.25)
100	1.3	0.084 (−0.084,0.26)	0.0006 (−0.10,0.10)	0.085 (−0.070,0.25)

The results were least sensitive to the correlation between mediators (see Assumption 4) and the NDE decreased (slightly) as epsilon increased but increased as the RR, χ increased. When we assumed independent uniform priors on the sensitivity parameters (based on their ranges elicited in Section 6.3), we drew similar conclusions (Table 5).

Table 5.

Posterior means and credible intervals for NDE, NIE, and TE for priors ρ ~ Unif[0, 1], ψ ~ Unif[50, 100], χ ~ Unif[1, 1.3].

NDE	NIE	TE
0.081 (−0.073,0.25)	0.003 (−0.086,0.12)	0.085 (−0.070,0.25)

Thus, based on our analysis, there was some evidence for the efficacy of the FTF treatment, but minimal evidence that the effect of the FTF treatment was mediated by the number of self-monitoring records completed over the 12 month management portion of the trial.

The maximal influence (on the posterior variance) for a violation of Assumption 5 is A ≤ .39.

6.5 Comparison with Baron and Kenny type estimators

For comparison, we also estimated the direct and indirect effects using the Baron and Kenny approach under the assumptions of sequential ignorability and no interaction. We use the R function mediate (Imai et al., 2010) and linear models as outlined in the Baron and Kenny approach in Section 1. The natural direct effect was estimated to be .031(−.12, 18) of similar magnitude to the natural indirect effect .054(−.000, .12), a quite different conclusion from the analysis above. However, the assumptions underlying the Baron and Kenny approach are unlikely to be reasonable in our (behavioral science) application and thus, we prefer the analysis (in Section 6.4) under the assumptions proposed in Section 2. Note that the sequential ignorability assumption is often weakened by including baseline covariates and conducting sensitivity analysis (Imai et al., 2010; vanderWeele, 2010), which we did not do here.

7. Discussion

We have proposed a Bayesian approach to the causal effect of mediation that involves three sensitivity parameters and no parametric models for the observed data. Strategies to elicit the sensitivity parameters were provided. Simulation studies suggested that estimation of the NIE is not very sensitive to small to medium size violations of Assumptions 3 and Assumption 5 provides an upper bound on the posterior variance of the NIE. For the TOURS trials, the effect of the face-to-face counseling treatment vs. the education control was marginally significant. However, based on our analysis, the potential mediator, the number of self-monitoring food records completed was not a mediator of this relationship. We propose this as a general approach to assess mediation that allows easy to interpret sensitivity parameters and realistic assumptions for behavioral trials.

There are several extensions to the current modeling approach. First, we might incorporate baseline covariates to weaken some of our assumptions and potentially gain efficiency in estimation of the natural indirect effects; we are currently working on this extension. Second, we could develop a more detailed framework for eliciting a prior (not just the range) for the sensitivity parameters. Third, extending the current framework (both defining causal effects and models) to the setting of multiple mediators is an open question. Fourth, we might consider alternatives to Assumption 2; in addition, we can generalize Assumption 2 by replacing the relative risk formulation with an odds ratio (exponential tilt) formulation that would be appropriate for both a binary and a continuous response.

There are also numerous interesting extensions based on the TOURS data. Twelve subjects (7.4%) dropped out before 18 months. We have not included them in the analysis. Future analyses will include these subjects under specific assumptions about the dropout. In addition, we have defined the mediator here as the total number of days with self-monitoring records of food intake over the 12 month period. However, this may be too coarse a summary. Future work will examine the record completion process, basically a 350-dimensional vector of 0 and 1’s (that sum up to our mediator) as there may be a (clinical) distinction between filling out no records per week versus one per week as opposed to two per week vs three per week (that both correspond to a difference of 50 days of records).

We are working on making the methods available as an R package.

Table 3.

Posterior means and credible intervals for NDE, NIE, and TE for ε ∈ {50, 75, 100}, χ ∈ {1.0, 1.15, 1.3} and ρ=0.3.

ε	χ	NDE	NIE	TE
50	1	0.078 (−0.073,0.25)	0.007 (−0.086,0.12)	0.085 (−0.070,0.25)
50	1.15	0.082 (−0.074,0.25)	0.003 (−0.10,0.10)	0.085 (−0.070,0.25)
50	1.3	0.087 (−0.078,0.26)	−0.0023 (−0.10,0.10)	0.085 (−0.070,0.25)
75	1	0.077 (−0.076,0.25)	0.007 (−0.095,0.12)	0.085 (−0.070,0.25)
75	1.15	0.081 (−0.076,0.25)	0.003 (−0.091,0.11)	0.085 (−0.070,0.25)
75	1.3	0.086 (−0.079,0.26)	−0.001 (−0.10,0.10)	0.085 (−0.070,0.25)
100	1	0.078 (−0.071,0.25)	0.006 (−0.095,0.12)	0.085 (−0.070,0.25)
100	1.15	0.080 (−0.076,0.26)	0.004 (−0.092,0.11)	0.085 (−0.070,0.25)
100	1.3	0.085 (−0.079,0.26)	0.0001 (−0.10,0.10)	0.085 (−0.070,0.25)