On the mechanics of growing thin biological membranes

Abstract

Despite their seemingly delicate appearance, thin biological membranes fulfill various crucial roles in the human body and can sustain substantial mechanical loads. Unlike engineering structures, biological membranes are able to grow and adapt to changes in their mechanical environment. Finite element modeling of biological growth holds the potential to better understand the interplay of membrane form and function and to reliably predict the effects of disease or medical intervention. However, standard continuum elements typically fail to represent thin biological membranes efficiently, accurately, and robustly. Moreover, continuum models are typically cumbersome to generate from surface-based medical imaging data. Here we propose a computational model for finite membrane growth using a classical midsurface representation compatible with standard shell elements. By assuming elastic incompressibility and membrane-only growth, the model a priori satisfies the zero-normal stress condition. To demonstrate its modular nature, we implement the membrane growth model into the general-purpose non-linear finite element package Abaqus/Standard using the concept of user subroutines. To probe efficiently and robustness, we simulate selected benchmark examples of growing biological membranes under different loading conditions. To demonstrate the clinical potential, we simulate the functional adaptation of a heart valve leaflet in ischemic cardiomyopathy. We believe that our novel approach will be widely applicable to simulate the adaptive chronic growth of thin biological structures including skin membranes, mucous membranes, fetal membranes, tympanic membranes, corneoscleral membranes, and heart valve membranes. Ultimately, our model can be used to identify diseased states, predict disease evolution, and guide the design of interventional or pharmaceutic therapies to arrest or revert disease progression.

1. Motivation

Biological membranes are fascinating structures: They are extremely delicate, with thicknesses rarely exceeding a few millimeters, while at the same time playing vital roles in the human body [26]. Typical examples are the skin membrane that is the largest protective organ of our body [55], the mucous membrane that lines the air-organ interfaces of our respiratory, digestive, and urogenital tracts [34], the fetal membrane that protects unborn life for the entire period of pregnancy [29], the tympanic membrane that separates our inner and outer ear and plays a crucial role in hearing [15], the corneoscleral membrane that has remarkable refractive properties and is essential for healthy vision [43], and the heart valve membranes that guarantee unidirectional blood flow within our circulatory system [45]. Biological membranes are functionally optimized thin structures, which continuously interact with their mechanical environment and, in many cases, support large physiological loads [50]. One of the most astonishing aspects of these structures is their ability to grow, change their external shape, and remodel their internal microstructure, to adapt to environmental changes [48]. The inability to adapt is often the underlying cause for fatal disease. For example, in some heart disease patients, the heart valves adapt to a pathologically enlarged opening area to maintain healthy valve function. In other patients with the same degree of enlargement, the valves are not able to adapt, which results in valve leakage, backflow, potentially heart failure, and ultimately death [9]. Understanding the interplay between thin biological membranes and their environment, and predicting their ability to functionally adapt, might be the key to solving many challenging clinical problems today.

During the past decade, mathematical modeling of thin biological membranes has become a powerful approach to explore tissue and organ function [49], to predict the response to internal and external loading [14], and to optimize medical devices and surgical techniques [37]. Because of its versatile nature, the finite element method is often the discretization tool of choice. Finite elements have been widely adapted to explore the mechanics of vascular membranes [13], skin membranes [7], mucous membranes [41], tympanic membranes [30], corneoscleral membranes [18], heart valve membranes [3], and many other thin biological structures [32]. Most of these approaches discretize the biological membrane using finite shell elements. When compared to standard three-dimensional solid elements, shell elements generally provide a number of computational advantages such as enhanced efficiency and improved conditioning [25]. Conditioning may become critical when modeling layered membranes such as skin, which consist of multiple layers with distinct microstructure, stiffness, and function [33]. In the context of biomedical modeling, a major advantage of shell elements is that they typically only require a midsurface representation, which is typically readily available from surface imaging data [46].

Traditionally, most finite element tools have been developed to explore the acute, short-term response to mechanical loading. Now, more and more finite element tools focus on predicting the chronic long-term response to environmental changes. Examples involve the simulation of arterial wall growth in hypertension [52], and in response to stenting [31], skin growth during tissue expansion [55], airway wall growth in chronic obstructive pulmonary disease [39], ocular growth in glaucoma [19], cardiac growth under physiological [16] and pathological [17] conditions, both in systemic and pulmonary hypertension [47], muscle growth during limb lengthening [56], to name but a few. Despite significant scientific progress throughout the past two decades [2], very few finite element algorithms can efficiently and robustly simulate growing biological structures of small thickness. This is of particular importance when studying growing biological membranes, which grow in membrane area but not in membrane thickness, such as skin [42, 57]. The goal of this manuscript is therefore to establish a finite element model for growing biological membranes using discrete Kirchhoff shell kinematics.

The remainder of this manuscript is organized as follows: In Section 2, we briefly summarize the continuum modeling of membrane growth, including the kinematic equations of growth, the constitutive equations of collagenous tissues with a pronounced microstructural direction, and the equations for stretch-driven membrane growth. In Section 3, we present the temporal discretization of the growth equation and its consistent algorithmic linearization. In Section 4, we illustrate the computational implementation of our growth model within a generalpurpose finite shell element. In Section 5, we demonstrate the basic features of our model using typical benchmark problems for thin shells. To illustrate the clinical relevance of membrane growth, we conclude with an example of mitral leaflet adaption in response to a heart attack. In Section 6, we conclude by discussing the current work, its relevance to the computational community, and its implications in biomechanical and biomedical research.

2. Continuum Modeling of Membrane Growth

2.1. Kinematics of Membrane Growth

In the following section, we lay out the framework for the theory of finite growth. We begin by introducing the deformation map φ, which maps a material point X of a body in the reference configuration B₀ onto its spatial counterpart x = φ(X, t) in the current configuration B_t at every point in time t. The key kinematic assumption of the theory of finite growth is the multiplicative decomposition of the deformation gradient,

$$\mathit{F}={\mathbf{\nabla }}_{\mathit{X}}\mathit{\phi }={\mathit{F}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{g}},$$ (1)

into a reversible elastic part F^e and an irreversible growth part F^g, where ∇_X denotes the gradient of a field with respect to the material placement X at fixed time t. Similarly, we can multiplicatively decompose the corresponding Jacobian,

$$J=\det (\mathit{F})={\mathit{J}}^{\mathrm{e}}{\mathit{J}}^{\mathrm{g}},$$ (2)

into a reversible elastic volume change J^e = det (F^e) and an irreversible grown volume change J^g = det (F^g). Subsequently, we will also utilize the area change according to Nanson’s formula,

$$\vartheta =\Vert J{\mathit{F}}^{-\mathrm{t}}·{\mathit{n}}_0\Vert ={\vartheta }^{\mathrm{e}}{\vartheta }^{\mathrm{g}},$$ (3)

where n₀ denotes the surface normal in the reference configuration. Here we consider the special case of area growth, for which growth takes place exclusively within the membrane plane, while the membrane thickness does not grow [7]. This implies that the total the area change ϑ obeys a multiplicative decomposition into a reversibly elastic area change ϑ^e and an irreversibly grown area change ϑ^g = ∥J^g F^g−t · n₀∥ = J^g. In the following, we will assume an isotropic in-plane growth, for which the growth tensor F^g takes the following simple format,

$${\mathit{F}}^{\mathrm{g}}=\sqrt{{\vartheta }^{\mathrm{g}}}\mathit{I}+[1-\sqrt{{\vartheta }^{\mathrm{g}}}]{\mathit{n}}_0\otimes {\mathit{n}}_0,$$ (4)

where the area growth ϑ^g takes the interpretation of a scalar-valued growth multiplier. Using the Sherman-Morrison formula, we can directly invert the growth tensor,

$${\mathit{F}}^{\mathrm{g}-1}=\frac{1}{\sqrt{{\vartheta }^{\mathrm{g}}}}\mathit{I}+\left[1-\frac{1}{\sqrt{{\vartheta }^{\mathrm{g}}}}\right]{\mathit{n}}_0\otimes {\mathit{n}}_0,$$ (5)

and obtain an explicit representation of the elastic tensor F^e,

$${\mathit{F}}^{\mathrm{e}}=\frac{1}{\sqrt{{\vartheta }^{\mathrm{g}}}}\mathit{F}+\left[1-\frac{1}{\sqrt{{\vartheta }^{\mathrm{g}}}}\right]\mathit{n}\otimes {\mathit{n}}_0,$$ (6)

where n = F · n₀ denotes the surface normal in the current configuration. We further introduce the right Cauchy-Green deformation tensor C and its elastic part C^e,

$${\mathit{C}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{e\; t}}·{\mathit{F}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{g}-\mathrm{t}}·\mathit{C}·{\mathit{F}}^{\mathrm{g}-1}\mathrm{with}\mathit{C}={\mathit{F}}^{\mathrm{t}}·\mathit{F},$$ (7)

along with the left Cauchy-Green deformation tensor b and its elastic part b^e,

$${\mathit{b}}^{\mathrm{e}}={\mathit{F}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{e\; t}}=\frac{1}{{\vartheta }^{\mathrm{g}}}\mathit{b}+\left[1-\frac{1}{{\vartheta }^{\mathrm{g}}}\right]\mathit{n}\otimes \mathit{n}\mathrm{with}\mathit{b}=\mathit{F}·{\mathit{F}}^{\mathrm{t}}.$$ (8)

It proves convenient to also introduce the growth deformation tensor, C^g = F^{g t} · F^g, and its inverse,

$${\mathit{C}}^{\mathrm{g}-1}={\mathit{F}}^{\mathrm{g}-1}·{\mathit{F}}^{\mathrm{g}-\mathrm{t}}=\frac{1}{{\vartheta }^{\mathrm{g}}}\mathit{I}+\left[1-\frac{1}{{\vartheta }^{\mathrm{g}}}\right]{\mathit{n}}_0\otimes {\mathit{n}}_0={\mathit{F}}^{-1}·{\mathit{b}}^{\mathrm{e}}·{\mathit{F}}^{-\mathrm{t}},$$ (9)

which follows directly from the covariant pullback of the elastic left Cauchy-Green deformation tensor b^e. In the following, we consider a transversely isotropic material with a characteristic microstructural direction m₀ in B_g, tangential to the shell midsurface, i.e., m₀ · n₀ ≐ 0, [8]. We characterize the material through the following kinematic invariants

$$J^{\mathrm{e}}=\det \left({\mathit{F}}^{\mathrm{e}}\right){\mathit{I}}_1^{\mathrm{e}}={\mathit{C}}^{\mathrm{e}}:\mathit{I}{\mathit{I}}_4^{\mathrm{e}}={\mathit{C}}^{\mathrm{e}}:{\mathit{m}}_0\otimes {\mathit{m}}_0,$$ (10)

and their derivatives

$$\frac{\partial J^{\mathrm{e}}}{\partial {\mathit{C}}^{\mathrm{e}}}=\frac{1}{2}{J}^{\mathrm{e}}{\mathit{C}}^{\mathrm{e}-1}\frac{\partial {\mathit{I}}_1^{\mathrm{e}}}{\partial {\mathit{C}}^{\mathrm{e}}}=\mathit{I}\frac{\partial {\mathit{I}}_4^{\mathrm{e}}}{\partial {\mathit{C}}^{\mathrm{e}}}={\mathit{m}}_0\otimes {\mathit{m}}_0.$$ (11)

Remark 1 (Kirchhoff Shell Kinematics)

In the following, we adopt Kirchhoff shell kinematics for thin shells and rotate the local coordinate system such that two of its base vectors lie within the shell midsurface, while the third base vector points in the direction of the shell normal. According to the Kirchhoff shell theory, the deformation gradient takes the following reduced format,

$$F_{13}=F_{23}=F_{31}=F_{32}\doteq 0.$$

Consequently, the right Cauchy-Green deformation tensor C = F^t · F adapts the same reduced format with

$$C_{13}=C_{23}=C_{31}=C_{32}\doteq 0.$$

For our particular form of growth of equation (4), for which the growth tensor F^g characterizes in-plane growth, a similar reduced format with

$$C_{13}^{\mathrm{e}}=C_{23}^{\mathrm{e}}=C_{31}^{\mathrm{e}}=C_{32}^{\mathrm{e}}\doteq 0$$

holds for the elastic right Cauchy-Green deformation tensor C^e = F^g−t · C · F^g−1.

Remark 2 (Incompressibility)

In the sequel, we assume that the reversible, elastic deformation is fully incompressible, i.e., that all volumetric changes are a consequence of growth,

$$J^{\mathrm{e}}=1\mathit{thus}J=J^{\mathrm{g}}={\vartheta }^{\mathrm{g}}.$$

Together with the Kirchhoff shell kinematics of the previous Remark and the particular format of the growth tensor in equation (4), this allows us to explicitly express the out-of-plane component of the elastic elastic right Cauchy-Green deformation tensor as

$$C_{33}^{\mathrm{e}}=1/{\vartheta }^{\mathrm{e}2}\mathit{with}{\vartheta }^{\mathrm{e}}=\Vert {\mathit{F}}^{-\mathrm{t}}·{\mathit{n}}_0\Vert .$$

where ϑ^e is the reversible elastic in-plane area change.

2.2. Constitutive Equations

We consider an incompressible, transversely isotropic, hyperelastic material [22], characterized through a free energy function ψ, which we additively decompose into a volumetric part U and an isochoric part ψ̄,

$$\psi =U(J^{\mathrm{e}})+\overline{\psi }(I_1^{\mathrm{e}},I_4^{\mathrm{e}})\mathrm{with}U=p[J^{\mathrm{e}}-1].$$ (12)

The volumetric part U enforces elastic incompressibility, J^e = 1, in terms of the pressure p, which we have to prescribe constitutively. The isochoric part ψ̄ is a function of the elastic invariants $I_1^{\mathrm{e}}$ and $I_4^{\mathrm{e}}$. We can then introduce the elastic Piola-Kirchhoff stress in the intermediate configuration,

$${\mathit{S}}^{\mathrm{e}}=2\frac{\partial \psi }{\partial {\mathit{C}}^{\mathrm{e}}}=p^{\mathrm{e}}{\mathit{C}}^{\mathrm{e}-1}+2{\psi }_1\mathit{I}+2{\psi }_4{\mathit{m}}_0\otimes {\mathit{m}}_0,$$ (13)

where we have introduced the abbreviations p^e = J^e p and ${\psi }_1=\partial \overline{\psi }/\partial I_1^{\mathrm{e}}$ and ${\psi }_4=\partial \overline{\psi }/\partial I_4^{\mathrm{e}}$. Through a contravariant pull back to the reference configuration, S = F ^g−1 · S^e · F^g−t, we obtain the total Piola-Kirchhoff stress,

$$\mathit{S}=2\frac{\partial \psi }{\partial \mathit{C}}=p^{\mathrm{e}}{\mathit{C}}^{-1}+2{\psi }_1{\mathit{C}}^{\mathrm{g}-1}+2{\psi }_4\frac{1}{{\vartheta }^{\mathrm{g}}}{\mathit{m}}_0\otimes {\mathit{m}}_0.$$ (14)

Here, because of the particular format of the growth tensor F^g, and because of the orthogonality of the characteristic directions for microstructure and growth, m₀ · n₀ = 0, the pull back of the microstructural direction, ${\mathit{F}}^{\mathrm{g}-1}·{\mathit{m}}_0=1\sqrt{{\vartheta }^{\mathrm{g}}}{\mathit{m}}_0$, is nothing but a scaling with the reciprocal square root of the area growth ϑ^g. Through a contravariant push forward to the current configuration, τ = F · S · F^t, we obtain the Kirchhoff stress,

$$\mathit{\tau }=p^{\mathrm{e}}\mathit{I}+2{\psi }_1{\mathit{b}}^{\mathrm{e}}+2{\psi }_4\frac{1}{{\vartheta }^{\mathrm{g}}}\mathit{m}\otimes \mathit{m},$$ (15)

where m = F^e · m₀ denotes the microstructural direction in the current configuration. We can then introduce the fourth order tensor of elastic moduli ℂ^e in the intermediate configuration as the derivative of the elastic Piola-Kirchhoff stress S^e with respect to the elastic right Cauchy-Green tensor C^e,

$$\begin{array}{lll}{ℂ}^{\mathrm{e}}=2\frac{\partial {\mathit{S}}^{\mathrm{e}}}{\partial {\mathit{C}}^{\mathrm{e}}}& =& -p^{\mathrm{e}}[{\mathit{C}}^{\mathrm{e}-1}\overline{\otimes }{\mathit{C}}^{\mathrm{e}-1}+{\mathit{C}}^{\mathrm{e}-1}\underset{\_}{\otimes }{\mathit{C}}^{\mathrm{e}-1}]\\ & & +2{\mathit{C}}^{\mathrm{e}-1}\otimes \partial p^{\mathrm{e}}/\partial {\mathit{C}}^{\mathrm{e}}\\ & & +4{\psi }_{11}\mathit{I}\otimes \mathit{I}\\ & & +8{\psi }_{14}{\left[\mathit{I}\otimes {\mathit{m}}_0\otimes {\mathit{m}}_0\right]}^{\mathrm{sym}}\\ & & +4{\psi }_{44}{\mathit{m}}_0\otimes {\mathit{m}}_0\otimes {\mathit{m}}_0\otimes {\mathit{m}}_0,\end{array}$$ (16)

where we have used the abbreviations ${\psi }_{11}={\partial }^2\overline{\psi }/\partial I_1^{\mathrm{e}2}$, ${\psi }_{14}={\partial }^2\overline{\psi }/\partial I_1^{\mathrm{e}}\partial I_4^{\mathrm{e}}$, and ${\psi }_{44}={\partial }^2\overline{\psi }/\partial I_4^{\mathrm{e}2}$ as well as the short hand notations ⊗̄ and ⊗̱ for the non-standard fourth order products {•⊗̄◦}_ijkl = {•}_ik{◦}_jl and {•⊗̱◦}_ijkl = {•}_il{◦}_jk. Last, for the algorithmic realization, it proves convenient to push the tensor of constitutive moduli ℂ^e to the current configuration,

$$\begin{array}{lll}{\mathrm{c}}^{\mathrm{e}}& =& -p^{\mathrm{e}}[\mathit{I}\overline{\otimes }\mathit{I}+\mathit{I}\underset{¯}{\otimes }\mathit{I}]\\ & & +2\mathit{I}\otimes \mathit{F}·\partial p^{\mathrm{e}}/\partial {\mathit{C}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{t}}\\ & & +4{\psi }_{11}\mathit{b}\otimes \mathit{b}\\ & & +8{\psi }_{14}{[\mathit{b}\otimes \mathit{m}\otimes \mathit{m}]}^{\mathrm{sym}}\\ & & +4{\psi }_{44}\mathit{m}\otimes \mathit{m}\otimes \mathit{m}\otimes \mathit{m}.\end{array}$$ (17)

Remark 3 (Plane Stress Condition)

To explicitly ensure the plane stress condition, S₃₃ ≐ 0, we impose the zero-normal stress condition and require that the out-of-plane component of the stress tensor vanishes identically [44]. Using equation (14), we can explicitly restate the plane stress condition as

$$S_{33}=p^{\mathrm{e}}{C}_{33}^{-1}+2{\psi }_1{C}_{33}^{\mathrm{g}-1}+2{\psi }_4\frac{1}{{\vartheta }^{\mathrm{g}}}{m}_{03}^2\doteq 0.$$

With the specific format of in-plane area growth F^g introduced equation (4), $C_{33}^{\mathrm{g}}=C_{33}^{\mathrm{g}-1}=1$, such that $C_{33}^{-1}=C_{33}^{\mathrm{e}-1}$, the condition of elastic incompressibility, J^e = 1 such that p^e = J^e p = p, and the fact that the microstructural direction m₀ with m₀ · n = 0 is always tangential to the shell midsurface, m₀₃ = 0, we can simplify the plane stress condition as follows,

$$S_{33}=p{C}_{33}^{\mathrm{e}-1}+2{\psi }_1\doteq 0.$$

We solve the above equation to obtain the following explicit expression

$$p=-2{\psi }_1{\mathit{C}}_{33}^{\mathrm{e}}=-2{\psi }_1/{\vartheta }^{\mathrm{e}2}.$$

for the pressure p.

2.3. Stretch Driven Membrane Growth

We assume that growth is a strain-driven process, and define the temporal evolution of the growth multiplier ϑ̇^g as the product of the growth function k^g and the growth criterion ϕ^g [17].

$$\dot{\vartheta }=k^{\mathrm{g}}{\varphi }^{\mathrm{g}}$$ (18)

The growth function

$$k^{\mathrm{g}}=\frac{1}{{\tau }^{\mathrm{g}}}{\left[\frac{{\vartheta }^{\max }-{\vartheta }^{\mathrm{g}}}{{\vartheta }^{\max }-1}\right]}^{\gamma }$$ (19)

governs the shape of the growth profile through three scalar parameters, the growth constant τ^g, the upper bound for area growth ϑ^max, and the non-linearity parameter γ. The growth criterion

$${\varphi }^{\mathrm{g}}=\langle {\vartheta }^{\mathrm{e}}-{\vartheta }^{\mathrm{crit}}\rangle =\langle \vartheta /{\vartheta }^{\mathrm{g}}-{\vartheta }^{\mathrm{crit}}\rangle$$ (20)

reflects the choice of elastic area-stretch ϑ^e as the driving force behind the growth response. The Macaulay brackets activate area growth, 〈ϑ^e − ϑ^crit〉 = ϑ^e − ϑ^crit, when the elastic area stretch exceeds a physiological threshold, ϑ^e ≥ ϑ^crit. They deactivate growth, 〈ϑ^e − ϑ^crit〉 = 0, for elastic area stretches within the physiological range, ϑ^e < ϑ^crit. Figure 1 illustrates the evolution of the total stretch ϑ, of the elastic stretch ϑ^e, and of the growth stretch ϑ^g in a virtual creep test, left, and in a virtual relaxation test, right.

Figure 1.

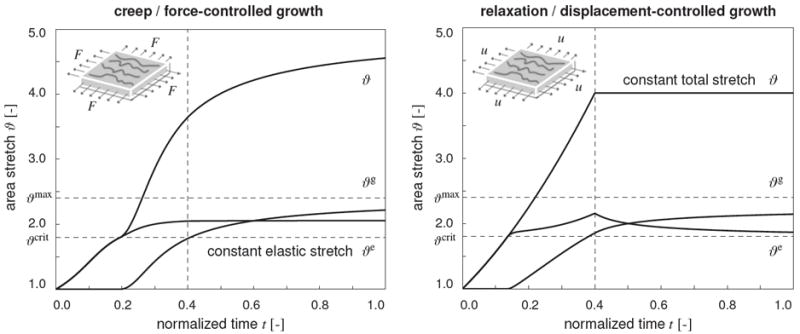
Creep and relaxation tests in growing thin biological membranes. Evolution of total area stretch ϑ, elastic area stretch ϑ^e, and growth area stretch ϑ^g under force control, left, and displacement control, right. Horizontal dashed lines represent the elastic stretch limit ϑ^crit beyond which growth is activated, and the maximum area growth ϑ^max to which growth is limited. Forces, left, and displacements, right, are increased linearly up to the vertical dashed lines and then held constant. Under force control, for a constant elastic stretch, the total stretch increases gradually as the growth stretch increases, left. Under displacement control, for a constant total stretch, the elastic stretch decreases gradually as growth stretch increases, right.

3. Computational Modeling of Membrane Growth

To embed the governing equations of membrane growth within a finite element setting, we discretize the growth equation (18) in time using a simple finite difference scheme. This allows us to express the temporal evolution of the area growth multiplier as

$${\dot{\vartheta }}^{\mathrm{g}}=[{\vartheta }^{\mathrm{g}}-{\vartheta }_n^{\mathrm{g}}]/\mathrm{\Delta }t,$$ (21)

where Δt = t−t_n denotes the time increment between the current time step t and the previous time step t_n. Now we introduce the residual R^ϑ using equation (18) and the discretized growth rate (21) as a function of the unknown growth multiplier ϑ^g,

$${\mathrm{R}}^{\vartheta }={\vartheta }^{\mathrm{g}}-{\vartheta }_n^{\mathrm{g}}-k^{\mathrm{g}}{\varphi }^{\mathrm{g}}\mathrm{\Delta }t.$$ (22)

To solve for the current growth multiplier ϑ^g, we employ a local Newton iteration and linearize the residual R^ϑ with respect to the growth multiplier ϑ^g,

$${\mathrm{K}}^{\vartheta }=\frac{\partial {\mathrm{R}}^{\vartheta }}{\partial {\vartheta }^{\mathrm{g}}}=1-\left[\frac{\partial k^{\mathrm{g}}}{\partial {\vartheta }^{\mathrm{g}}}{\varphi }^{\mathrm{g}}+k^{\mathrm{g}}\frac{\partial {\varphi }^{\mathrm{g}}}{\partial {\vartheta }^{\mathrm{g}}}\right]\mathrm{\Delta }t,$$ (23)

where ∂k^g/∂ϑ^g = −γk^g/[ϑ^max − ϑ^g] and ∂ϕ^g/∂ϑ^g = −ϑ/ϑ^{g 2}. For each local Newton iteration, we update the growth multiplier ϑ^g according to

$${\vartheta }^{\mathrm{g}}\leftarrow {\vartheta }^{\mathrm{g}}-{\mathrm{R}}^{\vartheta }/{\mathrm{K}}^{\vartheta },$$ (24)

until we reach a user-defined convergence criterion. From a workflow perspective, this implies that once the elastic area stretch ϑ^e exceeds the critical value ϑ^crit, we enter the local Newton iteration to iteratively solve for ϑ^g. Once we have determined the amount of area growth, we can update the growth tensor F^g, calculate the elastic tensor F^e, determine the elastic deformation tensors C^e and b^e, calculate the elastic Piola-Kirchhoff stress S^e, the total Piola-Kirchhoff stress S and Kirchhoff stress τ.

To efficiently solve the equations of membrane growth within a finite element setting, we linearize the second Piola-Kirchhoff stress S with respect to the right Cauchy-Green deformation tensor C to obtain the total fourth order tangent moduli ℂ in the reference configuration [17],

$$ℂ=2\frac{\mathrm{d}\mathit{S}}{\mathrm{d}\mathit{C}}=2\frac{\partial \mathit{S}}{\partial \mathit{C}}{|}_{{\mathit{F}}^g}+\left[\frac{\partial \mathit{S}}{\partial {\mathit{F}}^{\mathrm{g}}}:\frac{\partial {\mathit{F}}^{\mathrm{g}}}{\partial {\vartheta }^{\mathrm{g}}}\right]\otimes 2\frac{\partial {\vartheta }^{\mathrm{g}}}{\partial \mathit{C}}{|}_{\mathit{F}}.$$ (25)

The first term represents the pull back of the elastic moduli ℂ^e of equation (16) from the intermediate configuration to the reference configuration,

$$2\frac{\partial \mathit{S}}{\partial \mathit{C}}{|}_{{\mathit{F}}^g}=[{\mathit{F}}^{\mathrm{g}-1}\overline{\otimes }{\mathit{F}}^{\mathrm{g}-1}]:{ℂ}^{\mathrm{e}}:[{\mathit{F}}^{\mathrm{g}-\mathrm{t}}\overline{\otimes }{\mathit{F}}^{\mathrm{g}-\mathrm{t}}].$$ (26)

The second term results in following expression,

$$\begin{array}{lll}\frac{\partial \mathit{S}}{\partial {\mathit{F}}^{\mathrm{g}}}& =& -[{\mathit{F}}^{\mathrm{g}-1}\overline{\otimes }\mathit{S}+\mathit{S}\underset{\_}{\otimes }{\mathit{F}}^{\mathrm{g}-1}]\\ & & -[{\mathit{F}}^{\mathrm{g}-1}\overline{\otimes }{\mathit{F}}^{\mathrm{g}-1}]:\frac{1}{2}{ℂ}^{\mathrm{e}}:[{\mathit{F}}^{\mathrm{g}-\mathrm{t}}\underset{\_}{\otimes }{\mathit{C}}^{\mathrm{e}}+{\mathit{C}}^{\mathrm{e}}\overline{\otimes }{\mathit{F}}^{\mathrm{g}-\mathrm{t}}].\end{array}$$ (27)

The third term is specific to the particular format of the growth tensor in equation (4),

$$\frac{\partial {\mathit{F}}^{\mathrm{g}}}{\partial {\vartheta }^{\mathrm{g}}}=\frac{1}{2\sqrt{{\vartheta }^{\mathrm{g}}}}[\mathit{I}\mathit{-}{\mathit{n}}_0\otimes {\mathit{n}}_0].$$ (28)

The fourth term depends on the algorithmic solution of the evolution equation for the growth multiplier ϑ^g,

$$2\frac{\partial {\vartheta }^{\mathrm{g}}}{\partial \mathit{C}}=\frac{k^{\mathrm{g}}\mathrm{\Delta }t}{{\vartheta }^{\mathrm{g}}{\mathrm{K}}^{\vartheta }}\left[\vartheta {\mathit{C}}^{-1}-\frac{J^2}{\vartheta }[{\mathit{C}}^{-1}·{\mathit{n}}_0]\otimes [{\mathit{C}}^{-1}·{\mathit{n}}_0]\right],$$ (29)

and follows from expanding the algorithmic derivative ∂ϑ^g/∂C = [∂ϑ̇^g/∂C + ∂ϑ̇^g/∂ϑ^g · ∂ϑ^g/∂C] Δt and solving for ∂ϑ^g/∂C = [1 − ∂ϑ̇^g/∂ϑ^g Δt]⁻¹ ∂ϑ̇^g/∂C Δt = Δt/K^ϑ ∂ϑ̇^g/∂C as illustrated in [20].

4. Finite Element Implementation of Membrane Growth

For the finite element implementation, we consider finite elements with discrete Kirchhoff shell kinematics, for which the in-plane and out-of-plane components are fully decoupled. It proves convenient, to first determine the in-plane components, here denoted through the overhead symbol, and then calculate the out-of-plane components in a post-processing step. Accordingly, we introduce the in-plane growth tensor,

$${\widehat{\mathit{F}}}^{\mathrm{g}}=\sqrt{{\vartheta }^{\mathrm{g}}}\widehat{\mathit{I}},$$ (30)

and its inverse,

$${\widehat{\mathit{F}}}^{\mathrm{g}-1}=\widehat{\mathit{I}}/\sqrt{{\vartheta }^{\mathrm{g}}},$$ (31)

in terms of the in-plane unit tensor Î. This allows us to introduce the following simplified expressions for the in-plane elastic tensor,

$${\widehat{\mathit{F}}}^{\mathrm{e}}=\widehat{\mathit{F}}/\sqrt{{\vartheta }^{\mathrm{g}}},$$ (32)

the in-plane elastic right Cauchy-Green tensor,

$${\widehat{\mathit{C}}}^{\mathrm{e}}={\widehat{\mathit{F}}}^{\mathrm{e\; t}}·{\widehat{\mathit{F}}}^{\mathrm{e}}=\widehat{\mathit{C}}/{\vartheta }^{\mathrm{g}}\mathrm{with}\widehat{\mathit{C}}={\widehat{\mathit{F}}}^{\mathrm{t}}·\widehat{\mathit{F}}$$ (33)

and the in-plane elastic left Cauchy-Green tensor,

$${\widehat{\mathit{b}}}^{\mathrm{e}}={\widehat{\mathit{F}}}^{\mathrm{e}}·{\widehat{\mathit{F}}}^{\mathrm{e\; t}}=\widehat{\mathit{b}}/{\vartheta }^{\mathrm{g}}\mathrm{with}\widehat{\mathit{b}}=\widehat{\mathit{F}}·{\widehat{\mathit{F}}}^{\mathrm{t}},$$ (34)

as the area-growth weighted elastic counterparts of the corresponding total components. According to equation (13), we introduce the elastic in-plane Piola-Kirchhoff stress,

$${\widehat{\mathit{S}}}^{\mathrm{e}}=p^{\mathrm{e}}{\widehat{\mathit{C}}}^{\mathrm{e}-1}+2{\psi }_1\widehat{\mathit{I}}+2{\psi }_4{\widehat{\mathit{m}}}_0\otimes {\widehat{\mathit{m}}}_0,$$ (35)

where m̂₀ is the referential in-plane microstructural direction. Through a contravariant in-plane pull back to the reference configuration, Ŝ = F̂^g−1 · Ŝ^e · F̂^g−t = Ŝ^e/ϑ^g, we obtain the in-plane Piola-Kirchhoff stress as the area-growth weighted elastic in-plane Piola-Kirchhoff stress,

$$\widehat{\mathit{S}}=[p^{\mathrm{e}}{\widehat{\mathit{C}}}^{\mathrm{e}-1}+2{\psi }_1\widehat{\mathit{I}}+2{\psi }_4{\widehat{\mathit{m}}}_0\otimes {\widehat{\mathit{m}}}_0]/{\vartheta }^{\mathrm{g}}.$$ (36)

Through a contravariant in-plane push forward to the current configuration, τ̂ = F̂ · Ŝ · F̂^t, we obtain the in-plane Kirchhoff stress,

$$\widehat{\mathit{\tau }}=p^{\mathrm{e}}\widehat{\mathit{I}}+2{\psi }_1{\widehat{\mathit{b}}}^{\mathrm{e}}+2{\psi }_4\widehat{\mathit{m}}\otimes \widehat{\mathit{m}}$$ (37)

where m̂ = F̂ · m̂₀ is the current in-plane microstructural direction. The in-plane tangent moduli in the reference configuration take the following simplified format,

$$\widehat{ℂ}=2\frac{\mathrm{d}\widehat{\mathit{S}}}{\mathrm{d}\widehat{\mathit{C}}}=\left[{\widehat{ℂ}}^{\mathrm{e}}-\frac{k^{\mathrm{g}}\mathrm{\Delta }t}{{\vartheta }^g{\mathrm{K}}^{\vartheta }}\left[{\widehat{\mathit{S}}}^{\mathrm{e}}+\frac{1}{2}{\widehat{ℂ}}^{\mathrm{e}}:{\widehat{\mathit{C}}}^{\mathrm{e}}\right]\otimes \vartheta {\widehat{\mathit{C}}}^{-1}\right]/{\vartheta }^{\mathrm{g}2},$$ (38)

where ℂ̂^e are the in-plane components of the elastic moduli according to equation (16). Last, for the algorithmic realization, we push the in-plane constitutive moduli to the current configuration,

$$\widehat{\mathrm{c}}={\widehat{\mathrm{c}}}^{\mathrm{e}}-\frac{k^{\mathrm{g}}\mathrm{\Delta }t}{{\vartheta }^{{\mathrm{g}}^2}{\mathrm{K}}^{\vartheta }}\left[\widehat{\mathit{\tau }}+\frac{1}{2}{\widehat{\mathrm{c}}}^{\mathrm{e}}:\widehat{\mathit{I}}\right]\otimes \vartheta \widehat{\mathit{I}},$$ (39)

where ĉ^e are the in-plane components of the elastic moduli according to equation (17). Rather than working directly with the Kirchhoff stress (37) and with the constitutive moduli (39), the user-defined subroutine for shell elements in Abaqus/Standard [1] utilizes the Cauchy or true stress, σ̂ = τ̂/J,

$${\mathit{\sigma }}^{\mathrm{abaqus}}=[p^{\mathrm{e}}\widehat{\mathit{I}}+2{\psi }_1{\widehat{\mathit{b}}}^{\mathrm{e}}+2{\psi }_4\widehat{\mathit{m}}\otimes \widehat{\mathit{m}}]/\mathit{J},$$ (40)

and the Green-Naghdi stress rate devided by the Jacobian, which requires the following modification of the tangent moduli [44],

$${\mathrm{c}}^{\mathrm{abaqus}}=[\widehat{\mathrm{c}}+\widehat{\mathit{\tau }}\overline{\otimes }\widehat{\mathit{i}}+\widehat{\mathit{i}}\overline{\otimes }\widehat{\mathit{\tau }}+[\widehat{\mathit{\tau }}\overline{\otimes }\widehat{\mathit{i}}]:\mathrm{\Lambda }-[\widehat{\mathit{i}}\overline{\otimes }\widehat{\mathit{\tau }}]:\mathrm{\Lambda }]/\mathit{J},$$ (41)

where ĉ + τ̂ ⊗̄ î + î ⊗̄ τ̂ is the Jauman stress rate and Λ is a material-independent fourth order tensor [53]. The local stress σ^abaqus of equation (40) and the local tangent moduli c^abaqus of equation (41) enter the righthand side vector and the iteration matrix of the global Newton iteration. Upon its convergence, we store the current area growth ϑ^g locally at the integration point level.

Remark 4 (Growing Thin Films)

The in-plane representation of membrane growth proves conceptually elegant, since it reduces the pull-back and push-forward operations (33), (34), and (36) to scalar scaling operations in terms of the area growth ϑ_g. Its underlying idea is based on reducing the generic continuum ansatz for the growth tensor of equation (4),

$${\mathit{F}}^{\mathrm{g}}=\sqrt{{\vartheta }^{\mathrm{g}}}\mathit{I}+[1-\sqrt{{\vartheta }^{\mathrm{g}}}]{\mathit{n}}_0\otimes {\mathit{n}}_0,$$

which characterizes area growth normal to the direction n₀ [7], to its membrane representation of equation (30),

$${\widehat{\mathit{F}}}^{\mathrm{g}}=\sqrt{{\vartheta }^{\mathrm{g}}}\widehat{\mathit{I}},$$

which characterizes isotropic in-plane growth. In the zero-thickness limit, this in-plane representation converges to the recently proposed formulation for surface growth [41], which provides a suitable framework to model biological systems coated by thin films of thicknesses in the nano- and micrometer regime [21].

5. Examples of Growing Thin Biological Membranes

We illustrate the key features of our model by means of four examples of membrane growth. The first example is a pinched thin-walled cylinder, which undergoes significant bending combined with a moderate area stretch. We demonstrate the irreversible nature of growth by showing that the grown cylinder will not return to its original configuration upon unloading. The second example is a stretched bilayered thin film consisting of a growing bottom layer and a purely elastic top layer. As the thin film is subjected to biaxial stretching, the bottom layer grows in area while the top layer does not. We show that when the load is released, the panel folds out of plane, in an attempt to release the elastic energy stored in the top layer. The third example is a pressurized thin membrane, which is initially planar, but displaces out of plane upon inflation. We show the effects of heterogeneous growth and elastic material anisotropy by comparing an isotropic and two fiber-reinforced membranes. The fourth and last example is the clinical problem of a stretched heart valve leaflet. We demonstrate the chronic adaptation of the leaflet membrane under pathological loading conditions. In particular, we expose the leaflet to annular dilation and papillary muscle displacement to quantify leaflet growth in a disease known as mitral regurgitation. In all four cases, we adapt a Holzapfel-type constitutive model [22], and specify the isochoric part of the free energy of equation (12) as follows,

$$\overline{\psi }=c_0[I_1-3]+\frac{c_1}{2c_2}[\exp (c_2{[I_4-1]}^2)-1].$$

This specific format introduces the coefficients

$${\overline{\psi }}_1=c_0\mathrm{and}{\overline{\psi }}_4=c_1[I_4-1]\exp (c_2{[I_4-1]}^2)$$

for the elastic and total Piola-Kirchhoff stresses S^e and S of equations (13) and (14), and the coefficients ψ̄₁₁ = 0, ψ̄₁₄ = 0, and

$${\overline{\psi }}_{44}=c_1[1+2c_2[I_4-1]]\exp (c_2{[I_4-1]}^2)$$

for the elastic tangent moduli ℂ^e and c^e of equations (16) and (17). The parameter c₀ governs the isotropic response and corresponds to one half of the shear modulus μ in the limit of infinitesimal strains. The parameters c₁ and c₂ govern the anisotropic response along the pronounced mircostructural direction m₀.

5.1. Example 1: Pinched Thin-Walled Cylinder

In the first example, a classical benchmark problem for shell elements [6], we subject a thin-walled hollow cylinder of l = 30 cm length, r = 9 cm outer radius, and t = 0.02 cm thickness to a prescribed a vertical pinching along the cylinder’s long-axis. We take advantage of structural symmetry, and model a quarter of the cylinder with 420 Abaqus S4 four-noded shell elements. We model the cylinder as isotropic elastic with c₀ = 1.0 MPa, c₁ = 0.0 MPa, and c₂ = 0.0, and assume it grows with ϑ^crit = 1.0, ϑ^max = 4.0, τ^g = 0.1/t*, and γ = 2.0, where t* is a characteristic time of growth. First, we load the top and bottom mantle line of the cylinder by increasing their vertical displacements until both sides touch each other. Then, we hold the load constant and allow the structure to growth until growth has converged. Finally, we gradually remove the applied load. Figure 2 displays five characteristic stages of this loading history. As the cylinder is deformed, it is primarily subject to bending, while its lateral walls experience a moderate area stretch. This area stretch gradually causes the membrane to grow. Membrane growth varies regionally with ϑ^g = 1.05 corresponding to 5% area growth at the lateral wall and ϑ^g = 1.00 corresponding to no area growth at the top and bottom walls. Once the load is removed, the cylinder relaxes but the growth remains. The inhomogeneous growth pattern induces residual stresses, which prevent the cylinder from returning to its original circular configuration.

Figure 2.

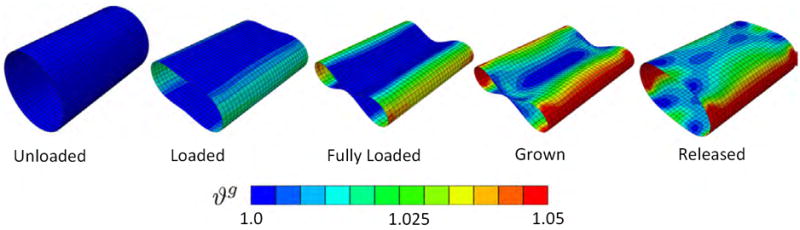
Pinched thin-walled cylinder: Irreversible nature of growth. As the cylinder is deformed, it is primarily subject to bending, while its lateral walls experience a moderate area stretch. This area stretch gradually causes the membrane to grow. Membrane growth varies regionally with ϑ^g = 1.05 corresponding to 5% area growth at the lateral wall and ϑ^g = 1.00 corresponding to no area growth at the top and bottom walls. Once the load is removed, the cylinder relaxes but the growth remains. The inhomogeneous growth pattern induces residual stresses, which prevent the cylinder from returning to its original circular configuration.

5.2. Example 2: Stretched Bilayered Thin Film

In the second example, we study the biaxial stretching of a bilayered thin film, which consists of a growing bottom layer and a purely elastic top layer. The 10 cm × 10 cm square sheet is modeled using 484 Abaqus S4 four-noded shell elements. Both layers are in perfect contact and have a thickness of t = 0.5 cm each. We first model the non-growing top layer as isotropic elastic with c₀ = 0.1 MPa, c₁ = 0.0 MPa, and c₂ = 0.0, and then as anisotropic elastic with c₀ = 0.1, c₁ = 0.1, and c₂ = 0.1. In both cases, we assume that the bottom layer is isotropic elastic with c₀ = 0.1 MPa, c₁ = 0.0 MPa, and c₂ = 0.0 and grows with ϑ^crit = 1.0, ϑ^max = 4.0, τ^g = 0.1 /t*, and γ = 2.0, where t* is a characteristic time of growth. The thin film is stretched biaxially with a displacement of d = 2 cm in all four directions corresponding to a total area increase of 96%. Once the growth process has converged, the load is removed and the sheet is allowed to relax. Figure 3 displays five characteristic stages of this loading history. Initially, both layers store elastic energy. As time evolves, the bottom layer releases its elastic energy as it grows, while the top layer does not. Once the load is removed, the bilayered film deforms out of plane in an attempt to achieve an energetically optimal configuration. Isotropy of the elastic layer results in a symmetric out-of-plane coiling, top row. Anisotropy of the elastic layer results in an anisotropic out-of-plane coiling, bottom row.

Figure 3.

Stretched bilayered thin film: Irreversible nature of growth under isotropic and anisotropic conditions. As the film is biaxially stretched, the bottom layer, shown here, gradually grows up to ϑ^g = 2.2 corresponding to more than 100% area growth, while the top layer, not shown, deforms elastically at to ϑ^g = 1.0 and stores elastic energy. Once the load is removed, the bilayered film deforms out of plane. Isotropy of the elastic layer results in a symmetric out-of-plane coiling, top row. Anisotropy of the elastic layer results in an anisotropic out-of-plane coiling, bottom row.

5.3. Example 3: Pressurized Thin Membrane

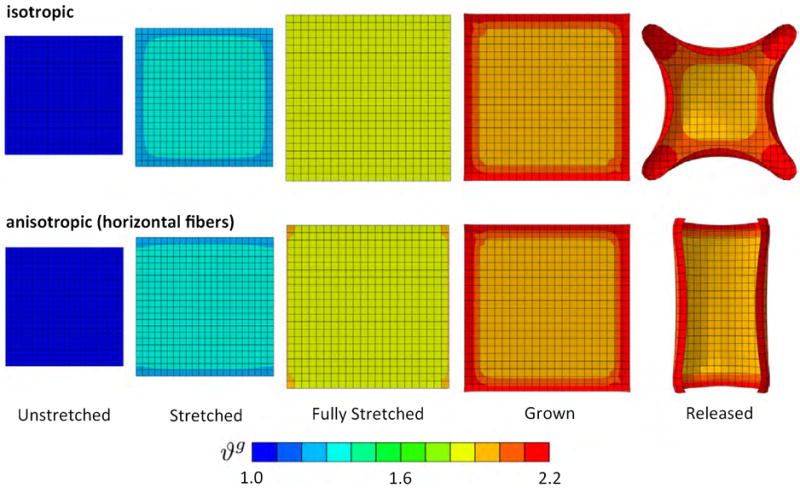
In the third example, to mimic the physiological loading conditions of biological membranes, we demonstrate growth of a thin membrane inflated by an external pressure p^ext. The membrane has a length of l = 200 cm, a width of w = 50 cm, and a thickness of t = 1 cm. We discretize the membrane with 6,942 Abaqus S3 and S4 three- and four-nodes shell elements. We first model the membrane as isotropic elastic with c₀ = 0.1 MPa, c₁ = 0.0 MPa, and c₂ = 0.0, and then as anisotropic elastic with c₀ = 0.1 MPa, c₁ = 0.1 MPa, and c₂ = 0.1, first with a vertical, then with a horizontal fiber reinforcement. In all three cases, we assume membrane growth with ϑ^crit = 1.0, ϑ^max = 4.0, τ^g = 0.1, and γ = 2.0, where t* is a characteristic time of growth. The outline of the structure is fixed in all three directions while all inner nodes are free to move. As the pressure is gradually increased to p^ext = 0.1 MPa, the membrane inflates in the out-of-plane direction, stretches, and grows. Figure 4 displays five characteristic stages of this loading history. To illustrate the effect of elastic anisotropy, we display the evolution of growth for an isotropic elastic membrane, top row, an elastic membrane with fibers in the vertical direction, middle row, and an elastic membrane with fibers in the horizontal direction, bottom row. All three membranes experience a substantial growth upon inflation. While the isotropic membrane develops spherical protrusions, the anisotropic examples display a distinct directionality in their protrusion patterns.

Figure 4.

Pressurized thin membrane: Regional variation of growth under isotropic and anisotropic conditions. As the membrane is inflated, it locally grows up to ϑ^g = 1.05 corresponding to 5% area growth, while other regions deform elastically at ϑ^g = 1.0 and do not grow. The isotropic membrane shows significant area growth and develops spherical protrusions, top row. Under the same pressure, the anisotropic membranes with vertical fibers, middle row, and with horizontal fibers, bottom row, develop anisotropic protrusions.

5.4. Example 4: Chronically Stretched Mitral Leaflet

In the fourth example, we present a clinically relevant problem, the adaptation of a thin biological membrane to altered mechanical forces following chronic disease [48]. Based on in vivo imaging data, we discretize the anterior leaflet of a mitral valve with 1,920 Abaqus S3 three-noded shell elements, and assign the leaflet a uniform thickness of 1mm. We subject the leaflet to a transvalvular pressure, which was acquired in vivo under physiological conditions [49]. In particular, we inflate the ventricular leaflet surface with the experimentally measured end-diastolic pressure. At the supported leaflet edge, we prescribe the experimentally measured leaflet positions as non-homogeneous Dirichlet boundary conditions. At the free leaflet edge and at the center, we locally support the leaflet through chordae tendineae. Choredae tendineae are cord-like tendons that connect regions of the leaflet to the papillary muscles to limit leaflet deformation as the pressure increases [50].

We represent the chordae tendineae as incompressible, tension-only elastic wires with a stiffness of c₀ = 10 MPa [49]. We model the elastic response of the leaflet as isotropic, incompressible Neo-Hookean with c₀ = 1.0 MPa, c₁ = 0.0 MPa, and c₂ = 0.0 and assume that the leaflet grows with ϑ^crit = 1.1, ϑ^max = 4.0, τ^g = 0.1, and γ = 2.0, where t* is a characteristic time of growth. To simulate the effects of myocardial remodeling following cardiac infarction, we impose two levels of annular dilation, λ=1.2 and λ=1.5 [51] combined with a symmetric and asymmetric papillary muscle displacement of δ=5 mm [48]. These values had previously been reported for controlled myocardial remodeling experiments in sheep. Figure 5 displays the initial configuration, the acute elastic response, and the chronic growth under these combined conditions. The top row illustrates the anterior mitral leaflet in the reference configuration, at end diastole, with the mitral annulus superimposed in white. The middle row shows the acute elastic area stretch ϑ^e in response to annular dilation of λ=1.2 and λ=1.5, in combination with asymmetric displacement of the posterior-medial papillary muscle, first and second column, and symmetric displacement of both papillary muscles, third and fourth column, by δ=5 mm in apical, septal, and posterior-medial directions. The bottom row shows the chronic area growth ϑ^g, which regionally exceed values of ϑ^g = 1.5, indicating more than 50% area growth upon leaflet adaptation.

Figure 5.

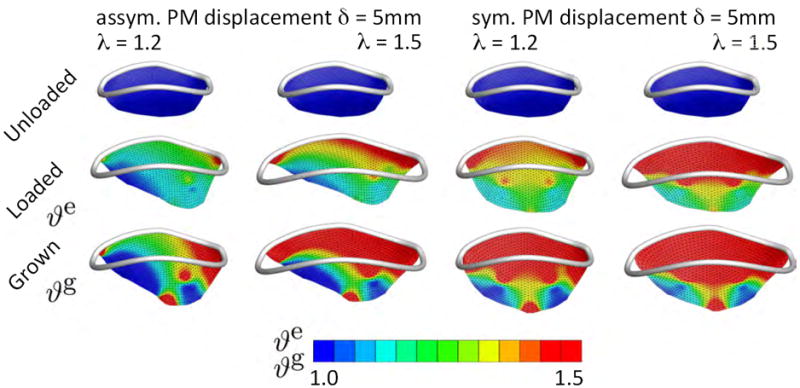
Chronically Stretched Mitral Leaflet: Mitral leaflet adaptation to annular dilation and papillary muscle displacement as seen in ischemic cardiomyopathy. Anterior mitral leaflet in the reference configuration at end diastole with the mitral annulus superimposed in white, top row. Acute elastic area stretch ϑ^e, middle row, in response to annular dilation of λ=1.2 and λ=1.5, in combination with asymmetric displacement of the posterior-medial papillary muscle, first and second column, and symmetric displacement of both papillary muscles, third and fourth column, by δ=5mm. Chronic area growth ϑ^g, bottom row, regionally exceed values of ϑ^g = 1.5 indicating more than 50% area growth upon leaflet adaptation.

6. Discussion

Thin biological membranes fulfill a number of crucial functions in the human body. Despite their seemingly delicate appearance, they often sustain tremendous loads [26]. Like many other soft and hard tissues, they interact with their chemical and physical environment to optimize their form and function [4, 10]. Especially load bearing biological membranes such as the skin, the pericardium, and the heart valve leaflets organize their microstructure and morphology in order to sustain internal and external forces [12]. Computational modeling holds tremendous potential to better understand the interplay of membrane form and function and to reliably predict the effects of disease or medical treatment. Because of their thin structure, biological membranes lend themselves ideally for spatial discretizations using shell elements [11]. However, to the best of our knowledge, the current work is the first to account for a biological growth model that is compatible with discrete shell kinematics.

In this manuscript, we employed a finite growth theory and introduced the total deformation gradient as the product of an elastic tensor and a growth tensor [52]. The functional format of the growth tensor mimics the modality of growth; whether the tissue grows isotropically or anisotropically, inplane or out-of-plane. The appropriate choice is usually answered by microstructural considerations [36]. For the current work, we selected a format that represents isotropic in-plane area growth [7]. Furthermore, we postulated that growth is mechanically driven as opposed to morphologically or chemically driven [41]. This implies that mechanics and growth are bidirectionally coupled: Growth affects the mechanics through the constitutive equations for the stress and the mechanics affect growth through the evolution equation for growth [21]. Motivated by physiological observations [55], we further assumed that growth is driven by the elastic area stretch, and that it is activated only if the elastic area stretch exceeds a physiological threshold value.

From an implementation standpoint, our approach is strictly modular and limited to local modifications at the constitutive level. To illustrate its universal character, we implemented the growth model into a generic, commercially available non-linear finite element package, Abaqus/Standard. Typically, for these types of platforms, at each global Newton iteration step, at each integration point, the deformation gradient is made available to a user-definable material subroutine, UMAT [1]. This material subroutine also provides access to the growth multiplier ϑ^g, which is stored locally as an internal variable to keep track of the current amount of growth [57]. In the material subroutine, we first split the deformation gradient into its elastic and growth contributions. We then evaluate whether the elastic area stretch exceeds a user-defined threshold, and update the growth multiplier if necessary. We then successively calculate the new growth tensor, the elastic tensor, the elastic stress, and, finally, the total stress and the tangent moduli. We pass the latter two back to Abaqus for the next iteration, and store the updated growth multiplier once the global Newton iteration has converged. This approach requires no additional modifications to the finite element code other than changes in the material subroutine, which is modularly replaceable in most non-linear finite element codes, commercial or non-commercial.

We have illustrated the features of our model by means of four examples with distinct characteristic loading conditions. The first example is a common benchmark problem for shell elements [6]. In a loading-holding-unloading scenario, this example nicely illustrates the irreversible nature of growth. The second example shows the effect of differential growth as it may occur in tissues subject to non-homoegeneous loading conditions across their thickness. A typical clinical example is differential growth in the arterial wall [27], which is closely related to the notion of prestrain and residual stress [21]. In arteries, layer-specific residual stresses have been studied in detail using different reference configurations for the individual layers [23, 24]. These residual stresses arise naturally as a consequence of growth [38] and can serve to identify critical conditions for growth-induced instabilities, for example in airway wall remodeling [28]. The third example presents a loading scenario characteristic of thin walled arterial aneurysms, where a surface pressure generates out-of-plane deformation, which induces membrane stretching and growth [54]. The fourth example illustrates the clinical problem of mitral leaflet growth in response to chronic overstretch. For this example, we directly extracted the mitral leaflet geometry from surface imaging data, and converted it into a triangular shell mesh [49]. We then reconstructed the pathologic mechanical environment as seen in ischemic cardiomyopathy [9]. A strong correlation between the experiments reported in the literature and the simulation presented here provides support for the hypothesis that a local increase in area stretch initiates local tissue adaption in the form of in-plane area growth: In controlled experiments in sheep, five weeks after induced myocardial infarction, the average mitral annulus had dilated by 25%, with local regions dilating by more than 50% [51]. In our simulation, we have represented this effect through imposing an annular dilation of λ=1.2 and λ=1.5 to induce mitral leaflet growth. In the sheep experiment, myocardial infarction caused a chronic papillary muscle displacement in the order of δ=5 mm [48]. In our simulation, we have represented this effect through displacing the posterior papillary muscle alone and both papillary muscles jointly to induce asymmetric and symmetric mitral leaflet growth. In the sheep experiment, the average mitral leaflet area had grown by 15.57%, with local regions growing up to 30% and more [48]. In our simulation, leaflet growth varied locally from no area change at ϑ^g = 1.00 to 50% of area increase at ϑ^g = 1.50. These values agree excellently with the experiment observations.

In conclusion, we have introduced a stretch-driven isotropic membrane growth model, which is conceptually embedded within the theory of finite growth and is compatible with standard shell kinematics. The model proved efficient and robust in four benchmark problems of thin biological membranes exposed to different loading scenarios. We believe that our membrane growth model will be widely applicable to simulate the chronic long-term response of thin layered biological structures such as skin membranes, mucous membranes, fetal membranes, tympanic membranes, corneoscleral membranes, and heart valve membranes. These structures are optimized in form and function and gradual deviations from their optimized design are critical indicators of disease. Computational models like the one presented here have the potential to identify diseased states, predict disease evolution, and, ideally, guide the design of interventional or pharmaceutic therapies to arrest or revert disease progression.