Using Dimers to Measure Biosignatures and Atmospheric Pressure for Terrestrial Exoplanets

Abstract

We present a new method to probe atmospheric pressure on Earth-like planets using (O₂-O₂) dimers in the near-infrared. We also show that dimer features could be the most readily detectable biosignatures for Earth-like atmospheres and may even be detectable in transit transmission with the James Webb Space Telescope (JWST). The absorption by dimers changes more rapidly with pressure and density than that of monomers and can therefore provide additional information about atmospheric pressures. By comparing the absorption strengths of rotational and vibrational features to the absorption strengths of dimer features, we show that in some cases it may be possible to estimate the pressure at the reflecting surface of a planet. This method is demonstrated by using the O₂ A band and the 1.06 μm dimer feature, either in transmission or reflected spectra. It works best for planets around M dwarfs with atmospheric pressures between 0.1 and 10 bar and for O₂ volume mixing ratios above 50% of Earth's present-day level. Furthermore, unlike observations of Rayleigh scattering, this method can be used at wavelengths longer than 0.6 μm and is therefore potentially applicable, although challenging, to near-term planet characterization missions such as JWST. We also performed detectability studies for JWST transit transmission spectroscopy and found that the 1.06 and 1.27 μm dimer features could be detectable (SNR>3) for an Earth analogue orbiting an M5V star at a distance of 5 pc. The detection of these features could provide a constraint on the atmospheric pressure of an exoplanet and serve as biosignatures for oxygenic photosynthesis. We calculated the required signal-to-noise ratios to detect and characterize O₂ monomer and dimer features in direct imaging–reflected spectra and found that signal-to-noise ratios greater than 10 at a spectral resolving power of R=100 would be required. Key Words: Remote sensing—Extrasolar terrestrial planets—Habitability—Radiative transfer—Biosignatures. Astrobiology 14, 67–86.

1. Introduction

Atmospheric pressure is a fundamental parameter for characterizing the environment and habitability of an extrasolar planet. Water's stability on a planetary surface as a liquid depends on both the surface temperature and pressure. While the freezing point of water is not strongly dependent on pressure, pressure does affect water's boiling point and sublimation. Thus, a reliable estimate of the surface pressure is an important part of the measurement suite required to determine the habitability of an exoplanet.

Despite the importance of atmospheric pressure, current proposed methods for measuring pressure by using remote-sensing techniques that could be applicable to exoplanetary atmospheres are challenging. The existing techniques include the use of Rayleigh scattering (Kasting and Traub, 2010) or the widths of individual absorption lines (Kaplan et al., 1964; Gray, 1966) or absorption bands (Chamberlain et al., 2006; Spiga et al., 2007; Ignatiev et al., 2009; Chamberlain et al., 2013). The presence and location of a blue Rayleigh scattering tail in a spectrum can provide information about the existence and pressure of an atmosphere. However, strong blue absorbers in the atmosphere (e.g., O₃, SO₂, NO₂, and many others) or surface features can mask this tail (Crow et al., 2011). Furthermore, the Rayleigh scattering tail is most prominent shortward of 0.6 μm, below the short wavelength cutoff of the James Webb Space Telescope (JWST) (Gardner et al., 2006). Lastly, planets around M dwarfs are likely to be the first to be characterized (Deming et al., 2009), and M dwarfs have relatively less visible-flux to Rayleigh scatter than solar-type stars. The Rayleigh tail would be more difficult to detect and characterize for planets orbiting stars of this stellar class.

It is also possible to use the widths of absorption features to estimate pressure. Pressure increases the widths of vibration rotation lines of gases. This method has been successful for Earth when using high-resolution spectra of the O₂ A band (Barton and Scott, 1986; Mitchell and O'Brien, 1987; Crisp et al., 2012), for Mars with CO₂ features near 2 μm (Gray, 1966; Chamberlain et al., 2006; Forget et al., 2007; Spiga et al., 2007), and for the cloud tops of Venus with the 1.6 μm CO₂ band (Ignatiev et al., 2009). This method provides unambiguous results when the spectral resolution is sufficiently high to resolve the profiles of individual spectral lines. It can also be used at lower spectral resolution but requires prior knowledge of the mixing ratio of the absorbing gas.

Here, we explore the feasibility of a new method to directly measure the pressure of an Earth-like atmosphere that combines the absorption features of dimers with those of monomer vibration-rotation bands to yield estimates of the atmospheric pressures even when the mixing ratio of the monomer is uncertain. Previous pressure estimates for which dimer absorption was used have been made for the cloud tops of Earth, but these techniques have required prior knowledge of the gas mixing ratio profile (Acarreta et al., 2004). Dimers are bound or quasi-bound states between two molecules driven together by molecular interactions. For example, the O₂-O₂ or O₄ dimer consists of two O₂ molecules temporarily bound to each other by Van der Waals forces. This dimer has its own rotational and vibrational modes and produces spectral features distinct from its constituent O₂ monomers. Additionally, absorption from dimer molecules is more sensitive to pressure than that of monomers. The optical depth (how much absorption occurs) for dimers and monomers can be expressed by the following equations:

where dτ_monomer and dτ_dimer are the monomer and dimer differential optical depths, σ is the monomer cross section, ρ is the number density of the gas, k is the dimer cross section, P is the pressure, T is the temperature, and dl is the path length. While the monomer (e.g., O₂) optical depth is directly proportional to pressure, the optical depth of the dimer (e.g., O₂-O₂) is dependent on the square of the density (and hence square of the pressure). This difference in pressure dependence allows us to estimate atmospheric pressure by comparing the dimer and monomer absorption features

For an oxygen-rich, Earth-like atmosphere, the best combination of bands to use for pressure determination at near-infrared wavelengths (>0.6 μm) would be the (O₂) A band at 0.76 μm and the 1.06 μm O₄ dimer band. The 0.76 μm O₂ A band is the strongest O₂ feature in the visible–near-infrared spectral region and is found in a relatively clean region of the spectrum between two water vapor bands. We have chosen the dimer feature at 1.06 μm as the likely best option, due to its combination of band strength and its location in a relatively uncluttered region of the planetary spectrum. Other O₄ features overlap with water features (dimer feature between 5.5 and 7 μm) or O₂ vibration-rotation bands (0.63, 0.76, and 1.27 μm dimer features) or are weaker than the 1.06 μm dimer feature (0.477 and 0.57 μm dimer features). Nevertheless, some other features, in particular the strong 1.27 μm feature, could be used if the 1.06 μm dimer feature is not detectable.

In the proposed technique, the O₂ 0.76 μm (monomer) band is used to provide an estimate of the atmospheric concentration of O₂ and combined with the O₄ 1.06 μm (dimer) band to constrain the atmospheric pressure. This method can be used with either transmission spectroscopy or directly detected reflection or emission spectra, and serves as a complement to pressure determination techniques such as Rayleigh scattering, which only work in the visible. Although the proof of concept is shown here with oxygen, this technique is not limited to the oxygen dimer in an Earth-like atmosphere in the visible to near-infrared. The same technique is applicable to pairs of monomer and dimer absorption features across a wider range of planetary atmospheric composition and spectral wavelength range.

2. Methods

In the present study, we generated transit transmission and direct imaging reflected spectra for cloud- and aerosol-free Earth-like exoplanets. The models we used to do this are described below.

2.1. Transmission spectroscopy model

2.1.1. Model overview

When an extrasolar planet transits or occults its host star, the planetary atmosphere is backlit, and some of the star's light traverses the planet's atmosphere on limb trajectories. This transmitted light can be used to characterize the planet's atmosphere (Seager and Sasselov, 2000; Brown, 2001; Hubbard et al., 2001). This has been done for a number of Jupiter- and Neptune-sized planets (e.g., Charbonneau et al., 2002; Vidal-Madjar et al., 2003; Pont et al., 2008) and the super-Earth/mini-Neptune GJ 1214 b (e.g., Bean et al., 2010).

The transmission spectroscopy model used here is based on Spectral Mapping Atmospheric Radiative Transfer (SMART) (Meadows and Crisp, 1996; Crisp, 1997), which is a spectrum-resolving (line-by-line), multi-stream, multiple-scattering radiative transfer model. We modified SMART to generate transit transmission spectra by combining the monochromatic absorption and scattering opacities for each atmospheric layer calculated by SMART with the limb path lengths inherent in a transit transmission event. The transmission model included gas absorption, Rayleigh scattering, interaction-induced absorption, extinction from clouds and aerosols, refraction, and limb darkening. Because multiple scattering was not included in the transit transmission component of the model, we considered only cloud- and aerosol-free atmospheres for this work.

2.1.2. Refraction

An important characteristic of the transit transmission spectroscopy model is the inclusion of refraction. As described by García Muñoz et al. (2012), refraction sets a fundamental limit on the range of pressures that can be probed during a transit, independent of absorption and scattering. Light refracts as it passes through an atmosphere, with a larger refraction angle as higher pressures and densities are probed. For every planet-star system, there will be a maximum tangent pressure in the planet's atmosphere that can be probed, because at greater pressures the light will be refracted by too large of an angle to be able to reach a distant observer during the transit.

For each tangent height in each atmosphere, we calculated the total angle of refraction for a beam of light emitted from the host star, using a modified version of the method described by Auer and Standish (2000). Their method was developed for calculating refraction for astronomical observations on Earth given a tangent altitude, apparent zenith angle, and an atmospheric density profile. We calculated the angle of refraction over a range of zenith angles to determine whether a path exists to connect the host star to a distant observer via the planetary atmosphere. Transit transmission spectroscopy cannot probe the tangent altitudes at which no such path exists.

The radius of the star, planet-star distance, and composition of the planet's atmosphere determine the maximum tangent pressure. The radius of the star and planet-star distance control the apparent angular size of the star from the planet's perspective. The larger the angular size, the greater the range of pressures that can be probed. For an Earth analogue orbiting a Sun-like star, the angular size of the star is ∼0.5°, while for an Earth analogue orbiting an M5 dwarf and receiving the same total flux, the angular size of the star is ∼2°. Therefore, transit transmission spectroscopy can probe higher pressures, that is, see deeper into the atmosphere, for the planet orbiting an M dwarf. Figure 1 shows this effect by comparing all possible paths at one tangent height for a planet around an M dwarf and a planet around a Sun-like star, with each planet receiving the same total flux.

FIG. 1.

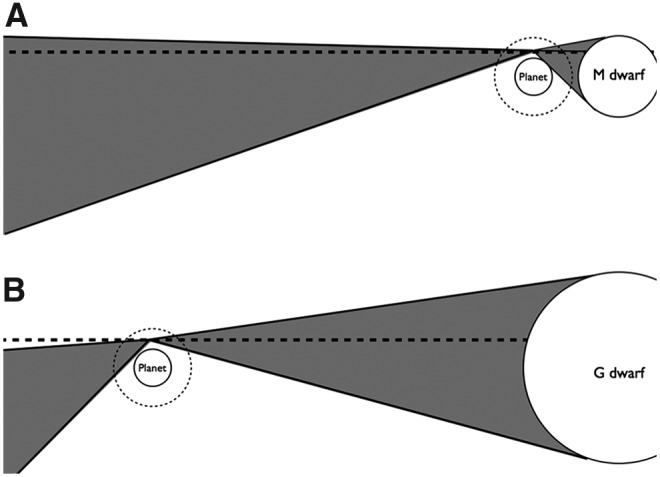
Comparison of the effect of refraction on (A) an exoplanet around an M dwarf and (B) a planet around a Sun-like star with both planets receiving the same total flux. The dashed circles are the planetary atmospheres. The solid lines represent different refracted paths through the atmosphere, and the dashed lines are the hypothetical paths to a distant observer observing the planet in transit transmission. Only paths that lie exactly on that dashed line will be observed. For the M dwarf case, there will be a path connecting the star to the observer through the atmosphere at this particular tangent height. However, there is no path in the Sun-like star case. This means that a transit transmission spectrum of the planet around the M dwarf can theoretically probe higher pressures of the atmosphere than in the Sun-like star case.

The composition of the atmosphere determines the refractivity (index of refraction −1) of the atmosphere. Atmospheres with greater refractivities will have lower maximum tangent pressures. The refractivity at standard temperature and pressure can vary from ∼1.5 times the refractivity of air for CO₂ to slightly less than half the refractivity of air for H₂, when considering only the common bulk atmospheric gases in the solar system. Therefore, in general it will be possible to probe higher pressures for an H₂ atmosphere than a CO₂ or air atmosphere.

2.2. Direct imaging (reflected) spectroscopy model

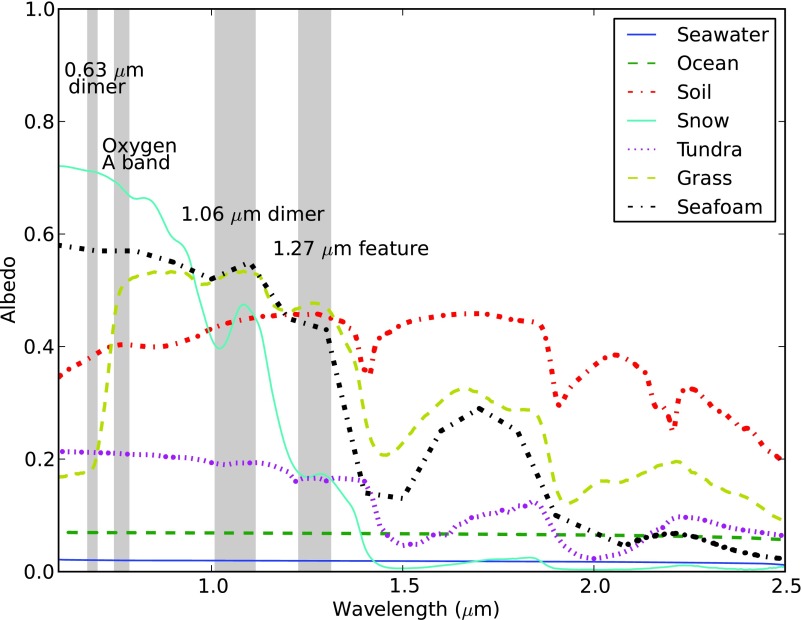
The reflected spectra were generated with the standard version of SMART, which can include multiple scattering from clouds and aerosols. However, to maintain consistency with the transmission spectrum model, clouds were not included in this study. The reflected spectra were generated assuming a surface with a constant albedo of 0.16, which is the average albedo of the cloud-free Earth (Pierrehumbert, 2010). We also assumed the surface is a Lambertian scatterer. Other surface types could have introduced an error into any quantitative estimates in this paper, unless explicitly included in a retrieval attempt. Figure 2 shows the wavelength dependence of a variety of surface types from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) spectral library (Baldridge et al., 2009) and the United States Geological Survey (USGS) digital spectral library (Clark et al., 2007). Surface albedos are nearly constant in the bands considered here, though, for example, snow fluctuates by ∼20% within the 1.06 μm dimer band. We modeled a test case with SMART with the snow surface to determine the error different surfaces can introduce. We found a difference of 15% between the seawater and snow cases when measuring the equivalent width (defined in Section 2.4) of the 1.06 μm dimer band. This difference was significantly less than the difference in measured equivalent widths for the cases considered in this paper. Therefore, we considered any discrepancies due to variations in surface albedo to be minimal for the present work.

FIG. 2.

Wavelength-dependent albedos for a variety of surfaces. The shaded regions correspond to O₂ monomer and dimer bands. For any absorption band, as long as the albedo does not vary widely within the band's wavelength range, it should be possible to measure an accurate equivalent width for each feature. The maximum variation within a band is no more than ∼20%. Therefore, we do not consider surface albedo variations important for this work. (Color graphics available online at www.liebertonline.com/ast)

2.3. Model inputs

2.3.1. Model atmospheres

The cloud-free model atmospheres were generated by a one-dimensional (altitude) photochemical code with an extensive history in early Earth (Zerkle et al., 2012), modern Earth (Catling et al., 2010), and exoplanet (Domagal-Goldman et al., 2011) research. The planetary radius and surface gravity used were the radius of Earth (6371 km) and surface gravity of Earth (9.87 m/s²). The vertical grid consists of 200 plane-parallel layers that are each 0.5 km thick in altitude, in which radiative transfer, atmospheric transport, and photochemical production and loss are solved simultaneously, subject to upper (stellar flux, atmospheric escape) and lower (volcanoes and biology) boundary conditions. The model calculates the mixing ratios of each species in each layer by solving the coupled mass-continuity/flux equations with the reverse Euler method (appropriate for stiff systems) and a variable time-stepping algorithm. Dimer concentrations were computed by using estimations from quantum mechanical calculations. First, we fit the temperature dependence of the equilibrium constant for O₂ dimer formation using the following equations:

where p(O₂)₂ and pO₂ are the dimer and monomer partial pressures and T is the temperature (Uhlik et al., 1993). The dimer mixing ratio was then computed as

where P is the pressure in atmospheres. The choice of quantum parameters in our fit of Eq. 4 ensures that our calculation is a lower limit to the dimer concentrations, an assumption which matches modern atmospheric data well (Slanina et al., 1994).

The model atmospheres used in this study started with boundary conditions that reproduce Earth's modern atmospheric chemistry. We then replaced the solar spectrum with the M dwarf spectrum described in 2.3.3 and decreased the surface albedo to 0.16 to account for cloud-free conditions. This “modified Earth around an M dwarf” model was then perturbed to examine changes to both total pressure and oxygen concentrations. Total atmospheric pressures of 0.1, 0.5, 1.0, 3.0, 5.0, and 10.0 bar were examined. At each of these total pressures, lower boundary conditions on O₂ mixing ratios were set at 0.1, 0.5, 1.0, and 2.0 times Earth's present level. This corresponds to oxygen mixing ratios from 2% to 42%, which is roughly the range of oxygen concentrations experienced throughout the past 2.5 billion years of Earth's history (Kump, 2008). Boundary conditions for all other species were held fixed at modern values. Figure 3 shows the pressure-temperature profile and volume mixing ratio profiles for the 1.0 times the present atmospheric level (PAL) O₂ cases for spectrally active gases in the wavelength region examined here. Stable steady-state solutions were analyzed in all but the three cases with the highest O₂ surface partial pressures. For those three cases, we extrapolated from our converged results at lower O₂ mixing ratios by increasing O₂ concentrations, scaling the dimer concentrations with the square of the O₂ mixing ratio, and keeping all other gas mixing ratios constant.

FIG. 3.

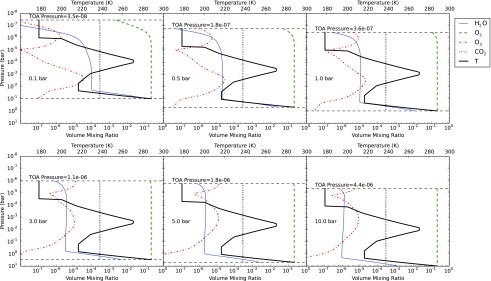
Pressure-temperature profiles and volume mixing ratio profiles for all pressures at 1.0×PAL O₂. The black dashed lines represent the surface pressures and top-of-atmosphere (TOA) pressures. We use the modern Earth temperature-altitude profile in all cases and calculate the pressures assuming hydrostatic equilibrium. The remainder of the atmosphere is N₂ for all cases. (Color graphics available online at www.liebertonline.com/ast)

For all tests presented here, we assumed Earth-like temperature and water vapor profiles, precluding the need for costly climate simulations. More specifically, we took the modern Earth temperature profile as a function of altitude and computed the corresponding pressure levels assuming hydrostatic equilibrium. This simplification provides a useful baseline but limits the range of validity of these results somewhat because the gas absorption cross sections and number densities depend on these atmospheric properties. The impact of this assumption is assessed in Section 3.4. For pressure/temperature regions corresponding to Earth's mesosphere, we adopted a temperature of 180 K, which likely overestimates the temperature in these regions. Dimer absorption preferentially occurs in higher-pressure regions and so is insensitive to assumed conditions in the tenuous upper atmosphere. Our model grid was capped at 100 km altitude, ensuring optically thin conditions for nearly all species, and made allowances for CO₂ and N₂ photolysis above the upper boundary. We used the modern measured eddy-diffusion profile to simulate convective motion for all atmospheres regardless of pressure. While this simplification would affect the prediction of trace gas concentrations, all species analyzed here are either well-mixed (CO₂, O₂, N₂) or short-lived (dimers) so are not sensitive to changes in turbulent mixing.

2.3.2. Absorption line lists and cross sections

We used the HITRAN 2008 database line lists (Rothman et al., 2009) to generate opacities in SMART. The dimer absorption cross sections for O₂ were taken from Greenblatt et al. (1990) and Maté et al. (1999).

2.3.3. Stellar properties

In the present study, we assumed that the planet orbits an M5V star, or an M dwarf with stellar radius of 0.20 R_sol and a luminosity of 0.0022 L_sol (Kaltenegger and Traub, 2009). The planet was placed at a distance of 0.047 AU so that the total integrated incoming stellar flux was equal to the total flux Earth receives from the Sun today. An M5 dwarf was chosen for these tests because there is a high probability that the terrestrial planets that will be the most easily characterized in the near future will be orbiting this class of star (Deming et al., 2009). Additionally, transit transmission spectroscopy can probe pressures up to the ∼1 bar level in an atmosphere for an Earth analogue around an M dwarf, while for the Earth around the Sun, it can only probe pressures as great as ∼0.2 bar. At these pressures and lower, the 1.06 μm dimer feature is very weak, even at 200% PAL O₂. Thus, using Earth-like atmospheres around an M dwarf instead of around the Sun provides a better demonstration of the pressure dependence of dimer features.

To simulate the spectrum of the star, we used a Phoenix NextGen synthetic spectrum (Hauschildt et al., 1999) for all wavelengths greater than ∼300 nm. For the shorter wavelengths, we used the UV spectrum of AD Leo (Segura et al., 2005). The Phoenix spectrum was normalized so that the total integrated flux was equal to 1373 W/m², which is the integrated flux Earth receives from the Sun. The AD Leo spectrum from Segura et al. (2005) was left unchanged, as it was already normalized to equal the amount of flux a planet near the inner edge of the habitable zone would receive.

2.3.4. Spectral resolution

We used a spectral resolving power of 100 to provide relevance to JWST, which will provide new opportunities for characterizing the atmospheres of transiting exoplanets (Lafreniere et al., 2013). Once JWST is launched, the Near-Infrared Spectrograph (NIRSpec) will provide spectra with a spectral resolving power 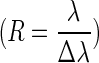of ∼100 between 0.6 and 5.0 μm in single prism mode (Köhler et al., 2005). We examine the effect of varying the spectral resolution in Sections 3.6 and 4.3.

2.4. Absorption strength measurements

To make a quantitative estimate of absorption strengths, we measured equivalent widths for the reflected spectra and measured part-per-million differences in flux for the transmission spectra. Equivalent widths were calculated with the following equation:

where W is the equivalent width, F_λ is the flux at each wavelength λ, and F₀ is the continuum flux at each wavelength. To obtain the equivalent widths, we first measured the area of the spectral band below the continuum. For each absorption band, we define the continuum by hand. For the O₂ A band, the continuum was assumed to be linear with wavelength; and for the 1.06 μm feature, the continuum was assumed to be constant with wavelength because in several of the cases the continuum at the longer wavelengths was difficult to define due to H₂O absorption. The equivalent width is the width, in units of wavelength, of a rectangle measured from the continuum to the level of zero flux with the same total area as the spectral band. We could not use this type of measurement for the transmission spectra because of the difficulty in defining the zero flux level. Therefore, we quantified the absorption strengths for the transmission spectra by measuring the change in flux from the continuum to the point of greatest absorption within a band.

2.5. Detectability calculations

We performed detectability studies (Deming et al., 2009; Kaltenegger and Traub, 2009; Belu et al., 2011; Rauer et al., 2011) for the model spectra, assuming the exoplanet-star system is at a distance of 5 pc. We calculated the expected signal-to-noise ratio (SNR_star) using the JWST Exposure Time Calculator (ETC)¹. The JWST ETC includes background noise from sky, dark, thermal, and zodiacal sources along with read-out noise and photon noise. The estimates provided are expected to be within 20% of the mission requirements. We note that for all the cases considered, the noise is dominated by photon noise. We do not include noise from detector intrapixel variations (Deming et al., 2009), but in principle calibration time could be devoted to mapping the pixels, as has been done with Spitzer Space Telescope Infrared Array Camera (Carey et al., 2012). We also note that noise levels within ∼20% of the photon noise limit have been obtained for transit transmission spectra with the Hubble Space Telescope in spatial scan mode, wherein the target star is trailed during each exposure by telescope motion perpendicular to the direction of dispersion (Deming et al., 2013; Wakeford et al., 2013). Spatial scan mode is being considered for JWST; so assuming photon-limited noise in our calculations, while optimistic, provides a reasonable estimate of the detectability of absorption features (Drake Deming, private communication, October 13, 2013).

We assumed that every possible transit is observed in JWST's 5-year mission lifetime, ignoring decreases in integration time due to non-zero impact parameters (where the planet does not traverse the center of the stellar disk and therefore has a lower transit duration) and limits on visibility based on the ecliptic latitude of the exoplanet (see Belu et al., 2011). For the Earth-Sun analogue, this corresponds to a total integration time of ∼2.3 * 10⁵ s, and for the Earth-M5V analogue, an integration time of ∼10⁶ s. We normalize the solar spectrum (using the Phoenix G2V model available on the site) to a Johnson V magnitude of 3.32 and the M5V spectrum to 2.1 * 10⁻¹³ erg cm⁻² s⁻¹ Å⁻¹ at 1 μm.

At each wavelength within an absorption band, we measured the signal as the magnitude of the difference from the continuum flux. The noise is expressed in parts per million (ppm, 10⁶/SNR_star) at each wavelength. The final SNR of the transit transmission spectrum is the square root of the sum of the squares of the SNR at each wavelength in the absorption band divided by 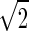, which is included because the transit transmission spectrum must be calibrated against the out-of-transit spectrum of the star.

We also performed detectability studies for the direct imaging reflected spectra that could be relevant to proposed direct imaging planet detection and characterization missions. For these calculations, we did not use an instrument simulator because the exact specifications for these missions are not currently defined. For each absorption band, we calculated two SNRs, one for detecting the spectral feature (SNR_D) and one for measuring the flux at the center of the band to a precision of 3σ (SNR_P). We calculated two SNRs because obtaining information about pressure from a spectral feature requires more than detection; it also requires a quantitative estimate of the strength of that spectral feature. To calculate SNR_D, we divided the reflected flux by the stellar flux, defined a continuum, and calculated the signal as the difference between the continuum and the normalized reflected flux. We assumed the noise is constant over the entire absorption band and then calculated the noise level required to detect the spectral feature with a SNR_band of 3 in the absorption band. The final SNR_D is the mean of the continuum reflected flux level divided by the calculated noise. To calculate SNR_P, we selected the wavelength within the band with the lowest radiance. We set the value of a second noise level as the lowest radiance divided by 3. SNR_P is the continuum flux level divided by the noise required to obtain a SNR of 3 at the lowest radiance in the absorption band.

3. Results

3.1. Transit transmission spectra

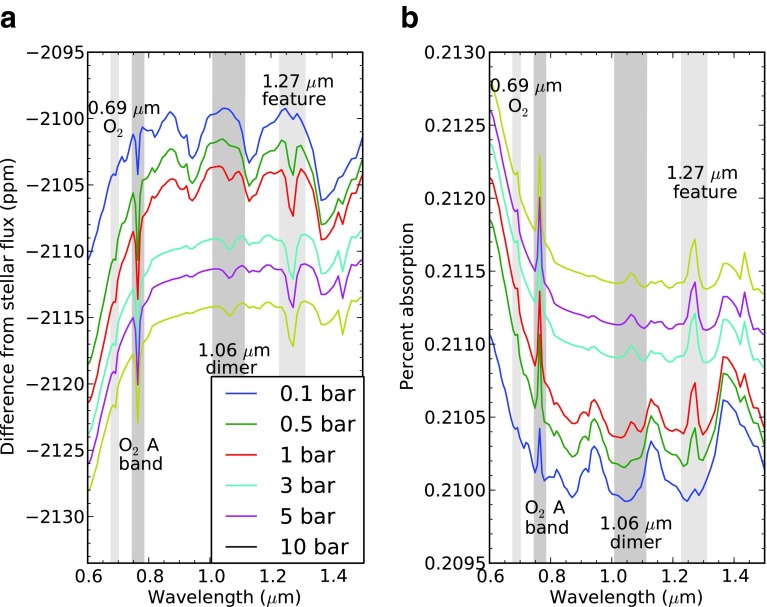
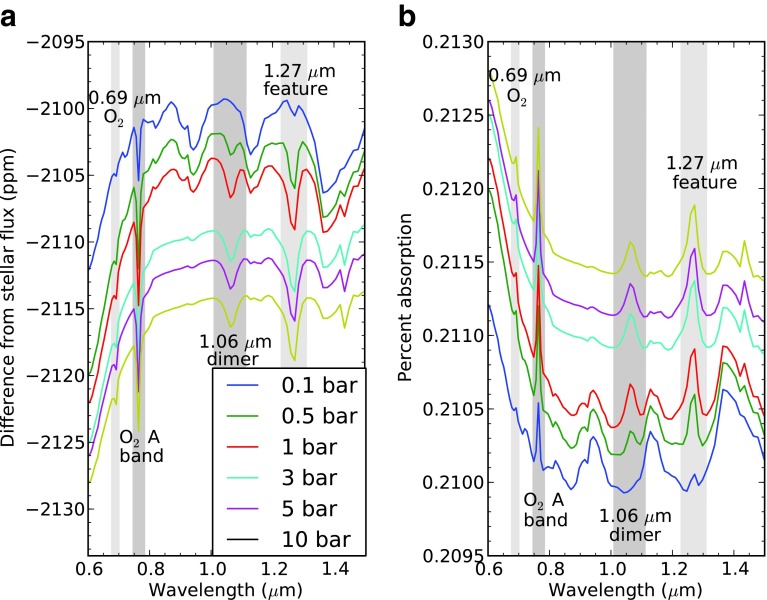
We generated transit transmission spectra and direct imaging spectra for atmospheres with O₂ concentrations of 10%, 50%, 100%, and 200% PAL and pressures of 0.1, 0.5, 1, 3, 5, and 10 bar. Figure 4 shows the resulting transit transmission spectra for 100% PAL O₂. Transmission spectra of atmospheres with pressures ≥1 bar are nearly identical for a given O₂ concentration because refraction limits depth of penetration to <1 bar. The dimer feature is weak for the 0.1 and 0.5 bar cases.

FIG. 4.

Transmission spectra of an Earth-like atmosphere with different total atmospheric pressures. (a) Difference in flux from the stellar flux. (b) Percent of stellar flux absorbed by the atmosphere. The 1.06 μm dimer feature is strong only in the spectra corresponding to atmospheric pressures greater than ∼0.5 bar. The spectra for atmospheres with pressure ≥1 bar are nearly identical except for an offset because there is a fundamental limit on which heights in an atmosphere can be probed by transmission spectroscopy. For an Earth-like atmosphere around the M5V used here, only the top 0.9 bar can be probed for all atmospheres at all wavelengths. This pressure corresponds to an altitude of ∼1 km above the surface for a 1 bar atmosphere and 19 km above the surface for a 10 bar atmosphere. The offset is due to the flux blocked by layers in the atmosphere with pressure greater than 0.9 bar.

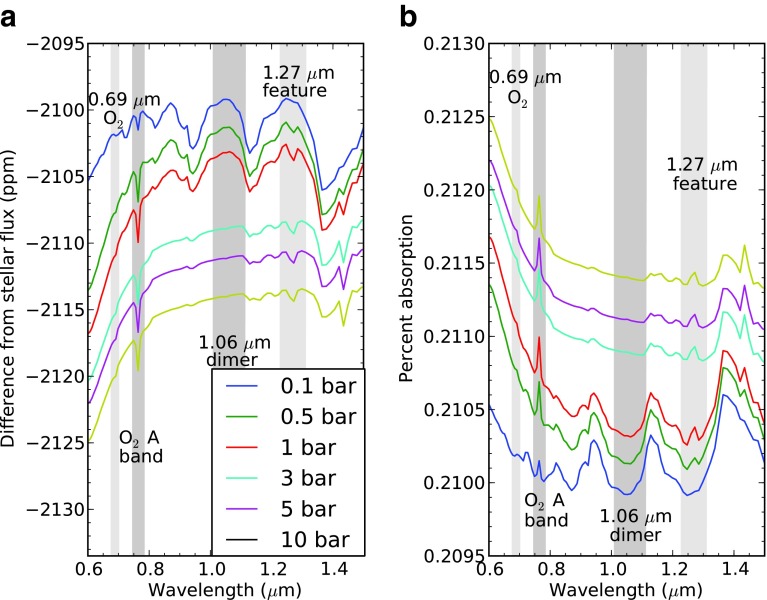
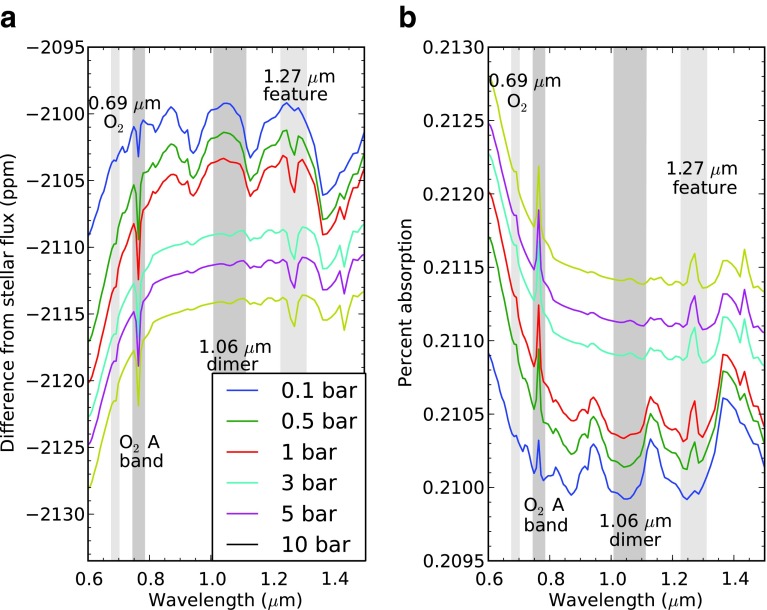
Figures 5, 6, and 7 show the resulting transit transmission spectra for O₂ concentrations of 10%, 50%, and 200% PAL. The 1.06 μm dimer feature is very weak at all pressures for O₂ concentrations at 10% PAL and weak for 50% PAL O₂, while it is very strong for pressures above 0.1 bar at 200% PAL O₂.

FIG. 5.

Same as Fig. 4 but for 10% of the present-day level of O₂. The dimer features do not appear at all because the O₂ concentration is too low.

FIG. 6.

Same as Fig. 4 but for 50% of the present-day level of O₂. The 1.06 μm dimer feature is very weak and is still weak for the highest surface-pressure atmospheres. (Color graphics available online at www.liebertonline.com/ast)

FIG. 7.

Same as Fig. 4 but for 200% of the present-day level of O₂. The 1.06 μm dimer feature is very strong in every case except for the 0.1 bar atmosphere. (Color graphics available online at www.liebertonline.com/ast)

3.2. Reflected spectra

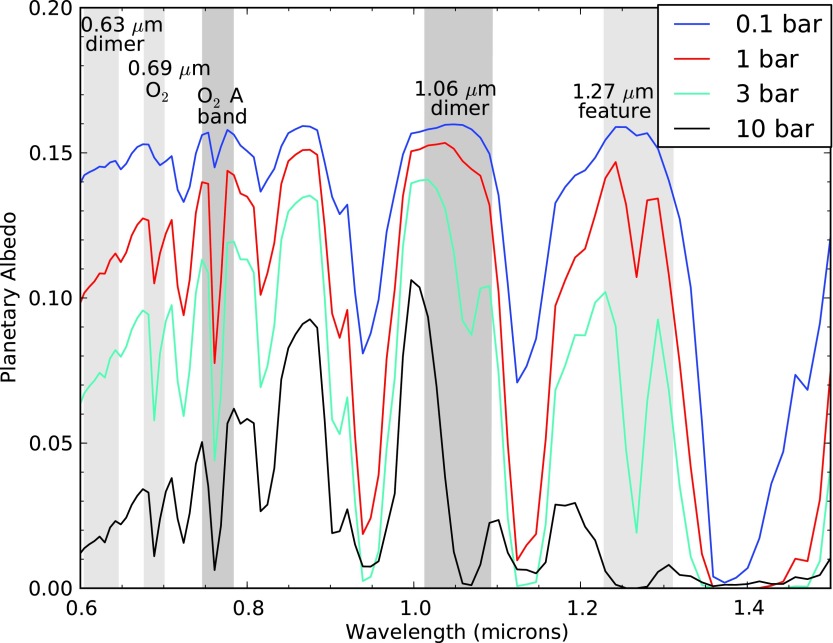
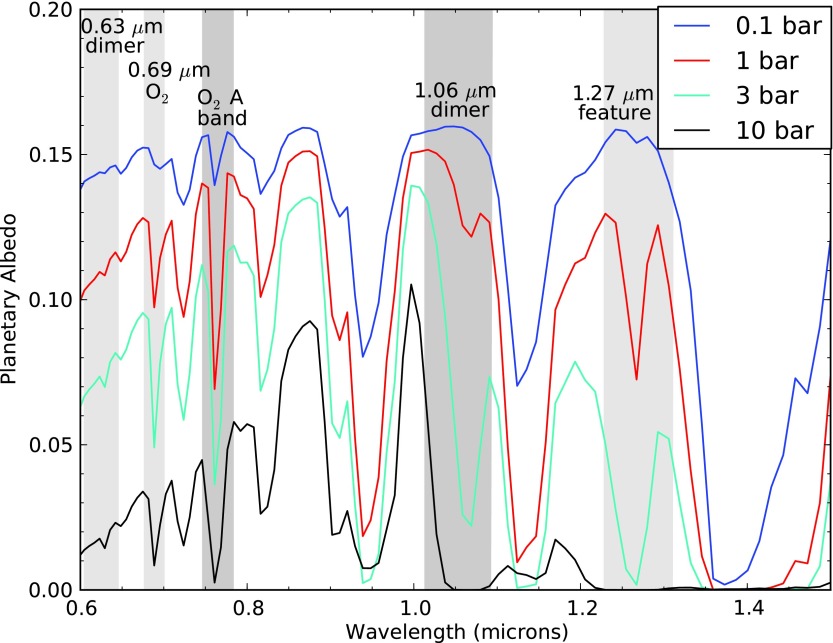
Figure 8 shows the reflected spectra for modern O₂ mixing ratios in atmospheres with a range of total pressure from 0.1 to 10 bar. The 0.5 and 5.0 bar cases are omitted from the plots to increase clarity but are still included in the equivalent width and SNR calculations. The 1.06 μm dimer feature is extremely weak for the present-day atmosphere, but in contrast to its behavior in the transmission spectra, it is a very prominent feature for the 3, 5, and 10 bar atmospheres.

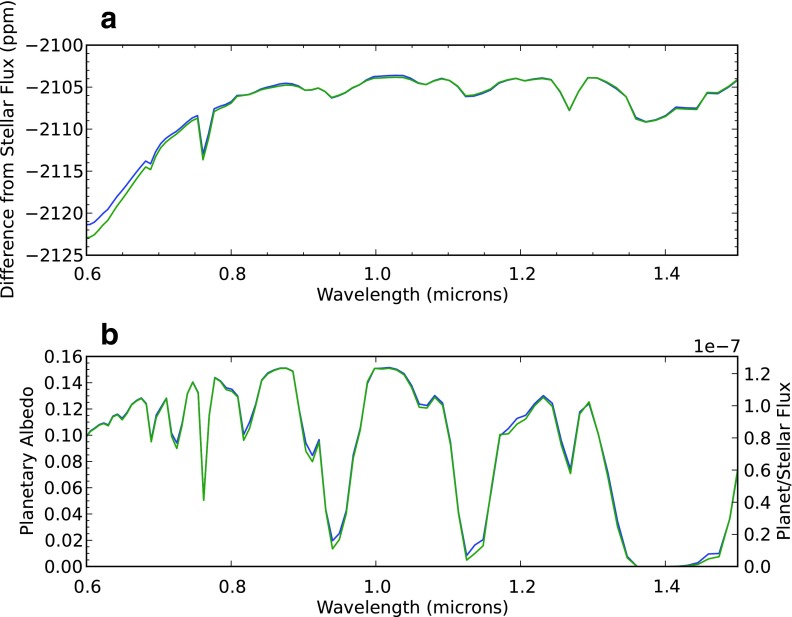
FIG. 8.

Reflected spectra for Earth-like atmospheres with 100% PAL O₂ but with different total atmospheric pressures. In the reflected spectrum, there is no fundamental limit to which pressures can be probed in an atmosphere. Assuming a cloud-free case, it is possible to probe the surface layers of the atmosphere. The 1.06 μm dimer feature is fairly weak in the present-day Earth's atmosphere, but it is a very strong feature in atmospheres with greater pressures. The 1.27 μm feature is very strong in most of the spectra.

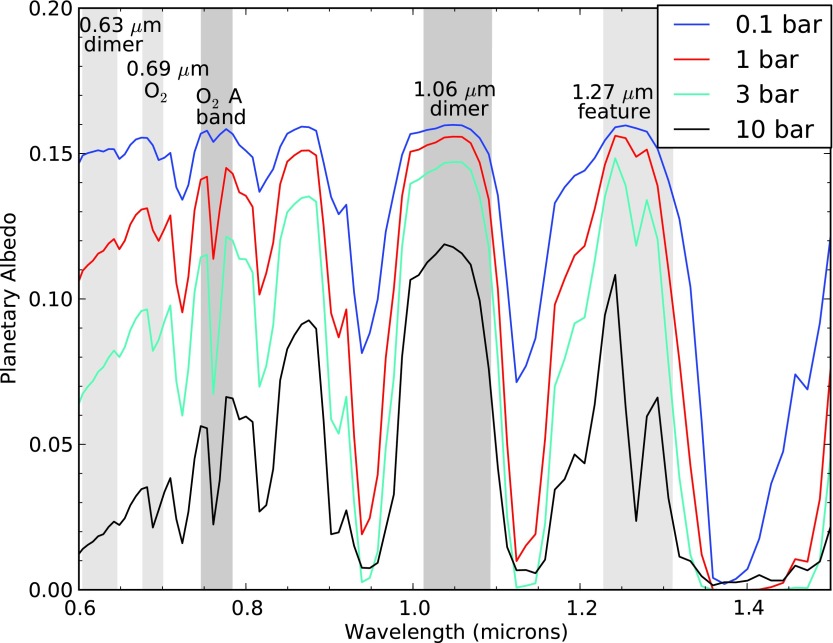
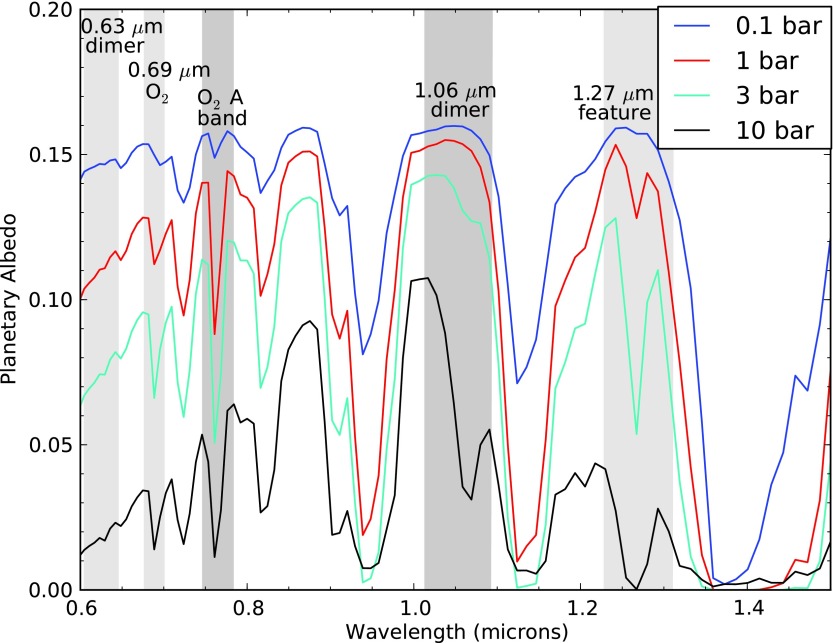
Figures 9, 10, and 11 show the reflected spectra at pressures between 0.1 and 10 bar for 10%, 50%, and 200% PAL O₂, respectively. In the 10% PAL case, the O₂ dimer feature at 1.06 μm is very weak because the total amount of O₂ is very low, even for a 10 bar atmosphere. The 1.06 μm dimer feature is stronger in the 3, 5, and 10 bar cases for atmospheres with 50% PAL O₂. Finally for the 200% O₂ atmospheres, the 1.06 μm dimer feature is one of the strongest spectral features, even in the 1 bar atmosphere.

FIG. 9.

Same as Fig. 8 but for an O₂ concentration of 10% PAL. For this amount of O₂, the 1.06 μm dimer feature is very weak. However, the 1.27 μm feature is still quite strong.

FIG. 10.

Same as Fig. 8 but for an O₂ concentration of 50% PAL. The 1.06 μm dimer feature is strong at pressures≥3 bar. (Color graphics available online at www.liebertonline.com/ast)

FIG. 11.

Same as Fig. 8 but for an O₂ concentration of 200% PAL. The dimer features are much stronger with more O₂ in the atmosphere, as expected. (Color graphics available online at www.liebertonline.com/ast)

3.3. Quantitative absorption measurements

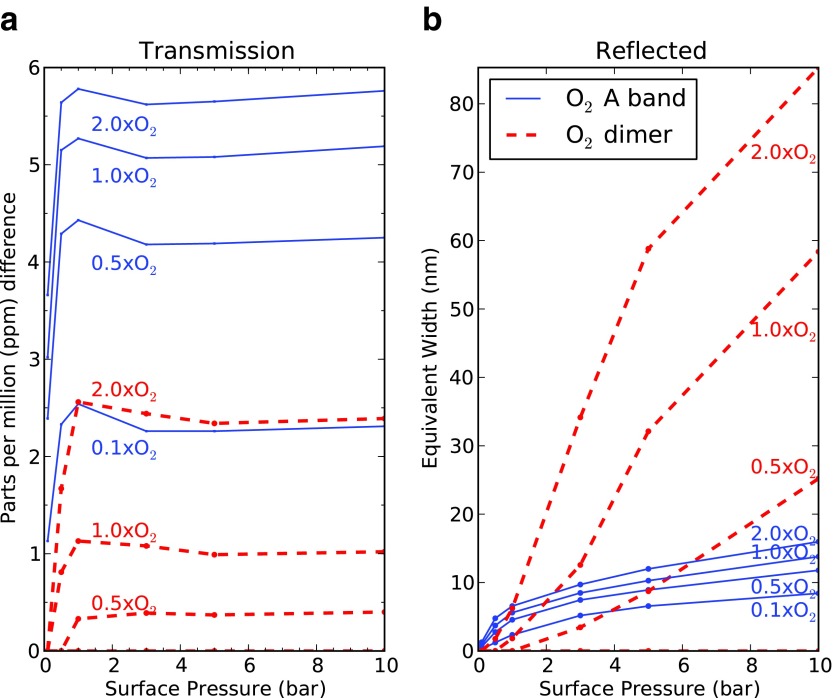
Figure 12 shows the flux change for the transmission spectra and equivalent widths for reflected spectra at different pressures and O₂ concentrations for the O₂ A band and the 1.06 μm dimer feature. For a given O₂ concentration, the transit transmission flux differences for the O₂ A band are roughly constant for pressures ≥1 bar due to refraction. The 1.06 μm dimer feature flux differences increase slightly with pressure but are also constant for pressures ≥1 bar for a given O₂ concentration. The dimer feature does not appear in transmission for cases with 10% PAL O₂.

FIG. 12.

(a) Flux differences (in ppm) for transit transmission spectra and (b) equivalent widths (in nm) for reflected spectra for the O₂ A band and the 1.06 μm dimer feature at various pressures and O₂ concentrations. In transmission, for the Earth-like planet orbiting an M5V star considered here, only the top 0.9 bar can be probed, meaning the dimer and A band equivalent widths are roughly constant with pressure above 1.0 bar for a given O₂ concentration. In comparison to the reflected spectra, the dimer equivalent widths are extremely sensitive to pressure. (Color graphics available online at www.liebertonline.com/ast)

For the direct imaging (reflected) spectra, both the O₂ A band and 1.06 μm dimer feature equivalent widths increase with pressure and increased O₂ concentrations. However, the dimer feature equivalent widths are much more sensitive to pressure. At higher pressures, the dimer feature is strong except for cases with 10% PAL O₂, in which the 1.06 μm dimer feature is too weak to quantify.

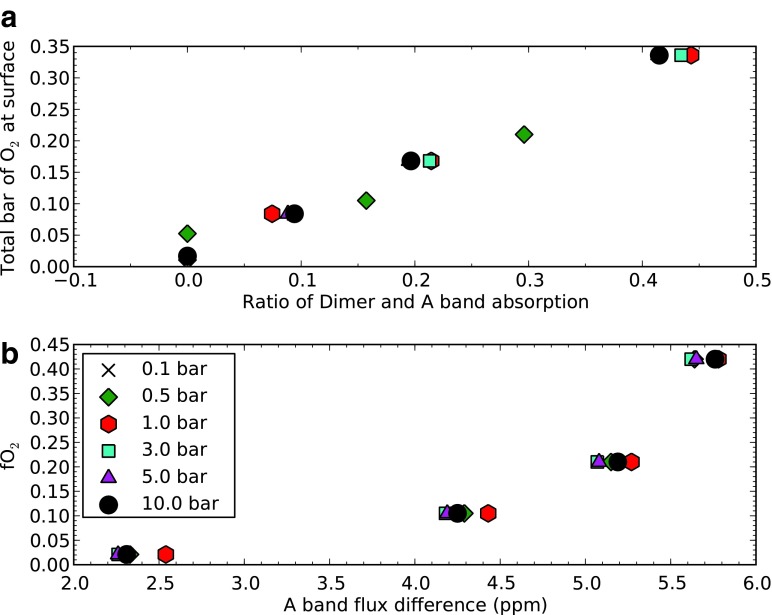
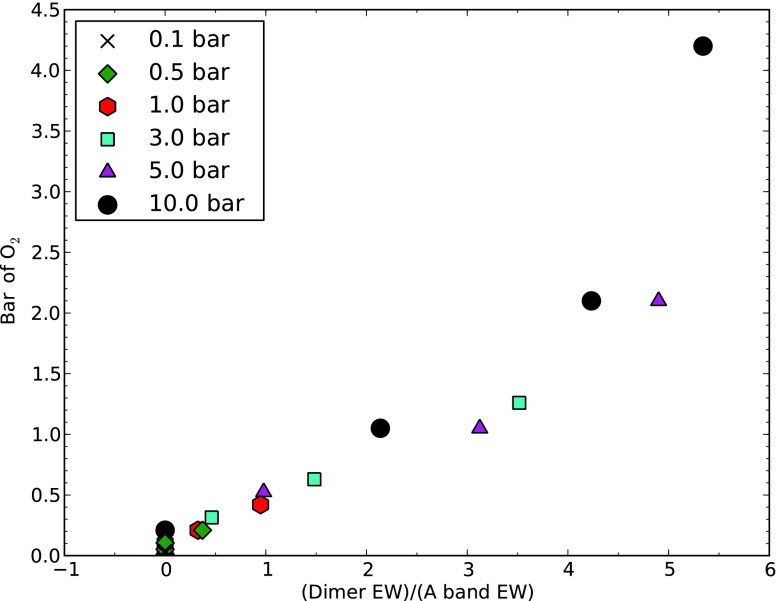
Figures 13–15 show the relationships between the quantitative absorption measurements described above and atmospheric quantities including the O₂ mixing ratio and the O₂ partial pressure at the surface. The part-per-million flux difference measured in transit transmission for the O₂ A band could be used to constrain the O₂ mixing ratio, as shown in Fig. 13b. The O₂ partial pressure at the surface can be estimated by using the ratio between the 1.06 μm dimer and O₂ A band absorption measurements. These ratios are shown in Fig. 13a with part-per-million flux differences and in Fig. 14 with equivalent widths. The O₂ mixing ratio and O₂ partial pressure at the surface can be combined to provide a unique estimate of the surface pressure of the planet. A more detailed description of the pressure measurement technique is given in Section 4.1.

FIG. 13.

This plot shows how one could determine a lower limit on the surface or cloud-top pressure using only a transmission spectrum. (a) O₂ partial pressure at maximum tangent pressure vs. the ratio of the dimer feature and O₂ A band flux difference ratio. The ratio can be used to determine the O₂ partial pressure. (b) fO₂ (or O₂ mixing ratio) vs. A band flux difference. The A band flux difference is roughly constant for a given O₂ mixing ratio. (Color graphics available online at www.liebertonline.com/ast)

FIG. 14.

Plot of total atmospheric O₂ vs. the ratio of the 1.06 μm dimer feature equivalent width (EW) to the O₂ A band equivalent width for the reflected spectrum. There is a trend between this ratio and the total amount of O₂. This could be used as a way to estimate the pressure if a transmission spectrum is not available. (Color graphics available online at www.liebertonline.com/ast)

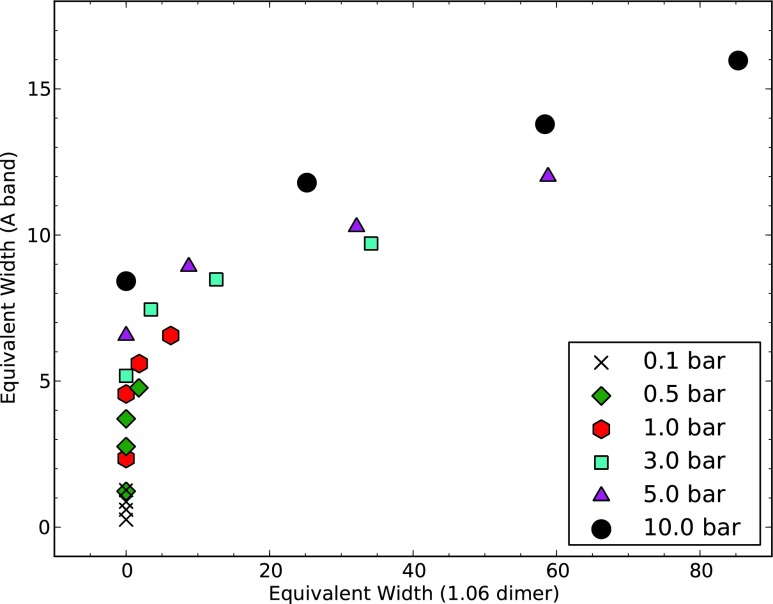
FIG. 15.

Atmospheric pressure as a function of the dimer and A band equivalent widths in the reflected spectrum. It will be possible to set a lower bound on the pressure with only the O₂ A band equivalent width and the 1.06 μm dimer equivalent width. (Color graphics available online at www.liebertonline.com/ast)

3.4. Sensitivity tests

To quantify the errors introduced by assuming the modern-day temperature profile, we generated spectra to test the sensitivity of our models to changes in the temperature profile and to changes in the water vapor profiles. We compared our 1.0 bar, 1.0×PAL O₂ spectra to a spectrum generated by using the same volume mixing ratio profiles but with an isothermal atmosphere at 250 K. We also compared our 1.0 bar, 1.0×PAL O₂ transit transmission spectrum to spectra generated with atmospheres with 0.1 and 10.0 times the H₂O levels. We perform a similar comparison for the 1.0 bar, 2.0×PAL O₂ reflected spectrum.

Figure 16 shows the sensitivity of the spectra to the temperature profile, with our Earth-like profile and an isothermal approximation profile compared. Both the transit transmission and reflected spectra show little sensitivity to the temperature profile. The 1.06 μm dimer band also shows little sensitivity to the temperature profile, despite the dependence of the dimer optical depth on the square of the temperature because the isothermal temperature profile approximates the average temperature of the troposphere, where the majority of dimer absorption occurs.

FIG. 16.

(a) Transit transmission spectra for Earth (blue) and an isothermal atmosphere at 250 K with the same pressure-composition profiles (green). (b) Reflected spectra for an Earth analogue with 2.0×PAL O₂ (blue) and an isothermal atmosphere at 250 K with the same pressure-composition profiles (green). In both cases, the spectra for the calculated temperature-pressure profile and the isothermal profile are very similar, showing that the spectra are not strongly dependent on the temperature profile.

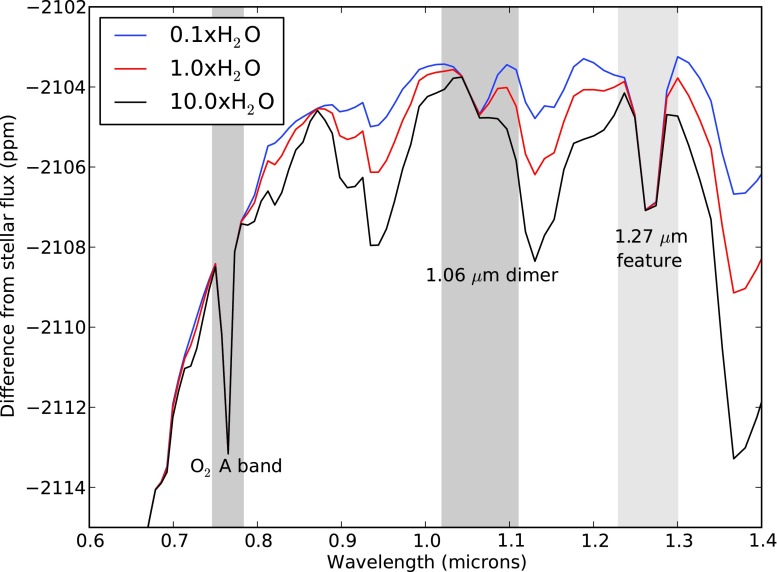
Figures 17, 18, and 19 show the results for the H₂O sensitivity tests. The O₂ A band equivalent widths and part-per-million flux differences are not strongly affected by changes in the H₂O profiles. However, changes in the H₂O mixing ratios affect the continuum flux in the wings of the 1.06 micron dimer feature, complicating measurements of the equivalent width of this feature. For the transit transmission spectra, the change in the total part-per-million flux difference (across the entire band) is less than 20% between the 0.1× and 10.0×H₂O cases. For the reflected spectra, the change in the equivalent width of the 1.06 μm dimer feature is less than 20%. For the reflected spectra, the equivalent widths can be much greater than that for the 1.0 bar, 2.0×O₂ case. For these greater equivalent widths, the effect of increasing or decreasing H₂O levels will diminish as the difference from the continuum flux (affected by H₂O), and the flux within the absorption band will increase.

FIG. 17.

Transit transmission spectra of a 1.0 bar, 1.0×PAL O₂ Earth analogue with H₂O concentrations varying from 0.1×to 10.0×PAL H₂O. While H₂O absorbs near the wings of the O₂ A band, the part-per-million flux difference and the SNR do not change greatly as the H₂O concentration changes. The continuum near the 1.06 μm dimer feature is strongly affected by the increases in H₂O. However, the magnitude of the change in the part-per-million flux difference over the entire band and the SNR is less than 20% when comparing the 1.0×PAL H₂O case to either the 0.1×or 10.0×H₂O cases.

FIG. 18.

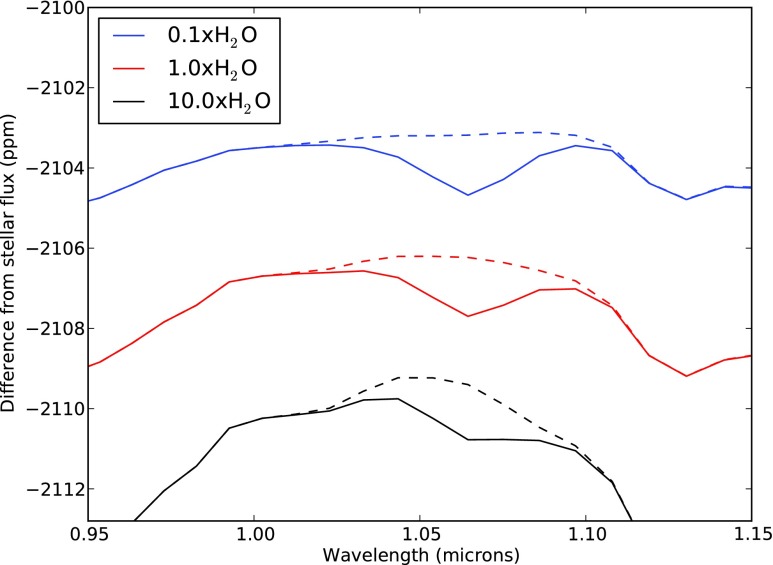
The 1.06 μm dimer feature in transit transmission with different amounts of H₂O. The spectra have been artificially offset for ease of viewing. The dashed lines are spectra that do not include any O₂ dimer absorption and are included to help show the continuum flux level. The total part-per-million flux difference and SNR for the dimer band vary by less than 20% with respect to the 1.0×H₂O case. (Color graphics available online at www.liebertonline.com/ast)

FIG. 19.

The 1.06 μm dimer feature in the direct beam reflected spectra with varying amounts of H₂O for an Earth analogue with a 1.0 bar, 2.0×PAL O₂ atmosphere. There is an artificial offset for ease of viewing, and the dashed lines are spectra that do not include any O₂ dimer absorption. As in transit transmission, the SNR of the dimer feature varies by less than 20% with respect to the 1.0×H₂O case. Additionally, the SNRs for higher-pressure cases should be less affected by changes in H₂O concentrations because of greater absorption within the dimer band. (Color graphics available online at www.liebertonline.com/ast)

3.5. Detectability of spectral features

Table 1 shows the SNRs for observations by JWST for the O₂ A band, 1.06 μm feature, and the 1.27 μm feature for the range of pressures and O₂ concentrations considered here for an Earth analogue at a distance of 5 pc. The SNR are calculated assuming that every transit of an Earth analogue orbiting an M5V star is observed over JWST's 5-year mission lifetime. In transit transmission, the O₂ A band SNRs are no greater than 1.1. The 1.06 μm dimer feature is detectable at a SNR of >3 for many of the 2.0×PAL O₂ cases. The 1.27 μm feature is the most detectable O₂ feature in this wavelength range, with SNRs greater than 5 for many of the 1.0×PAL O₂ cases and greater than 7 for many of the 2.0×PAL O₂ cases. JWST will not be able to detect O₂ species for Earth-like exoplanets in secondary eclipse in the visible and near-infrared, as shown by the secondary eclipse SNR levels. Even for the highest-pressure cases, the SNRs are no greater than ∼0.2.

Table 1.

Signal-to-Noise Ratios for the O₂ A Band, the 1.06 μm Dimer Feature, and the 1.27 μm Feature for All the Cases Considered in Both Transit Transmission and Secondary Eclipse

Pressure	fO2	Transit transmission			Secondary eclipse
Bar	PAL	O2 A band	O2-O2 1.06 μm	O2 1.27 μm	O2 A band	O2-O2 1.06 μm	O2 1.27 μm
0.1	0.1	0.2	0.0	0.0	5.2e-04	0.0e+00	2.7e-03
0.1	0.5	0.5	0.0	0.9	1.2e-03	0.0e+00	3.4e-03
0.1	1.0	0.6	0.0	1.2	1.7e-03	0.0e+00	4.2e-03
0.1	2.0	0.8	0.0	1.5	2.4e-03	0.0e+00	5.5e-03
0.5	0.1	0.5	0.0	1.1	2.3e-03	0.0e+00	5.5e-03
0.5	0.5	0.8	0.0	2.5	5.0e-03	0.0e+00	1.2e-02
0.5	1.0	1.1	1.2	3.7	6.7e-03	0.0e+00	1.8e-02
0.5	2.0	1.1	2.3	5.1	8.5e-03	1.2e-02	2.7e-02
1.0	0.1	0.5	0.0	1.6	4.1e-03	0.0e+00	9.5e-03
1.0	0.5	0.8	0.5	3.9	7.8e-03	0.0e+00	2.6e-02
1.0	1.0	1.1	1.5	5.2	9.4e-03	1.3e-02	3.9e-02
1.0	2.0	1.1	3.4	7.5	1.1e-02	3.5e-02	6.3e-02
3.0	0.1	0.5	0.0	1.2	7.3e-03	0.0e+00	3.2e-02
3.0	0.5	0.8	0.6	3.5	1.0e-02	2.1e-02	8.4e-02
3.0	1.0	1.1	1.5	5.0	1.1e-02	6.2e-02	9.9e-02
3.0	2.0	1.1	3.5	7.2	1.2e-02	1.5e-01	1.2e-01
5.0	0.1	0.5	0.0	1.1	7.5e-03	0.0e+00	5.8e-02
5.0	0.5	0.8	0.6	3.3	9.6e-03	4.3e-02	1.1e-01
5.0	1.0	1.1	1.4	4.9	1.1e-02	1.2e-01	9.4e-02
5.0	2.0	1.1	3.3	7.2	1.2e-02	2.1e-01	1.1e-01
10.0	0.1	0.5	0.0	1.1	5.9e-03	0.0e+00	9.2e-02
10.0	0.5	0.8	0.7	3.4	7.8e-03	9.3e-02	6.1e-02
10.0	1.0	1.1	1.4	5.0	8.6e-03	1.7e-01	6.1e-02
10.0	2.0	1.1	3.4	7.4	9.0e-03	2.1e-01	5.0e-02

The calculations were done for an Earth analogue orbiting an M5V star at a distance of 5 pc. The total integration time was assumed to be 10⁶ s, equal to the total amount of time spent in transit for this case over JWST's 5-year mission lifetime. The 1.06 μm dimer feature and the 1.27 μm feature could be detectable, allowing a lower limit for atmospheric pressure to be set.

Table 2 shows the SNRs necessary to detect and characterize the O₂ A band, 1.06 μm band, and the 1.27 μm feature for the range of pressures and O₂ concentrations considered here for the direct imaging reflected spectra at R=100. The SNRs in Table 2 would be relevant to a direct imaging characterization mission. While these SNRs were calculated for an Earth analogue orbiting an M5V star, the results should be independent of stellar spectral type because we divided out the stellar flux in our calculations. The O₂ A band, 1.06 μm dimer feature, and 1.27 μm feature are detectable at an average SNR_D of 14, 9, and 14, respectively, for the cases when the features are strong enough to identify in the model spectra. The average required SNR_P to use the features for pressure estimation are 11, 31, and 34.

Table 2.

Signal-to-Noise Ratios for Detection (SNR_D) and to Obtain Precision of 3σ in the Center of the Band (SNR_P) for the O₂ A Band, the 1.06 μm Dimer Feature, and the 1.27 μm Feature at Pressures Ranging from 0.1 to 10.0 Bar and O₂ Concentrations Ranging from 0.1 to 2.0 Times PAL O₂ for Direct Imaging Reflected Spectra

Pressure	fO2	O2 A band		1.06 μm dimer		1.27 μm feature
Bar	PAL	SNRD	SNRP	SNRD	SNRP	SNRD	SNRP
0.1	0.1	>100	3.1	—	—	—	—
0.1	0.5	50.0	3.2	—	—	>100	3.0
0.1	1.0	35.0	5.4	—	—	>100	5.1
0.1	2.0	24.4	3.4	—	—	89.8	3.1
0.5	0.1	25.1	3.4	—	—	>100	3.1
0.5	0.5	11.4	3.9	—	—	38.8	3.2
0.5	1.0	8.6	7.3	—	—	23.8	5.6
0.5	2.0	6.8	5.0	30.9	3.2	14.3	3.7
1.0	0.1	13.4	3.8	—	—	62.0	3.1
1.0	0.5	7.1	4.8	—	—	16.4	3.6
1.0	1.0	5.8	9.1	29.0	5.4	9.9	6.9
1.0	2.0	5.0	6.1	9.6	3.7	5.9	5.4
3.0	0.1	6.2	5.3	—	—	12.8	3.8
3.0	0.5	4.4	6.9	16.5	3.4	4.3	7.2
3.0	1.0	3.9	13.2	4.9	8.1	2.9	26.7
3.0	2.0	3.5	9.4	1.9	18.9	1.7	>100
5.0	0.1	5.0	6.3	—	—	6.5	5.0
5.0	0.5	3.8	8.6	6.8	4.1	2.7	20.9
5.0	1.0	3.4	17.7	2.3	18.1	1.9	>100
5.0	2.0	3.0	15.2	1.3	>100	1.3	>100
10.0	0.1	4.1	8.1	—	—	3.0	13.7
10.0	0.5	3.0	15.2	2.3	10.4	1.8	>100
10.0	1.0	2.7	44.9	1.4	>100	1.2	>100
10.0	2.0	2.4	61.6	1.0	>100	1.0	>100

3.6. Effect of spectral resolving power

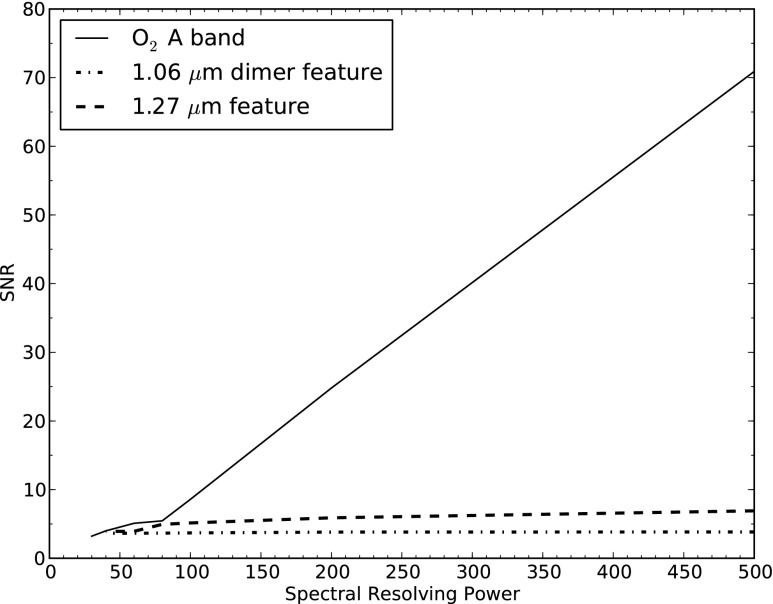
We examined the effect of spectral resolving power on the detectability of spectral features by generating transit transmission spectra for the 1.0 bar, 1.0×PAL O₂ case with spectral resolving powers of 500, 200, 100, 80, 60, 40, 30, and 20. Figure 20 shows the spectra for each of these cases. We also measured the SNR of each feature at each resolving power. The SNRs were calculated assuming a noise profile equivalent to the JWST NIRSpec noise profile but with the noise level at each wavelength divided by (100/R)², so that the noise at each wavelength decreased as the resolving power decreased. Figure 21 shows how the total SNR in each absorption band changes with resolving power. In general, the SNRs drop off rapidly as resolving power decreases for R<60.

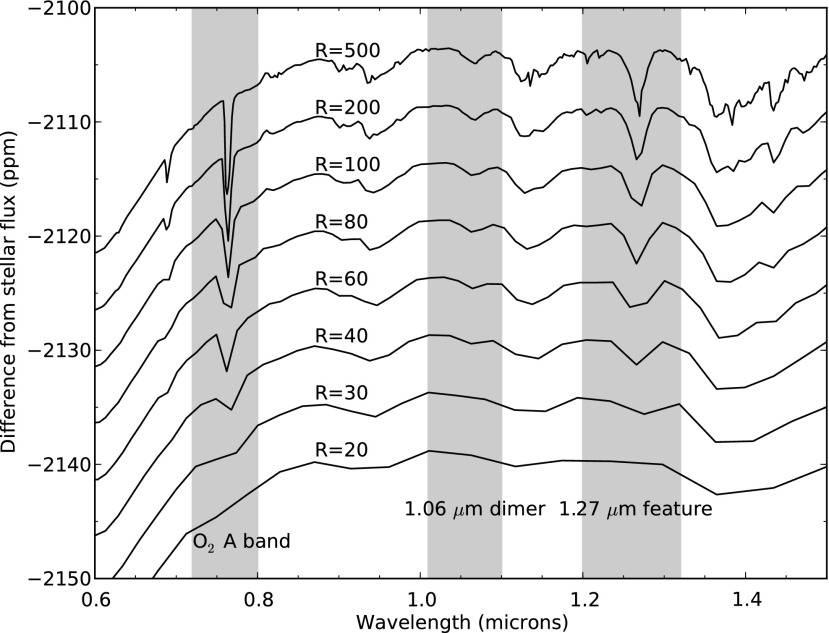
FIG. 20.

Transit transmission spectra for the 1.0 bar, 1.0×PAL O₂ case at various spectral resolving powers. The wavelengths for the O₂ A band, the 1.06 μm dimer band, and the 1.27 μm band are highlighted. An artificial offset has been added to the spectra for ease of viewing. At the lowest resolving powers, it is difficult to identify spectral features.

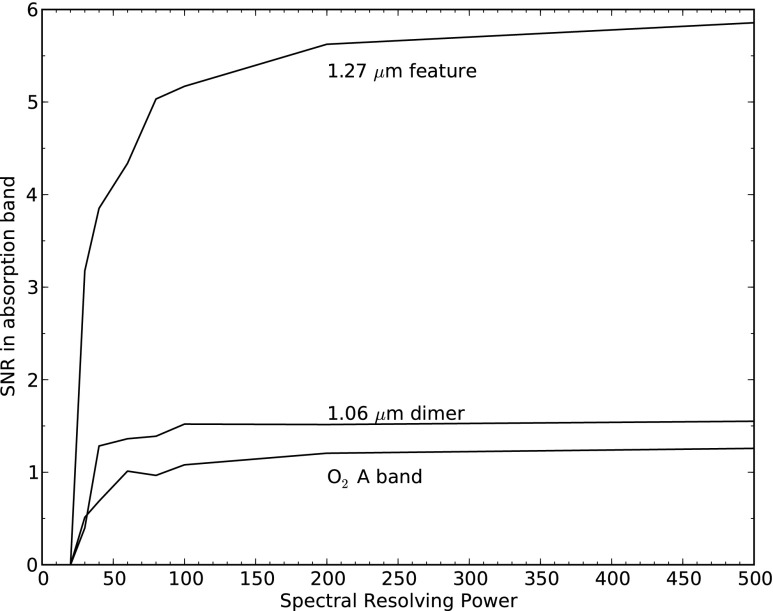
FIG. 21.

Signal-to-noise ratios of absorption features for the spectra shown in Fig. 20. The SNRs decrease as resolving power decreases because the absorption bands can no longer be resolved from the continuum. For R=30 and R=20 it is very difficult to identify any of the O₂ spectral features.

We also generated direct imaging reflected spectra for the 1.0 bar, 2.0×PAL O₂ case at resolving powers of 500, 200, 100, 80, 60, 40, 30, and 20, as shown in Fig. 22. Figures 23 and 24 show how the SNR for detection and precision vary with resolving power for the O₂ A band, 1.06 μm dimer feature, and the 1.27 μm feature. The SNR required to detect each feature increases as resolving power decreases. At R=20, the SNRs are not shown because no spectral features could be identified, and at R=30 only the O₂ A band was identified. The SNR required to quantify the flux at the center of each spectral feature decreases as resolving power decreases, because the lowest radiance level increases as the spectral resolving power decreases.

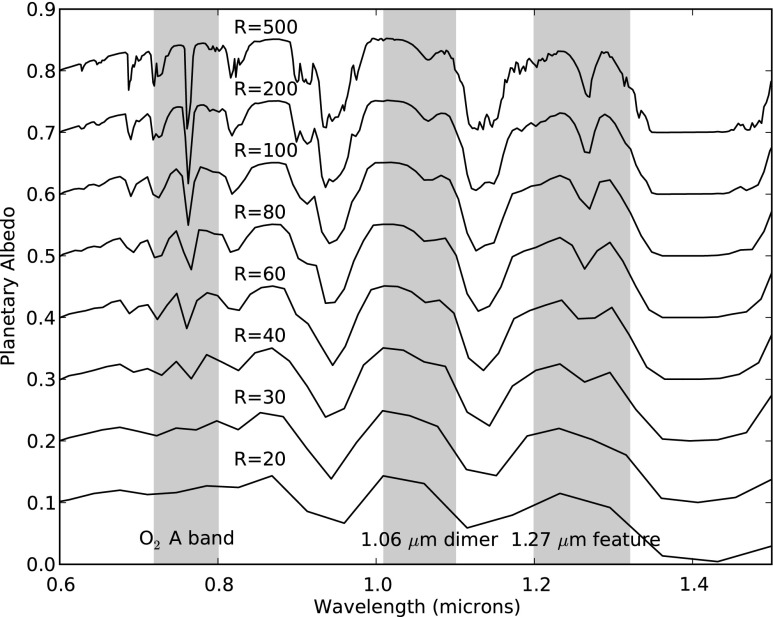
FIG. 22.

Direct imaging reflected spectra generated at spectral resolving powers from 500 to 20. The y axis is the planetary albedo with an arbitrary offset added for ease of viewing. The O₂ A band, 1.06 μm dimer feature, and 1.27 μm feature are highlighted. At resolving powers of R=30 and R=20 it is difficult to identify any O₂ absorption features.

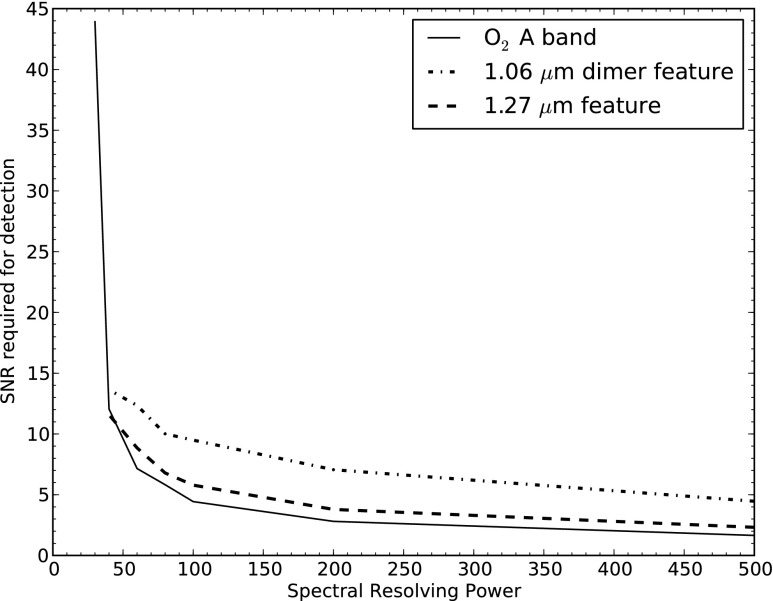
FIG. 23.

Signal-to-noise ratios needed to detect the O₂ A band, 1.06 μm dimer feature, and the 1.27 μm feature for direct imaging reflected spectra. As resolving power decreases, the required SNR to detect each feature increases because the continuum level decreases, resulting in a lower overall signal in the absorption band. Furthermore, at the lowest resolutions, the absorption bands cannot be resolved. Thus, this decreases the measurable signal even more, leading to an increase in the required SNR.

FIG. 24.

Signal-to-noise ratios required to quantify the flux within 3σ in the center of the absorption band (defined as the lowest flux level) for the O₂ A band, 1.06 μm dimer feature, and the 1.27 μm feature. The SNR required for this level of precision decreases as resolving power decreases because the flux is averaged over fewer wavelength bins, leading to an increase in the lowest flux. This decrease in required resolving power occurs for all three absorption features, though the trend is most apparent for the O₂ A band, as it has the narrowest spectral shape of the three features considered here.

4. Discussion

The 1.06 μm dimer feature is prominent in transit transmission for atmospheres with ≥50% PAL O₂ and surface pressures ≥0.5 bar. It is a prominent feature in the reflected spectra for atmospheres with ≥50% PAL O₂ and surface pressure ≥3 bar. For the reflected spectra, the dimer feature equivalent width is highly dependent on surface pressure when compared to the O₂ A band; therefore the dimer feature can be used to constrain pressure. Here, we discuss how to do this for the cases investigated in this study.

4.1. Pressure measurement technique

Figure 12 confirms that dimer absorption features are more strongly dependent on pressure than monomer features. Therefore, dimer features can be combined with monomer features to determine pressure, even if the mixing ratio of the absorbing gas is not known. With only transit transmission spectroscopy, it is impossible to probe pressures over ∼1 bar for the cases examined here, but it may be possible to constrain the O₂ mixing ratio and set a lower bound for pressure. In reflected spectra, it is possible to determine the surface partial pressure of O₂ and set a lower bound for pressure by using the 1.06 μm dimer feature as an on/off pressure gauge. With both a transit transmission spectrum and a reflected spectrum, it should be possible to determine total atmospheric surface pressure for an Earth-like exoplanet.

4.1.1. Transmission spectra pressure measurement

Transmission spectroscopy provides only a lower bound on the atmospheric pressure because refraction provides a fundamental limit to which pressures can be probed when using this technique. For the spectra presented here, a lower limit of ∼1 bar can be set for the high-pressure atmospheres. For a given O₂ concentration, a unique estimate of the pressure can be retrieved from the ratio between the part-per-million flux differences of the 1.06 μm dimer feature and the O₂ A band. Figure 13a shows the relationship between this ratio and the total amount of O₂ above 0.9 bar, which is the highest pressure that can be probed in this particular case. There is a clear trend between this ratio and the amount of O₂ in the atmosphere. When combined with an O₂ mixing ratio, this relationship can provide a quantitative estimate of a lower level of the surface or cloud-top pressure.

The O₂ mixing ratio can be estimated from the flux difference of the O₂ A band in transmission. Figure 13b shows the relationship between the O₂ mixing ratio (which is constant throughout the atmosphere) and the O₂ A band flux difference. For pressure ≥0.1 bar, the O₂ flux difference is roughly constant for a given O₂ concentration, meaning that a measurement of the O₂ A band flux difference should correlate with the O₂ mixing ratio.

4.1.2. Reflected spectra pressure measurement

Reflected spectra alone can provide an estimate of the surface partial pressure of O₂ by examination of the ratio of the 1.06 μm dimer equivalent width and the O₂ A band equivalent width. Figure 14 shows the relationship between this ratio and the surface partial pressure of O₂. The strength of the 1.06 μm dimer feature could also be used as an on/off gauge to set a lower bound for pressure. Determining total atmospheric pressure with only a reflected spectrum is difficult due to degeneracies between the O₂ concentration and total atmospheric pressure, as shown in Fig. 15. For large equivalent widths of the dimer feature, the pressure will certainly be above 1 bar. However, it is difficult to differentiate between atmospheres with the same O₂ surface partial pressure. Nevertheless, it appears that it is possible to set a lower limit on pressure by measuring the 1.06 μm dimer feature equivalent width. For example, a 1.06 μm dimer feature equivalent width greater than ∼10 nm would imply a surface pressure >1 bar.

4.1.3. Pressure measurement with both transit transmission and reflected spectra

If both a transit transmission spectrum and a reflected spectrum are available, it should be possible to directly measure the total atmospheric surface pressure in the absence of clouds. Transit transmission spectroscopy can provide an estimate of the O₂ mixing ratio as described previously. A reflected spectrum can theoretically probe to the reflecting surface and therefore can be used to constrain the O₂ partial pressure at the surface. By combining the O₂ mixing ratio and O₂ partial pressure, we can determine the total pressure at the reflecting surface, which could either be a reflective cloud layer or the physical surface of the planet.

4.2. Relevance to planet characterization

The methods described here could be used in the near future by the JWST NIRSpec instrument, which will potentially be able to characterize transiting planets between 0.6 and 5.0 μm. The O₂ A band will likely not be detectable for a nearby Earth analogue with JWST. Although this feature is strong in the spectrum, the sensitivity of NIRSpec is poor at shorter wavelengths. The 1.06 μm dimer feature is detectable at the 3σ level in transit transmission for cases with 2.0×PAL O₂ and high surface pressures. Thus, the detection of the 1.06 μm dimer feature would imply a surface or cloud-top pressure greater than or equal to 1.0 bar. For cases in which the 1.06 μm dimer feature is not detectable, the 1.27 μm feature could be used to constrain the pressure. This feature is not as strongly dependent on pressure as the 1.06 μm dimer feature, but it is more detectable in all cases explored here.

Terrestrial Planet Finder or a similar direct imaging mission will be required to characterize the reflected spectra of nearby Earth analogues in the visible and near-infrared. The SNR values for secondary eclipse applicable to JWST are all less than 1, so JWST will not be able to characterize the reflected spectra of Earth analogues in secondary eclipse. Table 2 shows the necessary SNRs to detect and characterize spectral features for a direct imaging planet characterization mission. While the SNRs were calculated for an Earth analogue orbiting an M5V star, the results should be largely independent of spectral type because we have divided the reflected flux by the stellar flux in our calculations. The required SNR values suggest that a SNR of >10 would be necessary to detect and quantify the O₂ A band, 1.06 μm dimer feature, and 1.27 μm feature for a true Earth analogue. However, because continuum brightness changes with pressure, a different SNR criteria would be necessary for higher-pressure atmospheres. For example, the continuum brightness near the O₂ A band is 3 times lower for the 10.0 bar cases than it is for the 0.1 bar cases. For most cases, a SNR of >7 would likely be sufficient to set a lower limit on the surface pressure when using the 1.06 μm dimer feature.

Clouds and aerosols will also affect the detectability of absorption features. In transit transmission, clouds can effectively mask the highest pressures of the atmospheres at which dimer absorption is most prominent. However, in partially cloudy atmospheres, some of the paths will probe pressures as high as the maximum tangent pressure; thus the planetary transmission spectrum could show evidence of dimer absorption. Furthermore, absorption in the 1.27 μm dimer band can be detected with SNR>1 in even some 0.1 bar cases, meaning that there could be a detectable dimer absorption signal for even a completely cloud-covered planet if the cloud deck pressure was ≥0.1 bar. For reflected spectra, clouds will truncate paths before they reach the surface and limit the dimer absorption for those paths. However, for partially cloudy atmospheres, dimer absorption could be detectable in the paths that do reach the surface. Additionally, because cloud albedos are typically greater than surface albedos, the presence of clouds will increase the continuum brightness levels and the brightness in the center of absorption bands. The increase in brightness has been shown to decrease the required SNR to detect and characterize O₂ monomer absorption in cloudy atmospheres when compared to cloud-free cases (Evans et al., 2011), though the effect of cloud albedo on the detectability of dimer absorption features has not been heretofore examined. Therefore, while clouds will impact the detectability of dimer features, using dimers to determine pressure and as biosignatures may still be feasible for cloudy atmospheres.

4.3. Detectability at different resolving powers

Figure 21 shows the SNRs for spectral features at varying resolving powers for transit transmission spectra of a 1.0 bar, 1.0×PAL O₂ atmosphere. The SNRs for each band are greatest at the highest resolving powers and then gradually decrease until R ∼ 60 or 80, at which the SNRs decrease strongly. This dramatic decrease with resolving power occurs because, at the lowest resolving powers, the absorption bands are indistinguishable from the continuum. Additionally, the highest flux levels in the continuum cannot be resolved at lower spectral resolving powers, decreasing the total signal. This effect can be seen most easily for the spectra with R=20, in which no absorption features can be identified.

Figures 23 and 24 show the SNRs for the direct imaging reflected spectra. In contrast to Fig. 21, these two figures show the required SNR to detect and characterize an absorption band, not the SNR that could be obtained with JWST. The required SNR to detect spectral features increases as resolving power decreases. However, this effect would be mitigated because the expected noise at each wavelength should decrease as resolving power decreases. The SNR required to quantify each absorption band decreases as resolving power decreases because the lowest radiance level increases. At R<40, however, spectral features are very difficult to identify, making these resolving powers unsuitable for detecting and characterizing O₂-related absorption features.

4.4. O₂ dimer biosignatures

In addition to their utility as pressure probes, the 1.06 μm dimer feature and 1.27 μm feature could potentially be detectable biosignatures for nearby Earth-like planets. The O₂ A band has long been considered the most viable O₂ biosignature, but it is unlikely to be the most detectable biosignature for an Earth-like planet in transit transmission. As initially described by Pallé et al. (2009), lunar eclipse observations show that the 1.06 and 1.27 μm dimer features are more detectable than O₂ monomer features like the A band, which is corroborated by our model spectra and detectability calculations. The 1.27 μm O₂ feature has been examined as a potential biosignature for ground-based telescopes by Kawahara et al. (2012), but to our knowledge detectability studies of neither the 1.06 μm dimer feature nor the 1.27 μm feature have been undertaken for JWST. Our results show that the 1.27 μm feature would be detectable with a SNR of 5 for a cloud-free Earth analogue at 5 pc. Therefore, we conclude that O₂ features, especially the 1.06 μm dimer feature and the 1.27 μm feature, could be detectable biosignatures for oxygenic photosynthesis with JWST.

4.5. Challenges to observations

Clouds and aerosols will make estimating pressure by using dimer features more difficult. A direct imaging observation of a partially cloud-covered planet will be able to probe to the surface for a fraction of the paths, such that the dimer feature will be weaker than for a cloud-free planet. Cloud and aerosol extinction can also be wavelength-dependent, which may complicate using equivalent widths or part-per-million flux differences to determine pressure. Nevertheless, dimer features can still provide a lower bound for pressure if clouds and aerosols cannot be explicitly included in the retrieval method.

Higher H₂O or CO₂ abundances in an atmosphere could also make this method more challenging. Higher H₂O abundances will make it more difficult to define a continuum for the 1.06 μm dimer feature, as shown in Figs. 18 and 19. However, as discussed in Section 3.4, the magnitude of this error should typically be less than 20% for most cases in which the 1.06 μm dimer feature could be detectable. CO₂ has an absorption feature near 1.06 μm (Segura et al., 2007), which could make using the 1.06 μm dimer feature difficult. This could be overcome by modeling out absorption from H₂O and CO₂ or by using other dimer features to supplement information from the 1.06 μm dimer feature, such as the 1.27 μm dimer feature.

Lastly, not knowing the mixing ratio of O₂ will make estimating pressure difficult when only a reflected spectrum is available. This is similar to the problem in using the absorption widths of rotation-vibration features to constrain pressure. However, the 1.06 μm dimer feature is more sensitive to pressure than a monomer feature and therefore can provide a better estimate of pressure than a monomer feature alone. Furthermore, monomer features cannot be used as an on/off pressure gauge, while dimer features can.

5. Conclusions

Spectrally resolved observations of O₂ dimer absorption can be combined with observations of the absorption by O₂ vibration-rotation bands to provide independent constraints on the O₂ concentration and the surface or cloud-top pressure in oxygenated atmospheres for planets around M dwarfs, and with low levels of CO₂. Even if a precise estimate for the pressure is not possible, the presence of dimer absorption is indicative of pressures greater than ∼0.5 bar in transmission spectroscopy and greater than ∼1 bar in reflected spectra.

We have shown that this method is feasible in the absence of clouds for oxygenated atmospheres. For transmission spectroscopy, this method can be used to estimate the surface or cloud-top pressure for O₂ concentrations ≥100% PAL and for pressures>0.5 bar. For reflected spectra, this method will work if the O₂ partial pressure at the surface is>0.3 bar. Clouds will reduce the absorption strength of dimer features by limiting the paths that can probe the highest pressures in transit transmission and by truncating paths before they reach the surface in the reflected spectra.

The James Webb Space Telescope may be able to detect the 1.06 μm dimer feature and the 1.27 μm O₂ feature for an Earth analogue orbiting an M dwarf in transit transmission. Thus, while not all the techniques described here will be applicable to JWST observations, a lower bound on pressure could be set for an exoplanet by using an O₂ dimer feature. Furthermore, we showed that a direct imaging mission operating in the visible and near-infrared like Terrestrial Planet Finder would require a spectral resolving power of R>40 and preferably higher. At R=100, a SNR of >10 would be required not only to detect O₂-related absorption features but also to provide an estimate of an exoplanet's atmospheric pressure.

Acknowledgments

We thank Drake Deming for helpful discussions on the detectability calculations and the two anonymous reviewers for their thorough and helpful reviews that greatly improved the paper.

This work was performed by the NASA Astrobiology Institute's Virtual Planetary Laboratory, supported by the National Aeronautics and Space Administration through the NASA Astrobiology Institute under Cooperative Agreement solicitation NNH05ZDA001C. This work has also been supported by a generous fellowship from the ARCS Seattle chapter and funding from the Astrobiology Program at the University of Washington under an NSF IGERT award.

Some of the work described here was conducted at the Jet Propulsion Laboratory, California Institute of Technology, under contract with NASA.

This research has made use of NASA's Astrophysics Data System.

Author Disclosure Statement

No competing financial interests exist.

Abbreviations

JWST, James Webb Space Telescope; NIRSpec, Near-Infrared Spectrograph; PAL, present atmospheric level; SMART, Spectral Mapping Atmospheric Radiative Transfer; SNR, signal-to-noise ratio.