Straightening: existence, uniqueness and stability

Abstract

One of the least studied universal deformations of incompressible nonlinear elasticity, namely the straightening of a sector of a circular cylinder into a rectangular block, is revisited here and, in particular, issues of existence and stability are addressed. Particular attention is paid to the system of forces required to sustain the large static deformation, including by the application of end couples. The influence of geometric parameters and constitutive models on the appearance of wrinkles on the compressed face of the block is also studied. Different numerical methods for solving the incremental stability problem are compared and it is found that the impedance matrix method, based on the resolution of a matrix Riccati differential equation, is the more precise.

1. Introduction

The rubber of a car tyre in contact with the road is slightly flattened, or straightened, with respect to its natural unloaded configuration. In other words, a portion of the rubber undergoes a deformation which can be quite accurately captured by Ericksen's solution [1] for the elastic straightening of a circular cylindrical sector into a rectangular block. Other examples of application for this deformation include the local behaviour of rubber-covered rollers in service or of extended body joints such as knees and elbows. Ericksen's exact solution is one of only a handful of universal deformations in incompressible isotropic nonlinear elasticity [2], but it has so far received scant attention in the literature, beyond the works of Hill [3], Aron et al. [4–6] and our recent contribution [7]. In this paper, we complete the picture with some additional results for the (plane strain) large straightening deformation of an incompressible isotropic sector and its stability with respect to incremental deformations.

In §2, we describe the considered deformation, the parameters it involves and the different boundary conditions under which it can be achieved, illustrated by use of the neo-Hookean strain-energy function. In §3, following a brief discussion of strong ellipticity of an incompressible isotropic strain-energy function, it is shown that if the sector is straightened either by the application of end couples alone or, in the absence of end couples, by lateral normal forces alone, then, under the inequalities associated with the strong ellipticity condition, existence of the straightening deformation is guaranteed irrespective of the particular form of strain-energy function. For a thin sector, asymptotic formulae in terms of the thickness to (outer) radius ratio, denoted ε, are then provided for these two cases to give explicit results for certain parameters of the problem. In particular, it is found that to third order in ε the results are independent of the choice of energy function.

In §4, we derive the equations of incremental equilibrium in the Stroh form with a view to solving them numerically in order to investigate the possible appearance of wrinkles (i.e. small amplitude undulations or instabilities) at a critical threshold of deformation. Then, in §5, the equations are effectively solved numerically for the corresponding, numerically stiff, two-point boundary value problem. First, we use the compound matrix method, which must be slightly modified from its usual form to circumvent a singularity problem. Impedance matrix techniques are then applied, and this approach proves to be more precise for the problem at hand. The results are illustrated for homogeneous sectors made of neo-Hookean and of Gent materials, and the effects of geometrical and constitutive parameters on stability are highlighted.

2. Basic equations

Consider the circular cylindrical sector of incompressible isotropic elastic material shown in figure 1a in terms of cylindrical polar coordinates (R,Θ,Z), with geometry defined by the reference region

2.1

where 0<2Θ₀<2π is the angle spanned by the sector. The sector can be deformed into a rectangular block, as shown in figure 1b with respect to Cartesian coordinates (x₁,x₂,x₃), by the deformation [2]

2.2

where A=Θ₀/l and 2l is the length of the block in the x₂-direction. Here, we are restricting the study to a plane strain deformation, although a uniform stretch could easily be included in the x₃-direction [1,2]. The deformed straightened sector occupies the region described by

2.3

where a and b are defined as

2.4

Figure 1.

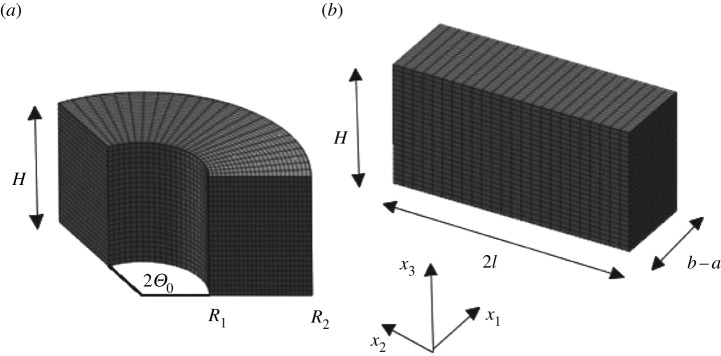
(a) A circular cylindrical sector with internal and external radii R₁ and R₂, respectively, and sector angle 2Θ₀ straightened (b) under plane strain conditions into a rectangular block of thickness b−a and length 2l.

The corresponding deformation gradient F has the form

2.5

where E_R,E_Θ,E_Z and e₁,e₂,e₃ are the cylindrical polar and Cartesian unit basis vectors in the reference and deformed configurations, respectively. It follows that the Eulerian principal directions of the deformation (defined as the directions of the eigenvectors of the left Cauchy–Green deformation tensor B=FF^T) are the Cartesian basis vectors and that the principal stretches are

2.6

We consider an incompressible isotropic hyperelastic material with strain energy W=W(λ₁,λ₂,λ₃) per unit volume, so that the Cauchy stress tensor can be written as

2.7

where σ₁,σ₂,σ₃ are the principal Cauchy stresses given by [8]

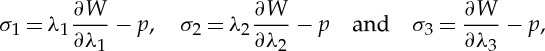2.8

p being a Lagrange multiplier associated with the incompressibility constraint λ₁λ₂λ₃=1, which is automatically satisfied by (2.6).

Henceforth, it is convenient to use the notation λ₂=λ, λ₁=λ⁻¹, and to introduce the function 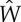of a single deformation variable defined by

2.9

from which, on use of (2.8), we obtain

2.10

As the deformation depends only on the single variable R (or x₁), the second and third components of the equilibrium equation div σ=0 in the absence of body forces show that p is independent of x₂ and x₃, and the first component yields simply dσ₁/dx₁=0; hence σ₁ is a constant. Then, by taking the boundary R=R₁, for example, to be traction free it follows that σ₁≡0, and hence

2.11

If required, the value of σ₃ needed to maintain the plane strain condition may be obtained in terms of λ from (2.8)₃ with p=λ₁∂W/∂λ₁.

Next, we compute the resultant normal force N and moment M (about the origin of the Cartesian coordinate system) on the end face x₂=l of the block. They are given by

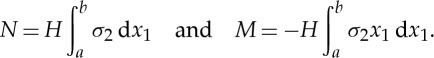2.12

Note that because σ₂ is independent of x₂, N and M are in fact the same on any section of the block normal to the x₂-direction. By a change of variables, we arrive at

2.13

where

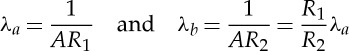2.14

are the values of the stretch λ on the faces x₁=a and x₁=b, respectively, of the straightened block. Except for large values of |N|, it is expected that the circumferential elements on the ‘inner’ face of the straightened block are extended and those on the ‘outer’ face are contracted, i.e. λ_a>1 and λ_b<1, in which case, by (2.14) and the definition of A, it would follow that l belongs to the interval

2.15

We do not insist that this ordering holds in general, but it turns out that it gives a necessary and sufficient condition for the existence of a plane where λ=1 (with equation x₁=l/2Θ₀) in the straightened block, which we refer to as the neutral plane, or neutral axis in the (x₁,x₂) plane. This is the case when either M=0 or N=0, the two examples we analyse in §3, if we impose the physically reasonable requirement that the stress σ₂ be positive (negative) when λ>1 (<1), i.e.

2.16

These inequalities certainly hold when the strain-energy function W satisfies the strong ellipticity condition. Indeed, by (2.10) we have

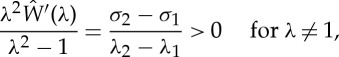2.17

because of the Baker–Ericksen inequalities, which are a consequence of the strong ellipticity condition [2]. Then, clearly, (2.16) readily follows.

As an example of the large straightening deformation, we consider the neo-Hookean material, for which

2.18

where μ>0 is the ground state shear modulus. For the plane strain problem this reduces to

2.19

We then calculate

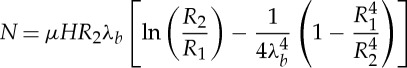2.20

and

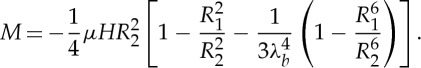2.21

Through this explicit example, which as far as we are aware is not available in the literature, it can be seen that in order to describe the straightening deformation, for any given Θ₀, either the loads can be prescribed, i.e. N (or M) can be prescribed and then the corresponding A and M (or N) can be computed from equation (2.13) with (2.14), or the deformed geometry can be described, i.e. the length 2l can be prescribed, hence fixing A, and then N and M deduced from equation (2.13) with (2.14). In this paper, following considerations of Hill [3] in respect of a spherical cap, we deal with three case studies that are important physically:

• (i) the sector is straightened by end couples alone (N=0);

• (ii) the sector is straightened by vice-clamps (M=0); and

• (iii) with NM≠0 in general, the final length 2l of the straightened sector is determined at the onset of instability.

For instance, if the deformation for the neo-Hookean material is achieved by the application of moments alone, as in Case (i), then N=0 and A is determined by

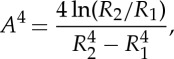2.22

in which case M depends on the geometry only through R₁ and R₂.

3. Examples of straightening

This section is concerned with deformations that are achieved by the application of two special systems of forces, that corresponding to zero resultant normal force, N=0, and that corresponding to zero resultant moment, M=0, i.e. Cases (i) and (ii) above, respectively. With reference to (2.12), we see that the difference between these two cases arises from the different distributions of the stress σ₂ with respect to x₁ in [a,b].

We focus on constitutive models that satisfy the strong ellipticity condition, which, for plane strain, consists of the inequalities [8]

3.1

These two inequalities are satisfied by many standard strain-energy functions, including the neo-Hookean model:

3.2

where I₁=tr B and μ is a constant; the Varga model [9]:

3.3

where i₁=tr(B^1/2); the Fung–Demiray model [10]:

3.4

where c is a constant and the Gent model [11]:

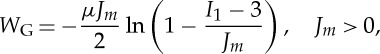3.5

where J_m is a constant and the range of deformation is limited by the condition that I₁−3<J_m. In each case, μ (>0) is the shear modulus of the material in the undeformed configuration, given by .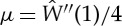

(a). Straightening by end couples

The system of loads consists of end couples alone when N=0, which is the case we consider here. If N=0 then σ₂ must take both positive and negative signs in the interval [a,b], and, in particular, there must be a value of x₂ where σ₂=0, and hence, by (2.16) λ=1, so that

3.6

By virtue of (2.14)₁, this leads to the restriction

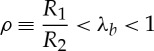3.7

on λ_b, wherein we have defined, for later convenience, the notation ρ. In this case, by (2.13)₁, we must investigate the existence of positive roots for λ_b in the interval (3.7) of the equation

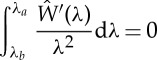3.8

with λ_a=λ_b/ρ for fixed ρ.

To this end, we introduce the function f(λ_b) defined by

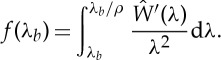3.9

By virtue of (2.16), we have

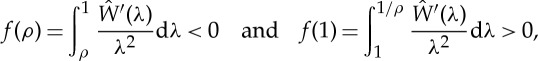3.10

and by differentiation

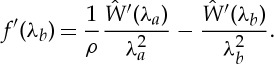3.11

By (2.16) and (3.6), this is clearly positive, and we conclude that f is strictly increasing, and so f has a unique zero, say 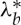, in interval (3.7). Consequently, a circular cylindrical sector made of an incompressible isotropic elastic material can be straightened by applying terminal couples only. This result is universal to all constitutive models with strain-energy functions 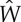continuously differentiable in 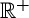and satisfying inequalities (2.16). The corresponding moment is

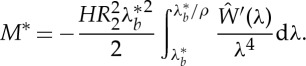3.12

For illustration, we now report some analytical and numerical results for the solution of equation (3.8).

For the neo-Hookean material (3.2), we obtain

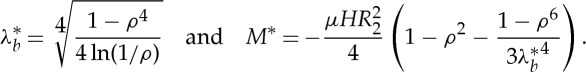3.13

For the Varga material, the explicit solution of (3.8) and the corresponding moment are given by

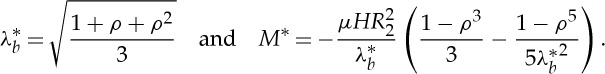3.14

For Fung–Demiray material (3.4), there are no explicit solutions, and a numerical resolution is required. Figure 2a,b displays the stretch as a function of the ratio ρ=R₁/R₂ for the neo-Hookean, Varga and Fung–Demiray materials. In particular, in plotting figure 2b, we took the Fung–Demiray energy density with constants used in [12] to model ‘young’ human arteries (c=1.0) and ‘old’ arteries (c=5.5).

Figure 2.

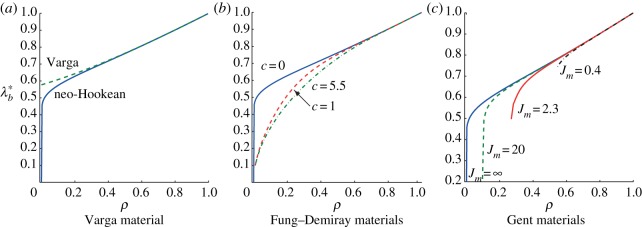
Circumferential stretch as a function of the radii ratio ρ=R₁/R₂ for the straightening of blocks by end-couples only: (a) Varga and neo-Hookean materials; (b) Fung–Demiray materials with stiffening parameters c=5.5, c=1.0 and (neo-Hookean limit) and (c) Gent materials with stiffening parameters J_m=0.4, J_m=2.3, J_m=20.0 and (neo-Hookean limit). (Online version in colour.)

As already pointed out, the assumptions that the function 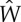is continuously differentiable and satisfies inequalities (2.16) are fundamental for proving the existence and uniqueness of the straightened configuration. We now show that, by means of slight changes, this result can be extended to Gent materials (3.5). For these materials, the function 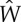reads

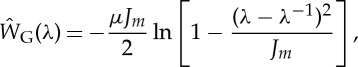3.15

and it is continuously differentiable in the interval , where

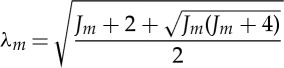3.16

is the upper bound on the stretch in (plane strain) uniaxial tension. Therefore, in order to straighten a circular cylindrical sector made of a Gent material, the circumferential stretch must belong to the interval 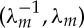throughout the thickness of the block. As a consequence of this restriction, if 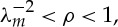then the condition 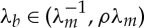implies that 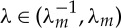throughout the block. On the other hand, as 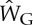satisfies the inequalities (2.16),

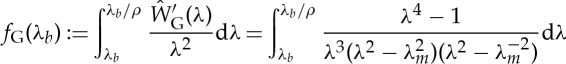3.17

is an increasing function such that

3.18

and, if 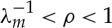, f_G(ρ)<0. We may then conclude that f_G has a unique zero at

3.19

It is worth noting that, in the light of (3.19), 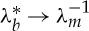as 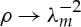(figure 2c).

(b). Straightening by vice-clamps

Now we investigate the existence of positive roots for λ_b in the interval (3.7) when M=0, that is

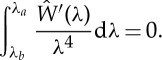3.20

Following arguments similar to those used in §3a, we introduce the function g(λ_b) defined by

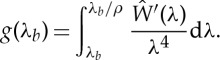3.21

By virtue of (2.16), we have

3.22

and by differentiation

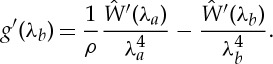3.23

which, in view of (2.16) and (3.6), is positive, implying that g is strictly increasing. Therefore, by virtue of (3.22), g has a unique zero, say 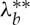, in the interval (ρ,1). Consequently, a circular cylindrical sector made of an incompressible isotropic elastic material can be straightened by applying a system of forces with zero resultant moment. By following the same arguments as in the previous section, one can prove that this result is valid not only for all the constitutive models with strain-energy functions 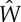continuously differentiable in and satisfying the inequalities (2.16), but also for Gent materials. The corresponding resultant normal force is

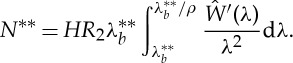3.24

For the neo-Hookean and Varga models, the explicit solutions of (3.20), which are illustrated in figure 3a, and the corresponding total normal force are, respectively,

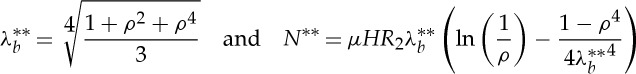3.25

and

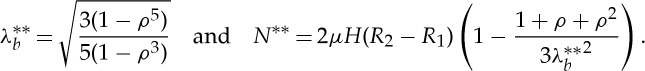3.26

For the Fung–Demiray and Gent materials, one can solve equation (3.20) only numerically. Figure 3b,c shows as a function of ρ for different values of the material parameters c and J_m.

Figure 3.

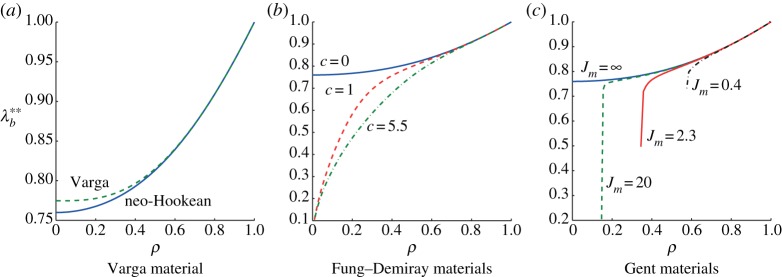
Circumferential stretch 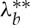as a function of the radii ratio ρ=R₁/R₂ for the straightening of blocks by vice-clamps: (a) Varga and neo-Hookean materials; (b) Fung–Demiray materials with stiffening parameters c=5.5, c=1.0 and (neo-Hookean limit) and (c) Gent materials with stiffening parameters J_m=0.4, J_m=2.3, J_m=20.0 and 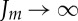(neo-Hookean limit). Note that different vertical scales are used in the three plots so as to avoid losing information. Thus, although not immediately apparent, the continuous curves in (a–c) are the same and are for the neo-Hookean model. (online version in colour.)

We end this section by pointing out that, independently of the form of the strain-energy function, we have

3.27

We have already shown that 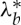and 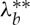belong to the interval (ρ,1). Furthermore, from (2.16), (3.9) and (3.21) we deduce that

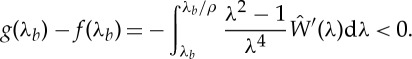3.28

Hence, as f and g are increasing in the interval (ρ,1), inequality (3.27) follows immediately.

(c). Thin sectors

For thin sectors, that is sectors with thickness much smaller than the radius of the (undeformed) inner face, some general conclusions can be established about the straightened configuration. For the asymptotic analysis, we introduce the small parameter ε>0 defined as

3.29

First we look at the straightening of a sector by the application of end couples, and we rewrite f in (3.9) as a function of ε, specifically

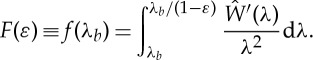3.30

Expanding F(ε) as a Maclaurin series in the parameter ε up to the fifth order, substituting into the equation f(λ_b)=0 and dropping a common factor ε, yields the equation

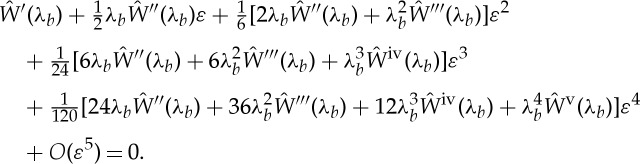3.31

Next, we expand λ_b in terms of ε to the fourth order

3.32

Substituting this into the previous expansion and equating to zero the coefficients of each power in the resulting expression, we obtain, at zero order

3.33

and hence, by (2.16), λ⁽⁰⁾=1. Using this result in the first-order term, we obtain

3.34

and because 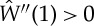, we deduce that 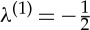. Then, the second-order term yields

3.35

The resulting expression for λ_b, to the second order in ε, is therefore

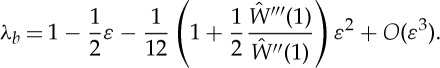3.36

However, for plane strain, there is the universal result 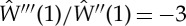(e.g. [13]), so that the above formula reduces to

3.37

Proceeding in a similar way (without showing the lengthy details), we obtain

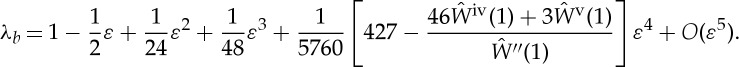3.38

Note, in particular, that the material properties do not enter until the fourth order, i.e. the results are independent of the form of strain-energy function up to order ε³.

Similarly, with an asymptotic analysis in the case of straightening by applying a resultant force only (M=0), we find that, for thin cylindrical sectors, the result analogous to (3.38) is

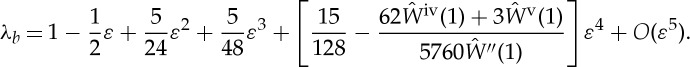3.39

The universal result used in (3.38) and (3.39) can be confirmed by, for example, expanding the strain-energy function in terms of the Green strain tensor E=(F^TF−I)/2 in the form

3.40

where μ, 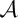and 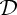are the second-, third- and fourth-order elastic constants, respectively (see Destrade & Ogden [14] and references therein). For the plane strain specialization, we have

3.41

and by computing the successive derivatives of 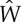we obtain

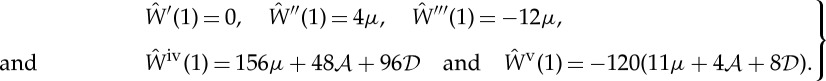3.42

Note that we established the last identity by expanding W to one order further than in (3.40) [15]. However, the next order terms do not contribute to the expression for .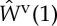

4. Incremental stability

We now study the stability of the deformed rectangular configuration by considering a superimposed incremental displacement u, with components (u₁,u₂,u₃). We denote the displacement gradient gradu by L, which has components L_ij=∂u_i/∂x_j. When linearized the incremental incompressibility condition reads

4.1

in the usual summation convention for indices, where a subscript i following a comma signifies differentiation with respect to x_i.

The corresponding linearized incremental nominal stress referred to the deformed configuration, denoted 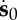, is given by [8]

4.2

where a superposed dot signifies an increment, the zero subscript indicates evaluation in the deformed configuration, I is the identity tensor and 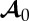is the fourth-order tensor of instantaneous elastic moduli. In components, this reads

4.3

where δ_ij is the Kronecker delta. Referred to the Eulerian principal axes of the underlying deformation, the only non-trivial components of 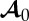are given by [8]

4.4

and

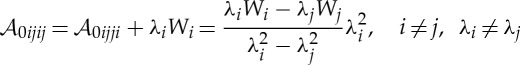4.5

with W_i=∂W/∂λ_i, W_ij=∂²W/∂λ_i∂λ_j, noting the major symmetry 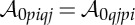. For λ_i=λ_j, the specializations of (4.5) can be obtained by taking the limit 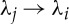but are not needed here.

For the neo-Hookean material (2.18), these reduce to

4.6

In the absence of body forces, the incremental equilibrium equation has the general form

4.7

but here we consider plane incremental deformations with u₃=0 and u₁ and u₂ independent of x₃, in which case the linearized incremental incompressibility condition becomes

4.8

Furthermore, as p and the deformation, and hence the components of 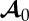, depend only on x₁, the components of equation (4.7) reduce to

4.9

Therefore, 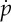is independent of x₃. From (4.2), the components of the incremental nominal stress 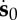appearing in (4.9) are

4.10

4.11

4.12

and

4.13

in the second of which we have used σ₁=0.

We seek solutions of the form

4.14

where n=kπA/Θ₀ is the mode number and the integer k is the number of wrinkles. Then, the components of incremental nominal stress (4.13) have a similar form, which we write as

4.15

with

4.16

4.17

4.18

and

4.19

and incremental incompressibility condition (4.8) yields

4.20

From (4.17), we obtain

4.21

where

4.22

On use of the above equations followed by elimination of S₂₁ and S₂₂ in favour of U₁, U₂, S₁₁ and S₁₂, incremental equilibrium equations (4.9) yield expressions for S′₁₁ and S₁₂′ in terms of U₁, U₂, S₁₁ and S₁₂.

Then, by introducing the four-component displacement–traction vector η=[U₁,U₂,iS₁₁,iS₁₂]^T, we can cast the governing equations in the Stroh form

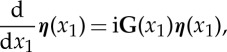4.23

where the real Stroh matrix G has the form

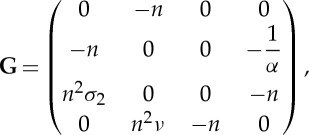4.24

with

4.25

We consider the incremental traction to vanish on the inner and outer faces, i.e.

4.26

If a solution of the incremental equations can be found subject to these boundary conditions, then possible equilibrium states exist in a neighbourhood of the straightened configuration, signalling the onset of instability of that configuration. The value of 1/(AR₂)=λ_b at this point is referred to as the critical value for the stretch and denoted by λ_cr. Then, from (2.4) it follows that

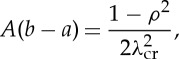4.27

which allows for the complete determination of the straightened geometry just prior to instability. In particular, the lengths of the block in the x₁ and x₂ directions are, respectively, given by

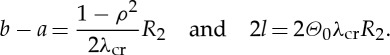4.28

Note that if 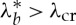, where 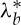is the unique positive solution of (3.8), then the cylindrical sector can be straightened by applying a moment alone without encountering any instability phenomenon. Similarly for a cylindrical sector straightened by vice-clamps, if 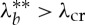(this case is illustrated in figure 4 for a neo-Hookean material).

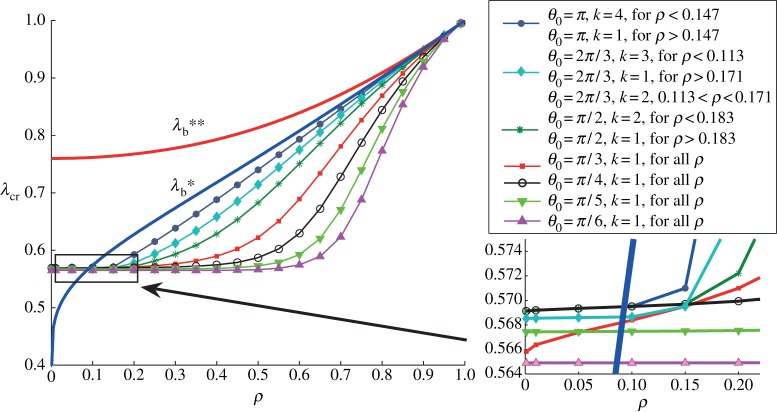
Figure 4.

Critical value of the stretch λ_cr as a function of the radii ratio ρ=R₁/R₂ for the straightening of a neo-Hookean material, for different angles Θ₀. (Online version in colour.)

5. Numerical results

In this section, we investigate the possibility of solving numerically the incremental instability problem. The Stroh form of the governing equations is numerically stiff and calls for the implementation of a robust algorithm. In the incremental stability literature, the compound matrix method has been used successfully to solve a variety of stiff problems, including eversion [16,17] and compression [18] of cylindrical tubes, bending [12,19,20] and combined bending and compression [21] of a straight block, bending of a sector [22], and pressurization of a spherical shell [23]. It turns out that for the problem considered here the compound matrix is itself singular, a feature that seems to be unique to the straightening stability problem. We manage to circumvent this problem by constructing a reduced, non-singular, compound matrix. We then use the impedance matrix method, which proves to be more precise numerically for this problem. It also provides for a complete field description of the incremental displacement solution.

(a). Compound matrix method

Let η⁽¹⁾(x₁), η⁽²⁾(x₁) be two linearly independent solutions of (4.23), and from them generate the six compound functions 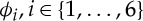, defined by

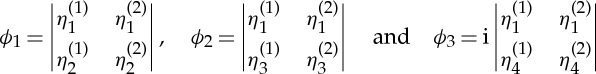5.1

and

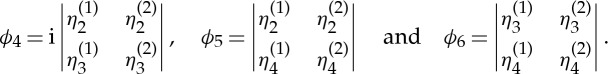5.2

Now, computing the derivatives of ϕ_i with respect to x₁ yields the so-called compound equations

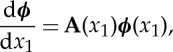5.3

where and A, the compound matrix, has the form

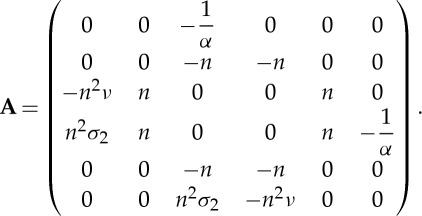5.4

Compound equations (5.3) must be integrated numerically, starting with the initial condition

5.5

and aiming at the target condition

5.6

according to (4.26).

However, we observe that , the first case in solid mechanics to our knowledge where a compound matrix is singular. Because of this situation, the numerical integration of Cauchy problem (5.3)–(5.5) will obviously encounter severe difficulties. In any event, the difficulty can be by-passed by noting that from (5.3) to (5.5) it follows that

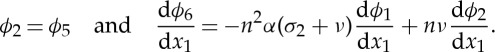5.7

It then follows that we can construct a reduced compound matrix by introducing five reduced compound functions 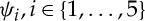, defined by

5.8

so that from (5.3) and (5.7)₂, the governing equations can be written as

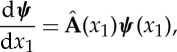5.9

where 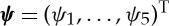and 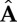has the form

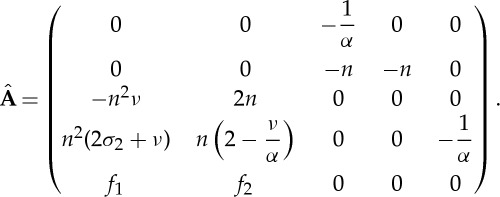5.10

Here,

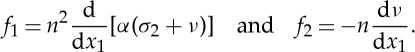5.11

It is easy to check that 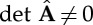. Hence, we may now integrate numerically the non-singular initial value problem (5.9) and (5.10) instead of the original compound equations with singular Jacobian. Finally, in view of (5.5) and (5.8), the initial condition for this system is

5.12

and in view of (5.6) and (5.8)₂, the target condition is

5.13

To implement the (reduced) compound matrix method, we first non-dimensionalized equations (5.9)–(5.12) and specialized them to the neo-Hookean model. Then we applied an initial value solver (ode45 or ode15s routines in Matlab), together with the dichotomy method in order to satisfy target condition (5.13).

This approach is a shooting-like technique for which convergence and stability can depend on the well- or ill-conditioning of the underlying boundary value problem and of the target root finder problem. The numerical drawbacks and challenges of the shooting techniques are highlighted in many textbooks (e.g. [24]).

In our case, for a set of fixed values of ρ=R₁/R₂∈(0,1), the bisection technique yields a sequence of values λ_j to approximate λ_cr and stops the iterations when: (a) the residual |F(λ_j)|=|ψ₅(b;λ_j)|≤tol_r and (b) the error estimate |λ_j−λ_j−1|≤tol_e. Both criteria must be used to check the goodness of the approximation. If the usual assumptions of the bisection method are satisfied on the starting localization interval I₀=[λ₀,λ₁] (that is F(λ₀)F(λ₁)<0) then the method will converge, i.e. by definition the criterion (b) will be always be satisfied. We set tol_e=10⁻¹² and tol_r=10⁻⁴, and included a control on the maximum number of iterations allowed (it_max=40). We applied the same shooting approach when using the compound matrix method and the impedance matrix method (next section). Both methods yielded the same results, although the former gave quite high residuals when k>2 and ρ is small. However, the values of λ_cr identified by the two methods were the same up to at least four significant digits even in the worst case of high residuals. For all intents and purposes, both the compound matrix and the impedance matrix methods provide the desired level of precision for the critical stretch of compression. The latter has the advantage of also providing a complete description of the incremental fields, as we now see.

(b). Impedance matrix method

Here, we follow Shuvalov [25] and introduce the matricant solution M(x₁,a) of (4.23) and (4.24) defined as the matrix such that

5.14

which has the following 2×2 block structure

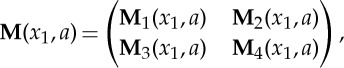5.15

I₍₄₎ being the fourth-order identity matrix.

We now use the incremental boundary condition S(a)=0 in (5.14) and (5.15) to establish that

5.16

is the conditional impedance matrix. Substituting this impedance matrix into the incremental equilibrium equations (4.23) and (4.24) gives

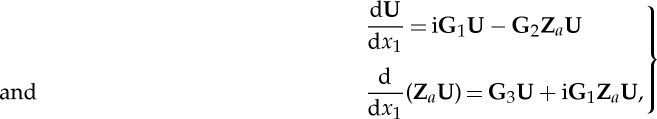5.17

where

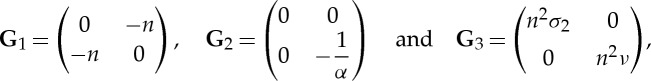5.18

are the 2×2 sub-blocks of G. Eliminating U between the two equations in (5.17) results in the following Riccati matrix differential equation for Z_a:

5.19

It is well behaved and can be integrated numerically in a robust way, subject to the initial condition,

5.20

which follows from (5.16)₂ and (5.14)₂. The target condition is

5.21

which is met by adjustment of the critical value λ_cr for the stretch λ_b, by using a bisection approach as described in §4a, with the same tolerance values for the stopping criteria. Then, S(b)=Z_a(b)U(b)=0 means that

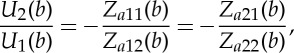5.22

and this ratio determines the form of the wrinkles on the outer face of the straightened block.

To proceed, we introduce the dimensionless quantities

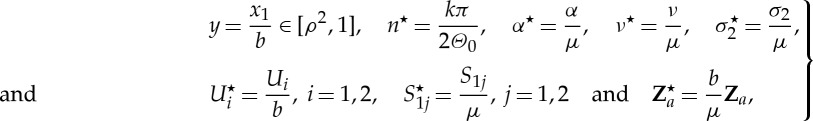5.23

where 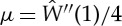is again the shear modulus in the reference configuration. Substitution of (5.23) into equations (4.23) and (4.24) yields

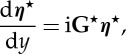5.24

with 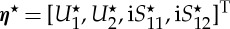and

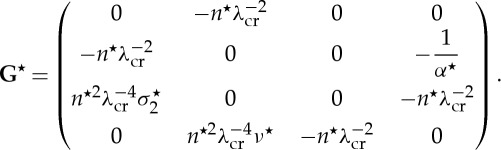5.25

The dimensionless version of the Riccati equation (5.19) is then

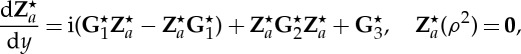5.26

where

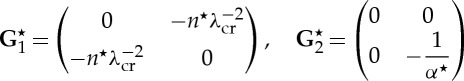5.27

and

5.28

The target condition to append to (5.26) for finding the critical stretch λ_cr is 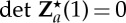. Finally, in order to determine the entire displacement field U throughout the straightened block once equation (5.26) is solved and the critical value λ_cr has been found, we integrate the equation

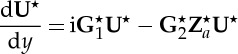5.29

numerically (again using the ode45 Matlab solver) from the initial conditions

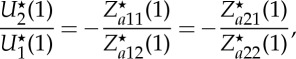5.30

at y=1 to the face at y=ρ².

(c). Neo-Hookean materials

For a neo-Hookean material with strain-energy function (2.18), we obtain the non-dimensional quantities

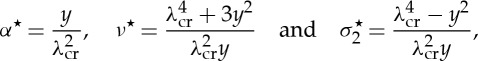5.31

which depend only on y and λ_cr.

In figure 4, we provide plots of the critical value λ_cr versus ρ=R₁/R₂ corresponding to loss of stability of some straightened sectors of neo-Hookean materials. We take in turn Θ₀=π,2π/3,π/2,π/3,π/4,π/5,π/6. The number of wrinkles k appearing on the compressed side of the block depends on the angle Θ₀ and on ρ. Hence, for Θ₀=π there are four wrinkles when ρ<0.1469 and only one when ρ>0.1469. For Θ₀=2π/3, there are three wrinkles when ρ<0.1131, two wrinkles when 0.1131<ρ<0.1717 and one wrinkle when ρ>0.1717. For Θ₀=π/2, there are two wrinkles when ρ<0.1833 and one wrinkle when ρ>0.1833. For all the other values of the opening angle, there is only one wrinkle for any value of ρ in (0,1). These results are summarized in the legend on the right of figure 4.

In the thick sector–small wavelength limit (i.e. as 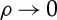and 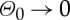), we recover the critical threshold for surface instability in plane strain of Biot [26] (i.e. ).

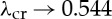We also plot the curves for 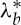and 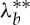, giving the circumferential stretch of a cylindrical sector straightened by end couples and by vice-clamps, respectively. We see that a sector straightened by applying a system of forces and no moment (vice-clamps) never buckles on its outer face because 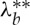is always greater than λ_cr. However, a sector straightened by moments alone and no normal forces (end couples) can buckle when ρ is smaller than 0.09 (see the zoom in figure 4). When ρ is greater than 0.09, a cylindrical sector straightened by end-couples does not present wrinkles on its outer face.

(d). Gent materials

To investigate the influence of material parameters on the behaviour of straightened blocks, we use the Gent model (3.5). For its non-dimensional quantities in the Riccati equation (5.26), we find

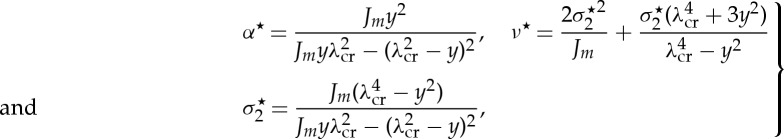5.32

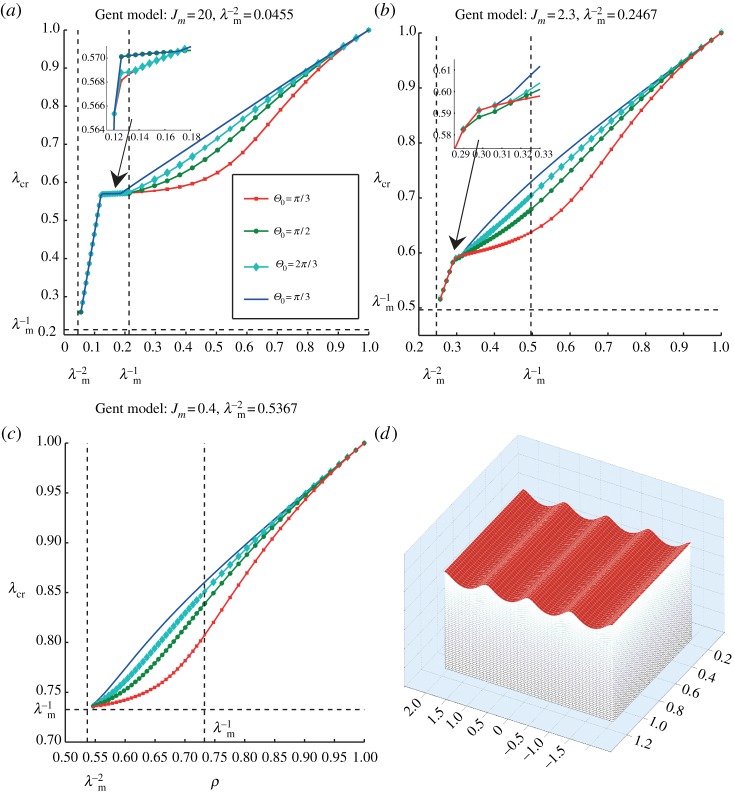
highlighting the role played by the stiffening parameter J_m; see the illustrations in figure 5.

Table 1.

Description of the results displayed in figure 5 for the bifurcation curves of straightened Gent materials. There are three different types of Gent materials (J_m=20, rubber; J_m=2.3, young artery; J_m=0.4, old artery) and four different angles (Θ₀=π/3,π/2,2π/3,π). Each curve is made of several pieces, each corresponding to the earliest bifurcation mode for a given value of ρ of the sector, with corresponding number of wrinkles k in the third column.

Jm	angle	number of wrinkles
20	Θ0=π/3	k=1 for 0.045<ρ≤1
20	Θ0=π/2	k=1 for 0.045<ρ<0.11 and 0.21<ρ≤1
		k=2 for 0.11<ρ<0.21
20	Θ0=2π/3	k=1 for 0.045<ρ<0.11 and 0.21<ρ≤1
		k=2 for 0.11<ρ<0.12 and 0.13<ρ<0.21
		k=3 for 0.12<ρ<0.13
20	Θ0=π	k=1 for 0.045<ρ<0.10 and 0.19<ρ≤1
		k=2 for 0.10<ρ<0.11
		k=3 for 0.11<ρ<0.12 and 0.17<ρ<0.19
		k=4 for 0.12<ρ<0.17
2.3	Θ0=π/3	k=1 for 0.25<ρ≤1
2.3	Θ0=π/2	k=1 for 0.25<ρ<0.28 and 0.30<ρ≤1
2.3	Θ0=2π/3	k=1 for 0.25<ρ<0.28 and 0.31<ρ≤1
		k=2 for 0.28<ρ<0.31
2.3	Θ0=π	k=1 for 0.25<ρ<0.27 and 0.31<ρ≤1
		k=2 for 0.27<ρ<0.28
		k=3 for 0.28<ρ<0.31
0.4	Θ0=π/3	k=1 for 0.54<ρ≤1
0.4	Θ0=π/2	k=1 for 0.54<ρ≤1
0.4	Θ0=2π/3	k=1 for 0.54<ρ≤1
0.4	Θ0=π	k=1 for 0.54<ρ≤1

Figure 5.

Instability of a straightened homogeneous circular cylindrical sector modelled by the Gent strain-energy function. (a–c) The critical stretch λ_cr for wrinkling versus the radii ratio ρ=R₁/R₂ for different open angles Θ₀, in the cases where the Gent stiffening parameter is (a) J_m=20 (rubber), (b) J_m=2.3 (old aorta) and (c) J_m=0.4 (young aorta). As summarized in table 1, the number of wrinkles k depends on the constitutive parameter J_m, on the angle Θ₀ and ρ. For instance, for J_m=20, Θ₀=π and ρ=0.15, the number of wrinkles is k=4; see (a) and (d). (Online version in colour.)

As a circular cylindrical sector made of a Gent material can be straightened provided that 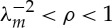and the circumferential stretch on the outer face λ_b belongs to the interval 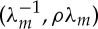, as indicated in §3a, λ_cr tends to as 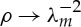. Consequently, when J_m is large enough but finite, the marginal stability curves for Gent and neo-Hookean materials are qualitatively similar in the interval 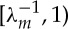, whereas they differ in the range 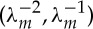; compare, for instance, figure 5a with figure 4. As 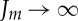, the behaviour of neo-Hookean material is recovered.

Finally, we integrated (5.29) for a case in which four wrinkles appear on the straightened face to generate the entire incremental displacement field (up to an arbitrary multiplicative factor), as illustrated in figure 5d.

Funding statement

Partial funding from the Royal Society of London (International Joint Project grant for M.D., R.W.O. and L.V.), from the Istituto Nazionale di Alta Matematica (Marie Curie COFUND Fellowship for L.V.; GNCS Visiting Professor Scheme for M.D. and I.S.) and from the Ministero dell'Istruzione, dell'Università della Ricerca (PRIN-2009 project Matematica e meccanica dei sistemi biologici e dei tessuti molli for I.S.) is gratefully acknowledged.