BOOTSTRAP INFERENCE FOR NETWORK CONSTRUCTION WITH AN APPLICATION TO A BREAST CANCER MICROARRAY STUDY

Abstract

Gaussian Graphical Models (GGMs) have been used to construct genetic regulatory networks where regularization techniques are widely used since the network inference usually falls into a high–dimension–low–sample–size scenario. Yet, finding the right amount of regularization can be challenging, especially in an unsupervised setting where traditional methods such as BIC or cross-validation often do not work well. In this paper, we propose a new method — Bootstrap Inference for Network COnstruction (BINCO) — to infer networks by directly controlling the false discovery rates (FDRs) of the selected edges. This method fits a mixture model for the distribution of edge selection frequencies to estimate the FDRs, where the selection frequencies are calculated via model aggregation. This method is applicable to a wide range of applications beyond network construction. When we applied our proposed method to building a gene regulatory network with microarray expression breast cancer data, we were able to identify high-confidence edges and well-connected hub genes that could potentially play important roles in understanding the underlying biological processes of breast cancer.

1. Introduction

The emergence of high-throughput technologies has made it feasible to measure molecular signatures of thousands of genes/proteins simultaneously. This provides scientists an opportunity to study the global genetic regulatory networks, shedding light on the functional interconnections among the regulatory genes, and leading to a better understanding of underlying biological processes. In this paper, we propose a network building procedure for learning genetic regulatory networks. Our work is motivated by an expression study of breast cancer (BC) that aims to infer the network structure based on 414 BC tumor samples (Loi et al., 2007). The proposed method enables us to detect high-confidence edges and well-connected hub genes that include both those previously implicated in BC and novel ones that may warrant further follow-up.

In practice, dependency structures of molecular activities such as correlation matrix and partial correlation matrix have been used to infer regulatory networks, (Pollack et al., 2002; Kim et al., 2006; Varambally et al., 2005; Nie et al., 2006). Such dependency structures are often represented by graphical models in which nodes of a graph represent biological components such as genes or proteins, and the edges represent their interactions. These interactions may be indirect (e.g., two genes are co-regulated by a third gene), or direct (e.g., one gene is regulated by another gene). For the latter case, Gaussian Graphical Models (GGMs), which represent dependencies between pairs of nodes conditioning on the remaining of nodes, are often used.

For the data obtained from high-throughput technologies, the number of nodes is typically much larger than the number of samples, which is where the classical GGM theory (Whittaker, 1990) generally fails (Friedman, 1989; Schäfer and Strimmer, 2005). This large-p-small-n scenario is usually addressed by assuming that the conditional dependency structure is sparse (Dobra et al., 2004; Li and Gui, 2006; Meinshausen and Bühlmann, 2006; Yuan and Lin, 2007; Friedman et al., 2007; Rothman et al., 2008; Peng et al., 2009). However, like many high-dimensional regularization problems, finding the appropriate level of sparsity remains a challenge. This is particularly true for network structure learning, since the problem is unsupervised in nature. Traditional methods, such as Bayes information criteria (Schwarz, 1978) and cross-validation, aim to find a model that minimizes prediction error or maximizes a targeted likelihood function. They tend to include many irrelevant features (e.g., Efron, 2004b; Efron et al., 2004, Meinshausen and Bühlmann, 2006 and Peng et al., 2010), and thus are not appropriate for learning the interaction structures.

Choosing the amount of regularization by directly controlling the false positive level would be ideal for structure learning. Recently, a few model aggregation methods have been proposed, and some of them provide certain control of false positives. For example, Bach (2008) proposed Bolasso, which chooses variables that are selected by all the lasso models (Tibshirani, 1996) built on bootstrapped datasets. In the context of network reconstruction, Peng et al. (2010) proposed choosing edges that are consistently selected across at least half of the cross-validation folds. More recently, Meinshausen and Bühlmann (2010) proposed the stability selection procedure to choose variables with selection frequencies exceeding a threshold. Under suitable conditions, they derived an upper bound for the expected number of false positives. In the same paper, they also proposed the randomized lasso penalty, which aggregates models from perturbing the regularization parameters. Combined with stability selection, randomized lasso achieves model selection consistency without requiring the irrepresentable condition (Zhao and Yu, 2006) that is necessary for lasso to achieve model selection consistency. In another work, Wang et al. (2011) proposed a modified lasso regression — random lasso — by aggregating models based on bootstrap samples and random subsets of variables. All these works have greatly advanced research in model selection in the high-dimensional regime. However, none of these methods provide direct estimation and control of the false discovery rate (FDR).

In this paper, we address the problem of finding the right amount of regularization in the context of high-dimension GGMs learning. In a spirit similar to the aforementioned methods, we first obtain selection frequencies from a collection of models built by perturbing both the data and the regularization parameters. We then model these selection frequencies by a mixture distribution to yield an estimate of FDR on the selected edges, which is then used to determine the cut-off threshold for the selection frequencies. This framework is rather general, as it only depends on the empirical distribution of the selection frequencies. Thus, it can be applied to a wide range of problems beyond GGMs.

The rest of this paper is organized as follows. In Section 2, we describe in detail the proposed method. In Section 3, an extensive simulation study is conducted to compare the method with the stability selection procedure and then evaluate its performance under different settings. In Section 4, the method is illustrated by building a genetic interaction network based on microarray expression data from BC study. The paper is concluded with some discussion in Section 5.

2. Method

2.1. Gaussian Graphical Models

In a Gaussian Graphical Model (GGM), network construction is defined by the conditional dependence relationships among the random variables. Let Y = (Y₁,…,Y_p) denote a p-dimension random vector following a multivariate normal distribution N(0, Σ), where Σ is a p × p positive definite matrix. The conditional dependence structure among Y is represented by an undirected graph G = (U, E) with vertices U = {1,2,…,p} representing Y₁,…,Y_p and the edge set E defined as

$$E=\{(i,j):Y_i\text{ and }{Y}_j\text{ are dependent given }{Y}_{-\{i,j\}},1\le i,j\le p\},$$

where Y_−{i,j} ≡ {Y_k : k ≠ i,j, 1 ≤ k ≤ p}. The goal of network construction is to identify the edge set E. Under normality assumption, the conditional independence between Y_i and Y_j is equivalent to the partial correlation ρ_ij between Y_i and Y_j given Y_−{i,j} being zero. It is also equivalent to the (i,j) entry of the concentration matrix (Σ⁻¹) being zero, i.e., σ_ij ≡ (Σ⁻¹)_ij = 0 (Dempster, 1972; Cox and Wermuth, 1996), since ${\rho }_{\text{ij}}=-\frac{{\sigma }_{\text{ij}}}{\sqrt{{\sigma }_{\text{ii}}{\sigma }_{\text{jj}}}}$.

There are two main types of approaches to fitting a GGM. One is the maximum-likelihood-based approach which estimates the concentration matrix directly. The other is the regression-based approach, which fits the GGM through identifying nonzero regression coefficients of the following regression

$$\begin{array}{cc}{Y}_i={\displaystyle \sum }_{j\ne i}{\beta }_{\text{ij}}{Y}_j+{∊}_i,& 1\le i\le p,\end{array}$$

where ∊_i is uncorrelated with Y_−i = {Y_k, k ≠ i, 1 ≤ k ≤ p}. The nonzero β_ij’s in the above regression setting correspond to nonzero entries in the concentration matrix since it can be shown that ${\beta }_{\text{ij}}=-{\sigma }_{\text{ij}}/{\sigma }_{\text{ii}}={\rho }_{\text{ij}}\sqrt{{\sigma }_{\text{jj}}/{\sigma }_{\text{ii}}}$. In both approaches, there are O(p²) parameters to estimate, which requires proper regularization on the model if p is larger than the sample size n. This can be achieved by making a sparsity assumption on the network structure, i.e., assuming that most pairs of variables are conditionally independent given all other variables. Such an assumption is reasonable for many real life networks, including genetic regulatory networks (Gardner et al. 2003; Jeong et al. 2001; Tegner et al. 2003). Methods have been developed along these lines by using L₁ regularization. For example, Yuan and Lin (2007) proposed a sparse estimator of the concentration matrix via maximizing the L₁ penalized log-likelihood. Efficient algorithms were subsequently developed to fit this model with high dimensional data (Friedman et al., 2007; Rothman et al., 2008). For regression-based approaches, Meinshausen and Bühlmann (2006) considered the neighborhood selection estimator by minimizing p individual loss functions

$$L^{(i)}(\beta ,Y)=\frac{1}{2}{\Vert Y_i-{\displaystyle \sum _{j:j\ne i}{\beta }_{\text{ij}}{Y}_j}\Vert }^2+\text{λ}{\displaystyle \sum _{j:j\ne i}|{\beta }_{\text{ij}}|,i=1,\dots ,p,}$$ (2.1)

while Peng et al. (2009) proposed the space algorithm by minimizing the joint loss

$$L(Y,\theta )=\frac{1}{2}\{{\displaystyle \sum _{i=1}^p{\Vert Y_i-{\displaystyle \sum _{j:j\ne i}\sqrt{\frac{{\sigma }_{\text{jj}}}{{\sigma }_{\text{ii}}}}{\rho }_{\text{ij}}{Y}_j}\Vert }^2\}+\text{λ}{\displaystyle \sum _{1\le i<j\le p}|{\rho }_{\text{ij}}|}}.$$ (2.2)

From objective functions (2.1) and (2.2), it is clear that the selected edge set depends on the regularization parameter λ. Since the goal here is to recover the true edge set, ideally λ should be determined based on considerations such as FDR and power with respect to edge selection. Moreover, when the sample size is limited, a model-aggregation-based strategy can improve the selection result compared to simply tuning the regularization parameter. Thus, in the following section, we introduce a new model-aggregation-based procedure that selects edges based on directly controlling the FDRs.

Throughout the rest of this paper, we refer to the set of all pairs of variables as the candidate edge set (denoted by Ω), the subset of those edges in the true model as the true edge set (denoted by E) and the rest as the null edge set (denoted by E^c). We denote the size of a set of edges by | · |. Note that Ω = E ∪ E^c and the total number of edges in Ω is N_Ω = |Ω| = p(p − 1)/2.

2.2. Model Aggregation

Consider a good network construction procedure, where good is in the sense that the true edges are stochastically more likely to be selected than the null edges. Then it would be reasonable to choose edges with high selection probabilities. In practice, these selection probabilities can be estimated by the selection frequencies over networks constructed based on perturbed data sets. In the following, we formalize this idea.

Let A(λ) be an edge selection procedure with a regularization parameter λ and S^λ(Y) ≡ S^λ(A(λ), Y) be the set of selected edges by applying A(λ) to data Y. The selection probability of edge (i,j) is defined as

$$p_{\text{ij}}=E(I\{(i,j)S^{\text{λ}}(Y)\}),$$

where I{·} is the indicator function. Let R(Y) be the space of resamples from Y (e.g., through bootstrapping or subsampling). For a random resample Y′ from R(Y), we define

$${\stackrel{\sim }{p}}_{\text{ij}}=E(I\{(i,j)\in S^{\text{λ}}(Y^{\prime })\})=E\left(E\right(I\{(i,j)\in S^{\text{λ}}(Y^{\prime })\}|Y)).$$

In many cases (see Section C in the supplemental article [Li (2012)]), p_ij’s and p̃_ij’s are close. For these cases, we can estimate p_ij by the selection frequency X_ij, which is the proportion of B resamples in which the edge (i,j) is selected:

$$X_{\text{ij}}^{\text{λ}}\equiv X_{\text{ij}}(A(\text{λ});Y^1,\dots ,Y^B\in R(Y))=\frac{1}{B}{\displaystyle \sum }_{k=1}^{B}I\{(i,j)\in S^{\text{λ}}(Y^k)\},1\le i<j\le p.$$ (2.3)

The aggregation-based procedures for choosing edges of large selection frequencies can be represented as:

$$\begin{array}{cc}{S}_c^{\text{λ}}=\{(i,j):X_{\text{ij}}^{\text{λ}}\ge c\},& \text{for }c\in (0,1]\end{array}.$$

$S_c^{\text{λ}}$ is reasonable as long as most true edges have selection frequencies greater than or equal to c and most null edges have selection frequencies less than c. Ideally we want to find a threshold c satisfying

$$\text{Pr}\left(\right\{\underset{(i,j)\in E}{\cap }\{X_{\text{ij}}^{\text{λ}}\ge c\}\}\cap \{\underset{(i,j)\in E^c}{\cap }\{X_{\text{ij}}^{\text{λ}}<c\}\left\}\right)\to 1\text{ as }n\to \infty ,$$ (2.4)

so that the corresponding procedure $S_c^{\text{λ}}$ is consistent, i.e., $\text{Pr}(S_c^{\text{λ}}=E)\to 1$. In fact, if A(λ) is selection consistent and $p_{\text{ij}}-{\stackrel{\sim }{p}}_{\text{ij}}\to 0$, then

$$\text{Pr}\left(\right\{\underset{(i,j)\in E}{\cap }\{X_{\text{ij}}^{\text{λ}}=c\}\}\cap \{\underset{(i,j)\in E^c}{\cap }\{X_{\text{ij}}^{\text{λ}}<c\}\left\}\right)\to 1\text{ as }n\to \infty ,$$ (2.5)

and thus any c ∈ (0,1] satisfies (2.4). Note that (2.4) is in general a much weaker condition than (2.5), which suggests that we might find a consistent $S_c^{\text{λ}}$ even when A(λ) is not consistent.

For the finite data case, an aggregation-based procedure could also perform better than the original procedure, as illustrated by the following simulation example (the simulation setup is provided in Section 3). Fig 1(a) shows the empirical distribution of selection frequencies based on a simulated data set and Fig 1(b) shows the empirical distributions of true edges (green triangles) and null edges (red crosses). Note that most null edges have low selection frequencies < 0.4 while most true edges have large selection frequencies > 0.6. This suggests that with a properly chosen c (say, c ∈ [0.4, 0.6]), $S_c^{\text{λ}}$ will select mostly true edges and only a small number of null edges. In fact, by simply choosing the cutoff c = 0.5, $S_c^{\text{λ}}$ outperforms A(λ) in both FDR and power (Fig 2).

Fig 1.

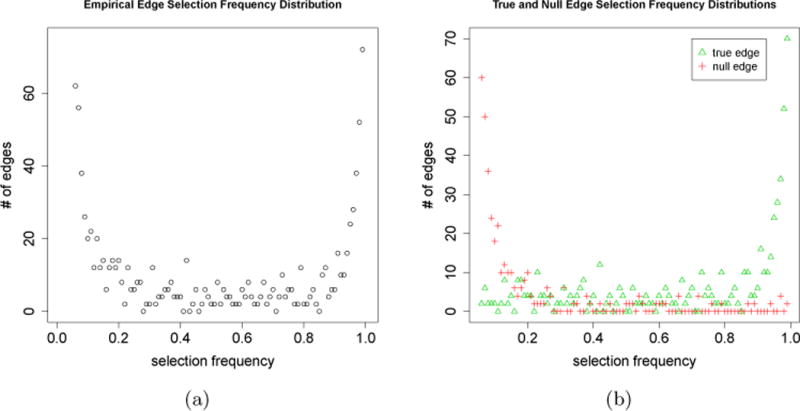
The distributions of selection frequencies based on a simulated dataset. (a) The distribution of selection frequencies of all edges. (b) Distributions of selection frequencies of null and true edges, respectively (note that, these are not observable in practice). Simulation is based on a power-law network with p=500, n=200, and the number of true edges is 495. The space algorithm with λ=135 is used as the original non-aggregation procedure A(λ). For illustrating the tail behavior of these distributions more effectively, we only show them on the selection frequency range [0.06,1], as there are too many edges with selection frequency less than 0.06.

Fig 2.

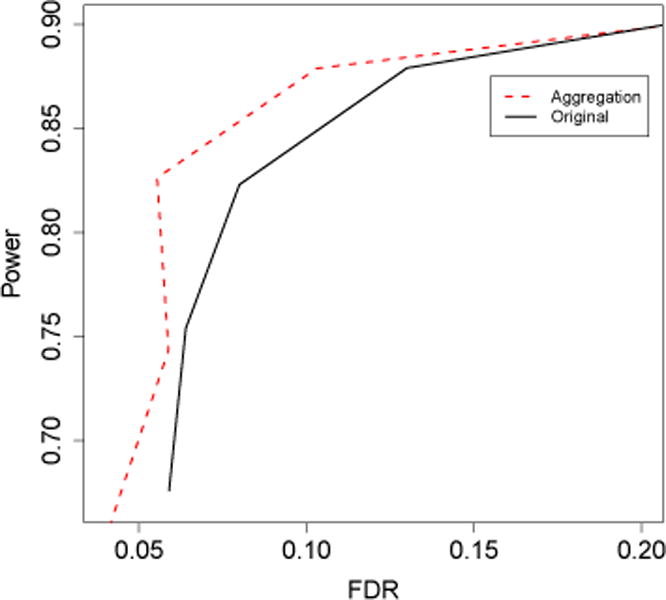
Power and FDR of the aggregation-based procedure $S_c^{\text{λ}}$ with cutoff c = 0.5 and the original procedure A(λ) for λ = 96, 114, 135, 160, with the rest of settings the same as in Fig 1.

2.3. Modeling Selection Frequency

Now we introduce a mixture model, similar in spirit to Efron (2004a), for estimating the FDR of an aggregation-based procedure $S_c^{\text{λ}}$. We will use this estimate to choose the optimal c and λ by controlling FDR while maximizing power. Assume that the selection frequencies $\{X_{\text{ij}}^{\text{λ}},(i,j)\in \Omega \}$, generated from B resamples, fall into two categories: “true” or “null”, depending on whether (i,j) is a true edge or a null edge. Let π be the proportion of the true edges. We also assume that $X_{\text{ij}}^{\text{λ}}$ has density $f_1^{\text{λ}}(x)$ or $f_0^{\text{λ}}(x)$ if it belongs to the “true” or the “null” categories, respectively. Note that both $f_1^{\text{λ}}$ and $f_0^{\text{λ}}$ depend on the sample size n but such dependence is not explicitly expressed in order to keep the notation simple. The mixture density for $X_{\text{ij}}^{\text{λ}}$ can be written as:

$$\begin{array}{cc}{f}^{\text{λ}}(x)=(1-\pi )f_0^{\text{λ}}(x)+\pi f_1^{\text{λ}}(x),& x\in \{0,1/B,2/B,\dots ,1\}\end{array}.$$ (2.6)

Based on this mixture model, the (positive) FDR (Storey, 2003) of the aggregation-based procedure $S_c^{\text{λ}}$ is

$$\text{FDR}(S_c^{\text{λ}})=\text{Pr}((i,j)\in E^c|(i,j)\in S_c^{\text{λ}})=\frac{{\displaystyle {\sum }_{x\ge c}(1-\pi )f_0^{\text{λ}}(x)}}{{\displaystyle {\sum }_{x\ge c}{f}^{\text{λ}}(x)}}.$$ (2.7)

Given an estimate $\widehat{\text{FDR}}(S_c^{\text{λ}})$ (which will be discussed below) from (2.7), the number of true edges in $S_c^{\text{λ}}$ can be estimated by

$$\widehat{N_E}(S_c^{\text{λ}})=|S_c^{\text{λ}}|(1-\widehat{\text{FDR}}(S_c^{\text{λ}})),$$ (2.8)

which can be used to compare the power of $S_c^{\text{λ}}$ across various choices of c and λ, as the total number of true edges is a constant. Consequently, for a given targeted FDR level α, we first seek for the optimal threshold c for each λ ∈ Λ:

$$c\ast (\text{λ})=\min \{c:\widehat{\text{FDR}}(S_c^{\text{λ}})\le \alpha \},$$ (2.9)

and then we find the optimal regularization parameter

$$\lambda \ast ={\text{argmax}}_{\lambda \in \Lambda }\widehat{N_E}(S_{c\ast (\lambda )}^{\lambda })$$ (2.10)

such that the corresponding procedure $S_{c\ast (\text{λ}\ast )}^{\text{λ}\ast }$ achieves the largest power among all competitors with estimated FDR not exceeding α.

The above procedure depends on a good FDR estimate, which in turn requires good estimates of the mixture density f^λ and its null-edge contribution $(1-\pi )f_0^{\text{λ}}$. A natural estimator of $f^{\text{λ}}$ is simply the empirical selection frequencies, i.e.,

$$\begin{array}{cc}{\widehat{f}}^{\text{λ}}\left(\frac{k}{B}\right)=\frac{n_k^{\text{λ}}}{N_{\Omega }},& k=0,1,\dots ,B\end{array},$$

where N_Ω = p(p − 1)/2 is the total number of candidate edges and $n_k^{\text{λ}}=|\{(i,j):X_{\text{ij}}^{\text{λ}}=k/B\}|$ is the number of edges with selection frequencies equal to k/B.

Before describing an approach to estimating π and $f_0^{\text{λ}}$, we note two observations from Fig 1(b). First, the contribution from the true edges to the mixture density f^λ is small in the range where the selection frequencies are small. Second, the empirical distribution of $f_0^{\text{λ}}$ is monotonically decreasing. These can be formally summarized as the following condition.

• Proper Condition: There exist V₁ and V₂, 0 < V₁ < V₂ < 1, such that as n → ∞,

• C1: $f_1^{\text{λ}}\to 0$ on (V₁, V₂];

• C2: $f_0^{\text{λ}}$ is monotonically decreasing on (V₁, 1].

This proper condition is satisfied by a class of procedures as described in the lemma below (the proof is provided in the Appendix).

Lemma 1

A selection procedure satisfies the proper condition if, as the sample size increases, p̃_ij tends to one uniformly for all true edges and has a limit superior strictly less than one for all null edges.

Remark 1

It is easy to verify that all consistent procedures applied to subsampling resamples satisfy the condition in Lemma 1. Other examples are procedures that use randomized lasso penalties (Meinshausen and Bühlmann, 2010). See Section 2.5 for more details.

The proper condition motivates us to estimate π and $f_0^{\text{λ}}$ by fitting a parametric model g_θ for f^λ in the region (V₁, V₂] and then extrapolating the fit to the region (V₂, 1]. This is because if C1 is satisfied then $(1-\pi )f_0^{\text{λ}}$ can be well approximated based on the empirical mixture density from the region (V₁, V₂]. If C2 is also satisfied, the extrapolation of g_θ will be a good approximation to $(1-\pi )f_0^{\text{λ}}$ on (V₂, 1] for a reasonably chosen family of g_θ.

We choose the parametric family as follows. Given p̃_ij, it is natural to model the selection frequency by a (rescaled) binomial distribution, denoted by b₁(·|p̃_ij), due to the independent and identical nature of resampling conditional on the original data. Moreover, we use a powered beta distribution (i.e., the distribution of Q^γ where Q ~ beta(a, b), a, b, r > 0) as the prior for p̃_ij’s, denoted by b₂(·|θ) with θ = (a, b, r). This is motivated by the fact that the beta family is a commonly used conjugate prior for the binomial family, and the additional power parameter γ simply provides more flexibility in fitting. Thus, the distribution of selection frequencies of null edges is modeled as

$$h_{\theta }(x)=\underset{0}{\overset{1}{\int }}{b}_1(x|\tau )b_2(\tau |\theta )d\tau .$$

The null-edge contribution $(1-\pi )f_0^{\text{λ}}$ can be estimated by fitting h_θ to the empirical mixture density f̂^λ in the fitting range (V₁, V₂], which, in practice, is determined based on the shape of f̂^λ (details are given in Section 2.4). Specifically, we estimate π and $f_0^{\text{λ}}$ by π̂ and h_θ̂, via

$$(\widehat{\pi },\widehat{\theta })={\text{argmin}}_{\pi ,\theta }L({\widehat{f}}^{\text{λ}}(·),(1-\pi )h_{\theta }(·)),$$ (2.11)

where L(f, g) ≡ − Σ_x∈(V1,V2][f(x) log g(x)], which amounts to the Kullback-Leibler distance.

2.4. Proper Regularization Range

Following what we propose in Section 2.3, we can evaluate the aggregation-based procedure $S_c^{\text{λ}}$ for different choices of (λ, c) with regard to model–selection–based criteria: the FDR and the number of selected true edges. For the range of λ, we consider those that yield “U-shaped” empirical distributions of selection frequencies, that is, f̂^λ decreases in the small-selection-frequency range and then increases in the large-selection-frequency range (see Fig 1(a) and Fig 3 for examples of “U-shaped” distribution). The decreasing trend is needed for the proper condition to hold while the increasing trend helps to control the FDR, since an $S_c^{\text{λ}}$ with FDR≤ α implies, by (2.7), that

$$\sum _{x\ge c}{f}^{\text{λ}}(x)\ge \frac{(1-\pi )\sum _{x\ge c}{f}_0^{\text{λ}}(x)}{\alpha }.$$ (2.12)

Therefore, if f̂^λ is not sufficiently large at the tail, FDR≤ α may not be achieved for a small value of α. The increasing trend also helps to obtain decent power since it guarantees a substantial size of $S_c^{\text{λ}}$. Based on our experience, the λ values chosen based on (2.9) and (2.10) indeed always corresponds to a “U-shaped” empirical selection frequency distribution.

Fig 3.

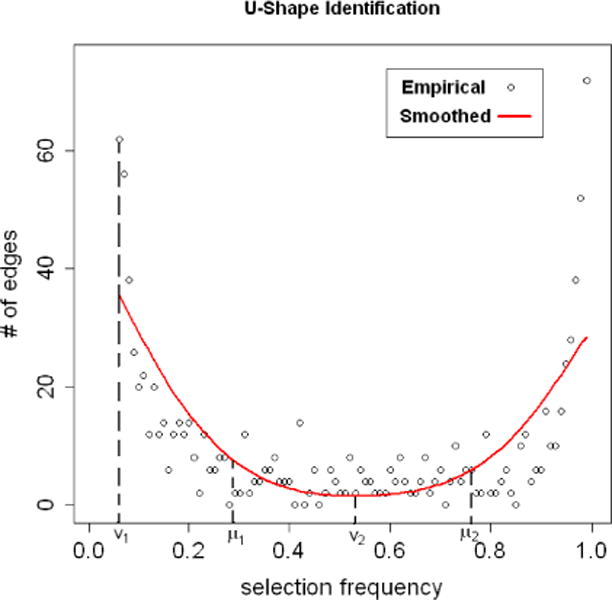
An illustration for the proposed U-shape identification procedure. The empirical distribution (f̂^λ) is the same as the one in Fig 1. The smooth curve (f̃^λ) is fitted by the R-function smooth.spline with df = 4. Locations of v₁, v₂, μ₁ and μ₂ are found by following steps in the U-shape detection procedure.

Thus, we propose the following simple procedure for identifying “U-shaped” f̂^λ’s to determine the proper regularization range in practice. An illustration for this procedure is given in Fig 3.

U-shape Detection Procedure
1.	INPUT f̂λ, the empirical density of selection frequencies. Set U = 1 (the U-shape indicator).
2.	Check U-shape.
	2.1.	Check valley point.
		2.1.1.	Calculate v2 = argminx f̂λ(x), the valley point position, where f̂λ is a smooth curve fitted based on f̂λ. (We use the R-function smooth.spline(), where the degree of freedom parameter is determined such that the derivative of f̂λ has only one sign change.)
		2.1.2.	IF v2 > 0.8
			Set U = 0, GOTO Step 3.
			END IF
	2.2	Calculate v1 = argmaxx<v2 f̂λ(x), the peak before v2.
	2.3.	Check if f̂λ is “roughly” decreasing on (v1, v2].
		2.3.1.	Calculate μ1 = (v1 + v2)/2, s1 = Σx∈[v1, μ1] f̂λ(x) and s2 = Σx∈[μ1, v2] f̂λ(x).
		2.3.2.	IF s1 < s2
			Set U = 0, GOTO Step 3.
			END IF
	2.4.	Check if f̂λ is “roughly” increasing on (v2,1].
		2.4.1	Calculate μ2 = (v2 + 1)/2, s3 = Σx∈[v2, μ2] f̂λ(x) and s4 = Σx∈[μ2, 1] f̂λ(x).
		2.4.2.	IF s3 > s4
			Set U = 0, GOTO Step 3.
			END IF
3.	RETURN v1, v2, U.

Remark 2

Step 2.1 is based on our extensive simulation where we find that a large value of v₂ often corresponds to a too-small λ, yielding too many null edges with high selection frequencies, which makes (2.12) difficult to hold for reasonably small FDR levels α (see Section D1 in the supplemental article [Li (2012)]). If f̂^λ is not recognized as “U-shaped” for a large range of λ’s, we would consider the data as lack of signals where a powerful $S_c^{\text{λ}}$ is not attainable. One example is the empty network (see Section 3.2 and Fig S-1 in the supplemental article [Li (2012)]).

Sections 2.2–2.4 provide a procedure for network inference based on directly estimating FDR. We name the procedure as BINCO — Bootstrap Inference for Network COnstruction, as we suggest to use bootstrap resamples. The main steps are summarized below.

BINCO Procedure
1.	INPUT Λ = (λ1,…, λk) the initial range of regularization parameter values; Yn×p the dataset; and α the desired FDR level.
2.	FOR i = 1 TO k
	2.1.	λ = λi
	2.2.	Generate f̂λ the empirical density of selection frequencies.
	2.3.	Check whether f̂λ is U-shaped based on the output (v1, v2, U) from the “U-Shape Detection Procedure”.
	2.4.	IF f̂λ is U-shaped (i.e., U = 1)
		2.4.1.	Obtain the null density estimate by (2.11).
		2.4.2.	Find the optimal threshold c* (λ) by (2.9), where the FDR is estimated based on (2.7) with fλ and replaced by f̂λ and , respectively.
		2.4.3.	Obtain and calculate , the estimated number of true edges being selected, based on (2.8).
		END IF
		ELSE , .
	2.5.	OUTPUT and .
	NEXT i
3.	Determine the optimal regularization λ* through (2.10). The optimal selection is .

2.5. Randomized Lasso

For an L₁ regularized procedure A(λ), the proper condition (Section 2.3) is satisfied if A(λ) is selection consistent, which usually requires strong conditions. For instance, the well-known irrepresentable condition under lasso regression setting (Zhao and Yu, 2006; Zou, 2006; Yuan and Lin, 2007; Wainwright 2009) or the so-called neighborhood stability condition under GGM setting (Meinshausen and Bühlmann, 2006; Peng et al., 2009). Recently, Meinshausen and Bühlmann (2010) proposed the randomized lasso which is a procedure based on randomly sampled regularization parameters. For example, the randomized lasso version of space would be

$$L(Y,\theta ,W)=\frac{1}{2}\{\sum _{i=1}^p{\Vert Y_i-\sum _{j:j\ne i}\sqrt{\frac{{\sigma }_{\text{jj}}}{{\sigma }_{\text{ii}}}}{\rho }_{\text{ij}}{Y}_j\Vert }^2\}+\text{λ}\sum _{1<i<j\le p}|{\rho }_{\text{ij}}|/w_{\text{ij}},$$ (2.13)

where w_ij’s are randomly sampled from a probability distribution p(w) supported on (l,1] for some l ∈ (0,1] (note that l = 1 corresponds to the ordinary L₁ penalty). The advantage of this randomized lasso procedure is that, by perturbing the regularization parameters, the irrelevant features may be decorrelated from the true features in some configurations of randomly sampled weights such that the irrepresentable condition is satisfied. Therefore, it selects all true features with probability tending to 1 and any irrelevant feature with a limiting probability strictly less than 1. As a result, a consistent aggregation-based procedure can be achieved under conditions “typically much weaker than the standard assumption of the irrepresentable condition” (Meinshausen and Bühlmann, 2010, Theorem 2). For this case, based on Lemma 1, the proper condition is also satisfied.

If (2.13) is used as the original (non-aggregated) procedure, an additional parameter l, which controls the amount of perturbation of the regularization parameter, needs to be chosen. A small l guards better against false positives but damages power, while a large l may result in a liberal procedure. Here we provide a two-step data-driven procedure for choosing an appropriate l in BINCO. We first fix l = 1, i.e. the ordinary L₁ penalty, to find a proper range Λ* for λ that corresponds to the “U-shaped” empirical mixtures. Then for each λ ∈ Λ*, we consider a set of pairs Λ₂ = {(λ_i, l_i), i = 1,…, m} such that ${\int }_{l_i}^1\frac{{\text{λ}}_i}{w}p(w)\text{dw}=\text{λ}$, i.e., keeping the average amount of regularization unchanged. For example, in the simulation study, we use l_i = i/10, i = 1,…, 9. We then pick the pair (λ*, l*) ∈ Λ₂ such that l* is the smallest among those l’s that yield U-shaped empirical mixture distributions. Our simulation shows that such a choice of (λ*, l*) ensures good power for BINCO while controlling FDR in a slightly conservative fashion.

3. Simulation

In this section, we first compare the performance of BINCO with stability selection (Meinshausen and Bühlmann, 2010), and then investigate the performance of BINCO with respect to various factors, including the network structure, dimensionality, signal strength and sample size.

We use space (Peng et al., 2009) coupled with randomized lasso (2.13) as the original non-aggregate procedure, where the random weights $\frac{1}{w_{\text{ij}}}$’s are generated from the uniform distribution U[1, 1/l] for l ∈ (0,1]. The selection frequencies are obtained based on B = 100 resamples. Since subsampling of size [n/2] is proposed for stability selection, we use subsampling to generate resamples when comparing BINCO and stability selection. For investigating BINCO’s performance, we use bootstrap resamples because that it yields slightly better performance (see Remark 4).

The performance of both methods are evaluated by true FDRs and power since for simulations we know whether an edge is true or null. In addition, we define ideal power, which is the best power one can achieve for $S_c^{\text{λ}}$ given the true FDR≤ α (in simulation we consider α = 0.05 and α = 0.1). Based on ideal power, we can evaluate the efficiency of the methods under different settings. For each simulation setting, results are based on 20 independent simulation runs.

3.1. Comparison between BINCO and Stability Selection

Stability selection procedure selects $S_{\text{stable}}^{\Lambda }(t)\equiv$ $\{(i,j):{\text{max}}_{\lambda \in \Lambda }(X_{\mathrm{ij}}^{\lambda })\ge t\}$, a set of edges with the maximum selection frequency over a pre-specified regularization set Λ exceeding a threshold t. Assuming an exchangeability condition upon the irrelevant variables (here the null edges), Mein-shausen and Bühlmann (2010, Theorem 1) derived an upper bound for the expected number of falsely selected variables for each choice of t > 0.5. Specifically, under suitable conditions, the expected number of null edges selected by the set $S_{\text{stable}}^{\text{Λ}}$, denoted by E(V), satisfies

$$E(V)=\frac{q_{\Lambda }^2}{(2t-1)N_{\Omega }}$$ (3.1)

where N_Ω = p(p − 1)/2 is the total number of candidate edges and q_Λ is the expected number of edges selected under at least one λ ∈ Λ. In practice, q_Λ can be estimated by $\frac{1}{B}{\sum }_{i=1}^B|{\cup }_{\text{λ}\in \Lambda }{S}^{\text{λ}}(Y^i)|$. Dividing both sides of (3.1) by $|S_{\text{stable}}^{\Lambda }(t)|$, we obtain

$$\frac{E(V)}{|S_{\text{stable}}^{\Lambda }(t)|}\le \frac{q_{\Lambda }^2}{(2t-1)N_{\Omega }·|S_{\text{stable}}^{\Lambda }(t)|}.$$ (3.2)

Although stability selection is intended to control E(V), for an easier comparison with BINCO, we use $\frac{E(V)}{|S_{\text{stable}}^{\Lambda }(t)|}$ to approximate FDR and obtain the optimal $S_{\text{stable}}^{\Lambda }(t)$ by finding the smallest threshold t such that the upper bound on the right hand of (3.2) is less than or equal to α.

For data generation, we first consider a power-law network with p = 500 nodes whose degree (i.e., the number of connected edges for each node) distribution follows P(k) ~ k^−γ. The scaling exponent γ is set to be 2.3, which is consistent with the findings in the literature for biological networks (Newman, 2003). There are in total 495 true edges in this network and its topology is illustrated in Fig 5(a). The sample size is n = 200. Two settings with different signal strengths are considered: (1) strong signal, the mean and standard deviation (SD) of nonzero |ρ_ij|’s are 0.34 and 0.13, respectively; (2) weak signal, the mean and SD of nonzero |ρ_ij|’s are 0.25 and 0.09, respectively. Note both positive and negative correlations are allowed in this network.

Fig 5.

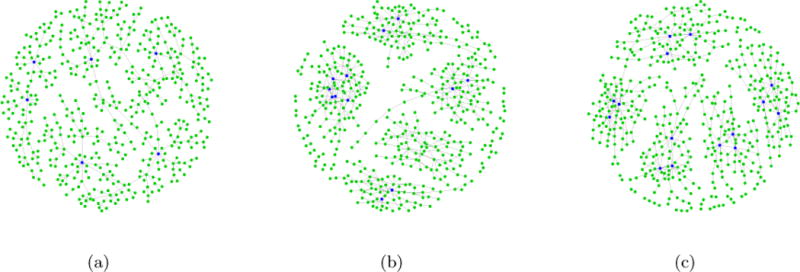
Different network topologies: (a) Power-law Network, number of true edges = 495; (b) Empirical Network, number of true edges=633; (c) Hub Network, number of true edges=587. All three networks have p = 500 nodes.

We compare the performance of BINCO and stability selection at a targeted FDR level of 0.05. For BINCO, we consider Λ₀ = {40, 50,…, 100} as the initial range for λ and then obtain the optimal final selection following the steps at the end of Section 2.4. For stability selection, since no specific guidance was provided for choosing Λ and l (the randomized lasso regularization perturbation parameter), we consider three different values for l ∈ {0.5, 0.8, 1} and a collection of intervals Λ = (λ_min, λ_max) with λ_min varying from 40 to 100 and λ_max = 100. This choice of Λ is due to the fact that the upper bound in (3.2) can not be controlled at 0.05 for any t for λ_min < 40, and the performance of stability selection is largely invariant for λ_max.

When the signals are strong, BINCO gives a conservative FDR= 0.026 but still maintains good power= 0.801 (Fig 4(a) and 4(c)). The performance of stability selection varies for different choices of λ_min and l. The FDRs are larger than the targeted level 0.05 for some λ_min’s when l = 0.8 and for all λ_min’s when l = 1. For other cases (some λ_min’s when l = 0.8 and all λ_min’s when l = 0.5), the FDR control is very conservative and the corresponding power is consistently lower than BINCO. When the signals are weak, stability selection is much more conservative than BINCO and results in much lower power (Fig 4(b) and 4(d)). In Table 1, we report the ideal power, the power for BINCO and the best power for stability selection (among different choices of λ_min) under l=0.5, 0.8 and 1. We also calculate the power efficiency as the ratio of the power for the method over the ideal power, for BINCO and stability selection, respectively. It can be seen that the power of BINCO is close to the ideal power for both levels of signal strength while stability selection is too conservative when the signal strength is weak. For more detailed results, see Section A1 in the supplemental article [Li (2012)].

Fig 4.

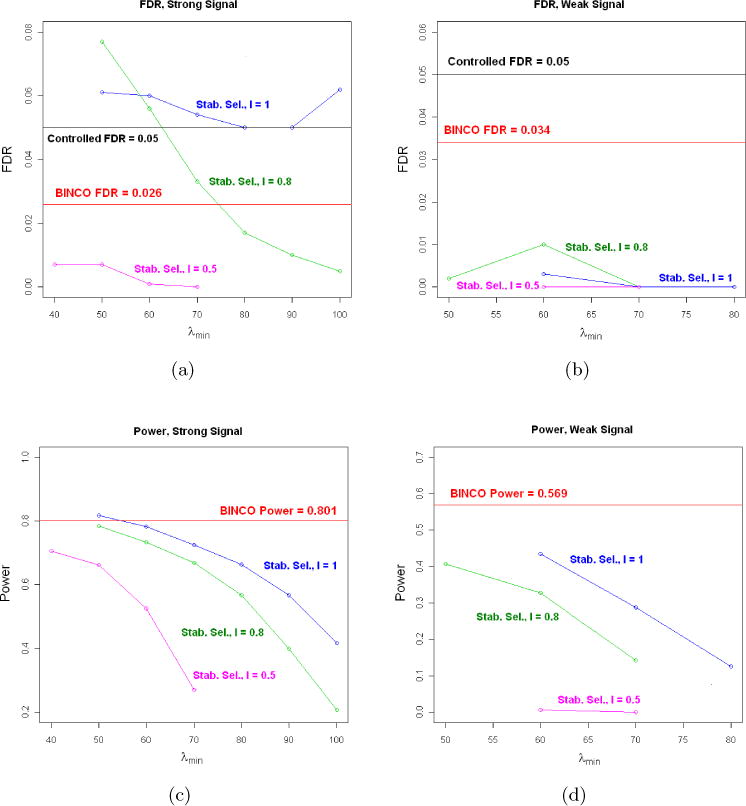
The FDR (top panels) and power (bottom panels) for BINCO and stability selection (Stab. Sel.). (a) and (c) are for the strong signal setting; (b) and (d) are for the weak signal setting.

Table 1.

Power comparison between BINCO and stability selection under strong and weak signals.

		Ideal1	BINCO	Stability Selection
				l = 1	l = 0.8	l = 0.5
Strong Signal	Power	0.853	0.801	0.8183	0.7853	0.706
	MPE2	1	0.939	0.9593	0.9203	0.828
Weak Signal	Power	0.616	0.569	0.434	0.407	0.170
	MPE2	1	0.924	0.705	0.661	0.276

¹“Ideal” refers to the ideal power that can be achieved when the true distribution of null edges is known.

²Method Power Efficiency (MPE) = method power / ideal power.

³FDR control failed.

Remark 3

In some cases we find that stability selection fails to control FDR. We suspect this may be due to the violation of the exchangeability assumption in Theorem 1 of Meinshausen and Bühlmann (2010). We examine the impact of the exchangeability assumption by simulation and find that when it is violated, the theoretical upper bound in (3.1) for E(V) may not hold (see Section D2 in the supplemental article [Li (2012)] for further details).

3.2. Further Investigation of BINCO

Now we investigate the effects of the network structure, dimensionality, signal strength and sample size on the performance of BINCO.

Network Structure

We consider four different network topologies: empty network, power-law network, empirical network and hub network. In each network, there are five disconnected components with 100 nodes each. Below is a brief description of the network topologies.

1. Empty network: there is no edge connecting any pair of nodes.

2. Power-law network: the degree follows a power-law distribution with parameter γ = 2.3 as described in Section 3.1 (Fig 5(a)).

3. Empirical network: the topology is simulated according to an empirical degree distribution of one genetic regulatory network (Schadt et al., 2005) (Fig 5(b)).

4. Hub network: three nodes per component have a large number of connecting edges (> 15) and all other nodes have a small number of connecting edges (< 5) (Fig 5(c)).

We set the sample size n = 200. The signal strength for all networks except for the empty network is fixed at the strong level as in Section 3.1.

For the empty network, the empirical mixture distributions of selection frequencies monotonically decrease on a wide range of λ (Fig S-1) and are not recognized by BINCO as “U-shaped”. Thus, we reach the correct conclusion that there is no signal in this case. In contrast, datasets from the other three networks produce the desired “U-shaped” mixture distributions for some λ (Fig S-2).

We compare BINCO results across networks 2–4 with FDR targeted at level α = 0.05 and 0.1. BINCO gives slightly conservative control on FDR and achieves reasonable power for all three networks (Table 2). The comparison to the ideal power shows that the network topologies investigated here have only a small effect on BINCO’s efficiency (Table 3).

Table 2.

Investigation of the Impact of Different Networks on BINCO Performance

	Targeted FDR = 0.05				Targeted FDR = 0.10
Network Topology	FDR		Power		FDR		Power
	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Power-law	0.046	0.009	0.810	0.013	0.096	0.013	0.845	0.013
Empirical	0.032	0.019	0.523	0.040	0.068	0.034	0.565	0.040
Hub	0.023	0.009	0.644	0.021	0.052	0.012	0.692	0.017

Table 3.

Comparison of BINCO power and ideal power under different networks.

	Targeted FDR = 0.05			Targeted FDR = 0.10
Topology	Power-law	Empirical	Hub	Power-law	Empirical	Hub
BINCO Power	0.810	0.523	0.644	0.845	0.565	0.692
Ideal Power	0.856	0.595	0.736	0.881	0.631	0.776
MPE1	0.946	0.879	0.875	0.959	0.895	0.892

¹Method Power Efficiency (MPE) = method power / ideal power.

Dimensionality

We investigate the impact of dimensionality on the performance of BINCO. We consider the power-law network and let the number of nodes p vary from 500, 800 to 1000. To keep the complexity of each component the same across different choices of p, we set the component size constant, being 100, and the number of components C = p/100. Again the sample size n = 200 is used for all three cases and the signal strength is fixed at the strong level as in Section 3.1.

For all three choices of p, BINCO performs similarly (Table 4), with slightly conservative FDR and power around 0.8. The dimensionality does not demonstrate a significant impact on BINCO. measurements of expression levels of 44928 BINCO’s result is also largely invariant when we compare networks of differing numbers of components with p fixed (such that component size varies, see Section A3 in the supplemental article [Li (2012)]).

Table 4.

Investigation of the Impact of Different Dimensionality on BINCO Performance

	Targeted FDR = 0.05				Targeted FDR = 0.10
Dimension	FDR		Power		FDR		Power
p	Mean	SD	Mean	SD	Mean	SD	Mean	SD
500	0.046	0.009	0.810	0.013	0.096	0.013	0.845	0.013
800	0.030	0.007	0.769	0.010	0.083	0.010	0.811	0.012
1000	0.043	0.007	0.784	0.008	0.096	0.011	0.821	0.007

Signal Strength

We consider three levels of signal strength: strong, weak and very weak. The corresponding means and SDs of nonzero |ρ_ij|’s are (0.34, 0.13), (0.25, 0.09) and (0.21, 0.07), respectively. The network is the power-law network with p = 500 and sample size is n = 200 for all settings.

BINCO provides good control on FDR, however the power decreases from 0.8 to 0.3 as the signal weakens (Table 5). Comparing the power of BINCO with the ideal power (Table 6), we see that BINCO remains efficient and the loss in power is largely due to reduction of signal strength.

Table 5.

Investigation of the Impact of Different Signal Strength on BINCO Performance

	Targeted FDR = 0.05				Targeted FDR = 0.10
Signal Strength	FDR		Power		FDR		Power
	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Strong	0.046	0.009	0.810	0.013	0.096	0.013	0.845	0.013
Weak	0.032	0.010	0.579	0.024	0.063	0.014	0.617	0.018
Very Weak	0.035	0.026	0.252	0.040	0.065	0.037	0.310	0.039

Table 6.

Power Comparison of BINCO power and ideal power when the signal strength is strong, weak and very weak.

	Targeted FDR = 0.05			Targeted FDR = 0.10
Signal Strength	Strong	Weak	Very Weak	Strong	Weak	Very Weak
BINCO Power	0.810	0.579	0.252	0.845	0.617	0.310
Ideal Power	0.856	0.615	0.279	0.881	0.651	0.345
MPE1	0.946	0.941	0.903	0.959	0.948	0.899

¹Method Power Efficiency (MPE) = method power / ideal power.

Sample Size

Now we consider the impact of sample size n by varying it from 200, 500 and 1000, while keeping the signal strength at the “very weak” level as in the previous simulation. The network structure is again the power-law network with p = 500.

With an increased sample size, the power of BINCO is significantly improved from 0.3 to nearly 0.9 while the FDRs are well controlled (Table 7).

Table 7.

Investigation of the Impact of Different Sample Size on BINCO Performance

	Targeted FDR = 0.05				Targeted FDR = 0.10
Sample Size	FDR		Power		FDR		Power
	Mean	SD	Mean	SD	Mean	SD	Mean	SD
200	0.035	0.026	0.252	0.040	0.065	0.037	0.310	0.039
500	0.024	0.010	0.684	0.012	0.049	0.011	0.714	0.014
1000	0.045	0.010	0.869	0.013	0.090	0.015	0.891	0.012

In summary, BINCO has good control for FDR under a wide range of scenarios. Its performance is shown to be robust for networks with different topologies and dimensionalities, and its efficiency is not influenced much even when the signal strength is weak. As the sample size increases, the power of BINCO is improved significantly.

Remark 4

We propose to use bootstrap over subsampling as the former appears to give slightly better power. Intuitively, bootstrap contains more distinct samples (0.632n, Pathak, 1962) than [n/2] subsampling (0.5n). However, the difference we have observed is rather small. For example, we compare the power over 20 independent samples between bootstrap and [n/2] subsampling under the power-law network setting. For FDR=0.05, the power is 0.810 for bootstrap and 0.801 for subsampling (compare Table 3 and Table 1); while for FDR=0.1, the power is 0.845 for bootstrap and 0.835 for subsampling (compare Table 3 and Table S-7). This observation is in agreement with the conclusions of several others (Menshausen and Bühlmann, 2010; Freedman, 1977; Bühlmann and Yu, 2002).

4. A Real Data Application

We apply the BINCO method to a microarray expression dataset of breast cancer (BC) (Loi et al., 2007) to build a gene expression network related to the disease. The data (http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE6532) contains measurements of expression levels of 44928 probes in tumor tissue samples from 414 BC patients based on the Affymetrix Human Genome U133A, U133B and U133 plus 2.0 Microarray platforms.

We preprocess the data as follows. First, a global normalization is applied by centering the median of each array to zero and scaling the Median Absolute Deviation (MAD) to one. Probes with standard deviation (SD) greater than the 25%-trimmed mean of all SDs are selected. We further focus on a subset of 1257 probes for genes from cell cycle and DNA-repair related pathways (http://peiwang.fhcrc.org/internal/papers/DNArepair_CellCircle_related.csv/view), as these pathways have been shown to play significant roles in BC tumor initiation and development. Clinical information including age, tumor size, ER-status (positive or negative) and treatment status (tamoxifen treated or not) is incorporated in the analysis as “fake genes” since we are also interested in investigating whether gene expressions are associated with these clinical characteristics. Finally we standardize each expression level to have mean zero and SD one. The resulting dataset has p = 1261 genes/probes (including four clinical variables) and n = 414 tumor samples.

We generate selection frequencies by applying the space algorithm with randomized lasso regularization to B = 100 bootstrap resamples. The initial range of the tuning parameter λ is set to be Λ = (100, 120, …, 580). We then apply the BINCO procedure and find that the optimal values for the regularization parameters are λ = 340 and l = 0.9. The empirical distribution of selection frequencies of all edges and the null density estimation are given in Fig 6. When the estimated FDR is controlled at 0.05, 0.1 and 0.2, BINCO identifies 125, 222 and 338 edges, respectively. The estimated network for FDR=0.2 is shown in Fig 7. In this figure, two components of large connectivity structure are observed. They contain most of the genes that are connected by a large number of high-selection-frequency edges. This constructed network can help to generate useful biological hypothesis and design follow up experiments to better understand the underlying mechanism in BC. For example, BINCO suggests with high confidence for the association between MAP3K4 and STAT3. MAP3K4 plays a role in the signal transduction pathways of BC cell proliferation, survival, and apoptosis (Bild and Johnson, 2001), and the constitutive activation of STAT3 is also frequently detected in BC tissues and cell lines (Hsieh et al., 2005). Interestingly, both MAP3K4 and STAT3 play roles in the regulation of c-Jun, a novel candidate oncogene whose aberrant expression contributes to the progression of breast and other human cancers (Tront et al., 2006; Shackleford et al., 2011). The association between MAP3K4 and STAT3 detected by BINCO suggests their potential cooperative roles in BC. It is also worth noting that for the four clinical variables, the only edge with high selection frequency is the one between age and ER-status (selection frequency = 0.96). All edges between clinical variables and the genes/probes are insignificant (selection frequencies < 0.12).

Fig 6.

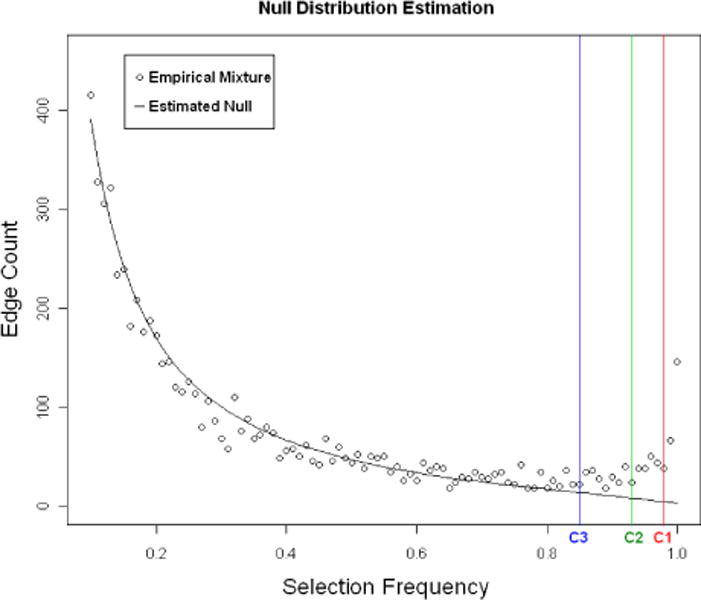
The empirical selection frequency distribution of all edges (dots) and the estimated selection frequency distribution of null edges (solid line). The three vertical lines are drawn at the cut-offs C1 = 0.98, C2 = 0.93 and C3 = 0.85 for FDR at 0.05, 0.1 and 0.2, respectively.

Fig 7.

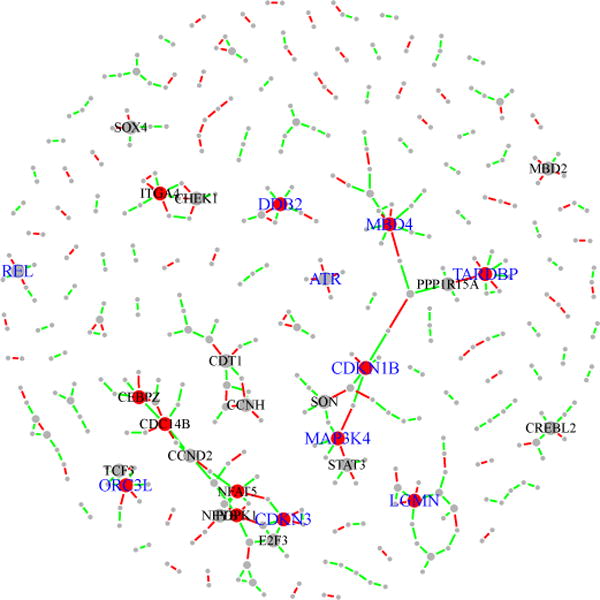
Inferred networks at FDR=0.2 from the BC expression data. A total of 338 edges (selection frequencies ≥ 0.85) are identified. Among these 338 edges, those with selection frequencies ≥ 0.98 (corresponding to the set with FDR= 0.05) are colored in red while other edges are colored in green. Genes with degree> 3 are labeled by their symbols; genes with degree> 4 are indicated by red nodes. In addition, the top ten genes with consistently high connection across perturbed datasets are labeled in blue symbols.

Networks built on perturbed datasets can also be used to detect hub genes (i.e., highly connected genes), which are often of great interest due to the central role these genes may play in genetic regulatory networks. The idea is to look for genes that show consistent high connection in estimated networks across perturbed datasets. Here, we propose to detect hub genes by the ranks of their degrees based on the estimated networks using λ = 340 and l = 0.9. The ten genes with the largest means and the smallest SDs of the degree rank across 100 bootstrap resamples (see Fig S-3, in black dots) are MBD4, TARDBP, DDB2, MAP3K4, ORC3L, CDKN1B, REL, ATR, LGMN and CDKN3. Nine out of these ten genes have been reported relevant to BC, while the remaining one (TARDBP) is newly discovered to be related to cancer (Postel-Vinay et al., 2012), although its role in BC is not clear at present. The neighborhood topologies of these hub genes in the network estimated by BINCO are illustrated in Fig 7. More details of these hub genes are given in the supplemental article [Li (2012)], Section B.

5. Discussion

In this paper we propose the BINCO procedure to conduct high-dimensional network inference. BINCO employs model aggregation strategies and selects edges by directly controlling the FDR. This is achieved by modeling the selection frequencies of edges with a two-component mixture model, where a flexible parametric distribution is used to model the density for the null edges. By doing this, BINCO is able to provide a good estimate of FDR and hence properly controls the FDR. To ensure BINCO works, we propose a set of screening rules to identify the U-shape characteristic of empirical selection frequency distributions. Based on our experience, a U-shape corresponds to a proper amount of regularization such that the FDR is well controlled and the sample from the set of selection power is reasonable. Extensive simulation results show that BINCO performs well under a wide range of scenarios, indicating that it can be used as a practical tool for network inference. Although we focus on the GGM construction problem in this paper, BINCO is applicable to a wide range of problems where model selection is needed because it provides a general approach to modeling the selection frequencies.

We use a mixture distribution with two components, one corresponding to true edges and the other corresponding to null edges, to model the selection frequency distribution. This two-component mixture model is adequate as long as the distribution of the null component is identifiable and can be reasonably estimated, as formalized in the proper condition. Note that the proper condition holds for a wide range of commonly used (non-aggregation) selection procedures (Lemma 1, Remark 1). To further ensure the FDR can be controlled at a reasonable level, we propose a U-shape detection procedure and only apply BINCO if the empirical distribution of selection frequencies passes the detection. These rules for U-shape detection are empirical but appear to work very well based on our extensive simulations.

BINCO works well despite the presence of correlations between edges (see Section D1 in the supplemental article [Li (2012)]), because we use the independence of edges only as a working assumption. It is well known that if the marginal distribution is correctly specified, the parameter estimates are consistent even in the presence of correlation. This is similar to the generalized estimating equations, where if the mean function is correctly specified, the parameters will be consistently estimated (Liang and Zeger, 1986). Towards this end, we use the three-parameter power beta distribution to allow for adequate flexibility in modeling the marginal distribution of selection frequencies.

BINCO is computationally feasible for high-dimensional data. The major computational cost lies in generating the selection frequencies via resampling. For each resample, the computational cost is determined by that of the non-aggregated procedure BINCO coupled with. In terms of space, it is O(np²). The processing time for a dataset with n = 200, p = 500, under a given λ and 100 bootstrap samples to generate selection frequencies is about 20 minutes on a PC with Pentium dual-core CPU at 2.8GHz and 1G ram. These selection frequencies can be simultaneously generated through parallel computing for different λ’s and weights. Fitting the mixture model takes much less time, which is about 2 minutes for the above example on the same computer.

Although we use GGM as our motivating example, BINCO works well even if the multivariate normality assumption does not hold. Note that, the multivariate normality assumption only concerns the interpretation of the edges. Under GGM, the presence of an edge means conditional dependency of the corresponding nodes given all other nodes. Without the normality assumption, one can only conclude nonzero partial correlation between the two nodes given the rest of nodes. The space method used in this paper is to estimate the concentration network (where an edge is drawn between two nodes if the corresponding partial correlation is nonzero) and has been shown to work well under non-normal cases such as multivariate-t distributions (Peng et al., 2009). We also generate data from non-normal distributions and found that BINCO works well in this situation (see Section D4 in the supplemental article [Li (2012)]).

BINCO is an aggregation-based procedure. In principle, it can be coupled with any selection procedure. In this sense, it has a wide range of applications as long as the features are defined (e.g., edges as in this paper, variables, or canonical correlations as in the example below), and the selection procedure is reasonably good, e.g., producing probabilities that satisfy the condition in Lemma 1. One application beyond GGM could be on the multi-attribute network construction where the links/edges are defined based on canonical correlations (Waaijenborg et al., 2008; Katenka and Kolaczyk, 2011; Witten et al., 2009). Another interesting extension may be on the time-varying network construction (Kolar et al., 2010) where appropriate incorporation of the time-domain structure across aggregated models will be important. These are beyond the scope of this paper and will be pursued in the future research.

The R package BINCO is available through CRAN.

APPENDIX A: PROOF OF LEMMA 1

Proof

Suppose as the sample size n increases, an edge selection procedure A(λ) gives selection probabilities $\{{\stackrel{\sim }{p}}_{\text{ij}}^{(n)}\}$ (with respect to resample space) which uniformly satisfy

$${\stackrel{\sim }{p}}_{\text{ij}}^{(n)}\to 1,\text{ if }(i,j\text{)}\in E$$ (A.1)

and

$$\lim \sup {\stackrel{\sim }{p}}_{\text{ij}}^{(n)}\le M<1,\text{ if }(i,j)\in E^c.$$ (A.2)

Suppose B is large such that $\frac{B+1}{B}M<1$. Let X be a random sample from the set of selection frequencies $\left\{X_{\text{ij}}^{\text{λ}}\right\}$ generated by applying A(λ) on B resamples, i.e., $\text{Pr}(X=X_{\text{ij}}^{\text{λ}})=1/N_{\Omega },(i,j)\in \Omega$. Also suppose X has density $f_{\text{ij}}^{\text{λ}}$ if $X=X_{\text{ij}}^{\text{λ}}$. Then the mixture model (2.6) becomes

$$f^{\text{λ}}(x)=(1-\pi )f_0^{\text{λ}}(x)+\pi f_1^{\text{λ}}(x)=\sum _{(i,j)\in E^c}\frac{1}{N_{\Omega }}{f}_{\text{ij}}^{\text{λ}}(x)+\sum _{(i,j)\in E}\frac{1}{N_{\Omega }}{f}_{\text{ij}}^{\text{λ}}(x)$$ (A.3)

with $(1-\pi )f_0^{\text{λ}}(x)={\sum }_{(i,j)\in E^c}\frac{1}{N_{\Omega }}{f}_{\text{ij}}^{\text{λ}}(x)$ and $\pi f_1^{\text{λ}}(x)={\sum }_{(i,j)\in E}\frac{1}{N_{\Omega }}{f}_{\text{ij}}^{\text{λ}}(x)$.

Because of the i.i.d. nature of resamples given the data, $f_{\text{ij}}^{\text{λ}}$ is a binomial density with ${\stackrel{\sim }{p}}_{\text{ij}}^{(n)}$ as the probability of success, i.e., $f_{\text{ij}}^{\text{λ}}(x)=(\begin{array}{c}B\\ k\end{array}){({\stackrel{\sim }{p}}_{\text{ij}}^{(n)})}^k{(1-{\stackrel{\sim }{p}}_{\text{ij}}^{(n)})}^{B-k}$ for x = k/B, k = 0,1,…, B. This binomial density is monotone decreasing for x greater than its mode ${\mu }_{\text{ij}}=\frac{[(B+1){\stackrel{\sim }{p}}_{\text{ij}}^{(n)}]}{B}\text{or}\frac{[(B+1){\stackrel{\sim }{p}}_{\text{ij}}^{(n)}]-1}{B}$. By (A.2), given $V_1=\frac{B+1}{B}M<1$ and ∊ > 0 such that V₁ + ∊ < 1, ∃N such that for all n > N max_{(i,j) ∈ E^c} (μ_ij) < V₁ + ∊ and hence for any null edge (i,j) ∈ E^c, $f_{\text{ij}}^{\text{λ}}(x)$ is monotone decreasing on [V₁ + ∊, 1], which implies C2 since $f_0^{\text{λ}}(x)=\frac{1}{(1-\pi )N_{\Omega }}{\sum }_{(i,j)\in E^c}{f}_{\text{ij}}^{\text{λ}}(x)$. Also, (A.1) implies, for (i,j) ∈ E, $f_{\text{ij}}^{\text{λ}}(x)\to 0$ uniformly for x < 1, which implies C1 for any V₂ < 1. Taking V₂ such that V₁ < V₂ < 1 satisfies the proper condition and completes the proof. □