Abstract
Bacteria face the challenging requirement to maintain their shape and avoid rupture due to the high internal turgor pressure, but simultaneously permit the import and export of nutrients, chemical signals, and virulence factors. The bacterial cell wall, a mesh-like structure composed of cross-linked strands of peptidoglycan, fulfills both needs by being semi-rigid, yet sufficiently porous to allow diffusion through it. How the mechanical properties of the cell wall are determined by the molecular features and the spatial arrangement of the relatively thin strands in the larger cellular-scale structure is not known. To examine this issue, we have developed and simulated atomic-scale models of Escherichia coli cell walls in a disordered circumferential arrangement. The cell-wall models are found to possess an anisotropic elasticity, as known experimentally, arising from the orthogonal orientation of the glycan strands and of the peptide cross-links. Other features such as thickness, pore size, and disorder are also found to generally agree with experiments, further supporting the disordered circumferential model of peptidoglycan. The validated constructs illustrate how mesoscopic structure and behavior emerge naturally from the underlying atomic-scale properties and, furthermore, demonstrate the ability of all-atom simulations to reproduce a range of macroscopic observables for extended polymer meshes.
Author Summary
The structure of the bacterial cell wall has been a point of controversy and contention since it was first discovered. Although the basic chemical composition of peptidoglycan, the key constituent of the cell wall, is now well established, its long-range organization is not. This dearth of information at the mesoscopic scale is a result of the inability of experimental imaging techniques to simultaneously visualize both the atomic-level detail of the peptidoglycan network and its macroscopic arrangement around the bacterium. Now, using molecular dynamics (MD) simulations, we have carefully constructed and validated models of sections of the Escherichia coli cell wall in full atomic detail. By comparing various properties of these models, including elasticity, pore size, and thickness with experiments, we can discriminate between them, resolving which best represents the native wall structure. In doing so, our study provides approaches for connecting measurements made in atomic-scale MD simulations with large-scale and even macroscopic properties.
Introduction
The cell wall rests outside the cytoplasmic membrane and provides bacteria with shape, rigidity, and protection from lysis due to the significant turgor pressure emanating from within [1]. It is primarily composed of a porous, mesh-like network of polymerized peptidoglycan, a repeating disaccharide/oligopeptide molecule. Because it is covalently connected, the cell wall is also the largest macromolecule in nature [2]. The chemical composition of peptidoglycan is largely conserved: relatively long glycan strands are cross-linked by short oligopeptides (see Fig. 1) [3]. In Gram-negative bacteria the cell wall presents as a relatively thin network (2–7 nm) between the inner and outer membranes, while in Gram-positive bacteria, it is much thicker, between 20 and 35 nm [1], [4].
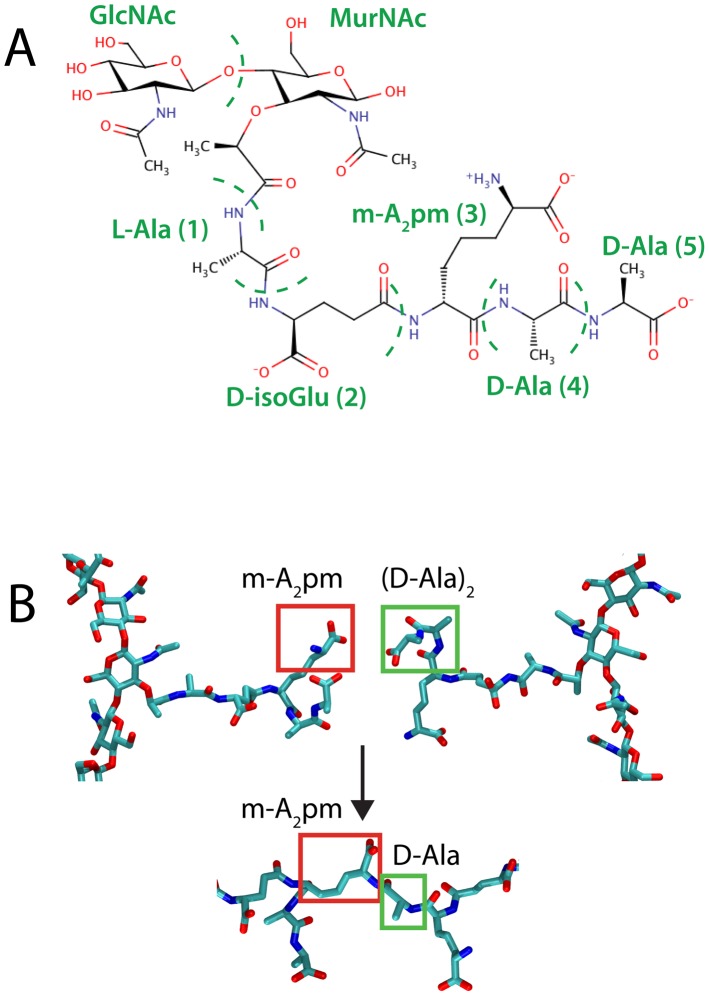
Figure 1. Peptidoglycan constituents.
(A) Chemical composition of the monomeric unit of peptidoglycan, consisting of a disaccharide with a connected five-residue peptide. (B) Transpeptidation reaction between two neighboring peptidoglycan strands. The reacting groups contributed by each peptide are boxed in red and green, respectively, before and after being linked.
Multiple theoretical models for the architecture of peptidoglycan at the mesoscopic scale have been conceived [1]. The models fall into two primary classes, a horizontal layer in which the glycan strands run parallel to the cell surface in a circumferential direction [5]–[7] and a scaffold in which the strands are oriented perpendicular to the surface [8], [9]. While some experiments have been interpreted as support for the scaffold model, e.g., the NMR structure of a peptidoglycan subunit [10], more recent electron cryo-tomography (ECT) on purified Gram-negative sacculi revealed circumferential glycan strands [11]. Even more complex models have been put forth, such as cables of coiled peptidoglycan encircling Gram-positive bacteria based on atomic force microscopy (AFM) measurements [12], although ECT on these bacteria failed to find distinct cable-like structures [4]. Using biochemical experiments and atomic-scale simulations, it was demonstrated that only layers composed of circumferential glycan strands could fully account for the ECT observations on Gram-positive bacteria, namely a distinct curling and thickening behavior of the sacculus, i.e., the part of the cell wall remaining after cell lysis, upon shearing [4].
One limitation of many of the previously developed models is that they are typically constructed with an idealized geometric arrangement, which is then deformed according to a set of mathematical rules. Not surprisingly, this procedure tends to generate cell walls with an unnatural degree of order [3]; indeed, regular patterns of quadrilateral or hexagonal shapes are often depicted [7], [8]. Furthermore, while apparent disagreement with a chosen set of experimental data has been used to indict some models over others [9], an alternative explanation is that the specific rules used to construct the model as well as the presumed experimental constraints were too strict [13].
In an attempt to circumvent some of the limitations of previous models, we have constructed and simulated patches of Gram-negative cell wall in their full atomic detail. By modeling the cell wall as a intricate composite of its individual components, we restrict the number of assumptions necessary for its construction. A single-layered model was chosen based on ECT of Gram-negative sacculi and on recent simulations of Gram-positive cell-wall patches [4]. Each patch of peptidoglycan was built from the level of individual residues on up, quantifying the behavior at each level, and connecting it with experimental measurements of various structural and mechanical properties. These comparisons are used both to validate the constructions and to illustrate the robustness of the cell wall to variations in average glycan strand length within the range of those observed in vivo. The widespread agreement with experimentally measured properties favors the disordered circumferential model of peptidoglycan in Gram-negative bacteria over other models.
Results
Modeling and validation of the physical properties of peptidoglycan components
While the glycan strand composition is uniform across all bacteria, composed of alternating  -1,4-linked GlcNAc and MurNAc saccharides, the peptide stem, connected to the lactyl moiety of the MurNAc residue, is quite diverse [3], [6]. In E. coli the full, five-residue sequence is L-Ala (1) D-isoGlu (2)
-1,4-linked GlcNAc and MurNAc saccharides, the peptide stem, connected to the lactyl moiety of the MurNAc residue, is quite diverse [3], [6]. In E. coli the full, five-residue sequence is L-Ala (1) D-isoGlu (2)  -
-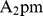 (3) D-Ala (4) D-Ala (5), where
(3) D-Ala (4) D-Ala (5), where  -
-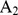 pm is
pm is 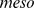 -diaminopimelic acid, a lysine derivative [3]. Also of note is that the D-isoglutamate is connected through a
-diaminopimelic acid, a lysine derivative [3]. Also of note is that the D-isoglutamate is connected through a  -carboxy linkage to the
-carboxy linkage to the 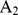 pm residue (see Fig. 1A). While alanine is already present in the CHARMM force field, the remaining four constituents were originally absent. Therefore, we developed new CHARMM-compatible topologies and parameters for these constituents, as well as for the connections between them (see Methods along with topology and parameter files provided in the Supporting Information). The novel force fields have already been successfully utilized for simulation of Gram-positive peptidoglycan [4].
pm residue (see Fig. 1A). While alanine is already present in the CHARMM force field, the remaining four constituents were originally absent. Therefore, we developed new CHARMM-compatible topologies and parameters for these constituents, as well as for the connections between them (see Methods along with topology and parameter files provided in the Supporting Information). The novel force fields have already been successfully utilized for simulation of Gram-positive peptidoglycan [4].
After parameterization, a single glycan strand 320 residues long was constructed without peptides. A useful property to quantitatively characterize the flexibility of a polymer is the persistence length 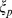 . It is defined as
. It is defined as
| (1) |
where  is the position along the strand,
is the position along the strand,  is the angle between the tangent vectors at positions
is the angle between the tangent vectors at positions 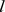 and
and 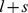 , and the average is taken over all starting positions
, and the average is taken over all starting positions 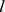 [14]. Effectively,
[14]. Effectively, 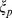 is a measure of the stiffness of the strand. Two 5-ns simulations of the 320-mer strand were carried out, and
is a measure of the stiffness of the strand. Two 5-ns simulations of the 320-mer strand were carried out, and 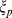 was determined by the initial decay of the correlation in Fig. 2
[15], [16]. The two simulations provided values of
was determined by the initial decay of the correlation in Fig. 2
[15], [16]. The two simulations provided values of 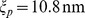 and 13.6 nm; extending the latter simulation to 10 ns changed this value only marginally (
and 13.6 nm; extending the latter simulation to 10 ns changed this value only marginally (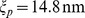 ). This persistence length is of the same order of magnitude as that found for other simple polysaccharides from experiments and/or modeling, which can span a large range, e.g., 4.5–13.5 nm for pectin [17] and 14.5 nm for cellulose [18]. Although not measured here, the persistence length of peptide cross-links is at least an order of magnitude less, being no more than 3–4 Å, making them significantly more stretchable than the relatively rigid glycan strands.
). This persistence length is of the same order of magnitude as that found for other simple polysaccharides from experiments and/or modeling, which can span a large range, e.g., 4.5–13.5 nm for pectin [17] and 14.5 nm for cellulose [18]. Although not measured here, the persistence length of peptide cross-links is at least an order of magnitude less, being no more than 3–4 Å, making them significantly more stretchable than the relatively rigid glycan strands.
Figure 2. Properties of single glycan strands.
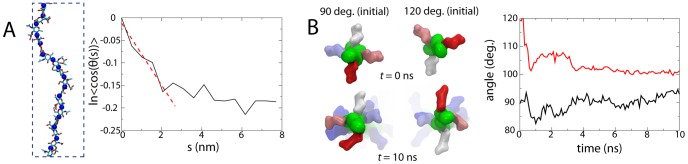
(A) Calculation of the persistence length of the 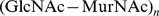 polysaccharide. Blue spheres along the strand on the left indicate the oxygen atoms involved in the glycosidic bonds between residues. (B) Average angle between neighboring peptides. On the left are images looking down on a portion of the strand (green) with the initial residues of the peptides shown, colored to indicate depth (red, then white, then blue). The plot on the right shows the average peptide-peptide angle as a function of time for one started at
polysaccharide. Blue spheres along the strand on the left indicate the oxygen atoms involved in the glycosidic bonds between residues. (B) Average angle between neighboring peptides. On the left are images looking down on a portion of the strand (green) with the initial residues of the peptides shown, colored to indicate depth (red, then white, then blue). The plot on the right shows the average peptide-peptide angle as a function of time for one started at 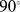 (black) and one started at
(black) and one started at 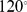 (red). Light restraints (
(red). Light restraints (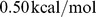 Å2) in the strand direction were placed on the glycosidic oxygen of every other GlcNAc residue to keep the strand elongated without preventing rotation. Also see Movie S1.
Å2) in the strand direction were placed on the glycosidic oxygen of every other GlcNAc residue to keep the strand elongated without preventing rotation. Also see Movie S1.
The peptides project outward from the glycan strand, presumably in a helical fashion (see Fig. 2B) [1]. The periodicity of these peptides is intimately connected to the orientation and degree with which neighboring glycan strands can form cross-links with one another. An angle of 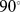 between successive peptide side chains was assumed in the classical layered model, thus placing every other one in the plane of the cell wall [5], [6]. An NMR structure of a peptidoglycan fragment, however, displayed an angle of
between successive peptide side chains was assumed in the classical layered model, thus placing every other one in the plane of the cell wall [5], [6]. An NMR structure of a peptidoglycan fragment, however, displayed an angle of 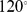 , in line with that in the scaffold model [10]. To determine the equilibrium angle for an isolated peptidoglycan strand, two 60-residue-long strands were constructed and simulated for 10 ns, one with an initial peptide-peptide angle of
, in line with that in the scaffold model [10]. To determine the equilibrium angle for an isolated peptidoglycan strand, two 60-residue-long strands were constructed and simulated for 10 ns, one with an initial peptide-peptide angle of 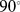 and one with an angle of
and one with an angle of 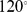 . For the strand initially at 120
. For the strand initially at 120 , the average angle relaxed to
, the average angle relaxed to 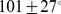 by the end of the 10-ns simulation, while the one initially at
by the end of the 10-ns simulation, while the one initially at 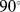 was
was 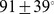 (see Fig. 2B). Based on these results, we conclude the native periodicity of the peptides is approximately four per turn. However, the significant variability in the angle in simulations, even within a single strand, indicates that this periodicity is not strictly maintained and could be easily modified by external forces.
(see Fig. 2B). Based on these results, we conclude the native periodicity of the peptides is approximately four per turn. However, the significant variability in the angle in simulations, even within a single strand, indicates that this periodicity is not strictly maintained and could be easily modified by external forces.
Mesoscale organization of the cell wall
In order to construct the full peptidoglycan network, individual glycan strands need to be covalently linked through their peptides. Although this linkage takes a variety of forms depending on species, in E. coli the most common link is a peptide bond made between the  amino group of the
amino group of the 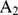 pm residue (position 3) and the carbonyl group of the penultimate D-Ala (position 4), shown in Fig. 1B
[6]. In the course of transpeptidation, the terminal D-Ala (position 5) is also cleaved, both processes being carried out by penicillin-binding proteins [19]. The degree of cross-linking varies between species and even growth states within a single species [1]; for E. coli it is typically around 50% on average, i.e., about half of the peptides are linked and half are free [20]. Although alterations to the cross-linking fraction likely affects the mechanical and structural properties of the peptidoglycan network, this variable is not explored in the current study.
pm residue (position 3) and the carbonyl group of the penultimate D-Ala (position 4), shown in Fig. 1B
[6]. In the course of transpeptidation, the terminal D-Ala (position 5) is also cleaved, both processes being carried out by penicillin-binding proteins [19]. The degree of cross-linking varies between species and even growth states within a single species [1]; for E. coli it is typically around 50% on average, i.e., about half of the peptides are linked and half are free [20]. Although alterations to the cross-linking fraction likely affects the mechanical and structural properties of the peptidoglycan network, this variable is not explored in the current study.
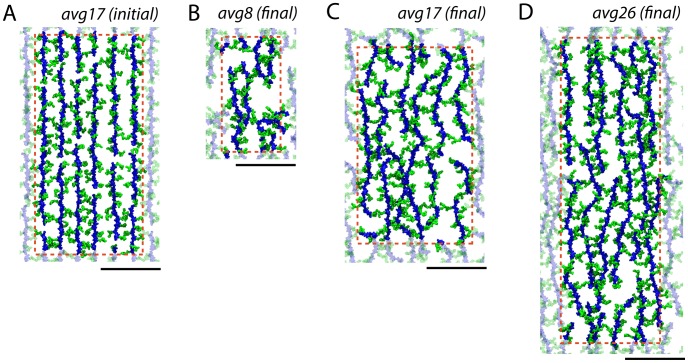
Two-dimensional periodic patches of peptidoglycan were constructed following a specific set of procedures designed to minimize user bias (see Methods); an example of a resulting system is shown in Fig. 3A. Despite being initially constructed as an organized, patterned network, the final organization of the peptidoglycan resembles the “disordered circumferential layered” model observed in cryo-tomography images of purified sacculi [11]. However, because no tension was applied, the possibility remains that the peptidoglycan becomes more ordered under native cellular conditions, which is explored below [1].
Figure 3. Peptidoglycan patches simulated.
In all parts, glycan strands are in blue and peptides in green. The dotted red line denotes the unit cell boundaries, with the transparent peptidoglycan being periodic copies. The black scale bars below are all equivalent at 10(A) Initially constructed state for avg17 (other patches appeared similarly at this state). (B–D) Final relaxed states for (B) avg8, (C) avg17, and (D) avg26. Inf1 and Inf2 are shown in Fig. S6 in Supporting Information. Relaxation of avg17 is shown in Movie S2.
Much like the fraction of peptides cross-linked, in the bacterial cell wall the average glycan strand length takes on a large range of values, as low as six disaccharides in the stationary growth phase of Helicobacter pylori
[21] and more than 50 in Proteus morganii
[22]. Even in E. coli, a range of values spanning from 9 to 60 disaccharides has been measured by different experimental techniques for different stages of growth [1]. To examine the dependence of mesoscale properties of peptidoglycan on the average length of the glycan strand, multiple models with a specific average, but non-uniform, number of disaccharides were constructed, including 8 3.2, 17
3.2, 17 5.8, and 26
5.8, and 26 2.4 disaccharides, denoted avg8, avg17, and avg26, respectively (see Fig. 3). Additionally, as an extreme case for comparison, two patches of cell wall with unbroken, periodic (and therefore effectively infinite) glycan strands with unit-cell lengths of 15 and 30 disaccharides, denoted Inf1 and Inf2, were modeled. Because of the small number of strands used (12 for avg17 and avg26, for example) it's not possible to reproduce distributions, although the limited range of lengths in avg17 (8–26 disaccharides) does agree with where the majority of the strand lengths in CG models falls [23].
2.4 disaccharides, denoted avg8, avg17, and avg26, respectively (see Fig. 3). Additionally, as an extreme case for comparison, two patches of cell wall with unbroken, periodic (and therefore effectively infinite) glycan strands with unit-cell lengths of 15 and 30 disaccharides, denoted Inf1 and Inf2, were modeled. Because of the small number of strands used (12 for avg17 and avg26, for example) it's not possible to reproduce distributions, although the limited range of lengths in avg17 (8–26 disaccharides) does agree with where the majority of the strand lengths in CG models falls [23].
Elastic properties of the peptidoglycan network
A defining property of the peptidoglycan layer is its tensile elasticity, i.e., its response to applied strain coming from the turgor pressure inside the bacterial cell, also referred to as Young's modulus. Elasticity also serves as a key metric for comparing the constructed models to experimental measurements. Because peptidoglycan is orthotropic, the elasticities along its two symmetry axes are not identical [24]. Based on the theory of mechanical deformation of a two-dimensional sheet (see SI for a full derivation starting from the material's constitutive relations), the Young's moduli in each orthogonal direction, 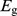 for the glycan strands and
for the glycan strands and 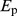 for the peptide cross-links, are given by
for the peptide cross-links, are given by
| (2) |
| (3) |
where 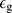 and
and 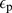 are the applied strains in each direction, defined as
are the applied strains in each direction, defined as 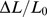 , and
, and 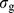 and
and 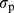 are the resulting stresses, measured in units of force/area. The dimensionless Poisson's ratios,
are the resulting stresses, measured in units of force/area. The dimensionless Poisson's ratios, 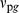 and
and 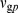 , relate the spontaneous strain arising in one direction given an applied strain in the other. In order to calculate the elasticity from simulation, varying strains were applied in the plane of the peptidoglycan by altering its dimensions, with one dimension stretched and the other held fixed at its equilibrium value, calculated from a minimum 20-ns constant-pressure simulation (see Methods). Because only one of
, relate the spontaneous strain arising in one direction given an applied strain in the other. In order to calculate the elasticity from simulation, varying strains were applied in the plane of the peptidoglycan by altering its dimensions, with one dimension stretched and the other held fixed at its equilibrium value, calculated from a minimum 20-ns constant-pressure simulation (see Methods). Because only one of 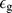 or
or 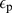 is allowed to be non-zero in each simulation, Eqs. 2 and 3 can be simplified to
is allowed to be non-zero in each simulation, Eqs. 2 and 3 can be simplified to
| (4) |
| (5) |
While the stresses,  and
and 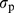 , are formally the derivatives of the free energy with respect to strain in the corresponding dimension, by virtue of the reversible work theorem they can be directly related to the thermodynamic pressure in that dimension, i.e., a mean force (see Text S1) [25], [26].
, are formally the derivatives of the free energy with respect to strain in the corresponding dimension, by virtue of the reversible work theorem they can be directly related to the thermodynamic pressure in that dimension, i.e., a mean force (see Text S1) [25], [26].
Determination of each model's elasticity was based on six or more 2-ns-minimum simulations in which the peptidoglycan was stretched in the direction parallel to the glycan strands between 1.25% and 17.5% (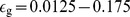 ) relative to the relaxed state and six more simulations between 5% and 45% (
) relative to the relaxed state and six more simulations between 5% and 45% (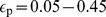 ) parallel to the peptide cross-links. Each simulation was repeated to ensure consistency of the results, giving at least 24 simulations per cell-wall patch (see Fig. S3 in SI). The resulting elasticities and Poisson's ratios are presented in Table 1, along with measurements and calculations from other studies [24], [27]–[30].
) parallel to the peptide cross-links. Each simulation was repeated to ensure consistency of the results, giving at least 24 simulations per cell-wall patch (see Fig. S3 in SI). The resulting elasticities and Poisson's ratios are presented in Table 1, along with measurements and calculations from other studies [24], [27]–[30].
Table 1. Poisson's ratios (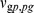 ) and Young's moduli
) and Young's moduli 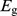 and
and 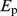 for simulated peptidoglycan patches compared with reported values from other studies.
for simulated peptidoglycan patches compared with reported values from other studies.
| Model |
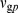
|
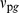
|
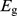 (MPa) (MPa) |
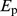 (MPa) (MPa) |
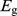 / /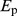
|
| avg08 | 0.670 | 0.175 | 11.4 | 4.0 | 2.84 |
| avg17 | 0.324 | 0.087 | 66.3 | 17.5 | 3.79 |
| avg26 | 0.363 | 0.062 | 62.5 | 6.1 | 10.25 |
| Inf1 | 0.216 | 0.020 | 125.7 | 11.3 | 11.05 |
| Inf2 | 0.302 | 0.018 | 212.6 | 11.6 | 18.39 |
| AFM [27] | 0.48 | 0.16 | 45 (35–60) | 25 (15–30) | 1.17–4.0 |
| exp. [29] | 0 | 0 | 49±20 | 23±8.0 | 2.13 |
| exp. [30] | 0.4 | 0.4 | - | 50–150 | - |
| theory [28] | - | - | - | 30 | - |
| theory [24] | 0.35–0.67 | 0.03–0.23 | 10–32 | 3–5 | 2.0–10.7 |
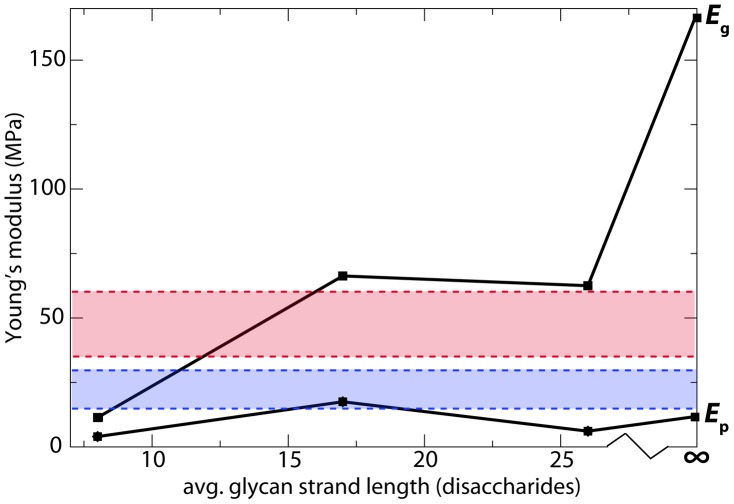
All simulated models reproduce the expected anisotropy of the elastic moduli in the two orthogonal directions [27]. The glycan strands are found to be much stiffer, with values of 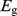 ranging from approximately 11 MPa to 66 MPa, compared to 4–18 MPa for
ranging from approximately 11 MPa to 66 MPa, compared to 4–18 MPa for 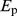 (both ranges for finite average strand lengths only). These values are similar to the ranges found in AFM measurements on E. coli, i.e.,
(both ranges for finite average strand lengths only). These values are similar to the ranges found in AFM measurements on E. coli, i.e., 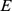 = 35–60 MPa perpendicular to the cell axis and 15–30 MPa parallel [27], as well as other theoretically derived elasticities [24], [29] (see Fig. 4). The glycan elasticity
= 35–60 MPa perpendicular to the cell axis and 15–30 MPa parallel [27], as well as other theoretically derived elasticities [24], [29] (see Fig. 4). The glycan elasticity 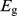 increases with average strand length, and for infinite strand lengths, it grows to as much as 200 MPa (see Inf1 and Inf2 in Table 1).
increases with average strand length, and for infinite strand lengths, it grows to as much as 200 MPa (see Inf1 and Inf2 in Table 1). 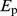 , on the other hand, has no apparent correlation with average strand length.
, on the other hand, has no apparent correlation with average strand length.
Figure 4. Young's modulus vs. average glycan strand length for the simulated patches.
The elasticity in the glycan-strand direction is labeled 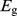 and that in the peptide direction is
and that in the peptide direction is 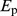 . The red and blue bars represent the range of values measured in AFM experiments for the circumferential and axial cellular directions, respectively [27].
. The red and blue bars represent the range of values measured in AFM experiments for the circumferential and axial cellular directions, respectively [27].
The relationship between the Poisson's ratios, specifically that 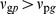 for all models, indicates that strain in the direction of the glycan strands induces a significant deformation in the peptide direction, but that the reverse is not true. Given that it is known that the glycan strands are aligned with the circumference of the cell and the peptide links with the long axis, the result is that stress applied to the cell wall will be primarily absorbed in the axial direction, leading to a lengthening of the cell, but not an increase in radius, just as observed experimentally [4], [31]. As average strand length increases, both Poisson's ratios decrease, effectively decoupling the two components of the peptidoglycan layer. One result of this decoupling is that the ratio of the two elasticities,
for all models, indicates that strain in the direction of the glycan strands induces a significant deformation in the peptide direction, but that the reverse is not true. Given that it is known that the glycan strands are aligned with the circumference of the cell and the peptide links with the long axis, the result is that stress applied to the cell wall will be primarily absorbed in the axial direction, leading to a lengthening of the cell, but not an increase in radius, just as observed experimentally [4], [31]. As average strand length increases, both Poisson's ratios decrease, effectively decoupling the two components of the peptidoglycan layer. One result of this decoupling is that the ratio of the two elasticities, 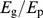 , increases monotonically with average strand length.
, increases monotonically with average strand length.
Quantifying macroscopic properties of the cell wall
Besides elasticity, other distinguishing physical characteristics of the cell wall as a whole include its thickness, the size of pores within it, the ordering of its strands, and the area per disaccharide. Using the five model patches developed, all of these characteristics were determined under different applied strains and compared to experimental measurements (see Table 2).
Table 2. Various properties of the simulated peptidoglycan patches under different applied strains.
| Model | Applied strain | thick (dens.) | thick (stress) | angle (°) | Pore rad. | unit area (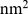 ) ) |
| avg8 |
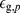 = 0 = 0 |
3.87 | 2.72 | −7.8 28.3 28.3 |
2.54 | 2.96 |
| avg8 |
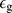 = 0.10 = 0.10 |
3.39 | 2.06 | −3.8 32.5 32.5 |
2.95 | 3.26 |
| avg8 |
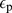 = 0.30 = 0.30 |
3.28 | 1.74 | −3.8 29.5 29.5 |
3.10 | 3.85 |
| avg17 |
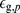 = 0 = 0 |
3.42 | 2.27 | −2.9 23.9 23.9 |
2.05 | 3.07 |
| avg17 |
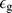 = 0.075 = 0.075 |
3.17 | 2.19 | −3.0 21.9 21.9 |
2.34 | 3.30 |
| avg17 |
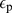 = 0.30 = 0.30 |
3.01 | 1.85 | −2.2 26.0 26.0 |
3.28 | 3.99 |
| avg26 |
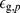 = 0 = 0 |
3.53 | 2.50 | −0.6 22.7 22.7 |
2.09 | 2.82 |
| avg26 |
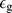 = 0.075 = 0.075 |
3.25 | 2.27 | −0.4 19.6 19.6 |
2.29 | 3.03 |
| avg26 |
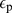 = 0.30 = 0.30 |
3.07 | 2.34 | 0.4 22.8 22.8 |
3.43 | 3.67 |
| Inf1 |
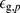 = 0 = 0 |
3.39 | 2.64 | −1.5 20.9 20.9 |
2.05 | 2.82 |
| Inf1 |
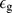 = 0.075 = 0.075 |
2.87 | 2.61 | −0.9 12.4 12.4 |
1.89 | 3.03 |
| Inf1 |
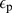 = 0.30 = 0.30 |
2.63 | 1.74 | −1.3 21.7 21.7 |
2.92 | 3.63 |
| Inf2 |
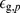 = 0 = 0 |
3.55 | 2.86 | −0.3 21.6 21.6 |
1.92 | 2.55 |
| Inf2 |
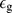 = 0.075 = 0.075 |
3.13 | 2.50 | 0.0 12.6 12.6 |
1.87 | 2.74 |
| Inf2 |
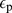 = 0.30 = 0.30 |
3.31 | 2.26 | −0.1 21.9 21.9 |
2.44 | 3.32 |
All thicknesses and radii are presented in units of nm. The most recent experiments have assigned a thickness of 2–4 nm at most [11], [34]. Pore sizes measured experimentally range from 2–3 nm in radius [5], [35] and even up to 5 nm in AFM experiments [34]. The experimental unit surface area is estimated to be 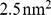 [37].
[37].
Based on different techniques, the thickness of the E. coli peptidoglycan layer has been assigned a range of values, including 2.5 nm (small-angle neutron scattering [32]), 6.0 nm (AFM [27]), and 6.4 nm (cryo-electron microscopy [33]). More recent ECT experiments estimated the thickness to be 4 nm at most [20] and AFM experiments measured ∼2 nm [34]. In contrast, cell walls from Pseudomonas aeruginosa appear even thinner, ranging from 2.4 nm (cryo-EM [33]) to 3.0 nm (AFM [27]), while that from Caulobacter crescentus is up to 7-nm thick [11].
The thickness in the simulated constructs was determined in two different ways. First, the mass density as a function of  , the coordinate orthogonal to the plane of the cell wall, was measured. This density was calculated for all the heavy atoms in the peptidoglycan, averaged over each trajectory. Values for the thickness were taken as the width of the density profile at 10% of its peak (see Fig. 5E). For the relaxed cell walls, the thickness ranged from 3.4–3.9 nm, in agreement with the most recent ECT measurements [11]. Under strain, this thickness decreased by up to 20%.
, the coordinate orthogonal to the plane of the cell wall, was measured. This density was calculated for all the heavy atoms in the peptidoglycan, averaged over each trajectory. Values for the thickness were taken as the width of the density profile at 10% of its peak (see Fig. 5E). For the relaxed cell walls, the thickness ranged from 3.4–3.9 nm, in agreement with the most recent ECT measurements [11]. Under strain, this thickness decreased by up to 20%.
Figure 5. Peptidoglycan under strain.
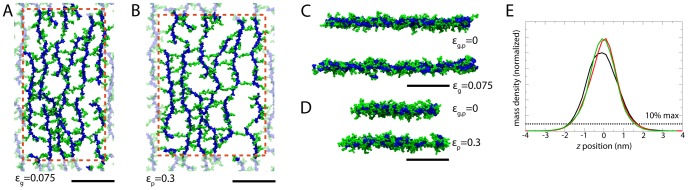
Shown in all panels is the avg17 cell-wall patch. The black bars in A–D are all 10 nm in length. (A,B) Top view with (A) 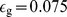 and (B)
and (B) 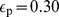 . (C) Axial view (glycan strands oriented in the plane of the page). (D) Circumferential view (glycan strains pointing into the page). (E) Normalized mass density for
. (C) Axial view (glycan strands oriented in the plane of the page). (D) Circumferential view (glycan strains pointing into the page). (E) Normalized mass density for 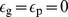 (black),
(black), 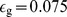 (red), and
(red), and 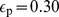 (green). Thickness was taken as the width at 10% of the maximum for each curve separately. A movie of stretching for
(green). Thickness was taken as the width at 10% of the maximum for each curve separately. A movie of stretching for 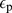 = 0.20 is also provided (Movie S3).
= 0.20 is also provided (Movie S3).
As a complementary measure of thickness, pressure profiles as a function of  were measured for the patch in each simulation. The thickness was then taken to be the stress-bearing part of the wall, i.e., that fraction of the simulation system with a significantly increased pressure compared to bulk water (see Fig. S1 in SI). This thickness was as much as 1–1.5 nm less than that derived from the mass density. Such a result is unsurprising, as the free peptide chains, which project outward from the cell wall, will contribute to the mass density but do not bear any stress (see SI for a detailed discussion of the pressure profile calculations).
were measured for the patch in each simulation. The thickness was then taken to be the stress-bearing part of the wall, i.e., that fraction of the simulation system with a significantly increased pressure compared to bulk water (see Fig. S1 in SI). This thickness was as much as 1–1.5 nm less than that derived from the mass density. Such a result is unsurprising, as the free peptide chains, which project outward from the cell wall, will contribute to the mass density but do not bear any stress (see SI for a detailed discussion of the pressure profile calculations).
The maximum pore size in the cell wall in different states has been measured indirectly by determining the largest objects that can pass through it. For example, fluorescently labeled dextran molecules were used to estimate the pore radius in the E. coli wall as 2.06 nm in the relaxed state [5]. In another study, proteins up to 100 kDa in size were released from osmotically shocked cells, giving an estimated pore radius of 3.1 nm for stretched peptidoglycan [35]. For the cell walls with finite glycan strand lengths studied here, i.e., avg8, avg17, and avg26, the maximum pore radius averaged over time was 2.05 to 2.44 nm in the relaxed state (see Fig. S4). This radius almost uniformly increased under strain, with the maximum observed being 3.43 nm, in agreement with the large pore size observed in the osmotic-shock experiments [35]. These pore sizes fall in the same range as those observed in CG simulations [23], although neither captures the very large pores (10-nm diameter) observed in recent AFM experiments [34], most likely explained by cell wall-spanning macromolecular machinery [36].
ECT images of frozen E. coli sacculi have revealed a lack of significant ordering of the glycan strands in the relaxed state [11], although some question remains as to whether this disorder persists when the cell wall is under tension as in a living cell [1]. For the simulated cell walls, the ordering was quantified by measuring the angle between segments of each strand and the circumferential axis (see Fig. S7). The temporally and spatially averaged angle was typically close to 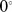 as expected, although persistently off-axis. The standard deviation in the angle was found to be significant at around 20–
as expected, although persistently off-axis. The standard deviation in the angle was found to be significant at around 20–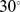 (see Table 2). For avg8, avg17, and avg26, the difference in this deviation was minimal under strain when compared to the relaxed state, suggesting that the wall does not become more ordered under tension. In contrast, for constructs Inf1 and Inf2, tension in the direction of the strands notably decreases their off-axis fluctuations. The sensitivity of these fluctuations to tension is due to the strands' inability to redirect the applied stress into the peptide cross-links, reflected also in their reduced Poisson's ratios (see Table 1).
(see Table 2). For avg8, avg17, and avg26, the difference in this deviation was minimal under strain when compared to the relaxed state, suggesting that the wall does not become more ordered under tension. In contrast, for constructs Inf1 and Inf2, tension in the direction of the strands notably decreases their off-axis fluctuations. The sensitivity of these fluctuations to tension is due to the strands' inability to redirect the applied stress into the peptide cross-links, reflected also in their reduced Poisson's ratios (see Table 1).
The average surface area per disaccharide has been estimated at 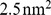 based on the number of
based on the number of 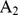 pm molecules in a given bacterium [37]. We note that this area can depend on a variety of factors, however, including ion concentration, pH, and the presence of denaturants [2], [4], although in the current study, only neutralizing
pm molecules in a given bacterium [37]. We note that this area can depend on a variety of factors, however, including ion concentration, pH, and the presence of denaturants [2], [4], although in the current study, only neutralizing 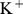 ions are used (see Methods). For the different patches examined here, the unit area for the relaxed cell wall ranges from 2.6 to
ions are used (see Methods). For the different patches examined here, the unit area for the relaxed cell wall ranges from 2.6 to 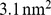 , and rises to 3–4
, and rises to 3–4 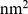 under strain (see Table 2). While at first, the discrepancy between experiment and modeling appears large, it should be noted that the cell wall may not be uniformly single layered, with up to three layers in some regions predicted [32]. Peptidoglycan in these additional layers would serve to lower the effective unit area for a single-layered cell wall. Considering a range of possible cell walls from completely single-layered to completely double-layered gives a range of possible unit areas of 2.5–5.0
under strain (see Table 2). While at first, the discrepancy between experiment and modeling appears large, it should be noted that the cell wall may not be uniformly single layered, with up to three layers in some regions predicted [32]. Peptidoglycan in these additional layers would serve to lower the effective unit area for a single-layered cell wall. Considering a range of possible cell walls from completely single-layered to completely double-layered gives a range of possible unit areas of 2.5–5.0 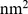 . If one assumes that the initial strand spacing used during modeling is linearly related to the resulting unit area, this implies that the average strand spacing can be no less than 2 nm (unit area of 2–2.67
. If one assumes that the initial strand spacing used during modeling is linearly related to the resulting unit area, this implies that the average strand spacing can be no less than 2 nm (unit area of 2–2.67 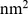 ) and no more than 4 nm (unit area of 4–5.33
) and no more than 4 nm (unit area of 4–5.33 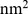 ).
).
Discussion
The native architecture and organization of the bacterial cell wall are largely inaccessible to direct imaging techniques, though at the very edge of the resolution of ECT, glycan strands could be discerned in a Gram-negative sacculus. These strands were, nonetheless, fragmented, and the cross-links were indiscernible [11]. Furthermore, the imaged samples are no longer part of living cells. For these reasons, modeling fills a critical gap between biochemical data on the cell wall's constituents and biophysical data on its macroscopic properties. In this paper, patches of an E. coli cell wall were made using a circumferential layered model, supported by ECT imaging of both Gram-negative and Gram-positive sacculi [4], [11], plausibility arguments based on the thickness and glycan strand length [1], and the average peptide-peptide angle measured above (see Fig. 2B). The patches were constructed using only a few initial parameters, including the initial strand spacing (roughly 3 nm), degree of cross-linking (50%), and average glycan strand length (between 8 and 26 disaccharides).
In the simulated cell-wall patches, peptidoglycan was found to be relatively inelastic in the direction of the glycan strands, while very elastic in the direction of the peptide cross-links. The calculated Young's moduli for the two directions, 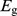 and
and 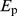 , respectively, were found to be in good agreement with multiple AFM measurements [27], [29], with the best agreement being found for the constructs avg17 and avg26 (see Table 1). The average glycan strand lengths for these two constructs also match those measured experimentally for E. coli cells in the stationary (17.8) and exponential growth (25.8) phases [20].
, respectively, were found to be in good agreement with multiple AFM measurements [27], [29], with the best agreement being found for the constructs avg17 and avg26 (see Table 1). The average glycan strand lengths for these two constructs also match those measured experimentally for E. coli cells in the stationary (17.8) and exponential growth (25.8) phases [20]. 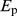 determined for live bacteria grown in aragose gel (5–15 MPa) was notably higher than our calculations, although other factors such as the outer membrane stiffness or incomplete gel polymerization may have inflated the number [30].
determined for live bacteria grown in aragose gel (5–15 MPa) was notably higher than our calculations, although other factors such as the outer membrane stiffness or incomplete gel polymerization may have inflated the number [30].
Further evidence of the relative stretchability of the peptide cross-links compared to the glycan strands comes from the decrease in Poisson's ratios as average glycan strand length increases. At short lengths, there is a significant coupling between the peptide cross-links and the glycan strands, allowing the former to absorb stress from the latter. At longer lengths, however, strain applied to the glycan strands is primarily absorbed by the strands alone, which, due to their inability to stretch much beyond their initial lengths, induces a large stress in the cell wall in their direction. This resistance to expansion, thus, does not depend on the peptide cross-links but is intrinsic to the glycan strands. Indeed, an intriguing suggestion is that longer glycan strands can compensate for a decrease in cross-linking percentage to maintain cell integrity [38]. While the fraction of peptides in cross-links was fixed near 50% for all models here, 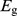 is directly related to the glycan strand length, whereas
is directly related to the glycan strand length, whereas  is independent. Although it remains to be shown, we hypothesize that, conversely,
is independent. Although it remains to be shown, we hypothesize that, conversely, 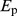 will be more sensitive than
will be more sensitive than 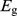 to the degree of cross-linking.
to the degree of cross-linking.
Beyond elasticity several other quantifiable properties were measured from the simulations, including the cell-wall thickness, maximum pore radius, and unit area per disaccharide. Excellent agreement with experimentally determined thicknesses [11] and pore sizes [5], [35] was found. The unit area measured in simulations (2.6–4 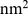 ) implies a cell wall that is more sparse than that estimated from experiment (2.5
) implies a cell wall that is more sparse than that estimated from experiment (2.5 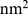 ). However, those experimental estimates are based on quantifying the total number of
). However, those experimental estimates are based on quantifying the total number of 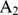 pm molecules per cell, irrespective of their place in the cell wall [37]. Neutron-scattering experiments have led to the suggestion that the Gram-negative cell wall is primarily a single layer, but includes regions of up to three layers over 25% of the surface [32]. The excess peptidoglycan in these additional, but limited and incomplete, layers would raise the experimental unit area for a single layer to 3.75
pm molecules per cell, irrespective of their place in the cell wall [37]. Neutron-scattering experiments have led to the suggestion that the Gram-negative cell wall is primarily a single layer, but includes regions of up to three layers over 25% of the surface [32]. The excess peptidoglycan in these additional, but limited and incomplete, layers would raise the experimental unit area for a single layer to 3.75 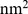 , in significantly better agreement with that from the models examined here, also supporting the choice of initial strand spacing of 3 nm.
, in significantly better agreement with that from the models examined here, also supporting the choice of initial strand spacing of 3 nm.
The average angle of the glycan strands with respect to the circumferential axis was found to be near 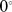 , although the standard deviation was typically 20–
, although the standard deviation was typically 20–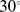 , even under tension (see Table 2). The lack of alignment amongst the strands argues in favor of a disordered circumferential model, as previously indicated by ECT [11]. A chiral patterning of peptidoglycan has been suggested based on recent experiments, and was attributed to a helical movement of MreB, a proposed cytoskeletal protein [39], [40]. Recent total internal reflection fluorescence and ECT experiments have indicated, however, that MreB moves circumferentially around the cell and does not form long filaments [41]–[44]. The glycan-strand angle measured here was often negative (range of −
, even under tension (see Table 2). The lack of alignment amongst the strands argues in favor of a disordered circumferential model, as previously indicated by ECT [11]. A chiral patterning of peptidoglycan has been suggested based on recent experiments, and was attributed to a helical movement of MreB, a proposed cytoskeletal protein [39], [40]. Recent total internal reflection fluorescence and ECT experiments have indicated, however, that MreB moves circumferentially around the cell and does not form long filaments [41]–[44]. The glycan-strand angle measured here was often negative (range of −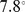 to
to 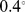 ), which hints at a slight intrinsic chirality in stressed peptidoglycan networks, irrespective of their assembly. Whether this could explain the experimental results remains unclear.
), which hints at a slight intrinsic chirality in stressed peptidoglycan networks, irrespective of their assembly. Whether this could explain the experimental results remains unclear.
The widespread agreement between simulation and experiment for all of the aforementioned properties, including elasticity, thickness, pore size, and unit area, serves to validate the connection made between the modeled atomic-scale properties of peptidoglycan and the macro-scale properties probed experimentally. The present molecular models support a cell wall composed predominantly of a single layer of peptidoglycan with glycan strands running circumferentially around the cell in a disordered fashion. Furthermore, assuming our model is correct, we predict that the disorder, which is primarily due to the random orientation of the peptide cross-links relative to the strands, persists under native cellular conditions. While we do not consider possible growth mechanisms here in detail, the insertion of new peptidoglycan strands has been predicted to be a function of such disorder, as well as mechanical tension and MreB [45], [46]. To examine tension-dependent insertion, we also created a peptidoglycan patch in which one strand was deleted, tension applied, and then the strand was added back to the gap that formed. Because some cross-links between the re-added strand and the rest of the patch formed in alternate locations, a slight decrease in the degree of connectivity resulted and one larger pore was observed (radius of 3.6 nm vs. 2.9 nm; see Text S1 and Fig. S5 for more details). Because this pore may serve as a site for addition of the next peptidoglycan strand, it cannot be assumed that larger pores are an inevitable product of tension-dependent insertion. However, over repeated growth cycles, the insertion mechanism used is likely to become increasingly relevant to the large-scale structure that develops.
While a number of other simulations of bacterial cell walls have been carried out in recent years [23],[39],[47], they are all highly coarse grained (CG), a necessary approach for modeling complete sacculi. Coarse graining the system requires, however, that one make a number of assumptions about the properties of individual “beads” in the CG model, including what underlying atoms they represent, how they are connected and interact with each other, and how they are affected by the surrounding environment, e.g., solvent. Where possible such assumptions are rooted in experimental data, although the reliability of those data and their conversion to model parameters is not always straightforward. On the other hand, models built starting from the atomic scale, in which the parameters are not specialized for each application, can utilize the same experimental data for validation, as done here. The atomic-scale model is limited in size compared to the CG models, however, and therefore cannot fully reproduce distributions in strand length [23] nor capture structural features beyond the modeled scale, e.g., pore sizes up to 10-nm in diameter [34]; additionally, a visual comparison of the previous CG models with the atomic-scale models here suggests that the latter models are still too ordered, likely a remnant of the initial construction [23]. Thus, future iterations will be used to probe more realistic growth models, the dependence of cellular-scale properties on the cross-linking fraction and strand spacing, and also the interactions of the network with various growth and remodeling enzymes and embedded proteins.
Methods
Parametrization of novel residues and linkages
Force-field parameters for GlcNAc were developed by linking glucose and acetamide, with those charges and parameters near the interface determined. Similarly, MurNAc parameters were developed by linking GlcNAc with lactic acid. Charges of interfacial atoms, namely C2 on the sugar ring and the the NH group on the acetamide side chain in both residues along with C3 on the ring, the 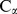 in the lactic acid side chain, and the bridging O3 oxygen in MurNAc, were modified. These charges were determined from ab initio quantum chemical calculations using a pre-release version of the Force Field Toolkit (ffTK) plugin for VMD, following the CHARMM parametrization procedures [48], [49]. Bond, angle, and dihedral parameters involving the interfacial atoms were similarly determined. Because D-isoglutamate and
in the lactic acid side chain, and the bridging O3 oxygen in MurNAc, were modified. These charges were determined from ab initio quantum chemical calculations using a pre-release version of the Force Field Toolkit (ffTK) plugin for VMD, following the CHARMM parametrization procedures [48], [49]. Bond, angle, and dihedral parameters involving the interfacial atoms were similarly determined. Because D-isoglutamate and 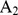 pm are nearly identical to their standard amino-acid counterparts, glutamate and lysine, their parameters were developed solely by analogy. The complete topology and parameter set used for subsequent simulations is provided in Text S2 and S3.
pm are nearly identical to their standard amino-acid counterparts, glutamate and lysine, their parameters were developed solely by analogy. The complete topology and parameter set used for subsequent simulations is provided in Text S2 and S3.
System construction
Because simulating the actual transpeptidase reactions is prohibited by both current knowledge of the order of events and available computational resources, a procedure was developed to build the peptidoglycan network with a statistical view of the general organization. In the first step, a set of E. coli peptidoglycan strands with the number of disaccharides chosen according to a random Gaussian distribution of specified mean are placed parallel to one another separated by a given distance (typically 2–3 nm, with a  0.5 nm random deviation). Each system is fully solvated in explicit water and sufficient
0.5 nm random deviation). Each system is fully solvated in explicit water and sufficient 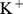 ions were added to the solution to neutralize the high negative charge in the peptidoglycan. The final atom count ranged from 100,000 to 545,000 atoms. Initially, the glycan strands are held fixed for a 2-ns simulation while the peptides are left free to move. Next, the trajectory is analyzed to find when each available
ions were added to the solution to neutralize the high negative charge in the peptidoglycan. The final atom count ranged from 100,000 to 545,000 atoms. Initially, the glycan strands are held fixed for a 2-ns simulation while the peptides are left free to move. Next, the trajectory is analyzed to find when each available 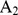 pm
pm  -nitrogen first comes near an available D-Ala carbonyl oxygen, and for what fraction of time they are within this distance. Finally, the list of possible links is ordered according to the first contact using a more stringent distance criterion along with a minimum time within range. Links are then added, in order, such that when a given
-nitrogen first comes near an available D-Ala carbonyl oxygen, and for what fraction of time they are within this distance. Finally, the list of possible links is ordered according to the first contact using a more stringent distance criterion along with a minimum time within range. Links are then added, in order, such that when a given 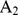 pm or D-Ala residue is linked, its entire peptide is removed from further consideration. The time and distance criteria are chosen to target roughly 50% cross-linking overall, as typically observed for E. coli
[1], [20].
pm or D-Ala residue is linked, its entire peptide is removed from further consideration. The time and distance criteria are chosen to target roughly 50% cross-linking overall, as typically observed for E. coli
[1], [20].
The cross-linked peptidoglycan network is first relaxed using energy minimization, and then allowed to equilibrate during MD simulations with no applied restraints. It should be noted that the network is periodic, with glycan strands as well as peptides covalently linked across the simulation system's periodic boundaries, thus mimicking a much larger patch of cell wall (see Fig. 3). The resulting network is simulated for at least 20 ns under constant pressure conditions, which allows its dimensions to fluctuate. The relaxed in-plane dimensions of each patch were taken as the average over the last 10 ns. These dimensions are: 9.3 0.2
0.2 18.1
18.1 0.5
0.5  (avg8), 18.7
(avg8), 18.7 0.2
0.2 33.4
33.4 0.25
0.25 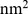 (avg17), 17.2
(avg17), 17.2 0.4
0.4 51.2
51.2 0.4
0.4 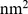 (avg26), 18.6
(avg26), 18.6 0.3
0.3 13.6
13.6 0.1
0.1 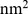 (Inf1), and 16.8
(Inf1), and 16.8 0.3
0.3 27.4
27.4 0.2
0.2 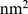 (Inf2).
(Inf2).
Molecular dynamics simulations
All simulations were run with the molecular dynamics package NAMD 2.9 [50] and the CHARMM force field [51]–[53]. A constant temperature of 310 K was held using Langevin dynamics; a pressure of 1 atm in the direction normal to peptidoglycan layer was maintained with a Langevin piston [54]. A 2-fs time step was utilized, with short-range non-bonded interactions (12-Å cutoff) evaluated every time step and long-range electrostatics every two time steps using the particle-mesh Ewald method [55]. All figures were made using VMD [56].
Supporting Information
Pressure profile along the glycan axis for simulation of avg17 patch with 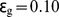 . The grey line is the original profile computed in 1-Å slabs, with the black curve representing a 5-Å running average. The red line is the stress-bearing thickness of the peptidoglycan at 10% of the peak stress.
. The grey line is the original profile computed in 1-Å slabs, with the black curve representing a 5-Å running average. The red line is the stress-bearing thickness of the peptidoglycan at 10% of the peak stress.
(PNG)
Pressure profiles along the  axis (normal to the peptidoglycan layer) for avg17 with
axis (normal to the peptidoglycan layer) for avg17 with 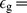 0.025, 0.05, 0.075, 0.1, 0.125, 0.15, and 0.175.
0.025, 0.05, 0.075, 0.1, 0.125, 0.15, and 0.175.
(PNG)
Stress as a function of strain for all simulated systems. In each plot, the black circles are data from simulations in which 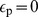 and
and 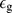 was varied, while the red squares are from simulations in which
was varied, while the red squares are from simulations in which 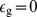 and
and 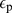 was varied. The corresponding lines are linear fits to the data.
was varied. The corresponding lines are linear fits to the data.
(PNG)
Patch of cell wall with maximum-radius spheres inscribed. Unlike in other figures, here the glycan strands are in grey and the peptides in tan. Sphere color is assigned based on size, with blue representing those with radius less than 1 nm, green less than 1.25 nm, yellow less than 1.5 nm, orange less than 1.75 nm, and red greater than 1.75 nm.
(PNG)
Strain-dependent insertion. In both panels, the avg17 patch is under strain 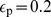 . Glycan strands are in blue and peptide cross-links in green. The strand selected for deletion and later replacement is shown in red and orange. (A) Original patch. (B) Patch after strand deletion, equilibration, and subsequent strand replacement.
. Glycan strands are in blue and peptide cross-links in green. The strand selected for deletion and later replacement is shown in red and orange. (A) Original patch. (B) Patch after strand deletion, equilibration, and subsequent strand replacement.
(PNG)
Peptidoglycan patches simulated with effectively infinite strand lengths, colored as in Fig. 3 in the main text. The black scale bars below are all equivalent at 10 nm in length. Final relaxed states for (A) inf15 and (B) inf30 are shown.
(PNG)
Quantifying glycan-strand angle as a measure of disorder. Shown are the NAG and NAM saccharide rings against a transparent outline of the full cell wall viewed from the outside. Individual angles made with the dashed line were measured for all vectors connecting the centers of rings spaced at least four saccharides apart, although only a subset of vectors are shown here. These vectors were then averaged over all separations within a given strand, over all strands within the simulated cell-wall patch, and over all frames in the simulation trajectory. The black, red, green, and purple vectors give positive angles, while the blue vector gives a negative angle. The dashed line represents the cell's circumferential axis with which the glycan strands were initially aligned during construction.
(PNG)
Simulation of a 320-mer glycan strand for 5 ns.
(MPG)
Relaxation of the avg17 patch after cross-linking of the peptides.
(MPG)
Response of the avg17 patch after a strain of 0.2 is applied in the peptide direction.
(MPG)
Formal derivation of the stress-strain relationships used in the study, expanded methods for measurements, and a discussion of simulations of strain-dependent strand insertion.
(PDF)
CHARMM-force field formatted topology file for the residues unique to this study.
(TXT)
CHARMM-force field formatted parameter file for the residues unique to this study.
(TXT)
Funding Statement
NIH K22-AI100927 to J.C.G. R01 GM062342 to B.R. HHMI to G.J.J. Gordon and Betty Moore Center for Integrative Study of Cell Regulation at Caltech to G.J.J. Computational resources were provided by the Computation Institute and the Biological Sciences Division of the University of Chicago and Argonne National Laboratory, under grant S10 RR029030-01. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Vollmer W, Seligman SJ (2010) Architecture of peptidoglycan: more data and more models. Trends Microbiol 18: 59–66. [DOI] [PubMed] [Google Scholar]
- 2. Koch AL, Woeste S (1992) Elasticity of the sacculus of Escherichia coli . J Bacteriol 174: 4811–4819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Vollmer W, Blanot D, de Pedro MA (2008) Peptidoglycan structure and architecture. FEMS Microbiol Rev 32: 149–167. [DOI] [PubMed] [Google Scholar]
- 4. Beeby M, Gumbart JC, Roux B, Jensen GJ (2013) Architecture and assembly of the Gram-positive cell wall. Mol Microbiol 88: 664–672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Demchick P, Koch AL (1996) The permeability of the wall fabric of Escherichia coli and Bacillus subtilis . J Bacteriol 178: 768–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Höltje JV (1998) Growth of the stress-bearing and shape-maintaining murein sacculus of Escherichia coli . Microbiol Mol Biol Rev 62: 181–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Pink D, Moeller J, Quinn B, Jericho M, Beveridge T (2000) On the architecture of the Gramnegative bacterial murein sacculus. J Bacteriol 182: 5925–5930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Dmitriev BA, Toukach FV, Schaper KJ, Holst O, Rietschel ET, et al. (2003) Tertiary structure of bacterial murein: the sca_old model. J Bacteriol 185: 3458–3468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Dmitriev B, Toukach F, Ehlers S (2005) Towards a comprehensive view of the bacterial cell wall. Trends Microbiol 13: 569–574. [DOI] [PubMed] [Google Scholar]
- 10. Meroueh SO, Bencze KZ, Hesek D, Lee M, Fisher JF, et al. (2006) Three-dimensional structure of the bacterial cell wall peptidoglycan. Proc Natl Acad Sci USA 103: 4404–4409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Gan L, Chen S, Jensen GJ (2008) Molecular organization of Gram-negative peptidoglycan. Proc Natl Acad Sci USA 105: 18953–18957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Hayhurst EJ, Kailas L, Hobbs JK, Foster SJ (2008) Cell wall peptidoglycan architecture in Bacillus subtilis . Proc Natl Acad Sci USA 105: 14603–14608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Young KD (2006) Too many strictures on structure. Trends Microbiol 14: 165–166. [DOI] [PubMed] [Google Scholar]
- 14.Doi M, Edwards SF (1986) The Theory of Polymer Dynamics. New York: Oxford. [Google Scholar]
- 15. Chu JW, Voth GA (2005) Allostery of actin filaments: Molecular dynamics simulations and coarse-grained analysis. Proc Natl Acad Sci USA 102: 13111–13116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Chu JW, Voth GA (2006) Coarse-grained modeling of the actin filament derived from atomistic-scale simulations. Biophys J 90: 1572–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Cros S, Garnier C, Axelos MA, Imberty A, Pérez S (1996) Solution conformations of pectin polysaccharides: determination of chain characteristics by small angle neutron scattering, viscometry, and molecular modeling. Biopolymers 39: 339–352. [DOI] [PubMed] [Google Scholar]
- 18. Kroon-Batenburg LMJ, Kruiskamp PH, Vliegenthart JFG, Kroon J (1997) Estimation of the persistence length of polymers by MD simulations on small fragments in solution. Application to cellulose. J Phys Chem B 101: 8454–8459. [Google Scholar]
- 19. Sauvage E, Kerff F, Terrak M, Ayala JA, Charlier P (2008) The penicillin-binding proteins: structure and role in peptidoglycan biosynthesis. FEMS Microbiol Rev 32: 234–258. [DOI] [PubMed] [Google Scholar]
- 20. Glauner B, Höltje JV, Schwarz U (1988) The composition of the murein of Escherichia coli . J Biol Chem 263: 10088–10095. [PubMed] [Google Scholar]
- 21. Costa K, Bacher G, Allmaier G, Dominguez-Bello MG, Engstrand L, et al. (1999) The morphological transition of Helicobacter pylori cells from spiral to coccoid is preceded by a substantial modification of the cell wall. J Biol Chem 181: 3710–3715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Quintela JC, Caparros M, de Pedro MA (1995) Variability of peptidoglycan structural parameters in Gram-negative bacteria. FEMS Microbiol Lett 125: 95–100. [DOI] [PubMed] [Google Scholar]
- 23. Huang KC, Wen B, Gitai Z, Wingreen N (2008) Cell shape and cell-wall organization in Gramnegative bacteria. Proc Natl Acad Sci USA 105: 19282–19287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Assidi M, Reis FD, Ganghoffer JF (2011) Equivalent mechanical properties of biological membranes from lattice homogenization. J Mech Behav Biomed Mater 4: 1833–1845. [DOI] [PubMed] [Google Scholar]
- 25. Ayton G, Smondyrev AM, Bardenhagen SG, McMurtry P, Voth GA (2002) Calculating the bulk modulus for a lipid bilayer with nonequilibrium molecular dynamics simulation. Biophys J 82: 1226–1238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Wells DB, Aksimentiev A (2010) Mechanical properties of a complete microtubule revealed through molecular dynamics simulation. Biophys J 99: 629–637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Yao X, Jericho M, Pink D, Beveridge T (1999) Thickness and elasticity of Gram-negative murein sacculi measured by atomic force microscopy. J Bacteriol 181: 6865–6875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Boulbitch A, Quinn B, Pink D (2000) Elasticity of the rod-shaped Gram-negative eubacteria. Phys Rev Lett 85: 5246–5249. [DOI] [PubMed] [Google Scholar]
- 29. Deng Y, Sun M, Shaevitz JW (2011) Direct measurement of cell wall stress stiffening and turgor pressure in live bacterial cells. Phys Rev Lett 107: 158101-1–158101-4. [DOI] [PubMed] [Google Scholar]
- 30. Tuson HH, Auer GK, Renner LD, Hasebe M, Tropini C, et al. (2012) Measuring the stiffness of bacterial cells from growth rates in hydrogels of tunable elasticity. Mol Microbiol 84: 874–891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. van den Bogaart G, Hermans N, Krasnikov V, Poolman B (2007) Protein mobility and diffusive barriers in Escherichia coli: consequences of osmotic stress. Mol Microbiol 64: 858–871. [DOI] [PubMed] [Google Scholar]
- 32. Labischinski H, Goodell EW, Goodell A, Hochberg ML (1991) Direct proof of a more-than-singlelayered peptidoglycan architecture of Escherichia coli W7: a neutron small-angle scattering study. J Bacteriol 173: 751–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Matias VRF, Al-Amoudi A, Dubocher J, Beveridge TJ (2003) Cryo-transmission electron microscopy of frozen-hydrated sections of Escherichia coli and Pseudomonas aeruginosa . J Bacteriol 185: 6112–6118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Turner RD, Hurd AF, Cadby A, Hobbs JK, Foster SJ (2013) Cell wall elongation mode in Gramnegative bacteria is determined by peptidoglycan architecture. Nat Commun 4: 1496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Vazquez-Laslop N, Lee H, Hu R, Neyfakh AA (2001) Molecular sieve mechanism of selective release of cytoplasmic proteins by osmotically shocked Escherichia coli . J Bacteriol 183: 2399–2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Scheurwater EM, Burrows LL (2011) Maintaining network security: how macromolecular structures cross the peptidoglycan layer. FEMS 318: 1–9. [DOI] [PubMed] [Google Scholar]
- 37. Wientjes FB, Woldringh CL, Nanninga N (1991) Amount of peptidoglycan in cell walls of Gramnegative bacteria. J Bacteriol 173: 7684–7691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Vollmer W, Höltje JV (2004) The architecture of the murein (peptidoglycan) in Gram-negative bacteria: vertical scaffold or horizontal layer(s)? J Bacteriol 186: 5978–5987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Wang S, Furchtgott L, Huang KC, Shaevitz JW (2012) Helical insertion of peptidoglycan produces chiral ordering of the bacterial cell wall. Proc Natl Acad Sci USA 109: E595–E604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Huang KC, Ehrhardt DW, Shaevitz JW (2012) The molecular origins of chiral growth in walled cells. Curr Opin Microbiol 15: 707–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Domínguez-Escobar J, Chastanet A, Crevenna AH, Formion V, Wedlich-Söldner R, et al. (2011) Processive movement of MreB-associated cell wall biosynthetic complexes in bacteria. Science 333: 225–228. [DOI] [PubMed] [Google Scholar]
- 42. Garner EC, Bernard R, Wang W, Zhuang X, Rudner DZ, et al. (2011) Coupled, circumferential motions of the cell wall synthesis machinery and MreB filaments in B. subtilis . Science 333: 222–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Swulius MT, Chen S, Ding HJ, Li Z, Briegel A, et al. (2011) Long helical filaments are not seen encircling cells in electron cryotomograms of rod-shaped bacteria. Biochem Biophys Res Commun 407: 650–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Swulius MT, Jensen GJ (2012) The helical MreB cytoskeleton in E. coli MC1000/pLE7 is an artifact of the N-terminal YFP tag. J Bacteriol 194: 6382–6386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Jiang HY, Sun SX (2010) Morphology, growth, and size limit of bacterial cells. Phys Rev Lett 105: 028101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Sun SX, Jiang H (2011) Physics of bacterial morphogenesis. Microbiol Mol Biol Rev 75: 543–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Furchtgott L, Wingreen NS, Huang KC (2011) Mechanisms for maintaining cell shape in rod-shaped Gram-negative bacteria. Mol Microbiol 80: 340–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Mayne CG, Saam J, Schulten K, Tajkhorshid E, Gumbart JC (2013) Rapid parameterization of small molecules using the force field toolkit. J Comp Chem 34: 2757–2770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Vanommeslaeghe K, Hatcher E, Acharya C, Kundu S, Zhong S, et al. (2010) CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J Comp Chem 31: 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, et al. (2005) Scalable molecular dynamics with NAMD. J Comp Chem 26: 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. MacKerell AD Jr, Bashford D, Bellott M, Dunbrack RL Jr, Evanseck J, et al. (1998) All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B 102: 3586–3616. [DOI] [PubMed] [Google Scholar]
- 52. Guvench O, Greene SN, Kamath G, Brady JW, Venable RM, et al. (2008) Additive empirical force field for hexopyranose monosaccharides. J Comp Chem 29: 2543–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Guvench O, Hatcher ER, Venable RM, Pastor RW, MacKerell AD Jr (2009) Additive empirical CHARMM force field for glycosyl linked hexopyranoses. J Chem Theory Comput 5: 2353–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Feller SE, Zhang YH, Pastor RW, Brooks BR (1995) Constant pressure molecular dynamics simulations —The Langevin piston method. J Chem Phys 103: 4613–4621. [Google Scholar]
- 55. Darden TA, York DM, Pedersen LG (1993) Particle mesh Ewald: An N log N method for Ewald sums in large systems. J Chem Phys 98: 10089–10092. [Google Scholar]
- 56. Humphrey W, Dalke A, Schulten K (1996) VMD - Visual Molecular Dynamics. J Mol Graphics 14: 33–38. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Pressure profile along the glycan axis for simulation of avg17 patch with 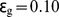 . The grey line is the original profile computed in 1-Å slabs, with the black curve representing a 5-Å running average. The red line is the stress-bearing thickness of the peptidoglycan at 10% of the peak stress.
. The grey line is the original profile computed in 1-Å slabs, with the black curve representing a 5-Å running average. The red line is the stress-bearing thickness of the peptidoglycan at 10% of the peak stress.
(PNG)
Pressure profiles along the  axis (normal to the peptidoglycan layer) for avg17 with
axis (normal to the peptidoglycan layer) for avg17 with 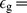 0.025, 0.05, 0.075, 0.1, 0.125, 0.15, and 0.175.
0.025, 0.05, 0.075, 0.1, 0.125, 0.15, and 0.175.
(PNG)
Stress as a function of strain for all simulated systems. In each plot, the black circles are data from simulations in which 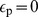 and
and 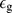 was varied, while the red squares are from simulations in which
was varied, while the red squares are from simulations in which 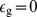 and
and 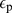 was varied. The corresponding lines are linear fits to the data.
was varied. The corresponding lines are linear fits to the data.
(PNG)
Patch of cell wall with maximum-radius spheres inscribed. Unlike in other figures, here the glycan strands are in grey and the peptides in tan. Sphere color is assigned based on size, with blue representing those with radius less than 1 nm, green less than 1.25 nm, yellow less than 1.5 nm, orange less than 1.75 nm, and red greater than 1.75 nm.
(PNG)
Strain-dependent insertion. In both panels, the avg17 patch is under strain 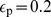 . Glycan strands are in blue and peptide cross-links in green. The strand selected for deletion and later replacement is shown in red and orange. (A) Original patch. (B) Patch after strand deletion, equilibration, and subsequent strand replacement.
. Glycan strands are in blue and peptide cross-links in green. The strand selected for deletion and later replacement is shown in red and orange. (A) Original patch. (B) Patch after strand deletion, equilibration, and subsequent strand replacement.
(PNG)
Peptidoglycan patches simulated with effectively infinite strand lengths, colored as in Fig. 3 in the main text. The black scale bars below are all equivalent at 10 nm in length. Final relaxed states for (A) inf15 and (B) inf30 are shown.
(PNG)
Quantifying glycan-strand angle as a measure of disorder. Shown are the NAG and NAM saccharide rings against a transparent outline of the full cell wall viewed from the outside. Individual angles made with the dashed line were measured for all vectors connecting the centers of rings spaced at least four saccharides apart, although only a subset of vectors are shown here. These vectors were then averaged over all separations within a given strand, over all strands within the simulated cell-wall patch, and over all frames in the simulation trajectory. The black, red, green, and purple vectors give positive angles, while the blue vector gives a negative angle. The dashed line represents the cell's circumferential axis with which the glycan strands were initially aligned during construction.
(PNG)
Simulation of a 320-mer glycan strand for 5 ns.
(MPG)
Relaxation of the avg17 patch after cross-linking of the peptides.
(MPG)
Response of the avg17 patch after a strain of 0.2 is applied in the peptide direction.
(MPG)
Formal derivation of the stress-strain relationships used in the study, expanded methods for measurements, and a discussion of simulations of strain-dependent strand insertion.
(PDF)
CHARMM-force field formatted topology file for the residues unique to this study.
(TXT)
CHARMM-force field formatted parameter file for the residues unique to this study.
(TXT)