Quantum and All-Atom Molecular Dynamics Simulations of Protonation and Divalent Ion Binding to Phosphatidylinositol 4,5-Bisphosphate (PIP₂)

Abstract

Molecular dynamics calculations have been used to determine the structure of phosphatidylinositol 4,5 bisphosphate (PIP₂) at the quantum level and to quantify the propensity for PIP₂ to bind two physiologically relevant divalent cations, Mg²⁺ and Ca²⁺. We performed a geometry optimization at the Hartree-Fock 6-31+G(d) level of theory in vacuum and with a polarized continuum dielectric to determine the conformation of the phospholipid headgroup in the presence of water and its partial charge distribution. The angle between the headgroup and the acyl chains is nearly perpendicular, suggesting that in the absence of other interactions, the inositol ring would lie flat along the cytoplasmic surface of the plasma membrane. Next, we employed hybrid quantum mechanics / molecular mechanics (QM/MM) simulations to investigate the protonation state of PIP₂ and its interactions with magnesium or calcium. We test the hypothesis suggested by prior experiments that binding of magnesium to PIP₂ is mediated by a water molecule that is absent when calcium binds. These results may explain the selective ability of calcium to induce the formation of PIP₂ clusters and phase separation from other lipids.

INTRODUCTION

The plasma membrane separates two highly distinct biological environments and is the site where intracellular signals are generated in response to binding of ligands, chemical stimuli, or the application of force. The production of second messengers depends on the lipid composition of the membrane and very often involves the synthesis, cleavage, or intercon version of polyphosphoinositides (PPIs) on the cytoplasmic face of the membrane^1,2. Defects in this process may lead to the acquisition of invasive or metastatic phenotypes or other cellular abnormalities in proliferation, differentiation, chemotaxis, exocytosis or endosomal and lysosomal membrane trafficking^1-3. The most abundant PPI is phosphatidylinositol 4,5-bisphosphate (PIP₂) which accounts for approximately 1% of the total phospholipid in the cell at a given time⁴. Due to its large headgroup and multivalent negative charge at physiological pH, PIP₂ also creates significant electrostatic interactions within the plane of the membrane^5-8. Investigations of PIP₂ containing monolayers at varying pH have demonstrated that the degree of ionization of the headgroup alters the phase behavior and transition temperature of such monolayers ⁹.

Hundreds of proteins interact in vitro with PIP₂ including the tumor suppressor PTEN and phosphoinositide 3-kinase (PI3K) which is activated by agonists for numerous cell surface receptors^1,2,10,11. Additionally, PIP₂ is capable of binding and activating mammalian potassium (Kir) channels through at least two putative binding sites, although no consensus PIP₂ binding sequence has been identified; PIP₂ may activate or inhibit channel gating in capsaicin receptors after phospholipase C activation^1-3,12-15. A major challenge in understanding the role of PIP₂ in vivo is determining how PIP₂ selectively activates or inhibits different proteins under different circumstances. One hypothesis is that PIP₂ exists in spatially distinct, or clustered, pools in the plasma membrane corralled by proteins that impede diffusion^4,16. Partitioning of PIP₂ leads to increased local concentration and a decreased diffusion rate, which may allow PIP₂ to act as a membrane scaffold, participate in endocytosis, promote actin assembly, or perform its other roles.

This hypothesis is supported by several recent experimental observations. Clusters of the SNAP receptor protein syntaxin-1 A on the plasma membrane require the formation of lipid domains^17-19. These domains are 80% PIP₂ in concentration and 73 nm in diameter. Transient formation of 100 nm domains containing the PIP₂ specific PLCδ PH domain have been observed to form within the cleavage furrow during cytokinesis ^2,3,9,18. Further, PIP₂ aggregation has been observed in model phospholipid monolayers using a Langmuir trough system^4,8,19. The introduction of 1 μM Ca²⁺ to the liquid subphase induces PIP₂ rich clusters 80 nm in diameter. Together, these data demonstrate that PIP₂ forms domains in vivo and that PIP₂ is able to form domains in the presence of divalent cations in vitro.

In this study, we use a multi-resolution computational framework to understand the atomic level structural details of the conformation of PIP₂, its protonation state, and its binding to divalent cations. An electronic structure geometry optimization was performed, which reveals the shape and orientation of PIP₂. Further investigation was carried out using hybrid quantum mechanics / molecular mechanics (QM/MM) simulations in the presence of pure water, or with added cations such as potassium, magnesium, or calcium. We applied the technique of umbrella sampling to delineate the free energy of binding and relative stability of the bound and unbound states. The outcome of these simulations lends insight into how PIP₂ is oriented with respect to the plasma membrane and possibly reacts to ion fluxes that occur at the membrane-cytoplasm interface of the cell.

METHODS

Geometry Optimization

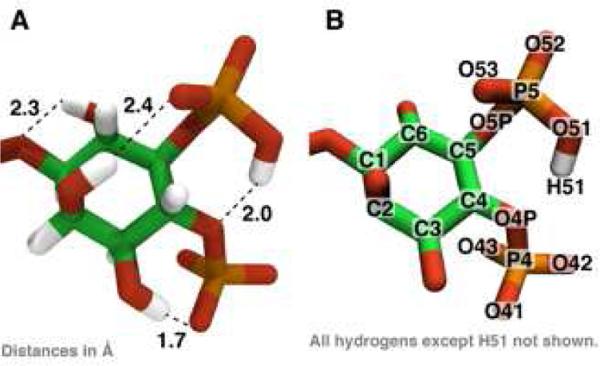
Geometry optimizations and vibrational calculations were performed primarily using the Gaussian 09 ^5-8,20 program with Hartree-Fock (HF) 6-31+G(d) model chemistry, which includes diffuse and polarizable functions, unless otherwise noted. For the electronic structure calculations, we truncated the stearate and arachidonate acyl chains after two carbons to improve the probability of selfconsistent field (SCF) convergence and decrease the computational resources (56 atoms, 300 electrons; see Supporting Information for the Z matrix). These methods are consistent with quantum mechanical (QM) calculations performed on other biomolecules parameterized in classical force fields^9,21,22. Charges were calculated using CHarges from ELectrostatic Potentials using a Grid based method (CHELPG)^10,11,23. The vibrational eigenvalues and eigenvectors were computed at HF/6-31G model chemistry and after applying suitable scaling factors^12-15,24 compared with ATR-FTIR experimental data on supported bilayers containing PIP₂^8,16. Relaxed potential energy scans of key angles and dihedrals were scanned in Gaussian 09 using the model chemistry as above and evaluated in increments of 10 or 20°. Atom names mentioned in the text refer to Figure 1.

Figure 1.

(A) The optimized geometry of PIP₂ highlighting several intramolecular hydrogen bonds. (B) The atom-naming scheme used in the text.

Hybrid QM/MM Simulations

The optimized PIP₂ geometry and charges were using in hybrid quantum mechanics / molecular mechanics (QM/MM)²⁵ molecular dynamics (MD) simula tions. A single PIP₂ molecule was placed in a water sphere containing approximately 10,000 TIP3 water molecules (10-15 Å buffer on all sides). Sodium, calcium, or magnesium were added to neutralize the −4 charge of the singly protonated PIP₂. Water molecules greater than 8 Å away from the PIP₂ were fixed in position. The system was split into two quantum regions: QM1, which contains only phospholipid atoms, and QM2, which contains interacting waters and ions. Two single-link atoms connect the QM regions to the classical regions (see e.g. ref ²⁶): the first link atom was placed between the third and fourth carbon of the inositol ring, the second link atom was placed between the fifth and sixth carbon of the inositol ring. The choice and sensitivity to location of link atoms on ring-structures has been investigated in our earlier studies and was found to not impact the optimized geometry significantly^27-29.

QM2 typically contains the five or six closest interacting waters and a divalent ion (if present). In one case, QM2 was expanded to include nine waters to cover all hydrogen bonds between the phosphomonoester groups and water molecules. We performed these calculations using a combination of GAMESS-UK³⁰ and CHARMM^31-33. Both QM regions (about 36 atoms) were treated with density functional theory (DFT) using the hybrid functional B3LYP/6-31G. We note that prior studies have investigated proton free energy landscapes using similar functionals²⁸. These studies have discussed the merits and limitations of these methods, such as accurate electrostatics, neglect of quantum effects, etc. Some of the simulations were repeated at a higher level of theory using either B3LYP/6-31G(d) or PBE/6-31G(d) to verify that we captured all salient hydrogen bonds and the correct orientation of the water molecules. The classical PIP₂ atoms and mobile ions are treated using the CHARMM36 all-hydrogen lipid forcefield parameterized for lipids and the CHARMM-consistent water model TIP3P³⁴. The CHARMM36 (C36) forcefield is significantly more accurate in reproducing experimental quantities for lipids than the previous iteration forcefield (C27r), particularly in matching the surface tension of bilayers simulated in the NPT ensemble^21,35. The parameters for the inositol ring and the phosphate groups have been derived from Hatcher, et al. ³⁶ and Mallajosyula, et al.³⁷ These combined parameters are obtained from the C36 version and differ from those of Li, et al.³⁸ who used the C27r forcefield, as discussed by Pastor and MacKerell²¹. Our parameters are also different from those used by Lupyan et al.³⁹ who parameterized PIP₂ at a net charge of −5 and explicitly included monovalent salts in all simulations.

In the QM/MM simulations, we performed the usual energy minimization (5000 steepest descent followed by 5000 steps of adopted basis Newton-Raphson) and constant temperature equilibration using Langevin dynamics at 300 K using a piston frequency of 10 ps⁻¹ before regular integration procedures in operation for pure MM systems using a standard 1 fs time step of integration. The QM/MM simulations were run for a total of 5 or 10 ps.

The reported average molecular area was computed by squaring the maximum distance between oxygens on different phosphomonoester groups over the course of a simulation. The error bar is the standard deviation of the measurement over the course of the trajectory.

Classical Simulations

All-atom classical MD simulations were run with the CHARMM program to determine starting structures for the hybrid QM/MM simulations and to perform analyses on a longer timescale. The same water sphere setup from the hybrid QM/MM simulations was employed, and waters on the edge were held fixed to prevent the sphere from expanding. The simulations were completed in the NVT ensemble using Langevin dynamics at 300 K. Starting structures for the QM/MM simulations and umbrella sampling analyses were vns of classical MD runs.

Umbrella Sampling and the Weighted Histogram Analysis Method

To test the dissociation of hydrogen H51 from oxygen O51, we began with one-dimensional umbrella sampling (US). The oxygen-hydrogen bond vector was used as the a priori reaction coordinate for US. Overlapping windows were chosen to span the distance from the equilibrium bond length of 0.962 Što 3.5 Šat which point we assume the covalent bond between oxygen and hydrogen is broken. A biasing potential of either 50 kcal/mol/Ų with 0.2-0.4 Šwindows or 100 kcal/mol/Ų with 0.1 Šwindows was applied for 1 ps of simulation using a 1 fs time step of integration. Three QM/MM simulations were performed at each window: 500 steps to force the US constraint to its target distance using 500 kcal/mol/ Ų, 500 steps to equilibrate the system at the new distance using 100 kcal/mol/Ų, and 1000 steps of dynamics (1 ps) following the QM/MM protocol described above. Only the last (dynamics) run for each window was chosen for analysis.

In the presence of monovalent salts (potassium or sodium) that are not within 8 Å of PIP₂, two-dimensional US was used to disfavor hydrogen H51 from forming a bond with the 4-phosphate ester oxygen, O4P. This distance was added as another US constraint and ranged from 1.5 to 4.5 Å at the same time the O51—H51 distance ranged from 0.962 to 3.5 Å.

One-dimensional US was also used to test for the dissociation of divalent ions from PIP₂. Here, the distance between the center of the divalent ion (either calcium or magnesium) and the nearest phosphate oxygen was used as the a priori reaction coordinate. Overlapping windows were chosen as above, spanning from about 1.75 to 10.0 Å. Three classical MD simulations were performed in each window: 500 steps to force the US constraint to its target distance using 500 kcal/mol/Ų, 500 steps to equilibrate the system at the new distance using 100 kcal/mol/Ų, and 100000 steps of dynamics (100 ps) using the classical MD protocol described above. Again, only the last (dynamics) run for each window was chosen for analysis.

The US runs enable the calculation of the potential of mean force (free energy density) along a priori reaction coordinates from which the free energy changes are calculated by numerical integration. For the free energy calculation, the probability distribution, P(ξ_i), is calculated by dividing the maximum range of the order parameter ξ_i (O51—H51 and O4P—H51 bond distances) into several windows. A histogram is made for each window i from which the mean force Λ_i(ξ_i) is calculated:

$$A_i\left({\xi }_i\right)=-k_{B}T\ln \left[\mathcal{P}\left({\xi }_i\right)\right]+\text{Constant}.$$

We processed the US data to calculate the multi-dimensional potential of mean force using the weighted histogram analysis method (WHAM)⁴⁰. The number of windows for US/WHAM ranged from 20-40 and the tolerance for the iterative convergence of the potential of mean force was set at 10⁻⁷.

RESULTS AND DISCUSSION

The conformation, charge, and size of PIP₂

The properties of PPIs are largely controlled by the position and amount of phosphorylation (1, 2, or 3 phosphate groups) on the inositol ring. Several proteins bind with high affinity to one of the three naturally occurring PIP₂ isomers – PI(3,4)P₂ or PI(4,5)P₂ or PI(3,5)P₂ – but not others, suggesting precise molecular targets. Recent work reported that one of the two solvent-accessible phosphomonoester groups on the inositol ring of PI(4,5)P₂ (referred to as PIP₂ in this article) is protonated, bringing the total lipid charge to −3.99 ± 0.10 e (see ref.⁴¹). We set out to determine (a) the position of the proton, (b) the charge distribution across atoms and the total charge of PIP₂, and (c) the optimal geometry adopted by PIP₂.

A Hartree Fock geometry optimization of PIP₂ with truncated acyl chains (see METHODS) was completed in the presence of a proton initially placed between the 4-phosphate and the 5-phosphate of the inositol ring. The proton found a stable position covalently bound to the 5-phosphate oxygen, O51 (see Figure 1 and Figure S1). Preliminary calculations at a lower level of theory showed that hydrogen H51 is 6 kcal/mol more stable bound to an oxygen on the 5-phosphate compared with the 4-phosphate. There are several intramolecular hydrogen bonds that span the inositol ring, which is in the chair conformation.

In a bilayer setting, the orientation of the headgroup determines the accessibility of PIP₂ to its myriad protein binding partners that manipulate the PPI content in the cell and generate second messengers responsible for responding to extracellular events. Crystal structures have revealed that PH domains form stereo-specific hydrogen bonding networks with the entire PIP₂ headgroup in an orientation that appears to be perpendicular to the membrane bilayer⁴². The structure of inositol 1,4,5-triphosphate bound to the ENTH domain, which is found in the protein epsin and required for clathrin-mediated endocytosis, further highlights coordination of multiple arginine and lysine residues to the 4- and 5-phosphate groups. If either 4- or 5-phosphate is not present, soluble inositol bisphosphate will not bind to the domain⁴³. Neutron diffraction studies have suggested the orientation of the PIP₂ headgroup is perpendicular to the membrane plane⁴⁴ while a prior simulation study found that the PIP₂ headgroup is titled at an average angle of ~40° with respect to a phosphatidylcholine bilayer³⁸.

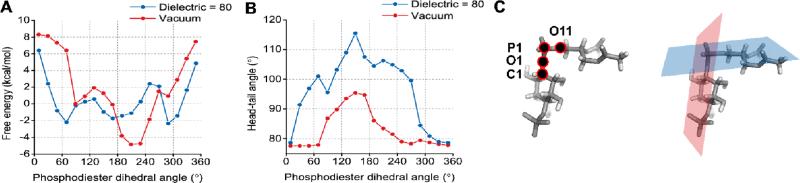
We define the angle between the inositol ring and the acyl chains (referred to as the “head-tail angle”), as the angle between the vector connecting the fourth carbon in the inositol ring to the phosphorus in the phosphodiester and the vector connecting the phosphorus in the phosphodiester to the first carbon in the glycerol moiety. For PIP₂, this angle is approximately 90° in the gas phase or in a polarized continuum solvent, suggesting that in the absence of other factors, the PIP₂ headgroup would lie parallel to the membrane bilayer. A relaxed potential energy scan of the two phosphodiester dihedral angles (C—O—P—O forward and reverse) was performed, and the head-tail angle varied from 80 to 115° (Figure 2). We were unable to obtain a relaxed structure with the head-tail angle near 0° or 180°. After 31 ns of all-atom molecular dynamics simulations of membrane bilayers of 800 total lipids containing PIP₂ in the presence of phosphatidylcholine, phosphatidylserine, phosphatidylethanolamine, and cholesterol with 150 mM NaCl, we find the average head-tail angle to be 103.9° (see Supporting Information for more details on the simulation and Figure S2), indicating that even in bilayer systems, the PIP₂ headgroup may lie nearly flat along the membrane.

Figure 2.

(A) The results of a relaxed potential energy scan of the phosphodiester dihedral angle joining the headgroup of PIP₂ to the glycerol moiety and the acyl chains. The dihedral angle is defined by the atoms labeled on the left of panel C. A value of 0 indicates that the plane defined by C1, O1, and P1 is aligned with the plane defined by O1, P1, and O11. (B) The angle between the ‘head’ and ‘tail’ of PIP₂ measured after a geometry relaxation at the values of the phosphodiester dihedral angle reported in panel (A). The head-tail angle corresponds to the angle between the planes on the right of panel (C).

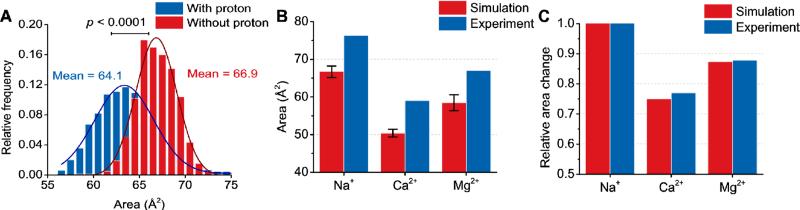
In the presence of neutralizing sodium ions kept at least 5 Å away from the PIP₂, the average area of the headgroup calculated from our QM/MM simulations is found to be 66.7 ± 1.5 Ų (Figure 3). The addition of magnesium, unconstrained in the water sphere, lowered the average surface area to 58.5 ± 2.1 Ų and the addition of calcium, also unconstrained, lowered the average surface area even further to 50.3 ± 1.0 Ų. These area estimates are expected to match experimental values from a Langmuir trough system only up to a constant, because in the simulations there is no external surface pressure acting on the PIP₂ molecule and there is only one PIP₂ molecule, eliminating the effect of electrostatic repulsion or hydrogen bonding between neighboring molecules. However, these data confirm the quantitative trend that binding of magnesium slightly lowers the size of PIP₂ and binding of calcium significantly increases this effect. When the surface area decreases are normalized by the average surface area of PIP₂ in pure water, the trend from the simulations compares favorably with the experimental results. These observations hint that the binding of calcium to PIP₂ may lead to desolvation of the ion and displacement of waters that hydrogen bond with the PIP₂ phosphomonoester groups. Bilayer simulations have shown a similar average surface area of PIP₂ in the presence of monovalent salts, although a much larger variance in the distribution of headgroup area (see Figure S3). These simulations are still in progress.

Figure 3.

(A) The average surface area of PIP₂ as calculated by squaring the maximum distance between oxygen atoms on two different phosphomonoester groups. The two histograms come from two separate QM/MM simulations with trajectories of 5 and 10 ps. (B) A comparison between the average surface area in simulations and Langmuir monolayer experiments of PIP₂ without a divalent ion present, with calcium, or magnesium. The error bars are the standard deviation of the area. (C) The same data as in panel (B) but the values for calcium and magnesium have been normalized by the experimental or simulation reported average surface area in the absence of divalent ions.

The preferred position of PIP₂ phosphomonoesters and divalent ion binding locations

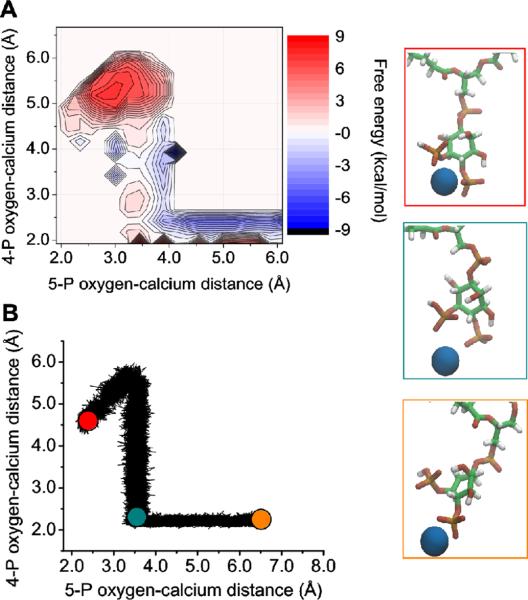
Two-dimensional classical US was used to investigate the free energy difference of calcium binding between the phosphomonoester groups and binding to only a single phosphomonoester. In classical simulations, the divalent ions prefer to localize to the fully charged 4-phosphate group. It is approximately 10 kcal/mol more favorable to bind solely to the 4-phosphate group relative to binding between the 4 and 5-phosphate groups (Figure 4). It is unclear whether binding to the 4-phosphate group can exist under physiological packing of phospholipids, so we also investigated the condition where calcium is chelated by both phosphomonoester groups together. Further, we hypothesize that if calcium is able to bind to the 4-phosphate group in patches of PIP₂, then it will act as an intermolecular bridge.

Figure 4.

(A) Free energy contours for calcium binding between the two phosphomonoester groups or to only the 4-phosphate group. (B) A scatter plot of the thermodynamic sampling path of the trajectory with renderings shown on the right for specific points along the path.

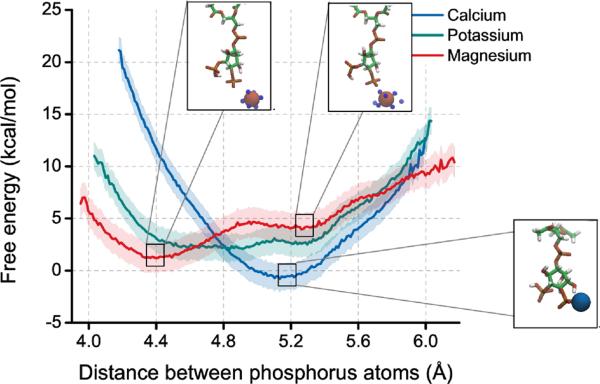
To investigate the energy barrier for spreading the phosphate groups and effectively increasing the size of PIP₂ in the presence of divalent ions, we employed one-dimensional US with a distance constraint on the two phosphorus atoms. If calcium is localized to the 4-phosphate group of PIP₂, then phosphate groups prefer to be separated by 5.1 Å. When the calcium is replaced by magnesium, the phosphate groups prefer to be closer, at around 4.4 Å and do not experience a large energy barrier for spreading (Figure 5). Potassium does not bind tightly to either of the phosphate groups and represents the intrinsic energy landscape for spreading the phosphate groups of PIP₂ while not bound to an ion.

Figure 5.

The free energy of spreading the phos phomonoester groups of PIP₂ in the presence of calcium, magnesium, or potassium using classical US simulations. The insets show renderings from the simulations. Calcium (blue) binds tightly to the 4-phosphate group of PIP₂. Magnesium (red) binds loosely to the 4-phosphate group and is coordinated by water molecules (TIP3 oxygens within 4 Å of the magnesium are shown as small blue spheres). Potassium does not appear to tightly bind PIP₂ and is not shown. The shaded background represents the mean square difference between analyzing only the first half umbrella sampling trajectories and the full window.

The free energy of protonating the PIP₂ phosphomonoester groups

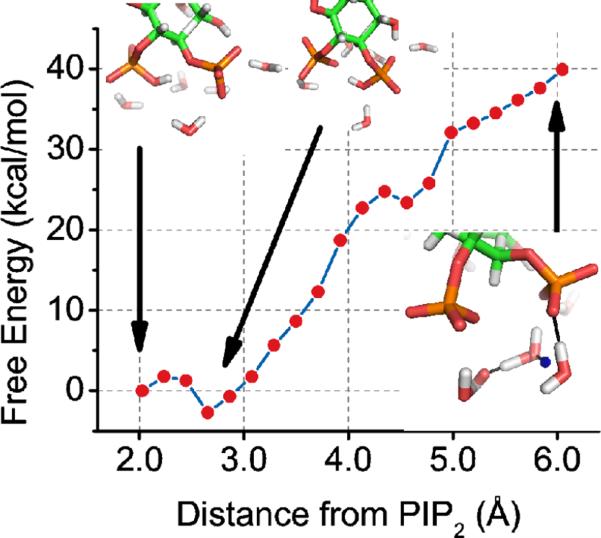
To ascertain the free energy of having a proton on the 5-phosphate group of PIP₂, we used two-dimensional QM/MM US to disfavor the proton H51 from the 4-phosphate and the 5-phosphate. This forced the proton to dissociate from PIP₂ and onto a nearby water molecule in the QM region. Two short-lived hydronium ions were formed during this process via the Grotthuss mechanism⁴⁵. In the last window of the US simulation, a water in the QM region forms a hydrogen bond with the 4-phosphate group of PIP₂. Complete deprotonation of PIP₂ is unfavorable by several dozen kcal/mol; this suggests that PIP₂ in vivo has a proton on the 5-phosphate group and the net charge of the phospholipid is −4 at pH 7 (Figure 6).

Figure 6.

The free energy of total deprotonation of the PIP₂ phosphomonoester groups using QM/MM US simulations. The insets show the initial configuration, with proton H51 bound to the 5-phosphate, an intermediate structure with proton H51 bound to the 4-phosphate, and the final configuration with proton H51 (blue) forming a hydronium ion and water molecules hydrogen bonding (black dashed line) with the PIP₂ phosphomonoester groups.

The distance between PIP₂ and calcium, magnesium, or potassium

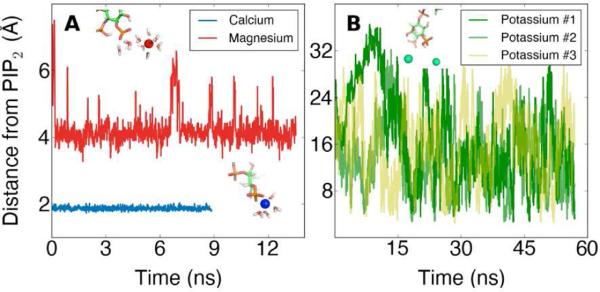
Classical simulations were performed to measure the binding of the divalent ions calcium and magnesium or the monovalent ion potassium to PIP₂ (Figure 7). Calcium and magnesium exhibit different preferred binding positions, and these preferred binding positions reflect their differential effects on the surface area of PIP₂. Potassium does not appear to stably bind to any of the phosphate oxygen atoms on PIP₂, unlike calcium and magnesium. Although the potassium ions may come within 5 Å of an oxygen, the ions leave freely and without always being replaced by another ion. From these data, we can conclude that calcium binds closest to PIP₂ compared to magnesium or potassium, and this fact may be crucial for the unique ability of calcium to induce cluster formation of PIP₂.

Figure 7.

(A) The equilibrium distance to PIP₂ obtained for the divalent ions, calcium or magnesium, in separate classical MD simulations and (B) the transient binding behavior of several potassium ions in a water sphere with a single PIP₂ molecule. Renderings of snapshots from simulations are shown in the insets.

The hydrogen bonds between PIP₂ and water in the presence of divalent ions

The results of the classical MD simulations that reported the binding of calcium and magnesium were used to seed QM/MM simulations. PIP₂ is able to form an average of 2.6 hydrogen bonds with water in the presence of calcium but only 1.6 hydrogen bonds with water in the presence of magnesium, although magnesium binds farther away. This difference is likely due to the fact that magnesium appears to retain its first hydration shell in its equilibrium binding position.

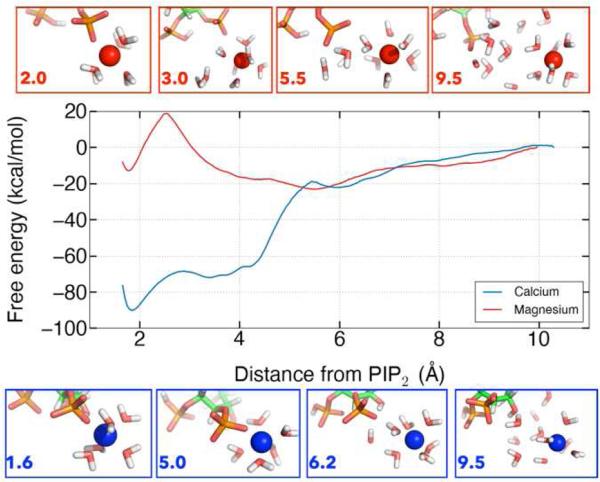
The free energy of calcium and magnesium binding to PIP₂

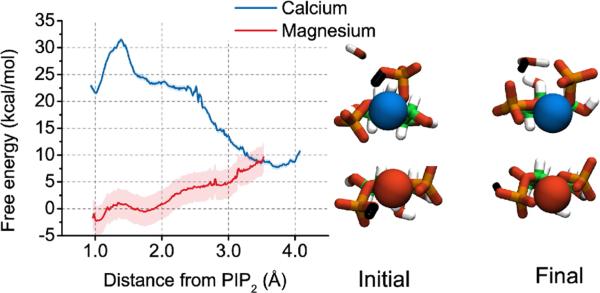
One-dimensional classical US was used to investigate the free energy landscape for dissociating calcium and magnesium from their respective preferred binding positions. Significantly more energy is required to pull calcium away from its equilibrium binding position, at 2 Å, into bulk water than it does for magnesium from its equilibrium binding position, at 5 Å (Figure 8). The analysis also revealed a second binding position for magnesium that was not sampled in the classical or QM/MM trajectories, corresponding to partial desolvation of the magnesium ion associated with a ~20 kcal/mol barrier. The minimum for magnesium at 5 Å is shallow and broad so many conformations can fit into this well. The broad shoulder of the calcium curve from 4-6 Å corresponds to increasing the distance between calcium and PIP₂ without a mediating water. The large difference in free energy for dissociating calcium and magnesium from a single PIP₂ molecule contrasts to the relatively modest difference in apparent affinity of these in for PIP₂ in lipid monolayers or bilayers. This difference between simulation and experiment suggests that long range electrostatic attraction of ions to the charged surfaces of membranes or differences in hydration or binding mode of ions to closely packed PIP₂ within a membrane contribute significant to the free energy of binding in these macroscopic systems.

Figure 8.

The free energy landscape for dissociating divalent ions from PIP₂.

The free energy of protonating the PIP₂ phosphomonoester groups in the presence of calcium and magnesium

We investigated whether the presence of calcium or magnesium affected the free energy, and thus likelihood, of the presence of a proton bound to the 5-phosphate group of PIP₂. Using one-dimensional QM/MM US, dissociating a proton from the 5-phosphate is unfavorable by 12 kcal/mol. However, after surmounting a barrier of ~5 kcal/mol to pull the proton more than 1.5 Å away from its covalently bound oxygen, the presence of calcium makes this process energetically favorable (Figure 9). The free energy landscape to describe proton confirmations beyond intramolecular hopping in the presence of magnesium is complex as indicated by Figure S4. The final state, with proton H51 dissociated from PIP₂ and bound to a hydronium ion is more favorable than the initial state (proton H51 bound to oxygen O51 of PIP₂) by approximately 8 kcal/mol. These data, combined with the free energy landscape for dissociating a proton from PIP₂ in pure water, suggest that PIP₂ is protonated on the 5-phosphate group of the inositol ring in pure water or with magnesium bound, but deprotonated with calcium bound.

Figure 9.

The free energy landscape for dissociating a proton from the 5-phosphate group of PIP₂ in the presence of calcium or magnesium. The shaded background represents the mean square difference between analyzing only the first half umbrella sampling trajectories and the full window. In the insets, the proton to be dissociated is shown in black, magnesium in red, and calcium in blue.

It is possible to calculate pKa values from the free energy landscape by comparing the integral over the bound state to the integral over the unbound state (see Supporting Information for further discussion and Figure S5). The pKa for proton binding in the presence of magnesium is similar to the pKa for proton binding in pure water. The pKa for proton binding in the presence of calcium is significantly more negative, indicating an increased probability for proton dissociation from PIP₂. We stress that the absolute value of these numbers should not be compared to the results of experiments due to the approximations involved in obtaining absolute free energy curves from the potentials of mean force along a single reaction coordinate. Furthermore, experimentally determined pKa values are calculated in lipid vesicles, which is different from our case in several respects (e.g., the effect of a negative surface charge density of the vesicle membrane) so a direct comparison is not strictly valid (see Supporting Information for more discussion).

Our results are consistent with observations that magnesium is only about one-third as effective as calcium ions in reducing the surface potential of mixed PIP₂ vesicles⁴⁶, leading to the implication that the intrinsic association between magnesium and PIP₂ is weaker than the intrinsic association between calcium and PIP₂. The protonation state of PIP₂ appears to follow the same trend as phosphatidic acid, whose phosphate group becomes doubly deprotonated at physiological pH in the presence of divalent or trivalent ions, particularly calcium, due to electrostatic correlations⁴⁷. Our results for ion binding to solvated PIP₂ can be extended to the membrane environment by following the methodology of Loew, et al. ⁴⁸

CONCLUSIONS

We have created a model of PIP₂ by using electronic structure calculations and hybrid QM/MM simulations to test hypotheses about divalent cation-mediated attractions between PIP₂, motivated by recent experimental data. We have found several key results that make predictions about the properties of PIP₂ under physiological conditions. The geometry of the PIP₂ headgroup, composed of an inositol ring and two vicinal phosphate groups, is held together by several intramolecular hydrogen bonds, including one between a proton on the 5-phosphate and an oxygen on the 4-phosphate, in the gas phase. The angle that is made between the headgroup and the acyl chains is nearly perpendicular, suggesting that the PIP₂ headgroup lies flat against the membrane until a protein binds to it or a chaotropic agent disrupts the local environment in a way that lowers the energy barrier to rotation. Several water molecules form stable hydrogen bonds with both the protonated and unprotonated form of the headgroup, but removing the proton on the 5-phosphate group in the presence of pure water is very unfavorable. These data imply that PIP₂ is protonated in pure water, consistent with the NMR results⁴¹.

The binding of the physiologically relevant divalent cations, calcium and magnesium, was also investigated. Both calcium and magnesium stably bind to a single PIP₂ in between the phosphomonoester groups or near the deprotonated 4-phosphate group. The free energy of removing calcium from binding to a single PIP₂ is much greater than for magnesium, but surface pressure measurements have estimated that magnesium binds only modestly weaker than calcium to PIP₂ in compressed lipid monolayers⁸. We have started simulations with multiple PIP₂ molecules to investigate whether these divalent cations are also able to bind between molecules, and whether this affects their preferred binding positions and free energy of binding. The free energy of removing a proton from the headgroup in the presence of magnesium is unfavorable, but the free energy of removing a proton from the headgroup in the presence of calcium is not unfavorable. Indeed, binding of calcium seems to displace the proton on the 5-phosphate group and is capable of decreasing the effective size of the PIP₂ headgroup. Taken together, we predict in vivo PIP₂ has a proton on the 5-phosphate group owing to the large intracellular concentration of magnesium ions, but during calcium influx when the concentration of free calcium increases to near μM, calcium is capable of binding to PIP₂ in place of a proton at the 5-phosphate group and decreasing the size of the phospholipid headgroup. Such changes in effective area at the inner leaflet of the plasma membrane might contribute to membrane curvature or restructuring that occur during vesicle trafficking or regulation of PIP₂-sensitive transmembrane protein complexes.

ABBREVIATIONS

PIP₂

phosphatidylinositol 4,5-bisphosphate

QM/MM

quantum mechanics / molecular mechanics

US

umbrella sampling