Nanowire nanocomputer as a finite-state machine

Significance

Fundamental limits soon may end the decades-long trend in microelectronic computer circuit miniaturization that has led to much technological and economic progress. Nanoelectronic circuits using new materials, devices, and/or fabrication methods face formidable challenges to provide alternatives for future microelectronics. A key advance toward overcoming these hurdles is achieved in this work through the construction of a nanoelectronic finite-state machine (nanoFSM) computer using “bottom–up” methods. The nanoFSM integrates both computing and memory elements, which are organized from individually addressable and functionally identical nanodevices, to perform clocked, multistage logic. Furthermore, the device density is the highest reported to date for any nanoelectronic system. Advances in logic and design in the nanoFSM are scalable and should enable more extensive nanocomputers.

Abstract

Implementation of complex computer circuits assembled from the bottom up and integrated on the nanometer scale has long been a goal of electronics research. It requires a design and fabrication strategy that can address individual nanometer-scale electronic devices, while enabling large-scale assembly of those devices into highly organized, integrated computational circuits. We describe how such a strategy has led to the design, construction, and demonstration of a nanoelectronic finite-state machine. The system was fabricated using a design-oriented approach enabled by a deterministic, bottom–up assembly process that does not require individual nanowire registration. This methodology allowed construction of the nanoelectronic finite-state machine through modular design using a multitile architecture. Each tile/module consists of two interconnected crossbar nanowire arrays, with each cross-point consisting of a programmable nanowire transistor node. The nanoelectronic finite-state machine integrates 180 programmable nanowire transistor nodes in three tiles or six total crossbar arrays, and incorporates both sequential and arithmetic logic, with extensive intertile and intratile communication that exhibits rigorous input/output matching. Our system realizes the complete 2-bit logic flow and clocked control over state registration that are required for a finite-state machine or computer. The programmable multitile circuit was also reprogrammed to a functionally distinct 2-bit full adder with 32-set matched and complete logic output. These steps forward and the ability of our unique design-oriented deterministic methodology to yield more extensive multitile systems suggest that proposed general-purpose nanocomputers can be realized in the near future.

It is widely agreed (1, 2) that because of fundamental physical limits, the microelectronics industry is approaching the end of its present Roadmap (1) for the miniaturization of computer circuits based upon lithographically fabricated bulk-silicon (Si) transistors. Therefore, much effort has been invested in the nanoelectronics field for the development of novel, alternative, nanometer-scale electronic device and fabrication technologies that could serve as potential routes for ever-denser and more capable systems to enable continued technological and economic advancement (3–17). These efforts have yielded simple nanoelectronic circuits (3–5, 8–17) and more complex circuit systems (6, 7) that use novel nanomaterials but are not integrated on the nanometer scale. In this regard, building a nanocomputer that transcends the ultimate scaling limitations of conventional semiconductor electronics has been a central goal of the nanoscience field and a long-term objective of the computing industry.

A finite-state machine (FSM) is a representation for a nanocomputer in that it is a fundamental model for clocked, programmable logic circuits (18, 19) and integrates key arithmetic and memory logic elements. In general, a FSM must maintain its internal state, modify this state in response to external stimuli, and then output commands to the external environment on that basis (18, 19). A basic state transition diagram for the 2-bit four-state FSM investigated in our work (Fig. 1A) highlights the four binary representations “00,” “01,” “10,” and “11,” and the transition from one state to another triggered by a binary input signal, “0” or “1.” Larger, more complex FSMs may be constructed using longer binary representations.

Fig. 1.

Architecture and fabrication of FSM. (A) Logic diagram of the FSM, with the gray circles representing the states. Upon triggering, the straight arrows indicate the transition of the current state to the next one for an input of 1; the curved arrows indicate maintaining the current state for an input of 0. (B) Schematic of the three-tile circuit of the nanoFSM. Each tile consists of two blocks, and each block consists of a nanowire array (vertical) with lithography-defined top gate lines (horizontal). A₁A₀, C_in, and CLK correspond to the 2-bit state, control, and clock signal, respectively. The green dots indicate the programmed active transistor nodes. For simplicity, the circuit only shows the drain contacts (blue) but not the source contacts or load resistors. The arrows indicate external wirings, with the red ones indicating feedback loops. (C) Deterministic fabrication scheme. Key steps include (l) definition of the anchoring sites (gray stripes), (Il) single-nanowire anchoring to the specific anchoring sites with highly directional alignment, (III) nanowire trimming to yield uniform lengths, and (lV) definition of contacts (light blue) and gates (orange) to the trimmed nanowires (dark blue) without registration. (D) SEM image of a 10 × 10 nanowire array from the nanoFSM circuit. The horizontal lines are metal gates with the top and bottom pads the source and drain contacts. (Scale bar, 1 µm.) (E) SEM image of the entire three-tile/six-array nanoFSM circuit. The red enclosed region corresponds to the image area shown in D. (Scale bar, 10 µm.)

Previous efforts have yielded circuit elements that perform simple logic functions using small numbers of individual nanoelectronic devices (8–17), but have fallen far short of demonstrating the combination of arithmetic and register elements required to realize a FSM. Specifically, integration of distinct functional circuit elements necessitates the capability to fabricate and precisely organize circuit systems that interconnect large numbers of addressable nanometer-scale electronic devices in a readily extensible manner. As a result, implementation of a nanoelectronic FSM (nanoFSM) via bottom–up assembly of individually addressable nanoscale devices has been well beyond the state of the art. Moreover, it represents a general gap between the current single-unit circuits and modular architectures for increasing complex and functional nanoelectronic systems (8, 20–24). Below we describe how we overcome the above challenges in design, assembly, and circuit fabrication for the realization of a nanoFSM in programmable multitile architecture, which also provides a general paradigm for further cascading nanoelectronic systems from the bottom up.

Results and Discussion

To realize the nanoFSM, we adopt a bottom–up compatible strategy using common circuit modules or tiles that are interconnected and programmed for distinct logic functions (21, 22). This strategy contrasts conventional circuit designs, which require different layouts for the distinct logic elements. Within the context of this bottom–up paradigm, our architecture for the nanoFSM interconnects three programmable nanowire tiles (Fig. 1B). Following fabrication, the common tiles or modules are differentiated by programming, with tile-1 programmed to perform arithmetic operations and tile-2 and tile-3 programmed to function as the register elements for the first and second digits of the state, respectively. Each tile in Fig. 1B consists of two programmable nanowire transistor arrays, where each cross-point in the arrays corresponds to a programmable transistor node having an active (transistor) or inactive (resistor) state. The output of the first array serves as the input to the second array such that the two-level NOR-logic structure of each tile can be programmed to yield complete Boolean logic (21, 22), and thus the necessary arithmetic and register elements of the nanoFSM.

The three-tile FSM design (Fig. 1B) represents a very substantial step forward in complexity compared with previous work (8–17), given the large number of individual nanowires that must be organized in an efficient and scalable manner and the stringent demands on individual logic devices with respect to input/output (I/O) voltage matching and control over threshold voltage variation. It also represents an experimental implementation of a bottom–up multitile or modular circuit architecture (8, 20–24).

We have made a general breakthrough in bottom–up organization by implementing a unique deterministic fabrication methodology (Fig. 1C and Fig. S1), which enables a design-oriented fabrication of the nanoFSM from postgrowth nanoscale elements. Our approach involves one initial patterning step, with all subsequent steps registered to this initial pattern including the assembly and interconnection of individual nanowire elements in the three-tile/six-array nanoFSM design. First, discrete periodic anchoring sites are defined based on the three-tile circuit design (Fig. 1 C, I and Fig. S1). Second, nanocombing (25, 26) of germanium (Ge)/Si core/shell nanowires (27) yields nanowires anchored at each site and aligned along the combing direction (Fig. 1 C, II and Fig. S1 A and B and Fig. S2). Third, the laterally periodic arrays of nanowires are trimmed registered to the initially patterned anchoring sites (Fig. 1 C, III and Fig. S1 A and C). Fourth, electrical contacts are made by registering to the initial anchoring sites (x axis) and the trimmed length (y axis) without nanowire registration (Fig. 1 C, IV and Fig. S1D).

The nanoFSM circuit and chip were completed by deposition of dielectric layers, metal gate lines, and interconnects to I/O pads for measurements (Materials and Methods). A scanning electron microscope (SEM) image of a crossbar array (Fig. 1D) highlights the high fidelity of the 10 pairs of electrodes with equal 1 µm pitch connecting to each of the well-aligned and periodic nanowires in the array. The high degree of alignment in all arrays prevents crossing of neighboring nanowires, which is critical for achieving uniform gate response at cross-point nodes. Focusing on the overall nanoFSM structure (Fig. 1E) reveals additional key features. First, regular I/O lines as a consequence of the near-deterministic assembly allow for layout and subsequent assembly of the three-tile/six-array circuit in accordance with our three-tile design versus typical postassembly design (9–16) (following nanowire registration). Second, a high yield of single-nanowire devices was achieved: for the 72 pairs of contacts made in the six arrays, 43 (60%) were single-nanowire devices, with the remainder double-nanowire (22%) and vacancies (18%). The initial circuit design took this yield into account by including sufficient contacts, such that each tile contained ample single-nanowire devices for the actual circuit. For even larger tiled circuits, peripheral routing logic elements could be integrated to yield systematic defect-tolerant crossbar architecture (28).

This single-nanowire device yield, nanowire pitch, and gate-line pitch (400 nm) results in 1.8 transistors/µm² or 1.8 × 10⁸/cm², at least a threefold increase in the density compared with other postassembly design strategies (9, 10, 13, 16). We note that the 10-fold improvement in nanowire alignment and 10-fold reduction in defeat density (e.g., crossing nanowires) by nanocombing (25) compared with typical shear printing assembly methods used previously (16) enable both the increase in circuit density and the multitile circuits in this work. Last, regular I/O lines of the nanoFSM (Fig. 1E) undergo fan-out (Fig. S3) to yield a ca. 4 × 4 mm² chip with 204 contact pads that mate to a probe card for testing.

The nanoFSM (Fig. 1B) requires extensive intra- and intertile signal flows, which require strict I/O voltage matching of the transistor nodes in fabricated three-tile structures (Fig. 1E). In this regard, we have characterized the voltage-out (V_out) versus voltage-in (V_in) characteristics of all of the individual nodes in the nanoFSM configured as inverters (Fig. S4). Specifically, the Al₂O₃–ZrO₂–Al₂O₃ dielectric layer (Materials and Methods) introduced as a charge-trapping medium (16, 29) can be programmed with a large gate input (e.g., +8/–8 V) to accumulate/deplete charge and thereby shift the transistor threshold (Fig. S4). In this way, representative V_out versus V_in data show a large hysteresis (Fig. 2A), in which the transistor node behaves as an active transistor (red) or an inactive resistor (blue) in a logic input range of 0–3 V (gray region) following the programming step. We define a circuit threshold voltage, V_c, as the value of V_in at which the inverter V_out is reduced to 1/10 of the supply voltage, V_d, and sets the minimum V_in for the inverter to output 0. I/O matching requires V_c ≤ V_d, so that the output 1 (∼V_d) is sufficient to serve as the input to drive the next element in the circuit without signal loss.

Fig. 2.

Programmable transistors and threshold-voltage map. (A) Characteristic output vs. input (V_out vs. V_in) from a programmable transistor node in the nanoFSM circuit; Fig. S4 provides additional details. The black arrows indicate the sweep directions of V_in. The red and blue curves correspond to programmed active transistor and inactive resistor states (inset schematics). The gray region indicates the 0–3 V logic window. (B) Spatial map of the threshold voltage V_c (at V_d = 2 V) in the active state for all of the 190 transistor nodes used for the three-tile circuit. Each box represents the corresponding transistor node shown in Fig. 1B. The blue color represents V_c < 2 V, which is capable of output gain or I/O matching; and the gray color represents V_c ≥ 2 V, which will yield reduced output.

We optimized the Ge/Si core/shell nanowire synthesis and device fabrication steps to control V_c and meet the design metric V_c ≤ V_d, where the principle challenges were minimizing positive shifts of V_c in the active state and achieving threshold uniformity (Fig. S5). Significantly, a map of the measured V_c values from the three-tile nanoFSM circuit (Fig. 2B) highlights the high yield of transistor nodes capable of gain or I/O matching. For the 190 transistor nodes in the three tiles, 177 out of 190 nodes (93%) meet the V_c ≤ V_d criteria, with an average V_c ±1 SD of 0.9 ± 0.7 V at V_d = 2 V. Last, a histogram for these same 190 nodes programmed to the inactive state (Fig. S6) demonstrates that 100% have V_c > 3.5 V (V_c ± 1 SD of 6.2 ± 0.5 V), which is outside the upper limit (3 V) of the logic window.

The operation of the FSM circuit, which had been verified by simulations before fabrication, was programmed (Fig. S7) as shown in Fig. 1B, with A₁A₀, C_in, and CLK representing the 2-bit state, control input, and clock signal, respectively. In this architecture, tile-1 is configured as a half adder that computes the summation of A₁A₀ + C_in. Its output A′₁A′₀ is the new state, where A′₀ = A₀ C_in, A′₁ = A₁ (A₀•C_in), and “” and “•” represent XOR and AND logic, respectively. The computed A′₀ and A′₁ values are input to tile-2 and tile-3, which are configured as D flip-flops (30) (DFFs). The DFFs register the new state on the rising edge of the synchronized CLK, and then this registered state is instantly fed back as input to the half adder to compute the next-level state. We first characterized the performance of the three “component” tiles in the nanoFSM; these results demonstrated that the half adder and DFF (Fig. S8 and Fig. S9) exhibited correct logic. For example, the DFF, which was not demonstrated previously in bottom–up circuits, involves two intratile feedback loops covering six of the seven functional nanowires in the circuit, and thus is substantially more complex and requires more stringent I/O matching and transistor uniformity than demonstrated circuits with single feedback loops (14–16). The fulfillment of rigorous I/O matching is reflected in the accurate logic flow and matching of the output Q to the input D and clock signal CLK (Fig. S9B). Moreover, the programmed DFF showed no obvious degradation after 10 h in ambient environment (Fig. S9C), thus demonstrating robustness and nonvolatility of the programmed tiles.

We have investigated the logic flow and fidelity of the nanoFSM for a variety of C_in and CLK sequences by continuously recording A₀ (V) and A₁ (V). First, for a constant control input C_in = 1 (Fig. 3A), the state A₁A₀ underwent a complete logic circle from 00→01→10→11→00, with each transition triggered by the CLK rising edge. The capability to fully control and lock the state by varying C_in is shown for t = 38–190 s. For example, for C_in = 0 (t = 38–55 s), the state A₁A₀ = 00 was locked and not triggered to the next level at the two consecutive rising edges of CLK (t = ∼45, 54 s). As the control input changed to C_in = 1, the state was unlocked and moved to A₁A₀ = 01 at the rising edge of CLK (t = ∼63 s). This high fidelity in the control is shown for all of the other states of 01, 10, and 11, which were locked when C_in = 0 and continued in the logic loop when C_in = 1 (t = 66–190 s). The robustness of the nanoFSM was further tested by inputting a more irregular control waveform (Fig. 3B), during which the states were intermittently locked. For example, the lock of the state 01 with C_in = 0 (t = 57–69 s) was followed by a continuous transition from 01→10→11 with C_in = 1 (t = 69–85 s) before the state 11 was locked with C_in = 0 (t = 85–101 s). Similar logic flow is shown for the transition from 00→01→10 (t = 111–165 s). Overall, the complete logic fidelity and arbitrary state control in these measurements highlight the successful implementation of a cascaded three-tile nanoFSM circuit.

Fig. 3.

nanoFSM output. (A and B) The logic flow of the output state A₁ (blue) and A₀ (red) with respect to the control input C_in (green) and clock signal CLK (gray) as indicated in Fig. 1B.

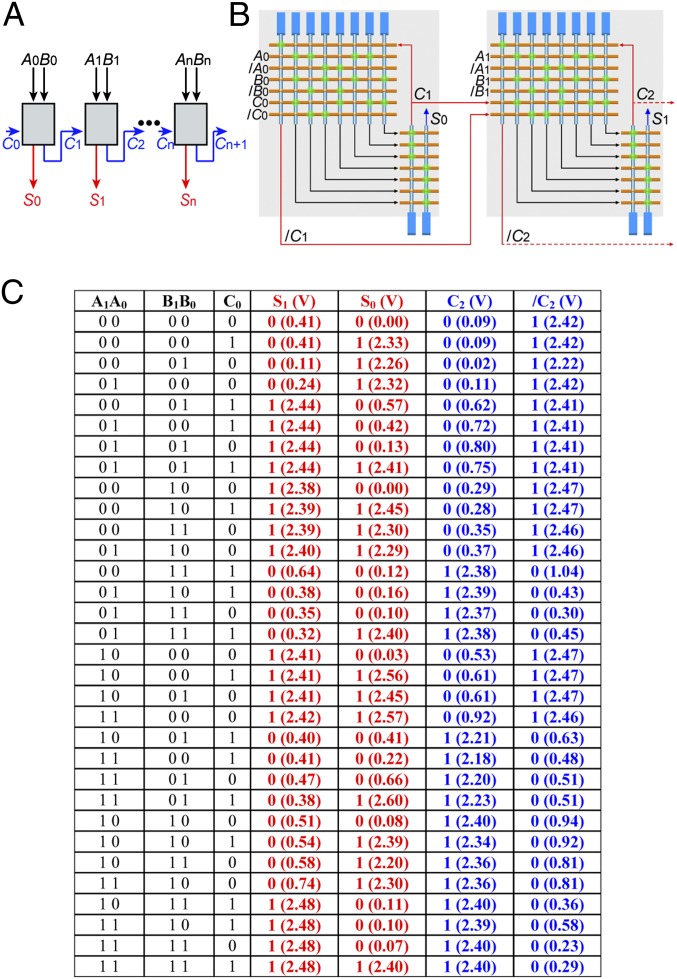
To investigate the feasibility of extending the number of cascaded tiles, we reprogrammed the circuit to a 2-bit full adder. Because a multibit full adder can be realized by serial interconnection of 1-bit full adders (31) (Fig. 4A), this output from successive interconnected tiles provides a critical measure of capability to extend the cascade. The high yield of transistor nodes capable of I/O matching (Fig. 2B) was exploited to reprogram the two DFFs of the nanoFSM such that the 2-bit full adder circuit contains a distinct configuration of active nodes (i.e., beyond the minimum changes required to realize the adder logic). In this cascaded two-tile circuit (Fig. 4B), each 1-bit full adder computes the sum S_i = A_i B_i C_i and carry-out C_i+1 = A_i•B_i+A_i•C_i+B_i•C_i (i = 1, 2; “+” denotes OR logic), with the computed C_i+1 and complementary /C_i+1 serving as the input to the higher-bit adder. Overall, the 2-bit full adder computes the summation of A₁A₀ + B₁B₀ + C₀, with S₀ and S₁ the first and second digits of the sum and C₂ the carry-out. Significantly, examination of the values for the complete 32-element truth table (Fig. 4C) demonstrates that the complete logic outputs for S₀, S₁, C₂, and /C₂ are correct, and that their average logic 1 output voltages 2.43 ± 0.03, 2.39 ± 0.12, 2.34 ± 0.08, and 2.43 ± 0.06 V, respectively, are well-matched (slightly enhanced) relative to the common logic input 1 value, 2.3 V. These results strongly validate the feasibility of implementing >2-bit full adders by cascading a larger number of tiles.

Fig. 4.

2-bit full adder. (A) Schematic of an n-bit full adder constructed from serial 1-bit full adders. (B) The two-tile circuit design for the 2-bit full adder. (C) Experimental truth table for the 2-bit full adder. The table consists of 32 sets of input combinations (A₁A₀, B₁B₀, C₀) with the corresponding outputs S₁, S₀, C₂, and /C₂. The voltage output values are shown in brackets. The input values for 1 and 0 are 2.3 and 0 V, respectively.

Conclusions

The multitile nanoFSM and 2-bit full adder programmable circuits demonstrated above highlight several distinct features compared with previous circuits based on bottom–up-assembled elements (8–17). First, the complexity is more than threefold in terms of number of devices (180 transistor elements) compared with all of the previous work (9–17), with the density of devices in the nanoFSM also much greater. This complexity is further enhanced in terms of circuit functionality by incorporation of both sequential and combinational logic elements. Second, this work provides concrete demonstration of tile integration and multiple intertile I/O critical to cascaded multitile architectures (8, 20–24) and complex circuits in general. In particular, the successful clocked operation of the nanoFSM required eight intertile and intratile feedback loops with matched I/O values, as opposed to a maximum of one demonstrated previously in single functional units (14–16). Third, instead of using an assembly-limited bottom–up fabrication strategy in all previous work (9–16), our high-precision, deterministic, bottom–up methodology has implemented a design-oriented circuit fabrication strategy that has been so successful in the conventional electronics industry. Taken together, we believe that these results represent a significant leap in scaling up electronic circuits from the bottom up. Our work suggests strongly that general-purpose nanoprocessors (20–24) can be realized in the near future.

Materials and Methods

Synthesis of Ge/Si Core/Shell Nanowires.

The Ge/Si nanowires were synthesized by the Au-nanocluster–catalyzed vapor–liquid–solid method described previously (27). The growth substrate (600 nm SiO₂/Si) dispersed with gold nanoparticles (10 nm, Ted Pella) was placed in a quartz-tube reactor system. The Ge core was synthesized at 255 °C and 450 Torr, with 30 sccm germane (GeH₄, 10% in H₂) and 200 sccm H₂ as the reactant and carrier gas, respectively. The growth time was 50 min, yielding an average length of ∼40 µm. The epitaxial Si shell was grown immediately after the growth of Ge core, at 460 °C and 5 Torr for 2 min, with 5 sccm silane (SiH₄) as the reactant gas, and yielded nanowires with an overall diameter of 15 nm.

Deterministic Nanocombing of Nanowires.

First, the device substrate (600 nm SiO₂/Si) was spin-coated with a thin layer (∼25 nm) of poly(methyl methacrylate) [PMMA 950-C2, 1:8 (v:v) diluted in ZEP-A, Microchem]. Based on the layout of the circuit design, electron-beam lithography was used to define arrays of exposed SiO₂ windows (300 nm × 10 µm) in the form of narrow stripes (Fig. S1 A, 1). The exposed stripes of SiO₂ surface were then functionalized with tetramethylammonium ions by rinsing the substrate in Microposit MF-319 developer for 50 s, followed by washing in deionized water (30 s) and isopropyl alcohol (30 s). This process selectively enhances the SiO₂-surface affinity to nanowires. The functionalized substrate was then brought into contact with the nanowire-growth substrate at a constant pressure of ∼5 N/cm², with ∼40 µL heavy mineral oil (#330760, Sigma-Aldrich) added between the surfaces as lubricant. The growth substrate was moved along the longitudinal direction of the stripes at a constant velocity of ∼5 mm/s, with the device substrate fixed (Fig. S1 A, 2). During this process, the protruding parts of nanowires were effectively anchored to the stripes of SiO₂ surface, with the rest length being drawn out over the resist (combing) surface. The weak interaction between the combing surface and nanowires maximizes the aligning shear force, resulting in the effective alignment of nanowires on the combing surface. The modulated lateral confinement in the anchoring stripes can produce a high yield of single-nanowire anchoring events, resulting in well-aligned and periodic single-nanowire arrays on the resist surface. The heavy mineral oil was then removed by drops of octane along the combing direction. A cleaning method by using acetone vapor (Fig. S5B) was used for the effective removal of the resist layer underneath the nanowires without disturbing their arrangement.

Fabrication of Logic Tiles.

A trimming process, which involved sacrificial mask (400 nm PMMA 950-C2) definition by electron-beam lithography and nanowire etching by reactive ion etching (Surface Technology Systems) using SF₆ as etchant gas, was used to define nanowire arrays with at predefined length (Fig. S1 A, 4–6). The source and drain contacts of the nanowires were defined by electron-beam lithography followed by the thermal evaporation of metal contacts (Cr/Ni, 1/40 nm) and liftoff process. The dielectric layers were deposited by atomic-layer deposition, followed by top-gate definition by electron-beam lithography, thermal evaporation of metals (Cr/Au, 4/65 nm), and liftoff process.

Growth of Dielectric Layers.

The trilayer Al₂O₃–ZrO₂–Al₂O₃ (2–5–5 nm) dielectric structure was grown by atomic-layer deposition at 200 °C, with trimethylaluminum {Al(CH₃)₃}, tetrakis(dimethylamino)zirconium {Zr[N(CH₃)₂]₄}, and water as precursors. Specifically, one Al₂O₃ growth cycle consisted of one water–vapor pulse (0.015 s), N₂ purge (8 s), one Al(CH₃)₃ pulse (0.015 s), and N₂ purge (8 s). One ZrO₂ growth cycle consisted of one water–vapor pulse (0.015 s), N₂ purge (8 s), one Zr[N(CH₃)₂]₄ pulse (0.25 s), and N₂ purge (8 s). A deposition sequence of 25 cycles Al₂O₃, 55 cycles ZrO₂, and 55 cycles Al₂O₃ was performed.

Programming and Testing of the Circuits.

The circuit chip was mounted in a probe station (Model 12561B, Cascade Microtech). A custom-designed 204-pin probe card (Accuprobe) was used to electrically access the device arrays. A computer-controlled analog I/O system (2× PXI-6723, 2× PXIe-6358 in a PXIe-1065 chassis, National Instruments), featuring 64 analog-voltage output channels and 24 analog-voltage input channels, was used for the electrical characterization. For each nanowire, an external resistor (8–15 MΩ, Vishay) was used, as illustrated in the dashed box in Fig. S4A. The resistance value of the load resistor was chosen to be at least one order of magnitude larger than the “ON” resistance of the active transistor node (<1 MΩ). Simplified circuit schemes without showing the load resistors are presented in Figs. 1 and 4 and Figs. S7–S9. The detailed programming scheme for each tile is described in Fig. S7. The tiles were programmed sequentially, with the interconnection between the tiles connected subsequently through an external switch box for the testing of the logic functionalities. For the logic outputs, drain voltages of 2.3–2.7 V were used for the DFF, FSM, and 2-bit full adder demonstrated in Fig. S9 and Figs. 3 and 4. Source voltages of –1 V were used for the DFF and FSM and 0 V for the 2-bit full adder. The input gate voltages were 0 V for logic 0 and 2.3–3 V for logic 1, as specified for each circuit in the main context.