Evolution and selection of river networks: Statics, dynamics, and complexity

Significance

Our focus is on a rich interdisciplinary problem touching on earth science, hydrology, and statistical mechanics—an understanding of the statics and dynamics of the network structures that we observe in the fluvial landscape, and their relation to evolution and selection of recurrent patterns of self-organization. It is an exemplar of how diverse ideas, numerical simulation, and elementary mathematics can come together to help solve the mystery of understanding a ubiquitous pattern of nature.

Abstract

Moving from the exact result that drainage network configurations minimizing total energy dissipation are stationary solutions of the general equation describing landscape evolution, we review the static properties and the dynamic origins of the scale-invariant structure of optimal river patterns. Optimal channel networks (OCNs) are feasible optimal configurations of a spanning network mimicking landscape evolution and network selection through imperfect searches for dynamically accessible states. OCNs are spanning loopless configurations, however, only under precise physical requirements that arise under the constraints imposed by river dynamics—every spanning tree is exactly a local minimum of total energy dissipation. It is remarkable that dynamically accessible configurations, the local optima, stabilize into diverse metastable forms that are nevertheless characterized by universal statistical features. Such universal features explain very well the statistics of, and the linkages among, the scaling features measured for fluvial landforms across a broad range of scales regardless of geology, exposed lithology, vegetation, or climate, and differ significantly from those of the ground state, known exactly. Results are provided on the emergence of criticality through adaptative evolution and on the yet-unexplored range of applications of the OCN concept.

A drainage basin of a river is the region from which rainfall becomes runoff flowing downhill and aggregating to form the river streams. Branching river networks in runoff-generating areas are naturally fractal (1)—there are basins within basins within basins, all of them looking alike. Fluvial landforms show deep similarities of the parts and the whole across up to six orders of magnitude despite the great diversity of their drivers and controls—geology, exposed lithology, vegetation, and climate (2). Observational data reveal the fine detail and large-scale patterns of fluvial landforms. Such data have been used to characterize river basins across our planet (2). River networks are spanning trees: spanning, because there is a route for water to flow from every location of the basin to the main stream; and a tree, because of the absence of loops. The scaling associated with the observed spanning trees is a topic of great interest (3–25). Remarkably, one observes approximate universality in the set of scaling exponents even though one is considering nonequilibrium conditions. As characteristic of conventional critical phenomena, the exponents were found not to be independent of each other. Rather, each of them can be derived through scaling relations postulating the knowledge of geometrical constraints. In addition, as is common in any good detective novel, our story comes with unexpected twists. The first surprise was that the observational exponents do not fall into any known standard universality class of spanning or directed trees with equal weight. A pivotal step in the story came through the notion of optimal channel networks (OCNs). This was directly inspired by the notable success of variational principles in physics. As water flows downhill, it loses potential energy. Could it be that nature selected those spanning trees for which the total energy dissipation was a minimum? Remarkably, numerical simulations compared with data suggested that this was likely the case. In a puzzling twist, it was found that one could solve OCNs exactly and the resulting exponents associated with the global minimum did not match either the observational data or the numerical simulations. The puzzles were resolved through a study of the dynamics of erosion sculpting the landscape. It was shown that the simplest dynamical equation, under reparametrization invariance, predicted that river networks were necessarily trees and had no loops. Even more interestingly, one could show that every local minimum of the OCN functional is a stationary solution of the general landscape evolution equation. The above observations suggested that the adaptation of the fluvial landscape to the geological and climatic environment corresponds to the dynamical settling of optimal structures into suboptimal niches of their fitness landscape and that feasible optimality, i.e., the search for optima that are accessible to the dynamics given the initial conditions, might apply to a broad spectrum of problems in nature. The puzzle was solved: The statics and dynamics of river networks had been collected in a neat package. It all fit in and a surprising outcome was the robust statistical features of the dynamically accessible minima.

This Inaugural Article provides technical details and references for the various steps of the development of the theory, explores results on the role of heterogeneity, and reviews recent developments and applications of the OCN concept in a variety of fields.

Scaling Fluvial Landscapes: Comparative Geomorphology

Accurate descriptions of the fluvial landscape across scales stem from digital terrain maps, i.e., discretized elevation fields 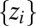on a lattice of pixels of unit area. The drainage network is determined by assigning to each site i a drainage direction through steepest descent at i, i.e., along local gradients 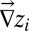. Drainage directions determine uniquely aggregation patterns and network lengths. To each pixel i, total drainage area (the number of upstream pixels connected to i through flow directions) is expressed in pixel units as 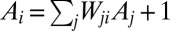, where: 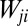is the arbitrary element of the connectivity matrix (i.e., 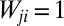if 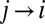and 0 otherwise), and 1 represents the unit area of the pixel unit that discretizes the surface. In the case of uniform rainfall injection for landscape-forming events, 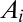provides a proxy of the flow at point i, i.e., accumulated flow 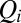, as the sum of the injections over all connected sites upstream of site i (included) 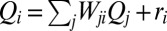[where 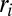is the distributed injection (2)]. In the case of constant injection 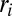for landscape-forming events, one has 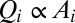, a commonly accepted hydrologic assumption (2, 3).

Many geomorphological features can be analyzed in the greatest detail. Channeled portions of the landscape are extracted from elevation fields through the exceedance of geomorphological thresholds of slope-dependent total contributing areas (6, 14). Contributing area 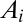at any point is related to the gradient of the elevation field (the topographic slope) at that point: , where a value of γ around 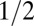is typically observed in runoff-generating areas (2, 6, 14, 26). Slope–area relations provide a powerful synthesis of the local physics. Upstream lengths 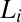(the along-stream distance from the farthest source draining into i) are also computed at any channeled site (2, 17, 18). The probability distributions of relevant random variables (like drainage area A and upstream length L sampled at any site of the catchment) are characterized by finite-size scaling (2, 17), i.e., 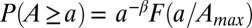, where 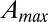is the area at the catchment closure limiting the distribution; and 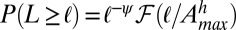, where 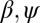are suitable scaling coefficients and h is Hack’s coefficient (27) (F and 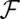are suitable cutoff functions; Fig. 1). 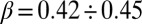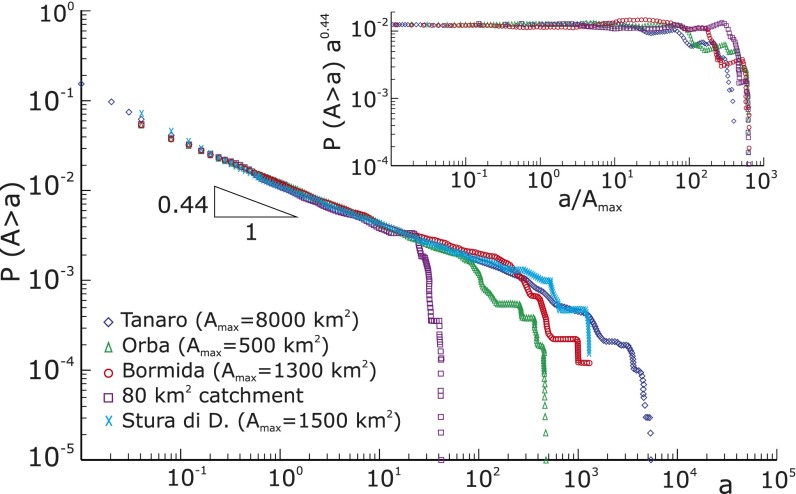The empirically defined scaling exponents, from vast comparative analyses (2, 17, 18), lie in a narrow [and related (28)] ranges (29) and 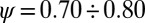(17), respectively. Fig. 1 shows one significant example of empirical probability distribution for total contributing area A. Here (to avoid binning issues), the cumulative probability of exceedance 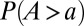is plotted for five nested subcatchments of a relatively large basin (∼3,000 km²), showing clearly its power-law character, jointly with the remarkable collapse of the rescaled plot defining the finite-size scaling effect induced by the cutoff dictated by the maximum area at each closure. The finite-size scaling ansatz provides a compelling observational proof of self-similarity and a strong version of Hack’s law (27) relating the largest upstream stream length 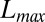to its total cumulative area: 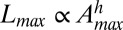, with 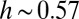. Hack’s coefficient h is a measure of the elongation of catchment shapes and an unmistakable signature of the fractal geometry of the river basin (1). The finite-size scaling argument requires the linkage of aggregation and elongation yielding 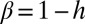(2, 17, 18), a framework in which the accepted standard values 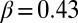and 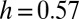fit perfectly. Scaling in the river basin has been documented in many other geomorphological indicators, including exact limit properties (22). Such measures will be used for comparative analyses with patterns derived from evolution and selection.

Fig. 1.

Statistical evidence of scaling behavior in the fluvial landscape: finite-size scaling of total contributing catchment area. Empirical probability distributions of contributing area are simply derived by computing A at every location from topography and plotting the probability obtained by counting the relative proportion of sites anywhere in the catchment whose total contributing area exceeds a current value a, here expressed in square kilometers. Empirical plot for five nested subcatchments of different maximum area 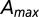indicated in the legend. (Inset) Collapse plot of the probability distribution once properly rescaled. The empirical cutoff function is argued to behave as 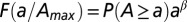, where β is estimated at 0.44. F is shown to behave properly by collapsing into a single curve regardless of widely varying 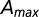. Note that 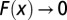for and 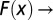const for 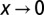. The nested catchments belong to the Tanaro river basin (Italy).

OCNs

We start from a review of the static model of river networks known as the OCN (11–13, 30). The OCN model was originally based on the ansatz that configurations occurring in nature are those that minimize a functional describing total energy dissipation and on the derivation of an explicit form for such a functional (using, locally, flow and energy loss, i.e., approximated by 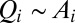and by the drop in elevation 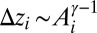). Spanning, loopless network configurations characterized by minimum energy dissipation are obtained by selecting the configuration, say s, that minimizes the functional:

where i spans the lattice, say of N sites. Given that 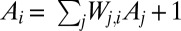, where 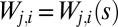is the element of the connectivity matrix, the configuration s determines uniquely, on a spanning tree, the values of 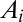. It is crucial, as we shall see later, that one has 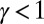directly from the physics of the problem subsumed by the slope–area relation.

Optimal arrangements of network structures and branching patterns result from the direct minimization of the functional in Eq. 1. The basic operational problem to obtain OCNs for a given domain is to find the connected path s draining it that minimizes 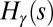without postulating predefined features, e.g., the number of sources or the link lengths (SI Text). Random perturbations of an initial structure imply disconnecting and reorienting a single link at a time. They lead to new configurations that are accepted, details aside (SI Text), if they lower total energy expenditure—iterated until many perturbations are unable to prompt change by finding better configurations. Loops possibly generated by the random configuration search in the fitness landscape were excluded at first without a rigorous basis. Only later it was shown exactly that they lead to energetically unfavorable configurations (23–25) (Dynamics and SI Text). Boundary conditions are required for the evolving optimal trees, as outlet(s) must be imposed (single or multiple outlets along drainage lines) as well as no-flux or periodic boundary conditions (2, 31, 32).

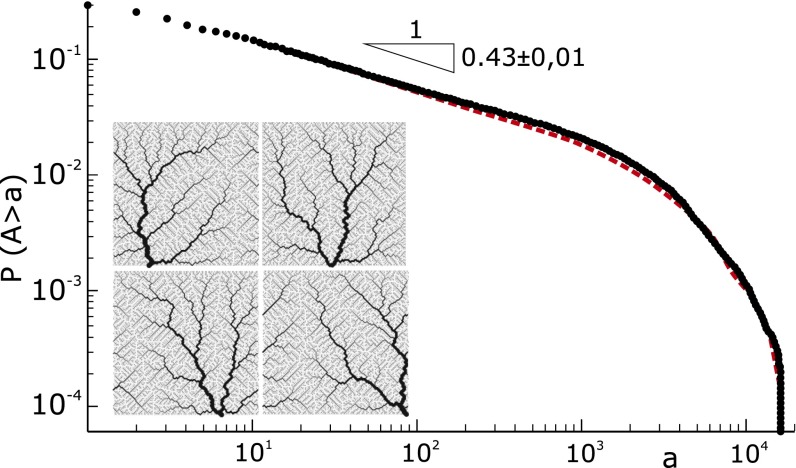
Fig. 2 illustrates the ensemble average of 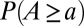for 128 OCNs obtained by a greedy algorithm (i.e., accepting only changes that decrease total energy dissipation; SI Text), in a Monte Carlo setting where the single outlet imposed as boundary condition changes for every realization. Note that this result, yielding local minima of the functional in Eq. 1, proves robust with respect to initial and boundary conditions or to the insertion of quenched randomness (2).

Fig. 2.

Scaling of total contributing area in single outlet OCNs: ensemble average of 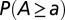from 128 OCNs of size 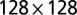obtained by shifting the outlet’s position for each realization. The dotted line represents an analogous ensemble of realizations endowed with periodic boundary conditions at the sides, which slightly steepen the ensemble mean scaling exponent from 0.43 to . (Inset) Four OCN realizations.

Interesting issues emerge on the statics, dynamics, and complexity (33) of OCNs. Here, we shall discuss the following: the existence of many dynamically accessible stable states; the practical impossibility of pointing out a priori the most stable feasible state among all metastable states without an evolutionary account of the history of the current configuration of the system; the hierarchical structure and the universality class of dynamically accessible states. Although the above are features that river networks share with other natural complex systems (33), the extent of observations and comparative analyses, the exact relation to the general evolution equations, and the broad range of scales involved suggest their interest as a general model system of how nature works (19).

Exact and Computational OCN Analyses

The OCN model has been thoroughly explored (2, 13, 20, 28, 34). A remarkable result is that local minima exhibit critical behavior characterized by scaling exponents indistinguishable from those observed in nature (2, 28). Before embarking in a technical discussion, we show examples of local and global minima of OCNs for a multiple-outlet setting (Fig. 3). Fig. 3A shows the result obtained by Eden growth generated by a self-avoiding random walk, known to lead to suboptimal structures analog to the ones attainable by enforcing only pointwise optimality (35, 36). Eden growth is a benchmark because of its chance-dominated selection (no necessity is implied by the self-avoiding random-walk dynamics, and only tree-like structures are selected by construction). Such structures were initially thought of as capturing the essentials of natural selection (3). That turned out to be an artifact of nondistinctive tests on tree structure (28) echoed by the statistical inevitability of Horton’s laws (37). Indeed, if topological measures alone (say, Horton numbers of bifurcation and length imposed on Strahler’s ordering, or Tokunaga matrices) are used to sort out the fine comparative properties of trees, one can be misled into finding spurious similarities with natural forms. The exercise of comparing Fig. 3 A and B is revealing as the two constructs have indistinguishable topological features, although they differ even at eyesight (18, 25, 28).

Fig. 3.

Different degrees of optimality in multiple-outlet networks obtained in the same rectangular domain imply substantial modifications only detected by truly distinctive statistics. (A) Optimality enforced only locally and tree-like constraints (35, 36) settle the system into unrealistic shapes whose topological structure is still indistinguishable from the one found in real rivers and in dynamically accessible states of total energy minimization: Eden growth patterns of self-avoiding random walks filling the domain. (B) An imperfect OCN (i.e., 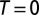; SI Text) leading to a local minimum of total energy dissipation. Note that OCNs bear long-lived signatures of the initial condition owing to the myopic search procedure, but actually reproduce perfectly, besides topology, also the aggregation and elongation structures observed in real river landscapes (2). (C) Ground-state OCNs obtained through simulated annealing using a very slow schedule of decreasing temperatures T (SI Text). The reaching of the ground state is confirmed by the matching of the exact mean field exponents (20) with those calculated for C. Note also the somewhat unrealistic regularity of the drainage patterns (redrawn after refs. 25 and 28).

Distinctive statistics of tree forms must rely on linked scaling exponents of aggregated areas, lengths, and elongation (28). Exact proofs are available like in the noteworthy case of Peano’s basin (1, 34, 38), where topological measures match those of real basins and OCNs, but fail to satisfy the requirements on aggregation and elongation. More subtle—but equally clear—is the failure of random-walk–type models (3) or topologically random networks (39, 40) to comply with stringent statistical comparisons (28). Note that the latter models were especially influential in suggesting that chance alone was behind the recurrence of natural patterns, because of the equal likelihood of any network configurations implied by the topologically random model. Instead, their purported similarity with natural patterns is now seen as an artifact of lenient comparative tools because statistical properties and “laws” derived in that context are inevitable for spanning trees. This applies to certain properties of directed networks as well (22).

Necessity is at work in the selection of natural networks because all spanning trees are not equally likely. Fig. 3B (18) shows a local minimum of Eq. 1 obtained by the greedy algorithm (SI Text). The fine features of the trees match perfectly those found in nature (2, 28). These results, obtained by accepting configurations perturbed by disconnecting and reorienting a single link at a time only if the new configuration lowers total energy dissipation, entail a myopic search capable of exploring only close configurations. Fig. 3C is instead obtained through the Metropolis procedure, where a massive annealing strategy has been implemented. This implies that many energetically unfavorable changes have been accepted owing to a schedule of slowly decreased temperatures (SI Text) reaching a ground state characterized by mean field scaling exponents (ref. 20; see below), here matched perfectly. Even at eyesight, the differences in the aggregation structure and in the regularity of the selected landforms are striking.

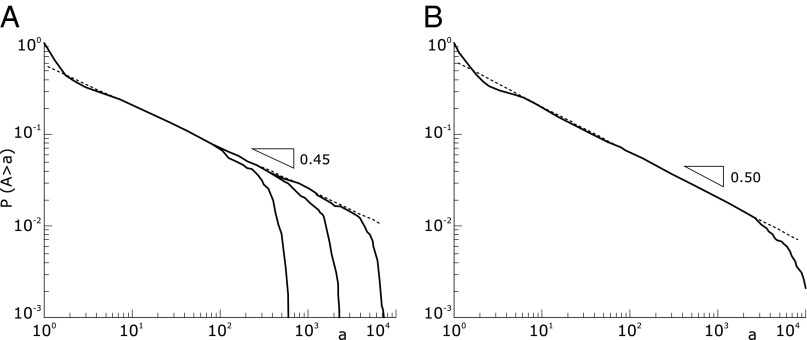
Fig. 4 further elaborates on this point. It shows the progressive departure of the exponent β from the typical observational value of 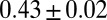along with refinements of the minimum search procedure (2). The scaling exponents of rapidly annealed minima on highly constrained OCNs are consistently found in the range 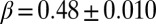, whereas the limit value 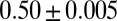, corresponding to the ground state (20), is consistently obtained only for the least constrained arrangements (Fig. 4B), that is, subject to multiple outlets, periodic boundary conditions, and through a schedule of slowly decreasing temperatures in the annealing scheme to avoid any legacy of the initial configuration. Each constraint affects the feasible optimal state to a different degree depending on its severity, matching the observation of consistent scaling exponents with minor but detectable variations in describing the morphology of different fluvial basins (2). Different fractal signatures embedded in linked scaling exponents thus suggest that evolution is adaptive to the climatic, lithologic, vegetational, and geologic environment. The worse energetic performance and yet the better representation of natural networks by suboptimal OCNs imply a defining role for geologic constraints in the evolution of a channel network. In fact, channel networks cannot change widely regardless of their initial condition, because these conditions leave long-lived geomorphic signatures (41). A question, arguably of general validity for open dissipative systems with many degrees of freedom, is whether the optimization that nature performs in the organization of the parts and the whole, could really be farsighted—that is, capable of evolving in a manner that completely disregards initial conditions. This would allow for major changes of structural features in the search for more stable configurations even though it would necessarily involve evolution through many unfavorable states. The experiments shown in Figs. 2–4 suggest that the type of optimization that nature performs, at least in the fluvial landscape, is myopic. The proof that river networks are not free to explore extended regions of their fitness landscapes suggests that nature might not search for global minima in general when striving for optimality but rather trades to settle in for dynamically accessible local minima whose features are still scaling, although differently from the universal features of inaccessible ground states.

Fig. 4.

Ensemble mean of the statistics of aggregated area in 100 realizations of OCNs generated with different boundary conditions: (A) plot of 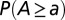obtained through ensemble averaging of the largest networks developing within 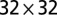, , 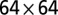and 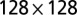lattices with multiple-outlet domains with lateral periodic boundary conditions (no-flux condition at the top boundary). Here, local minima are found through a greedy search procedure (SI Text). Note that the imposed periodicity relaxes constraints on the aggregation of the accessible minimum energy configurations. (B) As above for the largest lattice. Here, the minimum search procedure is a carefully annealed Metropolis algorithm (SI Text). Note that the ensemble mean exponent is 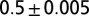, matching the characteristics of the ground state (redrawn from ref. 2).

Analytical results complete our static view of dynamically accessible optimal states (2, 17, 20, 28, 34). Exact properties for the global minimum of the functional 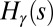in Eq. 1 are addressed first. Let us consider two limit cases ( 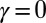and 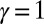). As per 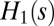, we denote with 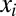the along-stream length of the pathway connecting the ith site to the outlet. It is straightforward to show that 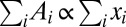(2, 20). Thus, the minimization of energy dissipation for 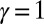corresponds to the minimization of the weighted path connecting every site to the outlet, i.e., the mean distance from the outlet, and the global minimum is the most direct network. The configurations yielding a minimum of 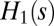is realized on a large subclass of the set of spanning trees, all of the directed ones where every link have positive projection along the diagonal oriented toward the outlet. The 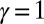case gives a minimum energy scaling 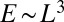(where L is the characteristic linear size of the lattice). This follows from the observation that any directed network corresponds to the Scheidegger model of river networks (4), where all directed trees are equally probable by construction. Such model can be mapped into a model of mass aggregation with injection exactly solved (8–10), later shown (42) to be map exactly the time activity of the abelian sandpile model of self-organized criticality (5). The corresponding scaling exponents are as follows:

All directed trees are equally probable having the same mean distance to the outlet, and each stream behaves like a single random walk (10).

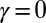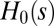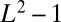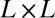The case, instead, implies the minimization of , the total weighted length of the spanning tree. Every configuration has the same energy because every spanning tree has the same number of links ( for a square lattice). The minimum energy E gives 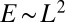for each network, in analogy to the problem of random spanning trees, and the related scaling exponents for a square lattice are as follows (20):

For arbitrary values of γ, it has been shown exactly (15) that a configuration s that minimizes 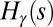also minimizes total potential energy. In fact, for that configuration, one has 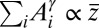, where the mean catchment elevation 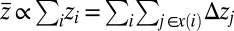[where 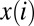is the path from i to the outlet] is constrained by 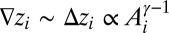(the local drop in elevation 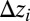along a drainage direction is added 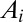times, i.e., as many times as the contributing sites upstream of i).

For all 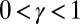, and in the thermodynamic limit 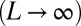, the global minimum in the space, 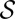, of all spanning trees of the functional 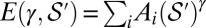scales with 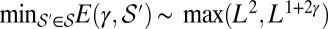(where 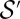denotes the subset of optimal trees). Because 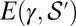is an increasing function of γ equal to 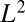for 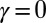, then for 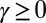one has 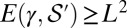(SI Text). The result (SI Text) is 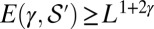yielding the lower bound

holding for every tree 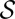, and thus also for the minimum over 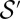(20). Relevant scaling exponents are derived from there. For instance, as undirected networks have 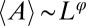, where , and recalling that β is the scaling exponent for total contributing area, and the above result yields, for 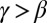(17) (SI Text):

valid for 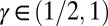. The exponents are the same as in mean field theory and for the Peano basin (34, 38), and indeed significantly different from the range of scaling exponents observed in nature (28). The most striking result is that the exponent of the distribution of aggregated areas is 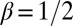, quite different from the consistent range 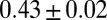for observational values (2).

The features of the minima of 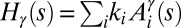, where 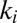condenses information on spatial heterogeneities, are also revealing. Two cases have been analyzed, namely the case of random bonds modeling local heterogeneity (21, 34), and the case of random spatial injections driving landscape-forming discharges. In the first case, one obtains a bound for total energy dissipation through an argument analogous to the homogeneous case—thus, all exact results for the homogeneous case apply (34). A different type of heterogeneity, however, may be introduced through the forcing injection field 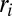[recall that the accumulated flow 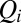is the sum of the injections over all connected sites upstream of site i (included), i.e., 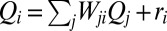]. One thus wonders about differences between the probabilities of accumulated flow, 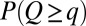, and area, 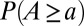(where 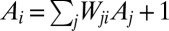). In fact, optimization would have to be carried out by minimizing 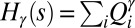, the proper energy dissipation functional, to collapse into equivalent formulations when 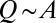for uniform injections. Hence one expects different degrees of aggregation, reflected in cumulated areas, depending on the spatial patterns of injection. This is actually the case (Fig. 5). Formally, this can be seen in the Kullback–Leibler (KL) divergence framework (43), where, given two probability distributions [like those yielding 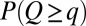and 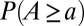], their KL divergence quantifies the loss of information incurred when one is used to approximate the other. Fig. 5 shows that the structure of the aggregation is altered by the correlation structure of the injection field (highlighted by diverging distributions for Q and A). Consistently with the ansatz labeled “practice makes critical” (43), the effect of added heterogeneity is that of making the system more critical, as underlined by the sharper finite-size effect (blue curves). The correlation scale of the forcing noise affects the scaling exponent of aggregation implying the selection of scaling landforms that adapt to environmental frustrations.

Fig. 5.

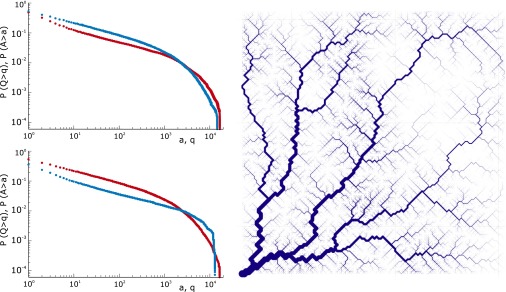
Ensemble average of the statistics of 100 OCNs obtained for a heterogeneous injection field. Here, the injection term 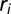(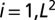, where L is the lattice size) is, for each OCN, one realization of a random space function (RSF) log-normally distributed with unit mean (for consistency) and variance equal to 2: (Upper Left) comparative analysis of the ensemble mean probabilities 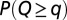(blue) and 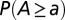(red). The correlation scale of the RSF 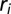is set at 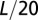. (Lower Left) Same for the above with correlation scale at 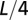. (Right) OCN where the size of the channel is drawn proportionally to Q. One notes thin channels extending at large contributing areas in correspondence to the patches of relatively weak injections.

Dynamics

River landscapes may be defined by nodes on a regular lattice representing the elevation field where network links are determined by steepest descent on the topography whose evolution determines the network structure. The equation that has been proposed to describe the evolution of the landscape, among a realm of essentially equivalent forms (e.g., refs. 2, 14, 21, 24, 44, and 45), is as follows:

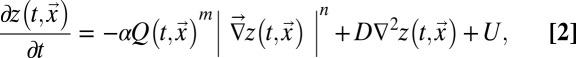where z again denotes the elevation at the point 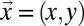of the substrate plane. The first term at the right-hand side is an erosional component relevant to channeled sites, and the second is a diffusive term known to portray hillslope evolution; the third term is a constant term modeling the geomorphologic uplift in tectonically active areas. The existence of uplift originating in tectonic forces allows a landscape to evolve forced by two concurrently active processes, uplift (endogenic) and degradation (exogenic). A stationary state results from their balance. A simple argument leading to Eq. 2 follows from the general form 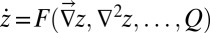, where an explicit dependence on z is excluded because it would break translational invariance (21, 24). Note that landscape-forming fluxes 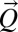(a 2D vector) become scalars, i.e., 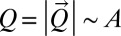because 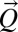is assumed parallel to 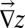(21, 24), where we introduce A, total contributing area at 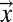, as a proxy the landscape-forming discharge (3). The diffusive term acts on the surface even at points with zero contributing areas unlike the first term, which vanishes when the flux becomes zero. In the absence of the diffusive term, the presence of maxima on the surface will cause the formation of singularities during the evolution, because, e.g., points at the top of a hill will never be eroded by the first term (both A and 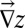vanish). The presence of a diffusive term, however small, is then essential (24). In the discretized version of the model, however, each site collects at least a unit area and thus no singularities appear even in the absence of the diffusive term. Reparametrization invariance in the small gradient approximation requires that to leading order one has 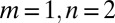(21, 24). The above is consistent with established geomorphological tenets: fluvial processes in landscape-forming events (whose erosive transport rates are defined by 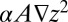) are responsible for the imprinting of the network by landscape-forming events. Hillslope processes—mass wasting defined by the divergence of a diffusive flux yielding the term 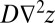in Eq. 2—act over larger timescales by smoothing landscapes without the capability of altering their basic fluvial signatures (41).

An interesting question is how networks resulting from the erosional dynamics are related to the landforms arising from minimization of total energy dissipation. Specifically, any landscape reconstructed from an optimal configuration using the slope–area relation has been shown to be a stationary solution of the evolution equation (Eq. 2). This superficially might seem obvious because the relation between topographic gradients and cumulative area is locally verified by construction [the stationary solutions of Eq. 2 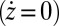require that 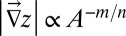if 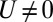, thus 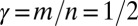]. One must notice, however, that the slope–area relation alone does not imply stationarity because the flow may not (and in general will not) be in the direction of the steepest descent in the reconstructed landscape (23). Thus, OCNs consist of the configurations s, which are local minima of Eq. 1 in the sense specified below: Two configurations, s and 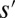, are close if one can move from one to the other just by changing the direction of a single link (i.e., the set of links 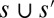represent a graph with a single loop). A configuration s is said a local minimum of the functional in Eq. 1 if each of the close configurations 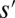corresponds to greater energy expended. Note that not all changes are allowed in the sense that the new graph again needs to be loopless. Thus, a local minimum is a stable configuration under a single link flip dynamics, i.e., a dynamics in which only one link can be flipped at a given time only when the move does not create loops and decreases the functional Eq. 1. Any elevation field obtained by enforcing the slope–area relation to a configuration minimizing at least locally the functional Eq. 1 is a stationary solution of the landscape evolution equation yielding the slope–area rule at steady state. This, in turn, implies that the landscape reconstructed from an optimal drainage network with the slope–area rule is consistent with the fact that the flow must follow steepest descent. The proof can be sketched as follows: consider a configuration realizing a local minimum of the dissipated energy, and a site i. The link issuing from i will join one of the nearest neighbors of i, say k. Let j be one of the remaining nearest neighbors such that changing the link from 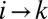to 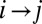one still gets an allowed configuration. Paths emerging from k and j will intersect downstream in a given point w (case a) or will never intersect until they reach their outlets (case b). Let 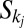denotes the set of all points in the path from k to w in the first case and from k to its outlet in the second. Likewise, one may define 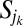. Changing the link from 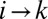to 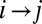will cause only the areas of sites belonging to the sets 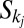and 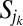to change. In particular, all areas in the set 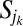will be increased of an amount equal to the area 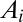contributing to the flow through i, and all areas in the set 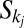will be decreased by that amount. Thus, such a change will cause a change 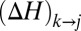in the dissipated energy equal to the following:

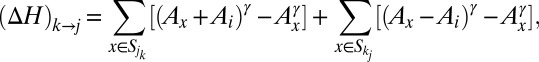where 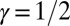and 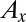are the contributing areas before the flip. The condition for a configuration to be a local minimum of 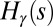translates into the set of conditions 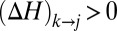for each i and j such that j is a nearest neighbor of i and gives rise to a loopless configuration. The elevation field determined by the local minimum configuration through the slope–area relation represents a stationary solution of the landscape evolution equation when the elevation field determined by a graph using slope–area relations is such that the drainage directions derived with the steepest descent rule yield again the graph from which the elevation field originated. This implies that if 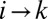is the drainage direction in the point i, the biggest drop in elevation from i to its nearest neighbors is in the direction of k. This condition yields 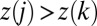for any j that is a nearest neighbor of i and different from k. The converse is not true, however, i.e., a stationary solution of the landscape evolution equation is not necessarily a local minimum of the dissipated energy under the single link flip dynamics. Thus, minimizing the functional in Eq. 1 leads exactly to configurations that solve Eq. 2 in stationary conditions. The proof for the general case 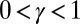is elsewhere (24).

Complexity

The transformations due to coarse graining of the state of a given system is termed renormalization, and the goal is to study quantitatively the change that a physical quantity undergoes under different degrees of aggregation. We will focus on the behavior of energy dissipation of OCNs under coarse graining. Because optimal energy expenditure is the foundation of the OCN concept, its variation under a change in the scale of observation of the landscape is of considerable importance. Although a full account is reported elsewhere (2), here it suffices to coarse grain the site of a lattice of size L in squares of side 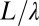, where the initial OCN is described at a resolution of pixels of side length L 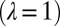. The conserved property is elevation: The 3D structure of the OCN is assigned everywhere through the exact slope–area relationship 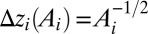, where 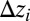approximates the topographic gradient. The original sites are then grouped in squares of side 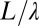, with 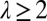(Fig. 6), such that, from an initial number of pixels N, one coarse grains the description of the terrain to a total number of pixels 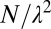. The elevation of each of the new sites (a larger pixels of side 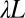) is computed as the average elevation of the 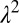constituent pixels of side length L. From this coarse-grained 3D landscape, a new drainage network is drawn following as flow directions the lines of steepest descent as in the original construct. The above transformation preserves the mean elevation of the basin [and thus its drainage network is still an OCN (2)]. Examples of OCNs progressively coarse-grained according to the previous rules are shown in the Inset of Fig. 6. The key result highlighted therein is that effectively the probability distribution of aggregated area is invariant under coarse graining, i.e., 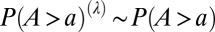. Under such premises, one obtains that total energy expenditure E of OCNs under coarse-graining scales as follows:

with 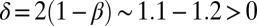(2). All of the above shows the statistical invariance of OCNs with the transformation group that preserves the mean elevation (and thus the total energy dissipation) of the system. This is deemed as fundamental evidence of the fractal features of minimum energy structures.

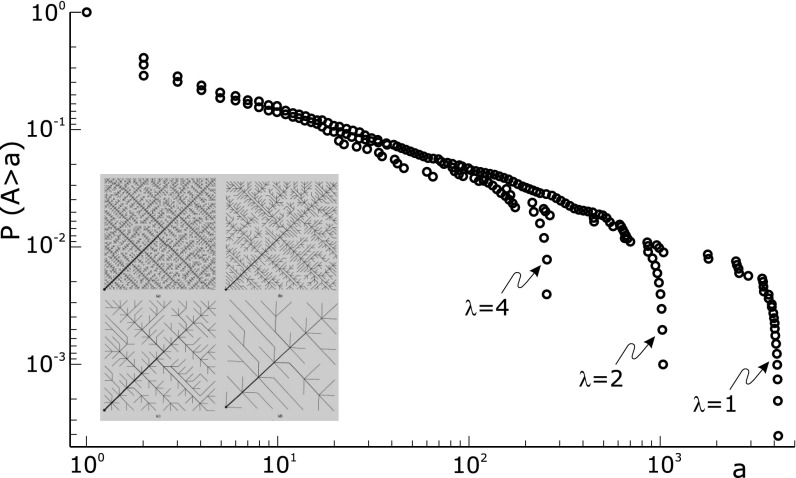
Fig. 6.

Effects of coarse graining at different levels λ of the probability of exceedence of total area A for the OCNs shown in Inset. It is remarkable the invariance of the probability distribution under coarse graining, a signature of the scaling aggregation structure. (Inset) Renormalized OCNs with 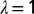(Upper Left), 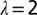(Upper Right), 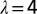(Lower Left), and 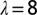(Lower Right).

A remarkable result is that every tree is a local minimum of Eq. 1 when 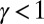, a result hinted at above and formally demonstrated elsewhere (23, 24). As noted above, it explains why the original ansatz of accepting only spanning tree configurations, as opposed to standard looping networks, was correct after all (SI Text). Fig. 7 illustrates the main result in the simple case of a four-bond lattice, a case that has been generalized to arbitrary lattices (23).

Fig. 7.

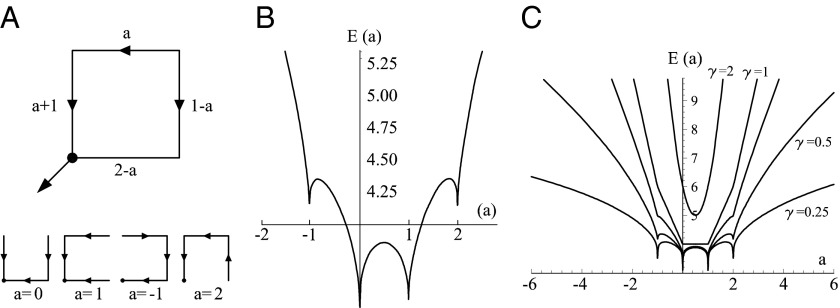
The four-bond lattice. (A) The four-node arrangement, with indications on the currents that respect continuity (note that a unit flux is injected at each node). The dot is the outlet. Here, the current a is taken as the parameter regulating the entire distribution of fluxes owing to continuity. (Lower Left) The only loopless configurations of the system are generated by integer values of a: possible trees correspond to the cases 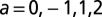. (B) Plot of the function E vs. a from 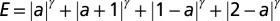(with 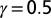), which is derived by computing energy dissipation after implementation of continuity at the nodes. In particular, the plot of 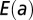highlights that there are local minima in correspondence with one of the four currents being zero (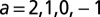), corresponding to the four trees shown in Lower Left (SI Text). (C) Energy functions 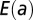vs. a for the cases 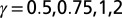. The particular behaviors highlighted in the plot are discussed in SI Text.

Finally, central to models postulating chance-dominated network selection is the assumption of equal likelihood of any tree-like configurations. The foundations of OCNs, however, postulate that certain spanning loopless network configurations are more likely than others. Indeed, their overall likelihood is controlled by the functional Eq. 1 defining total energy expenditure of the network structure both as a whole and in its parts. The set of possible configurations for the system is constituted by the ensemble of all rooted trees spanning a given lattice of sites defined by a complete set of oriented links among connected neighbor sites. Following ref. 46, the thermodynamic rationale behind the scaling properties of the energy and entropy of OCNs can be studied by assigning a probability 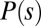to each particular spanning tree configuration s, i.e., 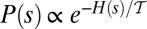, where 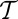is a suitable parameter resembling Gibbs’ temperature of ordinary thermodynamic systems. The functional 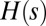is the Hamiltonian of the system, i.e., a global property related to energetic characters. Network models where all spanning trees are equally likely is the limit case for 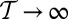. OCNs belong to the class of configurations where 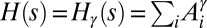(where i spans the 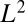sites occupied by a 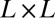square lattice) and represent the maximum probability case for 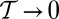. We show, following ref. 46, that the OCN concept applies at any finite temperature for 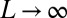. For a fixed γ, let 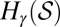denote the finite set of all possible values that may be taken on by 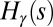for trees 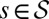. Given an energy level, E, let 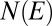be the degeneracy, or the number of different spanning trees s for which 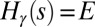. One has 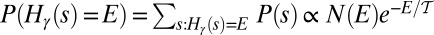. Defining formally the thermodynamic entropy as 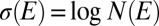, one obtains 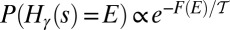, where a free energy 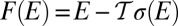has been introduced. Indeed, the most probable states correspond to an energy level E that minimizes 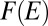. 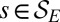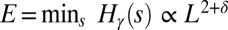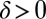One has exactly that for the set of OCNs it is with for 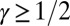(SI Text). For spanning trees, the number 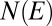of configurations s with given energy E scales as 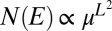(46). We thus conclude that, for OCNs with 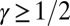, in the limit 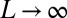, entropy scales subdominantly to the energy with system size (SI Text), i.e., the configuration s that minimizes 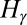also minimizes 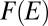whatever the value Gibbs’ parameter 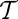, provided that the system is large enough. Hence OCNs, which would correspond to 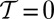, reproduce natural conditions for any “temperature.” Because fluvial networks usually develop migration of divides and competition for drainage in the absence of geologic controls over domains large with respect to the scale of channel initiation, it is likely that natural networks evolve under conditions that well approximate the thermodynamic limit .

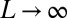The OCN model has been shown to belong in the class of self-organized critical approaches (2, 19) through a sandpile-like cellular automaton of river network evolution (15). Developments and applications of OCNs have appeared recently. For example, OCN arrangements have been used to design laboratory experiments with protist metacommunities where patches (true living ecosystems) are arranged in optimal network shapes to simulate the type of directional biological dispersal one expects in fluvial environments (47, 48), or used in spatially explicit models of epidemics of waterborne disease where river networks act as ecological corridors for pathogens (49). The OCN concept of feasible optimality has inspired a number of studies on fractal structures in nature not necessarily related to true equilibrium properties of the system, e.g., a class of nonequilibrium interfaces in random exchanges Ising ferromagnets (50). Also, 3D OCNs have been proposed and compared with metabolite distribution networks in organisms to deduce allometric scaling properties (32). Preliminary comparisons of Steiner trees with OCNs also promise avenues of research (32). The finding that 3D OCNs have characteristics analogous to 2D versions, as well as scaling properties similar to metabolic networks in biological organisms, suggest that they may prove more than academic exercises.