A Pluralistic Account of Homology: Adapting the Models to the Data

Abstract

Defining homologous genes is important in many evolutionary studies but raises obvious issues. Some of these issues are conceptual and stem from our assumptions of how a gene evolves, others are practical, and depend on the algorithmic decisions implemented in existing software. Therefore, to make progress in the study of homology, both ontological and epistemological questions must be considered. In particular, defining homologous genes cannot be solely addressed under the classic assumptions of strong tree thinking, according to which genes evolve in a strictly tree-like fashion of vertical descent and divergence and the problems of homology detection are primarily methodological. Gene homology could also be considered under a different perspective where genes evolve as “public goods,” subjected to various introgressive processes. In this latter case, defining homologous genes becomes a matter of designing models suited to the actual complexity of the data and how such complexity arises, rather than trying to fit genetic data to some a priori tree-like evolutionary model, a practice that inevitably results in the loss of much information. Here we show how important aspects of the problems raised by homology detection methods can be overcome when even more fundamental roots of these problems are addressed by analyzing public goods thinking evolutionary processes through which genes have frequently originated. This kind of thinking acknowledges distinct types of homologs, characterized by distinct patterns, in phylogenetic and nonphylogenetic unrooted or multirooted networks. In addition, we define “family resemblances” to include genes that are related through intermediate relatives, thereby placing notions of homology in the broader context of evolutionary relationships. We conclude by presenting some payoffs of adopting such a pluralistic account of homology and family relationship, which expands the scope of evolutionary analyses beyond the traditional, yet relatively narrow focus allowed by a strong tree-thinking view on gene evolution.

The meaning of scientific terms cannot and should not remain fixed forever by the priority of the original definition. This is simply because our experience constantly outruns our terminology.

  —Theodosius Dobzhansky (Dobzhansky 1955)

Defining Gene Families: A Central Complex Task in Evolutionary Studies

Homology is acknowledged as an elusive concept, and yet it is central to comparative evolutionary biology, underpins phylogeny reconstruction (Felsenstein 2004) and developmental biology (Brigandt 2003), and is used extensively in ethology and psychology (Ereshefsky 2007). On the one hand, we have ontological concepts of homology, and on the other hand, practical homology definitions and the relationship between these theoretical and operational issues is a neglected area of evolutionary biology. In this manuscript, we explore a plurality of ontological bases for understanding homology in macromolecular sequences, and by extension, we explore concepts and definitions of gene family. The ontology—the study of what objects exist and how they relate to one another—is an important aspect of enquiry that is generally addressed before any practical effort to apply this ontology. We contend that a tree-thinking perspective has strongly influenced consideration of what the ontological basis of homology might be and has needlessly and unhelpfully constrained understanding through the notion that homologs fit into neat genealogical families that have evolved their differences according to some underlying phylogenetic tree.

It has long been recognized that sequence evolution is not tree-like, in particular because of domain shuffling (Enright et al. 1999; Marcotte et al. 1999; Portugaly et al. 2006). It has also long been recognized that this non-tree–like evolution results in a network of sequence relationships (Sonnhammer and Kahn 1994; Park et al. 1997; Enright and Ouzounis 2000; Heger and Holm 2003; Ingolfsson and Yona 2008; Song et al. 2008). However, for an almost equally long period of time, it has been assumed that the right way to process this network was to carve it into homologous parts by clustering (Tatusov et al. 1997; Enright and Ouzounis 2000; Yona et al. 2000). Relevant clusters have generally been considered to be gene families with all members presenting full homology with one another. Smaller relevant clusters have also been proposed by identifying homologous domains, for example, families of sequences presenting homology over their entire length but frequently of smaller size than entire genes (Sonnhammer and Kahn 1994; Park and Teichmann 1998; Apic, Gough, Teichmann 2001b; Wuchty 2001; Enright et al. 2003; Song et al. 2008). Both of these relatively local perspectives on sequence relationships are familiar to most biologists.

Consequently, the task of defining gene families has been generally delegated to software programs that search for clusters or communities of phylogenetically related sequences. Increasingly, with genomic data sets of genuinely enormous sizes, the problem is considered best handled by such programs. And yet, the practice of placing genes into discrete gene families seems somehow at odds with the existence of domain databases (Corpet et al. 2000; Majumdar et al. 2009) that clearly demonstrate the pervasive influence of non-tree-like processes in molecular evolution (Levitt 2009). We propose not to carve up this network but to analyze its local (Sasson et al. 2003; Atkinson et al. 2009) and global structure (Adai et al. 2004).

In the last 20 years, as public repositories of macromolecular data have been greatly expanded, it has become increasingly apparent that a tree-thinking perspective on molecular evolution, while useful in many situations, is inadequate in a broader context and is far short of universality (because for instance, many, perhaps most genomes do not evolve solely in a tree-like fashion). We address the fundamental meanings of homology and its processual causes because, without precise insights into their meanings, we can only design algorithms or methods of defining homologies and families that carry caveats about the kinds of homologies that are being prioritized.

Without wishing to be critical of the useful and important work of others, it nonetheless seems unavoidable that we must take examples from the literature to provide some context. The TribeMCL (Enright et al. 2003) approach to defining gene families illustrates the problem quite clearly. In the manuscript describing the algorithm, analysis of a database of 311,257 proteins is reported. Depending on the settings of the software, 82,692 “families” could be identified, or 75,635 families or 60,934 families, with the entire automated process taking ∼14 h on a large computing cluster (Enright et al. 2003). In this case, the “concept” of family was not explicitly explored at an ontological level (though it built on a general understanding of gene family at that time); therefore, the “definition” of a family was an operational one, based on a setting in a software programme instead of exploring evolutionary history and whether it might be simple or complex. In this case, family definition is a uniformly applied rule where one software option fits all. Here, we suggest that alternatives to such simple approaches are desirable, though perhaps more difficult to achieve. Similarly, while we stress that the TribeMCL approach has proved to be of enormous benefit, we argue that many important evolutionary events and types of family relationship can be missed if this kind of approach is the only one that is taken.

A number of points should be made at this stage before getting to the main argument of the article. In this article, we specifically wish to discuss homology in the context of genes and other genetic components, such as promoters and subgene elements—what we term genetic goods (McInerney et al. 2011). For such data, the notion of “homolog” and “gene family” has been written about extensively, but there is still no universally agreed consensus on what either of these terms mean (Duret et al. 1994; Natale et al. 2000; Perriere et al. 2000; Tatusov et al. 2000; Dessimoz et al. 2012; Miele et al. 2012). Additionally, there are significant technical limitations for the detection of homologies. Certain cutoffs are imposed on any analysis, which leads to de facto homologies being missed because the sequences no longer manifest a level of similarity that is greater than expected by random chance. Despite ambitious efforts to reduce this complication, it is likely that large-scale underdetection of homologs is still a problem (Weston et al. 2004; Noble et al. 2005). The argument therefore might be made that every sequence is possibly homologous to every other sequence. That is to say, all extant molecular sequences can trace their ancestry to a single nucleotide that has evolved by duplication and mutation. This idea is not better than the alternative hypothesis that they do not all share common ancestry, because terminal transferase enzymes that exist can generate DNA sequences in a template-independent manner (Greider and Blackburn 1985). Nonetheless, fundamental limitations for software programs do not mean we cannot make progress in understanding homology concepts and improve gene family classification. Acknowledging a plurality of concepts will enhance practical gene family classifications. In particular, we wish to acknowledge that homologies are embedded within a wider set of relationships that we call “family resemblances,” and this is fundamentally different to the traditional notion of homology.

Homology Concepts and Homology Definitions

The notion of homology has a long and rich history, starting from before DNA was discovered. In 1868, Owen (1868) wrote a now classic book summarizing his ideas on homologies of the vertebrate skeleton. Owen did not have an evolutionary explanation for homology and interpreted the homologies that he inferred as variants on some kind of “archetype”—an ideal form of the organ that was constructed by a creator. In his book, Owen (1868) declared that there were three different kinds of homology. Special homology describes when two organs had the same connection to the body and performed the same function. This meant that the pectoral fin of a porpoise was homologous to the pectoral fin of a fish, even though they were manifestly different otherwise. General homology referred to morphological features or parts of features that were of “the same organ” under every variety of form and function. Finally, serial homology referred to organs that were repeated on the body—bristles on the legs of a fly for instance. Owen’s chief reason for writing this book seems to have arisen from his frustration with his fellow scientists using the word “analog” when they meant homolog.

Since then, within the field of morphology, the concept of homology has been subject to substantial debate, much of which can be seen as reflecting tensions between qualitative comparative anatomy and quantitative phylogenetics on the one hand, and causal and acausal accounts on the other. Thus, there have been proposals to synonymize homology with the cladistic concept of synapomorphy and accounts of “biological homology” (Mindell and Meyer 2001) that seek to accommodate new data from developmental biology on patterning and differential gene expression by explicating the notion of homology in terms of shared developmental pathways. The importance of ontogeny notwithstanding, of particular conceptual interest, is the notion of genetic piracy (Roth 1988) in which homology of some morphological character persists despite the genetic basis of the trait changing more or less completely over evolutionary time. These other debates illustrate how new data and new understandings of evolution often necessitate new usage of terms and clarification of concepts and models.

When similar frustrations arose almost 140 years after Owen’s work, a collection of prestigious scientists felt the need to clarify the meaning of the word homology in molecular sequence data (Reeck et al. 1987). Interestingly, this clarification did not entertain the notion that different types of homology may be required to handle molecular data, possibly because to a certain extent, there was a general consensus on the ontological concept of homology (corresponding to Owen’s general homology) though a lack of consensus on the practical identification of homologs. A reading of the literature today would corroborate the feeling that the practical level seems to be the one at which the problems of “defining” homologous genes lies, though in fact, the problems have much deeper ontological roots.

Walter Fitch commented that “homology […] is indivisible” (Fitch 2000). This sentiment is often used in the teaching of evolutionary biology classes and indeed is often quoted. However, Fitch (2000) also allowed for chimeric genes as one exception to this general model. Thus, he wrote:

If the domain that is homologous to the low-density lipoprotein receptor constitutes 20% of enterokinase, then enterokinase is only 20% homologous to that lipoprotein receptor, irrespective of its percent identity. If at the same time, this common domain were half of the lipoprotein receptor, the receptor would be 50% homologous to the enterokinase. The homologies are not the same in both directions if the proteins are of unequal length! This is the only situation where “percent homology” has a legitimate meaning and, even there, it is dangerous and better called, as Hillis has suggested, partial homology.

In Fitch’s view, saying that two proteins were homologous along part of their length was fraught with the potential for misinterpretation. Therefore, the phrase “partial homology” needs to be used with care and should only mean that “this part (X%) of sequence 1 is homologous to that part (Y%) of sequence 2.” In this case, some parts of sequences 1 and 2 do have a common ancestor, but we are implicitly acknowledging that their last common ancestor is not also a common ancestor of sequences 1 and 2 in their entirety. It would be a mistake to consider such a change in phrasing merely as a matter of rhetoric. Reeck et al. (1987) pointed out that a precise definition of homology would indeed be “an unimportant semantic issue” if it did not “interfere with our thinking about evolutionary relationships.” At that time, in the late 1980s, the problem stemmed from the common interchanging of the words “similarity” with “homology” (e.g., saying that two sequences were 80% homologous when the authors really meant that they were 80% similar in sequence). Reeck et al. offered the solution that “homology should mean ‘possessing a common evolutionary origin’ and in the vast majority of reports should have no other meaning.” Accordingly, Fitch later offered the opinion that homology was “[…] an abstraction, in that it is a relationship, common ancestry […]” (Fitch 2000). This last point, we feel, is particularly important.

Thus, the consensus among molecular biologists became that similarity was defined as quantitative by comparing the sequences in question, but that homology was qualitative—sequences are homologs or they are not. In fact, the majority of the literature from that time to present day suggests that homology is a term that specifically refers to genes or proteins that manifest significant sequence similarity along the majority of their length. Databases such as homologene (http://www.ncbi.nlm.nih.gov/homologene, last accessed December 10, 2013) and COG (http://www.ncbi.nlm.nih.gov/COG/, last accessed December 10, 2013) only contain genes that are allowed to be in one family. Although we do not deny that database entries of such sequences are likely or certain to be homologs, sole focus on those kinds of evolving entities (entries that trace their heredity to a single common ancestor) and the heuristic of requiring homologs to manifest near- or full-length significant sequence similarity has clearly resulted in biases and information loss, as has been demonstrated (Sonnhammer and Kahn 1994; Park et al. 1997; Enright and Ouzounis 2000; Heger and Holm 2003; Ingolfsson and Yona 2008; Song et al. 2008). Even if we had a universally agreed definition of the gene (Epp 1997), it remains much more complicated to decide what might be a gene family. Gene length can vary from dozens of nucleotides (the shortest human gene is 252 nucleotides in length) to several hundreds of thousands of nucleotides. Genes evolve by point mutation, legitimate and illegitimate recombination, exon shuffling, fusion, fission, invasion by selfish mobile elements, domain replacement, and so forth. Is a gene that has a transposon inserted into the middle no longer considered to be a member of this family? If a gene loses an exon and is now quite different in length from other members, then is it no longer considered to be a member of this family? In other words, our current knowledge of the diversity of evolutionary processes means that the generally agreed upon concept of homology needs revision and clarification, and other concepts such as family resemblance need to be introduced.

Recently, there has been an increased focus on the problems that domain shuffling in particular has created for efforts to distinguish orthologs and paralogs from sequences that appear to be orthologous and paralogous, when in fact they are not. Strictly speaking, two genes are orthologous when they are found in different species and can trace a direct lineage back to a single genomic locus in a common ancestor. It can be expected that the sequence in this common ancestor was not significantly different in domain architecture to the orthologs we observe today—though it is not clear how different is too different. Paralogs can trace their most recent common ancestor to a duplication event, again with the expectation that the most recent common ancestor will have had a similar structure. However, in the event that two genes or proteins look similar because they have been independently assembled through domain shuffling, they will not fulfill these criteria. In such cases, the word “Epaktolog” has been suggested to reflect similarity that is a consequence of independently “imported” domains (Nagy, Bányai, et al. 2011; Nagy, Szláma, et al. 2011). Specifically, the authors “[…] refer to proteins that are related to each other only through acquisition of the same type of mobile domains as epaktologs” (Nagy, Bányai, et al. 2011). This is an important consideration, and to date we do not have a rigorous analysis of known proteins to understand the extent to which similar proteins are in fact epaktologs and not orthologs or paralogs. However, we argue here that there are additional important relationships beyond those found in epaktologs (see later).

The most widely used method of allocating genes to a gene family is the Markov Clustering Algorithm (MCL) (Enright et al. 2002), which simulates flow through a network of sequence similarity and cuts the network at those places where flow is most restricted. A sequence similarity network is composed of nodes and edges, with the nodes representing gene or protein sequences and the edges representing some measure of similarity between the sequences. In practice, only “significant” levels of sequence similarity are represented at all, and these significant similarities are likely to represent homologous relationships because they are too similar to have arisen by random chance. Examples of such networks are given in figures 2, 4, and 5 and will be discussed later in this article. The idea behind the clustering approaches such as MCL is that unimportant relationships as defined by small, common, promiscuous domains can be safely deleted, leaving the more important relationships, and these can be used to define families. This approach is hugely successful, garnering well in excess of 1,500 citations at the time of writing. The authors have been careful to say that this method should be used with care, and indeed, appropriate usage of MCL for conservative analyses of particular kinds of homologs is expected to result in few if any errors. However, an ontological premise for this method is that a gene can only belong to one homologous family—the method explicitly does not allow a gene to belong to more than one family. This is because it is assumed that either there are “natural” discrete families and the relative strength of association between a gene and its family will emerge from the analysis or that some relationships are more important than others and the minor relationships can be dismissed as relatively unimportant. Although the philosophy of the approach (clearly influenced by the underlying assumption that gene evolution might be tree-like and takes place independently in different families) has not been explored extensively in the literature, we will argue that the effect of this algorithm is to principally enforce a tree-based viewpoint on gene families. This introduces persistent issues in homology definition that can best be overcome by first adopting more realistic starting assumptions on how genes evolve, second by adopting new concepts of homology, and third by adjusting our methods accordingly.

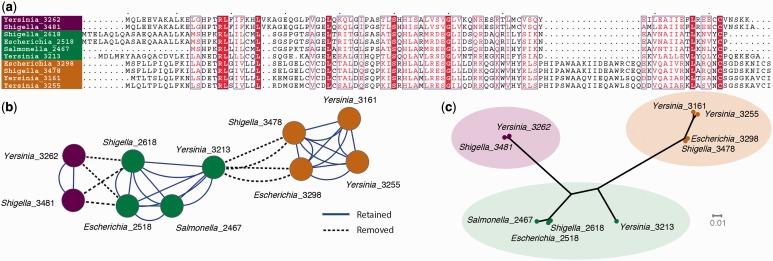
Fig. 2.

A ten-gene data set of a family of short proteins with considerable variation, including segmental length variation and possibly a chimeric history. (a) Multiple sequence alignment with completely conserved positions in the alignment are indicated by columns with a red background and white typeface, strongly conserved positions are in red typeface and surrounded by a blue rectangle, and the most variable positions are in black typeface. Positions where there is no homologous residue are represented by a dot. (b) Results of an all-versus-all Blast search with all proteins represented by a node and all significant hits represented by an arc drawn between nodes. Arcs drawn as dashed lines reflect those edges that are removed in a standard TribeMCL (Enright et al. 2002) analysis. (c) A phylogenetic tree inferred from the alignment. See main text for details of analysis.

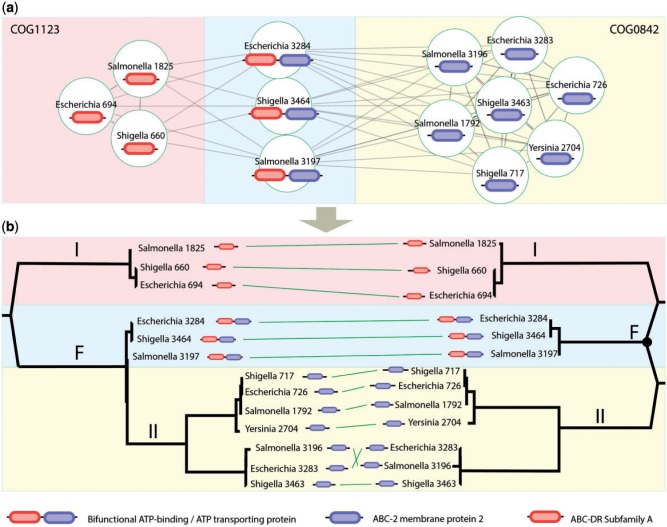
Fig. 4.

An example of a data set that cannot fit onto a conventional phylogenetic tree diagram. The sequence similarity network displays the significant similarity results from a Blast search of the collection of proteins against one another. The tree on the left is the tree recovered from a concatenated data analysis and rooted arbitrarily on the internal branch separating the COG1123 proteins from the rest. The network on the right is what we call an N-rooted network (in this case N = 2, so it is a two-rooted network).

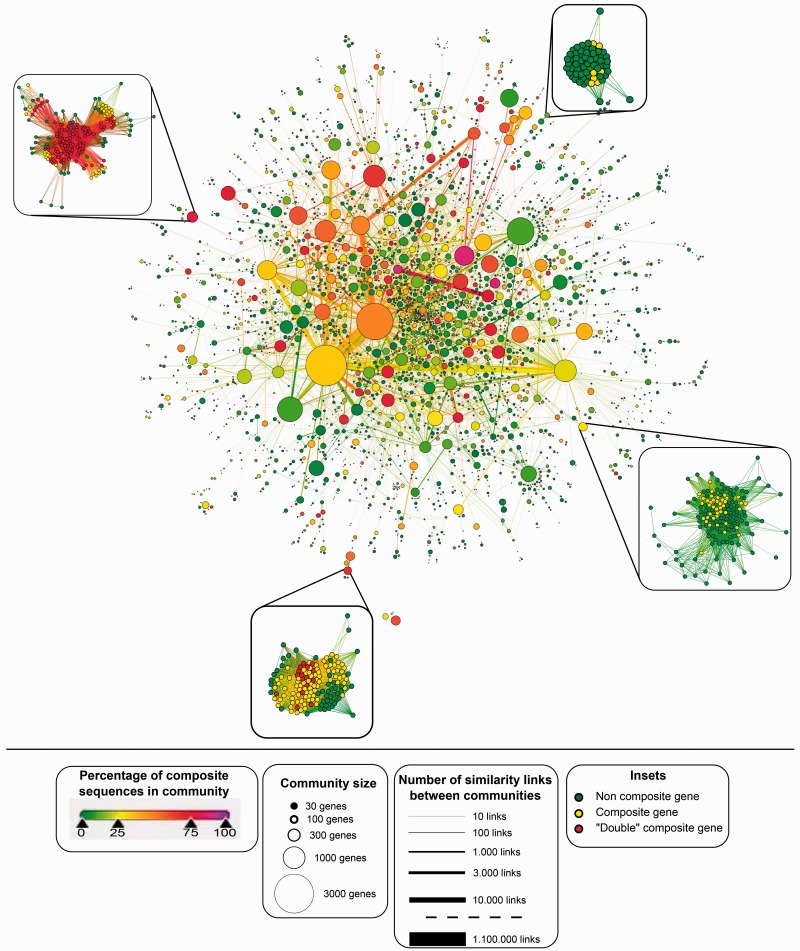
Fig. 5.

GCC from all-against-all BlastP search of 15 eukaryotic genomes. Nodes represent communities as identified using a single pass of the Louvain algorithm. Node area representing size of community and edge thickness is the square root of the number of edges connecting two nodes, with the exception of the largest edge that has its size represented by a thickness five times smaller (corresponding to 220,000 edges instead of the actual 1,100,00). Nodes on the left diagram are colored according to the proportion of composite genes in the community (from green = 0% to purple = 100%). Subnetworks of four communities are displayed around the figure. These communities have been chosen along the range of composite proportion (from light green to light red) to illustrate the variety of community structures. Nodes from these insets are colored in green for noncomposite sequences, yellow for composite sequences, and red for multicomposite sequences, that is, composites sequences whose component genes are themselves composites. See supplementary figure S1 (Supplementary Material online) for a pie chart representation of the proportion of noncomposite, composite, and multicomposite genes in each community.

Defining Homologs Meets Different Kinds of Problems

The lack of agreement in how to define homologs (Fitch 2000; Enright et al. 2003; Li et al. 2003; Wong and Ragan 2008; Majumdar et al. 2009; Dessimoz et al. 2012; Miele et al. 2012) reflects the historical ideas concerning homology and the attempt to fit notions that were developed for one purpose (morphological systematics and comparative anatomy) to data that are only obliquely related to this purpose. The first evolutionary character matrices (Abel 1910; Tillyard 1919) were rectangular consisting of M rows × N columns. Most phylogenetic software programs today require such rectangular matrices, and if the sequence data do not fit into a matrix, then the user has two choices—either add characters to represent “missing” data or prune the data until it becomes rectangular (Capella-Gutierrez et al. 2009). Therefore, there is an implicit assumption that data matrices should look like this and an explicit requirement that the data is made to look this way. Given that discussions of the pruned parts of alignments rarely make their way into the final manuscript, we have no clear idea how often these nonconforming data sets arise as a result of introgression and gene family membership that involves more than one family.

Additionally, focusing on different aspects of sequence relationships, that is, the homology of entireties or of parts, leads to different inferences of relationships and, consequently, to a lack of consensus. The reality is of course that different parts of a gene sequence might have different histories, so an honest appraisal of homology might require a more radical view of homology than is traditional. Recently, Song et al. (2008) offered a good example of this when they asserted the restrictive caveat that homologous genes must be descended from a common ancestor that had the same multidomain structure as contemporary sequences. Two genes that share a single domain and whose common ancestor had quite a different structure are not considered to be homologous in their model. The distinction between the two different kinds of evolutionary trajectory is of course important; however, it does seem to confuse the notion of homology being the concept of relationship through common ancestry, irrespective of how subsequent introgressive events have changed the overall domain neighbourhood. It is quite likely that what Song et al. (2008) call domain sharing but not homology is what Fitch (2000) and Hillis (1994) would call partial homology. Though it is perfectly reasonable to say that convergently remodeled proteins with similar structures cannot be true orthologs or paralogs, they are homologs, nonetheless.

Three Homology Models

In terms of homology concept and delineating homology groupings, a fundamental problem lies in the a priori model that we apply to our approach. Here we define three sets of models, and we discuss how these models can affect notions of homology. First, we have “strong tree thinking” (STT). This perspective sees that the important, perhaps only, relationships are those that have arisen along a diversifying phylogenetic tree, and events such as residue substitution and small indel events account for the changes between sequences. A phylogenetic tree, we emphasize, allows no introgressive events (Bapteste et al. 2012). STT is useful when analyzing sets of homologs that have a tree-like history and is generally seen in the analysis of nonrecombining orthologs to determine species relationships (Doherty et al. 2012) or nonrecombining paralogs to understand duplication events (e.g., Feuda et al. 2012). Next, we define “phylogenetic network thinking” (PNT) where legitimate recombination events are allowed, and these turn a phylogenetic tree into a phylogenetic web (Huson and Scornavacca 2011) relating closely related sequences without affecting homology relationships. PNT is extremely useful for analyzing legitimate recombination (Huson and Bryant 2006) and understanding incongruence in gene or genome histories. Finally, we have “goods thinking” (GT) that sees evolutionary history as being characterized by the vertical and horizontal transmission of genetic goods, allowing introgressive evolutionary events (e.g., legitimate and illegitimate recombination events, fusion, fission, etc.) and depicting relationships between sequences in a more pluralistic manner (McInerney et al. 2011; Bapteste et al. 2012). GT is the least conservative perspective and is the main focus of this manuscript. Its biological implications are potentially huge because it has been proposed that introgression of domains has resulted in the evolution of various signaling systems (Apic and Russell 2010) and a correlation has been suggested between the prevalence of proteins with multidomain architectures and organismal complexity (Apic, Gough, Teichmann 2001a). Indeed, a modest increase in number of domains allows for numerous novel genetic interactions, thus a small increase in genes sharing goods could be largely sufficient to construct complex hosts (Koonin et al. 2002).

Going back to Reeck et al. (1987) important definition according to which “homology should mean ‘possessing a common evolutionary origin’ and in the vast majority of reports should have no other meaning,” we want to stress that a fundamental issue stems from the interpretation of the word “a” in the quoted sentence. Traditionally, evolutionary biologists have used the word “a” in the STT sense (O'Hara 1997) or the PNT sense and judge that it means “one.” For both of these perspectives, the definition of homology can only mean that homologs must trace back to a single common ancestor without gene remodeling by sharing of DNA from other lineages. According to these perspectives, the community of descent that unites complete genes with complete genes corresponds to the objects such as the branches on phylogenetic trees or networks when these structures have been constructed from genes that are homologous along their entire length (Li et al. 2003) and where the genes have not been remodeled by illegitimate recombination throughout their history. This is probably the most commonly understood definition of homology, and it is certainly the focus of many software tools and algorithmic developments. Embracing this perspective (STT/PNT homology concept), a standard operational criterion (STT/PNT homology definition) for homology is, for instance, that homology extends for at least, say, 70% or 90% of the length of the two genes being examined.

However, if we interpret a in GT sense; McInerney et al. 2011), “a common ancestor” means “at least one” ancestor in common with other proteins. Then, our concept of homology is quite different and allows us to analyze a greater number of evolutionary events and relationships, though we must be much more careful about what we say about these evolving entities. So far, this GT perspective has not been explored much. The concept of homology has usually been described in terms of just the STT/PNT viewpoint—rather than the GT viewpoint—and software and databases have been geared toward the analysis of homologs defined under the aegis of the STT/PNT concept.

Instead of the traditional, narrower view of homology, we advocate that the pluralistic account of evolutionary processes and thus a pluralistic interpretation of the term “a” in Reecks et al.’s definition is now scientifically most fruitful, because it results in definitions of GT-style homologs and family resemblances that can encompass a greater variety of our empirical observations on sequence structures and is a better fit to our observations on the processes responsible for sharing of genetic “parts,” at the molecular level, in evolution. Indeed, STT/PNT expectations for how homologs should look have resulted in practical definitions of homology that have often restricted how we have viewed gene, genome, and protein evolution, have affected the software and databases that have been developed to analyze genomic data, have affected the ways in which we think we should analyze macromolecular sequence data and may have frequently succeeded in blinding us to many crucial evolutionary events. For instance, a recent publication (Miele et al. 2012) that deals with finding homologs from an exhaustive comparison of all macromolecular sequences in a data set against all other sequences in that data set starts with an opening line in the “motivation” section of the abstract thusly: “Proteins can be naturally classified into families of homologous sequences that derive from a common ancestor.” The manuscript then goes on to describe a very promising method for clustering protein sequences into groups that manifest extensive similarity along almost their entire length. This clearly is a STT/PNT view of protein evolution, where a family is defined in explicit, though narrow terms and all segments of sequence are expected to descend from one same common ancestor, not many ancestors. While being a completely legitimate way of thinking about some protein relationships, the complexity of the majority of data falls outside this narrow framework, and we advocate that additional homology concepts can provide an augmented view of protein evolution.

Homology Concepts That Do Not Assume Tree-Like Evolution

Is there a homology concept that fits the data better than the STT/PNT concept and could it conceivably reduce the likelihood of overly restrictive and potentially incorrect inferences occurring? We think that the most efficient way to ameliorate the risk of error and to really account for evolutionary relationships between sequences is to realize where the most fundamental problem lies. Most algorithms would run quickly if genetic data had genuinely evolved in a tree-like way. In fact, no sophisticated algorithm would be necessary at all, as the gene families could be easily parsed from an all-versus-all gene similarity search and, assuming the search was sensitive enough, they would naturally fit into their respective families. However, real data have experienced more complex evolutionary processes (Nagy, Bányai, et al. 2011; Nagy, Szláma, 2011).

We propose that methods for defining homologous genes (gene families) that require homology to extend along most of the sequence (Miele et al. 2012) might be described by the search for “tribes” of proteins. We choose the word tribes, because this is the original meaning for the word phylogeny (from the Greek Phylos meaning “tribe” and Genis meaning “origin”; Sapp 2009). Therefore, such tribes of sequences are likely to be amenable to phylogenetic tree or network construction using standard software currently available (Felsenstein 2004; Huson and Scornavacca 2011). We note that this fits well with the objective of such programs as TribeMCL (Enright et al. 2003).

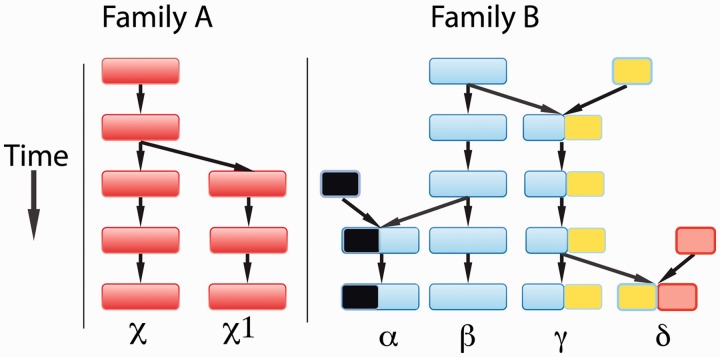
In continuing with the etymology of the word phylogeny, we wish to point out, however, that tribes are known to split and merge with other tribes, to subsume, and to be subsumed. Although analyzing homology along the entire length of a sequence is somewhat akin to a tribal origin analysis (a phylogenetic analysis of that tribe), it is by no means the only way that we can look at homology. We might consider that at one extreme there are tribes of sequences that are mostly isolated “closed” tribes (fig. 1, Family A) but that there are also tribes that are more “open” in terms of tribal mergers and divisions (fig. 1, Family B; Boucher and Bapteste 2009). In the case of Family B, it would be standard practice to split the family into four tribes to carry out phylogenetic analyses, thereby missing out the context in which the entire family has evolved. These open tribes are not readily analyzed using current phylogenetic methods, because the components of some of the sequences have separate origins and separate roots (in our toy example, the black, blue, yellow, and red gene parts all have separate roots). In other words, evolution has frequently occurred through introgression (Bapteste et al. 2012) with genes and parts of genes acting as goods (McInerney et al. 2011) that can be shared, such that a homology concept that only accommodates STT/PNT is likely to be incomplete as a basis for categorizing and describing the evolutionary histories (Bapteste et al. 2012). To demonstrate this, we explore the assumptions and expectations of STT/PNT.

Fig. 1.

Two extremes of family evolution. Family A is a closed family shown to evolve according to a strict tree-like process, Family B is an open family that evolve by horizontal and vertical evolutionary processes. Its members display family resemblances, as they can be connected through intermediates and relationships of GT homology (see main text).

Building on the historical role of morphology in the study of homology, STT/PNT considers either a complete organ or a significant part of an organ. This perspective has some consequences for the breadth and depth of analyses that can be carried out. The first consequence is that the organ should be clearly defined as a 1:1 correspondence. In contrast, most new genes are constructed from existing parts; fusions of genes, promoters, introns, exons, and motifs are common (Levitt 2009; Bapteste et al. 2012). This means that different parts of proteins can be expected to have different evolutionary histories. The different parts of a protein-coding gene might themselves be homologs of one another and may have arisen by tandem duplication or introgression of previously spatially separated DNA sequences (Bapteste et al. 2012). Even within morphology, it has been recognized that partial homologies offer a much broader view of evolution (Sattler 1984).

The second consequence of STT/PNT-based explanations of homology is that the notion of homology being indivisible is easy to understand—two organs/genes are either homologs or they are not. The problem we have with molecular sequence data is that we now know that a great number of molecular sequences are related to a great many other molecular sequences with varying amounts of structural (e.g., domain content) similarity (Adai et al. 2004; Halary et al. 2010; McInerney et al. 2011; Bapteste et al. 2012; Alvarez-Ponce et al. 2013). Consider the thought experiment where we have four proteins (see table 1), each protein has two domains and we have four domains in total. Gene1 has domains A and B, Gene2 has domains B and C, Gene3 has domains C and D, and Gene4 has domains A and D. All four proteins have particular kinds of relationships to the others that cannot be described by an “all or nothing” model. This problem affects both the homology concept and the homology definition. We will refer to this thought experiment when dealing with real data in “case 4” later.

Box 1.

Term	Meaning
Homologs	Having a relationship through descent from at least one common ancestor
Family resemblance	Having an evolutionary relationship through intermediate sequences and common descent
Clique	A subgraph in a network where every member of the subgraph is connected to all other members
STT	Strong tree thinking: A perspective that sees homology statements as valid when the homologs have evolved down the branches of a bifurcating phylogenetic tree
PNT	Phylogenetic network thinking: A perspective that sees homology statements as valid when the homologs have evolved through tree-like processes, but allowing for some homologous recombination, thereby making a phylogenetic network.
GT	Goods thinking: A perspective that sees homology relationships encompass illegitimate recombination, fusion, and fission of evolving entities in addition to vertical descent. Gene evolution is expected at times to be very complex and involve merging of evolving entities.
N-rooted fusion networks	A new kind of network that depicts rooted networks with at least one fusion node and at least two roots.
TRIBES	Homologs that have a 1:1 correspondence in terms of being homologous for most or all their length.
TribeMCL	One of the most successful approaches to finding communities in networks of gene similarity.

Table 1.

An Illustration of Four Hypothetical Genes That Manifest a History of Introgressive Processes.

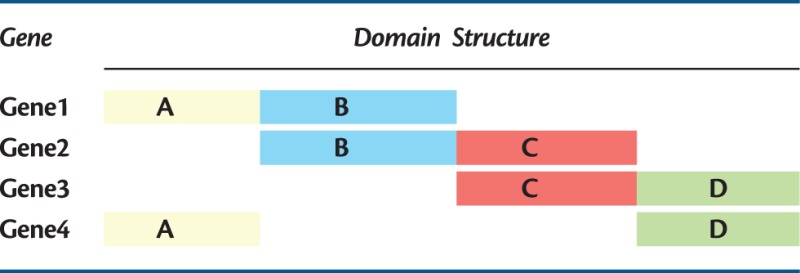Note.—Each gene consists of two domains, the colors are the same for homologous domains.

Current STT/PNT thinking does not address most of the issues we have just raised, because, being founded on an assumption of tree-like evolution, it produces a bias against the detection of introgressive processes. Relied upon exclusively, it prevents us from investigating those non-tree-like evolutionary events and relationships that could be revealed through a more pluralistic view of homology. In the following three examples, we use a standard set of analytical tools to demonstrate how our views of what constitutes a homologous family are influenced by the use of such heuristic approaches. We use BlastP (Altschul et al. 1997) and then pass the data through the MCL software (Enright et al. 2002) using default parameters.

Case 1: A Ten-Gene Data Set from Four Enteric Bacterial Genomes

In this case, we analyze data from four enteric bacterial genomes—one Escherichia coli, one Salmonella, one Yersinia, and one Shigella genome (data available as supplementary information S1, Supplementary Material online, Case1.aln). Homologous proteins with a helix-turn-helix motif are found ten times in these four genomes using a standard similarity search algorithm (Altschul et al. 1997). However, these genes are short and quite variable. Short gene length reduces the possibility that Blast can detect significant sequence similarity. Figure 2 depicts the gene similarity network that can be constructed from this gene family when an all-versus-all Blast analysis is carried out with a cutoff e-value of 10⁻⁶. As can be seen, not all genes show significant sequence similarity with all other genes according to this analysis. However, using Clustal Omega (Sievers et al. 2011), the alignment shown in figure 2 can be produced, and using FastTree with the default parameters (Price et al. 2010), the tree shown in figure 2 can be produced from that alignment. The Blast network also shows an analysis of what happens if the MCL software (Enright et al. 2002) is used to identify homologs with the default inflation value set at 2.0. MCL cuts this graph into three tribes. The color coding of the sequences on the Blast graph, the alignment, and the phylogenetic tree reflects how MCL would carve up the data. The STT/PNT proposition is that a gene family would be characterized by all members of the gene family recognizing all other members in a similarity analysis. This does not happen, so MCL divides up the gene family into three tribes. In these tribes, all members recognize all other members.

One of the features of note in this alignment is that the proteins are quite variable in length, and indeed, this is likely to be part of the reason why Blast does not produce a completely connected component where all sequences show significant similarity to all other sequences. The four sequences shaded in brown contain a conserved 18-amino acid stretch that has either been gained by these sequences or lost in the others. In addition, there is considerable length variation at the N- and C-termini of the sequences.

In the analysis of this alignment of sequences, an STT/PNT perspective will be faced with a conundrum. The four sequences at the bottom of the alignment, identified by the brown taxon labels on the alignment, brown nodes on the network, and brown tip labels in the tree, have an 18-amino acid stretch that is clearly homologous among these four sequences and is absent in the other six sequences. Although the sequences clearly manifest homologous relationships, should this process of insertion or deletion occur frequently, then descendants of these sequences might not contain any amino acid residues homologous to the residues that exist today. As a thought experiment, imagine if we discovered a series of proteins that differed from each other by the presence or absence of small domains, eventually leading to a collection of sequences where at the two extremes of this series we have proteins that do not share any domains (as in table 1). Then, both the STT and PNT perspectives would say that these proteins at the extremes do not have a relationship through common ancestry, whereas a GT perspective would say that they do. A GT model for homology that we could designate as the “open tribes” or family resemblance model would better accommodate this kind of situation, which we show later in this manuscript to be a very common situation.

Case 2: A Set of Orthologs from Closely Related Yeast Species

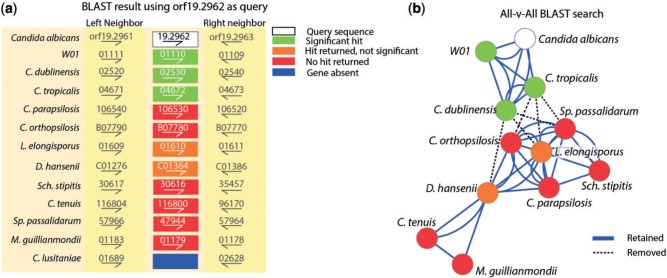
The Candida Gene Order Browser (CGOB) database (http://cgob.ucd.ie, last accessed December 11, 2013) is a carefully curated data set of 13 yeast (mostly Candida) genomes that have been aligned so that any particular gene can act as a “focus point,” and all its orthologs (if present) are presented to the viewer as pillars and their neighbors are also visible (see Fitzpatrick et al. 2010 for details). Figure 3a shows an example from this database. Open reading frame 19.2962 from the genome of Candida albicans is the focus gene and its orthologs are displayed underneath it. On the left and the right of this gene are two genes that are strongly conserved in all species. Orthology is easily recognized in these neighbors using standard analyses of similarity. In the pillar that is in focus (the orf19.2962 pillar) are 11 orthologs of this gene, with the ortholog being absent in the genome of C. lusitaniae. Figure 3b shows a network representation of the all-versus-all database search for this set of orthologs. The nodes in green produce a significant Blast hit when compared with orf19.2962. As can be seen, only three genes produce a significant result. The other orthologs are included in the network only as a consequence of the full analysis of Blast searches. Applying MCL to this data set results in six Blast hits (statements of homology) being discarded and consequently splits the data into two communities. In standard phylogenomic analyses, this set of orthologs that are weakly conserved in sequence but strongly conserved in genomic location might be analyzed as though they are two separate families, when in fact by any reasonable criterion, they should be analyzed as a single, albeit quite variable, family.

Fig. 3.

Analysis of a family of divergent orthologs in Candida and close relatives. (a) A view of three pillars from the CGOB database showing orthologous genomic locations for 13 organisms, with gene names as per the CGOB database. The focus gene (orf19.2962) is colored in white, the three orthologs that are identified in a standard Blast search are colored in green, and the other orthologs are colored in orange if they are identified in the Blast search as a “hit” but not a significant hit an the gene is colored red if no hit was returned. (b) A sequence similarity network constructed using Cytoscape (Shannon et al. 2003) based on the pattern of significant Blast hits from an all-versus-all search. Dashed lines indicate where the MCL algorithm splits the data into two partitions.

We used the CGOB database to explore how often the standard Blast approach to detecting orthology would fail to detect de facto orthologs. The CGOB contains 6,548 orthology pillars that obviously contain two or more orthologs. Of these, 707 contain at least one ortholog that would be missed in an all-against-all Blast search of the database. They have been manually included in orthology pillars based on synteny and weak Blast hits. This constitutes ∼10.8% of CGOBs orthology pillars, where on the basis of Blast alone, the orthologs would be split into more than one family. Naturally, we anticipate that this figure will increase substantially as we move toward examining organisms that are more distantly related than a group of closely related Ascomycota. Many or most “unknown” proteins could or should be placed into existing families, were it not for the limitations on computational tools and—very specifically—approaches.

Case 3: N-Rooted Networks

Figure 4 presents the results of two analyses of proteins that have likely experienced a gene fusion. This gene fusion is clearly seen in figure 4a, which is a sequence similarity network based on Blast searches. There are in fact two maximal cliques (completely connected subgraphs that do not exist exclusively within the vertex set of a larger clique) in this network. The collection of three genes on the left of the network and the three genes in the middle of the network collectively form a clique. In addition, the three genes in the center of the network and the seven genes on the right also form a clique. The three genes on the left and the seven genes on the right are not directly connected to each other. This kind of graph topology strongly suggests a gene fusion or fission event. In this example, we are going to assume that the three genes in the middle clique are derived fusion genes and not ancestral (note that the following will be true for any genuine product of gene fusion even if this specific network is not).

One set of proteins (the three genes on the left in fig. 4a) are members of the COG1123 family as defined in the COG database (Tatusov et al. 2000) and they function as ATP-binding proteins. The second family of seven genes on the right belong to COG0842 and function as ABC-2 type transporters. The fusion genes are bifunctional ATP-binding and transport proteins. For this analysis, we aligned the fusion proteins (a total of three proteins) separately with the COG1123 proteins (a total of three proteins in this family, resulting in a six-sequence alignment), and separately, we aligned the three fusion proteins with the seven members of COG0842. These two alignments were merged into a single alignment (available in supplementary information S1, Supplementary Material online) and two analyses were carried out.

The first analysis is seen in figure 4b, left tree. This tree was constructed from a complete alignment of the data, with missing parts padded out in the alignment using gap characters. The resulting tree is manifestly incorrect from two perspectives. First, COG1123 and COG0842 should have two different roots because they have two different origins, yet this diagram depicts a single origin of the entire tree. Second, there is no rooting of this tree that can depict the fusion event properly. This is because this representation—a tree—is not how the data have arisen. A fusion event is accurately represented by a node with an in-degree of two, and standard phylogenetic trees do not contain such nodes. The network on the right of figure 4b is an accurate representation of how the data have arisen. In this case, the N-terminal end of the fusion proteins were aligned to the COG1123 sequences (resulting in a six-sequence alignment) and the C-terminus portions of the fusion proteins were aligned to COG0842. The FastTree software (Price et al. 2010) was used to construct two maximum likelihood trees from the data, and then these trees were midpoint rooted and merged manually using the Adobe Illustrator software (naturally, there is more than one way to generate such a graph, but for illustration purposes, we chose this method). The resulting network, which we call an N-rooted fusion network, is a more accurate representation of the evolutionary history of these sequences. The two roots of the network are indicated, and the approximate location of the fusion event is indicated using the black dot. We note that this is an ad hoc placement of the fusion event—future work can focus on methods for accurately investigating the location of a fusion node. We cannot rule out the possibility or indeed likelihood that the genes described here are in fact related through some ancient undetectable community of descent. This would mean that, for the two-rooted network in figure 4b, we would simply be leaving out the edges of the network that would unite the two root edges further back in time, turning this two-rooted network into a more classic phylogenetic network, as expected in PNT. Of course, it is also possible that these two roots would join other kinds of families that would join other kinds of families and so forth, consistent with GT. Thus, although this simple example has two root nodes (it is a two-rooted fusion network), large multidomain proteins probably need to have their evolutionary history represented by 3-, 4-, or N-rooted networks, as indicated by our next example.

Is it possible that COG1123 and COG0842 are indeed homologous in the PNT sense, but this homology cannot be detected? As we have said earlier and as seen in Cases 1 and 2, there is a severe technical limitation that means that many homologies are not detected. This affects our homology definitions more than our homology concepts. Even if there is deep, undetected homology of the PNT variety between these two groups of genes, N-rooted networks are useful for providing a more complete picture of evolutionary relationships.

Case 4: Composite Genes in the Genomes of 15 Eukaryotes

The single connected component shown in figure 5 illustrates the value of GT (McInerney et al. 2011) in the study of homology. To generate this figure, we have used sequences from a total of 15 eukaryotic genomes (see supplementary information S1, Supplementary Material online). The total number of genes was 199,592. A similarity network was constructed from this data set using the BlastP program (Altschul et al. 1997) with the cutoff set to an e-value threshold of 1e−10. We searched through this network for composite genes, using the program FusedTriplets.py (Jachiet et al. 2013) and a verification test at 1e−20 threshold. Thus, a gene C is identified as composite if there are two component genes A and B such that: A and C are similar, with an e-value less than 1e−20; B and C are similar with an e-value less than 1e−20. In addition, A and B Blast matches on C do not overlap, and A and B are not similar, with an e-value greater than 1e−10. Next, we looked for multicomposite genes, which is the name we give to composite genes whose component genes (A and B) are themselves composites.

The similarity network has a giant connected component (GCC). This GCC contains 41.4% of the nodes (82,702) and more than 90% of the edges (8,826,323). It is very dense, with a mean degree of 200. This makes it impossible to visualize with Cytoscape (Shannon et al. 2003) or Gephi (Bastian et al. 2009).

Interestingly, we have a situation for this relatively small data set of just 15 genomes, where we can find a chain of significant sequence similarity between any two pairs of genes for almost half of the genes in the network. Under the conventional homology concept, the distant homology between any pair of dissimilar sequences is only retrieved by a chain of homologous intermediates with entire length similarities. An alternative GT-based explanation is that sequences with different ancestors recombine to create intermediate sequences that share partial homology with both of their ancestral sequences. Figure 5 illustrates that this alternative explains most of this pattern in the data. This is the situation that is outlined in table 1. In this case, we do not suggest that we alter the meaning of homology so extensively that sequences that have no ancestor–descendent relationship to one another are still considered homologous. Instead, homologous relationships are those where descent from at least one common ancestor has occurred and family resemblance relationships (Wittgenstein 2009) are those where a path of significant similarity can be found through a graph like we see in figure 5 that links the two sequences.

Composite sequences as identified by FusedTriplets (Jachiet et al. 2013) uncover this kind of nontransitive relationship that may result from nonhomologous recombination, domain shuffling, gene fusion, or indeed fission events. Most of the represented communities—and almost all of the largest and central communities—contain at least a small proportion of such composite sequences. A total of 24% of the sequences in the GCC contain a composite signature (which explains the yellowish look of the result), to be compared with the 6% proportion of composite sequences for the rest of the network (outside the GCC). Furthermore, some composite sequences also tend to recombine, with 10% of sequences identified as multicomposite sequences in the GCC. The structure of the GCC (and of some communities) exhibits large cycles without chords (holes), which also provides evidence of multiple introgressive events in the history of these proteins. This demonstrates the extent to which we can see non-tree-like evolution in many places in this data set.

Phylogenetic software tools or methods have not tackled the evolution of composite molecular sequences, despite the pervasiveness of introgression. The complex, yet real relationships between remodeled genes remains a blind spot for most analyses, because most analyses are performed at a much more local scale after the clustering steps. It is not clear why this perspective is the one usually adopted, because there are several databases of multidomain proteins (Majumdar et al. 2009), and a high level of interest in how domains combine (Sonnhammer and Kahn 1994; Park and Teichmann 1998; Enright et al. 1999; Marcotte et al. 1999; Apic, Gough, Teichmann 2001b; Wuchty 2001; Enright et al. 2003; Portugaly et al. 2006; Song et al. 2008). However, the dominant concept of STT homology, the focus on tree thinking as the prism through which we should view evolutionary histories, has undoubtedly played a role.

A Pluralistic Account of Homology

The concept of homology is defined as “descent from a common ancestor.” However, unless we include situations where the number of ancestors is greater than one, then it is necessary to ignore many real relationships—at the moment, this is a very common situation. The standard classifications of homologs place them into the category of ortholog (originating as a consequence of speciation), paralog (created by gene duplication), xenolog (created by horizontal gene transfer of an entire sequence), or ohnolog (created by whole genome duplication), all of whom are divergent events that are expected to appear under the standard concept of homology and are adequately analyzed using phylogenetic trees or phylogenetic networks. In contrast, the merger of two evolving entities (Bapteste et al. 2012) is not expected under a tree-thinking perspective and the standard concept of homology. Very little software has been developed to take account of this kind of process, and indeed, where software has been developed to analyze introgressive events, the resulting homologs have been described as not being homologs at all (Song et al. 2008).

Evolutionary biologists might wish to know about the evolution of more complex gene families, for example, the origins of entire connected components in a gene network and not just members of the same tribe. Alternatively, it might not be interesting to carry out such a broad-scale analysis and instead a narrower focus on a closed family or a subset of members of an open tribe is desired. If the latter, is it possible to clearly articulate why this subset of evolutionary events are the only ones to be studied? We do not say that this is an invalid thing to do—far from it, but it is necessary to be clear a priori why this is the only kind of evolutionary event that is to be studied when a more pluralistic account of evolutionary processes is possible. Gene evolutionary analyses and phylogenetic analyses are not the same thing (Bapteste et al. 2009). Complete reliance upon only full-length homologs in phylogenetic analysis has the potential to censor our understanding of nature (see Dagan [2011] for instance). The pervasive contribution of introgression is a strong incentive to develop tools to handle data created by such events.

It would be absurd to suggest that all the genes in figure 5 are homologs of one another (in the traditional sense); however, it is clear that there are relationships that can be explored that are outside what is conventionally expected of homologs. Going back to our earlier thought experiments with four genes and four domains, with each gene having two domains (see table 1), these genes will form a ring structure in a network analysis (a situation we see repeatedly in the empirical data used to construct fig. 5). We can clearly see that Gene1 has partially homologous relationships with Gene2 and Gene4. Likewise, Gene2 has partially homologous relationships with Gene3 and Gene1. Gene3 has partially homologous relationships with Gene4 and Gene2. Gene4 has partially homologous relationships with Gene1 and Gene3. We can also say that Gene1 and Gene3 have a family resemblance relationship that is only evident because of the presence of intermediates. Gene2 and Gene4 also have a family resemblance relationship. This is to say that they are not related through common ancestry but through intermediate gene sequences that show a line of common ancestry. In the vernacular form, it might be said that they are related through marriage (a union of their relatives). In terms of network analyses, two nodes that are directly connected to one another on a network are homologs (shortest path length of 1), while two nodes that are connected with a shortest path length that is greater than 1 can be considered to have a family resemblance (whose origin can be explored: do they display STT/PNT homology that is no longer detectable by Blast? Are they made of components that are shared within an open tribe?, etc.). Thus, molecular data are complex, with pairs of genes that have only one last common ancestor and other pairs that have more than one last common ancestor.

By stating a pluralistic concept of homology, emphasizing the possibility of both partial homology and linkages that lead to family resemblances between pairs of sequences in the absence of any direct homology (partial or complete), we wish to offer some ways to deal more inclusively with a greater range of homologies and similarities in sequences. For the most part, such pluralistic homology relationships have been depicted using connected components in sequence similarity networks (Dagan et al. 2008; Dagan and Martin 2009; Dagan 2011; Kloesges et al. 2011; Bapteste et al. 2012; Jachiet et al. 2013; also, see figs. 2–5 in this manuscript). However, in this article, we have also introduced the idea of using N-rooted fusion networks as an additional means of analyzing such data. Thus, a combination of gene similarity networks and N-rooted fusion networks could provide a more inclusive analysis and visualization approach with the ability to deal with multiple (>1) multiple sequence alignments, generating multiple phylogenetic trees or networks that can be fused together to reflect evolutionary histories more realistically.

The timing of fusions could be estimated using, for instance, maximum likelihood or Bayesian approaches, by reference to a fossil record or some such external timing. Relative or absolute timescales for fusion events can place them in the context of environmental change, for instance. Currently, estimating historical dates is restricted to ramifications on bi- or multifurcating phylogenetic trees (e.g., Tamura et al. 2012). However, the amount of introgression we see in figure 5 suggests the presence of large-scale introgressive events whose timing and context are poorly understood.

Enzymatic properties and how they change can be mapped onto these new structures, and the frequency of “emergent” properties (Fani et al. 2007) or shifts in selective pressures on individual amino acids can be estimated with respect to N-rooted fusion networks. Currently, tracing functional evolution is most often carried out by mapping traits onto phylogenetic trees of full-length homologs (e.g., see Feuda et al. 2012 and also Adai et al. 2004). The hotly debated “ortholog conjecture” states that orthologs are more similar in function despite being in different species, compared with paralogs that are to be found in the same species (Nehrt et al. 2011; Altenhoff et al. 2012; Chen and Zhang 2012). Sequence similarity network and N-rooted fusion networks offer the possibility of tracing functional evolution in a much more inclusive manner. We can ask whether functional variation and family resemblance are strongly or weakly linked and whether there are patterns that can emerge from such an analysis. Because there are many constraints on the kinds of genetic goods that can be joined together (see e.g., the content of the fusionDB database that clearly shows patterns of fusions are not random), a “family resemblance conjecture,” for instance, would suggest that nonhomologous sequences that have a closer family resemblance relationship are more similar in function than sequences that lack or have a more distant family resemblance relationship.

Adjusting our models to the data may well demonstrate whether there are as-yet unknown barriers to introgression, whether gene fusion occurs at different rates at different times and in different contexts and whether there are preferred routes for introgression and preferred partners. Although it is well known that homology relationships strongly suggest functional similarities, analysis of networks could reveal additional functional connections through the analysis of extended family resemblances (Bapteste et al. 2012). It has already been shown that additional evolutionary information can be obtained by the analysis of extended gene similarity networks (Alvarez-Ponce et al. 2013; Jachiet et al. 2013); however, there are further analyses that can be carried out.

In figures 2–4, we show that a rush to “atomize” evolutionary relationships and to only use a conservative perspective when analyzing homologies can completely blind us to interesting evolutionary events. Similarity network analyses can be used not only to understand recombination and fusion but also to find if there are transitive homology statements that can be made (Alvarez-Ponce et al. 2013). Distant homologies may be recognized through intermediate sequences, so if GeneX and GeneY manifest homology along a particular region and GeneY and GeneZ manifest homology along the same region, then even if a tool such as Blast cannot directly detect the homology between GeneX and GeneZ, we can use the network information to assign homology, even though our standard software tools might not see this homology.

Concluding Remarks

At this stage, we know much more about evolutionary relationships than we did 26 years ago when Reeck et al. (1987) felt the need to clarify the terminology. It is now much clearer that fusion and fission (Snel et al. 2000; Kummerfeld and Teichmann 2005; Pasek et al. 2006; Durrens et al. 2008; Jachiet et al. 2013) of (parts of) molecules is a frequent process and a significant source of genetic and genomic novelty. The consequent muddying of gene-level relationships affect sequence relationships to a point that justifies proposition of an extended notion of evolutionary relationships and of what constitutes a gene family. Overlooking of introgressive processes is causing considerably fewer evolutionary events to be appraised than would be the case if family relationships were defined more broadly. For this reason, future notions about homology should be explicit about the kind of homologous relationship that is observed—the model must be informed by the data and not just assumed at the cost of excluding massive amounts of data. Recognizing different homology and family resemblance concepts (STT, PNT, and GT) is useful and important. In other words, any operational definition of homology must be pragmatically oriented. Under that condition, reconsidering how we define relationships between genes may open the door to a new biology.

To conclude, adopting a more pluralistic view of homology entails that a number of methodological issues need to be resolved. Proteins or genes must be allowed to be a member of more than one family. Sequence similarity that is due to extensive remodeling (e.g., Epaktology [Nagy, Bányai, et al. 2011; Nagy, Szláma, et al. 2011]) must be distinguished from similarity that is not due to remodeling. Methods for assessing the importance of family resemblance relationships need to be developed—whether such family resemblances are relevant for function, for instance, or whether they are not. Statistically robust approaches for constructing N-rooted networks need to be developed in addition to methods for timing introgressive events on these structures. The analysis of connected component topological features must be developed so that we can understand the relationship between topology, protein function, and evolutionary history. Embedding phylogenetic trees or networks into networks of gene sharing can allow a far greater level of detail in assessing evolutionary histories.

Supplementary Material

Supplementary information S1 and figure S1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).