Skip to main content
PMC home page
Molecular Biology and Evolution logoLink to Molecular Biology and Evolution
. 2013 Nov 27;31(3):723–735. doi: 10.1093/molbev/mst229

Characterizing Bias in Population Genetic Inferences from Low-Coverage Sequencing Data

Eunjung Han 1, Janet S Sinsheimer 1,2, John Novembre 3,4,*
PMCID: PMC3935184  PMID: 24288159

Abstract

The site frequency spectrum (SFS) is of primary interest in population genetic studies, because the SFS compresses variation data into a simple summary from which many population genetic inferences can proceed. However, inferring the SFS from sequencing data is challenging because genotype calls from sequencing data are often inaccurate due to high error rates and if not accounted for, this genotype uncertainty can lead to serious bias in downstream analysis based on the inferred SFS. Here, we compare two approaches to estimate the SFS from sequencing data: one approach infers individual genotypes from aligned sequencing reads and then estimates the SFS based on the inferred genotypes (call-based approach) and the other approach directly estimates the SFS from aligned sequencing reads by maximum likelihood (direct estimation approach). We find that the SFS estimated by the direct estimation approach is unbiased even at low coverage, whereas the SFS by the call-based approach becomes biased as coverage decreases. The direction of the bias in the call-based approach depends on the pipeline to infer genotypes. Estimating genotypes by pooling individuals in a sample (multisample calling) results in underestimation of the number of rare variants, whereas estimating genotypes in each individual and merging them later (single-sample calling) leads to overestimation of rare variants. We characterize the impact of these biases on downstream analyses, such as demographic parameter estimation and genome-wide selection scans. Our work highlights that depending on the pipeline used to infer the SFS, one can reach different conclusions in population genetic inference with the same data set. Thus, careful attention to the analysis pipeline and SFS estimation procedures is vital for population genetic inferences.

Keywords: site frequency spectrum, base-calling errors, maximum likelihood, accuracy

Introduction

The availability of full-genome sequence data promises to increase understanding of molecular evolution in a broad array of organisms. These large-scale data sets also raise statistical challenges because inferred genotypes from sequencing data are often inaccurate due to high error rates (e.g., base-calling and alignment errors) (Bentley et al. 2008; Nielsen et al. 2011). If these errors not accounted for, population genetic inference based on the genotype calls could be misleading (Pool et al. 2010).

Population genetic inference often proceeds by compressing large-scale variation data into simple and informative summary statistics, such as allele frequencies, heterozygosity, and nucleotide diversity. The distribution of allele frequencies across sites, the so-called site frequency spectrum (SFS), is of primary interest, as many summary statistics are simple functions of the SFS and a number of population genetic inferences can proceed directly from the SFS. For example, a family of unbiased estimators of the population mutation rate 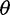Inline graphic, called 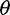Inline graphic estimators, is a simple function of the SFS (Achaz 2009). These include Watterson’s 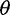Inline graphic estimator that uses the number of segregating sites (Watterson 1975) and Tajima’s 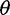Inline graphic estimator that is based on the average number of pairwise nucleotide differences between two sequences (Tajima 1983; Gutenkunst et al. 2009). Inferring demographic history (such as rates of ancestral population growth) can proceed from the SFS directly (Gutenkunst et al. 2009) or using approximate Bayesian computation approaches (Beaumont 2010) that often rely on summary statistics of the SFS. Another use of the SFS is in testing neutrality based on the frequency spectrum (Tajima 1989; Fu and Li 1993; Fay and Wu 2000; Achaz 2008, 2009). Neutrality tests based on the SFS compare different estimators of 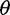Inline graphic to determine whether the observed SFS deviates from that expected under the standard constant-size equilibrium mutation-drift model. Large deviations from a background distribution have been used to detect local gene regions under selection, and this approach is used in many empirical genome-wide selection scans (Andolfatto 2007; Begun et al. 2007; Andersen et al. 2012; Axelsson et al. 2013).

A number of approaches can be taken to infer the SFS from NGS data. These can be classified into two broad categories. The first of these is a call-based approach, in which individual genotypes are first inferred from aligned short reads and then the SFS is estimated based on these inferred genotypes by allele counting. To infer genotypes from short-read data, a number of programs have been developed, which identify single-nucleotide variants (SNVs) and call genotypes. Among them, two of the most popular tools are the Genome Analysis Toolkit (GATK) (McKenna et al. 2010; DePristo et al. 2011) and SAMtools (Li, Handsaker, et al. 2009; Li 2011). The details of the differences in the implementation of SAMtools and GATK are presented in table 1. Both programs determine whether a site is polymorphic based on the pileup of reads at a given site (SNV calling) and estimate individual genotypes if the site is variable (genotype calling). Each program has two different SNV and genotype calling pipelines, a single-sample and a multisample calling mode. With the single-sample calling pipeline, aligned sequencing read data are analyzed for one individual at a time and then the most likely genotypes for that individual alone are determined. In contrast, with the multisample calling pipeline, aligned sequencing read data are analyzed for all individuals in a sample simultaneously and then the most likely genotype configurations for all individuals are determined. Imputation methods represent an extension of multisample calling in which a reference panel is used and often linkage disequilibrium (LD) from multiple variant sites is integrated into making calls at any one variant (Li, Willer, et al. 2009). In practice, imputation methods are generally restricted to well-studied species with reference samples such as the 1000 Genomes panel in humans (Abecasis et al. 2012) and the Drosophila Genome Reference panel in Drosophila melanogaster (Mackay et al. 2012).

Table 1.

Comparison of a GATK and SAMtools’s Multisample Calling Pipeline.

Step GATK SAMtools
[Calculating Genotype Likelihoods] For each individual, at each site, the likelihoods for 10 possible genotypes (AA,GG,CC,TT,AC,AG,AT,CG,CT,GT) are computed based on aligned reads. Independent errors assumed. Dependent errors assumed.
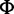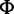[SNP calling] At each site, determine whether a site is polymorphic based on posterior probabilities of nonreference allele counts P(Xa|D,Inline graphic) where Inline graphic is an expected SFS under the standard model and D is aligned reads. A site is polymorphic if a 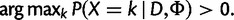Inline graphic A site is polymorphic if 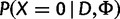Inline graphic < cutoff (default = 0.5).
[Genotype Calling] If a site is considered polymorphic, the maximum a posteriori genotype is assigned to each individual. At each site, the same genotype prior probabilities are used: P(AA) = 1 − 3θ/2 P(Aa) = θ P(aa) = θ/2, where θ is an expected heterozygosity (default = 0.001) At each site, genotype prior probabilities are computed based on the estimated nonreference allele frequency q and assuming Hardy–Weinberg equilibrium: P(AA) = p2 P(Aa) = 2pq P(aa) = q2
Open in a new tab

aX denotes nonreference allele counts in a sample of n individuals.

The second approach is a direct estimation approach, in which the SFS or summary statistics are directly inferred from aligned short reads. This approach makes an implicit assumption that inferred genotypes from sequencing data are inaccurate and model this uncertainty. Several approaches have been developed in this framework (Johnson and Slatkin 2008; Lynch 2008, 2009; Liu et al. 2009, 2010; Kang and Marjoram 2011; Keightley and Halligan 2011; Kim et al. 2011). Recently, Li (2011) proposed an EM algorithm and Nielsen et al. (2012) proposed an approach using Broyden–Fletcher–Goldfarb–Shanno (BFGS) steps to obtain the maximum likelihood estimate (MLE) of the SFS based on individual genotype likelihoods across all individuals and all sites. Both of these methods are implemented in the ANGSD software (Nielsen et al. 2012).

In this article, we use detailed, realistic simulations to investigate the accuracy of these approaches to infer the SFS from NGS data and the impact of bias in the inferred SFS on the downstream analysis, such as genome-wide selection scans based on rank statistics and parameter estimates for a given demographic model. Motivated by an interest in populations and species that have nonexistent or poor imputation panels, we focused here on two-stage approaches that use single-sample and multisample calls to infer the SFS. On the basis of our findings, we conclude with guidelines and recommendations for conducting population genetic inference using low-coverage sequencing data to avoid spurious conclusions.

Results

Evaluating Accuracy of the Inferred SFS under the Standard Model

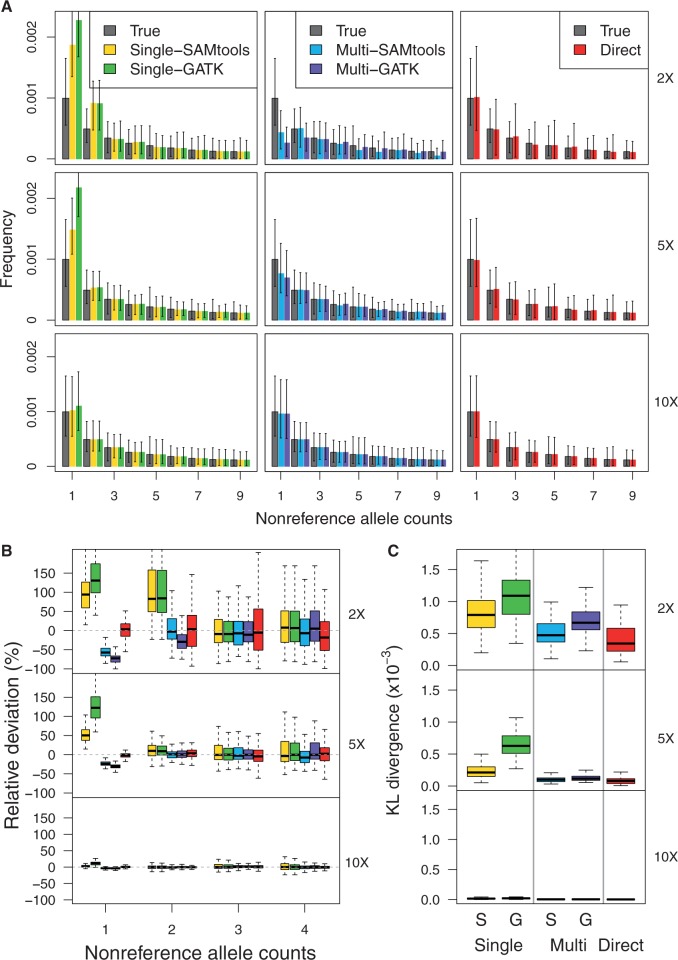
We first evaluated the performance of the two SFS estimation approaches (the call-based and direct estimation approach) as a function of sequencing coverage. For this comparison, we simulated 100 replicates of sequencing data for 10 diploid individuals each from genomic regions of length 100 kb under the standard model. The accuracy of the inferred SFS was evaluated by two metrics: 1) the shape of the inferred SFS in comparison to the ground-truth SFS (fig. 1A and B) and 2) the distance between the inferred SFS from the ground-truth SFS as measured by the Kullback–Leibler divergence metric (KL divergence, see Materials and Methods) (fig. 1C).

Fig. 1.

Fig. 1.

Open in a new tab

Evaluation of accuracy of inferred SFS by the call-based and direct estimation approach based on 100 replicates of genomic regions of length 100 kb. (A) Shapes of the inferred SFS (shown in colors in legend) compared with the ground-truth SFS (shown in gray) for coverage 2× (top), 5× (middle), and 10× (bottom). (B) Relative deviation of a fraction of sites with the nonreference allele counts of 1–4. (C) Distance between the inferred and ground-truth SFS as measured by KL divergence.

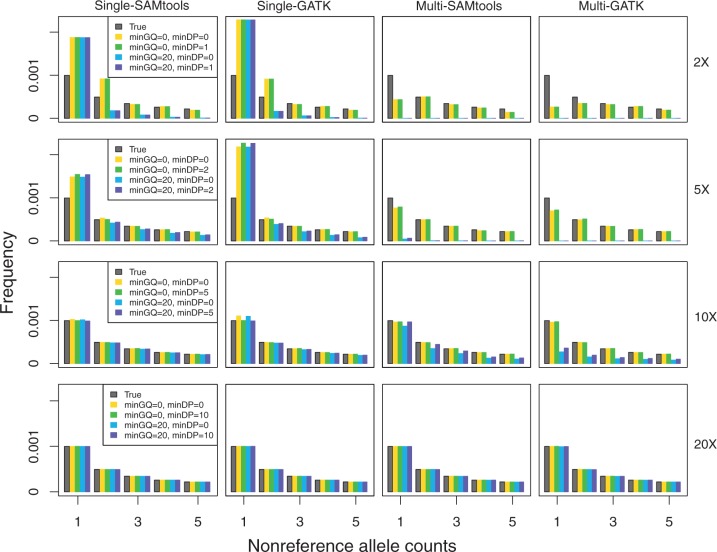
Fig. 2.

Fig. 2.

Open in a new tab

The effect of filtering of on the SFS construction for each call-based approach (panel columns) and coverages of 2×, 5×, 10×, and 20× (panel rows).

We found that the direct estimation approach (represented as Direct) outperformed the call-based approach (represented as Single-GATK, Multi-GATK, Single-SAMtools, and Multi-SAMtools) across all coverage ranges (fig. 1). The inferred SFS by the direct estimation approach was most similar to the ground-truth SFS. In contrast, the estimated SFS by the call-based approach became less accurate as coverage decreased and most of the deviation came from the sites with low allele frequency, such as singletons and doubletons (fig. 1A and B). For higher coverage data (10× per individual), the estimated SFS by the call-based methods approaches the ground-truth SFS, but the difference does not become negligible until 20× or higher (data not shown).

We also found that, depending on the genotyping pipeline (single-sample or multisample calling), the call-based approach resulted in different levels of performance in estimating the SFS. Interestingly, bias at the sites with rare variants went in opposite directions—single-sample calling led to overestimation of rare variants, whereas multisample calling led to underestimation of rare polymorphisms (fig. 1A and B). At coverage 2×, on average, singleton calls by single-sample calling were increased by more than 100% and doubleton calls were increased by 90%, thus leading to a skew in the SFS toward rare variants. In comparison, singleton calls by multisample calling were decreased by 60% and doubleton calls were decreased by 10%. This led to a distortion of the observed SFS, so that singletons were observed less often than doubletons, which is unexpected under the standard model. Overall though, we observed that the call-based approach with multisample calling (represented as Multi-GATK and Multi-SAMtools) performed better than the call-based approach with single-sample calling (represented as Single-GATK, Single-SAMtools) as reflected by the smaller KL divergence for multisample calling (fig. 1C).

The opposite performance of the single-sample and multisample caller (i.e., the multisample caller leading to underestimation of rare variants, whereas single-sample caller leading to overestimation of rare variants) is likely because a small number of erroneous reads strongly affects a single-sample caller, whereas a small number of correct alternate reads tends to be ignored in multisample caller. For example, at a site for an individual, suppose that we observe three aligned reads with two reference bases (R) and one nonreference base (V). If the base quality is reasonable, a single sample caller will often weigh the nonreference base as a real variant and produce a heterozygote call (G = R/V) even though a site is truly fixed for a reference allele. In contrast, if all other individuals are fixed for the reference, the multisample caller will more often consider the nonreference base as a sequencing error and produce a homozygote call (G = R/R) even though a site is a truly singleton site and reads come from a heterozygous individual.

Finally, controlling for the genotype calling pipeline, the KL divergence was smaller for SAMtools than GATK (fig. 1C). Consistent with this, we observed that SAMtools led to less overestimation (with single-sample calling) or less underestimation (with multisample calling) problems at sites with low frequency (fig. 1A and B). That said, SAMtools appears to be systematically underestimating minor allele frequencies, which causes underestimation for low-frequency nonreference alleles and overestimation for high-frequency nonreference alleles. Around frequency 1/2, SAMtools either underestimates or overestimates nonreference allele frequencies (depending on which allele is minor) leading to the lowest accuracy around frequency 1/2. The different performance between GATK and SAMtools might be due to different models for calculating genotype likelihoods (step 1 in table 1) and different priors for inferring genotypes (step 3 in table 1).

Impact of Filtering

When analyzing sequencing data, researchers often use strict filters to account for uncertainty associated with genotype calls. A common practice is to use genotype calls that exceed some threshold for genotype quality (GQ) or depth of coverage (DP) and treat less confident genotype calls as missing data. However, these filters can adversely affect SFS estimation based on genotype calls (Johnson and Slatkin 2008; Kim et al. 2011). Therefore, we explored whether it is better to estimate the SFS with filtering or without filtering. As a filter, we used a combination of GQ of 0 or 20, and DP of 0 or half of mean coverage (i.e., 1 for 2×, 2 for 5×, 5 for 10×, and 10 for 20×). Figure 2 shows that filtering based on GQ or DP does not alleviate the bias associated with called-based approaches.

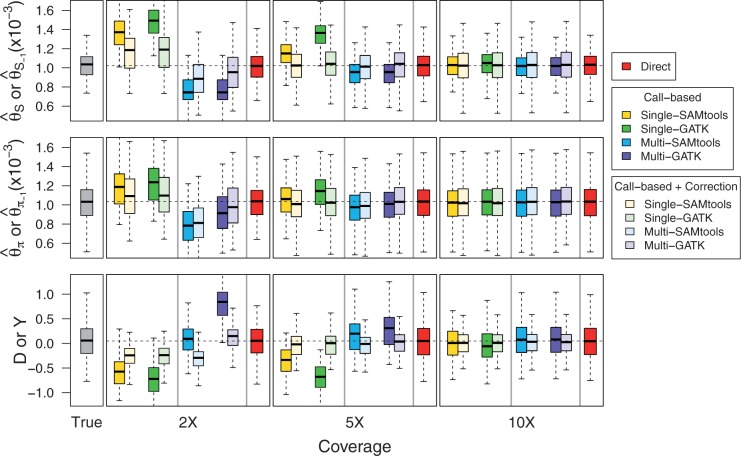
Impact on 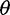Inline graphic Estimators and on Neutrality Tests under the Standard Model

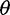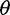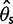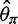Next, we investigated the impact of bias in inferred SFS on Inline graphic estimators and a neutrality test. With the call-based approach, both Inline graphic estimators and the neutrality test were biased. The bias direction depended on the genotype calling pipeline (fig. 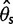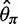3, call based): with the single-sample calling pipeline, Inline graphic and Inline graphic were overestimated and Tajima’s D was negatively skewed because of an excess of low frequency variants in the inferred SFS, whereas with the multisample calling pipeline, Inline graphic and Inline graphic were underestimated and Tajima’s D was skewed toward positive values due to a deficit of low frequency variants in the inferred SFS. 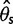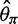Comparing Inline graphic and Inline graphic, the bias was bigger in 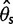Inline graphic than in 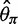Inline graphic for a sample size of 10. This is because adding a new artificial singleton by sequencing errors adds a new segregating site but adds only 2/10 to the average pairwise differences. 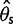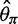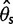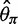In contrast, for the direct estimation approach, both Inline graphic and Inline graphic were unbiased (mean Inline graphic and Inline graphic were close to true value of 0.001) and consequently Tajima’s D was unbiased (mean D was close to zero as expected under the standard model (fig. 3, Direct).

Fig. 3.

Fig. 3.

Open in a new tab

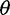Bias in Inline graphic estimators (top, middle) and neutrality test statistics (bottom) by the call-based approach alone, the call-based approach plus Achaz's correction, and the direct estimation approach, as a function of mean coverage.

Motivated by the fact that sequencing errors typically appear as artificial singletons and result in a false excess of observed singletons, Achaz (2008) proposed to ignore singletons when computing 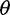Inline graphic estimators to reduce bias while retaining a powerful enough test to detect deviations from the standard model. We explored if using Achaz’s correction followed by the call-based approach can reduce bias in 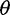Inline graphic estimators and in the neutrality test (fig. 3, call based + correction). In our simulated sequencing data, however, his assumptions about sequencing errors occurring as only singletons were violated: We observed sequencing errors affected not only singletons but also other allele-frequency bins (supplementary fig. S2, Supplementary Material online) and sequencing errors led to either an excess of singletons (with the single-sample calling pipeline) or a deficit of singletons (with the multisample calling pipeline). Nevertheless, Achaz’s correction followed by the call-based approach could reduce bias in 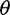Inline graphic estimators and Tajima’s D across ranges of coverage.

SFS and Parameter Estimation under the Exponential Population Growth

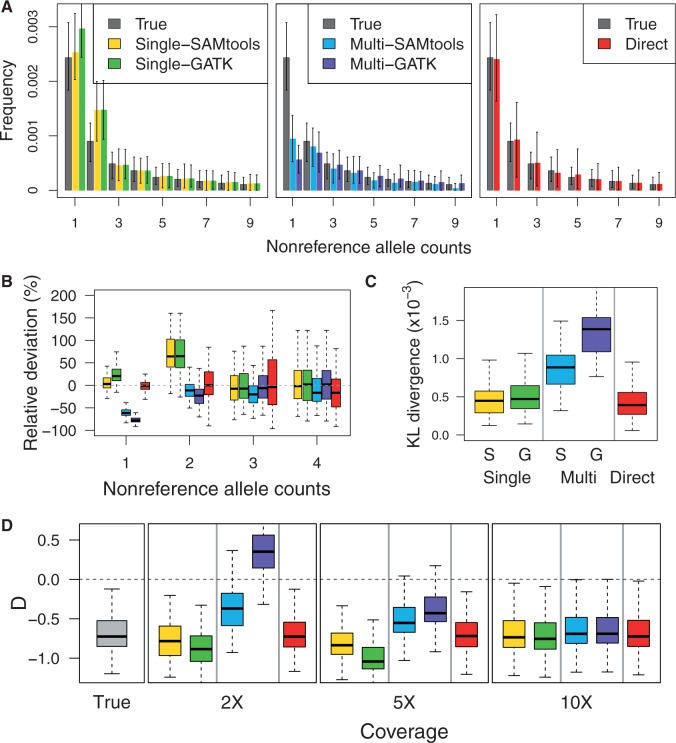
To explore robustness of SFS estimation to departures from the standard model, we evaluated the performance based on the simulated sequencing data under an exponential population expansion model with a growth rate of 0.01% (fig. 4). As expected, we observed that the ground-truth SFS under the exponential population growth model showed an excess of rare polymorphisms compared with that under the constant population size model (supplementary fig. S3, Supplementary Material online) and resulted in a negative Tajima’s D (fig. 4D).

Fig. 4.

Fig. 4.

Open in a new tab

Accuracy of the inferred SFS (A–C) for coverage 2× and bias in the neutrality test (D) under the exponential population growth model for coverage 2×, 5×, and 10×.

We observed similar bias patterns as in figure 1: The direct estimation outperformed that the call-based approach. The estimated SFS by the direct estimation approach was most similar to the ground-truth SFS across the range of coverages simulated, whereas the estimated SFS by the two-step estimation approach had bias in that rare variants were overestimated with the single-sample calling pipeline and underestimated with the multisample calling pipeline at low coverage (fig. 4A and B). Furthermore, bias in the estimated SFS subsequently influenced neutrality tests: Tajima’s D with the multisample calling pipeline was more positive than the ground-truth Tajima’s D, whereas Tajima’s D with the single-sample calling pipeline was more negative (fig. 4D).

Interestingly, under the population growth model, the single-sample calling pipeline performed better than the multisample calling pipeline as shown by the KL divergence (fig. 4C). In particular, at coverage 2×, the estimated SFS with the multisample calling pipeline in GATK was extremely distorted in that singleton calls were less than doubleton calls (fig. 4A), which in turn led to a positive Tajima’s D showing an evidence of population contraction (fig. 4D). The poor performance of the multisample calling pipeline is because the Bayesian inference for SNP discovery and genotype calling in GATK and SAMtools is based on priors that are derived under a constant size model.

Next, we investigated how the bias in the estimated SFS affects demographic inference based on the inferred SFS. By using dadi, we estimated parameters for the exponential population growth model, such as a present population size (N) and a time when population growth has started (T), based on the inferred SFS from sequencing data (fig. 5). The MLE of the growth rate with the direct estimation approach was almost unbiased across all ranges of coverage (close to the true growth rate 0.01%), whereas the growth rate was overestimated with the call-based approach with the single-sample calling pipeline and underestimated with the call-based approach with the multisample calling pipeline. This bias became more serious as coverage decreases: In particular, at coverage 2×, the growth rate estimate from GATK multisample calling becomes negative (–1%) indicating the inappropriate inference of population contraction rather than growth.

Fig. 5.

Fig. 5.

Open in a new tab

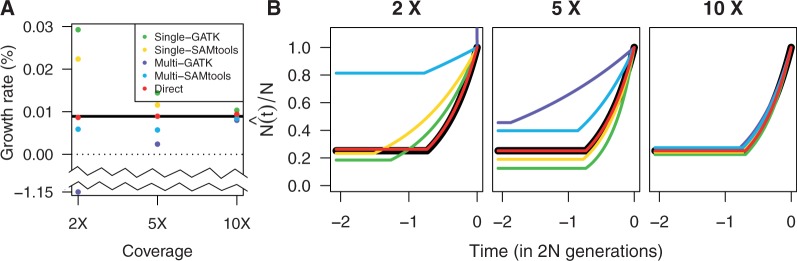
Estimation of a population growth rate by using dadi as a function of coverage. (A) Inferred growth rates for each method and the true growth rate (shown in black, 0.01%). (B) Inferred population size trajectory over time compared with the simulated trajectory (shown in black).

Impact of Changes in Parameters

To assess the robustness of our results, we explored how changes in nucleotide diversity (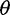Inline graphic), sequencing error rates (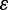Inline graphic), and underlying coalescent models affect the SFS estimation. To allow a straightforward comparison, we used the same parameters as in figure 1 apart from varying one parameter of interest at a time.

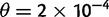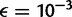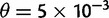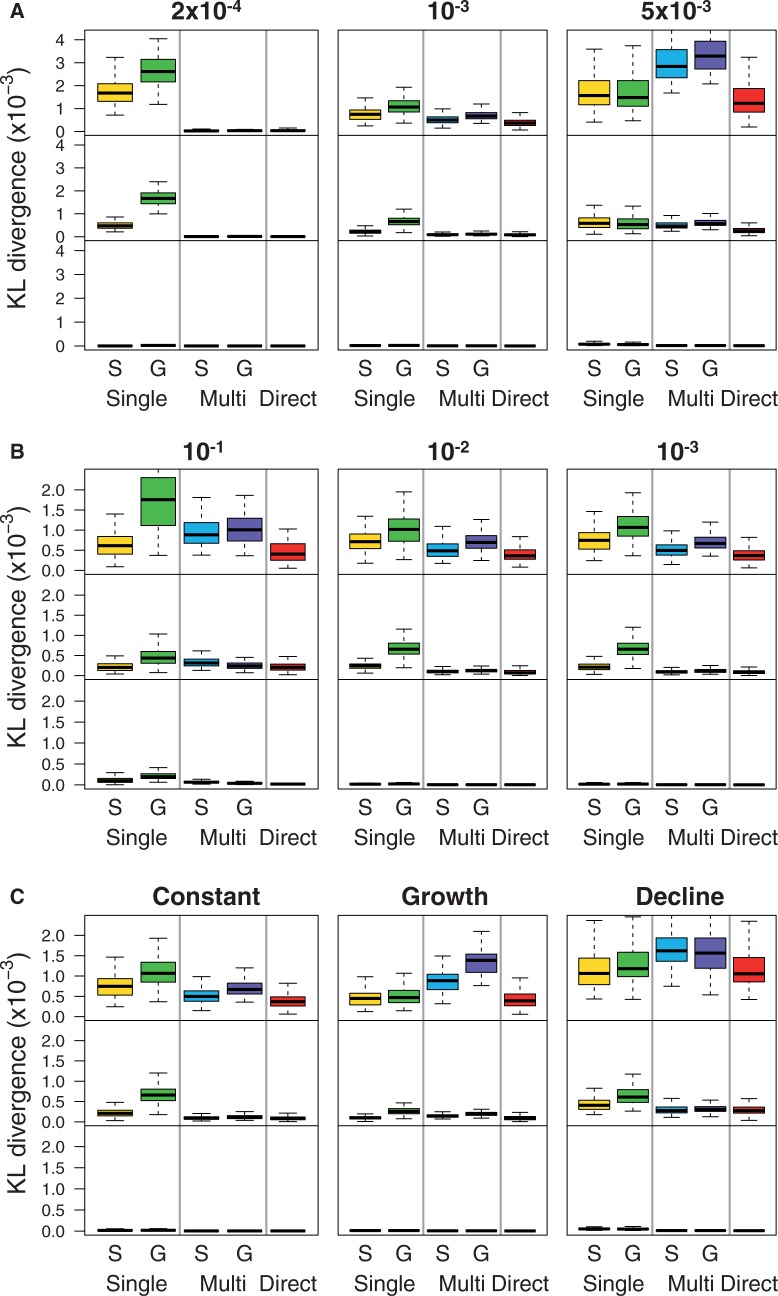
First, we examined the case where expected nucleotide diversity is five times smaller than the sequencing error rate (Inline graphic, Inline graphic) and five times larger than the error rate (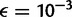Inline graphic, Inline graphic). Supplementary figures S2 and S3, Supplementary Material online, show that the SFS reconstruction methods behave almost identically as in figure 1—we observe that the SFS estimated by the direct estimation method is close to the true SFS even at 2×, whereas the SFS by the call-based approach is biased in that the single-sample caller overestimates rare variants and the multisample caller underestimates rare variants. However, when diversity gets smaller than the error rate, we observe that the KL divergence is larger for the single-sample caller compared with the multisample caller (fig. 6A). When diversity becomes larger than the error rate, the KL divergence for both single-sample and multisample caller becomes larger (fig. 6A).

Fig. 6.

Fig. 6.

Open in a new tab

The effect of changes in parameters on the SFS estimation. The distance between the inferred and ground-truth SFS is measured by KL divergence. We modified the following parameter with others fixed as in figure 1. (A) Nucleotide diversity. (B) Sequencing error rate. (C) Underlying coalescent model.

Next, we explored the effect of sequencing error rates on the SFS reconstruction with a fixed diversity of 10−3 under the standard model. We observed similar bias patterns to previous cases (supplementary fig. S5, Supplementary Material online), but when the error rate reaches 10−1, we need coverage higher than 20× for the estimated SFS by the call-based approach to be correct.

Finally, we examined how underlying coalescent models affects the SFS reconstruction based on sequencing data. We examined the case where the SFS is skewed to rare variants (population growth model) and the SFS is skewed to medium frequencies (population decline model) (supplementary fig. S6, Supplementary Material online). In both cases, we observed that the bias pattern in the inferred SFS was similar to that for the constant population size model (fig. 4 for the population growth model, supplementary fig. S7, Supplementary Material online, for the population decline model). We also observed that the violation to the constant size model led to a larger KL divergence for the multisample caller than the single-sample caller (fig. 6).

Genome-Wide Selection Scans

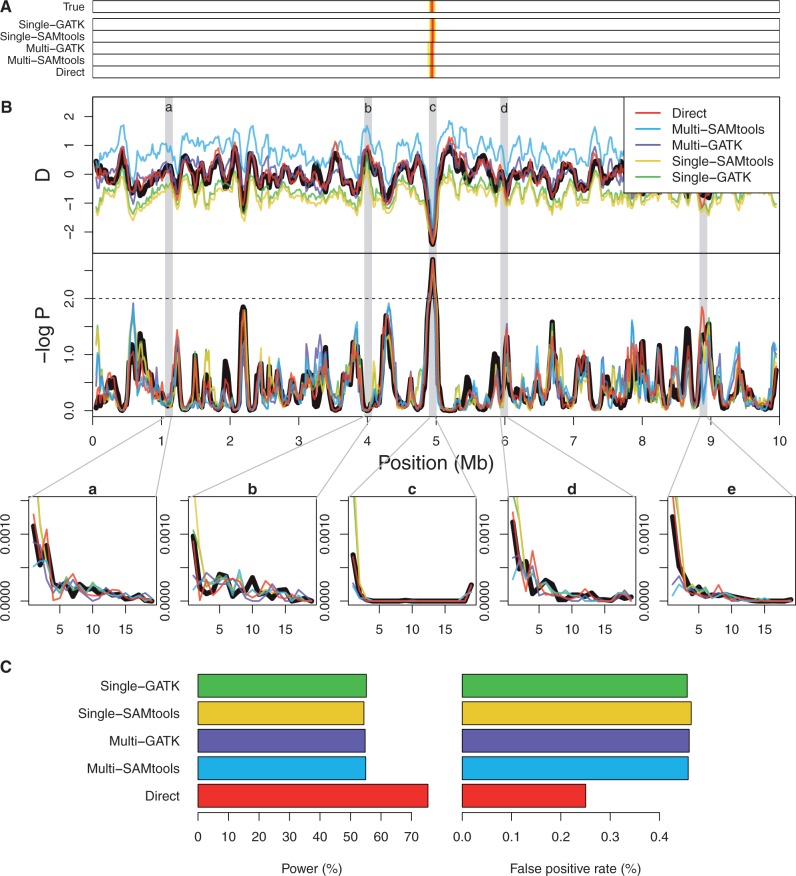
We next explored how error in the SFS affects the performance of genome-wide selection scans by an outlier detection approach. For this evaluation, we simulated sequencing data of length 10 Mb where a new beneficial mutation arose around 5 Mb, increased in frequency, and became fixed at the time of sampling. Figure 7B shows that at coverage 2×, Tajima’s D with the direct estimation approach was almost unbiased in both neutral and selected regions, whereas Tajima’s D was skewed positive with the call-based approach with multisample calling and skewed negative with the call-based approach with the single sample calling. However, after converting Tajima’s D to rank-based statistics, such as empirical P values, the difference between the direct estimation and call-based approach became negligible enough to select the same set of windows as a candidate region of a positive selection even at low coverage (fig. 7A). This indicates that rank-based statistics are less sensitive to bias in the inferred SFS, and if a positive selection is strong enough to be distinguishable from the neutral background, one can identify regions of positive selection with relative robustness to the SFS estimation approach used. However, over 100 replicates, the direct method had a higher power and smaller false-positive rates than the call-based approaches, and all call-based approaches performed with similar power and false-positive rates (fig. 7C).

Fig. 7.

Fig. 7.

Open in a new tab

Genome-wide selection scans by an outlier detection approach based on 10 Mb genomic region simulated with mean coverage 2×. (A) Classification of neutral vs. positively selected windows by empirical P values. The windows associated with empirical P values less than top 1% are shown with heat-map colors (the smaller the P value is, the more red the color is). These colored windows are candidate regions of having undergone positive selection. (B) Tajima's D (top), empirical P values (middle), and inferred SFS (bottom five panels) for 10 Mb genomic region. Bottom five panels corresponding to gray bars above (labeled a–e) are chosen to contrast SFS patterns in neutral regions (panels a, b, d, and e) and those in positively selected regions (panel c). (C) Power and false position rates in percent for each of the five approaches.

Discussion

With the rapid development of sequencing technologies, the obstacle in population genetic studies is in our ability to interpret such data with precision. The results shown here demonstrate that, depending on the pipeline used to analyze sequencing data, one can reach starkly different conclusions with the same data set. Simple allele counting after inferring individual genotypes from aligned sequencing data (call-based approach) leads to bias in the estimated SFS toward the sites with rare variants, and this bias is in opposite directions depending on the pipeline to infer genotypes: Multisample calling leads to underestimation of rare variants, whereas single-sample calling leads to overestimation of rare variants. Next, the bias in the inferred SFS subsequently results in bias in 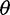Inline graphic estimators, neutrality test, and demographic inference. In contrast, we have shown that the SFS directly estimated from aligned sequencing data (direct estimation approach) was almost unbiased across ranges of coverage. Finally, genome-wide selection scans based on rank-based statistics are less sensitive to bias in the inferred SFS enough to capture the correct regions of positive selection even at low coverage. Given that many current studies using low to medium coverage sequencing data often use inferred genotypes to precede population genetic inference, our studies highlight that care is vital to avoid any potential bias problems and incorrect conclusions.

We reason that the increased performance of the direct estimation approach over the call-based approach is that it gains information from other individuals across all sites, whereas the call-based approach with multisample calling gains information from other individuals only at a given site and that with single-sample calling considers read data only for a given individual at a given position. Moreover, because the direct estimation approach can easily handle missing data, more information can be utilized to infer the SFS. To estimate the SFS from genotype calls by allele counting, we only used fully observable sites. The fraction of fully observable sites rapidly decreases as coverage decreases. We observed that for a sample of 10 individuals, only 20% of sites are fully observable at coverage 2×, 90% of sites at coverage 5×, and 99.9% of sites at coverage 10×. Handling missing data in SFS-based approaches has been a problem before short-read sequencing data and approaches to ameliorate the problem include subsampling the data down to a sample size for which most sites are observed (e.g., Nelson et al. 2012). An advantage of the direct estimation approach is that it can easily handle missing data during SFS estimation: It assigns a noninformative genotype likelihood for missing genotypes and maximized the likelihood of the SFS. In this way, it can utilize full information available in data, though it comes at a greater computational cost associated with the EM algorithm.

It is worth noting that there exist other frequently used tools for SNP discovery and genotype calling other than GATK and SAMtools. Among them, Stacks (Catchen et al. 2013) is a popular pipeline commonly used. Stacks is similar to the single sample calling in that it only considers read data for a given individual at a given site: It models read data for a single individual at a specific site with a multinomial distribution with a sequencing error rate for each site estimated by maximum likelihood (Hohenlohe et al. 2010). Then, it uses a likelihood ratio test (LRT) to assess the support for the most likely genotype at a 5% significance level. If the LRT is not significant, then the model assigns a homozygote genotype for the most commonly observed nucleotide. Another tool, Beagle (Browning and Browning 2009; Browning and Yu 2009), takes advantage of the pattern of LD at nearby sites to infer genotypes, and as a result, genotype calling accuracy is significantly improved and missing genotypes can be imputed. However, Beagle requires a modest sample size (e.g., on the scale of 50 individuals or higher) for LD information and imputation, and this can be challenging for studies with nonmodel organisms.

We should emphasize that our simulation studies are based on multiple assumptions that can be often violated in reality. In our simulation of sequencing data, we assumed that reads had been aligned to the reference without errors. In practice, however, this assumption is often violated in a region with repeats, insertions, deletions, and copy number variants. Hence, it might be important to catalog such regions to avoid potential bias due to alignment errors. Furthermore, we assumed that the number of reads at each site for a given individual is distributed according to a Poisson distribution. It is well known that the distribution of the number of reads follows an overdispersed Poisson distribution. Therefore, even though we concluded that the bias is almost negligible at mean coverage greater than 20× from our simulation studies, in reality, we might still observe nonnegligible bias at such coverage.

One may argue that future studies will have increased coverage and many of these problems will disappear. However, with limited budgets, we expect a category of experimental work will continue in which it is most advantageous to maximize the number of individuals by using low coverage. The insights gained here suggest how careful analysis of low-coverage data can provide useful population genetic inferences and that unquestioning use of basic analysis pipelines will be problematic.

Materials and Methods

To compare different approaches for estimating the SFS from sequencing data, we first conducted population genetic simulations to produce haplotype data and then overlaid sequencing errors assuming a paired-end short read sequencing approach.

Population Genetic Simulations

We simulated phased haplotypes for individuals by coalescent simulations under three different scenarios: the standard model (a neutral model with a constant population size) and two deviations from the standard models: a neutral model with an exponential population growth and positive selection on a new beneficial allele (a hard sweep model where a newly arisen beneficial allele increases in frequency and ultimately is fixed in a population). All coalescent simulations were performed using MSMS (Ewing and Hermisson 2010) with an effective population size of 10,000 diploid individuals, a mutation rate per-base per-generation of 2.5 × 10−8 and a recombination rate of 1 × 10−8. To simulate exponential population growth, we assumed that the population began with an initial population size of 10,000 to reach a present size of 40,000 in 16,000 generations (i.e., growth rate of 0.01%). To simulate exponential population decline, we used the initial population size of 40,000 that reached a present size of 10,000 in 16,000 generations (i.e., growth rate of −0.01%). To simulate positive selection, we introduced a new advantageous mutation with a selective advantage of 0.01 in the middle of the simulated region and conditioned the simulations on the allele just reaching fixation in a population. Under each scenario, we simulated 100 replicates of 100 kilobase pair (kb) genomic regions for a sample size of 10 diploid individuals to evaluate the accuracy of the estimated SFS. To perform genome-wide selection scans and parameter estimation for the exponential population growth, we simulated 10 megabase pair (Mb) genomic regions for a sample size of 10 diploid individuals. Finally, we randomly combined pairs of haplotypes to create genotype data, an assumption of panmixia.

Sequencing Experiment Simulations

To simulate 100-bp paired-end short read sequencing data for a given individual, we first sampled one of two haplotypes with an equal probability and then picked a starting position of the first read uniformly and a starting position of the second read by adding a paired-end distance from the last position of the first read. The paired-end distance was chosen according to a Poisson distribution with a rate set to 204 bp based on analysis of an Illumina 100 bp paired-end library of Drosophila melanogaster sequences (results not shown). On the basis of the two starting positions for the paired reads, we generated each read based on the underlying haplotype but with errors introduced according to the empirical distribution of base quality scores (after recalibration) from the same sequence library. The distribution of observed error rates from sequencing experiment simulations is shown in supplementary figure S4, Supplementary Material online.

Estimating the SFS

We assessed two ways to infer the SFS: the call-based and direct estimation approaches. With the call-based approach, we first inferred individual genotypes from aligned sequencing data and then computed the SFS from genotype calls by simple allele counting. In this case, we ignored uncertainty associated with genotype calls. To infer individual genotypes, we used one of two freely available programs, GATK (version 2.1-11) and SAMtools (version 1.4), and in each program we used either their single-sample or multisample calling procedures. Through this article, we refer to the results of these procedures as Single-GATK, Single-SAMtools, Multi-GATK, and Multi-SAMtools. To reconstruct the SFS from genotype calls by allele counting, we only used fully observable sites: the sites in which all individuals in a sample have at least one short read covering the site (hence, a genotype is observable for all individuals). With the direct estimation approach, we directly estimated the SFS from aligned sequencing data without inferring genotypes (Nielsen et al. 2012). We used the freely available program ANGSD (version 0.522) with an EM algorithm option to obtain the MLE of the SFS (Nielsen et al. 2012). We refer to results of this procedure as Direct.

Computing Summary Statistics for Population Genetic Inference

On the basis of the estimated SFS, we computed 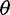Inline graphic estimators and neutrality test statistics. We computed four 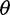Inline graphic estimators: 1) two original 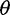Inline graphic estimators, Watterson’s 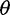Inline graphic estimator (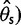Inline graphic based on the number of segregating sites (S) and Tajima’s 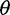Inline graphic estimator (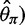Inline graphic based on the average pairwise differences (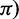Inline graphic, and 2) two more recent 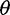Inline graphic estimators that ignore singletons to increase robustness to sequencing error, one derived from Watterson’s 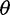Inline graphic-estimator (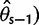Inline graphic and one derived from Tajima’s 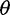Inline graphic-estimator (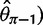Inline graphic (Achaz 2008, 2009). In the absence of sequencing errors and under a strict neutral model, these 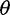Inline graphic estimators are unbiased estimators of a population mutation rate 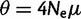Inline graphic, where 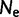Inline graphic is an effective population size and 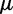Inline graphic is a mutation rate per-site per-generation.

For neutrality tests based on the SFS, we used Tajima’s D as it is a well used and powerful test of neutrality (Simonsen et al. 1995; Fu 1997) and Achaz’s Y (Achaz 2008), which is derived from Tajima’s D by ignoring singletons. Without sequencing errors and under the standard model with a constant population size, the expected value of D and Y are near zero regardless of sample size (Tajima 1983; Achaz 2009). The variance of D is expected to be one, but recombination reduces the variance in D to be smaller than one (Tajima 1989).

Quantification of Accuracy of the SFS Estimation

To evaluate the accuracy of the SFS estimated from sequencing data as a function of coverage, we computed the KL divergence of the estimated SFS from the ground-truth SFS (computed from genotype data) for each SFS estimation method.

We also evaluated the accuracy of the estimated SFS in each nonreference allele frequency bin i/(2n) in a sample of n diploid individuals. For each nonreference allele frequency bin, we computed a relative deviation of the fraction of sites with frequency i/(2n) in the estimated SFS fseq(i/2n) from that in the ground-truth SFS ftrue(i/2n).

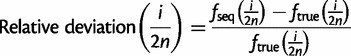graphic file with name mst229um1.jpg

To compare ground-truth SFS to the estimated SFS by each allele frequency bin, we made error matrices E of dimension (2n + 1) by (2n + 1). Each element 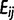Inline graphic of the error matrix E (i, j = 0, 1, … , 2n) is the fraction of the sites where the observed counts (the nonreference allele counts at each site computed from sequencing data) are j and the ground-true counts (the nonreference allele counts from genotype data) are i. Hence, diagonal elements 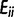Inline graphic of E represent the fraction of correctly estimated sites (true positives) for each allele frequency bin i/(2n).

Genome-Wide Selection Scans

To simulate a genome-wide selection scan, we generated 10-Mb genomic regions in which a new beneficial mutation arose in the middle of the region and identified a candidate region of positive selection by an outlier detection approach scan (Andolfatto 2007; Begun et al. 2007; Andersen et al. 2012; Axelsson et al. 2013):

  1. Estimated the SFS by using the call-based or the direct estimation approach in sliding windows of size 100 kb with an increment of 20 kb.

  2. Computed Tajima’s D associated with each window based on the estimated SFS.

  3. Converted Tajima’s D to empirical P values based on their ranks.

  4. Identified outlier windows if the empirical P value associated with a given window is ≤1%. The cutoff of 1% was chosen based on visual identification of an outlier mode presumed to represent selected loci (supplementary fig. S4, Supplementary Material online).

Estimating Parameters in an Exponential Population Growth Model

For demographic inference, we used the python module dadi (Gutenkunst et al. 2009). Dadi finds MLEs of parameters for a user-specified demographic model based on the observed SFS. We simulated a 10-Mb genomic region under the exponential population growth model and then estimated the present population size (N) and time when the growth had started (T, measured in units of 2 N generations). We found the MLEs first by a grid search to find a peak of likelihood surface and then by BFGS steps to localize the peak.

Supplementary Material

Supplementary figures S1–S7 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).

Supplementary Data
supp_31_3_723__index.html (1,005B, html)

Acknowledgments

The authors thank Darren Kessner for assistance with sequencing experiment simulations and Daniel Wegmann for assistance with programming. This work was supported by the National Institutes of Health (T32 HG002536 to E.H., GM053275 to J.S.S., and HG007089 to J.N.).

References

  1. Abecasis GR, Auton A, Brooks LD, DePristo MA, Durbin RM, Handsaker RE, Kang HM, Marth GT, McVean GA. An integrated map of genetic variation from 1,092 human genomes. Nature. 2012;491:56–65. doi: 10.1038/nature11632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Achaz G. Testing for neutrality in samples with sequencing errors. Genetics. 2008;179:1409–1424. doi: 10.1534/genetics.107.082198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Achaz G. Frequency spectrum neutrality tests: one for all and all for one. Genetics. 2009;183:249–258. doi: 10.1534/genetics.109.104042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andersen EC, Gerke JP, Shapiro JA, Crissman JR, Ghosh R, Bloom JS, Felix MA, Kruglyak L. Chromosome-scale selective sweeps shape Caenorhabditis elegans genomic diversity. Nat Genet. 2012;44:285–290. doi: 10.1038/ng.1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Andolfatto P. Hitchhiking effects of recurrent beneficial amino acid substitutions in the Drosophila melanogaster genome. Genome Res. 2007;17:1755–1762. doi: 10.1101/gr.6691007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Axelsson E, Ratnakumar A, Arendt ML, Maqbool K, Webster MT, Perloski M, Liberg O, Arnemo JM, Hedhammar A, Lindblad-Toh K. The genomic signature of dog domestication reveals adaptation to a starch-rich diet. Nature. 2013;495:360–364. doi: 10.1038/nature11837. [DOI] [PubMed] [Google Scholar]
  7. Beaumont MA. Approximate Bayesian computation in evolution and ecology. Annu Rev Ecol Evol Syst. 2010;41:379–406. [Google Scholar]
  8. Begun DJ, Holloway AK, Stevens K, Hillier LW, Poh YP, Hahn MW, Nista PM, Jones CD, Kern AD, Dewey CN, et al. Population genomics: whole-genome analysis of polymorphism and divergence in Drosophila simulans. PLoS Biol. 2007;5:e310. doi: 10.1371/journal.pbio.0050310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bentley DR, Balasubramanian S, Swerdlow HP, Smith GP, Milton J, Brown CG, Hall KP, Evers DJ, Barnes CL, Bignell HR, et al. Accurate whole human genome sequencing using reversible terminator chemistry. Nature. 2008;456:53–59. doi: 10.1038/nature07517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Browning BL, Browning SR. A unified approach to genotype imputation and haplotype-phase inference for large data sets of trios and unrelated individuals. Am J Hum Genet. 2009;84:210–223. doi: 10.1016/j.ajhg.2009.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Browning BL, Yu Z. Simultaneous genotype calling and haplotype phasing improves genotype accuracy and reduces false-positive associations for genome-wide association studies. Am J Hum Genet. 2009;85:847–861. doi: 10.1016/j.ajhg.2009.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Catchen J, Hohenlohe PA, Bassham S, Amores A, Cresko WA. Stacks: an analysis tool set for population genomics. Mol Ecol. 2013;22:3124–3140. doi: 10.1111/mec.12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. DePristo MA, Banks E, Poplin R, Garimella KV, Maguire JR, Hartl C, Philippakis AA, del Angel G, Rivas MA, Hanna M, et al. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat Genet. 2011;43:491–498. doi: 10.1038/ng.806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ewing G, Hermisson J. MSMS: a coalescent simulation program including recombination, demographic structure and selection at a single locus. Bioinformatics. 2010;26:2064–2065. doi: 10.1093/bioinformatics/btq322. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fay JC, Wu CI. Hitchhiking under positive Darwinian selection. Genetics. 2000;155:1405–1413. doi: 10.1093/genetics/155.3.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fu YX. Statistical tests of neutrality of mutations against population growth, hitchhiking and background selection. Genetics. 1997;147:915–925. doi: 10.1093/genetics/147.2.915. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Fu YX, Li WH. Statistical tests of neutrality of mutations. Genetics. 1993;133:693–709. doi: 10.1093/genetics/133.3.693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. PLoS Genet. 2009;5:e1000695. doi: 10.1371/journal.pgen.1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hohenlohe PA, Bassham S, Etter PD, Stiffler N, Johnson EA, Cresko WA. Population genomics of parallel adaptation in threespine stickleback using sequenced RAD tags. PLoS Genet. 2010;6:e1000862. doi: 10.1371/journal.pgen.1000862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Johnson PL, Slatkin M. Accounting for bias from sequencing error in population genetic estimates. Mol Biol Evol. 2008;25:199–206. doi: 10.1093/molbev/msm239. [DOI] [PubMed] [Google Scholar]
  21. Kang CJ, Marjoram P. Inference of population mutation rate and detection of segregating sites from next-generation sequence data. Genetics. 2011;189:595–605. doi: 10.1534/genetics.111.130898. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Keightley PD, Halligan DL. Inference of site frequency spectra from high-throughput sequence data: quantification of selection on nonsynonymous and synonymous sites in humans. Genetics. 2011;188:931–940. doi: 10.1534/genetics.111.128355. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kim SY, Lohmueller KE, Albrechtsen A, Li Y, Korneliussen T, Tian G, Grarup N, Jiang T, Andersen G, Witte D, et al. Estimation of allele frequency and association mapping using next-generation sequencing data. BMC Bioinformatics. 2011;12:231. doi: 10.1186/1471-2105-12-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics. 2011;27:2987–2993. doi: 10.1093/bioinformatics/btr509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, Marth G, Abecasis G, Durbin R. The Sequence Alignment/Map format and SAMtools. Bioinformatics. 2009;25:2078–2079. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Li Y, Willer C, Sanna S, Abecasis G. Genotype imputation. Annu Rev Genom Hum Genet. 2009;10:387–406. doi: 10.1146/annurev.genom.9.081307.164242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Liu X, Fu YX, Maxwell TJ, Boerwinkle E. Estimating population genetic parameters and comparing model goodness-of-fit using DNA sequences with error. Genome Res. 2010;20:101–109. doi: 10.1101/gr.097543.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Liu X, Maxwell TJ, Boerwinkle E, Fu YX. Inferring population mutation rate and sequencing error rate using the SNP frequency spectrum in a sample of DNA sequences. Mol Biol Evol. 2009;26:1479–1490. doi: 10.1093/molbev/msp059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lynch M. Estimation of nucleotide diversity, disequilibrium coefficients, and mutation rates from high-coverage genome-sequencing projects. Mol Biol Evol. 2008;25:2409–2419. doi: 10.1093/molbev/msn185. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lynch M. Estimation of allele frequencies from high-coverage genome-sequencing projects. Genetics. 2009;182:295–301. doi: 10.1534/genetics.109.100479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Mackay TF, Richards S, Stone EA, Barbadilla A, Ayroles JF, Zhu D, Casillas S, Han Y, Magwire MM, Cridland JM, et al. The Drosophila melanogaster Genetic Reference Panel. Nature. 2012;482:173–178. doi: 10.1038/nature10811. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. McKenna A, Hanna M, Banks E, Sivachenko A, Cibulskis K, Kernytsky A, Garimella K, Altshuler D, Gabriel S, Daly M, et al. The Genome Analysis Toolkit: a MapReduce framework for analyzing next-generation DNA sequencing data. Genome Res. 2010;20:1297–1303. doi: 10.1101/gr.107524.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nelson MR, Wegmann D, Ehm MG, Kessner D, St Jean P, Verzilli C, Shen J, Tang Z, Bacanu SA, Fraser D, et al. An abundance of rare functional variants in 202 drug target genes sequenced in 14,002 people. Science. 2012;337:100–104. doi: 10.1126/science.1217876. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Nielsen R, Korneliussen T, Albrechtsen A, Li Y, Wang J. SNP calling, genotype calling, and sample allele frequency estimation from new-generation sequencing data. PLoS One. 2012;7:e37558. doi: 10.1371/journal.pone.0037558. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Nielsen R, Paul JS, Albrechtsen A, Song YS. Genotype and SNP calling from next-generation sequencing data. Nat Rev Genet. 2011;12:443–451. doi: 10.1038/nrg2986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pool JE, Hellmann I, Jensen JD, Nielsen R. Population genetic inference from genomic sequence variation. Genome Res. 2010;20:291–300. doi: 10.1101/gr.079509.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Simonsen KL, Churchill GA, Aquadro CF. Properties of statistical tests of neutrality for DNA polymorphism data. Genetics. 1995;141:413–429. doi: 10.1093/genetics/141.1.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tajima F. Evolutionary relationship of DNA sequences in finite populations. Genetics. 1983;105:437–460. doi: 10.1093/genetics/105.2.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Tajima F. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics. 1989;123:585–595. doi: 10.1093/genetics/123.3.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Watterson GA. On the number of segregating sites in genetical models without recombination. Theor Popul Biol. 1975;7:256–276. doi: 10.1016/0040-5809(75)90020-9. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_31_3_723__index.html (1,005B, html)
supp_mst229_11.1.13_suppFigures_EHan.pdf (1MB, pdf)

Articles from Molecular Biology and Evolution are provided here courtesy of Oxford University Press

RESOURCES