Abstract
Objective Demonstrate multivariate multilevel survival analysis within a larger structural equation model. Test the 3 hypotheses that when confronted by a negative parent, child rates of angry, sad/fearful, and positive emotion will increase, decrease, and stay the same, respectively, for antisocial compared with normal children. This same pattern will predict increases in future antisocial behavior. Methods Parent–child dyads were videotaped in the fall of kindergarten in the laboratory and antisocial behavior ratings were obtained in the fall of kindergarten and third grade. Results Kindergarten antisocial predicted less child sad/fear and child positive but did not predict child anger given parent negative. Less child positive and more child neutral given parent negative predicted increases in third-grade antisocial behavior. Conclusions The model is a useful analytic tool for studying rates of social behavior. Lack of positive affect or excess neutral affect may be a new risk factor for child antisocial behavior.
Keywords: behavior problems, family functioning, longitudinal research, structural equation modeling
Pediatric psychologists are often interested in predictors and consequences of social interaction patterns among children because many leading theories of child development focus on such interaction. In fact, many times the theoretical focus is primarily on social interaction in the context of a particular dyad (e.g., parent–child) thought to play a critical role in healthy or pathological development. Patterson and colleagues’ coercion theory (Granic & Patterson, 2006) is an example where coercive social interaction between parent and child has been shown to be a major risk factor of the most common of child behavior problems, externalizing (i.e., aggressive, acting out behavior). This has led to the development of therapeutic interventions aimed at teaching and motivating parents to use more effective discipline strategies (Forgatch & Patterson, 2010). Coercive family interaction has also been implicated in other problems as well such as poor adherence to complex glycemic control regimens for managing type 1 diabetes (Duke et al., 2008). Finally, there is evidence to suggest that extreme coercive parent–child interaction in the family leads to exaggerated responses to stress. If this process continues on chronic basis, it can lead to a proinflammatory phenotype in adolescence that sets the stage for future susceptibility to degenerative disease (Miller & Chen, 2010).
Applying new and advanced statistical methods may provide a better understanding of patterns of behavior than previously implemented traditional methods. Thus, the goal of this article is to demonstrate multivariate multilevel survival analysis (MMSA), an advanced statistical method that is useful in general to answer research questions about the timing of events and in particular can be applied to research questions about dyadic social interaction. Using MMSA to study predictors and consequences of dyadic social interaction, however, requires extensions to basic survival analysis that have only recently become available. It is these extensions that are the primary focus of this article. Readers interested in more details should see the Supplementary Material that accompanies and extends this article.
As motivation for an example application, consider the following research question: For young children just starting kindergarten, are current child externalizing behavior problems related to over and under use of angry and sad/fearful emotions, respectively, in the parent–child dyad but not associated with positive emotion? Does this pattern predict increases in future externalizing problems several years later in third grade? More specifically, if the child is in a neutral affective state but the parent is in a negative affective state, as often happens in a discipline encounter, is the aforementioned pattern predicted by child antisocial and predictive of increases in future child antisocial behavior? On a macro level, such research questions involve an attempt to integrate aspects of coercion theory with emotion regulation theory to advance understanding of child antisocial behavior (Dagne & Snyder, 2011; Snyder, Stoolmiller, Wilson, & Yamamoto, 2003). On a micro level, the research question focuses on the rate of specific child responses (from neutral to anger, sad/fearful, or positive) to a specific antecedent parent behavior (parent negative). These child responses terminate episodes where the child is affectively neutral and the parent is affectively negative. For shorthand, we refer to these patterns as, for example, child anger given parent negative with the understanding that the child was neutral to begin with. For more information about the macro/micro distinction and the important role it plays in coercion theory, see Granic and Patterson (2006).
To understand how MMSA methodology could be applied, it is helpful to have a rough idea of the required data structure and how such data might be obtained. Suppose we bring parent–child dyads into the laboratory, ask them to engage in some problem-solving interaction task that is likely to result in parent–child conflict, and we videotape and code in proper sequence the durations of the displayed emotions of both parent (mutually exclusive and exhaustive categories of positive, neutral, or negative) and child (mutually exclusive and exhaustive categories of positive, neutral, angry, or sad/fearful) in real time. At the same time, we get ratings from the child’s parent about the child’s externalizing behavior, and in a follow-up 3 years later, we get the same ratings. At this point, MMSA can be used to estimate the rates of interest (usually referred to as hazard rates), the correlations among the child hazard rates, and whether the hazard rates are predicted by concurrent child externalizing and in turn are predictive of increases in future child externalizing.
Survival analysis is well developed and covered in detail in many sources (see Allison, 1984, for an introduction). Other terms for the same model include hazard rate regression or event history analysis. Generally, the nomenclature reflects the fact that the model estimates the underlying hazard rate, which controls the timing of occurrence of events of interest. A higher hazard rate means that the waiting time until the event happens is shorter and, on average, more events per unit time will occur. Hazard rates are not necessarily constant but can in fact change over time due to either observed or unobserved influences. Survival analysis also incorporates information about censoring, which is what happens when the observation period ends before the event happens for some of the subjects in the sample. Survival models incorporate all that is known about the waiting time for censored subjects, namely, that the waiting time is not known exactly but it was at least as long as the observation period.
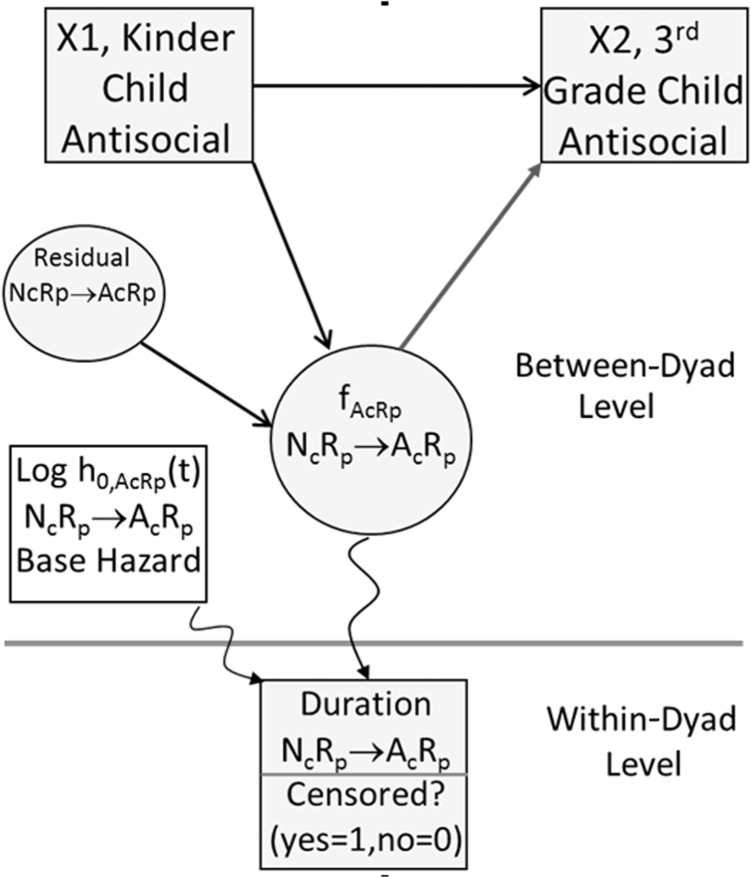
The extension to MMSA is more recent but is still covered in number of other sources (Dagne & Snyder, 2009; Goldstein, 2011; Stoolmiller & Snyder, 2006). At this point in time, however, what the existing sources have in common is that the survival process that is generating the event(s) of interest is treated as the ultimate end point or outcome to be predicted. This is most clear in medical applications where the process is disease and the event of interest is death and the goal is to study predictors of the disease process. In contrast, in our application, which utilizes recent advances in the Mplus program (Muthén & Muthén, 2013), the rate of child anger given parent negative is both an outcome and a predictor of future psychological adjustment. This is what makes our application of MMSA novel and an advance over our previous work (Stoolmiller & Snyder, 2006). A heuristic path diagram at the dyad level is shown in Figure 1 to illustrate the concept.
Figure 1.
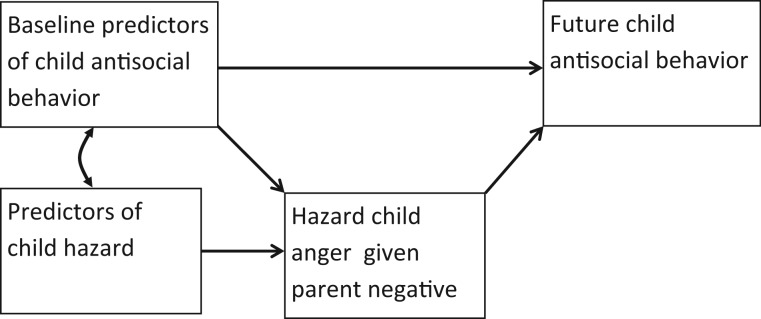
Heuristic diagram of the multivariate multilevel survival model.
Mplus, a commercially available program, contains the necessary MMSA functionality but also links and embeds MMSA in a larger SEM framework, which is what makes it possible to fit models such as the one shown in Figure 1. Indeed, the researcher has many tools available, if necessary, that are part of the SEM framework that are not available in more traditional survival regression programs. To name a few, it is possible to address questions about mediation, or include latent continuous variables if measurement error is a concern, or include latent categorical variables if the population is believed to consist of unobserved sub-populations, or include dyads with partial data (missing observation data or missing dyad-level data) either by design or by accident. The modeling opportunities in Mplus are very rich.
The particular MMSA we focus on is the Cox model that has several features that make it attractive for working with real-time observed behavior data (Therneau & Grambsch, 2000). First, the Cox model is a continuous-time survival model. When the time of occurrence of events is known more precisely, as it is when events are recorded in real time on electronic recording devices, time is usually conceptualized as continuous. In contrast, for less precise time scales, when many events can apparently happen simultaneously, time is usually conceptualized as discrete. Second, the Cox model is semi-parametric because the baseline hazard function need not be specified, which eliminates one potential source of model misspecification. The baseline hazard function, usually denoted h0(t), shows how the hazard rate changes as a function of time, t, while waiting for the event to happen and is somewhat analogous to a combination of both the intercept and residual term in standard regression. Like an intercept, it is the same for all subjects. Like a residual term, it is the source of randomness in the survival model. We will give more details on h0(t) shortly as we use our example application to illustrate the details of the Cox model.
A more detailed but still heuristic path diagram is shown in Figure 2 for a single hazard rate, child anger given parent negative, which we abbreviate AcRp (A = anger, c = child, R = negative, p = parent). The diagram is heuristic because there are no well-established conventions for depicting multilevel models or survival models, but the rest of the diagram follows the usual conventions with observed variables in boxes, latent variables in circles, double-headed arrows indicating correlation, and single-headed arrows indicating linear regression effects. The dyad-level model is shown above the horizontal gray line and the within-dyad model is shown below. Because the hazard rate is required to be non-negative to make sense, the Cox model is a multiplicative model involving two pieces, both of which are non-negative, the baseline hazard function, h0,AcRp(t) and an exponential term that includes all the predictors, latent or observed (e.g., exp(bX1i + fAcRp,i)). Notice that the baseline hazard function lacks a subscript i for individuals but does allow the hazard to vary continuously across time, and the exponential term has a collection of terms inside it that have subscripts for individuals, which allows the hazard to vary across individuals. Together the product of the baseline hazard and the exponential term constitute the hazard rate, hAcRp,i(t), for any individual dyad. Estimation is typically easier, however, and carried out on the log scale, which converts the multiplicative hazard model to an additive model. Thus, the latent variable in the Figure 2 represents individual differences on the log of the hazard scale and this is important to keep in mind when interpreting effect sizes. The within-dyad observed variables that define the latent hazard rates are shown as both a duration, NcRp→AcRp, identifying the initial state, child neutral parent negative and the terminating event, child anger and a dichotomous censoring indicator variable within a single square box. This is to remind readers that although these are two separate variables, they must go together to avoid biased estimates of hazard rates. Finally, the arrows that connect latent log AcRp, fAcRp,i, and the baseline hazard function for AcRp, h0,AcRp(t), to the overall hazard function, hAcRp,i(t), and to the episode durations and censoring indicators are shown as crooked arrows to remind readers that the Cox model is a nonlinear model.
Figure 2.
Heuristic path diagram of the multilevel Cox model for hazard rate for child anger.
Because the baseline hazard function is not specified in the Cox model, we could just ignore it and focus on the predictor effects, fixed and random, and indeed, this is a large part of the appeal of the Cox model. After all, almost nothing is known about the nature of any of the baseline hazard functions for typical parent–child social interaction behaviors. The baseline hazard function, however, can still be estimated after model fitting and it may be interesting in some applications, so we will spend a bit more time exploring it.
The most unusual thing about the baseline hazard function, compared with a standard regression intercept or residual term, is that it is a function of time. What this means is that the population rate of event occurrence can change over time while we are waiting for the events to occur independent of any predictors in the model, including moment-to-moment predictors. So the baseline hazard function captures the sum total of all moment-to-moment influences that have been omitted from the model over all individuals in the sample. An intuitive example of a baseline hazard function is the death rate in the United States. The death rate is not constant across the lifespan in the United States but rather starts out higher in the first years of life, drops in early childhood, and is fairly constant for a long period of years, and then gradually increases again in old age as people begin to wear out.
The final extension of our model is to add two more multilevel Cox models for the hazard rates for child sad/fear given parent negative and child positive given parent negative, which is what makes the model multivariate as well as multilevel. The only new additions to the model parameters beyond those in Figure 2 are the three correlations among the log hazard rates, which get at research questions such as, “When confronted by a negative parent, are children who are quick to get angry also slow to get sad/fearful?” See Supplementary Material for the path diagram for the full model.
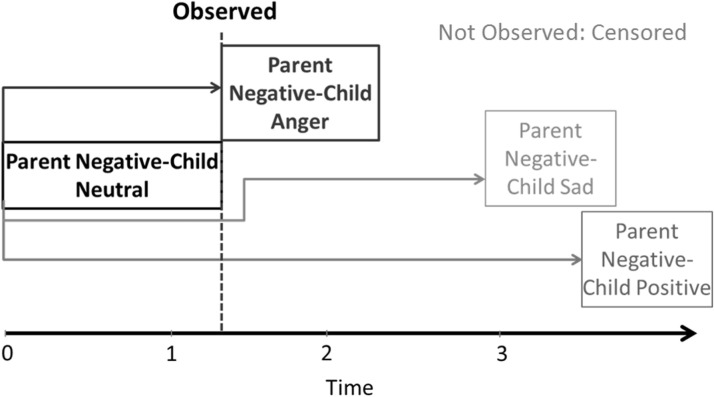
The last issue to cover is the issue of censoring in MMSA. Censoring is more complicated in MMSA because for any particular episode of child neutral parent negative, there are multiple competing end states that could happen and the occurrence of one necessarily precludes the occurrence of all the others. This is illustrated schematically in Figure 3 for a single episode shown in dark black that lasted for 1.5 s and ended in child sad/fear. For the other two child states that could have happened, the occurrence of child sad/fear censored their waiting times at 1.5 s, as indicated by the gray lines. The complete durations for this episode for the hypothetical alternative states are not known, except that they were longer than 1.5 s. This type of MMSA is typically referred to as a “competing risks” survival analysis, terminology that arises from the underlying concept that the possible end states are competing in a race to terminate the current episode and only the winning state’s time is recorded (Therneau & Grambsch, 2000). More importantly, the implication of competing risks style censoring for MMSA is that censoring will always be inherent and extensive in social interaction data and must be accounted for in the model to get accurate results. Next we present a few more details about the study sample and measures and then present a series of analyses to illustrate the methods.
Figure 3.
Schematic diagram of censoring in models of competing risks. What actually happens is the behavior shown at the end of the black arrow, and alternatives that could have happened but did not are shown at the end of the gray arrows; the length of the arrow indicating the waiting time. The behavior with the higher rate will tend to have the shorter waiting time and will censor (dashed black line) the occurrence of the behaviors with the lower rates and longer waiting times.
Methods
The participants were 275 children, (and their parents), 49% male, who were recruited at kindergarten entry to one elementary school that exclusively served a low-income, mixed industrial-residential neighborhood. Seventy-one percent of the children were European Americans, 19% were African American, 5% were Hispanic/Latino, and the remaining children were Native- and Asian American. The median per-capita annual family income was $8,300, and 34% of the parents had education beyond high school. The recruitment rate of children at kindergarten entry was 76%. The sample of children and families who participated in the study reflected the demographics of those in the neighborhood and (with the exception of family income) of the metropolitan area (MSA pop. = 550,000) in which the sample was located. Of these 275 families, 5 had missing data on all the measures in all the models and so were dropped, leaving the analytic sample at 270.
Child and Parent Emotion Displays
The interaction of parent–child dyads was videotaped for 2 hr on each of two occasions, separated by a minimum of 1 week (average = 2.3 weeks). The first hour of each session was structured around a series of tasks that were completed at a table, permitting a continuous and simultaneous observation of the facial expressions and frontal gestures of the parent and the child as well as their verbal and vocal behavior. The structured activities of the two sessions were very similar but not identical. The first hour of interaction of each parent–child dyad was coded using the Specific Affect Coding System (SPAFF; Gottman, McCoy, Coan, & Collier, 1996). Observers were trained extensively to a criterion of 75% agreement before initiating coding of videotaped interaction derived from participants in the current research. Weekly recalibration training was completed to minimize observer drift. Two observers independently coded 15% of all the sessions to assess coder agreement. Observers were blind to which sessions were used to assess observer agreement. The average between-observer agreement on the occurrence of SPAFF codes (using a +/−6-s window) was 83% (kappa = .73).
In the hazard analyses, super-ordinate categories labeled child “anger,” “positive,” “sad-fearful,” and “neutral” were defined by combining the SPAFF codes of anger, contempt, and disgust; SPAFF codes of validation, interest, enthusiasm, and humor; SPAFF codes of sad and fear–tension; and all other codes, respectively, except an out-of-view code. Super-ordinate categories labeled parent “negative,” “positive,” and “neutral” were defined by combining the SPAFF codes of anger, contempt, disgust, criticism, domineering, belligerence, threats, whining, stonewalling, defensiveness, fear/tension, and sadness; SPAFF codes of validation, interest, enthusiasm, and humor; and all other codes, respectively, except an out-of-view code. Observers used the out-of-view code when the child or parent’s affect could no longer be accurately coded because they were not visible. Out-of-view codes were treated just like the end of the session in the hazard analyses.
Child Antisocial Behavior
A measure of child antisocial behavior was obtained in the fall (child age 5.5 years) of the kindergarten year and in the spring of third grade consisting of the mean of 23 items scored 0, 1, or 2 from the parent Child Behavior Checklist (Achenbach & Edelbrock, 1991) describing aggressive and oppositional child behavior. The scale reliabilities (alpha) were greater than .90 on each measurement occasion. Based on 255 subjects with fall K data and 203 subjects with third-grade data, observed means at fall K and third grade were .49 and .43, respectively; standard deviations were .31 and .38, respectively; minimum scores were both 0; and maximum scores were 1.61 and 1.91, respectively. Although the antisocial measures were positively skewed (.89 and 1.32 for K and third grade, respectively), pronounced floor effects (many subjects with the identical minimum score of 0) were absent. The correlation between K and third-grade antisocial was .64 based on 189 subjects. See Snyder et al., 2003, for a more thorough description of the sample, the family-level measures, the observational procedures, and coding for parent–child emotion displays.
The data structure for multilevel Cox models is the same as that for standard two-level models in Mplus with the repeated measures, the episode durations, in “tall” format, one line for each repeated observation within a higher-level unit, in our case the dyad, which is identified by an ID variable. The dyad ID variable and any dyad-level predictors get duplicated across the repeated rows for the durations. The steps by which the observation data get combined with the dyad-level data will vary depending on how the observation data are stored but we briefly describe the process for our data to give readers some idea of how to proceed. For more detail about data preparation, see the Supplementary Material. For a family at a single session, the child and parent were coded independently of each other in separate passes through the video tape and the data stored in two separate files. The raw data consisted of multiple rows of session times and child or parent states; each time the child or parent changed state, the session time was recorded, called the start time, along with the new state called the start state. The parent and child codes were aggregated into the super-ordinate categories described previously and then merged using start time as the merging key. Merging creates missing values in the child start state and start time when the parent changes but the child does not and vice versa. These missing values were filled in using the last nonmissing values. A dyadic start state indicator was created by concatenating the start state of the child and parent in that order. A lag 1 time variable called end time and a lag 1 dyadic state variable called end state were computed, which for the jth row were just the j + 1 row values of the same variables. Duration was computed by subtracting the start time from the end time. Thus on any row, the data would indicate when a dyad started and ended a state, which state they started in and ended on, and the duration of the state.
Mplus requires a censoring indicator variable that by default takes the value of 1 if the episode duration was censored and 0 otherwise. The very last row in both parent and child files was always an end-of-session time and an end-of-session code, which allowed us to indicate that the duration of the final dyadic state was always censored. Out-of-view codes were treated just like end-of-session codes. As explained previously, for competing risks, it is also necessary to have a censoring indicator for each possible end state. This is a set of dummy variables that we named according to the end state (e.g., AcRp was the name of the dummy variable censoring indicator that indicated whether the NcRp episode ended in AcRp, scored 0 for not censored, or ended in some other state, scored 1 for censored). A dyad ID variable was added, and all the dyadic files were concatenated to make one very large file for all episodes for all dyads in Session 1 in the sample. The same procedure was followed for Session 2 and for Session 1, and two files were combined for use in the example analyses reported in this article. The final step consisted of selecting just the transitions of interest (episodes of NcRp ending in AcRp, ScRp, or PcRp) and merging in the additional dyad-level predictors or outcomes (K and third-grade antisocial), which like the dyad ID repeat across the multiple rows of durations within a dyad.
Results
Basic descriptive statistics for the survival data are important and interesting for a number of reasons. First, we have the possibility that the sub-sample that agrees to participate in the laboratory task is not representative of the larger sample in the study. Our models are based on 270 of the 275 dyads in the sample (five dyads were missing all data for all measures). However, 30 of the 270 dyads or 11% of the sample did not participate in any laboratory session. These 30 dyads are still included in the models and selection bias is minimized to the extent that the missing observation data are missing completely at random or at least random conditional on other predictors in the model. Although we will not pursue it here, we could use baseline data beyond child K antisocial to predict laboratory participation and include any significant predictors in our models to further minimize the possibility of selection bias. Second, we have the possibility that having experienced the first laboratory session, some dyads may decide not to participate in the second laboratory session, further augmenting the possibility of biased sampling. In our case, of the 239 dyads that participated in Session 1, 19 or 8% declined to come back for a second session. One dyad participated in the second but not the first session, so the total number of dyads in the second session was 221.
Third, given a fixed sample size of dyads, the precision of the estimates of the latent log hazards is strongly determined by the number of events. Most of the child transitions were from neutral to positive, 952 or 68%, followed by transitions to anger, 219 or 17%, and sad/fear, 186 or 15%; and most dyads, 208 or 82%, had at least one child positive transition, but fewer dyads had at least one child anger or child sad/fear transition, 98 or 41% and 89 or 37%, respectively. Two types of transitions omitted from the analyses are simultaneous dyadic transitions in which both dyad members change states at the exact same moment (at least they appear to at the resolution of time we used for coding, 1/30th of a second) and parent transitions where the child does not change state but the parent changes to either neutral or positive. The former can be safely ignored because they are very rare, making up a tiny fraction (0.3%) of the total number of transitions for NcRp, and the latter, while more numerous, are omitted to keep the demonstration models simple. In actual practice, because the parent hazard rates may be correlated with both the child hazard rates and third-grade child antisocial, it would be important to eventually include them in the model as competing predictors of third-grade child antisocial to avoid biased estimates for the child hazard effects.
As a preliminary, fitting smaller pieces of bigger models is usually a very good strategy, especially when complex estimation techniques like numerical integration are involved, as is the case with the multilevel Cox model. These smaller models are easier to debug, run much faster, are more likely to successfully converge to a final solution, and they can provide good initial estimates for the bigger models. A smart choice for small models in this context is to minimize the dimensions of integration required, which can be accomplished by focusing on a single multilevel survival process at a time. For example, the model shown in Figure 2 for the antisocial measures and just the hazard rate of child anger requires only a single dimension of integration. This model and the corresponding single hazard rate models for child positive and sad/fear could be used to get baseline hazard plots, preliminary estimates of dyad-level covariances and correlations, check for curvilinear regression effects, and assess normality assumptions on the latent variables. Mplus will compute and export estimates of the latent log hazards and their standard errors and these can be plotted against normal quantiles to look for possible violations of assumptions like clusters of points that might indicate latent subtypes, extreme outliers, or just highly non-normal distributions.
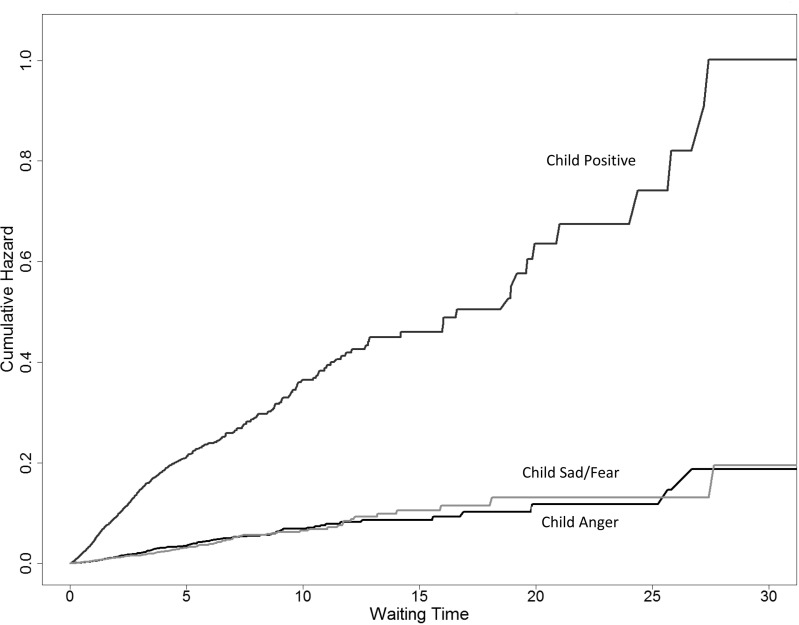
After fitting the Cox model, the baseline hazard parameters can be used to make plots of the hazard and the cumulative hazard across the waiting time. To our knowledge, baseline hazard functions for emotional displays of children interacting with their parents have never been published, so it is instructive to do so. The single hazard models for each of the three child transitions were used to obtain baseline hazard parameters and these in turn were used to compute the cumulative hazard curve, which is often easier to visualize than plotting the baseline hazard parameters against waiting time. The cumulative hazard curve gives the expected cumulative number of transitions in the interval from 0 to any particular value of time for a hypothetical average child, one who scores 0 on the latent log hazard variable. All three curves are shown in Figure 4. The waiting time axis has been limited to 30 s to show more detail in that part of the waiting time where the vast majority of transitions take place. Immediately obvious is the fact that positive transitions are accumulating much quicker than anger or sad/fear transitions, which are quite similar. By 5 s, about 0.2 positive transitions but only about 0.05 anger and sad/fear transitions have accumulated. The child positive cumulative hazard appears to slow down at about 5 s, but the anger and sad/fear cumulative hazards appear to steadily increase in a fairly linear fashion. A linear cumulative hazard curve corresponds to a constant hazard rate throughout the waiting time and this appears to describe fairly well anger and sad/fear transitions. The nonlinear cumulative hazard for positive transitions suggests that the hazard rate is not constant but drops after about 5 s. Perhaps children are willing to try a positive response to the parent’s negative behavior early in the episode, but as the parent’s negative behavior drags on, children become more reluctant to respond positively.
Figure 4.
Cumulative hazard curves for child hazard rates of anger, positive, and sad/fearful given parent negative.
Using the single hazard models to obtain initial estimates, the full model including all three child hazard rates converged in about 10 min on a multicore desktop computer, taking advantage of Mplus’ multicore capabilities to speed up the computations. Results are shown in Table I. The variances of the log hazards are all strongly significant (ps < .001), indicating ample individual differences to predict and to use as predictors of future outcomes. For the predictor, K child antisocial, the signs of the standardized effects are in the expected direction for anger (positive) and sad/fear (negative), but the standardized effect for anger at 0.188 is not significant (p = .098). The standardized effect for sad/fear, however, at −0.29 is significant (p = .012). Contrary to what was hypothesized, the standardized effect for the log hazard of positive at −.20 is also significant (p = .029). All the standardized effects are modest in magnitude, regardless of the level of statistical significance. The results indicate that antisocial children did not differ from normal children in their likelihood of an angry response to a negative parent but were less likely to show positive or sad/fear emotions. The raw effects of K child antisocial on the three hazards can also be interpreted in terms of hazard risk ratios, although space limitations preclude their presentation here (see Stoolmiller & Snyder, 2006, for more details of these kinds of interpretations).
Table I.
Parameter Estimates, Standard Errors, Critical Ratios, and p Values for MMSA Corresponding to Figure 4
| Effect | Estimate | SE | Estimated/SE | p |
|---|---|---|---|---|
| Standardized effects | ||||
| K child antisocial to | ||||
| Anger log hazard | 0.188 | 0.114 | 1.654 | 0.098 |
| Positive log hazard | −0.203 | 0.093 | −2.182 | 0.029 |
| Sad/fear log hazard | −0.292 | 0.116 | −2.526 | 0.012 |
| Third child antisocial on | ||||
| Anger log hazard | −0.151 | 0.150 | −1.008 | 0.314 |
| Positive log hazard | −0.230 | 0.120 | −1.916 | 0.055 |
| Sad/Fear log hazard | −0.135 | 0.156 | −0.869 | 0.385 |
| K child antisocial | 0.567 | 0.089 | 6.342 | 0.000 |
| Correlations | ||||
| Anger log hazard with | ||||
| Positive log hazard | −0.348 | 0.152 | −2.283 | 0.022 |
| Sad/fear log hazard | 0.287 | 0.188 | 1.529 | 0.126 |
| Positive log hazard with | ||||
| Sad/fear log hazard | −0.101 | 0.178 | −0.567 | 0.571 |
| Means or intercepts | ||||
| K child antisocial | 0.491 | 0.019 | 25.954 | 0.000 |
| Third child antisocial | 0.102 | 0.053 | 1.934 | 0.053 |
| Variances | ||||
| K child antisocial | 0.096 | 0.01 | 9.805 | 0.000 |
| Third child antisocial | 0.077 | 0.012 | 6.543 | 0.000 |
| Anger log hazard | 0.599 | 0.145 | 4.128 | 0.000 |
| Positive log hazard | 0.334 | 0.063 | 5.310 | 0.000 |
| Sad/fear log hazard | 0.703 | 0.159 | 4.434 | 0.000 |
For the prospective prediction to third-grade antisocial over and above K antisocial, only the log hazard of positive emotion was marginally significant with a small standardized effect of −0.23 (p = .055). Anger and sad/fear log hazards were also negatively related to third-grade antisocial but not strongly enough to be significant (p = .314 and p = .385, respectively). The fact, however, that all three log hazards were negatively related to third-grade antisocial suggests that longer durations of neutral child behavior would also significantly predict third-grade antisocial. We can test this by re-estimating the model and ignoring the terminating state. The results indicate that the standardized effect of K antisocial on child log neutral termination rates is small but significant at −0.23, (p = .011, i.e., lower termination rates or longer durations go with higher antisocial), and in turn, child log neutral termination rates are significantly predictive of third-grade antisocial net of K antisocial (standardized effect = −0.24, p = .027, i.e., lower termination rates or longer durations go with higher antisocial). Evidently, antisocial children are less likely to terminate NcRp states than normal children and hence spend more time in a neutral emotional state given that the parent is negative, and children who are less likely to terminate NcRp states and hence spend more time in a neutral emotional state given that the parent is negative increase in antisocial behavior from K to third grade.
Mplus will compute estimates of the latent log hazard scores for each child for each type of transition. These estimated log hazard scores can be plotted to check underlying model assumptions. In particular, the MMSA corresponding to Figure 4 is based on the assumption that all the latent variables are multinormally distributed, which implies a linear regression with constant residual variance between any two variables. If these assumptions are not at least roughly true, then model inferences may be inaccurate. Mplus does offer robust estimation methods to minimize the risk but perhaps, more critical, however, there may be important substantive implications if the multinormality assumptions are clearly violated. One possible source of theoretically interesting non-normality is the presence of latent classes of dyads, which could represent qualitatively distinct subpopulations with differing patterns of dyadic interaction (Berlin, Williams, & Parra, 2013). Clearly it would be important to know if the risk of child externalizing behavior was highly associated with latent class membership, and although it is beyond the scope of this work, Mplus has facilities for incorporating latent classes in to survival analyses.
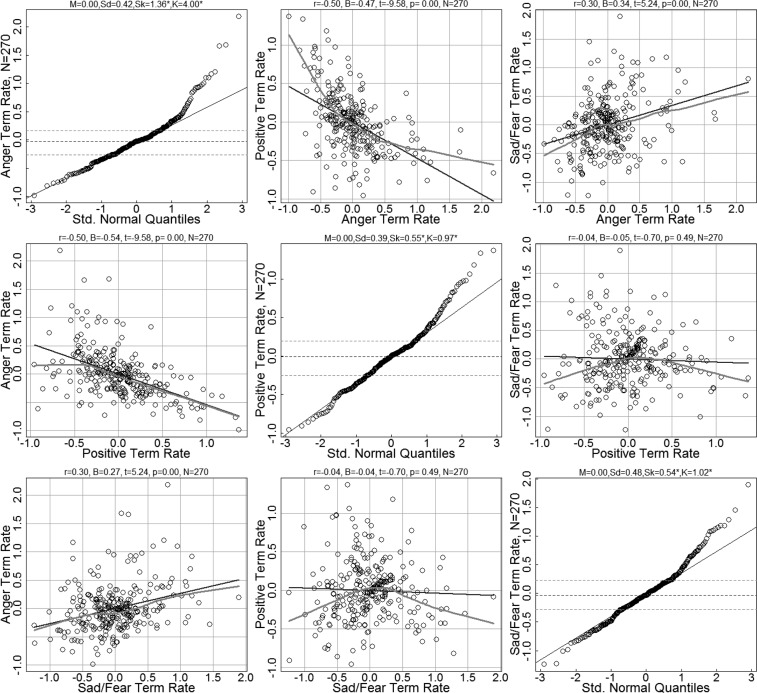
Figure 5 shows a scatter plot matrix with normal quantile plots on the main diagonal for the three estimated log hazard scores. The data points should fall roughly on the diagonal reference line in the normal quantile plots if the data are sampled from a normal distribution. The bottom, middle, and top dashed lines mark off the 25th, 50th, and 75th percentiles of the distribution of the observed data and as is apparent, the highest 20% or so of the data for each type of transition departs from the diagonal reference line, indicating positive skewness. Descriptive statistics are also printed in the top margin of the normal quantile plots, and the values for skewness confirm that all of the hazard distributions are positively skewed, although the anger distribution is the most extreme. The anger and sad/fear distributions also have several data points that are quite extreme, 4 or more standard deviations from the mean. Although we will not pursue it here, it might be a good idea to re-run the model and exclude several of these dyads to make sure they are not unduly influencing the results.
Figure 5.
Normal quantile plots (main diagonal) and scatter plots for model estimated latent log hazard rates. Lower, middle, and upper dashed lines in the normal quantile plots indicate 25th, 50th, and 75th quantiles, respectively, of the distributions. A normal distribution tends to track the diagonal solid reference line in the normal quantile plots. The black straight and gray curvy lines in the scatter plots are linear and nonparametric regression fits. The nonparametric regression is the lowess procedure. Descriptive statistics are printed in the top margins of the plots. For the normal quantile plots, the statistics are mean, standard deviation, skewness, and kurtosis, abbreviated M, Sd, Sk, and K, respectively. For the scatter plots, the statistics are correlation, regression weight, t value, p value, and bivariate sample size, abbreviated r, b, t, p, and N, respectively.
Discussion
For simplicity, our example application focuses only on hazard rates of child anger, positive, and sad/fear given parent negative, ignoring the hazard rates for parent positive and neutral. The substantive results provide mixed support for the hypotheses that compared with normal children, antisocial children have higher anger terminations rates, lower sad/fear termination rates, and the same positive termination rates. Of these three hypotheses, only the second was supported by the data; antisocial children had lower hazard rates of sad/fear emotions compared with normal children. Contrary to our predictions, antisocial children had about the same anger termination rates and significant lower positive termination rates. For prospective prediction, the only significant effect (p = .049) was that positive termination rates were negatively related to third-grade antisocial behavior, contrary to what was hypothesized. Sad/fear termination rates were negatively related to third-grade antisocial behavior, as hypothesized, but the effect was too small to be significant. Anger termination rates were also negatively related to third-grade antisocial, contrary to expectation, but too small to be significant.
The fact that all three child termination rates were negatively related to third-grade antisocial behavior suggested that what is most predictive of future antisocial behavior is long durations of neutral child behavior. In fact, when we re-estimated the model ignoring the different types of termination, the overall child neutral termination rate was significantly negatively related to third-grade antisocial behavior net of K antisocial. This indicates that children who spend long durations in neutral affect (when their parent is negative) tend to increase in antisocial behavior. It is not clear why the apparent absence of child affect would predict increases in antisocial behavior.
The novel part of our example application is the use of dyad-level log hazard rates as predictors of future child-level outcomes. MMSA are not new but most programs do not allow for subject-level log hazard rates to be embedded within a subject-level SEM and used as both outcomes and predictors at the same time. The current version of Mplus is capable of such modeling, and all the usual tools of SEM can be deployed to test hypotheses of interest. To keep the example application simple, we used a single predictor of hazard rates and a single outcome to be predicted by the hazard rates. It would be straightforward to add in more predictors or outcomes or to structure additional subject-level predictor or outcome variables as growth models, cross-lagged panel models, discrete time survival models, latent class models, latent factor models, etc.
The within-dyad survival part of the model can be extended in a number of interesting ways as well. At the most micro level, we could include predictors that can change during an episode or, alternatively, we could allow dyad-level predictors that are time-fixed to have time-varying effects during an episode. Both of these possibilities make the model a nonproportional hazards model. For example, besides just differences in rates for the three child transitions we studied, antisocial children may have a distinctly different baseline hazard functions as well and by allowing the child antisocial predictor to have time-varying effects, we could test this possibility (Muthén, Asparouhov, Boye, Hackshaw, & Naegeli, 2009). Stepping up a level, we could include predictors that vary during the session but are constant during an episode. For example, does the number of previous child anger terminations extend or shorten the current episode of NcRp? (e.g., Dagne & Snyder, 2009, 2011). The model could also be extended to include time-fixed but session-varying predictors. For example, if we obtained mood ratings from the participants just before each session, we could include these as predictors of session-level latent NcRp termination rates. The modeling possibilities are very diverse.
Limitations and Future Directions
Computing speed is a serious current limitation for MMSA. In our data, the parent can be in one of three states and the child can be in one of four states, so there are 12 possible dyadic states. In addition, if we want to distinguish hazard rates according to the end state, then there are 11 possible end states for the 12 possible start states or 132 hazard functions in all. Fortunately, some of these may be safe to ignore because they almost never happen, which is usually the case for the situation when both members of the dyad change simultaneously to new states. This eliminates 72 hazard functions but still leaves 60. Clearly, investigators will need to be selective because the computational burden increases exponentially with the number of hazard functions in the model due to the necessity of using numerical integration to estimate the models. Current desktop computing power makes including more than five or six hazard functions in a single model difficult. On the other hand, access to super computers is becoming more common now and this opens up possibilities for extending the models.
Observational designs that included planned missingness (Little, Jorgensen, Lang, & Moore, 2014) are badly needed to minimize costs associated with coding behavior. For example, an investigator could recruit a large and representative sample and then randomly select a subset for dyadic interaction tasks that will be coded. Very little is known about statistical power for MMSA under these types of circumstances. A related issue is the adequacy of large sample size assumptions at both the dyad-level and the within-dyad level. How many dyads are necessary for sampling distributions to approximate normality? Fortunately, many of the tools to address these issues are now available in Mplus, so the future outlook for MMSA is bright.
Supplementary Data
Supplementary data can be found at: http://www.jpepsy.oxfordjournals.org/
Funding
National Institute of Mental Health grant R01 57342.
Conflicts of interest: None declared.
Supplementary Material
References
- Achenbach T M, Edelbrock C. Manual for the child behavior checklist and revised child behavior profile. Burlington, VT: University of Vermont Department of Psychiatry; 1991. [Google Scholar]
- Allison P D. Event history analysis: Regression for longitudinal event data. In: Sullivan J L, Niemi G G, editors. Quantitative applications in the social sciences. Beverly Hills, CA: Sage; 1984. pp. 9–67. [Google Scholar]
- Berlin K S, Williams N A, Parra G R. An introduction to latent variable mixture modeling (part 1): Cross sectional latent class and latent profile analyses. Journal of Pediatric Psychology. 2013 doi: 10.1093/jpepsy/jst084. In press. [DOI] [PubMed] [Google Scholar]
- Dagne G A, Snyder J. Bayesian hierarchical duration model for repeated events: An application to behavioral observations. Journal of Applied Statistics. 2009;36:1267–1279. doi: 10.1080/02664760802587032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dagne G A, Snyder J. Relationship of maternal negative moods to child emotion regulation during family interaction. Development and Psychopathology. 2011;23:211–223. doi: 10.1017/S095457941000074X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duke D C, Geffken G R, Lewin A B, Williams L B, Storch E A, Silverstein J H. Glycemic Control in youth with type 1 diabetes: Family predictors and mediators. Journal of Pediatric Psychology. 2008;33:719–727. doi: 10.1093/jpepsy/jsn012. [DOI] [PubMed] [Google Scholar]
- Forgatch M S, Patterson G R. Parent management training – Oregon model: An intervention for antisocial behavior in children and adolescents. In: Weisz J R, Kazdin A E, editors. Evidence-based psychotherapies for children and adolescents. 2010. (2nd ed., pp. 159–178). New York, NY: Guilford. [Google Scholar]
- Goldstein H. Multilevel statistical models. Hoboken, NJ: Wiley; 2011. [Google Scholar]
- Granic I, Patterson G R. Toward a comprehensive model of antisocial development: A systems dynamic systems approach. Psychological Review. 2006;113:101–131. doi: 10.1037/0033-295X.113.1.101. [DOI] [PubMed] [Google Scholar]
- Little T D, Jorgensen T D, Lang K M, Moore W G. On the joys of missing data. Journal of Pediatric Psychology. 2014;39:151–162. doi: 10.1093/jpepsy/jst048. doi:10.1093/jpepsy/jst048. [DOI] [PubMed] [Google Scholar]
- Miller G E, Chen E. Harsh family climate in early life presages the emergence of a proinflammatory phenotype in adolescence. Psychological Science. 2010;21:848–856. doi: 10.1177/0956797610370161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthén B O, Asparouhov T, Boye M, Hackshaw M, Naegeli A. Applications of continuous-time survival in latent variable models for the analysis of oncology randomized clinical trial data using Mplus. Los Angeles, CA: Muthén & Muthén; 2009. [Google Scholar]
- Muthén L K, Muthén B O. Mplus user’s guide. 7th ed. Los Angeles, CA: Muthén & Muthén; 2013. [Google Scholar]
- Snyder J, Stoolmiller M, Wilson M, Yamamoto M. Child anger regulation, parental responses to children’s anger displays, and early child antisocial behavior. Social Development. 2003;12:335–360. [Google Scholar]
- Stoolmiller M, Snyder J. Modeling heterogeneity in social interaction processes: Using multilevel survival analysis. Psychological Methods. 2006;11:164–177. doi: 10.1037/1082-989X.11.2.164. [DOI] [PubMed] [Google Scholar]
- Therneau T M, Grambsch P M. Modeling survival data: Extending the Cox model. New York, NY: Springer; 2000. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.