Abstract
Statistical positioning, the localization of nucleosomes packed against a fixed barrier, is conjectured to explain the array of well-positioned nucleosomes at the 5′ end of genes, but the extent and precise implications of statistical positioning in vivo are unclear. We examine this hypothesis quantitatively and generalize the idea to include moving barriers as well as nucleosomes actively packed against a barrier. Early experiments noted a similarity between the nucleosome profile aligned and averaged across genes and that predicted by statistical positioning; however, we demonstrate that aligning random nucleosomes also generates the same profile, calling the previous interpretation into question. New rigorous results reformulate statistical positioning as predictions on the variance structure of nucleosome locations in individual genes. In particular, a quantity termed the variance gradient, describing the change in variance between adjacent nucleosomes, is tested against recent high-throughput nucleosome sequencing data. Constant variance gradients provide support for generalized statistical positioning in ∼50% of long genes. Genes that deviate from predictions have high nucleosome turnover and cell-to-cell gene expression variability. The observed variance gradient suggests an effective nucleosome size of 158 bp, instead of the commonly perceived 147 bp. Our analyses thus clarify the role of statistical positioning in vivo.
INTRODUCTION
Nucleosomes, consisting of 147 bp of DNA wrapping around histone octamers, constitute the repeating subunits of chromatin and modulate the accessibility of DNA. Nucleosome positioning in promoters and enhancers can critically regulate the activity of DNA-binding proteins and, consequently, transcription rates (1). The gene body and regulatory elements display distinct patterns of nucleosome positioning, but the forces that shape local chromatin structure are still largely unknown. Understanding the principles that guide nucleosome positioning thus remains an important problem in biology.
Recent studies highlighted the difficulty and complexity of this problem and demonstrated that no single mechanism alone can explain nucleosome positioning everywhere in the genome, suggesting that different mechanisms may play dominant roles at distinct genomic loci. For example, two salient features of chromatin observed to date are the nucleosome free regions (NFRs) upstream of transcription start sites (TSSs) and flanking arrays of well-positioned nucleosomes (2). On one hand, sequence-dependent physical properties of DNA are critical for establishing NFR; in particular, Poly(dA:dT) sequences are rigid and hinder nucleosome formation (3,4), while, to a lesser extent, certain periodic patterns with period 10 bp may facilitate wrapping around histones (5,6). On the other hand, ATP-dependent chromatin remodeling complexes can override sequence-specific biases and may be necessary for organizing nucleosome arrays, as demonstrated in vitro (7).
In addition to site-specific local factors, nucleosomes also interact with each other. To study the biophysical consequences of their interaction, several investigators have modeled nucleosomes as non-overlapping one-dimensional rods, known in statistical physics as Tonks gas (8), under the influence of a one-dimensional potential. Although the predicted nucleosome occupancy generally correlates with in vitro data obtained from high-throughput sequencing, predicting the in vivo nucleosome positioning (as opposed to occupancy) remains challenging (9–12). Adding inter-nucleosomal interactions can improve the agreement between theory and observation, although a consensus on the set of interactions has yet to emerge (13–16). For example, biophysical effects, such as electrostatic attractions and histone tail interactions, may influence nucleosome positioning, but these effects are currently difficult to characterize genome wide. Every model, however, should account for the steric hindrance interaction between adjacent nucleosomes—the topic of this article—because two nucleosomes cannot occupy the same genomic sequence.
The effect of steric exclusion is especially pronounced near barriers that limit nucleosome movement. In a classic theoretical paper (17), Kornberg and Stryer studied nucleosomes without binding preference, but confined to a finite or semi-infinite genomic region by barriers, e.g. those representing DNA-binding proteins. They predicted that arrays of well-positioned nucleosomes are caused by hard barriers and steric constraints that restrict the movement of densely packed nucleosomes, a phenomenon termed statistical positioning. Along this line, one interpretation of the nucleosome organization at the 5′ end of genes is that the NFR functions as a barrier, and the downstream nucleosomes are positioned through statistical positioning. High-throughput microarray and sequencing data have recently been used to either support or refute this hypothesis (7,18–21).
In support of the hypothesis, the gene length dependence of the nucleosome occupancy is similar to that predicted by statistical positioning (20). Furthermore, the nucleosome density aligned at TSS and averaged across genes exhibits an oscillating pattern with sharp peaks close to the TSS and decreasing amplitudes farther away (18). Möbius and Gerland (21) rigorously compared this pattern to the density predicted by statistical positioning and found a striking agreement, assuming that each nucleosome occupies 147 bp. Although this analysis is compelling, we demonstrate that the observed averaged density can be an artifact of effects other than statistical positioning.
In contrast, challenging statistical positioning, Zhang et al. (7) found that reconstituted nucleosomes incubated with whole-cell extract can form the arrays seen in vivo only if ATP is added, advocating a model where nucleosomes are actively packed toward a barrier at the 5′ end of genes. Although this packing model differs from statistical positioning in that the pressure of the Tonks gas is modeled to be high only at the 5′ end of genes, it is similar in that the array of positioned nucleosomes results from the combination of a barrier, steric constraints and high nucleosome density.
The role of statistical positioning thus needs to be resolved in light of these recent studies which provide seemingly conflicting views. One approach to probing the role of steric constraints is to analyze the fuzziness, i.e. the variance in position, of individual nucleosomes. Mavrich et al. (19) found that the average fuzziness increases downstream of the TSS, in agreement with the heuristics of statistical positioning. This paper extends that analysis by quantitatively comparing the fuzziness profiles of individual genes to the predictions of statistical positioning. We first generalize the concept of statistical positioning to quantify how a restriction on one nucleosome influences the surrounding nucleosomes through steric hindrance. The rate at which this influence diminishes with genomic distance is captured by a quantity we term the ‘variance gradient’, defined to be the rate of change in fuzziness between adjacent nucleosomes. We present analytic formulae describing the variance of nucleosome locations in the general cases of both moving and fixed barriers for finite and semi-infinite nucleosome arrays. Irrespective of the nature of the restriction, the generalized model of statistical positioning predicts a constant variance gradient for long genes, with the magnitude of the gradient set by the size of the gap between regions occupied by nucleosomes. This relation between the variance gradient and gap length generalizes to the case of nucleosomes packed against a barrier by constant forces, highlighting that the notions of statistical positioning and nucleosome packing can be combined into a single theory and, thus, partially resolving the competing view points.
We then test the variance-gradient predictions against the nucleosome architecture of gene bodies experimentally observed in Saccharomyces cerevisiae (22). Our calculation shows that the variance gradient in individual genes is much lower than that expected for nucleosomes occupying just 147 bp. The observed variance gradient instead indicates a steric exclusion length of 158 bp. One interpretation of this result is that three-dimensional steric constraints prevent or disfavor the unbound DNA close to a nucleosome from being wrapped by the neighboring nucleosomes, thereby extending the steric footprint of the nucleosome. Because the effective length of steric hindrance determines how a restriction imposed on one nucleosome, either by chromatin remodeling or DNA sequence preference, affects other nucleosomes in an array, this finding may help explain how local chromatin structure is established in vivo. Our work highlights the need for more rigorous quantitative models to parallel the development in experimental data generation and warns against the common practice of averaging data to represent chromatin structure.
MATERIALS AND METHODS
Statistical positioning predicts constant variance gradients for long genes
Kornberg and Stryer (17) argued that DNA-binding proteins can act as barriers and cause the appearance of nucleosomes well positioned across a population of cells. In its simplest form, statistical positioning refers to a model in which N nucleosomes are represented as finite segments of length d and placed at random in a region of length w, as shown in Figure 1A. The nucleosomes may be placed in any non-overlapping configuration within the prescribed region, and all allowed configurations are given equal probability.
Figure 1.
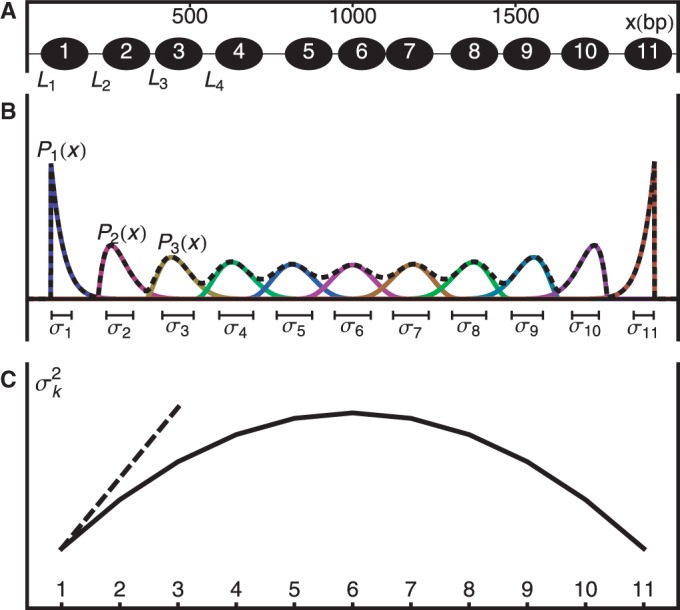
Hard barrier statistical positioning. (A) Example of a valid configuration. Nucleosomes are represented as non-overlapping intervals of width d constrained to lie between two infinite potential barriers. (B) The probability  of finding the kth nucleosome centered at x and the associated variance
of finding the kth nucleosome centered at x and the associated variance 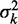 . Dashed black line is the mixture probability. (C) Solid line shows how
. Dashed black line is the mixture probability. (C) Solid line shows how 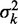 varies between two barriers. Dashed line indicates the asymptotic variance for the single barrier case, as the right barrier is moved to infinity while fixing the average nucleosome density constant.
varies between two barriers. Dashed line indicates the asymptotic variance for the single barrier case, as the right barrier is moved to infinity while fixing the average nucleosome density constant.
Interestingly, the probability of finding a nucleosome centered at position x is non-uniform and oscillates with decreasing amplitude and sharpness away from the barriers (Figure 1B). If nucleosomes can be clearly resolved and labeled (+1 at the barrier), this statement can be made quantitatively sharper by considering the marginal probability 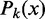 of finding the kth nucleosome centered at position x. To find
of finding the kth nucleosome centered at position x. To find 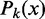 , note that the problem of finding distinct configurations is equivalent to partitioning the
, note that the problem of finding distinct configurations is equivalent to partitioning the 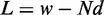 base pairs uncovered by nucleosomes into N + 1 gap regions of non-negative integer lengths
base pairs uncovered by nucleosomes into N + 1 gap regions of non-negative integer lengths 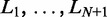 , where d is the effective nucleosome size. The distribution of the total gap length
, where d is the effective nucleosome size. The distribution of the total gap length 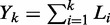 to the left of the kth nucleosome is then
to the left of the kth nucleosome is then
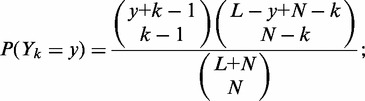 |
(1) |
see Supplementary Methods for details. Using this distribution to calculate the mean and variance of the dyad position 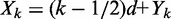 of the kth nucleosome gives
of the kth nucleosome gives
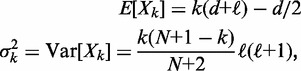 |
(2) |
where 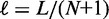 is the mean gap length (see Supplementary Methods for details). The variance expression simplifies further as the number of nucleosomes increases with the mean gap length
is the mean gap length (see Supplementary Methods for details). The variance expression simplifies further as the number of nucleosomes increases with the mean gap length 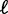 kept fixed:
kept fixed:
| (3) |
In this limit, statistical positioning predicts that the fuzziness 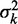 increases linearly with the nucleosome index k, with the slope depending only on the average gap length. We call this slope,
increases linearly with the nucleosome index k, with the slope depending only on the average gap length. We call this slope, 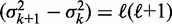 , the ‘variance gradient’.
, the ‘variance gradient’.
The length d is the minimal inter-nucleosome distance allowed by steric constraints, and it is related to the mean gap length 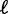 and the nucleosome density ρ through
and the nucleosome density ρ through 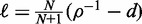 . Several hitherto-proposed models of nucleosome positioning assume this length d to be equal to the 147 bp wrapped in histones, in which case
. Several hitherto-proposed models of nucleosome positioning assume this length d to be equal to the 147 bp wrapped in histones, in which case 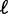 is the mean linker DNA length (9,10,11,21). However, stronger steric constraints, forcing adjacent nucleosomes to have non-zero linker DNA, would violate this assumption. In that case, the effective steric exclusion length d is > 147, and the effective gap size
is the mean linker DNA length (9,10,11,21). However, stronger steric constraints, forcing adjacent nucleosomes to have non-zero linker DNA, would violate this assumption. In that case, the effective steric exclusion length d is > 147, and the effective gap size 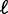 between nucleosomes is smaller; consequently, the observed variance gradient is lower than the case d = 147. Conversely, the gap length
between nucleosomes is smaller; consequently, the observed variance gradient is lower than the case d = 147. Conversely, the gap length 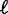 can be estimated from the observed variance gradient; and then, together with the observed inter-nucleosome distance, one can computationally infer the effective nucleosome size d, as described below.
can be estimated from the observed variance gradient; and then, together with the observed inter-nucleosome distance, one can computationally infer the effective nucleosome size d, as described below.
While the above analysis assumes a fixed number N of nucleosomes, N may fluctuate in biological systems. Such variations can be modeled using the grand canonical ensemble (GCE), which allows N to vary and weighs each valid configuration by 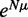 , where μ is the chemical potential. Note that this assumption does not affect the single barrier result, as the GCE is equivalent to the canonical ensemble in the thermodynamic limit, with
, where μ is the chemical potential. Note that this assumption does not affect the single barrier result, as the GCE is equivalent to the canonical ensemble in the thermodynamic limit, with 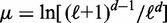 ; see Supplementary Methods for details. For a pair of barriers, multiple N values can give contributions of similar magnitude, resulting in the appearance of dephased nucleosomes, as shown in Supplementary Figure S1A and B (20). Such mixing occurs for only certain values of w, and the occurrence is attenuated with increasing μ. For example, for
; see Supplementary Methods for details. For a pair of barriers, multiple N values can give contributions of similar magnitude, resulting in the appearance of dephased nucleosomes, as shown in Supplementary Figure S1A and B (20). Such mixing occurs for only certain values of w, and the occurrence is attenuated with increasing μ. For example, for 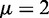 , one nucleosome count dominates (
, one nucleosome count dominates (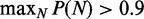 ) for 64% of interval length w in the range
) for 64% of interval length w in the range 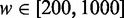 ; for
; for 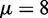 , however, this fraction is 93% of the range, and the nucleosome count does not fluctuate much (Supplementary Figure S1C). Supplementary Figure S1D and E shows that Equation (2) is still accurate in a broad range of interval length w for which one nucleosome count dominates the GCE. We shall subsequently demonstrate that the chemical potential in S. cerevisiae is actually very high in long genes, further justifying our simpler canonical ensemble approach.
, however, this fraction is 93% of the range, and the nucleosome count does not fluctuate much (Supplementary Figure S1C). Supplementary Figure S1D and E shows that Equation (2) is still accurate in a broad range of interval length w for which one nucleosome count dominates the GCE. We shall subsequently demonstrate that the chemical potential in S. cerevisiae is actually very high in long genes, further justifying our simpler canonical ensemble approach.
Actively packed nucleosomes
A key assumption of statistical positioning is bidirectionality; non-overlapping nucleosomes move freely in both directions. However, reconstituted nucleosomes incubated with whole-cell extract require ATP to form ordered arrays; and, within the arrays, the nucleosomes preferentially accumulate at the 5′ end of genes, suggesting that nucleosomes are unidirectionally packed against a barrier at the 5′ end (7). Furthermore, maps of nucleosome movement reveal that ancestral nucleosomes accumulate at the 5′ end of genes, and quantitative modeling suggests transcription-related retrograde nucleosome movement may be the cause of the directionality (23).
To model the effect of actively packed nucleosomes, consider a generalization of the single flexible barrier model, where the nucleosomes are pushed against the barrier by position-independent forces fk. In this model, each valid configuration has a relative weight 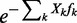 , where Xk is the distance between the kth nucleosome and the barrier. The forces modulate the nucleosome spacing and variance gradient, the effects that can be described in terms of the pressure pk on the kth nucleosome exerted by the
, where Xk is the distance between the kth nucleosome and the barrier. The forces modulate the nucleosome spacing and variance gradient, the effects that can be described in terms of the pressure pk on the kth nucleosome exerted by the  nucleosomes and the packing force fk. It can be seen that pk satisfies the recursion relation
nucleosomes and the packing force fk. It can be seen that pk satisfies the recursion relation
| (4) |
and that
| (5) |
from which it follows that
| (6) |
see Supplementary Methods for details. Equation (4) indicates that the pressure change is the greatest near regions where the packing force is the greatest and that in the absence of any packing force, the pressure is constant across nucleosomes. In turn, Equation (5) suggests that higher pressure on the kth nucleosome leads to a smaller gap relative to the 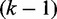 th nucleosome and that in the absence of any packing force, the expected gap distance between adjacent nucleosomes is constant. Finally, combined with these observations, Equation (6) implies that the variance gradient of nucleosome positioning is small near regions with high packing force and increases as the packing force decreases, eventually becoming constant as the packing force vanishes. Small forces acting on all nucleosomes along a gene will give a slowly varying pressure and a nucleosome distribution that is similar to that of statistical positioning near the 5′ end. Large forces applied only on the 5′ most nucleosomes will, on the other hand, give rapidly increasing variance gradient and nucleosome spacing away from the 5′ end. Thus, while statistical positioning and active nucleosome packing differ in the source of the nucleosome pressure, they share the common feature that the variance gradient is a reflection of the gap between the regions sterically occupied by nucleosomes.
th nucleosome and that in the absence of any packing force, the expected gap distance between adjacent nucleosomes is constant. Finally, combined with these observations, Equation (6) implies that the variance gradient of nucleosome positioning is small near regions with high packing force and increases as the packing force decreases, eventually becoming constant as the packing force vanishes. Small forces acting on all nucleosomes along a gene will give a slowly varying pressure and a nucleosome distribution that is similar to that of statistical positioning near the 5′ end. Large forces applied only on the 5′ most nucleosomes will, on the other hand, give rapidly increasing variance gradient and nucleosome spacing away from the 5′ end. Thus, while statistical positioning and active nucleosome packing differ in the source of the nucleosome pressure, they share the common feature that the variance gradient is a reflection of the gap between the regions sterically occupied by nucleosomes.
Statistical positioning with moving barriers
In its original form, statistical positioning only considers fixed barriers. However, a number of factors can affect the nucleosome distribution at gene boundaries and make barrier nucleosomes neither free nor fixed: (i) ATP-dependent remodeling may move the first nucleosome in a gene, (ii) Poly(dA:dT) sequences common in the NFR increase the free energy of nucleosome formation and (iii) the nucleosome promoter architecture may vary in an ensemble of cells. To model such ‘soft’ barriers, we consider N + 2 nucleosomes, where the first and last nucleosomes act as moving barriers. We assume that the barrier nucleosomes, indexed as the 0th and (N + 1) th, are positioned according to a joint probability distribution 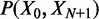 and that the in-between nucleosomes are distributed through statistical positioning conditioned on X0 and
and that the in-between nucleosomes are distributed through statistical positioning conditioned on X0 and 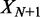 . The variance of the kth nucleosome,
. The variance of the kth nucleosome,  , is then:
, is then:
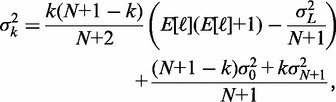 |
(7) |
where 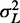 is the variance of the total gap length (see Supplementary Methods for details). Note that
is the variance of the total gap length (see Supplementary Methods for details). Note that 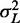 simplifies to
simplifies to 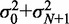 when the barrier nucleosomes move independently. The first term in the above expression has the same parabolic k dependence as in the fixed barrier case, with
when the barrier nucleosomes move independently. The first term in the above expression has the same parabolic k dependence as in the fixed barrier case, with 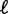 replaced by its expected value and offset by a small contribution. The second term is a linear interpolation of the fuzziness of the barrier nucleosomes.
replaced by its expected value and offset by a small contribution. The second term is a linear interpolation of the fuzziness of the barrier nucleosomes.
The variance structure downstream of a single soft barrier is found in the large N limit of Equation (7), with mean gap length and 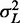 kept fixed:
kept fixed:
| (8) |
A partial restriction on the first nucleosome thus increases the overall fuzziness of the downstream nucleosomes, but leaves the variance gradient unchanged. Furthermore, statistical positioning, in essence, is the statement that a restricted nucleosome also restricts its neighbors and, consequently, that the positions of tightly packed nucleosomes are correlated. Equation (8) thus describes how the organizing effect of statistical positioning degrades with genomic distance. In fact, the constancy of the variance gradient in Equation (8) generalizes to models with more complex nearest-neighbor interactions (see Supplementary Methods for a simple derivation).
Quantifying variance gradient using paired-end sequenced data
Nucleosome position and fuzziness were calculated from paired-end MNase-seq data in S. cerevisiae (GEO accession number GSM756482) (22). Nucleosomes were identified by scanning the strand-specific read density profiles for pairs of offset peaks on opposite strands. Peaks were located using the statistic
where 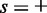 and
and 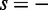 correspond to the positive and negative strands, respectively, and
correspond to the positive and negative strands, respectively, and 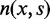 is the number of s-strand reads starting (for
is the number of s-strand reads starting (for 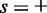 ) or ending (for
) or ending (for 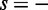 ) in a window of width 50 bp centered at x. A greedy search was performed by (i) finding the first peak at
) in a window of width 50 bp centered at x. A greedy search was performed by (i) finding the first peak at 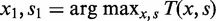 , (ii) finding an offset peak on the opposite strand at
, (ii) finding an offset peak on the opposite strand at 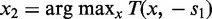 , where
, where 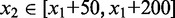 or
or 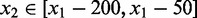 depending on s1 and (iii) iteratively repeating the first two steps to find new pairs of peaks under the constraint that new peaks are at least 100 bp away from previous peaks and have
depending on s1 and (iii) iteratively repeating the first two steps to find new pairs of peaks under the constraint that new peaks are at least 100 bp away from previous peaks and have 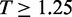 . Next we identified the region of support (ROS) around each peak to be the interval between two flanking troughs at
. Next we identified the region of support (ROS) around each peak to be the interval between two flanking troughs at 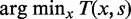 where
where 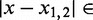
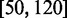 . We associated to each nucleosome all paired-end reads starting and ending in the corresponding paired ROS.
. We associated to each nucleosome all paired-end reads starting and ending in the corresponding paired ROS.
MNase digestion is an inherently stochastic process that cuts unprotected DNA fragments randomly, albeit with some sequence bias. Sequencing provides direct information about the locations of flanking cleavage sites, denoted as forward F and reverse R random variables; but, importantly, the dyad location X itself is not observable. The locations F and R are related to X via offset random variables 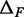 and
and 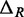 as
as 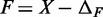 and
and 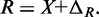 Paired-end sequencing provides an empirical joint distribution of F and R, from which one can compute the covariance
Paired-end sequencing provides an empirical joint distribution of F and R, from which one can compute the covariance 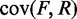 . If we assume that the distance between a cleavage site and the dyad of a nucleosome is independent of the genomic location of the nucleosome, then
. If we assume that the distance between a cleavage site and the dyad of a nucleosome is independent of the genomic location of the nucleosome, then 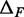 and
and 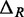 are uncorrelated with X. If we further assume that MNase digestion on one side of the nucleosome does not influence the digestion on the other side, then
are uncorrelated with X. If we further assume that MNase digestion on one side of the nucleosome does not influence the digestion on the other side, then 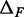 are
are 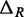 are also uncorrelated. Under these assumptions, we obtain
are also uncorrelated. Under these assumptions, we obtain 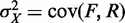 . The fuzziness of each nucleosome was estimated using this formula and the set of paired-end reads spanning between the corresponding ROSs. We used the MNase-seq data without size selection (22), but restricted our analysis to reads of length 120–200 bp to minimize the contribution from DNA-binding proteins other than histones. Nucleosomes with less than a quarter of the median number of reads were discarded.
. The fuzziness of each nucleosome was estimated using this formula and the set of paired-end reads spanning between the corresponding ROSs. We used the MNase-seq data without size selection (22), but restricted our analysis to reads of length 120–200 bp to minimize the contribution from DNA-binding proteins other than histones. Nucleosomes with less than a quarter of the median number of reads were discarded.
For accurate estimates of nucleosome fuzziness, it is important that the sequenced reads are assigned to correct nucleosomes. Assigning reads to the closest peak is reasonable for well-separated nucleosomes, but it will lead to an underestimation of 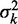 for fuzzy nucleosomes, as illustrated in Supplementary Figure S2A. [This effect may explain why the fuzziness approaches a fixed value far from the TSS in (19).] We thus estimate the range
for fuzzy nucleosomes, as illustrated in Supplementary Figure S2A. [This effect may explain why the fuzziness approaches a fixed value far from the TSS in (19).] We thus estimate the range 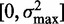 of fuzziness where each read can be accurately assigned to a single nucleosome, and denote nucleosomes with greater fuzziness as delocalized. To estimate
of fuzziness where each read can be accurately assigned to a single nucleosome, and denote nucleosomes with greater fuzziness as delocalized. To estimate 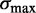 , note that a uniform random variable defined on
, note that a uniform random variable defined on 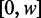 has variance
has variance 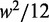 . Taking w to be the mean inter-nucleosome distance 167 bp, a completely delocalized nucleosome uniformly distributed in the interval will have variance ∼2324 bp2. A conservative estimate (see Supplementary Figure S2B) is to set
. Taking w to be the mean inter-nucleosome distance 167 bp, a completely delocalized nucleosome uniformly distributed in the interval will have variance ∼2324 bp2. A conservative estimate (see Supplementary Figure S2B) is to set 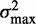 to be roughly half this number, i.e.
to be roughly half this number, i.e.  , which was sufficiently large to consider up to eight nucleosomes away from barriers.
, which was sufficiently large to consider up to eight nucleosomes away from barriers.
Nucleosomes were assigned to genes using TSS and transcription termination site (TTS) annotations based on RNA-seq (24), allowing dyads to be at most 50 bp outside the annotated gene bodies. Only genes classified as ‘verified’ in the Saccharomyces Genome Database (SGD, R61) were used. To prevent ambiguous reads from complicating our analysis, genes overlapping ‘dubious’ genes or regions classified as long terminal repeats, LTR-retrotransposon, repeat regions, transposable element gene or rRNA as defined by SGD were removed; genes overlapping simple repeats longer than 500 bp as defined in the UCSC Genome Browser (sacCer2) also were removed. The variance gradient a was calculated at the 5′ and 3′ ends of each gene separately by performing least-squares fitting of the truncated linear function 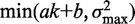 to the observed values of the variance
to the observed values of the variance 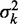 of the first and last eight nucleosomes in the gene body. The R2 values are the fraction of variance explained by these fits.
of the first and last eight nucleosomes in the gene body. The R2 values are the fraction of variance explained by these fits.
Nomenclature and notation
By +1 nucleosome, we mean the first nucleosome after TSS. By −1 nucleosome, we mean the last nucleosome just before the TTS. For positive k, we count the kth nucleosome downstream from +1; for negative k, we count the kth nucleosome upstream from 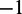 . We use
. We use 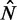 to denote the number of nucleosomes observed from sequencing data.
to denote the number of nucleosomes observed from sequencing data.
RESULTS
Averaged read density is not suitable for validating statistical positioning
A commonly used method for analyzing nucleosome mapping data is to align and average the density profiles across many genes at either the TSS (18,19) or the +1 nucleosome (21), yielding an oscillating pattern with decreasing amplitudes, as shown in Figure 2A. Ostensibly, this alignment agrees well with the nucleosome distribution predicted by the single barrier statistical positioning with exclusion length d = 147 bp and mean gap length 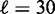 bp, corresponding to a variance gradient of 930 bp2/nucl and in line with the previous study (21).
bp, corresponding to a variance gradient of 930 bp2/nucl and in line with the previous study (21).
Figure 2.
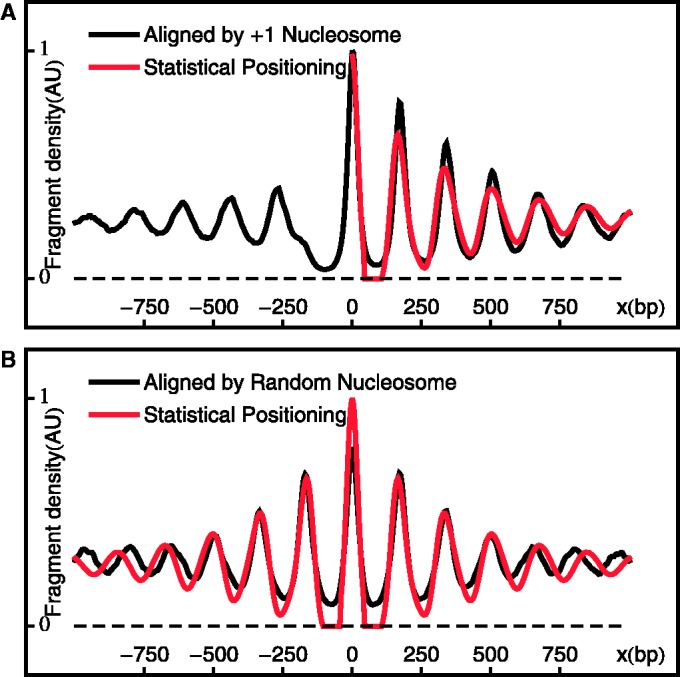
Aligned and averaged density of paired-end read centers. (A) Black curve shows the alignment across genes at the +1 nucleosomes. Red curve shows the single-barrier statistical positioning prediction with 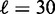 bp and
bp and 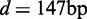 , smoothed with a Gaussian filter. (B) Black curve shows the average density aligned at randomly chosen downstream (
, smoothed with a Gaussian filter. (B) Black curve shows the average density aligned at randomly chosen downstream (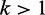 ) nucleosomes. Red curve shows the same statistical positioning model as in (A).
) nucleosomes. Red curve shows the same statistical positioning model as in (A).
However, we shall subsequently show that this estimate of variance gradient is an order of magnitude larger than that actually found in individual genes, indicating that this averaging approach is not suitable for studying statistical positioning. Moreover, averaging the nucleosome profile across different genes blurs the distinction between gene-to-gene variations in nucleosome location with respect to TSS (or +1 nucleosome) and nucleosome fuzziness within a single gene, making it difficult to interpret the peaks in the resulting profile. That is, the increasing width of the peaks in Figure 2A can result from either (i) increasingly fuzzy nucleosomes centered at the same relative positions across genes or (ii) sharply positioned nucleosomes that differ in relative positions across genes. Whereas the former is a signature of statistical positioning, the latter could result from a multitude of reasons, such as differences among genes in the remodeling of nucleosome arrays relative to TSS.
Even if all nucleosomes are equally well positioned, across-gene variations in nucleosome spacing can indeed induce decaying oscillation in averaged nucleosome occupancy, with the variance gradient equal to the variance of spacing across genes. Because the observed variance in spacing across genes is 770 bp2, comparable to the variance gradient of 930 bp2 in Figure 2A, most of the decay in oscillations in Figure 2A can be accounted for by the variations in spacing. To further test this fact, we aligned and averaged the nucleosome profile at random nucleosomes sampled from gene bodies, thereby averaging over trends in nucleosome fuzziness away from the randomly chosen nucleosomes. Figure 2B shows that the resulting profile is almost identical to that found by aligning at the +1 nucleosomes and artificially fits the predicted probability distribution of statistical positioning. This analysis shows that the variation in inter-nucleosome distance among genes by itself, without increasing fuzziness in nucleosome positioning away from barriers, is sufficient to generate the damped oscillation pattern that has been previously attributed to statistical positioning.
Low variance gradient is observed at the 5′ end of long genes
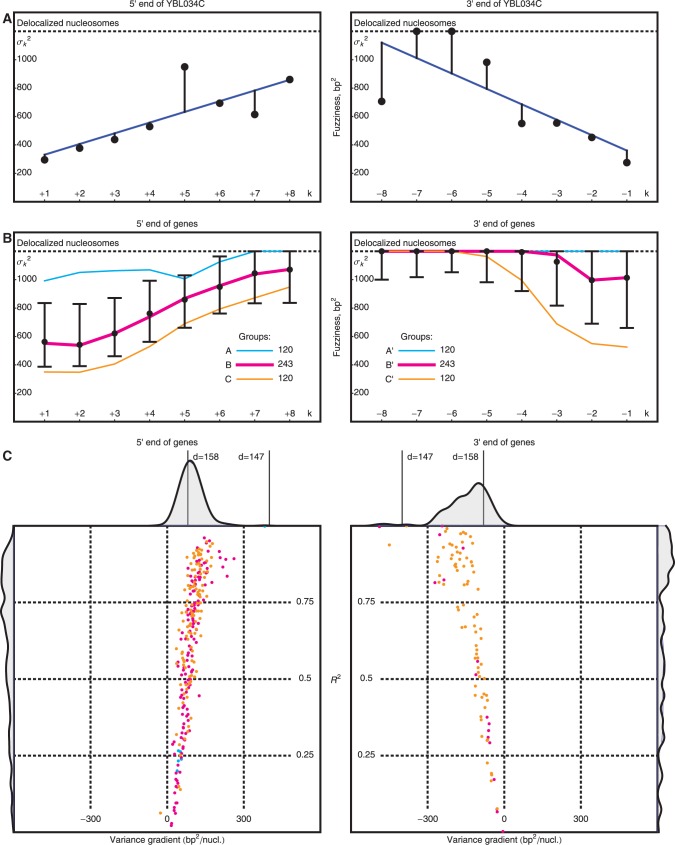
To avoid the aforementioned problems associated with averaged read densities, we measured the fuzziness of each nucleosome and analyzed whether its variation along individual genes agrees with Equation (8) (Figure 3A; ‘Materials and Methods’ section). For long genes with 16 or more nucleosomes, the median fuzziness 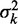 stays constant between the +1 and +2 nucleosomes and increases linearly between the +2 and +8 nucleosomes with a variance gradient of 88 bp2/nucl (Figure 3B). This rate is close to Mavrich et al.’s earlier calculation showing that
stays constant between the +1 and +2 nucleosomes and increases linearly between the +2 and +8 nucleosomes with a variance gradient of 88 bp2/nucl (Figure 3B). This rate is close to Mavrich et al.’s earlier calculation showing that 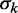 increases from 20 to 29 bp between the +1 and +5 nucleosomes, corresponding to a variance gradient of 110 bp2/nucl (19). The observed linear increase in
increases from 20 to 29 bp between the +1 and +5 nucleosomes, corresponding to a variance gradient of 110 bp2/nucl (19). The observed linear increase in 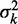 fits Equation (8) well for
fits Equation (8) well for 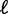 ∼ 9 bp, indicating that single-barrier statistical positioning may explain the array of nucleosomes downstream of the 5′ end of long genes. Because the median distance between well-positioned nucleosomes is 167 bp, this interpretation implies an effective steric exclusion length d = 158 bp. Interestingly, nucleosomes can be packed this tightly only with the large chemical potential
∼ 9 bp, indicating that single-barrier statistical positioning may explain the array of nucleosomes downstream of the 5′ end of long genes. Because the median distance between well-positioned nucleosomes is 167 bp, this interpretation implies an effective steric exclusion length d = 158 bp. Interestingly, nucleosomes can be packed this tightly only with the large chemical potential 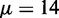 (Supplementary Figure S4).
(Supplementary Figure S4).
Figure 3.
Variation of nucleosome fuzziness along long genes. (A) Nucleosome fuzziness (black dots) for the first and last eight nucleosomes in the gene YBL034C. Nucleosomes that are poorly resolved (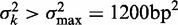 ; ‘Materials and Methods’ section) are designated as delocalized. Variance gradient a for each gene is found by fitting the truncated linear function
; ‘Materials and Methods’ section) are designated as delocalized. Variance gradient a for each gene is found by fitting the truncated linear function 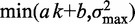 to the observed values of
to the observed values of 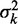 using least squares (blue line). (B) Distribution of fuzziness (
using least squares (blue line). (B) Distribution of fuzziness (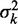 ) for 483 genes with 16 or more nucleosomes. Genes are grouped based on the quartiles of the projection of eight-dimensional fuzziness profiles onto the first principal component at the 5′ and 3′ ends, separately (Supplementary Figure S3). The groups A and A′ correspond to the first quartile, B and B′ to the two central quartiles and C and C′ to the last quartile. Colored lines show the median
) for 483 genes with 16 or more nucleosomes. Genes are grouped based on the quartiles of the projection of eight-dimensional fuzziness profiles onto the first principal component at the 5′ and 3′ ends, separately (Supplementary Figure S3). The groups A and A′ correspond to the first quartile, B and B′ to the two central quartiles and C and C′ to the last quartile. Colored lines show the median 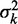 of the genes in the respective groups. Black vertical bars show the first and third quartiles of fuzziness at each nucleosome. (C) Scatter plot of variance gradient [slope in (A)] and R2 for fitting statistical positioning at the 5′ (left) and 3′ (right) ends of genes, colored by the groups in (B). Only genes with well-positioned +1 or –1 nucleosomes (
of the genes in the respective groups. Black vertical bars show the first and third quartiles of fuzziness at each nucleosome. (C) Scatter plot of variance gradient [slope in (A)] and R2 for fitting statistical positioning at the 5′ (left) and 3′ (right) ends of genes, colored by the groups in (B). Only genes with well-positioned +1 or –1 nucleosomes (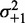 or
or  ) are used in the respective plots. Horizontal and vertical plots show the marginal distributions of variance gradient and R2, respectively. Vertical lines in the top marginal plots show the theoretical variance gradient predictions from single-barrier statistical positioning for different values of the steric exclusion length d, using an average inter-nucleosome distance of 167 bp.
) are used in the respective plots. Horizontal and vertical plots show the marginal distributions of variance gradient and R2, respectively. Vertical lines in the top marginal plots show the theoretical variance gradient predictions from single-barrier statistical positioning for different values of the steric exclusion length d, using an average inter-nucleosome distance of 167 bp.
To check that the observed low variance gradient is not an artifact of averaging, we calculated the variance gradients in individual genes using linear regression truncated at 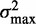 , the upper boundary of the range of sensitivity within which we can confidently assign each read to a single nucleosome (‘Materials and Methods’ section). The distribution of variance gradients across genes with 16 or more nucleosomes is shifted distinctly toward positive values compared to the null distribution of permuted nucleosomes (Supplementary Figure S5; Kolmogorov–Smirnov test
, the upper boundary of the range of sensitivity within which we can confidently assign each read to a single nucleosome (‘Materials and Methods’ section). The distribution of variance gradients across genes with 16 or more nucleosomes is shifted distinctly toward positive values compared to the null distribution of permuted nucleosomes (Supplementary Figure S5; Kolmogorov–Smirnov test 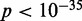 ). For each gene, we also calculated the goodness-of-fit R2 value of the regression and compared the observed distributions of the variance gradient and R2 with those obtained by permuting the nucleosomes; 46% of genes have significantly high R2 (at 5% significance after 100 permutations). Although the median R2 is high (0.48, compared to 0.08 after permutation), many genes have a relatively poor fit, low variance gradient and poorly positioned +1 nucleosome (Supplementary Figure S5). Because statistical positioning can give arrays of positioned nucleosomes only if the +1 nucleosome is well positioned, we restricted our attention to genes where
). For each gene, we also calculated the goodness-of-fit R2 value of the regression and compared the observed distributions of the variance gradient and R2 with those obtained by permuting the nucleosomes; 46% of genes have significantly high R2 (at 5% significance after 100 permutations). Although the median R2 is high (0.48, compared to 0.08 after permutation), many genes have a relatively poor fit, low variance gradient and poorly positioned +1 nucleosome (Supplementary Figure S5). Because statistical positioning can give arrays of positioned nucleosomes only if the +1 nucleosome is well positioned, we restricted our attention to genes where 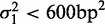 (roughly 50% of long genes). This set of genes has a roughly linear fuzziness profile (median
(roughly 50% of long genes). This set of genes has a roughly linear fuzziness profile (median 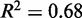 ) and a median variance gradient of 93 bp2/nucl, consistent with statistical positioning with
) and a median variance gradient of 93 bp2/nucl, consistent with statistical positioning with 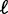 ∼ 9 bp (Figure 3C); these values were insensitive to the
∼ 9 bp (Figure 3C); these values were insensitive to the 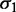 cutoff. In sharp contrast, fitting a statistical positioning model to the averaged read density gave
cutoff. In sharp contrast, fitting a statistical positioning model to the averaged read density gave 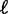 = 30 bp and thus a variance gradient of 930 bp2/nucl, almost one order of magnitude larger than the observed value. This discrepancy further demonstrates the difficulty of studying trends in nucleosome fuzziness using an averaged read density profile.
= 30 bp and thus a variance gradient of 930 bp2/nucl, almost one order of magnitude larger than the observed value. This discrepancy further demonstrates the difficulty of studying trends in nucleosome fuzziness using an averaged read density profile.
Nucleosomes at the 3′ end of genes are overall fuzzier than those at the 5′ end, with 49% of the −1 nucleosomes classified as delocalized (‘Materials and Methods’ section), compared to 18% at the 5′ end. Nevertheless, in genes where the last nucleosome is well positioned, i.e. 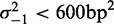 , the quality of fit is high (median
, the quality of fit is high (median 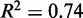 ), and the variance gradient is typically greater than that at the 5′ end (median gradient = 127 bp2/nucl), as is the average inter-nucleosome distance, suggesting that statistical positioning may play a role also at the 3′ end of this subset of genes, albeit at a lower nucleosome density. It should be noted, however, that the median distance between the −1 nucleosome and the TSS of the nearest downstream gene is only 446 bp for genes with
), and the variance gradient is typically greater than that at the 5′ end (median gradient = 127 bp2/nucl), as is the average inter-nucleosome distance, suggesting that statistical positioning may play a role also at the 3′ end of this subset of genes, albeit at a lower nucleosome density. It should be noted, however, that the median distance between the −1 nucleosome and the TSS of the nearest downstream gene is only 446 bp for genes with 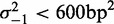 , compared to 1200 bp for all genes (see Supplementary Figure S6). This observation suggests that it may actually be the next TSS, and not the TTS, that acts as a barrier at the 3′ end, in line with (21).
, compared to 1200 bp for all genes (see Supplementary Figure S6). This observation suggests that it may actually be the next TSS, and not the TTS, that acts as a barrier at the 3′ end, in line with (21).
Delocalized nucleosomes are associated with high nucleosome turnover and gene expression variability
To characterize the variation in nucleosome organization across genes, we performed principal component analysis of the fuzziness profiles at the 5′ and 3′ ends separately. The fuzziness profiles projected along the first principal component were then used to group genes: in Figure 3B, Groups A and C contain the genes with fuzziness in the upper and lower quartiles, respectively, while Group B contains the remaining genes (Supplementary Figure S3). Group A is characterized by chaotic nucleosome organization with no clear trend in fuzziness (median 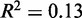 , median variance gradient = 14 bp2/nucl) and has 39% of nucleosomes classified as delocalized. Groups B and C have arrays of well-positioned nucleosomes, differing in the fuzziness of the +1 nucleosome, but having similar variance gradients (median of 72 bp2/nucl and 96 bp2/nucl, respectively).
, median variance gradient = 14 bp2/nucl) and has 39% of nucleosomes classified as delocalized. Groups B and C have arrays of well-positioned nucleosomes, differing in the fuzziness of the +1 nucleosome, but having similar variance gradients (median of 72 bp2/nucl and 96 bp2/nucl, respectively).
Statistical positioning requires the nucleosomes to be in thermal equilibrium. Earlier studies have found two contrasting promoter architectures: promoters with a distinct nucleosome depletion next to the TSS are associated with well-positioned nucleosomes, low histone turnover rate and low transcriptional plasticity, whereas promoters lacking such depletion have a more chaotic chromatin architecture and transcription signature (25). Similarly, to investigate how these activities are associated with statistical positioning, we ranked all genes from 0.0 to 1.0 according to the turnover rate (26) of nucleosomes in the interval [−100 bp, +1 kb] relative to the TSS and calculated the median rank of the genes in each group. Consistent with the fact that Group A exhibits significant deviation from statistical positioning, Figure 4A shows that this group is enriched for high histone turnover rate (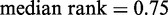 ,
, 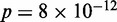 , see Supplementary Methods), suggesting that persistent perturbations at TSS may disrupt nucleosome arrays. Statistical positioning also assumes homogeneous conditions across a cell population, and the strong deviation of Group A genes from the predicted nucleosome fuzziness profile indicated that those genes may be subjected to high cell-to-cell transcriptional variability. Comparing our groups of genes to published measures of variability (27), we found that Group A is significantly enriched for genes with high intrinsic stochastic noise (
, see Supplementary Methods), suggesting that persistent perturbations at TSS may disrupt nucleosome arrays. Statistical positioning also assumes homogeneous conditions across a cell population, and the strong deviation of Group A genes from the predicted nucleosome fuzziness profile indicated that those genes may be subjected to high cell-to-cell transcriptional variability. Comparing our groups of genes to published measures of variability (27), we found that Group A is significantly enriched for genes with high intrinsic stochastic noise ( ,
, 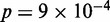 ) and responsiveness (
) and responsiveness (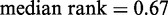 ,
, 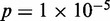 ), as defined in (27) (Figure 4B). Conversely, Group C, having the most well-positioned nucleosomes, was depleted of genes with high stochastic noise (
), as defined in (27) (Figure 4B). Conversely, Group C, having the most well-positioned nucleosomes, was depleted of genes with high stochastic noise (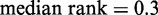 ,
, 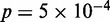 ). TATA-containing genes are known to be associated with stress response (28) and were highly enriched in Group A relative to Groups B and C (25% in A versus 7% in B and 3% in C,
). TATA-containing genes are known to be associated with stress response (28) and were highly enriched in Group A relative to Groups B and C (25% in A versus 7% in B and 3% in C, 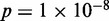 ), in agreement with earlier observations for aligned reads (29).
), in agreement with earlier observations for aligned reads (29).
Figure 4.
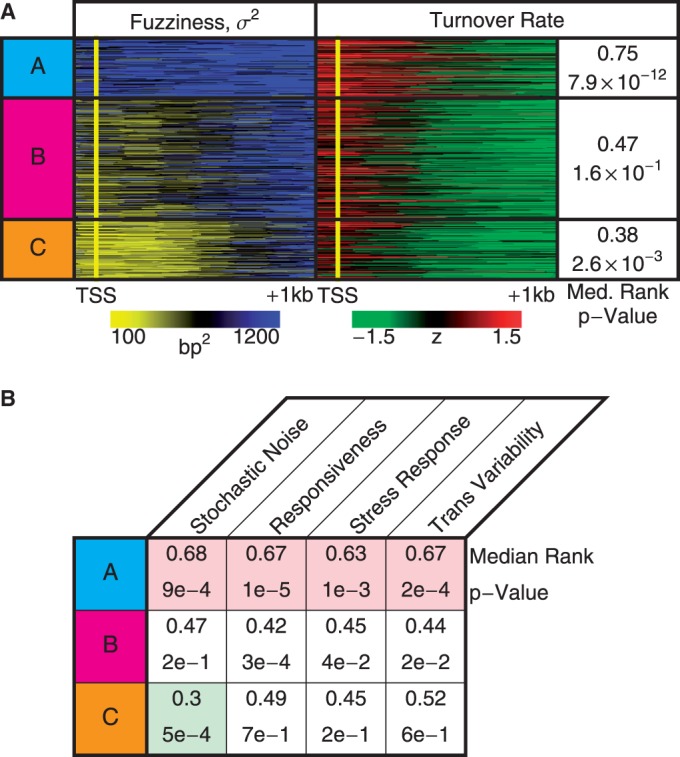
Functions associated with nucleosome profiles. (A) Nucleosome fuzziness and histone turnover rate (26) in the [−100 bp, +1 kb] region relative to TSS for the gene groups defined in Figure 3. Genes were ranked between 0 and 1 by their turnover rate in the [−100 bp, +1 kb] region; median rank of each group and its P-value were calculated (‘Materials and Methods’ section). The Group A genes that deviate from statistical positioning have a significantly high median turnover rate. (B) Enrichment analysis for gene variability [intrinsic stochastic noise, responsiveness, stress response and trans-variability from (27)]. The Group A genes again show a significantly high level of variability.
Fuzziness profile is highly asymmetric between the 5′ and 3′ ends of short genes
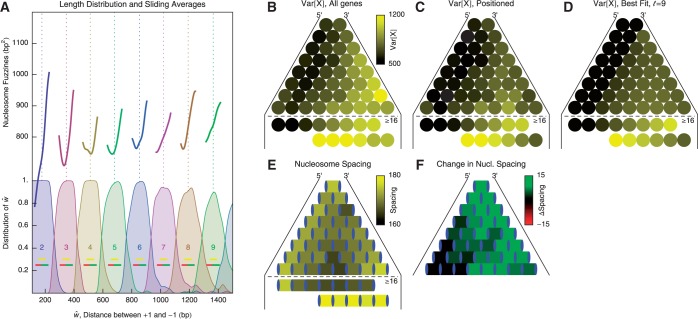
Statistical positioning predicts the variance gradient to be lower for a pair of barriers compared to a single barrier (Figure 1C). It also predicts that as the barrier separation length w increases, the gap length 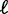 and fuzziness should both increase until an additional nucleosome is added, whereupon both quantities drop and the cycle restarts (20).
and fuzziness should both increase until an additional nucleosome is added, whereupon both quantities drop and the cycle restarts (20).
To test these predictions, we use the observed distance 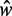 between the +1 and −1 nucleosomes as a proxy for w and the number
between the +1 and −1 nucleosomes as a proxy for w and the number 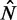 of identified nucleosome peaks as an estimate of N. For
of identified nucleosome peaks as an estimate of N. For 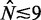 , the
, the 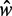 axis is partitioned into alternating stable regions, dominated by a single
axis is partitioned into alternating stable regions, dominated by a single 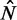 value, and transitional regions, where
value, and transitional regions, where 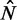 may vary (Figure 5A). In the language of statistical physics, for each
may vary (Figure 5A). In the language of statistical physics, for each 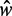 , we consider a GCE of nucleosomes, where the total number of nucleosomes can fluctuate. The stable regions, centered at
, we consider a GCE of nucleosomes, where the total number of nucleosomes can fluctuate. The stable regions, centered at 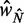 , are spaced 170 bp apart. Figure 5A shows that the median fuzziness mostly increases with increasing
, are spaced 170 bp apart. Figure 5A shows that the median fuzziness mostly increases with increasing 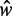 within each stable region, as predicted by statistical positioning. For
within each stable region, as predicted by statistical positioning. For 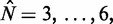 however, the fuzziness increases slightly with decreasing
however, the fuzziness increases slightly with decreasing 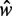 for
for 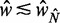 , suggesting that a nucleosome may get evicted as
, suggesting that a nucleosome may get evicted as 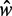 decreases and thus that the GCE may be important for these short genes. Taken together, these results show that the confining effect of double barriers can be detected in the nucleosome organization of short genes, in line with (20). To make a quantitative assessment of whether this effect agrees with statistical positioning, we next examine if the observed dependence of fuzziness on
decreases and thus that the GCE may be important for these short genes. Taken together, these results show that the confining effect of double barriers can be detected in the nucleosome organization of short genes, in line with (20). To make a quantitative assessment of whether this effect agrees with statistical positioning, we next examine if the observed dependence of fuzziness on 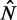 and k is consistent with the prediction in Equation (7). Because Equation (7) assumes fixed N, we focus on genes with
and k is consistent with the prediction in Equation (7). Because Equation (7) assumes fixed N, we focus on genes with 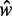 in the stable regions, i.e.
in the stable regions, i.e. 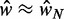 . For these genes, the median fuzziness profile is highly asymmetric between the 5′ and 3′ ends and has the following three main features: (i) a linear increase from the 5′ end across most of the gene body with variance gradient 76 bp2/nucl, (ii) a rapid decrease down to 1000 bp2 at the 3′ end for sufficiently long genes and (iii) constant values between the +1 and +2 nucleosomes (see Figure 5B and Supplementary Figure S7A and B). It needs to be checked whether these features are consistent with statistical positioning.
. For these genes, the median fuzziness profile is highly asymmetric between the 5′ and 3′ ends and has the following three main features: (i) a linear increase from the 5′ end across most of the gene body with variance gradient 76 bp2/nucl, (ii) a rapid decrease down to 1000 bp2 at the 3′ end for sufficiently long genes and (iii) constant values between the +1 and +2 nucleosomes (see Figure 5B and Supplementary Figure S7A and B). It needs to be checked whether these features are consistent with statistical positioning.
Figure 5.
Nucleosome distribution in short genes, organized by the total nucleosome count. (A) Top: Sliding average (Gaussian weighted, 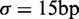 ) of fuzziness as a function of
) of fuzziness as a function of 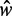 , the distance between the +1 and –1 nucleosomes and the number of identified nucleosomes
, the distance between the +1 and –1 nucleosomes and the number of identified nucleosomes 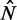 . Bottom: Distribution of
. Bottom: Distribution of 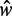 for different values of
for different values of 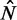 . Dashed vertical lines indicate
. Dashed vertical lines indicate 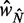 . Horizontal yellow bars indicate genes used in (B–E) and red and green bars indicate genes used in (F). (B) Median nucleosome fuzziness of the kth nucleosome (disks, left to right) out of N total (rows), calculated from genes with
. Horizontal yellow bars indicate genes used in (B–E) and red and green bars indicate genes used in (F). (B) Median nucleosome fuzziness of the kth nucleosome (disks, left to right) out of N total (rows), calculated from genes with 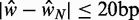 . Last two lines indicate the values for the first eight and last six nucleosomes in long genes with
. Last two lines indicate the values for the first eight and last six nucleosomes in long genes with 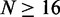 . (C) Same as (B), restricted to genes with well-positioned first and last nucleosomes (
. (C) Same as (B), restricted to genes with well-positioned first and last nucleosomes (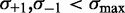 ). (D) Best fit of the model in Equation (7) to the values in (C), giving parameters
). (D) Best fit of the model in Equation (7) to the values in (C), giving parameters 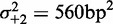 ,
, 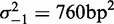 and
and 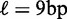 . (E) Mean nucleosome spacing (colored boxes) for the set of genes used in (B). Blue ovals represent nucleosomes. (F) Difference in mean nucleosome spacing (colored boxes) between genes slightly longer (
. (E) Mean nucleosome spacing (colored boxes) for the set of genes used in (B). Blue ovals represent nucleosomes. (F) Difference in mean nucleosome spacing (colored boxes) between genes slightly longer (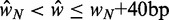 ) than
) than 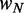 relative to genes slightly shorter (
relative to genes slightly shorter (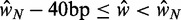 ).
).
Statistical positioning predicts that nucleosomes positioned by a pair of sharp barriers should have a symmetric fuzziness profile. Restricting the +1 nucleosome (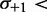
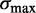 ) suppresses the linearly increasing part, while restricting the
) suppresses the linearly increasing part, while restricting the  1 nucleosome (
1 nucleosome (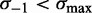 ) makes the 3′ drop in fuzziness steeper (see Figure 5C and Supplementary Figure S7C), consistent with statistical positioning. However, the fuzziness continues to increase linearly from the 5′ end into the gene body for a much greater distance than predicted by statistical positioning. The rapid decrease in median fuzziness at the 3′ end is present mostly for long genes (
) makes the 3′ drop in fuzziness steeper (see Figure 5C and Supplementary Figure S7C), consistent with statistical positioning. However, the fuzziness continues to increase linearly from the 5′ end into the gene body for a much greater distance than predicted by statistical positioning. The rapid decrease in median fuzziness at the 3′ end is present mostly for long genes ( ) where the linear increase exceeds 1000 bp2; in shorter genes, the characteristic profile is truncated in the linear stage (
) where the linear increase exceeds 1000 bp2; in shorter genes, the characteristic profile is truncated in the linear stage (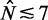 ) or is followed by a plateau at 1000 bp2. This asymmetric pattern and the extensive linearity of increasing variance at the 5′ end thus deviate from the parabolic variance structure predicted by double-barrier statistical positioning.
) or is followed by a plateau at 1000 bp2. This asymmetric pattern and the extensive linearity of increasing variance at the 5′ end thus deviate from the parabolic variance structure predicted by double-barrier statistical positioning.
More precisely, Figure 5D shows the best fit of Equation (7) to the median fuzziness of short (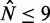 ) genes in Figure 5C with well-positioned +1 and −1 nucleosomes, assuming that
) genes in Figure 5C with well-positioned +1 and −1 nucleosomes, assuming that 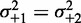 and that the term containing
and that the term containing 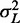 is negligible; the latter assumption is natural for long genes, where the term is inversely suppressed, and it can also apply to short genes if the movement of the first nucleosome causes a back reaction on the last nucleosome. While the agreement with data is decent (
is negligible; the latter assumption is natural for long genes, where the term is inversely suppressed, and it can also apply to short genes if the movement of the first nucleosome causes a back reaction on the last nucleosome. While the agreement with data is decent (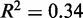 ) and the fitted gap length
) and the fitted gap length  consistent with the long gene results, this model severely under-estimates the fuzziness profile in the central regions of medium-long genes
consistent with the long gene results, this model severely under-estimates the fuzziness profile in the central regions of medium-long genes 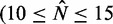 ) (cf. Supplementary Figure S7C versus Supplementary Figure S7E). Including longer genes in the fit gives
) (cf. Supplementary Figure S7C versus Supplementary Figure S7E). Including longer genes in the fit gives 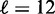 and thus alleviates the fuzziness suppression in the middle of gene body, but it still fails to recapitulate the steady linear increase in fuzziness extending along a much greater distance than predicted by statistical positioning. The linear increase observed for a wide range of
and thus alleviates the fuzziness suppression in the middle of gene body, but it still fails to recapitulate the steady linear increase in fuzziness extending along a much greater distance than predicted by statistical positioning. The linear increase observed for a wide range of 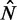 instead suggests that the nucleosomes are packed against the 5′ barrier and that the effect of a second barrier, located either at the TTS or further downstream, is limited because of low 3′ nucleosome pressure.
instead suggests that the nucleosomes are packed against the 5′ barrier and that the effect of a second barrier, located either at the TTS or further downstream, is limited because of low 3′ nucleosome pressure.
Contrary to the even nucleosome spacing predicted by statistical positioning, the nucleosome spacing has been observed to be suppressed at the 5′ end of genes (7). In genes with length 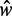 in the sable region, we find that nucleosomes are relatively evenly distributed in short genes except for a slight decrease in spacing in the middle of gene body (Figure 5E). For longer genes (
in the sable region, we find that nucleosomes are relatively evenly distributed in short genes except for a slight decrease in spacing in the middle of gene body (Figure 5E). For longer genes (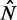 ≳ 10), however, the spacing is contracted away from the 5′ end and then expanded toward the 3′ end (Supplementary Figure S7D), significantly deviating from the prediction of statistical positioning. If this spacing asymmetry results from packing of nucleosomes toward the 5′ end, the resulting pressure variations could also explain the observed differences in variance gradient at the 5′ and 3′ ends of genes.
≳ 10), however, the spacing is contracted away from the 5′ end and then expanded toward the 3′ end (Supplementary Figure S7D), significantly deviating from the prediction of statistical positioning. If this spacing asymmetry results from packing of nucleosomes toward the 5′ end, the resulting pressure variations could also explain the observed differences in variance gradient at the 5′ and 3′ ends of genes.
Finally, the +1 and +2 nucleosomes behave differently from other nucleosomes; they have similar fuzziness, and the spacing between them is larger than that found for downstream nucleosomes (see Supplementary Figure S7D). Comparing the nucleosome spacing between two groups of genes, those with length 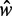 either slightly above or below the characteristic length
either slightly above or below the characteristic length 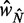 (Figure 5F), we find that the spacing between the +1 and +2 nucleosomes increases only slightly and that most additional space is distributed further downstream. This finding suggests that the +1 and +2 nucleosomes are relatively fixed and that those two nucleosomes are not likely to be positioned by statistical positioning.
(Figure 5F), we find that the spacing between the +1 and +2 nucleosomes increases only slightly and that most additional space is distributed further downstream. This finding suggests that the +1 and +2 nucleosomes are relatively fixed and that those two nucleosomes are not likely to be positioned by statistical positioning.
DISCUSSION
Although the initial theoretical (17) and experimental (30) studies of nucleosome positioning in the vicinity of barriers are more than two decades old, recent experimental progress, based on both high throughput sequencing and alternative experimental techniques (31), has sparked a renewed interest in the role of steric constraints in nucleosome positioning.
This article rigorously examines the theory of statistical positioning and presents a strikingly simple, yet robust, prediction: given that the position of one nucleosome is restricted, the variance in the position of surrounding nucleosomes increases at a constant rate away from the restricted nucleosome. The variance gradient—the rate of this increase—is entirely determined by the average size of the gap between the regions sterically occupied by nucleosomes. While the original formulation of statistical positioning models the restriction as a sharp repulsive barrier, our generalized result is also valid for a partial restriction, may it be due to sequence preference or chromatin remodeling, as long as the adjacent nucleosomes can move freely.
To test this generalized model, we calculated the empirical value of the variance gradient and R2 in individual genes in S. cerevisiae. About 50% of long genes exhibited constant variance gradient at the 5′ end, with a median value of ∼100 bp2/nucl. In contrast, statistical positioning based on each nucleosome occupying 147 bp at the observed density of one nucleosome per 167 bp would yield a variance gradient of 420 bp2/nucl. One interpretation of the observed low variance gradient is that nucleosomes effectively occupy around 158 bp and impose steric constraints longer than the 147 bp that are directly bound by histones. This extension of steric exclusion can easily arise from simple geometric considerations of how nucleosomal DNA wraps 1.6 times around a histone octamer, such that two nucleosomes may collide well before they bind adjacent base pairs. Furthermore, just like beads on a necklace can make it semi-rigid, small inter-nucleosomal separations curtail the allowed three-dimensional chromatin configurations, inducing a free energy cost for small separations and widening the region effectively occupied by a nucleosome. Interestingly, most models in the literature describe nucleosomes as non-overlapping finite intervals distributed along the genome according to a free energy potential (9–11). While the methods used for determining the potential differ, the region occupied by the nucleosome is commonly set to 147 bp, potentially underestimating the effect of steric constraints.
Nucleosome breathing, or transient unwrapping of nucleosomal DNA, also affects the effective size of nucleosomes. Cross-species variations in the aligned read density can be explained by letting the average length of unwrapped DNA depend on the species-specific nucleosome density, as previously demonstrated (16). It was found that the free energy potential associated with unwrapping spans 167 bp, in line with our conclusion that the region of steric constraints extends beyond 147 bp. However, it is difficult to infer the dynamics governing nucleosome positioning from the aligned and averaged sequencing read density; if the inter-nucleosomal distance varies across genes while the individual nucleosomes are well positioned, the averaged profile will appear fuzzy, yielding a fictitious profile mimicking the effects of statistical positioning, as demonstrated by aligning random nucleosomes. The fact that the variance gradient observed in individual genes is one order of magnitude lower than that seen in the averaged read density illustrates how the averaging procedure can lead to incorrect conclusions and demonstrates the importance of testing models of nucleosome positioning in individual genes.
While the steady variance gradient in the 5′ end is consistent with statistical positioning, the pattern of variance gradient in short genes, overall fuzziness and nucleosome spacing in the 3′ end suggest that the full gene body is not described by statistical positioning in its original form. An alternative interpretation of these findings is that ATP-dependent remodeling push nucleosomes toward the 5′ end and cause arrays of well-positioned nucleosomes (7). While differing from statistical positioning in its original form, even in this scenario, the arrays of well-positioned nucleosomes result from high nucleosome density, steric constraints and barriers. One reflection of this similarity is that the relation among steric constraints, nucleosome spacing and the variance gradient for packed nucleosomes in the case of a single barrier, as described by Equations (4–6), is the same as in statistical positioning. Therefore, our interpretation that the low and constant variance gradient reflects strong steric constraints is unchanged even when packing forces are present. The relatively even variance gradient and nucleosome spacing from the +2 through +8 nucleosomes near the 5′ end of long genes indicate that the ‘nucleosome pressure’ does not decrease abruptly in this range. The 5′/3′ asymmetry in nucleosome spacing is negligible for short genes, but becomes more pronounced with increasing gene length. This observation suggests a small packing force acting on all nucleosomes; the 5′/3′ asymmetry induced by such a force grows with the number of nucleosomes, creating wider nucleosome spacing and higher variance gradient in the 3′ end of long genes.
While arrays of well-positioned nucleosomes are ubiquitous at the 5′ end of genes, the 3′ end has a much higher fraction of delocalized nucleosomes. In short genes, where the effect of a second barrier at the TTS is predicted to be most pronounced and suppress the overall variance gradient to a parabola, the observed median fuzziness actually increases steadily toward the 3′ end. This disagreement indicates that most short genes do not have a sharp barrier at the TTS. In long genes, for which the ordering influence of the distant 5′ barrier is presumably smaller at the 3′ end, the median fuzziness drops toward the 3′ end, suggesting either a partial restriction at the TTS or a barrier further downstream. The latter hypothesis is supported by the correlation between the fuzziness of the last nucleosome and the distance to the closest downstream TSS (Supplementary Figure S6), in line with (21).
The +1 and +2 nucleosomes have very similar fuzziness, and perturbations in gene length leaves the spacing between them fixed, suggesting packing of the +2 nucleosome. However, the large spacing between these two nucleosomes seems to contradict this interpretation. Further studies would be needed to understand how these special nucleosomes are positioned.
Finally, although the simplified model of freely moving nucleosomes may be too crude to account for the full nucleosome landscape, steric restriction will be an important part of any description of nucleosome positioning; fixing the location of one nucleosome will certainly affect the possible configurations of its neighbors. In finding the balance between statistical positioning and other factors, such as histone binding preferences or higher order chromatin structure, this article shows that the effect of the former is characterized by the variance gradient 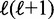 , where
, where 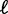 is the mean gap distance between sterically constrained regions. Measuring the variance gradient will thus give important clues about nucleosome dynamics, as demonstrated in S. cerevisiae.
is the mean gap distance between sterically constrained regions. Measuring the variance gradient will thus give important clues about nucleosome dynamics, as demonstrated in S. cerevisiae.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
NSF CAREER Award [1144866]; NIH [R01CA163336]. Funding for open access charge: NSF CAREER Award [1144866].
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Abhinav Nellore, Aaron Diaz and Courtney Onodera for helpful discussion.
REFERENCES
- 1.Radman-Livaja M, Rando OJ. Nucleosome positioning: how is it established, and why does it matter? Dev. Biol. 2010;339:258–266. doi: 10.1016/j.ydbio.2009.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rando OJ, Chang HY. Genome-wide views of chromatin structure. Annu. Rev. Biochem. 2009;78:245–271. doi: 10.1146/annurev.biochem.78.071107.134639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Iyer V, Struhl K. Poly(dA:dT), a ubiquitous promoter element that stimulates transcription via its intrinsic DNA structure. EMBO J. 1995;14:2570–2579. doi: 10.1002/j.1460-2075.1995.tb07255.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Anderson JD, Widom J. Poly(dA-dT) promoter elements increase the equilibrium accessibility of nucleosomal DNA target sites. Mol. Cell. Biol. 2001;21:3830–3839. doi: 10.1128/MCB.21.11.3830-3839.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Satchwell SC, Drew HR, Travers AA. Sequence periodicities in chicken nucleosome core DNA. J. Mol. Biol. 1986;191:659–675. doi: 10.1016/0022-2836(86)90452-3. [DOI] [PubMed] [Google Scholar]
- 6.Ioshikhes I, Bolshoy A, Derenshteyn K, Borodovsky M, Trifonov EN. Nucleosome DNA sequence pattern revealed by multiple alignment of experimentally mapped sequences. J. Mol. Biol. 1996;262:129–139. doi: 10.1006/jmbi.1996.0503. [DOI] [PubMed] [Google Scholar]
- 7.Zhang Z, Wippo CJ, Wal M, Ward E, Korber P, Pugh BF. A packing mechanism for nucleosome organization reconstituted across a eukaryotic genome. Science. 2011;332:977–980. doi: 10.1126/science.1200508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tonks L. The complete equation of state of one, two and three-dimensional gases of hard elastic spheres. Phys. Rev. 1936;50:955. [Google Scholar]
- 9.Segal E, Fondufe-Mittendorf Y, Chen L, Thastrom A, Field Y, Moore IK, Wang JP, Widom J. A genomic code for nucleosome positioning. Nature. 2006;442:772–778. doi: 10.1038/nature04979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Field Y, Kaplan N, Fondufe-Mittendorf Y, Moore IK, Sharon E, Lubling Y, Widom J, Segal E. Distinct modes of regulation by chromatin encoded through nucleosome positioning signals. PLoS Comput. Biol. 2008;4:e1000216. doi: 10.1371/journal.pcbi.1000216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Locke G, Tolkunov D, Moqtaderi Z, Struhl K, Morozov AV. High-throughput sequencing reveals a simple model of nucleosome energetics. Proc. Natl Acad. Sci. U.S.A. 2010;107:20998–21003. doi: 10.1073/pnas.1003838107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang Y, Moqtaderi Z, Rattner BP, Euskirchen G, Snyder M, Kadonaga JT, Liu XS, Struhl K. Evidence against a genomic code for nucleosome positioning Reply to [ldquo] Nucleosome sequence preferences influence in vivo nucleosome organization [rdquo] Nat. Struct. Mol.Biol. 2010;17:920–923. doi: 10.1038/nsmb0810-920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lubliner S, Segal E. Modeling interactions between adjacent nucleosomes improves genome-wide predictions of nucleosome occupancy. Bioinformatics. 2009;25:i348–i355. doi: 10.1093/bioinformatics/btp216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chereji RV, Tolkunov D, Locke G, Morozov AV. Statistical mechanics of nucleosome ordering by chromatin-structure-induced two-body interactions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;83(5 Pt 1):050903. doi: 10.1103/PhysRevE.83.050903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chereji RV, Morozov AV. Statistical mechanics of nucleosomes constrained by higher-order chromatin structure. J. Stat. Phys. 2011;144:379–404. doi: 10.1007/s10955-011-0214-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Möbius W, Osberg B, Tsankov AM, Rando OJ, Gerland U. Toward a unified physical model of nucleosome patterns flanking transcription start sites. Proc. Natl Acad. Sci. U.S.A. 2013;110:5719–5724. doi: 10.1073/pnas.1214048110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kornberg RD, Stryer L. Statistical distributions of nucleosomes: nonrandom locations by a stochastic mechanism. Nucleic Acids Res. 1988;16:6677–6690. doi: 10.1093/nar/16.14.6677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yuan GC, Liu YJ, Dion MF, Slack MD, Wu LF, Altschuler SJ, Rando OJ. Genome-scale identification of nucleosome positions in S. cerevisiae. Science. 2005;309:626–630. doi: 10.1126/science.1112178. [DOI] [PubMed] [Google Scholar]
- 19.Mavrich TN, Ioshikhes IP, Venters BJ, Jiang C, Tomsho LP, Qi J, Schuster SC, Albert I, Pugh BF. A barrier nucleosome model for statistical positioning of nucleosomes throughout the yeast genome. Genome Res. 2008;18:1073–1083. doi: 10.1101/gr.078261.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chevereau G, Palmeira L, Thermes C, Arneodo A, Vaillant C. Thermodynamics of intragenic nucleosome ordering. Phys. Rev. Lett. 2009;103:188103. doi: 10.1103/PhysRevLett.103.188103. [DOI] [PubMed] [Google Scholar]
- 21.Möbius W, Gerland U. Quantitative test of the barrier nucleosome model for statistical positioning of nucleosomes up- and downstream of transcription start sites. PLoS Comput. Biol. 2010;6 doi: 10.1371/journal.pcbi.1000891. e1000891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Krassovsky K, Henikoff JG, Henikoff S. Tripartite organization of centromeric chromatin in budding yeast. Proc. Natl Acad. Sci. U.S.A. 2012;109:243–248. doi: 10.1073/pnas.1118898109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Radman-Livaja M, Verzijlbergen KF, Weiner A, van Welsem T, Friedman N, Rando OJ, van Leeuwen F. Patterns and mechanisms of ancestral histone protein inheritance in budding yeast. PLoS Biol. 2011;9:e1001075. doi: 10.1371/journal.pbio.1001075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nagalakshmi U, Wang Z, Waern K, Shou C, Raha D, Gerstein M, Snyder M. The transcriptional landscape of the yeast genome defined by RNA sequencing. Science. 2008;320:1344–1349. doi: 10.1126/science.1158441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tirosh I, Barkai N. Two strategies for gene regulation by promoter nucleosomes. Genome Res. 2008;18:1084–1091. doi: 10.1101/gr.076059.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dion MF, Kaplan T, Kim M, Buratowski S, Friedman N, Rando OJ. Dynamics of replication-independent histone turnover in budding yeast. Science. 2007;315:1405–1408. doi: 10.1126/science.1134053. [DOI] [PubMed] [Google Scholar]
- 27.Choi JK, Kim YJ. Intrinsic variability of gene expression encoded in nucleosome positioning sequences. Nat. Genet. 2009;41:498–503. doi: 10.1038/ng.319. [DOI] [PubMed] [Google Scholar]
- 28.Basehoar AD, Zanton SJ, Pugh BF. Identification and distinct regulation of yeast TATA box-containing genes. Cell. 2004;116:699–709. doi: 10.1016/s0092-8674(04)00205-3. [DOI] [PubMed] [Google Scholar]
- 29.Ioshikhes IP, Albert I, Zanton SJ, Pugh BF. Nucleosome positions predicted through comparative genomics. Nat. Genet. 2006;38:1210–1215. doi: 10.1038/ng1878. [DOI] [PubMed] [Google Scholar]
- 30.Fedor MJ, Lue NF, Kornberg RD. Statistical positioning of nucleosomes by specific protein-binding to an upstream activating sequence in yeast. J. Mol. Biol. 1988;204:109–127. doi: 10.1016/0022-2836(88)90603-1. [DOI] [PubMed] [Google Scholar]
- 31.Milani P, Chevereau G, Vaillant C, Audit B, Haftek-Terreau Z, Marilley M, Bouvet P, Argoul F, Arneodo A. Nucleosome positioning by genomic excluding-energy barriers. Proc. Natl Acad. Sci. U.S.A. 2009;106:22257–22262. doi: 10.1073/pnas.0909511106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.