An implicit embedding of the space of Niggli-reduced cells in a higher-dimensional space to facilitate calculation of distances between cells is described. This distance metric is used to create a program, BGAOL, for Bravais lattice determination. Results from BGAOL are compared with results from other metric based Bravais lattice determination algorithms. This embedding depends on understanding the boundary polytopes of the Niggli-reduced cone N in the six-dimensional space G 6.
Keywords: Niggli reduction, Bravais lattice determination, computer programs
Abstract
Niggli reduction can be viewed as a series of operations in a six-dimensional space derived from the metric tensor. An implicit embedding of the space of Niggli-reduced cells in a higher-dimensional space to facilitate calculation of distances between cells is described. This distance metric is used to create a program, BGAOL, for Bravais lattice determination. Results from BGAOL are compared with results from other metric based Bravais lattice determination algorithms. This embedding depends on understanding the boundary polytopes of the Niggli-reduced cone N in the six-dimensional space G 6. This article describes an investigation of the boundary polytopes of the Niggli-reduced cone N in the six-dimensional space G 6 by algebraic analysis and organized random probing of regions near one-, two-, three-, four-, five-, six-, seven- and eightfold boundary polytope intersections. The discussion of valid boundary polytopes is limited to those avoiding the mathematically interesting but crystallographically impossible cases of zero-length cell edges. Combinations of boundary polytopes without a valid intersection in the closure of the Niggli cone or with an intersection that would force a cell edge to zero or without neighboring probe points are eliminated. In all, 216 boundary polytopes are found. There are 15 five-dimensional boundary polytopes of the full G 6 Niggli cone N.
1. Introduction
In a quantitative science, usable metrics should be defined. In the study of crystal lattices, only a few metrics have been proposed for describing the distance between two lattices (i.e. unit cells). The V7 metric (Andrews et al., 1980 ▶) is quite nonlinear and has known issues in many cases. The metric of Oishi-Tomiyasu (2012 ▶) is nonlinear and changes algorithm in some regions. This study and the work of Macíček & Yordanov (1992 ▶) use a metric based on the differences in metric tensors. This metric is nonlinear outside the Niggli cone. Here we propose a process for obtaining a linear measure from the differences of metric tensors by remaining inside the Niggli cone.
BGAOL (Bravais general analysis of lattices) is a Bravais lattice identification program based on the  analysis of Niggli reduction described below. Niggli reduction defines a complex space that has not previously been fully analyzed. Several authors have published interesting commentaries on the properties of this complex space (Hosoya, 2000 ▶; Oishi-Tomiyasu, 2012 ▶; Gruber, 1997 ▶). These studies use the space
analysis of Niggli reduction described below. Niggli reduction defines a complex space that has not previously been fully analyzed. Several authors have published interesting commentaries on the properties of this complex space (Hosoya, 2000 ▶; Oishi-Tomiyasu, 2012 ▶; Gruber, 1997 ▶). These studies use the space  (Andrews & Bernstein, 1988 ▶), or a similar metric tensor-based space, or a projection of
(Andrews & Bernstein, 1988 ▶), or a similar metric tensor-based space, or a projection of  to a space of lower dimensionality, respectively.
to a space of lower dimensionality, respectively.
Failure to correctly identify the Bravais lattice of a crystal can compromise subsequent least-squares calculations or even the solution of a structure. There are two commonly used ways to obtain a unique representative of the infinite number of cells that may be used to generate a given lattice: Niggli reduction (Niggli, 1928 ▶) and Delaunay reduction (Delaunay, 1932 ▶). We follow the conventions of International Tables for Crystallography (Burzlaff et al., 1992 ▶) in basing this article on Niggli reduction, and we will recast the discussion in terms of Delaunay reduction in a future study.
Given a precisely determined reduced cell, the lattice symmetry may be unambiguously inferred. In addition, reduced cells are useful in searching for sub- and super-cells, in indexing of powder patterns, and in twinned crystal studies. Without a suitable metric and a clear understanding of the geometry of the boundaries of the space, either searches of lattices in the neighborhood of a given cell must be excessively broad and produce many false positives, or, if made tighter, they risk missing important candidates, especially in the vicinity of 90° angles.
As noted by Azaroff & Buerger (1958 ▶), the concept of a reduced cell is strongly related to the concept of a reduced ternary quadratic form (Seeber, 1831 ▶; Selling, 1874 ▶). Reduced cells have become an important computational tool in crystallography (just as reduced quadratic forms are an important tool in computational number theory), but much of the literature focuses on an essentially qualitative approach, taking a reduced cell as an absolute indicator of symmetry and not considering the impact of experimental error (Andrews & Bernstein, 1988 ▶). Consideration of experimental error requires the use of a distance metric dealing with reduced cells. Such metrics have been used in a six-dimensional approach (Zimmermann & Burzlaff, 1985 ▶), another six-dimensional approach (Andrews & Bernstein, 1988 ▶), a similar six-dimensional approach with a modified  norm (Oishi-Tomiyasu, 2012 ▶), a lattice-specific six-dimensional approach (Kabsch, 2013 ▶), a B-matrix approach (Macíček & Yordanov, 1992 ▶) and a ‘distortion index’ approach (Minor & Otwinowski, 1997 ▶).
norm (Oishi-Tomiyasu, 2012 ▶), a lattice-specific six-dimensional approach (Kabsch, 2013 ▶), a B-matrix approach (Macíček & Yordanov, 1992 ▶) and a ‘distortion index’ approach (Minor & Otwinowski, 1997 ▶).
In addition, because the processes of both Niggli and Delaunay reduction can produce large discontinuities in reduced cell parameters from small changes in the lattice, an effective use of a metric must allow for such discontinuities, either by a combinatorial search or by a metric preserving embedding in a higher-dimensional space that removes the discontinuities. Until now, crystallographic software appears either to have used a demanding combinatorial approach or simply to have given up on doing a complete search. The purpose of this article is to take the necessary first steps towards adding an embedding to the existing combinatorial approaches by clearly mapping the boundary discontinuities and their related transformations.
Two principal uses of Niggli reduction are the determination of Bravais lattice type and the construction of a database using a representation of the unit cell for its key (Andrews et al., 1980 ▶; Toby, 1994 ▶; Byram et al., 1996 ▶).
Both uses can be viewed as distance determinations in  . In the former case the distances to the Bravais lattice subspaces are used, and in the latter case the distances between pairs of unit cells are used. However, the complexity of the space has consequences in some regions; it is not adequate to consider only one representation of a unit cell in
. In the former case the distances to the Bravais lattice subspaces are used, and in the latter case the distances between pairs of unit cells are used. However, the complexity of the space has consequences in some regions; it is not adequate to consider only one representation of a unit cell in  . A standard mathematical solution is to create an ‘embedding’ (Nash, 1956 ▶) of the space with an appropriate associated metric. In such an embedding, separate regions of the space under consideration are sewn together into a single fundamental region preserving distances from the original piecewise presentation.
. A standard mathematical solution is to create an ‘embedding’ (Nash, 1956 ▶) of the space with an appropriate associated metric. In such an embedding, separate regions of the space under consideration are sewn together into a single fundamental region preserving distances from the original piecewise presentation.
In the case being considered the regions contain sets of cells that appear to be far apart originally but which can be seen to represent similar lattices as the regions are sewn together, and sets of cells that remain far apart after the sewing can be seen as not representing similar lattices. In concept, this is similar to what we do in folding of atomic coordinates into the asymmetric unit of a crystal. This is an example of a simple embedding, allowing us to see which atoms interact. This is the approach followed in BGAOL. The present article discusses the application to Bravais lattice identification. McGill et al. (2014 ▶) discuss the database application.
In order to define an embedding, the operations defining the fundamental region must be specified. In the case of Niggli reduction, the complete space is  , and the fundamental region is the fraction of the space containing only Niggli-reduced cells. Proper unit cells in any other region of
, and the fundamental region is the fraction of the space containing only Niggli-reduced cells. Proper unit cells in any other region of  can be transformed into the fundamental region by the rules of Niggli reduction. The transformations at the boundaries must be enumerated and their combinations analyzed as in Appendix A
(see Table 1 ▶).
can be transformed into the fundamental region by the rules of Niggli reduction. The transformations at the boundaries must be enumerated and their combinations analyzed as in Appendix A
(see Table 1 ▶).
Table 1. Fifteen five-dimensional boundary polytopes of Niggli-reduced cells in  .
.
For a given boundary polytope  , the column ‘Condition’ gives the
, the column ‘Condition’ gives the  constraints (prior to closure) of the boundary polytope. Boundary polytopes 1 and 2 apply in both the all-acute (
constraints (prior to closure) of the boundary polytope. Boundary polytopes 1 and 2 apply in both the all-acute ( ) and the all-obtuse (
) and the all-obtuse ( ) branches of the Niggli-reduced cone. Boundary polytopes 8, B, E and F are restricted to the all-obtuse (
) branches of the Niggli-reduced cone. Boundary polytopes 8, B, E and F are restricted to the all-obtuse ( ) branch of the Niggli-reduced cone,
) branch of the Niggli-reduced cone, 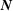 . Boundary polytopes 6, 7, 9, A, C and D are restricted to the all-acute (
. Boundary polytopes 6, 7, 9, A, C and D are restricted to the all-acute (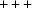 ) branch of
) branch of 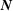 . Boundary polytopes 3, 4 and 5 are boundaries of both the all-acute (
. Boundary polytopes 3, 4 and 5 are boundaries of both the all-acute (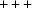 ) and the all-obtuse (
) and the all-obtuse ( ) branches.
) branches.
| Class | Boundary | Condition | Transformation matrix |
|---|---|---|---|
| Equal cell edges | 1 |
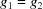
|
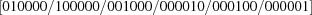
|
| 2 |
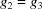
|
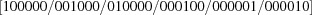
|
|
| 90° | 3 |
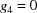
|
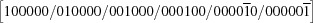
|
| 4 |
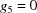
|
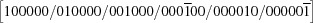
|
|
| 5 |
|
|
|
| Face diagonal | 6 |
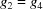 and and 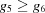
|
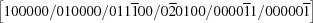
|
| 7 |
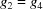 and and 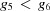
|
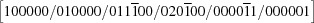
|
|
| 8 |
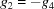
|
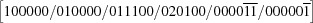
|
|
| 9 |
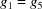 and and 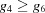
|
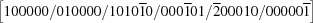
|
|
| A |
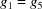 and and 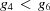
|

|
|
| B |
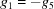
|
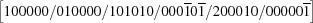
|
|
| C |
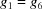 and and 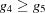
|
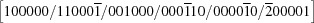
|
|
| D |
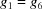 and and 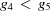
|
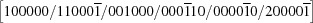
|
|
| E |
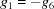
|
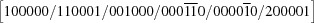
|
|
| Body diagonal | F |
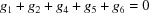
|
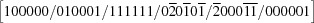
|
Given the complete set of conditions that define all boundaries of the fundamental unit and their relationships to adjacent units, the transformations of coordinates on crossing the boundaries are enumerated. Oishi-Tomiyasu (2012 ▶) has enumerated transformations in a related space.
There have been multiple investigations of such boundaries, albeit without a consideration of experimental error in most cases. See, for example, Gruber (1997 ▶, 2006 ▶) for a review and an approach using a five-dimensional space based on the metric tensor. Gruber’s 1997 ▶ approach partitions the space of reduced cells into 127 disjoint components (genera), based on 67 one- to four-dimensional ‘hyperfaces’ further subdivided into 227 hyperfaces in order to achieve a common partitioning applicable to both Niggli and Delaunay reduction. Unfortunately, Gruber’s reduction to five dimensions, and any purely topological approach without a metric that allows error propagation from the experimental data, makes it difficult or impossible to carry out a full perturbation analysis of the impact of experimental errors. The linear  metric used in the embedding makes such error analysis simpler.
metric used in the embedding makes such error analysis simpler.
Therefore, in this investigation we return to the full six-dimensional space (Andrews & Bernstein, 1988 ▶),  , of unit cells based on the metric tensor and use algebraic techniques confirmed by a Monte Carlo technique to explore the ‘natural’ five-, four-, three-, two- and one-dimensional boundary polytopes of the six-dimensional polytope of Niggli-reduced cells. The two techniques are mutually supportive. The lower-dimensional boundaries are an algebraic consequence of the five-dimensional boundaries. The lower-dimensional boundaries derived algebraically are confirmed by the Monte Carlo technique, which helps to identify unpopulated boundaries and boundaries that drop to lower dimension owing to glancing intersections with multiple other boundaries.
, of unit cells based on the metric tensor and use algebraic techniques confirmed by a Monte Carlo technique to explore the ‘natural’ five-, four-, three-, two- and one-dimensional boundary polytopes of the six-dimensional polytope of Niggli-reduced cells. The two techniques are mutually supportive. The lower-dimensional boundaries are an algebraic consequence of the five-dimensional boundaries. The lower-dimensional boundaries derived algebraically are confirmed by the Monte Carlo technique, which helps to identify unpopulated boundaries and boundaries that drop to lower dimension owing to glancing intersections with multiple other boundaries.
There are 15 five-dimensional boundary polytopes and a total of 216 boundary polytopes. In this approach, all the boundary polytopes are on the surface of the closure of the six-dimensional Niggli-reduced polytope. Identification of these boundary polytopes and the reduction transformations to be applied in crossing them is an essential step either in a combinatorial error analysis or in embedding  into a higher-dimensional space for an analytical error analysis, and it is useful for database searches.
into a higher-dimensional space for an analytical error analysis, and it is useful for database searches.
The 15 five-dimensional boundary polytopes give the complete shape of the space of Niggli-reduced cells (see Appendix A ). All of the primitive lattice types can be represented as combinations of the 15 five-dimensional boundary polytopes. All of the non-primitive lattice types can be represented as combinations of the 15 five-dimensional boundary polytopes and of the seven special-position subspaces of the five-dimensional boundary polytopes. By confining our attention to just the Niggli reduction, the result is a simpler classification than Gruber’s with more direct applicability to an embedding and database searching.
2. Background
Crystallography began with the study of crystal morphology and the classification of substances by the shapes of their crystals, a database concept before the creation of databases. Von Laue (1952 ▶) provided an accessible description. Two themes have developed: Bravais lattice assignment and database searches to identify substances by their unit-cell parameters. In this article we consider only the Bravais lattice identification issues.
The following glossary may be helpful in reading the subsequent discussion.
(1)  . The six-dimensional space of vectors
. The six-dimensional space of vectors
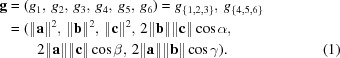 |
See § A1.
(2) N, Niggli cone, Niggli-reduced polytope. The locus of points in G 6 that are Niggli reduced. See § A2.
(3) Negative or positive portions of the Niggli cone. Those parts of the Niggli cone that have 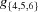 either all negative or all positive. Together they constitute the entire Niggli cone.
either all negative or all positive. Together they constitute the entire Niggli cone.
(4) Manifold. A space that in local regions has mappings that establish Euclidean coordinates.
(5) Polytope. A portion of a space with flat sides.
(6) Boundary of a set. The points that have some immediate neighbors in the set and some immediate neighbors not in the set, i.e. the interface between the inside of the set and the points outside of the set. Boundary points need not themselves be members of the set.
(7) Boundary transformations. The transformations to be applied to a point as it crosses from inside the Niggli cone to outside in order to transform its position to the corresponding position inside the Niggli cone.
(8) Boundary polytope. A portion of the boundary that is a polytope, i.e. has flat sides.
(9) Special-position subspace of a boundary polytope. The locus of points in a boundary manifold that are invariant under the boundary transformation. See § A4.
(10) Embedding (in topology). The mapping of one space into another, often of higher dimensionality.
(11) Isometric embedding. An embedding that preserves distances.
(12) L1 norm. Manhattan or city-block distance, the sum of the magnitudes of the differences of the vector components.
(13) L2 norm. Euclidean distance, the square root of the sum of the squares of the differences of the vector components.
(14) Fundamental region. For a repeating mathematical structure, one is chosen as the starting point. For instance, in crystallography, the 0–1, 0–1, 0–1 unit cell is often chosen as the basic cell.
(15) Bravais lattice subspace. Any polytope in  that is occupied by a single Bravais lattice type. For instance, cF lattices fall on a line with base vector (1, 1, 1, 1, 1, 1).
that is occupied by a single Bravais lattice type. For instance, cF lattices fall on a line with base vector (1, 1, 1, 1, 1, 1).
(16) Hyperface. Term used by Gruber (1997 ▶) for subspaces.
(17) Monte Carlo. Mathematical technique of random multiple probing of a system to discover its responses.
(18) Glancing intersection. An intersection of a manifold with the intersection of two or more other manifolds, but of measure zero. For instance, in a plane, the line (−1, 1) has a glancing intersection with the all-plus quadrant.
(19) Boundary maps. The list of transformations that must be applied to points exiting the fundamental unit.
(20) Projector into a subspace. A linear mapping from an arbitrary point in a space to the nearest point in the subspace.
(21) Closure. For an open manifold, the closure is the content of the manifold plus the content of the boundary. For instance, the closure of a circular region is the interior of the circle plus the bounding circle.
2.1. Bravais lattice assignment
Modern work on Bravais lattice assignment has taken two directions: qualitative absolute assignment of lattice type versus quantitative assignment using a metric to measure the distance from the 14 Bravais lattice types. This is a fuzzy distinction because all methods are fundamentally quantitative, being rooted in numeric cell parameters. The advantage of the methods based on, and making full use of, a metric is that they perform well in the presence of experimental error. The more fine grained the metric used, the more easily and efficiently can the alternatives be ranked. Gruber’s work (Gruber, 1997 ▶) is the latest in qualitative assignment of lattice types. DELOS (Zimmermann & Burzlaff, 1985 ▶) is a popular example of a rather coarse-grained metric. Kabsch has incorporated a fine-grained metric in XDS (Kabsch, 1993 ▶, 2010 ▶) based on the sum of the magnitudes of deviations from the various Niggli reduction conditions. See Macíček & Yordanov (1992 ▶) for a reasonably complete review of the relevant literature.
The use of a fine-grained metric under which it is meaningful to ask precisely how far a probe cell is from a given lattice and to compare that distance with the experimental error began with Andrews & Bernstein (1988 ▶), in which the space  , consisting of vectors
, consisting of vectors
(a modified metric tensor), was introduced. The concept is simple, but the implementation is complex because a very large number of iterations may be necessary to apply the boundary transformations of the Niggli cone. BLAF (Macíček & Yordanov, 1992 ▶) and OT-BLD (Oishi-Tomiyasu, 2012 ▶) cut off the iterations, creating the possibility of missed symmetries. The implementation of Andrews & Bernstein (1988 ▶), ITERATE, continues without a cutoff until no new candidates are found, to avoid missed symmetries but at the expense of additional execution time. BGAOL resolves this conflict by specifically using the 15 five-dimensional boundaries cited in Appendix A , labeled 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, from which the many remaining internal boundaries of the Niggli cone may be derived as intersections, and by using an isometric (i.e. distance-preserving) embedding that sharply limits the boundary transforms to be applied to the ones directly involved with those 15 five-dimensional boundaries, plus three of the four-dimensional boundaries (8F, BF and EF) in the negative portion of the Niggli cone and two boundaries (69 and 6C) in the positive portion of the Niggli cone that contains the images of 8F, BF and EF under their boundary transforms. For the database application involving points far from the boundaries, additional four-dimensional boundaries and three-dimensional boundaries are used.
2.2. Embeddings
In mathematics, an embedding is an instance of some mathematical structure within another, described as a map from one structure to the other. Among the purposes of embedding is to map coordinates from a discontinuous space onto a continuous one. An example would be a computer screen where objects exiting to the right reappear on the left. That can be modeled by mapping the screen onto a cylinder and treating the screen coordinate as an angle with range zero to 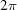 . Two of the ways that embeddings can be implemented are by analytical embedding, where an equation would map between the spaces, and by a collection of boundary maps with actions at the boundaries specified in the map. Treating the above example as cylinder is an analytical embedding. Using a boundary map that says at the right side subtract the screen width and at the left side add the screen width is a boundary map embedding. The latter are frequently used when an analytical embedding is difficult to determine or simply unknown. Often an analytical embedding is a more understandable, compact description, but boundary maps are frequently the more practical. We implemented our embedding of
. Two of the ways that embeddings can be implemented are by analytical embedding, where an equation would map between the spaces, and by a collection of boundary maps with actions at the boundaries specified in the map. Treating the above example as cylinder is an analytical embedding. Using a boundary map that says at the right side subtract the screen width and at the left side add the screen width is a boundary map embedding. The latter are frequently used when an analytical embedding is difficult to determine or simply unknown. Often an analytical embedding is a more understandable, compact description, but boundary maps are frequently the more practical. We implemented our embedding of  as boundary maps (there is no known analytical mapping), unfolding some transformations that are isometric across the boundaries (essentially an analytical embedding). This may seem to be an overly complex way to describe the distance measure, but it is useful in this case where the distance measure varies outside the fundamental unit (see §2.3).
as boundary maps (there is no known analytical mapping), unfolding some transformations that are isometric across the boundaries (essentially an analytical embedding). This may seem to be an overly complex way to describe the distance measure, but it is useful in this case where the distance measure varies outside the fundamental unit (see §2.3).
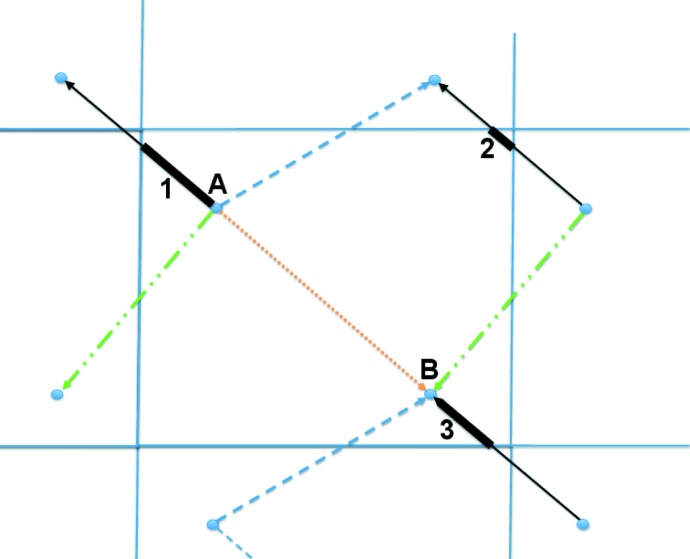
The problem of finding how far cells in the Niggli cone are from other cells in the Niggli cone is similar to the problem of finding the distance between atoms in a crystal, where the shortest distance may not be the distance within the asymmetric unit of the chosen cell. For example, in Fig. 1 ▶, two atoms, A and B, are shown in the asymmetric unit of a cell chosen from a two-dimensional lattice, with symmetry-related copies of those atoms in neighboring cells. In this case, a symmetry-related copy of B is closer to A (shown with a solid black line) than is the original B in the same asymmetric unit. An alternative to searching through neighboring cells in two dimensions examining all the translational copies would be to pick up the matching left and right edges of the cell and glue them together to form a tube, and then bend the tube to glue the remaining edges together to form a torus. Then we can navigate between points on the surface of the torus (where there is only one copy of B) looking for the shortest distance. Mapping the torus back onto the flat lattice, the shortest path from A to B consists of the three pieces shown in Fig. 1 ▶ as the bold black segments 1, 2 and 3. Even though they appear to be disjoint in the two-dimensional representation, they are contiguous in the embedding.
Figure 1.
Example of the difficulty of finding the shortest distance in a lattice. The distance within the asymmetric unit of the chosen cell is shown as a light dotted line. However, the shortest distance, shown as a heavy solid line, crosses multiple unit cells.
This process of picking up a lower-dimensional manifold in which we know the geometry in Euclidean patches and gluing the edges of the patches together to form a closed surface in a higher-dimensional space but with the same distances between points is called an isometric embedding. ‘All’ we need to know is the distance function on that embedded surface.
2.3. Metric distortions
Embedding the Niggli cone in  into a higher-dimensional space is, as one might expect, more complicated than embedding a three-dimensional lattice as a torus-like object into a six-dimensional space. In addition to having more dimensions, the symmetry operations generated by the boundary transformations in Table 1 ▶ are not, in general, isometric. The face-diagonal boundary transformations
into a higher-dimensional space is, as one might expect, more complicated than embedding a three-dimensional lattice as a torus-like object into a six-dimensional space. In addition to having more dimensions, the symmetry operations generated by the boundary transformations in Table 1 ▶ are not, in general, isometric. The face-diagonal boundary transformations 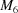 through
through 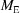 and the body-diagonal boundary transformation
and the body-diagonal boundary transformation 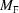 significantly compress space in some directions and expand it in others. In measuring the distance between cells in the Niggli cone, we always have to measure distances between representatives of cells within the Niggli cone and not between a representative in the cone and one outside. However, the equal-cell-edge (
significantly compress space in some directions and expand it in others. In measuring the distance between cells in the Niggli cone, we always have to measure distances between representatives of cells within the Niggli cone and not between a representative in the cone and one outside. However, the equal-cell-edge (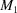 ,
, 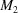 ) and 90° boundary transforms (
) and 90° boundary transforms (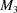 ,
, 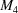 ,
, 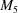 ) are isometric. Therefore we can safely ‘unroll’ the cone into multiple images using those transforms and then measure distances between those cell representatives. The non-isometric boundary transforms have anisotropic expansions and contractions, ranging from an expansion by a factor of nearly 3.6 in one direction and a contraction by a factor of less than 0.28 in another direction for the
) are isometric. Therefore we can safely ‘unroll’ the cone into multiple images using those transforms and then measure distances between those cell representatives. The non-isometric boundary transforms have anisotropic expansions and contractions, ranging from an expansion by a factor of nearly 3.6 in one direction and a contraction by a factor of less than 0.28 in another direction for the  vectors (corresponding to an expansion factor of nearly 1.9 and a contraction factor of less than 0.53 for the
vectors (corresponding to an expansion factor of nearly 1.9 and a contraction factor of less than 0.53 for the 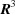 cells) for the body-diagonal boundary transform (
cells) for the body-diagonal boundary transform (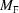 ). For the face-diagonal boundaries (
). For the face-diagonal boundaries (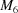 ,
, 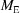 ) the corresponding expansions and contractions are 2.8 and 0.36 for the
) the corresponding expansions and contractions are 2.8 and 0.36 for the  vectors (corresponding to expansions and contractions of nearly 1.7 and less than 0.6 for the
vectors (corresponding to expansions and contractions of nearly 1.7 and less than 0.6 for the 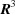 cells). For those transforms, boundary maps are used to map the transition through a boundary back into another part of the Niggli cone. If, instead of applying these boundary maps, we were to step past those boundaries into the surrounding
cells). For those transforms, boundary maps are used to map the transition through a boundary back into another part of the Niggli cone. If, instead of applying these boundary maps, we were to step past those boundaries into the surrounding  environment, the effect of those metric distortions would be very much like looking through glass of a high anisotropic refractive index, thereby potentially creating a very large number of distorted images of the distances within the Niggli cone. Using the embedding and confining distance measurements to those entirely within the cone greatly reduces this computationally expensive effect and the need for inappropriately early terminations of iterations. As noted above, a large indeterminate number of iterations may be necessary.
environment, the effect of those metric distortions would be very much like looking through glass of a high anisotropic refractive index, thereby potentially creating a very large number of distorted images of the distances within the Niggli cone. Using the embedding and confining distance measurements to those entirely within the cone greatly reduces this computationally expensive effect and the need for inappropriately early terminations of iterations. As noted above, a large indeterminate number of iterations may be necessary.
3. The BGAOL embedding distance
There are two ways in which to compute an embedded distance. In the first way, one maps the lower-dimensional space into a higher-dimensional space and computes distances along the resulting curved surface using the coordinate system of the higher-dimensional space, much as one computes spherical distances on the surface of the Earth to determine the distance between cities (A Society of Gentlemen in Scotland, 1771 ▶). In the second way, one uses the coordinate system of the lower-dimensional space and computes distances in those terms, using the rules of the embedding to join patches together (Helgason, 1962 ▶). Both approaches can involve comparisons of multiple alternative distances, just as one might have to compare going east versus going west in deciding on the shortest distance between New York, USA, and Sydney, Australia. In BGAOL, we chose to work with the coordinate system in  rather than with curvilinear coordinates in a higher-dimensional space.
rather than with curvilinear coordinates in a higher-dimensional space.
The program BGAOL computes the embedded distance between  vectors
vectors 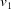 and
and 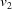 , which must both lie within the Niggli cone. This restriction is important because the boundary transformations are not isometric and have significant anisotropies, causing the regions outside the Niggli cone to be viewed as if through glass of anisotropic refractive index. The distances are computed from the
, which must both lie within the Niggli cone. This restriction is important because the boundary transformations are not isometric and have significant anisotropies, causing the regions outside the Niggli cone to be viewed as if through glass of anisotropic refractive index. The distances are computed from the  coordinates as follows.
coordinates as follows.
(1) Unroll the Niggli cone by applying the six permutations resulting from interchanging the cell edges and the four possible acute–obtuse angle changes, for an initial set of 24 alternative presentations of each cell, v: v, 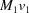 ,
, 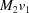 ,
, 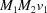 ,
, 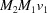 ,
, 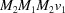 ,
, 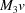 ,
, 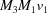 ,
, 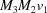 ,
, 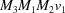 ,
, 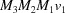 ,
, 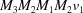 ,
, 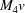 ,
, 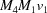 ,
, 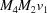 ,
, 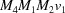 ,
, 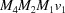 ,
, 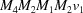 ,
, 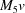 ,
, 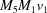 ,
, 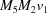 ,
, 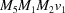 ,
, 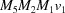 ,
, 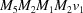 .
.
(2) For each of the 24 resulting cells from step 1, compute the distances to and projections onto each of the 15 five-dimensional Niggli cone boundaries.
(3) For each of the 24 resulting cells from step 1, compute the distances to and projections onto each of the three intersections between the face-diagonal cases and the body-diagonal case in the negative (obtuse angle) portion of the Niggli cone (8F, BF, EF) as well as the distances to and boundary mapping onto the images of those intersections in the positive (acute angle) portion of those intersections. Specifically, for each cell, v, compute the distance, projections and images
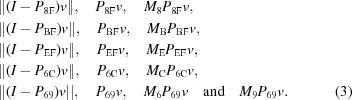 |
(4) For all subsequent distance calculations, also unroll the Niggli standard-form transformations that restrict the Niggli cone to 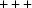 or
or  , by defining
, by defining
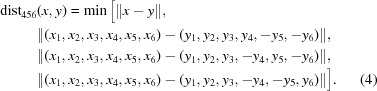 |
This is the minimum distance between two images where one is in the positive branch of the Niggli cone and the other is in the negative branch.
(5) Compute the minimum Euclidean distance from each of the 24 images of the first cell from step 1 to each of the 24 images of the second cell from step 1.
(6) For each of the 15 five-dimensional boundaries and for each of the 576 combinations of one of the 24 images of the first cell and one of the 24 images of the second cell, determine the minimum of the distances computed thus far and the distance going from the first cell to the chosen boundary and then from the boundary to the second cell, treating as equivalent each projection into a boundary and its transformation using the boundary transformation.
(7) For each member of each set of permutations, compute the distance from each permutation to each of the face-diagonal and body-diagonal boundary manifolds. The face-diagonal boundaries are grouped together as three cases (6-7-8, 9-A-B, C-D-E), with two subcases each. In the first three cases these are the full five-dimensional boundaries, and in the subcases these are the four-dimensional boundaries produced by the intersections with the body-diagonal boundary manifold (8F, BF, EF).
(8) For each face-diagonal or body-diagonal boundary manifold, Γ, consider a member 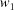 from the first set of permutations and
from the first set of permutations and 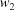 from the second set of permutations. Let
from the second set of permutations. Let 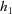 be the distance from
be the distance from 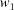 to Γand
to Γand 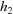 be the distance from
be the distance from 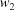 to Γ.
to Γ.
(9) If 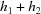 is less than the minimum distance already found, let
is less than the minimum distance already found, let 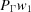 be the projection of
be the projection of 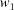 onto Γ and
onto Γ and 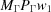 be the image of that projection under the boundary transformation, and let
be the image of that projection under the boundary transformation, and let 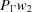 be the projection of
be the projection of 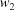 onto Γ and
onto Γ and 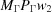 be the image of that projection under the boundary transformation. For the 8F, BF and EF four-dimensional boundaries, use the transformations for the corresponding face-diagonal boundaries (
be the image of that projection under the boundary transformation. For the 8F, BF and EF four-dimensional boundaries, use the transformations for the corresponding face-diagonal boundaries (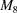 ,
, 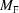 ,
, 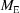 ). Compare the minimum distance thus far with {
). Compare the minimum distance thus far with {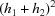 +
+ 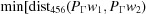 ,
, 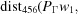
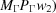 , dist
, dist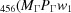 ,
, 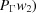 , dist
, dist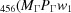 ,
, 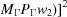 }
}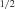 and keep the smallest value.
and keep the smallest value.
The raw distance in  is not sufficient for comparison of lattices of different symmetries and does not consider distances in relationship to the size of experimental errors. The anorthic lattices have the full six degrees of freedom of the space, the monoclinic have four, the orthorhombic have three, the hexagonal and tetragonal have two, and the cubic have one. Multiplying the reported
is not sufficient for comparison of lattices of different symmetries and does not consider distances in relationship to the size of experimental errors. The anorthic lattices have the full six degrees of freedom of the space, the monoclinic have four, the orthorhombic have three, the hexagonal and tetragonal have two, and the cubic have one. Multiplying the reported  distances by the square root of the number of degrees of freedom provides better comparisons between possible lattices. If one then divides by the
distances by the square root of the number of degrees of freedom provides better comparisons between possible lattices. If one then divides by the  experimental error estimate, one gets a dimensionless ‘Z score’.
experimental error estimate, one gets a dimensionless ‘Z score’.
Computationally, the multiplicities of the combinations used is lower than one might expect because of constant pruning by comparing the distance computed at each stage with the distance to the boundary under consideration. If the boundary distance that was precomputed in step 2 or 3 is larger than the previously computed minimum distance between cells, there is no need to compute path lengths that include that boundary distance.
4. Implementation of the embedding
BGAOL is a modification of our earlier iteration-based program ITERATE (Andrews & Bernstein, 1988 ▶) using embedding-based distances to search for likely Bravais lattice matches. The only other lattice matching programs that the authors know of that use a metric are BLAF (Macíček & Yordanov, 1992 ▶), DELOS (Zimmermann & Burzlaff, 1985 ▶), XDS (Kabsch, 2010 ▶) and OT-BLD, the lattice matching part of CONOGRAPH (Oishi-Tomiyasu, 2012 ▶). Because of the metric distortions outside the Niggli cone, none of these measures is assured to actually be linear. BLAF uses an 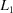 (i.e. Manhattan street grid) measure on the metric tensor, while ITERATE and BGAOL use an
(i.e. Manhattan street grid) measure on the metric tensor, while ITERATE and BGAOL use an 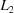 (i.e. Euclidean) measure. DELOS uses a coarse measure based on ‘cycles’. OT-BLD reports matches using a fractional measure, also based on the metric tensor. XDS uses a ‘quality index’ based on the sum of the extents to which the inequalities of Niggli reduction are not satisfied for components of the metric tensor, essentially an
(i.e. Euclidean) measure. DELOS uses a coarse measure based on ‘cycles’. OT-BLD reports matches using a fractional measure, also based on the metric tensor. XDS uses a ‘quality index’ based on the sum of the extents to which the inequalities of Niggli reduction are not satisfied for components of the metric tensor, essentially an 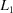 measure of the distance from each Niggli-cone boundary polytope. Table 2 ▶ shows a comparison of BGAOL results with those of other programs, except XDS. Table 3 ▶ shows a comparison of the BGAOL
Z score with the XDS quality indicator.
measure of the distance from each Niggli-cone boundary polytope. Table 2 ▶ shows a comparison of BGAOL results with those of other programs, except XDS. Table 3 ▶ shows a comparison of the BGAOL
Z score with the XDS quality indicator.
Table 2. Search results for BGAOL, BLAF, DELOS, OT-BLD and ITERATE for basic beryllium acetate, 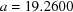 ,
, 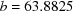 ,
, 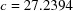 Å,
Å, 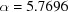 ,
, 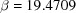 ,
,  ° (Himes & Mighell, 1987 ▶).
° (Himes & Mighell, 1987 ▶).
The BGAOL, BLAF and ITERATE columns show distances in Å2 from the probe to the appropriate boundary manifold for the indicated Niggli lattice character in  . The BLAF column uses
. The BLAF column uses 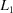 distances versus
distances versus
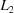 distances for the others. The DELOS column shows the numbers of cycles of relaxation of the Delaunay reduction needed to find the indicated symmetry. The OT-BLD column is a dimensionless fractional measure of the agreement of metric tensors. The significant differences between the BGAOL and ITERATE values in some cases are a result of the expansion and contraction factors (see the text) when
distances for the others. The DELOS column shows the numbers of cycles of relaxation of the Delaunay reduction needed to find the indicated symmetry. The OT-BLD column is a dimensionless fractional measure of the agreement of metric tensors. The significant differences between the BGAOL and ITERATE values in some cases are a result of the expansion and contraction factors (see the text) when  measures are applied outside the Niggli cone.
measures are applied outside the Niggli cone.
| Lattice character | BGAOL | BLAF | DELOS | OT-BLD | ITERATE |
|---|---|---|---|---|---|
| cF | 0.067 | – | 1 | 1 × 10−5 | 0.096 |
| tI | 0.038 | 0.014 | 1 | 6 × 10−6 | 0.038 |
| hR | 0.065 | 0.013 | 1 | 7 × 10−6 | 0.076 |
| oF | 0.038 | – | 1 | 6 × 10−6 | 0.038 |
| oI | 0.019 | 0.007 | 1 | 4 × 10−6 | 0.018 |
| mI | 0.007 | 0.004 | 1 | 1 × 10−6 | 0.007 |
Table 3. Partial search results for BGAOL and XDS for the test cell, 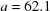 ,
, 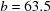 ,
, 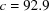 Å,
Å, 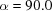 ,
, 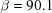 ,
, 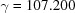 ° from Kabsch (1993 ▶).
° from Kabsch (1993 ▶).
The BGAOL columns show the  distance and the
distance and the  degrees-of-freedom weighted Z score, assuming errors of 0.2 in edges and 0.1 on angles, which in this case corresponds to a
degrees-of-freedom weighted Z score, assuming errors of 0.2 in edges and 0.1 on angles, which in this case corresponds to a  error estimate of 61.3 Å2. The XDS QI (quality indicator) and scaled QI columns show the raw deviations from Niggli reduction and the same deviations scaled by
error estimate of 61.3 Å2. The XDS QI (quality indicator) and scaled QI columns show the raw deviations from Niggli reduction and the same deviations scaled by 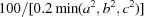 and capped at 999 as per Kabsch (2013 ▶). Only the three most promising lattice types are shown. The structure solution gave oC.
and capped at 999 as per Kabsch (2013 ▶). Only the three most promising lattice types are shown. The structure solution gave oC.  distances are in units of Å2.
distances are in units of Å2.
| Lattice character |
 distance distance |
BGAOL Z score | XDS QI | Scaled QI |
|---|---|---|---|---|
| mP | 20.138 | 0.657 | 1.0 | 0.13 |
| oC | 125.958 | 3.560 | 23.8 | 3.09 |
| mC | 125.150 | 4.085 | 23.4 | 3.03 |
4.1. Distance calculation
BGAOL distances are calculated using the function NCDIST, which computes the distance between pairs of reduced cells. Bravais lattice determination for a given probe cell consists of finding which boundary polytopes or subspaces among the Bravais lattice subspaces of the Niggli cone are closest to the probe. Constructing and using a cell database requires computing the distance between cells as points in  that are arbitrarily far apart. Fig. 2 ▶ illustrates the use of NCDIST to compute distances between well separated points.
that are arbitrarily far apart. Fig. 2 ▶ illustrates the use of NCDIST to compute distances between well separated points.
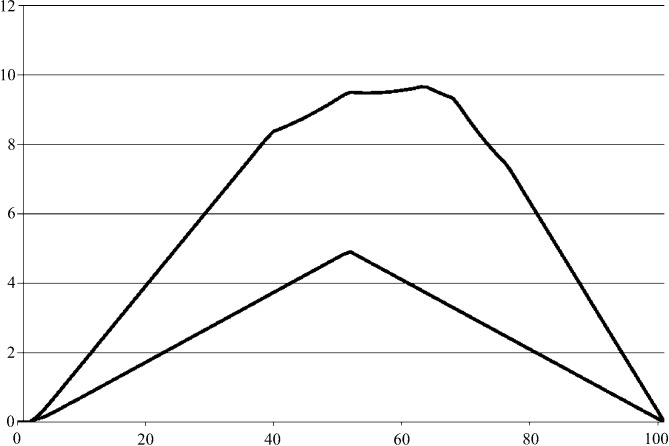
Figure 2.
To illustrate distance calculations between arbitrary points, a line was drawn in  between an unreduced point close to cF and its reduced image. Each curve shows the distances at 100 points along each line to the corresponding reduced cell of the starting point. The upper curve starts from
between an unreduced point close to cF and its reduced image. Each curve shows the distances at 100 points along each line to the corresponding reduced cell of the starting point. The upper curve starts from 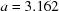 ,
, 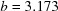 ,
, 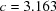 Å,
Å, 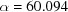 ,
, 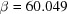 ,
, 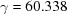 ° and ends at
° and ends at 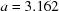 ,
, 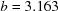 ,
, 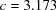 Å,
Å, 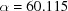 ,
, 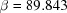 ,
, 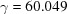 °. The lower curve starts from
°. The lower curve starts from 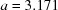 ,
, 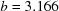 ,
, 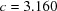 Å,
Å, 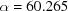 ,
, 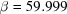 ,
, 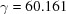 ° and ends at
° and ends at 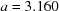 ,
, 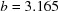 ,
, 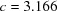 Å,
Å, 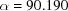 ,
, 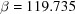 ,
, 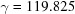 °.
°.
4.2. Availability and test results
A BGAOL-based lattice identification web server is available at http://iterate.sf.net/bgaol. A source kit may also be downloaded from a link on that page.
The prior ITERATE-based lattice identification web server is available at http://www.bernstein-plus-sons.com/software/ITERATE/.
The latest version of the source code of BGAOL is maintained on SourceForge (http://sourceforge.net/) for svn access at
svn checkout
svn://svn.code.sf.net/p/iterate/code/trunk/bgaol
bgaol-code
The source kit contains the test program, Follower.for, that computes the distance for database work as shown in Fig. 2 ▶.
The database code, which will be discussed in a subsequent article, is available from the ‘sauc’ module in the same repository.
Supplementary Material
Appendix B. DOI: 10.1107/S1600576713031002/kk5144sup1.pdf
Acknowledgments
The authors acknowledge the invaluable assistance of Frances C. Bernstein. The work by HJB has been supported in part by NIH NIGMS grant GM078077. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agency. LCA would like to thank Frances and Herbert Bernstein for hosting him during hurricane Sandy and its aftermath. Elizabeth Kincaid has contributed significant support in many ways. The authors wish to thank the referee who caught some errors in the dimensions assigned to some of the boundary polytopes in an earlier draft of this article. The necessary recheck produced one additional boundary polytope, and was the inspiration for the discussion of the reduction in the number of degrees of freedom for some of the twofolds and threefolds. The authors also wish to thank R. Oishi-Tomiyasu for helpful conversations, use of her code and providing preprints to her work.
Appendix A. The boundary polytopes
The embedding requires an understanding of the space  , the process of Niggli reduction, and the resulting Niggli cone and boundaries created thereof on
, the process of Niggli reduction, and the resulting Niggli cone and boundaries created thereof on  .
.
A1. The space G 6
 is a reformulation of the crystallographic metric tensor and the ‘Niggli matrix’ (itself a reformulation of the metric tensor) (Andrews & Bernstein, 1988 ▶). A vector
is a reformulation of the crystallographic metric tensor and the ‘Niggli matrix’ (itself a reformulation of the metric tensor) (Andrews & Bernstein, 1988 ▶). A vector 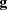 in
in  is defined as
is defined as
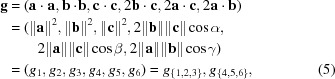 |
where  ,
, 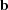 ,
,  are the unit-cell edge vectors, and
are the unit-cell edge vectors, and  indicates the dot product. The unit cell is chosen to be primitive.
indicates the dot product. The unit cell is chosen to be primitive.
The notation 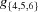 is used to denote the elements
is used to denote the elements 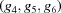 from the full
from the full  vector.
vector.
A2. The Niggli conditions
The Niggli-reduced cell of a lattice is a unique choice from among the infinite number of alternative cells that generate the same lattice (Niggli, 1928 ▶). A Buerger-reduced cell for a given lattice is any cell that generates that lattice, chosen such that no other cell has shorter cell edges (Buerger, 1960 ▶). Even after allowing for the equivalence of cells in which the directions of axes are reversed or axes of the same length are exchanged, there can be up to five alternative Buerger-reduced cells for the same lattice (Gruber, 1973 ▶). The Niggli conditions allow the selection of a unique reduced cell for a given lattice from among the alternative Buerger-reduced cells for that lattice.
Niggli reduction consists of converting the original cell to a primitive one and then alternately applying two operations: conversion to standard presentation and reduction (Niggli, 1928 ▶; Andrews & Bernstein, 1988 ▶). The convention for meeting the combined Buerger and Niggli conditions is based on increasingly restrictive layers of constraints: if  ,
,  ,
, 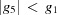 ,
, 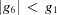 and either
and either 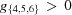 or
or 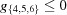 then we have a Niggli-reduced cell, and we are done.
then we have a Niggli-reduced cell, and we are done.
The remaining conditions are imposed when any of the above inequalities becomes an equality or the elements of 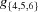 are not consistently all strictly positive or are not consistently all less than or equal to zero.
are not consistently all strictly positive or are not consistently all less than or equal to zero.
The full set of combined Buerger and Niggli conditions in addition to those for the cell edge lengths being minimal is as follows:
The  transformations associated with each of these steps are enumerated by Andrews & Bernstein (1988 ▶). Application of these operations must be repeated until all are satisfied.
transformations associated with each of these steps are enumerated by Andrews & Bernstein (1988 ▶). Application of these operations must be repeated until all are satisfied.
A3. Notation and boundary polytopes
We define the manifold of the Niggli-reduced cells in  as
as 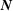 and refer to it as the ‘Niggli cone’.
and refer to it as the ‘Niggli cone’.
The interior of 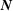 ,
, 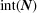 , is defined as the set of
, is defined as the set of 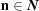 such that there exists
such that there exists 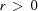 such that for all
such that for all 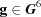 such that
such that 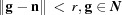 .
.
The closure of 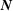 ,
, 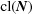 , is defined as the set of
, is defined as the set of 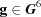 such that for all
such that for all 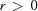 there exists
there exists 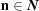 such that
such that 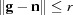 .
.
The boundary of 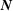 ,
, 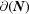 , is defined as the set of points in
, is defined as the set of points in 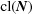 not in
not in 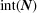 .
.
The boundary of 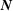 is created by the linear constraints of Niggli reduction and therefore can be decomposed into the union of ‘polytopes’, i.e. flat facets with straight edges.
is created by the linear constraints of Niggli reduction and therefore can be decomposed into the union of ‘polytopes’, i.e. flat facets with straight edges.
We distinguish the primary boundary polytopes from their edges, which are also polytopes, by ‘dimension’, which is the number of vectors in a basis for the interior of the polytope.
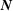 is a six-dimensional polytope.
is a six-dimensional polytope. 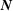 is a double-ended cone-like region going through the origin to infinity in both directions. The boundary polytopes are flat facets created by the intersections of hyperplanes through the origin. The boundary polytopes are, of course, of lower dimension than
is a double-ended cone-like region going through the origin to infinity in both directions. The boundary polytopes are flat facets created by the intersections of hyperplanes through the origin. The boundary polytopes are, of course, of lower dimension than 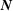 . Therefore any randomly selected vector in
. Therefore any randomly selected vector in  has a vanishingly small probability of occupying any particular five-dimensional boundary polytope, and it has an even lower probability of occupying one of the lower-dimensional boundary polytopes resulting from the intersections of five-dimensional boundary polytopes. Some boundary polytopes are ‘open’, i.e. while there are Niggli-reduced cells near that boundary, some or all of the points on those boundary polytopes are not themselves Niggli reduced.
has a vanishingly small probability of occupying any particular five-dimensional boundary polytope, and it has an even lower probability of occupying one of the lower-dimensional boundary polytopes resulting from the intersections of five-dimensional boundary polytopes. Some boundary polytopes are ‘open’, i.e. while there are Niggli-reduced cells near that boundary, some or all of the points on those boundary polytopes are not themselves Niggli reduced.
Our task is to identify the five-dimensional boundary polytopes that give 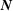 its shape. Those five-dimensional boundaries and the transforms involved in crossing them generate all the rest of the structure. However, in order to understand the shape of a given five-dimensional boundary polytope, we need the four-dimensional edges that bound it. In order to understand the shape of a given four-dimensional boundary polytope, we need the three-dimensional edges that bound it. In order to understand the shape of a given three-dimensional boundary polytope, we need the two-dimensional edges that bound it. In order to understand the shape of a given two-dimensional boundary polytope, we need the one-dimensional edges that bound it. From this classification we gain a better understanding of the relationships between Bravais lattice types, and, perhaps more importantly, this provides essential information needed to organize computations. Hosoya (1990 ▶) addressed a different, but related, classification. We discuss the relationship between boundary polytope identification, lattice types and Hosoya’s approach in §
A10. Hosoya recognized the complexity of boundary identifications for
its shape. Those five-dimensional boundaries and the transforms involved in crossing them generate all the rest of the structure. However, in order to understand the shape of a given five-dimensional boundary polytope, we need the four-dimensional edges that bound it. In order to understand the shape of a given four-dimensional boundary polytope, we need the three-dimensional edges that bound it. In order to understand the shape of a given three-dimensional boundary polytope, we need the two-dimensional edges that bound it. In order to understand the shape of a given two-dimensional boundary polytope, we need the one-dimensional edges that bound it. From this classification we gain a better understanding of the relationships between Bravais lattice types, and, perhaps more importantly, this provides essential information needed to organize computations. Hosoya (1990 ▶) addressed a different, but related, classification. We discuss the relationship between boundary polytope identification, lattice types and Hosoya’s approach in §
A10. Hosoya recognized the complexity of boundary identifications for 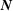 and introduced the use of Monte Carlo searching to clarify the relationships. We apply a Monte Carlo search in Appendix B (Andrews & Bernstein, 1976 ▶; Beltrami, 1873 ▶; Jordan, 1874 ▶; Stewart, 1993 ▶), which is available as supplementary material.2
and introduced the use of Monte Carlo searching to clarify the relationships. We apply a Monte Carlo search in Appendix B (Andrews & Bernstein, 1976 ▶; Beltrami, 1873 ▶; Jordan, 1874 ▶; Stewart, 1993 ▶), which is available as supplementary material.2
The reduction steps convert a non-reduced cell into one that has at least one edge shorter than the starting edges, and other steps in the case of equality convert a non-reduced cell into a cell that is more orthogonal than the starting cell. These operations are accomplished by choosing a face or body diagonal to replace one of the cell edges. The conditions added to remove the ambiguities in the case of equalities allow for a unique choice of Niggli cell in all cases but thereby create complex boundary conditions (Andrews & Bernstein, 1988 ▶). For example, the cell edge equalities in equations (7) and (8) create boundary polytopes across which elements of both 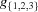 and
and 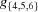 are exchanged, while equations (3) and (4)
create boundary polytopes across which edges are exchanged for face diagonals.
are exchanged, while equations (3) and (4)
create boundary polytopes across which edges are exchanged for face diagonals.
A boundary polytope does not necessarily consist entirely of Niggli-reduced cells but can contain non-Niggli-reduced cells including nearly reduced cells as well. We define a boundary polytope 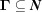 as a subset of
as a subset of 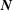 for which there is an associated matrix
for which there is an associated matrix 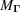 such that for all points
such that for all points 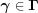 there exists
there exists 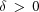 such that for all
such that for all 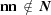 where
where 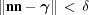 ,
, 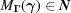 . Each boundary polytope is a portion of the boundary for which there is a single transformation matrix that maps the nearby non-Niggli-reduced cells to Niggli-reduced cells. This is not necessarily a mapping back to the starting point, or even to a point near the starting point, not even for points on the boundary polytope itself. We look for point-by-point invariance in defining special-position subspaces in §
A4.
. Each boundary polytope is a portion of the boundary for which there is a single transformation matrix that maps the nearby non-Niggli-reduced cells to Niggli-reduced cells. This is not necessarily a mapping back to the starting point, or even to a point near the starting point, not even for points on the boundary polytope itself. We look for point-by-point invariance in defining special-position subspaces in §
A4.
Each boundary polytope  has an associated ‘projector’
has an associated ‘projector’ 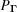 , which is the linear transformation that maps an arbitrary
, which is the linear transformation that maps an arbitrary 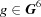 to the point
to the point 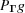 closest to g in the hyperplane containing
closest to g in the hyperplane containing  . It is important to understand that
. It is important to understand that 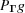 may not be Niggli reduced or even close to the Niggli cone.
may not be Niggli reduced or even close to the Niggli cone.
A4. Special-position subspaces
In an analysis of symmetry, special positions play an important role. A special position is a point invariant under a symmetry transformation, an eigenvector, of eigenvalue 1, of the transformation. We define a special-position subspace of a boundary polytope  as the intersection of the eigenspace of eigenvalue 1 of
as the intersection of the eigenspace of eigenvalue 1 of 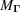 with the boundary polytope. Formally, for a boundary polytope
with the boundary polytope. Formally, for a boundary polytope  with associated transformation matrix
with associated transformation matrix 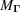 , the special-position subspace
, the special-position subspace 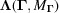 is defined as the set of points
is defined as the set of points 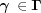 such that
such that 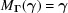 . In the case of boundary polytopes associated with a transformation matrix that goes from the all-acute
. In the case of boundary polytopes associated with a transformation matrix that goes from the all-acute  case to the all-obtuse
case to the all-obtuse  case or vice versa, there cannot be any Niggli-reduced special-position subspace, because the axial planes of the
case or vice versa, there cannot be any Niggli-reduced special-position subspace, because the axial planes of the 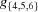 subspace are excluded from the all-acute
subspace are excluded from the all-acute 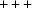 case. As we will see, while the special-position subspaces of the boundary polytopes are not needed in order to classify the primitive lattice types, they come into play in classifying the non-primitive lattice types.
case. As we will see, while the special-position subspaces of the boundary polytopes are not needed in order to classify the primitive lattice types, they come into play in classifying the non-primitive lattice types.
If we have two boundary polytopes 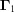 ,
, 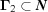 , we denote the intersection of the closure of
, we denote the intersection of the closure of 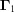 and the closure of
and the closure of 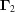 as
as 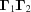 . Note that intersection is a commutative operation, i.e.
. Note that intersection is a commutative operation, i.e.
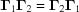 .
.
Because we have restricted the boundary polytope in this article to have only one associated matrix, we use the notation 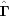 for
for 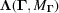 . In general, an infinite number of higher-dimensional polytopes will intersect
. In general, an infinite number of higher-dimensional polytopes will intersect  in
in 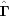 . We distinguish such a higher-dimensional polytope as
. We distinguish such a higher-dimensional polytope as 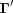 . Thus
. Thus 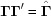 .
.
A5. The 15 five-dimensional boundary polytopes
The 15 five-dimensional boundary polytopes and their special-position subspaces may be organized as shown in Table 1 ▶, in which we use the hexadecimal digits 1 through F as identifiers. For each five-dimensional boundary polytope  in Table 1 ▶ having a nontrivial special-position subspace, we designate the particular choice of higher-dimensional polytope intersecting
in Table 1 ▶ having a nontrivial special-position subspace, we designate the particular choice of higher-dimensional polytope intersecting  in
in 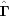 as
as 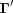 . See §
A5.3 for a concrete example.
. See §
A5.3 for a concrete example.
In the discussions of the 15 five-dimensional boundary polytopes below, we give the condition being satisfied, the right-handed 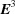 representation of the boundary transformation cell edge by cell edge, a
representation of the boundary transformation cell edge by cell edge, a  matrix representation of the same boundary transformation and a
matrix representation of the same boundary transformation and a  matrix representation of a projector into the hyperplane of that boundary. Note that both a right-handed
matrix representation of a projector into the hyperplane of that boundary. Note that both a right-handed 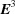 representation and its negative (left-handed) representation would map into the same
representation and its negative (left-handed) representation would map into the same  representation.
representation.
A5.1. Equal-cell-edge case
Cases 1 and 2 arise when two cell edges have equal length. In this section some scalar components are in bold face to direct the attention of the reader to values that are changing. The conditions of Niggli reduction impose a secondary condition on the associated angles for those two edges that resolves the ambiguity in ordering them. For example, in case 1, 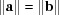 (
(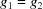 ) and the Niggli-reduced
) and the Niggli-reduced  vector
vector 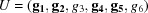 produces the same lattice as
produces the same lattice as 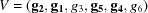 , which is not Niggli reduced if
, which is not Niggli reduced if  and
and  have different values. In going from Niggli-reduced cells near U to Niggli-reduced cells near V (e.g. by decreasing
have different values. In going from Niggli-reduced cells near U to Niggli-reduced cells near V (e.g. by decreasing  slightly), we are crossing a boundary polytope with a discontinuity in each of
slightly), we are crossing a boundary polytope with a discontinuity in each of 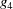 and
and 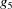 (Andrews & Bernstein, 1988 ▶). We may represent the transformation that takes U into V at the first boundary polytope by the matrix
(Andrews & Bernstein, 1988 ▶). We may represent the transformation that takes U into V at the first boundary polytope by the matrix 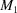 that maps U into V and the projector
that maps U into V and the projector 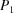 that maps any
that maps any  vector into the
vector into the 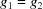 boundary polytope.
boundary polytope.
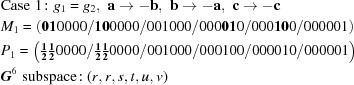 |
Similarly, for case 2, 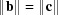 (
(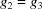 ),
), 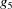 and
and 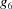 are exchanged, yielding
are exchanged, yielding
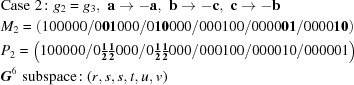 |
The remaining equal-cell-edge case, in which 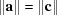 (
(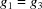 ), is only considered under Niggli reduction when
), is only considered under Niggli reduction when 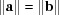 and
and 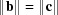 , which is a combination of case 1 and case 2. This requires two simultaneous five-dimensional constraints, thereby making
, which is a combination of case 1 and case 2. This requires two simultaneous five-dimensional constraints, thereby making 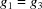 a four-dimensional rather than a five-dimensional case.
a four-dimensional rather than a five-dimensional case.
The special-position subspaces 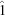 and
and 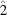 are obtained by adding the constraints
are obtained by adding the constraints 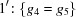 and
and 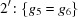 , respectively.
, respectively.
A5.2. Ninety degree case
Cases 3, 4 and 5 arise when a reduced cell angle is 90°. In those cases, the remaining cell angles both can be replaced by their supplements. This changes the sign of 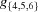 .
.
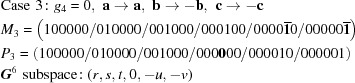 |
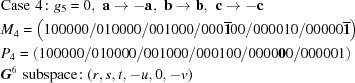 |
 |
In each 90° case, the special-position subspace consists of 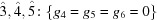 , i.e. the primitive orthorhombic case, and we take
, i.e. the primitive orthorhombic case, and we take 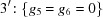 ,
, 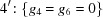 ,
, 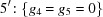 .
.
A5.3. Face-diagonal case
Cases 6 through E are all face-diagonal cases, in which a cell edge is equal in length to a face diagonal. Some complexity arises in the analysis because, unlike Delaunay reduction, Niggli reduction permits non-obtuse angles. We can always change the sign of any two elements of 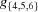 by changing the direction of the cell edge involved with those two elements. For example, if we transform
by changing the direction of the cell edge involved with those two elements. For example, if we transform  to
to 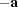 then, while
then, while 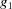 remains unaffected, the signs of each of
remains unaffected, the signs of each of 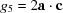 and
and 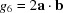 will change. Thus we can transform a cell having three acute angles to a cell having one acute angle and two obtuse angles, and we can transform a cell having three obtuse angles to a cell having one obtuse angle and two acute angles. The complete list of possible sign changes in
will change. Thus we can transform a cell having three acute angles to a cell having one acute angle and two obtuse angles, and we can transform a cell having three obtuse angles to a cell having one obtuse angle and two acute angles. The complete list of possible sign changes in 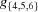 by changing the directions of axes are
by changing the directions of axes are
Unless one of the angles is 90° (which introduces a zero into 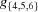 ), we cannot ordinarily transform a Niggli-reduced cell with all-acute angles to one with all-obtuse angles by changing the directions of axes, nor can we transform a Niggli-reduced cell with all-obtuse angles to one with all-acute angles by changing the directions of the axes. Note that changing the direction of all three axes has no effect because all the sign changes cancel.
), we cannot ordinarily transform a Niggli-reduced cell with all-acute angles to one with all-obtuse angles by changing the directions of axes, nor can we transform a Niggli-reduced cell with all-obtuse angles to one with all-acute angles by changing the directions of the axes. Note that changing the direction of all three axes has no effect because all the sign changes cancel.
The face-diagonal cases do include cases in which transformations from, for example,  to
to  do occur. Let us look in detail at cases 6 and 7,
do occur. Let us look in detail at cases 6 and 7, 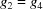 .
.
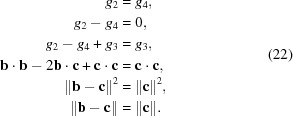 |
Thus transforming  to
to  will not change the cell edge lengths. In this case,
will not change the cell edge lengths. In this case, 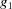 ,
, 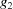 and
and 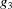 are, of course, unchanged and
are, of course, unchanged and
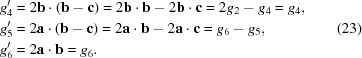 |
This shows that a single element of 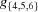 ,
, 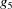 , will change sign depending on the sign of
, will change sign depending on the sign of  . Cases 6 and 7 cannot start from the all-obtuse case because
. Cases 6 and 7 cannot start from the all-obtuse case because 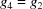 and because
and because 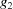 must be nonnegative. Starting from an all-acute case,
must be nonnegative. Starting from an all-acute case, 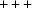 , we will remain in the all-acute case if
, we will remain in the all-acute case if 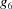 is greater than or equal to
is greater than or equal to  but go to one having one obtuse angle (not reduced) if
but go to one having one obtuse angle (not reduced) if  is less than
is less than  . We then change to having all-obtuse angles,
. We then change to having all-obtuse angles,  , by reversing the direction of b. The resulting matrices in these face-diagonal cases are
, by reversing the direction of b. The resulting matrices in these face-diagonal cases are
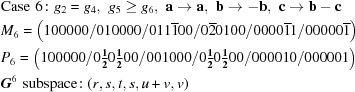 |
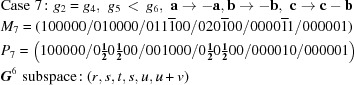 |
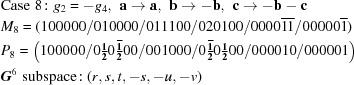 |
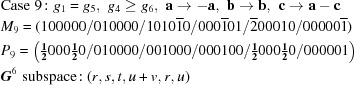 |
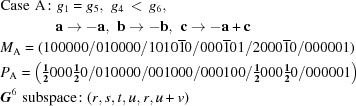 |
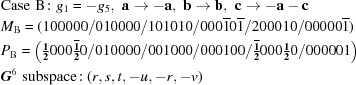 |
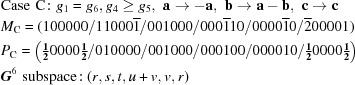 |
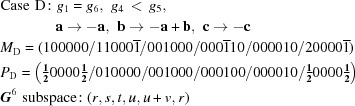 |
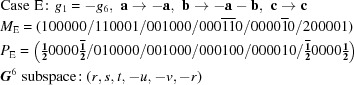 |
The special-position subspaces of the face-diagonal boundary polytopes 6, 8, 9, B, C and E are empty because such a special position would require a common point in the all-acute  and all-obtuse
and all-obtuse  cases that only meet at the axial planes of the
cases that only meet at the axial planes of the 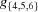 subspace, which are excluded from the all-acute
subspace, which are excluded from the all-acute  case. For cases 7, A and D there are non-trivial special-position subspaces. An invariant point in case 7 would have to satisfy
case. For cases 7, A and D there are non-trivial special-position subspaces. An invariant point in case 7 would have to satisfy  or
or 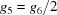 . Thus we define
. Thus we define 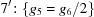 and similarly define
and similarly define 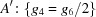 and
and 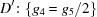 .
.
A5.4. Body-diagonal case
There is only one five-dimensional body-diagonal case, 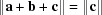 :
:
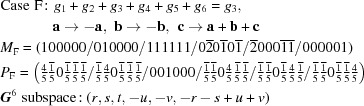 |
In order to have a special-position subspace in case F, in addition to 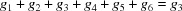 , we need (from the fourth and fifth rows of
, we need (from the fourth and fifth rows of 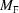 )
) 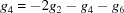 and
and 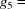
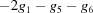 , from which we have
, from which we have 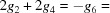
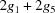 , from which we take
, from which we take 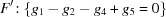 . This is equivalent to
. This is equivalent to 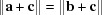 , i.e. that the shorter b-face diagonal is the same length as the shorter a-face diagonal.
, i.e. that the shorter b-face diagonal is the same length as the shorter a-face diagonal.
A6. The four-dimensional boundary polytopes
The four-dimensional boundary polytopes are created by the intersection of two five-dimensional boundary polytopes. Certain intersections are degenerate. For example, cases 8, B, E and F are restricted to the  branch of the boundary of the Niggli cone, while cases 6, 7, 9, A, C and D are restricted to the
branch of the boundary of the Niggli cone, while cases 6, 7, 9, A, C and D are restricted to the 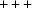 branch. More subtly, cases 6 and 7 require
branch. More subtly, cases 6 and 7 require 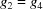 , maximizing
, maximizing 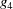 , forcing
, forcing 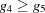 and
and 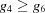 which would conflict with cases A and D. Only cases 9 and C, taken to their boundaries with A and D, respectively, are possible. Those boundaries are designated 9A and CD, respectively. Similarly, cases 9 and A maximize
which would conflict with cases A and D. Only cases 9 and C, taken to their boundaries with A and D, respectively, are possible. Those boundaries are designated 9A and CD, respectively. Similarly, cases 9 and A maximize 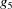 , which would conflict with case 7 and force 6 to the 67 boundary, and cases C and D maximize
, which would conflict with case 7 and force 6 to the 67 boundary, and cases C and D maximize 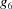 , which would conflict with case 6 except at the 67 boundary. Thus cases 6A, 7A, 6D, 7D, 79, 7A and 6C actually are the lower dimension cases 69A, 79A, 6CD, 7CD, 79A, 79A and 6CD, respectively. This process can result in three- or even two-dimensional boundary polytopes from the intersection of two five-dimensional boundary polytopes (see below). After excluding the cases that involve any of
, which would conflict with case 6 except at the 67 boundary. Thus cases 6A, 7A, 6D, 7D, 79, 7A and 6C actually are the lower dimension cases 69A, 79A, 6CD, 7CD, 79A, 79A and 6CD, respectively. This process can result in three- or even two-dimensional boundary polytopes from the intersection of two five-dimensional boundary polytopes (see below). After excluding the cases that involve any of 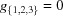 , there are 55 four-dimensional cases as shown in the supporting information (Appendix B, Table 3). The relative populations for all the two-dimensional boundary polytopes except 26, 28, 2A and 2D have Z scores above −1. The Z scores for those four cases range from −1.1 down to −1.9. (See the supplementary materials for a discussion of Z scores).
, there are 55 four-dimensional cases as shown in the supporting information (Appendix B, Table 3). The relative populations for all the two-dimensional boundary polytopes except 26, 28, 2A and 2D have Z scores above −1. The Z scores for those four cases range from −1.1 down to −1.9. (See the supplementary materials for a discussion of Z scores).
The edges of the five-dimensional polytopes can be read directly from Appendix B, Table 3. For example the 6 polytope is bounded by 16, 26, 56, 67 and 69, and the F polytope is bounded by 1F, 2F, 8F, BF and EF. It is important to note that the polytopes 1, 2, 3, 4 and 5 extend into the boundaries of both the 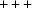 and the
and the  branches of
branches of 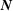 . Even though the polytopes 3, 4 and 5 do not contain any valid Niggli-reduced
. Even though the polytopes 3, 4 and 5 do not contain any valid Niggli-reduced 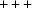 cells, they are part of both branches of
cells, they are part of both branches of 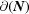 even for
even for 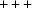 .
.
A7. The three-dimensional boundary polytopes
The three-dimensional boundary polytopes are created by the intersection of three five-dimensional boundary polytopes. In some cases the boundary polytope is better represented by a fourfold intersection. The boundary polytope 34CD is equivalent to 34C and 34D, 359A is equivalent to 359 and 35A, 4567 is equivalent to 456 and 457, 679C is equivalent to 69C and 79C, and 9ACD is equivalent to 9AD and ACD. These are ‘flat boundary intersection’ cases in which one side of the flat boundary intersection implies the other. On the other hand 126 and 127, 12A and 129, 12C and 12D, 2AD and 29C, and 69C and 79C are distinct rather than equivalent pairs of flat boundary intersections. Six twofold intersections of five-dimensional boundary polytopes (6A, 6C, 79, 7D, 9D and AC) result in three-dimensional boundary polytopes, rather than in four-dimensional boundary polytopes. In each case both boundary polytopes have mismatched partners from ‘flat boundary intersections’. Let us examine the 6A case in detail, elaborating on the discussion of the four-dimensional boundary polytopes above.
Cases 6 and A are 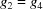 and
and 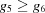 , and
, and 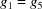 and
and 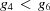 , respectively. For intersections, we use the closures of the boundary polytopes, so we have the closure of A as
, respectively. For intersections, we use the closures of the boundary polytopes, so we have the closure of A as 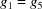 and
and 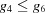 . The Niggli cone itself imposes the additional restrictions
. The Niggli cone itself imposes the additional restrictions 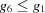 and
and 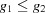 , but from 6,
, but from 6, 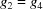 , and from the closure of A,
, and from the closure of A, 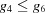 , so we have
, so we have
and from the Niggli reduction conditions
Thus 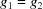 and
and 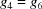 , meaning that, in addition to satisfying the constraints of case A, we also satisfy the constraints of case 9,
, meaning that, in addition to satisfying the constraints of case A, we also satisfy the constraints of case 9, 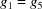 and
and 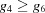 . Thus case 6A is actually case 69A, producing a true three-dimensional boundary polytope from the intersection of two five-dimensional boundary polytopes owing to the additional constraints of Niggli reduction. As we will see in the discussion of the two-dimensional boundary polytopes, the Niggli reduction constraints can result in shedding one or more degrees of freedom, allowing some twofold intersections of five-dimensional boundary polytopes to result in two-dimensional boundary polytopes.
. Thus case 6A is actually case 69A, producing a true three-dimensional boundary polytope from the intersection of two five-dimensional boundary polytopes owing to the additional constraints of Niggli reduction. As we will see in the discussion of the two-dimensional boundary polytopes, the Niggli reduction constraints can result in shedding one or more degrees of freedom, allowing some twofold intersections of five-dimensional boundary polytopes to result in two-dimensional boundary polytopes.
After excluding the cases that involve any of 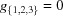 , there are 79 cases as shown in Appendix B, Table 4. The relative populations for all the three-dimensional boundary polytopes have Z scores greater than −1.1.
, there are 79 cases as shown in Appendix B, Table 4. The relative populations for all the three-dimensional boundary polytopes have Z scores greater than −1.1.
For completeness, if one wished to include the boundary polytope with 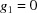 it would be considered in the three-dimensional polytopes. In
it would be considered in the three-dimensional polytopes. In 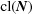 ,
, 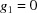 forces
forces 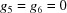 ,
, 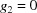 , leaving only three degrees of freedom at
, leaving only three degrees of freedom at 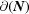 . Note that
. Note that 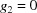 is of even lower dimension, one, because
is of even lower dimension, one, because 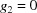 forces
forces 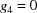 as well as
as well as 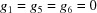 , leaving only one degree of freedom (
, leaving only one degree of freedom (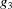 ).
). 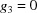 is just the origin.
is just the origin.
A8. The two-dimensional boundary polytopes
The two-dimensional boundary polytopes are, in general, created by the intersection of four five-dimensional boundary polytopes, but several well populated fourfold intersections result in three-dimensional boundary polytopes rather than two-dimensional boundary polytopes. Several fourfold intersections are most naturally presented as higher multiplicity intersections, and in some cases the intersection of as few as two five-dimensional boundary polytopes is sufficient to create a two-dimensional boundary polytope. After excluding the cases that involve any of 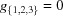 , there are 55 cases as shown in Appendix B, Table 5. The combination of seven boundary polytopes 1679ACD is the hexagonal rhombohedral hR, lattice character 9, Roof/Niggli symbol 49B, subspace
, there are 55 cases as shown in Appendix B, Table 5. The combination of seven boundary polytopes 1679ACD is the hexagonal rhombohedral hR, lattice character 9, Roof/Niggli symbol 49B, subspace 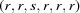 . Alternatively, lattice character 9 can be viewed as any of 81 other intersections, including two twofolds (6D, 7A), 18 threefolds (179, 16A, 16C, 16D, 17A, 17D, 19D, 1AC, 67A, 67D, 69D, 6AC, 6AD, 6CD, 79A, 79D, 7AC, 7AD), 33 fourfolds (1679, 167A, 167C, 167D, 169A, 169C, 169D, 16AC, 16AD, 16CD, 179A, 179C, 179D, 17AC, 17AD, 17CD, 19AC, 19AD, 19CD, 1ACD, 679A, 679D, 67AC, 67AD, 67CD, 69AC, 69AD, 69CD, 6ACD, 79AC, 79AD, 79CD, 7ACD), 21 fivefolds (1679A, 1679C, 1679D, 167AC, 167AD, 167CD, 169AC, 169AD, 169CD, 16ACD, 179AC, 179AD, 179CD, 17ACD, 19ACD, 679AC, 679AD, 679CD, 67ACD, 69ACD, 79ACD) and seven sixfolds (1679AC, 1679AD, 1679CD, 167ACD, 169ACD, 179ACD, 679ACD), and is a very highly populated two-dimensional boundary polytope. If we exclude this case, the remaining 54 cases have Z scores ranging from −1.36 (for 1456) to 0.84 (for 123E) to 2.75 (for 29ACD).
. Alternatively, lattice character 9 can be viewed as any of 81 other intersections, including two twofolds (6D, 7A), 18 threefolds (179, 16A, 16C, 16D, 17A, 17D, 19D, 1AC, 67A, 67D, 69D, 6AC, 6AD, 6CD, 79A, 79D, 7AC, 7AD), 33 fourfolds (1679, 167A, 167C, 167D, 169A, 169C, 169D, 16AC, 16AD, 16CD, 179A, 179C, 179D, 17AC, 17AD, 17CD, 19AC, 19AD, 19CD, 1ACD, 679A, 679D, 67AC, 67AD, 67CD, 69AC, 69AD, 69CD, 6ACD, 79AC, 79AD, 79CD, 7ACD), 21 fivefolds (1679A, 1679C, 1679D, 167AC, 167AD, 167CD, 169AC, 169AD, 169CD, 16ACD, 179AC, 179AD, 179CD, 17ACD, 19ACD, 679AC, 679AD, 679CD, 67ACD, 69ACD, 79ACD) and seven sixfolds (1679AC, 1679AD, 1679CD, 167ACD, 169ACD, 179ACD, 679ACD), and is a very highly populated two-dimensional boundary polytope. If we exclude this case, the remaining 54 cases have Z scores ranging from −1.36 (for 1456) to 0.84 (for 123E) to 2.75 (for 29ACD).
Let us consider how one of the twofolds, 6D, results in only two degrees of freedom. Cases 6 and D are  and
and  , and
, and  and
and 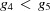 , respectively. The closure of D is
, respectively. The closure of D is 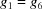 and
and 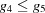 , and Niggli reduction requires
, and Niggli reduction requires 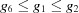 , from which it follows that
, from which it follows that
and therefore
creating the subspace 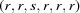 , i.e. two degrees of freedom.
, i.e. two degrees of freedom.
A9. The one-dimensional boundary polytopes
There are 14 distinct one-dimensional boundary polytopes, with many equivalent presentations. The most complex situation is best presented as an eightfold intersection, 12679ACD, i.e.
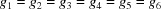 , which is the face-centered cubic
, which is the face-centered cubic 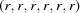 . There are 81 other equivalent presentations of the face-centered cubic, inherited from the sevenfold intersection hexagonal rhombohedral discussed above by adding case 2 to each of those presentations, thereby providing two threefolds for the face-centered cubic case (26D and 27A). The remaining 13 one-dimensional boundary polytopes are 12345
. There are 81 other equivalent presentations of the face-centered cubic, inherited from the sevenfold intersection hexagonal rhombohedral discussed above by adding case 2 to each of those presentations, thereby providing two threefolds for the face-centered cubic case (26D and 27A). The remaining 13 one-dimensional boundary polytopes are 12345 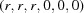 , 1234CD
, 1234CD 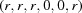 (equivalent to 1234C, 1234D, 123CD, 124CD), 1234E
(equivalent to 1234C, 1234D, 123CD, 124CD), 1234E 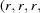
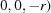 , 12359A
, 12359A 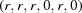 (equivalent to 12359, 1235A, 1239A, 1259A), 1235B
(equivalent to 12359, 1235A, 1239A, 1259A), 1235B 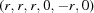 , 123AD
, 123AD 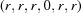 , 123BEF
, 123BEF 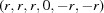 (equivalent to 123BE, 123BF, 123EF, 12BEF, 23BEF), 124567
(equivalent to 123BE, 123BF, 123EF, 12BEF, 23BEF), 124567 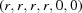 (equivalent to 12456, 12457, 12467, 12567), 12458
(equivalent to 12456, 12457, 12467, 12567), 12458 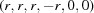 , 1247C
, 1247C 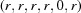 , 1248EF
, 1248EF 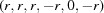 (equivalent to 1248E, 1248F, 124EF, 128EF), 12569
(equivalent to 1248E, 1248F, 124EF, 128EF), 12569 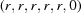 and 1258BF
and 1258BF 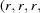
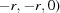 (equivalent to 1258B, 1258F, 125BF, 128BF).
(equivalent to 1258B, 1258F, 125BF, 128BF).
These 14 one-dimensional boundary polytopes of 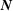 correspond exactly to the 14 vertices of the hyperpolyhedra given by Gruber (1997 ▶, Table 1) for which none of
correspond exactly to the 14 vertices of the hyperpolyhedra given by Gruber (1997 ▶, Table 1) for which none of 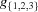 are zero. The 14 that match are a confirmation of the completeness of this analysis. Owing to the distortion introduced by projection, the rejection of the cases for which any of
are zero. The 14 that match are a confirmation of the completeness of this analysis. Owing to the distortion introduced by projection, the rejection of the cases for which any of 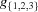 are zero is important in preserving the metric for incommensurate edges near the origin.
are zero is important in preserving the metric for incommensurate edges near the origin.
If we exclude the highly populated face-centered cubic, the Z scores for the relative populations of the remaining 13 one-dimensional boundary polytopes range from more than −1.1 for 12569 to 1.44 for 123BEF.
A10. Relationship between boundary polytopes and lattice type
‘Lattice characters’ provide a finer-grained division of lattice type than the 14 Bravais lattice types (International Tables for Crystallography, Vol. A, Burzlaff et al., 1992 ▶). In order to understand the relationship between the 216  boundary polytopes and the 44 lattice characters in International Tables, we use combinations of the 15 five-dimensional boundary polytopes and of the special-position subspaces of those polytopes. There are multiple alternative representations of some of the lattice characters. We discuss some of them below.
boundary polytopes and the 44 lattice characters in International Tables, we use combinations of the 15 five-dimensional boundary polytopes and of the special-position subspaces of those polytopes. There are multiple alternative representations of some of the lattice characters. We discuss some of them below.
We refer to Roof’s redrawn Niggli figure identifiers (Roof, 1967 ▶) as ‘Roof/Niggli symbols’. We may associate the Roof/Niggli symbols, lattice characters and Bravais lattice types with the indicated subspaces of  and combinations of boundary polytopes and special conditions as shown in Table 4 ▶. The triclinic lattice characters 31 and 44 are not included because no boundary polytopes are needed for the triclinic case as they fill the Niggli-reduced cone.
and combinations of boundary polytopes and special conditions as shown in Table 4 ▶. The triclinic lattice characters 31 and 44 are not included because no boundary polytopes are needed for the triclinic case as they fill the Niggli-reduced cone.
Table 4. Roof/Niggli symbol, International Tables (IT) lattice character, Bravais lattice type,  subspace (Andrews & Bernstein, 1988 ▶) and
subspace (Andrews & Bernstein, 1988 ▶) and  boundary polytope.
boundary polytope.
| Roof/Niggli symbol | IT lattice character | Bravais lattice type |
 subspace subspace |
 boundary polytope boundary polytope |
|---|---|---|---|---|
| 44A | 3 | cP |
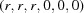
|
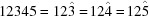
|
| 44C | 1 | cF |
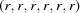
|
12679ACD |
| 44B | 5 | cI |
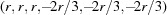
|
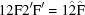
|
| 45A | 11 | tP |
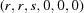
|
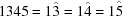
|
| 45B | 21 | tP |
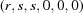
|
|
| 45D | 6 | tI |
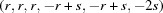
|
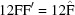
|
| 45D | 7 | tI |
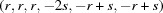
|
|
| 45C | 15 | tI |
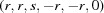
|
158BF |
| 45E | 18 | tI |
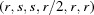
|
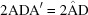
|
| 48A | 12 | hP |
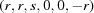
|
134E |
| 48B | 22 | hP |
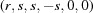
|
2458 |
| 49C | 2 | hR |
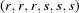
|
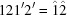
|
| 49D | 4 | hR |
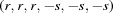
|
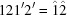
|
| 49B | 9 | hR |
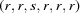
|
1679ACD |
| 49E | 24 | hR |
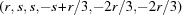
|
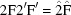
|
| 50C | 32 | oP |
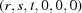
|
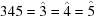
|
| 50D | 13 | oC |
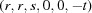
|
134 |
| 50E | 23 | oC |
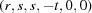
|
245 |
| 50A | 36 | oC |
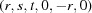
|
35B |
| 50B | 38 | oC |
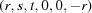
|
34E |
| 50F | 40 | oC |
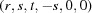
|
458 |
| 51A | 16 | oF |
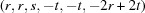
|
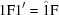
|
| 51B | 26 | oF |
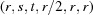
|
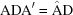
|
| 52A | 8 | oI |
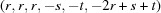
|
12F |
| 52B | 19 | oI |
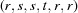
|
29C = 2AD |
| 52C | 42 | oI |
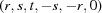
|
58BF |
| 53A | 33 | mP |
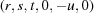
|
35 |
| 53B | 35 | mP |
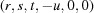
|
45 |
| 53C | 34 | mP |
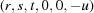
|
34 |
| 55A | 10 | mC |
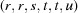
|
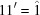
|
| 55A | 14 | mC |
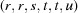
|
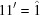
|
| 57B | 17 | mC |
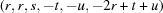
|
1F |
| 55B | 20 | mC |
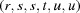
|
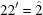
|
| 55B | 25 | mC |
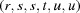
|
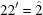
|
| 57C | 27 | mC |
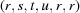
|
9C = AD |
| 56A | 28 | mC |
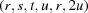
|
|
| 56C | 29 | mC |
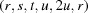
|
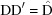
|
| 56B | 30 | mC |
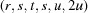
|
|
| 54C | 37 | mC |
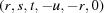
|
5B |
| 54A | 39 | mC |
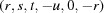
|
4E |
| 54B | 41 | mC |
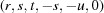
|
58 |
| 57A | 43 | mC |
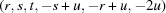
|
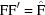
|
The primitive Bravais lattice types have a simple relationship to the boundary polytopes. The primitive cubic, which has one degree of freedom as a  subspace, is the intersection of five five-dimensional boundary polytopes. The primitive tetragonal and primitive hexagonal lattice types each have two degrees of freedom as
subspace, is the intersection of five five-dimensional boundary polytopes. The primitive tetragonal and primitive hexagonal lattice types each have two degrees of freedom as  subspaces and each is the intersection of four five-dimensional boundary polytopes. The primitive orthorhombic lattice type has three degrees of freedom as a
subspaces and each is the intersection of four five-dimensional boundary polytopes. The primitive orthorhombic lattice type has three degrees of freedom as a  subspace and is the intersection of three five-dimensional boundary polytopes. The primitive monoclinic lattice types each have four degrees of freedom as
subspace and is the intersection of three five-dimensional boundary polytopes. The primitive monoclinic lattice types each have four degrees of freedom as  subspaces, and each is the intersection of two five-dimensional boundary polytopes.
subspaces, and each is the intersection of two five-dimensional boundary polytopes.
The combination of eight boundary polytopes 12679ACD (equivalent to the threefold combinations 26D and 27A) is the face-centered cubic cF, lattice character 1, Roof/Niggli symbol 44C, subspace 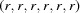 (Andrews & Bernstein, 1988 ▶). Alternatively, cF can be viewed as any of
(Andrews & Bernstein, 1988 ▶). Alternatively, cF can be viewed as any of  ,
,  or
or  and of several other intersections. As one would expect from the large number of intersecting boundary polytopes, this is a very complex region of
and of several other intersections. As one would expect from the large number of intersecting boundary polytopes, this is a very complex region of  and will be the subject of a later article.
and will be the subject of a later article.
The one-dimensional combinations of six boundary polytopes 1234CD (equivalent to the fivefolds 1234C, 1234D, 123CD, 124CD), 12359A (equivalent to the fivefolds 12359, 1235A, 1239A, 1259A), 123BEF (equivalent to the fivefolds 123BE, 123BF, 123EF, 12BEF, 23BEF), 124567 (equivalent to the fivefolds 12456, 12457, 12467, 12567), 1248EF (equivalent to the fivefolds 1248E, 1248F, 124EF, 128EF) and 1258BF (equivalent to the fivefolds 1258B, 1258F, 125BF, 128BF) form the subspaces
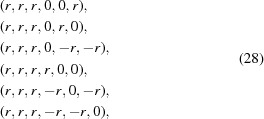 |
of which none are Niggli-reduced and which are therefore a set of open-boundary polytopes.
Most of the 216  boundary polytopes are non-Niggli-reduced open-boundary polytopes of the Niggli region. Therefore only two of the fivefold boundary polytopes, five of the fourfold boundary polytopes, eight of the threefold boundary polytopes and 11 of the twofold boundary polytopes correspond directly to lattice characters. None of the single five-dimensional boundary polytopes correspond to lattice characters.
boundary polytopes are non-Niggli-reduced open-boundary polytopes of the Niggli region. Therefore only two of the fivefold boundary polytopes, five of the fourfold boundary polytopes, eight of the threefold boundary polytopes and 11 of the twofold boundary polytopes correspond directly to lattice characters. None of the single five-dimensional boundary polytopes correspond to lattice characters.
We are working from the boundary polytopes, looking for the resulting symmetries. Hosoya (1990 ▶) started, instead, from the three highest-symmetry lattice types (the three cubics), added the lower-symmetry primitive hexagonal lattice type, and inferred boundary polytopes from the symmetries, having to treat open-boundary polytopes as if they were Niggli reduced. The resulting six boundary polytopes of the three cubics and the primitive hexagonal restated in terms of  are given in Table 5 ▶.
are given in Table 5 ▶.
Table 5. The Hosoya boundary polytopes of the three cubic lattice types and the primitive hexagonal in terms of  .
.
| Hosoya1 |
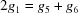
|
| Hosoya2 |
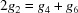
|
| Hosoya3 |
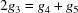
|
| Hosoya4 |
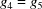 , the special-position subspace of case 1 , the special-position subspace of case 1 |
| Hosoya5 |
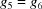 , the special-position subspace of case 2 , the special-position subspace of case 2 |
| Hosoya6 |
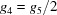 , the special-position subspace of case D , the special-position subspace of case D |
A11. Boundary polytope summary
The widespread use of Niggli reduction in crystallography implies that it should be thoroughly understood. Robust identification of Bravais lattices and lookup of unit-cell parameters in databases would be improved if a successful embedding of the Niggli space could be achieved. We have investigated and enumerated the several kinds of boundary polytopes on the Niggli cone and enumerated the transformations and projectors specific to each. While other, related, work has often used three-dimensional sections, our work natively addresses the boundary polytopes and transformations in the Euclidean space  . The single point of view and the simple linear algebra involved makes the presentation more consistent.
. The single point of view and the simple linear algebra involved makes the presentation more consistent.
Some unexpected complexities have been encountered, such as the occurrence of one boundary polytope that is the intersection of eight five-dimensional boundary polytopes, a fruitful area for further investigation.
Footnotes
This article is derived from one originally submitted to Acta Crystallographica Section A on 16 November 2011.
Supporting information for this paper is available from the IUCr electronic archives (Reference: KK5144).
References
- Andrews, L. C. & Bernstein, H. J. (1976). Acta Cryst. A32, 504–506.
- Andrews, L. C. & Bernstein, H. J. (1988). Acta Cryst. A44, 1009–1018.
- Andrews, L. C., Bernstein, H. J. & Pelletier, G. A. (1980). Acta Cryst. A36, 248–252.
- A Society of Gentlemen in Scotland (1771). Editor. Encyclopedia Britannica, or, a Dictionary of Arts and Sciences, Compiled upon a New Plan, Vol. II(54), p. 677. Edinburgh: A. Bell and C. Macfarquhar.
- Azaroff, L. V. & Buerger, M. J. (1958). The Powder Method in X-ray Crystallography, ch. 11, pp. 124–159. New York: McGraw-Hill.
- Beltrami, E. (1873). G. Mat. Uso Studenti Univ. 11, 98–106.
- Buerger, M. J. (1960). Z. Kristallogr. 113, 52–56.
- Burzlaff, H., Zimmermann, H. & de Wolff, P. M. (1992). International Tables for Crystallography, Vol. A, edited by T. Hahn, ch. 9, pp. 734–744. Dordrecht: Kluwer Academic Publishers.
- Byram, S. K., Campana, C. F., Fait, J. & Sparks, R. A. (1996). J. Res. NIST, 101, 295–300. [DOI] [PMC free article] [PubMed]
- Delaunay, B. N. (1932). Z. Kristallogr. 84, 109–149.
- Gruber, B. (1973). Acta Cryst. A29, 433–440.
- Gruber, B. (1997). Acta Cryst. A53, 505–521.
- Gruber, B. (2006). International Tables for Crystallography, Vol. A, 1st online ed., edited by T. Hahn, ch. 9.3, pp. 756–760. Chester: International Union of Crystallography.
- Helgason, S. (1962). Differential Geometry and Symmetric Spaces New York, London: Academic Press.
- Himes, V. L. & Mighell, A. D. (1987). Acta Cryst. A43, 375–384.
- Hosoya, M. (1990). Bull. Coll. Sci. Univ. Ryukyus, 50, 1–13.
- Hosoya, M. (2000). Acta Cryst. A56, 259–263. [DOI] [PubMed]
- Jordan, C. (1874). J. Math. Pures Appl. Deuxiéme Ser. 19, 35–54.
- Kabsch, W. (1993). J. Appl. Cryst. 26, 795–800.
- Kabsch, W. (2010). Acta Cryst. D66, 133–144. [DOI] [PMC free article] [PubMed]
- Kabsch, W. (2013). Personal communication.
- Macíček, J. & Yordanov, A. (1992). J. Appl. Cryst. 25, 73–80.
- McGill, K. J., Mojgan, A., Karakasheva, M. T., Andrews, L. C. & Bernstein, H. J. (2014). J. Appl. Cryst. 47, 360–354. [DOI] [PMC free article] [PubMed]
- Minor, W. & Otwinowski, Z. (1997). Crystallographic Computing 7. Proceedings from the Macromolecular Crystallography Computing School. Chester: International Union of Crystallography.
- Nash, J. (1956). Ann. Math. 63, 20–63.
- Niggli, P. (1928). Krystallographische und Strukturtheoretische Grundbegriffe, Handbuch der Experimentalphysik, Vol. 7(1). Leipzig: Akademische Verlagsgesellschaft.
- Oishi-Tomiyasu, R. (2012). Acta Cryst. A68, 525–535. [DOI] [PubMed]
- Roof, R. B. Jr (1967). A Theoretical Extension of the Reduced-Cell Concept in Crystallography Report No. LA-4038, TID-4500. Los Alamos Scientific Laboratory, New Mexico, USA. http://lib-www.lanl.gov/cgi-bin/getfile?00378045.pdf.
- Seeber, L. A. (1831). Untersuchungen über die Eigenschaften der positiven ternæren quadratischen Formen, Vol. 1. Mannheim: Tobias Loeffler.
- Selling, E. (1874). J. Reine Angew. Math. 1874, 143–229.
- Stewart, G. W. (1993). SIAM Rev. pp. 551–566.
- Toby, B. (1994). Personal communication.
- Von Laue, M. (1952). International Tables for X-ray Crystallography, Vol. I, edited by N. F. M. Henry & K. Lonsdale, pp. 1–5. Birmingham: Kynoch Press.
- Zimmermann, H. & Burzlaff, H. (1985). Z. Kristallogr. 170, 241–246.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix B. DOI: 10.1107/S1600576713031002/kk5144sup1.pdf