A 3,500-year tree-ring record of annual precipitation on the northeastern Tibetan Plateau

Significance

This paper describes the production and climatic interpretation of a tree-ring width chronology that is currently the longest, absolutely dated series produced for the northeastern Tibetan Plateau and one of the longest in the world. The method of chronology construction enables comparison of variations in precipitation totals over long timescales as well as shorter periods. Precipitation in this region during the last 50 years has been historically high—likely higher than for any equivalent length period in at least 3,500 years, even when considering the chronology and interpretational uncertainty. Notable dry periods occurred in the 4th century BCE and in the second half of the 15th century CE.

Abstract

An annually resolved and absolutely dated ring-width chronology spanning 4,500 y has been constructed using subfossil, archaeological, and living-tree juniper samples from the northeastern Tibetan Plateau. The chronology represents changing mean annual precipitation and is most reliable after 1500 B.C. Reconstructed precipitation for this period displays a trend toward more moist conditions: the last 10-, 25-, and 50-y periods all appear to be the wettest in at least three and a half millennia. Notable historical dry periods occurred in the 4th century BCE and in the second half of the 15th century CE. The driest individual year reconstructed (since 1500 B.C.) is 1048 B.C., whereas the wettest is 2010. Precipitation variability in this region appears not to be associated with inferred changes in Asian monsoon intensity during recent millennia. The chronology displays a statistical association with the multidecadal and longer-term variability of reconstructed mean Northern Hemisphere temperatures over the last two millennia. This suggests that any further large-scale warming might be associated with even greater moisture supply in this region.

The value of high-resolution proxy climate data for reconstructing climate variability beyond the limited time span of direct instrumental observations is borne out by their use in contemporary studies of the causes of late-Holocene climate changes, in particular research that seeks to distinguish the fingerprint of anthropogenic change from the background of natural climate variability (1). Long paleoclimate records, with annual resolution and good dating control, represent an ideal basis for rigorous statistical comparison of hypothetical climate forcing and observed climate responses, whether based on statistical climate change detection methodology (2) or through the “validation” of climate model simulations of past climate (3). Climate proxy data are more valuable where it can be demonstrated that they represent a wide spectrum of climate variability, encompassing year-to-year, decadal, and multicentennial timescale evidence of past changes. Such records are rare, and tree-ring–based reconstructions are among the most prominent (4). Many of these records provide evidence of past warm-season temperature variability and are located in near–tree-line regions at high-elevation or high-latitude sites (5, 6). Long precipitation-sensitive tree-ring chronologies are generally from lower latitudes and elevations (7–12).

In the last decade, dendroclimatic research on the Tibetan Plateau (TP) has expanded rapidly, with numerous localized studies of past tree growth and its climate controls and temporal ranges extending from hundreds to thousands of years. Here we build on previous studies (13–17) by describing a new multimillennial-length chronology constructed from a combination of moisture-sensitive ring-width measurements from archaeological, subfossil and living trees from multiple sites on the northeastern TP. Processing these data in a manner designed to identify and preserve common low-frequency variability provides a history of tree growth stretching over 4,000 y and one that is shown to be a likely reliable indicator of yearly moisture changes encompassing interannual up to millennial scales of variability back at least to –1500 (Methods).

Chronology Development

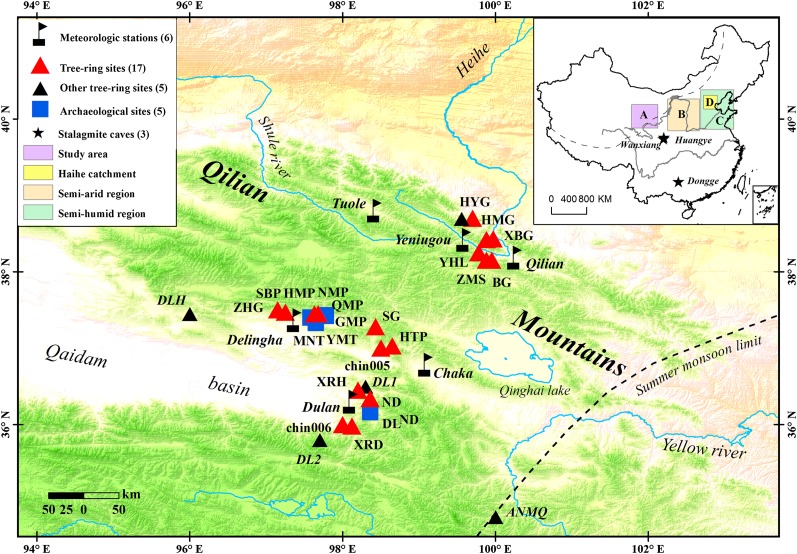
In the cold and arid conditions of the northeastern TP, Qilian juniper (Juniperus przewalskii Kom.) grows widely on high, south-facing slopes. Exceptionally, these trees can reach ages above 3,000 y, and living trees over 2,000 y old are not rare. Numerous core samples from living trees and from standing or fallen dead trees have been collected from a total of 17 sites in the Qilian Mountains, all located between ∼37–38.7°N and 97–100°E, with elevations ranging from 2,863 to 4,175 m above sea level. These sites are clustered in two areas, centered near Yeniugou and Delingha (Fig. 1 and SI Appendix, Table SA1). Ring-width measurements from these samples are combined here with similar data from around Dulan: previously published measurements from archaeological wood from a series of tombs just south of Dulan (∼35.8–36.3°N; 98–99°E), living trees from Shenge (37.0°N; 98.3°E) and Dulan (36.0°N; 98.0°E) (14), and more recently collected tree-ring data from Dulan (∼35.5–36.3°N; 98.1–98.7°E). By combining the measurement series from a total of 1,203 trees, it has been possible to establish an absolutely dated ring-width chronology that represents a continuous record of year-to-year growth variability for this species and general location spanning 4,649 y from –2637–2011.

Fig. 1.

Map of the study region. Locations of tree-ring and weather station sites (refer to the key; metadata provided in SI Appendix). (Inset) Study location (A) within China in relation to the locations of other paleoclimate records considered here and to the approximate limit of the direct summer monsoon (dashed line in the main map and Inset).

Having established the firm dating of the measurement series using high-frequency cross-matching (SI Appendix), they must then be processed for interpreting past climate influences on tree growth at longer as well as short timescales. The tendency for annual growth rings to become thinner in old trees must be removed from the measurement data, but information about past long-term changes in climate must be retained to produce a chronology that represents climate changes over a wide spectrum of timescales. Here, we use a recent form of processing known as Signal-Free Regional Curve Standardization (SF-RCS). This establishes an empirical model of “expected” ring width as a function of tree age, but with the influence of changing climate on tree growth having been removed (18). Dividing measured ring widths by the appropriate expected values for the correct ring age converts the measurements into relative indices, effectively removing a tree-age–related trend from the measurement data for each tree: a process known in dendroclimatology as standardization. The resulting standardized indices are averaged in the correct calendar years to produce an annually resolved chronology representing the changing signal of common tree-growth forcing over past millennia.

In practice, trees show a range of growth rates even when growing in parallel under the same climate conditions, and so multiple standardization curves are used, each curve applied as described above but to standardize a specific subset of the total data, representing a particular growth-rate class of trees (Methods). The growth habit of this species is characteristically complex with older trees growing slowly and forming convoluted multistem shapes. In very old age it is not unusual for the trees to grow around a contorted stem (SI Appendix, Figs. SA3–SA6). The ring-width series can exhibit large interannual variability compared with the amplitude of longer-term growth trends, with the latter displaying notable variability within and between trees. These complex growth forms present a particular problem for extracting a reliable chronology of low-frequency variability. The multiple-curve RCS method can account for part of this issue—namely, different mean growth rates between different trees—but cannot account for inhomogeneous changes in growth rate during the lifespan of a tree that might arise from changes in growth form or from sampling along different paths through the tree cross-section. Like inhomogeneities that can occur in trees with simpler growth forms (e.g., with a change from suppression to release), they introduce additional noise and uncertainty into a chronology. Combining data from a large sample of trees will reduce the influence of this noise, to an extent that depends on how systematic its occurrence is. Here, due to the complex growth forms in some of the sampled trees, data from a large number of trees are required to achieve an acceptable signal-to-noise ratio in the expression of long-timescale variability. Parallel variability displayed in the chronologies produced from independent subdivisions of the data (into growth-rate classes) corroborates the interpretation that the common external influence on the growth of these trees over time is being expressed reliably.

Fig. 2A shows a group of four independent SF-RCS chronologies, each produced using its own RCS curve. Each RCS curve is produced for one of four growth-rate classes (i.e., from faster- to slower-growing trees) by aligning the measurement data from inner (pith) year to outer rings and averaging for each ring age. Where there are progressively fewer series reaching older ages, the mean curves become noisy, but each is smoothed to provide the reference SF-RCS curve for standardizing the measurements from trees within that class (Methods and SI Appendix). The resulting four subchronologies are shown superimposed, after smoothing with a 50-y filter, to emphasize the longer-timescale variance.

Fig. 2.

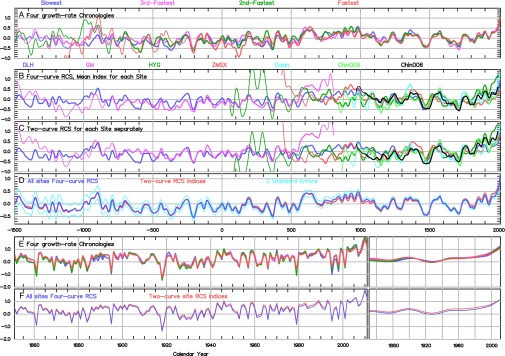
Consistency between subsets of tree-ring data. Chronologies formed by averaging tree indices (i.e., standardized tree-ring width) across different subsets of trees and using different SF-RCS standardization approaches. (A) Four growth-rate chronologies (an equal number of trees are assigned to each set, grouped according to their mean growth rate), each standardized with a separate SF-RCS curve. (B) Seven site chronologies, each the average of indices obtained using the four overall growth-rate SF-RCS curves. (C) Seven site chronologies, where each site dataset was standardized using two growth-rate SF-RCS curves. (D) Overall QLS chronologies formed from either the four growth-rate chronologies (blue, with ±2 chronology SEs in light blue) or the seven site chronologies (red). All chronologies are smoothed with a 50-y spline (end values are more uncertain), and sections comprising less than six trees are shown as thinner lines. Chronology values after 1850 are repeated with (Right) and without (Left) smoothing for the (E) four growth-rate chronologies and (F) two overall QLS chronologies.

Similar multicentennial and even millennial timescale variability is apparent in these independent series back to about –1500. Before this, where the number of samples in each series becomes very small, the series diverge although they still display clear common variability on annual and multidecadal timescales (SI Appendix, Figs. SB9 and SB10). Fig. 2B shows the same index data but averaged by site location to provide local-area chronologies. Fig. 2C shows similar local-site chronologies but with the original measurement data for each site having been separately standardized using only two RCS curves, one for faster and one for slower growth trees at that site. Similar variability is again apparent in these local chronologies where replication is high (Fig. 2 B and C), but less agreement when it is low. The average chronologies produced from the indices shown in Fig. 2 A and C are shown as red and blue curves, respectively, in Fig. 2D. The correspondence in low-frequency variability between these alternatively processed chronologies is excellent.

Using only a single RCS curve to standardize all data series overestimates the expected growth of slower-growing trees over their lifetime and underestimates that of faster-growing trees, producing overly small indices for the slower (earlier) growing archaeological data and overly large indices for the faster (predominately later) growing trees, respectively (SI Appendix). We note that using different numbers of multiple RCS curves to standardize different growth-rate classes of trees produces largely the same pattern of millennial variability (whether two, three, four, five, or six RCS curves are used), but all remove the likely bias seen in the single-RCS curve implementation (SI Appendix, Fig. SB1). We adopt the four-curve SF-RCS chronology (blue curve in Fig. 2D) to interpret as a climate proxy for this region. Henceforth this is referred to as the Qilian Mts. Chronology (QLS).

The recent data from the alternative chronologies (shown smoothed in Fig. 2 A and D) are shown as annual values in Fig. 2 E and F. This demonstrates that the unusually high chronology values apparent in the final decades of the record are real and not an artifact of the smoothing filter used in Fig. 2 A–D.

Climatic Interpretation and Reconstruction

Correlations between the QLS chronology and monthly mean temperature and precipitation series over 56 y, 1956–2011, are shown in SI Appendix, Fig. SD1, using either the original data or detrended series. Positive temperature correlations are apparent for a number of individual months, principally in the autumn and winter preceding tree growth, but these largely disappear when the detrended data series are compared. However, the pattern of strong positive correlations with precipitation variability in the summer of the previous and current year is similar whether the data are detrended or not (note that measured precipitation, like temperature, has a positive trend over this period). These results suggest an optimal association (SI Appendix, Fig. SD1 b and c) between annual tree growth and precipitation averaged over either a short 2-month spring/summer season (May to June) or a longer “annual water year” (encompassing all months from July of the previous year up to June of the current year).

The interpretation of a dominant moisture control on tree growth in this region is supported by a number of previous studies (16, 19–22). Interpreting local tree growth for this species as a predominant response to interannual variability of prior July to current-year June precipitation is consistent with the results of refs. 14 and 16, although their analyses were based on shorter precipitation records. It is also consistent with the early wood contributing more than 80% of the total ring-width increment (23).

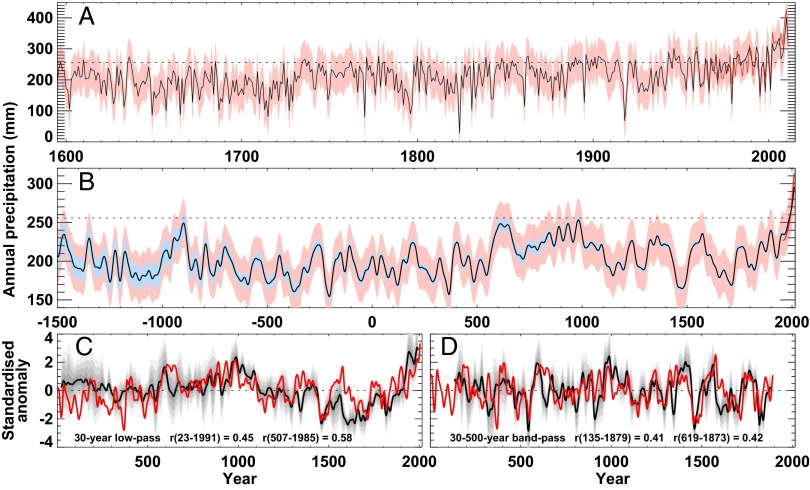
The QLS chronology was scaled so that the mean and variance of the detrended chronology match those of a similarly detrended regional precipitation series over the period 1957–2011 (Methods). The scaling factor was applied to the chronology data to produce a reconstruction of annual precipitation spanning the period over which the chronology is considered here to be sufficiently reliable (i.e., –1500 to 2011; SI Appendix, Section F) to use as an indicator of regional precipitation. The correlation between the reconstruction and the observed precipitation is 0.84 (P < 0.01). Other methods of calibration give similar results, and cross-validation tests demonstrate the robustness of this association (to the extent possible using the relatively short instrumental data record; SI Appendix, Section D). Fig. 3 A and B shows the rescaled chronology along with uncertainty estimates that incorporate both ring-width chronology error and the error associated with using the chronology to represent precipitation (estimated from the residuals between the reconstructed and observed precipitation).

Fig. 3.

Reconstructed annual precipitation for the northeastern Tibetan Plateau and comparison with a composite NH temperature reconstruction. (A) Estimates of annual precipitation from the calibrated QLS chronology, showing yearly values since 1595, together with the total uncertainty (pale red) and the part of the uncertainty arising from chronology uncertainty (pale blue), and the observed regional precipitation since 1957 (red). The horizontal dotted line indicates the mean precipitation over the calibration period (1957–2011). Note that the calibration residuals show that the estimated values somewhat exaggerate the dryness in some dry years (e.g., 1978 and 1998), and this should be borne in mind when interpreting extremely dry years in the reconstruction. (B) As A, except the data are shown for the period since –1500 with 50-y smoothing (smoothed values will be more uncertain near the end of the time series). (C) Comparison of the precipitation reconstruction (red) with a composite of NH temperature reconstructions (black line, composite mean; four levels of gray shading, composite mean ± 0.5, 1.0, 1.5, and 2.0 composite SDs). All series have been normalized to have zero mean and unit SD over the common overlap period (Methods) and smoothed with a 30-y low-pass Gaussian-weighted filter, truncated seven values from each end to reduce the influence of filter end effects. Correlations between the precipitation and composite-mean temperature reconstructions are indicated on the panel for the full overlap period and the shorter period when at least six NH temperature reconstructions are available. (D) As C, except that all series have been band-pass–filtered to retain variance on timescales between 30 and 500 y, and the truncation is extended to 119 values from each end because the end effects of a 500-y filter are much greater (SI Appendix, Fig. SG1).

In addition to the large interannual variance, there is significant long-term variability at millennial and centennial timescales in the QLS precipitation reconstruction. Perhaps the most fundamental feature of the reconstruction is an apparent rise in the general level of precipitation that occurred between 500 and 600: the prominently wetter ninth century BCE was followed by 14 centuries (–900 to 500) with mean precipitation of only 192 mm, compared with 228 mm for the five centuries from 601 to 1100. In the 50-y smoothed record, besides the ninth century BCE (when the QLS chronology is more uncertain than in following centuries), the periods –950 to –885, 575–670, 800–1000, 1310–1420, 1520–1580, 1740–1770, and 1840–1915 are consistently above the long-term mean, but the recent period 1940–2011 is notably wetter. The periods of highest and lowest reconstructed rainfall estimates for different time spans are listed (SI Appendix, Table SE1). Considering the chronology only after –1500, 11 of the wettest 20 y reconstructed occurred after 1940, whereas 7 of the wettest 10 y occurred after 1998 (the wettest individual year is 2010). The wettest 10-, 25-, and 50-y periods are all the most recent in the record. However, comparing all 100-y nonoverlapping periods shows that the most recent century (1912–2011) is only the third wettest since –1500, with 579–678 and 888–987 the wettest and second wettest, respectively. The driest reconstructed year is –1049 (note the caveats given in Fig. 3A and SI Appendix, Table SE1). Focusing on the putative “medieval warm” and “little ice age” periods in the circa 9th to 11th and 14th to 19th centuries, respectively (e.g., refs. 4 and 24), the reconstruction (Fig. 3B) indicates corresponding predominately wetter conditions during the former and drier conditions during the latter (notably, 1450–1500 and 1650–1700).

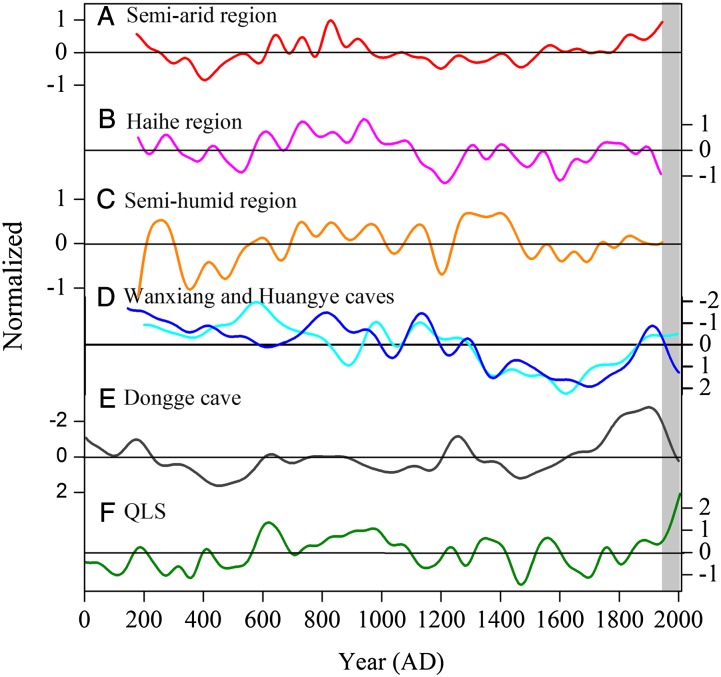
Analyses of precipitation data and comparisons of multiple, circa 500-y-long, tree-ring series have previously shown (22, 25) that decadal-scale moisture variations are largely coherent over a wide region of the northeastern TP, encompassing multiple semiarid areas of the Qilian Mountains and the more humid regions of the Hasi mountains some 400 km east of our tree-ring sites (Fig. 1 and SI Appendix, Table SA1). Fig. 4 compares the last 2,000 y of the QLS precipitation reconstruction with six relatively well-dated, published records indicative of moisture variability in China (Fig. 1). Some similarity in centennial timescale precipitation variability over northwestern China is evident, although there is only a partial agreement. They suggest widespread predominately drier conditions in the fourth to early sixth centuries, wetter conditions for the century centered on circa 600, predominantly wet conditions persisting during the ninth and 10th centuries and during the 14th century, with drier conditions throughout most of the late 15th to early 18th centuries except for some decades in the middle 16th century. Moisture supply appears near or above the two-millennia normal after about 1800 up until the mid 20th century. However, the Huangye and Dongge Cave records indicate drying in the late 20th century, whereas on the evidence of the QLS series, as we show, it became unusually wet during the late 20th and especially in the early 21st centuries across the northeastern TP, a positive precipitation trend which is also apparent in the locally measured precipitation data (SI Appendix, Figs. SA1c and SD1e).

Fig. 4.

Multiple records of moisture variability in central and western China. A comparison of the last 2,000 y of the QLS precipitation reconstruction (F) with six relatively well-dated, published records indicative of moisture variability in western China. All records are normalized to have zero mean and unit SD and are smoothed to emphasize their multidecadal to centennial timescale variability. The first three series are independent reconstructions based on documentary records of the frequency of floods and droughts for (A) the semiarid area of the Great Bend of the Yellow River (26), (B) the Haihe River Basin (27), and (C) the semihumid lower reaches of the Yellow River Basin (26). The three “cave” records are oxygen isotope series (δ¹⁸O) derived from cave speleothems in (D) Wanxiang (28) (cyan) and Huangye (29) (blue) Caves, located very close to each other in southern Gansu some 700 km to the southeast of Dulan and (E) Dongge Cave (30), situated much further south (25°17'N, 108°5′E) in northern Guizhou some 1500 km from the region of the tree-ring data (Fig. 1 gives all locations). The Dongge Cave record has been widely interpreted as a proxy for summer monsoon intensity throughout the Holocene and has been linked with changes in Total Solar Irradiance (ref. 32 and SI Appendix).

Prior tree-ring work has also drawn attention to a coincidence in the occurrence of dry conditions on the eastern TP and cool conditions indicated in reconstructions of mean Northern Hemisphere (NH) temperatures, especially during the late 15th century (23). This observation was based on decadally resolved data for only the last 600 y. Our current work enables this comparison to be extended back to the start of the first millennium, when the longest NH reconstructions begin. Fig. 3C lends strong support for an association between these records at multidecadal and centennial timescales (but there is no correlation at the interannual timescale; SI Appendix). The QLS chronology is positively correlated with every one of the 11 individual NH temperature reconstructions used to make the composite shown in Fig. 3C (SI Appendix, Table SG1), as well as with the composite itself. The correlation arises from common variance on timescales longer than 30 y and is apparent even if the millennial timescale variance is removed by filtering (Fig. 3D). Ref. 23 discusses the possible association between the variability of rainfall at Henan (northeastern TP) and the recent variability of sea-surface temperatures (SST), suggesting links with early and late summer monsoon rainfall. However, correlations between TP rainfall and SST are strongly influenced by trends in the data during recent decades, and little association is apparent in detrended data (SI Appendix, Fig. SE6). An analysis of stable isotopes in precipitation and river water samples from different locations in western China (31) indicates that the majority of precipitation on the northern TP derives from the recycling of continental moisture through summer convective processes and that the southwest monsoon is not a direct source of precipitation over our study region. This suggests that the link with larger-scale temperature variability indicated in Fig. 3 may arise from direct, mainly summer heating of the TP, although there is no evidence for this at the interannual timescale (SI Appendix, Fig. SD1).

A lack of any strong association with monsoon precipitation in our region could also explain why we find only limited association between our QLS precipitation reconstruction and variability in either monsoon intensity inferred from the longer Dongge Cave oxygen isotope data (30) or in total solar irradiance series (reconstructed from cosmogenic radionuclides in polar ice cores and low-latitude tree rings) which have been shown to covary during much of the Holocene (32) (SI Appendix, Fig. SE2).

In conclusion, we note that interpretation of the temporal variability of the QLS chronology, in terms of changing annual precipitation amounts, is based on a simple, albeit strong, correlation with a short record of observed regional precipitation during what appears to be the wettest 50 y in at least 3,500 y but also during a period that may also be unusually warm on a hemispheric scale. However, it may be that in previous, possibly cooler periods the association between tree growth and available moisture might not have been as strong. It is also possible that aspects of the local environment other than moisture supply may have recently promoted tree growth, such as increased nitrogen deposition or enhanced water use efficiency associated with rising atmospheric concentrations of carbon dioxide (33, 34). If, however, our interpretation of unusually high, recent precipitation levels is correct, this would be consistent with a general expectation of increasing precipitation in this region indicated by climate model projections under increasing levels of greenhouse gases (e.g., figure 14.24 of ref. 35).

Materials and Methods

Calendar.

Unless otherwise explicitly stated (such as where the BCE, CE calendar convention is used), the Astronomical Calendar is used throughout; i.e., the year before 1 CE is designated as year zero, and progressively earlier years are indicated by increasingly larger negative values.

Chronology Construction.

The ring-width data from newly collected samples were cross-dated, and the dating of additional (published) measurements, some accessed from the International Tree-Ring Data Bank, was similarly assessed, using multiple comparisons of high-pass–filtered series. The dated measurements and the evidence of dating fidelity in the form of cross-correlation tables are available at www.cru.uea.ac.uk/cru/papers/yang2013pnas/. Where there are multiple cores from the same tree, the measurements were averaged to form mean tree series. These data series were then “standardized” to remove nonclimate-related variance associated with changes in tree geometry that affect the distribution of radial wood production through the life of a tree. The method used is Signal-Free Regional Curve Standardization (SF-RCS) as discussed in the main text. Indices are measured ring-width values divided by expected values, defined by the appropriate SF-RCS curve values for the appropriate ring age. Simple arithmetic means of raw (measured) ring width by ring age (including pith offset estimates), or of indices by calendar year, were used to produce the RCS curve(s) or standardized chronology values, respectively. The RCS curves were smoothed using an age-dependent low-pass spline, applied only where sample replication was greater than three trees; where replication falls to three trees or less, a horizontal linear extension of the RCS curve was applied. The RCS curve was allowed to rise when representing the expected ring width for trees older than 1,500 y to allow for increasing ring width sometimes apparent in old-age trees that develop a strip-bark–like form. Chronologies created from subdivisions of the full measurement data set were used to explore potential source bias (SI Appendix). All SF-RCS curves and subchronologies are shown in SI Appendix. Where multiple RCS curves were used for different growth-rate classes of tree, the data were sorted into subgroups (of nearly equal numbers) according to the mean relative growth rate, i.e., the radial increment for each tree relative to the radial increment of a single RCS curve generated using all trees, where the comparison is over the (common) period of growth of the specific tree. An empirical method was used to transform the values of all tree indices so that their probability distribution function follows a normal distribution (SI Appendix). Chronology confidence is represented by the SEM (SE), usually shown as ±2 SE, calculated for the timescale of chronology variance being represented. An “adjusted” Expressed Population Signal (EPS) is also used to measure chronology confidence, as shown in SI Appendix.

Regional Precipitation Time Series.

Monthly mean observations from six weather stations were combined to represent precipitation over the study region (Fig. 1) for 1957–2011. The three southern stations are drier than the northern stations (SI Appendix, Figs. SA1 and SA3) and, because some monthly values are missing, a simple average of the station series could result in a biased regional mean series (e.g., the data from the drier Chaka station are not available after 2000, and a simple average would increase after 2000). Instead, each station series is first scaled so that its long-term mean is equal to the average long-term mean across all stations. The scaling is calculated separately for each month of the year, using long-term mean values calculated only from those years when all six stations have an observed value for the given month. The SD of a station series is also affected by the scaling, such that the coefficient of variation is constant. A simple average of the scaled station series is then used as the regional precipitation series. Note that the scaling increases the contribution of the drier stations relative to the wetter stations.

Reconstruction Calibration.

Multiple methods of scaling the QLS tree-ring chronology to represent annual (prior July to current June) regional precipitation were compared (SI Appendix, Section D), in all cases using the calibration data for the period 1957–2011. The results for the different calibrations (shown as scatter diagrams; SI Appendix, Fig. SD2) are all similar, with the explained variance (r²) ranging from 61% (high-pass–filtered case) to 79% (detrended, low-pass–filtered case). When expressed as the deviation in mm of annual rainfall represented by one SD of the chronology, the scaling coefficients (β) range from 33 to 65 mm/SD. The reconstruction shown in the main paper (Fig. 3) is based on the detrended case with β = 45 mm/SD; r = 0.79 [i.e., SI Appendix, Section D, case (iii)(b)]. Additional cross-validation tests were used to demonstrate the validity of the calibration process. These and the calculation of chronology and rainfall reconstruction uncertainty are also described in detail in SI Appendix.

Composite of Northern Hemisphere Temperature Reconstructions.

A compilation of 11 NH temperature reconstructions (SI Appendix) was assembled from previously published estimates, selecting only those reconstructions that began on or before 1000 and that were not considered to have been closely related to, or superseded by, later versions. Each reconstruction was filtered with a low- or band-pass filter to represent the timescale considered, with truncation to remove values near each end of the filtered time series that are more uncertain due to the end effects of the filter. Each filtered series was then “normalized” to have zero mean and unit SD over a common overlap period, and the composite mean and SD were calculated in each year.

Data and Software.

Tree-ring measurement and chronology data, precipitation observations and the precipitation reconstruction data, and the CRUST software (18) used to standardize and process the tree-ring data are all available at www.cru.uea.ac.uk/cru/papers/yang2013pnas/. Data are also available from the World Data Center for Paleoclimatology (www.ncdc.noaa.gov/paleo/).