Accuracy of Computational Cerebral Aneurysm Hemodynamics Using Patient-Specific Endovascular Measurements

Abstract

Computational hemodynamic simulations of cerebral aneurysms have traditionally relied on stereotypical boundary conditions (such as blood flow velocity and blood pressure) derived from published values as patient-specific measurements are unavailable or difficult to collect. However, controversy persists over the necessity of incorporating such patient specific conditions into computational analyses. We perform simulations using both endovascular-derived patient-specific and typical literature-derived inflow and outflow boundary conditions. Detailed three-dimensional anatomical models of the cerebral vasculature are developed from rotational angiography data, and blood flow velocity and pressure are measured in situ by a dual-sensor pressure and velocity endovascular guidewire at multiple peri-aneurysmal locations in ten unruptured cerebral aneurysms. These measurements are used to define inflow and outflow boundary conditions for computational hemodynamic models of the aneurysms. The additional in situ measurements which are not prescribed in the simulation are then used to assess the accuracy of the simulated flow velocity and pressure drop. Simulated velocities using patient-specific boundary conditions show good agreement with the guidewire measurements at measurement locations inside the domain, with no bias in the agreement and a random scatter of ≈25%. Simulated velocities using the simplified, literature-derived values show a systematic bias and over-predicted velocity by ≈30% with a random scatter of ≈40%. Computational hemodynamics using endovascularly measured patient-specific boundary conditions have the potential to improve treatment predictions as they provide more accurate and precise results of the aneurysmal hemodynamics than those based on commonly accepted reference values for boundary conditions.

Introduction

The hemodynamic environment of intracranial aneurysms is thought to strongly influence aneurysm formation, growth and, rupture¹⁸. Computational fluid dynamics (CFD) modeling of aneurysms and the surrounding cerebral vasculature allows investigators to calculate important hemodynamic characteristics, such as wall shear stress^6;8;19 (WSS), which have been implicated in aneurysm growth and rupture.

CFD oftentimes relies on stereotypical boundary conditions (such as blood flow velocity and blood pressure) derived from published values of healthy volunteers since patient-specific measurements are unavailable or difficult to collect. However, CFD calculations based on reference values are subject to potential uncertainty based on their sensitivity to patient-to-patient variability of pressure and/or flow rate waveforms^13;16;32.

The uncertainties in image-based CFD hemodynamics are thought to be primarily due to uncertainties in the reconstruction of the vessel lumen^2;12;30. However, significant errors are also introduced in the specification of the boundary condition velocities and pressures which, in turn, introduce uncertainties in pressure drop and wall shear stress calculations¹⁶. In particular, recent controversy has originated over the accuracy of CFD using either simplified literature-based vs. patient-specific flow rates for hemodynamic simulations of intracranial aneurysms²⁵.

Previous reports of CFD using blood flow velocity boundary conditions derived from transcranial Doppler (TCD) ultrasonography²⁸ or phase-contrast magnetic resonance angiography (pcMRA)^3;13;16 have attempted to apply patient-specific measurements to improve CFD accuracy. These measurements, however, lack blood pressure information and may suffer from anatomical and physiological inaccuracies.

The dual-sensor pressure and Doppler velocity guidewire has been used to measure patient-specific blood pressure and blood flow velocity in cerebral vessels²³ with excellent anatomical specificity and correlation to measured blood flow in animal models⁹. We previously applied measurements of blood flow velocity and blood pressure taken with this wire as boundary conditions for CFD modeling of intracranial aneurysms before treatment and after treatment with flow-diverting stents¹⁴. The CFD simulations in this study use either patient-specific boundary conditions or typical, but idealized, boundary conditions from the literature. The present study aims to evaluate, quantitatively, the degree to which computational simulations of intracranial aneurysm hemodynamics using patient-specific boundary conditions are more accurate and precise than those using simplified boundary conditions by comparing against the in situ wire measurements of velocity and pressure.

Materials and Methods

Population

Ten patients with unruptured intracranial aneurysms are included in this IRB-approved study, and their informed consent was obtained. The aneurysms are all located in either the internal carotid artery or the proximal middle cerebral artery. Three-dimensional rotational angiography was obtained before aneurysm treatment. The patient characteristics as well as the aneurysm geometric characteristics derived from the angiography are shown in table 1. All patients underwent endovascular aneurysm treatment under general anesthesia. This study, however, focuses on the hemodynamics before the aneurysm treatment.

Table 1.

Patient and Aneurysm Characteristics

N	Age	Sex	Aneurysm Location	Neck Width (mm)	Aneurysm Volume (cm3)	Parent Artery Diameter (mm)
1	75	M	L Supraclinoid Internal Carotid	10.6	3.80	4.3
2	64	F	L Supraclinoid Internal Carotid	3.6	0.21	3.5
3	77	F	L Supraclinoid Internal Carotid	4.9	1.31	3.8
4	46	F	L Internal Carotid Cave	5.0	0.02	4.4
5	37	F	R Cavernous Internal Carotid	3.7	0.05	4.3
6	33	F	R Supraclinoid Internal Carotid	3.4	0.05	3.7
7	83	F	R Supraclinoid Internal Carotid	5.4	0.26	5.3
8	73	F	L Paraclinoid Internal Carotid	8.6	0.21	3.8
9	24	F	R Proximal Middle Cerebral	17.1	1.82	2.6
10	50	F	L Paraclinoid Internal Carotid	6.8	0.28	4.1

Patient-Specific Data Collection

Blood flow velocity and blood pressure were measured using the dual-sensor pressure and Doppler velocity guidewire (ComboWireⓇ, Volcano Corporation, San Diego, CA) and workstation (ComboMapⓇ, Volcano). The tip of the 0.014” (0.36 mm) wire contains a piezoresistive pressure sensor and piezoelectric pulsed Doppler device which measures velocity. The Doppler device emits a 45° beam and insonifies a circular plane of 4 mm in diameter centered at 5 mm in front of tip. The maxiumum frequency curve of the Doppler spectrum is taken to be equal to the flow velocity at the measurement location. Pressure and velocity readings have a 5 ms temporal resolution. Systolic, diastolic, and average pressures and velocities are calculated automatically by the workstation based on the cardiac cycle. The workstation also continuously sampled systemic blood pressure from radial artery catheterization.

Prior to aneurysm treatment, the dual-sensor guidewire is placed in three predetermined peri-aneurysmal locations: 1) proximal petrous carotid artery, 2) 5 mm proximal to the aneurysm neck, and 3) 5 mm distal to the aneurysm neck. The wire was oriented along the vessel axis aligned with the main component of the flow in order to maximize the flow velocity signal. Radiographs of the wire location are obtained. Blood pressure and blood flow velocity are recorded for at least ten cardiac cycles at each location before wire removal. Systemic and wire-measured blood pressure and blood flow velocity measurements are exported to a workstation for CFD analysis.

Computational Modeling

Three-dimensional reconstructions of the vessels are created from the rotational angiographic images using the Vascular Modeling Toolkit (VMTK, release 1.0.0, www.vmtk.org). Tetrahedral meshes are generated for all simulations using the ANSYS GAMBIT package, release 2.4 (ANSYS Inc., Canonsburg PA). The characteristic width of the computational mesh cells is 0.2 mm for all cases. The number of computational cells ranges from about 0.5 to 2 million depending on the size of the aneurysm. Simulations are executed using ANSYS FLUENT, release 12.1 (ANSYS), a finite-volume-based solver. The blood is assumed to be incompressible and Newtonian with a density of 1050 kg m^–3 and a viscosity of 3.5 cP.

Patient-Specific Flow Rates

At the 3D model inlets, the time-dependent Womersley velocity profile is prescribed as the boundary condition using the velocity measurements from the dual-sensor guidewire at position 1 (petrous segment of the internal carotid artery). These in situ measured velocities are matched to the centerline velocity of the Womersley flow. At distal vessels, pressures are prescribed using the pressure measurements from the dual-sensor guidewire at position 3 (5mm distal to the aneurysm neck) as the outflow conditions. Velocity and pressure waveforms were phase-averaged over at least ten cardiac cycles before CFD modeling. Flow rates were computed directly from integrating the wire-derived Womersley velocity profile.

Simplified Flow Rates

Although many CFD studies have used non-patient-specific waveforms for the inflow boundary conditions of cerebral aneurysms hemodynamics, the assumptions involved in the process are not always consistent across studies. Many different conditions have been prescribed such as averaged flow rates derived from TCD or pcMRA of healthy subjects^19;33, flow rates from age- and-sex matched control subjects²⁷, or an allometric scaling, i.e. flow rate scales with vessel diameter raised to some exponent⁷. See the publication from Marzo et al.¹⁶ for a summary of the inflow/outflow boundary conditions of cerebral aneurysm used in the literature up to 2010.

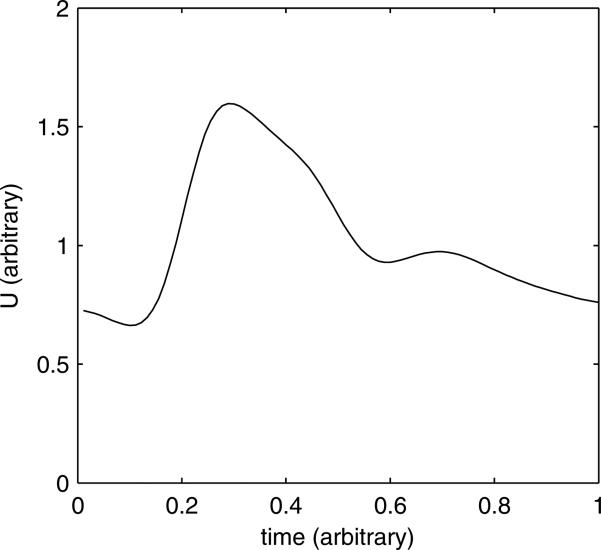
For this study, we use a waveform for the cross-sectionally-averaged velocity in the internal carotid artery which is based on the average of pcMRA-measured flow rates in 17 young, healthy subjects¹¹. The inflow velocity profile is then derived by assuming axisymmetric Womersley flow. Additionally, the flow waveform is scaled in proportion to the internal carotid artery diameter such that the time-average WSS is equal to 1.5 Pa (15 dyn cm^–2) which is consistent with a Murray's law scaling (flow rate scales with the cube of the diameter). The waveform shape used in this study is shown in figure 1. Although this is one of several possible simplified boundary conditions, we have chosen it in this study as it is representative, qualitatively and quantitatively, of the inlet boundary condition which has been used by multiple, independent research groups^7;12;16;21 for simulations of cerebral aneurysm hemodynamics. The period of the cardiac cycle for the simplified waveform is taken to be 0.91 s. At distal vessels, a constant pressure of 0.0 mmHg is applied as the outflow pressure boundary condition. As the simulation is an incompressible flow with rigid walls, the pressure is arbitrary to within an additive constant.

Fig. 1.

Velocity waveform vs. time used for the simplified boundary conditions.

Treatment of Vessel Branches

Very small side branches, e.g. the ophthalmic artery, are removed from the 3D reconstruction. Models are also truncated proximal to the circle of Willis where possible. However, three models do include the posterior communicating artery (PCom) as the aneurysms are at or near the base of the circle of Willis. The pressure in the PCom in these cases is adjusted relative to the internal carotid artery pressure such that some specified fraction of the total flow rate enters the PCom¹⁴. The fraction of the flow split is determined by assuming Murray's law (the ratio of the flow rates is equal to the cube of the ratio of the vessel diameters).

Accuracy Testing

To assess the CFD models incorporating dual-sensor guidewire boundary conditions, we identify two anatomical positions where velocity is measured by the dual-sensor guidewire but is not incorporated into CFD calculations. These locations are positions 2 (5 mm proximal to the aneurysm neck) and 3 (5 mm distal to the aneurysm neck). At these locations, axial components of the peak systolic and mean velocities simulated by CFD are compared with guidewire velocity measurements. The specific positions of the guidewire measurement locations are determined by visually inspecting the fluoroscopy images so that velocities could be extracted at the corresponding locations in the CFD. The “centerlines” function in VMTK is used to estimate the streamwise normal direction of the CFD velocity at a specific measurement point. The wire-measured velocity is assumed to be the streamwise normal component of the flow velocity.

Pressure drops, both peak and time-averaged, from position number 1 to position number 3 (petrous carotid to 5 mm distal to aneurysm neck) are computed from both the CFD and from the guidewire pressure measurements. The wire-derived pressure drop is not a true differential measurement; rather, we take the difference between the peak systolic (or mean) pressure between the petrous carotid and 5 mm distal measurements to compute the peak systolic (or mean) pressure drops. The pressure measurement at the petrous carotid location is not prescribed into the CFD, and can therefore be used for comparison purposes.

Bland-Altman plots are constructed to compare CFD-simulated vs. wire-measured velocities and pressure drops. Both sets of CFD simulations, patient-specific and simplified boundary conditions, are compared to the wire measurements. Bias is always calculated as f_CFD – f_Wire, where f is a generic hemodynamic variable. Biases in the Bland-Altman analysis are assessed statistically using the Wilcoxon signed-rank test. The coefficient of variation (CoV) is also computed for the differences which gives an estimate of the random errors. The CoV is computed by the formula

$$\mathrm{CoV}=\frac{s}{\frac{1}{2}\mathrm{Mean}(f_{CFD}+f_{Wire})}\cdot 100\%$$ (1)

where s is the sample standard deviation of (f_CFD – f_Wire).

Results

Blood flow velocity and in situ pressures are measured in each patient. There were no intra- or peri-procedural complications associated with the use of the dual-sensor guidewire. No vascular injury, thromboembolic event, or new neurological deficit was observed in any patient. Out of 20 desired velocity comparison measurements (10 patients and 2 locations each), 3 measurements from two separate patients are excluded from the analysis. In each of these excluded cases the wire-measured velocities are obscured by noise artifacts during acquisition. However, velocity measurements in the petrous carotid artery are sufficient in these cases such that the CFD analysis could be performed. Pressure drop measurements are excluded in three out of ten separate patients also due to measurement artifacts.

Hemodynamic quantities at the CFD inflow derived from both the endovascular measurements and the simplified reference values are shown in table 2. Scattergrams of the cohort shear stress and flow rate are provided in the supplementary material. In almost all cases, flow rates, both mean and maximum, using the simplified boundary conditions are larger than those using the wire-derived patient-specific boundary conditions. The mean flow rate derived from the wire measurements is 144.7±46.1 mL min^–1, while the mean flow rate derived with simplified conditions is 227.9±90.8 mL min^–1.

Table 2.

Hemodynamic Parameters with Patient-Specific and Simplified Boundary Conditions

Hemodynamic Variable	Patient-Specific	Simplified	p value
Mean Flow Rate (mL min–1)	144.7 ± 46.1	227.9 ± 90.8	< .01
Peak Flow Rate (mL min–1)	268.1 ± 99.5	364.8 ± 145.2	< .01
Mean Shear Stress in Internal Carotid Artery (Pa)	1.00 ± 0.29	1.50 ± 0.00	< .01
Peak Shear Stress in Internal Carotid Artery (Pa)	2.13 ± 0.57	2.71 ± 0.11	< .05
Womersley Number (-)	2.83 ± 0.57	2.94 ± 0.63	.25
Diameter of Internal Carotid Artery (mm)	4.44 ± 0.56	4.44 ± 0.56	-

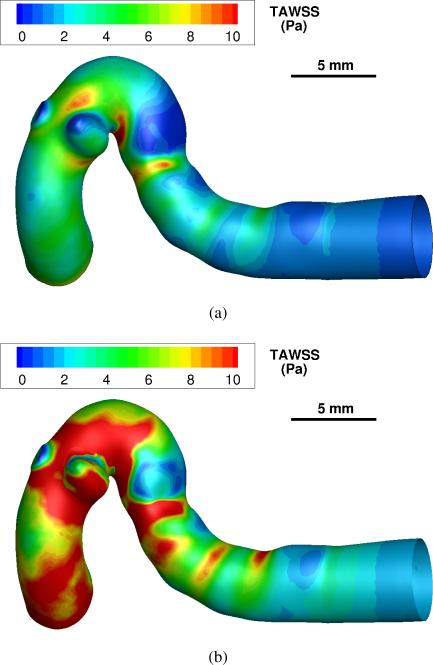
Simulations of the intra- and peri-aneurysmal hemodynamics, using both the patient-specific and simplified velocity waveforms, have been successfully computed in each case. Since the flow rates using the simplified boundary conditions are higher, the increased flow rates cause a significant increase in WSS within the vessels. A visualization of the spatial distribution of the time-averaged WSS for patient 4 is shown in figure 2. Additional WSS visualizations are included in the supplementary material. The simulation using simplified boundary conditions predicts systematically higher values of the time-averaged WSS. The spatially averaged WSS on the aneurysm wall is also computed for both patient-specific and simplified boundary conditions, and the results are summarized in table 3. Using the simplified conditions, the sample intra-aneurysmal WSS is about twice that of the patient-specific flow rate cases.

Fig. 2.

Spatial distributions of the time-averaged wall shear stress (TAWSS) in Pa for a single patient model (case no. 4). (a) simulation using patient-specific boundary conditions. (b) simulation with simplified boundary conditions.

Table 3.

Intra-aneurysmal WSS with Patient-Specific vs. Simplified Boundary Conditions

Hemodynamic Variable	Patient-Specific	Simplified	p value
Mean WSS (Pa)	1.85 ± 1.34	4.06 ± 3.57	< .01
Peak WSS (Pa)	4.41 ± 3.41	8.39 ± 7.50	< .01
Normalized Mean WSS (-)	1.98 ± 1.63	2.70 ± 2.38	< .01
Normalized Peak WSS (-)	2.29 ± 2.02	3.02 ± 2.58	< .01

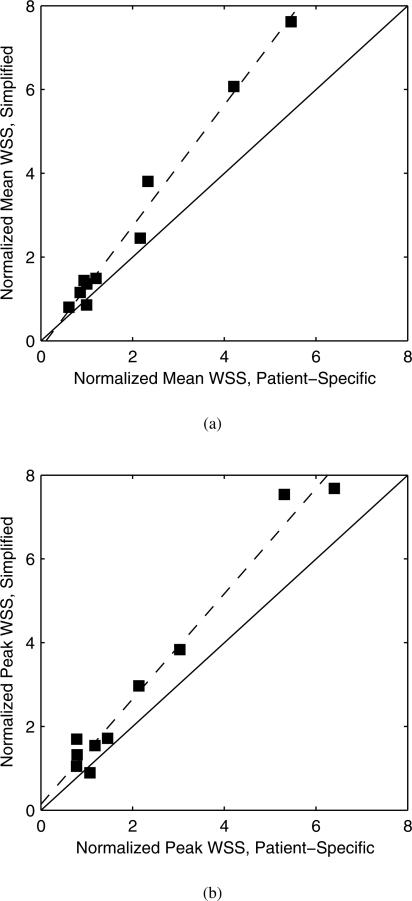
Intra-aneurysmal hemodynamic quantities, like WSS, are oftentimes normalized relative to some reference value^16;19, such as that of the parent artery, in order to adjust for inter-subject hemodynamic variability. The intra-aneurysmal WSS results are therefore normalized using the WSS in the petrous carotid artery for either the mean or peak values, respectively. The petrous carotid artery WSS is computed directly from the Womersley flow used as the inflow boundary condition. Normalized WSS values are presented in table 3. The differences between the patient-specific and simplified boundary condition cases are not as dramatic after normalization. Indeed the mean and peak normalized WSS using the simplified boundary conditions are highly correlated with the analogous normalized WSS using patient-specific boundary conditions, as shown in figure 3. Correlation coefficients are r = 0.991 and r = 0.986 (Pearson correlation coefficient) for the mean and peak values, respectively. A linear least squares regression between the simplified vs. patient-specific boundary conditions gives a slope of 1.45 and an intercept of −0.16 for the normalized mean WSS and a slope of 1.26 and an intercept of 0.14 for the normalized peak WSS. Therefore, the simplified boundary condition cases still predict significantly larger intra-aneurysmal WSS than the patient-specific cases even after a normalization.

Fig. 3.

Normalized WSS of simplified vs. patient-specific boundary condition cases for (a) mean values and (b) peak values. Solid line is the identity line, and dashed line is the linear least squares fit.

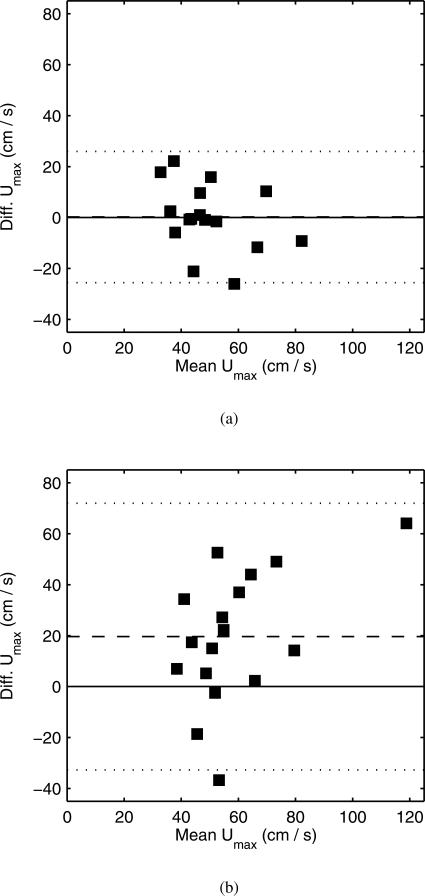
Bland-Altman analysis is conducted comparing the time-averaged and peak systolic streamwise velocity between the CFD and the wire-measured values. Comparisons are made at two independent perianeurysmal locations: position 2, located 5 mm proximal to the aneurysm neck, and position 3, located 5 mm distal to the aneurysm neck. These measurements were not prescribed in the CFD analysis. The Bland-Altman plots for the peak systolic velocity agreement, both using patient-specific and simplified boundary conditions, are shown in figure 4. There is no significant bias in the agreement between the wire-measured and CFD-derived velocities, either peak systolic or time averaged, using patient-specific boundary conditions. However, there is a significant bias in the agreement between the wire-measured and CFD-derived velocities at comparison locations, both peak systolic and averaged values, when using simplified boundary conditions; the CFD predicted systematically higher velocities compared to the wire measurements. Table 4 summarizes the Bland-Altman analysis for the wire-measured and CFD-derived velocities. There are relatively large CoV for both cases, which indicates the level of random error in the methodology.

Fig. 4.

Comparison of CFD and phase-averaged wire peak systolic velocity measurements. (a) Comparison using patient-specific boundary conditions. (b) Comparison using simplified boundary conditions. Dashed line is the mean bias, and dotted line is ±2 standard deviations from the mean bias.

Table 4.

Bland-Altman Analysis for CFD vs. Wire-measured Quantities

Hemodynamic Variable	Bias	Std. Dev.	p value of bias	CoV (%)	No. of Measurements
Systolic ΔP - Patient-Spec. (mmHg)	−0.144	1.58	.59	37.6	7
Systolic ΔP - Simplified (mmHg)	1.89	2.17	.11	41.6	7
Mean ΔP - Patient-Spec. (mmHg)	−2.30	1.43	.016*	57.6	7
Mean ΔP - Simplified (mmHg)	−0.790	1.40	.22	43.1	7
Peak Systolic Velocities - Patient-Spec. (cm s–1)	.205	12.9	.83	26.3	17
Peak Systolic Velocities - Simplified (cm s–1)	19.6	26.2	.0070**	44.6	17
Mean Velocities - Patient-Spec. (cm s–1)	−2.10	7.36	.19	24.4	17
Mean Velocities - Simplified (cm s–1)	12.3	14.0	.0056**	37.4	17

^*Significant at p < .05

^**Significant at p < .01

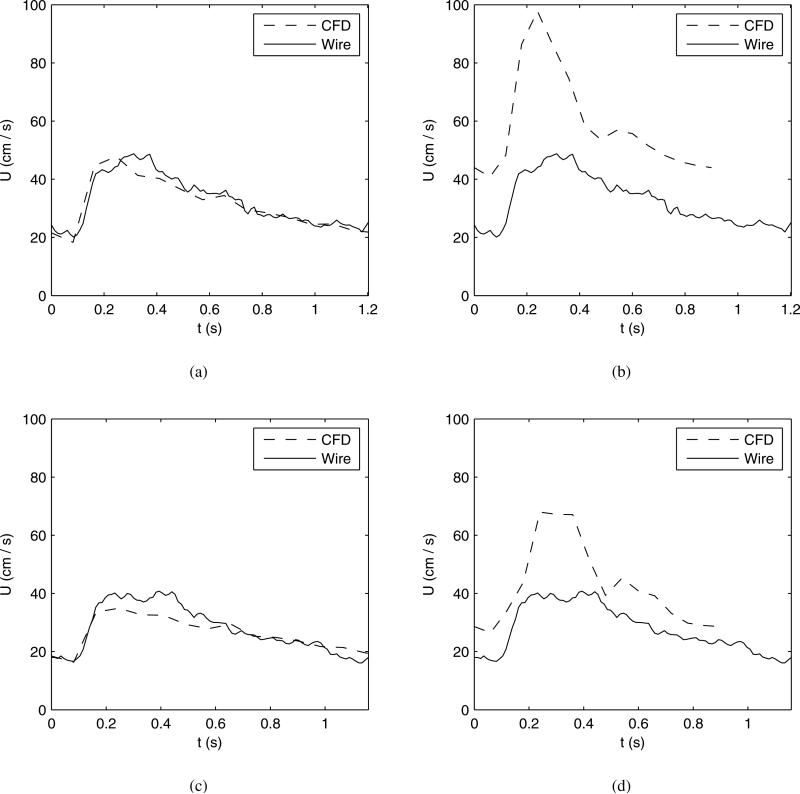
A typical comparison of the CFD velocity waveforms using patient-specific boundary conditions vs. the wire-measured waveforms is shown in figure 5 for the case of patient 4. A visual inspection reveals similar waveform shapes and amplitudes. Likewise, a comparison of the CFD velocity waveforms using simplified boundary conditions vs. the wire waveforms is also shown in figure 5. Visual inspection reveals high average and peak systolic velocity when using the simplified boundary conditions. The velocity waveform is characterized, for example, by a different peak-to-mean velocity ratio than that measured by the wire.

Fig. 5.

Comparison of CFD and phase-averaged wire velocity measurements vs. time for a single patient model (case no. 4). (a) Location 2 using patient-specific boundary conditions. (b) Location 2 using simplified boundary conditions. (c) Location 3 using patient-specific boundary conditions. (d) Location 3 using simplified boundary conditions.

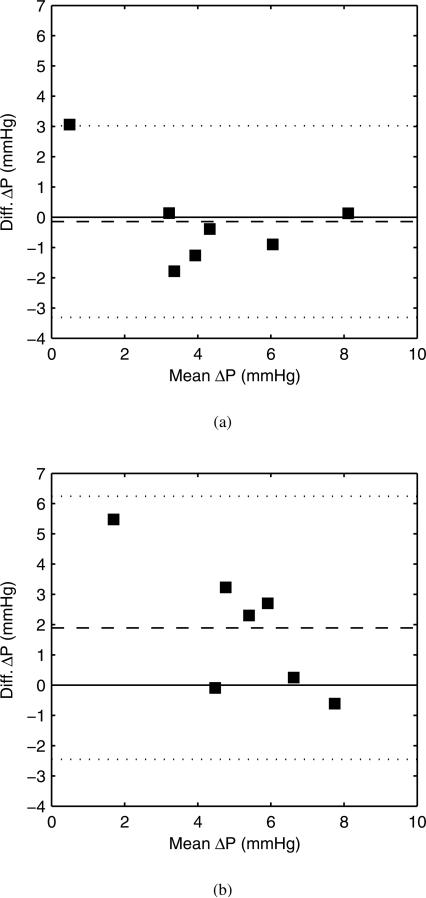
The wire-derived pressure drops between the petrous carotid and 5 mm distal-to-aneurysm location are compared with a Bland-Altman analysis against CFD-derived pressure drops for cases using the patient-specific and simplified boundary conditions. The pressure drop from the petrous carotid to the 5 mm distal-to-aneurysm location represents most of the pressure drop across the CFD model. The Bland-Altman plots for peak systolic pressure drop are shown in figure 6, and the analysis is summarized in table 4. The CFD with patient-specific boundary conditions did not show a bias in peak systolic pressure drop vs. the wire measurements. However, the mean pressure drop with patient-specific conditions did predict a significant negative bias. The CFD with simplified boundary conditions did not predict a significant bias with respect to the pressure drops. This apparent contradiction is addressed in the discussion section. There are also large CoV for the pressure drops which again indicates the degree of random errors in the methodology.

Fig. 6.

Comparison of CFD and wire-derived peak systolic pressure drops. (a) Comparison using patient-specific boundary conditions. (b) Comparison using simplified boundary conditions. Dashed line is the mean bias, and dotted line is ±2 standard deviations from the mean bias.

Discussion

We have demonstrated that CFD models of the cerebral vascular system based on boundary conditions from patient-specific velocity and pressure measurements from the dual-sensor guidewire are more accurate than those based on common reference or simplified values. More importantly, we have quantified the degree of the errors, both with respect to systematic biases and random scatter, using both classes of boundary conditions, allowing for a more precise interpretation of computational hemodynamic studies of the cerebral vasculature.

Velocities from the CFD models with patient-specific boundary conditions compared with in situ guidewire values at anatomical locations not used in CFD simulations show good agreement; there is no detectable bias for either peak systolic or time-averaged velocities using the Bland-Altman method. The CFD does predict slightly lower, albeit non-significant, mean velocities compared to the in situ measurements. The agreement between the velocities data suggests that using the guidewire to estimate simulation boundary conditions reduces systematic errors in the overall CFD analysis. The degree of random errors, as quantified by the CoV, is still relatively large, about 25-30%, for the velocity measurements. Using the simplified conditions, averaged and peak systolic velocities are biased significantly higher statistically than the wire measurements. The standard deviations and CoV are also larger, about 40-45%, when using the simplified conditions. Therefore, CFD with patient-specific boundary conditions more accurately and more precisely reflects the in vivo conditions within the cerebral vasculature than simulations that rely on simplified reference boundary conditions.

There are several possible sources of errors which we identify here. First, the imposed inflow rate derived from the endovascular measurements in the internal carotid artery assumes that the flow follows the axisymmetric Womersley velocity profile. Non-symmetric velocity profile skewing can introduce random errors of 10-15% when using the Womersley profile to interpolate the flow rate²⁰. Only at large degrees of velocity profile skewing does the Womersley profile systematically under-estimate the true mean flow rate. But the Womersley profile does not appear to systematically under-estimate the peak flow rate under the same conditions²⁰. If our wire-derived flow rates were systematically too low, then our CFD-derived velocities would also likely be too low when compared to the wire measurements which were not prescribed in the CFD. However, as our CFD-derived velocities showed no bias compared to the wire measurements, we would consider it unlikely that the flow rates were systematically too low.

Another key source of random error may be the wire velocity measurements themselves. While we attempted to recreate the exact location of the dual-sensor guidewire in the CFD conditions, small variations in the axial and radial position or angle of the wire may have influenced the velocity measurements. These localization errors were minimized by using multiple-projection radiographs. The wire was also manipulated in situ to attempt to measure the most robust velocity signal. It is possible that the wire was not perfectly aligned within the center of the vessel and thus did not truly measure the streamwise velocity component.

A third source of random error is the 3D reconstruction of the vessel itself, which can be due to the limited spatial resolution of the imaging modality or even the algorithm used to segment the vessel boundary⁵. For 3D rotational angiography, the reconstruction of the vessel diameter is reproducible to within about 10%¹². Random errors typically compound themselves in a root-mean-square manner. So if we posit a 10% random error for the wire velocity measurements, then the composite error due to these three sources (15% for the prescription of the flow rate, 10% for the limited precision of the wire, and 10% for the 3D reconstruction of the vessel) would amount to a 21% random error between the CFD- and wire-derived velocities. This estimate is in close agreement with the 25-30% random error computed with the Bland-Altman method, suggesting that these three effects are the dominant sources of error.

Regarding the wire-derived flow rates, the inter-subject mean flow rate in the petrous carotid is 144.7 mL min^–1. This is in contrast to normal internal carotid artery flow rates typically used in reference or literature-based CFD analyses. Studies of ultrasound²² and pcMRA^4;11 velocities of volunteers showed average flow rates of 234, 243, and 277 mL min^–1, respectively. However, subjects in those studies were young, awake, and healthy volunteers. The patients in our study are older and were anesthetized when hemodynamic measurements were acquired. Although older age¹⁷ and anesthesia²³ can reduce the measured blood flow rate in the cerebral vasculature by as much as 30%, it is not known if these factors fully explain the lower blood flow rates reported here.

Along similar lines, our reported value of patient-specific mean WSS in the internal carotid artery, 1.00±0.29 Pa, is very close to that reported by Cebral et al. using pcMRA⁴ who reported a mean WSS of 0.96±0.23 Pa. Our value is also reasonably close to the mean value reported in a meta-analysis by Cheng et al.¹⁰ of 1.16 Pa (range 0.95-1.5 Pa) for the common carotid artery in young, healthy subjects. This further provides support for the validity of the wire measurements, including flow rates, in this patient population.

With respect to the wire's pressure measurements, the precision of the instrument given by the manufacturer's specification is ±1-2 mmHg. By taking the difference between the inflow and outflow pressure measurements, and by assuming that the precision in the pressure measurement propagates in a root-mean-square manner, the precision in the pressure drop is ±1.4-2.8 mmHg. However, the relevant pressure drops computed by the CFD simulations are 2-5 mmHg for systolic values and only 1-2 mmHg for mean values. Indeed in some cases, the wire-measured mean pressure drop was actually greater than the corresponding peak systolic value. This illustrates the limited precision of the instrument when measuring such small pressure differences.

A significant negative bias is recorded in the time-averaged, but not peak systolic, pressure drops using the patient-specific flow rates. Although, we cannot fully identify the source of this bias, we conjecture possible sources of the bias. One possibility is that the imposed CFD flow rates derived from the wire measurements are systematically too low, thus producing a systematically low pressure drop in the CFD. But we would consider this possibility to be unlikely given the low bias in the velocity measurements. Additionally, the in situ pressure measurements from the wire are highly susceptible to noise artifacts which may introduce large errors. Thus, the source of the negative bias may be due to the limited precision of the wire rather than the CFD analysis per se.

There have been previously conflicting results regarding the need to incorporate patient-specific boundary conditions, such as flow rates, into imaged-based hemodynamic simulations of intracranial aneurysms. Cebral et al.⁵ found that variations <25% of blood flow rate did not significantly affect hemodynamic modeling results, but Venugopal et al³² reported that incorporating the variability of flow rate found in reference population studies substantially altered aneurysmal hemodynamics. Karmonik and colleagues¹³ found large differences between reference values and pcMRA-derived patient-specific flow rates in CFD models, including differences of up to 43% in peak systolic WSS results. This controversy is further complicated by methodological and technical difficulties in acquiring patient-specific flow rates. It is therefore important to discern the accuracy and sensitivity of CFD-derived hemodynamics as the effect of intra-aneurysmal WSS is widely thought to influence the growth and rupture of cerebral aneurysms¹⁸.

In this study, the intra-aneurysmal WSS using simplified boundary conditions is systematically higher, by a factor of 2, than that of the patient-specific case. Even after normalizing by the parent artery WSS, significant differences persist between the cases, albeit the magnitude of the differences is reduced as shown in table 3. Normalizing the CFD-derived WSS to some reference value does alleviate some of the systematic bias, therefore making the CFD less sensitive to the choice of inflow boundary condition. The two sets of data are highly correlated with each other (see figure 3) so a normalized WSS may still be correlated to clinical outcomes and would still be of important clinical utility. Nevertheless, a significant upward bias persists, about 30-40%, when using simplified conditions even after a normalization. Thus, the the utilization of patient-specific boundary conditions remains preferable for calculations of cerebral aneurysm hemodynamics.

Alternative methods of patient-specific data collection, such as TCD or pcMRA, have relative disadvantages to the endovascular technology of the current study. Acquiring flow rates with TCD is fast and noninvasive, but may not be accurate in the vertebrobasilar system²⁹ or in small-caliber vessels or in those near the skull base³¹ and cannot be obtained in up to 16% of patients lacking adequate temporal bone windows¹. When compared to TCD²⁴, flow rates acquired with pcMRA have a lower temporal resolution and may underestimate peak velocity by up to 30%, especially in smaller-diameter vessels. Additionally, pcMRA velocity data must be obtained outside of the angiographic workflow, and is both time-consuming and expensive to acquire.

The dual-sensor guidewire, while invasive, has several advantages over the above techniques in acquiring patient-specific measurements. Previous studies demonstrate good correlation with actual blood flow measurements⁹ and TCD¹⁵. Compared to TCD, it can be employed in a highly anatomically-specific manner in any major blood vessel including in the vertebrobasilar system, and does not require temporal bone windows. It also offers advantages over pcMRA including the real-time integration of blood flow velocity measurements into the angiographic workflow, eliminating the need for patient transport to and from the MRI suite. In addition, a previous report of direct comparison between blood flow velocity measured by pcMRA and the Doppler wire showed that pcMRA underestimated peak systolic velocity, which could alter CFD-derived hemodynamic calculations²³. Finally, neither TCD nor pcMRA acquire blood pressure measurements, while the dual-sensor nature of the guidewire allows additional integration of this physiological parameter into CFD modeling, though the wire precision may reduce the veracity of pressure measurements.

Limitations

The foremost limitation is the fact that the endovascular measurements were acquired with patients under anesthesia which may have reduced the cerebral blood flow from that of normal, awake conditions²³. The simulated hemodynamics may not fully reflect the typical hemodynamics within a patient's cerebral circulation. Future work should investigate the degree of bias in blood flow velocity between anesthetized and awake patients.

Secondly, even though our choice of using 1.5 Pa as the mean WSS in the petrous carotid artery for the simplified conditions is based on common values used in previous reports, it remains somewhat arbitrary. For example, a recent study²⁶ suggested scaling flow waveforms in cerebral aneurysms so that the mean WSS is 1.2 Pa, a value which is in turn based on that reported by Cheng et al.¹⁰ for the common carotid artery. Re-scaling the simplified waveform such that the mean inlet shear stress is 1.0 Pa (the inter-subject mean) would likely reduce the biases in the velocity comparisons. It is not known how closely this and other simplified conditions might mimic the true patient conditions. However, re-adjusting the waveform scaling would likely not provide better agreement in the velocity scatter than the simulations with the full patient-specific boundary conditions.

Third, a small number of patients were studied with variable aneurysmal size and morphology, reducing the study's generalizability. Fourth, biases in the Bland-Altman analysis may have been obscured since the standard deviations were relatively large. Fifth, a few wire velocity and pressure measurements were excluded from the Bland-Altman analysis due to noise artifacts. This highlights the technical challenges with acquiring wire measurements for use in CFD analyses. Nevertheless, most measurements were successfully acquired. Lastly, differences between patients’ systemic hemodynamic status over the course of the procedure may have influenced velocity and pressure measurements, though we attempted to keep systemic blood pressure, temperature and end-tidal CO₂ constant throughout each procedure.

Conclusions

Using the dual-sensor Doppler velocity guidewire, we have incorporated patient-specific measurements of blood flow velocity and blood pressure as inflow and outflow boundary conditions for CFD modeling of unruptured intracranial aneurysms. This study has quantified the degree of accuracy of using the wire-derived boundary conditions, specifically flow velocity and pressure drop, when compared against separate, independent wire measurements. Using the wire-derived boundary conditions gave results which were in better agreement with the in situ measurements when compared to cases using simplified boundary conditions typically employed in imaged-based hemodynamic analysis of cerebral aneurysms. There appears to be negligible systematic error in the CFD predicted velocity, and random errors are about 25-30% when using wire-derived boundary conditions. The dual-sensor guidewire is therefore a feasible and effective technique to measure patient-specific boundary conditions for hemodynamic analysis. CFD using wire-derived boundary conditions may provide better results than the commonly accepted reference values or scaling laws for boundary conditions.