Abstract
Background
The two most common models for the evolution of metabolism are the patchwork evolution model, where enzymes are thought to diverge from broad to narrow substrate specificity, and the retrograde evolution model, according to which enzymes evolve in response to substrate depletion. Analysis of the distribution of homologous enzyme pairs in the metabolic network can shed light on the respective importance of the two models. We here investigate the evolution of the metabolism in E. coli viewed as a single network using EcoCyc.
Results
Sequence comparison between all enzyme pairs was performed and the minimal path length (MPL) between all enzyme pairs was determined. We find a strong over-representation of homologous enzymes at MPL 1. We show that the functionally similar and functionally undetermined enzyme pairs are responsible for most of the over-representation of homologous enzyme pairs at MPL 1.
Conclusions
The retrograde evolution model predicts that homologous enzymes pairs are at short metabolic distances from each other. In general agreement with previous studies we find that homologous enzymes occur close to each other in the network more often than expected by chance, which lends some support to the retrograde evolution model. However, we show that the homologous enzyme pairs which may have evolved through retrograde evolution, namely the pairs that are functionally dissimilar, show a weaker over-representation at MPL 1 than the functionally similar enzyme pairs. Our study indicates that, while the retrograde evolution model may have played a small part, the patchwork evolution model is the predominant process of metabolic enzyme evolution.
Background
In 1945 one of the first theories regarding the evolution of metabolic pathways, often referred to as the retrograde evolution model, was proposed by Horowitz [1]. It states that during evolution pathways assembled backward compared to the direction of the pathway in response to depletion of substrates from the environment. As an example consider the following scenario: Enzyme E1 catalyzes reaction A → B, where B is essential to the organism. A is depleted from the environment, which means that an organism harboring an enzyme E2 that can catalyze a reaction producing A from some other substrate in the environment would be at an advantage. Since E1 can already bind A there is a greater chance that El rather than an enzyme without an affinity for A will be duplicated and mutated into E2.
In 1976 Jensen [2] proposed the recruitment evolution theory, more often referred to as the patchwork evolution model [3]. The patchwork evolution model states that enzymes initially have broad substrate specificities and that specialization takes place by way of gene duplication. As an example consider the following: An enzyme E1 catalyzes a reaction where either one of the substrates S1 and S2 is accepted. Through gene duplication and random mutation two different versions of E1 evolve; E1', which only accepts S1 as a substrate, and E1" which only accepts S2 as a substrate.
The retrograde evolution model was at first supported by the discovery of operons, where the functionally related genes in operons were thought to have evolved through tandem duplications [4]. The theory that operons are the remnants of tandem duplication has recently been criticized by Lawrence and Roth [5], who instead proposed that horizontal gene transfer may be the underlying mechanism for the occurrence of gene clusters. There are a few known homologous genes coding for enzymes which catalyze consecutive reactions and which therefore represent possible cases of retrograde evolution: trpC, trpA and trpB (in E. coli trpA and trpB are fused) that catalyze consecutive steps of the tryptophan biosynthesis [6], hisF and hisA in the histidine biosynthetic pathway [7] and metB and metC in the methionine biosynthesis [8].
A few recent studies give some support for the retrograde evolution model. Saqi & Sternberg [9] showed that a super-family has a general tendency to appear in one or two particular pathway(s). Rison et al [10] showed that homologous enzymes are found at close distances within the (extended) pathways of E. coli and Alves et al [11] showed that homologous enzymes are also found close to each other in the whole metabolic network using a modified version of the KEGG database[12,13].
The patchwork evolution model holds that there should be many pairs of homologous enzymes that catalyze basically the same kind of reaction, where one or more substrates are non-identical but similar. Support for this theory is more abundant than for the retrograde evolution model [14-17]. The TIM-barrel containing enzymes have been found in many different pathways [14] and the homologous pairs of small molecule metabolism enzymes of E. coli have been shown to be evenly distributed within and across pathways [15,16].
Metabolic networks are often partitioned into pathways, which are considered to be functionally separate units of the network. The partitioning of the metabolic network into pathways is not always straightforward [18]. As a result there may be correlations that are not visible in a pathway oriented perspective which will emerge in a whole-network oriented view. There is also an element of arbitrariness involved in which compounds are considered promiscuous (compounds involved in many reactions, e. g. H2O, ATP and cofactors) and which are not. We have chosen to apply a simple network-based criterion. We count the number of reactions a compound participates in within the complete metabolic network of E. coli. The most common compounds are then considered promiscuous and are excluded from part of the analysis.
In the study presented here we investigate whether homologous E. coli enzymes can be found close to each other in the complete, unpartitioned metabolic network of E. coli as derived from the EcoCyc database [19]. We subsequently investigate the homologous enzyme pairs found close to each other in the network and classify these enzyme pairs as cases of retrograde evolution and patchwork evolution respectively. Finally we investigate whether the correlation between metabolic network distance and homology differs for the enzyme pairs classified as retrograde evolution cases compared to the patchwork evolution cases.
Results and Discussion
Databases
Metabolic pathway information is available in several different databases such as EcoCyc [19], WIT [20], BRENDA [21] and KEGG [12]. EcoCyc is an E. coli-specific database and contains the metabolic complement of E. coli. We chose EcoCyc over the other available databases for three reasons: 1) EcoCyc contains information about the directionality of the enzymatic reactions, 2) Some enzymes have not yet been classified according to the Enzyme Commission (EC) system [22] (EcoCyc contains both EC-classified enzymes and enzymes that fall outside of the EC classification; There are 1172 enzyme entries in the database and 781 of these have EC numbers.) and 3) EcoCyc is freely available for universities and non-profit research institutes.
Representation framework
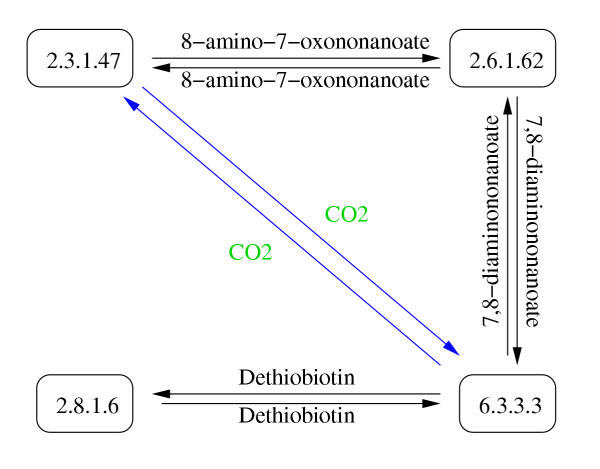
The vertices of the graph we use represent the enzymes catalyzing the reactions. One edge represents one or more compounds. There will be an edge leading from an enzyme E1 to an enzyme E2 if E1 catalyzes a reaction where compound A is produced and E2 takes A as a substrate. Reversible reactions, such as A 
B, are separated into two reactions, A → B and B → A. There can be at most one edge in each direction between a pair of enzymes. Note that the representation used herein is different from the common representation of metabolic pathways where the substrates and products are the vertices and the enzymes catalyzing the reactions are the edges (Figure 1). The type of network representation used in our study has been used before for metabolic network analysis where it has been referred to as 'protein-centric' graphs [23] and 'reaction graphs' [24] (Figure 2).
Figure 1.
Common representation of the biotin metabolism. In the most common representation of biochemical reactions the reactants represent the vertices of the network and the enzymes represent the edges. The drawing of the biotin metabolism was redrawn from EcoCyc [19].
Figure 2.
Protein-centric representation of the biotin metabolism. The protein-centric or reaction graph representation which was used in our study has enzymes as vertices and reactants as edges. EC 2.3.1.47 is a neighbor of EC 2.6.1.62 because there is an edge leading from EC 2.6.1.62 to EC 2.3.1.47. In the same manner, EC 2.6.1.62 is a neighbor of 2.3.1.47. In the biotin metabolism example there are 8 enzyme neighbor pairs. Note that in our definition an edge can consist of one or more compounds and there can only be one edge in each direction between two enzymes. The edges in blue font, representing CO2, between EC 2.3.1.47 and EC 6.3.3.3, are eliminated when the 20 most promiscuous compounds are removed from the network.
Some reactions are physiologically irreversible and should be represented accordingly. To encompass the directionality information we use a directed graph to represent the metabolic network of E. coli. As a result there are not necessarily paths from every enzyme vertex in the network to every other enzyme vertex.
One of the most problematic aspects with metabolic network analysis is how to handle the promiscuous compounds. One may argue that because promiscuous compounds are usually not the limiting factors of reactions, the network would become more biochemically meaningful if these compounds are removed [25]. However, to our knowledge there is no generally accepted criterion to determine whether a compound participating in a reaction is a current compound, cofactor or main metabolite. In this study, we have chosen to formulate and apply a simple network-based criterion. We count the number of times a compound occurs as part of an edge in the network. The most common compounds are then considered as promiscuous compounds [11]. As in the study performed by Wagner and Fell [24] we here conduct our study with one network that includes all compounds, including the promiscuous compounds, and another network where the most promiscuous compounds have been removed.
Determination of network parameters
The directed graph derived from EcoCyc contains 1,172 vertices and 224,972 edges (Table 1). The network consists of two components; one contains 2 vertices and a single edge while the other component consists of the remaining vertices. Except for the two enzymes (two chloride ion transporters) the whole metabolic network of E. coli is therefore connected as one would expect from a unicellular, autonomous and non-parasitic organism.
Table 1.
Network parameters. The table contains some important characteristics of the network (see text for more detailed description). The second column contains the network parameters for the whole network while the third column contains the network parameters for the network where the 20 most promiscuous compounds have been removed. The average path length (D) is determined by taking the average over the MPLs between all vertex pairs. The connectivity of a vertex is defined as the number of vertices which it is connected to by an outgoing edge.
| NETWORK PARAMETERS | 0 COMPOUNDS REMOVED | 20 COMPOUNDS REMOVED |
| Number of vertices (u) | 1,172 | 1,172 |
| Number of edges (k) | 224,972 | 11,365 |
Mean connectivity ( ) |
192 | 9.7 |
| Connectivity standard deviation | 151 | 10 |
| Average path length (D) | 1.9 | 4.2 |
| Average path length (random network) (Dr) | 1.3 | 3.0 |
| Clustering coefficient (Cn) | 0.72 | 0.48 |
| Clustering coefficient (random network) (Cr) | 0.16 | 0.0074 |
We examined which compounds are the most promiscuous in the metabolic network graph by determining the number of times the compounds occur as part of edges connecting two vertices in the network. The most promiscuous compound is H2O, which appears as part of an edge between 79,485 enzyme pairs (Table 2). The compound frequency plot shows some scale-free network characteristics in that there are a few compounds that occur very often and most compounds occur as parts of edges 1, 2 or 3 times (Figure 3). We also determine which enzymes are the most highly connected. The most highly connected enzyme has 735 enzyme neighbors (Carbamoyl phosphate synthase) (Table 3).
Table 2.
The most promiscuous compounds in the network. The frequency of a compound is the number of times the compound occurs as part of an edge in the network.
| RANK | COMPOUND | FREQUENCY |
| 1 | H2O | 79,485 |
| 2 | ATP | 46,579 |
| 3 | H+ | 27,033 |
| 4 | Mg2+ | 26,384 |
| 5 | ADP | 23,954 |
| 6 | Orthophosphate | 23,189 |
| 7 | Pyridoxal phosphate | 10,091 |
| 8 | NAD | 7,710 |
| 9 | NADH | 5,742 |
| 10 | CO2 | 4,245 |
| 11 | Pyruvate | 4,130 |
| 12 | NADP | 3,638 |
| 13 | NADPH | 3,284 |
| 14 | AMP | 2,964 |
| 15 | NH3 | 2,692 |
| 16 | Coenzyme A | 2,638 |
| 17 | L-Glutamate | 2,302 |
| 18 | Acetyl-CoA | 982 |
| 19 | Phosphoenolpyruvate | 941 |
| 20 | O2 | 920 |
| 21 | 2-Ketoglutarate | 808 |
| 22 | Mn2+ | 650 |
| 23 | S-Adenosylmethionine | 454 |
| 24 | L-Aspartate | 408 |
| 25 | FAD | 378 |
| 26 | Fructose-6-phosphate | 312 |
| 27 | GAP | 277 |
| 28 | Zn2+ | 272 |
| 29 | Sucrose | 272 |
| 30 | K+ | 268 |
Figure 3.
Compound frequency distribution histogram for the metabolic network of E. coli. The 20 most promiscuous compounds have been removed in the network analyzed here. The histogram shows how many compounds (y-axis, logged scale) that occur with a certain frequency (x-axis) in the network. Compound frequency is defined as the number of times a compound occurs as part of an edge.
Table 3.
The enzymes with the highest connectivities (k) of the network for the whole and the reduced networks. The connectivity of an enzyme is here defined as the number of enzymes which it is connected to by an outgoing edge.
| WHOLE NETWORK | REDUCED NETWORK | |||
| RANK | ENZYME | K | ENZYME | K |
| 1 | Carbamoyl phosphate synthase | 735 | Taurine dioxygenase | 61 |
| 2 | ATP synthase | 704 | Aspartate transaminase | 57 |
| 3 | Phosphoenolpyruvate synthase | 604 | Isocitrate dehydrogenase | 56 |
| 4 | S-adenosylmethionine synthetase I | 603 | Malate oxidase | 53 |
| 5 | NAD+ synthase | 599 | Quinolinate synthetase | 48 |
| 6 | NADP phosphatase | 583 | Alpha-galactosidase | 46 |
| 7 | Asparagine synthase B | 578 | 3-dimethylubiquinone 3-methyltransferase | 46 |
| 8 | Selenophosphate synthase | 563 | Transketolase I | 45 |
| 9 | Methionine adenosyltransferase 2 | 558 | Fructose 1,6-bisphosphatase II | 45 |
| 10 | Mg2+-importing ATPase | 558 | Glutamate synthase (NADPH) | 45 |
It has been shown in previous studies that the metabolic network of E. coli is a small world network [24-26]. The definition of a small world graph is that its average path length (D) is on the same order as the average path length for a random graph, with the same number of vertices (n) and mean connectivity (), but its clustering coefficient (Cn) exceeds that of the random graph by far [27]. Cn is a measure between 0 and 1 of the cliquishness of the graph [27]. Each vertex' clustering coefficient (C) is calculated by taking the number of edges between the vertex' neighbors (m) divided by the maximum number of edges between the vertex' neighbors, i.e if u is the number of neighbors and the graph is directed C = m/(u(u - 1)). Cn is the average clustering coefficient for the graph.
Our network graph has Cn = 0.72 which is large compared to the clustering coefficient of the random graph Cr = ( - 1)/n = 0.16 (Table 1). The average path length for the Erdös-Rényi random graph [28] is Dr ~ ln(n)/ln() = 1.3, which is smaller than but on the same order as the average path length for the metabolic network (Table 1). Given the large Cn and the small D we can conclude that the metabolic network of E. coli constructed from EcoCyc shows some characteristics of a small world network.
Correlation between MPL and homology
We used PSI-BLAST [29] with an E-value cut-off of 10-6 and 3 iterations for an all-against-all sequence comparison of the 1105 protein sequences coding for the metabolic enzymes in E. coli. We chose the relatively strict E-value cut-off in order to minimize the number of false positives. We also ran PSI-BLAST against the SCOP database [30] to increase the sensitivity and collect further pairs of homologous enzymes. The proteins in the SCOP database are ordered into a hierarchy consisting of class, fold, super-family and family, with an increasing level of structural similarity between the proteins. In our study, enzymes belonging to the same super-family are considered homologous. Using these methods 8,218 homologous enzyme pairs were found.
There are 72 cases where two homologous genes code for the same enzyme. The reason may for instance be that the genes code for different subunits of the enzyme, that there are multiple copies of one gene or that the genes code for two isozymes. In addition there are 169 pairs of enzymes which are clearly isozymes because they are homologous, identified as separate enzymes in EcoCyc and catalyze the same reaction. It is not clear what relationship these 241 pairs should have in our graph representation of the metabolic network. They may be included at minimal path length (MPL, Figure 4) 1 since they catalyze identical reactions, or they may be included as a special category at MPL 0. For our analysis however, since we are interested in the relationship between clearly different enzymes, we chose not to include these probably fairly recent gene duplications.
Figure 4.
Minimal path length (MPL) between enzymes. a) The reactions catalyzed by EC 1.1.1.1 (alcohol dehydrogenase), EC 1.5.1.12 (1-pyrroline-5-carboxylate dekydrogenase) and EC 1.2.1.3 (aldehyde dehydrogenase). b) There are severeral paths leading from EC 1.1.1.1 to EC 1.2.1.3. The shortest path goes from EC 1.1.1.1 through aldehyde to EC 1.2.1.3 and is of length 1 (MPL = 1).
There are 209 E. coli genes which are each associated with at least two enzymatic functions. Most of these multifunctional enzymes are enzymes with broad substrate specificities. 18 of these genes consist of two separate regions which are clearly associated with two (or more) different enzymatic functions (see Additional file 1 and for instance [31,32]). We used EcoCyc to identify these genes and Pfam [33] to localize the domains on the genes. The domains were separated from each other and included in the analysis as partial genes.
There are 644,656 pairs of enzymes in the whole network (Table 4). Of these, only 7,989 (1.2%) are homologous enzyme pairs. There are 121,295 enzyme pairs at MPL 1. 4,662 (3.8%) of these are homologous enzyme pairs. There appears to be a 3-fold over-representation of homologous enzyme pairs at MPL 1 in the whole network. In order to determine whether the observed over-representation of homologous enzyme pairs at MPL 1 is statistically significant randomized networks were constructed. There are many alternative ways to construct randomized networks. We have chosen an approach that preserves the topological properties of the network since it has been shown that the metabolic network of many organisms have some of the properties of scale-free networks [26]. We constructed many randomized networks by starting from the original real network and shuffling the enzyme identities between randomly chosen pairs of vertices in the graph which preserves the network topology (Figure 5).
Table 4.
The numbers of homologous enzyme pairs and enzyme pairs found at MPLs 1–12. The fraction is simply the ratio between the number of homologous enzyme pairs and the enzyme pairs. The reduced network is the network where the 20 most promiscuous compounds have been removed.
| WHOLE NETWORK | REDUCED NETWORK | |||||
| MPL | HOMOLOGS | ENZYME PAIRS | FRACTION | HOMOLOGS | ENZYME PAIRS | FRACTION |
| 1 | 4.662 | 121,295 | 0.0384 | 429 | 6,035 | 0.071 |
| 2 | 2,982 | 452,081 | 0.0066 | 561 | 33,203 | 0.017 |
| 3 | 340 | 67,857 | 0.0050 | 1,115 | 105,254 | 0,011 |
| 4 | 5 | 2,861 | 0.0017 | 1,472 | 146,932 | 0.010 |
| 5 | 0 | 553 | 0 | 1,188 | 99,240 | 0.012 |
| 6 | 0 | 9 | 0 | 611 | 47,115 | 0.013 |
| 7 | - | - | - | 265 | 18,975 | 0.014 |
| 8 | - | - | - | 97 | 5,707 | 0.017 |
| 9 | - | - | - | 25 | 1,217 | 0.021 |
| 10 | - | - | - | 9 | 230 | 0.039 |
| 11 | - | - | - | 1 | 17 | 0.059 |
| 12 | - | - | - | 0 | 2 | 0 |
| Total | 7.989 | 644,656 | 0.0124 | 5,773 | 463,927 | 0.013 |
Figure 5.
Preservation of network topology. The left side of the figure shows the numbers of vertices and edges in the original example graph. The right side of the figure shows the numbers of vertices and edges for the randomized graph where the vertex identities (A, B, C. D, E, F, G, H) have been shuffled. The topological properties of the original graph are preserved in the randomized graph.
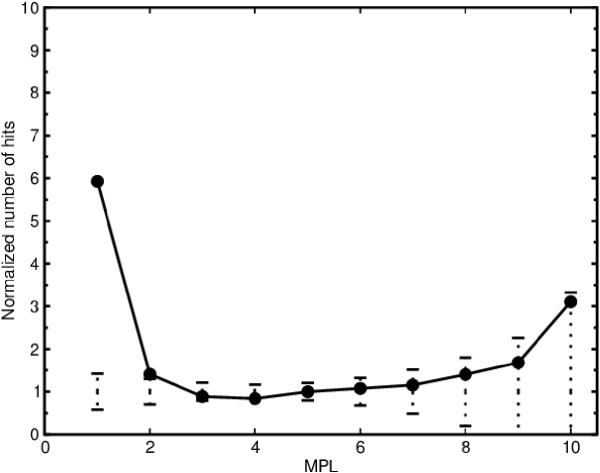
The number of homologous enzyme pairs plotted against MPL for the whole metabolic network of E. coli and the standard deviations for the 1,000 randomized networks are shown in Figure 6. In the real network there are 4,662 pairs of homologous genes at MPL 1, which is 58% of all homologous pairs found (Table 4). In contrast typically 1,454 homologous enzyme pairs (18%) are found at MPL 1 in the randomized networks. Compared to the randomized networks there is again a 3-fold over-representation of homologous enzyme pairs at MPL 1. If the homologies were randomly distributed in the network we would expect to see the line representing the real network within the boundaries of the standard deviations for the randomized networks in Figure 6. Instead, we find that there is a significantly greater likelihood of enzymes at distance 1 from each other to be homologous in the metabolic network of E. coli than in the randomized network.
Figure 6.
Homology vs minimal path length (MPL) for the whole metabolic network of E. coli. The plot shows the correlation between homology and MPL when all compounds are included. The solid line represents the real metabolic network of E. coli. The dotted vertical lines represent three standard deviations of the number of homologous enzyme pairs for the randomized networks. The number of homologous enzyme pairs has been normalized by the average number of homologous enzyme pairs for the randomized networks.
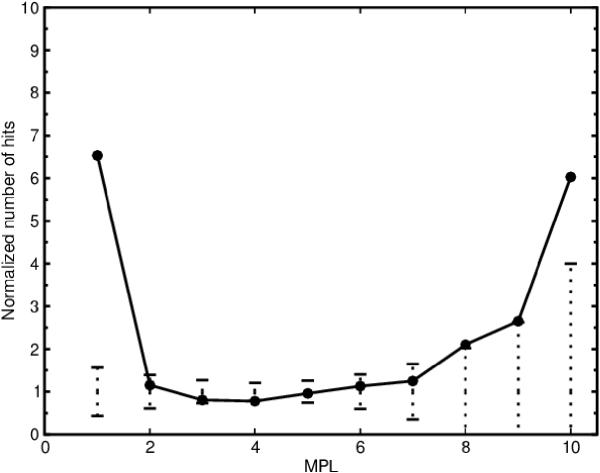
The network includes promiscuous compounds such as H2O, ATP and NAD. There are therefore homologous enzyme pairs containing for instance NAD-binding domains that are at MPL 1 because their gene products catalyze reactions involving that cofactor. It could be argued that such coenzyme binding domains give rise to skewed results in our analysis. To remedy this complication we removed 20 compounds, starting from the most promiscuous compound (H2O) down to the 20th most promiscuous compound (O2). We find that the correlation between MPL and homology is preserved (Figure 7), indicating that the abundance of homologous enzyme pairs at MPL 1 is not the result of common cofactor-binding domains alone. We could also detect a marginally significant correlation between MPL and homology at MPL 2 when the 20 most promiscuous compounds had been excluded from the network (Figure 7). No correlation could be detected at MPLs greater than 2. These results were robust for variations in the number of compounds that were removed from the network, i.e. removing between 17 and 23 of the most promiscuous compounds generated the same result (data not shown).
Figure 7.
Homology vs minimal path length (MPL) without the 20 most promiscuous compounds. The plot shows the correlation between homology and MPL when the 20 most promiscuous compounds (Table 2) have been removed. The solid line represents the metabolic network of E. coli.The dotted vertical lines represent three standard deviations of the number of homologous enzyme pairs for the randomized networks. The number of homologous enzyme pairs has been normalized by the average number of homologous enzyme pairs for the randomized networks.
It could be argued that the over-representation of homologous enzyme pairs at MPL 1 is due to the fact that not all cofactors have been removed by removing the 20 most promiscuous compounds. To investigate this possibility an alternative network was constructed where all the cofactors, as defined by EcoCyc, were removed from the network. In this alternative network the number of homologous enzyme pairs at MPL 2 is just within the boundaries of 3 standard deviations for the randomized networks. The correlation at MPL 1 remained unchanged (data not shown). Hence, the correlation between homology and MPL at MPL 1 is not due to cofactor-binding regions alone.
Rison et al [10] found an over-representation within the extended pathways of E. coli at pathway distances 1, 2 and 3. Alves et al found that there is clustering of homologous enzyme pairs at MPL 1 and 2 in the metabolic networks of several organisms. We detect a clearly significant over-representation only at MPL 1 in the metabolic network of E. coli. Two possible explanations for the differences between our results are that Alves et al performed a multi-organism analysis while we analyze only E. coli and that Rison et al looked at extended pathways rather than at the whole network.
Analysis of the homologous enzyme pairs
We wished to investigate to which extent the retrograde evolution model and the patchwork evolution model respectively are responsible for the over-representation of homologous enzyme pairs seen at MPL 1. In order to be able to analyze the homologous enzyme pairs at MPL 1 further we use a rough criterion for discriminating between cases that fit the retrograde evolution model or the patchwork evolution model:
1) Patchwork model: Homologous enzymes with similar functions probably evolved through patchwork evolution events. Therefore homologous enzymes that evolved through the patchwork evolution model should share the same primary EC number.
2) Retrograde evolution: Homologous enzymes with dissimilar functions are less likely to have evolved through patchwork evolution events. Therefore homologous enzymes that have different primary EC numbers are candidates for retrograde evolution.
We find that 304 enzymes (26%) have not been EC classified. Reactions that do not have EC numbers have been classified by EcoCyc according to an EcoCyc-specific scheme. We consider enzymes that belong to the same EcoCyc reaction type as functionally similar. There are some reactions that remain unclassified in EcoCyc. Pairs including such enzymes are regarded as 'undetermined' in our analysis.
240 (56%) of the homologous enzyme pairs at MPL 1 have similar functions (Table 5). One instance is 1-phosphofructokinase and 6-phosphofructokinase, which catalyze similar reactions with the difference that 1-phosphofructokinase catalyzes a reaction involving fructose-1-phosphate while 6-phosphofructokinase has fructose-6-phosphate as a substrate (Figure 8a). These are clearly analogous reactions whose homology can readily be explained by the patchwork evolution model.
Table 5.
The numbers of functionally similar /dissimilar/undetermined homologous enzyme pairs at MPLs 1–11 in the network where the 20 most promiscuous compounds have been removed.
| MPL | SIMILAR | DISSIMILAR | UNDETERMINED | |||
| NO. HOMOLOGS | % | NO. HOMOLOGS | % | NO. HOMOLOGS | % | |
| 1 | 240 | 56 | 90 | 21 | 99 | 23 |
| 2 | 233 | 42 | 207 | 37 | 121 | 22 |
| 3 | 515 | 46 | 395 | 35 | 205 | 18 |
| 4 | 693 | 47 | 553 | 38 | 226 | 15 |
| 5 | 579 | 49 | 469 | 40 | 140 | 12 |
| 6 | 326 | 53 | 231 | 38 | 54 | 8.8 |
| 7 | 146 | 55 | 101 | 38 | 18 | 6.8 |
| 8 | 74 | 76 | 22 | 23 | 1 | 1.0 |
| 9 | 20 | 80 | 5 | 20 | 0 | 0 |
| 10 | 9 | 100 | 0 | 0 | 0 | 0 |
| 11 | 1 | 100 | 0 | 0 | 0 | 0 |
| Total | 2836 | 49 | 2073 | 36 | 864 | 15 |
Figure 8.
Different types of homologous enzyme pairs at minimal path length (MPL) 1. a) Enzymes that catalyze similar reactions. The enzymes are at MPL 1 because they both catalyse reactions involving the metabolite fructose-1,6-bisphosphate. b) Enzymes that catalyze reactions that are mechanistically different. These enzymes are at MPL 1 because they both catalyse reactions involving chorismate.
90 (21%) of the homologous enzyme pairs at MPL 1 are functionally dissimilar (Table 5). One instance is component I of anthranilate synthase (trpE) which is homologous to the two isozymes of isochorismate synthase (entC and menF) (Figure 8b). If substrate depletion was the primary selective pressure for the E. coli ancestor of these enzymes, chorismate was probably the substrate being depleted because it is the only compound that these two reactions have in common. It is primarily among the 297 homologous enzyme pairs with dissimilar functions at MPL 1 and 2 that the candidates for retrograde theory enzymes can be found. However, it should be noted that some of the candidates for retrograde evolution that have been identified before are not included among our retrograde evolution candidates: We classify the enzymes, coding for the last two consecutive steps in the tryptophan biosynthesis (trpA/trpB and trpC) as functionally conserved because these two enzymes have the same primary EC numbers (4.1.1.48 and 4.2.1.20). In the same manner we classify the enzymes, coding for two consecutive steps in methionine biosynthesis (metB and metC) (4.2.99.9 and 4.4.1.8) as functionally similar as well as the four homologous consecutive enzymes in the peptidoglycan biosynthesis (6.3.2.8, 6.3.2.9, 6.3.2.13, 6.3.2.10).
The functionally similar, dissimilar and undetermined homologous enzyme pairs were plotted against MPL and normalized against 1,000 randomized networks by the same method as described above. From this procedure we could determine that most of the correlation between homology and MPL at MPL 1 can be attributed to enzymes with similar functions (Figure 9) and enzymes with undetermined function (data not shown). However, there is still an over-representation of functionally dissimilar homologous enzyme pairs at MPL 1 (Figure 10) indicating that there is a statistically significant proportion of the homologous enzyme pairs whose homology cannot be attributed to chemical similarity. We also note an over-representation at MPL 10 for the functionally similar homologous pairs (Figure 9). The over-representation consists of 9 pairs of homologous inner membrane MFS transporters which show 15–20% sequence identity.
Figure 9.
Homology vs minimal path length (MPL) without the 20 most promiscuous compounds for functionally similar enzyme pairs. The plots show the correlation between homology and MPL for functionally similar (shared primary EC number) enzyme pairs when the 20 most promiscuous compounds have been removed. The solid line represents the metabolic network of E. coli. The dotted vertical lines represent three standard deviations of the number of homologous enzyme pairs for the randomized networks. The number of homologous enzyme pairs has been normalized by the average number of homologous enzyme pairs for the randomized networks.
Figure 10.
Homology vs minimal path length (MPL) without the 20 most promiscuous compounds for functionally dissimilar enzyme pairs. The plots show the correlation between homology and MPL for functionally dissimilar (different primary EC number) enzyme pairs when the 20 most promiscuous compounds have been removed. The solid line represents the metabolic network of E. coli. The dotted vertical lines represent three standard deviations of the number of homologous enzyme pairs for the randomized networks. The number of homologous enzyme pairs has been normalized by the average number of homologous enzyme pairs for the randomized networks.
The correlation between homology and network distance at MPL 1 is mostly due to the homologous enzyme pairs with similar functions which have evolved through patchwork evolution and to homologous enzyme pairs with undetermined function. While there is some statistically significant over-representation of functionally dissimilar homologous enzyme pairs at MPL 1 which cannot easily be explained by the patchwork evolution model, it appears that the evolution of an enzyme that catalyzes a new type of reaction is rare and increased enzyme specificity driven evolution is more common which is in general agreement with recent studies [16,15].
Conclusions
We constructed a representation of the whole metabolic network of E. coli from EcoCyc and analyzed the distribution of homologous enzyme pairs over the network. We conclude from our study that homologous pairs of enzymes are more common at minimal path length (MPL) 1 than expected by chance. This correlation persists after the systematic removal of the most promiscuous compounds from the network.
The retrograde evolution model predicts that homologous enzyme pairs will be found at close distances in the metabolic network. Like previous studies our study seems to lend some support to the retrograde evolution model. To investigate the support for the retrograde evolution model further we analyzed the homologous pairs of enzymes in order to distinguish between on the one hand cases of patchwork evolution (broad-to-narrow evolution of enzyme substrate specificity) and on the other hand cases of retrograde evolution (evolution of a different reaction mechanisms). We found that the correlation between homology and network distance at MPL 1 is mostly due to homologous enzyme pairs with similar functions which have evolved through patchwork evolution and to homologous enzyme pairs with undetermined function. However, there is a statistically significant over-representation of functionally dissimilar homologous enzyme pairs at MPL 1 which cannot easily be explained by the patchwork evolution model. In conclusion, our study indicates that while the retrograde evolution model may have played a small part, the patchwork evolution model is the predominant process of metabolic enzyme evolution.
The record of evolutionary history that is present in modern genome sequences does not give much support for the retrograde evolution model [1] while Jensen's patchwork evolution model [2] has substantially more support. Horowitz aimed at explaining the emergence of metabolic pathways at the origin of life. It is possible that the subsequent mutations and gene rearrangements have obliterated the traces of ancient retrograde evolution. The patchwork evolution cases that we identify could be the examples of more recent events in evolutionary history. Further phylogenetic analysis of other genomes may shed light on this issue.
Methods
Databases
EcoCyc is arranged into several different flat-files. We used the enzrxns.dat file to extract the enzyme identifiers and the reaction directions, the proteins.dat file to extract the proteins coding for the enzymes, the genes.dat file to find the genes coding for the proteins, the genes.col file to find the Blattner identification number and the compounds.dat file to extract the compounds that are included in the reactions.
There were some reactions that were EC-number classified but did not have a link to the corresponding enzyme in the enzrxns.dat file. We could find 46 such cases and used KEGG [12] and BRENDA [21] to correct this problem (see Additional file 2).
Of the 1,172 enzyme identifiers available in EcoCyc, 44 were not connected to the rest of the network. Some other enzymes have not yet been located in the genome, which makes sequence comparison impossible, leaving the final number of enzymes for our study at 1,085. The 1,105 protein sequences coding for these enzymes were extracted from the Wisconsin-Madison E. coli genome project's flat-file [34]. There were 519 compounds that were involved in the reactions extracted.
Programs
A set of programs were constructed for determination of the minimal path lengths (MPLs) for all enzyme pairs in the network graph. For each E. coli enzyme the neighboring enzymes were determined (Figure 11a). The main program is a breadth-first search implementation which determines all possible MPLs between all pairs of enzymes (Figure 11b). The general idea for the algorithm is the same as described in Jeong et al [26]. It should be noted that because the graph representing the metabolic network of E. coli is directed there may not be paths between all enzyme pairs in one graph component. All the scripts used in this study were written in Python.
Figure 11.
Main algorithm. a) Determination of neighbors for each enzyme. b) Determination of minimal path length (MPL). The algorithm is a bread-first search for the shortest distance between all pairs of enzymes. MAX_MPL is the maximum MPL under investigation.
Authors' contributions
SL performed the analysis as a graduate student under the supervision of PK.
Supplementary Material
The text file additional_file_1.txt contains a list of some of the genes in E. coli which code for multifunctional enzymes. In this study these genes were separated into two partial genes because the functions could be clearly associated with different domains. Each line in the text file consists of the name for the partial gene, the EcoCyc ID for the enzyme associated with the gene, the EcoCyc gene ID and the gene's Blattner ID.
The text file additional_file_2.txt contains enzymatic reactions from EcoCyc's reactions.dat file which were associated with complete EC numbers and did not have links to the enzyme objects in EcoCyc's enzrxns.dat file. These reactions were added to our study using information from KEGG [12] and BRENDA [21]. The enzymatic reactions are included in this file with the EcoCyc reaction ID, EC number, common name, left side reactants, right side reactants, genes and reaction direction.
Acknowledgments
Acknowledgements
This work was supported by the Foundation for Strategic Research (SSF).
Contributor Information
Sara Light, Email: sara@sbc.su.se.
Per Kraulis, Email: Per.Kraulis@biovitrum.com.
References
- Horowitz NH. On the evolution of biochemical syntheses. Proc Natl Acad Sci USA. 1945;31:153–157. doi: 10.1073/pnas.31.6.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen RA. Enzyme recruitment in evolution of new function. Annu Rev Microbiol. 1976;30:409–425. doi: 10.1146/annurev.mi.30.100176.002205. [DOI] [PubMed] [Google Scholar]
- Lazcano A, Miller SL. The origin and early evolution of life: prebiotic chemistry, the pre-RNA world, and time. Cell. 1996;85:793–798. doi: 10.1016/S0092-8674(00)81263-5. [DOI] [PubMed] [Google Scholar]
- Horowitz NH. The evolution of biochemical syntheses – retrospect and prospect. In: Bryson V, Vogel HJ, editor. In Evolving genes and proteins. New York: Academic Press; 1965. pp. 15–23. [Google Scholar]
- Lawrence JG, Roth JR. Selfish operons: horizontal transfer may drive the evolution of gene clusters. Genetics. 1996;143:1843–1860. doi: 10.1093/genetics/143.4.1843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilmanns M, Hyde CC, Davies DR, Kirschner K, Jansonius JN. Structural conservation in parallel beta/alpha-barrel enzymes that catalyze three sequential reactions in the pathway of tryptophan biosynthesis. Biochemistry. 1991;30:9161–9169. doi: 10.1021/bi00102a006. [DOI] [PubMed] [Google Scholar]
- Fani R, Lio P, Lazcano A. Molecular evolution of the histidine biosynthetic pathway. J Mol Evol. 1995;41:760–774. doi: 10.1007/BF00173156. [DOI] [PubMed] [Google Scholar]
- Belfaiza J, Parsot C, Martel A, de la Tour CB, Margarita D, Cohen GN, Saint-Girons I. Evolution in biosynthetic pathways: two enzymes catalyzing consecutive steps in methionine biosynthesis originate from a common ancestor and possess a similar regulatory region. Proc Natl Acad Sci USA. 1986;83:867–871. doi: 10.1073/pnas.83.4.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saqi MA, Steinberg MJ. A structural census of metabolic networks for E. coli. J Mol Biol. 2001;313:1195–1206. doi: 10.1006/jmbi.2001.5107. [DOI] [PubMed] [Google Scholar]
- Rison SC, Teichmann SA, Thornton JM. Homology, pathway distance and chromoso mal localisation of the small molecule metabolism enzymes in Escherichia coli. J Mol Biol. 2002;318:911–932. doi: 10.1016/S0022-2836(02)00140-7. [DOI] [PubMed] [Google Scholar]
- Alves R, Chaleil RA, Sternberg MJ. Evolution of enzymes in metabolism: a network perspective. J Mol Biol. 2002;320:751–770. doi: 10.1016/S0022-2836(02)00546-6. [DOI] [PubMed] [Google Scholar]
- Kanehisa M, Goto S, Kawashima S, Nakaya A. The KEGG databases at GenomeNet. Nucleic Acids Res. 2002;30:42–46. doi: 10.1093/nar/30.1.42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goto S, Okuno Y, Hattori M, Nishioka T, Kanehisa M. LIGAND: database of chemical compounds and reactions in biological pathways. Nucleic Acids Res. 2002;30:402–404. doi: 10.1093/nar/30.1.402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Copley RR, Bork P. Homology among (β/α)8 barrels: implications for the evolution of metabolic pathways. J Mol Biol. 2000;303:627–641. doi: 10.1006/jmbi.2000.4152. [DOI] [PubMed] [Google Scholar]
- Teichmann SA, Rison SC, Thornton JM, Riley M, Gough J, Chothia C. The evolution and structural anatomy of the small molecule metabolic pathways in Escherichia coli. J Mol Biol. 2001;311:693–708. doi: 10.1006/jmbi.2001.4912. [DOI] [PubMed] [Google Scholar]
- Tsoka S, Ouzounis CA. Functional versatility and molecular diversity of the metabolic map of Escherichia coli. Genome Res. 2001;11:1503–1510. doi: 10.1101/gr.187501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petsko GA, Kenyon GL, Gerlt JA, Ringe D, Kozarich JW. On the origin of enzymatic species. Trends Biochem Sci. 1993;18:372–376. doi: 10.1016/0968-0004(93)90091-Z. [DOI] [PubMed] [Google Scholar]
- Schuster S, Fell DA, Dandekar T. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nat Biotechnol. 2000;18:326–332. doi: 10.1038/73786. [DOI] [PubMed] [Google Scholar]
- Karp PD, Riley M, Saier M, Paulsen IT, Collado-Vides J, Paley SM, Pellegrini-Toole A, Bonavides C, Gama-Castro S. The EcoCyc database. Nucleic Acids Res. 2002;30:56–58. doi: 10.1093/nar/30.1.56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overbeek R, Larsen N, Pusch GD, D'Souza M, Jr, Selkov E, Jr, Kyrpides N, Fonstein M, Maltsev N, Selkov E. WIT: integrated system for high-throughput genome sequence analysis and metabolic reconstruction. Nucleic Acids Res. 2000;28:123–125. doi: 10.1093/nar/28.1.123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schomburg I, Chang A, Schomburg D. BRENDA, enzyme data and metabolic information. Nucleic Acids Res. 2002;30:47–49. doi: 10.1093/nar/30.1.47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nomenclature Committee of the International Union of Biochemistry and Molecular Biology (NC-IUBMB) Enzyme Nomenclature. San Diego, California: Academic Press; 1992. [Google Scholar]
- Gerrard JA, Sparrow AD, Wells JA. Metabolic databases – what next? Trends Biochem Sci. 2001;26:137–140. doi: 10.1016/S0968-0004(00)01759-X. [DOI] [PubMed] [Google Scholar]
- Wagner A, Fell DA. The small world inside large metabolic networks. Proc R Soc Lond B Biol Sci. 2001;268:1803–1810. doi: 10.1098/rspb.2001.1711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma H, Zeng AP. Reconstruction of metabolic networks from genome data and analysis of their global structure for various organisms. Bioinformatics. 2003;19:270–277. doi: 10.1093/bioinformatics/19.2.270. [DOI] [PubMed] [Google Scholar]
- Jeong H, Tombor B, Albert R, Oltvai ZN, Barabasi AL. The large-scale organization of metabolic networks. Nature. 2000;407:651–654. doi: 10.1038/35036627. [DOI] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of 'small-world' networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Erdös P, Rényi A. On random graphs. I. Publicationes Mathematicae (Debrecen) 1959;6:290–297. [Google Scholar]
- Schaffer AA, Aravind L, Madden TL, Shavirin S, Sponge JL, Wolf YI, Koonin EV, Altschul SF. Improving the accuracy of PSI-BLAST protein database searches with composition-based statistics and other refinements. Nucleic Acids Res. 2001;29:2994–3005. doi: 10.1093/nar/29.14.2994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LoConte L, Ailey B, Hubbard TJ, Brenner SE, Murzin AG, Chothia C. SCOP: a structural classification of proteins database. Nucleic Acids Res. 2000;28:257–259. doi: 10.1093/nar/28.1.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun DH, Bonner CA, Gu W, Xie G, Jensen RA. The emerging periplasm-localized subclass of AroQ chorismate mutases, exemplified by those from Salmonella typhimurium and Pseudomonas aeruginosa. Biol Genome. 2001;2 doi: 10.1186/gb-2001-2-8-research0030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veron M, Falcoz-Kelly F, Cohen GN. The threonine-sensitive homoserine dehydrogenase and aspartokinase activities of Escherichia coli K12. The two catalytic activities are carried by two independent regions of the polypeptide chain. Eur J Biochem. 1972;28:520–527. doi: 10.1111/j.1432-1033.1972.tb01939.x. [DOI] [PubMed] [Google Scholar]
- Sonnhammer EL, Eddy SR, Durbin R. Pfam: a comprehensive database of protein families based on seed alignments. Proteins. 1997;28:405–420. doi: 10.1002/(SICI)1097-0134(199707)28:3<405::AID-PROT10>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- Blattner FR, Plunkett G, 3rd, Bloch CA, Perna NT, Burland V, Riley M, Collado-Vides J, Glasner JD, Rode CK, Mayhew GF, Gregor J, Davis NW, Kirkpatrick HA, Goeden MA, Rose DJ, Mau B, Shao Y. The complete genome sequence of Escherichia coli K-12. Science. 1997;277:1453–1474. doi: 10.1126/science.277.5331.1453. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The text file additional_file_1.txt contains a list of some of the genes in E. coli which code for multifunctional enzymes. In this study these genes were separated into two partial genes because the functions could be clearly associated with different domains. Each line in the text file consists of the name for the partial gene, the EcoCyc ID for the enzyme associated with the gene, the EcoCyc gene ID and the gene's Blattner ID.
The text file additional_file_2.txt contains enzymatic reactions from EcoCyc's reactions.dat file which were associated with complete EC numbers and did not have links to the enzyme objects in EcoCyc's enzrxns.dat file. These reactions were added to our study using information from KEGG [12] and BRENDA [21]. The enzymatic reactions are included in this file with the EcoCyc reaction ID, EC number, common name, left side reactants, right side reactants, genes and reaction direction.