Whole brain mapping of water pools and molecular dynamics with rotating frame MR relaxation using gradient modulated low-power adiabatic pulses

Abstract

Nuclear magnetic resonance (NMR) relaxation in the rotating frame is sensitive to molecular dynamics on the time scale of water molecules interacting with macromolecules or supramolecular complexes, such as proteins, myelin and cell membranes. Hence, longitudinal (T1ρ) and transverse (T2ρ) relaxation in the rotating frame may have a great potential to probe the macromolecular fraction of tissues. This stimulated a large interest in using this MR contrast to image brain under healthy and disease conditions. However, experimental challenges related to the use of intense radiofrequency irradiation have limited the widespread use of T1ρ and T2ρ imaging. Here, we present methodological development to acquire 3D high-resolution or 2D (multi-)slice selective T1ρ and T2ρ maps of the entire human brain within short acquisition times. These improvements are based on a class of gradient modulated adiabatic pulses that reduce the power deposition, provide slice selection, and mitigate artifacts resulting from inhomogeneities of B₁ and B₀ magnetic fields. Based on an analytical model of the T1ρ and T2ρ relaxation we compute the maps of macromolecular bound water fraction, correlation and exchange time constants as quantitative biomarkers informative of tissue macromolecular content. Results obtained from simulations, phantoms and five healthy subjects are included.

1. INTRODUCTION

Longitudinal (T1ρ) and transverse (T2ρ) relaxation in the rotating frame of nuclear magnetic resonance can probe water molecules loosely bound (hydration layer) to macromolecules. The macromolecular fraction is tissue specific and changes with disease, hence T1ρ and T2ρ have been proposed (Sepponen et al., 1985) as a candidate for non-invasive imaging solid tissue matrix, albeit indirectly through the relaxation of water interacting with macromolecules. Several studies have investigated the value of T1ρ and T2ρ imaging in the context of neurological diseases, including Alzheimer’s Disease (Borthakur et al., 2008, Haris et al., 2011), Parkinson Disease (Michaeli et al., 2007, Haris et al., 2011), stroke (Jokivarsi et al., 2009, Jokivarsi et al., 2010a), and brain cancer (Aronen et al., 1999, Hakumaki et al., 1999). These studies revealed that T1ρ and T2ρ relaxation times have a broader range of values compared to T1 and T2 across disease spectrum, and better separate patients from controls. Also, T1ρ and T2ρ relaxation times seem to correlate better and earlier with therapy response or disease progression when compared to other MRI markers such as laboratory frame T1 and T2 relaxation, or ADC values (Duvvuri et al., 2001, Hakumaki et al., 2002, Jokivarsi et al., 2010a).

Experimental challenges related to high specific absorption rate (SAR), non-selective spatial excitation, long acquisition times, and artifacts from B₀ and B₁ inhomogeneity currently prevent a wide spread adoption and usage of T1ρ and T2ρ in the neuroimaging community. Here, we present methodological development for clinically feasible and robust T1ρ and T2ρ mapping of the whole human brain based on a recent class of gradient modulated adiabatic pulses (Andronesi et al., 2010). Further, using an analytical model and fitting of relaxation curves we extract tissue specific maps for parameters of molecular dynamics such as correlation times, exchange times, and water pools.

Nuclear spin relaxation in the rotating frame is obtained when a radiofrequency field (B₁) is applied either along or perpendicular to the nuclear magnetization for longitudinal T1ρ relaxation or transverse T2ρ relaxation, respectively. Typically, T1ρ and T2ρ imaging of the human brain is done with B₁ amplitudes in the range of 0.5–1 kHz and durations between 50–100 ms. The combination of high B₁ amplitude and long duration leads to increased SAR, which is often circumvented by increasing repetition times (TR) leading to long acquisition times (TA). Moreover, in all imaging studies so far T1ρ and T2ρ relaxation has been achieved via spatially non-selective radiofrequency (RF) irradiation, which further imposes limits on the TR in multislice experiments due to relaxation and saturation of magnetization in neighboring slices. As a result, rotating frame relaxation imaging is usually performed as a single slice or very few (1–4) slices at a time.

Three main approaches are currently used to achieve T1ρ relaxation: i) the on-resonance continuous wave (CW) method were the magnetization is first flipped in the transverse plan and a B₁ field with a constant amplitude is applied along magnetization for spin-lock (Aronen et al., 1999), ii) the off-resonance continuous wave (CW) method were an offset is used to create an effective field and magnetization is flipped along the direction the effective field (Ramadan et al., 1998), and iii) a train of adiabatic inversion pulses producing repeated passages of the longitudinal magnetization between the +Z and −Z orientations via amplitude and frequency modulation of B₁ field (Michaeli et al., 2008). In the case of T2ρ relaxation the initial magnetization is first flipped perpendicular to the direction of the spin-lock or the effective field for precession around it. The spin-lock method is easier to implement and model analytically, but it is more sensitive to artifacts induced by B₀ and B₁ inhomegeneities. These artifacts can be compensated over a reduced B₀ and B₁ range by composite pulses and phase alternation of the CW spin-lock (Witschey et al., 2007). On the other hand, due to its simultaneous frequency and amplitude sweep adiabatic pulses can cover a much larger bandwidth of B₀ offsets and can tolerate several-folds of B₁ inhomogeneity above the adiabatic threshold (Garwood and DelaBarre, 2001). In addition, adiabatic pulses have lower SAR compared to a CW spin-lock of the same amplitude.

Our focus in this work was to address the major limitations of current T1ρ and T2ρ imaging techniques, namely high SAR and long acquisition times, while at the same time compensating for B₀ and B₁ inhomogeneities. Gradient modulated adiabatic pulses such as GOIA-W(16,4) (Andronesi et al., 2010) simultaneously meet all these requirements. The Gradient Offset Independent Adiabaticity (GOIA) design (Tannus and Garwood, 1997) lowers the maximum B₁ amplitude by 55%, resulting in 80% less SAR, compared to conventional adiabatic pulses of the same bandwidth and duration. Alternatively, GOIA-W(16,4) can be made shorter and still have lower B₁ amplitude than conventional adiabatic pulses, allowing more flexibility in choosing the duration of T1ρ and T2ρ preparation. Compared to a CW spin-lock of the same amplitude GOIA-W(16,4) pulses would have 20% less SAR.

The use of gradient modulation in GOIA-W(16,4) pulses naturally provides slice-selectivity for T1ρ and T2ρ. In the case of 2D imaging, slice selectivity allows the use of a short TR to acquire a stack of slices without saturating magnetization of neighboring slices. Although strategies have been proposed for the CW spin-lock method to reduce SAR (Wheaton et al., 2004a) or acquire multiple slices with less magnetization saturation (Wheaton et al., 2004b), these have limitations in fully achieving those goals. In terms of the SAR deposition, GOIA pulses compare favorably also to relaxation along the fictitious field (RAFF) method (Liimatainen et al., 2010) which uses sub-adiabatic RF frequency and amplitude modulations to lower B₁ requirements, at the cost of more sensitivity to B₁ inhomogeneity and without slice selectivity.

Here we demonstrate the use of GOIA-W(16,4) pulses trains in combination with 2D spin-echo EPI (EPI-SE) and 3D turbo FLASH (TFL) readouts as a new method for robust and feasible T1ρ and T2ρ imaging of the human brain.

2. THEORY

2.1 Relaxation in the rotating frame of GOIA pulses

Relaxation in the rotating frame has been an important research topic reach in applications since the beginning of nuclear magnetic resonance (Redfield, 1957). The semi-classical theory of Bloch-Wangsness-Redfield (BWR), often used for practical reasons, treats the spins quantum mechanically and the lattice as random perturbation described by classical statistics (Wangsness and Bloch, 1953, Redfield, 1957, Abragam, 1961). Significant progress has been made over the last decade in laying out the analytical framework for relaxation in the rotating frame under adiabatic pulses (Sorce et al., 2007, Michaeli et al., 2008, Mangia et al., 2009). In this work we extend the theory of rotating frame relaxation for the case of gradient modulated adiabatic pulses.

GOIA pulses (Tannus and Garwood, 1997) are obtained by simultaneously modulating the amplitude B₁(t) and frequency Δω(t) of RF field, together with the slice selection gradient G(t) according to:

$$\mathrm{\Delta }\omega (t)=\frac{1}{Q}G(t)\underset{0}{\overset{t}{\int }}\frac{{\gamma }^2{B}_1^2(t\prime )}{G(t\prime )}dt\prime$$ [1]

where Q is the adiabatic factor, and γ is the nuclear gyromagnetic ratio.

In particular, for GOIA-W(16,4) pulses (Andronesi et al., 2010) the modulation functions B₁(t) and G(t) are based on the wideband uniform rate and smooth truncation WURST (Kupce and Freeman, 1995) function:

$$B_1(t)=B_{1,\mathit{\text{max}}}(1-{\left[\text{sin}\right(\pi /2(2t/T_p-1)\left)\right]}^{16})G(t)=G_{\mathit{\text{max}}}((1-g_m)+g_m{\left[\text{sin}\right(\pi /2(2t/T_p-1)\left)\right]}^4)$$ [2]

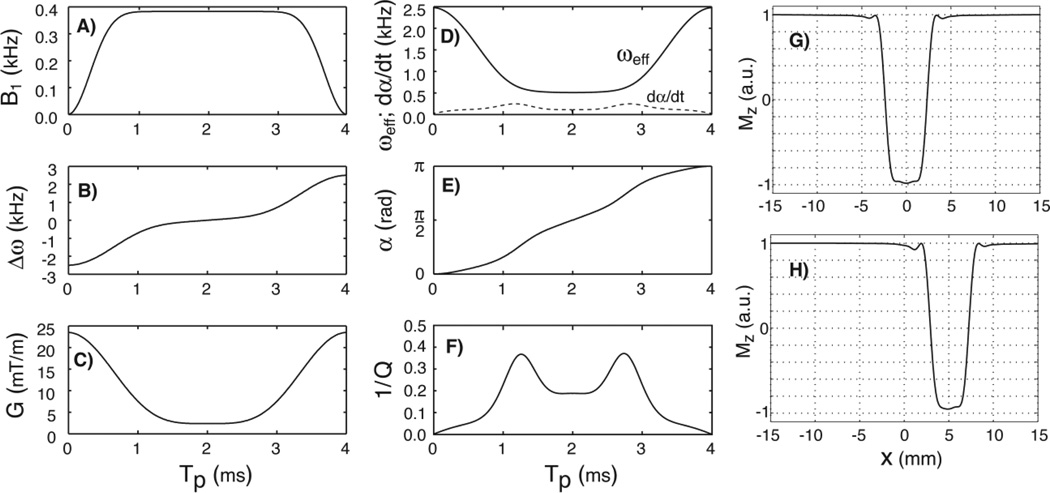
where T_p is the pulse duration, B_1,max is the maximum RF amplitude, G_max is the maximum gradient, and g_m ∈ [0, 1] is the gradient modulation factor. The larger the g_m factor the more the gradient drops in the middle of the pulse and correspondingly lesser RF amplitude is required, an effect also known as the variable rate selective excitation VERSE (Conolly et al., 1988). Alternatively, GOIA-HS(8,4) (Andronesi et al., 2010) pulses are obtained if stretched hyperbolic-secant functions are used instead of WURST. Besides pulse duration and gradient modulation factor, the exponents of trigonometric functions can be varied too, providing great flexibility in obtaining new pulses. Modulations of GOIA-W(16,4) pulse of 4ms duration and 5kHz bandwidth are shown in Figs. 1A–C.

Figure 1.

Plots of GOIA-W(16,4) pulse: A) B₁ amplitude modulation function; B) frequency sweep; C) gradient modulation; D) effective field; E) nutation angle; F) inverse of the adiabatic factor; G) slice profile at the isocenter; H) slice profile off-isocenter. A pulse duration of 4ms and bandwidth of 5kHz were assumed. In Fig.1D the rate of the nutation angle is also shown with the dashed line.

In order to calculate the rates of rotating frame relaxation we need the effective field (ω_eff) and the magnetization nutation angle (α):

$${\omega }_{\mathit{\text{eff}}}(t,x)=\sqrt{{(\gamma B_1(t))}^2+{((\mathrm{\Delta }\omega (t)+\gamma xG(t)))}^2}\alpha (t,x)=\mathrm{a}\text{tan}(\gamma B_1(t)/(\mathrm{\Delta }\omega (t)+\gamma xG(t)))$$ [3]

The adiabatic condition states that the effective field should be much greater than the rate nutation angle ω_eff (t, x) ≫ α̇(t, x) at all times and positions. In practice an adiabatic factor Q = ω_eff/α̇ ≥ 5 and a time-bandwidth product R ≥ 20 are needed to have an adiabatic pulse. Plots of the effective field modulation, nutation angle and inverse of adiabatic factor during the GOIA-W(16,4) pulse are shown in Figs. 1D–F. The adiabatic factor is greater than 5 for the most part of the pulse with the exception of short periods in the vicinity of 1.2ms and 2.8ms where it decreases to 3. By increasing the R product the pulse becomes more adiabatic.

An important observation is necessary at this point. Due to gradient modulation the effective field and nutation angle in Eqs. [3] become dependent on the spatial coordinate x in the slice direction. However, there is dependency only of the intra-slice isochromats, and not of the slice position relative to the isocenter. The effect of slice position is cancelled by the additional frequency modulation that is used to excite slices off-isocenter. For simplicity this term was not included in Eq. [1], but more details are given in (Andronesi et al., 2010). Thus, the slices at isocenter and off-isocenter positions have the same effective field and nutation angle, and consequently the relaxation rate does not depend on the slice position. As we will show next, what is relevant for the measurement is the average relaxation rate over the pulse duration and slice thickness, which can be exactly calculated.

A physical model that satisfactorily approximates the rotating frame relaxation of water in-vivo includes two main relaxation mechanisms: dipolar coupling and exchange interactions (Michaeli et al., 2004, Michaeli et al., 2005, Sorce et al., 2007, Michaeli et al., 2008). Random fluctuations due to reorientation of the direct proton-proton dipolar coupling and exchange of protons between sites with different chemical shifts or diffusion through microscopic field inhomogeneities lead to decoherence of the spin system. The stochastic nature of random perturbations is described by the spectral density functions of the type (n = 0,1,2):

$$J_n(\tau )~\tau /(1+{(n\omega \tau )}^2)$$ [4]

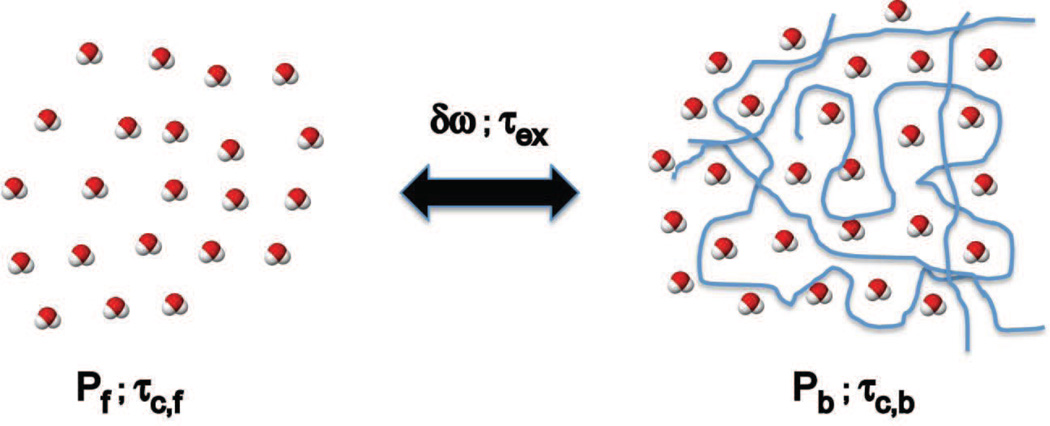
where τ may represent the correlation time τ_c or exchange time τ_ex, and ω may represent the Larmor frequency ω₀ = γB₀ or the effective field ω_eff from Eq. [3]. The most commonly employed model (Michaeli et al., 2008, Sierra et al., 2008, Jokivarsi et al., 2009, Mangia et al., 2009) for deriving rotating frame relaxation in tissues assumes a two sites exchange model (2SX) at equilibrium between the free water (slow relaxing component) and the water bound to macromolecules (fast relaxing component), as shown schematically in Figure 2.

Figure 2.

Two site exchange (2SX) model depicting the pool of free water and pool of water bound to macromolecules. In each pool water molecules experience dipolar coupling relaxation governed by the correlation times τ_c of each pool. The two pools are considered in an equilibrium anisochronous exchange determined by the exchange time τ_ex and the chemical shift difference δω_ex. The model is specified by four independent parameters: correlation time τ_c,b of bound water, τ_ex, δω_ex and bound water fraction P_b (Pf = 1− P_b and τ_c,f ≈ 5 ps). The fast exchange limit (FXL) it is assumed in-vivo δω_exτ_ex ≪ 1.

Relaxation rates in the rotating frame (Blicharski, 1972) can be cast in a time dependent form for adiabatic pulses as instantaneous relaxation rates (Michaeli et al., 2008, Mangia et al., 2009). In the case of GOIA-W(16,4) pulses the instantaneous relaxation rate for dipolar coupling interaction becomes dependent on the intra-slice isochromat at position x

$$R_{1\rho }^{dd}(t,x)=\frac{D_c}{10}{\tau }_c\times [\frac{3{\text{sin}}^2\alpha (t,x){\text{cos}}^2\alpha (t,x)}{1+{({\omega }_{\mathit{\text{eff}}}(t,x){\tau }_c)}^2}+\frac{3{\text{sin}}^4\alpha (t,x)}{1+{(2{\omega }_{\mathit{\text{eff}}}(t,x){\tau }_c)}^2}+\frac{2+3{\text{sin}}^2\alpha (t,x)}{1+{({\omega }_0{\tau }_c)}^2}+\frac{8-6{\text{sin}}^2\alpha (t,x)}{1+{(2{\omega }_0{\tau }_c)}^2}]R_{2\rho }^{dd}(t,x)=\frac{D_c}{40}{\tau }_c\times [3{(3{\text{cos}}^2\alpha (t,x)-1)}^2+\frac{30{\text{sin}}^2\alpha (t,x){\text{cos}}^2\alpha (t,x)}{1+{({\omega }_{\mathit{\text{eff}}}(t,x){\tau }_c)}^2}+\frac{3{\text{sin}}^4\alpha (t,x)}{1+{(2{\omega }_{\mathit{\text{eff}}}(t,x){\tau }_c)}^2}+\frac{20-6{\text{sin}}^2\alpha (t,x)}{1+{({\omega }_0{\tau }_c)}^2}+\frac{8+12{\text{sin}}^2\alpha (t,x)}{1+{(2{\omega }_0{\tau }_c)}^2}]$$ [5]

where the dipolar coupling constant D_c 2I(I + 1)[μ₀ ħ γ² / (4πr³)]², I = 1/2 is the spin number, and the physical constants are μ₀ = 4π·10⁻⁷ H/m the vacuum magnetic permeability, ħ = 1.055·10⁻³⁴ Js the Planck's constant, γ = 2π·42.576·10⁶ rad/(sT) the gyromagnetic ratio, and r = 1.58 Å is the proton-proton distance in water molecule. Simulations of dipolar relaxation rates for GOIA-W(16,4) pulses are shown in Figure 3(A,C).

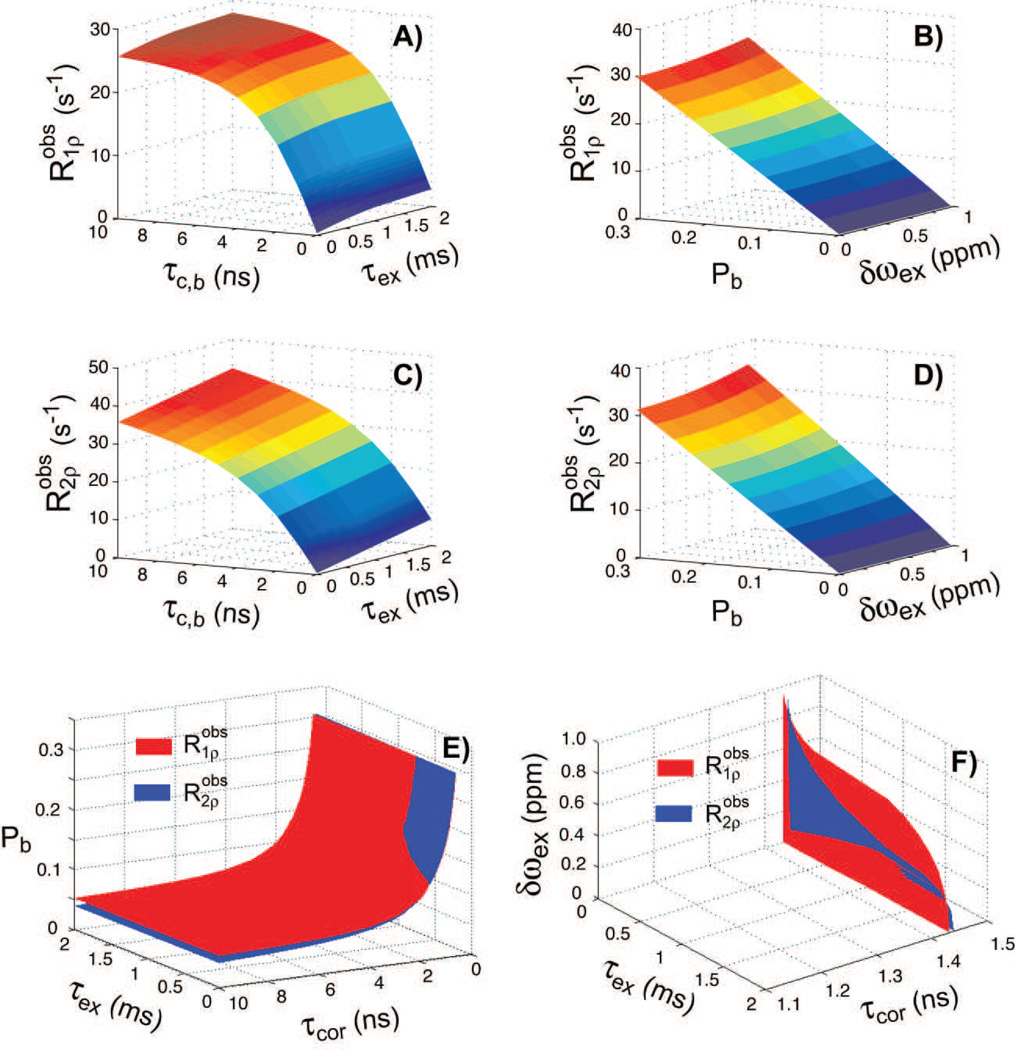
Figure 3.

Simulations of longitudinal and transverse rotating frame relaxation rates for dipolar coupling (Eqs. 5) and exchange (Eqs. 6) interactions during GOIA-W(16,4) pulses of 4 ms duration, 5 kHz bandwidth and 0.382 kHz peak amplitude. For exchange interaction (Figs. 3B,D) P_b was fixed at 0.15 and δω_ex was assumed 0.8 ppm at 2.89T (≈ 100 Hz). The B0 field was considered 2.89T.

Similarly, the instantaneous relaxation rates for the anisochronous exchange interaction can be obtained in the form of

$$R_{1\rho }^{ex}(t,x)=P_b{P}_f{(\delta {\omega }_{ex})}^2{\tau }_{ex}\frac{{\text{sin}}^2\alpha (t,x)}{1+{({\omega }_{\mathit{\text{eff}}}(t,x){\tau }_{ex})}^2}{R}_{2\rho }^{ex}(t,x)=P_b{P}_f{(\delta {\omega }_{ex})}^2{\tau }_{ex}{\text{cos}}^2\alpha (t,x)$$ [6]

where P_b is the pool of bound water, P_f is the pool of free water (P_b + P_f = 1), and δω_ex is the chemical shift difference between the two exchanging sites. Simulations for exchange relaxation rates during GOIA-W(16,4) pulses are presented in Figure 3B,D.

The intrinsic instantaneous relaxations rates Eqs. [5–6] are further used to compute the observed relaxation rates. First, the average dipolar and exchange relaxation rates over pulse duration need to be calculated for each slice isochromat:

$$\overline{R_{1\rho ,2\rho ;b,f}^{dd,ex}(x)}=\frac{1}{T_p}\underset{0}{\overset{T_p}{\int }}{R}_{1\rho ,2\rho ;b,f}^{dd,ex}(t,x)dt$$ [7]

For each isochromat we can then calculate the observed (or apparent) relaxation rate averaged over the pulse duration. Under in-vivo conditions the fast exchange limit δω_exτ_ex ≪ 1 (FXL) is assumed (Sierra et al., 2008, Jokivarsi et al., 2009), and the observed relaxation rate is obtained as a linear combination between dipolar relaxation of free and bound water, and exchange relaxation:

$$\overline{R_{1\rho ,2\rho }^{\mathit{\text{obs}}}(x)}=P_b(x)\overline{R_{1\rho ,2\rho ;b}^{dd}(x)}+P_f(x)\overline{R_{1\rho ,2\rho ;f}^{dd}(x)}+\overline{R_{1\rho ,2\rho }^{ex}(x)}$$ [8]

By integrating the exponential decays of all isochromats over the slice thickness we can obtain the time-spatial average of the observed relaxation rate:

$$\overline{\overline{R_{1\rho ,2\rho }^{\mathit{\text{obs}}}}}=-\frac{1}{T_p}\mathit{\text{ln}}[\frac{1}{\mathrm{\Delta }x{\mathrm{S̄}}_0}\underset{-\mathrm{\Delta }x/2}{\overset{\mathrm{\Delta }x/2}{\int }}{S}_0(x)\mathit{\text{exp}}(-\overline{R_{1\rho ,2\rho }^{\mathit{\text{obs}}}(x)}·T_p)dx]$$ [9]

where the mean initial magnetization (signal) over the slice is $\overline{S_0}=1/\mathrm{\Delta }x{\int }_{-\mathrm{\Delta }x/2}^{\mathrm{\Delta }x/2}{S}_0(x)dx$. Note that under the most general conditions the correlation times, exchange times, exchange rate, water pools and initial signal can be vary spatially across isochromats. In certain conditions, such as activation, the model parameters could vary also on the time scale of the pulse. This variation is captured implicitly in the Eqs. [6–9]. Simulations for the average observed relaxation rates during GOIA-W(16,4) pulses are presented in Figure 4 as a function of model parameters.

Figure 4.

Simulations of observed longitudinal and transverse rotating frame relaxation rates for the 2SX/FXL model (Eqs. 7–9) during GOIA-W(16,4) pulses of 4 ms duration, 5 kHz bandwidth and 0.382 kHz peak amplitude. For simulations in Fig. 4(A,C) P_b was fixed at 0.15 and δω_ex was assumed 0.8 ppm at 2.89T (≈ 100 Hz). For simulations in Fig. 4(B,D) τ_c,b = 2ns and τ_ex = 0.2 ms. In Figs 4(E,F) the isosurfaces and their intersection through the parameter space are shown corresponding to T1ρ = 90ms and T2ρ = 85ms. Because of the 4 dimensional parameter space the isosurfaces are shown when one of the model parameters is fixed to a particular value. In Fig. 4E δω_ex was assumed 0.8 ppm, and Fig. 4F P_b was assumed 0.15. The correlation time of free water was assumed τ_c,f ≈ 5 ps. The B₀ field was considered 2.89T.

In the case when the change in the relaxation rates and initial signal is small among isochromats Eqs. [7–9] may be linearized and the average relaxations can be very well approximated by:

$$\overline{\overline{R_{1\rho ,2\rho ;b,f}^{dd,ex}}}=\frac{1}{T_p}\frac{1}{\mathrm{\Delta }x}\underset{-\mathrm{\Delta }x/2}{\overset{\mathrm{\Delta }x/2}{\int }}\underset{0}{\overset{T_p}{\int }}{R}_{1\rho ,2\rho ;b,f}^{dd,ex}(t,x)dtdx\overline{\overline{R_{1\rho ,2\rho }^{\mathit{\text{obs}}}}}=P_b\overline{\overline{R_{1\rho ,2\rho ;b}^{dd}}}+P_f\overline{\overline{R_{1\rho ,2\rho ;f}^{dd}}}+\overline{\overline{R_{1\rho ,2\rho }^{ex}}}$$ [10]

Simulations performed in Figure 5C–F show the results for the average observed relaxation rates obtained from Eqs. [7–9] or Eqs. [10].

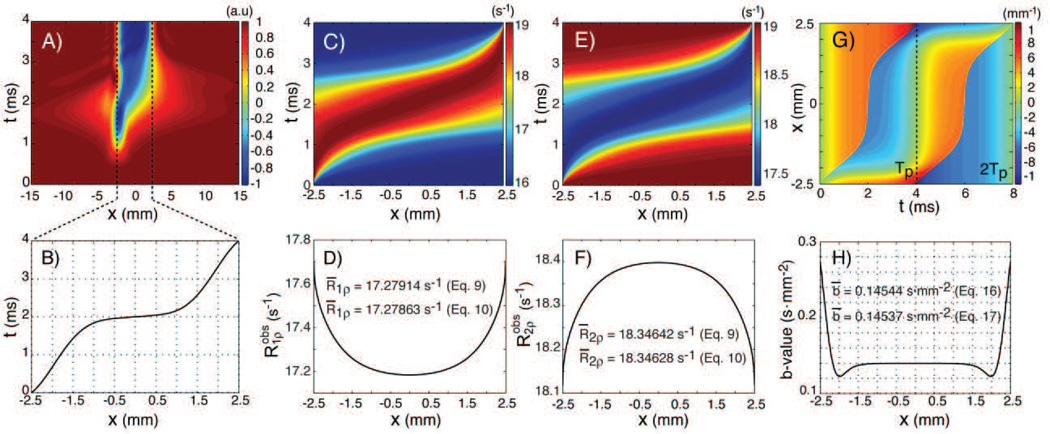
Figure 5.

Simulations of the magnetization inversion, rotating frame relaxation rates and b-values for the GOIA-W(16,4) pulse of 4ms and 5kHz. A) magnetization inversion during pulse across slice isochromats; B) isochromat inversion times; C) instantaneous and D) time averaged R1ρ relaxation rate across slice isochromats; E) instantaneous and F) time averaged R2ρ relaxation rate across slice isochromats; G) gradient moment for a pair of GOIA-W(16,4) pulses; H) b-values across slice isochromats for a pair of GOIA-W(16,4) pulses. For simulations of Figs 5C–F it was assumed that τ_c,b = 2ns, τ_ex = 0.2 ms, δω_ex = 0.8 ppm, P_b = 0.15, and τ_c,f ≈ 5 ps. The B₀ field was considered 2.89T.

The 2SX/FXL model depicted in Figure 2 is described by a maximum number of seven independent parameters: two correlation times (for bound and free water), two proton-proton distances (for bound and free water), population of bound site (P_f = 1− P_b), exchange time, and chemical shift difference. However, three parameters can be readily eliminated considering the same proton-proton distance (1.58 Å) for both bound and free water, and a standard value for the correlation time of free water (5 ps). In this case the observed relaxation rate is determined by the four remaining parameters: the correlation time of bound water, exchange time, chemical shift difference, and the population of bound water. In the ideal situation of no measurement noise a minimum number of four experimental time points are necessary to obtain the molecular parameters of interest, however experimentally extra time points are beneficial. Figure 4 shows simulations of the observed rotating frame relaxation rate under GOIA-W(16,4) pulses for relevant in-vivo model parameters.

2.2 Diffusion weighting during rotating frame relaxation under GOIA pulses

The use of the gradient modulation during relaxation in the rotating frame of GOIA pulses raises the question of what is the effect of diffusion on the signal decay. The effect of diffusion may be expected particularly for T2ρ where magnetization precesses around the effective field and diffusion may produce signal decay similarly like in spin echo experiments. In the case of T1ρ magnetization spends most of the time longitudinally and there is no evolution of the spin echo type.

A few papers have investigated the effects of diffusion during adiabatic pulses in spin echo experiments (Sun and Bartha, 2007, Valette et al., 2010). In deriving an expression for the b-value produced by the T2ρ preparation with GOIA-W(16,4) pulses we will follow the approach proposed in (Valette et al., 2010). Most generally, the b-value associated with a gradient G(t) is obtained as the integral of the square of the gradient moment k(t)

$$b(t)=\underset{0}{\overset{t}{\int }}{k}^2(t\prime )dt\prime \text{where}k(t\prime )=\gamma \underset{0}{\overset{t\prime }{\int }}G(t″)dt″$$ [11]

To calculate the gradient moment for the GOIA-W(16,4) pulse we can use the commonly assumed approximation (Pipe, 1995, Park and Garwood, 2009) that for a given isochromat located at position x within the slice (−Δx/2 ≤ x ≤ Δx/2) the magnetization is flipped instantaneously when Δω(t_x) = γxG(t_x). Under this assumption, it has been shown (Valette et al., 2010) that during adiabatic frequency-swept pulses the only contribution to diffusion weighting comes from the phase scrambling due to gradient, while the scrambling effect due to the quadratic phase induced by the frequency modulation of the B₁ field cancels out. The 180° flip of magnetization will change the sign of the gradient moment at the instant time t_x

$$k(t\prime ,x)=\{\begin{array}{cc}\gamma \underset{0}{\overset{t\prime }{\int }}G(t″)dt″,\hfill & 0\le t\prime \le t_x\hfill \\ \gamma \underset{0}{\overset{t\prime }{\int }}G(t″)dt″-2·\gamma \underset{0}{\overset{t_x}{\int }}G(t″)dt″,\hfill & t_x<t\prime \le T_p\hfill \end{array}$$ [12]

where the flipping time t_x ∈ [0, T_p] is given by the solution of

$$\gamma \underset{0}{\overset{t_x}{\int }}{B}_1^2(t)/G(t)dt=Qx$$ [13]

with B₁(t) and G(t) defined by Eqs. [2]. While solving Eq. [11] by integration of B₁(t) and G(t) modulations given in Eqs. [2] leads to a very complicated analytical solution, it can be shown that the inversion time for each isochromat can be simply calculated from:

$$t_x=\frac{T_p}{2}(1+\frac{2x·G(t)}{\mathrm{\Delta }x·G_{\mathit{\text{max}}}}),x\in [-\frac{\mathrm{\Delta }x}{2},\frac{\mathrm{\Delta }x}{2}]$$ [14]

This can be verified also numerically by simulations of the slice profile during the pulse as shown in Figure 5A. Plots of the inversion times and gradient moment are shown in Figs. 5B and 5G, respectively.

From Eqs. [12–14] it can be seen that the gradient moment and b-value become dependent on the isochromat position. Considering a pair of two GOIA-W(16,4) pulses as the diffusion weighting element the spatial dependent b-value can be calculated:

$$b(x)=\underset{0}{\overset{2T_p}{\int }}{k}^2(t,x)dt$$ [15]

Simulation of the b-values across the slice profile for a pair of GOIA-W(16,4) pulses is shown in Fig. 5H. An average b-value for the entire slice can be calculated similarly like in the relaxation case:

$$\mathrm{b̄}=-\frac{1}{\mathrm{D̄}}\mathit{\text{ln}}[\frac{1}{\mathrm{\Delta }x{\mathrm{S̄}}_0}\underset{-\mathrm{\Delta }x/2}{\overset{\mathrm{\Delta }x/2}{\int }}{S}_0(x)\mathit{\text{exp}}(-b(x)·D(x)\left)dx\right]$$ [16]

where D(x) is the diffusion coefficient, which most generally may vary across slice, and the mean coefficient $\mathrm{D̄}=1/\mathrm{\Delta }x·{\int }_{-\mathrm{\Delta }x/2}^{\mathrm{\Delta }x/2}D(x)dx$, and S̄₀ is defined similarly like in the case of relaxation. In the case there is small change in b-value b(x), diffusion coefficient D(x) and initial signal S₀(x) across the slice Eq. 16 can be liniarized

$$\mathrm{b̄}=\frac{1}{\mathrm{\Delta }x}\underset{-\mathrm{\Delta }x/2}{\overset{\mathrm{\Delta }x/2}{\int }}b(x)dx$$ [17]

Assuming that rotating frame relaxation and diffusion weighting are acting independently their combined effect on the signal decay during the train of GOIA-W(16,4) pulses:

$$S(t_m)=S(0)·\mathit{\text{exp}}[-({\mathrm{R̄}}_{2\rho }·t_m+(\mathrm{b̄}+b_r)·\mathrm{D̄}·t_m/2T_p)];t_m=4m·T_p;m=\overline{0,5}$$ [18]

where t_m is the T2ρ preparation time (multiple of four GOIA-W(16,4) pulses) and b_r is the b-value associated with the ramping of the gradient at the beginning and the end of the preparation time. The calculated b-values are 0.294, 0.589, 0.872, 1.178 and 1.473 s·mm⁻² for preparation times of 16, 32, 48, 64 and 80 ms, respectively (GOIA-W(16,4) of 4ms duration and 5kHz bandwidth).

We found experimentally (Fig. 6) that an effect of diffusion weighting can be observed on the signal decay in the case of T2ρ preparation for 2D imaging sequences. However, the experimental effect is much higher than predicted by the above theory:

$$S(t_m)=S(0)·\mathit{\text{exp}}[-({\mathrm{R̄}}_{2\rho }·t_m+\beta ·\mathrm{D̄}·t_m^3\left)\right]$$ [19]

with the diffusion term contributing more than linearly to the exponential signal decay. A coefficient β = 1.87·10⁶ (mm·s)⁻² has found to fit both phantom and in-vivo data, resulting in b-values of 1.6, 12.8, 43.1, 102.2, and 199.6 s·mm⁻² for preparation times of 16, 32, 48, 64 and 80 ms are, respectively. Possible explanations for the departure between experiments and theory are considered in the Discussion section.

Figure 6.

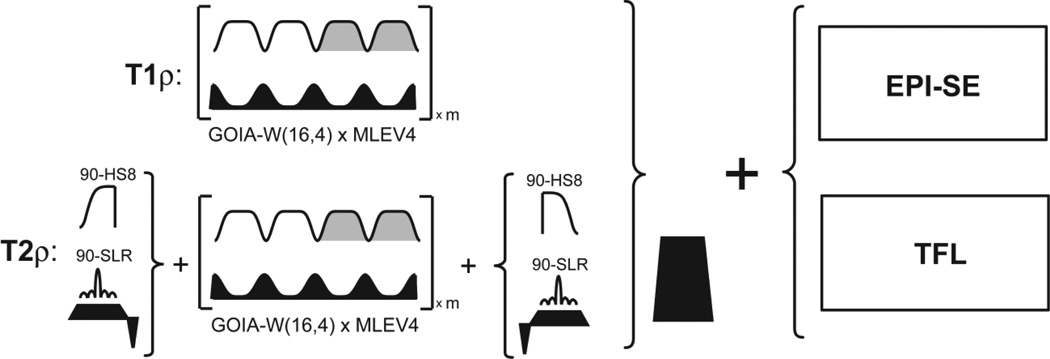
Pulse sequences for T1ρ and T2ρ mapping using GOIA-W(16,4) pulse trains. Turbo FLASH (TFL) or spin-echo EPI (EPI-SE) are used for image readout. GOIA-W(16,4) pulses are concatenated without gaps according to MLEV-4 phase cycle. For T2ρ mapping the GOIA-W(16,4) pulse train is preceded and followed by 90° pulses. For 2D slice selective T2ρ mapping 90° SLR pulses are used, while for 3D mapping 90° AHP-HS8 pulses are used. The gradient ramps of GOIA-W(16,4) pulses and the gradient of 90° SLR pulses are refocused. After T1ρ and T2ρ preparation a spoiler gradient is used to spoil any transverse magnetization that was not stored on the longitudinal direction.

3. METHODS

3.1. Simulations

Simulations for relaxation rates in the rotating frame of GOIA-W(16,4) pulses have been performed assuming the two site exchange model in the fast exchange limit (2SX/FXL) with the model parameters specified in Figure 2. A static magnetic field B₀ of 2.89T (Siemens Tim Trio magnet) was assumed.

GOIA-W(16,4) pulse parameters were: 4 ms duration, 5 kHz bandwidth (time-bandwidth product R = 20), and a gradient modulation factor g_m = 0.9 (Eqs. [1,2]). Under these conditions the peak amplitude (B_1,max) of the RF field was 0.382 kHz. A slice thickness of Δx = 5 mm was considered, requiring a maximum gradient G_max = 23.49 mT/m. A piecewise constant approach was used in all calculations by assuming that the RF field and gradient are constant over infinitesimal elements of time and space. The GOIA-W(16,4) pulse was discretized in steps of 10 µs, matching the experimental implementation. To account for the gradient modulation, the slice thickness has been divided in 400 thin intra-slice isochromats. Thus the number of isochromats matches the number of samples in the RF pulse waveforms. We verified that this time and slice discretization produced stable results, and further increase in digitization did not change results for two decimals precision.

The four independent parameters (correlation time constant of bound water, exchange time constant, chemical shift difference, and pool of bound water) were varied over a four dimensional grid spanning the ranges that are relevant for in-vivo conditions. The correlation and exchange time constants were varied logarithmically over four orders of magnitude (τ_c ∈ [10⁻², 10²] ns; τ_ex ∈ [10⁻³, 10¹] ms; 40 values each), while the chemical shift difference and pool of bound water were varied linearly over their range (P_b ∈ [0, 1]; δω_ex ∈ [0, 5] ppm; 50 values each). In total 4 · 10⁶ combinations of model parameters were simulated. The correlation time of free water was assumed to be 5 ps, and the proton-proton distance to be 1.58 Å in both sites. Simulations were performed in Matlab 2012b (Natick, MA). Results of simulations are shown in Figures 3 and 4.

3.2. Pulse sequences

Pulse sequences for T1ρ and T2ρ mapping were implemented on a 3T Tim Trio clinical MR scanner (Siemens Healthcare, Erlangen). The body transmit coil, capable of 1 kHz peak RF field, was used for excitation, and a 32-channels head coil was used for signal reception. The body gradient coil of a 3T Tim Trio has a maximum gradient amplitude of 40 mT/m per axis and a rise time of 200 mT/(m·ms).

The low-power slice selective magnetization preparation module for rotating frame relaxation was realized by concatenating GOIA-W(16,4) pulses according to the MLEV4 (Levitt et al., 1982) phase cycling scheme. No gaps were introduced in the pulse train during concatenation. A single continuous pulse shape was calculated for each preparation time. The maximum preparation time was 80 ms to avoid introducing delays in the shape due to limitations with the maximum possible pulse duration. This time duration is comparable with the rotating frame relaxation time in-vivo and is sufficient to map the relevant portion of the rotating frame relaxation curve. The phase modulation of GOIA-W(16,4) was calculated dynamically for each repetition time in order to shift the slice position for multislice imaging. For T1ρ, magnetization can be intuitively visualized as making repeated flip-flops between +Z and −Z directions of the static magnetic field B₀, following the effective field of GOIA-W(16,4) pulses. For T2ρ, magnetization is first flipped perpendicular to the direction of the effective field of GOIA-W(16,4) pulses to precess around it, and at the end of preparation it is stored again along the direction of B₀ field. In the case of 3D T2ρ mapping the 90° pulses bracketing the GOIA-W(16,4) pulse train were stretched adiabatic half passage hyperbolic-secant AHP-HS8 (Garwood and DelaBarre, 2001), or Shinnar-LeRoux SLR (Pauly et al., 1991) slice selective pulses for 2D T2ρ mapping. After both T1ρ and T2ρ preparation a gradient spoiler (5 ms, 25 mT/m) is used to spoil any transverse magnetization that was not stored along longitudinal direction. The prepared magnetization was sampled with a 3D turbo FLASH (TFL) or 2D spin echo EPI (EPI-SE) readout. Details of the T1ρ and T2ρ pulse sequences are given in Figure 6.

In particular, the T1ρ and T2ρ preparations for in-vivo measurements were done using: 1) GOIA-W(16,4) pulses of 4 ms and 5 kHz bandwidth, 2) preparation times of 0, 16, 32, 48, 64, 80 ms, and 3) AHP-HS8 90°pulses of 4 ms and 5 kHz bandwidth for T2ρ 3D TFL, or SLR 90° pulses of 3ms and 2 kHz bandwidth for T2ρ 2D EPI-SE. Shapes of the GOIA-W(16,4) pulse were sampled each 10 µs (400 samples for 4 ms). Short ramps were needed for the GOIA-W(16,4) gradient at the beginning and the end of preparation period. The ramps were 30 µs for the 3D TFL sequence, and 160 µs for 5 mm slices in 2D EPI-SE. In the case of T2ρ preparation the ramps of the GOIA gradients were refocused (balanced) with gradients of opposite sign and moment. In addition, for slice selective T2ρ the gradient of SLR 90° pulses was also balanced and superimposed on the GOIA balancing gradient. The balancing gradient was 30 µs for the 3D TFL readout, and 480 µs for 5 mm slices in 2D EPI-SE. The total time delay at the beginning and the end of T2ρ preparation were 60 µs for the 3D TFL readout, and 640 µs for the 2D EPI-SE with 5 mm slices.

The 3D TFL image acquisition was performed in sagittal orientation with the following parameters: matrix = 192×192×128, voxel size = 1.33×1.33×1.33 mm³, partial Fourier factor of 6/8 in the slice and phase encoding directions, parallel acquisition (PAT) factor 2, readout bandwidth = 1530 Hz/Pixel, flip angle = 8°, echo time TE = 0.98 ms, repetition time TR = 0.8 s, 10 dummy scans, 5 preparation times (0, 16, 32, 48, 64 ms). The total acquisition time was 5:40 min. The T1ρ and T2ρ preparation were also positioned sagitally to excite a slab of 350 mm thickness, roughly twice the right-left diameter of the head. The TR of 0.8 sec was chosen to be 8 to 10 times larger than the rotating frame relaxation times of gray and white matter tissue to allow complete relaxation of the rotating frame prepared magnetization. With this TR the SAR was 50–60% of the maximum allowed SAR (3W/kg) as monitored by the Siemens console.

The 2D EPI-SE image acquisition was performed axially with the following parameters: matrix = 128×128, 20 slices, voxel size = 2×2×5 mm³, partial Fourier factor of 6/8 in the phase encoding direction, interleaved slice acquisition, slice gap 50% (2.5 mm), parallel acquisition (PAT) factor 2, readout bandwidth = 1562 Hz/Pixel, excitation flip angle = 90°, refocusing flip angle = 180°, echo time TE = 27 ms, repetition time TR = 7 s (350 ms/slice), 4 dummy scans, 6 preparation times (0, 16, 32, 48, 64, 80 ms), fat suppression. The total acquisition time was 1:17 min. The slice selective T1ρ and T2ρ preparations were prescribed axially and their position was updated according to the interleaved 2D EPI-SE slice acquisition. With this TR the SAR was 80–90% of the maximum allowed SAR (3W/kg) as monitored by the Siemens console.

Importantly, for 2D imaging the slice profile of the T1ρ and T2ρ preparations have to match the slice profile of the EPI-SE sequence or any other sequence that is used for 2D image acquisition. The slice profile of GOIA-W(16,4) pulses is sharper than the slice profile of non adiabatic pulses that are typically used in the EPI-SE sequence. If slice thickness is not matched, only the central part of the EPI-SE slice will experience rotating frame relaxation while the edges will experience relaxation in the laboratory frame, resulting in a multi-exponential behavior. To avoid this situation the slice of GOIA-W(16,4) was chosen to be twice thicker (10 mm) than the slice of 2D EPI-SE (5 mm). Considering that a slice gap of 50% is typically used in 2D imaging, together with the interleaved slice excitation and sharpness of GOIA pulses, the doubling of slice thickness of GOIA pulses does not produce saturation of neighboring slices. However, the slice profiles of rotating frame preparation and image encoding can be perfectly matched if the same GOIA-W(16,4) pulses are used for refocusing in the 2D EPI-SE.

For comparison T1ρ and T2ρ mapping sequences with continuous wave spin-lock and conventional adiabatic pulses were implemented. The continuous wave (CW) spin-lock was implemented using the B₀ and B₁ compensation method of (Witschey et al., 2007). The conventional adiabatic preparation was implemented with stretched hyperbolic-secant HS8 pulses of 4 ms and 5 kHz bandwidth (Michaeli et al., 2008, Mangia et al., 2009). Single slice measurements were performed and compared using all three rotating frame relaxation methods CW, HS8, and GOIA-W(16,4) as detailed in the following section.

3.3. Phantom experiments

Two phantoms were imaged to develop and optimize our methodology. A uniform agar phantom (3% w/v) with an inner diameter of 16 cm was used to test uniformity and artifacts of rotating frame preparation. A second phantom that contained 3 agar tubes (1%, 2% and 3% w/v) immersed in saline solution was used to verify and calibrate the modeling and fitting routines.

Uniformity of multislice T1ρ and T2ρ mapping with GOIA-W(16,4) pulses was verified on the uniform phantom with both 2D EPI-SE and 3D TFL readouts. Relaxation under GOIA-W(16,4) pulses was compared with relaxation under HS8 and CW using the same image readout in single slice experiments. The B_1,max of HS8 was 0.886 kHz for 4 ms duration and 5 kHz bandwidth, and the B_1,max of CW was set to the same value as HS8. For GOIA-W(16,4) pulses two situations were considered: 1) GOIA-W(16,4) having the same duration and bandwidth as HS8 but half of the B_1,max (0.382 kHz), and 2) GOIA-W(16,3) pulses having similar B_1,max (0.821 kHz) as HS8, but half duration (2 ms) and 10 kHz bandwidth. To investigate the compensation of B₀ inhomogeneity the carrier frequency during CW, HS8 and GOIA-W was placed off-resonance from the water signal, and the durations of the preparation periods were matched to the same duration (48 ms) for all measurements. Diffusion in the slice direction was measured with a pulsed gradient spin echo (PGSE) EPI sequence using five b-values in the range 200–1000 s/mm², and matching the slice thickness and resolution of T2ρ 2D EPI-SE.

3.4. Volunteer measurements

Brain imaging was performed on five young healthy volunteer (4 males, 1 female, 26–33 years age interval) with informed consent using a protocol approved by the IRB of our institution. T1ρ and T2ρ mapping were obtained with GOIA-W(16,4) pulses using the acquisition parameters mentioned for 3D TFL and 2D EPI-SE in Section 3.2. A structural scan was acquired at 1 mm isotropic resolution with the MEMPRAGE sequence (van der Kouwe et al., 2008) to perform brain segmentation and statistical analysis of T1ρ, T2ρ and molecular parameters in region of interests (ROI) of the brain. Diffusion in the slice direction was measured with a pulsed gradient spin echo (PGSE) EPI sequence using five b-values in the range 200–1000 s/mm², and matching the slice thickness and resolution of T2ρ 2D EPI-SE.

3.5. Data analysis

Maps of relaxation time constants were calculated by fitting a mono-exponential law S_1ρ,2ρ (t) = S (0)exp (−t/T_1ρ,2ρ) to the phenomenological relaxation curves measured for T1ρ with 3D or 2D sequences and T2ρ with 3D sequences. In practice a first order polynomial was fit to the log-linear time series signal to obtain the relaxation rates. In the case of T2ρ relaxation measured with 2D sequences Eq. [19] was fit to the data using the diffusion constant that was independently estimated from PGSE measurements.

To extract parametric maps of correlation times, exchange times, water bound fraction, and chemical exchange frequency the experimental time series were fitted according to the 2SX/FXL model from Eqs. 5–8 and assuming the GOIA-W(16,4) modulation functions of Eqs. 1–3. The slice or slab thickness was considered for both 2D and 3D measurements. For 2D measurements 500 isochromats were considered for each slice as mentioned for simulations. For 3D measurements since the slab excited by T1ρ and T2ρ preparations was much thicker (350 mm) than the individual slice thickness (1.33 mm), each slice was considered its own isochromat. This was verified to give stable results compared to the case when more isochromats were calculated for each slice. The slice position within the 3D slab was included in the calculation. However, since the maximum gradient for a 350 mm slab is very weak (G_max = 0.34 mT/m in Eq. [2]) no effect of slice position within the brain was detected on the measured T1ρ and T2ρ relaxation times. As mentioned earlier, for 2D acquisition the effect of slice position is completely removed by the frequency modulation that is needed to shift the slice position. Nonlinear curve fitting of time series signal was employed to obtain the model parameters.

All fitting was performed in Matlab R2012b (Natick, MA). Each voxel was fit independently and parallel computation toolbox was used to speed up calculations. The fitting was done in the least square sense for both linear and nonlinear curve fitting.

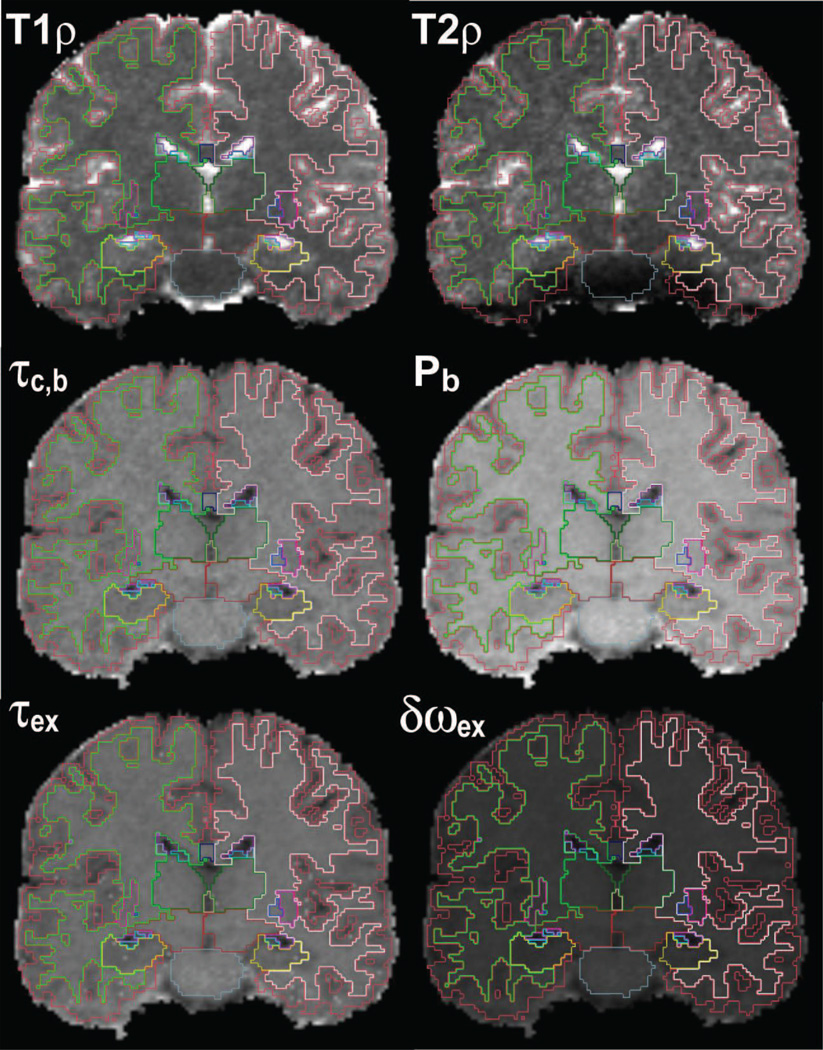
An ROI analysis was done for all the maps. The structural 3D MEMPRAGE image was segmented using Freesurfer 5.1 software (Fischl et al., 2002) and then coregistered using the bbregister (Greve and Fischl, 2009) method of Freesurfer to the maps derived from 3D T1ρ and T2ρ measurements. Mean values and standard deviations were calculated for eight brain ROIs (cortical gray matter, white matter, thalamus, caudate, putamen, pallidum, hippocampus, ventral diencephalon that includes substancia nigra). Only the voxels with an R² coefficient of determination larger than 0.95 were included in the statistical analysis. Edge voxels at the border of two ROIs were excluded to reduce ambiguity in classification and coregistration. Hundreds to a few thousands voxels were available in each ROI for statistical analysis.

4. RESULTS

4.1. Simulations of rotating frame relaxation and diffusion weighting under GOIA pulses

In Figure 1(G,H) simulations of the slice profiles at the isocenter and off-isocenter locations are shown for an inversion GOIA-W(16,4) pulse of 4 ms duration, 5 kHz bandwidth, 0.382 kHz maximum RF amplitude and slice thickness of 5mm (Eqs. [1–3]). Note, in all subsequent simulations the same GOIA-W(16,4) and slice thickness have bee assumed. The slice profile at the isocenter is characterized by 100% inversion in the center of the slice and 98% inversion at the edge of the flat top, transition bands (flat top to baseline) that represent 40% of the slice thickness, one very small sideband with less than 3% inversion symmetrically on each side of the slice. The slice at the off-isocenter position shows a very similar profile with minimal smearing due to the gradient versing. Increasing the BW of the pulse reduces the transition bands and can eliminate completely the sidebands at the cost of increased B_1,max. However, the pulse of Fig. 1 represents a good compromise between inversion performance, slice selectivity, duration and B_1,max requirements.

Simulations of rotating frame relaxation rates for the same GOIA-W(16,4) pulse and assuming a 2.89T static magnetic field. In Figure 3 longitudinal (Fig. 3A,B) and transverse (Fig. 3C,D) rotating frame relaxation rates for dipolar coupling and exchange interactions were calculated (Eqs. [5,6]) over the range of correlation and exchange time constants expected in-vivo. The bound water fraction P_b was assumed 0.2 and the exchange chemical shift difference δω_ex was considered 0.8 ppm (~100 Hz at 2.89T). Due to pulse modulation the relaxation rates are time dependent, reaching a maximum (R_1ρ) or a minimum (R_2ρ) in the middle of the pulse. The exchange T1ρ relaxation time constant (Fig. 3B) exhibits a maximum around an exchange time constant of 3 ms. The other relaxation rates increase with the correlation (Fig. 3A,C) and exchange time constants (Fig. 3D). This is a similar behavior as noticed for conventional adiabatic pulses in the absence of magnetic field gradients (Michaeli et al., 2008, Mangia et al., 2009).

In Figure 4 the observed longitudinal (Fig. 4A,B) and transverse (Fig. 4C,D) rotating frame relaxation rates are simulated assuming the 2SX/FXL model for several combinations of model parameters. The four dimensional parameter space was sampled over ranges relevant for in-vivo conditions and FXL regime (τ_c,f was fixed at 5 ps). The correlation time and exchange time constants were sampled logarithmically over four orders of magnitude, while the exchange range and water bound fraction were sampled linearly. For each slice isochromat the time average relaxation was first calculated according to Eqs. [7,8] and then the slice averaged relaxation was obtained using Eq. [9]. Model parameters were assumed not to vary across isochromats (this is discussed in the case of Fig. 5). Figs. 4A,C show the hyperplanes through the four dimensional space when two of the model parameters are fixed: bound water fraction P_b of 0.15 and exchange rate δω_ex of 0.8 ppm. The longitudinal rotating frame relaxation rate (Fig. 4A) exhibits a steep increase with correlation time constant in the 0–5 ns interval, and a smaller increase in the 5–10 ns interval. The change over the exchange time constant is less pronounced compared to change over the correlation time constant, indicating that dipolar coupling is the major relaxation mechanism. The transverse rotating frame relaxation rate (Fig. 4C) shows slightly larger changes across correlation and exchange time constants. However, the interplay between dipolar coupling and exchange interactions can change based on the water pools populations and exchange rates. In Figs. 4B,D a hyperplane through the four dimensional space is shown when the correlation time constant τ_c,b was fixed at 2 ns and the exchange time constant τ_ex was set to 0.2 ms. These values are relevant for in-vivo conditions and fulfill the fast exchange condition. The longitudinal (Fig. 4B) and transverse (Fig. 4D) rotating frame relaxation rates exhibit almost a linear dependency on water bound fraction in the FXL regime. A parabolic dependency starts to become evident, as expected from Eqs. [6] when bound water fraction or exchange rate increase.

Figures 4E,F show the isosurfaces through the parameter space corresponding to particular values of rotating relaxation times T1ρ = 90 ms and T2ρ = 85 ms. While the parameter space and number of solutions that can fit each relaxation is very large, the intersection of both spaces is relatively small and indicate that combining longitudinal and transverse rotating relaxation can lift this degeneracy and converge the fit on a small number of solutions for model parameters.

In Figure 5 the isochromat dependency on relaxation and diffusion are illustrated. Figure 5A shows the progressive inversion of the magnetization as the pulse sweeps through each isochromat of the slice. It can be seen that the assumption of instant magnetization inversion of each isochromat a good approximation. Although the inversion at the end of the pulse is perfectly confined to the slice it can be noticed that at intermediate times, particularly in the middle part of the pulse between 1–3 ms, magnetization outside of the slice is slightly affected. Magnetization may be temporarily flipped up to 40% in the immediate vicinity of the slice in regions extending out up to half of slice thickness from the edge of the slice. This effect becomes small beyond this limit and is unnoticeable at a distance of 15 mm (3 times the slice thickness). With interleaved slice acquisition and 50% slice gap the rotating frame magnetization history between chronologically excited slices can be avoided. The inversion times for each isochromat are plotted in Fig. 5B, which as expected show faster inversion at the edges of the slice where the pulse is swept faster.

Simulations performed in Fig. 5C–F show that there is very little difference in the average relaxation rates obtained by the exact calculation of Eqs. [7–9] or approximate calculation of Eqs. 10. A single value was assumed for each model parameter (τ_c,b = 2ns, τ_ex = 0.2ms, δ_ex = 0.8ppm, P_b = 0.15, τ_c,f = 5ps) and equal distribution of initial magnetization across isochromats. Using the exact calculations Eqs. [7–9], a symmetric distribution is obtained, with less than 3% difference between the relaxation rates of different isochromats. This is explains why the linearization and calculation with Eqs. [10] yields very close results. Although these results are contingent on the assumption that model parameters are the same for all isochromats, even when including a variation of ±25% for the model parameters across the slice thickness the average values calculated by Eqs. [7–9] or Eqs. [10] differ by less than a 5%. For thin slices (≤5mm) a limited variation of model parameters across slice thickness may be an acceptable assumption.

Figures 5G,H plot the gradient moment and b-values as a function of isochromat calculated using Eqs. [12–15] for a pair of GOIA-W(16,4) pulses. A symmetric distribution of b-values is obtained. The b-values are much higher at the edge of the slice compared to the middle part, which is expected since the gradient is much stronger for the isochromats at the edge of the slice. The difference between the mean b-value of the slice calculated with the exact Eq. [16] or approximate Eq. [17] approach is very small because the first order contribution dominates in the Taylor expansion of the exponentials. A diffusion coefficient of 0.8·10⁻³ mm²·s⁻¹ was considered for all isochromats.

4.2. Experimental diffusion weighting during GOIA pulse trains

First, the possible effects of diffusion on the signal decay during the gradient modulated GOIA-W(16,4) pulse train were investigated experimentally for both T1ρ and T2ρ relaxations. Measurements performed in an agar phantom and volunteers are presented in Figure 7. Relaxation curves were measured using GOIA-W(16,4) pulses of 4 ms for two situations: 1) a strong gradient (G_max = 23.5 mT/m) used to prepare T1ρ and T2ρ for a 5 mm slice, and 2) a very weak gradient (G_max = 0.34 mT/m) used to prepare T1ρ and T2ρ for a 350 mm thick slab. In both cases a single slice of 2.5 mm was acquired with the 2D EPI-SE sequence in the middle of the region prepared by rotating frame relaxation. The experiment with the weak gradient did not produced any detectable diffusion weighting, and in this respect is similar with the spatially non-selective rotating frame relaxation.

Figure 7.

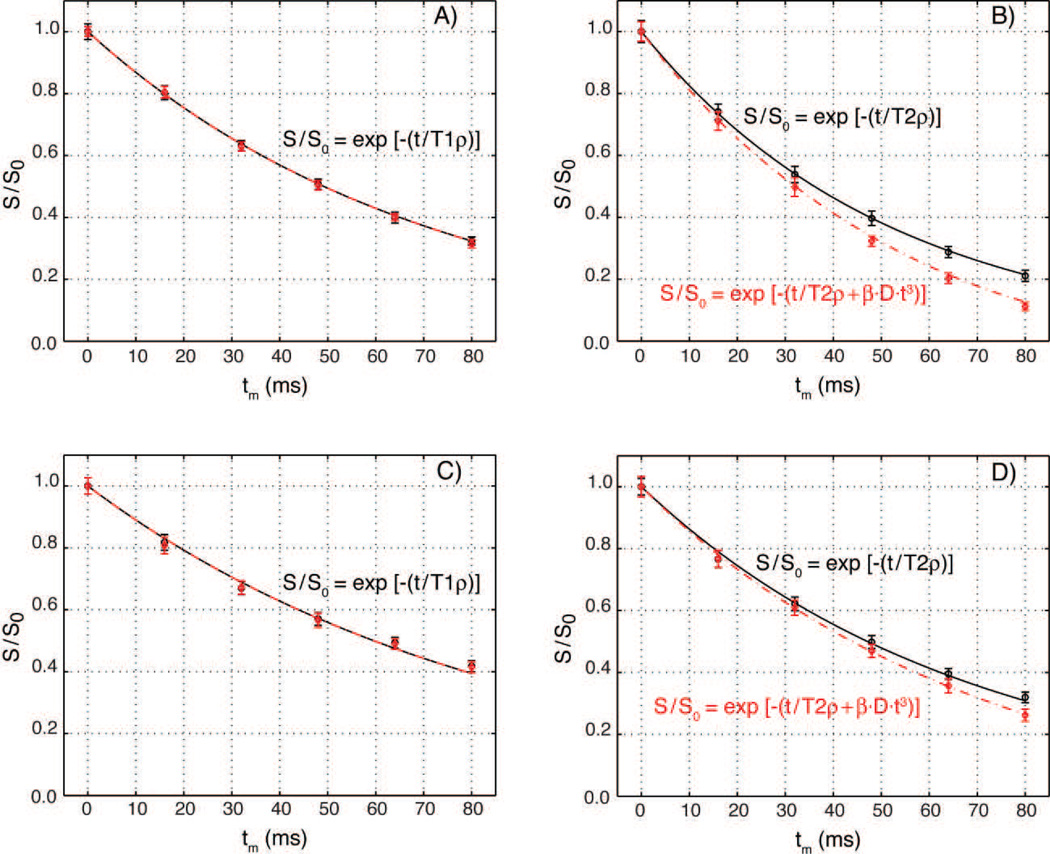
Diffusion effects in slice selective T1ρ and T2ρ experiments using GOIA-W(16,4) pulses of 4 ms duration and 5 kHz bandwidth. Relaxation curves were measured with a strong gradient (23.5 mT/m, 5 mm slice, red diamonds) and a very weak gradient (0.34 mT/m, 350 mm slab, black circles). T1ρ experiments in an agar phantom (Fig. 7A) and volunteers (Fig. 7C) show no difference in relaxation curves and can be fitted with the same relaxation time constant and an exponential decay (T1ρ = 71 ms for agar, and T1ρ = 87 ms for in-vivo). T2ρ experiments show differences between relaxation curves measured with strong and weak gradients in both agar (Fig. 7B) and volunteers (Fig. 7D). Signal decay with a weak gradient can be fitted with transverse relaxation time T2ρ = 52 ms for agar and T2ρ = 68 ms for volunteers. For strong gradient an additional diffusion term has to be included in the exponential signal decay. Data can be fitted with a coefficient β = 1.87·10⁶ mm⁻²·s⁻², diffusion constant D = 2.1·10⁻³ mm²·s⁻¹ for agar and D = 0.8·10⁻³ mm²·s⁻¹ for volunteers, and the same transverse relaxation times used for the weak gradient. Diffusion constants were independently measured in the slice direction with a PGSE experiment. The difference between the weak and strong gradient transverse relaxation curves increases with diffusion constant. Error bars equal plus/minus two standard deviations.

In the case of T1ρ experiments (Figs. 7A,C) the experimental relaxation curves obtained for the 5 mm slice (red diamonds) and the 350 mm thick slab (black circles) are identical and can be fitted with a mono-exponential function in both agar phantom (Fig. 5A, T1ρ = 71 ms) and volunteers (Fig. 5C, T1ρ = 87 ms), proving that diffusion weighting does not affect T1ρ measurements. In the case of T2ρ experiments (Figs. 5B,D) the effects of diffusion become apparent as the signal decay curves for the 5 mm slice and the 350 mm thick slab are different. As expected for diffusion weighting, the difference between T2ρ signal decay curves measured in the thin slice (red diamonds) and thick slab (black circles) increases with diffusion coefficient (agar D = 2.1·10⁻³ mm²·s⁻¹, white matter D = 0.8·10⁻³ mm²·s⁻¹). The signal decay for the 5 mm slice selective T2ρ measurements can be fitted empirically by Eq. [19], which includes in the exponential a non-linear time contribution of the diffusion term in addition to transverse rotating relaxation. Good agreement between Eq. [19] (red dashed line) and the 5 mm slice experimental time points (red diamonds) is obtained using the same transverse rotating frame relaxation rate that fits the 350 mm thick slab relaxation (black circles and line) and the diffusion constant measured from the PGSE (agar T2ρ = 52 ms and D = 2.1·10⁻³ mm²·s⁻¹ in Fig. 5B, in-vivo T2ρ = 68 ms and D = 0.8·10⁻³ mm²·s⁻¹ in Fig. 5D). The same β coefficient (1.87·10⁶ mm⁻²·s⁻²) fits both phantom and volunteer data, and is characteristic for the particular GOIA pulse used. The corresponding b-values are, respectively, 1.6, 12.8, 43.1, 102.2, and 199.6 s·mm⁻² for T2ρ preparation times of 16, 32, 48, 64 and 80 ms. These experimental b-values are much larger as predicted from Eqs. [12–16]. This is further analyzed in the Discussion section.

4.3. Measurements of GOIA rotating frame relaxation in phantoms

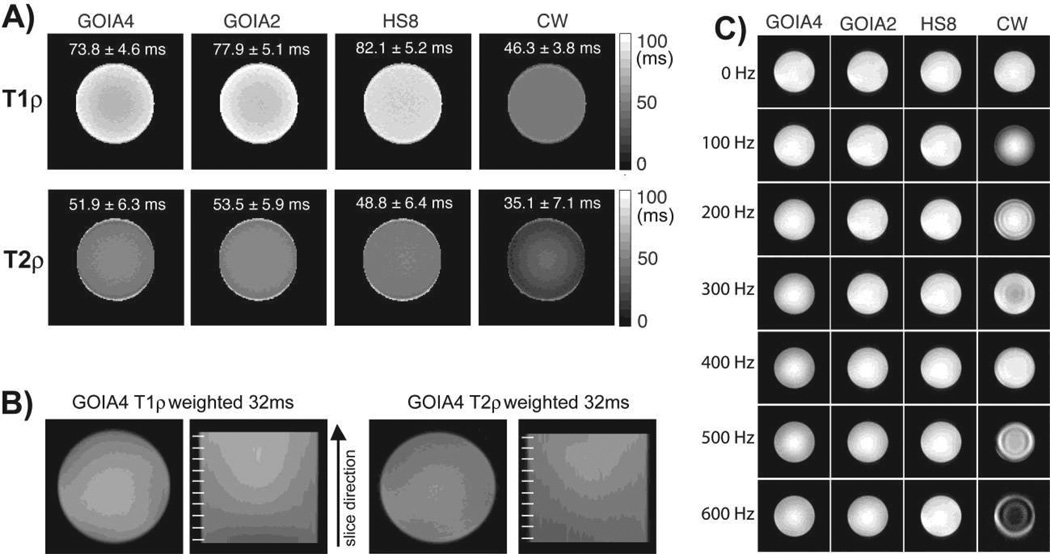
Results obtained on the agar phantoms are presented in Figures 8–10. Figure 8A shows the T1ρ and T2ρ relaxation maps obtained on the uniform agar phantom with GOIA-W(16,4) pulses, HS8 pulses and CW spin-lock. GOIA-W(16,4) pulses that match either the duration of the HS8 pulses (abbrev. GOIA4 for 4 ms duration) or the amplitude of HS8 pulses (abbrev. GOIA2 for 2 ms duration) have been used. The amplitude of CW spin-lock matched the amplitude of HS8 pulses. As shown previously (Michaeli et al., 2008, Mangia et al., 2009) relaxation times depend on the modulation functions, and longer relaxation times are measured with adiabatic pulses of higher B_1,max. The shortest T1ρ and T2ρ relaxation time constants are measured with CW spin-lock, which also shows the smallet difference between longitudinal and transverse relaxation times. This is expected since CW spin-lock acts on magnetization that is in the transverse plane for both T1ρ and T2ρ relaxation, while adiabatic pulses act on longitudinal magnetization in the case of T1ρ relaxation and transverse magnetization for T2ρ relaxation. The uniformity of multislice T1ρ and T2ρ imaging with GOIA-W(16,4) pulses is proven in Fig 8B. The sagittal views taken along the slice direction indicate no saturation or magnetization history between slices. In Fig. 8C the effect of B₀ inhomogeneity was investigated. The carrier frequency of pulses was shifted off-resonance from the water as noted on the left side. Despite using the B₀ and B₁ compensation scheme for CW spin-lock (Witschey et al., 2007) the compensation of the offset is not perfect and works for a limited range of offsets. Artifacts are observed for offsets over 100 Hz. Adiabatic pulses exhibit a much better compensation and image uniformity across a wide range of offsets.

Figure 8.

T1ρ and T2ρ maps in an uniform agar phantom. Fig. 8A shows maps obtained with: i) GOIA-W(16,4) pulses of 4 ms, 5 kHz bandwidth, 0.382 kHz peak amplitude (abbrev. GOIA4), ii) GOIA-W(16,3) pulses of 2 ms, 10 kHz bandwidth, 0.821 kHz peak amplitude (abbrev. GOIA2), iii) HS8 pulses of 4 ms, 5 kHz bandwidth, 0.886 kHz peak amplitude, iv) CW spin-lock with 0.886 kHz amplitude and B₁ and B₀ compensation. Fig. 8B shows multislice T1ρ and T2ρ weighted images acquired with the slice selective GOIA-W(16,4) preparation. The sagittal views shown in the slice direction have good uniformity and no slice cross-talking (slice position is indicated by the white lines on the right of each sagittal image). Fig 8C show the compensation of B₀ inhomogeneity. The carrier frequency during T1ρ preparation was changed as noted on the left side. It can be seen that the CW spin-lock method shows artifacts due to B₀ inhomogeneity despite using a B₀ and B₁ compensation scheme. Adiabatic methods show good compensation of B₀ inhomogeneity over the entire range of offset frequencies.

Figure 10.

Parametric maps of water molecular dynamics in a multi-compartment phantom containing three agar tubes prepared with 1%, 2% and 3% w/v. Good contrast can be seen between tubes in T1ρ, T2ρ, τ_c,b, τ_ex and P_b. Chemical shift exchange frequency δω_ex is approximately 1 ppm in all tubes, showing, as expected, no dependency on agar concentration. Importantly, the map of water bound fraction P_b is able to distinguish a difference of 1% agar concentration. Goodness of fit is indicated by the coefficient of determination R² showed in the bottom figures.

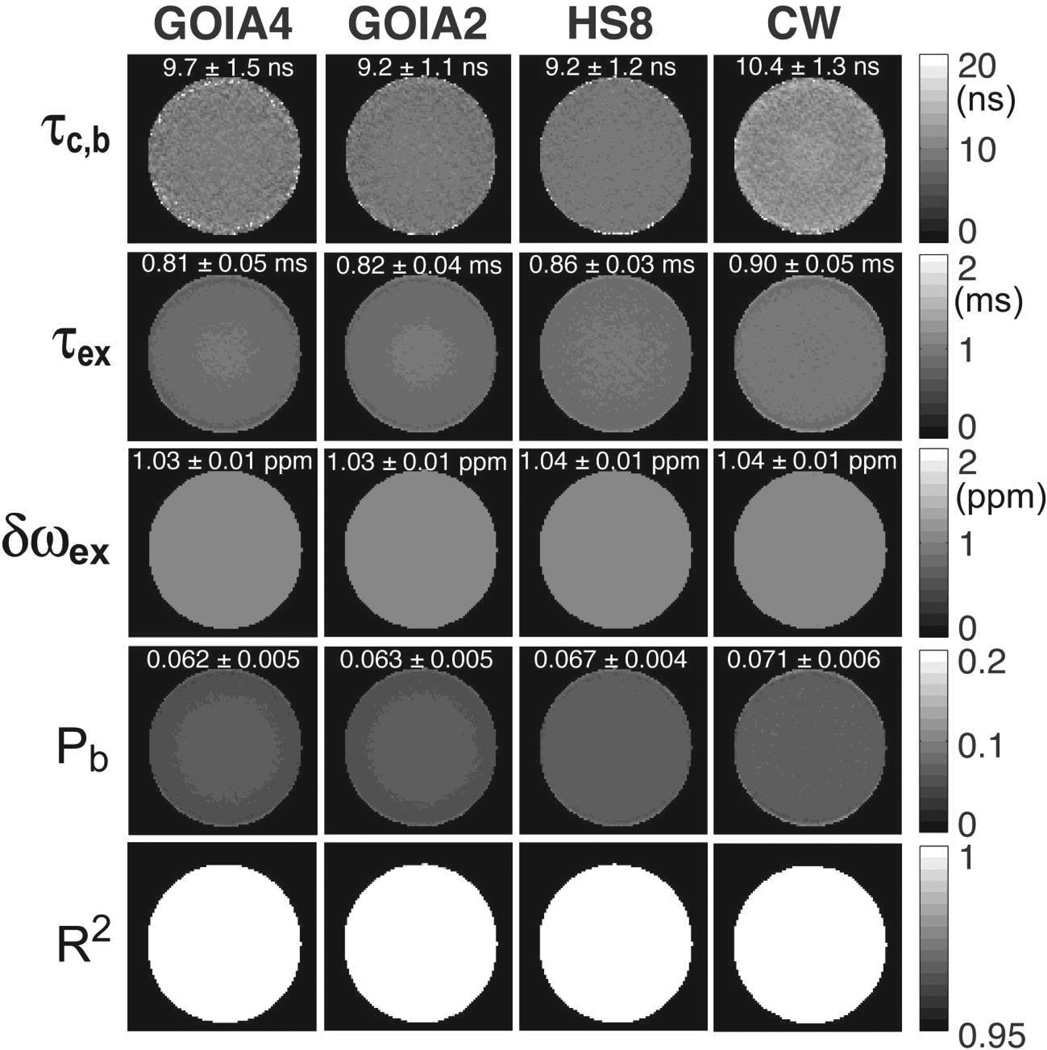
Molecular dynamics parameters in the agar phantom were estimated by fitting the 2SX/FXL model to the relaxation measurements from Fig 8A. In order to restrict the possible solution space of the non-linear least square fit the data from both T1ρ and T2ρ measurements were used. As shown by simulations (Figs. 4E,F) the intersection of the two solution spaces is very small. The maps of correlation time constant, exchange time constant, water bound fraction and chemical exchange difference that best fit the experimental data are shown in Figure 9. The range of values for the molecular parameters is much smaller compared to the values of relaxation times obtained with different approaches. While the relaxation time constants depend on both sample and the pulse sequence, molecular parameters are sample specific and are more appropriate for quantitation and comparing measurements done with different techniques if the same relaxation model is used for fitting.

Figure 9.

Parametric maps of water molecular dynamic in the agar phantom obtained by fitting the 2SX/FXL model to experimental data from Fig. 8A. Uniform maps are obtained for all paramters. Mean values and standard deviation for each parameter and measurement are calculated. Mean values obtained with different methods are much closer than the relaxation times in Fig. 7A. The goodness of fit is indicated by the map of coefficient of determination R² at the bottom.

Figure 10 shows results obtained on the multi-compartment agar phantom with GOIA-W(16,4) pulses of 4 ms and 5 kHz. Relaxation and parameter maps of molecular dynamics are shown in the upper two rows. It can be seen that T1ρ and T2ρ relaxation maps show visible contrast between tubes differing only by 1% in agar concentration. T1ρ relaxation times were: 135.8 ± 5.1 ms for 1% agar, 107.4 ± 4.8 ms for 2% agar, and 84.2 ± 3.5 ms for 3% agar. T2ρ relaxation times were: 119.3 ± 4.6 ms for 1% agar, 97.2 ± 4.1 ms for 2% agar, and 72.3 ± 3.9 ms for 3% agar. Differences are noted also in the maps of the molecular dynamics parameters. Importantly, the bound water fraction (P_b) map is sensitive to the difference in agar concentration. The bound water fraction was found to be 4.8 ± 0.3% for 3% agar, 3.1 ± 0.3% for 2% agar and 1.9 ± 0.2% for 1% agar. The bound water fractions derived from the relaxation measurements are slightly higher than the agar weight/volume ratio that was used to prepare the phantoms. This may be explained by the syneresis phenomenon of agar hydrogels which are known to expel water (Boral et al., 2010). A layer of water was macroscopically observed at the interface between the agar gel and the wall of the tubes. The maps in the bottom row of Fig. 10 show the R² coefficient of determination of the fitting. For T1ρ and the 2SX/FXL model fitting the R² values are above 0.99 inside agar tubes. For T2ρ fit the R² values are above 0.9 inside agar tubes.

In order to investigate whether model parameters would be overfitted when using relaxation data measured with a single GOIA modulation we also fitted model parameters from dispersion data obtained at multiple GOIA modulations in the uniform agar phantom. For this purpose, T1ρ relaxation decay curves were acquired at four different GOIA modulations and the T1ρ relaxation constants were derived first. The four T1ρ relaxation constants were further used as input data for the model fitting. Independently, the model parameters were estimated also by fitting the relaxation decay curve measured with a fifth GOIA modulation that was different from the four dispersion GOIA modulations. It was found that the main difference lies in the fitted τ_c,b correlation time constants which differ by approximately 11%. The fits of the exchange time constant τ_ex, exchange chemical shift δω_ex, and water bound fraction P_b are very similar, and differ by less than 4%. It can be also noticed that the standard deviations of the dispersion fits are smaller. However, the differences noticed between the two fits are much smaller compared to the range of variation obtained for example when agar concentration was varied by 1% as in Fig. 10. The results are summarized in Table 1.

Table 1.

2SX/FXL modeling of agar T1ρ relaxation. Comparison of the model parameters obtained by fitting dispersion data or single relaxation decay curves. Dispersion data included rotating frame relaxation rates obtained at four different GOIA modulations as specified on the first raw. Single fit data represented the relaxation decay curve measured with one GOIA modulation (4ms, GOIA-W(16,4), g_m = 0.9, B_1max = 382 Hz) different from the previous four. The model parameters were: correlation time constant τ_c,b, exchange time constant τ_ex, exchange chemical shift δω_ex, water bound fraction P_b.

GOIA	4ms, W(16,4), gm=0.6	4ms, W(8,4), gm=0.8	5ms, W(16,4), gm=0.9	6ms, W(16,4), gm=0.9
B1max (Hz)	640	510	305	255
T1ρ (ms)	90.04±7.05	87.69±7.40	80.38±9.19	79.02±8.59
Model parameters	τc,b (ns)	τex (ms)	δωex (ppm)	Pb
Dispersion fit	8.403±0.346	0.815±0.044	0.997±0.003	0.065±0.003
Single fit	9.429±2.301	0.827±0.063	1.034±0.006	0.063±0.006

4.4. Measurements of rotating frame relaxation in volunteers

Results obtained from the T1ρ and T2ρ measurements performed on volunteers are summarized in Figures 11–15. Relaxation in the rotating frame has been prepared with GOIA-W(16,4) pulses of 4 ms duration, 5 kHz bandwidth, and 0.382 kHz peak RF amplitude.

Figure 11.

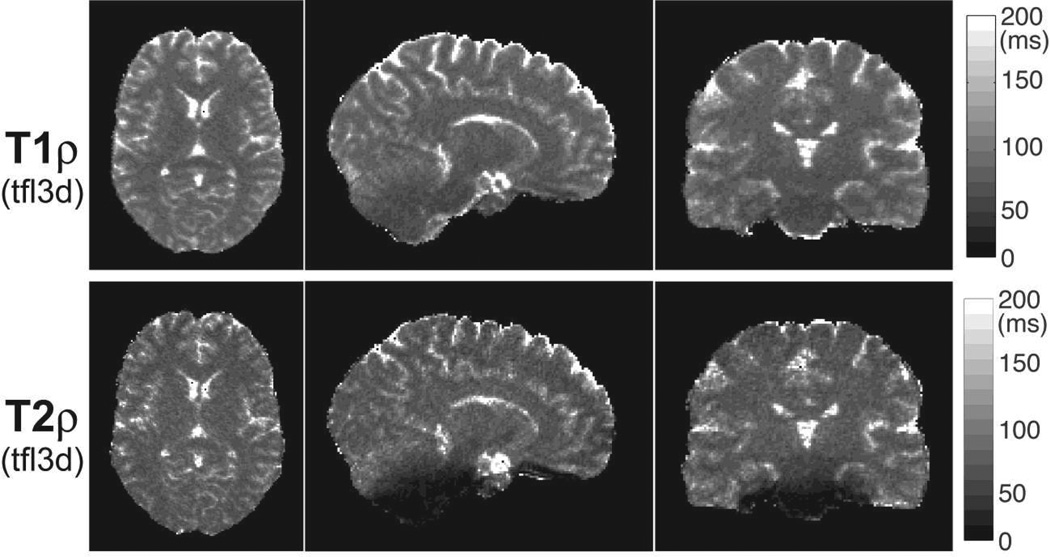
3D T1ρ and T2ρ maps of the brain acquired in a volunteer. Five preparation periods of 0, 16, 32, 48 and 64 ms consisting of 0, 4, 8, 12 and 16 GOIA-W(16,4) pulses were acquired with 3D turbo FLASH at 1.33 mm isotropic resolution in 5:40 min. T1ρ map shows good uniformity in all three orthogonal cross-sections. T1ρ map shows good uniformity in all three orthogonal cross-sections. T2ρ map shows signal loss towards the base of the skull, predominantly in vermis and pons as seen in the sagittal and coronal views. Good contrast can be seen between gray and white matter, and subcortical structures.

Figure 15.

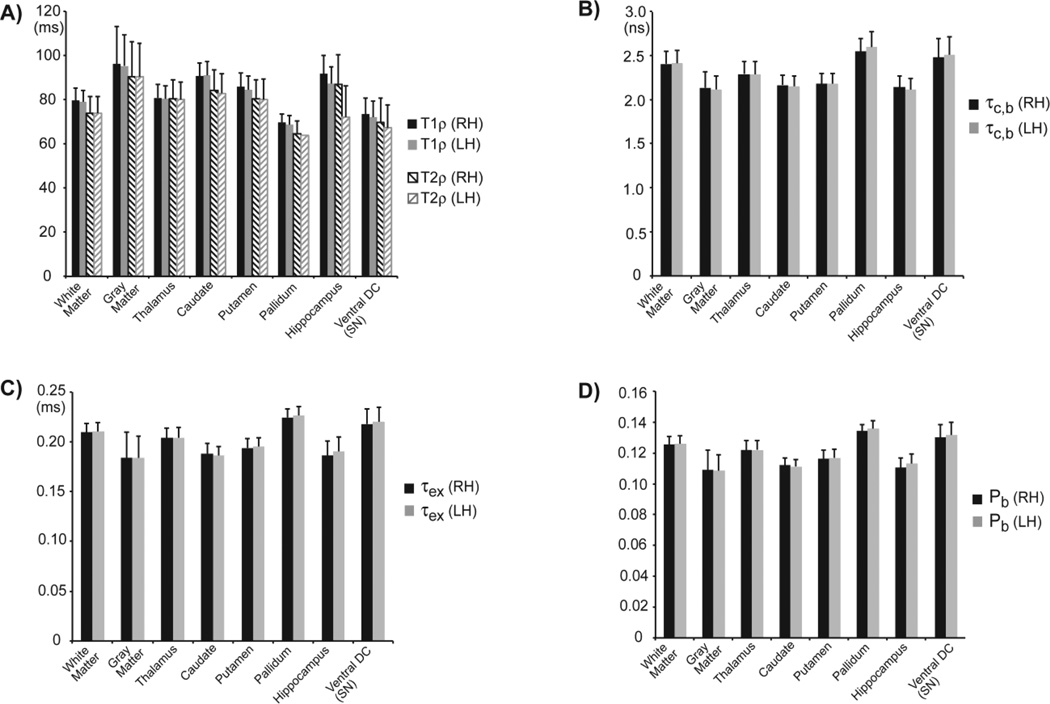
Statistical analysis of T1ρ, T2ρ and water molecular dynamics in eight ROIs segmented by Freesurfer in each hemisphere of the brain (RH - right hemisphere, LH - left hemisphere). Mean and standard deviation values are shown for all subjects. Only voxels with goodness of fit R² > 0.95 were included. Edge voxels at the border of two ROIs were excluded.

Figure 11 shows 3D maps of T1ρ and T2ρ relaxation times acquired in the brain at 1.33 mm isotropic resolution in 5:40 min using the 3D TFL image readout. Three orthogonal sections are shown for both maps. The T1ρ map shows good uniformity across brain in all three sections. The T2ρ map shows some signal loss in regions of the pons and cerebellar vermis, which are near the base of the skull close to big air cavities such as pharynx. This signal loss is related to areas of large B₀ inhomogeneity which leads to additional dephasing of transverse magnetization that precess around the effective field during the T2ρ preparation. In the case of T1ρ mapping the longitudinal magnetization is locked along the effective adiabatic field and its evolution is not susceptible to B₀ inhomogeneities.

Figure 12 shows 2D multi-slice maps of T1ρ and T2ρ relaxation times from the brain of the same volunteer acquired in 1:17 min with slice selective rotating frame preparation and 2D EPI-SE readout. Four axial slices were selected for display at different levels in the brain, i.e. centrum semiovale, ventricles, and infratentorial. The coronal view on the right side shows the prescription of all slices and proves, as in the phantom case, that multislice excitation can be obtained without saturation and magnetization history. The effects of B₀ inhomogeneity are observed in T2ρ maps towards the base of the skull. Diffusion coefficients were independently measured to separate the diffusion weighting from the T2ρ relaxation in the signal decay curves.

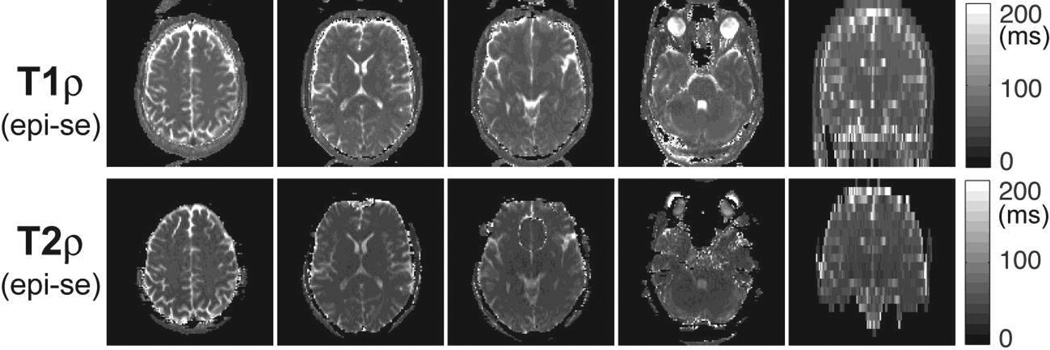
Figure 12.

2D slice selective T1ρ and T2ρ maps of the brain acquired in a volunteer. Six preparation periods of 0, 16, 32, 48, 64 and 80 ms consisting of 0, 4, 8, 12, 16 and 20 GOIA-W(16,4) pulses were acquired for 20 slices with 2D EPI-SE at 2×2×5 mm³ resolution in 1:17 min. T1ρ map shows good uniformity in all slices, while T2ρ map shows signal loss in slices at the base of the skull in regions with large susceptibility anisotropy. The coronal views on the right side indicate the prescription of slices and show no magnetization history between neighboring slices.

Maps of molecular dynamics parameters were calculated using the 2SX/FXL model to fit the 3D rotating frame relaxation measurements, and results are presented in Figure 13. Again as in the phantom case, the data from both T1ρ and T2ρ measurements were used in order to restrict the possible solution space of the non-linear least square fit. Since in the case of 3D mapping the slab inverted by the GOIA-W(16,4) was very thick (350 mm) while on the other hand each slice in the 3D volume was much thinner (1.3 mm) we can safely use Eqs. [10] and assume there is little variation of model parameters across each thin slice. All parameter maps show good uniformity and contrast across the brain in all three orthogonal directions that are displayed. Anatomical features of the cortical and subcortical structures can be easily noticed. Segmentation of the T1ρ, T2ρ and parametric maps of molecular dynamics are shown in Figure 14. At 1.33 mm isotropic resolution the boundaries between cortical gray matter, white matter, and subcortical structures can be followed on all the maps. Mean values and standard deviations of rotating frame relaxation time constants, correlation time constants, exchange time constants, and bound water fraction in eight ROIs of the brain are plotted in Figure 15. The values for all parameters are also given in Table 2. A difference (contrast) of 20–30% among mean parameter values of different brain structures is noticed. Only the voxels with an R² coefficient of determination larger than 0.95 were included in the statistical analysis. Except for CSF, the majority of voxels (~99% for T1ρ, and ~85% for T2ρ) in the brain parenchima had R² > 0.95. Values of the molecular dynamics parameters were in the range of values reported in the literature for in-vivo measurements (Michaeli et al., 2008, Sierra et al., 2008, Jokivarsi et al., 2009, Mangia et al., 2009).

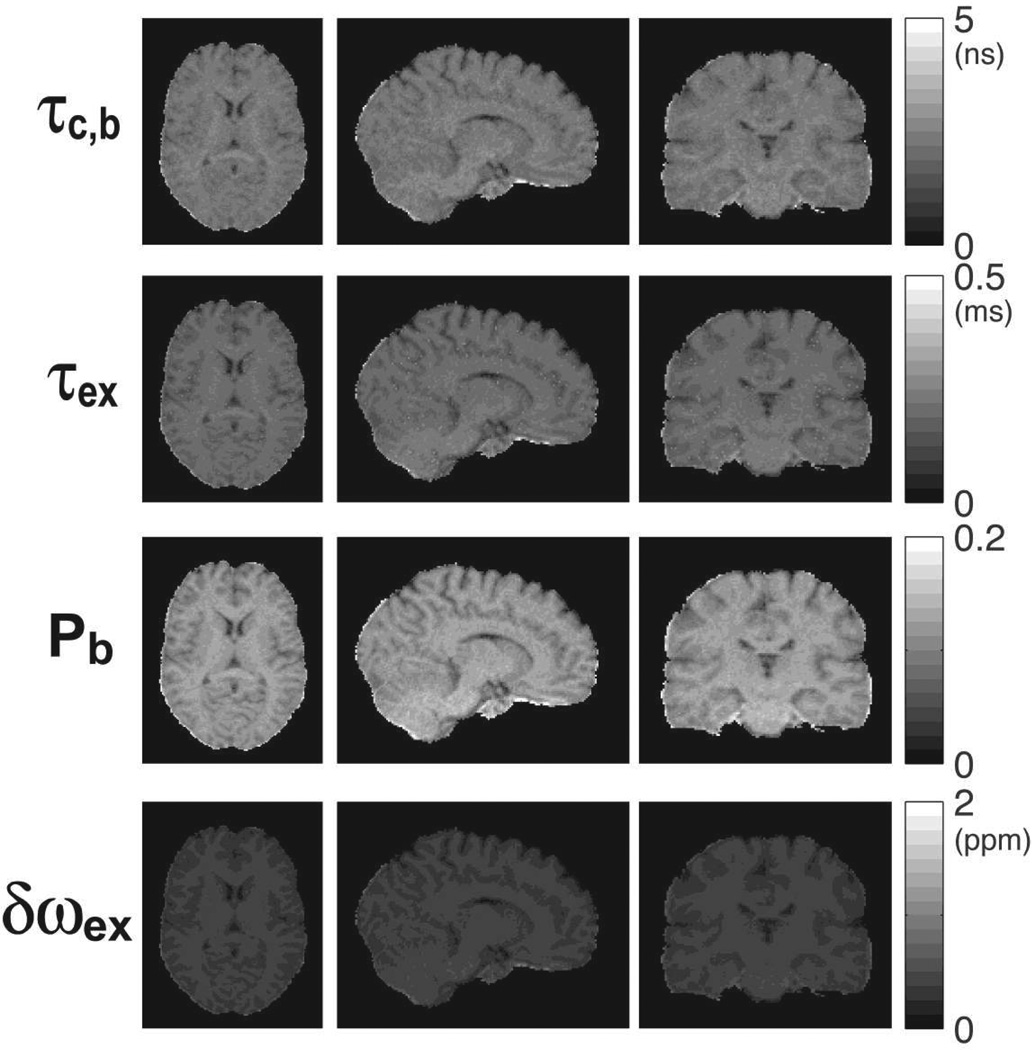
Figure 13.

3D parametric maps of water molecular dynamics in the brain of a human volunteer. The maps were obtained by fitting the 2SX/FXL model to rotating frame relaxation data from Fig. 11. Maps are uniform and without artifacts in all three orthogonal sections. Good contrast can be seen in all maps between gray and white matter, and subcortical structures.

Figure 14.

Segmentation of the T1ρ, T2ρ and water molecular dynamics maps. Cortical gray matter, white matter and subcortical structures were segmented on a high-resolution scan using Freesurfer 5.1. The high-resolution scan and segmentation were coregistered to the rotating frame relaxation data.

Table 2.

Mean and standard deviation values for longitudinal T1ρ relaxation, transverse T2ρ relaxation, correlation time constant τ_c,b, exchange time constant τ_ex, exchange chemical shift δω_ex, water bound fraction P_b. Values are calculated in eight ROIs segmented by Freesurfer 5.1 on high-resolution 3D anatomical scans and coregistered to the 3D rotating frame relaxation maps acquired in the brains of five human volunteers. Only voxels with a coefficient of determination R² > 0.95 were used for statistical analysis. Voxels at the boundary of ROIs were also excluded. RH – right hemisphere, LH – left hemisphere, Ventral DC – ventral diencephalon, SN – substancia nigra.

Brain ROI		T1ρ (ms)	T2ρ (ms)	τc,b (ns)	τex (ms)	δωex (ppm)	Pb
White Matter	RH	79.5 ± 5.5	73.9 ± 7.5	2.40 ± 0.15	0.21 ± 0.01	0.42 ± 0.02	0.125 ± 0.005
	LH	79.0 ± 5.4	73.9 ± 7.4	2.41 ± 0.15	0.21 ± 0.01	0.42 ± 0.02	0.126 ± 0.005
Gray Matter	RH	96.1 ± 16.9	90.4 ± 15.8	2.13 ± 0.18	0.18 ± 0.03	0.36 ± 0.04	0.109 ± 0.013
	LH	95.3 ± 13.9	90.3 ± 15.1	2.11 ± 0.15	0.18 ± 0.02	0.36 ± 0.03	0.108 ± 0.010
Thalamus	RH	80.8 ± 6.2	80.5 ± 8.6	2.29 ± 0.14	0.20 ± 0.01	0.41 ± 0.02	0.122 ± 0.006
	LH	80.3 ± 6.0	80.0 ± 8.1	2.29 ± 0.15	0.20 ± 0.01	0.41 ± 0.02	0.122 ± 0.006
Caudate	RH	90.7 ± 5.9	84.2 ± 9.5	2.16 ± 0.11	0.19 ± 0.01	0.37 ± 0.02	0.112 ± 0.005
	LH	90.9 ± 6.3	82.9 ± 8.9	2.15 ± 0.12	0.19 ± 0.01	0.37 ± 0.02	0.111 ± 0.005
Putamen	RH	85.8 ± 6.5	80.4 ± 8.6	2.18 ± 0.11	0.19 ± 0.01	0.39 ± 0.02	0.116 ± 0.006
	LH	84.5 ± 6.2	80.0 ± 9.2	2.18 ± 0.11	0.20 ± 0.01	0.39 ± 0.02	0.117 ± 0.005
Pallidum	RH	69.8 ± 3.7	64.5 ± 5.8	2.55 ± 0.15	0.22 ± 0.01	0.45 ± 0.01	0.134 ± 0.004
	LH	68.7 ± 3.9	64.0 ± 5.3	2.59 ± 0.17	0.23 ± 0.01	0.45 ± 0.02	0.136 ± 0.005
Hippocampus	RH	91.8 ± 8.2	86.8 ± 13.7	2.14 ± 0.13	0.19 ± 0.01	0.37 ± 0.02	0.111 ± 0.006
	LH	87.2 ± 7.7	72.2 ± 14.1	2.11 ± 0.13	0.19 ± 0.01	0.38 ± 0.02	0.113 ± 0.006
Ventral DC (SN)	RH	73.4 ± 7.4	69.9 ± 10.7	2.48 ± 0.21	0.22 ± 0.01	0.43 ± 0.03	0.130 ± 0.008
	LH	72.1 ± 7.3	67.2 ± 10.4	2.50 ± 0.21	0.22 ± 0.01	0.44 ± 0.03	0.132 ± 0.008

5. DISCUSSIONS

The use of GOIA-W(16,4) pulses solves simultaneously three major problems in T1ρ and T2ρ mapping: i) reduction of SAR, ii) compensation of B₁ and B₀ inhomogeneity, and iii) slice selectivity. The last aspect is relevant particularly for 2D imaging, while the second aspect is specifically improved when compared to CW approaches. Consequently, GOIA-W(16,4) pulses allow for faster and more robust imaging of T1ρ and T2ρ relaxation in both 2D and 3D sequences.

Compared to the more familiar T1 and T2 relaxation in the laboratory frame, the T1ρ and T2ρ relaxation in the rotating frame are weighted more towards water molecules interacting with macromolecules. The water bound fraction experience dynamics on the ns-ms time scale which is better accessed with the weaker B₁ radiofrequency field (~10µT) than with the stronger B₀ static field (~1T). In addition, the B₁ field can be easily varied compared to the B₀ field, enabling detailed investigation of relaxation mechanisms via relaxation dispersion curves. Modulation functions of adiabatic pulses can be varied too, adding more versatility than CW spin-lock. In the case of GOIA pulses simultaneous modulation of the RF field and gradient enables shorter pulses in-vivo within the limits of available B_1,max and SAR, which provides more flexibility for preparation times. Another effect leading to further decrease of SAR is related to the fact that relaxation times scale with the size of the effective field. Relaxation time constants are longer under the higher effective field of conventional adiabatic HS4 pulses, and shorter under the smaller effective field of GOIA-W(16,4). A comparison of the frequency sweep and time evolution of the nutation angle between the two pulses indicate that frequency is swept slower in the middle of the pulse and magnetization spends more time in the region near to the transverse plane in the case of GOIA-W(16,4) pulse, which may explain shorter rotating relaxation time constants. To accurately measure relaxation times the duration of magnetization preparation has to approach the relaxation time constant. Hence, the longest preparation time with HS4 pulse may need to exceed 100 ms (Mangia et al., 2009), while for GOIA-W(16,4) pulses 80 ms preparation may be sufficient. Reduced SAR with GOIA-W(16,4) pulses might facilitate the use of T1ρ and T2ρ relaxation at higher fields (7T) in humans.

Often rotating frame relaxation experiments performed under CW spin-lock try to match the amplitude of the RF field to a certain value for the molecular dynamics parameter of interest. In-vivo this might not be necessary or counterproductive since tissue conditions are spatially heterogeneous. For example, pH variations in disease could change exchange rates across the lesion. Adiabatic pulses with their sweep of frequency might actually be suited to address this spatial heterogeneity of molecular parameters. GOIA-W(16,4) pulses have a slow linear frequency sweep over the central part of the pulse (aprox. 45% of the pulse duration). The sweep of GOIA-W(16,4) over the middle part of the pulse is slower compared to HS4 pulses, which might be more advantageous to step through the range of values for in-vivo molecular dynamics parameters.

The use of a slice selective gradient during T1ρ and T2ρ could result in relaxation rates being sensitive to slice position or diffusion. These two aspects are relevant only for 2D imaging, since in 3D sequences the gradient is very weak (0.34 mT/m). First, as proven in the theory and experiments, the dependency on the slice position is removed from the relaxation curve by the frequency modulation used to excite slices off-isocenter. The dependency of the relaxation rate on intra-slice isochromats can be calculated and a slice mean relaxation rate can be exactly computed. Second, diffusion may play a role only during 2D T2ρ preparation. Signal attenuation can be fitted with a combined T2ρ relaxation and diffusion equation. In the case of T1ρ preparation longitudinal magnetization is locked along the adiabatic effective field and signal attenuation due to diffusion cannot occur. The b-values for a particular GOIA-W(16,4) pulse can be calibrated on phantoms. We found that experimental b-values are smaller than 200 s·mm⁻² for T2ρ preparation times up to 80 ms. However, the experimental b-values are much larger than those predicted by the theory employed in the theory section. Several possible explanations for the departure between theory and experiment may exist. First the theoretical derivation of b-values is based on the assumption of instantaneous inversion of isochromats, a reversal of the gradient moment and the exact cancellation of the radiofrequency contribution to the phase scrambling. However, slight imperfections in the gradient and RF waveforms, such as delays between the two waveforms or phase inaccuracies in the RF modulation may render this assumption less accurate. In this case the phase scrambling due to the radiofrequency term may not cancel but accumulate over the preparation time. Second, the contribution to the diffusion of the magnetization from the transition bands was not included. The b-values in the transition bands are larger than in the center of the slice, however the magnetization trajectory is more complicated. Third, an imperfect inversion of the magnetization in the presence of the gradient could accumulate over the pulses, however such an effect would be more linear and should be visible in both T1ρ and T2ρ experiments. Fourth, crossterms from other imaging gradients were not included, although the effect of the ramps was considered. Fifth, a possible crossterm between rotating frame relaxation and diffusion may exist if the time scale of molecular dynamics and diffusion were similar. While the dipolar coupling is much faster than diffusion, the exchange interaction could happen on a similar time scale like diffusion. However considering also the length scale and the strength of the macroscopic gradient this is a less likely situation.

On the other hand, a magnetization preparation module that simultaneously probes relaxation in the rotating frame and diffusion could be useful. When analyzed separately, ADC and rotating frame relaxation rates correlate strongest with disease stage and treatment response (Kettunen et al., 2007, Jokivarsi et al., 2010b). It may be plausible that a combined diffusion-relaxation contrast might show even more specificity and sensitivity to pathology, linking macromolecular fraction and cell density. By analogy, relaxation along the fictitious field that combines T1ρ and T2ρ relaxation seems to correlate stronger with pathology than either relaxation alone (Liimatainen et al., 2012). Diffusion weighting during GOIA-W(16,4) pulse can be adjusted by the gradient modulation factor. Moreover, the gradient modulation during T2ρ preparation is periodic, resembling the oscillating gradient diffusion (OSGE) method (Aggarwal et al., 2012), and the frequency of oscillation can be changed by changing pulse duration. These features provide flexibility in tuning the diffusion component of the sequence.

For slice selective T1ρ and T2ρ relaxation it is important that the slice profiles of magnetization preparation and the imaging readout are matched. This can be perfectly achieved in spin echo sequences that use the same GOIA-W(16,4) pulses for preparation and readout. The slice profile of GOIA-W(16,4) pulses is sharper than for typical pulses used in MRI sequences. Doubling the slice thickness of the GOIA-W(16,4) pulses ensures that all the magnetization that is imaged is also prepared by the rotating frame relaxation, if different pulses are used for readout. With a slice gap of 50% the neighboring slices are not excited and magnetization saturation does not occur. Also interleaved slice acquisition provides a temporal separation of 2·TR between adjacent slices allowing more time for relaxation and magnetization recovery to proceed compared to a single TR in spatially non-selective rotating frame relaxation. While slice selectivity could also be obtained with conventional adiabatic pulses using a gradient, GOIA pulses offer the advantage of 80% less SAR for the same duration and bandwidth. Obviously slice selectivity cannot be achieved for CW by applying a gradient during spin-lock, and GOIA-W(16,4) pulse has 20% less SAR compared to a CW spin-lock of the same peak amplitude.

Maps of T1ρ relaxation time obtained with GOIA-W(16,4) pulses show good uniformity and no artifacts over the entire brain in human volunteers. The T2ρ relaxation maps show artifacts as signal loss in structures at the base of the skull (pons, cerebellar vermis), that are located in the vicinity of big air cavities. This is due to large B₀ inhomogeneity in these regions, resulting in dephasing the precession of transverse magnetization around the effective field.

Previous investigators showed that parameters of molecular dynamics can be calculated from rotating frame relaxation curves (Michaeli et al., 2006, Michaeli et al., 2008, Sierra et al., 2008, Jokivarsi et al., 2009). We show here, for the first time to our knowledge, 3D maps of water molecular dynamics in the human brain. Molecular dynamics parameters depend solely on tissue properties, and represent a more useful quantification that is suited for comparing results among different investigators. Relaxation rates depend on both the tissue properties and sequence, which leads to variability among results reported by different investigators. For a given relaxation model, such as 2SX/FXL, the fitted molecular parameters are independent of the measurement method and reflect more faithfully the intrinsic properties of the tissue. Of particular interest is the map of the bound water fraction, which correlates with the macromolecular content. A change of 1% in the macromolecular content could be detected in agar phantoms. In the brains of young healthy volunteers 20–30% contrast has been observed in the maps of bound water fraction among different brain structures. This suggests the possibility that such an approach may be able to discover subtle differences across the entire brain in neurological diseases.

Caution has to be exercised regarding overfitting the relaxation curves. Our relaxation curves had five or six time points, while our model had four free parameters, hence the system is overdetermined. However, due to the system of non-linear equations multiple solutions are possible. By restricting the possible range of each parameter and selecting the starting point appropriately for in-vivo conditions, the solution space can be narrowed. One more free parameter can be eliminated by fixing the chemical shift exchange difference. In our case a value of 0.45 ppm (~50 Hz at 2.89T) fits well the in-vivo data. Additionally, to reduce more the ambiguity in determining the model parameters dispersion data can be collected at different modulations of the RF field or by combining T1ρ and T2ρ relaxation. Our results from the agar phantom indicate that the difference in the parameter fits is relatively small when using dispersion versus single relaxation data, and compares favorably with the differences noticed at different agar concentrations or between gray and white matter. This is particularly true for the water bound fraction, which may be the most meaningful and useful parameter. On the other hand, acquiring dispersion data would be difficult to do routinely in patients due to increased acquisition time and the higher likelihood of motion artifacts. Further research and development is necessary to find the best and most feasible strategy to derive accurate model parameters.

Although the relaxation model that we adopted excludes other possible relaxation mechanisms such as auto-relaxations, cross-relaxations and cross-correlations, it is a good compromise in explaining the experimental data while maintaining the complexity within practical limits. More advanced in-vivo relaxation models using three spins system and additional relaxation channels have been discussed (Michaeli et al., 2008) but the number degrees of freedom quickly increases, leading to assumptions for the value of certain parameters.

Alternative methods to rotating frame relaxation have been proposed for investigating the macromolecular content, such as magnetization transfer - MT (Hu et al., 1992), and chemical exchange saturation transfer - CEST (Zhou et al., 2003). All these methods share in common the concept of creating contrast by preparing magnetization with spatially non-selective RF irradiation. Spatial selectivity can be easier incorporated with relaxation in the rotating frame than with MT and CEST.

The current work has implications also for other applications of T1ρ relaxation, such as functional activation studies (Hulvershorn et al., 2005), cerebral metabolic rate of oxygen consumption (CMRO2) (Mellon et al., 2010), and pH imaging (Kettunen et al., 2002, Kogan et al., 2012). Multi-slice and faster acquisition with GOIA-W(16,4) pulses should benefit these applications too. Our method can be used also outside the brain.

For clinical applications it is expected that the proposed sequences are more robust and patient friendly in a clinical environment, providing high-resolution whole head measurements in feasible scan time. In particular, the selective multislice acquisition in roughly 1 min could be useful to translate rotating frame relaxation mapping in humans with acute stroke, where T1ρ has been shown to predict time to onset in animal models (Jokivarsi et al., 2010a).

6. CONCLUSIONS

In summary, we demonstrated a new imaging method for relaxation in the rotating frame that addresses several limitations of the existing methods. The improvements shown for SAR reduction, compensation of B0 and B1 inhomogeneity related artifacts, and spatial selectivity may facilitate the routine acquisition of T1ρ and T2ρ relaxation maps in clinical examinations. Validation studies in patients are necessary, and further development of the proposed method at 3T and 7T may provide new contrast.

Highlights.

• Reduction of specific absorption rate (SAR) for T1ρ and T2 ρ mapping

• Compensate B1 and B0 inhomogeneity and minimize image artifacts

• Slice selective T1ρ and T2 ρ mapping

• Whole brain high resolution T1ρ and T2 ρ mapping with reduced acquisition time

• Modeling, segmentation and statistical analysis of water dynamics in brain