Diffusion Coefficients of Endogenous Cytosolic Proteins from Rabbit Skinned Muscle Fibers

Abstract

Efflux time courses of endogenous cytosolic proteins were obtained from rabbit psoas muscle fibers skinned in oil and transferred to physiological salt solution. Proteins were separated by gel electrophoresis and compared to load-matched standards for quantitative analysis. A radial diffusion model incorporating the dissociation and dissipation of supramolecular complexes accounts for an initial lag and subsequent efflux of glycolytic and glycogenolytic enzymes. The model includes terms representing protein crowding, myofilament lattice hindrance, and binding to the cytomatrix. Optimization algorithms returned estimates of the apparent diffusion coefficients, D(r,t), that were very low at the onset of diffusion (∼10⁻¹⁰ cm² s⁻¹) but increased with time as cytosolic protein density, which was initially high, decreased. D(r,t) at later times ranged from 2.11 × 10⁻⁷ cm² s⁻¹ (parvalbumin) to 0.20 × 10⁻⁷ cm² s⁻¹ (phosphofructose kinase), values that are 3.6- to 12.3-fold lower than those predicted in bulk water. The low initial values are consistent with the presence of complexes in situ; the higher later values are consistent with molecular sieving and transient binding of dissociated proteins. Channeling of metabolic intermediates via enzyme complexes may enhance production of adenosine triphosphate at rates beyond that possible with randomly and/or sparsely distributed enzymes, thereby matching supply with demand.

Introduction

Glycolysis is a multistep anaerobic chemical process that converts glucose or one glucosyl moiety of glycogen into two pyruvate molecules. The free energy released assists in the formation of the high-energy compounds ATP and NADH used in cellular metabolism. Glycolysis occurs in nearly all organisms, and although specific aspects of the metabolic pathways may vary, the ubiquity of this metabolic process reflects both its evolutionary age and importance in cellular homeostasis.

Glycolysis is of particular importance to the function of vertebrate fast-twitch muscle fibers. These fibers are rich in glycogen granules that give the muscle its whitish tint. By rapidly breaking down glycogen and glucose, the linked processes of glycogenolysis and glycolysis represent an immediate source of ATP, complementing the aerobic pathways mediated by the mitochondria. The mechanical work and power produced by ATP-consuming actomyosin cross-bridges is limited, however, both by the amount of available substrate (one glycosyl unit yields three molecules of ATP and one glucose unit yields two molecules of ATP) and by the rate at which ATP is formed at the intermediate steps of glycolysis. The level of this anaerobic capacity (1) is important to the whole organism and establishes the level of success for a variety of motile activities; e.g., from the fight-and-flight response crucial to our early survival as a species to the performance of an elite sprinter in the modern Olympics. Furthermore, although aerobic pathways are the main conduit of ATP delivery, in many multisystem diseases that exhibit underlying mitochondrial dysfunction (e.g., myalgic encephalomyelitis) (2), glycolysis may be an important compensatory pathway for generating ATP.

Previous studies have established that within the muscle cell, the glycolytic enzymes are located in the fluid cytoplasm (3), specifically, within the I-band region of the sarcomere (4). Indirect evidence suggests that within the crowded interior of the I-band, glycolytic enzymes aggregate and form complexes. The close proximity of the enzymes would enable channeling of metabolic substrate intermediates (3–11). Although the expected enhancement in ATP production may help explain how ATP supply matches demand during high power output (1,12), direct evidence establishing the existence of putative complexes in situ, upon which the concept of metabolic channeling is predicted, remains elusive.

In a previous report (3), we identified and estimated the concentrations of the 15 most abundant cytosolic proteins in rabbit psoas (fast twitch) fibers, including 10 glycolytic enzymes. The glycolytic enzymes were present at the predicted stoichiometric ratios, where the mole fraction of each enzyme in the triose (three-carbon sugar) section of the pathway was roughly twice that of each enzyme in the hexose (six-carbon sugar) section, consistent with a mechanism of metabolic channeling. Here, we examine the rate at which these glycolytic enzymes and other cytosolic proteins diffuse out of skinned psoas fibers after being transferred from oil to physiological salt solution. We looked for evidence of whether the glycolytic enzymes are dissociated and freely diffusible under physiological conditions or exist as organized complexes that may assist their functional role. We reasoned that if the glycolytic enzymes exist as complexes, then the complexed enzymes should diffuse together with the same characteristic diffusion coefficient (which could be very small if the size of the complexed enzymes prevented movement through the actin-myosin lattice structure), and the rate of diffusion should be considerably less than that of the individual molecules in the same aqueous medium. If, however, the glycolytic enzymes are not complexed, the diffusion coefficients should scale more or less according to molecular weight and hydrodynamic radius (for example, smaller molecules like enolase would diffuse faster than larger molecules like pyruvate kinase). We based the model fits on measurements of the radial efflux time courses for 11 of the 15 cytosolic proteins examined previously. The results of the modeling are consistent with the hypothesis that supramolecular complexes exist for both glycogenolytic and glycolytic enzymes in the crowded intracellular environment of the living muscle cell. In this interpretation, complexes rapidly break apart under conditions where the cytosol becomes depleted of diffusible proteins. The apparent diffusion coefficients of the dissociated proteins, reduced by steric hindrance and transient binding in the meshlike myofilament lattice, increase with time as the hindering effect of cytosolic protein crowding diminishes.

Materials and Methods

Experimental preparation and solutions

Muscle fiber segments from the psoas (fast-twitch fiber type IID) of New England white rabbits were used. Long segments of intact fibers were isolated in water-saturated mineral oil (7°C), peeled of their sarcolemma using a sharp needle, and cut into ∼6-mm-long segments. Each segment was transferred through adjacent drops of relaxing solution (also at 7°C unless otherwise indicated) according to the procedures described below and illustrated in Fig. 1 A. Details of the method are given elsewhere (13). The width and length of each segment were measured using a digital micrometer both before and after transfer of the segment to relaxing solution. Sarcomere spacing was ∼2.2 μm (i.e., at slack length, untethered). The standard relaxing solution contained (as in Maughan et al. (3)) 6 mM MgCl₂, 5 mM Na₂ATP, 20 mM imidazole, 5 mM EGTA, 45 mM K₂ creatine phosphate, 50 mM sucrose, 4% w/v Dextran T500, and 174 mM ionic strength, pH 7.0 at 20°C (pH 7.3 at 7°C). In some cases, pH and temperature were varied as indicated in the text. As reported previously (14,15), 4% w/v of the high-molecular-weight polymer Dextran T500 (M_w = 465 kDa) osmotically constrains the otherwise swollen skinned fiber and its myofilament lattice to approximately its in vivo width (i.e., the fiber width measured initially in oil, ranging from 38.9 μm to 65.7 μm) and lattice spacing (i.e, the center-to-center thick-filament distance measured by small angle x-ray diffraction).

Figure 1.

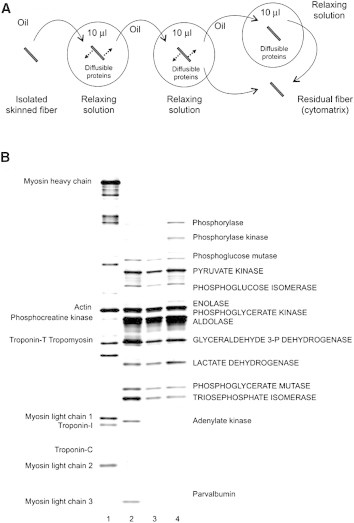
Experimental setup and radial diffusion of endogenous cytosolic proteins into relaxing solution from skinned fiber segments of rabbit psoas muscle. (A) The experimental protocol, where each fiber is placed sequentially in either two or three drops of relaxing solution (∼10 μL each) for a specified period of time ranging from 2 s to 20 min (see text). (B) Proteins separated by SDS polyacrylamide gel electrophoresis with silver-stained gel. Proteins are identified as in Maughan et al. (3). Lanes 2–4, cytosolic protein fractions obtained by sequentially incubating the skinned fiber for 35 s (lane 2, load 5.4 μL = 51% of total volume), 80 s (lane 3, load 7.2 μL = 68% of total), and 1440 s (lane 4, load 10 μL = 90% of total) in 10 μL relaxing solution drops. Lane 1, cytomatrix fraction (residual fiber, load 5 μL = 14% of total). Fiber radius, 29.5 μm; fiber length, 6.56 mm.

Protein radial diffusion protocols

Intracellular protein diffusion rates were measured by transferring the skinned fiber segments through a series of two or three drops (each 10 μL) of relaxing solution on the floor of a glass-bottomed dish containing 2–3 mL water-saturated mineral oil (Fig. 1 A). The volume into which the proteins diffused (10 μL) was very much larger than the fiber volume (3.7 ± 1.2 nL), thereby allowing us to neglect back diffusion in the diffusion models. Stainless steel tweezers were used to clasp one end of a fiber and to quickly transfer it from one drop to another. Fluid adhering to the surface of the fiber between drops was stripped off as the fiber was drawn through the oil phase. Transfers were accomplished within 1 s, unless otherwise indicated. Fibers remained in each drop for 2–1440 s; e.g., 2 s in the first drop, 30 s in the second drop, and 600 s in the last drop; or 35 s in the first drop, 80 s in the second drop, and 1140 s in the last drop, as in Fig. 1 A. (Very few experiments were run with a time of 2–4 s in the first drop; most were run with a time of 20–30 s in the first drop.) Each drop, except the last, was stirred by slowly moving the fiber in a circle or figure eight. The last drop was stirred occasionally. Incubation in the last drop was terminated by transferring the fiber (i.e., the cytomatrix fraction) to sodium dodecyl sulfate (SDS) sample buffer for electrophoretic separation of proteins (see below). In most cases, 5 μL aliquots of each drop containing part of the cytosolic fraction were combined with 2.5 μL of SDS sample buffer and 2.5 μL 50% glycerol, loaded onto the gel, and subjected to electrophoresis alongside diluted samples of the cytomatrix fractions (0.5 nL fiber volume per μL).

SDS polyacrylamide gel electrophoresis

Proteins were separated by SDS polyacrylamide gel electrophoresis, and gels were analyzed as described elsewhere (3). Sample volumes were adjusted to achieve an average load of ∼5 ng per protein band (determined by trial and error). The sample volumes, thus established, also set the maximum number of drops through which the fibers were transferred (nominally three) that allowed the gel analysis to remain within the lower limit of the sensitivity of the assay (1 ng, with a linear range of 1–25 ng). The dilution factors were used to correct band densities during subsequent analysis.

Modeling and parameter optimization

The skinned fiber segment was modeled as a long cylinder bathed in a relatively large, well-stirred volume of solution, as follows: Net movement of protein is directed radially outward, with net outward diffusion of individual species (coupled to dissociation of protein complexes, if present) beginning the moment the cylindrical fiber is transferred from oil to solution. Immediately before transfer, the bath is free of protein and the diffusible proteins and/or protein complexes within specific repeating subsegments of the fiber (defined later) are assumed to be uniformly distributed. Transfer times between drops of solution are neglected, since the time it took to transfer a fiber from one drop to another was short (<1 s) compared to the time a fiber remained in each drop. Taking these conditions into consideration for a specific fiber segment, diffusion in its simplest form is represented by the one-dimensional radial diffusion equation (16):

$$\frac{\partial C\left(r,t\right)}{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left[Dr\frac{\partial C\left(r,t\right)}{\partial r}\right]$$ (1)

and is subject to the following boundary and initial conditions:

$$\begin{array}{l}\text{Boundary}C\left(a,t\right)=0;\frac{\partial C\left(0,t\right)}{\partial t}=0\hfill \\ \text{Initial}C\left(r,0\right)=C_0\text{for}r\text{<}a,\hfill \end{array}$$ (2)

where C is the concentration of the specified cytosolic protein, r is the radial location inside the fiber (ranging between 0 and 20.6 μm in our simulations), and t is the time measured from the moment the fiber is initially transferred into the relaxing solution, D is the corresponding diffusion coefficient, a is the radius of the muscle fiber, and C₀ represents the initial concentration of the specified protein, assumed to be distributed uniformly throughout the specified region (or segment) of the skinned fiber.

We considered two models, the Constant D model, in which D is constant for all radial positions and times, and the Variable D model, in which D varies with radial position and time due to changes in local cytosolic protein density. Both models were evaluated by solving Eqs. 1 and 2 numerically, as described below. We determined the diffusional characteristics of 11 cytosolic proteins for which efflux time course data from experiments were available. These proteins included seven glycolytic enzymes (phosphoglucose isomerase, phosphofructose kinase, triosephosphate isomerase, glyceraldehyde-3-phosphate dehydrogenase, phosphoglycerate mutase, enolase, and pyruvate kinase) and four other abundant proteins in rabbit muscle cytosol (parvalbumin, adenylate kinase, phosphoglucose mutase, and glycogen phosphorylase, of which the latter two are glycogenolytic enzymes).

Previous immunohistochemical studies show that the glycolytic enzymes (as well as diffusible phosphocreatine kinase) reside in the I-band region of the sarcomere (17,18). Localization to the I-band is consistent with these enzymes being part of a supramolecular complex, the size of which would restrict diffusion into the more congested A-band (3). However, since we do not know a priori whether the enzymes are initially complexed or not, we referred all concentrations to total cytosolic volume. These concentrations included glycolytic enzyme concentrations as well as those of proteins more broadly distributed in the cytoplasm.

In both models, the initial conditions are established by the cytosolic diffusible protein density at the onset of diffusion (t = 0) and the fixed parameters listed in Table 1. We assumed, as an approximation, that the total initial diffusible protein density at t = 0 is equal to the sum of the 15 most abundant cytosolic proteins in rabbit psoas muscle, 1121 μmol/L cytosolic fluid volume (Tables II and III in Maughan et al. (3)). We neglected other cytosolic proteins and polypeptides, since their contribution to the total is relatively small (3,19).

Table 1.

Fixed and free parameters and defined variables used in models

Fixed parameters
Symbol	Description	Value	Units	Reference
a	Average radius of fibers	20.6 ± 4.3	μm	Fig. 2 legend
Mo	Oligomeric molecular weight of proteina	11.9–340.3	kDa	Table 2
Dw	Diffusion in dilute aqueous solution of proteina	(2.48–7.75) × 10−7	cm2 s−1	Table 2
Rh	Hydrodynamic radius of proteina	1.83–5.69	nm	Table 2
Vh	Hydrodynamic volume of proteina	0.0129–0.0137	dL/g	Interpolated from (22)
Rthin	Radius of thin filament	4	nm	(66)
Rthick	Radius of thick filament	6.5	nm	(66)
Ro	Average radius of thick and thin filaments	5.25	nm	(66)
L	Half center-to-center thick-thin filament spacing	12.85	nm	(15)
ns	Supramolecular binding cooperativity exponentb	5c	unitless	—
k	Boltzmann constant	1.381 × 10−23	J K−1
η	Viscosity of water at 7°C, at 39.4°C	1.45, 0.65	cP	(37)
T	Temperature of experimental conditions	280, 312.4	K
Free parameters
Symbol	Description	Optimization ranged	Optimum Values	Units
φ	Ease of vacancy, hydrodynamic volume product	0.01–1.00	0.12 ± 0.01	dL g−1
kb	Apparent binding constant of proteins to lattice	0–15	0.96 ± 0.17	unitless
ksmax	Maximal supramolecular complex binding constant	10–1500	628 ± 111	unitless
ρ50	Total cytosolic protein density at 50% binding	0–50	21.96 ± 0.90	mmol L−1
D	Optimized diffusion coefficient (Constant D)	(0–1.00) × 10−7	(0.08–0.68) × 10−7	cm2 s−1
Variables
Symbol	Description	Returned value rangee		Units
ρ(r,t)	Total cytosolic protein density in a radial annulus	0–1.121		mmol L−1
D(r,t)	Variable diffusion coefficient (Variable D)f	0.20–1.60 × 10−7		cm2 s−1

^aValues depend on protein species.

^bIndex of the steepness of the transition from maximal to minimal supramolecular binding, defined in Eq. 6.

^cFor the simulations, the value was fixed at 5, corresponding to an arbitrarily high value for cooperativity of the supramolecular binding and dissociation (see text for details).

^dRange of values over which optimum value is determined.

^eRange of values returned from simulations. The values tabulated here for the optimized parameters are the mean ± SD over the 20 best fits to the data. The RMS error between simulation and data of the 20 best fits is 1.66 ± 0.02%.

^fEvaluated at t/a² = 0.035.

In the Constant D model, the diffusion coefficients are independent of protein density, fiber radius, and time; therefore, the diffusion of one protein is uncoupled from that of another, allowing the normalized efflux time course to be solved for each protein species independently of all others. As shown later (Results), the Constant D model does not adequately fit the time course data, especially at short times.

In the Variable D model, the diffusion coefficients depend on radial and temporal variations in protein density, thereby introducing a conceptual basis for a more accurate model fit to the diffusion time course data. Included in this model are four mechanisms that contribute to the time-varying reduction of the diffusion coefficients (20–22).

Obstructions and tortuosity due to cytomatrix proteins

The actin and myosin filaments in a muscle fiber form a regular lattice structure that impedes free diffusion of proteins. The reduced diffusion coefficient, D_h, resulting from cytoskeletal hindrance is determined from the expression for a hexagonal arrangement of myofilaments (23) and the assumption that a protein of hydrodynamic radius, R_h, diffuses through a lattice structure at the same rate as a point particle through an altered structure reduced in spacing by R_h (20):

$$D_h=D_w\frac{1-{\left[\left(R_h+R_o\right)/L\right]}^2}{1+{\left[\left(R_h+R_o\right)/L\right]}^2},$$ (3)

where D_w is the diffusion coefficient of a given protein in aqueous solution, R_o is the mean radius of the myofilaments, and L is the half-mean center-to-center spacing of the myofilaments. Although the structural differences between A- and I-band lattices may differentially affect the radial efflux of protein from each region, we assume, for simplicity, nominal values of R_o and L that reflect those of the A-band (Table 1). We assume this because 1), I-band values roughly approximate those of the A-band if the presence of titin, which runs alongside the thin filaments in the I-band (24) and nebulin, another actin-binding protein (25), are taken into account; and 2), at the sarcomere length at which the present experiments were conducted (2.2 μm), the A-/I-band volume ratio is 3:1 (3), so it is likely that the radial efflux of diffusible proteins from the A-band exceeds that from the I-band. Even complexed proteins initially confined to the I-band, once dissociated, will likely contribute to the radial efflux of proteins from the A-band, since the equilibration times associated with local axial fluxes between flanking I- and A-band regions of the 2.2 μm sarcomere will be short compared to equilibration times associated with the radial efflux of protein between the core and periphery of the ∼20 μm radius skinned fiber.

Excluded volume due to cytosolic proteins

The diffusion rate of a protein in solution is reduced in the presence of a high concentration of other nonreactive background proteins, because the diffusing proteins are excluded from the space occupied by the other proteins (22,26). In this case, the reduced diffusion coefficient, D_c, is given by (22)

$$D_c\left(r,t\right)=D_w\exp \left[\frac{-\gamma V_h\rho \left(r,t\right)}{1-V_h^b\rho \left(r,t\right)}\right],$$ (4)

where γ is a unitless constant that represents the ease-of-vacancy formation of the protein, V_h is the average protein exclusion volume, which is equated to the hydrodynamic volume of the protein in accordance with O’Leary (22), V_h^b is the average hydrodynamic volume of the background proteins in the cytosol, and ρ(r,t) is the sum of the product of the concentrations of each protein (mmol/dL) and their respective molecular weights (g/mmol) present in the cytosol within a specific radial annulus at a given time, hereafter referred to as the total cytosolic protein density within that annulus.

Binding to cytomatrix proteins

There is ample evidence that some diffusible proteins bind transiently to structural proteins of the cytoskeleton (6,7,27–30). Gershon et al. (21) investigated the generic properties of protein binding to the cytoplasmic matrix in eukaryotic cells, which lead to a simple expression for the reduced diffusion coefficient, D_b:

$$D_b=\frac{D_w}{1+k_b},$$ (5)

where k_b is the apparent binding constant of diffusible proteins to the cytomatrix, indicating the ratio of bound to free protein molecules.

Supramolecular complexes

From thermodynamic principles (31,32), it is likely that enzymes in the crowded cytosol of the I-band and other regions of the myofibril form supramolecular complexes, the diffusion of which is severely restricted due to steric hindrance and binding to the myofilaments, as noted above. Clearly, enzymes within the complex must dissociate before they are free to diffuse. To factor in this circumstance, we adopt a form of the reduced diffusion coefficient similar to that in Eq. 5, incorporating a variable supramolecular binding term, k_s:

$$k_s=k_s^{\max }\frac{{\left[\rho \left(r,t\right)/{\rho }_{50}\right]}^{n_s}}{1+{\left[\rho \left(r,t\right)/{\rho }_{50}\right]}^{n_s}}$$ (6)

where k_s^max is the maximal supramolecular complex binding constant (i.e., the maximum ratio of complexed to free protein molecules), ρ₅₀ is the total cytosolic protein density at half-maximum binding, and n_s is the supramolecular binding cooperativity parameter (i.e., an index of the steepness of the transition from maximal to minimal supramolecular binding). For simplicity, we assume that k_s^max, ρ₅₀, and n_s are the same for all complexes (whether glycolytic or glycogenolytic) and are independent of position and time.

We combined all factors described by Eqs. 3–6 to yield an expression for an apparent diffusion coefficient of a given cytosolic protein in the muscle fiber, D(r,t), that is independent of axial position but depends on radial position and time through the variation of total cytosolic protein density, ρ(r,t):

$$D\left(r,t\right)=D_w\frac{\frac{1-{\left[\left(R_h+R_o\right)/L\right]}^2}{1+{\left[\left(R_h+R_o\right)/L\right]}^2}\exp \left[\frac{-\gamma V_h\rho \left(r,t\right)}{1-V_h^b\rho \left(r,t\right)}\right]}{1+k_b+k_s^{\max }\frac{{\left[\rho \left(r,t\right)/{\rho }_{50}\right]}^{n_s}}{1+{\left[\rho \left(r,t\right)/{\rho }_{50}\right]}^{n_s}}},$$ (7)

where, as defined in Eqn. 4, $\rho \left(r,t\right)={\sum }_i^N{C}_i\left(r,t\right)M_{o,i}$, where N is the total number of cytosolic proteins accounted for in this model (14), C_i(r,t) is the concentration of protein i at radius r and time t, and M_o,i is the molecular weight of protein i. The apparent diffusion coefficient is different for each protein and increases with time at any given position as ρ(r,t) decreases. The formulation for D(r,t) in the Variable D model does not account for specific protein-cytomatrix binding, protein-protein binding, or the competitive inhibition between these kinetic processes. Accounting for these possible interactions would either require detailed biochemical experiments to quantify the associated binding kinetics or would greatly increase the number of free parameters in this model. Units for all model parameters (fixed and free) and variables, assumed values for fixed parameters and the value ranges for each of the free parameters are given in Table 1.

The 15 partial differential equations, representing diffusion for each diffusible protein included in the Variable D model, are coupled through the protein crowding term (Eq. 4) and the supramolecular binding term (Eq. 6), both functions of ρ(r,t). Therefore, the equations must be solved simultaneously. Of the 10 glycolytic enzymes whose diffusional characteristics are provisionally assumed to be governed by Eqs. 1, 2, and 7, experimental efflux data were available for only seven: phosphoglucose isomerase, phosphofructose kinase, triose-phosphate isomerase, glyceraldehyde-3-phosphate dehydrogenase, enolase, pyruvate kinase, and phosphoglycerate mutase. The diffusional characteristics of the remaining four (aldolase, phosphoglycerate kinase, lactate dehydrogenase, and phosphocreatine kinase) were specified by the global fit to the efflux time courses for the seven for which data are available, as was the diffusion of phosphocreatine kinase, since diffusible phosphocreatine kinase has been shown to bind to phosphofructose kinase and aldolase in the I-band of skeletal muscle (33). Two glycogenolytic enzymes for which experimental efflux data were available (phosphoglucose mutase and glycogen phosphorylase) are closely associated with particles of aggregated glycogen located in the extramyofibrillar space (34) and were therefore provisionally included in the Variable D model as complexed enzymes also governed by Eqs. 1, 2, and 7. Finally, in applying the Variable D model to adenylate kinase and parvalbumin (broadly distributed small proteins involved in cell metabolism and Ca²⁺ handling), we omitted terms in Eq. 7 that correspond to supramolecular equilibrium binding (Eq. 6), because both of these proteins have been shown to diffuse freely in skeletal muscle (10,13).

The data sets for each protein were composed from experiments run on multiple muscle fibers of different fiber radii. The time associated with the protein diffusion for each fiber was normalized by the square of the fiber radius. This normalized time value is denoted as t/a² and is scaled with a different a determined by the specific radius of each fiber. Data were pooled from multiple fibers to obtain data sets that were sufficiently large for analysis. Pooling was necessary because it was not possible to obtain more than one or two data points per fiber and because free parameters defined from model fits to a small number of data points have limited value (especially those from the Variable D model). When fitting a model to the data, we used the average fiber radius in the data set ($\overline{a}$ = 20.6 μm; Fig. 2 legend); thus, for both the Constant D and Variable D model simulations, the normalized time is equivalent to $t/{\overline{a}}^2$.

Figure 2.

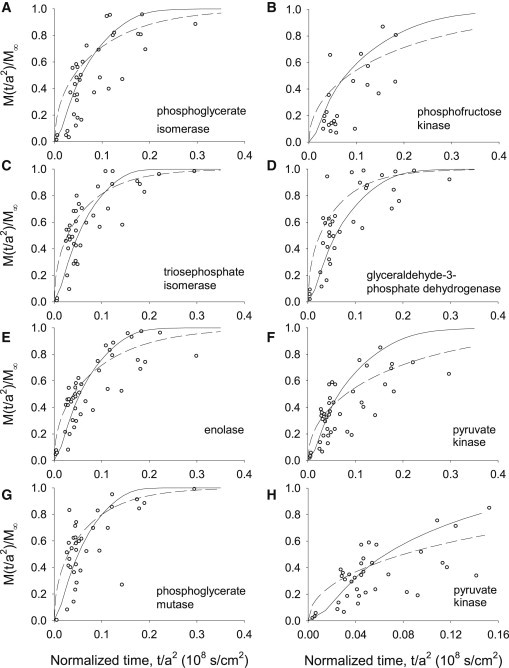
(A–G) Radial diffusion time courses for seven glycolytic enzymes. Ordinate, amount of protein, M(t/a²), relative to the total, M_∞, that diffuses from a segment of a skinned psoas fiber; abscissa, elapsed time fiber remains in each drop divided by the square of the fiber radius. Experiments were performed according to the following protocol. Skinned fibers were transferred sequentially from oil to drop 1, where they remained for variable periods of time, then through oil (<1 s) to drop 2, where they remained for 600 s. Average length of fiber segments, ∼6 mm; average radius, 20.6 ± 4.3 μm (mean ± SD) In a subset of fibers (the three-drop experiment), fibers remained for variable periods in drops 1 and 2 before being transferred to drop 3 (600 s). Curves are generated from numerical solutions of the Constant D model (hatched lines) and Variable D model (solid lines). (H) Duplicate of F (pyruvate kinase) at expanded timescale. The equilibration time for endogenous pyruvate kinase is comparable to that reported for exogenous Rh-pyruvate kinase (55). See text for details.

From the simulation solution, the amount of each protein that diffuses out of the fiber as a function of time, M(t/a²), was determined by integrating the concentration profile at a given time across the fiber cross section (yielding the total amount of diffusible protein retained in the myofiber) and then subtracting that amount from the initial amount. The initial amount was assumed to be equivalent to the total amount of protein that diffused out of the fiber after a long (infinite) time, M_∞. This value was used to normalize M(t/a²) to give data points of M(t/a²)/M_∞ ranging from 0 to 1, which were used to calculate the simulation curves of M(t/a²)/M_∞.

O’Leary (22) examined the diffusion rates of human and earthworm hemoglobin at different concentration levels. In modeling his results O’Leary noted that the product of the ease-of-vacancy formation (γ) and the hydrodynamic volume (V_h) is roughly constant across both proteins, despite their extreme difference in V_h. Thus, for our simulation, we assumed φ = γV_h is constant across all 15 proteins, whose V_h values lie almost entirely between the two extremes. Because there are no literature values for the hydrodynamic volumes of the proteins examined here, we used a linear fit to the plot of hydrodynamic volume versus molecular weight for human and earthworm hemoglobin reported by O’Leary (22) to obtain an interpolated hydrodynamic volume for each protein in this study (see Section B in the Supporting Material). As a check, we used these estimated hydrodynamic volumes and the Stokes-Einstein relationship to calculate the diffusion coefficients of the 15 proteins in bulk water. These calculated diffusion coefficients were slightly larger (by 7–10%) compared to those calculated from a general equation (35) based on experimental values obtained from other proteins. In addition to the parameter φ, we assumed for simplicity that the following parameters are constant across all proteins: the apparent binding constant of diffusible protein to cytomatrix (k_b), the binding constant of maximal supramolecular complex formation (k_s^max), and the total cytosolic protein density at half-maximum complex formation (ρ₅₀). In applying Eqs. 1, 2 and 7, we returned optimized values for these four free parameters that yielded the best (simultaneous) fit to the seven glycolytic and four cytosolic proteins for which we had diffusion time course data. Preliminary optimizations were performed with the steepness index of supramolecular binding (equivalent to the cooperativity of binding), n_s, included as a free parameter. However, optimization of fit was found to be relatively insensitive to this parameter. Because values of n_s > 5 appear to make very little difference in the transition from maximal to minimal supramolecular binding, optimizations were therefore performed with n_s = 5 in the Variable D model. Minimizing the error between simulation and data returned optimum values for the four free parameters using a hybrid simulated annealing/gradient-based method. The same optimization method was used to specify the apparent diffusion coefficient in the Constant D model. Simulations and optimizations were performed on a MATLAB computational cluster utilizing 32 dual-core AMD Opteron-based servers (HP DL145 G2, 4GB RAM). The MATLAB Parallel Computing Toolbox was incorporated to distribute the computational tasks across the cores of the cluster to speed up the optimization procedure. Complete details of the hydrodynamic volume estimation method and calculation of error between simulation and data used during optimization are included in the Supporting Material.

Results

Radial diffusion of proteins from skinned fiber

We measured the diffusion coefficients of 11 cytosolic protein species by assessing the fractional amount of each that diffused from a skinned muscle fiber. The fiber was skinned under oil and subsequently transferred through drops of relaxing solution. Comparison of skinned-fiber dimensions before and after transfer from oil to solution confirmed that the fiber dimensions remained virtually unaltered due to the physiological colloidal pressure replicated by the osmotic agent, Dextran T500, in the relaxing solution. Our ability to separate the proteins on polyacrylamide gels and to measure the relative density of each band from aliquots from each drop allowed us to quantify the efflux of each protein. Fig. 1 B demonstrates the expected outcome that small proteins diffuse out of the fiber more rapidly than large proteins. For example, monomeric parvalbumin (11.9 kDa) and adenylate kinase (21.6 kDa) are present only in the first drop (lane 2, efflux 0–35 s) whereas oligomeric glycogen phosphorylase (194.3 kDa) and to a lesser degree pyruvate kinase (231.7 kDa) are most conspicuous in the third drop (lane 4, efflux 80–1440 s). Fig. 1 B indicates that only myofibrillar proteins remain in the fiber at the end of the diffusion time. Preliminary (not shown) and previous experiments (3) confirmed that 10- to 20-min incubations were sufficient to clear the fiber of diffusible cytosolic proteins.

Fig. 2, A–G, summarizes the diffusion time courses for seven glycolytic enzymes. Data from fibers of different radii were pooled by normalizing the elapsed time (t) with the square of the fiber radius (a²). The fractional amount of protein in the solution drop, M(t/a²)/M_∞ (where M(t/a²) is the total amount diffused out at time t and M_∞ is the total amount diffused out at infinite time for a specific protein) is plotted against t/a² to yield the efflux trajectories. The solid lines represent the best optimized fit of the Variable D model to the data. Constant D model fits (Fig. 2, dashed lines) are shown for comparison. Least-squares analysis and visual inspection of the model fit to the data confirm that the Variable D model represents the data more accurately than does the Constant D model (RMS error = 0.0158 vs. 0.0169, respectively). Although this small difference in RMS error is not by itself sufficient to distinguish between the two models, other criteria (such as Akaike or Bayesian information criteria (see Supporting Material) strongly favor the Variable D model. Furthermore, fitting the Constant D model to the 11 data sets requires 11 adjustable parameters, i.e., one diffusion coefficient for each of the 11 proteins, whereas fitting the Variable D model requires only four adjustable parameters that apply globally to all the proteins. In addition, the adjustable parameters of the Variable D model give us insight into mechanisms that could be contributing to the noted reduction in diffusion of proteins within these fibers. Columns 6 and 5 of Table 2 list values for the diffusion coefficients returned from the best fits to the Constant D and Variable D models, respectively. The optimized parameter average and standard deviation values for the 20 best fits of the Variable D model to the experimental data are given in Table 1.

Table 2.

Physical constants and radial diffusion coefficients for cytosolic proteins of rabbit psoas muscle fibers.

1	2	3	4	5	6	7
Protein	Mo (kDa)	Rh (nm)	Dw (× 10−7 cm2/s)	D(r,t) (× 10−7 cm2/s)	D (× 10−7 cm2/s)	n
Phosphoglucose isomerase	125.2	4.0	3.51	0.57	0.15	31
Phosphofructose kinase	340.3	5.7	2.48	0.20	0.08	19
Triosephosphate isomerase	53.3	3.0	4.69	0.99	0.23	32
Glyceraldehyde-3-phosphate dehydrogenase	144.7	4.2	3.34	0.50	0.25	29
Phosphoglycerate mutase	57.0	3.1	4.59	0.96	0.21	30
Enolase	93.9	3.7	3.87	0.70	0.16	38
Pyruvate kinase	231.7	5.0	2.84	0.33	0.08	39
Glycogen phosphorylase	194.3	4.7	3.02	0.39	0.08	23
Phosphoglucose mutase	61.4	3.2	4.47	0.91	0.16	28
Adenylate kinase	21.6	2.2	6.35	1.6	0.50	21
Parvalbumin	11.9	1.8	7.75	2.1	0.68	12

Column 1 lists the diffusible protein, with glycolytic enzymes in bold type. Column 2 lists the oligomeric molecular weight, M_o (sources listed in Table I of Maughan et al. (3)). Column 3 lists the hydrodynamic radius, R_h, calculated from R_h³ = (3/4π) V_h, where V_h is the hydrodynamic volume of each protein interpolated from the hydrodynamic volume versus molecular weight data of O’Leary (22). See text and Supporting Materials for details. Column 4 lists the estimated value of the diffusion coefficient of the protein in bulk water, D_w (47), calculated from D_w = (kT)/(6πηR_h), where k is the Boltzmann constant, T = 280 K, η = 1.45 cP at 7°C, and R_h is from column 3. Column 5 lists values for the Variable D model radial diffusion coefficients D(r,t) at t/a² = 0.35 and r ∼ a, calculated from an optimized global fit to the experimental data. Column 6 lists values for the Constant D model radial diffusion coefficients (D, constant over the diffusional time course). Column 7 lists the number (n) of fibers sampled. Temperature, 7 ± 1°C; pH 7.3.

Fig. 3, A–D, summarizes the results for four other diffusible cytosolic proteins. Fits of the Constant D model (Fig. 3, solid lines) and Variable D model (Fig. 3, dashed lines) were generated as in Fig. 2. Like the glycolytic enzymes, the diffusion time courses for the glycogenolytic enzymes glycogen phosphorylase and phosphoglucose mutase are better represented by the Variable D model than by the Constant D model. In contrast, the diffusion time courses for adenylate kinase and parvalbumin generated by the Variable D model could not be distinguished from those of the Constant D model given the available data.

Figure 3.

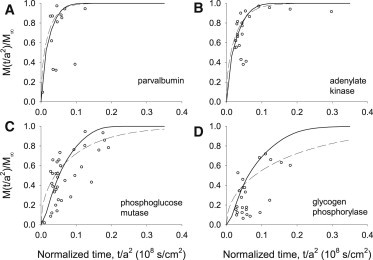
(A–D) Radial diffusion time courses for four cytosolic proteins. Ordinate, abscissa, and procedures are as in Fig. 2. Curves are generated from numerical solutions of the Constant D model (hatched lines) and Variable D model (solid lines). Note that the initial diffusional lag is evident in C and D. Fiber dimensions are as in Fig. 2. See text for details.

Although most experiments were carried out at 7°C and pH 7.3, some were conducted at a temperature and intracellular pH that were closer to those in vivo (39.4°C and pH 6.8 (3,36). An approximation of the mean radial diffusion coefficient at a specific t/a², denoted as D_t/a², was calculated by applying the Constant D model to drops 1 and 2, given the value of M(t/a²)/M_∞ measured at the time the fiber was withdrawn from drop 1. For the case where ∼2 s had elapsed, i.e., where t/a² = 0.049 (± 0.0032) × 10⁸ s cm⁻²), D_t/a²=0.049 at 39.4°C was found to be approximately double that at 7°C (D_t/a²=0.049^39.4°C/D_t/a²=0.049^7°C = 1.93 ± 1.16). The average Q₁₀ of D_t/a²=0.049 (calculated according to the formula Q₁₀^{(39.4°C−7.4°C)/10} = D_t/a²=0.049^39.4°C/D_t/a²=0.049^7°C) was 1.21 ± 0.19 for 9 of 11 proteins listed in Table 2 (the Q₁₀s of parvalbumin and adenylate kinase were not calculated, because the rates were too rapid at 39.4°C to be measured accurately). The value of 1.21 for Q₁₀ is consistent with that for passive diffusion (1.32) (36,37). Because enzymatic reactions generally have Q₁₀s between 3 and 4, we conclude that metabolic processes do not play a significant role in determining the diffusion coefficients.

Oil or unstirred layer artifact?

Inspection of the data points of Fig. 2 reveals an apparent delay in diffusion of the order of 10 s after the onset. Although we provisionally attribute this to a delayed break-up of a putative supramolecular complex, it is possible that the lag reflects the presence of oil or an unstirred layer of polarized water (38) that dissipates with stirring. However, because we started stirring immediately upon transfer from oil to solution, it is unlikely that a stagnant layer of oil or polarized water, even if present initially, would be sustained for more than a second or two. The results of a three-drop experiment (presented in Table S2 in the Supporting Material) are consistent with this view. A freshly skinned fiber was transferred from oil to a drop of relaxing solution and after 2 s was returned to oil. During this brief period in solution, 3–9% of the diffusible protein left the fiber, the exact amount depending on the protein species and fiber diameter. After a 60 s equilibration period in oil, the fiber was transferred to a second drop of relaxing solution for 2 s. That is, the initial conditions were reestablished and the procedure repeated, during which the fiber was depleted of a slightly greater amount of diffusible protein. Finally, the fiber was transferred rapidly through oil to a third drop of relaxing solution for a final washout period of 10 min. Values of D_t/a² at t/a² = 0.049 (i.e., D of the Constant D model evaluated at t/a² = 0.049) were calculated for a representative set of proteins by applying the Constant D model to drops 1–3 and to drops 2–3, respectively, as explained in the Supporting Material. D_t/a² at t/a² = 0.049 derived from the second transfer exceeded those from the first by a factor of 2.8 ± 0.6. If oil or polarized water were responsible for the lag, and it dissipated similarly for both transfers, roughly similar values of D_t/a² at t/a² = 0.049 would be expected, and this was not the case. However, if a diffusion lag occurred because a protein complex (which takes time to dissociate) is initially present in the first transfer but not in the second, then a significantly higher value of D_t/a² = 0.049 would be expected, and this is what was observed.

The relative contributions of viscosity and steric hindrance to reduced protein diffusivity

Fig. 4 A shows how the apparent diffusion coefficient returned from either the Constant D model (open circles) or the Variable D model (solid circles) is inversely proportional to molecular weight. This reciprocity can be at least partially explained by a Stokes-Einstein relationship (dotted line), where diffusion in water, D_w, is given by (39,40)

$$D_w=\frac{kT}{6\pi {\eta }_w{R}_h},$$ (8)

where k is Boltzmann’s constant, T is temperature, η_w is the viscosity of water and R_h is the hydrodynamic radius of the diffusing protein calculated from the linear-fit estimate of hydrodynamic volume described earlier.

Figure 4.

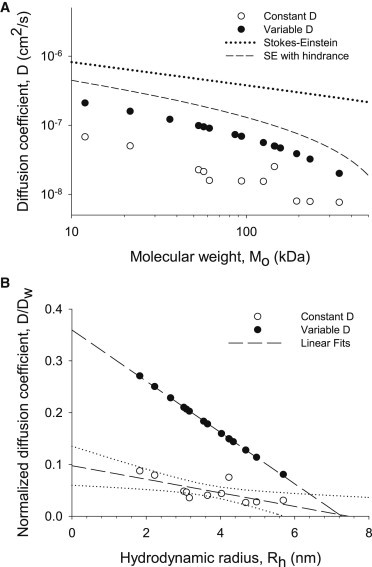
(A) D (Constant D model) and D(r,t) (Variable D model) evaluated at later times versus protein molecular weight contrasted against predicted Stokes-Einstein relationships, with and without steric hindrance. Open and solid circles represent diffusion coefficients determined with the Constant D model, and those determined with the Variable D model (D(r,t) evaluated at t/a² = 0.35 where r = a, i.e., the fiber radius), respectively. The dotted and dashed lines give the Stokes-Einstein relations using diffusion coefficients determined experimentally by Young et al. (35), without and with, respectively, the lattice hindrance term. The slopes of the double log plots are about −1, consistent with an inverse relationship between diffusion coefficient and hydrodynamic radius. (B) D/D_w (Constant D model) and D(r,t)/D_w (Variable D model) at t/a² = 0.35 and r ∼ a as functions of the hydrodynamic radius. The Variable D curve is plotted according to Eq. 9, where values of D(r,t), D_w, and R_h are from Table 2. Straight dashed lines are linear regression fits, and curved dotted lines are 95% confidence limits. Although the general form of Eq. 9 is nonlinear, the resulting plot (solid circles) is, to the naked eye, essentially linear for the parameter values used (R_o = 5.25 nm, L = 12.85 nm, and R_h = 1.83–5.69 nm), yielding an x axis intercept (i.e., the sieving radius) of 7.6 nm, i.e., a value close to that obtained by the linear fit.

Note, however, the substantial reduction in the magnitude of the diffusion coefficients beyond that predicted from a Stokes-Einstein relationship. The marked discrepancy indicates the presence of other retardation factors. As noted above, an important contributor is steric hindrance due to the lattice structure (Eq. 3) which, when factored in, further attenuates the diffusion coefficients (Fig. 4 A, dashed line):

$$D_h=\left[\frac{kT}{6\pi {\eta }_w{R}_h}\right]\left\{\frac{1-{\left[\left(R_h+R_o\right)/L\right]}^2}{1+{\left[\left(R_h+R_o\right)/L\right]}^2}\right\}.$$ (9)

In generating curves from Eq. 9, values of k, T, η_w, R_o, and L are given in Table 1, and values of R_h for each protein are given in Table 2.The first bracketed term accounts for the Stokes-Einstein relationship, and the second bracketed term accounts for steric hindrance, as in Eq. 3. Steric hindrance appears to moderately attenuate the diffusion coefficients returned from the Constant D model (51–87%; open circles) or the Variable D model at long diffusional times (55–91%; solid circles). However, steric hindrance alone does not explain the much lower initial diffusion rates, implying that additional factors, as considered in the Variable D model above, come into play.

Fig. 4 B recasts Fig. 4 A by showing the ratio of the apparent diffusion coefficients to their values in bulk water (D_w) plotted against the hydrodynamic radius, R_h. Both D/D_w (Constant D model, open circles) and D(r,t)/D_w evaluated at long times, i.e., t/a² = 0.35 (Variable D model, solid circles) decline linearly with R_h, as would be expected of a molecular sieve of impenetrable rods (discussed in more detail later).

Discussion

Glycolytic and other cytosolic enzymes that serve anaerobic metabolic pathways are abundant in fast skeletal muscle fibers. At the high concentrations found (3,4,41) and references therein), it is expected from thermodynamic and other considerations that multiprotein complexes would form (31,32,42). This study measures the diffusion coefficients of nine representative metabolic enzymes to assess whether their values are very low and not significantly different from one another, thereby supporting the existence of large complexes, or whether their values are higher and scale inversely with their hydrodynamic radii, thereby supporting a dissociated state. The results for seven glycolytic (Fig. 2) and two glycogenolytic (Fig. 3) enzymes show features of both scenarios, namely, an initial lag in diffusion with correspondingly low values of D(r,t), suggesting that the enzymes exist as complexes in vivo, but with higher values at later times and a dependency of D(r,t) on oligomeric size, suggesting that the enzymes dissociate upon immersion of the skinned fiber in relaxing solution. Adenylate kinase and parvalbumin do not appear to be complexed, since the initial lag in diffusion is absent (Fig. 3). The ability of the Variable D model to more accurately reproduce the general features of the diffusion time course for each species supports this interpretation.

Origin of diffusion lag

We considered several alternative mechanisms that could generate a diffusion lag, including one in which a barrier (a layer of oil or polarized water) is present initially but dissipates with time. As mentioned earlier, it is unlikely that a stagnant layer of oil or polarized water could be sustained because of continuous stirring, a conclusion bolstered by results of the three-drop experiment (Table S2). In this experiment, significantly lower values of D_t/a² were associated with the initial transfer of the fiber from oil to solution compared to the values associated with reequilibration of the fiber in oil and a second transfer to solution. A mechanism in which an envelope of oil or polarized (highly structured) water reforms and dissipates during the second reequilibration in oil and transfer to solution would be expected to produce similar coefficients, which was not the case. Substantial experimental evidence suggests that an aqueous phase resembling bulk water constitutes nearly all (>96%) of the total water in the muscle (43–46), although this conclusion is somewhat controversial (38,47). The putative remainder (<4%) strongly absorbed to cytomatrix proteins or highly structured is probably of insufficient quantity to appreciably retard diffusion of cytosolic proteins.

We suggest a more realistic possibility, that native complexes of glycolytic and glycogenolytic enzymes break apart as the pool of monomers in equilibrium with the complexes becomes rapidly depleted. Cytosolic protein crowding and dissociation of such complexes, whose constituent molecules occupy a large volume fraction of the I-band in particular, provide a reasonable mechanism for the dependency of D(r,t) on total protein density, reflected in the diffusional time lag. With dissociation of enzymes at reduced protein density, lattice hindrance and binding become the primary contributors to the reduced diffusivity at a later time. This interpretation is supported by the better fit of the Variable D model to the data (Figs. 2 and 3). Table 1 lists the average optimized parameter values with standard deviations for the 20 best fits to the data. The relatively narrow range of optimized values for parameters specifying the ease of vacancy-hydrodynamic volume product (φ), lattice binding equilibrium (k_b), and half dissociation activity density (ρ₅₀) indicates that these parameters are more sensitively prescribed by the data presented here than is the maximal complex dissociation equilibrium constant (k_s^max), which has a relatively wide range of optimized values. Despite these differences in parameter sensitivity, the overall goodness of fit achieved with the optimized parameter values lends credence to the Variable D model.

There is considerable circumstantial evidence that glycolytic enzymes form complexes (7–9,17,47), a notion consistent with the results of the Variable D model. Further, concentration measurements of the glycolytic enzymes in related experiments with rabbit psoas muscle fibers (3) indicate a 1:2 stoichiometric relationship of enzymes in the hexose/triose pathways. Together, these results suggest the presence of a complex that effectively channels substrate intermediates through a potential bottleneck at the hexose/triose interface, enabling two pyruvate molecules to synchronously exit the complex for every glucose molecule that enters.

Diffusion after the lag

Our results show that the diffusion constants evaluated at a later time (after most of the putative complexes break up) scale roughly with molecular weight and hydrodynamic radius (Fig. 4). Obstructions and tortuosity appear to contribute most to the reduced diffusivity. Linear regressions through the data points intercept the hydrodynamic radius axis at 7.4 nm for the Constant D model and 7.3 nm for the Variable D model, indicating the radius at which particles are unable to diffuse out of the myofibril. The intercept from these models (and Eq. 9; see Fig. 4 B, legend) corresponds to a mesh size (2x) of 14.6–14.8 nm, and at 2.2 μm sarcomere spacing this range of sizes is within the range of surface-to-surface distances between adjacent myofilaments (14 nm in the A-band and 20 nm in the I-band (Table 2)). Thus, in regions of the sarcomere where cytosolic proteins are localized or into which they may diffuse, the myofilament lattice is of the appropriate size to be the molecular sieve.

The linear regression for the Variable D model in Fig. 4 B (solid circles and dashed line) gives D(r,t)/D_w = 0.36 (at r = a and t/a² approaching 0.35 × 10⁻⁸ s cm⁻²) for a point particle in the matrix (R_h = 0), indicating that the diffusion coefficients of small particles, such as metal ions or metabolites, are also attenuated by tortuosity and molecular sieving. The 64% reduction in radial diffusion coefficients for small particles inferred in this study is greater than the 50% reduction in longitudinal diffusion coefficients reported elsewhere for ionic potassium, sodium, sulfate, and adenosine triphosphate in vertebrate skeletal muscle (43). The greater reduction in radial diffusion compared to longitudinal diffusion is surprising in light of additional obstructions to longitudinal diffusion (Z-, M-, and A-band structures, including myosin heads, C-proteins, and myosin light chain extensions), but the diffusion anisotropy is consistent with that observed in previous experimental (48,49) or theoretical (50) work, where diffusion of water or small molecules in skeletal muscle was reported to be slower in the radial than in the longitudinal direction.

Electrostatic interactions with other proteins also appear to contribute to the reduced diffusion coefficients, but to a lesser extent. Muscle glycolytic enzymes have been shown to bind to one another differentially and to actin filaments under physiological ionic conditions (29,51–54). Indeed, the Variable D model returns an average apparent binding constant, k_b, of 0.96, implying that an appreciable fraction (∼0.49 = k_b/(1 + k_b) (21)) of the diffusible molecules is bound to the cytomatrix at any moment. The corresponding binding free energy, ΔG, of that bound fraction is 0.10 kJ mol⁻¹ (= −RT lnk_b (21)).

Relationship to other studies

In complementary studies, Kraft and colleagues (55) used confocal microscopy to examine the influx of exogenous fluorescently labeled molecules into chemically skinned fibers from rabbit psoas. Equilibration times varied widely, from minutes (e.g., rhodamine (Rh)-labeled pyruvate kinase) to days (e.g., Rh-labeled NEM-myosin S1), with large differences in equilibration times attributed to a combination of myofilament lattice obstruction and binding to fixed structures. Although diffusion coefficients were, for technical reasons, not reported and therefore cannot be compared with those listed in Table 2, the timescales over which equilibration occurs appear to be in rough accord. For example, the 8- to 10-min equilibration time for exogenous Rh-pyruvate kinase (Fig. 3 of Kraft et al. (55)) is comparable to that of endogenous pyruvate kinase (Fig. 2, F and H).

Other studies have been conducted in a variety of cell types to assess the relative contributions of geometrical hindrance and of binding to cytomatrix proteins to the reduced diffusion coefficient of cytosolic proteins. In most cases, a combined effect of interference by other proteins in the cytosol and obstruction by fixed cytomatrix proteins accounts for most of the reduced diffusivity (21). In some cases, steric hindrance by the myofilament lattice alone appears to account for most of the reduced diffusivity, as, for example, the 10-fold decrease in diffusion coefficients of native myoglobin observed in intact frog (56) and rat (57) skeletal muscle fibers. In a follow-up study, Papadopoulos and colleagues (58) found that the molecular sieve property of the filament lattice progressively reduced the diffusion coefficients of the microinjected proteins in relation to their size, from ∼1/6 (cytochrome c, 3.1 nm diameter) to ∼1/63 (ferritin, 12.2 nm) of their value predicted in water, with the exact values depending on fiber type. The marked dependence of the diffusion coefficients on protein size was explained by the high viscosity of the myoplasm (due to the high soluble protein content) and steric hindrance (due to the presence of the myofilament lattice and other structural barriers). These results also indicate that about half the number of otherwise freely diffusible cytosolic proteins are bound to the cytomatrix at any given moment, with a surprisingly low average binding free energy (0.10 kJ mol⁻¹) compared to those reported for other cell systems (21).

The low initial diffusivity and apparent dependence of the diffusion coefficients on total cytosolic protein concentration reported here in skinned fibers are consistent with the low diffusion coefficient values reported elsewhere in intact muscle fibers (noted above). However, only at the outset of diffusion, when protein associations are most pronounced and soluble protein content (and cytosol viscosity) is highest, would one expect diffusion coefficients to be as low as those observed in intact cells, i.e., a tenth or less of that measured for a particular species in water. Only after the putative associations disperse and soluble protein content diminishes do individual molecules diffuse out more rapidly and in an ever-changing temporal pattern according to Eqs. 1, 2, and 7.

As noted previously, there is considerable circumstantial evidence, backed by strong thermodynamic arguments (31,59), that glycolytic enzymes form complexes in the crowded cytosol of muscle cells (3,9,32,47,60,61). Recently, Brownian dynamic simulations have contributed to our understanding of the critical residues involved in the molecular interactions between specific glycolytic enzyme species (53) and between glycolytic enzymes and globular and filamentous actin (53,54,62,63) in the formation of the putative complexes. The troponin-tropomyosin complex may help seed cytosolic protein aggregates, since binding of glycolytic enzymes to actin is enhanced by the presence of thin-filament-associated proteins (29). Aldolase, in particular, displays a preferred binding to thin filaments at troponinlike intervals of 38 nm, similar to that of the so-called I-bridges that appear to bridge neighboring thin filaments in the I-band of fast skeletal muscle fibers (64). These studies and others led to the hypothesis that glycolytic complexes (or aggregates of enzymes) are involved in metabolic channeling of substrate intermediates, which could elevate the rate of ATP production beyond that achievable with dissociated enzymes (8,9,53). The complexes are probably unstable, since the binding forces appear to be relatively weak in light of their propensity to dissociate readily. The complexes must also be dynamic, since myosin heads slide easily into the I-band region during rapid shortening.

Similar thermodynamic arguments can be applied to glycogenolytic enzymes associated with glycogen particles, which together with the bound enzymes constitute the glycosome (59). Glycogen phosphorylase and phosphoglucose mutase, which bind to these extramyofibrillar particles, catalyze the breakdown of glycogen (65). We speculate that exposing the skinned segment to the bathing medium releases the enzymes from the glycogen particle, resulting in the slight lag in efflux (Fig. 3, C and D).

Conclusion

The results of this study are consistent with a primary mechanism of reduced protein diffusivity in which the compact myofilament lattice of the I-band restricts diffusion of complexes (or aggregates) of glycolytic enzymes located within that region, whereas the more compact lattice of the A-band (containing the myosin heads and other structural proteins) excludes the complexes (3). When muscle fibers are stripped of their sarcolemma and immersed in a physiological bathing solution, the complexes break up into monomers normally in equilibrium with the complexed enzymes, and the monomers diffuse out of the fiber into the bath. The diffusion coefficient of individual species is reduced significantly at the outset due to associations between proteins when the cytosol is crowded, but as the total protein content in the cytosol falls, the complexes dissociate and the individual proteins diffuse out at rates that are inversely proportional to their size. Collisions with cytomatrix proteins (molecular sieving and tortuosity) hinder diffusion, eventually rendering diffusion coefficients that are a tenth to a fifth of those in bulk water.