Advances in Modeling Ventricular Arrhythmias: from Mechanisms to the Clinic

Abstract

Modern cardiovascular research has increasingly recognized that heart models and simulation can help interpret an array of experimental data and dissect important mechanisms and interrelationships, with developments rooted in the iterative interaction between modeling and experimentation. This article reviews the progress made in simulating cardiac electrical behavior at the level of the organ and, specifically, in the development of models of ventricular arrhythmias and fibrillation, as well as their termination (defibrillation). The ability to construct multi-scale models of ventricular arrhythmias, representing integrative behavior from the molecule to the entire organ, has enabled mechanistic inquiry into the dynamics of ventricular arrhythmias in the diseased myocardium, in understanding drug-induced pro-arrhythmia, and in the development of new modalities for defibrillation, to name a few. In this article we also review the initial use of ventricular models of arrhythmia in personalized diagnosis, treatment planning, and prevention of sudden cardiac death. Implementing individualized cardiac simulations at the patient bedside is poised to become one of the most thrilling examples of computational science and engineering approaches in translational medicine.

INTRODUCTION

As advances in computer modeling are transforming many traditional areas of physics and engineering, they are also transforming the understanding of heart function in health and disease. Modern cardiac research has increasingly recognized that appropriate models and simulation can help interpret an array of experimental data and dissect important mechanisms and interrelationships. Decades of development in cardiac simulation have rendered the heart the most highly integrated example of a “virtual organ”.^1-4 These developments are firmly anchored in the long history of cardiac cell modeling, and are rooted in the iterative interaction between modeling and experimentation. Cardiac cell action potential models often take the form of coupled systems of nonlinear ordinary differential equations (ODEs) representing current flow through ion channels, pumps, and exchangers as well as sub-cellular calcium cycling; model equations are solved to observe how states (concentrations of molecules) evolve in time as they interact with one another and respond to inputs.

Over the last two decades, cardiac modeling has also progressed to the level of the tissue and the whole heart, where the propagation of a wave of action potentials is simulated by a reaction–diffusion partial differential equation (PDE). The reaction-diffusion PDE describes current flow through tissue composed of myocytes that are electrically connected via low-resistance gap junctions. Cardiac tissue ha orthotropic electrical conductivities that arise from the cellular organization of the myocardium (cardiac muscle) into fibers and laminar sheets. Global conductivity values are obtained by combining fiber and sheet organization with myocyte-specific local conductivity values. Current flow in the tissue is driven by ionic exchanges across cell membranes during the myocyte action potential. Simultaneous solution of the PDE with the set of action potential ODEs over the tissue volume represents simulation of electrical wave propagation in the myocardium. In certain cases, such as when external current delivery to the myocardium is simulated, a system of coupled PDEs is used (instead of a single PDE), allowing for the explicit representation of current flow in the interstitial space outside cardiac cells.

As documented in reviews by Fink et al.⁵ and Roberts et al.⁶, recent advancements in single-cell action potential modeling have produced building blocks for constructing models of the ventricles^7-10 and cardiac conduction system^11-15 with unprecedented levels of biophysical detail and accuracy. Such developments have helped to fuel the exciting progress made in simulating cardiac electrical behavior at the organ level, which this review is devoted to chronicling. In general, many of the emergent, integrative behaviors in the heart result not only from complex interactions within a specific level but also from feed-forward and feedback interactions that connect a broad range of hierarchical levels of biological organization. The ability to construct multi-scale models of the electrical functioning of the heart, representing integrative behavior from the molecule to the entire organ, is of particular significance since it paves the way for clinical applications of cardiac organ modeling. The review below, while not exhaustive, focuses on both achievements in mechanistic understanding of heart function and dysfunction, and on the trends in the computational medicine aspect of biophysically-detailed ventricular modeling applications.

Modeling of Arrhythmia in the Ventricles

Effects of Cardiac Microstructure on Reentrant Arrhythmia Dynamics

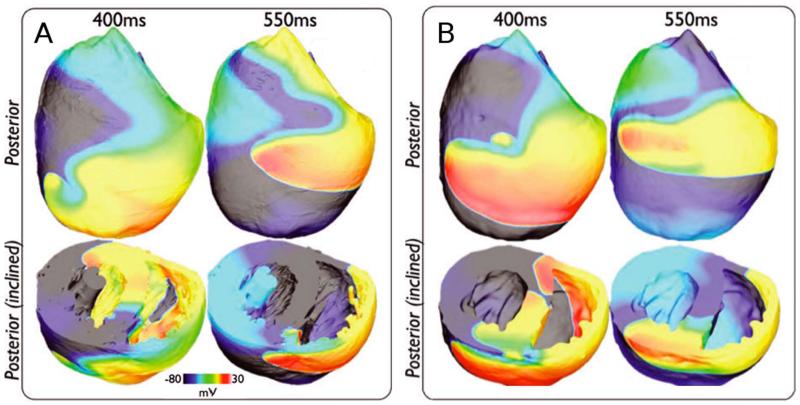
An ongoing concern in cardiac modeling is striking an appropriate balance between anatomical detail and computational tractability. Incorporating high-resolution representation of small-scale ventricular structures can push simulation runtimes beyond the realm of feasibility, even on powerful supercomputers¹⁶. Several recent studies^16-18 have systematically explored how different types of anatomical detail affect the dynamics of reentrant arrhythmia initiation and maintenance in realistic ventricular models. For example, Bishop et al.¹⁷ compared reentrant wavefront propagation in a complex ventricular model, which included fine-grain anatomical structures such as blood vessels, papillary muscles, and endocardial trabeculations, and a simplified version of the same model ventricles, which represented the ventricular wall geometry but lacked those anatomical features. The authors showed (Fig. 1) that there was no marked difference in arrhythmia dynamics between the two models. However, not all anatomical details are safe to ignore – in a separate study¹⁶, the same group showed that electric loading effects caused by the fluid surrounding the myocardium (such as blood in the cavity) reduced arrhythmia inducibility and complexity in ventricular models. Overall, these studies suggest that reentrant arrhythmia dynamics could be reliably and efficiently simulated in ventricular models without high-resolution anatomical detail as long as the proper steps are taken to account for the loading effects exerted by the fluid surrounding the heart.

Figure 1.

A&B. Wavefront dynamics during reentry are qualitatively similar in ventricular models with (A) and without (B) high-resolution representation of anatomical micro-structures. Figure modified with permission from Bishop et al.¹⁷

Arrhythmias Involving the Purkinje System

The Purkinje system (PS) plays a critical role in the coordination of ventricular excitation but it has also been implicated as a key player in arrhythmia initiation and maintenance.^19-22 Unfortunately, detailed analysis of PS contributions is difficult because its spatiotemporal excitation sequence in the intact heart must be inferred from low-amplitude electrograms.²²

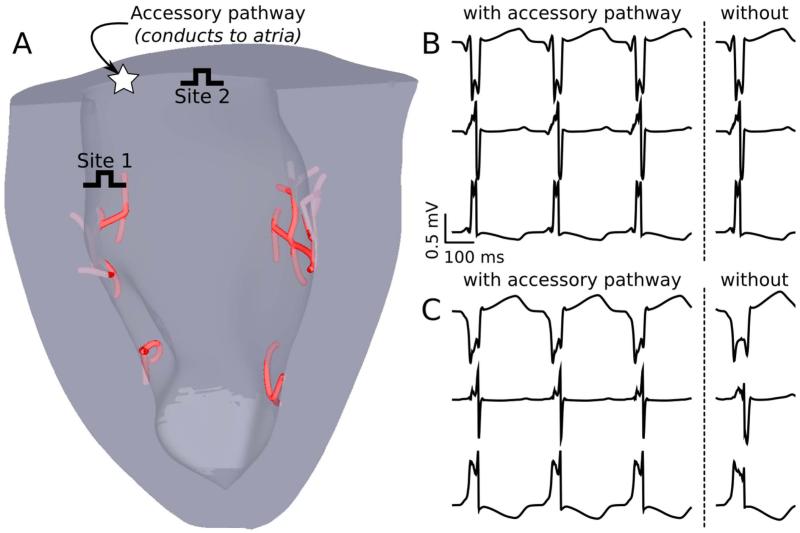
Moreover, chemical ablation of the PS to isolate arrhythmogenic mechanisms is non-selective, since it also destroys several layers of endocardial cells.²³ Circumventing these limitations, computational modeling has provided important insights on arrhythmias involving the PS that would be impossible to achieve otherwise.^24-26 For example, ectopic activations from the PS are known to drive catecholaminergic polymorphic ventricular tachycardia (CPVT),²¹ but exact organ-scale mechanisms are unknown; Baher et al.²⁴ provided an answer by showing that delayed afterdepolarization-driven reciprocating activation of the left and right sides of the PS gave rise to a bidirectional ECG pattern consistent with CPVT. Another recent study²⁵ used models of the ventricles with and without the PS to clarify whether elevated endocardial activation rates observed during ventricular fibrillation (VF) were due to activity from nearby PS terminals. Simulations revealed that although PS effects increased the local complexity of VF, transmural rate heterogeneity was most likely caused instead by locally increased expression of ATP-sensitive potassium channels. Finally, in arrhythmias where the PS is a critical part of the reentrant pathway, simulations can be used to guide improvements in clinical diagnosis and treatment. Boyle et al.²⁶ used models with and without a conductive accessory pathway (AcP) between the ventricles and atria to identify optimal sites for overdrive pacing, a technique used to distinguish AcP-mediated arrhythmia from other tachyardias.²⁷ As shown in Fig. 2, the diagnostic value of this maneuver was greatly improved by pacing near the suspected AcP and far from PS endpoints, since these sites were most likely to produce a visibly distinct QRS complex. These three studies demonstrate how computer modeling can bypass limitations of in vitro experiments to provide mechanistic insights on arrhythmias involving the PS.

Figure 2.

A. Model of the rabbit ventricles and PS with two possible overdrive pacing sites for supraventricular tachycardia diagnosis. B&C. Pseudo-ECG recordings (leads I, II, and III) during overdrive pacing from sites 1 and 2, respectively; sites closer to the PS are a poor choice in terms of diagnostic quality since they fail to produce distinct QRS complexes in simulations with (left) vs. without (right) the accessory pathway. Figure modified with permission from Boyle et al.²⁶

Thus far, arrhythmia contributions have only been studied with simple branching network models of the PS, such as those described above;^24-26 these models adequately simulate the macroscopic functional role of the specialized tissue but lack geometric complexity. In dissected hearts, PS fibers on the endocardium form a distinct network but 3D imaging of these structures remains difficult²⁸ as such, another recent research trajectory has focused on the generation of anatomically realistic PS models that mimic the physiological network, which could provide insight on how interactions of myocardial tissue with the conduction system affect ventricular arrhythmia dynamics. Ijiri et al. used fractal growth patterns to generate networks that qualitatively resembled the physiological PS.²⁹ Other groups have adapted this technique^{28, 30} to construct patient-specific PS models and explore how PS network complexity affects sinus activation sequence. It will be interesting to see what new insights on PS-mediated arrhythmia dynamics can be gained from simulations that incorporate PS models with increased geometric complexity, which are now a possibility.

Dynamics of Alternans and Ventricular Fibrillation

Simulation studies of ventricular electrophysiology have made major contributions to understanding the onset of alternans and the dynamics of VF, the most lethal of all arrhythmias. Particularly interesting are the studies on human hearts,³¹ which revealed that human VF is driven by a small number of reentrant sources, and is thus much more organized than VF in animal hearts of comparable size; the human action potential duration (APD) was found to be responsible for the specific VF dynamics in the human heart. Electrical alternans, which is beat-to-beat variation in APD, has long been recognized as a precursor to the development of VF. Alternans can be concordant, with the entire tissue experiencing the same phase of oscillation, or discordant, with opposite-phase regions distributed throughout the tissue. The restitution curve slope has been viewed as a major factor both in the onset of arrhythmias following the development of discordant alternans and in the dynamic destabilization of reentrant waves leading to the transition of VT into VF. In what has become known as the restitution hypothesis, flattening the APD restitution curve is postulated to inhibit alternans development and subsequent conduction block, and prevent the onset of VF.³² Simulation studies employing ventricular models^33-35 have made important contributions to ascertaining the intricate set of mechanisms by and the conditions under which steep APD restitution could lead to VF onset. These include, but are not limited to, the role of electrotonic and memory effects in suppressing alternans and stabilizing reentrant waves, and the effect of heterogeneous restitution properties on human VF.

Wavefront breakup due to steep APD restitution is not the only possible cause of electrical turbulence seen in VF; Alonso et al. recently showed that in a ventricular model with modestly reduced excitability and APD, the organizing centers (filaments) around which scroll waves rotate tend to increase in length, a phenomenon called “negative tension”.³⁶ As first characterized in geometrically simple 3D models,^37,38 negative tension destabilizes scroll waves, causing increased vorticity and leading to degradation from orderly, VT-like arrhythmias into chaotic VF. Better understanding of negative filament tension could explain situations where VF can be induced despite flat APD restitution.

Stretch-Mediated Ventricular Arrhythmias

One of the most important mechanisms of mechanoelectric coupling in the heart is the existence of sarcolemmal channels that are activated by mechanical stimuli. Of these, stretch-activated channels (SACs) have long been implicated as important contributors to the pro-arrhythmic substrate in the heart. However, uncovering the mechanisms by which SACs contribute to ventricular arrhythmogenesis is hampered by the lack of experimental methodologies that can record the 3D electrical and mechanical activity simultaneously and with high spatiotemporal resolution. Thus, computer simulations have emerged as a valuable tool to dissect the mechanisms by which SACs contribute to the ventricular arrhythmogenic substrate.

Early whole-heart modeling attempts to address the role of SACs in the initiation and termination of arrhythmia by a mechanical impact to the chest used pseudo-electromechanical models, in which mechanical activity was not represented but its effect on ventricular electrophysiology was, through SAC recruitment.^39,40 True electromechanical models of the ventricles have been recently developed,^41,42 aimed at investigating the effect of mechanoelectric coupling via SACs on ventricular reentrant wave stability. The study by Hu⁴² used an MRI-based electromechanical model of the human ventricles to test the hypothesis that SAC recruitment affects scroll wave stability differently depending on SAC reversal potential and conductance. The study thus provided a mechanistic insight into the change of organization of VF under abnormal stretch.

Drug-induced Pro-arrhythmia

Relating effects of drugs on ion channels beyond the action potential requires virtual tissue or whole heart organ simulation, so that arrhythmia onset, termination and prevention can be explored. Moreno et al. incorporated both state-dependent Markov modeling of drug effects and full integration to the human action potential (AP), human tissue, and finally realistic MRI image-based human heart.⁴³ This is the first instance of such massive integration across the space and time scales at play. Their study showed that the effects of flecainide and lidocaine on sodium current (I_Na) block are globally similar in response to dynamic protocols. However, clinical trials have shown previously that flecainide tended to be pro-arrhythmic at therapeutic doses, while lidocaine was not. Simulation results made clear that neither simple reduction in I_Na, nor single cell behavior could explain this paradox. However, at the macroscopic scale, the vulnerable window was greater for flecainide than for lidocaine (especially in heart failure simulations due to shortened diastole) and reentrant arrhythmia in the ventricle persisted; as discovered by examining Markov states, this was due to the relatively slow accumulation of and recovery from use-dependent block with flecainide.

A common approach to testing potential drugs for cardiotoxicity is to measure hERG channel binding affinity, which indicates whether a compound will prolong the QT interval of the ECG by blocking the rapid delayed rectifier potassium current (I_Kr). Many recent studies have sought to use computer modeling to overcome limitations of this screening methodology, such as its high rate of false positives and false negatives. Wilhelms et al.⁴⁴ use detailed multiscale models of healthy and ischemic hearts to examine the effects of two drugs that both fail the hERG screening test: cisapride, which is pro-arrhythmic, and amiodarone, which is anti-arrhythmic. Simulations revealed the amiodarone is comparatively safe because in addition to QT prolongation (which was seen for both drugs on simulated ECGs) it also flattened APD restitution. This study and others^45-47 demonstrate the feasibility of predicting specific drug dose effects on the thoracic ECG. It is hoped that this approach will lead to the development of screening systems that will accelerate cardiotoxicity testing by providing improved reliability compared to the present standard.

Ventricular Arrhythmias in Disease

Simulations have also been conducted to understand ventricular arrhythmia mechanisms for a variety of diseases. Models representing regional ischemia^48,49 have characterized the substrate for ischemia phase 1B arrhythmias by examining how the interplay between different degrees of hyperkalemia in the surviving layers, and the level of cellular uncoupling between these layers and the mid-myocardium combine with the specific geometry of the ischemic zone in the ventricles to result in reentrant arrhythmias. Jie et al.⁵⁰ used a model of the beating rabbit ventricles to gain insight into the role of electromechanical dysfunction in arrhythmogenesis during acute regional ischemia, both in the induction of ventricular premature beats and in their subsequent degeneration into ventricular arrhythmia.

Computer simulations of ventricular ischemia and infarction and the corresponding body surface potentials have also been used to determine how the extent of the ischemic zone is reflected in the 12-lead ECG. Specifically, modeling research has provided insight on how ECG signals are influenced by the size and shape of acute⁵¹ and healed⁵² myocardial infarction. Simulations have also been employed to distinguish between diseases that have similar ECG properties but different underlying cause, which can confound diagnosis and treatment. Potse et al.⁵³ used ventricular models to show that left bundle branch block and diffuse electrical uncoupling, both of which prolong the QRS complex, can be differentiated by examining ECG amplitude.

Uncovering arrhythmia mechanisms in genetically inherited diseases has also benefitted significantly from models of ventricular function^54-57. Adeniran et al.⁵⁴ developed a Markov model of a mutant I_Krchannel known to cause short QT syndrome. Whole heart simulations revealed that increased arrhythmia susceptibility was due to a both APD abbreviation caused by the mutation and intrinsic transmural heterogeneity of I_Krchannel expression; when combined, these two factors gave rise to arrhythmogenic APD dispersion. Deo et al.⁵⁵ characterized an inward rectifier potassium channel (I_K1) mutation from an individual with a different type of short QT syndrome. In addition to reproducing the electrocardiographic phenotype, ventricular simulations with the mutant channel showed that slight (20%) I_Na reduction dramatically increased arrhythmia inducibility, suggesting that the use of class I anti-arrhythmic drugs must be closely monitored in the patient. Finally, Hoogendijk et al.⁵⁶ showed that I_Nareduction, which is associated with Brugada syndrome, leads to conduction block due to source-sink mismatch at microscopic tissue heterogeneities; simulations revealed that the severity of this effect is modulated by other Brugada-linked mutations, such as increased transient outward potassium current and decreased L-type calcium current.

Effects of Fibroblast Activation on Ventricular Arrhythmias

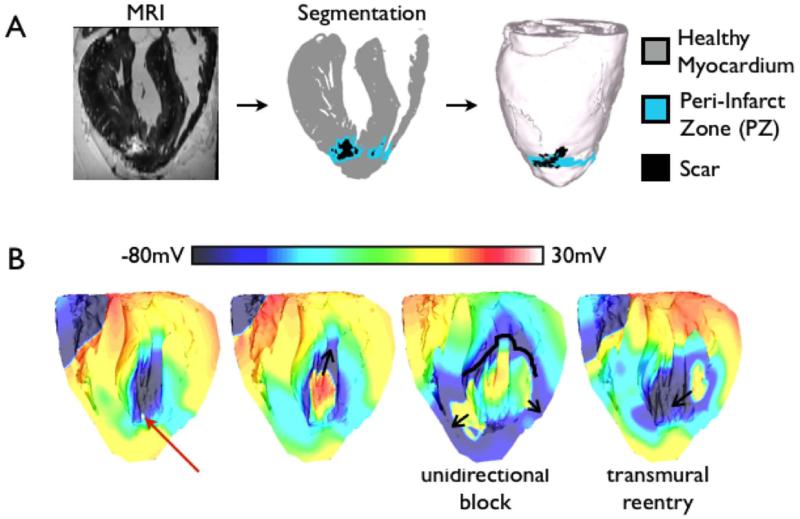
Simulation studies of ventricular arrhythmogenesis have recently begun to incorporate the role of cells other than myocytes in creating the arrhythmogenic substrate; the majority of nonmyocytes in the heart are fibroblasts.⁵⁸ Pathological conditions could trigger fibrotic remodeling of myocardium, resulting in a substrate susceptible to arrhythmias. Specifically, differentiating fibroblasts, called myofibroblasts, have been reported to couple to myocytes, affecting their electrophysiology, as demonstrated by simulation results from lower-scale (0-, 1-, and 2-dimensional) models.^59-63 McDowell et al.⁶⁴ developed the first ventricular model that incorporated both myocytes and fibroblasts; the authors employed a novel MRI-based computational model of the chronically infarcted rabbit ventricles (Fig. 3A) to characterize the arrhythmogenic substrate resulting from myofibroblast infiltration. It was found that myofibroblasts at low densities do not alter arrhythmia propensity, while at intermediate densities, myofibroblasts cause APD shortening and exacerbate arrhythmia propensity (Fig. 3B). Interestingly, at high densities, myofibroblasts were found to protect against arrhythmia by causing resting depolarization and blocking propagation.

Figure 3.

A. High-resolution MRI-based model of the infarcted rabbit ventricle with fibroblasts incorporated in the zone of infarct. B. Coupling of fibroblasts to myocytes results in arrhythmia. Red arrow indicates the location of the premature activation. Figure modified with permission from McDowell et al.⁶⁴

Risk Stratification for Ventricular Arrhythmias

Robust methods for stratifying the risk of lethal cardiac arrhythmias decrease morbidity and mortality in patients with cardiovascular disease and reduce health care costs.⁶⁵ The most widely used approaches currently used for stratifying cardiac arrhythmia risk involve testing for ECG abnormalities, then using the results to identify patients who would benefit from implantable cardioverter defibrillator (ICD) therapy. However, the mechanisms underlying these ECG indices, and their relationship to lethal arrhythmias, are not fully understood. Computational models of the heart have made inroads in this clinical cardiology arena.^66-73 Specifically, research has reported a strong correlation between increased arrhythmia risk and the presence of microvolt T-wave alternans (MTWA).^74,75 However, the mechanistic basis of MTWA preceding lethal ventricular arrhythmias has been under debate since MTWA is most successful in stratifying risk in patients at heart rates < 110 bpm, where APD restitution is flat.⁷⁶ Computational models of the left ventricular (LV) wall in combination with clinical data revealed that abnormal intracellular calcium handling underlies alternans in action potential voltage, which result in MTWA at heart rates < 110 bpm;^66,67 abnormalities in intracellular calcium have long been linked to ventricular fibrillation.^77,78 Computational modeling studies have also shown that under the conditions of abnormal calcium dynamics, the magnitude of T-wave alternans is enhanced by structural heterogeneities in the myocardium.⁶⁸

Recently, a computational model of the human ventricles was used to demonstrate that detecting instabilities in the QT interval in the clinical ECGs could predict the onset of VT, particularly in patients with acute myocardial infarction.⁷³ The study found that increased frequency of premature activation, which was easily controlled in the model, could precede VT onset, with premature activations placing the system in a state where QT interval is unstable. Therefore, screening the QT interval of the ECG for instabilities using the novel algorithm developed by Chen and Trayanova^{73, 79} could potentially be a robust risk stratification method for patients with acute myocardial infarction. Recently, the approach was successfully applied to stratify the risk of arrhythmias in 114 patients with ICDs.⁸⁰ These studies pave the way for executing computer simulations to determine patient-specific thresholds for arrhythmia stratification ECG indices, rather than relaying on clinical guidelines based on large and diverse patient cohorts. Another approach to arrhythmia risk stratification that has recently gained traction is the use of computer models to predict the arrhythmia outcome in patients that exhibit potentially lethal mutations in genes encoding cardiac proteins associated with long QT syndrome.^69-72 These studies chart new directions for future genotype-based risk stratification and personalized gene therapy.

Cardiac Optogenetics

Cardiac optogenetics is an emerging field that involves inserting light-sensitive ion channels (opsins) in heart tissue to enable control of bioelectric behavior with illumination instead of electric current.⁸¹ This technology is poised to open a new avenue for the development of safe and effective anti-arrhythmia therapies by enabling the evocation of spatiotemporally precise responses in targeted cells or tissues. Abilez et al.⁸² conducted ventricular simulations with a Markov model of light-sensitive current incorporated at the cell scale in selected regions; a later study from the same group⁸³ showed that differences between optically and electrically stimulated cells were limited to mild changes in intracellular sodium and potassium concentrations. Boyle et al.⁸⁴ developed a comprehensive whole-heart optogenetics simulation platform that incorporates realistic representations of opsin delivery as well as the response to illumination at the molecular, cell, tissue, and organ scales. This framework was then used to explore how opsin delivery characteristics determine energy requirements for optical stimulation and to identify cardiac structures that are potential pacemaking targets with low optical excitation threshold. Optical stimulation was found to be more efficient when cell-specific optogenetic targeting was used to express opsins in the PS compared to ventricular cells. This suggests that similar strategies could be used to develop low-energy approaches for managing ventricular arrhythmia.

Translating Arrhythmia Simulations to the Clinic

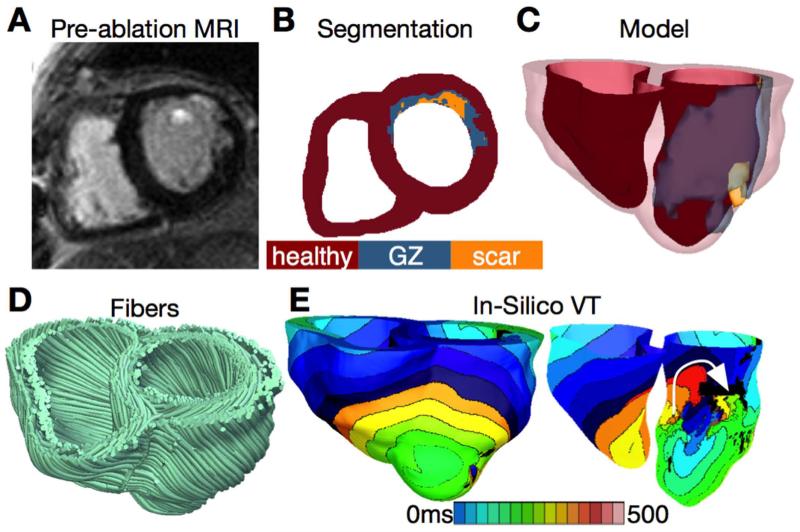
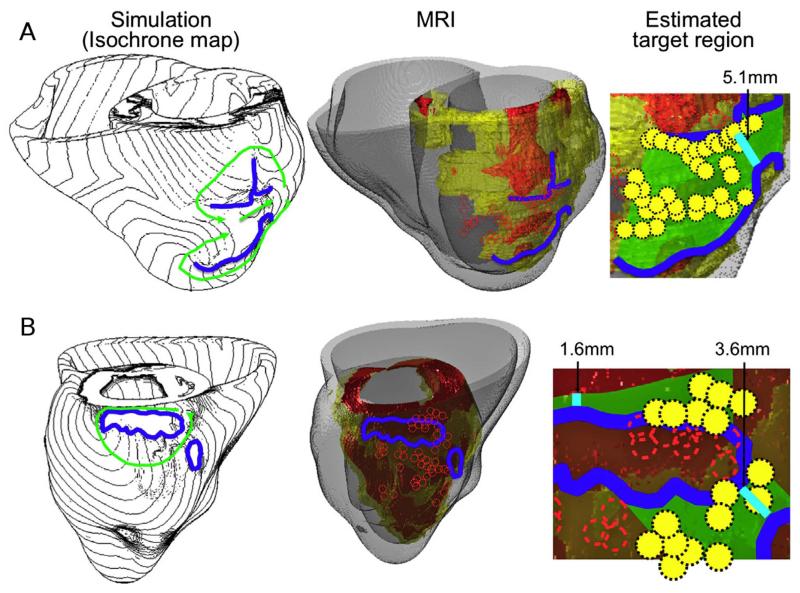
Recent years have witnessed revolutionary advances in imaging, including ex vivo structural and diffusion tensor (DT) magnetic resonance imaging (MRI) that facilitate acquisition of the intact structure of explanted hearts with high resolution. Leveraging these advances, a new generation of whole-heart image-based models with unprecedented detail has emerged.^85,86 Such models are currently being used, in combination with experimental electrophysiological data, to provide better understanding of the role of the individual infarct region morphology in the generation and maintenance of infarct-related VT, the most frequent clinical ventricular arrhythmia, present in 64% of patients with ventricular rhythm disorder and in 89% of patients with sudden cardiac death.⁸⁷ Using a model of the infarcted pig ventricles reconstructed from ex-vivo MRI and DTMRI data, Pop et al.⁸⁸ demonstrated good correspondence between in-silico and experimental electroanatomical voltage maps, and successfully predicted infarct-related VT inducibility after programmed electrical stimulation. Arevalo et al.⁸⁹ examined the role infarct border zone extent in arrhythmogenesis, establishing that a minimum volume of remodeled tissue is needed for VT maintenance and demonstrating that the organizing center of infarct-related VT is located within the border zone, regardless of the pacing site from which VT is induced. Such simulation methodology could have a major clinical impact in predicting the optimal targets for catheter ablation of infarct-related VT in individual hearts, should the methodology be able to reconstruct patent hearts from clinical imaging data and evaluate the 3D patterns of infarct-related VT in the patient. The first attempts in this direction have already been made. Fig. 4 presents a simulation of arrhythmia in a patient-specific model of the infarcted ventricles; it shows model generation from clinical MR scans of the patient heart as well as simulated infarct-related ventricular tachycardia.⁴ Fig. 5, from the recent study by Ashikaga et al.,⁹⁰ demonstrates that non-invasive simulation prediction of optimal targets for ablation of infarct-related VT could result in lesions that are much smaller than those executed in the clinic.

Figure 4.

A&B. Clinical MRI scan of an infarcted patient heart and the corresponding segmentation. C. 3D geometric model of the patient heart with the epicardium and the infarct border zone rendered semi-transparent. D. Estimated fiber orientations. E. Simulated activation map of ventricular tachycardia (VT) revealing reentry on the left ventricular endocardium. VT frequency is 3.05Hz. Figure modified with permission from Winslow et al.⁴

Figure 5. A&B. Comparison between simulation-guided and standard electrophysiological approaches for identifying ablation targets in two patients with infarct-related VTs. Left column: propagation pathways (green) and lines of conduction block (blue) are overlaid over VT activation maps simulated in image-based patient heart models. Middle column: pre-ablation infarct geometry (infarct scar: orange, border zone: yellow, non-infarcted: gray) along with ablation lesions delivered by the standard approach (red circles) and conduction block lines as calculated from ventricular simulations. Right column: optimal ablation zones (green shading) predicted by simulations, with narrowest isthmuses indicated (cyan); in both cases, only a fraction of the ablation sites from the standard approach were within the predicted optimal ablation zone (yellow circles). Figure modified with permission from Ashikaga et al.⁹⁰

Several additional studies are noteworthy. Zhu et al.⁹¹ showed that models of the heart can be used to carry out non-invasive localization of accessory pathways in patients with Wolff-Parkinson-White syndrome. Ng et al.⁹² demonstrated the feasibility of using simulations to predict VT circuits. Relan et al.⁹³ used a hybrid X-ray and MR environment to image a patient heart, which was further personalized with voltage measurements. The results demonstrated that the heart model could successfully be used to assess infarct-related VT inducibility from sites not accessible in the clinic. Further translation of ventricular simulations in the clinic will be facilitated by the development of methodologies to estimate patient-specific fiber orientations from clinical MRI scans.^94,95

Modeling Termination (Cardioversion and Defibrillation) of Ventricular Arrhythmias

Understanding Defibrillation Mechanisms

Controlling the complex spatio-temporal dynamics underlying life-threatening cardiac arrhythmias such as fibrillation is extremely difficult because of the nonlinear interaction of excitation waves within the heterogeneous anatomical substrate. In the absence of a better strategy, strong electrical shocks have remained the only reliable treatment for cardiac fibrillation. Over the years, biophysically-detailed multi-scale models of defibrillation have made major contributions to understanding how defibrillation shocks used in clinical practice interact with cardiac tissue;^96-105 these models have been validated by comparing to the results of optimal mapping experiments.^106-108 Computer modeling of whole-heart defibrillation has been instrumental in the development of the virtual electrode polarization (VEP) theory for defibrillation. Research has found that mechanisms for shock success or failure are multifactorial, depending mainly on the postshock distribution of transmembrane potential as well as the timing and propagation speed of shock-induced wavefronts. Recent simulation studies have been instrumental in understanding mechanisms of the isoelectric window that follows defibrillation shocks with strength near the defibrillation threshold (DFT): one of the proposed explanations for the isoelectric window duration is propagation of postshock activations in intramural excitable areas (“tunnel propagation”), bounded by long-lasting postshock depolarization of the cardiac surfaces.^109,110

Ventricular simulations have also ascertained the role of cardiac microstructure in the mechanisms of defibrillation. For example, Bishop et al. applied shocks to a very high-resolution (≈25 μm voxel size) image-based rabbit ventricular model; VEPs formed at the boundaries between blood vessels and myocardium,¹¹¹ which gave rise to secondary sources that eliminated excitable gaps and led to successful defibrillation.¹¹² Simulations have also contributed to understanding of the process of defibrillation in hearts with myocardial ischemia and infarction,^113-115 uncovering the role of electrophysiological and structural remodeling in the failure or success of the shock. Finally, simulations were conducted in a rabbit ventricular electromechanics model to examine vulnerability to strong shocks and defibrillation under the conditions of LV dilation and determine the mechanisms by which mechanical deformation may lead to increased vulnerability and elevated DFT.^116-118 The results suggested that ventricular geometry and the rearrangement of fiber architecture in the deformed ventricles is responsible for the reduced defibrillation efficacy in the dilated ventricles.

Developing New Modalities for Arrhythmia Cardioversion and Defibrillation

Recently, defibrillation modeling has focused on the development of new methodologies for low-voltage termination of lethal arrhythmias or for applying defibrillation in novel, less damaging ways. The study by Tandri et al.¹¹⁹ used sustained kilohertz-range alternating current (AC) fields for arrhythmia termination. Termination of arrhythmia with AC fields has been attempted previously in simulations^120-122 with limited success; the frequencies used in these studies were, however, substantially lower. The premise of the Tandri et al. study was that such fields have been known to instantaneously and reversibly block electrical conduction in nerve tissue. Aided by ventricular modeling, the article provided proof of the concept that electric fields, such as those used for neural block, when applied to cardiac tissue, similarly produce reversible block of cardiac impulse propagation and lead to successful defibrillation; it also showed that this methodology could potentially be a safer means for terminating life-threatening reentrant arrhythmias. Since the same AC fields block equally well both neural and cardiac activity, the proposed defibrillation methodology could possibly be utilized to achieve high-voltage yet painless defibrillation. The follow-up study by Weinberg et al.¹²³ provided, again using ventricular simulations, a deeper analysis of the mechanisms that underlie the success and failure of this novel mode of defibrillation.

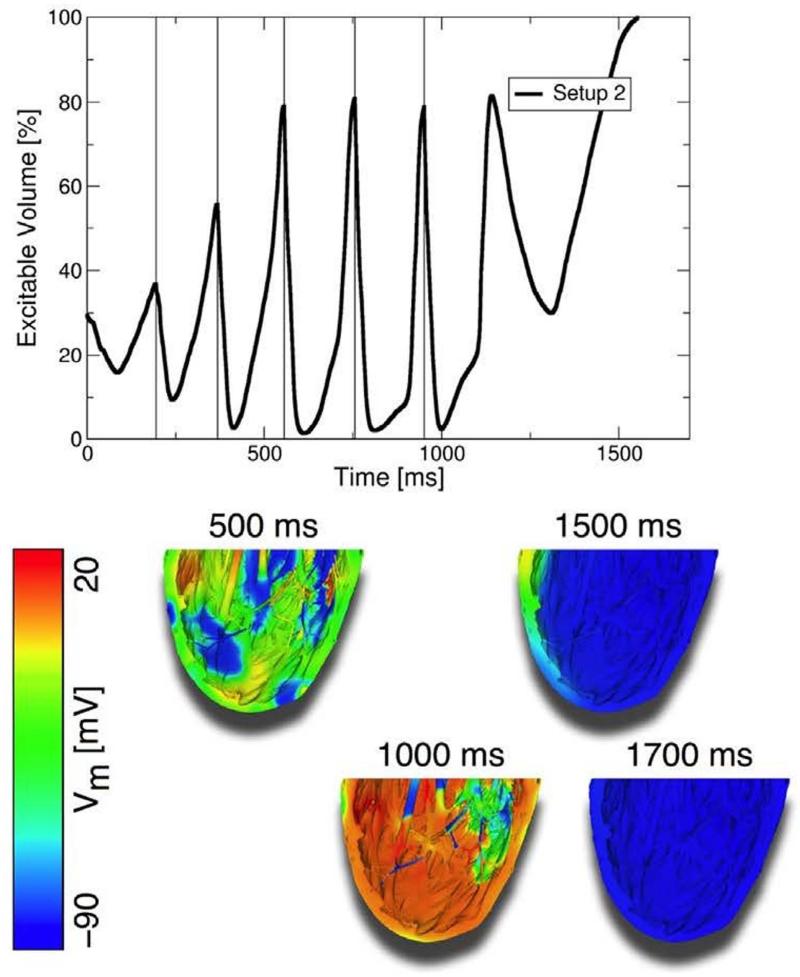
Recent experimental studies have shown that applied electric fields delivering multiple far-field stimuli at a given cycle length can terminate VT, atrial flutter, and atrial fibrillation with less total energy than a single strong shock.^124-126 However, the mechanisms and full range of applications of this new mode of defibrillation have remained poorly explored. The recent simulation study by Rantner at al.¹²⁷ aimed to elucidate these mechanisms and to develop an optimal low-voltage defibrillation protocol. Based on the simulation results using a complex high-resolution MRI-based ventricular wall model, a novel two-stage low-voltage defibrillation protocol was proposed that did not involve the delivery of the stimuli at a constant cycle length. Instead, the first stage converted VF into VT by applying low-voltage stimuli at instants of maximal excitable gap, capturing large tissue volume and synchronizing depolarization. Fig. 6 illustrates this approach; in this case the applied far-field pulse train directly terminated VF. The second stage was designed to terminate VT, in cases where it persisted, by multiple low-voltage stimuli given at constant cycle lengths. The energy required for successful defibrillation using this protocol was 57.42% of the energy for low-voltage defibrillation when stimulating at the optimal fixed-duration cycle length.

Figure 6.

Low-voltage defibrillation with a train of pulses. Low-energy shocks (250 mV/cm) delivered at the instants when the maximal amount of myocardial volume was excitable terminated VF. Figure modified with permission from Rantner et al.¹²⁷

Translating Arrhythmia Cardioversion and Defibrillation Simulations to the Clinic

Finally, a recent study¹²⁸ has made the first attempt towards clinical translation of computer models of arrhythmia termination. It addressed a clinical need: ICDs with transvenous leads often cannot be implanted in a standard manner in pediatric and congenital heart defect (CHD) patients; currently, there is no reliable approach to predict the optimal ICD placement in these patients. The study provided proof-of-concept that patient-specific, biophysically detailed computer simulations of the dynamic process of defibrillation could be used to predict optimal ICD lead location in these patients. A pipeline for constructing personalized, electrophysiological heart-torso models from clinical MRI scans was developed and applied to a pediatric CHD patient, and the optimal ICD placement was determined using patient-specific simulations of defibrillation. In a patient with tricuspid valve atresia, two configurations with epicardial leads were found to have the lowest defibrillation threshold. The study demonstrated that by using such methodology the optimal ICD placement in pediatric/CHD patients could be predicted computationally, which could reduce defibrillation energy if the pipeline is used as part of ICD implantation planning.

Outlook for the Field of Computational Cardiac Electrophysiology

As this review demonstrates, the key in attaining predictive capabilities of multi-scale biophysically-detailed cardiac models at the level of the organ has been the use of geometrically realistic (typically MRI- or CT- based) models of the ventricles, and the application of diffusion tensor MR imaging (DTMRI) to measure the anatomy, fiber, and sheet structure of the heart, in cases of ex-vivo studies. This has led to a new generation of image-based ventricular models with unprecedented structural and biophysical detail. Clearly, models of cardiac function have benefited significantly from this revolution in medical imaging.

As outlined above, cardiac models have been used to gain insights into mechanisms of arrhythmia in many disease settings and to understand how external currents can terminate ventricular arrhythmias. In addition, a major thrust in computational cardiac electrophysiology is to use models as a test bed for evaluation of new antiarrhythmic drugs. It is now possible to test hypotheses regarding mechanisms of drug action on the scale of the whole heart. Multi-scale heart models of antiarrhythmic drug interactions with ion channels have provided insights into why certain pharmacological interventions result in pro-arrhythmia, whereas others do not. This work has the potential to more effectively guide the drug development pipeline—a process that currently has high failure rates and high costs.

The use of heart models in personalized diagnosis, treatment planning, and prevention of sudden cardiac death is also slowly becoming a reality, as reviewed here. The feasibility of subject-specific modeling has been demonstrated through the use of heart models reconstructed from clinical MRI scans. Computer simulations of the function of the diseased heart represent a profound example of a research avenue in the new discipline of computational medicine. Biophysically detailed models of the heart assembled with data from clinical imaging modalities that incorporate electrophysiological and structural remodeling in cardiac disease are poised to become a first line of screening for new therapies and approaches, new diagnostic developments, and new methods for disease prevention. Implementing patient-specific cardiac simulations at the patient bedside could become one of the most thrilling examples of computational science and engineering approaches in translational medicine.