Kinetics of Fast Changing Intramolecular Distance Distributions Obtained by Combined Analysis of FRET Efficiency Kinetics and Time-Resolved FRET Equilibrium Measurements

Abstract

Detailed studies of the mechanisms of macromolecular conformational transitions such as protein folding are enhanced by analysis of changes of distributions for intramolecular distances during the transitions. Time-resolved Förster resonance energy transfer (FRET) measurements yield such data, but the more readily available kinetics of mean FRET efficiency changes cannot be analyzed in terms of changes in distances because of the sixth-power dependence on the mean distance. To enhance the information obtained from mean FRET efficiency kinetics, we combined the analyses of FRET efficiency kinetics and equilibrium trFRET experiments. The joint analysis enabled determination of transient distance distributions along the folding reaction both in cases where a two-state transition is valid and in some cases consisting of a three-state scenario. The procedure and its limits were tested by simulations. Experimental data obtained from stopped-flow measurements of the refolding of Escherichia coli adenylate kinase were analyzed. The distance distributions between three double-labeled mutants, in the collapsed transient state, were determined and compared to those obtained experimentally using the double-kinetics technique. The proposed method effectively provides information on distance distributions of kinetically accessed intermediates of fast conformational transitions induced by common relaxation methods.

Introduction

Inter- and intramolecular distance determination by means of Förster resonance energy transfer (FRET) measurements is an ideal source of information on fast conformational transitions in biopolymers such as protein folding (1–6) or protein ligand interactions (1,7–14). The common mode of measurement of macromolecular conformational transitions, by determination of the time dependence of the mean transfer efficiency between the probes can yield the mean distance between the probes only in ensembles where all molecules share similar distances. However, in ensembles of multiple conformers, where an intramolecular distance should be characterized by a distribution of distances, the mean transfer efficiency has no relationship to any type of mean distance. This limitation is due to the sixth-power dependence of the transfer efficiency on the interprobe distance (13,15–17). The actual mean distances between the probes can be obtained by time-resolved FRET (trFRET) experiments where distance distributions and their fast fluctuations can readily be determined (15,18). The double-kinetics methods (14,19–23) enable fast acquisition of the trFRET data at different time points along a kinetic track. Using this method, the transient ensemble of conformers can be characterized in terms of their transient distributions of intramolecular distances (12,24). The transitions between them produce a superposition of the distributions of that intramolecular distance (16,25), weighted by the fraction of each subpopulation of conformers (initial and final in the case of a two-state transition) at each time point, which is dictated by the transition rate constants.

These experiments are not always possible, mainly due to limitations of sample quantities, as well as expensive instrumentation. However, in many cases the intramolecular distance distribution of a fast changing ensemble of conformers at the initial phases of the transition and throughout the duration of the transition can be obtained even though only mean transfer efficiency is measured. This can be achieved by joint analysis of time-dependent mean transfer efficiency values obtained during the time course of an induced conformational change (e.g., a protein folding transition) and trFRET data obtained at the end states of the transition (e.g., the unfolded and fully folded protein ensembles).

In many relaxation experiments, in which a conformational transition is induced by fast change of conditions, an initial state is formed immediately after relaxation of the perturbation. The characteristics of the ensemble of macromolecules thus formed are of much interest because they represent the actual initial ensemble from which the conformational relaxation starts. This ensemble, in most cases, is different from the pretransition equilibrium ensemble, which is under chemical or physical perturbation (2,6,8,14,24,26,27). Typical examples are found in protein refolding kinetic experiments, where folding is induced by fast removal of the perturbation that induces unfolding (e.g., change of solvent from high concentrations of denaturants to a physiological solution), which initiates a very fast initial adaptation to the perturbation-free conditions (folding conditions), followed by a slower transition to the ensemble of folded conformers (5,6,22).

Practically, in most experiments, the initial phase is too fast to be detected by stopped-flow experiments (28) and data acquisition follows the slower transition between the initial and folded states. Thus the question of the characteristics of ensembles of unfolded protein molecules under folding conditions, i.e., at the starting point of the folding transition, as well as the transition progresses, is of great interest but difficult to measure. That was our motivation for developing a method to determine the distance distribution between two FRET probes located at sites of interest in a protein molecule immediately after the removal of the unfolding perturbation (∼1 ms). The method is based on combined analysis of mean FRET efficiency kinetic traces together with trFRET data obtained at the end of the refolding transition once equilibrium is reached under folding conditions.

This analysis yields the intramolecular distance distribution at the initiation and also in the two-state case during the refolding transition. In the case of a two-state transition, this believed-new method yields the relative fractions of the initial and final conformers at each stage of the transition, avoiding the need for a double-kinetics experiment. The method was tested by simulation and applied experimentally in a study of the mechanism of refolding of Escherichia coli adenylate kinase (AK). Three structural elements in the CORE domain of the AK molecule (PDB:4AKE (29)) were examined: a β-strand element (residues 79–86), a loop-forming element (residues 28–71) (22,24), and two residues (residues 18 and 203) (22,24) which are in close proximity in the folded state. The initial state distance distributions, obtained from model fitting, were compared to those obtained experimentally using the double-kinetics FRET technique.

Materials and Methods

Protein preparation and labeling

Escherichia coli AK mutants were constructed by site-directed mutagenesis, overexpressed, and purified as described in the literature (22,24,30). All variants were derived from the Cys-free C77S pseudo-AK form. In each labeled AK mutant, the donor, Trp, was genetically inserted at a predefined position. In addition, a single Cys was genetically inserted at the desired acceptor positions. The Donor Only (DO) variant was prepared by Cys blockage by reaction with iodoacetamide (Sigma, St. Louis, MO). The Donor in the presence of Acceptor (DA) variants were labeled by reaction with 7-iodoacetamidocoumarin-4-carboxylic acid (Cou) or 5-aminosalicylic acid (Sal). Labeling and purification procedures were described previously in Sinev et al. (31) and Jacob et al. (32).

Spectroscopic measurements

Steady-state fluorescence kinetic measurements were performed by a stopped-flow SFM 400 (Bio-Logic, Claix, France) as reported previously in Ben Ishay et al. (22). The bandpass filter (Cat. No. 357/44; Semrock, Rochester, NY), which was used for selection of the tryptophan emission, efficiently blocks the acceptor emissions. Refolding experiments were performed by a two-step dilution (double jump) to minimize the effect of proline isomerization on the rate of refolding (24). Measurements were carried out using the μFC-08 cell (Bio-Logic), with a 1-ms dead-time.

The system used for the fluorescence kinetic measurements in time-resolved mode, double-kinetics, was described recently in Ben Ishay et al. (23), and the measurement protocols were reported previously in Ben Ishay et al. (22).

Equilibrium time-resolved fluorescence measurements were performed as described previously in Ben Ishay et al. (22) and Orevi et al. (24). Equilibrium intramolecular distance distributions (IDDs) were calculated from the best-fit results of the Haas-Steinberg model (33,34) to the DO and DA donor fluorescence decays. Possible errors due to photochemistry of the probes were absent due to the short time intervals of data collection. No changes of emission intensity were detected after test irradiation at the excitation wavelengths with duration 10 times longer than the average data collection times.

Model implementation

Two independent data sets were used. The first was the trace of kinetics of change for transfer efficiencies obtained by the stopped-flow experiment where the emission intensity of the donor was monitored in the absence and presence of an acceptor. The second data set was the parameters of the distribution for the intramolecular distance between the donor and the acceptor in the folded state at the end of the refolding transition. A rate constant for the kinetics of change of the transfer efficiency was obtained by fitting a theoretical trace of the kinetics of the change for the transfer efficiency to the experimental one obtained in the refolding experiment. The free parameters in this fitting procedure were the parameters of the distribution of the labeled intramolecular distance in the collapsed subpopulation and the ratio of the population ratios. The constraints used in this analysis were the two (at times three) subpopulations that were included in the model (where one is known and the other unknown), and the known parameters of the distance distribution of the final (folded) subpopulation.

The fitting procedure searched for a combination of the free parameters that would yield a time-dependent theoretical transfer efficiency trace, based on integration of the contribution of the two subpopulations best fitted to the experimental trace. The analysis was implemented in the software MATLAB Ver. R2008b (The MathWorks, Natick, MA). All model fittings performed, whether on simulated or experimental data, were achieved by use of the lsqcurvefit function for nonlinear least-squares curve fitting using the Levenberg-Marquardt algorithm. The final distance distribution parameters were calculated by analysis of trFRET experiments performed under equilibrium, at the end of the refolding transition. The analysis is based on fitting the donor fluorescence decays in the absence and presence of acceptor to corresponding decay curves created using the Haas-Steinberg model implemented in FORTRAN (33,35). The nonexponential nature of the donor fluorescence decay and its possible effect on the Förster constant were taken into account as described earlier in Orevi et al. (35) and Haran et al. (36). According to the best-fit χ-square values, a 95% confidence interval was calculated and used to determine model parameter error ranges in a rigorous error analysis process, in which the model’s parameter range was fixed at different values around the best-fit result.

Results

Theory

Two-state process

Consider a first-order, two-state nonequilibrium kinetic process, e.g., folding of a protein from the initial state which we shall call the “collapsed state” (C) (unfolded under folding conditions), to its native folded state (F), C→F, with a rate constant, k_f, while neglecting the minor effect of the slow reverse reaction under the given conditions. Assuming that at time zero, only state C is occupied, the rate equation for the change of the fraction of the folded state occupancy, f(t), is given as

$$f\left(t\right)=1-e^{-k_{F}t}.$$ (1)

The ensemble of each state, C and F, can be characterized by an IDD, P_C(r,t) and P_F(r,t), respectively. For a solution that contains both ensembles, F and C, one can calculate the overall transient IDD, P(r,t), as a superposition of the two ensembles weighted by the fraction of the two subpopulations, as

$$P\left(r,t\right)=f\left(t\right)P_F\left(r\right)+\left[1-f\left(t\right)\right]P_C\left(r\right).$$ (2)

The time dependence of the mean energy transfer efficiency (ETE) obtained for that solution during the transition is given by the Förster relation, weighted by the relative contribution of the transient two component IDDs of Eq. 2 (18), as

$$\langle E\rangle \left(t\right)=\underset{r_{\min }}{\overset{r_{\max }}{\int }}\frac{P\left(r,t\right)}{1+{\left[r/R_0\left(t\right)\right]}^6}dr,$$ (3)

where R₀(t) is the Förster critical distance at different time points along the kinetics, and r_min and r_max are distance boundaries. The IDDs can be modeled as three-dimensional radial distributions,

$$p_i\left(r\right)=Norm\cdot r^2{e}^{-b_i{\left(r-a_i\right)}^2},$$

having i ∈ {C, F}, where b_i and a_i are parameters related to the mean distance and to the reciprocal of the width of the distribution of ensemble i, respectively, and Norm is a normalization parameter.

Assuming that R₀(t) stays constant during the time course of the transition, substitution of Eqs. 1 and 2 into Eq. 3 yields the time dependence of the mean ETE during the transition, as

$$\langle E\rangle \left(t\right)=\left(1-e^{-k_{F}t}\right)\underset{r_{\min }}{\overset{r_{\max }}{\int }}\frac{\left[P_F\left(r\right)-P_C\left(r\right)\right]dr}{1+{\left(r/R_0\right)}^6}+\underset{r_{\min }}{\overset{r_{\max }}{\int }}\frac{P_C\left(r\right)dr}{1+{\left(r/R_0\right)}^6},$$ (4)

which is now reduced to a monoexponential function of time.

The refolding rate constant, k_F, can be obtained by a curve-fitting procedure using the experimental ETE, 〈E〉(t). The quality of fit is judged by statistical tests (9,37). To determine the unknown distribution of the distance in the collapsed state, P_C(r), one can use Eq. 4 and the following independent data:

• 1.The value k_F obtained by fitting the 〈E〉(t) trace; and
• 2.The distance distribution obtained for the ensemble of folded molecules by trFRET, P_F(r).

Then, a fitting procedure can be applied for determination of the collapsed state distribution by fitting the kinetics of the mean transfer efficiency and using the folded state distribution P_F(r) as constants in the model.

There are two additional phenomena that might affect the FRET parameters and should be considered when analyzing FRET experiments: 1), possible time dependence of R₀ due to changes of spectral properties of the probes (e.g., due to changes of local environments in the conformers) (15); and 2), enhancement of the transfer efficiency by fast conformational fluctuations (15,38). Moreover, significant deviation of the transfer efficiency kinetics, 〈E〉(t), from an exponential shape might indicate a possible underlying three-state transition (9). Simulations of FRET kinetics including these possible effects were performed to test the applicability and validity of the proposed model.

Assessment of the applicability of the method and its limits

Simulation of two-state transitions

Simulation of a transition from a collapsed to a folded ensemble of conformers represented by the corresponding intramolecular distance distributions was performed. The kinetics of the change of the mean transfer efficiency was calculated using the parameters of the simulated distributions and the predetermined value of k_F. The simulated P_C(r) was recovered assuming the two-state model using the values of P_F(r) and k_F by means of Eq. 4. The simulation setup is explained in the Supporting Material and the results are reported in Spreadsheet S1 in the Supporting Material.

The analyses of the simulated experiments show the limits of applicability of the combined approach for obtaining significant values of the distribution, P_C(r):

• 1.The greater the distance difference between the means of the two distance distributions (P_C(r) and P_F(r)), the narrower the fitting error ranges.
• 2.The method is effective when the change of the transfer efficiency is within the range of 0.1 and 0.9.
• 3.The range of overall change in the transfer efficiency during the full transition should be at least five times higher than the standard deviation of the experimental noise on the FRET scale.
• 4.The mean of the distance distributions of both the collapsed and folded ensembles should be in the range determined by the Förster critical distance (0.5 R₀ < r < 1.5 R₀).
• 5.The fitting error range of the calculated parameters of the distribution P_C(r) is reduced for distributions with higher full width at half-maximum (FWHM) whenever their mean distance is larger than that of the known distribution P_F(r). The fitting error range for the calculated parameters is smaller for the case of distribution with smaller FWHM, when the mean of P_C(r) is smaller than that of P_F(r).
• 6.Selection of pairs of probes with known R₀ values whose range covers the mean of both P_F(r) and P_C(r), (0.5 R₀ < r_mean< 1.5 R₀), can be difficult when the mean of the range of possible values of the mean P_C(r) is unknown. In that case, the classic experimental FRET strategy of repeating experiments with more than one pair of probes can be very helpful.

Effect of various deviations from two-state transition on analysis using Eq. 4

We tested the effect of various variables on the quality of fit of the time-dependent mean transfer efficiency trace 〈E〉(t) to a monoexponential function of the type

$$\langle E\rangle \left(t\right)=n{e}^{-kt}+m.$$ (5)

We tested the limits of fitting a monoexponential function to 〈E〉(t) traces produced by simulation of experiments where deviations from a two-state transition are possible, and studied the performance of fitting to the resulting simulated traces (see the Supporting Material and Spreadsheet S1 in the Supporting Material).

For the dataset chosen for simulations, the conclusions of these simulations are as follows.

• 1.In the case of a simulated three-state transition, modeled by Eqs. S1–S4 in the Supporting Material, the 〈E〉(t) trace can be fitted to a monoexponential function (pseudo two-state case) under two different scenarios, here given.
• (i)The rate of formation of the intermediate conformers and of their transition to the folded conformers is similar (standard error of k_i < 10%), and its mean distance is between those of the initial and folded ensembles, and
• (ii)The intramolecular distance distribution of the intermediate ensemble is similar to the distributions of the collapsed or the folded states. A three-state transition in which the characteristics of the distribution of the measured intramolecular distances differ from the above scenarios would yield an acceptable fit of the 〈E〉(t) trace to the monoexponential model, and Eq. 4 would not be applicable.
• 2.In the case of a two-state transition with distribution of rate constants where the variation is within one order of magnitude, an acceptable fit to a monoexponential 〈E〉(t) curve would be obtained.
• 3.Unimodal (one-state) (39–41) FRET kinetics cannot be fitted to a monoexponential model (see Fig. S1 in the Supporting Material).
• 4.The effect of dependence of the R₀ values on the change of conformations during a two-state transition is small and does not preclude application of Eq. 4.
• 5.The effect of high intramolecular flexibility (interprobe diffusion coefficient of up to 20 Å²/ns) (15) in the collapsed state conformers is within the uncertainty range of the analysis based on Eqs. 3 and 4.

Experimental evaluation of the method—collapsed state conformations of AK

The method was applied in a study focused on the refolding of three different double-labeled segments in AK (each having a single donor and a single acceptor at the specified positions). The labeled AK mutants had a Trp as donor at residues 86, 71, or 203 and either a coumarin (Cou) derivative or a salicylic acid derivative (Sal) as acceptors of FRET at residues 79, 28, or 18, respectively, as described in the Materials and Methods (22,24). The labeled AK mutants were denatured by fast mixing into a final Guanidinium Hydrochloride (GndHCl) concentration of 1.8 M; after 3 s, the denaturant was diluted to a final concentration of 0.3 M GndHCl, in a stopped-flow experiment, as described by Orevi et al. (24).

The measured segments of AK represent the following structures in the AK folded state (PDB:4AKE (29)): residues 79 and 86 are at the two ends of a β-strand element; 28 and 71 are at the node of a fast closing loop (24); and 18 and 203 are two spatially proximate residues in the CORE domain (Fig. 1). The R₀ values at 0.3 M GndHCl of the pair 79–86 with Trp as a donor and Sal or Cou as acceptor were 18.1 and 23.9 Å, respectively, and the values of the pairs 28–71 and 18–203 labeled with Trp and Sal were 17.2 and 15.9 Å, respectively. The folded state intramolecular distance distributions, P_F(r), between the ends of the labeled segments were obtained by trFRET measurements performed at equilibrium under final solution conditions used in the stopped-flow experiment (0.3 M GndHCl) (12,16,17,24) (Fig. 2 D, black trace, and Table 1). The distributions were also determined for the labeled mutants in 1.8 M GndHCl (unfolded state) (Fig. 2 D, magenta trace, and Table 1). These results are based on the best fit to the donor fluorescence decays at equilibrium (Fig. 3) (15,33).

Figure 1.

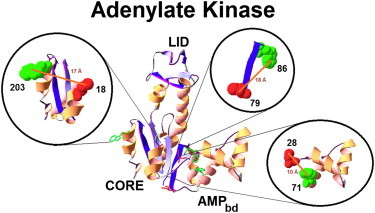
The crystal structure of E. coli adenylate kinase and three pairs of sites that were labeled to test the experimental method. (Circles each represent one double-labeled mutant, in which the donor Trp residue is represented by a green space-filling structure and the Cys residue, the site for attachment of the acceptor, is represented by a red space-filling structure.) Expected mean distance between the labeled sites in the folded state (as represented by orange lines connecting to site centers). To see this figure in color, go online.

Figure 2.

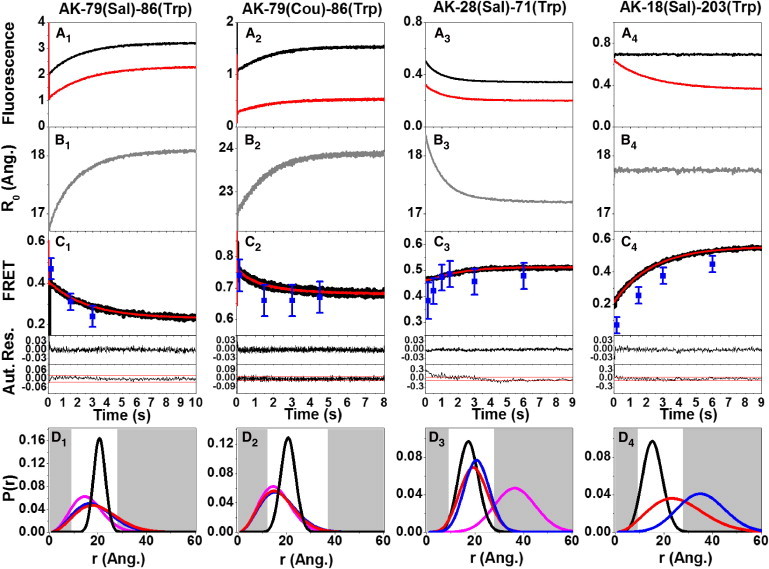
Emission intensity detected FRET efficiency kinetics during the refolding of E. coli AK mutants initiated by rapid mixing in stopped-flow experiment and the corresponding intramolecular distance distributions determined by the combined analysis. The kinetics of the change of the emission intensity of the donor in the absence (black) and presence (red) of an acceptor is presented in the top row (A). The resulting time dependence of the Förster critical distance (R₀; see the Supporting Material) is shown in the second row (B); experimental traces of the kinetics of change of FRET efficiencies were obtained based on the data presented in panels A and B, and are shown in the third row (C, in black; also see the Supporting Material). The residuals of the fitting (Res.) of the kinetic trace (C) with that obtained by the combined analysis of Eqs. 3 and 4 and the autocorrelation of the residuals of fitting (Aut.) are shown in the bottom panels of row C (red lines are lower and upper bounds of 95% statistical significance of the autocorrelation of the residuals). Mean transfer efficiency obtained from the double-kinetics trFRET experiments at selected time points during the refolding kinetics (shown by the blue squares in panel C). The corresponding calculated intramolecular distance distributions are shown in the last row (D) for the following states: the initial (collapsed) state obtained by the combined analysis of data shown in panel C (red); by the experimental double-kinetics experiment (blue); the folded state (black); and the denatured state, analyzed by equilibrium trFRET experiment (magenta). To see this figure in color, go online.

Table 1.

Comparison of parameters of distributions for three intramolecular distances in the Escherichia coli AK molecule

AK mutanta	PF(r)b		PC(r) double-kineticsc		PC(r) intensityd		kF (s−1)g
	Peak (Å)e	FWHM (Å)f	Peak (Å)	FWHM (Å)	Peak (Å)	FWHM (Å)
79(Sal)-86(Trp)	20.7 (20.0–20.9)	6 (4–8)	16.6 (16.1–20.5)	19 (5–20)	17.8 (17.7–18.7)	20 (12–21)	0.40 (0.31–0.47)
79(Cou)-86(Trp)	20.7 (20.0–20.9)	6 (4–8)	15.2 (15.2–21.7)	18 (6–18)	14.7 (14.4–16.4)	17 (13–18)	0.56 (0.50–0.62)
28(Sal)-71(Trp)	17.2 (16.4–17.7)	10 (8–12)	20.6 (17.7–21.8)	12(9–17)	19.2 (17.6–20.1)	13 (5–21)	0.63 (0.60–0.66)
18(Sal)-203(Trp)	15.2 (14.2–15.9)	9 (8–11)	34.9 (32.2–38.1)	23 (16–31)	23.3 (20.2–26.1)	27 (9–30)	0.43 (0.42–0.45)

The comparisons were performed at the initial phase of refolding determined by analysis of the emission intensity detected kinetics, and by double-kinetics methods. AK, adenylate kinase; FWHM, full width at half-maximum.

^aThe two labeled residues and the probes used as FRET donor and acceptor.

^bThe final (folded) state intramolecular distribution obtained by trFRET measurements at 0.3 M GndHCl.

^cThe initial (collapsed) state intramolecular distance distribution obtained by double-kinetics FRET measurements at the first few milliseconds of folding.

^dThe initial (collapsed) state distribution obtained as extrapolation to zero-time from best-fit results of the combined analysis.

^eMost probable distance out of a skewed Gaussian radial distance distribution model.

^fThe FWHM of a skewed Gaussian radial distance distribution model.

^gThe first-order apparent refolding rate constant.

Figure 3.

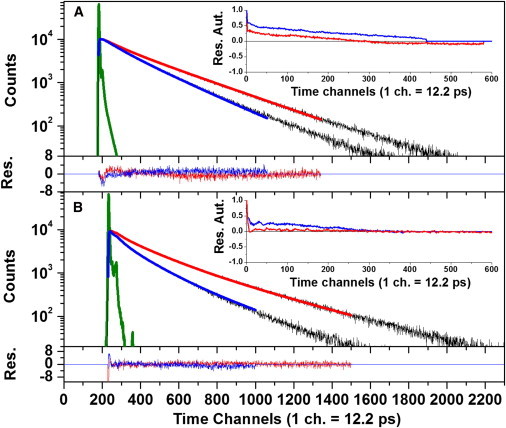
trFRET data obtained under equilibrium conditions for the mutant AK-79(Sal)-86(Trp) in 0.3 (A), and 1.8 M (B) GndHCl and the best-fit results of global analysis employing the Haas-Steinberg model (33). The experimental donor fluorescence decay (black) in the absence (DO) and presence (DA) of an acceptor and the best-fit results (down to 1% amplitude relative to the maximum count) in the absence of acceptor (red), as well as in the presence of the acceptor (Sal) (blue); the instrument response function is also shown (green). Corresponding fitting residuals (Res.) are given (bottom of each panel) as well as their autocorrelation (Aut.; see inset). To see this figure in color, go online.

We then performed fluorescence emission intensity-detected stopped-flow measurements of the mutant labeled by the donor without an acceptor (the DO mutant) (Fig. 2 A, black), and of the mutant labeled by both the donor and the acceptor (the DA mutant) (Fig. 2, A, red trace). For experiments in which the intensity of the donor significantly changed over the course of DO mutant refolding, a Förster critical distance time vector, R₀(t) (Fig. 2 B), was prepared using Eq. S5 in the Supporting Material. The experimental 〈E〉(t) traces were calculated using Eqs. S6 and S7 in the Supporting Material, and fitted to the theoretical trace using Eq. 3. The values of 〈E〉(∞) (i.e., at the end of the transition) were obtained from the equilibrium trFRET data of the folded state ensemble (Fig. 2 C).

Experimental intramolecular distance distributions of each labeled segment were obtained by means of the trFRET detected double-kinetics experiments within the first few milliseconds after the mixing dead-time (Fig. 2, D, blue, and Table 1). The parameters of the distance distribution of the collapsed state ensemble (P_C(r)) were obtained both experimentally by the double-kinetics experiment, and by analysis of the 〈E〉(t) data using Eqs. 3 and 4 (Fig. 2 D, red, and Table 1). Excluding AK-18(Sal)-203(Trp), the collapsed state distance distributions, P_C(r), extracted from the double-kinetics measurements were well within the Förster critical distance range of the pairs of probes, and the FRET efficiencies from both double-kinetics and steady-state detected fluorescence kinetics were similar throughout the course of the transition, within an error of <2% (Fig. 2 C, blue squares).

The fit quality of the calculated 〈E〉(t) using Eqs. 4 and 5 to the experimental values was excellent, as can be judged by the fitting residuals and their autocorrelation. The collapsed-state intramolecular distance distributions, P_C(r), calculated from the experimental 〈E〉(t) traces and the final state distance distribution, P_F(r), were very similar to the ones obtained experimentally from the double-kinetics experiments (excluding the case of AK-18(Sal)-203(Trp)). The mean and FWHM error ranges of the best-fit results were similar to those of the experimental intramolecular distance distributions (Table 1).

In summary, the method presented here may be used to determine distributions of intramolecular distances in ensembles of molecules undergoing fast changes at the initiation of the transition; this approach is based solely on the folded state equilibrium intramolecular distance distributions, and emission intensity-based determination of the kinetics of the mean transfer efficiency data.

Discussion

The kinetics of the response of macromolecules to changing conditions, such as induction or removal of physico-chemical perturbations (e.g., change of solvent) (2,5,6,24,42), ligand binding (4,8,9,13,14,26,27,43), or formation of macromolecular complexes (1,3,7,10–12), contains a wealth of information regarding key biochemical and biophysical processes. The popularity of applications based on the FRET effect in the detection of the kinetics for the macromolecular conformational transitions is based on the simple relationship between the transfer efficiency and the intra- or intermolecular distances (6,9,20,25,27). Deduction of features of the mechanism of any transition requires knowledge of the structural characteristics of the ensemble of molecules at the starting point of the transition (1,14,16).

The method presented here helps overcome a major limitation of FRET experiments based on fluorescence intensity measurements, namely, the nonlinear relationship between the distance and the mean transfer efficiency (15,18). The sixth-power dependence of the transfer efficiency prevents determination of mean interprobe distances in ensembles of multiple conformers or of heterogeneous systems without application of trFRET. Here, we developed and verified the applicability of a method to determine the transient distribution of intramolecular distances at the initiation and over the full duration of the kinetics of a conformational transition, even when trFRET measurements cannot be applied for detection of the fast transient state at the initial phase of the transition. Our approach is based on combined analysis of fluorescence intensity-detected fast kinetics, and application of trFRET measurements at the end of the transition under equilibrium conditions. The method further enables determination of the population ratio of two ensembles, the initial and the final, during the full duration of the transition in two-state transitions. The applicability of the method was demonstrated and tested in comparison to double-kinetics data, in studies of the folding transition of double-labeled mutants of AK.

Two-state model

In a case characterized by a marked difference between the equilibrium intramolecular distance distribution in the ensemble of the conformers in the state before the initiation of the transition (e.g., proteins under denaturing conditions) and the one immediately after initiation of the transition, the process can be described as a three-state transition (5,24) where the first and second sequential transitions are fast and slow, respectively. In most such cases, the kinetics of change of the monitored signal appears to be monoexponential (6,24,27). The method presented here, which assumes a two-state transition, does not depend on knowledge of the characteristics of the ensemble before the initiation of the transition. Only the characteristics of the final ensemble and the kinetics of change at the signal are used, and hence the two-state model can be applied.

The detailed simulations performed showed the limits of application of the method and its dependence on the parameters of the experimental system. Of particular influence is the difference between the selected intramolecular distance distributions of the initial and final ensembles and the value of the Förster critical distance, R₀, with respect to the mean of the two distance distributions. These two key parameters can be tuned by careful selection of the pair of probes and the distance to be monitored, respectively. Ideally, one would like to repeat experiments using more than one pair of probes and monitor more than a single intramolecular distance in separate experiments. The simulations also set the limit of application of the method for recovery of the initial distance distribution in the case of pseudo two-state transitions due to the existence of an intermediate state. The simulations presented in the Supporting Material can be used for design of FRET kinetics experiments with additional sets of parameters by multiplying the data presented by a single factor.

This kind of kinetic approach is well documented in other steady-state stopped-flow FRET measurements (2,6,8,24,27). The FRET kinetics fit well with a monoexponential rate law, characteristic of a two-state transition. This can be described by a three-state model having the first transition much faster than the mixing dead-time, followed by a second, slower transition. Based on a large database of both published and unpublished results studying different elements within AK (24), this molecule contains elements, such as AK-18(Sal)-71(Trp), with such characteristic three-state behavior, whereas other elements, such as AK-79(Sal/Cou)-86(Trp), show a slow two-state transition directly from unfolded to folded state equilibrium distance distributions. Thus, the overall dimension of the ensemble of conformers, but not all parts of the chain, change dimensions upon the change of solvent. We call this intermediate state “a collapsed state” (5,6) and describe here the distance distributions that characterize it.

The test case: folding of AK mutants

The three intramolecular distance distributions obtained for the initial (collapsed) ensemble of refolding AK molecules determined by the method presented here, and previous double-kinetics experiments, provide strong validation of our believed-new method.

The excellent agreement between the trFRET-detected double-kinetics experiment and the best-fit results of the emission intensity-based FRET detection kinetics proves its viability, at least for two-state transitions within the limits established by the simulations.

In one case, agreement was poor. The mean transfer efficiency obtained for the mutant AK-18(Sal)-203(Trp) in the collapsed state by analysis of the double-kinetics experiment in comparison to that obtained by analysis of the emission intensity determined that the 〈E〉(t) trace was ∼2 vs. 20%, respectively. This deviation is probably the result of the very large mean distance of the collapsed state distance distribution, which exceeds the Förster distance range of this specific pair of probes (Fig. 2 D, row 4, blue, and Table 1).

The distributions of three intramolecular distances in the AK molecule were obtained for ensembles of AK molecules in three states: denatured in 1.8 M GndHCl at the initiation of refolding; initial (collapsed) state; and at the end of the refolding transition. The folded state in 0.3 M GndHCl, shown in Fig. 2 reveals two major transitions in refolding of the CORE domain. The first transition is a fast partial reduction of the distance between residues separated by a very long chain segment (residues 18 and 203), which can be assigned to a solvent-induced collapse. The second major transition is a complex hierarchic succession of folding transitions of subdomain elements. Some elements fold by a slow two-state transition (the formation of β-strands between residues 79 and 86) and some fold very rapidly, immediately within the dead-time of the stopped-flow mixing experiment (the closure of the loop between residues 28 and 71). Even though the process is probably much more complex, the two-state approximation may be used for recovery of the parameters of the three intramolecular distance distributions by the method presented here.

Three-state transition

In some cases, distinctive three-state kinetics are expected (5,6,16,44). It could be valuable to use the proposed methodology when a three-state transition is expected, by employing the extension to a possible three-state transition (see Eqs. S1–S4 in the Supporting Material). We performed auxiliary simulations testing the applicability of the proposed three-state model, in cases where both the initial and final state intramolecular distance distributions are known from equilibrium trFRET, and the unknowns are the intermediate state distance distribution and the two rate constants (see the Supporting Material and Spreadsheet S1 in the Supporting Material). The factors that improve the accuracy in predicting the known parameters are the time variation between the two transitions, the difference between the mean of the intermediate distance distribution and those of the known initial and final states, and the proper choice of a pair of probes with optimal R₀ value. Moreover, one should remember that without early knowledge of an underlying three-state transition, the usage of a three-state transition model will be assessed in comparison to the simpler two-state model by the traditional statistical model comparison tools.

Concluding Remarks

The protein folding transition, which is the most extensive type of conformational transition of biopolymers, is a sum of formation of multiple interacting pairs; hence, even the main transition is often very cooperative, and mapping of each subdomain transition is essential for a full description and understanding of the mechanism of folding. Methods based on magnetic resonance measurements (45–49) are powerful, enabling many atoms to serve as structural probes in a single mutant molecule. However, partially folded macromolecular systems generally form ensembles of multiple conformers that should be characterized in statistical terms of distributions of structural parameters. The trFRET-based methods, although limited to a single pair per measurement, can be used to determine intramolecular distance distributions and their fast changes down to the nanosecond timescale. The double-kinetics methods, which can be applied with any kind of fast or ultrafast induction or relaxation of structural perturbations, yield such information. So why go back to emission intensity-based FRET measurements? The importance of the method presented here stems from the need to measure many distributions of intramolecular distances in many mutants to ultimately relate structural elements to subdomain and global folding events, and their progression. Because the double-kinetics method requires much larger amounts of each sample and very sophisticated instrumentation, the high throughput work needed in the study of protein folding, as well as any other conformational transitions, can gain much from the combination of recording traces of emission intensity measurements and equilibrium trFRET measurements.