Abstract
In this paper, the oscillations and synchronization status of two different network connectivity patterns based on Izhikevich model are studied. One of the connectivity patterns is a randomly connected neuronal network, the other one is a small-world neuronal network. This Izhikevich model is a simple model which can not only reproduce the rich behaviors of biological neurons but also has only two equations and one nonlinear term. Detailed investigations reveal that by varying some key parameters, such as the connection weights of neurons, the external current injection, the noise of intensity and the neuron number, this neuronal network will exhibit various collective behaviors in randomly coupled neuronal network. In addition, we show that by changing the number of nearest neighbor and connection probability in small-world topology can also affect the collective dynamics of neuronal activity. These results may be instructive in understanding the collective dynamics of mammalian cortex.
Keywords: Cortical neuronal network, Randomly-coupled network, Small-world network, Oscillation and synchronization
Introduction
Neuronal synchronization is known to play a crucial role in many physiological functions such as information binding and wake-sleep cycles (Haken 2002; Suykens and Osipov 2008; Stephens et al. 2010). Experiments have shown that synchronization can occur in many special areas of the brain such as the visual cortex and hippocampus regions (Mehta et al. 2002; Gray and Singer 1989). The synchronization of neuronal signal was proposed as one of the mechanisms to transmit and code information in the human brain (Singer 1994; Pikovsky et al. 2001). Hence, the synchronous firing of interconnected neurons has been extensively investigated by means of the theory of nonlinear dynamics (Nomura et al. 2003; Sato and Shiino 2007; Wang et al. 2011; He et al. 2003; Kitajo et al. 2007; Liu and Cao 2011; Sun et al. 2010; Qu et al. 2012; Shi et al. 2008; Zhou and Kurths 2005; Kiss et al. 2003; Liu et al. 2012). Synchronization of fast-spiking neurons interconnected by GABA-ergic and electrical synapses was investigated by Nomura and his team. It was observed that a fast-spiking pair connected by electrical and chemical synapses could achieve both synchronous and anti-synchronous firing states in a physiologically plausible range of the conductance ratio between electrical and chemical synapses (Nomura et al. 2003). Sato and Shiino investigated effects of the width of an action potential on synchronization phenomena using an integrate-and-fire neuron model and a piecewise linear version of the FitzHugh-Nagumo neuron model. It was shown that the duration of the impulse had a critical role in assuring synchronization (Sato and Shiino 2007). Wang et al. investigated the dependence of synchronization transitions of bursting oscillations on the information transmission delay over scale-free neuronal networks with attractive and repulsive coupling. It is shown that for both types of coupling, the delay always plays a subtle role in either promoting or impairing synchronization (Wang et al. 2011). Moreover, noise-induced synchronization has also been reported in realistic neuronal systems. He et al. studied numerically in two realistic models, the Pikovsky-Rabinovich circuit model and the Hindmarsh-Rose neuron model. It is found that two none-coupled identical systems can been synchronized by forcing with common Gaussian noise term (He et al. 2003).
To study the oscillations and synchronization of a brain system, modeling of network consisting of thousands of neurons is required (Rulkov et al. 2004; Rulkov, and Bazhenov 2008). In any study of network dynamics, there are two crucial issues which are: (1) what model describes spiking dynamics of each neuron and (2) how the neurons are connected (Izhikevich 2004b). As we develop such a brain model consisting of spiking neurons, the model for a single neuron must be computationally simple and capable of producing rich firing patterns exhibited by real biological neurons. The widely used models of spiking and bursting neurons can be expressed in the form of ordinary differential equations such as Hodgkin-Huxley model (Hodgkin and Huxley 1952), integrate-and-fire (Stein 1967), spiking model by Izhikevich (Izhikevich 2003, 2004a), FitzHugh-Nagumo model (FitzHugh 1961), Hindmarsh-Rose model (Rose and Hindmarsh 1989), Morris-Lecar model (Morris and Lecar 1981) and so on. The most realistic approach for simulation of neuronal behavior is based on Hodgkin-Huxley model (Hodgkin and Huxley 1952). In general, scientists refer to all conductance-based models as being of the Hodgkin-Huxley type. Such models are important because their parameters are biophysically meaningful and measurable. However, only a handful of neurons can be simulated in real time since it is computationally prohibitive with four differential equations and tens of parameters. In contrast, using integrate-and-fire model is computationally effective, but the model is too simple to produce rich spiking and bursting firings exhibited by cortical neurons (Stein 1967). So, Izhikevich et. al. proposed a simple spiking model that is as biologically plausible as the Hodgkin-Huxley model and as computationally efficient as integrate-and-fire model (Izhikevich 2003, 2004a).
How the neurons are connected is another important issue to study network dynamics. Most of the existing work on synchronization of coupled networks assumes that the coupling configuration is completely regular (Heagy et al. 1994; Wu and Chua 1995), while a few studies address the issue of synchronization in randomly coupled networks (Gade 1996; Manrubia and Mikhailov 1999). However, many biological, technological and social networks are neither completely regular nor completely random. To interpolate between these two extremes, Watts and Strogatz introduced the interesting concept of small-world networks (Watts and Strogatz 1998). In this small-world network, neurons of the brain are coupled mainly locally, but in addition, are also connected through sparse long-range connections linking physically distant units. The so-called small-world networks have intermediate connectivity properties but exhibit a high degree of clustering as in the regular networks and a small average distance between vertices as in the random networks. Convincing evidences have been presented which support the idea that small-world networks provide a powerful and versatile tool, leading us towards understanding the structure and function of the human brain (Yu et al. 2008; Bassett and Bullmore 2006; Volman et al. 2005). Hence, much attention has been devoted to studying the dynamics of small-world neuronal networks (Roxin et al. 2004). Furthermore, Kwon and Moon (2002) investigated the effects of small-world networks on the phenomenon of coherence resonance in ensembles of Hodgkin-Huxley neurons. It has been reported that increasing the network randomness may lead to an enhancement of temporal coherence and spatial synchronization. Spatiotemporal chaos and synchronization on complex neuronal networks have also been studied (Gong et al. 2006; Wei and Luo 2007). Both works report that the synchronization, which is absent in the regular network, can be greatly enhanced by random shortcuts between distant neurons. Moreover, Perc et al. have recently investigated the stochastic resonance and spatial synchronization on excitable (Perc 2007) as well as bitable (Perc and Gosak 2008) small-world networks, whereby previously it has also been reported that the synchronization of small-world networks depends not only on their topology but also on the type of coupling (Hasegawa 2005).
In the present paper, a network model based on Izhikevich simple model is proposed to study the dynamics of cortical neural networks. This network model will exhibit different types of collective behavior such as gamma and alpha rhythm corresponding to that of mammalian cortex. Both randomly-coupled and small-world network connectivity patterns are studied. In randomly coupled network, it will exhibit various oscillation and synchronous status by tuning the key parameters of coupling connection weights, the external current injection, the noise of intensity and the neuron number. It is proven that the synchronization status of neuronal network has relationship with these four key parameters. Moreover, the external input has more effects on spiking of inhibitory neurons than that of excitatory neurons. Moreover, in WS small-world network (Watts and Strogatz 1998), it is proven that the synchronization has relationship with two parameters of network. One is the connection probability and the other is the number of nearest neighbor of each node of network.
The paper is organized as follows: Section “Model” presents the model equations and network connections, including different spiking patterns in a single neuron. Section “Result” gives the main simulation results of neuronal networks with different connection patterns, the randomly-coupled network and the small-world network. It is shown that this neuronal network will exhibit various collective behaviors by tuning control parameters. Finally, a brief conclusion is given in Section “Conclusion”.
Model
Single neuron pattern generator
For a single neuron, a Izhikevich simple spiking model is presented in this paper (Izhikevich 2003), which is as biologically plausible as the Hodgkin-Huxley model (Hodgkin and Huxley 1952), yet as computationally efficient as integrate-and fire model (Stein 1967). This model consists of two ordinary differential equations as below
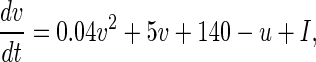 |
1 |
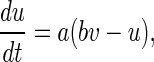 |
2 |
with the auxiliary after-spike resetting
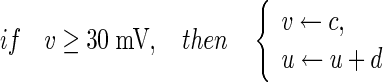 |
3 |
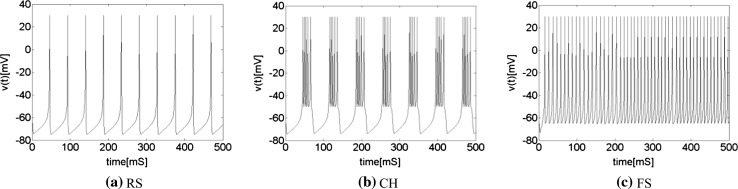
where v represents the membrane potential of the neuron, u represents a membrane recovery variable and it provides negative feedback to v. Synaptic currents or dc-currents are delivered via the variable I. After the spike reaches its apex (+30 mV), the membrane voltage and the recovery variable are reset according to the Eq. (3). There are a, b, c, d four parameters in this simple model. Various setting of the parameters results in various intrinsic firing patterns including excitatory and inhibitory cortical cells in intracellular recordings. Neocortical neurons in the mammalian brain can be classified into several types according to spiking patterns. All excitatory cortical cells are divided into RS (regular spiking), CH (chattering) neurons while FS (fast spiking) is typical behavior of inhibitory neurons. Figure 1 gives three most typical types of neurons to different values of the parameters.
Fig. 1.
Typical types of neurons to different values of the parameters. RS and CH are typical cortical excitatory neurons. FS is cortical inhibitory neuron. In this simulation, time step is 1 ms and time length is 500 ms. a Regular spiking (RS), the parameters are set as a = 0.02, b = 0.2, c = −65 mV, d = 8. b Chattering (CH), the parameters are set as a = 0.02, b = 0.2, c = −50 mV, d = 2. c Fast spiking (FS), the parameters are set as a = 0.1, b = 0.2, c = −65 mV, d = 2
Network geometry
To study the network geometry, a pulse-coupled neuronal networks is simulated in this paper. The network is described as follow equation.
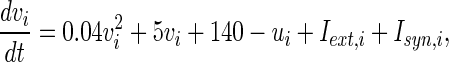 |
4 |
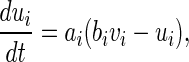 |
5 |
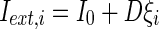 |
6 |
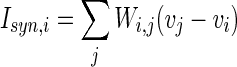 |
7 |
where 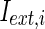 is the external current to the neuron. Each neuron in the network receives a noisy thalamic input.
is the external current to the neuron. Each neuron in the network receives a noisy thalamic input. 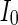 is the intensity of the dc current. D is the intensity of the noise.
is the intensity of the dc current. D is the intensity of the noise. 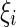 is a random process without time correction and the random variables are identically and uniformly distributed in [−1, 1].
is a random process without time correction and the random variables are identically and uniformly distributed in [−1, 1]. 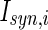 accounts for the synaptic current received by the neuron. The synaptic connection weights between the neurons are given by
accounts for the synaptic current received by the neuron. The synaptic connection weights between the neurons are given by 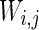 . The firing of jth neuron instantaneously changes variable
. The firing of jth neuron instantaneously changes variable 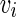 by
by 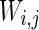 .
.
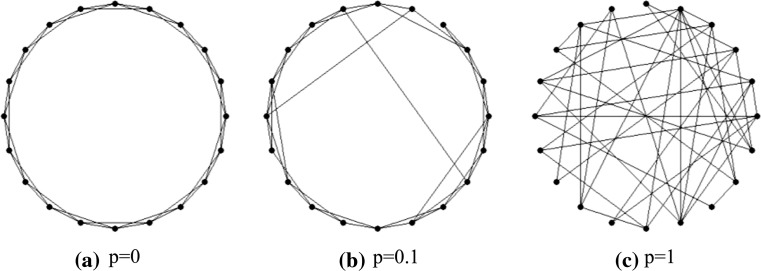
Figure 2 gives the three typical examples of network topologies. The parameter p determines the probability of rewiring a link, whereby  constitutes a regular graph (as Fig. 2a), while
constitutes a regular graph (as Fig. 2a), while  results in a random network (as Fig. 2c). For
results in a random network (as Fig. 2c). For 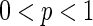 , as exemplified in Fig. 2b, the resulting network may have small-world properties in that the normalized characteristic path length between distant units is small comparable with that of a random network, while the normalized clustering coefficient is still large comparable with that of a regular nearest-neighbor graph. In this paper, both small-world network and randomly-coupled network connectivity patterns are studied. Regular network is excluded since it has been investigated in our previous work (Qu et al. 2012).
, as exemplified in Fig. 2b, the resulting network may have small-world properties in that the normalized characteristic path length between distant units is small comparable with that of a random network, while the normalized clustering coefficient is still large comparable with that of a regular nearest-neighbor graph. In this paper, both small-world network and randomly-coupled network connectivity patterns are studied. Regular network is excluded since it has been investigated in our previous work (Qu et al. 2012).
Fig. 2.
Examples of considered network topologies. Only 20 vertices are displayed in each panel. a Regular ring characterized by p = 0 with periodic boundary conditions. Each vertex is connected to its k = 4 nearest neighbors. b Realization of WS small-world topology via random rewiring of a certain fraction p of links, p = 0.1. c Realization of randomly connected network, p = 1
For convenience, we construct a neural network consisting of 1,000 neurons. Based on the anatomy of a mammalian cortex, the ratio of excitatory to inhibitory neurons is chosen as 4:1. The numbers of excitatory neurons are from 1 to 800 while inhibitory ones are from 801 to 1,000. RS cells are used to model all excitatory neurons and FS cells to model all inhibitory neurons. In the model, each excitatory neuron has 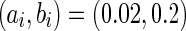 . To make different neurons have different dynamics, the excitatory neurons are assigned
. To make different neurons have different dynamics, the excitatory neurons are assigned 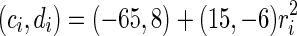 , where
, where 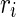 is a random variable uniformly distributed on the interval [0, 1]. So,
is a random variable uniformly distributed on the interval [0, 1]. So, 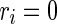 corresponds to a regular spiking (RS) cell and
corresponds to a regular spiking (RS) cell and 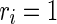 corresponds to a chattering (CH) cell. We use
corresponds to a chattering (CH) cell. We use 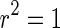 to bias the distribution towards RS cells. Each inhibitory cell has
to bias the distribution towards RS cells. Each inhibitory cell has 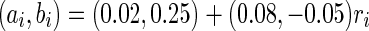 and
and 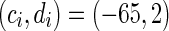 . During the simulation, all equations are numerically integrated using the fourth-order Runge–Kutta method. The time step is 0.5 ms.
. During the simulation, all equations are numerically integrated using the fourth-order Runge–Kutta method. The time step is 0.5 ms.
Results
Dynamics based on randomly connected network
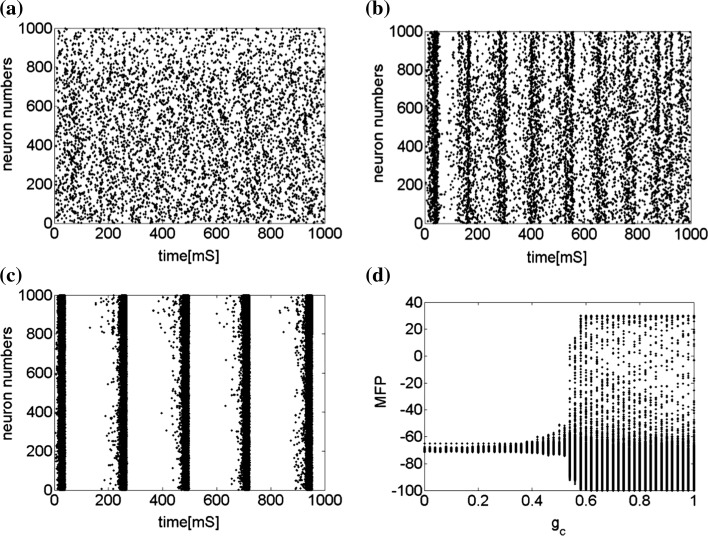
The effects of connection weights are simulated firstly. The synaptic connection weights between the neurons are given by the matrix. Figure 3 shows that by changing the relative strength of synaptic connections, the network will produce different collective behaviors. In this simulation, the connection weights with inhibitory neurons are always set as −1 while those with excitatory neurons are tuned from 0 to 1. If the connection weight with excitatory neuron is 0.25, 1,000 neurons randomly spike (Fig. 3a). Figure 3b shows that as the connection weight are tuned to 0.5, although the network is connected randomly and there is no synaptic plasticity, the neurons self-organize into assemblies and they exhibit collective rhythmic behavior in the frequency range corresponding to that of mammalian cortex in the awake state such as alpha and gamma band rhythm (10 and 40 Hz, respectively). As Fig. 3c, the connection weight continuously increases to 0.75, all the neurons spike with the same rhythm (time interval is about 250 ms) and reach the complete synchronization.
Fig. 3.
Characteristic of a network of randomly coupled spiking neurons for different connection weights 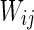 . The connection weight with the inhibitory neuron is always set as −1. The connection weights with excitatory neuron are set as a 0.25, b 0.5, c 0.75, d mean field potential (MFP) plot versus connection weight. Other system parameters are neuron number
. The connection weight with the inhibitory neuron is always set as −1. The connection weights with excitatory neuron are set as a 0.25, b 0.5, c 0.75, d mean field potential (MFP) plot versus connection weight. Other system parameters are neuron number 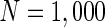 , the external input
, the external input 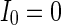 , the noise intensity for excitatory neuron
, the noise intensity for excitatory neuron 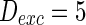 and that of the inhibitory neuron
and that of the inhibitory neuron 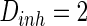
Figure 3d provides the mean field potential (MFP) plot versus connection weight, which will provide more information about the effect of connection weight. MFP is adopted as a global parameter for visualization of the synchronization of multiple neurons. It is the mean membrane potential of all neurons in the network. Since the most pronounced voltage changes occur during the action potentials, significant MFP deflections can only be expected when a high percentage of the neurons generate action potentials at the same time. The maximum amplitude will only be achieved when all neurons fire in exact coincidence (Postnova et al. 2010). Figure 3d shows that the values of MFP increase very slowly as the synaptic connection weights increases from 0 to 0.5, which means the system are in asynchronous and randomly spiking. With further increasing the synaptic connection weights from 0.5 to 0.6, the MFP increases very quickly, reaches the maximum and remains there, which means that the synchronization is already complete. In a summary, with increasing the synaptic connection weights, the system becomes more and more synchronous, from random spiking (from 0 to 0.5) to almost synchronous(from 0.5 to 0.6), then to complete synchronization(larger than 0.6).
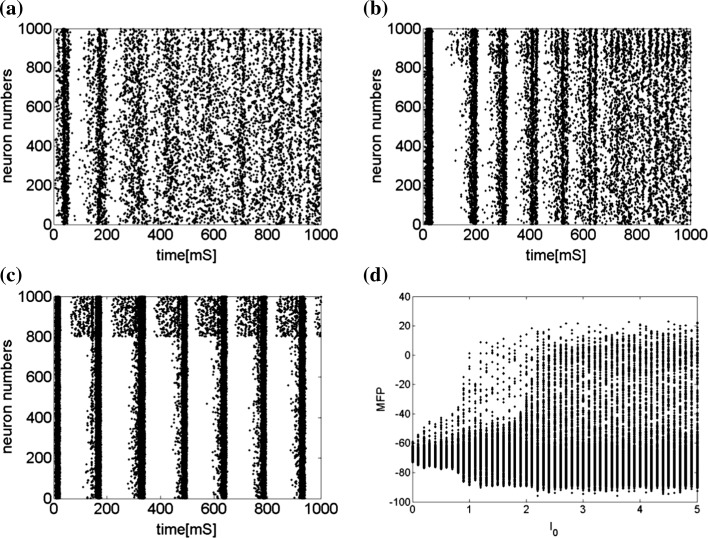
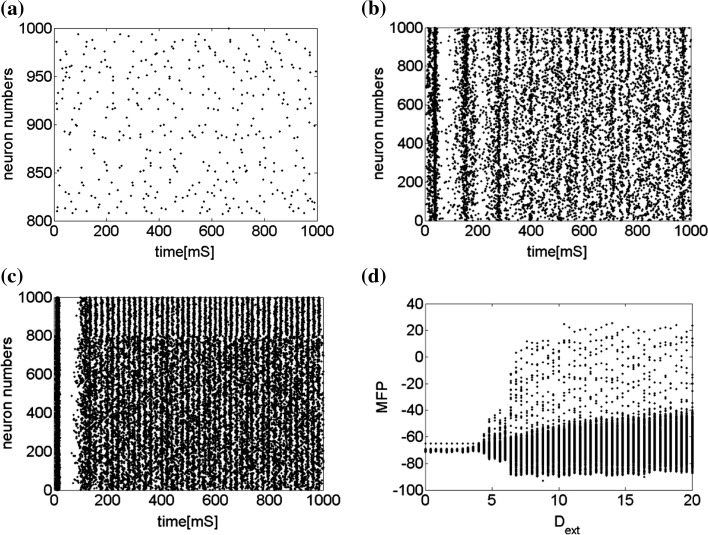
Secondly, the collective dynamics of network by tuning the parameter external current 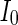 is simulated. Figure 4 gives the characteristic of a network of randomly coupled spiking neurons for different external input
is simulated. Figure 4 gives the characteristic of a network of randomly coupled spiking neurons for different external input 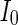 . When
. When 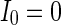 (Fig. 4a), the situation is as same as that of Fig. 4b. If
(Fig. 4a), the situation is as same as that of Fig. 4b. If 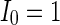 , the coupled neurons of network become more synchronous and keep the rhythm of the spiking. With increasing the intensity
, the coupled neurons of network become more synchronous and keep the rhythm of the spiking. With increasing the intensity 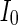 to 3, all the neurons spike at the same time interval (about 150 mS). However, the excitatory neurons (from number 1 to 800) and inhibitory neurons (from number 801 to 1,000) show obviously different behavior. The spiking frequency of inhibitory neurons is higher than that of excitatory ones. Figure 4d provides the MFP plot versus connection weight. It is shown that with increasing the external current
to 3, all the neurons spike at the same time interval (about 150 mS). However, the excitatory neurons (from number 1 to 800) and inhibitory neurons (from number 801 to 1,000) show obviously different behavior. The spiking frequency of inhibitory neurons is higher than that of excitatory ones. Figure 4d provides the MFP plot versus connection weight. It is shown that with increasing the external current 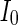 , the network will display the behavior from random spiking (
, the network will display the behavior from random spiking (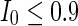 ) to almost synchronous (
) to almost synchronous (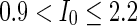 ), then to complete synchronization (
), then to complete synchronization (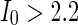 ).
).
Fig. 4.
Characteristic of a network of randomly coupled spiking neurons for different external input 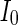 . a
. a
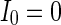 , b
, b
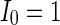 ,c
,c
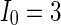 , d MFP plot versus external input
, d MFP plot versus external input 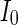 . Other system parameters are: neuron number
. Other system parameters are: neuron number 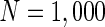 , the connection weights of excitatory neuron
, the connection weights of excitatory neuron 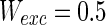 , and that of inhibitory neuron
, and that of inhibitory neuron 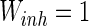 , noise intensities for excitatory neuron
, noise intensities for excitatory neuron 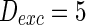 and that for inhibitory neuron
and that for inhibitory neuron 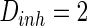
Thirdly, how the parameter of noise intensity influences the collective dynamics is discussed. The noise intensities for excitatory and inhibitory neurons are set as 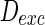 and
and 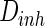 , respectively. Here, for easy discussion, only tune one parameter
, respectively. Here, for easy discussion, only tune one parameter 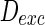 while setting the other parameter
while setting the other parameter 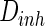 as constant (
as constant (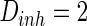 ). Neuron spiking results with different noise intensity of excitatory neurons is shown in Fig. 5. If the noise intensity of excitatory neurons
). Neuron spiking results with different noise intensity of excitatory neurons is shown in Fig. 5. If the noise intensity of excitatory neurons  , only a few neurons randomly spike due to the current input is too small to make neurons spike. As the noise intensity of excitatory neurons increases to 5 while that of inhibitory neurons maintain 2, dark vertical lines indicate episodes of alpha and gamma band rhythm (Fig. 5b). If the noise intensity of excitatory neurons increases to 10 (Fig. 5c), all the neurons are in almost synchronous state. However, neither excitatory nor inhibitory neurons spike during the time interval from 0 to 150 mS. Figure 5d provides MFP plot versus noise intensities for excitatory neurons. It is demonstrated that with increasing the noise intensities for excitatory neurons
, only a few neurons randomly spike due to the current input is too small to make neurons spike. As the noise intensity of excitatory neurons increases to 5 while that of inhibitory neurons maintain 2, dark vertical lines indicate episodes of alpha and gamma band rhythm (Fig. 5b). If the noise intensity of excitatory neurons increases to 10 (Fig. 5c), all the neurons are in almost synchronous state. However, neither excitatory nor inhibitory neurons spike during the time interval from 0 to 150 mS. Figure 5d provides MFP plot versus noise intensities for excitatory neurons. It is demonstrated that with increasing the noise intensities for excitatory neurons 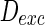 , the network will display the behavior from random spiking (
, the network will display the behavior from random spiking (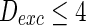 ) to almost synchronous (
) to almost synchronous (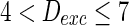 ), then to complete synchronization (
), then to complete synchronization (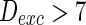 ).
).
Fig. 5.
Spiking results of neurons with different noise intensity D. In our simulation, noise intensities of excitatory neuron and inhibitory neuron are set as 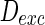 and
and 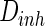 , respectively. a
, respectively. a
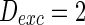 . b
. b
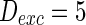 . c
. c
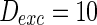 . d MFP plot versus noise intensities of excitatory neuron. Other system parameters are:
. d MFP plot versus noise intensities of excitatory neuron. Other system parameters are: 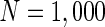 ,
, 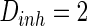 ,
, 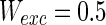 ,
, 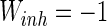 ,
, 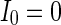
From Figs. 3, 4, and 5, what happens for large values of parameters? If noise intensity is set as sufficiently large value such as 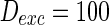 , the simulation result shows that all the neurons will spike in any time (from 0 to 1,000 m) in randomly-coupled network. There occurs same phenomenon if the other two parameters of synaptic weights and external current are set as large values.
, the simulation result shows that all the neurons will spike in any time (from 0 to 1,000 m) in randomly-coupled network. There occurs same phenomenon if the other two parameters of synaptic weights and external current are set as large values.
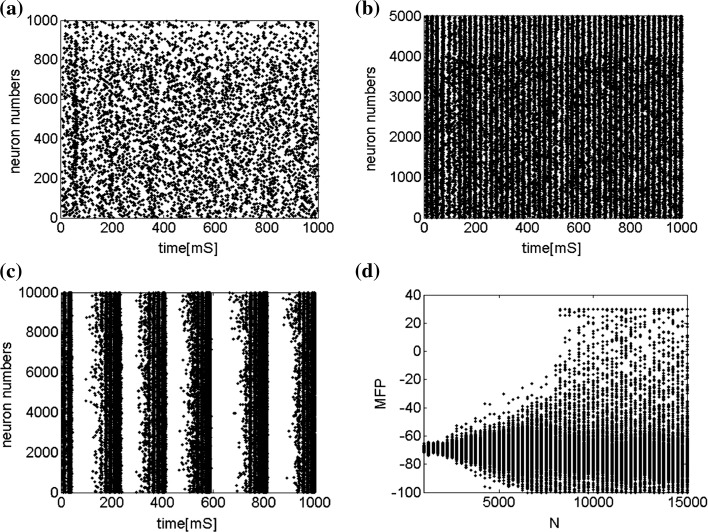
Finally, since we think that the MFP may be a kind of order parameter describing the synchronous transition, the effect of the number of neurons N should be studied. Figure 6a shows that if the neuron number is 1,000, the neurons randomly spike. As neuron number increases to 5,000 (Fig. 6b), the neurons will self-organize into assemblies. As the neuron number are tuned to 10,000, all the neurons spike with the same rhythm (time interval is about 200 ms) and reach the complete synchronization. Figure 6d provides MFP plot versus neuron number. It is proven that as the neuron number increases from 1,000 to 8,000, the values of MFP increase at the same speed, with increasing neuron number, the system becomes more and more synchronous. With further increasing the neuron number, the MFP reaches the maximum and remains there, which means that the synchronization is already complete.
Fig. 6.
Spiking results of neurons with different neuron number N. a
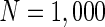 . b
. b
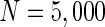 . c
. c
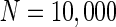 . d MFP plot versus neuron number. Other system parameters are:
. d MFP plot versus neuron number. Other system parameters are: 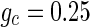 ,
, 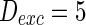 ,
, 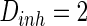 ,
, 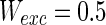 ,
, 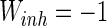 ,
, 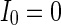
Dynamics based on small-world network
In this section, we will discuss the dynamics based on WS small-world network (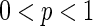 ) instead of randomly-coupled network (
) instead of randomly-coupled network ( ). The effects of two important parameters of WS small-world network are investigated, respectively. One parameter is the connection probability p and the other one is the number of nearest neighbor of each node k. Setting various values of p and k will lead to the change of topology of the network.
). The effects of two important parameters of WS small-world network are investigated, respectively. One parameter is the connection probability p and the other one is the number of nearest neighbor of each node k. Setting various values of p and k will lead to the change of topology of the network.
Firstly, the effect of connection probability p is simulated. As tuning p, the other parameters are set as constants. If two neurons i, j are connected, 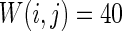 , otherwise,
, otherwise, 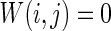 . The half of the number of nearest neighbor of each node
. The half of the number of nearest neighbor of each node  . The external input
. The external input 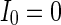 , the noise strength for excitatory and inhibitory neurons are set as
, the noise strength for excitatory and inhibitory neurons are set as 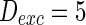 and
and 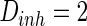 . Figure 7a shows the small-world topology via random rewiring of a small fraction
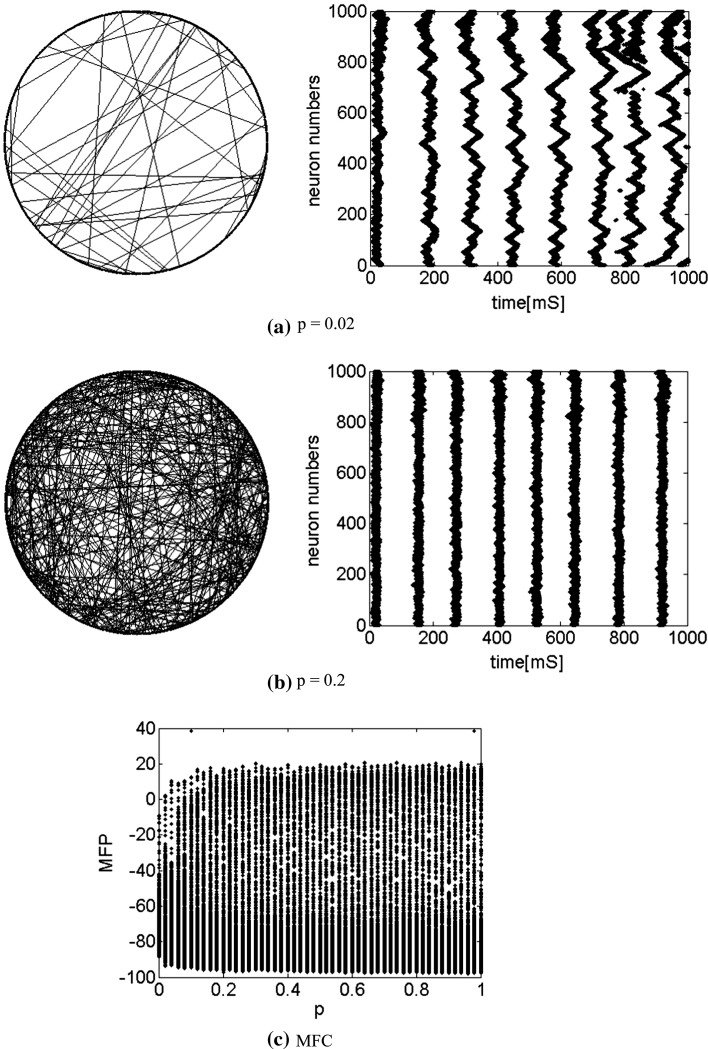
. Figure 7a shows the small-world topology via random rewiring of a small fraction 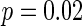 (left part) and its corresponding neuron spiking result (right part). It is demonstrated that if
(left part) and its corresponding neuron spiking result (right part). It is demonstrated that if 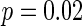 , all the neurons are in almost synchronous state, neither randomly spiking nor completely synchronization. Figure 7b gives the small-world topology via random rewiring of a bigger fraction
, all the neurons are in almost synchronous state, neither randomly spiking nor completely synchronization. Figure 7b gives the small-world topology via random rewiring of a bigger fraction 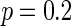 (left part) and its corresponding neuron spiking result (right part). It is shown that all the neurons are in complete synchronization state in case of
(left part) and its corresponding neuron spiking result (right part). It is shown that all the neurons are in complete synchronization state in case of 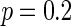 and maintains the interval of spiking. To give a globe view of the synchronization of neuronal network, Fig. 7c gives MFP plot versus the connection probability p. It is demonstrated that with increasing the connection probability p, the network will display the behavior from almost synchronous (
and maintains the interval of spiking. To give a globe view of the synchronization of neuronal network, Fig. 7c gives MFP plot versus the connection probability p. It is demonstrated that with increasing the connection probability p, the network will display the behavior from almost synchronous (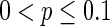 ), then quickly changes into complete synchronization and maintains it with the range of connection probability
), then quickly changes into complete synchronization and maintains it with the range of connection probability 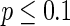 .
.
Fig. 7.
Characteristics of a WS small-world network for different connection probability p. The connection probabilities p are set as a 0.02 and b 0.2. c MFP plot versus connection probability p. If two neurons i, j are connected, 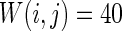 , otherwise,
, otherwise, 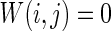 . Other system parameters are:
. Other system parameters are:  ,
, 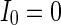 ,
, 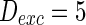 and
and 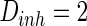 . The time length is 1,000 mS and the neuron number is 1,000
. The time length is 1,000 mS and the neuron number is 1,000
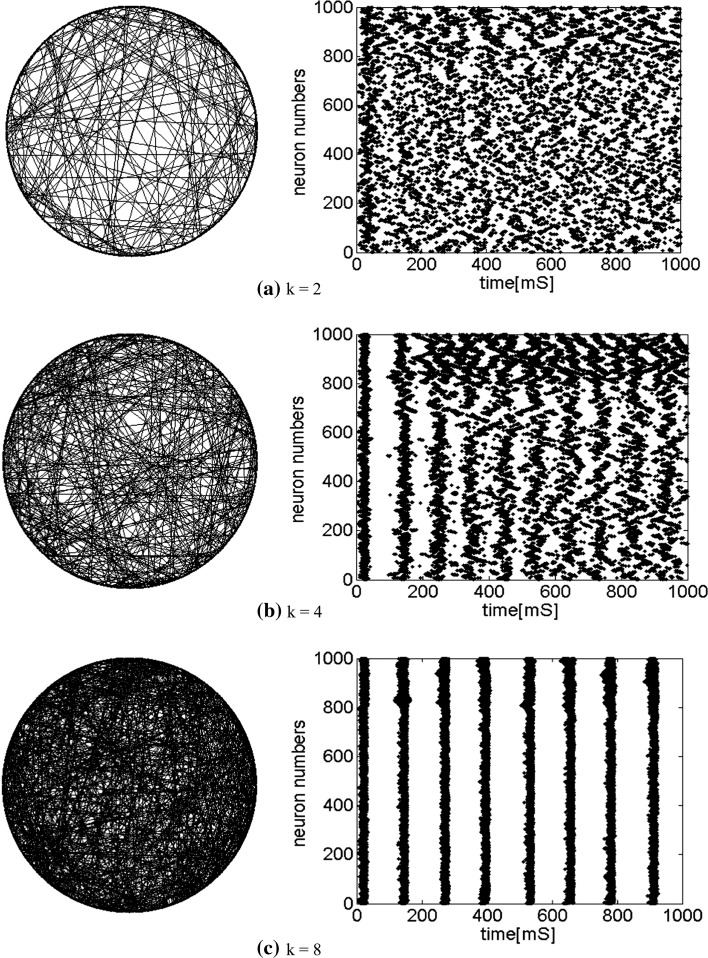
How the number of nearest neighbor of each node k effects the synchronization is further discussed. Small-world topologies and corresponding neuron spiking results with different values of k are shown in Fig. 8. Other parameters are set as connection probability p equals 0.2. If two neurons i, j are connected, 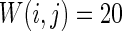 , otherwise,
, otherwise, 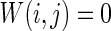 . The external input
. The external input 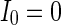 , the noise strength for excitatory and inhibitory neurons are set as
, the noise strength for excitatory and inhibitory neurons are set as 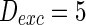 and
and 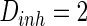 , respectively. If
, respectively. If  , 1,000 neurons randomly spike (Fig. 8a). Figure 8b shows that as the number of nearest neighbor of each node k is increased to 4, although the network is connected randomly, the neurons self-organize into assemblies and they exhibit collective rhythmic behavior. As Fig. 8c, the value of k continuously increases to 8, all the neurons spike with the same rhythm (time interval is about 130 ms) and reach the complete synchronization. So, as the number of nearest neighbor of each node increases, the network will become more and more synchronous.
, 1,000 neurons randomly spike (Fig. 8a). Figure 8b shows that as the number of nearest neighbor of each node k is increased to 4, although the network is connected randomly, the neurons self-organize into assemblies and they exhibit collective rhythmic behavior. As Fig. 8c, the value of k continuously increases to 8, all the neurons spike with the same rhythm (time interval is about 130 ms) and reach the complete synchronization. So, as the number of nearest neighbor of each node increases, the network will become more and more synchronous.
Fig. 8.
Characteristic of a WS small-world network for the number of nearest neighbor of each node k. The number of nearest neighbor of each node k are set as a 2, b 4, c 8. If two neurons i, j are connected, 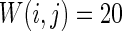 , otherwise,
, otherwise, 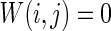 . Other system parameters are:
. Other system parameters are: 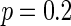 ,
, 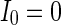 ,
, 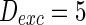 and
and 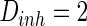 . The time length is 1,000 mS and the neuron number is 1,000
. The time length is 1,000 mS and the neuron number is 1,000
Conclusion
In conclusion, the oscillations and synchronization status of two different network connectivity patterns based on Izhikevich model have been investigated in this paper. One of the connectivity patterns is randomly connected neuronal network, the other one is small-world neuronal network. The coupled neurons will exhibit types of collective behavior by tuning some key parameters such as connection weights, external current injection, noise intensity, neuron number, connection probability and the number of nearest neighbor.
Four major outcomes are found based on this network model. (1) One of them is the demonstration that the synchronization status is much related with these four key parameters in randomly connected neuronal network. By increasing the synaptic connection weights, external current injection, noise intensity and neuron number, respectively, the system becomes more and more synchronous, from random spiking to almost synchronous, then to complete synchronization. (2) It can be seen that tuning the intensity of external input has much effects on spiking of inhibitory neurons than that of excitatory neurons. (3) In addition, we show that by changing the connection probability in small-world topology can also affect the collective dynamics of neuronal activity. It is demonstrated that with increasing the connection probability, the network will display the behavior from almost synchronous to complete synchronization and maintains it. (4) Moreover, it is presented that increasing the number of nearest neighbor in small-world topology can also significantly affect the collective dynamics of neuronal activity, from randomly spiking to completely synchronization. These methods and results provide some guidelines to understand the collective dynamics of mammalian cortex.
Acknowledgments
The work is supported by Science and Technology Support Plan Topics (No. 2011BAH24B12), Key Program of National Natural Science Foundation of China (No. 11232005), Fundamental Research Funds for the Central Universities (No. ZXH2012C004) and Start-up Funds of Civil Aviation University (No. 2012QD09X).
References
- Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. 2006;12(6):512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
- FitzHugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophys J . 1961;1(6):445–466. doi: 10.1016/S0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gade PM. Synchronization of oscillators with random nonlocal connectivity. Phys Rev E. 1996;54:64–70. doi: 10.1103/PhysRevE.54.64. [DOI] [PubMed] [Google Scholar]
- Gong YB, Xu B, Xu Q, Yang CL, Ren TQ, Hou ZH, Xin HW. Ordering spatiotemporal chaos in complex thermosensitive neuron networks. Phys Rev E. 2006;73:046137. doi: 10.1103/PhysRevE.73.046137. [DOI] [PubMed] [Google Scholar]
- Gray CM, Singer W. Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proc Natl Acad Sci USA. 1989;86:1698–1702. doi: 10.1073/pnas.86.5.1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haken H. Brain dynamics-synchronization and activity patterns in pulse-coupled neural nets with delays and noise. Berlin: Springer; 2002. [Google Scholar]
- Hasegawa H. Synchronizations in small-world networks of spiking neurons: diffusive versus sigmoid couplings. Phys Rev E. 2005;72:056139. doi: 10.1103/PhysRevE.72.056139. [DOI] [PubMed] [Google Scholar]
- He DH, Shi PL, Stone L. Noise-induced synchronization in realistic models. Phys Rev E. 2003;67:027202. doi: 10.1103/PhysRevE.67.027202. [DOI] [PubMed] [Google Scholar]
- Heagy JF, Carroll TL, Pecora LM. Synchronous chaos in coupled oscillator systems. Phys Rev E. 1994;50(3):1874–1885. doi: 10.1103/PhysRevE.50.1874. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A qualitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM. Simple model of spiking meurons. IEEE Trans Neural Networks. 2003;14(6):1569–1572. doi: 10.1109/TNN.2003.820440. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Which model to use for cortical spiking neurons? IEEE Trans Neural Networks. 2004;15(5):1063–1070. doi: 10.1109/TNN.2004.832719. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Spike-timing dynamics of neuronal groups. Cereb Cortex. 2004;14(8):933–944. doi: 10.1093/cercor/bhh053. [DOI] [PubMed] [Google Scholar]
- Kiss IZ, Zhai Y, Hudson JL, Zhou C, Kurths J. Noise enhanced phase synchronization and coherence resonance in sets of chaotic oscillators with weak global coupling. Chaos. 2003;13(1):267–278. doi: 10.1063/1.1513081. [DOI] [PubMed] [Google Scholar]
- Kitajo K, Doesburg SM, Yamanaka K, Nozaki D, Ward LM, et al. Noise-induced large-scale phase synchronization of human-brain activity associated with behavioural stochastic resonance. EPL. 2007;80:40009. doi: 10.1209/0295-5075/80/40009. [DOI] [Google Scholar]
- Kwon O, Moon HT. Coherence resonance in small-world networks of excitable cells. Phys Lett A. 2002;298:319–324. doi: 10.1016/S0375-9601(02)00575-3. [DOI] [Google Scholar]
- Liu XY, Cao JD. Local synchronization of one-to-one coupled neural networks with discontinuous activations. Cogn Neurodyn. 2011;5(1):13–20. doi: 10.1007/s11571-010-9132-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Liu LG, Wang H. Study on congestion and bursting in small-world networks with time delay from the viewpoint of nonlinear dynamics. Chin Phys Lett. 2012;29(6):060504. doi: 10.1088/0256-307X/29/6/060504. [DOI] [Google Scholar]
- Manrubia SC, Mikhailov SM. Synchronization and clustering in randomly coupled chaotic dynamical networks. Phys Rev E. 1999;60:1579–1589. doi: 10.1103/PhysRevE.60.1579. [DOI] [PubMed] [Google Scholar]
- Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature. 2002;417:741–746. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
- Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J . 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nomura M, Fukai T, Aoyagi T. Synchrony of fast-spiking interneurons interconnected by GABAergic and electrical synapses. Neural Comput. 2003;15:2179–2198. doi: 10.1162/089976603322297340. [DOI] [PubMed] [Google Scholar]
- Perc M. Stochastic resonance on excitable small-world networks via a pacemaker. Phys Rev E. 2007;76:066203. doi: 10.1103/PhysRevE.76.066203. [DOI] [PubMed] [Google Scholar]
- Perc M, Gosak M. Pacemaker-driven stochastic resonance on diffusive and complex networks of bistable oscillators. New J Phys. 2008;10:053008. doi: 10.1088/1367-2630/10/5/053008. [DOI] [Google Scholar]
- Pikovsky A, Rosenblum M, Kurths J. Synchronization, a universal concept in nonlinear sciences. New York: Cambridge University Press; 2001. [Google Scholar]
- Postnova S, Christian F, Jin W, Schneider H, Braun HA. A computational study of the interdependencies between neuronal impulse pattern, noise effects and synchronization. J Physiol Paris. 2010;104:176–189. doi: 10.1016/j.jphysparis.2009.11.022. [DOI] [PubMed] [Google Scholar]
- Qu JY, Wang RB, Du Y, Cao JT. Synchronization study in ring-like and grid-like neuronal networks. Cogn Neurodyn. 2012;6(1):21–31. doi: 10.1007/s11571-011-9174-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose RM, Hindmarsh JL. The assembly of ionic currents in a thalamic neuron. I The three-dimensional model. Proc R Soc Lond B. 1989;237:267–288. doi: 10.1098/rspb.1989.0049. [DOI] [PubMed] [Google Scholar]
- Roxin A, Riecke H, Solla SA. Self-sustained activity in a small-world network of excitable neurons. Phys Rev Lett. 2004;92:198101. doi: 10.1103/PhysRevLett.92.198101. [DOI] [PubMed] [Google Scholar]
- Rulkov NF, Bazhenov M. Oscillations and synchrony in large-scale cortical network models. J Biol Phys. 2008;34:279–299. doi: 10.1007/s10867-008-9079-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rulkov NF, Timofeev I, Bazhenov M. Oscillations in large-scale cortical networks: map-based model. J Comput Neurosci. 2004;17:203–223. doi: 10.1023/B:JCNS.0000037683.55688.7e. [DOI] [PubMed] [Google Scholar]
- Sato YD, Shiino M. Generalization of coupled spiking models and effects of the width of an action potential on synchronization phenomena. Phys Rev E. 2007;75:011909–011915. doi: 10.1103/PhysRevE.75.011909. [DOI] [PubMed] [Google Scholar]
- Shi X, Wang QY, Lu QS. Firing synchronization and temporal order in noisy neuronal networks. Cogn Neurodyn. 2008;2(3):195–206. doi: 10.1007/s11571-008-9055-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer W. Time as coding space in neocortical processing. Berlin: Springer; 1994. [Google Scholar]
- Stein RB. Some models of neuronal variability. Biophys J . 1967;7(1):37–68. doi: 10.1016/S0006-3495(67)86574-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens GJ, Silbert LJ, Hasson U. Speaker-listener neural coupling underlies successful communication. Proc Natl Acad Sci USA. 2010;107:14425–14430. doi: 10.1073/pnas.1008662107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun WG, Wang RB, Wang WX, Cao JT. Analyzing inner and outer synchronization between two coupled discrete-time networks with time delays. Cogn Neurodyn. 2010;4(3):225–231. doi: 10.1007/s11571-010-9118-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suykens JAK, Osipov GV. Synchronization in complex networks. Chaos. 2008;18:037101. doi: 10.1063/1.2985139. [DOI] [PubMed] [Google Scholar]
- Volman V, Baruchi I, Ben-Jacob E. Manifestation of function-follow-form in cultured neuronal networks. Phys Biol. 2005;2(2):98–110. doi: 10.1088/1478-3975/2/2/003. [DOI] [PubMed] [Google Scholar]
- Wang QY, Chen GR, Perc M. Synchronous bursts on scale-free neuronal networks with attractive and repulsive coupling. PLoS ONE. 2011;6(1):el5851. doi: 10.1371/journal.pone.0015851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of ‘small world’ networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Wei DQ, Luo XS. Ordering spatiotemporal chaos in discrete neural networks with small-world connections. Europhys Lett. 2007;78:68004. doi: 10.1209/0295-5075/78/68004. [DOI] [Google Scholar]
- Wu CW, Chua LO. Synchronization in an array of linearly coupled dynamical systems. IEEE Trans Circ Syst I. 1995;42(8):430–447. doi: 10.1109/81.404047. [DOI] [Google Scholar]
- Yu S, Huang DB, Singer W, et al. A small world of neuronal synchrony. Cereb Cortex. 2008;18(2):2891–2901. doi: 10.1093/cercor/bhn047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou CS, Kurths J. Noise-sustained and controlled synchronization of stirred excitable media by external forcing. New J Phys. 2005;7:18. doi: 10.1088/1367-2630/7/1/018. [DOI] [Google Scholar]