Modeling Protein Assemblies in the Proteome

Abstract

Most (if not all) proteins function when associated in multimolecular assemblies. Attaining the structures of protein assemblies at the atomic scale is an important aim of structural biology. Experimentally, structures are increasingly available, and computations can help bridge the resolution gap between high- and low-resolution scales. Existing computational methods have made substantial progress toward this aim; however, current approaches are still limited. Some involve manual adjustment of experimental data; some are automated docking methods, which are computationally expensive and not applicable to large-scale proteome studies; and still others exploit the symmetry of the complexes and thus are not applicable to nonsymmetrical complexes. Our study aims to take steps toward overcoming these limitations. We have developed a strategy for the construction of protein assemblies computationally based on binary interactions predicted by a motif-based protein interaction prediction tool, PRISM (Protein Interactions by Structural Matching). Previously, we have shown its power in predicting pairwise interactions. Here we take a step toward multimolecular assemblies, reflecting the more prevalent cellular scenarios. With this method we are able to construct homo-/hetero-complexes and symmetric/asymmetric complexes without a limitation on the number of components. The method considers conformational changes and is applicable to large-scale studies. We also exploit electron microscopy density maps to select a solution from among the predictions. Here we present the method, illustrate its results, and highlight its current limitations.

Proteins function through interactions with other molecules. In vivo, the overwhelming majority of proteins function when they are part of not only of binary interactions but multimolecular assemblies. Protein assemblies are responsible for the vast majority (or all) of the processes in a cell (1); the RNA polymerase transcription machinery (2), the ribosome, the translation engine (3), chaperonins (4), the proteasome, and the protein degradation machine (5) are some examples. It is essential to model protein assemblies in order to figure out cellular mechanisms. Three-dimensional structural data are crucial in order to correctly determine assemblies. Experimentally, structures of protein complexes can be obtained via several techniques, such as x-ray crystallography (6, 7), nuclear magnetic resonance (NMR) spectroscopy (8), electron microscopy (EM) (9), FRET spectroscopy (10), and small angle x-ray scattering (11), albeit at different resolutions.

The experimental determination of protein complexes can be difficult. Despite the many experimental methods, shortcomings abound: x-ray crystallization is applicable only to molecules that can be cloned, crystallized, and purified in large quantities, and often crystals suitable for the structural determination of protein assemblies cannot be obtained (7). NMR is limited to relatively small molecular sizes (12). Cryo-EM, cryo-electron tomography, FRET spectroscopy, and small angle x-ray scattering are more suitable for the structural determination of large molecules and assemblies, but their resolution is not at an atomic scale (9, 13).

Computational methods are essential for obtaining the structures of protein assemblies. Even though they also are associated with inherent shortcomings and hurdles, they can be of use in experimental techniques. Integrative structural determination methods combine experimental results from different sources with computational constraints, models, and theory. EM maps are combined with atomic structures of single protein components (14–20) or atomic models (21), and binary interaction data of the protein components of a complex obtained by means of affinity purification and mass spectrometry (MS) are integrated with comparative modeling (22). Structures of complexes are modeled based on NMR-derived data (23, 24). Eventually, several structures of protein complexes, such as the nuclear pore complex (15), the eukaryotic ribosome (25), human RNA polymerase II (26), the AAA-ATPase/20S core particle subcomplex of the 26S proteasome (27), and histone methyltransferase complex Set1C from yeast (28), were predicted using integrative methods. Despite their immense potential power, to date, these methods have been limited to a small set of proteins, especially to the most highly studied ones; this is because of the need for a broad range of different types of data, manual adjustment, and data curation.

Ab initio docking approaches have been used for the prediction of structures of protein complexes. These methods utilize different types of experimental data to increase their accuracy. MolFit (29, 30) and ATTRACT (31, 32) consider experimentally determined interface residues. ZDOCK (33, 34) blocks non-interface residues in docking and can use experimental data to filter the solutions; M-ZDOCK (35) uses this idea to construct cyclic symmetric multimers. PatchDock (36, 37) finds solutions based on shape complementarity and can use experimental data to detect binding sites. SymmDock (36, 38) restricts the search to symmetric cyclic transformations and constructs homocomplexes with cyclic symmetry. PROXIMO (39) and MultiFit (18) use radical probe MS and EM data in docking, respectively. Another useful docking tool is HADDOCK (40). It utilizes a variety of experimental data, mainly derived from NMR, to extract information about the interface, contacts, and relative orientations. Six subunit complexes can be constructed, and the method has been tested on symmetrical cases. However, expensive computation of the ab initio docking is a barrier for large-scale protein complex predictions. Computationally, modeling of multimolecular assemblies from the structures of their monomeric components is challenging because of the large number of possible combinations of the components (41).

Some studies have focused on the symmetry of the components of the complex. Eisenstein et al. (42) constructed the symmetrical structure of the helical protein coat of tobacco mosaic virus. Later, a similar approach was used to assemble cyclic and dihedral symmetrical structures (43, 44). Comeau and Camacho (45) also predicted cyclic and dihedral symmetrical structures. In addition, they assembled oligomers starting from dimers. Schneidman-Duhovny et al. (38) developed a protocol for the construction of cyclic symmetrical structures, and Huang et al. (46) were able to dock C2 symmetrical dimers. Andre et al. (47) developed a protocol for predicting symmetrical assemblies starting from the structure or the sequence of a single subunit. Imposing symmetry constraints in the protocol limits the space of the predictions, making it unsuitable for the prediction of nonsymmetrical protein complexes. Nonsymmetrical complexes have not been studied as much as symmetrical ones. Inbar et al. (41) developed a protocol for the construction of hetero-multimolecular protein assemblies. In this multimolecular assembly protocol, CombDock, subunits are considered as “puzzle pieces” and the native complex as the “puzzle solution.” CombDock considers all pairwise dockings and combinatorially builds the final assembly. Finding the right combination is computationally hard (nondeterministic polynomial-time hard) (41); therefore, CombDock uses a heuristic based on the greedy construction of subassemblies. The protocol has been used successfully to reconstruct a protein complex from its components. However, computing all pairwise dockings (N units, N(N − 1)/2 pairwise sets of docking configurations) still presents challenges in terms of the computation time and, in particular, might miss solutions where the complexes are less stable as dimers but gain stability in the larger assembly.

Thus, the capabilities of current procedures are limited. Integrative procedures mainly depend on the experimental data, and manual adjustment and curation are necessary. Ab initio docking procedures are computationally expensive; others are limited by considerations of symmetry. There is a need for a procedure that constructs homo-/hetero-complexes and symmetric/asymmetric complexes without the computational cost of ab initio docking, considers possible conformational changes, and is applicable to large-scale studies. This study aims to take steps toward addressing this need. Here, we exploit a template-based protein interaction prediction tool, PRISM (Protein Interactions by Structural Matching) (48–50), to predict binary interactions through structural motif searching and use these predictions to construct protein assemblies. This is done based on the observation that proteins tend to interact via recurring motifs, regardless of the global similarity of the structures of the chains (51, 52). Previously, we tested it on a docking benchmark dataset and on interactions of different pathways. It was able to predict almost all the “easy” cases (87 out of 88 cases) (53) and two-thirds of the “difficult” cases (54) of a docking benchmark dataset, and it had high accuracy in predictions of the interactions in the ubiquitination (76% accuracy) (55) and apoptosis (78% accuracy) (56) pathways. In addition, we have shown that it can be used to model structural networks (57, 58). The success of PRISM is encouraging with regard to the much-needed modeling of multimolecular assemblies. One major difference between our approach and CombDock is that we do not consider all possible pairwise interactions and instead use template-based pairwise interactions, expected to be much fewer than N(N − 1)/2.

MATERIALS AND METHODS

This section presents the input data; PRISM, the tool used to predict binary protein–protein interactions; the method used to construct protein assemblies based on the PRISM predictions; and the identification of different conformations of the proteins.

Protein Assembly Benchmark and Evaluations of the Predictions

We prepared a benchmark of the protein assembly structures from the Protein Data Bank (PDB).¹ The benchmark included eight structures (Table I): three three-chain and three four-chain assemblies with different numbers of homologous chains, and one assembly of five- and seven-chain assemblies. Assemblies were selected in different sizes, ranging between 290 and 1,452 residues in total, and subunits ranged between 58 and 363 residues. Asymmetric/symmetric and homo-/hetero-complexes were experimentally obtained in different resolutions ranging between 1.50 and 2.90 Å and covering small proteins and four main Structural Classification of Proteins (59) classes: all α proteins, all β proteins, α or β proteins (a/b), and α and β proteins (a+b). The similarity of chain sequences to other chain sequences was between 0.3% and 32.6% (the average was 11.1%, and the median was 9.8%), and the identity was between 0.3% and 18.5% (the average was 6.7%, and the median was 5.7%). The benchmark included symmetrical cyclic structures (PDB I.D.s: 2e86, 1b0c, and 1wnr), which are the most challenging structures for our method, because it is difficult to add the last protein and complete the cyclic structure based on binary interactions. Unbound forms of the proteins and their structural difference relative to bound forms are given in supplemental Table S1. Predictions are evaluated based on structural similarity to the PDB structure and the energy score. Structural similarity was measured based on the root-mean-square deviation (RMSD) values calculated for backbone atoms (N, Cα, C, O) of all residues. The energy value of an assembly is the summation of energy values calculated for the addition of each protein. Chimera (60) version 1.6.2 was used to dock structures into an EM density map. The EM density map data was taken from the EMDataBank (61), and the “fit” command was used to obtain 30 results.

Table I. Structural features of the benchmark proteins.

PDB I.D.	Protein name	Number of chains	Homologous chains	Number of residues in chains	Total residue	Resolution (Å)	Structural type	SCOP class
2e86	Copper-containing nitrite reductase trimer	3	3	3 × 337	1011	1.50	Symmetric, homocomplex	All β proteins
1eer	Erythropoietin complexed with its receptor	3	2	2 × 227	620	1.90	Asymmetric, heterocomplex	All β proteins
			+1	+166				All α proteins
1gp2	G protein heterotrimer: Gi α 1–β 1–γ 2	3	1	353	764	2.30	Asymmetric, heterocomplex	α and β
			+1	+340				Proteins (a/b)
			+1	+71				All β proteins
								All α proteins
1ado	Aldolase tetramer	4	4	4 × 363	1452	1.90	Asymmetric, homocomplex	α and β
								Proteins (a/b)
1z0k	Rab GTPase complexed with rabenosyn-5	4	2	2 × 172	482	1.92	Asymmetric, heterocomplex	α and β
			+2	+2 × 69				Proteins (a/b)
								All α proteins
1akj	MHC class I glycoprotein HLA-A2 with T-cell coreceptor CD8	4	1	276	615	2.65	Asymmetric, heterocomplex	All β proteins
			+1	+99				α and β
			+2	+2 × 120				Proteins (a+b)
1b0c	Pancreatic trypsin inhibitor	5	5	5 × 58	290	2.80	Symmetric, homocomplex	Small proteins
1wnr	10-kDa chaperonin	7	7	7 × 94	658	2.90	Symmetric, homocomplex	All β proteins

Pairwise Protein Interaction Prediction Using PRISM

PRISM (48–50) is a knowledge-based method. It is a motif-based protein interaction modeling tool that can be used in proteome-scale studies (48). PRISM structurally compares query proteins with the known interacting protein pairs. If it is known that proteins A and B interact, that query protein A′ has a surface similar to the binding site of protein A, and that query protein B′ has a surface similar to the binding site of protein B, it is claimed that there may be an interaction between proteins A′ and B′. PRISM considers interaction A–B as a template and offers a potential interaction A′–B′ according to the structural similarity of A′ to the interface site of A and of B′ to the interface site of B. The template set is constructed from all known interactions in the PDB (62, 63). Interfaces of known interacting pairs are extracted and clustered according to their structural similarity. The template set organization depends only on the structural similarity of the interfaces (Fig. 1, step 0); this is because interface structures are conserved independently of the proteins' functions and global structures (64–67). Homologous chains with similar structures (90% of residues are matched within 2.0 Å) are counted only once in the target set. The surfaces of query proteins (or target proteins) are extracted (Fig. 1, step 1) and aligned onto template interfaces to check whether there is structural similarity among the structures (Fig. 1, step 2). PRISM uses three conformations for each target protein–template alignment. To guarantee that there is a proper match between the target surfaces and the template interfaces in the alignment, PRISM checks whether the matched residues of both sides are against each other and at least one residue of the target surface matches identically with a hotspot of the template interface. Hotspots are residues that contribute more to the binding energy of the interaction than the other interacting residues (68). There is also a high correlation between hotspots and conserved residues (69–71). Thus, PRISM searches both structural and evolutionary similarities in protein interaction predictions. After that, PRISM checks whether the candidate interaction is physically and chemically meaningful. First, physical clashes between residues of two interacting proteins are found, and the interaction is discarded if there are many clashes (Fig. 1, step 3). The side chains of residues undergo a reorientation process to eliminate clashes, and the global energy score of the candidate protein complex is calculated (Fig. 1, step 4). In this flexible refinement process, backbones of proteins are also slightly reoriented. At the end, PRISM predicts the three-dimensional structures of the interacting proteins.

Fig. 1.

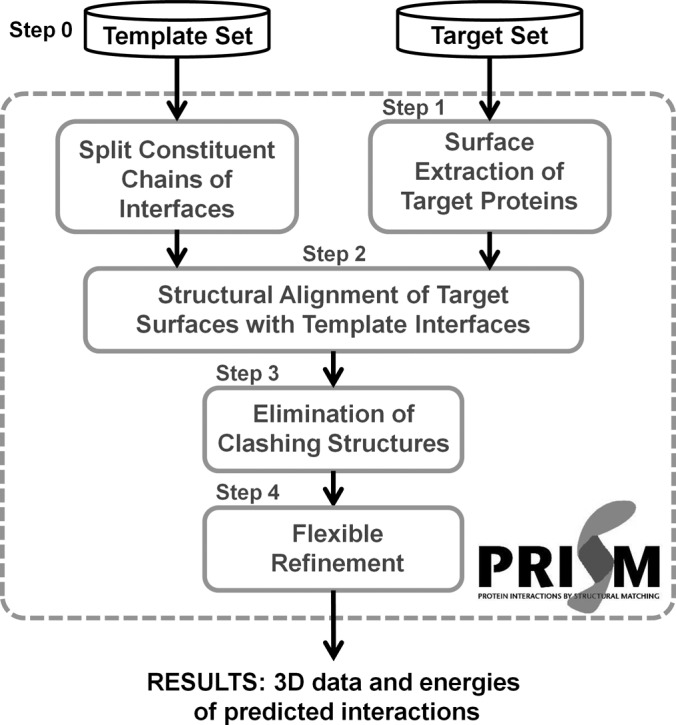
PRISM algorithm. Steps 1–4 constitute the PRISM flowchart. Inputs are template and target datasets, and outputs are three-dimensional structures of predicted binary interactions and their energies. Step 0 is the template organization, step 1 is surface extraction of target proteins, step 2 is the structural alignment process, step 3 is elimination of clashing structures, and step 4 is the flexible refinement process.

Constructing Protein Assemblies Based on PRISM Predictions

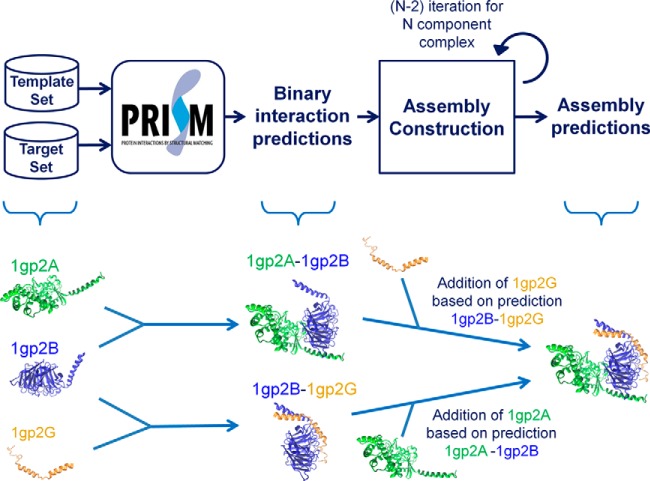
The construction of the protein assemblies based on PRISM predictions is illustrated in Fig. 2. In the prediction of binary interactions, query proteins are submitted as the target set, and the template set can be chosen according to the types of interactions being searched. It can include interface templates related to a certain pathway (such as ubiquitination (55) or apoptosis (56)), a certain template interface group (interfaces of obligate or non-obligate interactions (72)), or all template interfaces (57). If there is no information about the assembly, interactions of the query proteins can be searched using the whole template set. Because we construct assemblies based on binary interactions, we need to set a threshold energy value for binary interactions. Supplemental Table S2 shows FiberDock energies of the interfaces in the benchmark. One pair of homologous chains is given in the table. The highest energy value is −13.74. In a previous study (54), we considered results with at most −10 energy units as biologically favorable. The user can set another threshold energy value. We processed nonredundant biologically favorable results in the assembly construction. Only one of the solutions for the same proteins and with the same energy value was selected for further processing to eliminate repetitious computation.

Fig. 2.

Assembly construction based on PRISM binary predictions. First PRISM predicts binary interactions among target proteins. Then, assembly is constructed in an iterative process. N − 2 iterations are needed to construct an N-component assembly. Proteins are added one by one at each iteration based on PRISM binary predictions. There the protein to be added is transformed according to the PRISM prediction and the flexible refinement step of PRISM is run for the addition. The protein is added if the energy calculated is favorable.

Assembly construction starts with an interacting protein pair, which is a PRISM prediction. In the first iteration, another protein is bound to one of these interacting proteins based on the corresponding predicted PRISM interaction between the protein to be added and the one in the first interaction. First, the protein to be added is transformed next to the subassembly structure (as in step 3 of PRISM in Fig. 1) and flexible refinement is done for this candidate interaction (as in step 4 of PRISM in Fig. 1). The candidate protein can be a new protein or one of the proteins in the first pair. The assembly construction process is carried out starting with each nonredundant biologically favorable PRISM interaction, and each candidate protein is assessed in terms of whether it can be added based on the interactions predicted by PRISM. All possible combinations are considered. The addition of a protein can give as many solutions as the number of nonredundant biologically favorable predictions. To shorten the computation time, some specific interactions (e.g. the ones with the lowest energy values) can be processed. However, there is no guarantee that the assembly will be constructed based on the biologically most favorable predictions.

For an N component assembly, the addition process is performed N − 2 times (because it starts with a binary interaction). At each iteration, nonredundant biologically favorable predictions are filtered. The protein is added to the subassembly if the interaction has an energy below the cutoff value of −10 energy units. The process is aborted before the assembly reaches the specified number of components if another protein cannot be added to the subassembly with a sufficiently low energy value. The solution set can have similar structures. We clustered assembly results based on their structural similarity. Alignment and RMSD calculations are performed using version 1.9.1 of the VMD (Visual Molecular Dynamics) tool (73). The RMSD threshold was taken as 3.0 Å, considering backbone heavy atoms (N, Cα, C, O) of all residues. We chose the structure with the lowest energy score as representative of the cluster.

Identification of Different Conformations of the Proteins

Different conformations of query proteins were identified from the PDB as in our previous study (54). Chains of PDB structures with the same sequence as the query protein are detected using sequence homology. 100% FASTA sequence homology between the molecules is considered. Then, the different structures are detected by structural alignment using MultiProt (74). If MultiProt matches the candidate structure with less than 90% of the query structure or if the RMSD value between the matched residues of the two structures is more than 2.0 Å, the candidate structure is considered as a different conformation of the query protein. The RMSD value is calculated for backbone heavy atoms of all residues. Assemblies are constructed considering each structure (query proteins and their alternative conformations) as individual structures.

RESULTS

Protein assembly construction was performed for three scenarios: first, starting from the bound forms of the components; second, starting from the unbound forms of the components; and third, considering alternative conformations of the unbound forms.

Reconstruction of Assemblies

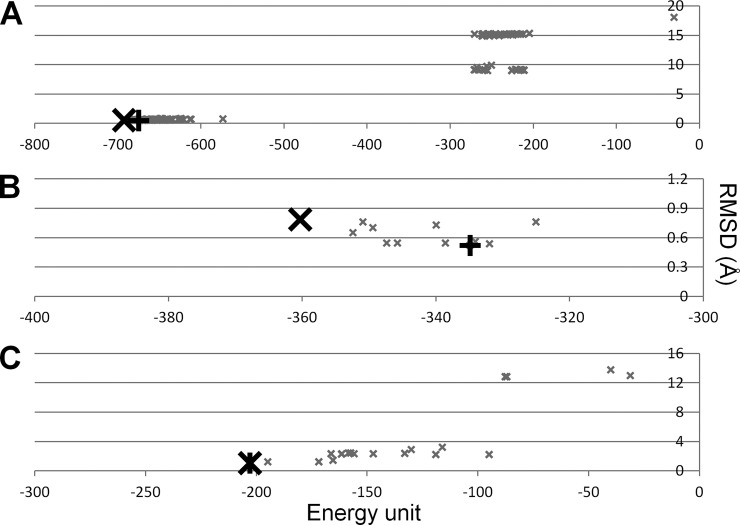
In the first part, assemblies were decomposed into their components and the components were treated as individual structures. Fig. 2 explains how the assembly was constructed based on PRISM predictions. Components (or chains) of the assemblies were submitted as the target set. We reconstructed three-unit assemblies in the benchmark with PDB I.D.s 2e86, 1eer, and 1gp2. We calculated the RMSD of predictions compared with the PDB structure and set the energy score of an assembly as the summation of the energy scores calculated at each protein addition. The RMSD versus energy score is plotted in Fig. 3. The best energy prediction is the best RMSD prediction (e.g. 1eer) or has an RMSD value close to the best RMSD value (e.g. in 2e86, the best energy and RMSD predictions have 0.53 and 0.51 Å, respectively, and for 1gp2 the best energy and RMSD predictions have 0.79 and 0.52 Å, respectively). We considered the energy as the indicator in subsequent steps. We clustered the predictions based on structural similarity. The RMSD values among the predictions were calculated using VMD. We selected the best energy prediction in each cluster as the representative. The best representative predictions (as judged by the similarity to the PDB structures) are given in Table II (details in supplemental Table S3, in which the first binary interaction prediction is given as step 0 and the nth iteration in the assembly construction is step n; all structurally different predictions are listed in supplemental Table S4). The reconstruction of the assemblies suggests that our method works, but we need to construct assemblies starting from the unbound forms of proteins to be more realistic.

Fig. 3.

Energy score versus RMSD of predictions. Energy score (energy unit) versus RMSD (Å) is given for three reconstructed assemblies: (A) 2e86, (B) 1gp2, and (C) 1eer. The best energy prediction and the best RMSD prediction are denoted by larger black crosses (X) and black plus signs (+), respectively. Others are shown with smaller gray crosses. In A, predictions with energy scores lower than −600 have RMSD values of 0.5 to 1.0 Å. The best energy and the best RMSD predictions are the same structure in C.

Table II. Results for construction of protein assemblies starting from their components.

PDB structure	Number of chains	Number of residues	Structurally different predictions	Energy unit	RMSD (Å)
2e86	3	1011	9	−692.94	0.53
1eer	3	620	6	−203.02	1.09
1gp2	3	764	1	−360.33	0.79

Predicted PDB structures are given with their PDB I.D., number of chains, and number of residues. RMSD was calculated compared to the PDB structures for all backbone atoms, and the energy value of an assembly is the summation of energy values calculated for the addition of each protein. These are the best RMSD representatives of the structurally clustered predictions.

Construction of Assemblies from Unbound Protein Structures

In the second part, PDB structures were assembled starting from the unbound forms of the components. The same procedure was followed as in the first part (Fig. 2). We constructed all assemblies in our benchmark starting from their unbound forms, listed in supplemental Table S1. Homologous chains are given together in the table. Predictions were structurally clustered, and the best energy prediction in each cluster was chosen as the representative. The best RMSD representatives, their unbound form sets, and the results are listed in Table III (details in supplemental Table S5, where the first binary interaction prediction is given as step 0 and the nth iteration in the assembly construction is given as step n; all structurally different predictions are given in supplemental Table S6). If a protein was used twice it is labeled “x2.”

Table III. Results for the construction of protein assembly starting from the unbound forms of the components.

PDB structure	Number of chains	Number of residues	Unbound forms	Structurally different predictions	Energy	RMSD
2e86	3	1011	1et5A x3	1	−694.70	0.52
1eer	3	620	1buy, 1ernA x2	9	−75.58	5.56
1gp2	3	764	1giaA, 1tbgA, 1tbgE	1	−279.38	3.57
1ado	4	482	1aldA x4	15	−324.79	2.79
1akj	4	615	2clrA, 2clrB, 1cd8A x2	5	−272.70	2.57
1z0k	4	482	2bmeA x2, 1yzmA x2	13	−104.58	3.07
1b0c	5	290	9ptiA x5	23	−109.12	5.15
1wnr	7	658	3nx6A x7	13	−426.80	4.60

Predicted PDB structures are given with their PDB I.D., number of chains, and number of residues. If an unbound structure is used twice, it is denoted by “x2.” RMSD was calculated compared to the PDB structures for all backbone atoms, and the energy value of an assembly is the summation of energy values calculated for the addition of each protein. These are the best RMSD representatives of the structurally clustered predictions.

Assembly construction of benchmark proteins resulted in up to 23 different structures. The construction of 2e86 and 1gp2 has one representative structure; the construction of 1b0c has 23 representative structures. In each case, one of these results matches the PDB structure; the RMSD values of the best representative structures ranged between 0.52 and 5.56 Å, which suggests that our method can construct assemblies starting from their unbound forms. However, we also had results that differed from the PDB structures. These may be different conformations of the assemblies or false positives. For example, one of the results for 1b0c had an RMSD value of 23.29 Å. In the construction of this assembly, the template interface 1aalAB was used four times. 1aalAB is a dimer interface of trypsin inhibitor, yet it is structurally different from interfaces in 1b0c. In 1b0c, trypsin inhibitors interact head-to-head and form a star shape. However, in 1aal, the interaction is head-to-tail with a wider angle. Besides structurally different results, we could obtain results structurally close to the PDB structures. However, we need methods to construct assemblies whose structures are unknown. Experimental data on mutations or from different techniques such as EM, small angle x-ray scattering, and FRET can help in the selection of the most appropriate structure as the result, which is covered below.

Exploiting EM Data in Assembly Construction

Here, we used experimental data to point out a predicted structure as the solution. 1wnr is a heptamer of 10-kDa chaperonin. In the construction of 1wnr starting from its unbound form, we obtained 13 different structures. We exploited the EM density map to select the solution. The EM density map of co-chaperonin protein 10 complexed with GroEL and ADP, where 10-kDa chaperonin is at the top of the structure, is available in the EMDataBank (EMD 1531). We docked 13 solutions into the EM density map using Chimera. Only one result matched with the top of the density map (Fig. 4). Chimera calculated the correlation as 0.85, and that result had the lowest RMSD (4.60 Å) among those 13 structures. It did not fit perfectly into the density map, because it does not have a perfectly symmetrical cyclic shape. However, an RMSD of 4.60 Å is still acceptable. The density map helped us to choose the structure with the best RMSD from among those 13, which suggests that experimental data such as EM density maps can help in choosing the solution.

Fig. 4.

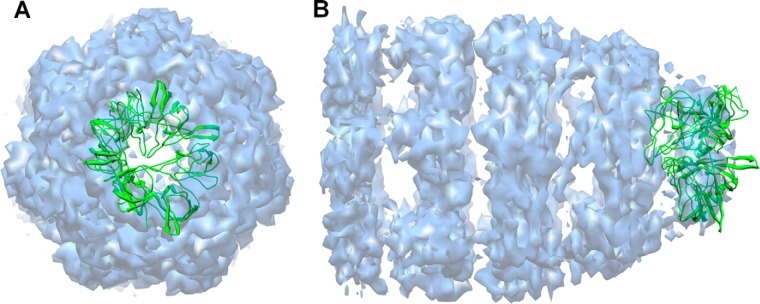
Predicted structure docked in the EM density map. The structure (green) is docked in the EM density map (blue, EMD I.D.: 1531) using Chimera. 30 solutions are created using the “fit” command. Top (A) and side (B) views are given.

Considering Alternative Conformations in the Construction of an Assembly

Proteins are flexible and can change their conformations upon binding. Therefore, constructing a protein assembly starting from unbound forms of the components might lead to unsuccessful predictions. An assembly can be constructed more successfully with the help of different conformations of the query proteins (54). The PDB offers different conformations of proteins, including their unbound, bound, or any alternative forms such as mutants, those obtained following post-translational modifications, or those of different crystal forms. We identified PDB structures with 100% sequence homology to the query proteins and determined the structurally different ones using structural alignment as described in “Materials and Methods.” We obtained better results in the construction of 1eer and 1gp2 using alternative conformations (3.23 Å RMSD rather than 5.56 Å for 1eer, and 2.50 Å RMSD rather than 3.57 Å for 1gp2). In this part, predictions with the lowest energy value were selected for each binary interaction, and the assemblies were constructed based on only these binary interactions. Alternative conformations of these proteins can be found in supplemental Table S7, and the results of the assembly construction using these alternative conformations are given in Table IV (details in supplemental Tables S5 and S8; the first binary interaction prediction is given as step 0 and nth iteration).

Table IV. Results for the construction of protein assemblies starting from alternative conformations of the unbound forms.

PDB structure	Number of chains	Number of residues	Target set	Energy unit	RMSD (Å)
1eer	3	620	1gia, 1tbgA, 1tbgE	−75.58	5.56
1eer	3	620	1gia, 1gg2A, 1tbgA, 1tbgE	−122.19	3.23
1gp2	3	764	1buyA, 1ernA x2	−279.38	3.57
1gp2	3	764	1buyA, 1ernA x2, 1cn4C, 1ebaA x2	−376.18	2.50

Predicted PDB structures are given with their PDB I.D., number of chains, and number of residues. Target set includes unbound forms and their alternative conformations found in the PDB. If an unbound structure is used twice, it is denoted by “x2.” Different target sets are used: (i) a target set of unbound forms and (ii) a target set of unbound forms and their alternative structures. Their best energy predictions are compared with respect to energy scores and RMSD values. RMSD was calculated for all backbone atoms, and the energy value of an assembly is the summation of energy values calculated for the addition of each protein.

DISCUSSION

The availability of structures of multimolecular associations, even if the interactions are short lived, is essential. This is our aim here. Using our method, we first reconstructed three-unit protein assemblies in the benchmark starting from the assembly components, obtaining low RMSDs. We next tested the modeling of protein assemblies starting from the unbound forms and also obtained good results (0.52 to 5.56 Å). Because we construct assemblies based on binary interactions, the most challenging cases are the symmetric cyclic assemblies. To complete the cyclic structure, the last protein is docked into limited space and interacts with more than one chain, which affects the energy calculation and may cause clashes. We obtained good results also in constructing such symmetric cyclic structures in the cases that we tried. Knowledge-based methods, including PRISM, do not consider the protein flexibility, except in the last refinement step, where backbones and side-chains of the structures can be slightly reoriented. To partially address this handicap, here we exploited different conformations of the proteins, if these were available in the PDB.

Modeling of multimolecular assemblies from monomeric structures of their components is computationally challenging with a broad solution space. To reduce this space, we select the energetically more favorable predictions of binary interactions. However, the possibility always exists that we will miss biological solutions that, although less favorable for binary interactions, become more stable as the assembly grows. Such a situation is also encountered in hierarchical folding strategies (75, 76), as discussed for CombDock (41), which also suffers from this handicap. Another problem is choosing the right prediction. Although the energy value can be an indicator, similar to protein folding, this is not always the case. Experimental techniques such as Cryo-EM, FRET, and small angle x-ray scattering, which provide low-resolution data on assemblies, can be used to help select the solutions. Here, we used EM data for 10-kDa chaperonin complexed with GroEL and ADP. Only one structure fit at the top of the EM density map, where 10-kDa chaperonin is present, and that is our best result.

Other caveats relate to PDB structures that do not always represent the entire protein or the functional state. In addition, flexible fragments and disordered domains are missing. Although it is often possible to model these when handled individually, it is more difficult on a large scale. We are currently including high-quality modeled structures (57), which may partially alleviate this problem. Further, the coverage of the interface architectures by a template set based on the PDB affects PRISM predictions and hence the assembly construction. Nonetheless, we were able to successfully construct protein assemblies thanks to the current PDB richness and experimental data such as EM density maps.