Homotropic Cooperativity from the Activation Pathway of the Allosteric Ligand-Responsive Regulatory Protein TRAP

Abstract

The trp RNA-binding Attenuation Protein (TRAP) assembles into an 11-fold symmetric ring that regulates transcription and translation of trp-mRNA in bacilli via heterotropic allosteric activation by the amino acid tryptophan (Trp). Whereas nuclear magnetic resonance studies have revealed that Trp-induced activation coincides with both μs-ms rigidification and local structural changes in TRAP, the pathway of binding of the 11 Trp ligands to the TRAP ring remains unclear. Moreover, because each of eleven bound Trp molecules is completely surrounded by protein, its release requires flexibility of Trp-bound (holo) TRAP. Here, we used stopped-flow fluorescence to study the kinetics of Trp binding by Bacillus stearothermophilus TRAP over a range of temperatures and we observed well-separated kinetic steps. These data were analyzed using non-linear least-squares fitting of several two- and three-step models. We found that a model with two binding steps best describes the data, although the structural equivalence of the binding sites in TRAP implies a fundamental change in the time-dependent structure of the TRAP rings upon Trp binding. Application of the two binding step model reveals that Trp binding is much slower than the diffusion limit, suggesting a gating mechanism that depends on the dynamics of apo TRAP. These data also reveal that Trp dissociation from the second binding mode is much slower than after the first Trp binding mode, revealing insight into the mechanism for positive homotropic allostery, or cooperativity. Temperature dependent analyses reveal that both binding modes imbue increases in bondedness and order toward a more compressed active state. These results provide insight into mechanisms of cooperative TRAP activation, and underscore the importance of protein dynamics for ligand binding, ligand release, protein activation, and allostery.

Ligand-responsive proteins are able to regulate essential biological functions because their structure and dynamics are altered via binding to partner molecules (8). These phenomena are understood not only by comparing different states of the protein, but by describing the pathways that link them. Here, we characterize the activation pathway of the undecameric (11-mer) trp RNA-binding Attenuation Protein (TRAP), which regulates biosynthesis of the amino acid tryptophan (Trp) in bacilli (9) via a feedback mechanism involving interaction of TRAP with the nascent trp-mRNA transcript in response to its ligand, Trp. In the absence of Trp, “apo” TRAP is inactive for binding trp-mRNA, which is therefore transcribed in full and translated. When Trp is abundant, up to eleven Trp molecules bind to TRAP, and its “holo” form is active for binding trp-mRNA. The binding of TRAP to trp-mRNA induces transcription termination prior to the structural genes of the operon, thereby precluding trp expression and Trp biosynthesis. TRAP also regulates translation of the trpE and trpD gene products by altering accessibility of the mRNA Shine-Dalgarno sequence (9). Apo TRAP is thought to be inactive for RNA binding because its flexibility masks the RNA binding site, and Trp binding both rigidifies and alters the local structure of TRAP (Fig. 1) such that the target RNA can bind tightly and specifically. This mechanism is supported by several prior studies: (i) nuclear magnetic resonance (NMR) studies that compare the μs-ms dynamics of apo and holo TRAP (1,10), (ii) calorimetric experiments that quantify a large reduction in heat capacity upon Trp binding (11), and (iii) gel mobility shift assays that indicate apo TRAP binds RNA at low temperature (i.e., conditions under which flexibility is reduced) (12). Crystallographic studies corroborate the disorder of apo TRAP (12) and reveal that holo TRAP forms many specific contacts with Trp (13,14), RNA (15), and an inhibitory protein Anti-TRAP (16).

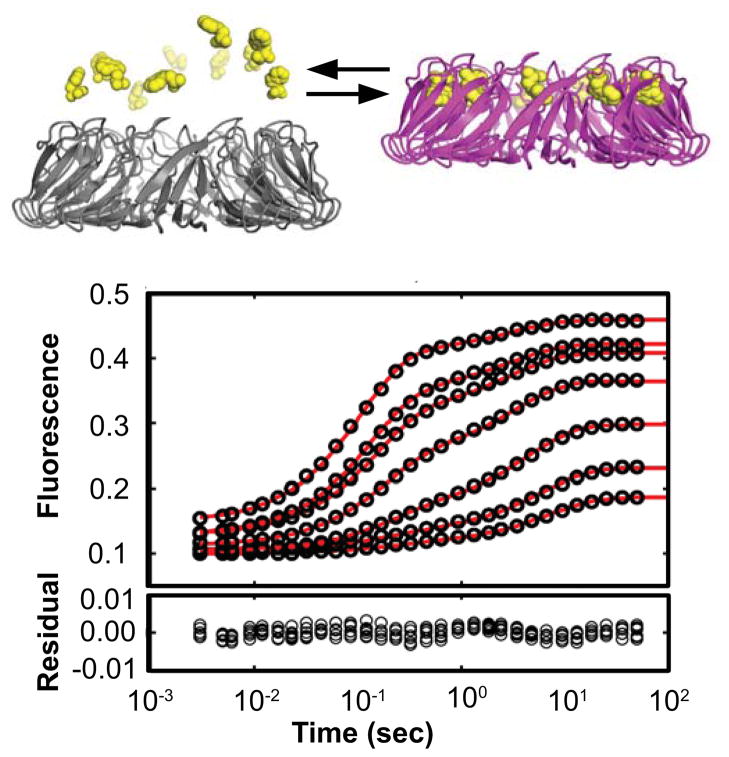
Figure 1.

Stopped-flow experiments reveal well-resolved kinetic steps during TRAP activation by Trp binding. (Top) Apo-TRAP is inactive for RNA binding (grey) due to its disordered loops and RNA binding surface. Un-decameric TRAP is activated (magenta) upon binding eleven Trp ligands (yellow), which results in coupled folding and rigidification of the RNA binding surface. (Bottom) The seven transients correspond to 1 μM Trp mixed with 0.1–2.0 μM TRAP 11-mer (1.0–22.3 μM binding sites). These transients were acquired at 25°C and similar high-quality data were obtained at seven temperatures in total: 15, 20, 25, 30, 35, 40, and 45°C (Fig. S3). The red line is the fit to a two step model describing Trp binding followed by a second Trp binding event (designated the Bind-Bind or “BB” model). Although the systematic residuals at ~1 second suggest an additional kinetic step, the BB model is a prudent simplification, as discussed in the text.

Whereas direct comparisons between the structure and flexibility of the free and bound states reveal features coincident with activation, considering that up to 11 Trp ligands can bind a TRAP ring, the pathway and time course of this activation process is less clear. Moreover, crystallographic data indicate that bound Trp is completely surrounded by protein (13,14), indicating that its release requires flexibility of holo TRAP. Finally, prior studies of Trp binding homotropic cooperativity have been limited in experimental breadth (17,18) and/or quantitative insight (19), leaving unresolved the magnitude and mechanism of the effect. Here, we used stopped-flow (SF) fluorescence to monitor binding-associated changes in Trp fluorescence that follow rapid mixing of Trp and apo TRAP from Bacillus stearothermophilus (Bst), and observed multiple kinetic steps (Fig. 1). We then used nonlinear least squares fitting to test and explore mechanisms that could explain the kinetic observations. Whereas several two- and three-step models were tested, the most parsimonious model that fits the data describes two binding steps. Application of this branched two binding step model (BB) reveals that Trp binding is much slower than the diffusion limit, which suggests a gating mechanism that depends on the dynamics of apo TRAP. These data also reveal that the second Trp binding event exhibits 1.5 times faster binding, 100 times slower dissociation, and thus 150 times tighter binding than the first Trp binding event, revealing the kinetic mechanism for positive homotropic cooperativity. Furthermore, temperature-dependent analyses indicate that both Trp binding events yield increases in bondedness and order toward the active state. Finally, the rate constants for Trp release reveal that holo TRAP is flexible on the second and millisecond timescale. Interpretation of this two-step model in the context of the undecameric TRAP ring describes a process by which a dynamic protein is initially transiently bound by a sub-saturating fraction of ligands, followed by tighter binding by a second set of ligands. This multi-step process thus leads to activation of TRAP for RNA binding and subsequent transcriptional and translational repression.

Materials and Methods

Sample preparation

Mutagenesis, expression, and purification of Bst A26I TRAP (designated “TRAP”) were described previously ((1); see Supporting Information), except that no isotope labeling scheme is utilized here. To accommodate these and other binding experiments, a large stock of TRAP and Trp were each stored in reaction buffer: 100 mM NaCl, 50 mM NaPO₄, pH 8.0 at 25°C, 0.02% NaN₃. TRAP stock was 60 mL at 6.82 ± 0.18 μM 11-mer (75 ± 2 μM binding sites), with concentration measured using UV absorbance at 280 nm with ε = 2,980 M⁻¹cm⁻¹, calculated using ProtParam (20). Trp stock was prepared by adding crystalline Trp (USB Corporation) to buffer matched to the TRAP stock via dialysis, at a concentration of 2,030 ± 43 μM based on diluted samples that were quantified by UV (278 nm, ε = 5,579 M⁻¹cm⁻¹ (21)). All SF experiments utilized one dilution of Trp: ~200 mL at 1.034 μM, and seven dilutions of TRAP: ~8 mL each at 11-mer concentrations of 0.093, 0.164, 0.323, 0.664, 1.008, 1.350, and 2.027 μM (1.022, 1.800, 3.558, 7.306, 11.088, 14.846, and 22.292 μM binding sites), designated A–G, respectively. Because accurate concentrations are essential for analysis, all samples were prepared from their respective stocks with dilution factors measured using an analytical balance that is precise to 0.1 mg (~0.1 μL).

Stopped-flow fluorescence measurements

SF experiments were performed 3–8 times to ensure high-quality data for averaging, using an Applied Photophysics SX.18MV instrument. For each time course, 75 μL of Trp was mixed with equal volume of TRAP (A–G) or buffer, resulting in 50% dilution of the solutes. Data were acquired in pseudo-random order through the temperature range of the instrument: 15, 20, 25, 30, 35, 40, and 45°C (also pseudo-randomized) for a duration of 50 sec (100 sec at 15°C) using 500 points during the first 0.1 sec, then 500 points for the remaining time with log-time sampling in each segment. The excitation wavelength was 295 ± 5 nm and the detection range was ≥ 320 nm with the photo-multiplier tube gain set to 450 volts.

Processing stopped-flow data

For each Trp-TRAP concentration and temperature, each time course was smoothed using a third degree polynomial Savitsky-Golay filter with a 5 point window size. Next, within each Trp-TRAP concentration and temperature, the smoothed time courses were averaged (the number of time courses ranged from 2–8; average ± standard deviation 3.8 ± 1.0; some time courses were removed due to experimental artifacts like air bubbles and the entire 1.350 μM TRAP time course at 15°C was anomalous and was therefore discarded completely). Then to allay the effects of photobleaching apparent especially at higher temperatures, each set of averaged traces was truncated to the time point as soon as the fluorescence signal reached its upper plateau, which occurred after 50, 50, 30, 20, 10, 5, and 5 sec for 15, 20, 25, 30, 35, 40, and 45°C traces respectively. Finally, the smoothed, averaged, and truncated time courses were resampled with exponential spacing to 30 points per trace in order to more equally weight the early and late phases of the time course in the subsequent nonlinear fitting analyses. These data processing steps were performed using DYNAFIT v. 4 (22,23).

Initial fits to stopped-flow data

For each Trp-TRAP concentration and temperature, the observed rate constant, k^Obs, for each of the kinetic phases was determined by fitting the time-dependent fluorescence signal F(t) to a sum of exponential functions, $F(t)=B+{\displaystyle \sum _i^N}{F}_i\left(1-exp\left(-{tk}_i^{\mathit{Obs}}\right)\right)$, where t is time and the fitted parameters are: B, the baseline fluorescence, F_i, the fluorescence maximum for phase i, and k_i^Obs, the observed rate constant for phase i. Fits to N = 2, 3, and 4 exponential functions were examined for each concentration and temperature (i.e., for each processed stopped flow trace described above). For each trace, the Bayesian Information Criterion (BIC) was used to assess whether the 2, 3, or 4 exponential fit was most appropriate. Nonlinear fitting and the subsequent calculation of the Bayesian Information Criterion was performed using DYNAFIT.

For each phase and temperature, the relationship between k^Obs and TRAP concentration were fit to either (a) a linear equation, k^Obs(c_TRAP) = k^F c_TRAP + k^B, where c_TRAP is the molar concentration of TRAP, and k^F and k^B are the forward and reverse kinetic rate constants in units of M⁻¹sec⁻¹ and sec⁻¹, respectively, or (b) a hyperbolic equation, k^Obs (c_TRAP) = k^F/(1 + K_d / c_TRAP) + k^B, with variable parameters K_d, k^F, and k^B, where K_d is the dissociation constant for the preceding phase, and k^F and k^B are the forward and reverse kinetic rate constants, both in units of sec⁻¹ (24). Non-linear fitting was performed using MATLAB (Mathworks, Inc.).

Testing kinetic models

To extend the simplified analysis, stopped flow data were fit directly to several discrete mechanistic models without simplifying assumptions of pseudo-first-order pre-equilibrium conditions by explicit derivation of appropriate differential equations, followed by numerical integration and iterative nonlinear fitting. The program DYNAFIT was used to globally fit all time courses for each temperature by specifying the post-mixing concentrations of Trp and TRAP for each time course, and to perform statistical model testing. For the two-step Bind-Bind (BB) model selected for further analysis, a pair of binding sites on TRAP (T_T) was modeled that can bind 0, 1, or 2 Trp molecules (W) (Scheme I).

Scheme I.

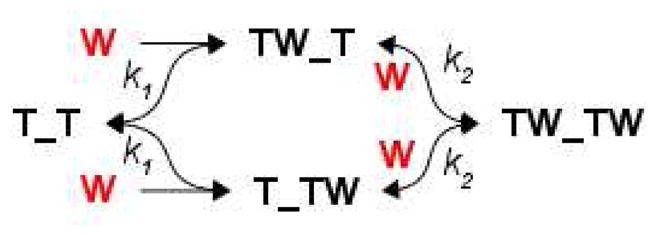
The fluorescent signal was fit to the sum of ordinary differential equations describing the signal from each species: (1) $\frac{d\left[T\_T\right]}{dt}=-2k_1^F\left[T\_T\right]\left[W\right]+k_1^B\left[T\_TW\right]+k_1^B\left[TW\_T\right]$,(2) $\frac{d\left[W\right]}{dt}=-2k_1^F\left[T\_T\right]\left[W\right]+k_1^B\left[T\_TW\right]+k_1^B\left[TW\_T\right]-k_2^F\left[T\_TW\right]\left[W\right]-k_2^F\left[TW\_T\right]\left[W\right]+2k_2^B\left[TW\_TW\right]$, (3) $\frac{d\left[T\_TW\right]}{dt}=k_1^F\left[T\_T\right]\left[W\right]-k_1^B\left[T\_TW\right]-k_2^F\left[T\_TW\right]\left[W\right]+k_2^B\left[TW\_TW\right]$, (4) $\frac{d\left[TW\_T\right]}{dt}=k_1^F\left[T\_T\right]\left[W\right]-k_1^B\left[TW\_T\right]-k_2^F\left[TW\_T\right]\left[W\right]+k_2^B\left[TW\_TW\right]$, and (5) $\frac{d\left[TW\_TW\right]}{dt}=k_2^F\left[T\_TW\right]\left[W\right]+k_2^F\left[TW\_T\right]\left[W\right]-2k_2^B\left[TW\_TW\right]$. The fitted parameters were the four microscopic kinetic rate constants for the forward and reverse paths of each step, k₁^F, k₁^B, k₂^F, k₂^B, the concentration-dependent fluorescence responses of the Trp-bound species R(T_TW) = R(TW_T) and R(TW_TW), all but one of the TRAP concentrations used (to account for volume-delivery errors during stopped-flow experiments), and baseline offsets for each time course. Note that because identical responses and microscopic rate constants are assumed, independent of pathway, the branched BB mechanism above is algebraically identical to an unbranched pathway with a single intermediate state, but we apply a branched pathway because the microscopic rate constants allow us to consider the statistical weights implicit in ligand binding to a molecule with two classes of sites. A similar set of differential equations were derived in an automated fashion for nine other multiple-step mechanisms using DYNAFIT (see Supporting Information). Confidence intervals in each fitted parameter were estimated using 1,000 iterations of Monte Carlo analysis that re-fit simulated data that were re-sampled by shuffling residuals from the best fit to the data (25), which was implemented in DYNAFIT. Confidence intervals in parameters derived from combinations of kinetic rates (e.g., K₁ = k₁^F / k₁^B) were estimated by computing the desired parameter within each of the 1,000 Monte Carlo simulations.

Calculation of encounter rate constants

To compare the experimentally observed binding rate to the diffusion limit, we estimated the encounter rate constant between Trp and its binding site on TRAP, as well as upper and lower limits of this value, based on geometric considerations (26). The upper limit considers TRAP as a sphere, with the encounter rate given by the Smoluchowski equation (27), k_Upper = 4πN₀(100R_Enc(D_Trp + D_TRAP))/1000, where N₀ is Avagadro’s number; the factors 100 and 1/1000 yield k_Upper in M⁻¹ sec⁻¹; R_Enc is the radius of the TRAP-sphere which was set to 36 Å based on the holo TRAP crystal structure (15) enlarged by 15% to reflect the more loosely-packed apo structure evidenced by diffusion measurements; D_Trp and D_TRAP are the diffusion coefficients in cm²sec⁻¹ for Trp and TRAP respectively, measured as 480 × 10⁻⁹ cm²sec⁻¹ and 5010 × 10⁻⁹ cm² sec⁻¹ at 25°C using dynamic light scattering and NMR, respectively (J. Sachleben, I. Kleckner, M. Foster, unpublished); subsequent analyses assumed 20% uncertainty in each quantity. The temperature-dependence of each diffusion constant was estimated from the Stokes-Einstein relation, D(T) = 1000k_BT / (6πR_Hη(T)), where k_B is the Boltzmann constant 1.23 × 10⁻²³ J·K⁻¹, T is the temperature in Kelvin, η(T) is the water viscosity at temperature T in N·sec·m⁻² (28), R_H is the Stokes hydration radius in meters, and the factor 1000 yields D in cm² sec⁻¹. The lower limit of encounter rate is given by the Solc and Stockmayer equation (29), k_Lower = k_UpperA_bind / (4πR_Enc²), which reduces k_Upper to account for the area of the Trp binding sites on TRAP, A_bind. Due to the lack of high-resolution structural details of apo TRAP, A_bind was estimated using the minimum cross-sectional area of a 11.1 × 7.5 × 7.2 ų rectangular prism that encloses the Van der Waals representation of a Trp molecule (i.e., 7.5 × 7.2 Ų = 54 Ų is the smallest area through which a single Trp molecule could fit). For first Trp binding, A_bind = 11 × 54 Ų = 594 Ų since there are 11 free sites per donut; for second Trp binding, A_bind = 6 × 54 Ų = 324 Ų since there are 6 free sites per donut (i.e., assuming that the first 5 Trp binding steps have no neighboring Trp molecules and the 2nd Trp binding steps have 1–2 neighboring Trp molecules). An intermediate value of the encounter rate constant is given by the Shoup equation (26), k_Intermed = k_Uppersqrt(A_bind/π) / (πR_Enc), which reduces the upper limit to account for A_bind, but is greater than the lower lower limit to account for rotational diffusion of TRAP, which effectively presents the binding area as larger than its geometric fraction. The probability of Trp binding upon encounter was calculated as the ratio of observed rate constant for binding to any single site, k₁^F, to the calculated rate constant for encounter with any single site: Pr(Bind) = k₁^F / k_Enc where k_Enc = k_Lower, k_Upper, or k_Intermed.

Extended Arrhenius analysis using temperature-dependence of rate constants

To thermodynamically describe three ground states, T_T, T_TW, and TW_TW, and the two transition states, [T_TW]^‡ and [TW_TW]^‡, the temperature-dependence of fitted rate constants were subjected to Arrhenius analysis using the extended relation, which includes a non-zero transition state heat capacity change ΔC_p^‡, as implied by curvature in the Arrhenius plots (30,31):

$$ln\left(\frac{k(T)}{k(T_0)}\right)=\frac{\mathrm{\Delta }{H}_0^{‡}}{R{T}_0}-\left(\frac{1}{RT}\right)\left(\mathrm{\Delta }{H}_0^{‡}+\mathrm{\Delta }{C}_p^{‡}\left(T-T_0-Tln\left(\frac{T}{T_0}\right)\right)\right)$$ (1)

Here, k(T) is the fitted rate constant from the SF data at absolute temperature T, with the reference temperature T₀ = 298 K used to compare dimensionless quantities among all the steps (32); R is the gas constant 1.985 cal·K⁻¹ mol⁻¹, ΔH₀^‡ is the activation enthalpy at T₀ with ΔH^‡(T) = ΔH₀^‡ + ΔC_p^‡(T-T₀), and ΔC_p^‡ is the activation heat capacity, assumed to be independent of temperature. For each of four steps, the fitted rate constants k(T) at seven temperatures were fit to equation (1) using MATLAB to extract either (a) only ΔH₀^‡, while ΔC_p^‡ was fixed to zero, or (b) both ΔH₀^‡ and ΔC_p^‡, if ΔC_p^‡ was allowed to be non-zero. Although introducing non-zero values of ΔC_p^‡ did not result in statistically significant improvements in fits for all rate constants (Fig. S4), these were employed to retain consistency with both the principle of microscopic reversibility and with results from van’t Hoff analysis (below). Note, the sign of ΔC_p^‡ was inverted from (31) for consistency in obtaining ground state thermodynamic quantities from their transition state counterparts (i.e., to ensure that X^GS = X_F^‡ − X_B^‡, where X = G, H, S, or C_p, and X^GS designates a ground state quantity). Using ΔH₀^‡, the relative reference activation entropy was obtained at temperature T₀:

$$\mathrm{\Delta }{S}_{0,\mathit{Rel}}^{‡}=R\text{ln}\left(k\left(T_0\right)\right)+R\text{ln}\left(\frac{h}{k_B}\right)+R\text{ln}\left(\frac{1}{T_0}\right)+\frac{1}{T_0}\mathrm{\Delta }{H}_0^{‡}-R\text{ln}\left(\kappa \right)$$ (2)

where h is Planck’s constant 6.626 × 10⁻³⁴ J·s, k_B is the Boltzmann constant 1.23 × 10⁻²³ J·K⁻¹, and κ is the transmission coefficient. Here, $\mathit{\Delta }{S}_{0,\mathit{Rel}}^{‡}$ was estimated using κ = 1, even though this violates the assumption of reversibility in the reaction mechanism (30), yielding a theoretical upper-limit for activation entropies and therefore a lower-limit for activation free energies, ΔG_0,Min^‡ = ΔH₀^‡ − TΔS_0,Max^‡. Moreover, although $\mathit{\Delta }{S}_{0,\mathit{Rel}}^{‡}$ is offset by an amount R·ln(κ) and therefore is inaccurate to the extent that κ is less than one (30), differences (but not ratios) in step-wise $\mathit{\Delta }{S}_{0,\mathit{Rel}}^{‡}$ values are accurate because factors of R·ln(κ) are subtracted away. Confidence intervals in these fitted parameters were estimated using 10,000 iterations of Monte Carlo resampling. Specifically, for each of 10,000 iterations, one data point at each temperature was randomly sampled from the 1,000 Monte Carlo fits used to generate confidence intervals in kinetic rate constants at that temperature (mentioned above). In this way, an across-temperature simulated dataset was generated and fit 10,000 times.

Extended van’t Hoff analysis using temperature-dependence of equilibrium constants

In the Arrhenius analysis the ΔS_0,Max^‡ values were lower-limits and the ΔG_0,Min^‡ values were upper limits because the value of the transmission coefficient κ in equation (2) is not known, but was assumed to be the maximum value of 1. In the van’t Hoff analysis, this limitation is circumvented because equilibrium constants are ratios of rate constants (or differences in ΔG^‡) and therefore the κ term is removed. Specifically, the equilibrium constants are K_i = k_i^F/k_i^B = exp(−ΔG_i/RT) for steps i = 1 or 2. Like the Arrhenius analyses, the extended form of the van’t Hoff relation was used to compare fits of the data using (a) ΔC_p fixed to zero, and (b) ΔC_p optimized to a non-zero value during fitting (33):

$$ln\left(\frac{K\left(T\right)}{K\left(T_0\right)}\right)=\frac{\mathrm{\Delta }{H}_0-T_0\mathrm{\Delta }{C}_p}{R}\left(\frac{1}{T_0}-\frac{1}{T}\right)+\frac{\mathrm{\Delta }{C}_p}{R}ln\left(\frac{T}{T_0}\right)$$ (3)

Here, K(T) is each equilibrium constant obtained from fits to the SF data at absolute temperature T, with reference temperature T₀ = 298 K used to compare dimensionless quantities among all the steps (32), R is the gas constant 1.985 cal·K⁻¹mol⁻¹, ΔH₀ is the enthalpy at T₀ with ΔH(T) = ΔH₀ + ΔC_p(T-T₀), and ΔC_p is the temperature-independent heat capacity. For each of three equilibria, the input data K(T) were supplied at seven temperatures and were fit to equation (3) using MATLAB to either (a) only ΔH₀, while ΔC_p was fixed to zero, or (b) both ΔH₀ and ΔC_p, if ΔC_p was allowed to be non-zero. Confidence intervals in these fitted parameters were estimated using 10,000 iterations of Monte Carlo resampling as described above for Arrhenius analyses. For ground state quantities, the following relations were used to obtain thermodynamic quantities at non-reference temperatures: ΔG(T) = −RTln(K(T)), ΔH(T) = ΔH(T₀) + ΔC_p(T-T₀), and ΔS(T) = (ΔH – ΔG) / T.

Results

Trp binding to TRAP occurs in multiple kinetic steps

To characterize the time-dependent pathway for Trp binding and TRAP activation, we used a stopped-flow (SF) apparatus to rapidly mix Trp and apo TRAP¹ in solution while measuring the time-resolved fluorescence of Trp, which is sensitive to its local electronic environment (Fig. 1)(34); the TRAP protein itself possesses no tryptophan residues, which would complicate data interpretation. Each of ~49 fluorescence time courses were acquired using a fixed concentration of Trp mixed with one of seven concentrations of TRAP acquired at one of seven temperatures between 15 and 45°C (Fig. S3). These data clearly demonstrated that Trp binding occurs through at least two time-resolved steps, with time constants ranging from ~0.1 sec to ~10 sec, (Fig. 1). Mechanistically, because these data reflect changes in bulk Trp fluorescence, the observed steps could report structural changes in TRAP related to its activation (i.e., isomerization) and/or multiple Trp-binding events, since each TRAP oligomer can bind up to eleven Trp molecules.

At most of the temperatures and TRAP concentrations sampled, the major features of the binding curves could be captured by a two-step process described by a two-phase exponential function, although additional kinetic steps are implied by the non-random small residuals (Fig. 1). Indeed, a three-step process is statistically preferred over two-step or four-step process when comparing two-, three-, and four-phase exponential functions in their ability to fit the data (Fig. S1, Table S3). As discussed below, although at least one additional step is implicit in the binding mechanism, we proceed with a two-step model for quantitative analyses of fitted rate constants because the two-step model captures most of the features of the data, and more complex models yield poorly constrained fitted parameters.

A two-step kinetic model for Trp binding to TRAP

To learn more about the mechanisms of the kinetic steps evident in the data, we explored the concentration-dependence of the apparent rate constants obtained from fitting the two- and three-phase exponential decay functions (a four-phase exponential fit is not discussed further because it is too complex, as mentioned above). The two-phase analysis revealed a near linear relationship between k₁^Obs and [TRAP], while k₂^Obs exhibits a hyperbolic relationship to [TRAP] (Figs. 2, S2). These relationships are consistent with a mechanism where the second step involves the product of the first step. The three-phase analysis suggests that an additional step occurs between the first and second steps from the two-phase analysis (i.e., the two-phase steps 1 and 2 correspond to the three-phase steps 1 and 3; Fig. S2). Although estimates of microscopic forward and reverse rate constants can be obtained by assuming linear and hyperbolic dependencies of the apparent rate constants for the kinetic phases (Table S2), we obtained more accurate forward and reverse rate constants by globally fitting data to differential equations via numerical integration because not all of the data were recorded under simplifying pseudo-first order conditions.

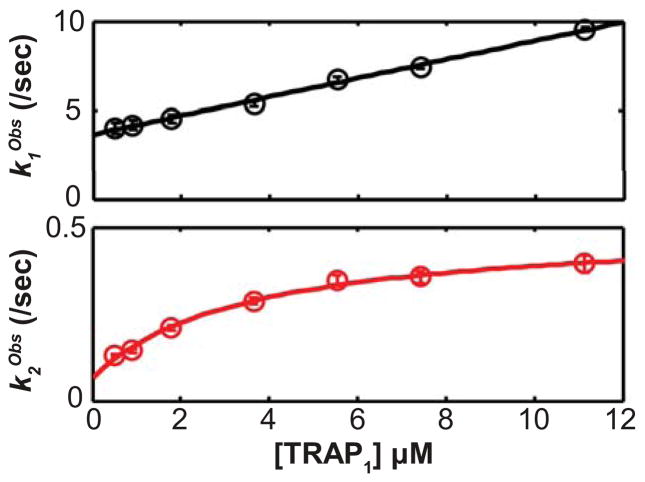
Figure 2.

The concentration-dependences of the mechanism-independent apparent rate constants for a two-step process reveal that the second step mechanistically follows the first step. (Top) The faster (first) step exhibits a linear relationship between k^Obs and the total TRAP concentration, [TRAP]. (Bottom) The second (slower) step exhibits a hyperbolic relationship between k^Obs and [TRAP]. These data correspond to 25°C and are corroborated by data at other temperatures (Fig. S2, Table S2). Error bars show the standard errors from fitting the time-dependent SF data to a two-phase exponential function. This behavior supports analysis of the data using a two-step mechanism.

To identify the best mechanism to describe these data, several candidate mechanisms were fit to the data by numerical integration of differential equations that arise from each mechanism, each of which included two or three binding and/or isomerization steps (see Supporting Information)². We used the program DYNAFIT to globally fit the 6–7 TRAP concentrations within each temperature and to statistically compare mechanistic models. As discussed in the supporting information, we found the two-step Bind-Bind (BB) model to best describe the data (Scheme I). The BB model describes Trp binding to a pair of binding sites (T_T) using four microscopic rate constants: (1) k₁^F for first Trp binding $\mathrm{T}\_\mathrm{T}+\mathrm{W}\stackrel{k_1^F}{\to }\mathrm{T}\_\text{TW}$ and $\mathrm{T}\_\mathrm{T}+\mathrm{W}\stackrel{k_1^F}{\to }\text{TW}\_\mathrm{T}$, (2) k₁^B for first Trp release $\mathrm{T}\_\text{TW}\stackrel{k_1^B}{\to }\mathrm{T}\_\mathrm{T}+\mathrm{W}$ and $\text{TW}\_\mathrm{T}\stackrel{k_1^B}{\to }\mathrm{T}\_\mathrm{T}+\mathrm{W}$, (3) k₂^F for second Trp binding $\mathrm{T}\_\text{TW}+\mathrm{W}\stackrel{k_2^F}{\to }\text{TW}\_\text{TW}$ and $\text{TW}\_\mathrm{T}+\mathrm{W}\stackrel{k_2^F}{\to }\text{TW}\_\text{TW}$, and (4) k₂^B for second Trp release $\text{TW}\_\text{TW}\stackrel{k_2^B}{\to }\mathrm{T}\_\text{TW}+\mathrm{W}$ and $\text{TW}\_\text{TW}\stackrel{k_2^B}{\to }\text{TW}\_\mathrm{T}+\mathrm{W}$. The model also includes parameters related to how each molecular species contributes to the observed fluorescence data, and it accounts for volume-delivery errors (see Materials and Methods). In TRAP, because the ligand binding sites are equivalent, differences in the rate constants for first and second binding events implies allosteric coupling between binding sites.

Tighter second Trp binding reveals the mechanism of homotropic allostery

To assess the degree of cooperativity between the first and second Trp binding modes, we compared the binding and dissociation rates (k_i^F and k_i^B) and affinities (K₁ = 1 / K_d1 = k₁^F / k₁^B and K₂ = 1 / K_d2 = k₂^F / k₂^B) of the first and second binding steps (Table 1). The microscopic rate constant for the second Trp binding mode is moderately faster (1.4 to 2.5 times) than that of the first, indicating that Trp binding exhibits modest positive cooperativity in a kinetic sense (i.e., the activation free energy ΔG^‡ decreases after first binding). However, a much greater difference was found in the rate constants for dissociation (k₁^B, k₂^B), which differ by two orders of magnitude (Table 1); the data indicate that ligand dissociation after the second binding mode is ~100 times slower than after the first mode. Consequently, the affinity of second Trp binding is ~130 times tighter than the affinity of first Trp binding, indicating that Trp binding is positively cooperative in a thermodynamic sense (i.e., the binding free energy G decreases after first binding).

Table 1.

Fitted parameters from analysis of kinetic data using the BB model^a

T (°C)	k1F (μM−1sec−1)	k1B (sec−1)	k2F (μM−1sec−1)	k2B (sec−1)	R(T_TW)	R(TW_TW)	Kd1 (μM)	Kd2 (μM)	K2/K1
15	0.23 [0.22, 0.24]	0.97 [0.92, 1.03]	0.33 [0.30, 0.36]	0.011 [0.010, 0.012]	0.75 [0.74, 0.77]	1.37 [1.35, 1.39]	4.25 [3.99, 4.54]	0.033 [0.029, 0.037]	128 [110, 154]
20	0.34 [0.34, 0.35]	1.80 [1.73, 1.88]	0.52 [0.49, 0.56]	0.018 [0.017, 0.019]	0.78 [0.76, 0.80]	1.35 [1.34, 1.36]	5.23 [4.98, 5.51]	0.034 [0.031, 0.037]	153 [134, 173]
25	0.51 [0.50, 0.52]	3.52 [3.37, 3.68]	0.80 [0.75, 0.85]	0.036 [0.035, 0.038]	0.84 [0.82, 0.87]	1.36 [1.35, 1.38]	6.93 [6.53, 7.32]	0.045 [0.042, 0.049]	153 [133, 175]
30	0.65 [0.63, 0.67]	6.87 [6.63, 7.13]	1.20 [1.13, 1.28]	0.077 [0.075, 0.080]	0.88 [0.85, 0.92]	1.34 [1.32, 1.35]	10.57 [9.99, 11.16]	0.064 [0.060, 0.069]	164 [145, 186]
35	0.83 [0.79, 0.86]	13.30 [12.83, 13.78]	1.70 [1.58, 1.84]	0.171 [0.166, 0.176]	0.94 [0.89, 0.99]	1.33 [1.31, 1.35]	16.03 [15.02, 17.22]	0.100 [0.092, 0.109]	160 [138, 188]
40	1.01 [0.92, 1.08]	24.04 [22.96, 25.13]	2.14 [1.84, 2.49]	0.420 [0.403, 0.435]	0.93 [0.84, 1.05]	1.34 [1.29, 1.40]	23.91 [21.23, 27.26]	0.196 [0.164, 0.231]	122 [92, 167]
45	1.18 [0.80, 1.48]	48.52 [45.01, 52.25]	2.93 [2.04, 4.80]	0.879 [0.834, 0.928]	1.08 [0.83, 1.66]	1.35 [1.21, 1.53]	41.12 [30.69, 64.00]	0.300 [0.177, 0.442]	137 [70, 359]

^aThe kinetic parameters k₁^F, k₁^B, k₂^F, and k₂^B correspond to the kinetic steps first Trp binding, first Trp release, second Trp binding, and second Trp release, respectively. The two “response” parameters, R(T_TW) and R(TW_TW), are proportional to the quantum yield of the bound states. The “μM” units on k₁^F and k₂^F correspond to the concentration of TRAP binding sites (i.e., 11 times [TRAP₁₁]). 95% confidence intervals estimated using Monte Carlo analyses are shown in the brackets. K₂/K₁ = K_d1/K_d2 and is the ratio of the equilibrium association constants obtained from the ratios of the forward and backwards rate constants, K_i = k_i^F/k_i^B.

Trp binding is much slower than the diffusion limit

The observed rate constant for first and second Trp binding, k₁^F and k₂^F, ranged from 0.22 to 2.9 μM⁻¹ sec⁻¹ from 15 to 45°C. To compare k₁^F and k₂^F with the diffusion-limited encounter rate constant between Trp and its binding site on TRAP, the area of the binding site is estimated as the minimum cross-sectional area of Trp, and two additional geometric considerations provide upper and lower limits for comparison (26) (Fig. 3a). Upon dividing the binding rates by the encounter rates at each temperature, we find that Trp binding upon encounter is highly unlikely, with only a 0.016% to 0.136% chance of binding upon encounter (i.e., only 1-in-6,000 to 1-in-700; Fig. 3b). Such unproductive collisions imply a large population of conformations that do not favor binding, either though occlusion or poor complementarity, and that binding-permissive conformations are sampled rarely.

Figure 3.

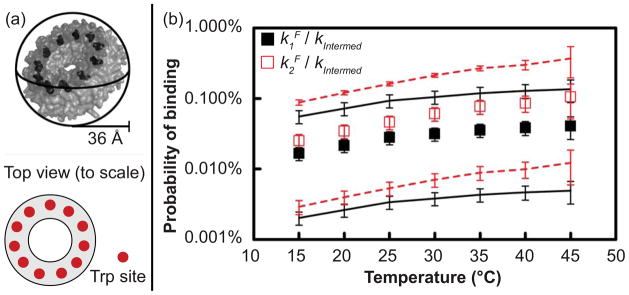
Low probability of Trp binding upon encounter with TRAP implies ligand gating. (a) Three geometric considerations of TRAP determine upper and lower limits of the Trp-TRAP encounter rate constants. The upper limit considers TRAP as a sphere, the lower limit reduces this value to account for the area of the Trp binding sites (eleven red circles on cartoon), and the intermediate value increases the lower limit to account for rotational diffusion of TRAP, which effectively presents the active area as larger than its geometric value. (b) The probability of binding upon encounter is obtained by dividing the observed binding rate constant, k₁^F or k₂^F, by the calculated encounter rate constant, k_Enc; this indicates only a 0.016% to 0.136% chance of binding upon encounter (i.e., only 1-in-6,000 to 1-in-700 events), which increases at higher temperatures. Black and red squares indicate the binding probabilities for binding steps 1 and 2, respectively, while the lines indicate upper and lower limits on the binding probability, as calculated using lower and upper limits of the encounter rate constant (see materials and methods). Error bars are propagated from 95% confidence intervals for k₁^F and k₂^F and uncertainties in geometric quantities. The probability of second binding is slightly higher than that of first binding, reflecting that k₂^F is greater than k₁^F and that fewer empty sites are available for second binding.

Arrhenius analysis reveals step-wise reduction in heat capacity upon Trp binding to TRAP

To gain structural insight regarding the two binding steps, the temperature-dependence of the four kinetic rate constants from the BB model are interpreted using an extended Arrhenius analysis. The analysis yields the activation enthalpies ΔH^‡, heat capacities ΔC_p^‡, minimum entropies ΔS_0,Min^‡, and maximum free energies ΔG_0,Max^‡ (31,35) (Table 2, Fig. 4) that compare each of the ground state and transition state structures. Data at 45°C were not included in the Arrhenius or van’t Hoff temperature dependent analyses, as the fitted rate constant values were outlying and poorly defined at this temperature (Fig S6). Curvature in the Arrhenius plots require the use of a non-zero ΔC_p^‡ term (Figs. 4, S4), which implies a change in both the extent of conformations sampled and in solvent accessible surface area (36) between the ground states and transitions states. The analysis reveals similar negative ΔC_p^‡ for the forward reactions k₁^F, k₂^F (−404, −335 cal mol⁻¹ K⁻¹), likely reflecting similar changes in solvation during the binding process. A much larger ΔC_p^‡ is observed for k₂^B than for k₁^B (+702, versus +104 cal mol⁻¹ K⁻¹), indicating that dissociation from the fully bound state involves an intermediate with substantially increased surface exposure and conformational diversity. The analysis reveals that the pathway for Trp binding to TRAP proceeds via intermediates with reduced C_p, and that dissociation from the doubly bound state involves much larger structural rearrangements than from the singly bound states.

Table 2.

Extended Arrhenius analysis fit results (T₀ = 25°C)^b

Thermodynamic Term	Step 1		Step 2
	Forward	Backward	Forward	Backward
ΔH0‡ (kcal·mol−1)	11.7 [11.0, 11.8]	22.8 [22.3, 23.6]	13.5 [13.1, 15.2]	25.2 [23.8, 25.4]
ΔCp‡ (cal·mol−1K−1)	−404 [−527, −349]	104 [40, 256]	−335 [−428, −23]	702 [640, 889]
ΔS0,Min‡ (cal·mol−1K−1)	108 [105, 108]	121 [120, 124]	114 [113, 120]	120 [116, 121]
ΔG0,Max‡ (kcal·mol−1)	−20.4 [−20.4, −20.4]	−13.4 [−13.4, −13.3]	−20.6 [−20.7, −20.6]	−10.7 [−10.7, −10.6]

^aThe thermodynamic terms ΔH₀^‡, ΔC_p^‡, ΔS_0,Minf^‡, and ΔG_0,Max^‡, an refer to the activation enthalpy, activation heat capacity, minimum activation entropy, and maximum activation free energy, respectively. The values of ΔH₀^‡ and ΔC_p^‡ are obtained by fitting the temperature-dependence of the kinetic rates (Table 1) to the extended Arrhenius equation (equation 1) using MATLAB. The values of ΔS_0,Min^‡ and ΔG_0,Max^‡ are obtained using ΔH₀^‡ in equation 2 and the relations in the materials and methods. 95% confidence intervals estimated using Monte Carlo analyses are shown in the brackets.

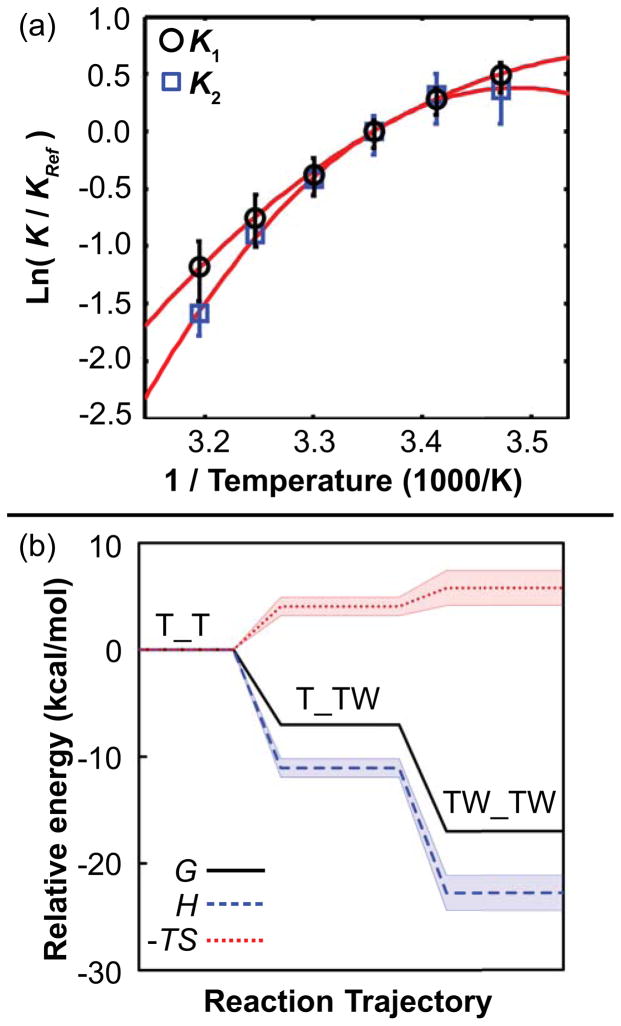
Figure 4.

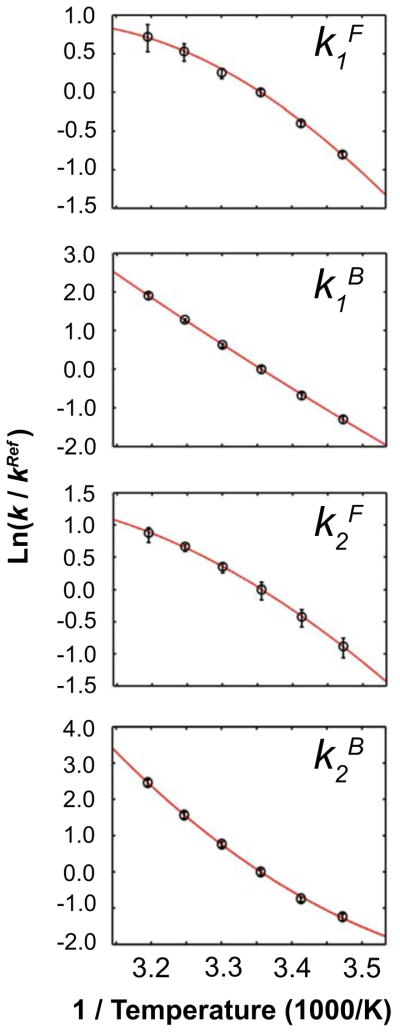
Extended Arrhenius analysis reveals the magnitude of heat capacity change for activation, ΔC_p^‡, that enable Trp binding to TRAP. The curvature in the Arrhenius plots describe the magnitude and sign of the activation ΔC_p^‡ between the ground state and transition states for each step. Error bars are 95% confidence intervals from a Monte Carlo error analysis propagated from the original stopped flow time courses. Negative values in the forward direction are indicated by convex curves while positive values of the reverse steps are determined by concave curves. ΔC_p^‡ is largest for binding of Trp to free TRAP, k₁^F, and dissociation of fully bound TRAP, k₂^B, indicating that those transitions involve larger changes in structure and solvation than the other two transitions.

Van’t Hoff analysis reveals that both binding steps increase bondedness and order

Ground state free energies G and entropies S were quantified by using the fitted rate constants to derive equilibrium constants and subjecting these to extended van’t Hoff analysis (33), which yields ΔG and TΔS in addition to ΔH and ΔC_p (Figs. 5a and S5, and Table 3). As shown from the reaction coordinate plot (Fig. 5b), both binding steps exhibit favorable changes in free energy and enthalpy, but an unfavorable loss of entropy (ΔG < 0, ΔH < 0, and −TΔS > 0, respectively). This reflects a step-wise increase in bondedness and order along the reaction coordinate, thus distinguishing the singly and doubly-bound states. Furthermore, as temperature increases from 15 to 45°C, Trp binding is favored less (K_d1 and K_d2 increase; Table 1).

Figure 5.

Extended van’t Hoff analysis reveals a step-wise increase in bondedness and order of the Trp-TRAP-solvent system upon Trp binding. (a) The van’t Hoff plot illustrates curvature for both steps, which are each fit with slope ΔH and curvature ΔC_p. Error bars are 95% confidence intervals from a Monte Carlo error analysis propagated from the original stopped flow time courses. (b) Energetic contributions from enthalpy H, and entropy -TS at 25°C along the reaction coordinate reveal that increased bondedness and order accompany favorable binding free energy G. The energy of the free state T_T is set to zero for reference, and the shaded regions enclose 95% confidence intervals from Monte Carlo analysis for obtaining G, H, and -TS via ΔH and ΔC_p from the extended van’t Hoff analysis.

Table 3.

Extended van’t Hoff analysis fit results (T_Ref = 25°C)^c

Thermodynamic Term	Step One (First Binding)	Step Two (Second Binding)
ΔH0 (kcal·mol−1)	−11.1 [−12.4, −10.7]	−11.7 [−11.9, −9.1]
ΔCp (cal·mol−1K−1)	−506 [−751, −419]	−1048 [−1240, −736]
ΔS0 (cal·mol−1K−1)	−13.6 [−18.0, −12.2]	−5.8 [−6.4, 3.0]
ΔG0 (kcal·mol−1)	−7.0 [−7.1, −7.0]	−10.0 [−10.1, −10.0]

^aThe thermodynamic terms ΔH₀, ΔC_p, ΔS₀, and ΔG₀, and refer to the enthalpy, heat capacity, entropy, and free energy, respectively. These values of ΔH₀ and ΔC_p are obtained by fitting the temperature-dependence of the equilibrium constants (Table 1) to the extended van’t Hoff equation (equation 3) using MATLAB. The values of ΔS₀ and ΔG₀ are obtained using additional equations described in materials and methods. 95% confidence intervals estimated using Monte Carlo analyses are shown in the brackets.

Discussion

Trp binding to TRAP proceeds via a well-defined kinetic intermediate

In vitro transcription assays indicate that the kinetics of RNA binding are important determinants to the effectiveness of transcription attenuation (37), thus drawing attention to the kinetics of TRAP activation via Trp binding. Stopped flow fluorescence experiments reported here reveal that the kinetics of Trp binding to TRAP proceed via at least two well-separated kinetic steps. We have applied a two-step Bind-Bind mechanism that is capable of describing the major features of the data, while judiciously ignoring the possibility that there are more than two configurations of partially bound TRAP 11-mer rings. Although this BB model is clearly a simplification, the fitted kinetic parameters and their temperature dependencies nevertheless provide bulk kinetic-thermodynamic insights into the pathway of ligand binding and activation of TRAP.

Trp binding to TRAP is positively cooperative

TRAP functions through heterotropic allostery, as RNA and Trp binding to TRAP are strongly coupled (38). Given the oligomeric structure of TRAP, its ligand-coupled disorder-order transition, and the geometric proximity of its ligand binding sites to one another, the question of its homotropic allostery, or cooperativity in Trp binding, have been of long-standing interest (39–41). Efforts to investigate this question using equilibrium dialysis and calorimetry have revealed weak positive cooperativity for B. subtilis TRAP (39), but not for Bst TRAP (42–44). The present results clearly establish positive cooperativity in Trp binding to Bst TRAP and provide a plausible mechanistic explanation for the phenomenon: initial weak binding by a fractional set of Trp ligands is followed by concerted structural changes that kinetically enable binding of additional Trp ligands, after which dissociation of the ligands is kinetically disfavored; we note also that the similar enthalpy changes for the two binding modes would complicate their detection by ITC as in references (43,44) (Table 1). Although the BB kinetic model does not explicitly include a kinetic step for conformational change, the fact that all of the Trp binding sites in the ring are structurally equivalent due to its axial symmetry requires that structural changes in the protein ring define the difference between binding modes that allow fast and slow ligand release. The nature of these structural changes is evident from the temperature dependence of the kinetic parameters, as described below.

The temperature dependence of stopped-flow data describe the structural differences between the ground states sampled by TRAP, and between their intermediates

The observed large reduction in heat capacity upon Trp binding (ΔC_p ~ −506 + −1048 = −1554 cal mol⁻¹ K⁻¹; Table 3) is much larger than obtained from equilibrium calorimetric studies of wild-type TRAP (−370 cal mol⁻¹ K⁻¹ (11); this difference in ΔC_p is perhaps due to different protein sequences and experimental observables, and perhaps because the value of −370 cal mol⁻¹ K⁻¹ was obtained under conditions where the energetics of each Trp binding event was not evident (33,45,46)). If a reduction in C_p is considered a metric for the conformational restriction/compression of TRAP, these results imply that (i) the free state T+W is relatively loosely packed, (ii) first Trp binding rapidly compresses TRAP through the transition state to the singly-bound ground state, and (iii) the singly bound state is compressed even further upon second binding to the doubly-bound ground state (Fig. 6). After accounting for solvation effects, this large negative ΔC_p implies a dramatic conformational restriction (36), which is mechanistically consistent with NMR studies that detail conformational restriction at the μs-ms timescale upon Trp binding (1,10).

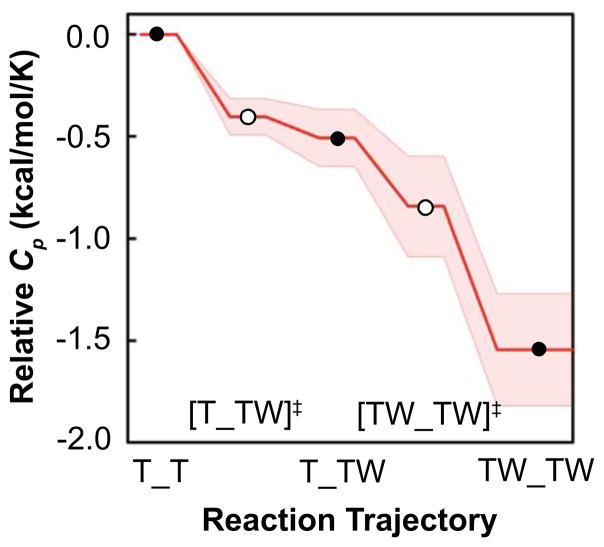
Figure 6.

Extended Arrhenius analysis reveals a step-wise structural compression of TRAP upon Trp binding, evidenced by reduction in heat capacity, C_p, along the reaction coordinate. The relative heat capacity along reaction coordinate results from changes in structure and dynamics between the three ground states marked with black circles (T_T, T_TW, and TW_TW) via the two transition states marked with white circles ([T_TW]^‡ and [TW_TW]^‡). A lower value of C_p is interpreted as a conformational restriction of the Trp-TRAP-solvent system that releases otherwise-bound solvent molecules. The C_p of the T_T state is set to zero for reference, and the shaded region encloses propagated fitting errors via the extended Arrhenius relation. The largest changes in C_p occur between the ground state of the free protein T_T and first transition state [T_TW]^‡, and between the second transition state [TW_TW]^‡ and fully bound state.

Kinetics and thermodynamics of TRAP isomerization influence function

The rate constant for Trp binding by TRAP, k₁^F, is small compared to that of other proteins that bind similarly-shaped ligands (i.e., 0.65 μM⁻¹sec⁻¹ at 30°C versus 1–1,000 μM⁻¹sec⁻¹ for other proteins (47)). For example, Trp binds to TRAP 6–100 times slower than it does to the trp repressor: NMR lineshape analyses found 4.4 μM⁻¹sec⁻¹ at 30°C (48), while stopped-flow fluorescence experiments with trp repressor yielded a rate constant of 4 μM⁻¹sec⁻¹ at 4°C (49); at that temperature, the Arrhenius analysis performed here predicts 0.066 μM⁻¹sec⁻¹ for TRAP. These kinetic differences highlight differences in the Trp binding modes, as for instance, Trp binds to the surface of each protomer in the trp repressor dimer, where it remains solvent-accessible (50), whereas Trp is buried between protomers in the TRAP 11-mer, where it is excluded from solvent (13). It is clear that Trp binding is orders of magnitude slower than hydrodynamic estimates of the diffusion limit for such encounters, even after considering uncertainties in the calculated encounter probability arising from estimates of the Trp binding area, and the diffusive encounter rate. Although low binding probability is not uncommon in other proteins (51,52), solution NMR studies have shown apo TRAP to be quite dynamic at the Trp site (1,10). This observation suggests that the flexible loops flanking the Trp binding site function as a dynamic gate, directly influencing the mechanism and rate of Trp entry and solvent exit (53–55).

In addition to modulating Trp binding to apo-TRAP, protein dynamics are important for allowing Trp release and deactivation. Because Trp is entirely buried in its fully-bound state, release of bound Trp implies flexibility of holo TRAP on the timescale of the release rate constant for the second bound state, k₂^B, which ranges from 0.01 sec⁻¹ to 0.88 sec⁻¹ between 15–45°C. Motions at these relatively slow timescales (1/k = 1.1 to 100 sec) are consistent with the observation that Ile 26δ₁ in the Trp loop samples two conformations in holo TRAP (1), though we note that Trp fluorescence likely only reports on dynamics of the binding pocket³. The fact that Trp release is slow relative to the timescale of bond rotations may reflect the requirement for a rare synchrony of individual local motions that occur at faster timescales (e.g., involving multiple residues or multiple protomers) (8). Indeed, such μs-ms motions have been observed near the RNA site and the core of holo TRAP, albeit to a small degree (1), and indicate that the dynamic landscape of holo TRAP is surprisingly rich.

Key insights and limitations

Technical limitations arise in interpretation of the physical observable in the stopped flow data, the Trp quantum yield Φ_Trp, because it is a one-dimensional value that is influenced by complex multi-dimensional effects from protein structure and dynamics (34). In the BB model applied here, the change in Φ_Trp that reports on the first and second steps are interpreted as reporting Trp binding in a manner independent of configuration or nearest-neighbor effects, but there also may be changes in Φ_Trp associated with a conformational change in TRAP surrounding bound Trp and/or a re-organization of Trp molecules within a TRAP 11-mer. Furthermore, Φ_Trp may change depending on the number of Trp molecules bound to a single TRAP 11-mer, but this change could not be quantitatively defined in models that describe conformational changes between binding events (e.g., model E [BIB] in the Supporting Information).

Moreover, although the BB model appears adequate to broadly describe the kinetics of Trp binding to TRAP, it is limited in its description of the eleven unique Trp binding sites on each TRAP ring. Considering the oligomeric nature of TRAP, the mechanism of the BB model implies two assumptions: (i) there are only two types of binding events in the 11-mer, implying that binding sites with one occupied neighbor are similar to those with two occupied neighbors (56), and (ii) each phase of the SF time course is exclusively binding. Thus, the BB model does not allow for a quantitative description of microscopic conformational changes in TRAP and/or a re-organization of Trp molecules within a TRAP 11-mer (i.e., Trp may be released from a kinetically favored site and rebound to a thermodynamically favored site). Despite these limitations, as discussed above the BB model represents a prudent simplification because more complex models cannot be quantitatively constrained by these data.

Conclusion

The functions of proteins are dependent on their structure and dynamics, which are characterized by a conformational landscape that is sensitive to a variety of factors including ligand binding, temperature, and pH (8). Here, we shed light on these phenomena by characterizing the pathway through which the protein TRAP is activated by the ligand Trp (Fig. 7). Prior studies have indicated that the flexibility of apo TRAP is important to prevent RNA binding (1,10). Here, we have expanded this view by showing that the flexibility of apo TRAP may play a role in gating the entry of Trp, shown here to involve over 6,000 unsuccessful attempts at some temperatures, as a possible mechanism for enhanced ligand selectivity (54,55). Moreover, the flexibility of apo TRAP may help characterize the extent to which any allosteric effects in TRAP involve induced fit or conformational selection mechanisms (51,52,57). Next, a two-binding-site kinetic model reveals the mechanism of positive homotropic cooperativity for Trp binding: weak binding by an initial set of Trp ligands is followed by a change in the structure and dynamics of TRAP that permits a higher affinity binding mode, from which Trp release is retarded by 100 fold. Next, although structural and thermodynamic studies have already indicated that holo TRAP is more bonded, more ordered, and more conformationally restricted than apo TRAP (11), our present kinetic data reveals that these interactions proceed in a step-wise manner through several intermediate states. Finally, despite the relative rigidity of holo TRAP (1,10), because Trp release from doubly-bound TRAP occurs on the sub-second timescale between two bound states, we conclude that the flexibility of holo TRAP on this timescale may be important for bound Trp to exit its otherwise buried binding site. Finally, considering that holo TRAP also exhibits flexibility on the μs-ms timescale (1,10), our results reveal that holo TRAP exhibits a rich dynamic behavior that illustrates how changes in the conformational landscape coincide with molecular function.

Figure 7.

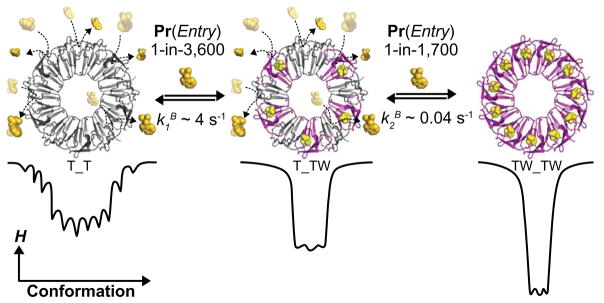
The Bind-Bind (BB) kinetic model for Trp binding to TRAP. The BB model might be understood structurally by considering binding of the first set of Trp molecule to sites without occupied neighboring sites, while the second set of Trp ligands bind after partial ring saturation has resulted in stabilization of a higher affinity binding mode; the figure illustrates one such possible intermediate. Quantitatively, the results of the Bind-Bind analysis reveal that in the free state (T_T), TRAP is conformationally diverse and Trp binding requires ~3,600 encounters before successful entry. Once the first Trp molecule binds, the Trp binding site undergoes a rapid conformational restriction (i.e. reduction in C_p) wherein initial Trp bonds are formed. Moreover, after first Trp binding, the neighboring Trp sites may be structurally and/or dynamically altered such that second Trp binding is ~50% faster and ~150 times tighter than first Trp binding. The binding probabilities and rate constants correspond to data at 25°C.

Abbreviations

TRAP

trp RNA-binding attenuation protein

Trp

tryptophan

W

tryptophan

NMR

nuclear magnetic resonance

SF

stopped-flow

Φ

quantum yield

sec

second

s

second

ms

millisecond (10⁻³ s)

μs

microsecond (10⁻⁶ s)

k

rate constant

K

equilibrium constant

G

Gibbs free energy

H

enthalpy

S

entropy

C_p

heat capacity

ΔX

change in quantity X (X,G, H, S, C_p)

X^‡

transition state quantity X