Insight into α-Synuclein Plasticity and Misfolding from Differential Micelle Binding

Abstract

Misfolded species of the 140-residue protein α-synuclein (αS) are implicated in the demise of dopaminergic neurons resulting in fatal neurodegeneration. The intrinsically unstructured protein binds curved synaptic vesicle membranes in helical conformations but misfolds into amyloid fibrils via β-sheet interactions. Breaks in helical αS conformation may offer a pathway to transition from helical to sheet conformation. Here, we explore the evolution of broken αS helix conformations formed in complex with SDS and SLAS micelles by molecular dynamics simulations. The population distribution of experimentally observed αS conformations is related to the spatial concentration of intrinsic micelle shape perturbations. For the success of micelle-induced αS folding, we posit the length of the first helical segment formed, which controls micelle ellipticity, to be a key determinant. The degree of micelle curvature relates to the arrangement and segmental motions of helical secondary structure elements. A criterion for assessing the reproduction of such intermediate timescale protein dynamics is introduced by comparing the sampling of experimental and simulated spin label distributions. Finally, at the sites of breaks in the elongated, marginally stable αS helix, vulnerability to forming a transient, intramolecular β-sheet is identified. Upon subsequent intermolecular β-sheet pairing, pathological αS amyloid formation from initial helical conformation is thus achievable.

Introduction

In aqueous solution, the 140-residue protein α-synuclein (αS) displays a high rate of spontaneous misfolding from intrinsically unstructured conformations into amyloid fibrils. This process correlates to protein mean charge, mean hydrophobicity, mean β-sheet propensity,^1,2 and the clustering but not the order of residues of high β-sheet propensity.³ The emergence of amyloid fibrils and misfolding intermediates relates to the demise of dopaminergic neurons in the substantia nigra region of the midbrain resulting in fatal neurodegeneration.^4–7 A hallmark of αS is an extensive amphiphilic sequence (residues D2-A89) of helical periodicity⁸ that interacts preferentially with negatively charged, highly curved membranes in helical conformation to stabilize such membranes.^9,10 In amyloid fibrils, a large portion of this sequence (residues L38-K96) converts to parallel, in-register β-sheet arrangements,^11,12 revealing a high structural plasticity for residues L38-K96. Amyloid formation by αS is a hierarchical process^3,13 and it is presently unclear what structural event(s) gives rise to the initial misfolded αS species that rapidly triggers further aggregation. Such insight is critical to rationalize and interfere with misfolding.

The association of αS with its in vivo target synaptic vesicles inhibits misfolding relative to its unfolded state, as determined by αS aggregation experiments using small unilamellar vesicles (SUV) as models for synaptic vesicles.¹⁴ However, the rarity of αS misfolding in vivo does not exclude contributions to misfolding from fluctuations in helical conformations on vesicle membranes.^15–18 On SUV, a single uninterrupted helix encompassing the αS amphiphilic sequence is stable^19,20 but only marginally, which can permit the emergence of transient helix breaks.¹⁶ We deem such breaks relevant to misfolding because they may offer the opportunity to form an intramolecular β-sheet structure that could initiate an intermolecular β-sheet assembly. Broken helix states are prevalent on a variety of spherical anionic micelles,^21–26 which makes these structures suitable starting points for molecular dynamics (MD) simulations to assess intermolecular β-sheet formation and general principles of αS-surfactant interactions.

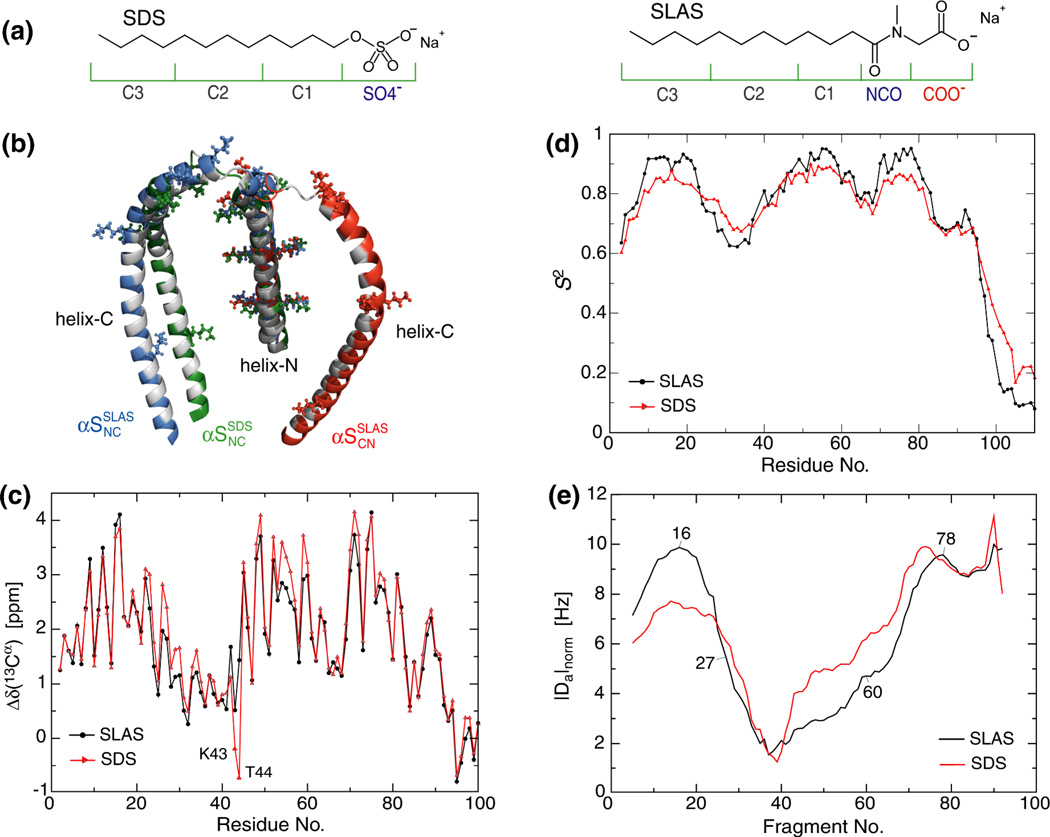
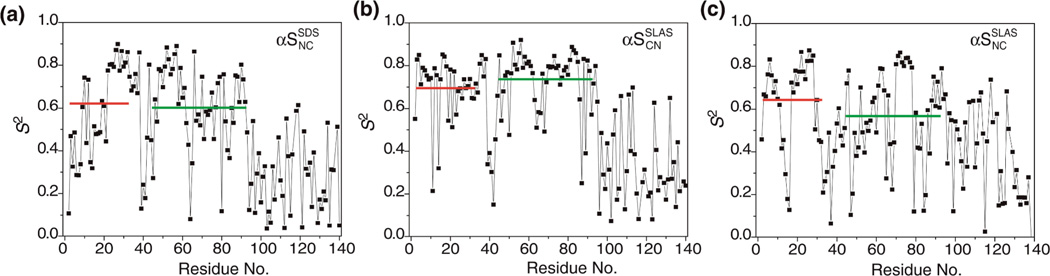
In complex with a sodium dodecyl sulfate (SDS; Figure 1a) micelle, the dominant conformation of αS, referred herein as αS^SDS_NC, was determined by NMR spectroscopy. It consists of two anti-parallel, non-interacting helices, termed helix-N and -C, that are connected by a short linker (Figure 1b).²¹ In complex with a sodium lauroyl sarcosinate (SLAS; Figure 1a) micelle, an innovative combinatorial NMR and EPR spectroscopic approach permitted the determination of all αS structures present.²⁷ Two conformations were revealed with the anti-parallel helices in NC and CN orientations at a relative ratio of 0.55:0.45, referred to as αS^SLAS_NC and αS^SLAS_CN, respectively (Figure 1b). Based on different detergent structures (Figure 1a), each micelle will provide a different folding scaffold for αS in terms of headgroup chemistry, surface area and curvature. Experimentally, the difference in scaffolding is reflected in the differences of a number of NMR parameters between SDS- and SLAS-bound αS states. For example, αS secondary ¹³C^[α] chemical shifts, Δδ(¹³C^[α]), which report on protein secondary structure conformation (Figure 1c), and general order parameters, S², and segmental variations in alignment tensor magnitudes, D_a, which reflect backbone dynamics on fast (pico- to nanosecond) and intermediate (nano- to millisecond) timescales, respectively (Figure 1d–e).^21,27

Figure 1.

Structural and dynamic properties of detergent micelle-bound α-synuclein. (a) Chemical structures of employed detergent molecules. The moieties that were represented by coarse grain beads are indicated. (b) Comparison of available micelle-bound αS structures. The structure of SDS-bound αS, termed αS^SDS_NC (PDB ID 1xq8, model 1), is colored in green. The structures of SLAS-bound αS, termed αS^SLAS_NC and αS^SLAS_CN (PDB ID 2kkw; model 34/configuration 93/N′C′/same and model 1/configuration 9/C′N′/same), are colored in blue and red, respectively. The structures were superimposed on the C^[α] coordinates of residues 13–29. The hydrophobic face of the amphiphilic αS helix is colored in gray and lysine residues are shown in ball-and-stick representation. (c) Comparison of SLAS- and SDS-bound αS secondary ¹³C^[α] chemical shifts. For ²H/¹³C/¹⁵N-labeled αS, random coil conformations are obtained at approximately −0.5 ppm, whereas positive and negative shifts relative to this value denote helical and extended backbone propensities, respectively.⁶⁷ Measurement uncertainties approximate the size of data symbols.²⁶ (d) General order parameter, S², derived from backbone ¹⁵N relaxation analysis using an isotropic model.^21,26,68,69 S² ranges from 0 for freely jointed motions to 1 for completely rigid bond vectors. Representative error bars are shown. (e) Variation of absolute alignment tensor magnitudes, |D_a|, obtained during molecular fragment replacement using a fragment length of 7 residues, along the sequence.^21,26 The fragment number denotes the center residue of each fragment. To compare SLAS- and SDS-bound αS, D_a values were normalized to minimize differences between fragments 78–88. The highly mobile, unfolded C-terminal tail residues of αS were omitted from all panels.

MD simulations have been used to probe the interaction of αS with SDS micelles and SDS micelle formation in the presence of αS,^28,29 providing important insight into the principles underlying the SDS-αS association. The present study compares αS interactions with SDS and SLAS micelles in initially coarse-grained MD simulations to examine the effects of different micelle scaffolds on the binding and evolution of broken αS helical conformations. To provide insight into αS folding and putative misfolding from helical conformations, the evolution of partially folded αS conformations on SDS and SLAS micelles is examined in all-atom MD simulations. To assess the level of αS folding and the extent of protein dynamics captured in these all-atom MD trajectories, experimental S² values (Figure 1d) and available EPR-derived spin label distance distributions²⁷ were compared to the corresponding computed parameters.

Experimental Methods

Translational diffusion measurements of SDS micelles

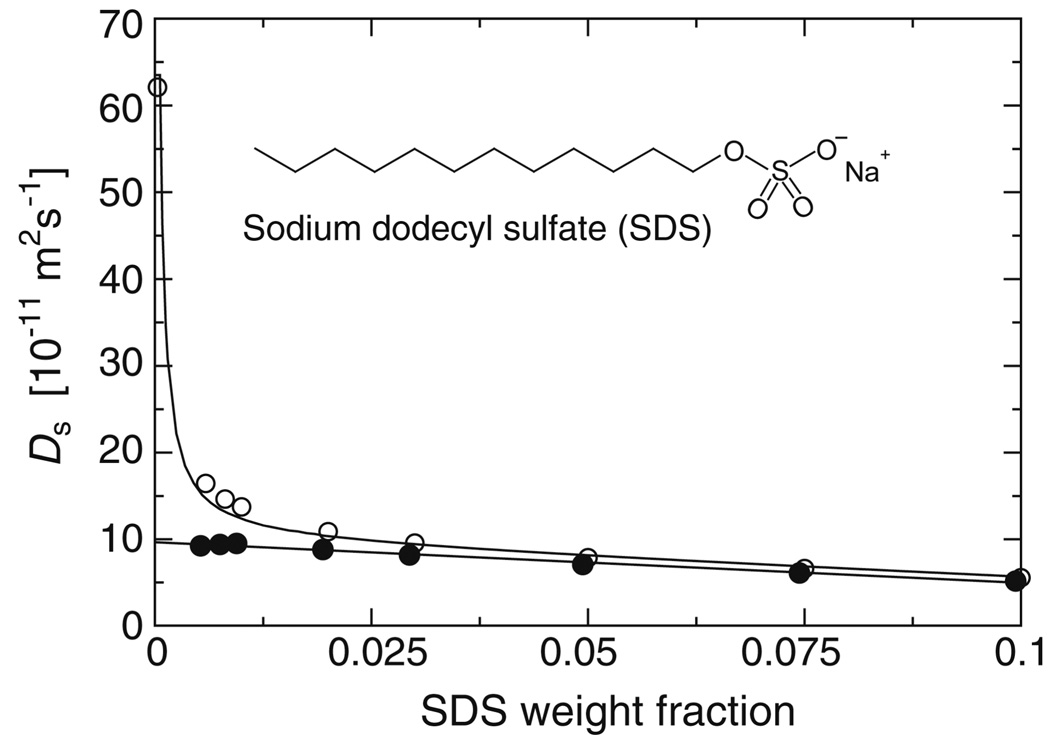
To ascertain the average size of SDS micelles at the experimental condition used to determine the αS^SDS_NC structure,²¹ the translational self-diffusion constants, D_s, of SDS assemblies were measured as a function of weight fraction by BPP-LED experiments (Figure 2).³⁰ The linearization of D_s to yield the corresponding self-diffusion coefficients of the SDS micelle alone, D_m,³⁰ is optimal for a free detergent concentration of 2 mM (Figure 2). Extrapolation to infinite dilution yields a diffusion constant, D₀, of 9.65×10⁻¹¹ m²s⁻¹. Relative to lysozyme (D₀= 11.3×10⁻¹¹ m²s⁻¹), an unhydrated micelle radius of 18.7 Å is thus obtained. When using a SDS density of 1.149 g/cm³,³¹ an average micellar mass of 19.0 kDa and an aggregation number of 66 were calculated (Table S1).

Figure 2.

Aggregation number of SDS micelles. Translational self-diffusion constant, D_s, of SDS as a function of weight fraction (open circles) in 25 mM NaH₂PO₄/Na₂HPO₄, pH 7.4. Linearization of D_s to yield the corresponding self-diffusion coefficients of the SDS micelle alone, D_m,³⁰ is optimal for a free detergent concentration of 2 mM (solid circles). Extrapolation to infinite dilution yields a micellar diffusion constant, D₀, of 9.65×10⁻¹¹ m²s⁻¹.

Micelle formation in coarse-grain MD simulations

The program GROMACS 4.5.4 was used to model surfactants within the context of the MARTINI CG force field (version 2.0).^32,33 This force field contains four principal types of interacting centers: Polar (P), nonpolar (N), apolar (C), and charged (Q). SDS was represented by three hydrophobic (C₁) beads and one negatively charged bead (type Q_a; Figure 1a).³⁴ To represent the SLAS hydrophobic tail three hydrophobic (C₁) beads were used. For its headgroup two beads were used, one of type Q_a with a charge of −1 and one of type N_a (Figure 1a). Table S2 summarizes the coarse grain topology for SLAS, while the analogous SDS topology is contained in the MARTINI force field. Hydrated sodium counterions were represented by a bead of type Q_d (charge of +1) and their number corresponded to the number of detergent molecules. The models are solvated in periodic water boxes using the CG water model implemented in the MARTINI force field. For each micelle type, two sets of simulations were performed starting from different random detergent distributions (Figure S1). Table 1 and Table S3 summarize the simulation details.

Table 1.

Summary of coarse-grained (CG) and all-atom (AA) simulation parameter.

Simulation	No. of water beads / atoms	Total no. of beads / atoms	Box dimension [Å]	Simulation time [ns]
CG (micelle self-assembly) a,b
SDS	2,383	2,713	68×68×68	100
SLAS	8,630	9,150	100×100×100	200
CG (micelle self-assembly)b
SDS-αSSDSNC	14,726	15,337	88×232×88	250
SLAS-αSSLASCN	8,488	9,393	92×101 ×113	250
SLAS-αSSLASNC	9,713	10,618	120×100×100	500
CG (micelle pre-equilibrated)b,c
SDS-αSSDSNC	6,739	7,350	60×240 ×60	200
SLAS-αSSLASCN	8,051	8,956	61×88×95	400
SLAS-αSSLASNC	10,008	10,913	120×100×100	400
AA (micelle-αS complex pre-assembled)
SDS-αSSDSNC	80,868	83,323	60×240 ×60	100
SLAS-αSSLASCN	96,612	99,959	92×101 ×113	100
SLAS-αSSLASNC	120,651	123,998	120×100×100	100

^aTwo independent simulations were performed for each detergent micelle (see Table S3).

^b264 SDS, 520 SLAS and 272 αS beads were employed.

^cThree independent simulations were performed for each αS structure (see Table S3).

After energy minimization (using the ‘steepest descent algorithm’, until the minimization force converges to a maximal value of 10 kJ·mol⁻¹·nm⁻¹), a simulation at constant number of particles, pressure and temperature (NPT) was performed for 5000 steps at 300 K and 1 bar with a time step of 0.4 fs, to remove bad contacts and bring the system close to equilibrium. Subsequently, NPT production runs were carried out (Figure S1). The Lennard-Jones and the Coulombic potentials were smoothly shifted to zero between 9–12 Å and 0–12 Å, respectively. The relative dielectric constant for explicit screening of MARTINI water was 15. The neighbor list was updated every 10 steps using a cutoff of 14 Å. In all simulations the surfactant molecules, ions and solvent particles were independently coupled to a 300 K bath with a relaxation time of τ_T of 1.0 ps. The pressure was maintained isotropically at 1 bar³⁵ with a coupling time of τ_P = 5.0 ps and an isothermal compressibility of 4.5×10⁻⁵ bar⁻¹. The equations of motion were integrated using the leap-frog algorithm with a time step of 40 fs.³⁶ Because CG potentials are much smoother than atomic potentials, the effective time sampled is four times larger than the actual simulation time.³⁷

Protein-micelle complex formation in CG MD simulations

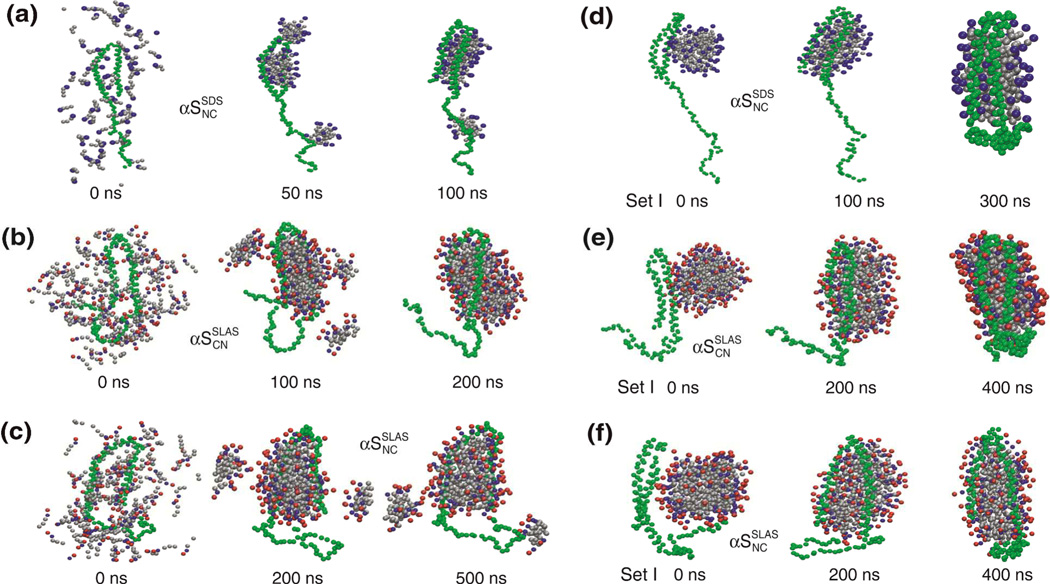
Simulations that observe the spontaneous self-association of SDS and SLAS molecules around the experimental αS^SDS_NC, αS^SLAS_NC and αS^SLAS_CN structures (Figure 1b) were performed (Figure 3a–c). In addition, the association of these structures with pre-equilibrated, fully hydrated micelles was evaluated in three independent simulations for each structure. Starting coordinates differed in relative αS-micelle orientations and micelle structures (Figure 3d–f and Figure S2). Simulation details are summarized in Table 1 and Table S3. For amino acids, the CG parameters as implemented in the MARTINI 2.1 force field were employed.³⁸ Specifically, each amino acid is represented by one backbone bead and up to four side chain beads. This force field has been validated for use in peptide-bilayer systems.^38–40

Figure 3.

Micelle-αS complex formation during coarse-grained molecular dynamics simulations. (a-c) Spontaneous self-association of randomly distributed detergent molecules around (a) αS^SDS_NC, (b) αS^SLAS_CN and (c) αS^SLAS_NC. (d–f) Complex formation of (d) αS^SDS_NC, (e) αS^SLAS_CN and (f) αS^SLAS_NC with pre-equilibrated M1 micelles (Figure S1). All protein geometrical restraints were released at 100 and 200 ns for SDS and SLAS, respectively.

All systems were solvated in a water box consisting of CG water molecules. Each system was first energy minimized as described above and equilibrated by a 20 ps NPT simulation. During this equilibration, the coordinates of the protein and micelle were harmonically restrained using a force constant of 1000 kJ mol⁻¹ nm⁻². During subsequent NPT production runs, the micelle was unrestrained and, after stable protein-micelle complex formation, the harmonic force on the protein was reduced stepwise to zero over a period of 50 ns for each simulation (Figure 3d–f and Figure S2). The temperature of the system was maintained at 300 K using the Berendsen thermostat with coupling constant 0.1 ps.³⁵ The pressure coupling was performed at 1 bar with the Berendsen barostat, using a coupling constant of 5.0 ps and a value of 4.5× 10⁻⁵ bar⁻¹ for the isothermal compressibility.³⁵ Long-range electrostatic interactions were treated using PME method⁴¹ with a real space cutoff of 12 Å. Periodic boundary conditions were applied with a van der Waals cutoff of 9 Å. All bond lengths were constrained using LINCS algorithm,⁴² allowing an integration time step of 2.5 fs.

Atomistic MD simulation of protein-micelle complex

To reconstruct atomistic details from CG coordinates, we used Marrink’s algorithm as implemented in the GROMACS package.⁴³ For protein, the GROMOS96 force field with 43a2 parameters was employed. For SDS and SLAS, topology files were generated using the program PRODRG⁴⁴ and modified manually to comply with 43a2 parameters⁴⁵ (Table S4). Each simulation setup (Table 1 and Table S3) was first energy minimized as described above followed by 1 ns of NPT simulation for equilibration. Then, 100 ns of NPT production runs were executed. The temperature of the system was maintained at 300 K, employing the Nose-Hoover thermostat with a coupling constant of 0.1 ps.^46,47 The pressure coupling was performed at 1 bar with the Parrinello-Rahman barostat, adopting a coupling constant of 5.0 ps and a value of 4.5×10⁻⁵ bar⁻¹ for the isothermal compressibility.⁴⁸ Long-range electrostatic interactions were treated using PME method⁴¹ with a real space cutoff of 12 Å. Periodic boundary conditions were applied with a van der Waals cutoff of 9 Å. All simulations were carried out on computers incorporating 6-core or multiple 4-core CPUs.

Results and Discussion

Size of free SDS and SLAS micelles

The aggregation numbers of micelles depend on solution conditions. Consequently, the aggregation numbers that are present at the solution conditions of the micelle-bound αS structures (Figure 1b) must be used to compute micellar assemblies. Using translation diffusion measurements, we had previously determined the radius of an unhydrated SLAS micelle to be 22.2 Å at the solution condition of the αS^SLAS_NC/αS^SLAS_CN structures (25 mM NaH₂PO₄/Na₂HPO₄, pH 7.4), which amounts to 104 SLAS molecules per micelle.²⁶ The αS^SDS_NC structure was determined under the same conditions, and here an average SDS micelle radius of 18.7 Å was measured, which amounts to an aggregation number of 66 (Figure 2 and Table S1). When titrating αS with SDS and SLAS, saturations are reached at protein-to-detergent ratios of ~1:70 and ~1:100, respectively.^21,22,26 This verifies that micelle aggregation numbers are unchanged upon αS association. Compared to SLAS micelles, SDS micelles will therefore produce a negatively charged surface area and volume that is smaller by 29 and 40%, respectively.

Properties of free SDS and SLAS micelles in coarse-grain simulations

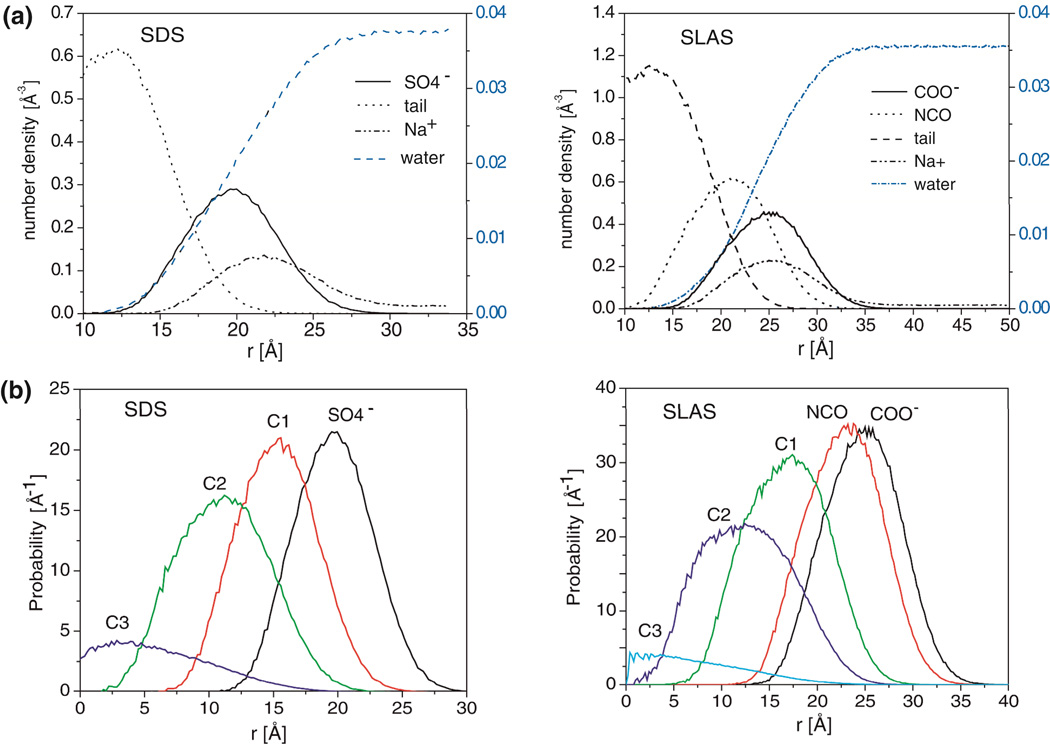
First, coarse-grain (CG) MD simulations of the free SDS and SLAS micelles were carried out at 300 K to understand their intrinsic structure and dynamics and to arrive at equilibrated micelles suitable for docking with αS. SDS and SLAS molecules were represented by four and five CG beads, respectively (Figure 1a). Upon commencing simulations from two randomly distributed detergent distributions for each SDS and SLAS, micelles assembled spontaneously (Figure S1). Following Bogusz et al., we define an effective micellar radius, R_s, based on the relationship between the radius of a solid sphere and its radius of gyration, R_g, as R_s = sqrt(5/3) × <R_g>.^49,50 R_g averaged over the last 80 ns of simulation time was 16.6 ± 0.6 Å for the two SDS simulation runs, identifying R_s as 21.4 ± 0.6 Å (Figure S1a). For the two conducted SLAS simulations (Figure S1b), R_g, averaged over the last 100 ns of simulation time was 20.5 ± 0.5 Å, yielding R_s= 26.5 ± 0.6 Å. To analyze the shape of the micelles, we calculated the eccentricity e, defined as 1- I_min/I_avg, where I_min is the moment of inertia along x, y or z axis with the smallest magnitude and I_avg the average of all three moments of inertia. For a perfect sphere, the value of e would be zero. The average eccentricities for SDS and SLAS micelles from the last 80 ns of simulations are 0.54±0.05 and 0.54±0.04, respectively, showing that both entities broke spherical symmetry (Table 2). The interfacial properties of the micelles, as represented by number density profiles, illustrate the complex transition from bulk water to the hydrophobic micelle core (Figure 4).

Table 2.

Micelle ellipticity, e, and ratios of moments of inertia, I, at the end of MD simulations

Simulation	I1/I3	I1/I2	I2/I3	e=1-Imin/Iave
CG (micelle self-assembly)
SDS	1.5 ± 0.1a	1.1 ± 0.1	1.3 ± 0.1b	0.54 ± 0.03
SLAS	1.5 ± 0.1	1.2 ± 0.1	1.3 ± 0.1	0.54 ± 0.02
CG (micelle self-assembly)c
SDS-αSSDSNC	–	–	–	–
SLAS-αSSLASCN	1.8 ± 0.2	1.2 ± 0.2	1.5 ± 0.2	0.70 ± 0.04
SLAS-αSSLASNC	–	–	–	–
CG (micelle pre-equilibrated)
SDS-αSSDSNC	2.2 ± 0.5	1.2 ± 0.1	1.9 ± 0.5	0.68 ± 0.05
SLAS-αSSLASCN	2.2 ± 0.5	1.1 ± 0.1	2.1 ± 0.5	0.67 ± 0.03
SLAS-αSSLASNC	1.9 ± 0.5	1.1 ± 0.1	1.7 ± 0.5	0.65 ± 0.03
AA (micelle-αS complex pre-assembled)
SDS-αSSDSNC	2.9 ± 0.5	1.0 ± 0.5	2.9 ± 0.5	0.76 ± 0.01
SLAS-αSSLASCN	1.6 ± 0.5	1.2 ± 0.1	1.4 ± 0.5	0.58 ± 0.09
SLAS-αSSLASNC	2.7 ± 0.5	1.1 ± 0.1	2.5 ± 0.5	0.74 ± 0.04

^aIn previous CG simulations, values of 1.52 and 1.39 were reported.^34,51

^bIn previous CG simulations, values of 1.29 and 1.24 were reported.^34,51

^cMultiple micelles were observed and no values were computed for SDS-αS^SDS_NC and SLAS-αS^SLAS_NC.

Figure 4.

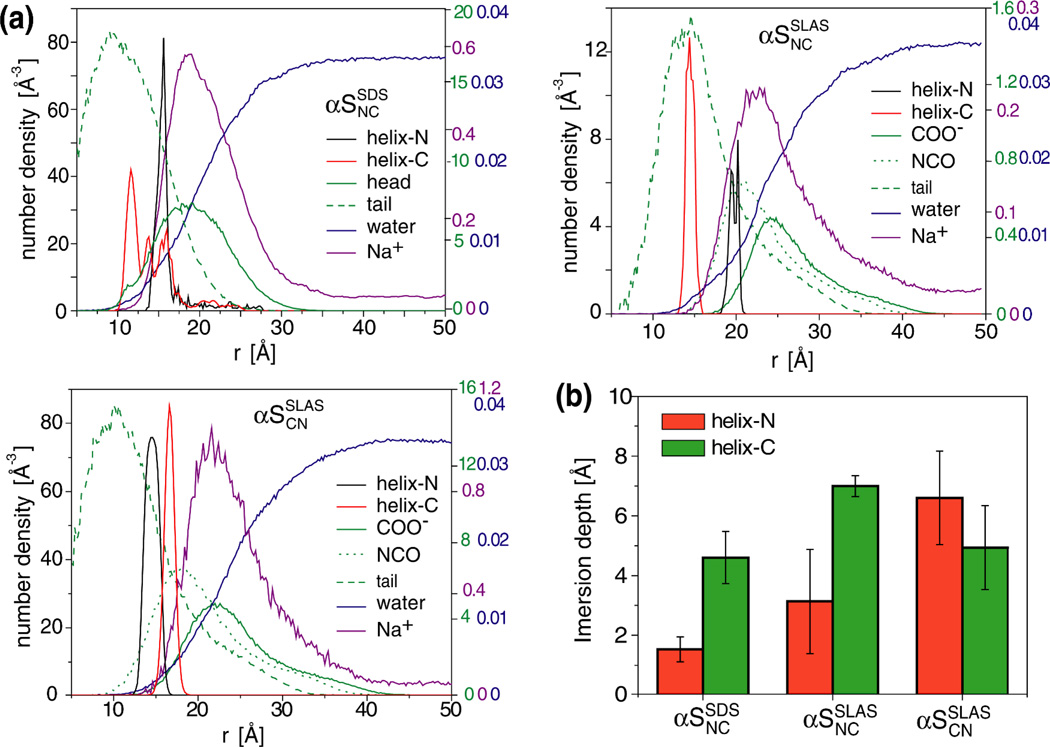
Structural properties of free SDS and SLAS micelles in CG MD simulations. (a) Number density profiles of the indicated groups relative to the micelle center of mass (COM). These plots represent the number of selected atoms present within 0.2 Å-wide shells at a given distance, r, from COM. (b) Radial probability distributions for the indicated groups with respect to the micelle COM. All profiles report on data that were obtained for the last 80 ns and 100 ns of SDS and SLAS simulations, respectively (Table 1).

In contrast to SLAS micelles, SDS micelles are well studied. A 500 ns CG-MD study of a SDS micelle containing 60 molecules reported R_g at 15.7 ± 0.2 and R_s at 20.3 ± 0.3 Å.³⁴ In another study, R_g was 15.5 Å when using a simplified potential and a united atom description of the dodecyl chain.⁵¹ Bruce et al. obtained values of 16.2 and 20.9 Å for R_g and R_s of a SDS micelle in all atom simulations.⁵⁰ From X-ray scattering, the experimental R_s value is 22.3 Å.⁵² Using small angle neutron scattering, a mean micelle radius of 18.9 Å and an average radius of gyration of 15.4 Å is reported for lithium dodecyl sulfate.⁵³ Thus, our coarse-grained description of the SDS micelle is in agreement with all-atom simulations and experimental values. With no previous SLAS simulations reported, this agreement also provides validation to our SLAS simulation protocol.

Micelle-αS association in coarse-grain simulations

To first examine αS interactions with individual detergent molecules, the spontaneous assembly of fixed micelle-bound αS structures with non-overlapping randomly positioned detergent molecules was tested in one simulation for each experimental αS structure. During the simulation period, this approach led to the formation of a single micelle only in case of αS^SLAS_CN whereas detergent molecules clustered around the C-terminal tail of αS^SLAS_NC and αS^SDS_NC in addition to the amphiphilic sequence (Figure 3a–c). Specifically, for αS^SDS_NC 15 detergent molecules assembled around M116–V118, which exhibit the highest hydrophobicity within the acidic C-terminal tail (residues 90–140; Figure S3a). With αS^SLAS_NC we found that Y125 clustered with SLAS molecules. Although we regard these associations to be transient, they highlight that the assembly of the protein-micelle complex experienced distinct contributions from hydrophobic interactions. The initial formation of relatively small micelles and a mixture of electrostatic and hydrophobic protein-detergent interactions are analogous to observations made in a recent SDS-αS all-atom MD simulation.²⁸ However, because of the absence of stable detergent interactions with the C-terminal tail,^{21–24,26,54} we focused on simulations with pre-equilibrated micelles.

By selecting from two different pre-formed micelle structures and choosing different relative αS-micelle orientations, three starting configurations were created for each experimental αS structure (Figure 3d–f and Figure S2). Complex formation was then allowed to take place with protein structures that were initially fixed. After initial complex formation, protein positional restraints were gradually removed over a period of 50 ns. This resulted in stable complexes between micelle and the αS amphiphilic region (Figure 3d–f and Figure S2) in agreement with the absence of stable detergent interactions with the C-terminal tail.^{21–24,26,54} Upon releasing all restraints on the protein structure, interhelical distances decreased significantly (Figure S4b). A previous experimental study suggested that the interhelical distance relates to micelle size²⁵ in accordance with αS^SLAS_NC and αS^SDS_NC structures (Figure 1b). To maintain close agreement with experimental αS structures, structural parameter in CG simulations were therefore not extracted beyond the time that all protein geometrical restraints were released.

Effect of αS association on SDS and SLAS micelle shape in coarse-grain simulations

The equilibrium structures of the SDS and SLAS micelles were perturbed by αS binding. Specifically, the micelles flattened into prolate spheroidal shapes (Figure 3d–f and Figure S2) as reflected in the increases in eccentricity relative to the free micelles (Table 2 and Figure S4a). This conforms to our earlier observations that the dimensions of the micelle-bound protein structures exceed the free micelle dimensions.^21,27 Moreover, it is analogous to reported SDS-αS^SDS_NC MD simulations.^28,29 The mechanism underlying these shape changes is likely to involve the spatially selective neutralization of detergent headgroups.²¹ As many as 12 Lys(ε-NH₃⁺) side chain charges (Figure 1b) can neutralize SDS(SO₄⁻) or SLAS(COO⁻) that decreases the effective detergent headgroup area. For example, with increasing concentration of the organic salt p-toluidine hydrochloride, SDS micelles increasingly adopt prolate spheroidal shapes in concert with an increase in aggregation number.⁵⁵

The positioning of αS relative to the micelles was evaluated after the formation of stable protein-micelle complexes. The observed complex dimensions illustrated the different sizes of SDS and SLAS micelles and confirmed that αS occupies a larger portion of the surface of SDS as compared to SLAS micelles (Figure 3d–f and Figure S2). Number density plots showed head group densities to peak at 16.8 ± 0.2 Å and 22.0 ± 0.5 Å for SDS and SLAS micelles, respectively (Figure 5a). Relative to the head groups, the backbone distribution of αS was evaluated for helix-N and -C, respectively. For αS^SDS_NC and αS^SLAS_NC, helix-C was preferentially immersed deeper than helix-N, whereas in αS^SLAS_CN differences between both helices were less pronounced and both helices immersed relatively deeply (Figure 5b). The experimental αS structures indicate that the orientation and distance of the hydrophobic helix faces differ between NC and CN helix orientations (Figure 1b and Figures S3b, S4b). In the αS^SLAS_CN structure, the relative orientations of the curved, hydrophobic helix faces are similar and expected to induce relatively concentrated micelle perturbations. For NC orientations, those helix faces appear less well aligned, causing spatially less concentrated perturbations to the micelle in correlation to their different micelle immersion depths and the relatively shallow helix-N immersion (Figure 5b). The experimental asymmetry in αS^SLAS_NC and αS^SLAS_CN populations of 0.55:0.45 is therefore explained by differences in the spatial orientations of protein-induced micelle perturbations.

Figure 5.

Association of αS with pre-equilibrated SDS and SLAS micelles in coarse grain MD simulations. (a) Number density profiles of the indicated groups relative to the center of micelle mass. For αS^SDS_NC the 50–100 ns simulation time period was considered (Table 1). For αS^SLAS_CN/αS^SLAS_NC the considered time period was 100–200 ns (Table 1). (b) Micelle immersion depths of αS helices in CG simulations. Immersion depths represent the distance between detergent head group and helix backbone densities relative to the center of micelle mass. Error bars denote standard deviations from three simulations with pre-equilibrated micelles (Table S3).

Evolution of partially folded, micelle-bound αS states in all-atom simulations

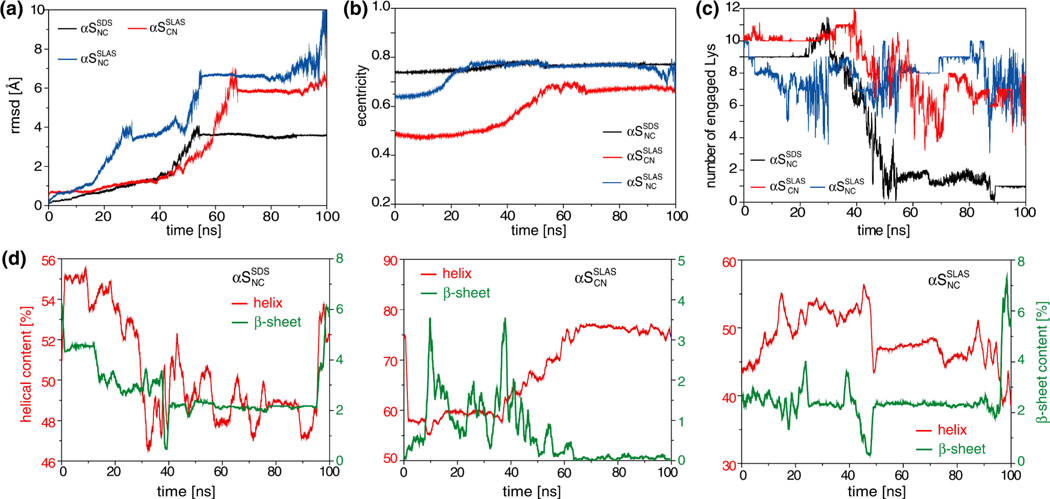
To observe possible αS interactions with the different micelle systems pertaining to its misfolding, all atom simulations were carried out starting from partially folded αS states. Atomistic configurations were created from the CG-MD configurations that were obtained before all protein restraints had been released (100 and 200 ns for SDS and SLAS simulations, respectively; Figure 3d–f), using the reverse-transformation algorithm of GROMACS.⁴³ This procedure resulted in initial αS conformations that deviated from ideal helical geometry in several instances (Figure 6), providing partially folded αS states. We note that, after transforming from CG to atomistic configuration, the micelles in the absence of protein were stable, as shown by separate simulations (Figure S6). As to be expected, substantial protein refolding/equilibration occurred in the course of the simulations as reflected by relatively large changes in protein backbone C^α coordinate rmsd, relative to the starting coordinates (Figure 7a). After approximately 50 ns of simulation time, relatively stable conformations were observed.

Figure 6.

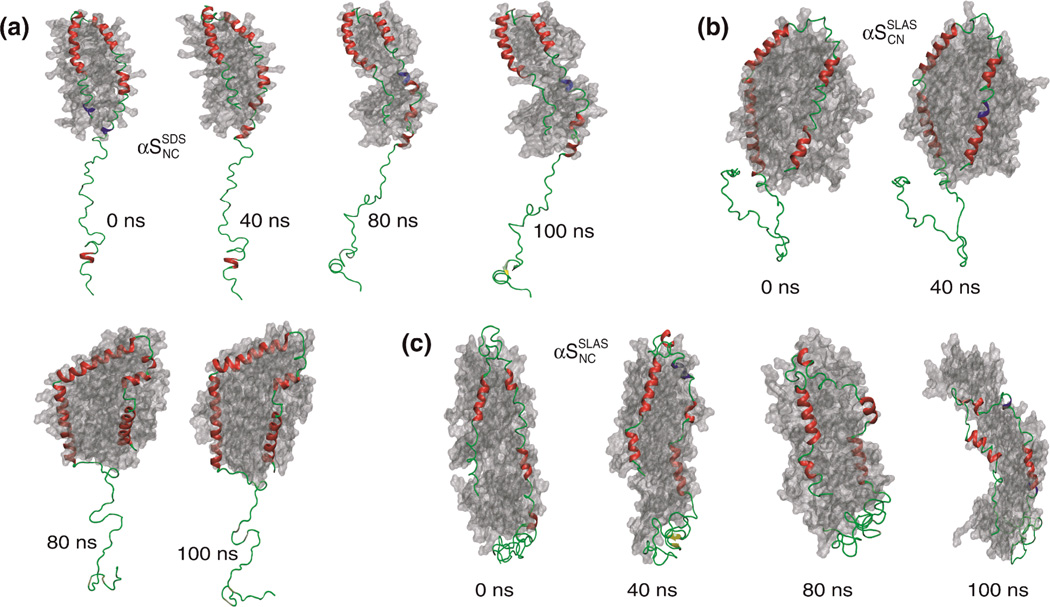
Snapshots from all-atom MD simulations of micelle-bound αS. Snapshots for (a) αS^SDS_NC, (b) αS^SLAS_NC and (c) αS^SLAS_CN during the simulation (0–100 ns). The micelle surface is shown in grey, α-helix in red, 3₁₀-helix in blue, β-sheet in yellow, and turn and coil in green. Protein secondary structures were classified with the program STRIDE.⁷⁰

Figure 7.

Evolution of structural parameter during all-atom MD simulations of micelle-bound αS. (a) Root-mean-square-deviation (rmsd) between C^[α] coordinates of αS residues 2–92 relative to the starting structures. (b) Micelle eccentricities. (c) Number of lysine ε-NH₃⁺ groups of αS within hydrogen bonding distance (≤ 3.5 Å) to SDS(SO₄⁻) or SLAS(COO⁻). (d) Contents of helical (α-helix and 3₁₀-helix) and β-sheet (β-bridge and β-bulges) secondary structures. Secondary structure was classified with the program DSSP.⁷¹

In the course of the αS^SDS_NC simulation, large rmsd changes were detected for residues at the beginning of helix-N and end of helix-C (Figure 6a and 7d), some of which did not recover helical conformation (Figure S7). Likewise, the SDS micelle rearranged considerably and interacted differently with helical and non-helical regions (Figure 6a). Number density plots revealed that, relative to the center of mass, the center of the SDS micelle was dispersed without well-defined hydrophobic core (Figure S5). At the end of the simulation, segments of helix-N dissociated visibly from the micelle surface (Figure 6a) in correlation to a dramatic loss of Lys(ε-NH₃⁺)-SDS(SO₄⁻) contacts (Figure 7c). At the end of the simulation the obtained SDS micelle shape (Figure 6b and 7b) appeared to be unsuitable to accommodate two helices, contributing to their unfolding and tendency to dissociate, respectively.

With αS^SLAS_CN, helical conformation was successfully recovered during the simulation (Figure 6b and 7d) in correlation to the emergence of a well-defined micelle interaction (Figure 6b). A few residues (E20, Q24, the linker residues Y39-G41 and G67) remained in non-helical conformations (Figure S8), which minimized the longitudinal dimension of helices and, thus, deformations to the intrinsic micelle shape (Figure 6b). Lys(ε-NH₃⁺)-SLAS(COO⁻) contacts remained intact but, interestingly, only 7 out of 12 possible interactions were populated on average (Figure 7c).

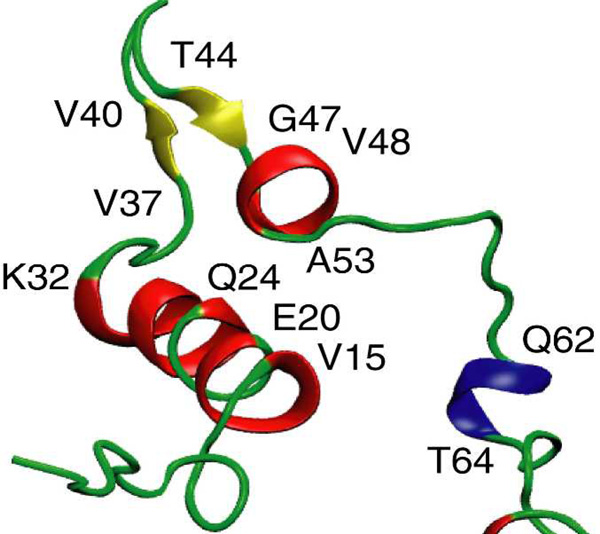
The SLAS-αS^SLAS_NC simulation commenced with the lowest helical content and was not able to recover helical conformations throughout the simulation (Figure 6c, 7d, and Figure S9). The protein-micelle interaction remained ill-defined (Figure S5) although Lys(ε-NH₃⁺)-SLAS(COO⁻) contacts did not disengage (Figure 7c). However, most notably in terms of αS pathology, an intramolecular β-sheet developed towards the end of the simulation run (Figure 6c and 7d) that encompassed V37–V40 and T44-G47 (Figure 8). In sum, the three performed all-atom simulations exemplify the theoretically possible outcomes of αS-micelle interactions, i.e., αS association, dissociation and misfolding. For each outcome, multiple interaction pathways are to be expected and each of the performed simulation represents one such possibility.

Figure 8.

Illustration of β-sheet formation in the SLAS-αS^SLAS_NC simulation. At 100 ns, residues V37–V40 and T44-G47 form an anti-parallel β-sheet. Protein secondary structures were classified using the program STRIDE⁷⁰ with α-helix shown in red, 3₁₀-helix in blue, β-sheet in yellow, and turn and coil in green.

Determinants of αS-micelle interaction

Upon αS deforming the micelles along its helix axes, the surface area orthogonal to the helix axes is invariably reduced (sphere-to-spheroid transition). With αS^SDS_NC and αS^SLAS_NC this correlation may contribute to their unsuccessful micelle interactions over the duration of the simulation. The micelle shape change is aided by the selective neutralization of detergent headgroups.⁵⁵ When assuming that all 12 lysines of αS interact with detergent headgroups, per micelle 18.1% of SDS(SO₄⁻) groups are neutralized but only 11.5% of SLAS(COO⁻) groups. In addition, the SLAS headgroup contains additional polar moieties unlike its SDS counterpart (Figure 1a). Based on these considerations, we posit the length of initially formed helical segment to be a key determinant of the success of micelle-induced αS folding. With the larger diameter of SLAS than SDS micelles (Table S1), a longer helix may prevail on the former micelle. On SLAS micelles, helix-C encompasses S42–T92 whereas on SDS micelles it ranges from K45 to T92 (Figure 1b)^21,27 in support of our expectation. This difference relates to the distinctly non-helical conformation of K43–T44 on SDS micelles, for which ¹³C^[α] shifts differ most between SDS- and SLAS-bound αS (Figure 1c). For SLAS-bound αS some helicity, i.e., positive ¹³C^[α] shifts, is maintained throughout the entire amphiphilic region (D2-A89) in agreement with its uninterrupted amphiphilic helical amino acid sequence periodicity.^8,26 Interestingly, for helix-N and -C ¹³C^[α] shifts are nonetheless often slightly higher for SDS- than SLAS-bound αS, suggesting that for SDS non-helical conformation is concentrated to the helix-helix linker as opposed to the more widely dispersed reduction of SLAS helicity.

To understand αS-micelle interactions better, it is insightful to discuss the experimental differences in protein dynamics between SDS- and SLAS-bound αS states (Figure 1d–e). Fast backbone dynamics exhibit an overall similar pattern (Figure 1d). Offsets in S² values between the two states may be related to their slightly different average structures (Figure 1b) and may also experience contributions from relaxation measurements that were carried out on different spectrometers.^21,26 Intermediate timescale dynamics modulate the obtainable degree of bond vector alignment relative to the magnetic field in an anisotropic milieu. When assuming that fluctuations for the relatively immobile section of helix-C (segments 78–88) are comparable on the surface of SLAS and SDS micelles, helix-N fluctuates more on SDS than on SLAS micelles (Figure 1e). On SLAS, the alignment of both helices is relatively balanced. On SDS, the C-terminal half of helix-C dominates the micelle interaction along its helix axis at the apparent expense of increased helix-N movements in correlation to its smaller, less accommodating surface area (Table S1). Interestingly, segmental motions along helix-C differ somewhat between SDS and SLAS micelle-bound αS states (Figure 1e). The helix-N/helix-C connector is approached more steeply on SDS than on SLAS micelles, which again may relate to the more compact SDS micelle size. When shortening helix-C by 11-residues, less segmental motions are observed on SLAS micelles for its N-terminal half as shown by experiments with β-synuclein,²⁶ indicating that segmental motions correlate with the degree of micelle deformation. In conclusion, we suggest that the degree of micelle curvature determines the arrangement and segmental motions of helical secondary structure elements of micelle-bound synucleins but micelle curvature has less influence on secondary structure formation and stability that drive the αS-micelle association.

Protein backbone dynamics from MD simulations

The initial setup of our all-atom simulation did not intend to capture the average protein dynamics of micelle-bound αS. However, the large conformational fluctuations encountered during simulations make a comparison to experimental backbone dynamics (Figure 1d–e) useful for judging the level of acquired αS folding. The MD trajectories permit the calculation of the generalized order parameter, S², describing the amplitude of backbone H-N bond fluctuations, according to

$$S^2=\frac{1}{2}(3\sum _{i=1}^3\sum _{j=1}^3{\langle {\mu }_i{\mu }_j\rangle }^2-1)$$

where µ_i are the Cartesian coordinates of the normalized internuclear N-H vector when the overall protein motion is not taken into account.⁵⁶ In order to treat internal motions solely, the overall translational and rotational movements of protein were removed by least-square fitting of C^[α] atoms to the initial coordinates. We computed S² for the 20–100 ns simulation period, which encompassed protein folding (Figure 7a). In case of αS^SDS_NC, this revealed that relative to helix-C, helix-N underwent larger fluctuations for its N-terminal half (Figure 9a), suggesting that it was difficult for this section to fold and maintain its micelle association. For αS^SLAS_CN, a noticeable correlation to experimental S² values started to emerge; fluctuations of S² in helix-N and -C diminished and the experimental dips at the helix-helix linker and N65-G68 were observed consistently (Figure 9b). As to αS^SLAS_NC no meaningful correlation to experimental S² values was observed (Figure 9c) in agreement with its perceived ongoing dissociation from the SLAS micelle.

Figure 9.

Backbone dynamics from all-atom MD simulations. The order parameter, S², was calculated for simulation trajectories obtained for simulations periods of 20–100 ns. The average S² values of helix-N″ (V3-K32) and helix-C″ (K45–T92) are indicated by horizontal bars.

To supplement our analysis of protein dynamics, dynamic information was also extracted from CG simulations. To identify possible collective atomic motions of CG particles, we performed principal component analysis (PCA)^43,57 on the CG-MD trajectories that involved the release of all geometrical restraints on protein (Figure 3d–f). Diagonalization of the covariance matrix of CG bead fluctuations provided a set of eigenvalues and eigenvectors or principal components (PC; Figure S10). As to be expected, the PC with the largest eigenvalue, termed PC1, could account for most fluctuations (Figure S10a). A measure of fluctuations along the directions of the PC illustrated the magnitudes of protein bead fluctuations as a function of simulation time (Figure S10b and S11). Perhaps most readily interpretable in terms of experimental order parameter S² (Figure 1d) are the root-mean-square fluctuations (RMSF) of amino acid beads calculated after projecting trajectories along the respective PC. Regions of helix breaks and the C-terminal tail region exhibited the largest fluctuations for most PC orientations (Figure 9 and Figure S12) in agreement with experimental data (Figure 1d).

The durations of MD simulations cannot provide quantitative insight into nano- to millisecond timescale dynamics but, because current all-atom simulations involved an unusual amount of protein refolding (Figure 7a), we highlight a few observations for the successfully folding αS^SLAS_CN configuration that may offer a glimpse into these unknown motions. Visual inspection of Figure 6b indicates that the relative invariance in the orientation of the first half helix-N and last half of helix-C conforms to their highest alignment magnitudes (Figure 1e). Likewise, the large reorientations, occurring at the end of helix-N and the beginning of helix-C, illustrate motions that can lead to the diminished alignments of these segments, including the connector between helix-N and -C. Dynamics on the nano- to millisecond timescale are therefore likely to encompass a dynamic partitioning of the helices, especially helix-C.

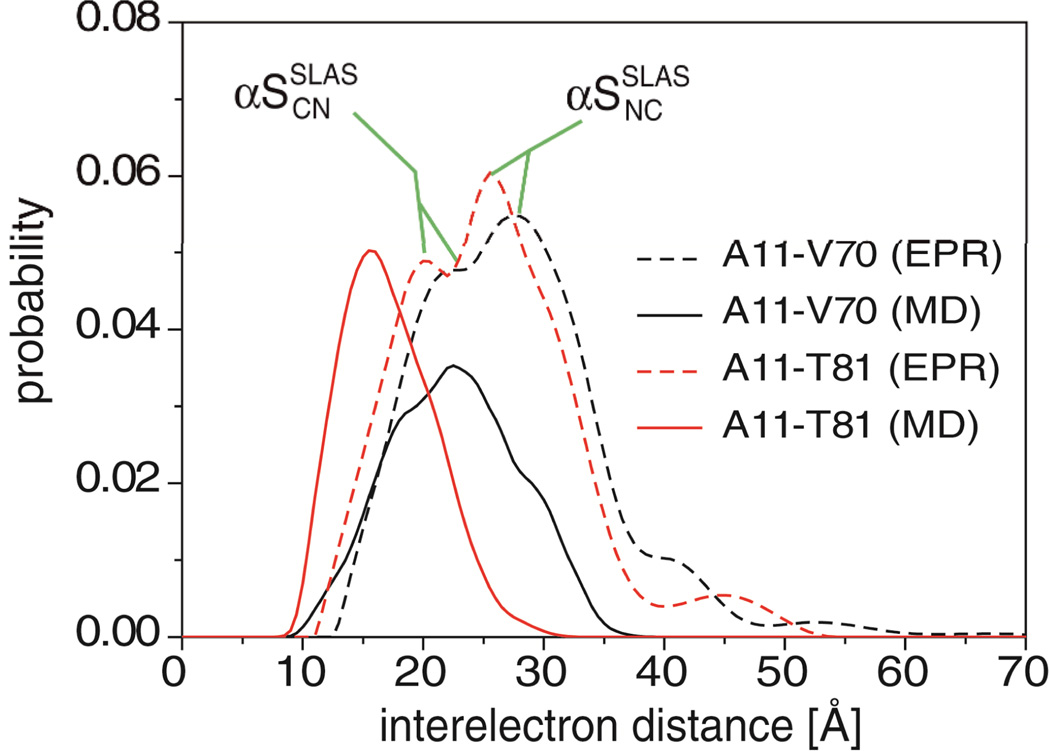
Whether a MD trajectory reproduces a dynamic process on an intermediate timescale represents an interesting question. We obtained a necessary but not sufficient condition for deciding this issue from the reconstruction of distance distributions between pairs of spin labels obtained previously from EPR spectroscopy of SLAS micelle-bound αS.²⁷ The interelectron distance distributions for the 11R1–70R1 and 11R1–81R1 spin-label pairs exhibit two maxima each (Figure 10), corresponding to the αS^SLAS_NC and αS^SLAS_CN conformations, respectively (Figure 1b). When reconstructing interelectron distance distributions individually for these spin-label pairs based on the αS^SLAS_CN all-atom MD trajectory, it was found that the simulation approximated the correct distribution maxima (Figure 10). For the 11R1–81R1 distribution, the maximum was offset to somewhat lower distances than experimentally detected. Nonetheless, the level of agreement is noteworthy. To reproduce both distribution maxima, αS would have to interconvert between CN and NC helix orientations, which represents an event outside of the scope of present simulations.

Figure 10.

Reconstruction of experimental interelectron distances from all-atom MD simulation. For every 1 ns one structure was extracted from SLAS-αS^SLAS_CN simulations. MTSL (S-(2,2,5,5-tetramethyl-2,5-dihydro-1H-pyrrol-3-yl)methyl methanesulfonothioate) spin labels were attached to the indicated residues, and interelectron distance distributions predicted with the program MMM 2010.⁷² For each spin label pair, distance distributions were calculated individually, i.e., spin labels shared between different spin label pairs were not correlated.²⁷ Shown is the frequency of all computed interelectron distances in comparison to experimental probabilities. The two distribution maxima observed experimentally correspond to αS^SLAS_CN and αS^SLAS_NC, respectively.²⁷

Conclusions

Aided by the comparative analysis of αS interactions with SDS and SLAS micelles (Figure 1), the present study used MD simulations to correlate αS structural and dynamic properties to experimentally determined micelles sizes and to computed deformations of micelle shapes. The study related the imbalance of SLAS-αS interactions between NC and CN helix orientations²⁷ to the asymmetry of protein-induced micelle deformation, i.e., the alignment and distance of curved hydrophobic helix faces. It exemplified protein and micelle determinants of αS folding and dynamics. Micelle curvature governs the arrangement and motions of helical αS segments but it is less influential in terms of secondary structure formation and stability, which drive the αS-micelle association.^9,10 Deformations in intrinsic micelle shapes and the dynamic partitioning of αS helices, which we suggested to contribute to dynamics on the intermediate timescale, serve to optimize the thermodynamics of αS-micelle complex formation. Employing EPR spectroscopy-derived distance distributions between pairs of spin labels, a simple method was introduced to compare protein dynamics between experiment and simulation. In the following, we discuss the potential relevance of the observed effects and principles to pathological αS events.

The deformation of intrinsic micelle shapes by αS is reminiscent of the remodeling of vesicles composed mainly of anionic lipids by αS.⁵⁸ The titration of αS with SUV composed of the anionic lipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-(1'-rac-glycerol) saturates at only 9±3 lipid molecules,¹⁶ implying a dense protein-lipid interaction network where one lipid interacts with multiple αS molecules. A remodeling of membranes by αS has therefore membrane-perturbing, pathological potential.⁵⁸ An imbalance of anionic lipid concentrations in synaptic vesicle membranes could favor such "misdirected" membrane stabilization. In synaptic vesicles, approximately 14% of phospholipids are anionic lipids.⁵⁹ However, age dependent changes in membrane lipid composition increase their prevalence in membranes⁶⁰ and age is the primary risk factor of neurodegeneration.

Based on the β-sheet secondary structure of αS fibrils^11,12 and the anti-parallel β-sheet conformations of αS oligomers,⁶¹ structural events that lead to the formation of β-sheet conformation are relevant to understanding the initial events of αS misfolding. In the course of the SLAS-αS^SLAS_NC simulation, V37–V40 and T44-G47 formed an anti-parallel β-sheet (Figure 8), suggesting that a transient αS intermediate exhibiting β-sheet conformation can originate in the context of surfactant surfaces. Moreover, this event reveals a pathway for converting helical αS structure into β-sheet structure. We note that α-helical intermediates have previously been implicated in the formation of β-sheet conformation in different amyloid fibrils including αS fibrils.^17,62,63 A first intramolecular β-sheet formation, taking place on membranes, may be followed by dimerization via intermolecular β-sheet pairing either on the membrane surface or when (partially) dissociated to create a more stable, longer-lived β-sheet assembly. Based on thermodynamic considerations, an αS helix break is a frequent event on SUV membranes and may occur at different positions.¹⁶ The β-sheet observed here therefore represents only one β-sheet pairing possibility. A recent Monte Carlo simulation of the conformational ensemble sampled by the free αS monomer highlights ample possibilities for intramolecular β-sheet formation.⁶⁴ The misfolding mechanism proposed here is conceptually similar to the suggested action of divalent cations that accelerate the fibrillogenesis of αS in aqueous solution.^65,66 Residues brought in proximity by Cu²⁺-binding have been proposed to form β-sheet structure in the course of Cu²⁺-accelerated misfolding.⁶⁶