Quantitative magnetic susceptibility mapping without phase unwrapping using WASSR

Abstract

The magnetic susceptibility of tissue within and around an image voxel affects the magnetic field and thus the local frequency in that voxel. Recently, it has been shown that spatial maps of frequency can be used to quantify local susceptibility if the contributions of surrounding tissue can be deconvolved. Currently, such quantitative susceptibility mapping (QSM) methods employ gradient recalled echo (GRE) imaging to measure spatial differences in the signal phase evolution as a function of echo time, from which frequencies can be deduced. Analysis of these phase images, however, is complicated by phase wraps, despite the availability and usage of various phase unwrapping algorithms. In addition, lengthy high-resolution GRE scanning often heats the magnet bore, causing the magnetic field to drift over several Hertz, which is on the order of the frequency differences between tissues. Here, we explore the feasibility of applying the WAter Saturation Shift Referencing (WASSR) method for 3D whole brain susceptibility imaging. WASSR uses direct saturation of water protons as a function of frequency irradiation offset to generate frequency maps without phase wraps, which can be combined with any image or spectroscopy acquisition. By utilizing a series of fast short-echo-time direct saturation images with multiple radiofrequency offsets, a frequency correction for field drift can be applied based on the individual image phases. Regions of interest were delineated with an automated atlas-based method, and the average magnetic susceptibilities calculated from frequency maps obtained from WASSR correlated well with those from the phase-based multi-echo GRE approach at 3 Tesla.

Introduction

The recent availability of high magnetic fields (3T and 7T) has caused a surge in the technology development for quantitative susceptibility mapping (QSM) (de Rochefort et al., 2010; Haacke et al., 2010; Liu et al., 2009; Rauscher et al., 2008; Schweser et al., 2011b; Wharton and Bowtell, 2010; Wharton et al., 2010), as well as the determination of the susceptibility tensor in tissue (Li et al., 2012a; Li et al., 2012b; Liu, 2010; Liu et al., 2012). Currently, such QSM methods rely on phase maps generated from gradient-recalled echo (GRE) images to determine the voxel frequency (Duyn et al., 2007; Li et al., 2011; Liu, 2010; Liu et al., 2010a; Shmueli et al., 2009; Wharton and Bowtell, 2010). Although GRE is fast and available as a standard sequence on all human MRI scanners, this method has a few disadvantages. In particular, phase wraps complicate data interpretation at interfaces of structures with very different susceptibilities (e.g., near the sinuses), as well as at positions further from the magnetic field center that exhibit significantly different frequencies due to static magnetic field inhomogeneity. Problems also occur when spatial resolution is low with respect to the spatial rate of field change, causing intra-voxel inhomogeneity and phase measurement errors. Thus, for GRE imaging, there is a dilemma: increasing the echo time (TE) increases frequency contrast between tissues, but phase images acquired at longer TEs have an increasing number of phase wraps, while the magnitude images exhibit lower signal-to-noise ratio (SNR). However, SNR of the phase image is maximum at TE = T₂* (Wu et al., 2012). Additionally, when high-resolution 3D imaging is performed, the GRE acquisition may take several minutes, thereby increasing sensitivity to motion artifacts and to static field drift, which may occur when gradient heating increases the bore temperature. Such drifts may range over several Hertz, which is on the order of magnitude of the measured frequency differences between tissues. When this occurs, the susceptibility measurements may not be reproducible.

The main parameter necessary for susceptibility quantification is the frequency shift in each voxel. Whole-brain resonance frequency maps without phase wraps can be obtained using the WAter Saturation Shift Referencing (WASSR) method, in which the resonance frequency per voxel is characterized by measuring direct water saturation as a function of saturation frequency offset (Kim et al., 2009; Smith et al., 2009). When using an RF pulse with low power and short duration, the frequency-dependent line shape is a Lorentzian that is not affected by inhomogeneous line broadening (Liu et al., 2010b; Mulkern and Williams, 1993) and has minimal contributions from conventional magnetization transfer (MT) and chemical exchange saturation transfer (CEST). The voxel resonance frequency can be determined from the minimum of the fitted Lorentzian curve, allowing the WASSR method to use only the signal magnitude for generating tissue frequency maps, which can then be processed to derive quantitative susceptibility maps with available technology. Here, we compare the use of WASSR and GRE for quantitative susceptibility mapping at 3 Tesla. This work has been presented partially in abstract form (Lim et al., 2011a; Lim et al., 2011b; Lim et al., 2012b).

Theory

Multi-Echo Gradient-Recalled Echo (GRE)

For each voxel, the rate of change of the signal phase as a function of echo time (TE) is related to Δ ω_H2O = ω_H2O − ω_ref, the radial resonance frequency of the voxel water shifted with respect to the scanner reference frequency (ω_ref):

$$\varphi (TE)={\varphi }_0+(\mathrm{\Delta }{\omega }_{H_{2}O})·TE$$ [1]

$$\mathrm{\Delta }{f}_{H_{2}O}=\frac{\mathrm{\Delta }{\omega }_{H_{2}O}}{2\pi }$$ [2]

where ϕ is the phase in radians, and ϕ₀ corrects for any non-zero intercepts.

WAter Saturation Shift Referencing (WASSR)

Direct saturation (DS) of the water protons is achieved by applying a radiofrequency (RF) saturation pre-pulse of low power and short duration, minimizing contributions from magnetization transfer (MT) and chemical exchange saturation transfer (CEST) (Henkelman et al., 2001; Kim et al., 2009; Smith et al., 2009). By applying the saturation pulse across a range of RF frequencies, the resulting signal intensity in each voxel can be plotted as a function of RF offset frequency, resulting in a Z-spectrum for each voxel, as shown in Figure 1. The saturation spectrum can be described by an exact solution to the Bloch equations (Mulkern and Williams, 1993; Smith et al., 2009), in which the magnetization at steady state gives a Lorentzian lineshape as a function of the RF irradiation frequency (ω_RF) with respect to the water frequency:

$$M_{ss}(\mathrm{\Delta }{\omega }_{RF})=\frac{M_0{R}_1[R_2^2+{(\mathrm{\Delta }{\omega }_{RF}-\mathrm{\Delta }{\omega }_{H_{2}O})}^2]}{R_1[R_2^2+{(\mathrm{\Delta }{\omega }_{RF}-\mathrm{\Delta }{\omega }_{H_{2}O})}^2]+{\omega }_1^2{R}_2}$$ [3]

where Δω_RF = ω_RF − ω_ref, M₀ is the initial signal without saturation in arbitrary units; R₁ and R₂ are the longitudinal and transverse relaxation rate constants in Hertz; ω₁ = γB₁ is the radial frequency of the saturation pulse field with amplitude B₁

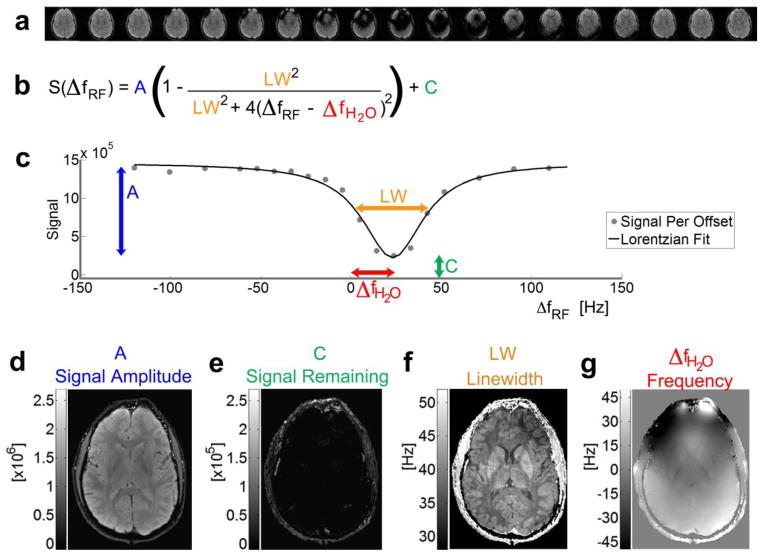
Figure 1.

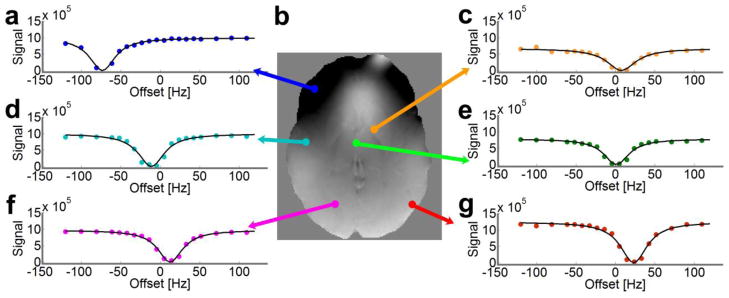
Direct saturation Z-spectra in various voxels of an axial-oblique slice. (a, c–g) The direct saturation signal magnitude is plotted as a function of RF offset frequency with respect to the scanner reference frequency (ω_ref) at 0ppm. (b) The resonance frequency map (field map) is calculated from the minimum of the direct saturation spectra using Lorentzian lineshape fitting. The colored dots in Z-spectra denote the experimental data points, and the black lines denote the fitted lineshape.

Several methods can be used to identify the water resonance frequency from the DS Z-spectrum, including polynomial fitting (Smith et al., 2009) and symmetry analysis with the Maximum Symmetry Algorithm with respect to the scanner reference frequency (Kim et al., 2009). The latter approach capitalizes on the fact that the shape of the direct saturation Z-spectrum is not affected by field inhomogeneities and is symmetric with respect to the center frequency (Kim et al., 2009). Dula et al. noted that the Maximum Symmetry Algorithm produced smoother frequency shift maps with less profound shift zones than seen in polynomial fitting (Dula et al., 2011; Dula et al., 2010), indicating that the Maximum Symmetry Algorithm produced a more robust map of the resonance frequency in a direct saturation experiment. However, the Maximum Symmetry Algorithm requires 16 to 33 points for accurate fitting (Kim et al., 2009).

To shorten the experiment and maintain a clinically viable scan time, we replaced Eqn. 3 with the equivalent general Lorentzian lineshape (Liu et al., 2010b; Sheth et al., 2011) to fit the direct saturation signal (Fig. 2a, b):

$$S(\mathrm{\Delta }{f}_{RF})=A-\frac{A·{LW}^2}{{LW}^2+4{(\mathrm{\Delta }{f}_{RF}-\mathrm{\Delta }{f}_{H_{2}O})}^2}+C$$ [4]

where A is the signal amplitude in arbitrary units (Fig. 2d), C the signal remaining after saturation (Fig. 2e), and LW the linewidth at full-width-half-maximum (Fig. 2f) that depends on R₁, R₂, and ω₁ = γB₁ (Mulkern and Williams, 1993). After fitting this Lorentzian lineshape to the direct saturation spectrum in each voxel, we can map the water resonance frequency (Fig. 2g) with respect to the scanner reference frequency, similar to GRE imaging. This approach also allows one to map the signal amplitude A and the signal remaining after saturation C to measure the efficiency of the saturation pulse, as well as the linewidth LW to assess relaxation effects. For instance, the linewidth map allows a separate view into the effect of iron content (Smith et al., 2009).

Figure 2.

Overview of the WASSR approach for mapping the voxel frequency. (a) Individual images are acquired with a saturation prepulse across a range of RF offset frequencies. (b) The direct saturation signal follows the equation for a Lorentzian lineshape. (c) The signal intensity in each voxel [gray dots] across the direct saturation spectrum is fit to this Lorentzian lineshape [solid black line]. The difference between the minimum of the Lorentzian curve and the scanner reference frequency at 0Hz shows the shift in (g) resonance frequency [Δf_H2O] per voxel. Other parameters included in the fitting result in maps of the (d) signal amplitude before saturation [A], (e) any signal remaining from incomplete saturation [C], and (f) linewidth [LW, the full-width at half maximum of the Lorentzian lineshape].

As shown in Figure 1e, voxels close to the center of the brain usually have a resonance frequency that corresponds to the scanner reference frequency (referenced to 0Hz), which is automatically set by the scanner. At various other locations in the brain (Fig. 1a, c–d, f–g), background gradients and susceptibility effects from tissues can shift the resonance frequency of the voxel, resulting in a horizontal shift of the Z-spectra in these voxels. In the iron-rich globus pallidus (Fig. 1c), the T₂ of the voxel is shortened, thereby changing the linewidth of the direct saturation spectra (Smith et al., 2009), so that the curve is not only shifted, but also broadened.

In direct saturation imaging, any B₁ inhomogeneities affect only the linewidth (and thus the depth) of the Z-spectrum, not the lineshape or resonance frequency. The WASSR method should therefore provide robust measurements of raw resonance frequency even in the presence of B₁ inhomogeneities.

Methods

Simulations

A Monte Carlo simulation was used to estimate the optimal parameters for WASSR imaging and to compare the robustness of finding the center frequency using a Lorentzian fit versus using the Maximum Symmetry Algorithm. The DS signal was simulated using Eqn. 3 (Mulkern and Williams, 1993), with added Rician noise to gauge the effect of SNR on the fitting. Variables included: the SNR of the volume acquired without a saturation prepulse, SNR(S₀); the sweepwidth (range) across which the RF offset frequencies were prescribed; and the number of RF offset frequencies prescribed within the sweepwidth. The linewidth, or full-width half-maximum, of the normalized direct saturation spectrum (S(ω_RF)/S₀) plotted as a function of RF offset frequency can be calculated as (Kim et al., 2009):

$$LW=\frac{1}{\pi }\sqrt{\frac{R_1{R}_2^2+{\omega }_1^2{R}_2}{R_1}}$$ [5]

For gray matter at 3T, R₁ and R₂ are approximately 0.88Hz and 13.5Hz (Lu et al., 2005). We used B₁ = 0.2μT so that ω₁ = 53.5rad/sec. For these simulations, LW = 67.2Hz.

A set multiplier (between 1 and 5) was used to generate the sweepwidth based on this linewidth. For example, for a SW/LW ratio of 2, the sweepwidth would be 134Hz, with endpoints of +/− 67Hz. For each sweepwidth to linewidth ratio, a set number of RF offset frequencies (ranging from 5 to 61 offset frequencies) was equally spaced over the sweepwidth; this is needed because the field varies over a sample and the position of the DS curve differs between voxels. Experimentally, when acquiring a direct saturation dataset for five subjects and creating a histogram of the resonance frequency shifts, we found that the range of resonance frequency shifts across the brain had a standard deviation of approximately 21.6Hz. To simulate a resonance frequency shift, we therefore modeled the resonance frequencies as a zero-mean normal distribution, with a standard deviation equal to 21.6Hz.

We simulated the true direct saturation signal at infinite SNR, with the resonance frequency shifted as described above as well as at different SNR levels. We subsequently fit the signal to a Lorentzian lineshape, gauging the error for determining these resonance frequencies as a function of SNR and the number of offset frequencies over a range of sweepwidth to linewidth ratios. The mean absolute error was calculated from the simulated resonance frequency minus the fitted resonance frequency. This WASSR resonance frequency error was computed as a function of the number of offset frequencies for SNR values of 10:1, 20:1, 30:1, 40:1, 80:1, 100:1, 1000:1, and infinite over 1000 Monte Carlo iterations. All processing was performed with in-house software written with Java and MATLAB (The MathWorks, Natick, MA, USA).

Image Acquisition

To optimize image acquisition, direct saturation spectra were first acquired using several saturation pre-pulse powers and durations. While there is no strict rule, the general requirements are 1) sufficiently low power to avoid MT and CEST effects as much as possible, since they may shift the average water frequency; 2) sufficiently high power to generate at least 50% water saturation in each voxel to allow accurate Lorentzian fitting; 3) sufficiently long saturation pulse for it to be selective enough for minimizing the curve width; 4) sufficiently short saturation pulse for the sequence to be fast enough to be clinically viable. Because a short saturation pulse has an increased bandwidth and decreased selectivity of irradiation, we chose the shortest pulse at the lowest power necessary for selective saturation, in which the direct saturation spectra demonstrated the least saturation broadening around the resonance frequency. In our experimental setup at 3T with a body coil, proper saturation was achieved with a 0.2μT sinc-gauss pre-pulse applied for 70ms at 3T.

After IRB approval and written informed consent, five healthy male volunteers (aged 30 to 32 years old) were studied at 3T (Philips Healthcare, Best, Netherlands) using body-coil excitation and 32-channel head coil receive. A T₁-weighted 3D MPRAGE scan was acquired for structural referencing (Turbo factor = 192, shot interval = 3000ms, SENSE = 2 × 1 × 2, TE = 3.5ms, TR = 7.5ms, α = 8°) with an acquired isotropic resolution of 1.1mm³ (FOV = 212mm × 212mm × 165mm, with a matrix reconstruction of 512). For all WASSR and GRE scans, the nominal resolution was 1.2mm isotropic, covering the entire brain (100 slices, FOV = 220mm × 220mm × 120mm, reconstructed resolution = 0.98mm × 0.98mm × 1.2mm). Fat suppression was accomplished using a water-selective ProSet 121 excitation pulse and one 60mm REST slab positioned inferior to the acquired volume. Phase images were acquired using a 3D ten-echo gradient-recalled echo sequence (SENSE = 2×1×2, TR = 70ms, TE₁ = 6ms, ΔTE = 6ms, α = 20°, Scan Duration = 7:46min). For WASSR, each volume for the direct saturation spectra was acquired with a 3D GRE multi-shot EPI readout (EPI factor = 33, SENSE = 2×1×2, TR = 150ms, TE = 22ms, α = 20°, volume acquisition time = 24s) preceded by a saturation prepulse. The overall scan time depended on the number of offset frequencies utilized to sample the spectrum.

To provide a gold standard for WASSR, a highly sampled direct saturation dataset (57 RF offset frequencies sampled every 5Hz) was acquired over a large sweepwidth (−140Hz to 140Hz) to encompass the range of frequencies across a brain at 3T. One volume with no saturation prepulse and one volume with a prepulse at an RF offset of 80kHz were also acquired, leading to a total scan duration of 20:41minutes. A subset of these data was then fit to the Lorentzian lineshape to determine the minimum number of offsets necessary for generating a resonance frequency map of sufficient quality. Customized MATLAB software utilized a least squares curve-fitting algorithm written in Java for increased processing speed to calculate the resonance frequency maps, as well as the goodness-of-fit for fitting the Lorentzian lineshape.

With a saturation pre-pulse of 70ms at 0.2μT, the linewidth of the direct saturation spectra over the brain ranged from approximately 20 to 50Hz. The range of offset frequencies fell primarily between +/−80Hz. Therefore, for each subject, we applied the saturation pulse across a sweepwidth of +/−120Hz with respect to the scanner reference frequency, with a close sampling interval of 5Hz between +/−80Hz and larger sampling interval of 10Hz between 80Hz and 120Hz, in order to gather detail within the range of tissue frequencies and also encompass the full range of frequencies across the brain, respectively. Combined with the no-saturation and 80kHz offset volumes, this scan could be completed in a total time of 8:25min.

Image Analysis

The SNR within a region of interest of experimental data was calculated by acquiring two images with identical parameters, Image A and B, and using (Firbank et al., 1999):

$$\mathit{SNR}=\frac{\mathit{average}(A+B)}{\mathit{std}(A-B)}$$ [6]

Frequency and Susceptibility Calculations

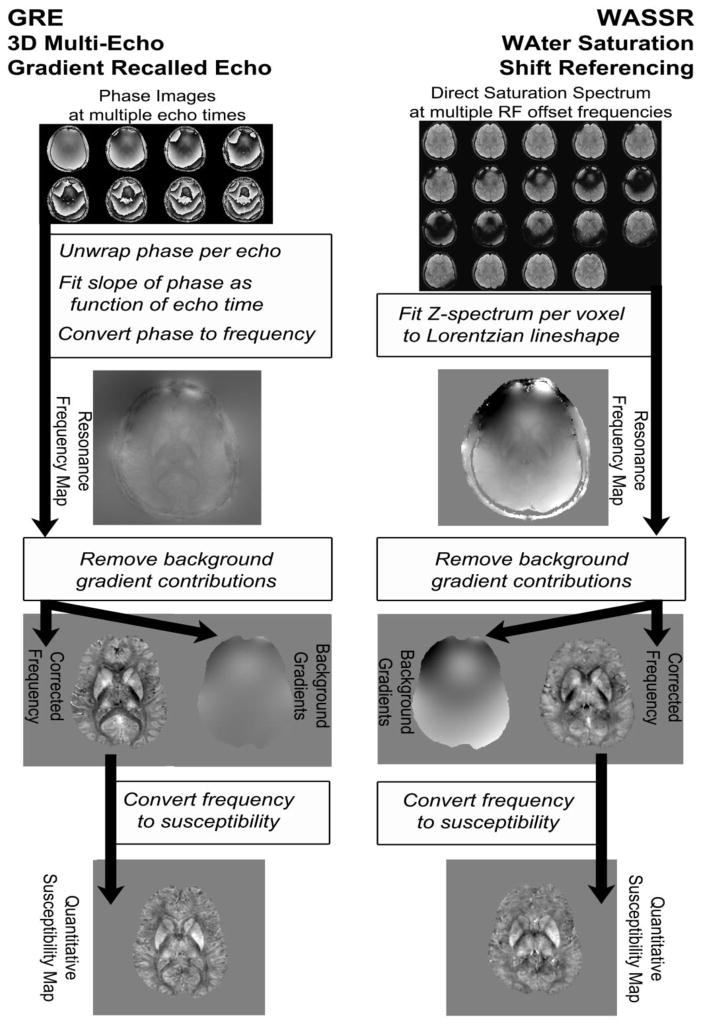
The data processing pipeline is illustrated by the flowchart in Figure 3. All processing was performed using custom-written scripts in MATLAB. It can be seen that the generation of the initial frequency maps is different between the two methods, as required by the different acquisition approaches, while the remainder of the processing is the same. However, because the phase-unwrapping procedure (Laplacian-based phase unwrapping) for the GRE QSM approach removes some of the large background gradients, the removal of these gradients is more demanding for WASSR processing.

Figure 3.

Overview of data processing approaches used to generate susceptibility maps from the GRE and WASSR methods.

Frequency mapping using gradient-recalled echo phase images was accomplished by first processing the phase signal from each echo with a Laplacian-based phase unwrapping method (Li et al., 2011), followed by linear fitting of the phase signal as a function of echo time for the first eight echoes (Eqn. 1) and calculation of the frequency map using Eqn. 2. The linear fitting of phase over time also gives an estimation of the initial phase (ϕ_offset), which can be used as a threshold to exclude some voxels with unreliable phase measurement (Schweser et al., 2011b). Our threshold was π/8, meaning that voxels with an intercept larger than this threshold were considered unreliable, possibly due to turbulent flow, partial volume effects, or an unusually high frequency shift.

Frequency mapping using WASSR direct saturation spectra consisted of three steps, namely (i) correction for the field drift; (ii) coregistration of the image volumes for each irradiation frequency; (iii) fitting the direct saturation curves to a Lorentzian lineshape.

The field drift was calculated using the phase images acquired for the direct saturation volume at each RF frequency. Because all of these images were acquired with the same TE and TR, the theoretical phase signal in each image without field drift should be identical; therefore, any variations between the average phase of these volumes can be attributed to the field drifting. The slices with the most homogeneous phase were used for this correction. Slices near the top of the brain, with few phase wraps, were processed to select the largest continuous phase region over these slices across the duration of the direct saturation spectrum acquisition. The mean and standard deviation of the phase within this region were calculated as a function of dynamic scan time and fit to a fifth order polynomial function. The phase difference with respect to the first acquired image was converted to a frequency difference and subtracted from the prescribed offset frequency used to acquire that particular volume. No phase unwrapping was required.

After field drift compensation, the magnitude signal of each direct saturation volume was coregistered to the volume acquired with no saturation pre-pulse, using the Oxford FMRIb Software Library (FSL) Linear Image Registration Tool (FLIRT) (Jenkinson and Smith, 2001; Smith et al., 2004; Woolrich et al., 2009) with rigid body registration and a normalized mutual information algorithm. The signal per voxel (Fig. 2a) was then fit to a Lorentzian lineshape (Eqn. 4) as a function of the field-drift compensated RF offset frequency of the saturation prepulse (Fig. 2b–c) using a least-squares curve fit. Output parameters from this fit were maps of the amplitude of the initial signal (Fig. 2d), any residual signal from incomplete saturation (Fig. 2e), the linewidth at full-width-half-maximum (Fig. 2f), and the resonance frequency shift with respect to the scanner reference frequency (Fig. 2g).

To assess the quality of the Lorentzian fit, we calculated a map depicting the squared 2-norm of the difference between the experimental points and the fitted points per voxel across N offset frequencies:

$$\mathit{resnorm}=\sum _n^N{({\mathit{data}}_{\mathit{fitted}}-{\mathit{data}}_{\mathit{original}})}^2$$ [7]

This residual norm map was combined with maps of the initial signal and residual signal from incomplete saturation to create a “goodness of fit” mask, indicating how well the Lorentzian lineshape fit the experimental data. For regions within the brain, we calculated a goodness of fit factor:

$$\mathit{GoodnessFitFactor}=\frac{\sqrt{\frac{\mathit{resnorm}}{N}}}{\mathit{eps}([A-C]<0)}·M_{\mathit{brain}}$$ [8]

with the square root of the residual norm map resnorm divided by the number of offset frequency points N, and A and C as defined with Eqn. 4 (Fig. 2). Because the signal remaining after saturation should generally be less than the initial signal without saturation, any negative differences in this “signal difference map” were set to very low values, using the “eps” function in MATLAB, which sets the selected voxels to the smallest values within a floating point precision of the software, approximately 2⁻⁵². The residual norm map divided by the signal difference map produced very high values in voxels with unreliable resonance frequency measurements, which could be due to incomplete saturation, noise, blood flow, or motion. The “goodness of fit” mask was created using all voxels having less than a ratio of 0.1.

To experimentally examine the effect of the number of collected points on the quality of fitting the direct saturation lineshape, we compared the highly-sampled dataset (57 offset frequencies) with datasets based on varying numbers of offset frequencies.

Susceptibility Calculation from the Field Map

The raw resonance frequency maps contain slowly-varying components from background gradient inhomogeneities that result in large field changes, as well as smaller local field changes from inhomogeneities due to the magnetic susceptibility of tissues. We used the dipole-fitting method (de Rochefort et al., 2010; Wharton and Bowtell, 2010) to model the background gradient field, first stripping the skull and dura and masking the brain, then solving a minimization problem to determine the susceptibility sources outside of the brain that would generate a background gradient field similar to that measured experimentally:

$${min}_x\left({\Vert W\left({FT}^{-1}\left\{\left(\frac{1}{3}-\frac{{\left(\left({\widehat{H}}_0^{\mathit{sub}}\right)·{\overline{k}}^{\mathit{sub}}\right)}^2}{{\Vert {\overline{k}}^{\mathit{sub}}\Vert }^2}\right)Ft\{\chi \}\right\}-\left(\delta B_z^{\mathit{sub}}\right)\right)\Vert }_2^2+\beta {\Vert M\chi \Vert }_2^2\right)$$ [9]

where FT is the Fourier Transform operation and FT⁻¹ is the inverse Fourier Transform operation, χ is the magnetic susceptibility distribution, ${\widehat{H}}_0^{\mathit{sub}}$ is the unit vector in the direction of the main magnetic field in the subject frame, k̄^subis the spatial frequency vector in the subject frame, and $\delta B_z^{\mathit{sub}}$ is the relative change in the magnetic field along the direction of the main magnetic field. W is a weighting matrix, chosen for the WASSR images to be the non-saturated volume from direct saturation imaging (TE = 22ms) multiplied by the goodness of fit mask. For the GRE images, W was chosen to be the corresponding fourth echo GRE magnitude image (acquired at TE = 24ms). M is a brain mask and β is a regularization parameter.

The mask of the brain region was created using the FSL Brain Extraction Tool (BET) (Smith, 2002; Smith et al., 2004; Woolrich et al., 2009), with areas outside the brain set at a value of zero, and areas inside the brain set at a value of one. This mask was then eroded by a disk element with a radius of three pixels, in order to eliminate extraneous signal from cerebrospinal fluid (CSF) surrounding the brain. The regularization parameter β was set to 1000, which makes the fitted susceptibility source inside the brain very small (less than 1 * 10⁻⁶ ppm), thereby emphasizing the susceptibility sources outside the brain as major contributions to field fluctuations. An iterative conjugate gradient-based solver was developed in MATLAB for solving the minimization problem, resulting in a map of the global magnetic field shift distribution from the fitted susceptibility sources. This global map was subtracted from the original resonance frequency map, which produced a map of the residual magnetic field shift.

The conversion from frequency to magnetic susceptibility is an ill-posed inverse problem (Wharton and Bowtell, 2010). We used the LSQR method (Li et al., 2011; Liu et al., 2009; Paige and Saunders, 1982; Wharton and Bowtell, 2010) to determine the magnetic susceptibilities. To calibrate the calculation for studies where we only have frequency maps for a single head orientation, we acquired a multi-orientation GRE and a multi-orientation WASSR dataset for one subject, then used the COSMOS method to find the solution χ to the following minimization problem (Liu et al., 2009; Wharton and Bowtell, 2010):

$${min}_x\left({\Vert O_1\Vert }_2^2+{\Vert O_2\Vert }_2^2+\dots +{\Vert O_N\Vert }_2^2+{\alpha }^2{\Vert M_{\mathit{out}}\chi \Vert }_2^2\right)$$ [10]

where

$$O_n=W_n\left({FT}^{-1}\left(C_n\stackrel{\sim }{\chi }\right)-\mathrm{\Delta }{B}_n\right)$$ [11]

with ΔB_n as the field shift produced by a susceptibility distribution (χ) in the n^th orientation across a total of N orientations, χ̃ indicating the three-dimensional Fourier Transform of the magnetic susceptibility, C_n being the Fourier transform of the dipole convolution kernel linking susceptibility and field for that n^th orientation from Eqn. 10, α as a regularization parameter set to 20, M_out as a mask that is zero inside the brain, and W_n as the chosen weighting matrix for the n^th orientation. With α set to 20, the resulting susceptibility outside the brain is fairly small (less than 1 * 10⁻⁵ppm), thereby emphasizing susceptibility contributions from within the brain.

For a single orientation (N = 1), a relative residual threshold was set as the stopping criteria for the developed LSQR solver for the minimization problem in Eqn. 10. The weighting matrices for WASSR and GRE images were generated as described above for the multi-orientation data set.

Region of Interest Analysis

We parcellated our datasets into over sixty regions of interest through automated coregistration and segmentation with the Eve atlas using MRI Studio (https://www.mristudio.org) from the National Research Resource for Quantitative Functional MRI (http://www.mri-resource.kennedykrieger.org/software) (Jiang et al., 2006; Lim et al., 2013; Oishi et al., 2009). The Eve atlas from Johns Hopkins University is a single-subject female brain at 1mm³ isotropic resolution, put in standard Montreal Neurological Institute (MNI) coordinates (Mori et al., 2009; Mori et al., 2008; Oishi et al., 2009). Here, the Eve atlas templates used for coregistration were a skull-stripped GRE magnitude image at TE = 24ms (“EveGreMag”) and a QSM image (“EveQSM”), downloadable from the MRI Studio website as “JHU_MNI_SS_GreMag_ss” and “JHU_MNI_SS_QSM_ss,” with coregistration described in the methods section of (Lim et al., 2013). To coregister the outer surface of the brain, the skull-stripped magnitude image from the fourth echo of the GRE (TE = 24ms) from each subject was coregistered to the EveGreMag using Automated Image Registration (AIR) (Woods et al., 1998a; Woods et al., 1998b), with affine rigid body registration and trilinear interpolation. The resulting AIR transformation matrix was applied to the subject QSM. To facilitate processing, the images were transformed from float to byte format and intensity-corrected with automated histogram matching. To coregister the internal brain structures, the GRE magnitude image and QSM from each subject were coregistered using dual-channel Large Deformation Diffeomorphic Metric Mapping (Beg et al., 2005; Miller et al., 2002) to the EveGreMag and EveQSM. For the WASSR datasets, the skull-stripped non-saturated volume of the WASSR dataset (TE = 22ms) and the QSM from WASSR were coregistered using the above process to the EveGreMag and EveQSM, respectively.

After coregistration, the inverse transformation matrices from AIR and LDDMM were applied to the “Everything” Parcellation Map with deep gray matter ROIs delineated from QSM images and deep white matter ROIs from DTI FA images (downloadable as “JHU_MNI_SS_EvePM_V1.0”), transforming these brain regions into subject coordinates. These brain regions include gyral areas that contain both cortical gray matter and white matter tracts, which are difficult to align exactly per volunteer due to individual gyral variation. For the purposes of this paper, we included only deep gray matter and deep white matter ROIs in our analyses.

During the automated prescan, the scanner reference frequency (ω_ref) is placed at the frequency of the maximum water signal, which may be different for each scan depending on shimming and subject position in the coil. Therefore, a susceptibility reference standard is needed when quantifying susceptibilities. For each subject, deep white matter regions from the transformed EvePM were selected as a reference ROI in order to analyze all subjects on the same reference scale. The calculated susceptibility maps were then shifted so that the mean magnetic susceptibility value of white matter was −0.03ppm (Li et al., 2012b; Lim et al., 2013). This value was chosen because it led to a mean susceptibility of approximately 0ppm for cerebrospinal fluid (CSF), which is a common reference region used in QSM when assuming an isotropic susceptibility. Using the EvePM, we were able to measure the average susceptibility in various regions containing CSF, such as the frontal portion of the lateral ventricle and the body of the lateral ventricle, and saw a wide range of average values within these ROIs. Unlike the ventricles that may have partial volume effects with surrounding tissue, large white matter regions are more straightforward to select, and the mean magnetic susceptibility values within these white matter regions have smaller spatial variations (Li et al., 2012b; Lim et al., 2013; Wharton and Bowtell, 2010). We therefore used this indirect method to allocate a reference susceptibility of 0ppm to the CSF.

The transformed EvePM was applied to each subject’s referenced QSM, and an average susceptibility was determined for each region of interest. Values equal to exactly zero were excluded from the mean susceptibility calculation. The automated coregistration and segmentation process is described in detail in a recent paper (Lim et al., 2013).

To compare the agreement between the two methods for deep white matter and deep gray matter ROIs, we plotted the average susceptibilities for GRE vs. the average susceptibilities for WASSR alongside an identity line of y = x. We also created a Bland-Altman plot, with the average of the susceptibility values for GRE and WASSR plotted against the difference of the susceptibility values for GRE and WASSR for each of the regions of interest (Bland and Altman, 1986).

Results

Simulations

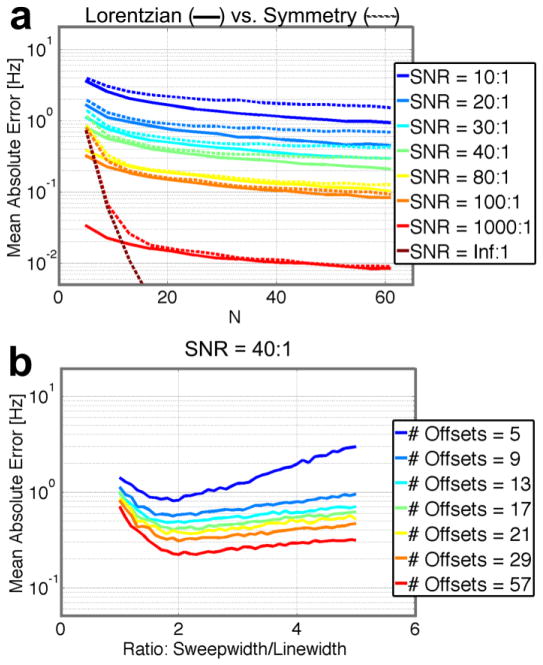
Monte Carlo simulations were used to compare the robustness of finding the resonance frequency with a Lorentzian fit or the Maximum Symmetry Algorithm. Figure 4a shows the mean absolute error in the resonance frequency as a function of the number of applied RF offset frequencies (N) for the optimal sweepwidth to linewidth ratio at different SNR levels of the non-saturated volume. As expected, using a higher number of points results in reduced error. Fitting with the Lorentzian lineshape consistently exhibited less error than with the Maximum Symmetry Algorithm. In the situation without noise, the mean absolute error for the Lorentzian fitting was about 10⁻⁸Hz (data smaller than axis limits of Fig. 4a), essentially the precision level of the software, whereas the Maximum Symmetry Algorithm reached an error limit of 10⁻⁶Hz.

Figure 4.

Simulations to gauge robustness of finding the resonance frequency. Mean absolute error is the absolute value of the mean difference between the generated resonance frequency and the fitted resonance frequency over 1000 Monte Carlo iterations. (a) Comparison between the Maximum Symmetry Algorithm (dashed lines) and Lorentzian fitting (solid lines) as a function of number of offset frequencies fitted (N) for the optimal sweepwidth to linewidth ratio at different SNR levels shows that Lorentzian fitting consistently exhibits equal or less error than the Maximum Symmetry Algorithm. (b) Error in Lorentzian fitting as a function of sweepwidth to linewidth ratio at an SNR of 40:1 shows that minimal error is around a ratio of 2.

Previous work on WASSR field mapping using the Maximum Symmetry Algorithm at 3T recommended acquiring 16 to 33 points (Kim et al., 2009). However, as seen in Figure 4a, with Lorentzian fitting (Liu et al., 2010b), a sub-Hertz error could be achieved using as few as nine offset frequencies with an SNR as low as 20:1. Experimentally, the SNR of the brain region for the non-saturated volume was determined to be 20 to 40 per slice, depending on the anatomical level of the slice. The pre-determined Lorentzian shape can be fitted quite well as long as there are some points without saturation and at least a few in the saturation dip. Figure 4b shows that using a sweepwidth to linewidth ratio greater than two does not improve the quality of the frequency determination but in fact reduces it slightly. As the accuracy reduces steeply below a ratio of two and linewidths vary, it is best to choose a conservative ratio between 2 and 4. That said, the shift range is also a factor, which generally requires one to increase the sweepwidth above optimal.

Determination of the Number of Points for WASSR Acquisition

Even though the simulations indicate that WASSR could measure frequency shifts with as few as nine data points for a sub-Hz error, the actual number of points (image volumes with different frequency offset) that is needed of course depends on the error required for determining accurate magnetic susceptibility differences from frequency differences on the order of a few Hz or less. The frequency shifts across a large organ like the brain fall across a fairly large range, which we experimentally determined to be approximately +/− 1ppm, or +/−128Hz at 3T. For these subjects, the linewidth (that is, the Full-Width Half Maximum of the fitted Lorentzian lineshape) generally ranged from 20Hz to 65Hz across the brain.

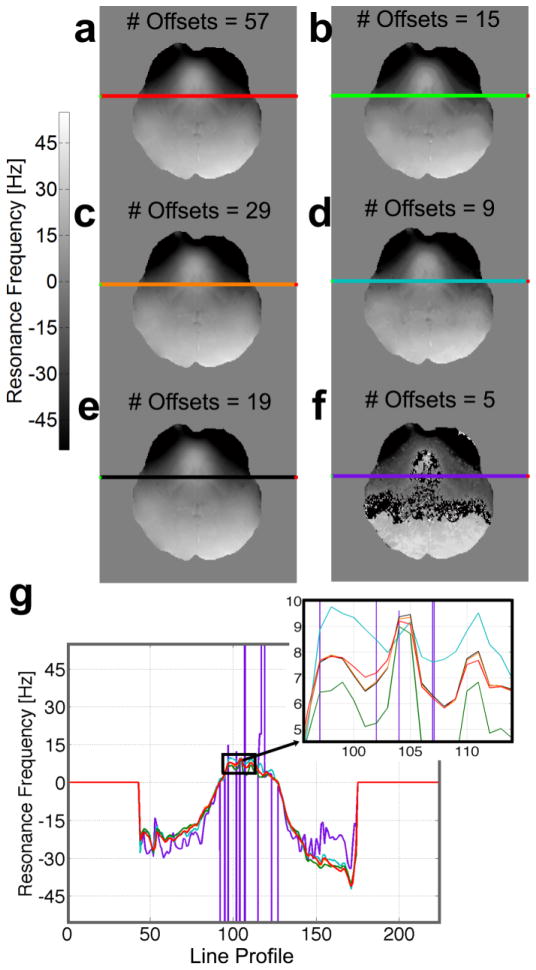
A 57-point direct saturation dataset was acquired with a saturation pre-pulse applied at an RF offset frequency every 5Hz between +/−140Hz. The SNR of the non-saturated signal ranged from 20 to 40, depending on the slice and structure in which the SNR was measured. Figure 5 shows a comparison between frequency maps calculated as a function of frequency resolution, ranging from 57-point 5Hz spacing (Fig. 5a) to 5-point 70Hz spacing (Fig. 5h). The highly-sampled dataset provided easy fitting of the frequency, but the total scan duration of 24 minutes is clearly not optimal for clinical studies. The sparse dataset with five points was insufficient for determining resonance frequency accurately (Fig. 5f). Acquiring fewer points shows a different profile from the gold standard, as seen in a graph of the line profiles (Fig. 5g inset) through the same slice of the resulting frequency maps.

Figure 5.

Resonance frequency maps calculated using different RF sampling densities within the same sweepwidth. (a) A highly sampled dataset of 57 volumes with 5Hz spacing over a +/− 140Hz range. This dataset was used as “gold standard,” then discretely down-sampled, from (b) 29 points acquired every 10Hz to (f) five volumes acquired every 70Hz. Note that (e) was sampled non-linearly every 5Hz between +/−80Hz and 10Hz from +/− 80 to +/−120Hz. (g) The line profiles through the same slice of the calculated resonance frequency maps show comparable behavior for numbers of offsets ranging from 19 to 57 (see inset with sub-Hertz range).

A histogram of resonance frequencies across the brain showed that the majority of the resonance frequencies within the brain occur between +/− 80Hz, with fewer frequencies around +/− 120Hz located closer to the skull and CSF. Therefore, we decided to use 19 points (image volumes) spaced at intervals of 10Hz within +/− 80Hz (for finer detail within the brain, in accordance with our simulations) and then 20Hz between 80Hz and 120Hz (to capture the areas more affected by background gradients on the outer edges of the brain). This provided data comparable to the gold standard (Figs. 5e, g), while adhering to a clinically viable scan duration of approximately eight minutes.

This 19-volume non-linear scan does propagate more noise from regions with lower SNR (e.g., regions that contain flowing liquids like the blood and CSF with longer T₁, which are less prone to complete saturation), but line profiles through resonance frequency maps from the 57-volume scan, 29-volume scan, and the 19-volume scan showed very comparable behavior (Fig. 5g, inset).

Field Drift Correction

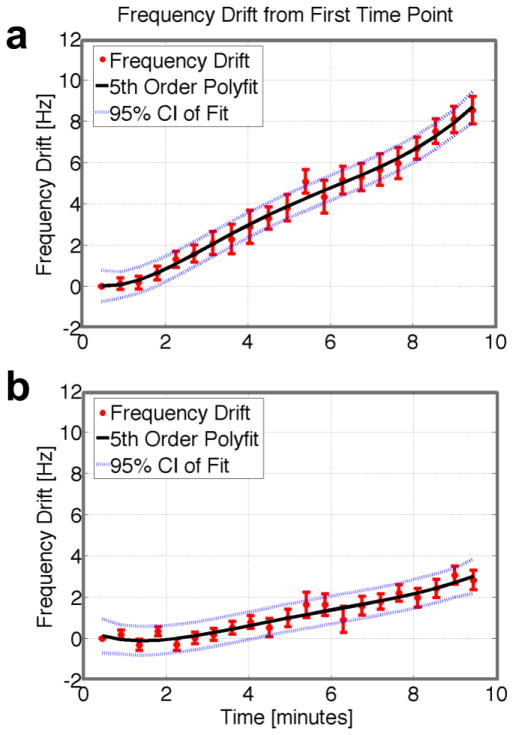
Rapid GRE scanning often heats the magnet bore components, especially the passive shims. As a result, the magnet frequency may drift several Hertz over the total scan time, with the amount of drift depending on scan history. Figure 6 illustrates how a correction for this field drift can be obtained using WASSR. If the WASSR (or other GRE-based acquisition) experiment is conducted at the beginning of the overall study starting from a cold scanner, the magnet bore heats up slowly and continuously during the scan, causing the field to drift up to 10Hz over ten minutes (Fig. 6a). If a gradient-intensive sequence (e.g., DTI) is performed before the series of GRE acquisitions in the WASSR sequence, however, the magnet bore is closer to thermal equilibrium, and the field drifts much less (Fig. 6b). Because we cannot correct for field drift in the normal 3D single-volume GRE datasets, we usually ran the GRE sequence used for quantitative susceptibility comparison after the WASSR sequence, so that the field would drift less during the GRE image acquisition. The field drift can be measured using the WASSR frequency as a function of time (Fig. 6a, b), the result of which can be used for correction of the data by fitting the trend with a polynomial and shifting the prescribed offset frequencies used in Lorenztian fitting.

Figure 6.

Illustration of field drift during GRE acquisition (a) starting from a cold magnet and (b) after prior gradient-intense scanning. Drift is defined as the difference between the average frequency in each dynamic and the average frequency in the first dynamic. Data acquired using WASSR allowed determination of field drift as each volume (one frequency offset) was acquired every 30 seconds. The field drift was fit with a fifth order polynomial, which was used to correct the prescribed offset frequencies. Abbreviations: CI = confidence interval.

Calibration of Magnetic Susceptibilities

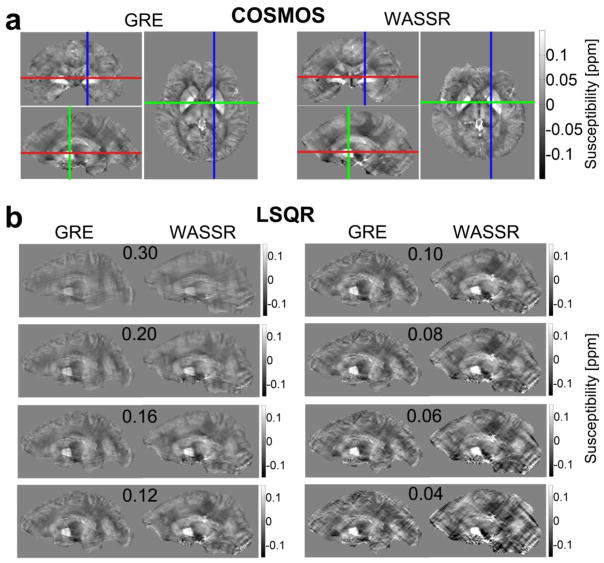
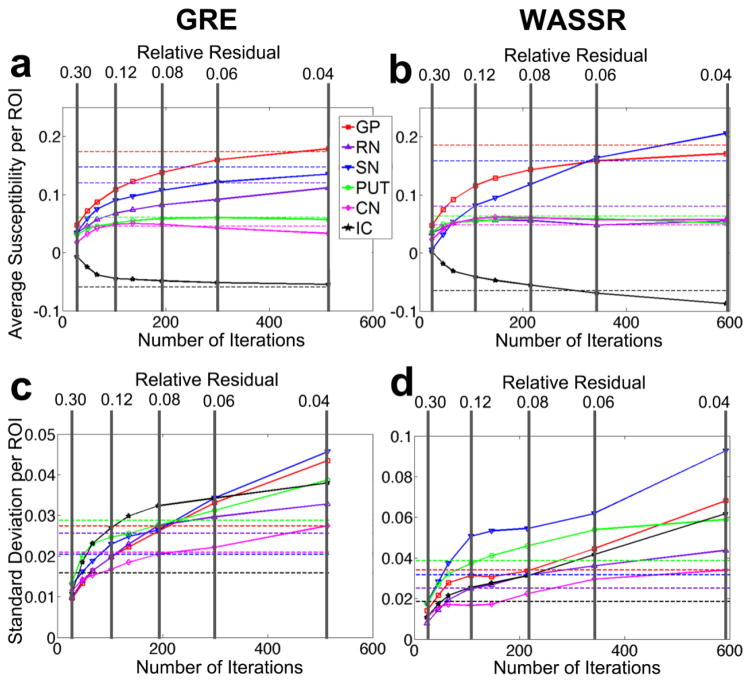
The COSMOS method, which utilizes data collected at multiple subject orientations, has the best inverse conditions compared to other methods (Liu et al., 2009). However, this is physically inconvenient for the subject and time consuming; therefore, most groups use only single orientation acquisitions. We used a COSMOS acquisition of one subject as the gold standard to calibrate the thresholds for stopping the iterative inverse calculation in the single orientation method. An example of this is shown in Figure 7 for both multi-echo GRE and WASSR. The LSQR iteration stopping criteria for the single-orientation susceptibility calculations were varied across a range of maximum relative residual thresholds (0.30, 0.20, 0.16, 0.12, 0.10, 0.08, 0.06, 0.04), as visualized in Fig. 7b. Figure 8 shows the average susceptibility (a, b) and standard deviation (c, d) within selected regions of interest for (a, c) GRE and (b, d) WASSR. The GRE single-orientation susceptibility maps corresponding to these relative residual thresholds converged at 28, 48, 67, 103, 136, 192, 299, and 514 iterations, respectively. The WASSR single-orientation susceptibility maps corresponding to these relative residual thresholds converged at 24, 46, 65, 108, 147, 215, 343, and 593 iterations, respectively. We determined the optimum relative residual threshold as the most consistent average susceptibility per ROI with the lowest standard deviation, which was approximately 0.06 for GRE and 0.06 − 0.08 for WASSR. We decided that the following parameters would produce appropriate susceptibility values for single-orientation acquisitions: α = 10, the maximum number of iterations = 200, and the tolerance threshold for the minimization = 0.08. For both acquisitions, the calculations generally converge within 80 to 200 iterations.

Figure 7.

Using COSMOS with multi-orientation datasets for multi-echo GRE and WASSR to calibrate the LSQR susceptibility calculation for single-orientation datasets. Susceptibility scale is in ppm relative to CSF. (a) The multi-orientation dataset was calculated with a convergence tolerance set at 1 × 10⁻⁵. (b) Single-orientation quantitative susceptibility maps for GRE and WASSR as a function of relative residual threshold (e.g., 0.30, 0.20, etc.) used as the LSQR iteration stopping criterion over a range from 0.30 to 0.04.

Figure 8.

Susceptibility measurements for the gold standard of COSMOS (dashed lines) and LSQR (solid lines), showing the average susceptibility per region of interest and the standard deviations within each region of interest for (a, c) GRE and (b, d) WASSR. The average and standard deviation per ROI for LSQR measurements are shown as both a function of the relative residual threshold (vertical gray lines) and the number of iterations (x-axis) for the calculation.

Frequency and Susceptibility Maps

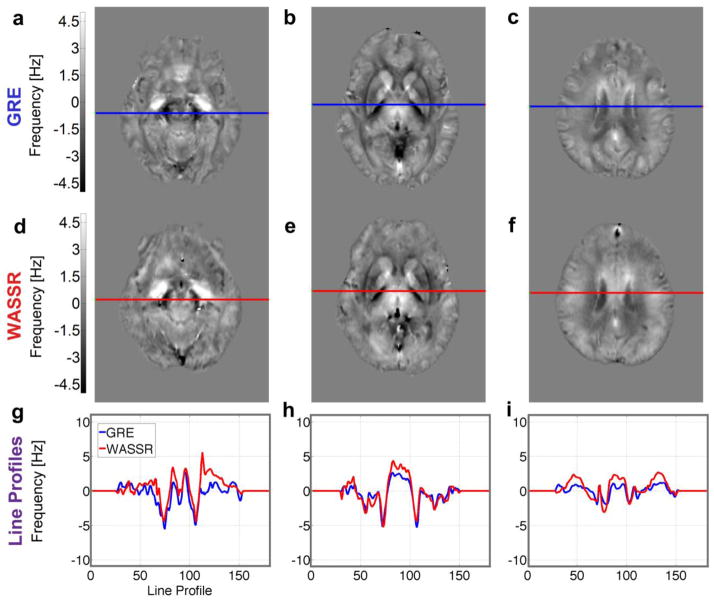
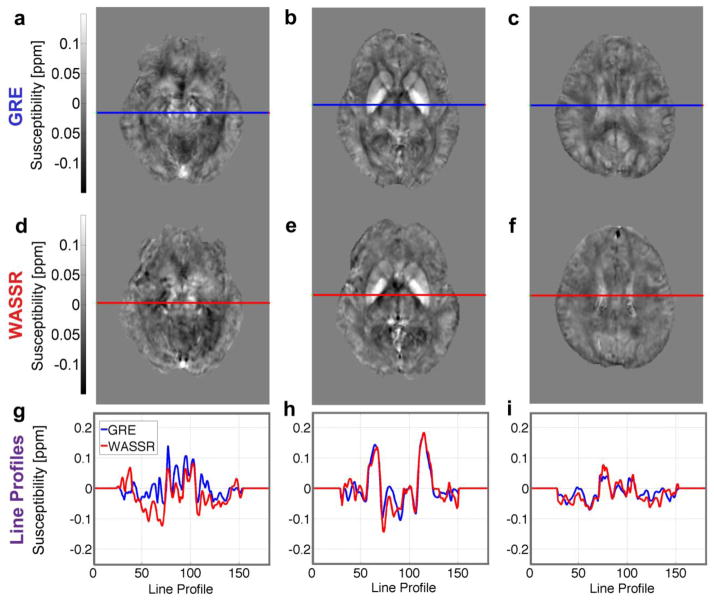
The multi-echo gradient echo and WASSR direct saturation images produced the frequency maps shown in Figure 9 and the susceptibility maps shown in Figure 10. These maps were coregistered to GRE magnitude and QSM images from the Eve atlas (Lim et al., 2013) in order to display line profiles (Figs. 9g–i, 10g–i) through the same slices at several levels in the brain, which illustrate similarities and differences between the two methods.

Figure 9.

Frequency maps from (a–c) multi-echo 3D GRE and (d–f) 3D WASSR obtained after dipole fitting to remove background gradients. Comparable scan times were used (~8 minutes). (g–i) Line profiles across these maps from GRE (blue lines) and WASSR (red lines) show similar trends in these slices through (a, d, g) the red nucleus and substantia nigra, (b, e, h) basal ganglia, and (c, f, i) corticospinal tract. Transformation matrices from coregistration were applied to these non-referenced frequency maps to show the comparison in the coordinates of the Eve atlas.

Figure 10.

Susceptibility maps from (a–c) multi-echo 3D GRE and (d–f) 3D WASSR calculated using the LSQR method (with a stopping relative residual set to 0.08) from one subject’s corrected frequency maps and coregistered to the Eve atlas. (g–i) Line profiles across these maps for GRE (blue lines) and WASSR (red lines) show similar trends for both methods in slices through (a, d, g) the red nucleus and substantia nigra, (b, e, h) basal ganglia, and (c, f, i) corticospinal tract.

Generally, the frequency and susceptibility maps for both GRE and WASSR show comparable trends; that is, the iron-rich deep gray matter structures such as the red nucleus and globus pallidus appear to be brighter, or more paramagnetic, than the reference of CSF, whereas the white matter structures such as the internal capsule of the corticospinal tract and the thalamic radiations appear darker, or more diamagnetic, than CSF.

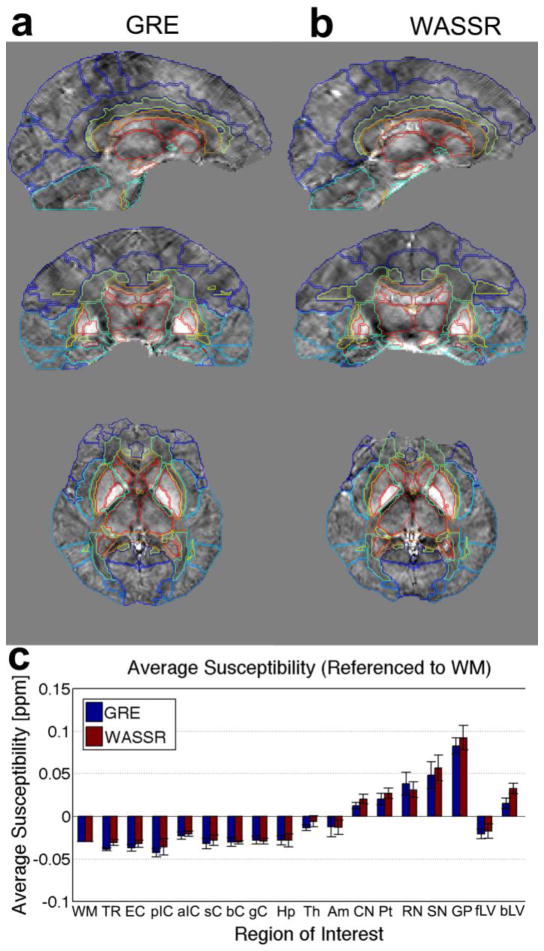
Regions of Interest Analysis to compare WASSR and GRE

Figure 11 shows the regions of interest delineated via automated segmentation of QSM maps in our EveQSM reference atlas (Lim et al., 2013) for (a) GRE and (b) WASSR. Figure 11c displays the average referenced susceptibility and standard deviations for several deep white matter and deep gray matter regions of interest across our five subjects, showing comparable measurements for GRE and WASSR within the standard deviation for each ROI. Generally, the deep white matter regions exhibit an average susceptibility that is more negative than the deep gray matter regions. The globus pallidus exhibited the highest average susceptibility for all five volunteers. As shown in Figure 11c, the average susceptibility in two CSF-filled regions, the frontal portion and the body of the lateral ventricle, was approximately −0.03 to 0.04 ppm for WASSR and −0.03 to 0.02ppm for GRE, respectively, across the five volunteers. This typical large variation prompted the combined usage of several deep white matter bundles as a reference region, as described in the Methods section.

Figure 11.

Over sixty brain regions can be selected using MRI Studio software and the Eve atlas for (a) multi-echo GRE and (b) WASSR. (c) Measured susceptibilities (ppm) in a selection of deep white matter and deep gray matter regions show comparable numbers for both methods within a standard deviation. Abbreviations: WM = white matter reference region, TR = thalamic radiations, EC = external capsule, pIC = posterior limb of the interior capsule, aIC = anterior limb of the interior capsule, sC = splenium of the corpus callosum, bC = body of the corpus callosum, gC = genus of the corpus callosum, Hp = hippocampus, Th = thalamus, Am = amygdala, CN = caudate nucleus, Put = putamen, RN = red nucleus, SN = substantia nigra, GP = globus pallidus, fLV = frontal portion of the lateral ventricle, bLV = body of the lateral ventricle.

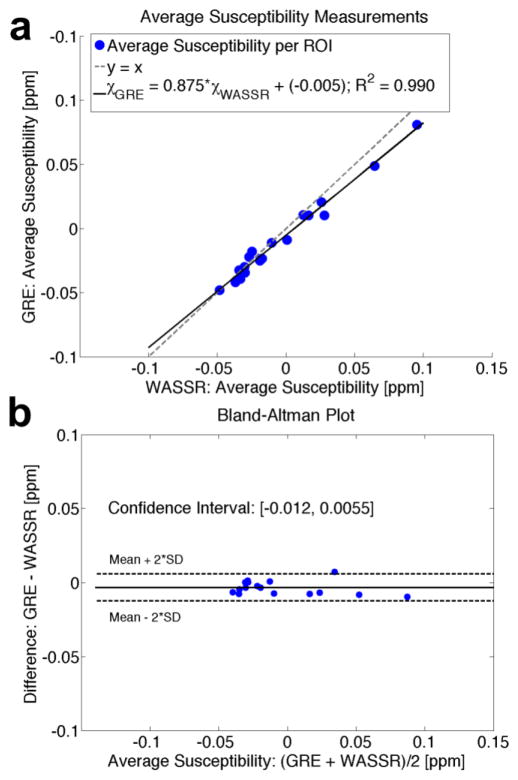
Figure 12a depicts the correlation between the GRE and WASSR methods for the mean susceptibilities across the white and gray matter regions of interest (R² = 0.992) in Fig. 11c, plotted alongside a line of identity (y = x). For this particular set of volunteers, the correlation between the average susceptibility calculated using GRE versus WASSR follows the equation:

$${\chi }_{\mathit{GRE}}=0.875·{\chi }_{\mathit{WASSR}}-0.005$$ [12]

Figure 12.

Comparison between average susceptibilities in ROIs from Figure 11c measured by WASSR and multi-echo GRE. (a) Correlation between average susceptibility measurements. (b) Bland-Altman plot showing that the mean difference between GRE and WASSR is very small. The confidence interval is narrow and encompasses zero difference, which signifies a high correlation between the two methods.

Figure 12b contains a Bland-Altman bias plot that shows the degree of agreement for the ROIs displayed in Figure 11c between multi-echo GRE and WASSR (Bland and Altman, 1986) by comparing the difference between the mean susceptibilities of the two methods with their average. The mean difference between susceptibility measurements from WASSR and GRE was −0.0035, with a 95% confidence interval of [−0.012, 0.0055] ppm. Because the confidence interval is narrow and includes zero, the zero bias likely is the real bias, indicating agreement between the two methods.

Discussion

Gradient-recalled echo imaging is a convenient pulse sequence for frequency mapping that is widely available on all human MRI scanners, but exhibits a few disadvantages that may affect the accuracy of susceptibility maps. Firstly, phase images may have phase wraps at the interfaces of structures with largely different susceptibilities, thereby complicating data interpretation around these structures. Faulty phase wrap removal results in areas of discontinuous phase signal, which propagates to discontinuous susceptibility maps. Many methods have been developed to remove these phase wraps, including high pass filtering (Haacke et al., 2009; Haacke et al., 2004), region-based unwrapping methods (Jenkinson, 2003; Rauscher et al., 2008; Witoszynskyj et al., 2009), and Laplacian-based phase unwrapping (Li et al., 2011; Schofield and Zhu, 2003). The method of phase unwrapping may affect the resonance frequency map; for example, when using a high-pass filter to remove background gradients, the size of the filter and number of iterations applied will affect the final contrast in the resulting frequency map. Laplacian-based phase unwrapping, the method utilized here in our GRE method, removes part of the background gradients before dipole fitting, which results in a blurred resonance frequency map.

Secondly, phase contrast relies on proper choice of echo times, resulting in images with longer overall imaging times at lower fields; for example, commonly utilized TEs are approximately 40ms at 1.5T (Schweser et al., 2010) and 3T (Li et al., 2011), and about 15ms at 7T (Wharton and Bowtell, 2010). Phase images acquired at longer echo times will exhibit more phase wraps across the acquired volume, with maximum SNR at TE = T2* (Wu et al., 2012). Fast-imaging readouts, such as EPI, utilize longer echo times, which result in more phase wraps; therefore, phase imaging with GRE usually does not use EPI.

Thirdly, when acquiring the entire 3D GRE volume at high resolution, the subject is more likely to move, leading to image blurring. Examples from the literature show that, at 3T, the time needed to acquire a four-echo GRE at 2mm isotropic resolution was 26 minutes (Yao et al., 2009) and to acquire a dual-echo GRE at 0.6mm isotropic resolution was 19 minutes (Schweser et al., 2011b). Here, we utilized a 3D eight-echo GRE at 1.2mm isotropic resolution with a scan duration of approximately 8 minutes, which is still a long period of time for a subject to lie in the scanner without moving.

Fourthly, in conventional GRE, B₁ inhomogeneities from RF transmission may affect the measured susceptibility (Schweser et al., 2011a). Fifthly, rapid GRE scanning often heats the magnet bore components, thereby changing the magnet frequency according to Curie’s Law, and the magnet frequency may drift over several Hertz during the acquisition.

Our results show that WASSR provides a comparable alternative, with several advantages over GRE imaging for QSM mapping. The WASSR method relies primarily on the signal magnitude, and no phase unwrapping is necessary. Because the generation of the resonance frequency map depends mainly on the direct saturation prepulse, any readout may be utilized; therefore, volumes may be acquired with a short TE (for higher SNR) and an EPI acquisition (approximately 20–30 seconds to acquire a whole-brain volume at 3T). A higher EPI factor may cause slight geometric distortions, but allows faster acquisition of each volume, which also decreases the likelihood of motion during acquisition. Even though structures may not correspond exactly between WASSR with EPI and 3D-GRE, which does not utilize EPI, the susceptibility measurements from WASSR were well reproducible and quite comparable to those from GRE. As shown by the Bland-Altman plot in Figure 12b, the susceptibility measurements using each of the two methods correlate well across regions of interest.

Acquiring separate volumes requires coregistration between the volumes, but also allows for quality control; if a subject moves while one volume is acquired at a particular RF offset frequency, that volume may be discarded without drastically affecting the entire experiment, because other volumes may still be fit to a Lorentzian lineshape. Therefore, the WASSR method is especially useful for acquiring susceptibility maps in subjects that are likely to move (e.g., children) or structures that are affected by involuntary motion. For example, acquiring direct saturation images and calculating frequency maps with WASSR has been used to calculate susceptibility maps in the cervical spinal cord (Lim et al., 2012a).

For our WASSR images at an SNR of 20 to 40 at 3T, while covering the entire brain from +/− 120Hz, we observed contributions from brain tissues within +/− 80Hz. Therefore, using simulations where the theoretical signal had a resonance frequency randomly selected from a distribution that had a mean of 0 and a standard deviation of 21.6Hz, we found that Lorentzian fitting had an error on the order of sub-Hertz even for low SNR conditions (Fig. 3b). The optimal sweepwidth to linewidth ratio was determined based on the number of volumes acquired; for 19 points, the optimal SW/LW was approximately 2 (Fig. 4b). A very low sweepwidth of acquired offset frequencies compared to the experimental linewidth (SW/LW ratio < 2) effectively undersamples the data, resulting in a high error for the Lorentzian fit. On the other hand, if the sweepwidth is too large (SW/LW > 4), the sampled points cannot adequately characterize the curve, also resulting in a slightly higher error. Experimentally, the sweepwidth should therefore encompass the distribution of frequency shifts across the brain, approximately +/− 1ppm from the scanner reference frequency. For subjects or structures across which the resonance frequency varies significantly, we recommend a longer scan to achieve higher offset frequency sampling across a larger sweepwidth.

With the WASSR method, any inhomogeneities from B₁ transmission affect only the linewidth of the direct saturation lineshape and not the resonance frequency per voxel; that is, B₁ inhomogeneities affect the breadth or width of the Lorentzian lineshape, but the Z-spectrum in each voxel will still be symmetric about and have a minimum signal occurring at the resonance frequency of that voxel. Because the calculated susceptibility is based on this resonance frequency, the WASSR method is expected to provide robust measurements of raw resonance frequency even in the presence of B₁ inhomogeneities.

Using the WASSR method, the Z-spectrum of direct saturation images consists of a series of 3D brain volumes, each of which is acquired in less than half a minute with the same TE and TR. Even though the signal magnitude changes as a function of RF offset frequency, the signal phase depends mainly on the timing parameters (e.g., TE), and therefore should be the same for each volume. Any changes in this average phase with respect to the first volume correlate with changes in the main magnetic field. By acquiring a phase image for each 30-second WASSR volume, a frequency correction based on the individual volumes could be applied to determine field drift between acquired volumes.

The resonance frequency maps from GRE and WASSR do appear somewhat different. This could be due to either technical or mechanistic differences. From a technical point of view, the Laplacian-based phase unwrapping in the 3D-GRE removes a portion of the background gradient effects, resulting in a blurrier GRE resonance frequency map before background removal. For the WASSR method, background gradient removal for the resonance frequency maps relies solely on dipole fitting, which is more calculation intensive and may be less able to show small differences. Also, the GRE images did not utilize an EPI readout, leading to fewer geometric distortions but a longer acquisition time per volume. That said, EPI could theoretically be used to speed up the GRE acquisition, especially when using one TE for the phase information. The application of motion correction between the direct saturation images acquired at different frequencies may lead to reduced sharpness in the contrast of the WASSR images. Possible ways to overcome these limitations would be to restrain the subject’s motion further and to acquire the images with a lower EPI factor or other acquisition method. (Also see Supplementary Material.) The WASSR resonance frequency maps contained more extreme values, mainly due to differences in CSF saturation between acquired volumes, possible coregistration errors, geometric distortions from EPI, and larger contributions from background gradients that were not removed with preprocessing; however, these factors all contribute to a low “goodness of fit” factor when assessing how well the Lorentzian fit matched the experimental data. Therefore, any voxels with a low “goodness of fit” metric were given low weighting values in subsequent calculations, allowing the determination of meaningful corrected frequency and susceptibility maps. We used 0.08 as the relative residual threshold in susceptibility calculations for both GRE and WASSR in order to provide a comparable standard for the resulting quantitative susceptibility maps. An advantage of multi-echo GRE imaging is the ability to calculate an R₂* map. The WASSR method allows for calculation of a linewidth map, which incorporates R₁, R₂, and B₁. R₂* maps (Haacke et al., 2005; Jensen et al., 2009) and saturation linewidth maps (Smith et al., 2009) have both been used to show iron distribution in the brain.

Interestingly, one feature that seems to differ between the methods is the appearance of some of the fiber bundles on the susceptibility images, for instance the optic radiations in Figures 9 and 10. In the future, we intend to perform higher resolution combined GRE and WASSR studies at 7T to see whether these differences can be used to study the mechanisms of contrast in susceptibility images. We hypothesize that these differences may be due to selection of different compartments (Sati et al., 2013) in the two methods, which provide an opportunity to learn more about the system. The WASSR approach is likely to measure different compartments from GRE for several reasons. First, with our current GRE approach, we calculated the resonance frequency maps as the average slope across eight echo times, ranging from TE₁ = 6ms to TE₈ = 48ms. The WASSR images were each acquired with a single TE of 24ms. Recent publications have suggested a difference in the frequency maps generated at different echo times, which could also contribute to the differences between these two images (Wharton and Bowtell, 2012). Using different echo times will affect the pools measured. At the longer TE used in the WASSR method, myelin water no longer contributes much to the water signal. Second, the water is saturated at a single frequency, after which this saturation can be transferred to other pools through multiple mechanisms of magnetization transfer, such as dipolar coupling (Henkelman et al., 2001; Wolff and Balaban, 1994), chemical exchange (van Zijl and Yadav, 2011), and physically through diffusion. Using a typical water diffusion constant in brain tissue of 1×10−9 m2/s, this can be as far as over a range of 29 μm. Of course, saturation is not instantaneous but follows T₁, so the situation is more complex. The effect of magnetization exchange on susceptibility mapping (Luo et al., 2010; Shmueli et al., 2011; Zhong et al., 2008) is still not fully elucidated. More work is needed to extract the details of these mechanisms, but comparing these two methods provides an opportunity to study the complex biophysical system in more detail.

The accuracy of susceptibility maps obtained using the WASSR method depends mainly on sampling rate; more volumes acquired at closely-spaced RF offset frequencies will result in a better Lorentzian fit and a more clearly-defined susceptibility map. GRE is more conducive at higher magnetic fields, at which a shorter TE induces larger frequency shifts and therefore more contrast between gray and white matter structures. However, at lower fields with lower frequency shifts, GRE is limited by spatial SNR, longer echo times required for phase contrast, and resulting longer scan times. In WASSR, the sweepwidth needed to cover the distribution of frequency shifts across the brain is proportional to the field in Hz, but the same in ppm, allowing the same number of RF offset frequencies to be acquired at each field, and resulting in susceptibility maps that will be comparable between varying field strengths. The WASSR method may be most useful for centers that do not have access to high-field magnet systems.

Conclusions

The WASSR method utilizes direct saturation images to identify susceptibility shifts. The overall scan time for WASSR depends on the number of volumes acquired; acquiring more volumes result in susceptibility maps with a higher SNR, but also make WASSR somewhat slower than GRE MRI at high fields. That said, because the individual volumes are acquired quickly and are not significantly hampered by B₁ or B₀ field inhomogeneities, WASSR should be especially advantageous for low-field imaging with subjects that are likely to move (e.g., children), or across areas with large susceptibility differences that would produce many phase wraps.

Supplementary Material

02

Supplemental Figure: Comparison between the (a) corrected frequency maps and (b) average susceptibility maps calculated using GRE (top), WASSR (middle), and difference between GRE minus WASSR (bottom) for one volunteer.

Highlights.

• We derived resonance frequency maps using WAter Saturation Shift Referencing (WASSR).

• With WASSR, we can correct for field drift and motion, then calculate QSM images.

• Quantitative Susceptibility Maps (QSMs) were also calculated from GRE signal phase.

• We used MRI Studio with the Eve atlas for coregistration and automated segmentation.

• QSM images and average QS per ROI were well correlated between WASSR and GRE methods.

Abbreviations

aIC

Anterior limb of the Internal Capsule

Am

Amygdala

bC

Body of the Corpus callosum

bLV

Body of the Lateral Ventricle

CC

Corpus Callosum

CI

Confidence Interval

CN

Caudate Nucleus

CSF

Cerebrospinal Fluid

COSMOS

Calculation of Susceptibility through Multiple Orientation Sampling

DS

Direct Saturation

EC

External Capsule

EvePM

“Everything” Parcellation Map from the Eve atlas at Johns Hopkins University

fLV

Frontal portion of the Lateral Ventricle

gC

Genu of the Corpus callosum

GM

Gray Matter

GP

Globus Pallidus

GRE

Gradient Recalled Echo

Hp

Hippocampus

IC

Internal Capsule

LSQR

Algorithm for sparse linear equations and sparse least squares

MTR

Magnetization Transfer Ratio

pIC

Posterior limb of the Internal Capsule

Pt

Putamen

QSM

Quantitative Susceptibility Mapping

RN

Red Nucleus

ROI

Region of Interest

sC

Splenium of the Corpus callosum

SN

Substantia Nigra

Th

Thalamus

TR

Thalamic Radiations

WASSR

WAter Saturation Shift Referencing

WM

White Matter