Abstract
Rule-based modeling was developed to address the limitations of traditional approaches for modeling chemical kinetics in cell signaling systems. These systems consist of multiple interacting biomolecules (e.g., proteins), which themselves consist of multiple parts (e.g., domains, linear motifs, and sites of phosphorylation). Consequently, biomolecules that mediate information processing generally have the potential to interact in multiple ways, with the number of possible complexes and post-translational modification states tending to grow exponentially with the number of binary interactions considered. As a result, only large reaction networks capture all possible consequences of the molecular interactions that occur in a cell signaling system, which is problematic because traditional modeling approaches for chemical kinetics (e.g., ordinary differential equations) require explicit network specification. This problem is circumvented through representation of interactions in terms of local rules. With this approach, network specification is implicit and model specification is concise. Concise representation results in a coarse graining of chemical kinetics, which is introduced because all reactions implied by a rule inherit the rate law associated with that rule. Coarse graining can be appropriate if interactions are modular, and the coarseness of a model can be adjusted as needed. Rules can be specified using specialized model-specification languages, and recently developed tools designed for specification of rule-based models allow one to leverage powerful software engineering capabilities. A rule-based model comprises a set of rules, which can be processed by general-purpose simulation and analysis tools to achieve different objectives (e.g., to perform either a deterministic or stochastic simulation).
How does the behavior of a cellular regulatory system emerge from the physical interactions of its constituent biomolecules? What information processing and decision-making functions are performed by these interactions? What are the design principles underlying these functions? The field of systems biology aims to address such questions using a suite of experimental and computational approaches1–3. Among the computational approaches is rule-based modeling4, 5, which is particularly useful for studying cell signaling6–26. A characteristic feature of this approach is the use of rules to represent interactions. As we will discuss, the use of rules streamlines specification and enables simulation of models that capture biomolecular site dynamics, the structurally-resolved chemical kinetics of biomolecular interactions. Studies of site dynamics are needed to understand the behavior of cell signaling systems because 1) biomolecular interactions (e.g., protein-protein interactions) depend on specific structural interfaces 27–31; and 2) these interactions are transient27, 32, 33. In the first two sections that follow, we discuss aspects of biomolecular interaction networks and modeling concerns that motivate the rule-based modeling approach. After these sections, we provide an introduction to basic rule-based modeling concepts, which features discussion of an example model. We then discuss simulation techniques, including the advantages and disadvantages of various methods, and issues related to knowledge representation, including model visualization and annotation and new high-level approaches to model specification. We conclude with a brief discussion of the potential for model reuse and collaborative model development to contribute to our predictive understanding of cell signaling.
BIOMOLECULAR INTERACTION NETWORKS: COMPLEX, DYNAMIC, AND MODULAR
Complex networks of interacting biomolecules are ubiquitous in cells, and form the regulatory machinery controlling fundamental biological processes34, such as metabolism, gene expression, and signaling, which are interdependent35. We focus here on networks that mediate intracellular signaling, i.e., detection of environmental stimuli and processing of this information to yield a cellular response. These networks are overlapping and interconnected36 partly due to promiscuity37 and crosstalk, which can have functional consequences38. The most prominent biomolecules in signaling systems are proteins39, 40, but lipids, nucleic acids, and small-molecule metabolites also play important roles. Proteins have been subject to a barrage of evolutionary pressures41,42, which has led to emergence of modular protein elements: functional units that can operate somewhat independently and that offer adaptive benefits43. These functional units can be combined into diverse arrangements through mechanisms such as gene duplication and fusion43, or through deliberate engineering44, to generate new connections between pathways and new capabilities45.
A protein with multiple functional components has the potential to interact with multiple binding partners simultaneously. A further layer of complexity arises because a protein may be subject to post-translational modifications at multiple sites46, 47, which regulate interactions and modulate catalytic activities. Many different combinations of interactions and multi-site modifications may be possible, with different combinations contributing to different signaling functions38. This hallmark feature of signaling systems has been termed combinatorial complexity48. The challenges posed by combinatorial complexity, discussed below, motivate the rule-based modeling approach.
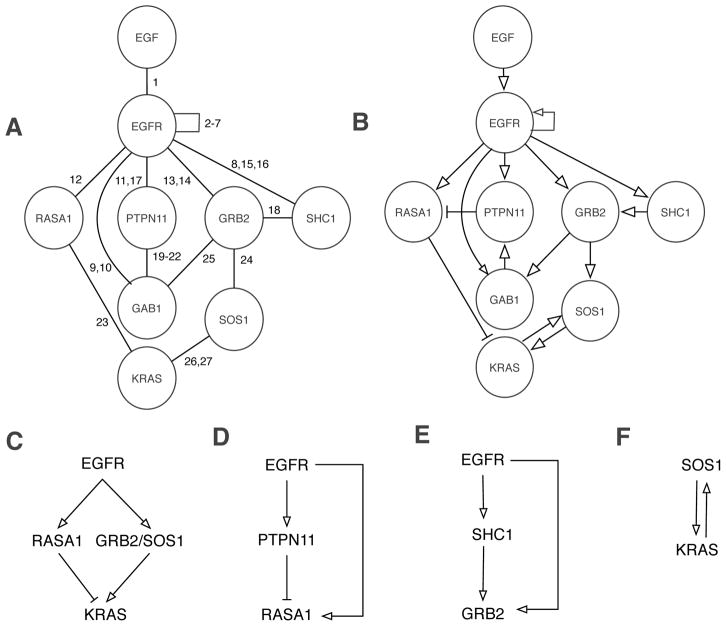
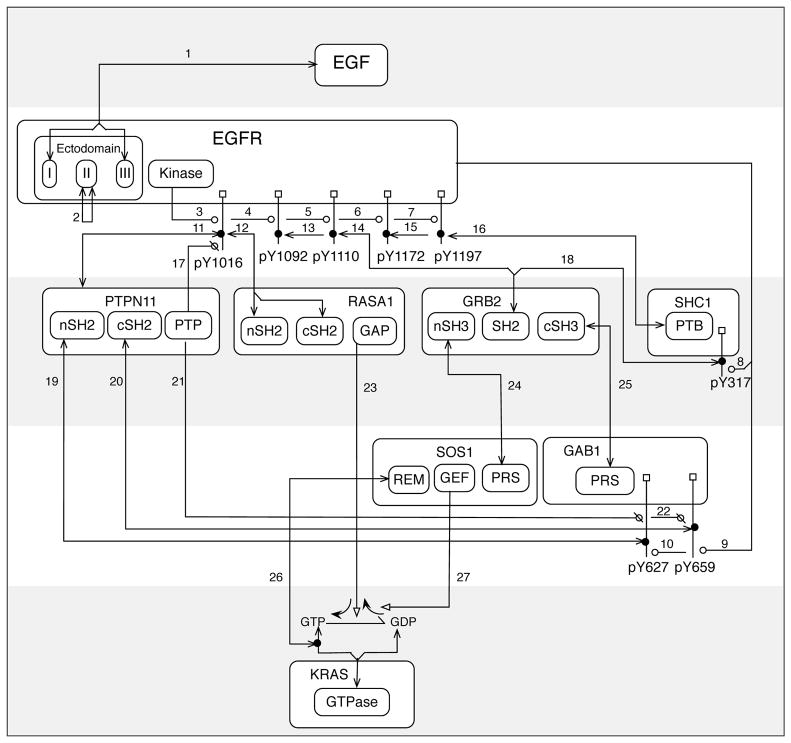
In addition to being intricately connected, signaling networks are highly dynamic. Most interactions among proteins in such a network are noncovalent and transient49, and the outcomes of enzyme-substrate interactions within these networks, such as serine, threonine, and tyrosine phosphorylation, are known to be condition- and time-dependent50, 51. However, these networks are commonly depicted as static diagrams or graphs, in which nodes correspond to biomolecules and edges or arrows correspond to interactions and/or influences (e.g. activation and inhibition)52. Examples of such diagrams are shown in Fig. 1, which illustrate proteins and interactions considered in various models for signaling by the epidermal growth factor (EGF) receptor (EGFR)15, 53–60, a member of the ErbB family of receptor tyrosine kinases61. The interactions considered in Fig. 1 are further described in Table 1. Diagrams such as those of Fig. 1 have clear utility; they can summarize large amounts of qualitative knowledge in an intuitive and visual format. However, the logical consequences of the interactions depicted in a diagram depend not only on qualitative factors (e.g., the connections and influences among the biomolecular components of a network) but also on quantitative factors (e.g., the copy number of a protein, which can modulate the abundance of a protein complex and/or the strength of a feedback loop)62, 63. Whenever quantitative factors are important, intuition alone is limited, and reasoning aids, such as computational models, are needed to accurately predict the behavior of a system.
Figure 1.
Illustration of proteins and interactions involved in EGFR signaling. (A) In this graph, nodes correspond to proteins and edges correspond to direct physical interactions. This type of graph is commonly used to visualize protein interaction networks195. Numbers next to edges refer to descriptions of interactions given in Table 1. (B) In this graph, arrows represent positive and negative influences. Note that there is a (negative) arrow connecting PTPN11 and RASA1 even though these proteins do not directly interact (cf. Panels A and B) because PTPN11 is responsible for dephosphorylation of a site in EGFR that interacts with RASA1 (Table 1). Interesting regulatory circuits embedded within the diagram of Panel B are highlighted in the panels at bottom. (C) EGFR generates competing positive and negative signals for KRAS activation. (D) An incoherent type 1 feed-forward loop (FFL) motif196. (E) A coherent type 1 FFL motif196. (F) A positive feedback loop197.
Table 1.
Description of interactions considered in figures.
| Index | Description |
|---|---|
| 1 | EGF binds EGFR201. |
| 2 | EGF-induced dimerization of EGFR via EGFR-EGFR interaction201 |
| 3 | EGFR autophosphorylation at Y1016204 |
| 4 | EGFR autophosphorylation at Y1092205 |
| 5 | EGFR autophosphorylation at Y1110206 |
| 6 | EGFR autophosphorylation at Y1172205 |
| 7 | EGFR autophosphorylation at Y1197205 |
| 8 | EGFR-mediated phosphorylation of Y317 in SHC1 (isoform p52Shc)207 |
| 9 | EGFR-mediated phosphorylation of Y627 in GAB1208 |
| 10 | EGFR-mediated phosphorylation of Y659 in GAB1208 |
| 11 | PTPN11 binds pY1016 in EGFR209. |
| 12 | The SH2 domains in RASA1 mediate interaction with pY1016 in EGFR78, 210. |
| 13 | The SH2 domain in GRB2 binds pY1092 in EGFR121, 211, 212. |
| 14 | The SH2 domain in GRB2 binds pY1110 in EGFR121, 211, 212. |
| 15 | The PTB domain in SHC1 binds pY1172 in EGFR122, 212. |
| 16 | The PTB domain in SHC1 binds pY1197 in EGFR122, 212. |
| 17 | PTPN11-mediated dephosphorylation of pY1016 in EGFR210 |
| 18 | The SH2 domain in GRB2 binds pY317 in SHC1 (isoform p52Shc)207. |
| 19 | The N-terminal SH2 domain in PTPN11 binds pY627 in GAB1213. |
| 20 | The C-terminal SH2 domain in PTPN11 binds pY659 in GAB1213. |
| 21 | PTPN11-mediated dephosphorylation of pY627 in GAB1213 |
| 22 | PTPN11-mediated dephosphorylation of pY659 in GAB1213 |
| 23 | The GAP domain in RASA1 binds KRAS causing an increase in GTPase activity that favors the GDP-loaded form of KRAS214. |
| 24 | The N-terminal SH3 domain in GRB2 interacts with several C-terminal proline-rich sequences (PRS) in SOS1215, 216. |
| 25 | The C-terminal SH3 domain in GRB2 interacts with two central proline-rich sequences (PRS) in GAB1217. |
| 26 | GTP-loaded KRAS binds the REM domain in SOS1, which increases the GEF activity of SOS1218, 219. |
| 27 | The GEF domain in SOS1 binds KRAS causing a release of guanine nucleotide that favors the GTP-loaded form of KRAS220. |
INVESTIGATING CELL SIGNALING WITH MODELS
Given the complexity of biomolecular interaction networks, researchers are increasingly using theoretical/computational methods to study biomolecular interactions5, 64. Among these methods is molecular dynamics (MD)65, 66, which is routinely used to simulate the motions of atoms in biomolecules. However, the computational expense of this approach imposes limits on the timescales that can be simulated (typically nanoseconds to milliseconds), which are shorter than the timescale on which many signaling events occur (seconds to minutes to hours). Thus, although MD can be useful for studying isolated interactions67, it is not useful for studying the integrated behavior of a network of biomolecular interactions, except with coarse graining68, which tends to be challenging and dependent on problem-specific details69. A menagerie of methods that overcome this limitation have been applied to characterize cell signaling systems, including Bayesian analysis70, regression analysis71, information theory72, constraint-based modeling73, 74, and Boolean/logical modeling75. However, the aforementioned approaches either ignore (without intentionally violating) physicochemical principles or are only loosely coupled to these principles. This disconnect can be beneficial (or irrelevant) for particular purposes. However, a model based on physicochemical principles has a number of highly desirable attributes. Such a model is grounded in causality (vs. correlation) and its parameters (e.g., protein copy numbers and binding affinities) can be measured independently76–79. Moreover, the interactions that underlie the structure of such a model can be (and have been) systematically elucidated through a variety of both reductionist and high-throughput approaches29, 80 (vs. imperfectly reconstructed through statistical inference81 on the basis of one or a few types of high-throughput data). Thus, there is a need for modeling approaches that are grounded in causality, constrained by physicochemical principles (e.g., the law of mass action, the thermodynamic principle of detailed balance82–84, and Fick’s laws of diffusion85, 86), and applicable at the timescales relevant for studying cell signaling.
Addressing this need is the framework of chemical kinetics, which has been widely applied in studies of cell signaling5, 32, 55, 87–90. A traditional approach for modeling chemical kinetics involves enumerating chemical species and reactions in a system to construct a reaction network, from which a system of coupled ordinary differential equations (ODEs) can be obtained91. These equations characterize changes in concentrations of chemical species (or comparable state variables) with time. ODEs have been used to model chemical kinetics for approximately 150 years92, 93. The intense interest in this approach within the systems biology community is evidenced by the popularity of tools such as COPASI94, 95 and the development and broad adoption of SBML96, 97, a standardized format for electronic storage and exchange of models that are defined in terms of reaction networks. However, it can be difficult or even impossible to specify a complete reaction network when one is interested in structurally-resolved chemical kinetics, meaning changes that occur at specific functional sites within biomolecules, because the modular functional components of these molecules can interact in myriad ways. These interactions have the potential to produce a vast number of chemical species.
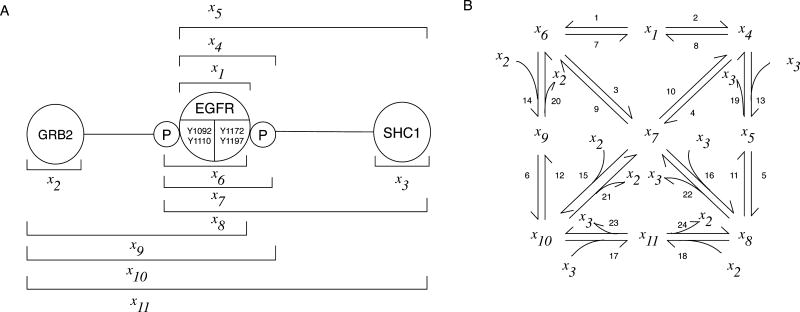
If we aim to translate a protein interaction network into a chemical reaction network, we must (in a traditional modeling approach) enumerate the chemical species that can be populated and the connections and influences amongst these species (i.e., their reactions). To obtain an ODE model for this network, we then must write an equation for each chemical species that includes a term for each relevant reaction. This task can be daunting. As illustrated in Fig. 2, the arrows in a typical pathway diagram imply many chemical species and hide a larger reaction network encompassing these species. As more biomolecular sites and interactions are considered, there is a combinatorial explosion and network size eventually becomes unmanageable. For example, Creamer et al.15 found that a subset of known post-translational modifications and interactions of an EGFR/ErbB3 heterodimer imply >10100 distinct potentially populated chemical species. Clearly, not all of these species are relevant, but which can be safely ignored? Often, ad hoc assumptions are made to limit the chemical species included in a model to a manageable number. For example, different sites of phosphorylation in a protein may be lumped together as a single “virtual phosphorylation site,” as discussed by Birtwistle et al. 58. Such approaches are certainly serviceable for some purposes56 but most such assumptions are never evaluated and lumping of sites and other simplifying assumptions can limit the resolution of a model56, 98. Moreover, these assumptions may have unintended and undesirable consequences. For example, if the phosphosites of a receptor are lumped together and these sites interact with different adaptor proteins, then lumping may introduce a false competition amongst the adaptor proteins for binding to the receptor. In cases where 1) site-specific details are important, 2) these details entail significant combinatorial complexity, and 3) commonly used simplifications aimed at overcoming the barrier of combinatorial complexity have limited utility or require careful evaluation, what approach should one take to model biomolecular site dynamics?
Figure 2.
The edges/arrows of a typical pathway diagram hide significant combinatorial complexity. (A) The interactions and phosphorylation states of the three proteins considered in this diagram (EGFR and two adaptor proteins, GRB2 and SHC1) imply 11 distinct chemical species. The horizontal bars serve to label the 11 species and to delineate their compositions. Note that EGFR is taken to be phosphorylated at two sites of EGFR autophosphorylation: Y1092 (or both Y1092 and Y1110, which are important docking sites of GRB2) and Y1172 (or both Y1172 and Y1197, which are important docking sites of SHC1). GRB2 and SHC1 interact with EGFR via domains that recognize phosphotyrosines: the SH2 domain in GRB2 and the PTB domain in SHC1. The diagram shown here does not comprehensively depict the known interactions and phosphorylation states of these proteins; for example, EGFR-mediated phosphorylation of SHC1 and interaction between GRB2 and phosphorylated SHC1 are not considered. (B) The 11 chemical species are connected in a reaction network encompassing 24 unidirectional reactions. Reactions 1–6 are phosphorylation reactions, Reactions 7–12 are dephosphorylation reactions, Reactions 13–18 are bimolecular association reactions, and Reactions 19–24 are dissociation reactions. For simplicity, all reactions are represented as single-step transformations and catalysts are considered implicitly. For more information about the interactions considered here, see Table 1.
RULE-BASED MODELING
From equations to rules
The key feature of rule-based modeling that makes this approach suitable for studying the site dynamics of biomolecular networks is the simplifying idea of representing biomolecular interactions in terms of local rules4. Modeling approaches based on local rules, as in agent-based modeling99, are used in many fields, including physics, chemistry, and computer science100.
Local rules can be formulated in different ways and on the basis of different formalisms, such as that of process algebra101–103, finite state machines104, 105 or graph rewriting106–109. In one approach106, 107, which underlies a number of useful methods and software tools, such as BioNetGen106, 110, 111, rules take the form of single-pushout graph transformations112, graph-rewriting rules with particular technical features, such as a mapping of vertices from the left-hand side (LHS) to the right-hand side (RHS) of a rule. (This mapping is usually implicit but can be made explicit, which is necessary for some purposes113.) Rules are applied to graphs representing biomolecules and connected sets of graphs representing biomolecular complexes to determine the outcomes of interactions. These graphs are simple, colored, attributed graphs, in which vertices represent molecular components, undirected edges connecting vertices represent (non-covalent) bonds between components, and the vertices representing the components of a particular molecule type are all associated with a common “color,” the name of the molecule type. Moreover, vertices are optionally associated with attributes or internal states, which take the form of alphanumeric strings. Internal states are abstractions useful for representing local properties of sites such as conformation, phosphorylation status, and subcellular location. For example, a vertex representing a tyrosine residue in a protein that is a substrate of a protein tyrosine kinase and phosphatase can be associated with the attribute “P” (or “0”) to indicate that the tyrosine is phosphorylated (or unphosphorylated). Accessible formal definitions of the graphs used in rule-based modeling are available114.
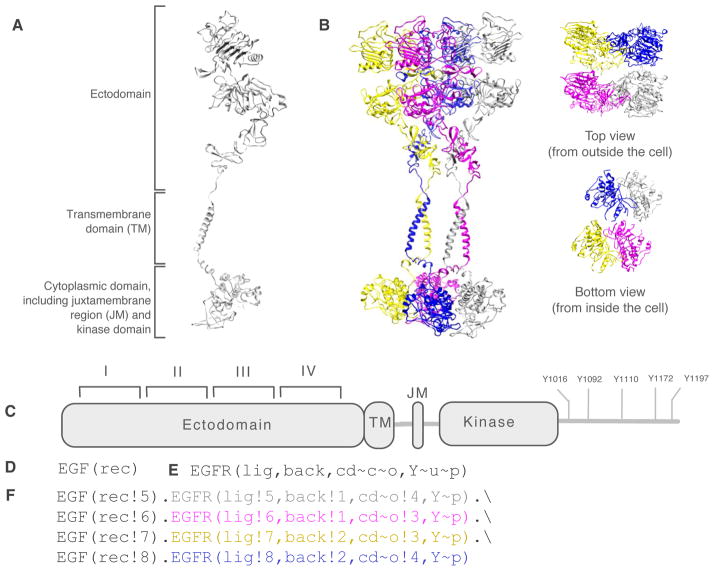
Model-specification languages, such as the BioNetGen language (BNGL)111 and Kappa115, which can be viewed as domain-specific programming languages, enable the graphs of a rule-based model, which represent biomolecules and complexes, to be encoded in a machine-readable plain-text format. In Fig. 3, we illustrate BNGL-encoded representations of two proteins (EGF and EGFR) and a particular chemical species considered in a recently reported rule-based model for EGF-induced oligomerization of EGFR22. The structural resolution of these representations is intermediate between the finer resolution of an atomic model and the coarser resolution of a traditionally formulated model for chemical kinetics, in which each chemical species is represented simply by a unique name. As can be seen by comparing Figs. 3B and 3F, BNGL enables the connectivity (or topology) of a protein complex to be explicitly represented. This level of resolution is most common; however, geometrical aspects of complexes have been considered in some rule-based models116–120.
Figure 3.
A protein or protein complex can be represented at different levels of resolution. (A) An atomic model of EGFR (amino acid residues 25–982). The model is based on experimentally determined structures of three domains of EGFR (PDB accession codes 3NJP, 2M20, and 2JIV)198–200. The model does not include the cytoplasmic tail of EGFR. (B) An atomic model of an EGF-induced oligomer of EGFR, a cyclic side-by-side dimer of dimers. EGF is not shown. The model was constructed with preservation of experimentally determined structural interfaces between domains and with preservation of the chemical integrity of individual domains, which were treated as rigid bodies. Consecutive domains are within the allowed lengths of the connecting loops. The top view highlights ectodomain-ectodomain interactions, and the bottom view highlights cytoplasmic domain-cytoplasmic domain interactions. (C) Domain architecture of EGFR. This diagram provides a schematic representation of EGFR and its component parts and includes a depiction of five sites of autophosphorylation (cf. Figs. 2 and 5). (D) BNGL-encoded representation of EGF. This encoding indicates that the molecule type EGF contains one functional component, rec. More formally, this line of code introduces a graph that has the color EGF and one vertex labeled rec. (E) BNGL-encoded representation of EGFR (cf. Panel A). This encoding indicates that the molecule type EGFR has four functional components: lig, back, cd, and Y. The lig component represents the ligand-binding site, which comprises domains I and III of the EGFR ectodomain201. The back component represents domain II of the EGFR ectodomain, which is responsible for a self-interaction201. The cd component, which is responsible for another self-interaction202, represents the cytoplasmic domain of EGFR and encompasses the juxtramembrane region and kinase domain. The cd component is taken to have two possible internal states (or more formally, vertex attributes): closed (c) and open (o). In the o state, the cd component is able to interact with a second copy of itself (also in the o state). The Y component represents an autophosphorylation site, which is taken to have two possible internal states. These states, u and p, represent different phosphorylation states, unphosphorylated and phosphorylated. (F) BNGL-encoded representation of a cyclic EGFR tetramer (cf. Panel B). As indicated, this complex is held together through alternating back-back and cd-cd interactions, which are abstractions of the interactions illustrated at atomic resolution in Panel B. Atomic models were visualized using the UCSF Chimera package203. The model of Panel B represents only one plausible structure.
BNGL111 enables rules to be encoded in plain text. For example, interactions of the adaptor proteins GRB2 and SHC1 with phosphotyrosines in EGFR (Fig. 2A) can be encoded as follows:
| (1) |
and
| (2) |
These rules indicate that the SH2 (PTB) domain in GRB2 (SHC1) can reversibly bind the phosphorylated form of Y1092 (Y1172) in EGFR121, 122. According to these rules, a free SH2 or PTB domain in an adaptor protein and the availability of a phosphorylated cognate binding site in EGFR are the only requirements for interaction. In general, rules define the necessary and sufficient conditions for interactions and transformations; the stringency of these conditions can be adjusted to match mechanistic understanding and assumptions. In accordance with the conventions of BNGL111, two components in direct physical interaction are identified (on the RHS of each of the above rules) through sharing of a bond name, which here is a number that is prefixed by a “!” symbol. The “~” symbol prefixes an internal state label. Here, the label “P” is used to represent “phosphorylated.” In a complete model specification, the rules above would each be associated with rate laws for association and dissociation (which are specified by simply providing single-site forward and reverse rate constants if mass-action kinetics is assumed). BNGL-encoded rules are further discussed in the sidebar. For readers interested in additional information about BNGL, a comprehensive description of BNGL is available111, as is a thorough tutorial123.
Formal aspects of BNGL-encoded rules.
In the formalism underlying BNGL106, 107, rules are strictly unidirectional. Thus, Eq. 1 or 2 is actually shorthand for two rules, one for association and one for dissociation. Rules are composed of pattern graphs representing molecular moieties106, 107. The set of pattern graphs on the LHS of a rule defines the necessary and sufficient conditions required of a set of sites for an interaction or transformation to occur. Pattern graphs identify reactants through “matching.” A pattern graph matches a chemical-species graph (and identifies the corresponding chemical species as a potential reactant) if the two graphs are related by a subgraph isomorphism107. The set of pattern graphs on the RHS of a rule, together with a LHS-to-RHS mapping of vertices, defines the outcome of a transformation. The transformation, given implicitly by the difference between LHS and RHS, could be addition of an edge, removal of an edge, or a change of a vertex attribute. Rules can also represent processes that add or remove molecules or complexes. If a site in a biomolecule or a site’s state does not affect an interaction, or if its influence is unknown and one wishes to make minimal assumptions, it is omitted from a rule. This practice is sometimes called the “don’t care, don’t write” convention. Rules that include only sites (vertices) directly involved in an interaction are maximally permissive. Rules with additional sites are more stringent. The purpose of including non-reactive sites in rules is to impose contextual constraints on interactions.
Representation of an interaction in the form of a local rule is appropriate (and advantageous) if the interaction is modular, i.e., entirely independent of molecular context or only loosely coupled to non-reactive aspects of the environment in which the interaction occurs. An assumption of modularity can often be justified by Occam’s razor and by the observation that proteins, as well as other biomolecules, tend to be composed of modular parts, as discussed earlier.
If the necessary and sufficient conditions for applicability of a rule are not highly stringent, then biomolecules in many distinct states are likely to satisfy the conditions and the rule will define multiple reactions. For example, the rules given above (Eqs. 1 and 2) each corresponds to multiple reactions in Fig. 2B: the forward transformation of the first rule (GRB2 association with EGFR) corresponds to Reactions 14, 15, and 18, and the forward transformation of the second rule (SHC1 association with EGFR) corresponds to Reactions 13, 16, and 17. It is this feature of rules that enables concise model specification. It should be noted that the benefit of concise representation comes with a cost. Because each (unidirectional) rule is associated with one rate law, all reactions implied by that rule are effectively assigned this rate law, which brings about a coarse graining of the chemical kinetics. However, the resolution/applicability of a rule can be adjusted as needed or desired. For example, if a non-local property of a site is a prerequisite for an interaction (e.g., through allostery, which is discussed below), this requirement can be specified in a rule to make the rule as specific as necessary. In general, the specification of a rule can be tuned to restrict or enlarge the set of species that qualify as reactants according to the rule. The most broadly applicable binding rule that could be specified would simply state that potentially reactive components must be free for binding to occur between them. At the other extreme, the finest rule would imply one and only one reaction, i.e., the rule would be equivalent to an individual reaction in the traditional sense. Thus, a set of rules can be viewed as a generalization of a reaction network.
Rule-based models are compositional, meaning that the rules that comprise these models can be specified somewhat independently. Often, adding consideration of an interaction to a model only requires adding a new rule for that interaction100. Although in practice some additional modifications of the model may be necessary, the effort of making these modifications is usually modest in comparison to the effort required when adding an interaction to an equivalent ODE model.100 The ability to specify rules independently makes a rule analogous to a line of code; a set of related rules, defining for example the interactions involved in a Michaelis-Menten reaction mechanism, analogous to a software routine; and the complete set of rules of a model analogous to a program. Because model specification is separated from model simulation111, simulation is analogous to compilation. This analogy has been leveraged by recently developed software tools, most notably RuleBender124, 125 and PySB126. RuleBender, an Eclipse rich client platform (RCP) application, provides an integrated development environment (IDE) for specification, visualization, and simulation of rule-based models. PySB is a Python module that enables high-level abstractions and treatment of rule-based models as Python-language programs, which has the potential to facilitate model reuse. PySB is further discussed below.
A simple example of a rule-based model
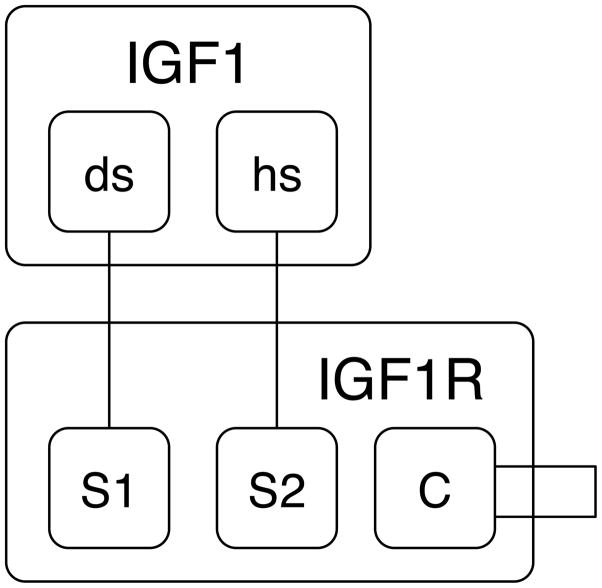
As an example of a rule-based model, we consider the model of Kiselyov et al.127 for insulin-like growth factor 1 (IGF1) binding to the IGF1 receptor (IGF1R) (Fig. 4). IGF1R is a dimeric receptor containing a total of four extracellular binding sites that can interact with IGF1. As illustrated in Fig. 4A, a single ligand (IGF1) can bind two receptor sites simultaneously, thereby crosslinking the receptor subunits containing these sites. Formation of a crosslink coincides with a conformational change that causes sites distal from the crosslink to shift away from each other, preventing formation of a second crosslink (Fig. 4A). Thus, ligand-receptor binding reactions depend on the states of sites that are capable of interacting directly (i.e., the states of the ligand and receptor sites), as well as non-local properties (e.g., the presence or absence of a crosslink). Another non-local property considered in this model is binding pocket occupancy; the model only allows one ligand per binding pocket (the space between opposing ligand-binding sites). The model of Kiselyov et al.127 exemplifies the role of structurally-resolved or site-specific details in modeling of biochemical kinetics. Two rules from this model are illustrated in Fig. 4B (for ligand binding and crosslinking) using the graphical conventions of Faeder et al.128. All rules of the model are shown in Fig. 4C in BNGL111, along with definitions of molecule types (for IGF1 and IGF1R); seed species, which define an initial system state; and an observable, which is defined because the last rule of the model includes a local function. For this model, the definition of seed species is important beyond providing initial conditions, because this section of the model (together with the absence of rules for receptor dimer formation or dimer dissociation) indicates that receptors are static dimers. Local functions, a fairly new feature of BNGL, are discussed in the sidebar.
Figure 4.
A rule-based model for IGF1 interaction with IGF1R. (A) Two reactions from the model of Kiselyov et al.127. Reversible capture of a free ligand (IGF1) by an inactive, unbound receptor (IGF1R) is illustrated at left, and reversible ligand-mediated crosslinking of receptor subunits containing Sites 1 and 2 (or S1 and S2) is illustrated at right. A receptor is dimeric and each monomer contains two ligand-binding sites. Common shading indicates sites that are found in the same receptor monomer. (B) Two rules from the model of Kiselyov et al.127 drawn according to the graphical conventions of Faeder et al.128. The rule at top (bottom) implies the left (right) reaction in Panel A. (C) Excerpts from an executable encoding of the model of Kiselyov et al.127 in BNGL111. In the listing shown here, definitions of graphs for IGF1 and IGF1R (i.e., molecule types) are given at top, definitions of seed species are given next, definition of a pattern used in a local function is given in the observables block, and definitions of rules are given at bottom. Rule 1 is the text encoding of the top rule in Panel B, and Rule 3 is the text encoding of the bottom rule in Panel B. Rule 2 is similar to Rule 1. Rules 3 and 4 together define crosslinking of Sites 1 and 2 when a ligand is bound at Site 1. Rule 5 defines crosslinking of Sites 1 and 2 when a ligand is bound at Site 2.
Local functions in BNGL.
In BNGL, “observables” are user-specified outputs of simulation111. An observable is defined by a set of pattern graphs and a type. For an observable of the “Molecules” type, its value, loosely speaking, is the number of times its pattern graphs match a set of chemical-species graphs. Usually this set represents all species present in a system. However, observables can also be computed for smaller sets of chemical-species graphs. Observables with limited scope are called local observables. In BNGL, a graph can be tagged using the syntax “%label” and the tag can be passed as an argument to an observable to limit its scope, as in the expression “Obs(label).” BNGL also allows for the use of functions that refer to local observables in rate laws, which are called local functions. If the rate law of a rule includes such a function, the rate of an individual reaction implied by that rule will depend on the number of matches of the local observable’s pattern graph(s) to the reactant chemical-species graph(s). In Rule 5 of Fig. 4C, a local function is used to restrict crosslinking of receptor subunits by IGF1 to situations where a crosslink does not already exist. The local function of Rule 5 accomplishes this restriction by setting the forward rate constant for crosslinking (kcr) to zero if a chemical-species graph matching the LHS of the rule also matches the “Crosslink” observable, i.e., if a crosslink is detected.
SIMULATION METHODS
Rule-based models can be simulated using a variety of approaches. These approaches fall into two broad categories: indirect methods and direct methods. Most available software tools for rule-based modeling, which are exhaustively listed in a recent review100, implement indirect methods. In an indirect approach, a rule-based model is first converted to a model having a traditional model form, such as a system of ODEs, and then a simulation method/tool available for that model form (e.g., an ODE solver) is applied. In a direct approach, the simulation procedure is tailored to the native form of a rule-based model129. Currently available direct approaches are particle-based kinetic Monte Carlo (KMC) methods130, in which rules are used as event generators. The algorithmic differences between available direct approaches are compared in a recent review100. A notable distinction between indirect and direct methods is the way in which system state is tracked. In an indirect method, system state is defined by traditional state variables, such as concentrations. In contrast, in a direct method, system state is defined by the collective states of individual sites or particles131. This aspect of direct methods is discussed further below.
Indirect methods
If either an indirect or direct method can be applied, it is usually the case that the indirect method is more efficient. However, indirect methods are not always feasible4.
Network generation
The first step in an indirect simulation method is network generation106, 107, 110, a process of enumerating the chemical species and individual reactions implied by a set of rules through iterative application of these rules to graphs representing seed species and their derivatives. In the first round of rule application, rules are applied to the graphs representing seed species, which are defined as part of a model specification. (A declaration of seed species is analogous to a declaration of an initial condition for an initial value problem.) In the second round of rule application, rules are applied to the graphs representing any novel products of reactions involving the seed species as reactants, which are generated in the first round of rule application. The novelty of a reaction product is detected through canonical labeling of chemical-species graphs107, 114. The process of network generation continues until no new products are generated or a specified stopping criterion is satisfied. In general, the process is not guaranteed to terminate. For example, network generation will not terminate, without specification of an arbitrary stopping criterion, if a model includes a rule defining a polymerization-like reaction4, 130. The size of a reaction network obtained via network generation can range from small (i.e., manageable) to large (i.e., unmanageable) depending on the details of the rules of a model and the initial data (i.e., the seed species). An important point that should be kept in mind is that the intrinsic complexity of a rule-based model is reflected by the number of rules of the model (which largely determines the number of parameters), not the number of chemical species or number of reactions implied by the rules. Analogously, the complexity of a model for protein dynamics is not defined by the number of molecular configurations that can potentially be sampled during an MD simulation. The reactions implied by the rules of a model are ancillary to the rules themselves, and these reactions would ordinarily only be derived for purposes such as simulation via an indirect method. A number of software tools provide network generation capabilities, including BioNetGen111, Simmune132–135, and SSC136. BioNetGen is the most used of these tools137 and it has been extensively tested, which is important given the technical complexity of network generation106, 107, 111, 114.
Simulation of well-mixed compartmental models
Once a reaction network has been generated, simulations can be performed using the armamentarium of network-based deterministic and stochastic simulation methods for well-mixed reaction compartments. For example, a list of reactions and associated reaction propensities, which are determined by rate constants and system state, can serve as the input for a stochastic simulation algorithm93, 138. Alternatively, under the assumption of a continuum limit, an ODE model can be derived91, 93. BioNetGen111 currently provides access to three built-in network simulators: 1) the stiff/nonstiff numerical ODE solver CVODE139, which offers multiple methods of numerical integration; 2) an implementation of an efficient version of Gillespie’s method for stochastic simulations of chemical kinetics138 with propensity sorting 140; and 3) a partitioned-leaping algorithm (PLA) for accelerated stochastic simulations141. Furthermore, stochastic simulations can be performed on-the-fly106, 142. Finally, BioNetGen is capable of exporting rule-derived reaction networks in SBML format96, 97, allowing for their simulation and analysis via SBML-compatible tools143, such as COPASI94, 95. It can also export a specification of the corresponding ODEs as a MATLAB M-file or MEX-file.
Simulation of models with coupled reaction and diffusion
Fully enumerated reaction networks can be simulated in a spatially resolved manner. The tools Simmune132–135 and SSC136 are designed to support spatial simulations of rule-based models, using subvolume-based continuum and stochastic simulators, respectively. Both tools enable native specification of rules. Smoldyn86 includes native rule-based modeling features144 and enables particle-based reaction-diffusion calculations, i.e., simulations based on Brownian dynamics (BD). A BioNetGen frontend utility is available for VCell145, a Web-based platform that provides access to continuum and particle-based spatial modeling capabilities. Particle-based simulations are performed through an interface with Smoldyn, and continuum simulations are performed on the basis of partial differential equations (PDEs) and PDE solvers.
Direct methods
Indirect methods are not always tenable. Inclusion of a rule that defines a polymerization-like reaction will often result in an implied network bounded (without information about the parameters of rate laws) only by the number of molecules in a system4, 130. Polymerization-like reactions arise, for example, in modeling of multivalent ligand-receptor binding146, 147. Even without rules that define polymerization-like reactions, the size of an implied reaction network can be effectively infinite15, simply because of the combinatorial explosion in network size that comes with consideration of more and more interactions. In some cases, a truncated network (e.g., a network obtained from a limited number of rounds of rule application) can be useful. However, in some cases, it is impossible to find a truncated network of manageable size that captures all of the populated chemical species in a system130. Various methods are available for obtaining reduced-order models from rules115, 148–153. However, these methods are not guaranteed to yield a significant or meaningful reduction in the size of a model. In cases where a model in a traditional form cannot be obtained from a set of rules, currently, direct methods must be used.
Simulating rule-based models that correspond to large-scale reaction networks requires changing the system state representation from a population (concentration) perspective to a particle-based perspective. Intuitively, the idea is that if the number of particles (molecules/reactive sites) in a system is less than the total number of chemical species that are potentially populated, then it is computationally more efficient to operate on the system of particles than it is to enumerate all of the distinct populations in which these particles can potentially be found. A system of particles can be simulated using particle-based KMC methods129–131, 154–158, which are variants of standard stochastic simulation algorithms100, such as Gillespie’s method138. Because a reaction network is not enumerated, these methods are commonly referred to as network-free methods. Available network-free methods are similar to each other100. The following steps are found in several algorithms: 1) rates (propensities) are calculated for the rules comprising a model by counting the number of molecular moieties, or reactive sites, that match the pattern graphs on the left-hand sides of rules; 2) the next rule to fire (i.e., to apply to the graphs representing the molecules in the system of interest) is chosen probabilistically based on the relative rates of rules; and 3) sites qualifying as reactive according to the rule chosen to fire are randomly selected and transformed in accordance with the rule.
A number of network-free simulators are available. The tools DYNSTOC156, RuleMonkey131 and NFsim157 are compatible with BNGL111. NFsim is conveniently distributed with RuleBender124, 125. KaSim159 is compatible with Kappa115. Hybrid methods, which combine aspects of direct and indirect simulation, are emerging160, 161. Although direct simulation methods allow one to perform new types of simulations and to ask new questions, such as questions about the composition of protein complexes at the proteome-wide scale16, these methods have drawbacks. For example, because these methods update system state one reaction event at a time, they can be computationally expensive. Acceleration of stochastic simulation for traditionally formulated models is a topic that has received much attention93, 160, 162. As noted above, a method for accelerated stochastic simulation, PLA141, is available with BioNetGen. However, there are many other useful methods in this class that have yet to become available in simulators for rule-based models. Another drawback of direct methods is the difficulty of identifying the parameters of a model that can only be simulated stochastically160, 163, 164. In general, the various known drawbacks of stochastic simulation arise when using direct methods.
MODELS AS VEHICLES OF UNDERSTANDING
Visualization and annotation
As it becomes possible to specify and simulate increasingly complex models, a new challenge arises in the question of how models can be communicated effectively. This challenge is two-fold: concise representation of molecules and interactions captured in a model, and connection of model elements to relevant experimental data. To address these challenges, methods for visualization and annotation of rule-based models have been developed165.
Individual rules in a model are easily visualized (see Fig. 4B), and more comprehensive model diagrams can be generated automatically by a number of software tools124, 125, 166. A useful type of diagram is a contact map167, which can be generated automatically from a BNGL- or Kappa-encoded model specification. A contact map for the model of Fig. 4 is shown in Fig. 5. A contact map illustrates the molecules, components, component states, and binding interactions captured in a model. A limitation of a contact map is that it only captures information explicitly encoded in a model. Thus, a contact map will not illustrate aspects of a system that are implicitly captured in a model165, such as an enzyme whose concentration is subsumed in an effective rate constant.
Figure 5.
Example of a contact map for the model of Kiselyov et al.127 (Fig. 4). The map shown here is essentially the same as the one that is generated automatically by RuleBender124, 125 from the model specification that is partially shown in Fig. 4C.
To encompass these details in visualization of a model, the concept of an extended contact map has been developed165. Extended contact maps provide several types of information typically absent in an automatically generated contact map: enzyme-substrate relationships are depicted explicitly, hierarchical protein substructures114 are illustrated through nesting of boxes representing the material constituents of a system, and the layout of a map is designed to reflect the flow of information during signaling. Construction of extended contact maps is aided by templates available online165. A number of examples of extended contact maps have been published14, 15, 21, 26, 168. Interactions and molecules illustrated in a map can be connected to formal model elements (e.g., rules) through a model guide, in which these elements are annotated with information from the primary literature or online resources165. In this way, a visualized and annotated rule-based model can serve as an easily navigated archive of available knowledge about a signaling system. An extended contact map for the proteins and interactions considered in Fig. 1 is shown in Fig. 6. As can be seen, an extended contact map illustrates site-specific details, which are often omitted in pathway diagrams (cf. Figs. 1 and 6). Because the elements of an extended contact map relate to the formal elements of a rule-based model165, summary of available mechanistic knowledge in the form of an extended contact map can be valuable during development of a model and for communication of the finished product.
Figure 6.
Example of an extended contact map165 for selected proteins and protein-protein interactions involved in EGFR signaling. The same proteins and interactions are considered in Fig. 1. Boxes with rounded corners represent selected proteins, domains, and linear motifs. Small square boxes attached to vertical lines represent sites of phosphorylation. Lines that begin and end with an arrowhead represent noncovalent direct-binding interactions. Lines that begin at a box representing a catalytic subunit and end with a circle point to substrates of an enzyme (a kinase or phosphatase). An open circle indicates a post-translational modification (phosphorylation); a circle with a line through it indicates reversal of a modification (dephosphorylation). See Table 1 for more information about the interactions represented in this map.
High-level modeling languages
With development of larger and more complex models59, 169, the potential usefulness of collaboration among modelers has become increasingly apparent170. In collaborative model development, approaches used in computer programming are likely to prove useful because teams of programmers routinely write, maintain, and extend complex codes. Two products of recent efforts to bring software engineering concepts to modeling in systems biology are PySB126 and LBS-κ171, which are tools designed to ease the specification of models. A model specified using PySB takes the form of a Python-language program, which can be executed to obtain models in other formats and to direct simulations and analyses. PySB provides an embedded language for high-level abstractions and a capability to translate these abstractions into BNGL111 and Kappa115. In contrast, LBS-κ is a domain-specific language that enables high-level abstractions. An earlier example of such a language is MetaKappa172.
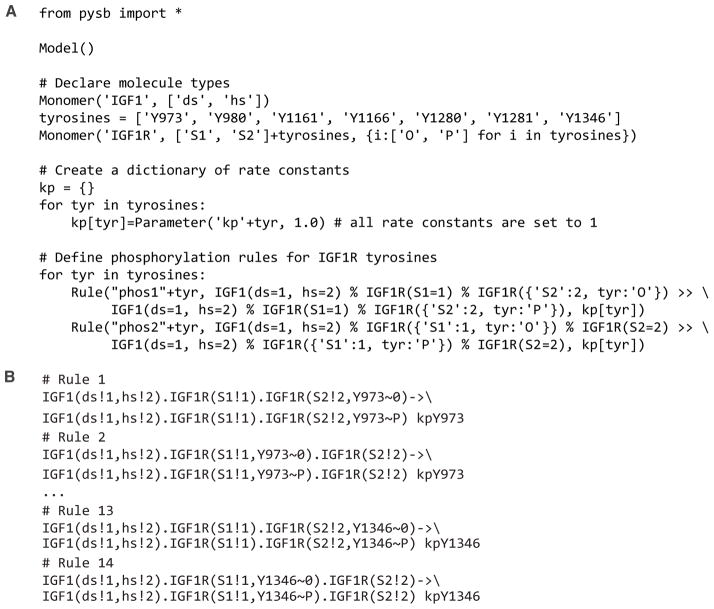
A PySB model may contain modules that represent sets of interactions. A module is useful for concisely representing a set of interactions that recurs many times within a single model or a set of interactions found in multiple models (e.g., the interactions of the reader/writer/eraser signaling motif173), in part because a user can define different but related sets of rules by passing different arguments to the same module and by using loops and conditionals. Adding a module to a PySB model contextualizes the interactions represented by the module (e.g., through user-specified arguments). A benefit of using PySB-defined modules is that it becomes unnecessary to manually specify nearly identical sets of rules, such as sets of rules capturing a common enzymatic mechanism but for which the identity of the substrate varies (Fig. 7). Another benefit is that modules can be assigned intuitive names and constructed through Python-native object-oriented composition so that a PySB model has a hierarchical structure that can be inspected at multiple levels of resolution.
Figure 7.
Illustration of how PySB126 can simplify the specification of related but distinct rules. (A) PySB code that specifies two phosphorylation rules for each of seven sites of IGF1R autophosphorylation. IGF1R is a receptor tyrosine kinase61. The rules all have the same form, differing only with respect to substrate and symmetry of ligand binding. It is assumed that an IGF1-crosslinked receptor can mediate autophosphorylation of sites in both of its monomer subunits. (B) Examples of the 14 rules defined by the PySB code in Panel A, in BNGL format111.
PySB enables model reuse at several levels. At the simplest level, an existing PySB model can be duplicated and its elements can be modified or new elements can be added. A second type of model reuse involves independent manipulation of modules, allowing a modeler to swap out part of a model while other parts of the model are maintained. A third approach involves automatic generation of a set of models, each with a different combination of features of interest. To facilitate identification and annotation of formal model elements across different models, PySB provides the capability to tag model elements with terms compatible with the conventions of MIRIAM174, a set of guidelines for model annotation. These capabilities combined with streamlined model specification and consistent annotation has the potential to make model development a more efficient and collaborative process than has previously been possible.
Because PySB provides an embedded language for high-level model specification (i.e., one that is used within a general-purpose programming language), a modeler using PySB inherits the benefits of mature software development tools, such as those available for version control. In addition, all the features of a general-purpose programming language (e.g., conditionals, loops, and classes) are made available to a modeler. However, this feature can be a disadvantage if the flexibility available is abused, such that a model becomes difficult to interpret due to absence of a standardized style for model specification. Moreover, the syntax of the host language (Python in the case of PySB) must be retained, and this restriction is not always desirable, especially if a modeler is unfamiliar with the language. In comparison, a high-level domain-specific language, such as LBS-κ or MetaKappa, can be easier to learn and to use and can be tailored to meet specific needs of modelers, but such a language will generally not offer as much flexibility as an embedded language, which can be a disadvantage if an unanticipated model-specification problem arises.
Conclusion
Cellular regulatory systems compute through interactions of biomolecules175–177, which generally comprise multiple functional components, or sites. These sites undergo continuous changes in state, as exemplified by the reader/writer/eraser signaling motif173, wherein a tyrosine residue is subject to the opposing activities of a kinase and phosphatase and serves as a docking site for SH2 domain-containing proteins when phosphorylated. The study of state changes at the functional sites of proteins and other biomolecules can be called biomolecular site dynamics. An appropriate theoretical framework for studying site dynamics, which evolve over seconds to minutes to hours, is that of chemical kinetics; however, traditional approaches for modeling chemical kinetics are difficult to apply48, which has necessitated the development of the specialized method of rule-based modeling4. This approach is based on the use of local rules to model biomolecular interactions and their consequences and appropriate data structures (viz. graphs) to capture the coarse structures (domain architectures) of biomolecules and the topological structures (connections) of biomolecular complexes. Nearly 30 software tools have been developed for rule-based modeling of cellular regulatory systems100. These tools deliver capabilities to perform a variety of simulations, including simulations based on ODEs, PDEs, KMC algorithms, and BD algorithms. Coarse MD simulations are even possible.119 However, development of simulation and analysis capabilities is ongoing, and indeed, building the theoretical foundations of rule-based modeling is an active area of research168. At present, the approach is mature enough to enable non-trivial modeling studies of intracellular signaling6–25 and other biological processes, such as metabolism178–180 and gene regulation181–183.
Two promising directions for future research are model-based analyses of proteomic data and further development of capabilities and resources that are relevant for collaborative model development and model reuse, such as model repositories184–186. Modeling and proteomics have not so far become intimately integrated, despite the ability to apply proteomic technologies to generate quantitative data in support of modeling efforts187. We expect that this situation will change because a rule-based model has the site-specific resolution needed to connect to high-throughput proteomic data15, such as (time-resolved) measurements of site-specific phosphorylation50, 188–190 and measurements of binding site-specific affinities78, 79. The approach can also leverage our growing knowledge of protein-protein interfaces28–31. Model reuse is an issue that must receive greater attention if we are to develop reliable comprehensive models for cellular regulatory systems that fully leverage our collective intelligence. Recent large-scale modeling efforts provide motivation for pursuing comprehensive models191, 192. As discussed here, rule-based models have features that should facilitate model reuse and community-driven model development. Efforts to model and analyze cellular regulatory systems in systems biology have tended to focus on small subsystems, such as the simple circuits illustrated in Figs. 1C–1F87, 193. Increasing the scope of modeling efforts (without degrading model reliability) should enable deeper insights into cellular regulation and predictions of greater health significance. Rule-based modeling approaches, which are scalable with respect to both specification and simulation, may offer solutions to some of the problems posed by this challenge194.
Footnotes
| Article ID | Article title |
|---|---|
| WSBM.52 | Computational modeling of mammalian signaling networks |
| WSBM.116 | Simulation of cellular biochemical system kinetics |
| WSBM.1185 | Post-translational modification: Nature’s escape from genetic imprisonment and the basis for dynamic information encoding |
Contributor Information
Lily A. Chylek, Department of Chemistry and Chemical Biology, Cornell University, Ithaca, New York 14853, USA
Leonard A. Harris, Department of Computational and Systems Biology, University of Pittsburgh School of Medicine, Pittsburgh, Pennsylvania 15260, USA
Chang-Shung Tung, Theoretical Division, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA.
James R. Faeder, Email: faeder@pitt.edu, Department of Computational and Systems Biology, University of Pittsburgh School of Medicine, Pittsburgh, Pennsylvania 15260, USA
Carlos F. Lopez, Email: c.lopez@vanderbilt.edu, Department of Cancer Biology and Center for Quantitative Sciences, Vanderbilt University School of Medicine, Nashville, Tennessee 37212, USA
William S. Hlavacek, Email: wish@lanl.gov, Theoretical Division and Center for Nonlinear Studies, Los Alamos National Laboratory, Los Alamos, New Mexico 87545, USA
References
- 1.Bhalla US, Iyengar R. Emergent properties of networks of biological signaling pathways. Science. 1999;283:381–387. doi: 10.1126/science.283.5400.381. [DOI] [PubMed] [Google Scholar]
- 2.Kitano H. Systems biology: a brief overview. Science. 2002;295:1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]
- 3.Nurse P. Life, logic and information. Nature. 2008;454:424–426. doi: 10.1038/454424a. [DOI] [PubMed] [Google Scholar]
- 4.Hlavacek WS, Faeder JR, Blinov ML, Posner RG, Hucka M, Fontana W. Rules for modeling signal-transduction systems. Sci STKE. 2006:re6. doi: 10.1126/stke.3442006re6. [DOI] [PubMed] [Google Scholar]
- 5.Kholodenko B, Yaffe MB, Kolch W. Computational approaches for analyzing information flow in biological networks. Sci Signal. 2012;5:re1. doi: 10.1126/scisignal.2002961. [DOI] [PubMed] [Google Scholar]
- 6.Artyomov MN, Lis M, Devadas S, Davis MM, Chakraborty AK. CD4 and CD8 binding to MHC molecules primarily acts to enhance Lck delivery. Proc Natl Acad Sci USA. 2010;107:16916–16921. doi: 10.1073/pnas.1010568107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gong H, Zuliani P, Komuravelli A, Faeder JR, Clarke EM. Analysis and verification of the HMGB1 signaling pathway. BMC Bioinformatics. 2010;11 (Suppl 7):S10. doi: 10.1186/1471-2105-11-S7-S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nag A, Faeder JR, Goldstein B. Shaping the response: the role of FcεRI and Syk expression levels in mast cell signaling. IET Syst Biol. 2010;4:334–347. doi: 10.1049/iet-syb.2010.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nag A, Monine MI, Blinov ML, Goldstein B. A detailed mathematical model predicts that serial engagement of IgE-FcεRI complexes can enhance Syk activation in mast cells. J Immunol. 2010;185:3268–3276. doi: 10.4049/jimmunol.1000326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dushek O, van der Merwe PA, Shahrezaei V. Ultrasensitivity in multisite phosphorylation of membrane-anchored proteins. Biophys J. 2011;100:1189–1197. doi: 10.1016/j.bpj.2011.01.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Geier F, Fengos G, Iber D. A computational analysis of the dynamic roles of Talin, Dok1, and PIPKI for integrin activation. PLoS ONE. 2011;6:e24808. doi: 10.1371/journal.pone.0024808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thomson TM, Benjamin KR, Bush A, Love T, Pincus D, Resnekov O, Yu RC, Gordon A, Colman-Lerner A, Endy D, et al. Scaffold number in yeast signaling system sets tradeoff between system output and dynamic range. Proc Natl Acad Sci USA. 2011;108:20265–20270. doi: 10.1073/pnas.1004042108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Barua D, Goldstein B. A mechanistic model of early FcεRI signaling: lipid rafts and the question of protection from dephosphorylation. PLoS ONE. 2012;7:e51669. doi: 10.1371/journal.pone.0051669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Barua D, Hlavacek WS, Lipniacki T. A computational model for early events in B cell antigen receptor signaling: analysis of the roles of Lyn and Fyn. J Immunol. 2012;189:646–658. doi: 10.4049/jimmunol.1102003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Creamer MS, Stites EC, Aziz M, Cahill JA, Tan CW, Berens ME, Han H, Bussey KJ, Von Hoff DD, Hlavacek WS, et al. Specification, annotation, visualization and simulation of a large rule-based model for ERBB receptor signaling. BMC Syst Biol. 2012;6:107. doi: 10.1186/1752-0509-6-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Deeds EJ, Krivine J, Feret J, Danos V, Fontana W. Combinatorial complexity and compositional drift in protein interaction networks. PLoS ONE. 2012;7:e32032. doi: 10.1371/journal.pone.0032032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kocieniewski P, Faeder JR, Lipniacki T. The interplay of double phosphorylation and scaffolding in MAPK pathways. J Theor Biol. 2012;295:116–124. doi: 10.1016/j.jtbi.2011.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Michalski PJ, Loew LM. CaMKII activation and dynamics are independent of the holoenzyme structure: an infinite subunit holoenzyme approximation. Phys Biol. 2012;9:036010. doi: 10.1088/1478-3975/9/3/036010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nag A, Monine M, Perelson AS, Goldstein B. Modeling and simulation of aggregation of membrane protein LAT with molecular variability in the number of binding sites for cytosolic Grb2-SOS1-Grb2. PLoS ONE. 2012;7:e28758. doi: 10.1371/journal.pone.0028758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Falkenberg CV, Loew LM. Computational analysis of Rho GTPase cycling. PLOS Comput Biol. 2013;9:e1002831. doi: 10.1371/journal.pcbi.1002831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kesseler KJ, Blinov ML, Elston TC, Kaufmann WK, Simpson DA. A predictive mathematical model of the DNA damage G2 checkpoint. J Theor Biol. 2013;320:159–169. doi: 10.1016/j.jtbi.2012.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kozer N, Barua D, Orchard S, Nice EC, Burgess AW, Hlavacek WS, Clayton AH. Exploring higher-order EGFR oligomerisation and phosphorylation--a combined experimental and theoretical approach. Mol BioSyst. 2013;9:1849–1863. doi: 10.1039/c3mb70073a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu Y, Barua D, Liu P, Wilson BS, Oliver JM, Hlavacek WS, Singh AK. Single-cell measurements of IgE-mediated FcεRI signaling using an integrated microfluidic platform. PLOS ONE. 2013;8:e60159. doi: 10.1371/journal.pone.0060159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mukherjee S, Zhu J, Zikherman J, Parameswaran R, Kadlecek TA, Wang Q, Au-Yeung B, Ploegh H, Kuriyan J, Das J, et al. Monovalent and multivalent ligation of the B cell receptor exhibit differential dependence upon Syk and Src family kinases. Sci Signal. 2013;6:ra1. doi: 10.1126/scisignal.2003220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mukhopadhyay H, Cordoba SP, Maini PK, van der Merwe PA, Dushek O. Systems model of T cell receptor proximal signaling reveals emergent ultrasensitivity. PLOS Comput Biol. 2013;9:e1003004. doi: 10.1371/journal.pcbi.1003004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Barua D, Hlavacek WS. Modeling the effect of APC truncation on destruction complex function in colorectal cancer cells. PLOS Comput Biol. doi: 10.1371/journal.pcbi.1003217. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Scott JD, Pawson T. Cell signaling in space and time: where proteins come together and when they’re apart. Science. 2009;326:1220–1224. doi: 10.1126/science.1175668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kuzu G, Keskin O, Gursoy A, Nussinov R. Constructing structural networks of signaling pathways on the proteome scale. Curr Opin Struct Biol. 2012;22:367–377. doi: 10.1016/j.sbi.2012.04.004. [DOI] [PubMed] [Google Scholar]
- 29.Zhang QC, Petrey D, Deng L, Qiang L, Shi Y, Thu CA, Bisikirska B, Lefebvre C, Accili D, Hunter T, et al. Structure-based prediction of protein-protein interactions on a genome-wide scale. Nature. 2012;490:556–560. doi: 10.1038/nature11503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhang QC, Petrey D, Garzon JI, Deng L, Honig B. PrePPI: a structure-informed database of protein-protein interactions. Nucleic Acids Res. 2013;41:D828–D833. doi: 10.1093/nar/gks1231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Johnson ME, Hummer G. Interface-resolved network of protein-protein interactions. PLOS Comput Biol. 2013;9:e1003065. doi: 10.1371/journal.pcbi.1003065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kholodenko BN, Hancock JF, Kolch W. Signalling ballet in space and time. Nat Rev Mol Cell Biol. 2010;11:414–426. doi: 10.1038/nrm2901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ozbabacan SE, Engin HB, Gursoy A, Keskin O. Transient protein-protein interactions. Protein Eng Des Sel. 2011;24:635–648. doi: 10.1093/protein/gzr025. [DOI] [PubMed] [Google Scholar]
- 34.Weng G, Bhalla US, Iyengar R. Complexity in biological signaling systems. Science. 1999;284:92–96. doi: 10.1126/science.284.5411.92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dang CV. MYC on the path to cancer. Cell. 2012;149:22–35. doi: 10.1016/j.cell.2012.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kirouac DC, Saez-Rodriguez J, Swantek J, Burke JM, Lauffenburger DA, Sorger PK. Creating and analyzing pathway and protein interaction compendia for modelling signal transduction networks. BMC Syst Biol. 2012;6:29. doi: 10.1186/1752-0509-6-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nobeli I, Favia AD, Thornton JM. Protein promiscuity and its implications for biotechnology. Nat Biotechnol. 2009;27:157–167. doi: 10.1038/nbt1519. [DOI] [PubMed] [Google Scholar]
- 38.Rowland MA, Fontana W, Deeds EJ. Crosstalk and competition in signaling networks. Biophys J. 2012;103:2389–2398. doi: 10.1016/j.bpj.2012.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hunter T. Signaling--2000 and beyond. Cell. 2000;100:113–127. doi: 10.1016/s0092-8674(00)81688-8. [DOI] [PubMed] [Google Scholar]
- 40.Kandasamy K, Mohan SS, Raju R, Keerthikumar S, Kumar GS, Venugopal AK, Telikicherla D, Navarro JD, Mathivanan S, Pecquet C, et al. NetPath: a public resource of curated signal transduction pathways. Genome Biol. 2010;11:R3. doi: 10.1186/gb-2010-11-1-r3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McLaughlin RN, Jr, Poelwijk FJ, Raman A, Gosal WS, Ranganathan R. The spatial architecture of protein function and adaptation. Nature. 2012;491:138–142. doi: 10.1038/nature11500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Clune J, Mouret JB, Lipson H. The evolutionary origins of modularity. Proc R Soc B. 2013;280:20122863. doi: 10.1098/rspb.2012.2863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bornberg-Bauer E, Albà MM. Dynamics and adaptive benefits of modular protein evolution. Curr Opin Struct Biol. 2013;23:459–466. doi: 10.1016/j.sbi.2013.02.012. [DOI] [PubMed] [Google Scholar]
- 44.Peisajovich SG, Garbarino JE, Wei P, Lim WA. Rapid diversification of cell signaling phenotypes by modular domain recombination. Science. 2010;328:368–372. doi: 10.1126/science.1182376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jin J, Pawson T. Modular evolution of phosphorylation-based signalling systems. Philos Trans R Soc Lond B Biol Sci. 2012;367:2540–2555. doi: 10.1098/rstb.2012.0106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Yang XJ. Multisite protein modification and intramolecular signaling. Oncogene. 2005;24:1653–1662. doi: 10.1038/sj.onc.1208173. [DOI] [PubMed] [Google Scholar]
- 47.Prabakaran S, Lippens G, Steen H, Gunawardena J. Post-translational modification: nature’s escape from genetic imprisonment and the basis for dynamic information encoding. Wiley Interdiscip Rev Syst Biol Med. 2012;4:565–583. doi: 10.1002/wsbm.1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hlavacek WS, Faeder JR, Blinov ML, Perelson AS, Goldstein B. The complexity of complexes in signal transduction. Biotechnol Bioeng. 2003;84:783–794. doi: 10.1002/bit.10842. [DOI] [PubMed] [Google Scholar]
- 49.Perkins JR, Diboun I, Dessailly BH, Lees JG, Orengo C. Transient protein-protein interactions: structural, functional, and network properties. Structure. 2010;18:1233–1243. doi: 10.1016/j.str.2010.08.007. [DOI] [PubMed] [Google Scholar]
- 50.Olsen JV, Blagoev B, Gnad F, Macek B, Kumar C, Mortensen P, Mann M. Global, in vivo, and site-specific phosphorylation dynamics in signaling networks. Cell. 2006;127:635–648. doi: 10.1016/j.cell.2006.09.026. [DOI] [PubMed] [Google Scholar]
- 51.Daub H, Olsen JV, Bairlein M, Gnad F, Oppermann FS, Korner R, Greff Z, Keri G, Stemmann O, Mann M. Kinase-selective enrichment enables quantitative phosphoproteomics of the kinome across the cell cycle. Mol Cell. 2008;31:438–448. doi: 10.1016/j.molcel.2008.07.007. [DOI] [PubMed] [Google Scholar]
- 52.Le Novère N, Hucka M, Mi H, Moodie S, Schreiber F, Sorokin A, Demir E, Wegner K, Aladjem MI, Wimalaratne SM, et al. The Systems Biology Graphical Notation. Nat Biotechnol. 2009;27:735–741. doi: 10.1038/nbt.1558. [DOI] [PubMed] [Google Scholar]
- 53.Kholodenko BN, Demin OV, Moehren G, Hoek JB. Quantification of short term signaling by the epidermal growth factor receptor. J Biol Chem. 1999;274:30169–30181. doi: 10.1074/jbc.274.42.30169. [DOI] [PubMed] [Google Scholar]
- 54.Schoeberl B, Eichler-Jonsson C, Gilles ED, Müller G. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nat Biotechnol. 2002;20:370–375. doi: 10.1038/nbt0402-370. [DOI] [PubMed] [Google Scholar]
- 55.Wiley HS, Shvartsman SY, Lauffenburger DA. Computational modeling of the EGF-receptor system: a paradigm for systems biology. Trends Cell Biol. 2003;13:43–50. doi: 10.1016/s0962-8924(02)00009-0. [DOI] [PubMed] [Google Scholar]
- 56.Blinov ML, Faeder JR, Goldstein B, Hlavacek WS. A network model of early events in epidermal growth factor receptor signaling that accounts for combinatorial complexity. BioSystems. 2006;83:136–151. doi: 10.1016/j.biosystems.2005.06.014. [DOI] [PubMed] [Google Scholar]
- 57.Kiyatkin A, Aksamitiene E, Markevich NI, Borisov NM, Hoek JB, Kholodenko BN. Scaffolding protein Grb2-associated binder 1 sustains epidermal growth factor-induced mitogenic and survival signaling by multiple positive feedback loops. J Biol Chem. 2006;281:19925–19938. doi: 10.1074/jbc.M600482200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Birtwistle MR, Hatakeyama M, Yumoto N, Ogunnaike BA, Hoek JB, Kholodenko BN. Ligand-dependent responses of the ErbB signaling network: experimental and modeling analyses. Mol Syst Biol. 2007;3:144. doi: 10.1038/msb4100188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Chen WW, Schoeberl B, Jasper PJ, Niepel M, Nielsen UB, Lauffenburger DA, Sorger PK. Input-output behavior of ErbB signaling pathways as revealed by a mass action model trained against dynamic data. Mol Syst Biol. 2009;5:239. doi: 10.1038/msb.2008.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Nakakuki T, Birtwistle MR, Saeki Y, Yumoto N, Ide K, Nagashima T, Brusch L, Ogunnaike BA, Okada-Hatakeyama M, Kholodenko BN. Ligand-specific c-Fos expression emerges from the spatiotemporal control of ErbB network dynamics. Cell. 2010;141:884–896. doi: 10.1016/j.cell.2010.03.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lemmon MA, Schlessinger J. Cell signaling by receptor tyrosine kinases. Cell. 2010;141:1117–1134. doi: 10.1016/j.cell.2010.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Prahallad A, Sun C, Huang S, Di Nicolantonio F, Salazar R, Zecchin D, Beijersbergen RL, Bardelli A, Bernards R. Unresponsiveness of colon cancer to BRAF(V600E) inhibition through feedback activation of EGFR. Nature. 2012;483:100–103. doi: 10.1038/nature10868. [DOI] [PubMed] [Google Scholar]
- 63.Stites EC. The response of cancers to BRAF inhibition underscores the importance of cancer systems biology. Sci Signal. 2012;5:pe46. doi: 10.1126/scisignal.2003354. [DOI] [PubMed] [Google Scholar]
- 64.Kitano H. Computational systems biology. Nature. 2002;420:206–210. doi: 10.1038/nature01254. [DOI] [PubMed] [Google Scholar]
- 65.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable molecular dynamics with NAMD. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Brooks BR, Brooks CL, III, Mackerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, et al. CHARMM: the biomolecular simulation program. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Sethi A, Goldstein B, Gnanakaran S. Quantifying intramolecular binding in multivalent interactions: a structure-based synergistic study on Grb2-Sos1 complex. PLoS Comput Biol. 2011;7:e1002192. doi: 10.1371/journal.pcbi.1002192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Saunders MG, Voth GA. Coarse-graining of multiprotein assemblies. Curr Opin Struct Biol. 2012;22:144–150. doi: 10.1016/j.sbi.2012.01.003. [DOI] [PubMed] [Google Scholar]
- 69.Lopez CF, Nielsen SO, Moore PB, Klein ML. Understanding nature’s design for a nanosyringe. Proc Natl Acad Sci USA. 2004;101:4431–4434. doi: 10.1073/pnas.0400352101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sachs K, Perez O, Pe’er D, Lauffenburger DA, Nolan GP. Causal protein-signaling networks derived from multiparameter single-cell data. Science. 2005;308:523–529. doi: 10.1126/science.1105809. [DOI] [PubMed] [Google Scholar]
- 71.Janes KA, Yaffe MB. Data-driven modelling of signal-transduction networks. Nat Rev Mol Cell Biol. 2006;7:820–828. doi: 10.1038/nrm2041. [DOI] [PubMed] [Google Scholar]
- 72.Cheong R, Rhee A, Wang CJ, Nemenman I, Levchenko A. Information transduction capacity of noisy biochemical signaling networks. Science. 2011;334:354–358. doi: 10.1126/science.1204553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Covert MW, Knight EM, Reed JL, Herrgard MJ, Palsson BØ. Integrating high-throughput and computational data elucidates bacterial networks. Nature. 2004;429:92–96. doi: 10.1038/nature02456. [DOI] [PubMed] [Google Scholar]
- 74.Papin JA, Palsson BØ. The JAK-STAT signaling network in the human B-cell: an extreme signaling pathway analysis. Biophys J. 2004;87:37–46. doi: 10.1529/biophysj.103.029884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Wynn ML, Consul N, Merajver SD, Schnell S. Logic-based models in systems biology: a predictive and parameter-free network analysis method. Integr Biol. 2012;4:1323–1337. doi: 10.1039/c2ib20193c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Low-Nam ST, Lidke KA, Cutler PJ, Roovers RC, van Bergen en Henegouwen PMP, Wilson BS, Lidke DS. ErbB1 dimerization is promoted by domain co-confinement and stabilized by ligand binding. Nat Struct Mol Biol. 2011;18:1244–1249. doi: 10.1038/nsmb.2135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Kleiman LB, Maiwald T, Conzelmann H, Lauffenburger DA, Sorger PK. Rapid phospho-turnover by receptor tyrosine kinases impacts downstream signaling and drug binding. Mol Cell. 2011;43:723–737. doi: 10.1016/j.molcel.2011.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Hause RJ, Jr, Leung KK, Barkinge JL, Ciaccio MF, Chuu CP, Jones RB. Comprehensive binary interaction mapping of SH2 domains via fluorescence polarization reveals novel functional diversification of ErbB receptors. PLoS ONE. 2012;7:e44471. doi: 10.1371/journal.pone.0044471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Koytiger G, Kaushansky A, Gordus A, Rush J, Sorger PK, MacBeath G. Phosphotyrosine signaling proteins that drive oncogenesis tend to be highly interconnected. Mol Cell Proteomics. 2013;12:1204–1213. doi: 10.1074/mcp.M112.025858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Linding R, Jensen LJ, Ostheimer GJ, van Vugt MA, Jorgensen C, Miron IM, Diella F, Colwill K, Taylor L, Elder K, et al. Systematic discovery of in vivo phosphorylation networks. Cell. 2007;129:1415–1426. doi: 10.1016/j.cell.2007.05.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Lefebvre C, Rieckhof G, Califano A. Reverse-engineering human regulatory networks. Wiley Interdiscip Rev Syst Biol Med. 2012;4:311–325. doi: 10.1002/wsbm.1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Yang J, Bruno WJ, Hlavacek WS, Pearson JE. On imposing detailed balance in complex reaction mechanisms. Biophys J. 2006;91:1136–1141. doi: 10.1529/biophysj.105.071852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Ederer M, Gilles ED. Thermodynamically feasible kinetic models of reaction networks. Biophys J. 2007;92:1846–1857. doi: 10.1529/biophysj.106.094094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Danos V, Oury N. Equilibrium and termination II: the case of Petri nets. Math Struct Comp Sci. 2013;23:290–307. [Google Scholar]
- 85.Kerr RA, Bartol TM, Kaminsky B, Dittrich M, Chang JCJ, Baden SB, Sejnowski TJ, Stiles JR. Fast Monte Carlo simulation methods for biological reaction-diffusion systems in solution and on surfaces. SIAM J Sci Comput. 2008;30:3126–3149. doi: 10.1137/070692017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Andrews SS, Addy NJ, Brent R, Arkin AP. Detailed simulations of cell biology with Smoldyn 2. 1. PLoS Comput Biol. 2010;6:e1000705. doi: 10.1371/journal.pcbi.1000705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Tyson JJ, Novák B. Functional motifs in biochemical reaction networks. Annu Rev Phys Chem. 2010;61:219–240. doi: 10.1146/annurev.physchem.012809.103457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Spencer SL, Sorger PK. Measuring and modeling apoptosis in single cells. Cell. 2011;144:926–939. doi: 10.1016/j.cell.2011.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Kolitz SE, Lauffenburger DA. Measurement and modeling of signaling at the single-cell level. Biochemistry. 2012;51:7433–7443. doi: 10.1021/bi300846p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Purvis JE, Lahav G. Encoding and decoding cellular information through signaling dynamics. Cell. 2013;152:945–956. doi: 10.1016/j.cell.2013.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Le Novère N, Endler L. Using chemical kinetics to model biochemical pathways. Methods Mol Biol. 2013;1021:147–167. doi: 10.1007/978-1-62703-450-0_8. [DOI] [PubMed] [Google Scholar]
- 92.Harcourt AV, Esson W. On the laws of connexion between the conditions of a chemical change and its amount. P R Soc London. 1865;14:470–474. [Google Scholar]
- 93.Gillespie DT, Hellander A, Petzold LR. Perspective: stochastic algorithms for chemical kinetics. J Chem Phys. 2013;138:170901. doi: 10.1063/1.4801941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Hoops S, Sahle S, Gauges R, Lee C, Pahle J, Simus N, Singhal M, Xu L, Mendes P, Kummer U. COPASI--a COmplex PAthway SImulator. Bioinformatics. 2006;22:3067–3074. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
- 95.Mendes P, Hoops S, Sahle S, Gauges R, Dada J, Kummer U. Computational modeling of biochemical networks using COPASI. Methods Mol Biol. 2009;500:17–59. doi: 10.1007/978-1-59745-525-1_2. [DOI] [PubMed] [Google Scholar]
- 96.Hucka M, Finney A, Sauro HM, Bolouri H, Doyle JC, Kitano H, Arkin AP, Bornstein BJ, Bray D, Cornish-Bowden A, et al. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics. 2003;19:524–531. doi: 10.1093/bioinformatics/btg015. [DOI] [PubMed] [Google Scholar]
- 97.Keating SM, Le Novère N. Supporting SBML as a model exchange format in software applications. Methods Mol Biol. 2013;1021:201–225. doi: 10.1007/978-1-62703-450-0_11. [DOI] [PubMed] [Google Scholar]
- 98.Chylek LA. Decoding the language of phosphorylation site dynamics. Sci Signal. 2013;6:jc2. doi: 10.1126/scisignal.2004061. [DOI] [PubMed] [Google Scholar]
- 99.Bonabeau E. Agent-based modeling: methods and techniques for simulating human systems. Proc Natl Acad Sci USA. 2002;99 (Suppl 3):7280–7287. doi: 10.1073/pnas.082080899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Chylek LA, Stites EC, Posner RG, Hlavacek WS. Innovations of the rule-based modeling approach. In: Prokop A, Csukás B, editors. Systems Biology: Integrative Biology and Simulation Tools. Vol. 1. Springer; 2013. [Google Scholar]
- 101.Regev A, Silverman W, Shapiro E. Representation and simulation of biochemical processes using the pi-calculus process algebra. Pac Symp Biocomput. 2001:459–470. doi: 10.1142/9789814447362_0045. [DOI] [PubMed] [Google Scholar]
- 102.Priami C, Regev A, Shapiro E, Silverman W. Application of a stochastic name-passing calculus to representation and simulation of molecular processes. Inform Process Lett. 2001;80:25–31. [Google Scholar]
- 103.Danos V, Laneve C. Formal molecular biology. Theor Comput Sci. 2004;325:69–110. [Google Scholar]
- 104.Cardelli L. Artificial biochemistry. Nat Comp Ser. 2009:429–462. [Google Scholar]
- 105.Yang J, Meng X, Hlavacek WS. Rule-based modelling and simulation of biochemical systems with molecular finite automata. IET Syst Biol. 2010;4:453–466. doi: 10.1049/iet-syb.2010.0015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Faeder JR, Blinov ML, Goldstein B, Hlavacek WS. Rule-based modeling of biochemical networks. Complexity. 2005;10:22–41. [Google Scholar]
- 107.Blinov ML, Yang J, Faeder JR, Hlavacek WS. Graph theory for rule-based modeling of biochemical networks. Lect Notes Comput Sci. 2006;4230:89–106. [Google Scholar]
- 108.Danos V, Harmer R, Winskel G. Constraining rule-based dynamics with types. Math Struct Comp Sci. 2013;23:272–289. [Google Scholar]
- 109.Hayman J, Heindel T. Pattern graphs and rule-based models: the semantics of Kappa. Lect Notes Comput Sci. 2013;7794:1–16. [Google Scholar]
- 110.Blinov ML, Faeder JR, Goldstein B, Hlavacek WS. BioNetGen: software for rule-based modeling of signal transduction based on the interactions of molecular domains. Bioinformatics. 2004;20:3289–3291. doi: 10.1093/bioinformatics/bth378. [DOI] [PubMed] [Google Scholar]
- 111.Faeder JR, Blinov ML, Hlavacek WS. Rule-based modeling of biochemical systems with BioNetGen. Methods Mol Biol. 2009;500:113–167. doi: 10.1007/978-1-59745-525-1_5. [DOI] [PubMed] [Google Scholar]
- 112.Löwe M. Algebraic approach to single-pushout graph transformation. Theor Comput Sci. 1993;109:181–224. [Google Scholar]
- 113.Mu F, Williams RF, Unkefer CJ, Unkefer PJ, Faeder JR, Hlavacek WS. Carbon-fate maps for metabolic reactions. Bioinformatics. 2007;23:3193–3199. doi: 10.1093/bioinformatics/btm498. [DOI] [PubMed] [Google Scholar]
- 114.Lemons NW, Hu B, Hlavacek WS. Hierarchical graphs for rule-based modeling of biochemical systems. BMC Bioinformatics. 2011;12:45. doi: 10.1186/1471-2105-12-45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Feret J, Danos V, Krivine J, Harmer R, Fontana W. Internal coarse-graining of molecular systems. Proc Natl Acad Sci USA. 2009;106:6453–6458. doi: 10.1073/pnas.0809908106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Jamalyaria F, Rohlfs R, Schwartz R. Queue-based method for efficient simulation of biological self-assembly systems. J Comput Phys. 2005;204:100–120. [Google Scholar]
- 117.Zhang T, Rohlfs R, Schwartz R. Implementation of a discrete event simulator for biological self-assembly systems. In: Kuhl ME, Steiger NM, Armstrong FB, Joines JA, editors. Proc 2005 Winter Simulat Conf. 2005. pp. 2223–2231. [Google Scholar]
- 118.Monine MI, Posner RG, Savage PB, Faeder JR, Hlavacek WS. Modeling multivalent ligand-receptor interactions with steric constraints on configurations of cell-surface receptor aggregates. Biophys J. 2010;98:48–56. doi: 10.1016/j.bpj.2009.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Gruenert G, Ibrahim B, Lenser T, Lohel M, Hinze T, Dittrich P. Rule-based spatial modeling with diffusing, geometrically constrained molecules. BMC Bioinformatics. 2010;11:307. doi: 10.1186/1471-2105-11-307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Tschernyschkow S, Herda S, Gruenert G, Doring V, Gorlich D, Hofmeister A, Hoischen C, Dittrich P, Diekmann S, Ibrahim B. Rule-based modeling and simulations of the inner kinetochore structure. Prog Biophys Mol Biol. 2013 doi: 10.1016/j.pbiomolbio.2013.03.010. [DOI] [PubMed] [Google Scholar]
- 121.Okutani T, Okabayashi Y, Kido Y, Sugimoto Y, Sakaguchi K, Matuoka K, Takenawa T, Kasuga M. Grb2/Ash binds directly to tyrosines 1068 and 1086 and indirectly to tyrosine 1148 of activated human epidermal growth factor receptors in intact cells. J Biol Chem. 1994;269:31310–31314. [PubMed] [Google Scholar]
- 122.Sakaguchi K, Okabayashi Y, Kido Y, Kimura S, Matsumura Y, Inushima K, Kasuga M. Shc phosphotyrosine-binding domain dominantly interacts with epidermal growth factor receptors and mediates Ras activation in intact cells. Mol Endocrinol. 1998;12:536–543. doi: 10.1210/mend.12.4.0094. [DOI] [PubMed] [Google Scholar]
- 123.Sekar JA, Faeder JR. Rule-based modeling of signal transduction: a primer. Methods Mol Biol. 2012;880:139–218. doi: 10.1007/978-1-61779-833-7_9. [DOI] [PubMed] [Google Scholar]
- 124.Xu W, Smith AM, Faeder JR, Marai GE. RuleBender: a visual interface for rule-based modeling. Bioinformatics. 2011;27:1721–1722. doi: 10.1093/bioinformatics/btr197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Smith AM, Xu W, Sun Y, Faeder JR, Marai GE. RuleBender: integrated modeling, simulation and visualization for rule-based intracellular biochemistry. BMC Bioinformatics. 2012;13 (Suppl 8):S3. doi: 10.1186/1471-2105-13-S8-S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Lopez CF, Muhlich JL, Bachman JA, Sorger PK. Programming biological models in Python using PySB. Mol Syst Biol. 2013;9:646. doi: 10.1038/msb.2013.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Kiselyov VV, Versteyhe S, Gauguin L, De Meyts P. Harmonic oscillator model of the insulin and IGF1 receptors’ allosteric binding and activation. Mol Syst Biol. 2009;5:243. doi: 10.1038/msb.2008.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Faeder JR, Blinov ML, Hlavacek WS. Proc 2005 ACM Symp Appl Computing. Santa Fe, NM: ACM Press; 2005. Graphical rule-based representation of signal-transduction networks; pp. 133–140. [Google Scholar]
- 129.Danos V, Feret J, Fontana W, Krivine J. Scalable simulation of cellular signaling networks. Lect Notes Comput Sci. 2007;4807:139–157. [Google Scholar]
- 130.Yang J, Monine MI, Faeder JR, Hlavacek WS. Kinetic Monte Carlo method for rule-based modeling of biochemical networks. Phys Rev E. 2008;78:031910. doi: 10.1103/PhysRevE.78.031910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Colvin J, Monine MI, Gutenkunst RN, Hlavacek WS, Von Hoff DD, Posner RG. RuleMonkey: software for stochastic simulation of rule-based models. BMC Bioinformatics. 2010;11:404. doi: 10.1186/1471-2105-11-404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Meier-Schellersheim M, Xu X, Angermann B, Kunkel EJ, Jin T, Germain RN. Key role of local regulation in chemosensing revealed by a new molecular interaction-based modeling method. PLoS Comput Biol. 2006;2:e82. doi: 10.1371/journal.pcbi.0020082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Meier-Schellersheim M, Klauschen F, Angermann B. Computational modeling of signaling networks for eukaryotic chemosensing. Methods Mol Biol. 2009;571:507–526. doi: 10.1007/978-1-60761-198-1_33. [DOI] [PubMed] [Google Scholar]
- 134.Angermann BR, Klauschen F, Garcia AD, Prustel T, Zhang F, Germain RN, Meier-Schellersheim M. Computational modeling of cellular signaling processes embedded into dynamic spatial contexts. Nat Methods. 2012;9:283–289. doi: 10.1038/nmeth.1861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Zhang F, Angermann BR, Meier-Schellersheim M. The Simmune Modeler visual interface for creating signaling networks based on bi-molecular interactions. Bioinformatics. 2013;29:1229–1230. doi: 10.1093/bioinformatics/btt134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Lis M, Artyomov MN, Devadas S, Chakraborty AK. Efficient stochastic simulation of reaction-diffusion processes via direct compilation. Bioinformatics. 2009;25:2289–2291. doi: 10.1093/bioinformatics/btp387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Chylek LA, Wilson BS, Hlavacek WS. Modeling biomolecular site dynamics in immunoreceptor signaling sytems. In: Corey SJ, Kimmel M, Leonard JN, editors. A Systems Biology Approach to Blood. Springer; in press. [DOI] [PubMed] [Google Scholar]
- 138.Gillespie DT. Stochastic simulation of chemical kinetics. Annu Rev Phys Chem. 2007;58:35–55. doi: 10.1146/annurev.physchem.58.032806.104637. [DOI] [PubMed] [Google Scholar]
- 139.Hindmarsh AC, Brown PN, Grant KE, Lee SL, Serban R, Shumaker DE, Woodward CS. SUNDIALS: suite of nonlinear and differential/algebraic equation solvers. ACM T Math Software. 2005;31:363–396. [Google Scholar]
- 140.Fricke T, Wendt D. The Markoff-automaton: a new algorithm for simulating the time-evolution of large stochastic dynamic systems. Int J Mod Phys C. 1995;6:277–306. [Google Scholar]
- 141.Harris LA, Clancy P. A “partitioned leaping” approach for multiscale modeling of chemical reaction dynamics. J Chem Phys. 2006;125:144107. doi: 10.1063/1.2354085. [DOI] [PubMed] [Google Scholar]
- 142.Lok L, Brent R. Automatic generation of cellular reaction networks with Moleculizer 1. 0. Nat Biotechnol. 2005;23:131–136. doi: 10.1038/nbt1054. [DOI] [PubMed] [Google Scholar]
- 143.Bornstein BJ, Keating SM, Jouraku A, Hucka M. LibSBML: an API library for SBML. Bioinformatics. 2008;24:880–881. doi: 10.1093/bioinformatics/btn051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Andrews SS. Spatial and stochastic cellular modeling with the Smoldyn simulator. Methods Mol Biol. 2012;804:519–542. doi: 10.1007/978-1-61779-361-5_26. [DOI] [PubMed] [Google Scholar]
- 145.Moraru, Schaff JC, Slepchenko BM, Blinov ML, Morgan F, Lakshminarayana A, Gao F, Li Y, Loew LM. Virtual Cell modelling and simulation software environment. IET Syst Biol. 2008;2:352–362. doi: 10.1049/iet-syb:20080102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Dembo M, Goldstein B. Theory of equilibrium binding of symmetric bivalent haptens to cell surface antibody: application to histamine release from basophils. J Immunol. 1978;121:345–353. [PubMed] [Google Scholar]
- 147.Perelson AS, Delisi C. Receptor clustering on a cell surface. I, Theory of receptor cross-Linking by ligands bearing two chemically identical functional groups. Math Biosci. 1980;48:71–110. [Google Scholar]
- 148.Conzelmann H, Fey D, Gilles ED. Exact model reduction of combinatorial reaction networks. BMC Syst Biol. 2008;2:78. doi: 10.1186/1752-0509-2-78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Conzelmann H, Gilles ED. Dynamic pathway modeling of signal transduction networks: a domain-oriented approach. Methods Mol Biol. 2008;484:559–578. doi: 10.1007/978-1-59745-398-1_33. [DOI] [PubMed] [Google Scholar]
- 150.Borisov NM, Chistopolsky AS, Faeder JR, Kholodenko BN. Domain-oriented reduction of rule-based network models. IET Syst Biol. 2008;2:342–351. doi: 10.1049/iet-syb:20070081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Harmer R, Danos V, Feret J, Krivine J, Fontana W. Intrinsic information carriers in combinatorial dynamical systems. Chaos. 2010:20. doi: 10.1063/1.3491100. [DOI] [PubMed] [Google Scholar]
- 152.Bugenhagen SM, Beard DA. Specification, construction, and exact reduction of state transition system models of biochemical processes. J Chem Phys. 2012;137:154108. doi: 10.1063/1.4758074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Klinke DJ, II, Finley SD. Timescale analysis of rule-based biochemical reaction networks. Biotechnol Prog. 2012;28:33–44. doi: 10.1002/btpr.704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Morton-Firth CJ, Bray D. Predicting temporal fluctuations in an intracellular signalling pathway. J Theor Biol. 1998;192:117–128. doi: 10.1006/jtbi.1997.0651. [DOI] [PubMed] [Google Scholar]
- 155.Shimizu TS, Bray D. Computational biology--the stochastic approach. In: Kitano H, editor. Foundations of Systems Biology. Ch 10. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- 156.Colvin J, Monine MI, Faeder JR, Hlavacek WS, Von Hoff DD, Posner RG. Simulation of large-scale rule-based models. Bioinformatics. 2009;25:910–917. doi: 10.1093/bioinformatics/btp066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Sneddon MW, Faeder JR, Emonet T. Efficient modeling, simulation and coarse-graining of biological complexity with NFsim. Nat Methods. 2011;8:177–183. doi: 10.1038/nmeth.1546. [DOI] [PubMed] [Google Scholar]
- 158.Yang J, Hlavacek WS. The efficiency of reactant site sampling in network-free simulation of rule-based models for biochemical systems. Phys Biol. 2011;8:055009. doi: 10.1088/1478-3975/8/5/055009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Feret J, Krivine J. KaSim3 reference manual. 2013 Available at: http://kappalanguage.org.
- 160.Mjolsness E. Time-ordered product expansions for computational stochastic system biology. Phys Biol. 2013;10:035009. doi: 10.1088/1478-3975/10/3/035009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Hogg JS, Harris LA, Stover LJ, Nair NS, Faeder JR. Exact hybrid particle/population simulation of rule-based models of biochemical systems. doi: 10.1371/journal.pcbi.1003544. Available at: http://arxiv.org/abs/1301.6854. [DOI] [PMC free article] [PubMed]
- 162.Anderson DF, Higham DJ. Multilevel Monte Carlo for continuous time Markov chains, with applications in biochemical kinetics. Multiscale Model Sim. 2012;10:146–179. [Google Scholar]
- 163.Daigle BJ, Jr, Roh MK, Petzold LR, Niemi J. Accelerated maximum likelihood parameter estimation for stochastic biochemical systems. BMC Bioinformatics. 2012;13:68. doi: 10.1186/1471-2105-13-68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Goutsias J, Jenkinson G. Markovian dynamics on complex reaction networks. Phys Rep. 2013;529:199–264. [Google Scholar]
- 165.Chylek LA, Hu B, Blinov ML, Emonet T, Faeder JR, Goldstein B, Gutenkunst RN, Haugh JM, Lipniacki T, Posner RG, et al. Guidelines for visualizing and annotating rule-based models. Mol BioSyst. 2011;7:2779–2795. doi: 10.1039/c1mb05077j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Tiger CF, Krause F, Cedersund G, Palmer R, Klipp E, Hohmann S, Kitano H, Krantz M. A framework for mapping, visualisation and automatic model creation of signal-transduction networks. Mol Syst Biol. 2012;8:578. doi: 10.1038/msb.2012.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Danos V, Feret J, Fontana W, Harmer R, Krivine J. Rule-based modelling of cellular signalling. Lect Notes Comput Sci. 2007;4703:17–41. [Google Scholar]
- 168.Faeder JR. Toward a comprehensive language for biological systems. BMC Biol. 2011;9:68. doi: 10.1186/1741-7007-9-68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Hlavacek WS. How to deal with large models? Mol Syst Biol. 2009;5:240. doi: 10.1038/msb.2008.80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Wang Z, Sagotsky J, Taylor T, Shironoshita P, Deisboeck TS. Accelerating cancer systems biology research through Semantic Web technology. Wiley Interdiscip Rev Syst Biol Med. 2013;5:135–151. doi: 10.1002/wsbm.1200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Pedersen M, Phillips A, Plotkin G. [Accessed August 16, 2013];A high-level language for rule-based modeling. doi: 10.1371/journal.pone.0114296. Available at: http://people.ds.cam.ac.uk/mdp40/papers/lbs-kappa.pdf. [DOI] [PMC free article] [PubMed]
- 172.Danos V, Feret J, Fontana W, Harmer R, Krivine J. Rule-based modelling and model perturbation. Lect Notes Comput Sci. 2009;5750:116–137. [Google Scholar]
- 173.Lim WA, Pawson T. Phosphotyrosine signaling: evolving a new cellular communication system. Cell. 2010;142:661–667. doi: 10.1016/j.cell.2010.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Le Novère N, Finney A, Hucka M, Bhalla US, Campagne F, Collado-Vides J, Crampin EJ, Halstead M, Klipp E, Mendes P, et al. Minimum information requested in the annotation of biochemical models (MIRIAM) Nat Biotechnol. 2005;23:1509–1515. doi: 10.1038/nbt1156. [DOI] [PubMed] [Google Scholar]
- 175.Bray D. Protein molecules as computational elements in living cells. Nature. 1995;376:307–312. doi: 10.1038/376307a0. [DOI] [PubMed] [Google Scholar]
- 176.Fisher J, Henzinger TA. Executable cell biology. Nat Biotechnol. 2007;25:1239–1249. doi: 10.1038/nbt1356. [DOI] [PubMed] [Google Scholar]
- 177.Regev A, Shapiro E. Cells as computation. Nature. 2002;419:343. doi: 10.1038/419343a. [DOI] [PubMed] [Google Scholar]
- 178.Asztalos A, Daniels M, Sethi A, Shen T, Langan P, Redondo A, Gnanakaran S. A coarse-grained model for synergistic action of multiple enzymes on cellulose. Biotechnol Biofuels. 2012;5:55. doi: 10.1186/1754-6834-5-55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Daoutidis P, Marvin WA, Rangarajan S, Torres AI. Engineering biomass conversion processes: a systems perspective. AIChE J. 2013;59:3–18. [Google Scholar]
- 180.Scotti M, Stella L, Shearer EJ, Stover PJ. Modeling cellular compartmentation in one-carbon metabolism. Wiley Interdiscip Rev Syst Biol Med. 2013;5:343–365. doi: 10.1002/wsbm.1209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Ray JCJ, Igoshin OA. Adaptable functionality of transcriptional feedback in bacterial two-component systems. PLoS Comput Biol. 2010;6:e1000676. doi: 10.1371/journal.pcbi.1000676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Marchisio MA, Colaiacovo M, Whitehead E, Stelling J. Modular, rule-based modeling for the design of eukaryotic synthetic gene circuits. BMC Syst Biol. 2013;7:42. doi: 10.1186/1752-0509-7-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Vilar JM, Saiz L. Reliable prediction of complex phenotypes from a modular design in free energy space: an extensive exploration of the lac operon. ACS Synth Biol. 2013 doi: 10.1021/sb400013w. [DOI] [PubMed] [Google Scholar]
- 184.Le Novère N, Bornstein B, Broicher A, Courtot M, Donizelli M, Dharuri H, Li L, Sauro H, Schilstra M, Shapiro B, et al. BioModels Database: a free, centralized database of curated, published, quantitative kinetic models of biochemical and cellular systems. Nucleic Acids Res. 2006;34:D689–691. doi: 10.1093/nar/gkj092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Li C, Donizelli M, Rodriguez N, Dharuri H, Endler L, Chelliah V, Li L, He E, Henry A, Stefan MI, et al. BioModels Database: an enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst Biol. 2010;4:92. doi: 10.1186/1752-0509-4-92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Chelliah V, Laibe C, Le Novère N. BioModels Database: a repository of mathematical models of biological processes. Methods Mol Biol. 2013;1021:189–199. doi: 10.1007/978-1-62703-450-0_10. [DOI] [PubMed] [Google Scholar]
- 187.Cox J, Mann M. Quantitative, high-resolution proteomics for data-driven systems biology. Annu Rev Biochem. 2011;80:273–299. doi: 10.1146/annurev-biochem-061308-093216. [DOI] [PubMed] [Google Scholar]
- 188.Wolf-Yadlin A, Hautaniemi S, Lauffenburger DA, White FM. Multiple reaction monitoring for robust quantitative proteomic analysis of cellular signaling networks. Proc Natl Acad Sci USA. 2007;104:5860–5865. doi: 10.1073/pnas.0608638104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.VanMeter AJ, Rodriguez AS, Bowman ED, Jen J, Harris CC, Deng J, Calvert VS, Silvestri A, Fredolini C, Chandhoke V, et al. Laser capture microdissection and protein microarray analysis of human non-small cell lung cancer: differential epidermal growth factor receptor (EGPR) phosphorylation events associated with mutated EGFR compared with wild type. Mol Cell Proteomics. 2008;7:1902–1924. doi: 10.1074/mcp.M800204-MCP200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Ciaccio MF, Wagner JP, Chuu CP, Lauffenburger DA, Jones RB. Systems analysis of EGF receptor signaling dynamics with microwestern arrays. Nat Methods. 2010;7:148–155. doi: 10.1038/nmeth.1418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Karr JR, Sanghvi JC, Macklin DN, Gutschow MV, Jacobs JM, Bolival B, Jr, Assad-Garcia N, Glass JI, Covert MW. A whole-cell computational model predicts phenotype from genotype. Cell. 2012;150:389–401. doi: 10.1016/j.cell.2012.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Thiele I, Swainston N, Fleming RM, Hoppe A, Sahoo S, Aurich MK, Haraldsdottir H, Mo ML, Rolfsson O, Stobbe MD, et al. A community-driven global reconstruction of human metabolism. Nat Biotechnol. 2013;31:419–425. doi: 10.1038/nbt.2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Alon U. Network motifs: theory and experimental approaches. Nat Rev Genet. 2007;8:450–461. doi: 10.1038/nrg2102. [DOI] [PubMed] [Google Scholar]
- 194.Hlavacek WS. Two challenges of systems biology. In: Stumpf MPH, Balding DJ, Girolami MA, editors. Handbook of Statistical Systems Biology. Wiley; 2011. pp. 3–14. [Google Scholar]
- 195.Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, Amin N, Schwikowski B, Ideker T. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 2003;13:2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Mangan S, Alon U. Structure and function of the feed-forward loop network motif. Proc Natl Acad Sci USA. 2003;100:11980–11985. doi: 10.1073/pnas.2133841100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197.Das J, Ho M, Zikherman J, Govern C, Yang M, Weiss A, Chakraborty AK, Roose JP. Digital signaling and hysteresis characterize Ras activation in lymphoid cells. Cell. 2009;136:337–351. doi: 10.1016/j.cell.2008.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 198.Lu C, Mi LZ, Grey MJ, Zhu J, Graef E, Yokoyama S, Springer TA. Structural evidence for loose linkage between ligand binding and kinase activation in the epidermal growth factor receptor. Mol Cell Biol. 2010;30:5432–5443. doi: 10.1128/MCB.00742-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Endres NF, Das R, Smith AW, Arkhipov A, Kovacs E, Huang Y, Pelton JG, Shan Y, Shaw DE, Wemmer DE, et al. Conformational coupling across the plasma membrane in activation of the EGF receptor. Cell. 2013;152:543–556. doi: 10.1016/j.cell.2012.12.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Yun CH, Mengwasser KE, Toms AV, Woo MS, Greulich H, Wong KK, Meyerson M, Eck MJ. The T790M mutation in EGFR kinase causes drug resistance by increasing the affinity for ATP. Proc Natl Acad Sci USA. 2008;105:2070–2075. doi: 10.1073/pnas.0709662105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Burgess AW, Cho HS, Eigenbrot C, Ferguson KM, Garrett TP, Leahy DJ, Lemmon MA, Sliwkowski MX, Ward CW, Yokoyama S. An open-and-shut case? Recent insights into the activation of EGF/ErbB receptors. Mol Cell. 2003;12:541–552. doi: 10.1016/s1097-2765(03)00350-2. [DOI] [PubMed] [Google Scholar]
- 202.Endres NF, Engel K, Das R, Kovacs E, Kuriyan J. Regulation of the catalytic activity of the EGF receptor. Curr Opin Struct Biol. 2011;21:777–784. doi: 10.1016/j.sbi.2011.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera--a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 204.Walton GM, Chen WS, Rosenfeld MG, Gill GN. Analysis of deletions of the carboxyl terminus of the epidermal growth factor receptor reveals self-phosphorylation at tyrosine 992 and enhanced in vivo tyrosine phosphorylation of cell substrates. J Biol Chem. 1990;265:1750–1754. [PubMed] [Google Scholar]
- 205.Downward J, Parker P, Waterfield MD. Autophosphorylation sites on the epidermal growth factor receptor. Nature. 1984;311:483–485. doi: 10.1038/311483a0. [DOI] [PubMed] [Google Scholar]
- 206.Margolis BL, Lax I, Kris R, Dombalagian M, Honegger AM, Howk R, Givol D, Ullrich A, Schlessinger J. All autophosphorylation sites of epidermal growth factor (EGF) receptor and HER2/neu are located in their carboxyl-terminal tails. Identification of a novel site in EGF receptor. J Biol Chem. 1989;264:10667–10671. [PubMed] [Google Scholar]
- 207.Salcini AE, McGlade J, Pelicci G, Nicoletti I, Pawson T, Pelicci PG. Formation of Shc-Grb2 complexes is necessary to induce neoplastic transformation by overexpression of Shc proteins. Oncogene. 1994;9:2827–2836. [PubMed] [Google Scholar]
- 208.Lehr S, Kotzka J, Herkner A, Klein E, Siethoff C, Knebel B, Noelle V, Bruning JC, Klein HW, Meyer HE, et al. Identification of tyrosine phosphorylation sites in human Gab-1 protein by EGF receptor kinase in vitro. Biochemistry. 1999;38:151–159. doi: 10.1021/bi9818265. [DOI] [PubMed] [Google Scholar]
- 209.Schulze WX, Deng L, Mann M. Phosphotyrosine interactome of the ErbB-receptor kinase family. Mol Syst Biol. 2005;1:2005 0008. doi: 10.1038/msb4100012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 210.Agazie YM, Hayman MJ. Molecular mechanism for a role of SHP2 in epidermal growth factor receptor signaling. Mol Cell Biol. 2003;23:7875–7886. doi: 10.1128/MCB.23.21.7875-7886.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Batzer AG, Rotin D, Urena JM, Skolnik EY, Schlessinger J. Hierarchy of binding sites for Grb2 and Shc on the epidermal growth factor receptor. Mol Cell Biol. 1994;14:5192–5201. doi: 10.1128/mcb.14.8.5192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212.Jorissen RN, Walker F, Pouliot N, Garrett TP, Ward CW, Burgess AW. Epidermal growth factor receptor: mechanisms of activation and signalling. Exp Cell Res. 2003;284:31–53. doi: 10.1016/s0014-4827(02)00098-8. [DOI] [PubMed] [Google Scholar]
- 213.Cunnick JM, Mei L, Doupnik CA, Wu J. Phosphotyrosines 627 and 659 of Gab1 constitute a bisphosphoryl tyrosine-based activation motif (BTAM) conferring binding and activation of SHP2. J Biol Chem. 2001;276:24380–24387. doi: 10.1074/jbc.M010275200. [DOI] [PubMed] [Google Scholar]
- 214.Pamonsinlapatham P, Hadj-Slimane R, Lepelletier Y, Allain B, Toccafondi M, Garbay C, Raynaud F. p120-Ras GTPase activating protein (RasGAP): a multi-interacting protein in downstream signaling. Biochimie. 2009;91:320–328. doi: 10.1016/j.biochi.2008.10.010. [DOI] [PubMed] [Google Scholar]
- 215.McDonald CB, Seldeen KL, Deegan BJ, Bhat V, Farooq A. Assembly of the Sos1-Grb2-Gab1 ternary signaling complex is under allosteric control. Arch Biochem Biophys. 2010;494:216–225. doi: 10.1016/j.abb.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216.McDonald CB, Balke JE, Bhat V, Mikles DC, Deegan BJ, Seldeen KL, Farooq A. Multivalent binding and facilitated diffusion account for the formation of the Grb2-Sos1 signaling complex in a cooperative manner. Biochemistry. 2012;51:2122–2135. doi: 10.1021/bi3000534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 217.Liu Y, Rohrschneider LR. The gift of Gab. FEBS Lett. 2002;515:1–7. doi: 10.1016/s0014-5793(02)02425-0. [DOI] [PubMed] [Google Scholar]
- 218.Margarit SM, Sondermann H, Hall BE, Nagar B, Hoelz A, Pirruccello M, Bar-Sagi D, Kuriyan J. Structural evidence for feedback activation by Ras·GTP of the Ras-specific nucleotide exchange factor SOS. Cell. 2003;112:685–695. doi: 10.1016/s0092-8674(03)00149-1. [DOI] [PubMed] [Google Scholar]
- 219.Boykevisch S, Zhao C, Sondermann H, Philippidou P, Halegoua S, Kuriyan J, Bar-Sagi D. Regulation of Ras signaling dynamics by Sos-mediated positive feedback. Curr Biol. 2006;16:2173–2179. doi: 10.1016/j.cub.2006.09.033. [DOI] [PubMed] [Google Scholar]
- 220.Bos JL, Rehmann H, Wittinghofer A. GEFs and GAPs: critical elements in the control of small G proteins. Cell. 2007;129:865–877. doi: 10.1016/j.cell.2007.05.018. [DOI] [PubMed] [Google Scholar]