Hydrological droughts in the 21st century, hotspots and uncertainties from a global multimodel ensemble experiment

Significance

Increasing concentrations of greenhouse gases in the atmosphere are widely expected to influence global climate over the coming century. The impact on drought is uncertain because of the complexity of the processes but can be estimated using outputs from an ensemble of global models (hydrological and climate models). Using an ensemble of 35 simulations, we show a likely increase in the global severity of drought by the end of 21st century, with regional hotspots including South America and Central and Western Europe in which the frequency of drought increases by more than 20%. The main source of uncertainty in the results comes from the hydrological models, with climate models contributing to a substantial but smaller amount of uncertainty.

Abstract

Increasing concentrations of greenhouse gases in the atmosphere are expected to modify the global water cycle with significant consequences for terrestrial hydrology. We assess the impact of climate change on hydrological droughts in a multimodel experiment including seven global impact models (GIMs) driven by bias-corrected climate from five global climate models under four representative concentration pathways (RCPs). Drought severity is defined as the fraction of land under drought conditions. Results show a likely increase in the global severity of hydrological drought at the end of the 21st century, with systematically greater increases for RCPs describing stronger radiative forcings. Under RCP8.5, droughts exceeding 40% of analyzed land area are projected by nearly half of the simulations. This increase in drought severity has a strong signal-to-noise ratio at the global scale, and Southern Europe, the Middle East, the Southeast United States, Chile, and South West Australia are identified as possible hotspots for future water security issues. The uncertainty due to GIMs is greater than that from global climate models, particularly if including a GIM that accounts for the dynamic response of plants to CO₂ and climate, as this model simulates little or no increase in drought frequency. Our study demonstrates that different representations of terrestrial water-cycle processes in GIMs are responsible for a much larger uncertainty in the response of hydrological drought to climate change than previously thought. When assessing the impact of climate change on hydrology, it is therefore critical to consider a diverse range of GIMs to better capture the uncertainty.

The global water cycle is expected to change over the 21st century due to the combined effects of climate change and increasing human intervention. In a warmer world, the water-holding capacity of the atmosphere will increase, resulting in a change in the frequency of precipitation extremes, increased evaporation and dry periods (1), and intensification of droughts (2). This process is represented by most global climate models (GCMs) by increased summer dryness and winter wetness over large areas of continental mid to high latitudes in the Northern Hemisphere (3), associated with a reduction in water availability at continental (4, 5) and global scales (6, 7). Because such changes have potentially very serious implications in some regions of the world, identifying areas where there is agreement in the direction and magnitude of changes in drought characteristics (hotspots) in response to climate change is essential information for water resource management aimed at ensuring water security in a changing climate.

Most GCMs, however, are not able to reproduce the fine-scale processes governing terrestrial hydrology (and hence runoff) and suffer from systematic biases (8). As land-atmospheric feedbacks are not yet fully understood and reproduced by global models (9), and because full coupling of GCMs and global impact models (GIMs) is not straightforward, GIMs forced by data from GCMs have been used as tools to quantify the impact of changed climate on the water cycle and droughts (10), despite by definition ignoring important feedbacks and their possible modification with climate change (11). GIMs vary in the types of processes represented and the parameterisations used. Some GIMs, particularly those designed to quantify water resources, calculate only the water balance (12) whereas others consider coupled water and energy balances, sometimes also representing the dynamic response of plants to changes in atmospheric CO₂ and climate (13). Until recently, the uncertainty in the simulation of the terrestrial water cycle related to the choice of a particular GIM had not been investigated. However, the Water Model Intercomparison Project (WaterMIP) (14) highlighted that simulated hydrological averages can vary substantially between GIMs, even when driven with the same bias-corrected climatic forcing (14, 15), and uncertainty in future projection due to GIMs can be as large as that from GCMs in some regions (16, 17). Although in the climate-to-impact modeling chain much effort has been directed to better understand the uncertainty due to GCMs, studies of the impact of climate change on water availability and drought have often been based on one or a few GIMs, potentially underestimating the overall uncertainty.

This study focuses on identifying regions where the impact of climate change on hydrological drought (henceforth simply “drought”) shows a strong signal of change between the end of the 20th and 21st centuries. We define drought as occurring when total runoff is less than a given threshold. Drought represents the time-integrated effect of several interlinked processes and stores, including precipitation, evaporation, and soil moisture storage (10); because some of these processes are represented by GCMs and some by GIMs, it is vital to quantify the relative uncertainty introduced by both GCMs and GIMs when assessing climate change impacts.

We use outputs from the Inter-Sectoral Impact Model Intercomparison Project (ISI-MIP) multimodel ensemble (MME) experiment (18) of 35 members [for representative concentration pathways (RCPs) 2.6 and 8.5; only 27 members available for RCP4.5 and 6.0] in which GIMs of different types were driven by bias-corrected (8) climate from state-of-the-art CMIP5 GCMs (19). These GIMs describe the terrestrial water cycle at global scale and include current understanding of hydrological systems (20). Note that statistical bias correction can influence the signal of runoff changes but that this effect generally remains smaller than uncertainty from GCMs and GIMs (21). The simulations we use did not consider water management or changes of land use so they represent the effects of climate change alone. We quantify changes in the space-time variability of drought that are projected to occur under four RCPs that span a wide range of radiative forcing (22) (Methods). We also evaluate the uncertainty associated with both GCMs and GIMs so as to identify hotspots of change where we have more confidence in the projections of future drought severity.

Results

We analyze future droughts by comparing the temporal and spatial patterns of simulated runoff in the years 2070–2099 (RCP forcings) with those from a reference period 1976–2005 (historical forcings). For each land cell and simulation, we define a runoff deficit index (DI) that is equal to 1 if the daily runoff (not river discharge) is less than a daily drought threshold (10th percentile) calculated from the reference period (Methods) and is zero otherwise; a grid cell with DI = 1 is therefore under drought conditions. As a measure of the severity of drought, global and regional deficit index (GDI and RDI) time series are calculated as the fraction of land area on the globe or a given region that is under drought conditions. Arid grid cells in which runoff is equal to zero more than 90% of time in the reference or future periods are excluded (white areas on Fig. 1). Also excluded were GIMs for which on average fewer than 75% of the remaining land cells could be used to calculate a DI because of a high proportion of zero runoff values; therefore, a total of seven GIMs driven by five GCMs are included in the MME for RCP2.6 and RCP8.5 (Methods; Figs. S1 and S2). The MME mean changes in GDI and RDI are examined at the annual and seasonal scale, with signal-to-noise ratios (S2N) (MME mean divided by its inter-quartile range) (Methods) used to quantify the relative sizes of variability due to GIMs and GCMs and to identify hotspots where the signal is strongest.

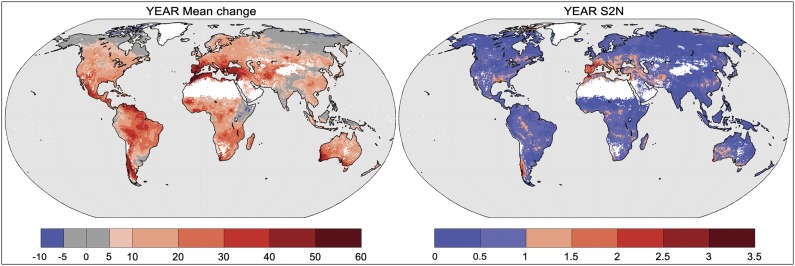
Fig. 1.

Percentage change in the occurrence of days under drought conditions for the period 2070–2099 relative to 1976–2005, based on a multimodel ensemble MME experiment under RCP8.5 from five global climate models and seven global impact models: MME Mean change (Left) and associated signal-to-noise ratio (S2N, MME mean change divided by its inter-quartile range, Right). See Methods for definition of drought, S2N, and masking procedure.

Global Changes.

Under RCP8.5, the MME mean change in the frequency of drought (i.e., DI = 1) shows a widespread increase of drought conditions across the globe and in particular in most parts of South and North America, large parts of tropical and southern Africa, the Mediterranean region, Southeast China, and Australia; little change or reduced occurrence of drought conditions are found in northern Canada, Northeast Russia, the Horn of Africa, and parts of Indonesia (Fig. 1). There is strong seasonality across many mid- to high-latitude regions in the Northern Hemisphere, with small changes or reductions in December to February (DJF) and larger increases in June to August (JJA) (Fig. S3). For 25 members (i.e., 70% of the ensemble), the frequency of drought increases in 60.3% of unmasked land cells, falling to 44.9% in DJF when there is the largest degree of disagreement between ensemble members as to the direction of changes. Over the whole year, S2N is largest in the Mediterranean and the Middle East, Chile, Southeast United States, and Western Australia (Fig. 1).

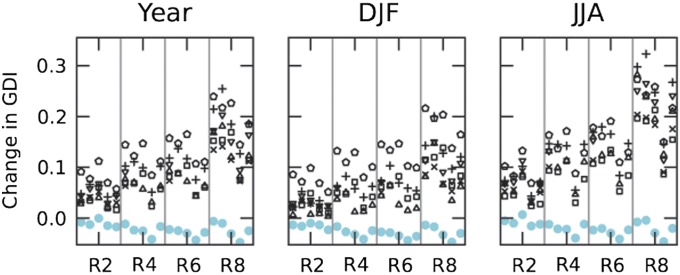
In Fig. 2, we calculate the mean change in GDI for the four RCPs. The results show a likely increase in drought severity with an MME mean increase of 3.9% under RCP2.6, 6.3% for RCP4.5, and 7.4% for RCP6.0 and reaching 13% under RCP8.5 (see ref. 23 for method and SI Text for detailed results); changes are largest in JJA (17.6%) and smallest in DJF (10.6%) under RCP8.5. The systematic increase in drought severity with radiative forcing (Fig. 2) is associated with considerable variation in the magnitude of the changes ranging from −1.7% to +11.2% under RCP2.6 and −4.8% to 25.4% under RCP8.5. S2N associated with GCMs and GIMs shows a stronger signal (less uncertainty) for GCMs (mean S2N = 2.44) than for GIMs (1.82) primarily due to smaller inter-quartile (IQ) for GCMs (mean IQ = 0.049) than for GIMs (0.070) (see SI Text for details). This result indicates that, at the global scale, the variability due to different GIMs is larger than that due to different GCMs.

Fig. 2.

Mean change in drought severity (Change in GDI, y axis) as measured by the daily global deficit index (GDI) for the period 2070–2099 relative to 1976–2005 based on a multimodel ensemble MME experiment calculated over the whole year (Left), December to February (DJF, Center), and June to August (JJA, Right). Changes are given for each MME member and are organized by radiative forcing (from left to right: RCP2.6, R2; RCP4.5, R4; RCP6.0, R6; RCP8.5, R8). In each RCP panel, results are organized according to driving GCMs from left to right: HadGEM2-ES, IPSLCM5-ARL, MIROC-ESM-CHEM, GFDL-ESM2M, and NorESM1-M. CO₂ effect in GIMs is described as color: black/open symbols, no CO₂; cyan/filled symbols, CO₂. GIMs are indicated by symbols: up triangle, HO8; circle, JULES; x, Mac-PDM.09; +, MPI-HM; pentagon, PRCGLOB-WB; down triangle, VIC; square, WBM.

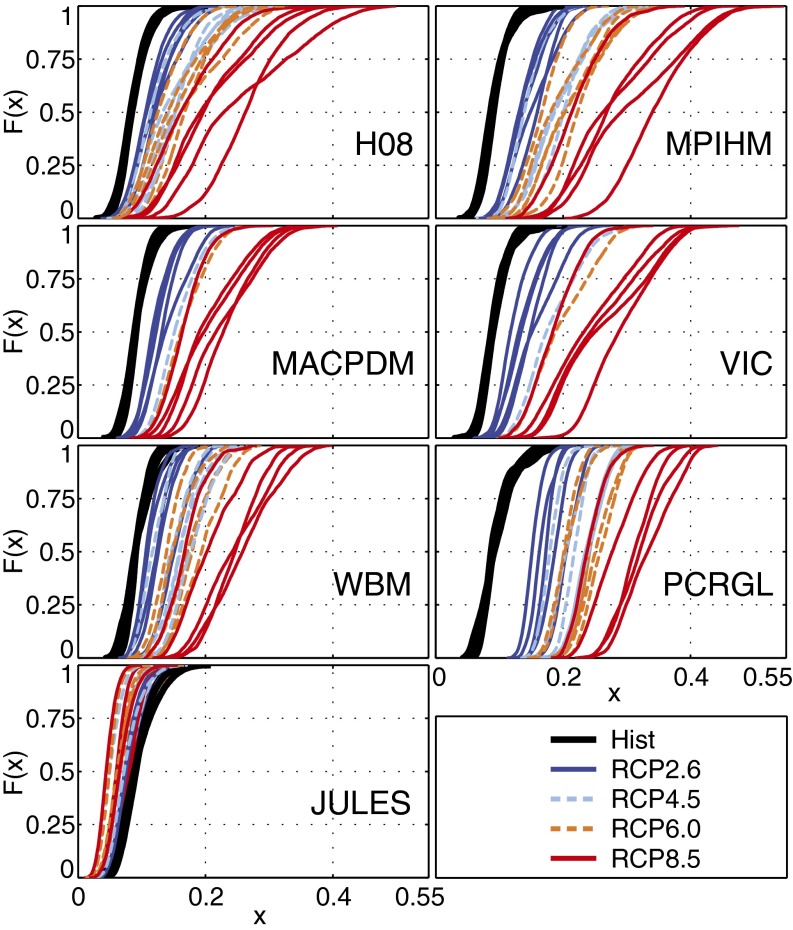
There is a statistically significant (Methods) increase in the frequency of severe events (large GDI) for all RCP/GCM/GIM combinations except for the Joint UK Land Environment Simulator (JULES), which shows a consistently smaller change signal [cumulative density function (CDF)] (Fig. 3). Under historical forcing, drought affects less than 21% of the global land area at any one time (GDI < 0.21; black lines), but this GDI of 21% is exceeded for 23 out of 35 simulations under RCP2.6 (dark blue) and for 30 under RCP8.5 (red). Largest increases are seen for RCP8.5, with maximum drought severity exceeding 40% of land in 16 simulations. There is greater temporal variability in the GDI in many simulations of the RCPs (flatter CDFs in Fig. 3), increasing with radiative forcing, and associated with more pronounced variability between GIMs.

Fig. 3.

Cumulative density functions (CDFs) of daily global deficit index (GDI) calculated over 30-y periods (1976-2005 for historical forcing and 2070–2099 for RCP forcings) for each multimodel ensemble member.

Effects of Model Structure.

All of the models shown in Fig. 3 calculate the water balance of the land, but only H08 and JULES consider the energy balance (Table S1), and only JULES represents the effects of CO₂ on stomatal opening and includes a dynamic vegetation model that allows vegetation to grow in response to its environment. To examine whether the different behavior of JULES was attributable to one of these differences in model structure, we used results from two further GIMs [Lund-Potsdam-Jena managed Land (LPJmL) and Minimal Advanced Treatments of Surface Integration and RunOff (MATSIRO)] that were excluded from the MME because of a high proportion of zero runoff values (Methods and Figs. S1 and S2) but that share some similarities with JULES in terms of model structure: MATSIRO and JULES are energy (and water) balance models whereas LPJmL and JULES both represent varying CO₂ and dynamic vegetation effects. For this analysis, the GDI was calculated using the smaller sample of land cells dictated by LPJmL and MATSIRO (Fig. S2) after the masking procedure was applied to those GIMs. CDFs from the energy balance GIMs show a strong response of H08 and MATSIRO to climate change (Fig. 4), broadly similar to those from the water balance models of Fig. 3, which is evidence that it is not the inclusion of an energy balance that makes JULES different. (The CDFs in Fig. 4 cannot be compared directly with those in Fig. 3 because of the different locations sampled. However, as the sampling does not substantially alter the distributions for JULES between these figures, qualitative comparisons of the figures can be made.)

Fig. 4.

Cumulative density functions (CDFs) of daily global deficit index (GDI) calculated over 30-y periods (1976-2005 for historical forcing and 2070–2099 for RCP forcings) from runs using HadGEM2-ES forcing. (A) Models that include water and energy balances, shown for historical (Hist) and RCP8.5 (R8.5) forcings. (B) and (C) Models that include the dynamic responses of vegetation to CO₂ and climate, shown for historical (Hist), RCP2.6 (R2.6) and RCP8.5 (R8.5) forcings. Results are shown separately for runs that were forced by time-varying CO₂ concentration (CO₂) and with CO₂ concentration held constant after the year 2000 (noCO₂). (B) shows results for JULES, (C) shows results for LPJmL. Note that all CDFs in this figure sample a smaller set of locations than those in Fig. 3.

In contrast, the CDFs for the models that include CO₂ and vegetation effects (JULES and LPJmL) (solid lines in Fig. 4 Right) show a weaker response to climate change. The effect on plants of increased CO₂ concentration is often considered to consist of physiological and structural components. The former results in the stomata opening less widely in a CO₂-enriched atmosphere, leading to less water loss through transpiration (24). However, increased growth can alter the structure of the vegetation, potentially resulting in increased leaf area (and increased transpiration) (25). Sensitivity experiments in which CO₂ was allowed to vary only until the year 2000, after which it remained constant, showed increased response to climate from both JULES and LPJmL (dashed lines in Fig. 4 Right), albeit the increase is much more pronounced in JULES. Both models gave less transpiration under higher CO₂ than when CO₂ was constant despite having increased biomass (Fig. S4) indicating a strong physiological effect of CO₂. Further runs of JULES in which all structural aspects of the vegetation (fractional coverage, leaf area, and height) were kept constant in time showed that the largest increase in drought occurred when both CO₂ and vegetation were constant (Fig. S5)—that is, for the configuration most similar to that of the other GIMs shown in Figs. 2 and 3. This result suggests that accounting for the dynamic response of plants to CO₂ and climate is largely responsible for the outlying (small) response of JULES in Fig. 3. This finding is consistent with a study showing that a substantially lower irrigation water demand under climate change is simulated by GIMs including CO₂ effect than those without (26).

Regional Changes.

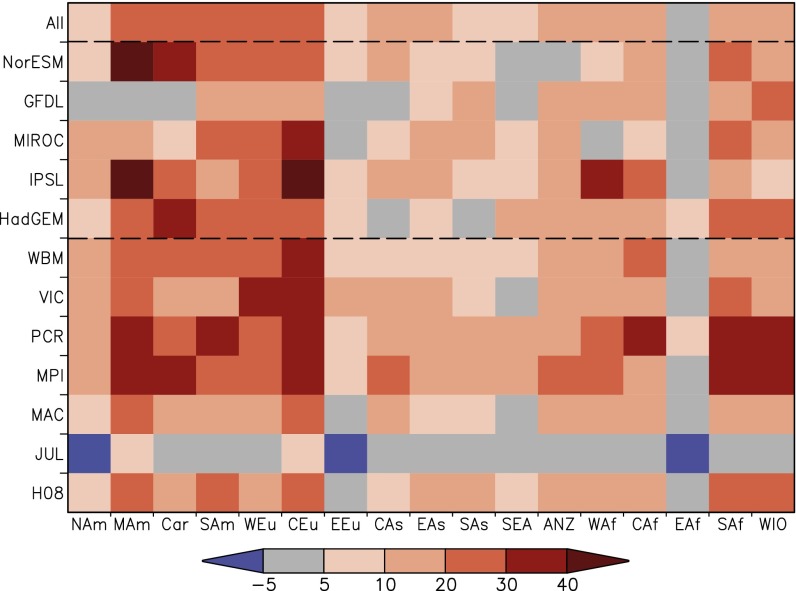
We calculate the RDI for the 17 GEO subregions (27) for which the DI could be calculated at more than 50% of the points in the region; note, however, the wide variation in size between regions (27). Average changes under RCP8.5 (top line in Fig. 5) vary between no change (Eastern Africa) to 28% (Central Europe), with five regions showing increases of at least 20% (South and Meso-America, Caribbean, and Central and Western Europe).

Fig. 5.

Mean percentage changes in regional deficit index (RDI) between 30-y simulations of reference (1976-2005) and future (2070-2099) under RCP8.5 for 17 world regions. Values are averaged over all of the MME members (All), by GCMs, and by GIMs. JULES includes CO₂ and vegetation effects. See SI Text and ref. 27 for GEO region descriptions and acronyms.

For RCP8.5 S2N is larger than 1 in 6 regions, and is larger than 1.5 in South America and Western and Central Europe. Uncertainty is largest in Eastern Europe, South and Southeast Asia, and Eastern Africa where S2N is less or equal to 0.7. When calculated separately for GCMs and GIMs ensembles, the average S2N resulting from different GIMs is larger than that from GCMs in 11 regions, and, in 4 of those, it is more than 2 times as large (Meso America, Central Europe, South East Asia and the Caribbean) (see Table S2 for details). Note results in Fig. 5 where the variation in mean change between the GCMs (lines near top of figure) is smaller than that between the GIMs (lines at bottom of figure). In North and South America, Eastern Europe, East and South Asia, and Central and Eastern Africa, S2Ns from GCMs and GIMs are comparable. When JULES is excluded from the ensemble (i.e., only six GIMs included), the mean change remains relatively similar to that from the seven GIMs ensemble, but the S2N ratio increases, with magnitude depending on the region (Tables S2 and S3 for details). Note, however, that, even with JULES excluded from the MME, the uncertainty from GIMs generally remains greater than that from GCMs, suggesting that JULES is not the dominant source of uncertainty within GIMs.

Discussion

Previous global modeling experiments have suggested that, under climate change, soil moisture and runoff would decrease (4–7, 10, 28, 29–32), albeit with large regional uncertainty in the magnitude of changes. However, most studies include only one or a few global impact models (GIMs) whereas recent work (17, 26) has shown that the uncertainty associated with the response of terrestrial hydrology to climate change simulated by different GIMs could be as large as the uncertainty in the response of the climate to greenhouse gas forcings simulated by global climate models (GCMs). The uncertainty associated with GIMs has been attributed to differences in the number and type of processes represented in the GIMs (e.g., water balance, energy balance) and to differences in the details of their implementations. We used a multi-model ensemble (MME) experiment including a relatively large number of GIMs of diverse types (which are able to reproduce the main characteristics of water deficits in terms of regional extent and duration) (15), forced by the same bias-corrected climate from simulations of five state-of-the-art GCMs, to assess changes in the frequency and severity of droughts, at the global and regional scales, under four different RCPs for the end of the 21st century.

At the regional scale, our results show that drought frequency (proportion of time under drought conditions) and severity (proportion of land under drought conditions) is very likely (i.e., more than 90% of ensemble members) to increase in the Caribbean, South America, Western and Central Europe, Central Africa, Australia and New Zealand, and the Western Indian Ocean under RCP8.5; this result reinforces earlier findings based on CMIP3/Special Report on Emissions Scenarios (SRES) projections (2). In Eastern Africa, the variation between GCMs is large and the signal-to-noise ratio (S2N) is close to zero. Both GCMs and GIMs contribute to the overall uncertainty in the response; improving the representation of regional changes in droughts is dependent on improved process representation in the models, for example, through analyses of GIMs biases when forced by observed climate. It is, however, beyond the scope of this paper to diagnose the reasons for the differences between particular GCMs and GIMs.

The MME shows a likely increase in the spatial extent (severity) of dry episodes under all four RCPs, with increasingly large changes under greater radiative forcing and S2N greater than 1 at the global scale and in some regions. Under RCP8.5, all five GCMs show a substantially warmer climate that will tend to drive increased evaporation. There is more variation in projected precipitation changes, both between regions and between GCMs (Fig. S6). Where evaporation increases and precipitation decreases, soil moisture deficit can build up, resulting in increased drought. In our results, areas with the largest signal of drought increase are generally located where precipitation is projected to decrease. However, even in those areas where precipitation increases, drought can still increase if this extra water is lost through greater evaporation. This is the case in tropical areas where GCMs indicate increased precipitation (e.g., parts of Central Africa) (Fig. S6), but increase in evaporation leads to more drought being simulated by GIMs (Fig. 1). Using S2N calculated over different subsets of the MME to describe the range of GCMs and GIMs, we showed that the total uncertainty associated with projected changes in drought is larger from GIMs compared with GCMs. GIMs uncertainty is particularly affected by an outlying GIM, JULES, that shows systemically lower response to climate change, but remains larger than the uncertainty in GCMs even when excluding JULES from the ensemble; e.g., GDI S2N is 2.48 from GIMs and 3.01 from GCMs when excluding JULES (Table S2; numbers in parentheses for details).

By investigating JULES simulations further, we show that its outlying signal is largely the result of the inclusion of a description of the plant response to enhanced CO₂, a process that is not represented in most GIMs used to simulate global water resources. The effects of CO₂ and dynamic vegetation on plant evapotranspiration and mean runoff have been studied before (24, 25, 33, 34), but the effect on drought and a direct comparison with hydrological models has not been presented before. When atmospheric CO₂ increases, the stomata can partially close (35), conserving the water and resulting in smaller changes of evaporatranspiration in a warmer climate (26, 36). This process leaves a wetter soil and thereby a less likely drought occurrence, as found in our results. At the leaf scale, the physiological effect of increased CO₂ is well characterized by laboratory and field studies (37), but models differ substantially in the predicted response of transpiration at the ecosystem level (38) and the net effect of physiological and structural changes is also highly uncertain (39). Our results suggest that the inclusion of CO₂ and vegetation dynamics can fundamentally change the drought response to climate change, but the magnitude of these changes remains uncertain. This finding underlines the importance of including a diverse range of GIMs describing various processes when designing multimodel experiments and that more research should be conducted to better understand the response of vegetation water use to CO₂ increase.

Our MME considered only the impact of climate change, with no representation of water management or changes in land use. Climate (including CO₂ effects on vegetation) is not the only forcing relevant to assessments of future droughts and water scarcity as water demand can generate water stress (40) and the projected future population increase will likely result in further increases in water stress (41). For a thorough investigation of water availability, the combined effect of climate, land use and water management should be taken into account, using a range of GCMs and GIMs to capture the uncertainty.

Methods

In this paper, we have analyzed simulations from the global impact models of the ISI-MIP ensemble experiments for which daily runoff data were available.

The experiments considered five different worlds: one representative of historical radiative forcing and four possible future worlds. These future scenarios included the following: a very high baseline (rising radiative forcing reaching 8.5 Wm⁻² by 2100; RCP8.5), a very low forcing level (radiative forcing peaking at 3 Wm⁻² before declining to reach 2.6 Wm⁻² by 2100; RCP2.6), and two medium stabilization scenarios (stabilization without overshoot pathway to 4.5/6.0 Wm⁻² at 2100; RCP4.5/RCP6.0) (22, 42). Each radiative forcing scenario was implemented by five global climate models (GCMs): HadGEM2-ES, IPSL-CM5A-LR, MIROC-ESM-CHEM, GFDL-ESM2M, and NorESM1-M (18). Transient GCM outputs were regridded to a common 0.5° latitude × 0.5° longitude grid, and a two-step bias correction procedure was implemented for each month independently (8) based on the WATer and global CHange (WATCH) Forcing data (43).

The bias-corrected GCM outputs (8) were used as inputs for nine global impact models: H08, JULES, LPJmL, Mac-PDM.09, MATSIRO, MPI-hm, PRCGlobWB, VIC, and WBM (see SI Text for references). For RCP4.5 and 6.0, VIC and Mac-PDM.09 were only driven by HadGEM2-ES. The GIMs were run on 0.5° grids (except JULES, which was run with grid cell size 1.875° longitude × 1.25° latitude, then regridded to 0.5° for analysis). GIMs were spun up to a quasi steady state by repeated use of detrended meteorology for 1951–1980, followed by a simulation of the period 1951–2005. Simulations for each RCP covered 2006–2099 (2005-2099 for HadGEM2-ES-forced runs). All GIMs considered contemporary patterns of land use, except JULES, which modeled natural vegetation only, with no land use. No anthropogenic storage (e.g., dams and reservoir) or water management was represented.

We have not investigated the extent to which the drought results from JULES depend on the grid scale, as no simulations at other scales are available. However, our best assessment from other work with JULES (not specifically on drought) is that results are generally not very sensitive to the size of the grid cells, at least for modest changes in resolution (say 0.5–3 degrees) and for regionally or globally averaged statistics.

Daily total runoff is the sum of surface and subsurface runoff. It is an integrated response to all basin input, storage and transfer processes, and the useable output of river basins for various water sectors. The daily total runoff outputs from the RCP/GCM/GIM combinations were extracted and analyzed for two time slices: 1976–2005 (historical forcing hist or reference period) and 2070–2099 (future forcing or RCP).

The ISI-MIP dataset also includes experiments of JULES and LPJmL in which CO₂ was allowed to vary only until the year 2000, after which it was kept constant (“noCO₂” runs) whereas the meteorological forcing included the climate change signal as before. “No CO₂” runs of JULES were used only in the sensitivity analysis of Fig. 4; all other analysis used JULES runs with varying CO₂.

Following ref. 6, drought episodes were defined relative to a time-varying threshold corresponding to the 10th percentile of total runoff (Q90) simulated under hist (notation follows convention from ref. 44 with Q90 being the runoff value exceeded or equaled 90% of the time). We calculated a daily Q90 value using a 30-d moving window to capture intramonthly temporal patterns, as in ref. 15. Q90 was used as a threshold to calculate daily runoff deficit indices (DIs), such that DI = 1 when runoff is <Q90 and DI = 0 otherwise. All years were treated as having 365 d, with data for 29 Feb removed from models that included that day. The difference in the frequency and fraction of land cells for which runoff is below this threshold between the future and historical runs quantifies any signal of increase in severity and frequency of drought. To capture geographical and seasonal characteristics of the runoff, thresholds were calculated for each land cell independently. To reduce uncertainty due to climate-impact modeling biases in the results, thresholds were also calculated for each climate-impact model combination as in ref. 45.

For each land cell of each simulation, we calculated a measure of drought frequency to be the fraction of days under drought for each hist and RCP scenario. We quantified a signal as the difference between the fraction of days under drought between each RCP scenario and the corresponding historical scenario. We calculated the signal-to-noise ratio (S2N) as the ensemble mean change divided by the inter-quartile IQ range of changes for the full MME and certain subsets of RCP/GCM/GIM combinations (i.e., S2N associated with GCMs is the S2N associated with each GIM driven by all GCMs, then averaged across all GCMs; for GIMs uncertainty, it is the S2N associated with each GCM for all GIMs, then averaged across all GIMs). Sensitivity of S2N to the definition of spread was tested (SI). It showed that values based on IQ range are similar but slightly more conservative (i.e., smaller S2N) than those based on SD, and therefore S2N-IQ was chosen.

Similarly to ref. 46, we removed arid regions from the analysis. We defined arid cells to be those that had more than 90% of the runoff time series equal to zero in any single climate-impact model combination; the land-mask of these cells is displayed in SI Text. Of the remaining cells, the seasonal variation in the runoff resulted in some very dry periods. We therefore also implemented a daily veto for each cell of each GCM/GIM combination, which discarded days for which the value of Q90 was zero. There were two GIMs (LPJmL and MATSIRO) for which the masking and vetoing removed too many points to be able to calculate global averages (see SI Text for details), so we did not consider them in the global analysis. After applying the masking procedure to the remaining seven GIMs, 82% of the total land cells (55,051 out of 67,420 grid cells) was included in the analysis. For JULES, the unmasked area corresponds to 83% of the total land cells (6,270 out of 7,558 grid cells). Note that we investigated the effects of model structure (inclusion of dynamic effect of CO₂ on plants) using the two discarded GIMs (LPJmL and MATSIRO) along with JULES, using the full 9GIMs mask, which retained only 64% of the total land cells (68% of the JULES land cells) (see SI Text for details). Therefore, these sensitivity tests are not global results.

The global impact of changing drought was studied by calculating a daily global deficit index (GDI) for each GIM/GCM/RCP combination over the unmasked land cells. This is the weighted average of the number of land cells under drought conditions, with weights proportional to the area of each grid cell. It represents the global proportion of land (or spatial extent) under drought and gives a measure of the global severity of a dry episode; it varies between 0 (no land cells under drought conditions that day) to 1 (all land cells under drought conditions that day). The method differs from that of ref. 47, which calculated the spatial extent of droughts over contiguous cells but is similar to that of ref. 6 to avoid potential discontinuity introduced by minor events. Seasonal GDIs were derived by extracting GDI time series for two specific 3-mo periods: December to February (DJF) and June to August (JJA).

We also calculated a daily regional deficit index (RDI) for 17 of the Geo regions defined in ref. 27. These regions were those for which we could calculate a DI value for at least 50% of the land cells.

Differences between hist and RCP GDIs were assessed using the 1-sided Kolmogorov–Smirnov (48) test, which measures the distance between the empirical cumulative distribution functions of two samples of n1 observations (here n1 = 365 × 30 = 10,950). Results are presented at the 95% level.