Joint Inference of Identity by Descent Along Multiple Chromosomes from Population Samples

Abstract

There has been much interest in detecting genomic identity by descent (IBD) segments from modern dense genetic marker data and in using them to identify human disease susceptibility loci. Here we present a novel Bayesian framework using Markov chain Monte Carlo (MCMC) realizations to jointly infer IBD states among multiple individuals not known to be related, together with the allelic typing error rate and the IBD process parameters. The data are phased single nucleotide polymorphism (SNP) haplotypes. We model changes in latent IBD state along homologous chromosomes by a continuous time Markov model having the Ewens sampling formula as its stationary distribution. We show by simulation that this model for the IBD process fits quite well with the coalescent predictions. Using simulation data sets of 40 haplotypes over regions of 1 and 10 million base pairs (Mbp), we show that the jointly estimated IBD states are very close to the true values, although the presence of linkage disequilibrium decreases the accuracy. We also present comparisons with the ibd_haplo program, which estimates IBD among sets of four haplotypes. Our new IBD detection method focuses on the scale between genome-wide methods using simple IBD models and complex coalescent-based methods that are limited to short genome segments. At the scale of a few Mbp, our approach offers potentially more power for fine-scale IBD association mapping.

1. Introduction

Identity by descent (IBD) is a fundamental concept in genetics that describes the ancestral relationships among current copies of homologous DNA. It was first introduced by Cotterman (1940) and Malécot (1948) to generalize the coefficients of inbreeding and relatedness of Wright (1921, 1922). Copies of DNA at a locus are IBD if they descend from the same ancestral DNA. Thus IBD is by definition relative to some ancestral reference population. The IBD state for a sample of homologous DNA copies can be specified as a partition into disjoint sets; copies within a set share a common ancestor relative to the ancestral reference population. To avoid confusion with alternate sets of chromosomes, alleles, or haplotypes, we will refer to the members of the sample of haploid DNA copies under consideration as gametes.

The concept of IBD has many uses in genetics, including detecting unknown familial relationships (Stevens et al., 2011), family or population-based genetic mapping (Albrechtsen et al., 2009, Han and Abney, 2011), genotype imputation and haplotype inference (Kong et al., 2008), measuring population structure (Weir and Cockerham, 1984), and detecting natural selection (Albrechtsen et al., 2010). There has therefore been much recent interest in inferring IBD from genetic marker data, but the focus of these approaches has been pairs of gametes or pairs of diploid individuals. Leutenegger et al. (2003) developed a method to estimate inbreeding coefficients from individual genotypic data, and Browning (2008) used the same model for pairs of population haplotypes. Purcell et al. (2007) and Albrechtsen et al. (2009) summarize the latent IBD state at a locus as the number (0, 1, or 2) of gametes that are IBD at the locus between two diploid individuals. Browning and Browning (2010, 2011) further reduced the state space at a locus to none (0) or any (1) shared IBD between two individuals. The primary goal of this article is to extend the models and methods to inference of IBD among an arbitrary number of gametes. This allows inference of joint patterns of IBD among individuals and across a segment of genome for use in subsequent genetic analyses (Browning and Thompson, 2012, Glazner and Thompson, 2012).

The complete historical relationship among current gametes can be described by the genealogical tree of coalescent theory (Kingman, 1982), in which ancestry is traced backward in time from the present to the most recent common ancestor of the gametes. However, for practical purposes, a reference population must be specified. In a pedigree-based study, the gametes of the pedigree founders serve naturally as the reference population. In other cases, there may be a well-defined founder population. However, in population samples without external pedigree information, there is often no clear way to specify the ancestral reference population. In this article, we define IBD by specifying a reference population at t₀ generations in the past. If mutations occurring subsequent to the t₀ time point are ignored, this specification is the same as the concept of equivalence class used by Kingman (1982) in the formulation of the standard coalescent.

The choice of t₀ will depend on the purpose of inferring IBD. Here we consider the range of time depth t₀ of tens to a hundred generations. This is “recent” IBD (Browning, 2008; Browning and Browning, 2010), intermediate between pedigree-based IBD among close relatives and the ancient IBD that is a source of linkage disequilibrium (LD) in population haplotypes. The time depth t₀ is often specified indirectly by the probability η of IBD between a pair of gametes. For a constant diploid population with effective size N_e, the ancestral coalescence rate between two gametes is 1/(2N_e) and thus η = 1 − exp [ − t₀/(2N_e)]. The pairwise probability η of IBD is approximately equal to the scaled time depth τ₀ = t₀/(2N_e), for small time depth t₀ (<10² generations) and large effective size N_e (>10⁴ for most recent human populations).

Since the IBD state at a site is the partition determined by a given time depth in the genealogical tree, the process of changing IBD states along a chromosome is determined by the process of changing genealogy due to historical recombination. In coalescent theory, it has been shown that the sequence of coalescent trees along a chromosome can be well approximated by a Markov process (McVean and Cardin, 2005; Marjoram and Wall, 2006). Stam (1980) first introduced a Markov model for the IBD process between two gametes, where the lengths of both IBD and non-IBD segments are exponentially distributed, and a parameter λ measures the overall rate of change in IBD state. The two parameters η and λ jointly determine the level of IBD at a site and the chromosomal extent of a segment of shared ancestry (IBD).

Thompson (2008) developed a continuous time Markov model for four gametes with a state space consisting of fifteen IBD states (the partitions of four gametes). Thompson (2009) extended the model to any number n of gametes, but used it to infer IBD states across a chromosome only for n = 2 and n = 4. In this model, transitions in IBD state were restricted to single gametes joining or leaving larger sets. Brown et al. (2012) relaxed the restriction by allowing any move of one gamete between the subsets of an IBD partition and implemented this model for sets of four gametes. Moltke et al. (2011) presented a model for multiple gametes, but with much more restricted state transitions.

Model-based approaches to inference of latent IBD states from population single nucleotide polymorphism (SNP) data generally use a hidden Markov model (HMM) approach. This includes the original two-gamete model of Leutenegger et al. (2003), the generalizations of Purcell et al. (2007) and Albrechtsen et al. (2009) to pairs of diploid individuals, and the more general 15-state model implemented by Brown et al. (2012). These approaches use exact HMM computational algorithms such as the forward-backward algorithm (Baum et al., 1970; Baum, 1972; Rabiner, 1989).

In this article, we extend the previous work of Brown et al. (2012) to jointly estimate IBD along a chromosome among any number n of gametes using the same IBD process model. However, exact HMM computations cannot be applied for larger numbers of gametes because the state space increases extremely fast with n (Bell, 1940). In the Methods section, we develop a Bayesian inference framework and a reversible jump Markov chain Monte Carlo (MCMC) method to estimate the latent IBD states along a chromosome, the IBD process parameters, and the allelic typing error rate. Reversible jump MCMC is needed since the number of IBD transition points can vary over MCMC realizations. We will call the new method JointIBD.

Earlier methods computed IBD probabilities (Brown et al., 2012) or sampled IBD realizations (Moltke et al., 2011) only at locations of SNP markers. By sampling IBD transition points, we achieve a more flexible MCMC process that realizes the IBD state at all points on the chromosome. This means that a long stretch of bases without SNPs may contain multiple IBD state transitions, allowing IBD state to change substantially between one SNP and the next. Moltke et al. (2011) achieve a similar effect by allowing multistep transitions between marker locations.

JointIBD combines five extensions to previous approaches. (1) It can handle an arbitrary number of gametes (we present results based on 40 gametes), as can the method of Moltke et al. (2011), whereas other methods can handle only a small number. (2) It models the full set of IBD partitions at a locus and relaxes some restrictions on IBD state transitions. (3) As do some earlier approaches, it explicitly models typing errors, and as a byproduct may be less sensitive to nonmodeled recent mutations. (4) It allows transitions of IBD at any point on the sequence, not only at SNP locations. (5) It provides Bayesian estimates of parameters, which can be related directly to the underlying processes of coalescence at a locus, and recombination across the genome.

In the Simulations section, we show results using simulated data from Brown et al. (2012). We compare JointIBD results for subsets of four gametes with results from exact computation using the ibd_haplo program as implemented in the MORGAN v3.2 (2013) release. We conclude with a Discussion section.

2. Methods

2.1. The HMM model

The data, y = {y_ij}, consist of SNP haplotypes, with y_ij being the observed allele at SNP site i (=1, ., m) of gamete 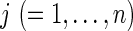. Within the population, we assume that there are only two alleles (denoted as allele 1 and allele 2) at each SNP site. Let ℓ be the length of the chromosome in base pairs (bp), and let π_i be the population frequency of allele 1 at SNP site i. These allele frequencies are assumed to be known. In practice, they would be estimated from a large population sample. We build a hidden Markov model for SNP data y, where the latent variables are the IBD states across a genome segment.

At genome location x, the IBD state, Z(x), among gametes is represented as a partition of the n gametes into IBD subsets, v, where each set is a collection of gametes that are IBD at a location. Thus an IBD state at a site is a partition of the set of integers 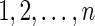. For example n = 6, Z(x) = {{1, 2, 6},{3, 5},{4}} means that at a given location x gametes 1, 2, and 6 are IBD, gametes 3 and 5 are IBD, and gamete 4 is not IBD with any of the others. The ordering of subsets and of the elements within each is irrelevant. Conventionally, here we order the elements in each subset in increasing order and order the subsets according to the smallest member of each. The Ewens sampling formula (ESF, Ewens, 1972) provides a single-parameter probability model for the n-gamete IBD partition at a site:

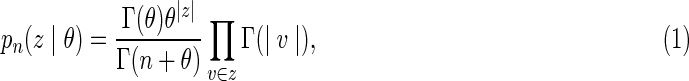where θ > 0, |v| denotes the number of elements in set v, and Γ(v) denotes the gamma function. From equation (1), p₂({{1, 2}} |θ) = 1/(1 + θ). Thus, the parameter θ is inversely related to the probability that two elements fall in the same subset, or, in our application, that two gametes are IBD at this site. The pairwise IBD probability η is simply 1/(1 + θ).

We model the latent process of IBD transitions along chromosomes by a continuous-time reversible Markov process whose stationary distribution is given by the ESF (1). We assume that the distance to the next potential transition event along the chromosome is exponentially distributed with mean 1/λ bp. Given current state z and a potential transition event, the resulting IBD state w is sampled from the transition probability p(w|z) specified by the modified Chinese restaurant process (MCRP, Brown et al., 2012). Thompson (2009) and Brown et al. (2012) model SNP-to-SNP transitions in IBD state and so build in additional flexibility by incorporating the possibility of IBD transitions independent of the current state, where the new IBD state is sampled from the stationary ESF distribution (1). Since our model IBD transitions occur in a continuum, multiple state transitions can occur between adjacent SNPs. There is therefore no need to include this additional model component.

We briefly describe the MRCP transition process as follows. First, insert a new gamete. The gamete is inserted into any set of size k with probability k/(n + θ) or as a new singleton with probability θ/(n + θ). Next, randomly delete one of the n + 1 gametes. The newly inserted gamete, if not deleted, takes the identity of the deleted one. Thus the MCRP allows any one gamete to move from one IBD subset to another. It has been shown that the IBD process along the chromosome is reversible with respect to ESF (Appendix A of Brown et al., 2012). Using the MCRP model, we formulate the transition probability for two consecutive IBD states z and w along a chromosome. These transitions can result in the same IBD state (z = w) or a different state (z ≠ w).

The probability of a transition for which z = w is given by:

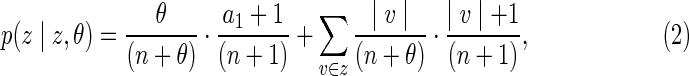where a₁ denotes the number of singletons in z. Here the first term on the right-hand side refers to the case in which the new gamete is inserted as a singleton and one of the singletons is then deleted, and the second term refers to the case in which the new gamete is inserted into an existing set (denoted v) and one of the gametes in that set is then deleted. Since some potential transitions do not produce state changes, the number of transitions predicted by a given value of λ will generally be greater than the number of actual (i.e., state-changing) transitions. Throughout this article, whenever we measure the number of transitions or the distance between transitions, we refer to actual transitions only. This is consistent with usage in earlier methods (Leutenegger et al., 2003; Thompson, 2009; Moltke et al., 2011).

In cases where the transition changes IBD state (z ≠ w), suppose that the new gamete is inserted into a set of size l₁, and the deleted gamete is from a set of size l₂. The transition probability p(w | z,θ) is given by

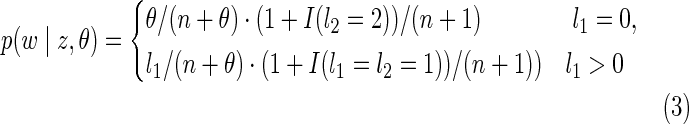where I(S) = 1 if the statement S is true and 0 otherwise. This extra term arises when one doubleton splits into two singletons (l₁ = 0, l₂ = 2) or two singletons merge into one doubleton (l₁ = 1, l₂ = 1). The same state will result in whichever of the two gametes is deleted (for the former case) or inserted (for the latter case). For any two states z and w, we define the IBD distance |z − w| to be the minimum number of IBD transitions necessary to transfer one into the other according to the MCRP.

We model the emission probability of SNP data given the latent IBD states. We do not model linkage disequilibrium in the ancestral reference haplotypes, so the SNP data at each site i are conditionally independent given the latent IBD states. We assume that the ancestral allelic states for each IBD subset are independent among subsets and across sites and are randomly sampled from a locus-specific ancestral allele frequency π_i. Since we consider common SNP variation and short-scaled time depth τ₀, we use separately estimated current allele frequencies as proxies for π_i.

Our typing error model assumes that each observed allele has a probability ɛ of being toggled to the alternative allele. Consider an IBD set of size l at site i. The probability of the corresponding data vector consisting of, for example, k alleles of type 1 and (l − k) alleles of type 2, is proportional to

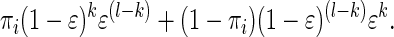We assume that the scaled time depth τ₀ defining the reference population is small enough that mutations on the lineages from ancestral reference alleles to the current sample can be ignored. Mutations that do occur will be interpreted as typing errors, potentially resulting in an overestimate of ɛ.

For our Bayesian prior distributions on parameters, we assign priors of high variance that suggest low levels of IBD among the n = 40 gametes. For the error probability ɛ, we assign a uniform distribution on the range [0, 1]. For the IBD level parameter θ we use a gamma distribution with shape α_θ = 2 and scale β_θ = 2n. This distribution has mean 160 and standard deviation ∼113, corresponding to values of η of order of magnitude 0.006, but permitting much higher values where the data provide evidence of IBD. For λ we use a gamma distribution with shape α_λ = 2 and scale β_λ = 10⁻⁴, giving a mean distance 5000 bp to the next potential transition point but again allowing for much longer or shorter segments.

For marker data with high levels of linkage disequilibrium (LD), our method tends to overestimate IBD levels due to haplotype similarities in the reference founder population (Purcell et al., 2007; Brown et al., 2012). This, in effect, increases the scaled time depth τ₀ of the ancestral reference population, and hence also the IBD level η. We therefore also used a more informative prior distribution for θ by including a constraint, truncating the gamma prior distribution, so that θ ≥ θ_c = n = 40. That is, the pairwise IBD probability η is bound above by 1/(1 + θ_c). In addition, we restrict the total number of transitions to be no greater than K_c = 2 × 10⁻⁵ℓ.

2.2. Parameter estimation

We update Z(x) by reversible jump MCMC and the model parameters θ, λ, and ɛ by Gibbs sampling. As the reversible jump MCMC procedure is the novel part of this process, we describe it here: updates for other parameters are described in Supplementary Material S4 (Supplementary Material available online at www.liebertonline.com/cmb).

We define three proposal distributions for use in MCMC updates. These are briefly described here; their formal definitions are in Supplementary Material S3.

(A) The proposal distribution q(z|z_A) or “one-side distribution” samples the IBD state of the new z, starting from the left side z_A, using the MCRP. This could, for example, be used to draw a new successor (z) to the most rightward interval on the chromosome (z_A).

(B) The proposal distribution q(z|z_A, z_B) or “two-side distribution” samples a new z that is an intermediate between the left side z_A and the right side z_B, which must be no more than two steps apart; the new z must be no more than one step from each of z_A and z_B.

(C) The proposal distribution q(z|z_A, z_B, z_C) or “propagation distribution” considers a situation in which z_A and z_B are consecutive IBD states along the chromosome and are thus no more than one step apart, and where z_C is a state exactly one step from z_A. If z_B and z_C are no more than one step apart, the propagation stops, that is, z is set to z_B. Otherwise, we choose a new z that is no more than one step from both z_B and z_C, and is two steps from z_A.

This proposal distribution is used when changes of an IBD state (modification, insertion, or deletion) have to be propagated through a subsequent interval in order to avoid a violation of the MCRP model. Proceeding rightward, new values for each of the IBD segments are drawn from the propagation distribution where z_B is the original state of the segment being redrawn, z_A is the state of its original leftward neighbor, and z_C is the state of its current leftward neighbor. This redrawing process stops as soon as a segment that is legal without modification is reached, or at the end of the chromosome.

Updates of K, x, and z use six move types briefly described here (details and proposal ratios are given in Supplementary Material S4, as well as handling for special cases such as the end of the chromosome).

(A) Update a transition location. A transition location is chosen at random and set to a new location chosen uniformly between its flanking transitions.

(B) Update an IBD segment. A segment is chosen at random. A new state for this segment is chosen from the two-side distribution, with its two neighbor IBD states being the two sides.

(C) Update an IBD state with adjustments to downstream material. A segment is chosen at random. A new state for this segment is chosen from the two-side distribution, with the leftward neighbor and the current IBD state as z_A and z_B. Downstream IBD segments are drawn from the propagation distribution.

(D) Insert a transition with adjustments to downstream material. A random IBD segment is chosen and a new transition location is chosen uniformly within it. The new IBD state associated with that transition is sampled from the one-side distribution based on its leftward neighbor. The downstream IBD segments are drawn from the propagation distribution.

(E) Delete a transition with adjustments to downstream material. A random IBD segment is deleted. The downstream IBD segments are drawn from the propagation distribution.

(F) Update segments of IBD by swapping their gamete labels. A pair of gametes is chosen at random and partitioned into segments that are IBD and segments that are not. Independently for each run of non-IBD material, we choose randomly whether or not to swap the labels for that pair of gametes.

3. Results

3.1. Generation and analysis of simulated data

We test model performance using part of the population simulation of Brown et al. (2012). In those data, a constant population of 3500 males and 3500 females was simulated over t₀ = 200 generations. In each generation, repeated 3500 times, a random male and a random female were chosen to generate a son and a daughter. This mating system yields a mean of two diploid offspring and a variance of four, resulting in an effective population size of N_e = 7000 × 4/6 ≈ 4667 (Crow and Kimura, 1970). The gamete segregating from a parent is obtained by generating recombinants between the two homologous chromosomes of the parent with rate 10⁻⁸ per bp. Each founder gamete is given a unique founder label; descendant gametes are specified as a list of segments descending from the founder genomes with the same label. Among a set of sampled gametes, homologous chromosome segments with the same founder label are IBD.

The haplotypes of descendant individuals can be created by assigning founder haplotypes to the labels. Briefly, Brown et al. (2012) generated founder haplotypes as follows. First a BEAGLE haplotype cluster model (Browning and Browning, 2007) was fit to a set of 1917 real haplotypes with high LD levels. These haplotypes also provided the assumed values of the SNP allele frequencies π_i. The program beaglesim (Glazner and Thompson, 2012) was then used to simulate new haplotypes from the BEAGLE model. In beaglesim, a parameter γ controls generation of data sets at varying LD levels. In generating a haplotype from the BEAGLE model, γ is the probability of random switching among haplotype clusters at each SNP marker and thus LD is broken on average every 1/γ markers. In this article, we use only the high-LD (γ = 0.05) and no-LD (γ = 1) data sets of Brown et al. (2012). We then impose additional typing errors on the data sets of Brown et al. (2012). After constructing the current generation-200 haplotypes from the founder haplotypes and the descendant founder genome segments, we simulate allelic typing errors using the same error model assumed by our analysis. We apply error independently for each marker and each gamete with probability ɛ = 0.005.

Simulated data were analyzed with JointIBD as follows: For each data set, two independent replicates were run. For each, four equally spaced temperatures were used, chosen adaptively during burn-in. (The length of burn-in varied among the data sets.) After burn-in, samples were taken every 20 iterations for a total of 20,000 iterations or 1000 samples. The two replicates were pooled to give 2000 samples. Potential scale reduction factors (PSRFs; Gelman and Rubin, 1992) were computed between the two replicates to assess MCMC mixing; a PSRF below about 1.05 indicates satisfactory mixing. Run conditions and PSRF values are shown in Table 1.

Table 1.

JointIBD Run Conditions

		PSRF
Data set	Total steps	logl	θ	ɛ	ρ	Transitions
S-NoLD	42,550	1.0007	1.0013	0.9995	1.0012	0.9998
S-LD	42,040	1.0171	1.0019	0.9996	0.9998	0.9997
L-NoLD	43,770	0.9997	0.9997	1.0037	1.0006	1.0013
L-LD	39,790	1.0480	0.9999	1.0090	0.9999	0.9998

3.2. Fit between simulated IBD and theoretical models

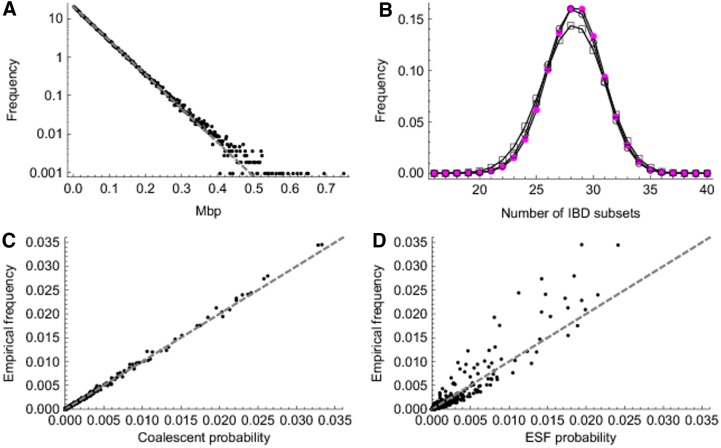
Here we test the adequacy of the ESF and the MCRP to model IBD data drawn from a more detailed population model. Using the simulated population of Brown et al. (2012), we first construct samples of sets of 40 gametes (20 individuals) from the final generation and examine the true IBD transitions in these data. We partition the gametes of 3500 final-generation females into 175 sets of 40 gametes. (Only females are chosen to minimize the chance of sampling full sibs.) Recall we define the IBD distance between states as the minimum number of MCRP transitions necessary to transform one into the other. Among 534,438 state transitions, 95% have distance 1, 4.7% have distance 2, and only 0.3% have distance 3 or more. These results indicate that it is reasonable to model only IBD transitions of distance 1; those involving the move of a single gamete. Our model can explain a transition of distance 2 or more as multiple closely spaced transitions. Figure 1A shows the distribution of the bp distances between transitions. It has somewhat heavier tails and larger variance than an exponential distribution with the same mean.

FIG. 1.

Comparison of simulated identity by descent (IBD) with theoretical predictions. (A) Distribution of the distances between successive IBD states along chromosomes. Dots show distances from the simulation, with y-axis frequencies binned using a bin size of 0.002 Mbp; the dashed gray line shows an exponential distribution with the same mean (0.049 Mbp). (B) Distribution of the number of IBD subsets. Magenta dots denote the simulated data, circles the distribution based on coalescent theory with scaled time depth τ₀ = 0.0214, and rectangles the distribution calculated from the Ewens sampling formula (ESF) with θ = 41. (C) Comparison of simulated frequency for each distinct IBD state with coalescent predictions. Here we represent an IBD state by vector a with element a_l being the number of IBD subsets of size 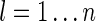. Dashed line denotes y = x. The linear correlation coefficient is 0.999. (D) Comparison of simulated frequency with ESF predictions. The linear correlation coefficient is 0.942.

We examine the empirical stationary distribution of the IBD process along chromosomes by sampling IBD states every 0.05 Mbp. As shown in Figure 1B and C, the simulated distribution of IBD states is very close to the distribution based on coalescent theory (Hein et al., 2005) with scaled time depth τ₀ = t₀/(2N_e) ≈ 0.0214. The slight discrepancies may be due to the use of only one realization of the underlying population pedigree or to differences between the coalescent model and the simulation model used for IBD descent.

Figure 1B and D compare the simulation distribution with the ESF (Eq. 1). The value of θ is set to 41 so that the mean number of IBD sets is the same as for the empirical distribution. This is slightly smaller than the value calculated from the relation θ = (1 − η)/η ≈ (1 − τ₀)/τ₀ ≈ 46. The distribution of the number of IBD sets based on the ESF is more dispersed than the simulated one (Fig. 1B). Consistently, Figure 1D shows that the more frequent IBD states are a little under-represented by the ESF, while the less frequent IBD states are a little over-represented. Overall, the ESF distribution fits the empirical distribution reasonably well.

3.3. MCMC inference of IBD

To assess the performance of JointIBD we use the 40 haplotypes of the first 20 female individuals from the 200^th generation of the simulated population of Brown et al. (2012). We reset the location of the first marker as the origin. Bayesian estimation via MCMC simulations is computationally intensive, and thus for each of the two data sets we analyze only the initial 1 Mbp (“short”) and 10 Mbp (“long”) from each haplotype, corresponding to distances used in fine-scale gene mapping. We analyze four data sets: short and long haplotypes with no LD (γ = 1, data sets S-NoLD and L-NoLD) and short and long haplotypes with strong LD (γ = 0.05, data sets S-LD and L-LD). There are 85 markers in the 1 Mbp data sets and 860 markers in the 10 Mbp data sets. In Figures 2–6, results for no-LD data are shown on the left.

FIG. 2.

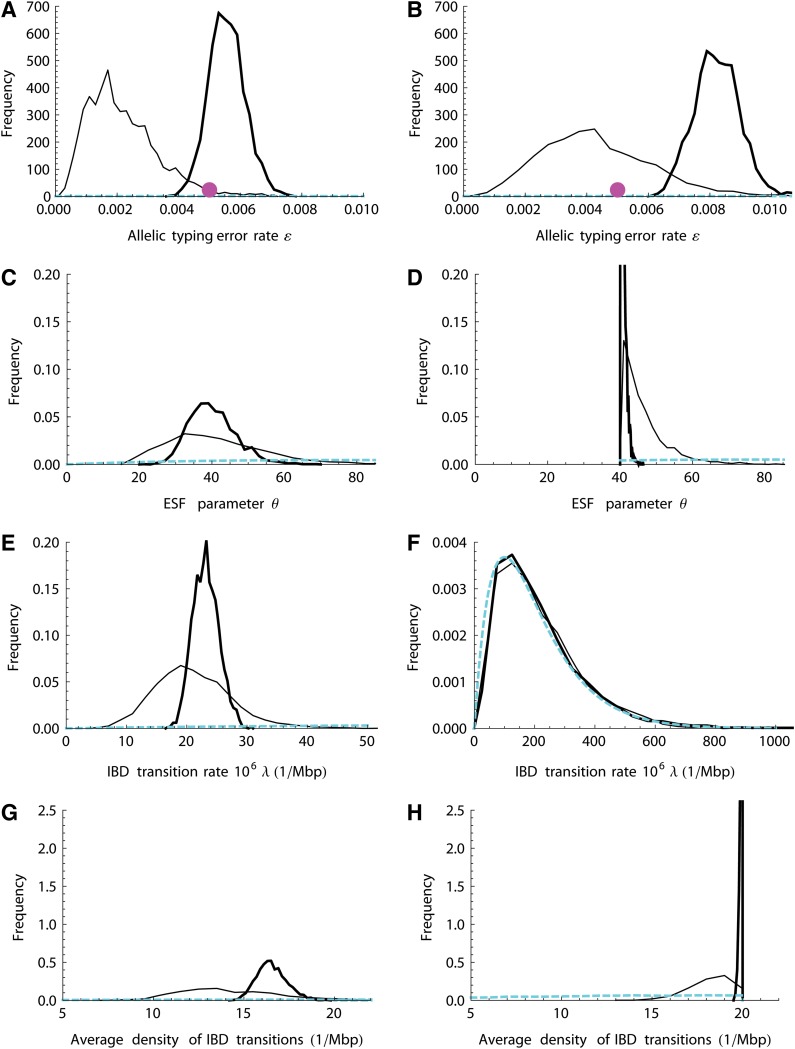
Posterior parameter distributions. Thin lines represent short data sets and thick lines long data sets; left panels are no-LD results and right panels are LD results. Panels show allelic typing error rate ɛ (A and B), ESF parameter θ (C and D), IBD transition rate 10⁶λ (E and F), and average density of actual (state-changing) IBD transitions (G and H). Cyan lines denote the marginal prior distributions, and the magenta dots in (A) and (B) denote the true typing error rate (0.005). LD, Linkage disequilibrium.

FIG. 3.

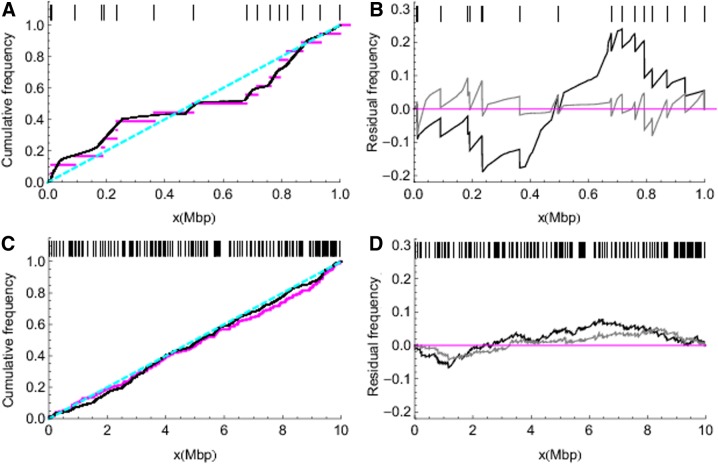
Estimation of IBD transition locations along chromosomes. Lefthand panels (A) and (C) show inferred cumulative transition frequency (black), true cumulative transition frequency (magenta), and the prior expectation (dashed cyan line) for S-NoLD and L-NoLD, respectively. Righthand panels (B) and (D) contrast results from data sets without LD (gray lines) and with LD (black lines) for short and long data sets, respectively. Residual frequency is defined as the inferred frequency minus the true frequency, so that a residual frequency of 0.0 represents perfect recovery. Short vertical lines on the top of each panel indicate the true transition locations.

FIG. 4.

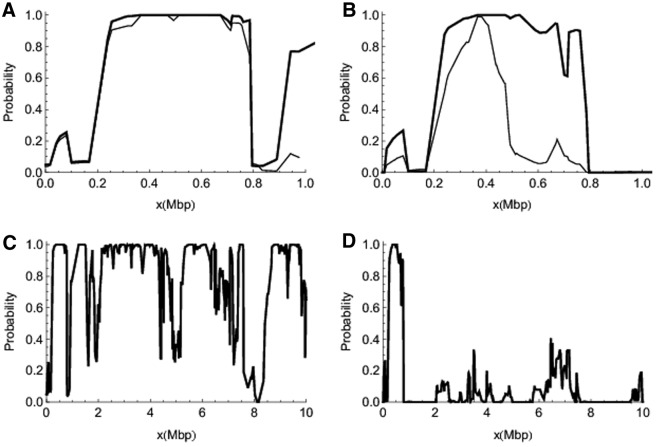
Detailed recovery of IBD states. Each panel shows the probability that the distance between a random estimated IBD state and the true IBD state is no greater than two at each SNP marker location. Throughout, heavy lines represent long data sets and narrow lines represent short ones. (A) contrasts S-NoLD and the first 1 Mbp of L-NoLD; (B) contrasts S-LD and the first 1 Mbp of L-LD. (C) and (D) show results for the full length of L-NoLD and L-LD, respectively.

FIG. 5.

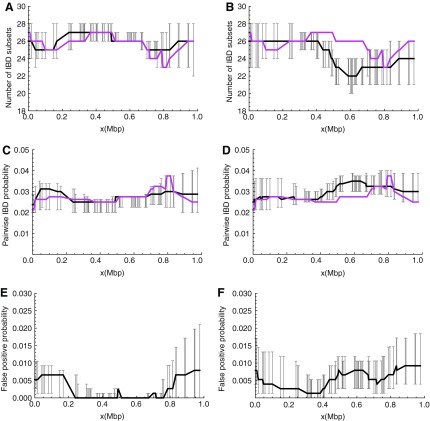
Overall IBD state recovery performance. This figure shows estimates of IBD states at each, single nucleotide polymorphism (SNP) location based on S-NoLD (left panels) and S-LD (right panels). They are evaluated in terms of the number of IBD sets (A and B), the pairwise IBD probability (C and D), and the false positive probability (E and F). Error bars denote the 95% central posterior intervals with black lines connecting the medians. In (A)–(D), magenta lines denote the true values.

FIG. 6.

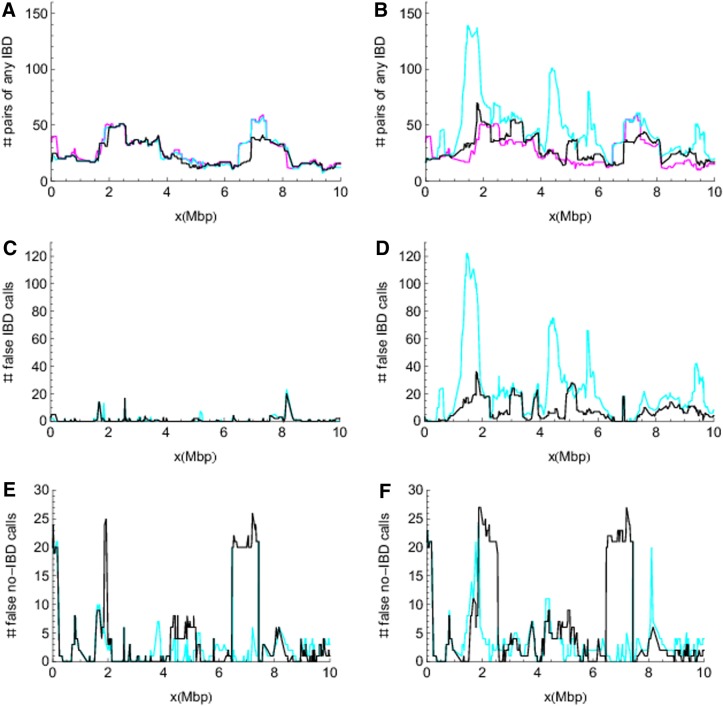
JointIBD versus ibd_haplo. Comparisons of JointIBD estimates (black lines) to the pairwise estimates (cyan lines) obtained by ibd_haplo from the data sets L-NoLD (left panels) and L-LD (right panels). Magenta lines denote the true values. (A) and (B) show the number of pairs inferred to have any IBD. (C) and (D) show the counts of false IBD calls (false positives), and (E) and (F) show the counts of false no-IBD calls (false negatives). “No IBD” refers to the IBD state consisting of four singletons; all other IBD states for two individuals are grouped as “any IBD.”

We first examine estimates from no-LD data for the parameters ɛ, θ, λ, and the average density of IBD transitions (the number of transitions divided by the length of the chromosome). As shown in the left panels of Figure 2, the prior distributions (dashed lines) are essentially noninformative. As expected, longer sequences give a tighter posterior distribution. By chance, S-NoLD had a realized error rate of only 0.0035, while L-NoLD had a realized error of 0.0053; as a result, the estimate of ɛ was low for the S data. The ESF parameter θ is estimated to be around 40 from both data sets (Fig. 2C), which is consistent with t₀ = 200 generations (see Section 3.1).

Since the “true” transition rate λ is unknown, we estimate it based on coalescent theory and then compare the result with its posterior distribution (Fig. 2E). The average number of lineages (or IBD sets) at τ₀ ≈ 0.0214 for n = 40 gametes is estimated to be around 28 (Hein et al., 2005; see also Fig. 5A). The average total coalescent branch length L(τ₀) backward to τ₀ can be obtained as 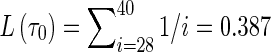. Thus, from N_e = 4667 and ρ = 10⁻⁸ per generation per bp we can roughly estimate λ = 2N_eρL ≈ 36 per Mbp. This estimate falls in the range of the posterior distribution from S-NoLD, although it is slightly larger than the estimate from L-NoLD.

The number of IBD state changes realized from S-NoLD (Fig. 2G) is not significantly smaller than the true empirical value of 18; the MCMC-based probability that this number of actual transitions is more than 18 is 0.083. The number of actual IBD transitions estimated from L-NoLD is around the true value of 169. Note that the transition rate λ suggests a higher number of transitions than are actually realized, because some potential transitions do not result in a changed IBD state.

Ancestral LD is due to shared population history beyond t₀ generations in the past and is not accounted for in our model. Ancestral LD results in decreased θ and increased λ and thus an increased number of IBD transitions (right panels of Fig. 2). Figures 2D and H show that, particularly for the large data set (L-LD), the estimated θ and the average density of IBD transitions become very sharply distributed just above the truncation thresholds (see Section 2.1). As a consequence, the posterior distribution of λ is essentially identical to its prior (Fig. 2E). Ancestral LD has effectively shifted the reference population backward and increased the scaled time depth τ₀. Our results confirm previous studies (Purcell et al., 2007; Brown et al., 2012) showing that high LD regions are miscalled as shared IBD segments. The mismatch between our model and the LD data also leads to an overestimate of the allelic typing error rate (Figure 2B), since the miscalled IBD segments show strong haplotypic similarity but not identity.

Figure 3 evaluates our estimation framework for the detection of IBD segments, beginning with the transition locations. The cumulative distributions of IBD transition location estimated from S-NoLD and L-NoLD are very close to the true distributions (Fig. 3A and C). Gray lines in Figure 3B and D show the difference between the cumulative distributions and the truth based on Figure 3A and C. Dark lines show the contrast with the method's performance in the presence of ancestral LD. Runs with LD deviate much further from the truth, especially for S-LD.

To assess accuracy of state reconstruction, at each SNP marker location we evaluate the inferred marginal IBD state by the probability that the distance between a random estimated IBD state and the true IBD state is no greater than two. As shown in Figure 4, IBD states are not well estimated in the presence of LD in the founder genomes. This is explained by the increased number of inferred IBD transitions (see Fig. 2G and H) so that on average fewer markers provide information about each IBD state. Estimation of IBD state is also affected by the local density of SNP markers, as indicated by the poorer estimation of IBD around the 8 Mbp location in Figure 4C. There are only 31 SNP markers between 7.5 and 8.5 Mbp, far less than the global average of 86 markers per Mbp. As shown in the left panels of Supplementary Figure S2, this region also shows high false-positive probability and large posterior uncertainties in the number of IBD subsets and pairwise IBD probability. Finally, longer data sets do better than shorter ones in their area of overlap (Fig. 4A and B), presumably because of better parameter inference.

In addition, at each SNP marker location we evaluate the inferred IBD state by the number of IBD subsets and the pairwise IBD probability. We define the false-positive probability at a location as the probability of a false claim of IBD between a random pair. Results from the short data sets are shown in Figure 5 and from the long data sets in Supplementary Figure S2. For the results estimated from S-NoLD (left panels of Fig. 5), the true values of the number of IBD sets and the pairwise IBD probability fall within their marker-specific posterior central 95% intervals (Fig. 5A and C), and the IBD states in the middle region are well estimated as shown by the small posterior intervals (Fig. 5A, C, and E) and low false-positive probability (Fig. 5E). In fact, a randomly sampled IBD state in the middle region (0.35 to 0.7 Mbp) has a probability of around 0.91, being exactly the same as the true state (data not shown).

In the presence of LD in the founder genomes (S-LD), the number of IBD sets at an SNP marker in the middle region is underestimated (Fig. 5B), consistent with our earlier interpretation of the increased scaled time depth. This results in a larger pairwise IBD probability and a higher false-positive probability than in the absence of LD. However, even in the presence of LD the rate of false claims of IBD remains below 1%.

3.4. Comparison with ibd_haplo

Browning and Browning (2010, 2011) compared the performance of fastIBD to that of PLINK (Purcell et al., 2007) and GERMLINE (Gusev et al., 2009), and Brown et al. (2012) compared ibd_haplo to fastIBD. Here we compare JointIBD to ibd_haplo, using data based on those in Brown et al. (2012). However, our results for ibd_haplo performance are not directly comparable to the previous results. First, the program has been substantially updated; we used the version of the MORGAN v3.2 (2013) release. More significantly, Thompson (2009) and Brown et al. (2012) incorporate the additional possibility of IBD transitions independent of the current state. The ibd_haplo program models SNP-to-SNP changes in IBD state, and this additional flexibility may be important in areas where SNPs are sparse. However, for closer analogy with the JointIBD model, we do not allow ibd_haplo these additional transitions. Finally, the data of Brown et al. (2012) did not include typing errors, but an error rate of 0.01 was used in the analysis to accommodate aberrant IBD changes or (in real data) mutations and other anomalies. In this article, we added typing errors at rate 0.005 but used only this same lower value in the ibd_haplo analyses.

For each of the two large data sets L-NoLD and L-LD, we ran ibd_haplo for all 190 possible pairs out of 20 individuals and obtained the most probable pairwise IBD state at each marker location. In each run, we set ɛ = 0.005, the simulation value, and η = 0.025 so that θ = 39 close to the “true” value in terms of the number of IBD sets (Fig. 1B). Following Brown et al. (2012), we used 0.05 per Mbp for the IBD change rate parameter since the analysis of that article has shown that keeping this parameter small provides more robustness in the presence of LD. To compare with the results of Brown et al. (2012), we first extracted the posterior distribution of pairwise IBD states from that of joint IBD states among n = 20 individuals, and then found the most probable pairwise state for each pair of individuals and at each marker location.

The results are shown in Figure 6. As shown in the left panels of Figure 6 for the results estimated from data without LD, both methods perform very well and ibd_haplo performs slightly better than JointIBD. The number of pairs showing any IBD as estimated by ibd_haplo is almost identical to the true value, whereas JointIBD underestimates this around the location of 7 Mbp (Fig. 6A). Additionally, ibd_haplo shows fewer false IBD calls (Fig. 6C) and fewer false no-IBD calls (Fig. 6E). On the other hand, in the presence of LD (right panels of Fig. 6), JointIBD performs better than ibd_haplo. The latter shows large overestimation of the probability of any IBD (Fig. 6B), which results in a large number of false IBD calls (Fig. 6D) at corresponding locations. Neither method does well at detecting all the pairwise IBD (Fig. 6F).

The differences in performance between ibd_haplo and JointIBD are partly due to the different specifications of the prior distributions. In the absence of LD in founder genomes, the data are informative for the number of IBD transitions, and thus the results are not sensitive to the ibd_haplo assumption of a relatively low IBD change rate. The ibd_haplo program also fixed the parameter values of ɛ and θ, whereas JointIBD uses non-informative prior distributions for these parameters. This may explain the slightly better performance of ibd_haplo.

In contrast, LD in founder genomes tends to be interpreted as IBD segments, as such LD is not modeled in these methods. Thus the number of IBD transitions is overestimated. While ibd_haplo puts a soft constraint on the number of IBD transitions by assigning a small value to the IBD change-rate, JointIBD puts a hard upper bound on the number of IBD transitions. Thus the false positive rate (calls of IBD given no IBD) is more effectively controlled by JointIBD (Fig. 6D).

4. Discussion

We have presented JointIBD, a Bayesian inference framework for the joint detection of IBD segments among multiple gametes. We discuss three main assumptions in our model. First, we assume that IBD processes along chromosomes are independent of allelic states. Thus, the SNP loci are assumed to be selectively neutral and the effects of mutation negligible. For the inference of IBD we use common SNP variation, not rare variants, and we aim to infer IBD relative to a reference population at scaled time depth τ₀ in the past. Processes such as natural selection and demographic history are relevant only from τ₀ to the present. Our interest is in relatively recent IBD, where τ₀ is of order 0.02. Therefore, in contrast to detection of ancient IBD (large τ₀), our method is largely immune to natural selection, unless the selection is very strong.

The second main assumption is the modeling of IBD processes along chromosomes by the modified Chinese restaurant process (MRCP) with the ESF as the stationary distribution. In the ESF the gametes are exchangeable, and thus we implicitly assume there is no geographical or social population structure among the small sample of individuals who provide the gametes. To validate the ESF, we make comparisons with coalescent theory, which assumes that the recent genealogical process of the population can be described by a Wright-Fisher model with constant effective population size. We have verified that the ESF is a good approximation of the probability distribution of IBD states at τ₀ predicted by coalescent theory, although the number of IBD subsets has slightly higher variance under ESF (Fig. 1B). The MRCP has an approximate biological basis. IBD transitions involving only one gamete correspond qualitatively to historical recombination events occurring on terminal branches of coalescent trees along chromosomes in the sequential Markov coalescent (McVean and Cardin, 2005; Marjoram and Wall, 2006). For small-scaled time depth τ₀, the large majority of recombination events occur in the terminal branches.

Lastly, we assume that the ancestral allelic states for IBD sets are independent both within loci and across loci. As we do not model LD in founder genomes, we have evaluated its impact on detection of IBD segments. Our results have shown that LD is confounded with the underlying IBD states, indicating the desirability of accommodating LD. Albrechtsen et al. (2009) modeled the nonindependence of marker data given hidden IBD states by pairwise haplotype probabilities. Browning (2008) and Browning and Browning (2010) built a joint hidden Markov model for haplotype frequencies and pairwise IBD states. Their model for haplotype frequencies incorporating LD models localized haplotype clusters as a variable-length Markov chain (Browning, 2006). However, to estimate joint IBD states among multiple gametes, we have necessarily simplified the data model. Joint inference in the presence of LD remains an important direction for future work.

We have compared JointIBD to ibd_haplo using data from Brown et al. (2012). In the absence of LD in founder genomes, both methods perform well and comparably. In the presence of LD in founder genomes, JointIBD controls the false positive calls of IBD more effectively, but otherwise does not outperform ibd_haplo in terms of inferring pairwise IBD. It is not surprising that the pairwise summaries of IBD are similar under the two methods, as both use almost the same model for the IBD process. However, although the output of JointIBD can be reduced to a pairwise summary, there is no straightforward way to obtain a joint inference from ibd_haplo. The IBD states for all the 190 pairs of individuals obtained separately from pairwise methods are not always consistent, and even at a single locus probabilities of IBD states obtained from different pairs cannot be easily combined. Combining pairwise inferences to form estimated IBD states among multiple individuals across loci is a challenging open problem. It is joint information, such as is provided directly by JointIBD, that helps to increase power in IBD-based mapping (Moltke et al., 2011).

The only comparable published method for detecting joint IBD states among multiple individuals is that of Moltke et al., (2011). Both methods use MCMC and are thus computationally intensive, and neither accommodates LD. However, their model specifications are very different. Moltke et al., (2011) use integer IBD indicators for a gamete at a locus, where 0 represents non-IBD with any other gamete (singletons), and gametes with the same positive indicator are IBD. The authors modeled IBD processes across a chromosome by a reversible birth and death process of zero indicators. Direct transitions between positive indicators are not allowed, so they must be implemented by inserting intermediate zero indicators. Thus, there are many more IBD transitions in their model than are required by the underlying historical recombination events.

In contrast to the single ESF parameter, θ, the stationary distribution of IBD indicators in Moltke et al., (2011) is determined by two parameters: the maximum positive indicator and the probability of being a zero indicator. Whereas the parameter η = 1/(1 + θ) has a natural interpretation as the pointwise probability of IBD between a pair of gametes, it is not clear how the Moltke et al., (2011) parameters relate to the reference population or to the descent from an ancestral origin allele to each IBD group. The maximum positive indicator limits the number of non-singleton IBD groups. It was fixed to be 1, 2, or 3 in various analyses of Moltke et al. (2011), but it is unclear how it should be set in practice.

JointIBD can only analyze haplotype data at this time. For genotype data, unknown phases could potentially be integrated out using the methods described by Albrechtsen et al. (2009) and Moltke et al. (2011). Missing data can be easily accommodated in our method, for example, by assuming that data are missing independently of allelic type. Alternatively, a program such as BEAGLE (Browning and Browning, 2007) can be used to infer the most probable phase and to impute missing allelic states, while incorporating additional information contained in reference panels of data if these are available.

Availability: JointIBD is freely available as Mathematica code from the software page of the corresponding author: http://www.stat.washington.edu/thompson/Genepi/pangaea.shtml. Other software of the authors used in comparison analyses (for example, MORGAN v3.2) is also available through this page.

Acknowledgments

We thank Serge Sverdlov and Jon Yamato for editing assistance. This research was supported by the National Institute of Health grants GM046255 (E.A.T and C.Z.) and GM099568 (E.A.T. and M.K.K.).

Author Disclosure Statement

The authors have no competing financial interests.