Solvent-Exposed Salt Bridges Influence the Kinetics of α-Helix Folding and Unfolding

Abstract

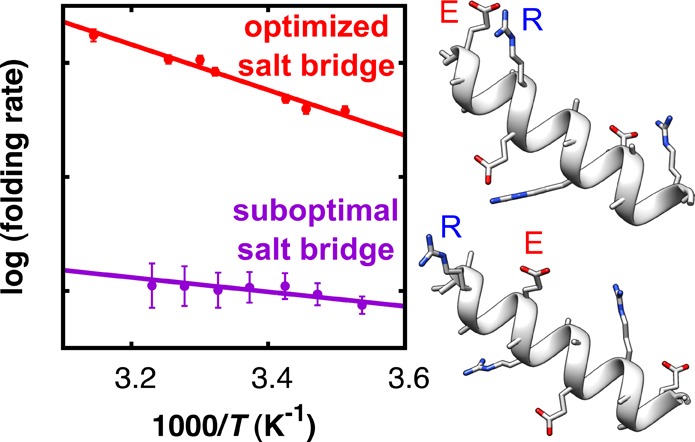
Salt bridges are known to play an essential role in the thermodynamic stability of the folded conformation of many proteins, but their influence on the kinetics of folding remains largely unknown. Here, we investigate the effect of Glu-Arg salt bridges on the kinetics of α-helix folding using temperature-jump transient-infrared spectroscopy and steady-state UV circular dichroism. We find that geometrically optimized salt bridges (Glu^– and Arg⁺ are spaced four peptide units apart, and the Glu/Arg order is such that the side-chain rotameric preferences favor salt-bridge formation) significantly speed up folding and slow down unfolding, whereas salt bridges with unfavorable geometry slow down folding and slightly speed up unfolding. Our observations suggest a possible explanation for the surprising fact that many biologically active proteins contain salt bridges that do not stabilize the native conformation: these salt bridges might have a kinetic rather than a thermodynamic function.

The folded conformation of proteins is determined by a complicated interplay of hydrophobic effects, van der Waals forces, hydrogen bonding, and electrostatic interactions, and their relative contributions are under ongoing discussion. The role of electrostatic interactions between oppositely charged residues (salt bridges) has proven to be particularly ambiguous.¹⁻³ Because the energetically favorable Coulomb interaction between salt-bridged charge pairs is often counteracted by entropy loss and energetically unfavorable desolvation,¹ the net free-energy contribution of a salt bridge can range from highly stabilizing to highly destabilizing.⁴⁻⁸ An interesting example of the latter is the Arc repressor of bacteriophage P22, for which mutation studies have shown that a buried Glu-Arg salt bridge destabilizes the native conformation.⁶ Similarly, the formation of the Asp-Arg salt bridge buried in the protein core of human salivary α-amylase increases the free energy of the folded state by as much as 44 kJ mol^–1.⁷ The question arises as to the evolutionary pressure for the conservation of such destabilizing salt bridges in biologically active proteins.

It has been speculated that salt bridges might influence not only the thermodynamic stability of the folded conformation but also the folding kinetics.⁹⁻¹² Molecular dynamics (MD) simulations even suggest that Glu-Lys salt bridges accelerate the formation of amyloids by acting as intramolecular folding nucleates.¹³ However, the relation between salt bridges and protein folding kinetics remains speculative, and whereas the thermodynamic effects of salt bridges have been extensively studied,¹⁻⁸ experimental data on how salt bridges affect folding kinetics is scarce.¹⁴⁻¹⁶ Fluorescence stopped-flow experiments indicate that the formation of electrostatic interactions in the early stage of the folding pathway of Barnase is likely to facilitate folding by stabilizing the transition state.¹⁴ On the other hand, transient temperature-jump (T-jump) infrared (IR) measurements indicate an unfavorable effect of salt-bridge formation on the folding kinetics of the α-helical neuroactive peptide Conantokin-T.¹⁶ To obtain a better understanding of the effects of salt bridges on folding kinetics, we here report on a systematic investigation of the effect of Glu-Arg salt bridges on the folding and unfolding rates of α-helical peptides. We study four alanine-based α-helical peptides, each of which has a nearly identical amino-acid composition with three repeating Glu (E) and Arg (R) residue pairs that only differ in E-R spacing and orientation (see Table 1 and Figure 1). Such short, helix-forming peptides with well-defined salt-bridge-forming residue pairs provide excellent model systems for understanding the impact of electrostatic side-chain interactions on protein stability and folding.⁵

Table 1. Sequence, Apparent Transition Enthalpy (ΔH_app^‡), and Entropy (ΔS_app) for the Folding (U → F) Transitions of the Four Investigated Peptides at Neutral pH (Salt Bridge Formation) and at Acidic pH (No Salt Bridge Effects).

		pH = 7.0 (with salt bridge)		pH = 2.5 (no salt bridge)
sequencea	peptidea	ΔHapp (U→F)‡ (kJ mol–1)	ΔSapp (U→F)‡ (J mol–1 K–1)	ΔHapp (U→F)‡ (kJ mol–1)	ΔSapp (U→F)‡ (J mol–1 K–1)
Ac-A(EAAAR)3A-NH2	(i + 4)ER	16.6 ± 1.2	–62.0 ± 4.0	15.3 ± 1.7	–69.3 ± 5.8
Ac-A(AEAAR)3A-NH2	(i + 3)ER	13.1 ± 1.1	–80.1 ± 3.6	17.5 ± 3.6	–67.3 ± 12.3
Ac-A(RAAAE)3A-NH2	(i + 4)RE	11.9 ± 1.9	–84.7 ± 6.4	14.1 ± 3.4	–75.0 ± 11.8
Ac-A(ARAAE)3A-NH2	(i + 3)RE	5.2 ± 1.5b	–115.4 ± 5.1b	16.7 ± 3.0	–72.2 ± 10.3

^aAc = acetyl; A = alanine; E = glutamic acid; R = arginine.

^bThese are asymptotic standard errors.³⁷

Figure 1.

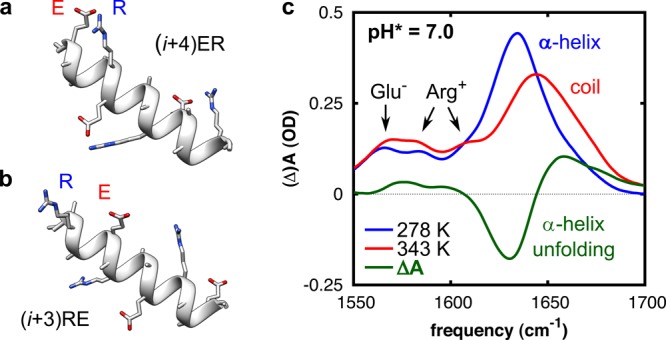
(a,b) Schematic representation of the folded structure of two of the investigated peptides, showing the salt-bridging side chains Glu^– (E) and Arg⁺ (R). (a) Peptide (i + 4)ER, in which E and R are spaced four peptide units apart. (b) Peptide (i + 3)RE, in which R and E are spaced three peptide units apart and in reverse order. Structures optimized and rendered with Chimera.¹⁷ (c) Temperature-dependent Fourier transform infrared (FTIR) spectra of peptide (i + 4)ER. The thermal difference spectrum (green) reflects the conformational changes upon thermal unfolding. The peptide concentration was 12 mM.

To determine the folding and unfolding rates, we use a combination of steady-state UV circular dichroism (UV-CD) and T-jump transient-IR measurements. The thermal unfolding curves of these peptides have a sigmoidal shape, and from a singular-value decomposition of the temperature-dependent CD spectra and global fitting, we find that the folding can be effectively described by a two-state model (see the Supporting Information). Comparison of the UV-CD and FTIR thermal melting curves shows no differences in the melting curves derived from the two different techniques (Figure S4, Supporting Information), further supporting effective two-state folding behavior. The thermodynamic stabilities follow the trend (i + 4)ER > (i + 3)ER ≈ (i + 4)RE > (i + 3)RE, indicating that the α-helix-stabilizing effect is largest for ER-ordered salt bridges in which E and R are spaced four peptide units apart (approximately one α-helical turn; see Figure 1a), as was reported previously.⁵ This order and distance dependence can be explained from sterical considerations and side-chain rotameric preferences (see the Supporting Information). Complementary MD simulations confirm that the thermal unfolding transition of the peptides involves breaking of the salt bridges (see the Supporting Information).

We investigate the folding/unfolding kinetics by monitoring the re-equilibration of the peptides in the amide I′ spectral region in response to a nanosecond T jump,¹⁸⁻²¹ starting from various initial temperatures. Figure 2a shows the solvent-corrected relaxation kinetics of peptide (i + 4)ER at neutral pH following a T jump from 301 to 307 K. The absorption change ΔA, presented as function of frequency and time delay, shows negative (blue) and positive (red) contributions reflecting the transient blue shift of the amide I′ band of the peptide as it undergoes conformational re-equilibration. As can be seen in Figure 2b, the transient spectra at long times resemble the equilibrium FTIR difference spectrum and exhibit the shape characteristic for the α-helix–coil transition.¹⁹ The T-jump-induced transient absorption changes show an instantaneous response followed by a well-resolved kinetic phase (Figure 2c). The former is due to the intrinsic temperature dependence of the amide I′ mode,²² the latter arises from the re-equilibration of the folded and unfolded populations. To confirm this, we also measured the transient absorption changes of an aqueous solution of N-methylacetamide, for which a very similar instantaneous T-jump response, but no kinetic phase is observed (Figure S6, Supporting Information). The relaxation kinetics at both 1630 cm^–1 (decay of the α-helical population) and 1658 cm^–1 (increase of the random coil population), for each peptide, and at all final T jump temperatures and pH values can be well described by a single-exponential function (Figure S7, Supporting Information). This single-exponential kinetics indicates that the α-helices effectively behave as two-state folders,²³ as already suggested by the steady-state UV-CD and IR data. Such effective two-state behavior is often observed for α-helical peptides.^16,24−30 It is believed to arise from a conformational free-energy landscape in which the α-helical and random coil ensembles are two broad free-energy minima separated by a single barrier that is higher than the barriers within these broad minima.²⁵⁻²⁷ When the free-energy barrier separating the two free-energy minima is much higher than the barriers between the conformational microstates within each of them, intrabasin relaxation proceeds on time scales much faster than interbasin population exchange.³¹⁻³⁴ The observation of single-exponential behavior indicates that the relative population distributions of all of the microstates relax to a pre-equilibrium within the time resolution of our T-jump pulse (∼5 ns). After this pre-equilibration, the relative populations of all microstates remain constant, and the population redistribution between the α-helical and random coil ensembles gives rise to a single effective kinetic time scale, which reflects the crossing of the main free-energy barrier of the folding process.³³ The effective folding and unfolding rates (k_F,eff and k_U,eff) involving the crossing of the main free-energy barrier can then be estimated using a kinetic two-state model.^33,34

Figure 2.

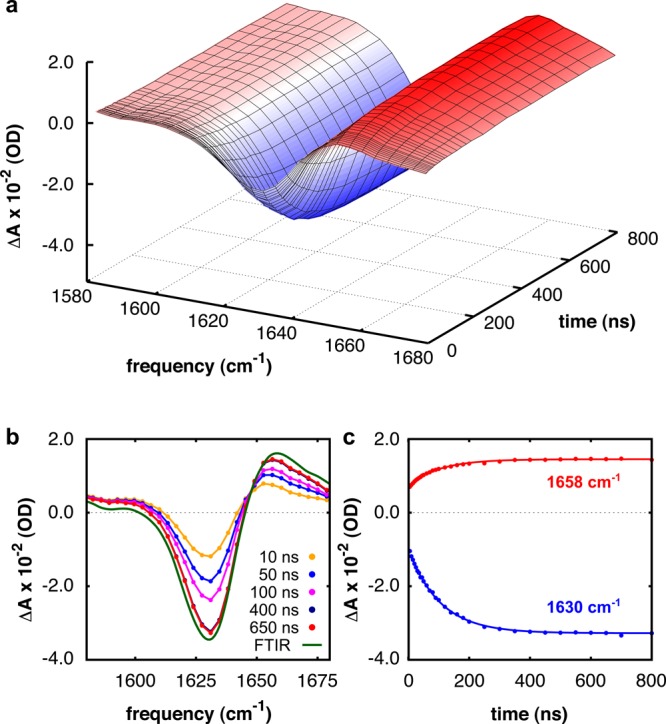
Relaxation kinetics of peptide (i + 4)ER in the amide I′ region following a T jump from 301 to 307 K at neutral pH (12 mM peptide concentration). (a) Absorption change ΔA versus frequency and time. (b) ΔA for selected delay times compared to the (scaled) equilibrium FTIR difference spectrum. (c) Relaxation kinetics at 1630 and 1658 cm^–1. The relaxation kinetics are globally fitted to a single-exponential decay function (solid curve), ΔA(t) = A₀ + A₁ exp(−t/τ), with an observed time constant of τ = 100 ± 4 ns.

We estimate the effective folding and unfolding rates (k_F,eff and k_U,eff) involving the crossing of the main free-energy barrier at a particular temperature from a combined analysis of the experimentally observed T jump relaxation rate (k_R) and the folding equilibrium constants (K_eq) deduced from our temperature-dependent CD measurements (because k_R = k_F + k_U and K_eq = k_F/k_U).^23,35 The results are shown in Figures 3 and 4 (see the Supporting Information for plots of all k_R, k_F,eff, and k_U,eff). To specifically determine the impact of the salt bridge on the kinetics, each of the peptides was also studied at acidic pH. At neutral pH, both the Glu and Arg side chains are charged, and formation of an ER- or RE-type salt bridge is possible, whereas at acidic pH (pH = 2.5), Glu is neutral, making salt-bridge formation impossible. We verified that the carboxylate groups of the Glu residues are completely protonated from the IR response of the COO^– and COOH groups (see the Supporting Information).

Figure 3.

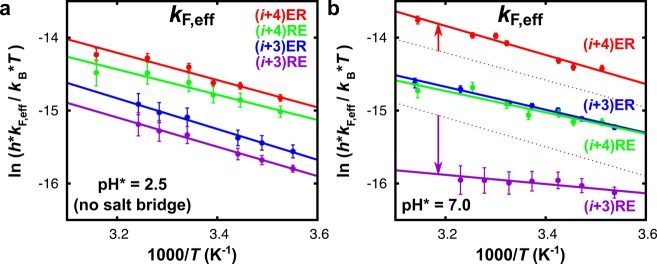
Eyring plots of the effective folding rates (k_F,eff) of each of the peptides measured at (a) acidic and (b) neutral pH. The lines are least-squares fits. For better comparison, in (b), the fits to k_F,eff at acidic pH (no salt bridges) are shown as dotted lines for peptides (i + 4)ER and (i + 3)RE. The values obtained for ΔH_app (U→F)^‡ and ΔS_app (U→F) at acidic and neutral pH are listed in Table 1

Figure 4.

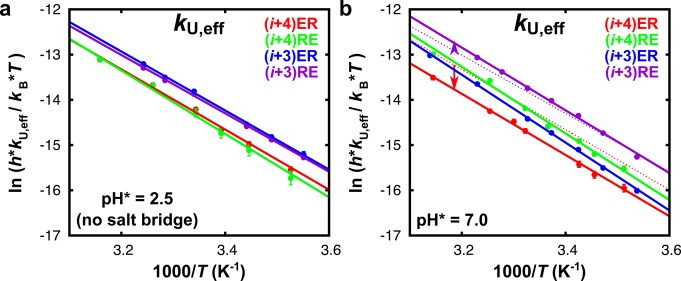
Eyring plots of the effective unfolding rates (k_U,eff) of each of the peptides measured at (a) acidic and (b) neutral pH. The lines are least-squares fits. The dotted lines in (b) correspond to the linear fit of k_U,eff measured at acidic pH of peptides (i + 4)ER and (i + 3)RE. The values obtained for ΔH_app (F→U)^‡ and ΔS_app (F→U) at acidic and neutral pH are listed in Table S2 (Supporting Information).

Comparing the effective folding rates k_F,eff of the four peptides in the absence of salt bridges (Figure 3a), we observe small differences, which are probably caused by a dependence of the side-chain rotameric preferences (and thus the helix-forming propensity) on the peptide sequence. As can be seen in Figure 3b, the ability to form salt bridges (neutral pH) significantly changes the folding dynamics. Interestingly, we find that a salt bridge can both speed up and slow down the folding, depending on the geometric orientation and relative distance between the interacting residues. Notably, a geometrically optimized ER-oriented salt bridge speeds up the rate of α-helix formation ((i + 4)ER, red data points), whereas a destabilizing RE-oriented salt bridge slows down the folding ((i + 3)RE, purple data points). Thus, inhibiting the formation of this unfavorable RE-oriented salt bridge by lowering the pH speeds up the folding (data in Figure 3a and dotted line in Figure 3b). The effective folding rates at neutral pH show the same trend as the stability of the folded conformation, namely. (i + 4)ER > (i + 3)ER ≈ (i + 4)RE > (i + 3)RE (see Figure S9, Supporting Information).

For unfolding, we find the opposite behavior (Figure 4); in the presence of stabilizing ER-oriented salt bridges (peptides (i + 4)ER and (i + 3)ER), the effective rates of unfolding are distinctly slower. In contrast, destabilizing RE-oriented salt bridges result in only marginally faster unfolding (peptide (i + 3)RE). The effective unfolding rates thus follow a trend exactly opposite to that of the effective folding rates, and we can conclude that geometrically optimized salt bridges not only speed up folding but can also serve as a kinetic barrier to unfolding.

We find that the effective folding and unfolding rates exhibit Eyring temperature dependence (Figures 3 and 4). The apparent transition enthalpies (ΔH_app^‡) and entropies (ΔS_app), both for the folding (U → F) and unfolding (F → U) transitions¹⁴ of all peptides, are listed in Table 1 (see Table S2 in the Supporting Information for the unfolding parameters). The apparent transition enthalpy and entropy of folding (ΔH_app (U→F)^‡ and ΔS_app (U→F)) in the presence of salt bridges shows a dichotomy between the peptides with ER- and RE-oriented salt bridges (Table 1). Peptides containing ER-oriented salt bridges have significantly higher apparent transition enthalpies of folding (ΔH_app (U→F)^‡) compared to slow-folding peptides that are destabilized by RE-type salt bridges. The unfavorable enthalpic contribution of stabilizing salt bridges to ΔG_U→F implies that their accelerating effect on the folding rates must originate from a substantial entropy–enthalpy compensation. Indeed, our results show that the transition entropies of folding ΔS_app (U→F)^‡ of the ER-type peptides are significantly higher compared to those of the slow-folding RE-oriented peptides (Table 1), and we can conclude that the increased folding rates in the presence of geometrically optimized salt bridges are mainly an entropic effect (a change in ΔS_app (U→F)), reflecting an ordering rather than an energetic effect of the salt bridge on the kinetics. A probable explanation for this entropic effect could be that optimized salt bridges speed up the folding by acting as a nucleation site, thereby limiting the number of low free-energy backbone conformations and restricting the time required for the conformational search of the entire protein or peptide.

To conclude, we find that salt bridges can have a strong impact not only on the thermodynamics of the investigated α-helical peptides but also on the kinetics of folding and unfolding. It has been speculated that such kinetic effects may explain the biological significance of salt bridges for which an equilibrium (stabilizing) function is of secondary importance, or even absent.^9,10,12 Such salt bridges might have a kinetic rather than a thermodynamic function, for instance, by stabilizing folding intermediates (but not necessarily the final folded state) or by preventing the protein from following nonproductive folding pathways in the early stages of the folding process.¹¹ Evidence for a kinetic function of salt bridges exists for several proteins. The solvent-exposed Glu-Arg salt bridge in Staphylococcal nuclease contributes only marginally to the stability of the native structure,³⁶ but MD simulations suggest that these salt bridges impose significant kinetic barriers, thereby preventing the protein from unfolding.¹⁰ Furthermore, an Arg-Asp salt bridge in triosephosphate isomerase⁹ and an Arg-Glu salt bridge in mouse Paneth cell α-defensin cryptidin-4¹² are both believed to play a role during the folding process, rather than to stabilize the native folds. One might speculate that the kinetic effect of salt bridges on the folding of the peptides observed here may thus be a more general phenomenon. This might provide a possible evolutionary explanation for the presence of apparently (namely, thermodynamically) nonfunctional salt bridges in many biologically active proteins.

Supporting Information Available

Experimental methods; temperature-dependent UV-CD data; FTIR thermal unfolding curves; rotameric state preferences; MD simulations; T jump control measurements; additional FTIR spectra; T jump relaxation kinetics at all final T jump temperatures; and the Eyring plots of all k_R, k_F,eff, and k_U,eff of each individual peptide. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.