Summary
The case-cohort study design, used to reduce costs in large cohort studies, is a random sample of the entire cohort, named the subcohort, augmented with subjects having the disease of interest but not in the subcohort sample. When several diseases are of interest, several case-cohort studies may be conducted using the same subcohort, with each disease analyzed separately, ignoring the additional exposure measurements collected on subjects with the other diseases. This is not an efficient use of the data, and in this paper, we propose more efficient estimators. We consider both joint and separate analyses for the multiple diseases. We propose an estimating equation approach with a new weight function, and we establish the consistency and asymptotic normality of the resulting estimator. Simulation studies show that the proposed methods using all available information gain efficiency. We apply our proposed method to the data from the Busselton Health Study.
Some key words: Case-cohort study, Multiple disease outcomes, Multivariate failure time, Proportional hazards, Survival analysis
1. Introduction
For large epidemiologic cohort studies, assembling some types of covariate information, e.g. measuring genetic information or chemical exposures from stored blood samples, for all cohort members may entail enormous cost. With cost in mind, Prentice (1986) proposed the case-cohort study design, which requires covariate information only for a random sample of the cohort, named the subcohort, as well as for all subjects with the disease of interest. One important advantage of the case-cohort study design is that the same subcohort can be used for studying different diseases, whereas for designs such as the nested case-control design, new matching of cases and controls is needed for different diseases (Langholz & Thomas, 1990; Wacholder et al., 1991).
Many methods have been proposed for case-cohort data under the proportional hazards model. Prentice (1986) and Self & Prentice (1988) studied a pseudo-likelihood approach, which is a modification of the partial likelihood method (Cox, 1975) that weights the contributions of the cases and subcohort differently. To improve the efficiency of the pseudo-likelihood estimator, Chen & Lo (1999) and Chen (2001b) studied different classes of estimating equations and used a local type of average as weight, respectively. Borgan et al. (2000) proposed using time-varying weights, and Kulich & Lin (2004) developed a class of weighted estimators by using all available covariate data for the full cohort. Breslow & Wellner (2007) considered the semiparametric model using inverse probability weighted methods with two-phase stratified samples. Various other semiparametric survival models have also been modified to accommodate case-cohort studies (e.g. Chen, 2001a; Chen & Zucker, 2009; Kong et al., 2004; Kulich & Lin, 2000; Lu & Tsiatis, 2006).
Taking advantage of the case-cohort design, several diseases are often studied using the same subcohort. In such situations, the information on the expensive exposure measure is available on the subcohort as well as any subjects with any of the diseases of interest. For example, in the Busselton Health Study, two case-cohort studies were conducted to investigate the effect of serum ferritin on coronary heart disease and on stroke, respectively (Knuiman et al., 2003). Serum ferritin was measured on the subcohort, a random sample of the cohort, as well as in all subjects with coronary heart disease and/or stroke. Typically, the coronary heart disease analysis would not include any exposure information collected on stroke patients not in the subcohort, and vice versa. In this paper, we develop more efficient estimators for a single disease outcome, which can effectively use all available exposure information. Because it is often of interest to compare the effect of a risk factor on different diseases, we propose a more efficient version of the Kang & Cai (2009) test of association across multiple diseases.
2. Model and Estimation
2·1. Model definitions and assumptions
Suppose that there are n independent subjects in a cohort study with K diseases of interest. Let Tik denote the potential failure time and Cik denote the potential censoring time for disease k of subject i. Let Xik = min(Tik, Cik) denote the observed time, Δik = I(Tik ≤ Cik) the indicator for failure, and Nik(t) = I(Xik ≤ t, Δik = 1) and Yik(t) = I(Xik ≥ t) the counting and at-risk processes for disease k of subject i, respectively, where I(·) is the indicator function. Let Zik(t) be a p × 1 vector of possibly time-dependent covariates for disease k of subject i at time t. The time-dependent covariates are assumed to be external (Kalbfleisch & Prentice, 2002). Let τ denote the end of study time. We assume that Tik is independent of Cik given the covariates Zik and follows the multiplicative intensity process (Cox, 1972)
| (1) |
where λ0k(t) is an unspecified baseline hazard function for disease k of subject i and β0 is p-dimensional vector of fixed and unknown parameters. Model (1) can incorporate disease-specific effect model, , as a special case. Specifically, we define and , letting 0T be a 1 × p zero vector. Then we have .
Assume that there are ñ subjects in the subcohort. Let ξi be an indicator for subcohort membership, i.e. ξi = 1 denotes that subject i is selected into the subcohort and ξi = 0 denotes otherwise. Let α̃ = pr(ξi = 1) = ñ/n denote the selection probability of subject i into the subcohort. The covariates Zik(t) (0 ≤ t ≤ τ) are measured for subjects in the subcohort and those with any disease of interest.
2·2. Estimation for univariate failure time
First, we consider the situation in which only one disease is of interest, but covariate information is available for subjects with other diseases. In the Busselton Health study, for example, this corresponds to the situation in which we are interested in the effect of serum ferritin on coronary heart disease with additional serum ferritin measurements available on subjects outside the subcohort who had stroke.
In this situation, the observable information is {Xik,Δik,ξi, Zik(t), 0 ≤ t ≤ Xik} when ξi = 1 or Δik = 1, and is (Xik,Δik,ξi) when ξi = 0 and Δik = 0 (k = 1,…, K). If we are interested in disease k and ignore the covariate information collected on subjects with other diseases, we can use Borgan et al. (2000)’s estimator with time-varying weights. Specifically, the estimator is the solution to
| (2) |
where for d= 0,1 and 2 with a⊗0 = 1, a⊗1 = a, and a⊗2 = aaT, and the time-varying weight with . Here α̂k(t), an estimator for the true selection probability α̃, is the proportion of the sampled censored subjects for disease k among censored subjects who remain in the risk set at time t for disease k. This estimator does not use the covariate information from subjects outside the subcohort who had other diseases.
To use the collected covariate information on subjects who are outside the subcohort and have other diseases, we consider the pseudo-partial likelihood score equations
| (3) |
where
and . Here α̃k(t) is the proportion of sampled subjects among subjects who do not have any diseases and are remaining in the risk set at time t. Our proposed weight for disease k is ψik(t) = 1 when Δij = 1 for some j, and when ξi = 1 and Δij = 0 for all j (j = 1,…, k). This weight takes the failure status of the other diseases into consideration, and thus our proposed estimator will use the available covariate information for other diseases.
2·3. Estimation for multivariate failure time
For multivariate failure time data in case-cohort studies, Kang & Cai (2009) proposed the pseudo-likelihood score equations
| (4) |
with the corresponding solution denoted β̂M.
As with Borgan et al. (2000)’s estimator, when calculating the contribution of disease k in the estimating equation, the quantity does not use the covariate information collected on subjects with other diseases outside the subcohort. In order to improve efficiency, we consider the pseudo-likelihood score equations with new weights
| (5) |
When there is only a single disease of interest, i.e. K = 1, (5) reduces to (3). Let β̃M denote the solution of equation (5). We estimate the baseline cumulative hazard function for disease k using a Breslow–Aalen type estimator , where
| (6) |
3. Asymptotic properties
Because the estimators for the univariate failure time are special cases of those for the multivariate failure time, we present results only for the multivariate case. We make the following assumptions:
(Ti, Ci, Zi, i = 1,…, n) are independently and identically distributed, where Ti = (Ti1,…, TiK)T, Ci = (Ci1,…, CiK)T, and Zi = (Zi1,…, ZiK)T ;
pr{Yik(t) = 1} > 0 for t ∈ [0,τ], i = 1,…, n and k = 1,…, K;
for i = 1,…, n and k = 1,…, K almost surely, where Dz is a constant;
for d = 0, 1, 2, there exists a neighborhood
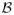 of
β0 such that are continuous functions and in probability, where ;
of
β0 such that are continuous functions and in probability, where ;the matrix is positive definite for k = 1,…, K, where and ;
for all β∈
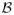 , t ∈
[0,τ], and k
= 1,…, K, , and , where , d = 0, 1, 2 are
continuous functions of β∈
, t ∈
[0,τ], and k
= 1,…, K, , and , where , d = 0, 1, 2 are
continuous functions of β∈ 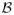 uniformly in t ∈
[0,τ] and are bounded on
uniformly in t ∈
[0,τ] and are bounded on
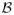 ×
[0,τ], and is bounded away from zero on
×
[0,τ], and is bounded away from zero on
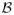 ×
[0,τ];
×
[0,τ];for all k = 1,…, K, ; and
limn→∞ α̃ = α, where α̃ = ñ/n and α is a positive constant.
Theorem 1
Under regularity conditions (a)–(h), β̃M converges in probability to β0 and n1/2(β̃M − β0) converges in distribution to a mean zero normal distribution with covariance matrix A(β0)−1Σ(β0)A(β0)−1, where
The outline of the proof is given in the Appendix. The covariance matrix Σ(β0) consists of two parts: VI (β0) is a contribution to the variance from the full cohort, and VII (β0) is due to sampling the subcohort from the full cohort.
We summarize the asymptotic properties of the proposed baseline cumulative hazard estimator in the next theorem.
Theorem 2
Under regularity conditions (a)–(h), is a consistent estimator of
Λ0k(t)
in t ∈
[0,τ] and converges weakly to the Gaussian process
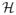 (t)
= {
(t)
= { 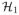 (t),…,
(t),…, 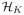 (t)}T in
D[0,τ]K
with mean zero and the following covariance function
(t)}T in
D[0,τ]K
with mean zero and the following covariance function 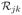 (t, s) between
(t, s) between
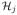 (t) and
(t) and
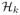 (s) for
j ≠ k
(s) for
j ≠ k
where
The proof of Theorem 2 is outlined in the Appendix.
4. Simulations
We conducted simulation studies to examine the performance of the proposed methods and to compare them with the Borgan et al. (2000) method for univariate outcomes and the Kang & Cai (2009) method for multiple outcomes. We also compared separate analysis with joint analysis. Suppose case-cohort studies have been conducted for diseases 1 and 2. Then covariate information is collected for the subcohort and all the subjects with disease 1 and/or 2. We generated bivariate failure times from the Clayton–Cuzick model (Clayton & Cuzick, 1985) with the conditional survival function
where λ0k(t) and βk (k = 1, 2) are the baseline hazard function and the effect of a covariate for disease k, respectively, and θ is the association parameter between the failure times of the two diseases. Kendall’s tau is τθ = (2θ+ 1)−1. Smaller Kendall’s tau values represent lower correlation between T1 and T2. Values of 0·1, 4, and 10 are used for θ, with corresponding Kendall’s tau values 0·83, 0·11, and 0·05, respectively. We set the baseline hazard functions λ01(t) ≡ 2 and λ02(t) ≡ 4. We consider the situation Z1 = Z2 = Z, where Z is generated from a Bernouilli distribution with pr(Z = 1) = 0·5. Censoring times are simulated from a uniform distribution [0, u], where u depends on the specified level of the censoring probability. We set the event proportions of approximately 8% and 20% for k = 1, and 14% and 35% for k = 2. The corresponding u values are 0·08 and 0·22, respectively, for β1 = 0·1; they are 0·06 and 0·16 for β1 = log 2. The sample size of the full cohort is set to be n = 1000. We create the subcohort by simple random sampling and consider subcohort sizes of 100 and 200. For each configuration, 2000 simulations were conducted.
In the first set of simulations, we consider the case that disease 1 is of primary interest. We compare the performance of our proposed estimator with the estimator of Borgan et al. (2000). Table 1 summarizes the results. We see that both methods are approximately unbiased. The average of the estimated standard error of the proposed estimator is close to the empirical standard deviation, and the coverage rate of the 95% confidence interval is close to the nominal level. As expected, the variation of the estimators in general decreases as the subcohort size increases. Our proposed estimators have smaller variance relative to the estimators of Borgan et al. (2000) in all cases. This shows that the extra information collected on subjects with the other disease helps to increase efficiency. The efficiency gain is larger in situations with larger event proportions, smaller subcohort sizes and lower correlation. We also considered disease 2 with β2 = log 2 and conducted additional simulations to compare our proposed estimator with those of Prentice (1986), Self & Prentice (1988), Kalbfleisch & Lawless (1988), and Barlow (1994). Similar results were obtained but are not presented in the paper due to space limitations.
Table 1.
Comparison of two methods with a single disease outcome: β1 = log 2 = 0·693
| Event proportion | Size of subcohort | τθ | The proposed method | Borgan et al.’s method | SRE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| β̃1 | SE | SD | CR | β̂1 | SE | SD | CR | ||||
| 8% | 100 | 0·83 | 0·706 | 0·32 | 0·32 | 94 | 0·705 | 0·33 | 0·33 | 94 | 1·04 |
| 0·11 | 0·718 | 0·31 | 0·32 | 94 | 0·719 | 0·33 | 0·33 | 94 | 1·07 | ||
| 0·05 | 0·708 | 0·32 | 0·32 | 94 | 0·705 | 0·33 | 0·33 | 94 | 1·06 | ||
| 200 | 0·83 | 0·715 | 0·28 | 0·28 | 95 | 0·716 | 0·28 | 0·28 | 95 | 1·02 | |
| 0·11 | 0·704 | 0·28 | 0·28 | 95 | 0·705 | 0·28 | 0·29 | 95 | 1·03 | ||
| 0·05 | 0·697 | 0·28 | 0·27 | 95 | 0·698 | 0·28 | 0·28 | 95 | 1·05 | ||
| 20% | 100 | 0·83 | 0·703 | 0·25 | 0·25 | 94 | 0·704 | 0·26 | 0·27 | 95 | 1·13 |
| 0·11 | 0·694 | 0·23 | 0·23 | 94 | 0·694 | 0·26 | 0·27 | 95 | 1·31 | ||
| 0·05 | 0·700 | 0·23 | 0·23 | 94 | 0·701 | 0·26 | 0·26 | 95 | 1·29 | ||
| 200 | 0·83 | 0·693 | 0·20 | 0·20 | 95 | 0·692 | 0·21 | 0·21 | 95 | 1·10 | |
| 0·11 | 0·696 | 0·19 | 0·19 | 95 | 0·699 | 0·21 | 0·21 | 95 | 1·17 | ||
| 0·05 | 0·694 | 0·19 | 0·19 | 95 | 0·695 | 0·21 | 0·21 | 95 | 1·26 | ||
SE, average standard errors; SD, sample standard deviation; CR, coverage rate (%) of the nominal 95% confidence intervals; , sample relative efficiency, where SDc and SDp are the sample standard deviation for the Borgan et al. (2000)’s method and the proposed method, respectively.
In the second set of simulations, we are interested in the joint analysis of the two diseases. We fit the following models:
We compare the performance of the proposed estimator with the estimator of Kang & Cai (2009). Table 2 provides summary statistics for the estimator of β1 for different combinations of event proportion, subcohort sample size, and correlation. The estimates from both methods are nearly unbiased, and their estimated standard errors are close to the empirical standard deviations. Our method is more efficient than that of Kang & Cai (2009). The efficiency gain is very limited when the event proportion is small. Higher efficiency gains are associated with smaller subcohort sizes. Estimates for β2 are not shown in Table 2, but the overall performance is similar to that of β1.
Table 2.
Comparison of two methods with multiple disease outcomes: [β1, β2] = [0·1, 0·7]
| Event proportion | Size of subcohort | τθ | The proposed method | Kang & Cai’s method | SRE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
SE | SD | CR |
|
SE | SD | CR | β̂1 | |||
| [8%, 14%] | 100 | 0·83 | 0·099 | 0·31 | 0·30 | 95 | 0·101 | 0·32 | 0·31 | 95 | 1·07 |
| 0·11 | 0·101 | 0·30 | 0·30 | 95 | 0·098 | 0·32 | 0·32 | 95 | 1·13 | ||
| 0·05 | 0·109 | 0·30 | 0·31 | 94 | 0·111 | 0·32 | 0·33 | 94 | 1·11 | ||
| 200 | 0·83 | 0·106 | 0·26 | 0·27 | 95 | 0·105 | 0·27 | 0·27 | 95 | 1·04 | |
| 0·11 | 0·096 | 0·26 | 0·26 | 94 | 0·096 | 0·27 | 0·27 | 94 | 1·05 | ||
| 0·05 | 0·098 | 0·26 | 0·27 | 94 | 0·098 | 0·27 | 0·27 | 94 | 1·05 | ||
| [20%, 35%] | 100 | 0·83 | 0·098 | 0·23 | 0·24 | 94 | 0·094 | 0·26 | 0·27 | 94 | 1·24 |
| 0·11 | 0·099 | 0·22 | 0·22 | 94 | 0·097 | 0·26 | 0·26 | 95 | 1·42 | ||
| 0·05 | 0·095 | 0·22 | 0·22 | 94 | 0·101 | 0·26 | 0·27 | 95 | 1·44 | ||
| 200 | 0·83 | 0·103 | 0·19 | 0·19 | 94 | 0·104 | 0·20 | 0·21 | 95 | 1·19 | |
| 0·11 | 0·098 | 0·18 | 0·18 | 95 | 0·097 | 0·20 | 0·20 | 95 | 1·29 | ||
| 0·05 | 0·098 | 0·18 | 0·18 | 95 | 0·100 | 0·20 | 0·20 | 96 | 1·31 | ||
SE, average standard errors; SD, sample standard deviation; CR, coverage rate (%) of the nominal 95% confidence intervals; , sample relative efficiency, where SDe and SDp are the sample standard deviation for the Kang & Cai (2009)’s method and the proposed method, respectively.
We also compared separate analysis of the two diseases with the joint analysis using the proposed method. Data were generated satisfying the following model:
where β1 represents the effect of Z on the risk of disease 1, β2 represents the effect of Z on the risk of disease 2, and β3 represents the common effect of Z* for both diseases. We set β1 = β2 = log 2 and β3 = 0·1. Table 3 summarizes the results for β1. The sample standard deviations of Kang & Cai’s estimator in the joint analysis are slightly smaller than Borgan’s estimator in the separate analysis. The sample standard deviations of the proposed estimators are similar in the joint and separate analyses, and they are smaller than Kang & Cai’s and Borgan’s estimators, respectively. Conclusions for the estimator of β2 are similar. We also conducted hypothesis tests for H0 : β1 = β2. Table 4 presents the Type I error rates and power of the tests at the 0·05 significance level. The tests under the separate analysis treat the two estimates, β̂1 and β̂2, as from two independent samples. Type I error rates from separate analyses are much lower than 5% while those from the joint analysis are close to 5%. The settings for power analysis are the same as before except that β1 = 0·1 and β2 = 0·7. Tests based on the proposed methods are more powerful than those based on Kang & Cai’s and Borgan’s methods, and the joint analysis produces more powerful tests than the separate analysis.
Table 3.
Comparison between separate and joint analysis: β1 = log 2 with event proportion 20%
| Size of subcohort | τθ | Separate analysis | |||||
|---|---|---|---|---|---|---|---|
| The proposed weight | Borgan at al.’s method | ||||||
| β̃1 | SE | SD | β̂1 | SE | SD | ||
| 100 | 0·83 | 0·713 | 0·244 | 0·245 | 0·716 | 0·263 | 0·265 |
| 0·11 | 0·702 | 0·226 | 0·236 | 0·705 | 0·262 | 0·270 | |
| 0·05 | 0·700 | 0·226 | 0·232 | 0·710 | 0·263 | 0·268 | |
| 200 | 0·83 | 0·703 | 0·196 | 0·194 | 0·704 | 0·206 | 0·206 |
| 0·11 | 0·697 | 0·186 | 0·193 | 0·699 | 0·205 | 0·213 | |
| 0·05 | 0·698 | 0·186 | 0·187 | 0·702 | 0·206 | 0·209 | |
| Size of subcohort | τθ | Joint analysis | |||||
|---|---|---|---|---|---|---|---|
| The proposed weight | Kang and Cai’s method | ||||||
|
|
SE | SD |
|
SE | SD | ||
| 100 | 0·83 | 0·711 | 0·243 | 0·245 | 0·713 | 0·262 | 0·264 |
| 0·11 | 0·701 | 0·226 | 0·235 | 0·701 | 0·261 | 0·267 | |
| 0·05 | 0·700 | 0·225 | 0·231 | 0·707 | 0·262 | 0·266 | |
| 200 | 0·83 | 0·703 | 0·195 | 0·194 | 0·703 | 0·205 | 0·205 |
| 0·11 | 0·696 | 0·186 | 0·193 | 0·697 | 0·205 | 0·212 | |
| 0·05 | 0·698 | 0·186 | 0·187 | 0·700 | 0·205 | 0·209 | |
SE, average standard errors; SD, sample standard deviation.
Table 4.
Type I error and power (%) in separate and joint analyses with event proportion 20%
| Size of subcohort | τθ | Type I error (β1 = β2 = log 2) | Power (β1 = 0·1, β2 = 0·7) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Separate analysis | Joint analysis | Separate analysis | Joint analysis | ||||||
| P | BR | P | KC | P | BR | P | KC | ||
| 100 | 0·83 | 0·6 | 0·6 | 6·3 | 6·7 | 49 | 42 | 90 | 78 |
| 0·11 | 0·8 | 1·7 | 5·9 | 5·9 | 56 | 42 | 83 | 61 | |
| 0·05 | 1·2 | 2·1 | 5·1 | 5·6 | 59 | 43 | 81 | 61 | |
| 200 | 0·83 | 0·2 | 0·3 | 5·2 | 5·8 | 80 | 72 | 98 | 94 |
| 0·11 | 1·6 | 1·9 | 5·4 | 5·4 | 77 | 65 | 89 | 78 | |
| 0·05 | 1·8 | 2·5 | 5·3 | 5·4 | 79 | 68 | 90 | 79 | |
P, the proposed weight; BR, the method of Borgan et al. (2000); KC, the method of Kang & Cai (2009).
5. Data analysis
We apply the proposed method to analyze data from the Busselton Health Study (Cullen, 1972; Knuiman et al., 2003), conducted in the south-west of Western Australia, and intended to evaluate the association between coronary heart disease and stroke and their risk factors. General health information for adult participants was obtained by questionnaire every three years from 1966 to 1981. This study population consists of 1612 men and women aged 40–89 who participated in 1981 and were free of coronary heart disease or stroke at that time. Coronary heart disease event is defined as hospital admission, any procedure, or death related to coronary heart disease. Stroke event is defined as hospital admission, any procedure, or death from stroke. The outcomes of interest were time to the first coronary heart disease event and time to the first stroke event. The event time for a subject was considered censored if the subject was free of that event type by December 31, 1998 or lost to follow-up during the study period.
One of the main interests of the study was to compare the effect of serum ferritin on coronary heart disease with its effect on stroke. To reduce cost and preserve stored serum, case-cohort sampling was used. Serum ferritin was measured for all the subjects with coronary heart disease and/or stroke as well as those in the subcohort. We conduct a joint analysis of the two diseases. In our analysis, the full cohort consists of 1210 subjects with viable blood serum samples, which includes 174 subjects with only coronary heart disease, 75 with only stroke, and 43 with both diseases. The subcohort consisted of 334 disease-free subjects, 61 with only coronary heart disease, 36 with only stroke, and 19 with both diseases. The total number of assayed sera samples was 626. If a subject was censored and free of both events at the censoring time, then the censoring times for the two disease events were the same. Two subjects died due to both coronary heart disease and stroke, for whom the times for both events were the same. No other subjects died at the first diagnosis of either disease. For this study, it is reasonable to assume, as in the original study (Knuiman et al., 2003), that censoring was conditionally independent of the event processes.
We fit the following model
where Z1, Z2, Z3, and Z4 denote the logarithm of serum ferritin level, age in years, triglycerides in millimoles per liter, and whether subjects had blood pressure treatment, respectively. We then tested H0 : β21 = β22, β31 = β32, β41 = β42 based on the proposed method, and the p-value is 0·138. Therefore, we fit the final model
Table 5 summarizes the results of the final fit. With a 1 unit increase in the logarithm of the serum ferritin level, the hazard ratio for coronary heart disease risk is increased by 16% and for stroke risk by 19%. When we tested H0 : β11 = β12, H0 was not rejected with the p-value = 0·823. We also fit the same model using Kang & Cai (2009)’s method. The standard errors for the effects of the logarithm of the serum ferritin level are slightly larger, 0·0949 for coronary heart disease and 0·1304 for stroke.
Table 5.
Analysis results for the Busselton Health Study
| Variables | Proposed method | Kang & Cai method | ||||||
|---|---|---|---|---|---|---|---|---|
| β̃M | SE | HR | 95% CI | β̂M | SE | HR | 95% CI | |
| log(ferritin) on CHD | 0·145 | 0·0897 | 1·16 | (0·97, 1·38) | 0·092 | 0·0949 | 1·10 | (0·91, 1·32) |
| log(ferritin) on Stroke | 0·172 | 0·1219 | 1·19 | (0·93, 1·51) | 0·186 | 0·1304 | 1·20 | (0·93, 1·56) |
| Age | 0·071 | 0·0069 | 1·07 | (1·06, 1·09) | 0·069 | 0·0070 | 1·07 | (1·06, 1·09) |
| Triglycerides | 0·239 | 0·0484 | 1·27 | (1·16, 1·40) | 0·232 | 0·0541 | 1·26 | (1·13, 1·40) |
| Blood pressure treatment | 0·423 | 0·1633 | 1·53 | (1·11, 2·10) | 0·408 | 0·1727 | 1·50 | (1·07, 2·11) |
CHD, coronary heart disease; SE, standard error; HR, hazard ratio; CI, confidence interval.
6. Concluding Remarks
When disease rates are low, the efficiency gain of the proposed method is not large. When the event rates are low, the number of cases is small, and consequently, the amount of extra information is small. In the case of common diseases, sampling all cases in the traditional case-cohort design with multiple diseases limits applications (Breslow & Wellner, 2007). Instead, a generalized case-cohort design (Cai & Zeng, 2007) in which cases are sampled can be considered. Extending the proposed weights to this general case merits further investigation.
In our proposed estimation framework, time-dependent covariates can be allowed. However, estimation generally requires one to know the entire history of time-dependent covariates. In many follow-up studies, this may not be true. One commonly used approach for handling time-dependent covariates is to consider the last-value-carry-forward, but this could introduce bias. A more sensible approach is to consider the joint modeling of survival times and longitudinal covariates via shared random effects, which has not been studied for case-cohort data.
When studying multiple diseases, different diseases may be competing risks for the same subject. In a competing risks situation, a subject can only experience at most one event; in the situation we considered, a subject can still experience the other events. Consequently, in the competing risks situation, a subject is at risk for all types of events simultaneously and will not be at risk for any other events as soon as one event occurs. Our approach in this paper can be adapted to competing risks by modifying the at-risk process and the weight function, but analysis will be based on the cause-specific hazards as studied in Sorensen & Andersen (2000).
The current method is based on estimating equations, which improves the estimation efficiency by incorporating a refined weight function for the risk set. However, it is not semiparametric efficient. To derive the most efficient estimator, we need to specify the joint distribution of the correlated failure times from the same subject and consider nonparametric maximum likelihood estimation based on the joint likelihood function for case-cohort sampling. This may be very challenging, especially when expensive covariates are continuous. This is an interesting topic which warrants future research.
Acknowledgments
We thank the editor, the associate editor, and two referees for the careful reading and the constructive comments which have led to great improvement of our manuscript. We thank Professor Matthew Knuiman and the Busselton Population Medical Research Foundation for permission to use their data. We also thank Professor Amy Herring and Forrest DeMarcus for their editorial assistance. This work was partially supported by grants from the National Institutes of Health.
Appendix. Outline of the Proofs of Theorems 1 – 2
Under the assumptions in Section 3, we outline the proofs for the main theorems. To prove the asymptotic properties for the proposed estimators, the following lemmas are used. The proof of Lemma 1 is in Lin (2000) and Lemma 2 is in Lemma A1 in Kang & Cai (2009).
Lemma 1
Let 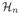 (t) and
(t) and 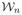 (t) be two sequences of bounded processes. If we
assume that the following conditions (i), (ii), and (iii) hold for some
constant τ, for which (i)
sup0≤t≤τ
||
(t) be two sequences of bounded processes. If we
assume that the following conditions (i), (ii), and (iii) hold for some
constant τ, for which (i)
sup0≤t≤τ
|| 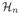 (t)
−
(t)
− 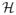 (t)
||→ 0 in probability for some bounded process
(t)
||→ 0 in probability for some bounded process 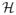 (t); (ii)
(t); (ii) 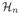 (t) is monotone on
[0,τ]; and (iii)
(t) is monotone on
[0,τ]; and (iii)
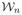 (t)
converges to a zero-mean process with continuous sample paths, then in probability, and in probability.
(t)
converges to a zero-mean process with continuous sample paths, then in probability, and in probability.
Lemma 2
Let Bi(t) (i = 1,…, n) be independent and identically distributed real-valued random process on [0,τ], and denote random process vector, B(t) = {B1(t),…, Bn(t)} with E{Bi(t)} ≡ μB(t), var{Bi(0)} < ∞, and var{Bi(τ)} < ∞. Let ξ= [ξ1,…,ξn] be random vector containing ñ ones and n − ñ zeros with each permutation equally likely. Let ξ be independent of B(t). Suppose that almost all paths of Bi(t) have finite variation. Then, converges weakly in l∞[0,τ] to a zero-mean Gaussian process, and converges in probability to zero uniformly in t.
Proof of Theorem 1
First, the proof of consistency of
β̃M can be shown by
the extension of Fourtz (1977):
(I) exists and is continuous in an open
neighborhood 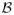 of
β0; (II) is negative definite with probability
going to one as n → ∞; (III) converges to
A(β0) in
probability uniformly for β in an open
neighborhood about β0; (IV) converges to 0 in probability, where . Clearly, (I) is satisfied. If we show
that converges to zero in probability
uniformly in β∈
of
β0; (II) is negative definite with probability
going to one as n → ∞; (III) converges to
A(β0) in
probability uniformly for β in an open
neighborhood about β0; (IV) converges to 0 in probability, where . Clearly, (I) is satisfied. If we show
that converges to zero in probability
uniformly in β∈ 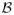 as n →
∞, then (II) and (III) are satisfied. We have . Each of the three parts converges to
zero in probability by Lemma 2, the Lenglart inequality, and conditions
(d), (e), (f), and (g). Convergence of to zero in probability shows that (IV)
is satisfied. Therefore, β̃M
converges to β0 in probability and
is a consistent estimator of β0.
as n →
∞, then (II) and (III) are satisfied. We have . Each of the three parts converges to
zero in probability by Lemma 2, the Lenglart inequality, and conditions
(d), (e), (f), and (g). Convergence of to zero in probability shows that (IV)
is satisfied. Therefore, β̃M
converges to β0 in probability and
is a consistent estimator of β0.
To establish the asymptotic normality of , we decompose it into two parts: . The first term is asymptotically equivalent to by Spiekerman & Lin (1998). The second term can be decomposed into two parts , where . The first term converges in probability uniformly in t to zero by van der Vaart & Wellner (1996), the Kolmogorov–Centsov Theorem, conditions (c), (d), and (f), and Lemma 1. The second term is asymptotically equivalent to by Lemma 1. Hence, is asymptotically equivalent to . By Spiekerman & Lin (1998), the first term converges weakly to a zero-mean normal vector with covariance matrix . The second term is asymptotically a zero-mean normal vector with covariance matrix by Hájek (1960)’s central limit theorem for finite sampling. In addition, and are independent. Thus n1/2(β̃M − β0) converges weakly to a zero-mean normal vector with covariance matrix A(β0)−1Σ(β0)A(β0)−1. This completes the proof of Theorem 1.
Proof of Theorem 2
We decompose as
| (A1) |
The first term here converges to zero in probability uniformly in t by Taylor expansion and Lemma 1. The second term can be written as n1/2lk(β, t)T (β̃M − β0) + op(1), where by Taylor expansion, uniform convergence of and , d=0,1, and boundedness of dΛ0k(u), where β* is on the line segment between β̃M and β0. Because can be written as a sum of two monotone functions in t and converges uniformly to , in which is bounded away from 0, and converges to a zero-mean Gaussian process with continuous sample path, the third term in (A1) can be written as . Due to the uniform convergence of to , where is bounded away from 0, the last term in (A1) is asymptotically equivalent to . Using a decomposition of n1/2(β̃M − β0), we have .
Let H(t) = {H(1)(t) + H(2)(t)}, where , and . By Spiekerman & Lin (1998), converges weakly to a Gaussian process whose mean is zero and covariance function between and is E{η1j(β0, t),η1k(β0, s)} for t, s ∈ [0,τ] in D[0,τ]K. By Lemma 1, Lemma 2, boundedness conditions, and the Cramer–Wold device, it can be shown that converges weakly to a Gaussian process whose mean is zero and covariance function between and is {1 − α}α−1E{ζ1j(β0, t),ζ1k(β0, s)} for t, s ∈ [0,τ] in D[0,τ]K. It can easily be shown that H(1)(t) and H(2)(s) are independent. Therefore the conclusion in Theorem 2 holds. This completes the proof of Theorem 2.
Contributor Information
S. KIM, Email: kimso@live.unc.edu, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599, U.S.A
J. CAI, Email: cai@bios.unc.edu, Department of Biostatistics, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599, U.S.A
W. LU, Email: lu@stat.ncsu.edu, Department of Statistics, North Carolina State University, Raleigh, North Carolina 27695, U.S.A
References
- Barlow W. Robust variance estimation for the case-cohort design. Biometrics. 1994;50:1064–72. [PubMed] [Google Scholar]
- Borgan O, Langholz B, Samuelsen SO, Goldstein L, Pogoda J. Exposure stratified case-cohort designs. Lifetime Data Anal. 2000;6:39–58. doi: 10.1023/a:1009661900674. [DOI] [PubMed] [Google Scholar]
- Breslow NE, Wellner JA. Weighted likelihood for semiparametric models and two-phase stratified samples, with application to Cox regression. Scand J Statist. 2007;34:86–102. doi: 10.1111/j.1467-9469.2007.00574.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai J, Zeng D. Power calculation for case-cohort studies with nonrare events. Biometrics. 2007;63:1288–95. doi: 10.1111/j.1541-0420.2007.00838.x. [DOI] [PubMed] [Google Scholar]
- Chen HY. Weighted semiparametric likelihood method for fitting a proportional odds regression model to data from the case-cohort design. J Am Statist Assoc. 2001a;96:1446–57. [Google Scholar]
- Chen K. Generalized case-cohort sampling. J R Statist Soc B. 2001b;63:791–809. [Google Scholar]
- Chen K, LOS Case-cohort and case-control analysis with Cox’s model. Biometrika. 1999;86:755–64. [Google Scholar]
- Chen Y, Zucker DM. Case-cohort analysis with semiparametric transformation models. J Statist Plan Inf. 2009;139:3706–17. [Google Scholar]
- Clayton D, Cuzick J. Multivariate generalizations of the proportional hazards model. J R Statist Soc A. 1985;148:82–117. [Google Scholar]
- Cox DR. Regression models and life-tables (with discussion) J R Statist Soc B. 1972;34:187–220. [Google Scholar]
- Cox DR. Partial likelihood. Biometrika. 1975;62:269–76. [Google Scholar]
- Cullen KJ. Mass health examinations in the Busselton population, 1996 to 1970. Aust J Med. 1972;2:714–8. doi: 10.5694/j.1326-5377.1972.tb103506.x. [DOI] [PubMed] [Google Scholar]
- Fourtz RV. On the unique consistent solution to the likelihood equations. J Am Statist Assoc. 1977;72:147–8. [Google Scholar]
- Hájek J. Limiting distributions in simple random sampling from a finite population. Publ Math Inst Hungar Acad Sci. 1960;5:361–74. [Google Scholar]
- Kalbfleisch JD, Lawless JF. Likelihood analysis of multi-state models for disease incidence and mortality. Statist Med. 1988;7:149–60. doi: 10.1002/sim.4780070116. [DOI] [PubMed] [Google Scholar]
- Kalbfleisch JD, Prentice RL. The Statistical Analysis of Failure Time Data. 2 New York: John Wiley; 2002. [Google Scholar]
- Kang S, Cai J. Marginal hazards model for case-cohort studies with multiple disease outcomes. Biometrika. 2009;96:887–901. doi: 10.1093/biomet/asp059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knuiman MW, Divitini ML, Olynyk JK, Cullen DJ, Bartholomew HC. Serum ferritin and cardiovascular disease: A 17-year follow-up study in Busselton, Western Australia. Am J Epidemiol. 2003;158:144–9. doi: 10.1093/aje/kwg121. [DOI] [PubMed] [Google Scholar]
- Kong L, Cai J, Sen PK. Weighted estimating equations for semiparametric transformation models with censored data from a case-cohort design. Biometrika. 2004;91:305–19. [Google Scholar]
- Kulich M, Lin DY. Additive hazards regression for case-cohort studies. Biometrika. 2000;87:73–87. [Google Scholar]
- Kulich M, Lin DY. Improving the efficiency of relative-risk estimation in case-cohort studies. J Am Statist Assoc. 2004;99:832–44. [Google Scholar]
- Langholz B, Thomas DC. Nested case-control and case-cohort methods of sampling from a cohort: A critical comparison. Am J Epidemiol. 1990;131:169–76. doi: 10.1093/oxfordjournals.aje.a115471. [DOI] [PubMed] [Google Scholar]
- Lin DY. On fitting Cox’s proportional hazards models to survey data. Biometrika. 2000;87:37–47. [Google Scholar]
- Lu W, Tsiatis AA. Semiparametric transformation models for the case-cohort study. Biometrika. 2006;93:207–14. [Google Scholar]
- Prentice RL. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73:1–11. [Google Scholar]
- Self SG, Prentice RL. Asymptotic distribution theory and efficiency results for case-cohort studies. Ann Statist. 1988;16:64–81. [Google Scholar]
- Sorensen P, Andersen PK. Competing risks analysis of the case-cohort design. Biometrika. 2000;87:49–59. [Google Scholar]
- Spiekerman CF, Lin DY. Marginal regression models for multivariate failure time data. J Am Statist Assoc. 1998;93:1164–75. [Google Scholar]
- van der Vaart AW, Wellner JA. Weak Convergence and Empirical Processes. New York: Springer; 1996. [Google Scholar]
- Wacholder S, Gail M, Pee D. Efficient design for assessing exposure-disease relationships in an assembled cohort. Biometrics. 1991;47:63–76. [PubMed] [Google Scholar]


